奥林匹克训练题库·找规律(word版)
奥数题目大全

第1讲 找规律(一)事物的发展中有规律的,只有认为观察事物,找到事物发展变化的规律,才能深入地了解和掌握它,从而找到解决问题的方法和途径。
在数学竞赛中,常常出现按规律填数的题目,找规律的方法是根据已知数的前后(可上下)之间的联系,找出其中的规律,求得相应的数。
例题与方法例1. 请找出下列各组数排列的规律,并根据规律在括号里填上适当的数。
(1)1,5,9,13,( ),21,25。
(2)3,6,12,24,( ),96,192。
(3)1,4,9,16,25,( ),49,64,81。
(4)2,3,5,8,12,17,( ),30,38。
(5)21,4,16,4,11,4,( ),( )。
(6)1,6,5,10,9,14,13,( ),( )。
例2.根据下表中数的排列规律,在空格里填上适当的数。
(1) (2)例3.下面每个括号里两个数按一定规律组合,在里填上适当的数。
(9,13),(17,5),(14,8),( ,16)。
例4.根据前面两个圈里三个数的关系,在第三个圈里的( )里填上适当的数。
练习与思考1.找出下面各组数排列的规律,并根据规律在括号里填上合适的数。
(1)1,4,3,6,5,( ),( )。
(2)1,4,16,64,( )。
(3)11,3,8,3,5,3,( ),( )。
13 20 7 9 17 8 5 9 24 7 5 36 12 6 14 16 10 20 20 8 18 16 ( ) 25 ( )(4)0,1,3,8,21,( )。
2.找规律,在空格里填上适当的数。
(1) (2)3.下面括号里和两个数是按一定规律组合,根据规律在 里填上适当的数。
(1)(8,7),(6,9),(10,5),( ,13)。
(2)(1,3),(5,9),(7,13),(9, )。
4.根据前面两个圈里三个数的关系,在第三个圈里的( )里填上适当的数。
(1) (2)(2)第二讲 找规律(二)例1.请先计算下面一组算式的前三题,然后找出其中的规律,并根据规律直接写出后六题的得数。
2020四年级奥林匹克数学基础资料库 第7讲 找规律(一)

第7讲找规律(一)我们在三年级已经见过“找规律”这个题目,学习了如何发现图形、数表和数列的变化规律。
这一讲重点学习具有“周期性”变化规律的问题。
什么是周期性变化规律呢?比如,一年有春夏秋冬四季,百花盛开的春季过后就是夏天,赤日炎炎的夏季过后就是秋天,果实累累的秋季过后就是冬天,白雪皑皑的冬季过后又到了春天。
年复一年,总是按照春、夏、秋、冬四季变化,这就是周期性变化规律。
再比如,数列0,1,2,0,1,2,0,1,2,0,…是按照0,1,2三个数重复出现的,这也是周期性变化问题。
下面,我们通过一些例题作进一步讲解。
例1节日的夜景真漂亮,街上的彩灯按照5盏红灯、再接4盏蓝灯、再接3盏黄灯,然后又是5盏红灯、4盏蓝灯、3盏黄灯、……这样排下去。
问:(1)第100盏灯是什么颜色?(2)前150盏彩灯中有多少盏蓝灯?分析与解:这是一个周期变化问题。
彩灯按照5红、4蓝、3黄,每12盏灯一个周期循环出现。
(1)100÷12=8……4,所以第100盏灯是第9个周期的第4盏灯,是红灯。
(2)150÷12=12……6,前150盏灯共有12个周期零6盏灯,12个周期中有蓝灯4×12=48(盏),最后的6盏灯中有1盏蓝灯,所以共有蓝灯48+1=49(盏)。
例2有一串数,任何相邻的四个数之和都等于25。
已知第1个数是3,第6个数是6,第11个数是7。
问:这串数中第24个数是几?前77个数的和是多少?分析与解:因为第1,2,3,4个数的和等于第2,3,4,5个数的和,所以第1个数与第5个数相同。
进一步可推知,第1,5,9,13,…个数都相同。
同理,第2,6,10,14,…个数都相同,第3,7,11,15,…个数都相同,第4,8,12,16…个数都相同。
也就是说,这串数是按照每四个数为一个周期循环出现的。
所以,第2个数等于第6个数,是6;第3个数等于第11个数,是7。
前三个数依次是3,6,7,第四个数是25-(3+6+7)=9。
奥数 找规律(30道选择题、20道解答题)试题及解析

找规律一、选择题(共30小题)1.一个数串219⋯,从第4个数字开始,每个数字都是前面3个数字和的个位数.下面有4个四位数:1113,2226,2125,2215,其中共有( )个不出现在该数串中.A.1B.2C.3D.42.有一种数,是以法国数学家梅森的名字命名的,它们就是形如21(n n -为质数)的梅森数,当梅森数是质数时就叫梅森质数,是合数时就叫梅森合数.例如2213-=就是第一个梅森质数,第一个梅森合数是( )A.4B.15C.127D.20473.一些小球按下面的方式堆放,第7堆小球有( )个.A.19B.20C.21D.22 4.如图由“”复制组合成的,探索复制组合100次后的阴影部分占整个组合图的几分之几问题,解决的最优策略是( )A.猜想与尝试B.特例找规律C.画图D.列表5.如图,一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人.像这样( )张桌子拼起来可以坐40人.A.17B.18C.19D.206.先找出规律,然后在括号里填上适当的数:23,4,20,6,17,8,14,10,( ),()( )A.12,13B.13,12C.11,12D.12,147.如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成45度角,最高的小树高2.8米,最低的小树高峰1.4米,那么从左向右数第4棵树的高度是( )米.A.2.6B.2.4C.2.2D.2.08.在下面的两个图形中发现其中四个数的关系,进而在第三个图形中的空白三角形中填入适当的数( ),使该图中四个数也符合上述关系.A.9B.12C.10D.119.如图,第(1)个多边形由正三角形“扩展”而来,边数记为3a ,第(2)个多边形由正方形“扩展”而来,边数记为4a ,⋯,依此类推,由正n 边形“扩展”而来的多边形的边数记为(3n a n … ),则345111120146051n a a a a +++⋯+=,那么(n = )A.2014B.2015C.2016D.201710.观察下列图形,“?”位置对应的图形是( )A. B. C. D.11.把足够大的一张厚度为0.1mm纸连续对折,要使对折后的整叠纸总厚度超过12mm,至少要对折()A.6次B.7次C.8次D.9次12.有一组式子:2a,32a-,43a,54a-⋯从左往右数的第10个式子是下面算式的第()个.A.1110aB.1110a- C.1011a- D.1111a-13.找出规律,将你认为合适的数填入(),2、4、3、9、4、16、5、()、()、36、7、⋯那么正确的数是()A.18、6B.22、6C.25、6D.2514.有一列数,开头四个是2,0,1,3;从第5个数开始,每个数是前面四个数的和除以4所得的余数,那么这列数中的第2013个数是()A.0B.1C.2D.315.有一列数,第1个数是22,第2个数是12,从第3个数开始,每个数是它前面两个数的平均数,这列数的第10个数的整数部分是()A.17B.14C.15D.1616.杰克和吉莉每人各有一只水壶,其中都装有1升水.第一天,杰克把他壶中的1毫升水倒入吉莉的壶中,第二天吉莉把她的壶中的3毫升水倒入杰克的壶中,第三天杰克把他壶中的5毫升水倒入吉莉的壶中,这样继续做下去,其中每个人倒出的水比前一天从对方得到的水多2毫升.那么第101天结束后,杰克壶中有()毫升水?(1升1000=毫升)A.799B.899C.900D.100017.下列图形,第10个图中△比〇多()个A.44B.60C.56D.4518.根据1()1A,1()8B,1()27C,1()64D,(E)⋯⋯中数的变化规律,E中的数是()A.165B.181C.1125D.121619.一本童话书,每两页之间有3页插图,也就是说3页插图前后各有1页文字.那么第36页是()A.插图B.文字20.下面空白的椭圆内应填入的数是()A.1730B.1750C.1780D.179021.观察下面图形我们发现:第一个图中有1个正方形,第2个图中共有5个正方形,第3个图中共有14个正方形,按照这种规律下去的第6个图形中正方形的个数是()A.80B.81C.90D.9122.下列一列数中:5、8、11、14⋯,第()个数为2009.A.667B.668C.669D.70023.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入⋯12345⋯输出⋯1225310417526⋯那么,当输入数据是8时,输出的数据是()A.861B.863C.865D.86724.动物园里猩猩比狒狒多,猴子比猩猩多.一天,饲养员拿了十箱香蕉分给它们.每只猩猩比每只狒狒多分一根,每只猴子比每只猩猩多分一根.分完后,只剩下2根香蕉.如果每箱香蕉数量相同,都是40多个,而且猴子比狒狒多6只,猩猩有16只.那么,动物.园里有( )只猴子.A.18B.19C.20D.1725.数列1,2,4,5,10,11,22,23,46,47⋯,它形成的规律:第2项等于第1项加1的和,第3项等于第2项的2倍,第4项等于第3项加1的和,第5项等于第4项的2倍,⋯,如此继续下去,得到上面的数列.那么,这个数列的第100项的个位数字是( )A.2B.5C.7D.826.盒中原有7个小球,魔术师从中取出若干个球,把每个球都变成7个小球,将其放回盒中;他又由其中取出若干个球,把每个球都变成7个小球,再将其放回盒中;⋯,如此进行到某一时刻,当魔术师停止变魔术时,盒中球的总数可能是()A.2003个B.2004个C.2005个D.2006个27.在一个没有余数的除法算式里,如果被除数扩大6倍,除数缩小2倍,那么商的变化是()A.扩大12倍B.缩小2l倍C.扩大3倍D.缩小3倍28.按照如图所示的规律,图6中小三角形共有()个.A.53B.51C.49D.4729.给出一列11,21,12,31,22,13,L,1k,12k-,L,1k.在这列数中,第40个值等于1的项是这列数中第()项.A.3120B.3121C.3200D.320130.观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放,那么第10个图形中的小黑点个数是( )个.A.100B.90C.91D.101二、解答题(共20小题)31.以下一串密码代表一句话,数字代表拼音字母顺序,其中(28,20)代表“我”,那么这串密码代表的这句话是什么?(28,20)(6,14)(19,14)(31,13,20,19,12)(12,26,20)32.小强编了一个程序:从a 开始,交错地做加法或乘法(第一次可以是加法,也可以是乘法).每次做加法时,将上次运算的结果加2或加(3)-;每次做乘法时,将上次运算的结果乘以2或乘以3.例如:24a 可以这样得到3a ⨯−−→2232322332646112212124224a a a a a a a a +⨯-⨯-⨯+−−→+−−→+−−→+−−→+−−→-−−→-−−→请你用此程序得到8a ,写出过程.33.有12个位置,每个位置放一个自然数.若第二个数与第一个数相等,从第三个数开始,每个数恰好是它前边所有数的总和,则我们称这样的12个数为“好串数”.请问含1992这个数的好串数共 个.34.称分母是分子的3倍少1的分数为“可儿”,例如25就是“可儿”,将分数320写成两个“可儿”之积,这两个“可儿”是 .35.2017位同学排成一列依次报数.若某位同学报的是一位数,后面的同学就报这个数的2倍;若某位同学报的是两位数,后面的同学就报其个位数字与5的和.已知一位同学报1,到了第100位同学,他却把前面那位同学报的数加上了另一个一位自然数,其他人都没有注意到,仍然按以前的规则继续报数,直到最后一位同学报的数是5.那么第100位同学所报的数是把前一位同学报的数加上了多少?36.有一列数2,9,8,2,6,⋯从第3个数起,每个数都是前面两个数乘积的个位数字.例如第四个数就是第二、第三两数乘积9872⨯=的个位数字是2.问这一列数第2003个数是几?37.2017位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报4,第二位同学报9,然后从第三位同学开始,每位同学都把自己前面两位同学所报的数相乘,再报出乘积的个位来.试问,最后一位同学报的是几?38.(1)今天是3月1日,小明买了一些橙子,他如果每天吃3个,十多天能吃完,最后一天只吃2个;如果小明每天吃4个,不到十天就吃完了,最后一天吃了3个,那么,这些橙子原来有多少个?(2)小明好奇地看了看这一年3月份的日历,发现3月份有四个星期日,却有五个星期六,那么今天(3月1日)是星期几?39.黑板上先写下一串数:1,2,3,⋯,100,如果每次都擦去最前面的6个,并在这串数的最后再写上擦去的6个数的和,得到新的一串数,再做同样的操作,直到黑板上剩下的数不足6个.问:(1)最后黑板上剩下的这些数的和是多少?(2)最后所写的那个数是多少?40.例2.根据下表中数的排列规律,在空格里填上适当的数.(1)13207917859(2)247536126141641.按照下面的规律在黑板上写整数,:一开始写1,然后每一次操作在它后面写上比它大1的数.例如,一开始的时候,黑板上的数是1.第一次操作:比1大1的数是2,就在它后面写上2,现在黑板上的数是12;第二次操作:比黑板上的12大1的数是13,就在它后面连写上13,现在黑板上的数就是1213;以此类推⋯(1)请求出第三次操作后黑板上的数是多少?(2)当黑板上第一次出现“321”时,是在第几次操作之后?(3)请求出从左数第2016位数字是多少?42.某年,端午节距离儿童节和父亲节的天数相同,在月历中与六月最后一天同列,父亲节是六月的第三个星期日,则该年的父亲节是六月日.(如图是某个月的月历示意图)43.将自然数1,2,3,4,从小到大无间隔地排列起来,得到:1234567891011121314,这串数码中,当偶数数码首次连续出现5个时,其中的第一个(偶)数码所在位置从左数是第多少位?44.等边三角形的边长3厘米,现将三角形ABC沿一条直线翻滚30次,如图:求A点经过的路程的长是多少厘米?(π取3.14).45.一棵生命力极强的树苗,第一周在树干上长出2条树枝(如图1),第二周在原先长出的每条树枝上又长出2条新的树枝(如图2),第三周又在第二周新长出的每条树枝上再长出2条新枝(如图3),这棵树苗按此规律生长,到第十周新的树枝长出来后,共有条树枝.46.1,1,3,2,5,4,7,8,9,16, , ,13,64.47.一列数,其前七项依次为1,1,3,4,5,9,7,第8项是什么?说明理由.48.在棋盘上滚动骰子,使骰子的一面和棋盘格的大小相等,然后将骰子以棱为轴,滚动到邻近的棋盘格,每滚动一次,骰子朝上一面的数字就会变化.如果骰子的初始位置如图1,当骰子滚动六次到达对角顶点时(如图2),那么,第一步、第四步、第六步朝上的面分别是几点?(说明:骰子的相对两个面的点数之和为7)49.在平面上用长度为5cm 的火柴棒摆正方形,摆出1个边长为5cm 的正方形需要4根火柴,摆出2015个这样的正方形最少需要多少根火柴?说明你的摆法(不必画图).50.如图所示,圆周上的两个点1A 、2A 将圆等分成2份,在这两个点处写上14;圆周上的两个点1A 、2A 再将两段半圆弧等分,在点3A 、4A 处分别写上相邻2个数之和;如此继续这样操作,问能否出现圆周上所有数字之和2015?若可能,请求出经过了多少次操作?若不能,请说明理由.参考答案与试题解析一、选择题(共30小题)1.一个数串219⋯,从第4个数字开始,每个数字都是前面3个数字和的个位数.下面有4个四位数:1113,2226,2125,2215,其中共有( )个不出现在该数串中.A.1B.2C.3D.4【答案解析】枚举法219的数字和是12,接下来就是2192数字和是12,接下来就是2922的数字和是13,接下来就是3223的数字和为7,接下来就是7237的数字和为12,接下来的数2以此类推数字为:2192237221584790651281102⋯规律总结数字和的尾数呈现两奇数两个偶数的周期规律.故选:C .2.有一种数,是以法国数学家梅森的名字命名的,它们就是形如21(n n -为质数)的梅森数,当梅森数是质数时就叫梅森质数,是合数时就叫梅森合数.例如2213-=就是第一个梅森质数,第一个梅森合数是( )A.4B.15C.127D.2047【答案解析】选项:214n A -=,n 无整数解;选项:2115n B -=,n 为4,但n 不是质数,故舍去;选项:21127n C -=,n 为7,127不是合数,故舍去;选项:212047n D -=,n 为11,n 为质数,且20472389=⨯,是合数,满足条件. 故选:D .3.一些小球按下面的方式堆放,第7堆小球有( )个.A.19B.20C.21D.22【答案解析】5813+=第7堆小球有:13821+=;故选:C.4.如图由“”复制组合成的,探索复制组合100次后的阴影部分占整个组合图的几分之几问题,解决的最优策略是()A.猜想与尝试B.特例找规律C.画图D.列表【答案解析】如图由“”复制组合成的,探索复制组合100次后的阴影部分占整个组合图的几分之几问题,解决的最优策略是特例找规律;故选:B.5.如图,一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人.像这样()张桌子拼起来可以坐40人.A.17B.18C.19D.20【答案解析】第一张桌子可以坐4人;拼2张桌子可以坐4216+⨯=人;拼3张桌子可以坐4228+⨯=人;故n张桌子拼在一起可以坐42(1)22+-=+.n n当2240n=,n+=时,19答:像这样19张桌子拼起来可以坐40人.故选:C.6.先找出规律,然后在括号里填上适当的数:23,4,20,6,17,8,14,10,(),()()A.12,13B.13,12C.11,12D.12,14【答案解析】根据上面的分析,第9个数应该是14311+=,-=,第10个数应该是10212故选:C.7.如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成45度角,最高的小树高2.8米,最低的小树高峰1.4米,那么从左向右数第4棵树的高度是()米.A.2.6B.2.4C.2.2D.2.0【答案解析】因为:树根成一条直线,树顶也成一条直线,45∠=︒,最高的小树高 2.8米,最低的小树高峰A1.4米,所以 2.8BC AC AB=-=米,AC=米, 1.4AB=米, 1.4又因为:这排树的间距相同,所以:÷=(米)1.470.2⨯+0.24 1.4=+0.8 1.4=(米)2.2答:那么从左向右数第4棵树的高度是2.2米.故选:C.8.在下面的两个图形中发现其中四个数的关系,进而在第三个图形中的空白三角形中填入适当的数(),使该图中四个数也符合上述关系.A.9B.12C.10D.11【答案解析】54210⨯÷=所以,第三个图形中的空白三角形中填入的数是10.故选:C.9.如图,第(1)个多边形由正三角形“扩展”而来,边数记为a,第(2)个多边形由正方3形“扩展”而来,边数记为a,⋯,依此类推,由正n边形“扩展”而来的多边形的边4数记为(3na n…),则345111120146051na a a a+++⋯+=,那么(n=)A.2014B.2015C.2016D.2017【答案解析】33(22)34a=+=⨯,44(23)45a=+=⨯,55(24)56a=+=⨯,⋯(1)na n n=+,∴11112014344556(1)6051n n+++⋯+=⨯⨯⨯+,∴11111111201434455616051n n-+-+-+⋯+-=+,∴112014316051n-=+,12017n∴+=,2016n∴=.10.观察下列图形,“?”位置对应的图形是()A. B. C. D.【答案解析】再逆时针旋转90︒是.故选:C .11.把足够大的一张厚度为0.1mm 纸连续对折,要使对折后的整叠纸总厚度超过12mm ,至少要对折( ) A.6次B.7次C.8次D.9次【答案解析】设对折n 次,由此可得, 0.1212n ⨯> 2120n = 72128= 6264= 64120128<<所以,7n = 答:至少要对折7次. 故选:B .12.有一组式子:2a ,32a -,43a ,54a -⋯从左往右数的第10个式子是下面算式的第( )个.A.1110a B.1110a -C.1011a -D.1111a -【答案解析】由题意,奇数项为正,偶数项为负,分母是正整数,分子是1n a +,所以从左往右数的第10个式子是1110a -,故选:B .13.找出规律,将你认为合适的数填入( ),2、4、3、9、4、16、5、( )、( )、36、7、⋯那么正确的数是( ) A.18、6B.22、6C.25、6D.25【答案解析】注意到:4是2的平方,9是3的平方,16是4的平方,25是5的平方,36是6的平方,⋯根据这个规律,可知中间两个括号分别应填25和6.故选:C.14.有一列数,开头四个是2,0,1,3;从第5个数开始,每个数是前面四个数的和除以4所得的余数,那么这列数中的第2013个数是()A.0B.1C.2D.3【答案解析】(2013)4+++÷64=÷=⋯12所以第5个数是2;(0132)4+++÷=÷64=⋯12第6个数是2;+++÷(1322)4=÷8420=⋯第7个数是0;+++÷(3220)4=÷74=⋯13(2203)4+++÷=÷74=⋯13第9个数是3;+++÷(2033)4 =÷8420=⋯第10个数是0;+++÷(0330)4 =÷64=⋯12第11个数是2;(3302)4+++÷=÷84=⋯20第12个数是0;+++÷(3020)4 =÷5411=⋯第13个数是1;+++÷(0201)4 =÷34=⋯03此时这些数是:2,1,0,3,2,2,0,3,3,0,2,0,1,3再向下计算又会是2,2,0,3,3,0,2,0,1,3⋯看以看出这些数是以“2,1,0,3,2,2,0,3,3,0”为一个循环不断循环出现这个循环节中有10个数字;2013102013÷=⋯余数是3,所以第2013个数第202个循环中的第3个数字,是0.故选:A.15.有一列数,第1个数是22,第2个数是12,从第3个数开始,每个数是它前面两个数的平均数,这列数的第10个数的整数部分是()A.17B.14C.15D.16【答案解析】第三个数:(2212)217+÷=第四个数:(1217)214.5+÷=第五个数:(1714.5)215.75+÷=第六个数:(14.515.75)215.125+÷=第七个数:(15.7515.125)215.4375+÷=⋯再向下计算由于两个数都不大于15.5,所以它们的平均数的整数部分只能是15.答:这列数的第10个数的整数部分是15.故选:C.16.杰克和吉莉每人各有一只水壶,其中都装有1升水.第一天,杰克把他壶中的1毫升水倒入吉莉的壶中,第二天吉莉把她的壶中的3毫升水倒入杰克的壶中,第三天杰克把他壶中的5毫升水倒入吉莉的壶中,这样继续做下去,其中每个人倒出的水比前一天从对方得到的水多2毫升.那么第101天结束后,杰克壶中有()毫升水?(1升1000=毫升)A.799B.899C.900D.1000【答案解析】-=(毫升)312752-=(毫升)⋯1012501÷=⋯(天)前100天杰克的壶中增加250100⨯=(毫升)第101天杰克倒出(1011)21201-⨯+=(毫升)201100101-=(毫升)1升1000=(毫升)1000101899-=(毫升)故选:B.17.下列图形,第10个图中△比〇多()个A.44B.60C.56D.45【答案解析】第10图中△的个数1010100⨯=(个)〇的个数4(102)444⨯+-=(个)1004456-=(个)故选:C.18.根据1()1A,1()8B,1()27C,1()64D,(E)⋯⋯中数的变化规律,E中的数是()A.165B.181C.1125D.1216【答案解析】35125=所以,这个分数是1 125.故选:C.19.一本童话书,每两页之间有3页插图,也就是说3页插图前后各有1页文字.那么第36页是()A.插图B.文字【答案解析】3649÷=(组),所以第36页和第四页相同,应该是插图;故选:A.20.下面空白的椭圆内应填入的数是()A.1730B.1750C.1780D.1790【答案解析】1700501750+=故选:B.21.观察下面图形我们发现:第一个图中有1个正方形,第2个图中共有5个正方形,第3个图中共有14个正方形,按照这种规律下去的第6个图形中正方形的个数是()A.80B.81C.90D.91【答案解析】第一个图形有1个正方形,第二个图形有22512=+个正方形,第三个图形有22214123=++个正方形,⋯第六个图形有14916253691+++++=个正方形.故选:D.22.下列一列数中:5、8、11、14⋯,第()个数为2009.A.667B.668C.669D.700【答案解析】这是一个首项是5,公差是3的等差数列由5(1)32009n+-⨯=,可得669n=.故选:C.23.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入⋯12345⋯输出⋯1225310417526⋯那么,当输入数据是8时,输出的数据是()A.861B.863C.865D.867【答案解析】28165+=,所以输出的数是8 65.故选:C.24.动物园里猩猩比狒狒多,猴子比猩猩多.一天,饲养员拿了十箱香蕉分给它们.每只猩猩比每只狒狒多分一根,每只猴子比每只猩猩多分一根.分完后,只剩下2根香蕉.如果每箱香蕉数量相同,都是40多个,而且猴子比狒狒多6只,猩猩有16只.那么,动物.园里有( )只猴子.A.18B.19C.20D.17【答案解析】动物园里有x只猴子,则狒狒6x-只,猩猩有16只,狒狒分y根香蕉,猩猩1y+根,猴子2y+根,(2)(6)16(1)400x y y x y++-++>,261616xy x xy y y++-++,2(1)1016x y y=+++,假设19x=,383810164854400y y y+++=+>,48346y>,7.2y>,设:8y=,4854438y+=. 符合题意.故选:B.25.数列1,2,4,5,10,11,22,23,46,47⋯,它形成的规律:第2项等于第1项加1的和,第3项等于第2项的2倍,第4项等于第3项加1的和,第5项等于第4项的2倍,⋯,如此继续下去,得到上面的数列.那么,这个数列的第100项的个位数字是( )A.2B.5C.7D.8【答案解析】(991)248-÷=,48412÷=,没有余数,个位数就是4,它的下一项(第100项)的个位数就是:故选:B.26.盒中原有7个小球,魔术师从中取出若干个球,把每个球都变成7个小球,将其放回盒中;他又由其中取出若干个球,把每个球都变成7个小球,再将其放回盒中;⋯,如此进行到某一时刻,当魔术师停止变魔术时,盒中球的总数可能是()A.2003个B.2004个C.2005个D.2006个【答案解析】根据以上分析知:-÷=⋯,2003减7的差不是6的倍数,(20037)63324-÷=⋯,2004减7的差不是6的倍数,(20047)63325-÷=,2005减7的差是6的倍数,(20057)6333-÷=⋯,2006减7的差不是6的倍数,(20067)63331所以盒中球的总数可能是2005个.故选:C.27.在一个没有余数的除法算式里,如果被除数扩大6倍,除数缩小2倍,那么商的变化是()A.扩大12倍B.缩小2l倍C.扩大3倍D.缩小3倍【答案解析】例如80108÷=,被除数扩大6倍,由80变成480,除数缩小2倍,由10变成5,则商变为:480596÷=,商由8变成96,是商扩大了12倍;据此可知:被除数扩大6倍,除数缩小2倍,那么商扩大6212⨯=倍.故选:A.28.按照如图所示的规律,图6中小三角形共有()个.A.53B.51C.49D.47【答案解析】根据分析可得,2++(16)453=(个)答:图6中小三角形共有53个.故选:A.29.给出一列11,21,12,31,22,13,L,1k,12k-,L,1k.在这列数中,第40个值等于1的项是这列数中第()项.A.3120B.3121C.3200D.3201【答案解析】分子分母和为2的有1个,分子分母和为3的有2个,分子分母和为4的有3个,⋯,分子分母和为79的数有78个,123783081+++⋯+=(项),第40个值等于1的项分子分母和为80且为4040是这一数列中的第40项,3081403121+=(项).故选:B.30.观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放,那么第10个图形中的小黑点个数是()个.A.100B.90C.91D.101【答案解析】根据图形分析可知:(用s表示图中小黑点的个数)1n=时,1s=;2n=时,3211s==⨯+;3n=时,7321s==⨯+;4n=时,13431s==⨯+;5n=时,21541s==⨯+;⋯;第n个图中小黑点的个数为(1)1n n-+.第10个图形中的小黑点个数是10(101)191⨯-+=.故选:C .二、解答题(共20小题)31.以下一串密码代表一句话,数字代表拼音字母顺序,其中(28,20)代表“我”,那么这串密码代表的这句话是什么?(28,20)(6,14)(19,14)(31,13,20,19,12)(12,26,20)【答案解析】28代表w ,20代表o ,根据这个规律可以确定:(6,14)代表ai(19,14)代表ni(31,13,20,19,12)代表zhong(12,26,20)guo这些拼音对应的中文是“我爱你中国”.答:这串密码代表的这句话是“我爱你中国”.32.小强编了一个程序:从a 开始,交错地做加法或乘法(第一次可以是加法,也可以是乘法).每次做加法时,将上次运算的结果加2或加(3)-;每次做乘法时,将上次运算的结果乘以2或乘以3.例如:24a 可以这样得到3a ⨯−−→2232322332646112212124224a a a a a a a a +⨯-⨯-⨯+−−→+−−→+−−→+−−→+−−→-−−→-−−→请你用此程序得到8a ,写出过程.【答案解析】利用其程序运算如下:2232322224214241828a a a a a a a a +⨯-⨯-⨯+−−→+−−→+−−→+−−→+−−→-−−→-−−→.33.有12个位置,每个位置放一个自然数.若第二个数与第一个数相等,从第三个数开始,每个数恰好是它前边所有数的总和,则我们称这样的12个数为“好串数”.请问含1992这个数的好串数共 4 个.【答案解析】通过以上分析得出含1992这个数的好串数共.4个:249 249 498 996 1992 3984498⋯ 498 996 1992 3984 7968996⋯ 996 1992 3984 7968159361992⋯ 1992 3984 7968 15936 31872⋯34.称分母是分子的3倍少1的分数为“可儿”,例如25就是“可儿”,将分数320写成两个“可儿”之积,这两个“可儿”是25、38.【答案解析】362323 20405858⨯===⨯⨯即,这两个“可儿”是25、38.故答案为:25、38.35.2017位同学排成一列依次报数.若某位同学报的是一位数,后面的同学就报这个数的2倍;若某位同学报的是两位数,后面的同学就报其个位数字与5的和.已知一位同学报1,到了第100位同学,他却把前面那位同学报的数加上了另一个一位自然数,其他人都没有注意到,仍然按以前的规则继续报数,直到最后一位同学报的数是5.那么第100位同学所报的数是把前一位同学报的数加上了多少?【答案解析】按照规则将前面几位同学所报数写出:1,2,4,8,16,11,6,12,7,14,9,18,13,8,16⋯可以发现从第3位同学开始,每10位同学为一个周期,所以第99位同学报的数为7;由于最后一位同学报的数是5,往前倒推,应该是5、10、5、10⋯可知,第100位同学报的数只能为倒数第偶数个,应该是10,所以第100位同学报的数是把前一位同学报的数加上了3.36.有一列数2,9,8,2,6,⋯从第3个数起,每个数都是前面两个数乘积的个位数字.例如第四个数就是第二、第三两数乘积9872⨯=的个位数字是2.问这一列数第2003个数是几?【答案解析】(20032)63333-÷=⋯,可以知道这一列数第2003个数为第333组后面的第3个数是“6”.答:这一列数第2003个数是6.故答案为:637.2017位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报4,第二位同学报9,然后从第三位同学开始,每位同学都把自己前面两位同学所报的数相乘,再报出乘积的个位来.试问,最后一位同学报的是几?【答案解析】从第三个同学开始,他们依次报出的数为6、4、4、6、4、4、6⋯(20172)36712-÷=⋯即循环周中的第2个数是4.答:最后一位同学报的是4.38.(1)今天是3月1日,小明买了一些橙子,他如果每天吃3个,十多天能吃完,最后一天只吃2个;如果小明每天吃4个,不到十天就吃完了,最后一天吃了3个,那么,这些橙子原来有多少个?(2)小明好奇地看了看这一年3月份的日历,发现3月份有四个星期日,却有五个星期六,那么今天(3月1日)是星期几?【答案解析】(1)【3,4】12=,12336-=(个)⨯=,36135答:这些橙子原来有35个.(2)31473-⨯=3月3日是星期六,那么3月2日是星期五,3月1日是星期四答:今天(3月1日)是星期四.39.黑板上先写下一串数:1,2,3,⋯,100,如果每次都擦去最前面的6个,并在这串数的最后再写上擦去的6个数的和,得到新的一串数,再做同样的操作,直到黑板上剩下的数不足6个.问:(1)最后黑板上剩下的这些数的和是多少?(2)最后所写的那个数是多少?【答案解析】依题意可知:(1)擦去1,2,3,4,5,6但是写上了21数字和没有变化.最后的数字和是123100+++⋯+的数字和为5050.(2)第一次擦下去的数字是1,2,3,4,5,6写上去的是21,第二次擦去的是7,8,9,10,11,12写上的数字是57.那么21与57的数字差为36.÷=⋯.说明擦去96个数字填上了16 个数字,这16个数字是以21位首项公差为100616436的等差数列.后来共20个数字.这20个数字为:97,98,99,100,21,57,93,129,165,201,237,273,309,345,381,417,453,489,525,561.然后20632÷=⋯.说明最后两个数字剩下了,新添加了3个数字,那么最后写的数字就是309,345,381,417,453,489的数字和为2394.答:(1)最后黑板上剩下的这些数的和是5050.(2)最后所写的那个数是2394.40.例2.根据下表中数的排列规律,在空格里填上适当的数.(1)13207917859(2)2475361261416【答案解析】(1)5914+=(2)(1416)260+⨯=故填14和60.41.按照下面的规律在黑板上写整数,:一开始写1,然后每一次操作在它后面写上比它大1的数.例如,一开始的时候,黑板上的数是1.第一次操作:比1大1的数是2,就在它后面写上2,现在黑板上的数是12;第二次操作:比黑板上的12大1的数是13,就在它后面连写上13,现在黑板上的数就是1213;以此类推⋯(1)请求出第三次操作后黑板上的数是多少?(2)当黑板上第一次出现“321”时,是在第几次操作之后?(3)请求出从左数第2016位数字是多少?【答案解析】(1)第二次操作:比黑板上的1213大1的数是1214,就是在它的后面写上1214,则需在黑板的数就是12131214答:第三次操作后黑板上的数是12131214.(2)黑板上的数是12,末位是12;第二次操作后,黑板上的数是1213,末两位是13;第三次操作后,黑板上的数是12131214,末两位14;⋯第n次操作后,黑板上的数的末两位是11n+,要想黑板出现“321”,须在末两位是32,与开头的1连起来才可以,第21。
2019年二年级奥林匹克数学找规律法习题

2019年二年级奥林匹克数学找规律法习题1.先计算下面的前几个算式,找出规律,再继续往下写出一些算式:①1×9+2= ②9×9+7=12×9+3= 98×9+6=123×9+4= 987×9+5=1234×9+5=9876×9+4=……2.先计算下面的奇妙算式,找出规律,再继续写出一些算式:19+9×9=118+98×9=1117+987×9=11116+9876×9=111115+98765×9=…3.先计算下面的前几个算式,找出规律,再继续写出一些算式:1×1=11×11=111×111=1111×1111=11111×11111=…4.有一列数是2、9、8、2、…,从第三个数起,每一个数都是它前面的两个数相乘积的个位数字(比如第三个数8就是2×9=18的个位数字)。
问这一列数的第100个数是几?5.如果全体自然数按下表进行排列,那么数1000应在哪个字母下面?6.如果自然数如下图所示排成四列,问101在哪个字母下面?7.3×3的末位数字是9,3×3×3的末位数是7,3×3×3×3的末位数字是1。
求35个3相乘的结果的末位数字是几?解答1.①1×9+2=1112×9+3=111123×9+4=11111234×9+5=1111112345×9+6=111111123456×9+7=11111111234567×9+8=1111111112345678×9+9=111111111。
②9×9+7=8898×9+6=888987×9+5=88889876×9+4=8888898765×9+3=888888987654×9+2=88888889876543×9+1=88888888。
最新-二年级奥林匹克数学 找规律练习试卷(二) 精品

二年级找规律(二)练习及答案1.仔细观察图7—14,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?2.仔细观察图7—15,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?3.仔细观察图7—16,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?4.按顺序仔细观察下列图形,猜一猜第3组的“?”处应填什么图?5.按顺序仔细观察下列图形,猜一猜第3组的“?”处应填什么图?6.按顺序仔细观察下列图形,猜一猜第3组的“?”应填什么图?7.按顺序仔细观察下列图形,猜一猜第3组的“?”应填什么图?8.仔细观察下列图形的变化,请先回答:①在方框(4)中应画出怎样的图形?②再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?9.仔细观察下列图形的变化,请先回答:①在方框(4)中应画出怎样的图形?②再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?答案1.答:(见图7—23)。
2.答:(见图7—24)。
3.答:(见图7—25)。
4.答(见图7—26)。
5.答:(见图7—27)。
6.答:(见图7—28)。
7.答:(见图7—29)。
8.答:(见图7—30)。
①先按(1)、(2)、(3)、……的顺序仔细观察,可以发现:在(1)中,*在左上角,在(2)中它在右上角,在(3)中它在右下角,……可见它在沿顺时针方向转动。
其他三个小图形,即□、△、○,也和*一样都在沿着顺时针方向转动。
发现规律:因方框中的每个小图形的位置的变化都是按顺时针方向旋转,可以说,方框连同内部的小图形及整体在按顺时针方向旋转。
②进一步猜想,根据所发现的规律进一步推测可知,第(4)个方框中的图形的样子。
③按(1)、(2)、(3)、……的顺序仔细观察,进一步还可发现,图形的变化是有“周期性”的,也就是说,每过4个方框后,完全同样的图形又重新出现,如第(1)、(5)、(9)个图形是完全一样的。
小学数学奥林匹克辅导及练习找出数列的排列规律(二)(含答案)-.doc

找出数列的排列规律(二)这一讲我们利用前面学习的等差数列有关知识和找规律的思想方法,解决数学问题。
(一)例题指导例1. 如果按一定规律排出的加法算式是3+4,5+9,7+14,9+19,11+24,……,那么第10个算式是()+();第80个算式中两个数的和是多少?分析与解:第一个加数如下排列:3,5,7,9,11……,这是一个等差数列,公差是2,第二个加数排列如下:4,9,14,19,24,……,这也是一个等差数列,公差是5。
根据等差数列的通项公式可以分别求出第10个算式的两个加数。
所以第10个算式是。
要求第80个算式的和,只要求出第80个算式的两个加数,再相加即可,当然也可以找一找和的规律。
想一想:第几个加法算式中两个数的和是707?例2. 有一列数:1,2,3,5,8,13,……,这列数中的第200个数是奇数还是偶数?分析与解:要想判断这列数中第200个数是奇还是偶,必须找出这列数中奇、偶数的排列规律。
不难看出,这列数是按照“奇偶奇”的顺序循环重复排列的,即每过3个数循环一次。
那么到第200个数一次循环了66次还余2。
这说明到第200个数时,已做了66次“奇偶奇”的循环,还余下2个数。
也就是说余下的两个数依次为“奇偶”,所以第200个数是偶数。
例3. 下面的算式是按某种规律排列的:1+1,2+3,3+5,4+7,1+9,2+11,3+13,4+15,1+17,……问:(1)第1998个算式是()+();(2)第()个算式的和是2000。
分析与解:(1)第1个加数依次为1、2、3、4,1、2、3、4……每4个数循环一次,重复出现。
,所以第1998个算式的第1个加数是2。
第二个加数依次为1,3,5,7,9,11……是公差为2的等差数列。
根据等差数列的通项公式可求出第1998个算式的第2个加数为,所以第1998个算式是。
(2)由于每个算式的第二个加数都是奇数,所以和是2000的算式的第1个加数一定是奇数,不会是2和4。
奥林匹克训练题库·最大与最小(word版)

最大与最小12在五位数 22576的某一位数码后面再插入一个该数码,能得到的六位数中最大的是几?13在六位数865473的某一位数码后面再插入一个该数码,能得到的七位数中最小的是几?14用1~8这八个数码组成两个四位数,要使这两个数的差尽量小,这个差是几?15要砌一个面积是72米2的长方形猪圈,长方形的边长都是自然数(单位∶米),这个猪圈的围墙总长是多少米?16三个质数的和是100,这三个质数的积最大是几?17有一类自然数,它的各个数位上的数字之和为8888,这类自然数中最小的是几?18在下面的一排数字之间添上五个加号,组成一个连加算式,求这个连加算式的结果的最小值。
1 2 3 4 5 6 7 8 919把16拆成若干个自然数的和,要求这些自然数的乘积尽量大,应如何拆?202050拆成若干个自然数的和,要求这些自然数的乘积尽量大,应如何拆?21将30拆成若干个互不相同的自然数之和,要求这些自然数的乘积尽量大,应怎样拆?22将546分解成四个不同自然数的乘积,这四个自然数的和最大是多少?23三个两位的连续偶数,它们的个位数字的和能被7整除,这三个数的和最少等于多少?24有两个三位数,构成它们的六个数码互不相同。
已知这两个三位数之和等于1771,求这两个三位数之积的最大可能值。
25用1,3,5,7,9五个数码组成一个两位数和一个三位数,这两个数的乘积记为A;用0,2,4,6,8五个数码也组成一个两位数和一个三位数,这两个数的乘积记为B。
问:(1)(A-B)最大是多少?(2)(B - A)最大是多少?26有一类自然数,从第三个数字开始,每个数字都恰好是它前面两个数字之和,如246,1347等等,这类数中最大的自然数是几?27在下面的数表中,上、下两行都是等差数列。
上、下对应的两个数字中,大数减小数的差最小是几?28一个三位数的各位数字都不是0,这个三位数与组成它的各位数字之积的比是M(如三位数432,M=432÷(4×3×2)=18),求 M的最大值。
小学一年级数学奥林匹克试卷25套+应用题专项训练6套+逻辑思维专项训练1套无水印

6. 小影到商店买文具用品。她用所带钱的一半买了 1 支自动铅笔,她又用剩下的钱的一
半买了 1 支圆珠笔,还剩下 1 元钱。那么,小影原来有( )元钱。(25 分) 列式:
试卷 10(30 分钟) 1. 一个三角形,切去一个角,还有( )个角。(10 分)
想法: 2. 瓶装汽水厂规定每 2 个空瓶可以换 1 瓶汽水。妈妈为小明共买了 6 瓶汽水,那么他最
想法:
列式:
2. 找规律填数。(15 分)
(1) 2、4、6、8、( )、( )、( )、( )、18、20。
(2) 19、17、15、( )、( )、( )、( )。
(3) 0、1、1、2、3、5、( )、( )。
3. 填空。(15 分)
(1)2+( )=3+( )。
(2)10-( )=6+( )。
试卷 5(30 分钟) 1. 在 3、9、12、13 这四个数中选三个数写出四道算式。(20 分) ( )+( )=( ),( )+( )=( ); ( )-( )=( ),( )-( )=( )。 2. 新星小学美术兴趣小组有学生 9 人,书法兴趣小组的人数和美术兴趣小组的人数同样
多,这两个兴趣小组共有( )名学生。(10 分) 列式: 3. 小明每天早上、中午、晚上各吃 1 个枣。一星期中,小明共吃( )个枣。(20 分) 列式: 4. 小红用同样的钱可以买 3 只蛋糕或者 4 只面包,( )比( )贵。(10 分) 想法: 5. 3 个男同学与 3 个女同学进行打球比赛,如果每个男同学都要与每个女同学比赛 1 次, 一共需要比赛( )次。(10 分) 列式: 6. 一根木头锯成 5 段,要锯( )次。(10 分) 想法: 7. 50 名运动员参加比赛,号码从 1 排到 50。这些号码中共出现了( )个 1。(20 分) 想法:
小学奥数图形找规律题库教师版word精品

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题•板块一数量规律【例1】请找出下面哪个图形与其他图形不一样•【解析】这组图形的共同特征是,连接各边上一点,组成一个复合图形•所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样【例2】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变•因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变•因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△ •(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?00OO O O O△O O O△△O?△△△O A△△△【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变•因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形•(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形【例3】观察下面的图形,按规律在“?”处填上适当的图形【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起, 每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形•【例4】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
奥林匹克训练题库·找规律

一找规律1.根据以下各串数的规律,在括号中填入适当的数:〔1〕1,4,7,10,〔〕,16,……〔2〕2,3,5,8,13,〔〕,34,……〔3〕1,2,4,8,16,〔〕,……〔4〕2,6,12,20,〔〕,42,……2.观察以下各串数的规律,在括号中填入适当的数:〔1〕2,3,5,7,11,13,〔〕,19,……〔2〕1,2,2,4,8,32,〔〕,……〔3〕2,5,11,23,47,〔〕,……〔4〕6,7,3,0,3,3,6,9,5,〔〕,……3.观察以下各串数的规律,并在每题的两个括号内填入适当的数:〔1〕1,1,2,4,3,9,4,16,〔〕,25,6,〔〕,……〔2〕 15, 16, 13, 19, 11, 22,〔〕, 25, 7,〔〕,……4.按规律填上第五个数组中的数:{1,5,10}{2,10,20}{3,15,30}{4,20,40}{ }5.下面各列算式分别按一定规律排列,请分别求出它们的第40个算式:〔1〕1+1,2+3,3+5,1+7,2+9,3+11,1+13,2+15,〔2〕1×3,2×2,1×1,2×3,1×2,2×1,1×3,……6.下面两张数表中的数的排列存在某种规律,你能找出这个规律,并根据这个规律把括号里的数填上吗?〔1〕2 6 7 11 〔2〕2 3 14 4 ( ) 1 35 23 5 5 64 ( ) 37.下面各列数中都有一个“与众不同〞的数,请将它们找出来:〔1〕3,5,7,11,15,19,23,……〔2〕6,12,3,27,21,10,15,30,……〔3〕2,5,10,16,22,28,32,38,24,……〔4〕2,3,5,8,12,16,23,30,……8.以下图所示的两组图形中的数字都有各自的规律,先把规律找出来,再把空缺的数字填上:〔1〕〔2〕9.观察下面图形中的数的规律,根据此规律,“?〞处是几?10.根据左以下图中数字的规律,在最上面的空格中填上适宜的数.11.观察右上图的规律,然后在括号内填上适宜的数.12◇按数字规律填出以下图中空缺的数:13.以下图中有一个圆内四个数字间的关系与另外三个圆不同,请找出这个圆,并修改其中的两个数,使圆内四个数字间的关系与另外三个圆相同.14.在下面各数阵中,第10行的第3个数分别是几?15.下面是两个根据一定规律排列的数字三角形,请根据规律填上空缺的数:〔1〕〔2〕16.以下图中已经画出了三个图,请将第四个图补全.17.根据下面的图和字母的关系,将ad的图补上.18.下面的每一个图形都是由△,□,○中的两个构成的.观察各图形与它下面的数之间的关系,“?〞应当是几?19.左以下图中大圆圈内的数字是由它周围的小圆圈里的数字确定的,那么小圆圈里的“?〞代表几?20.右上图的数字之间存在着某种关系,请根据这一关系求出数字a 和b.21.左以下图中共有12个小图形,每一个不同的小图形表示1~9中的一个数码,每行的三个图形表示一个三位数,四行表示四个三位数:146,521,658和692.问第二行表示哪个三位数?22.右上图中,每个圆代表一个数码,每横行的三个圆从左到右看做一个三位数,四行表示的四个三位数是890, 784,361,256.那么,。
小学数学竞赛数学奥林匹克竞赛中心 找规律填数

找规律填数例1 找出每道题前面几个数的排列规律,并填出括号里的数。
(1)、1、2、3、4、5、()、()、8、9(2)、1、3、5、7、9、()、()、15、17(3)、20、18、16、14、()、()、8、6、4(一例一练)找出每道题前面几个数的排列规律,并填出括号里的数。
(1)、1、7、13、19、()、()、37、43(2)、40、35、30、25、()、()、10、5例2 按照规律,在()里填上合适的数。
15、3、12、3、9、3、()、()(一例一练) 34、5、30、5、26、5、22、5、()、()例3 按照规律,在()里填上合适的数。
(1)、1、2、4、5、7、8、10、()(2)、19、9、17、8、15、7、()、()(一例一练)按照规律,在()里填上合适的数。
(1)、1、3、7、12、18、25、( )、()(2)、29、19、27、18、25、17、()、()例4 按照规律,在()里填上合适的数。
(1)、1、1、2、3、5、8、( )、()(一例一练)按照规律,在()里填上合适的数。
(1)、2、2、4、6、10、16、26、()例5 按照规律,在()里填上合适的数。
(1)、1、3、9、()(2)、16、8、4、2()一例一练)按照规律,在()里填上合适的数。
(1)、1、2、4、8、16、()(2)、32、16、8、()例6 按照规律,在()里填上合适的数。
(1)、1、2、4、7、11、()、()、29 (2)、1、2、3、6、7、()、()(一例一练)按照规律,在()里填上合适的数。
(1)、18、9、10、5、6、()、()(2)、1、3、4、12、13、()、()练习题1、照规律,在()里填上合适的数。
(1)、4、5、6、()、8、9 (2)、19、17、15、13、()、()(3)80、70、()、()40、30 (4)5、9、13、()、21、()2、照规律,在()里填上合适的数。
奥数试题三年级找规律填数(完整资料).doc

此文档下载后即可编辑找规律填数观察下面各组数,你发现它们的排列各有什么规律吗?⑴ 2、4、6、8、10、12、14⑵ 5、10、15、20、25、30、35⑶ 5、6、6、7、7、8、8、9⑷ 13、11、9、7、5、3、11、找规律,再填数⑴ 78、74、70、66、()、()⑵()、90、85、80、()、()⑶ 1、3、9、27、()、()⑷ 1、4、9、16、25、()、()⑸ 7、8、10、13、17、()、()⑹ 3、2、4、3、5、4、()、()、7、6⑺ 1、50、3、40、5、30、()、()⑻ 128、64、32、16、()、()2、先找规律,再继续画下去或写下去。
⑴ ODAAODAAODAA……⑵□△"△口△[△口△O……⑶ 357913579135791••…⑷ 896889966888999666 ••…3、找出与其他四行不同的一行数。
填数时,要注意_____________________________________________________O第一部分必做题1、在括号里填上适当的数。
⑴(☆)11、13、15、()、()⑵(☆)& 17、8、15、10、13、12、()、()⑶(☆)△ 6、18、54、()、()⑷(☆)()、()、65、60、55⑸(☆☆)6、5、9、8、12、11、15、()、()⑹(☆)()、()、84、81、78、75、()⑺(☆)3 7、5、9、7、11、9、13、11、15、()、(⑻(☆☆)30、15、45、15、60、()、()2、先找规律,再继续画下去或写下去。
(1)(☆) OAOAAOAAAOAAAAO(☆^)△△。
△△△△。
△△△△△△^⑶(☆)135113355111333⑷(☆)4327274327274327⑸(☆)135791357913(6)(^)OAAOOOAAAAOOOOOAAAAAA(7)(☆)□□□ □□□□□□□□□□⑻(☆☆)345456 567 6783、找规律填上合适的数。
2019年找规律奥数题及答案-推荐word版 (1页)

2019年找规律奥数题及答案-推荐word版
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!
== 本文为word格式,下载后可方便编辑和修改! ==
找规律奥数题及答案
1.找规律
找规律填数: 1、2、4、5、7、8、10、()、()
解答:在1、2、4、5、7、8、10、()、()中,第二个数比第一个数多1,第三个数比第二个数多2……,根据这一规律,第八个应填11,第九个数应填13。
2.算式问题
找规律奥数题及答案:已知:□+○=8,○+○=6,□+△+△=13。
那么:
□=(),○=(),
△=()
解答: (1)984-(84+67)=984-84-67。
去掉小括号,然后按顺序先算984-84=900。
它们的差为整百数,这样计算比较简便。
(2)143+(57-29)=143+57-29=200-29去掉括号,然后按顺序先算143+57,
它们的差为整百数,这样计算比较简便。
六年级上册数学试题 - 奥数竞赛找规律填图形 全国通用(含答案)
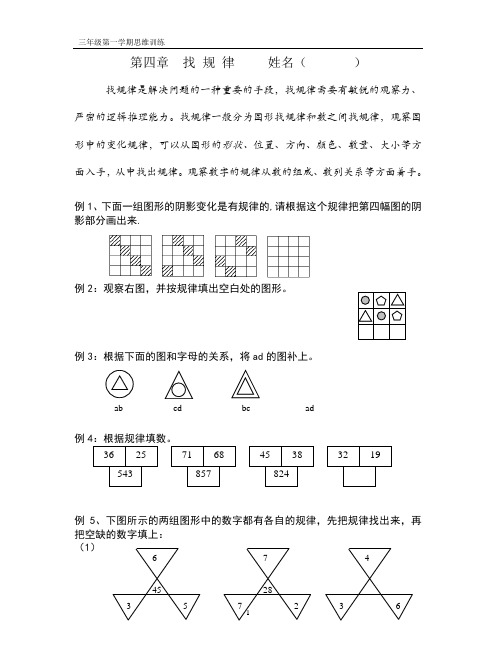
6 45 35 7 287 2 4 3 6第四章 找 规 律 姓名( )找规律是解决问题的一种重要的手段,找规律需要有敏锐的观察力、严密的逻辑推理能力。
找规律一般分为图形找规律和数之间找规律,观察图形中的变化规律,可以从图形的形状、位置、方向、颜色、数量、大小等方面入手,从中找出规律。
观察数字的规律从数的组成、数列关系等方面着手。
例1、下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影部分画出来.例2:观察右图,并按规律填出空白处的图形。
例3:根据下面的图和字母的关系,将ad 的图补上。
例4:根据规律填数。
例5、下图所示的两组图形中的数字都有各自的规律,先把规律找出来,再把空缺的数字填上:(1)ab cd bcad 36 25 543 71 68 857 45 38 824 3219(2)例6:仔细观察下图,根据规律填出所缺的数。
例7:下面三块正方体的六个面,都是按相同的规律涂有红、黄、蓝、白、黑、绿六种颜色。
那么请你根据这一规律,白色的对面是什么颜色?红色的对面是什么颜色?黄色的对面是什么颜色?(1) (2) (3)练习:1、下面括号里两个数按一定规律组合,在( )里填上适当的数。
(1)、(8,7)、(6,9)(10、5)、( 、13 )。
(2)、(2,3)、(5,9)、(7、13)、( 、23 )。
(3)、(18,10)、(10,6)、(20、11)、( 、4(4)、 1、 2、 3、 6、 11、 20、( )2、仔细观察一右图,并按它的变化规律, 在“?”处填上适当的图。
3、在右图空格里填数白 黑 黄 绿 白 红 黄蓝 红 ? 3 12 6 4 16 8 5 206 124.下面的每一个图形都是由△,□,○中的两个构成的。
观察各图形与它下面的数之间的关系,“?”应当是几?5、找规律,从a,b,c,d,e中选入一幅图填入空格内.6. 找规律,画出第四幅图的答案.7、下图是由9个小人排列的方阵,但有一个小人没有到位,请你从右面的6个小人中,选一位小人放到问号的位置.你认为最合适的人选是()号.8、根据规律填数。
奥林匹克ABC题库·探索与归纳训练B卷(word版)

探索与归纳训练B卷班级______姓名______得分______1.找规律,填上恰当的数。
3.原先甲、乙、丙、丁四人分别坐在1、2、3、4号位子上(如图所示)。
后来不停地调换位子。
第一次是上下两排交换,第2次是在第一次交换后再左右两排交换,第三次再上下交换,第四次再左右交换……问第73次交换位子后,甲坐在第几号位子上?4.有一长串珠子是由1994颗红、白两种颜色的珠子穿成。
且2颗白珠子中间总穿着4颗红珠子,无连续串4颗以上的红珠子。
问这一串珠子共有多少颗红珠子?5.3÷7的商是一个循环小数,这个循环小数的小数点后面第1995位上的数字是几?如果数到某一位小数时,这位小数前的小数各位数字之和是500,这位小数是第几位小数?6.原有5根绳子,取其中若干根,将每根剪成5段后放回。
然后再取出、剪短、放回……。
是否可能在某次放回后,绳子的段数刚好是1995段?8.求证:27个72的连乘积与23个32的连乘积的差是10的倍数。
9.在8个连续自然数1986、1987……1993中挑选出两个,使这两数的积是6的倍数,有多少种不同的挑选法?10.把连续偶数2、4、6、8……按右图的方法排列。
(1)数1990属 A、 B、 C、 D列的哪一列上?(2)第101行B列上的数是几?11.下表中,上下两个对应的字和字母配成一组。
例如第一组是(我、A),第五组是(国、E)……(1)第65组是( )。
(2)如果1993组是(我、B),那么第2020组应是( )。
12.紧接1992后面写一串数字,写下的每一个数字,都是前面两个数字乘积的个位数。
例如 9×2=18,在 2后面写 8,又∵ 2×8=16,在 8后面写6……,这样得到一串数字:1992868……(1)这串数字从1开始往右数,第1995个数字是几?(2)这串数字的前1995个数字的和是多少?13.70个数排成一列,除了两头的两个数以外,每个数的3倍都恰好等于它两边两个数的和,这一列数最左边的几个是这样的:0、1、3、8、21……,问最右边的一个数被6除余几?14.把连续奇数1、3、5、7……,按右边的方法排列。
找规律小学奥数题100道及答案(完整版)

找规律小学奥数题100道及答案(完整版)题目1:1,3,5,7,9,()答案:11(相邻两个数的差为2,依次递增)题目2:2,4,6,8,10,()答案:12(相邻两个数的差为2,依次递增)题目3:5,10,15,20,25,()答案:30(相邻两个数的差为5,依次递增)题目4:1,4,9,16,25,()答案:36(分别是1、2、3、4、5 的平方,下一个是 6 的平方)题目5:3,6,9,12,15,()答案:18(相邻两个数的差为3,依次递增)题目6:1,2,4,8,16,()答案:32(后一个数是前一个数的2 倍)题目7:2,6,12,20,30,()答案:42(相邻两个数的差依次为4、6、8、10、12)题目8:1,1,2,3,5,8,()答案:13(前两个数相加等于后一个数)题目9:3,4,7,11,18,()答案:29(前两个数相加等于后一个数)题目10:1,3,7,13,21,()答案:31(相邻两个数的差依次为2、4、6、8、10)题目11:2,5,10,17,26,()答案:37(相邻两个数的差依次为3、5、7、9、11)题目12:9,16,25,36,()答案:49(分别是3、4、5、6 的平方,下一个是7 的平方)题目13:1,8,27,64,()答案:125(分别是1、2、3、4 的立方,下一个是5 的立方)题目14:5,12,19,26,33,()答案:40(相邻两个数的差为7,依次递增)题目15:3,8,15,24,()答案:35(相邻两个数的差依次为5、7、9、11)题目16:2,3,5,8,13,()答案:21(前两个数相加等于后一个数)题目17:1,4,10,22,46,()答案:94(相邻两个数的差依次为3、6、12、24、48)题目18:1,5,14,30,55,()答案:91(相邻两个数的差依次为4、9、16、25、36)题目19:2,6,18,54,()答案:162(后一个数是前一个数的3 倍)题目20:7,14,28,56,()答案:112(后一个数是前一个数的2 倍)题目21:1,2,6,24,120,()答案:720(后一个数依次是前一个数乘2、3、4、5、6)题目22:3,5,9,17,33,()答案:65(相邻两个数的差依次为2、4、8、16、32)题目23:1,3,8,19,42,()答案:89(相邻两个数的差依次为2、5、11、23、47,这些差依次增加3、6、12、24)题目24:2,4,10,28,82,()答案:244(相邻两个数的差依次为2、6、18、54、162,后一个差是前一个差的 3 倍)题目25:5,9,17,33,65,()答案:129(相邻两个数的差依次为4、8、16、32、64)题目26:1,4,27,256,()答案:3125(分别是1、2、3、4 的1、2、3、4 次方,下一个是5 的 5 次方)题目27:1,6,21,66,201,()答案:606(相邻两个数的差依次为5、15、45、135、405,后一个差是前一个差的3 倍)题目28:3,8,15,24,35,()答案:48(相邻两个数的差依次为5、7、9、11、13)题目29:2,3,7,18,47,()答案:123(7 = 3×2 + 1,18 = 7×2 + 4,47 = 18×2 + 11,下一个数应为47×2 + 16 = 123)题目30:1,2,5,14,41,()答案:122(相邻两个数的差依次为1、3、9、27、81,后一个差是前一个差的3 倍)题目31:2,5,11,23,47,()答案:95(相邻两个数的差依次为3、6、12、24、48)题目32:4,9,16,25,36,()答案:49(分别是2、3、4、5、6 的平方,下一个是7 的平方)题目33:6,12,20,30,42,()答案:56(相邻两个数的差依次为6、8、10、12、14)题目34:1,3,7,15,31,()答案:63(相邻两个数的差依次为2、4、8、16、32)题目35:3,9,27,81,()答案:243(后一个数是前一个数的3 倍)题目36:5,13,25,41,()答案:61(相邻两个数的差依次为8、12、16、20)题目37:2,8,32,128,()答案:512(后一个数是前一个数的4 倍)题目38:7,16,29,46,()答案:67(相邻两个数的差依次为9、13、17、21)题目39:1,5,13,25,()答案:41(相邻两个数的差依次为4、8、12、16)题目40:6,18,54,162,()答案:486(后一个数是前一个数的3 倍)题目41:8,18,32,50,()答案:72(相邻两个数的差依次为10、14、18、22)题目42:1,4,13,40,()答案:121(相邻两个数的差依次为3、9、27、81)题目43:3,10,21,36,()答案:55(相邻两个数的差依次为7、11、15、19)题目44:5,15,45,135,()答案:405(后一个数是前一个数的3 倍)题目45:2,6,14,30,()答案:62(相邻两个数的差依次为4、8、16、32)题目46:9,25,49,81,()答案:121(分别是3、5、7、9 的平方,下一个是11 的平方)题目47:7,19,37,61,()答案:91(相邻两个数的差依次为12、18、24、30)题目48:4,12,36,108,()答案:324(后一个数是前一个数的3 倍)题目49:1,6,15,28,()答案:45(相邻两个数的差依次为5、9、13、17)题目50:8,20,36,56,()答案:80(相邻两个数的差依次为12、16、20、24)题目51:3,11,23,39,()答案:59(相邻两个数的差依次为8、12、16、20)题目52:6,15,35,77,()答案:143(相邻两个数的差依次为9、20、42、66,差依次增加11、22、24)题目53:2,9,28,65,()答案:126(分别是1、2、3、4 的立方加1,下一个是5 的立方加1)题目54:1,7,19,37,()答案:61(相邻两个数的差依次为6、12、18、24)题目55:5,16,29,46,()答案:67(相邻两个数的差依次为11、13、17、21)题目56:3,12,27,48,()答案:75(相邻两个数的差依次为9、15、21、27)题目57:7,18,33,52,()答案:77(相邻两个数的差依次为11、15、19、25)题目58:2,10,30,68,()答案:130(相邻两个数的差依次为8、20、38、62,差依次增加12、18、24)题目59:4,15,32,55,()答案:84(相邻两个数的差依次为11、17、23、29)题目60:6,21,42,72,()答案:106(相邻两个数的差依次为15、21、30、34)题目61:1,9,25,49,()答案:81(分别是1、3、5、7 的平方,下一个是9 的平方)题目62:8,24,48,80,()答案:120(相邻两个数的差依次为16、24、32、40)题目63:3,13,31,57,()答案:91(相邻两个数的差依次为10、18、26、34)题目64:5,19,41,71,()答案:105(相邻两个数的差依次为14、22、30、34)题目65:2,11,26,47,()答案:76(相邻两个数的差依次为9、15、21、29)题目66:9,27,51,81,()答案:117(相邻两个数的差依次为18、24、30、36)题目67:7,17,33,55,()答案:83(相邻两个数的差依次为10、16、22、28)题目68:4,14,30,52,()答案:78(相邻两个数的差依次为10、16、22、26)题目69:6,18,36,60,()答案:90(相邻两个数的差依次为12、18、24、30)题目70:1,11,27,51,()答案:81(相邻两个数的差依次为10、16、24、30)题目71:5,17,33,53,()答案:77(相邻两个数的差依次为12、16、20、24)题目72:3,14,31,58,()答案:91(相邻两个数的差依次为11、17、27、33)题目73:8,22,42,70,()答案:106(相邻两个数的差依次为14、20、28、36)题目74:2,13,30,53,()答案:84(相邻两个数的差依次为11、17、23、31)题目75:9,29,55,91,()答案:133(相邻两个数的差依次为20、26、36、42)题目76:7,20,39,64,()答案:95(相邻两个数的差依次为13、19、25、31)题目77:4,16,36,64,()答案:100(分别是2、4、6、8 的平方,下一个是10 的平方)题目78:3,15,33,57,()答案:87(相邻两个数的差依次为12、18、24、30)题目79:6,22,44,74,()答案:110(相邻两个数的差依次为16、22、30、36)题目80:1,13,29,53,()答案:89(相邻两个数的差依次为12、16、24、36)题目81:5,21,41,67,()答案:99(相邻两个数的差依次为16、20、26、32)题目82:8,26,50,82,()答案:118(相邻两个数的差依次为18、24、32、36)题目83:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目84:7,23,45,73,()答案:107(相邻两个数的差依次为16、22、28、34)题目85:2,14,32,56,()答案:88(相邻两个数的差依次为12、18、24、32)题目86:9,31,59,95,()答案:139(相邻两个数的差依次为22、28、36、44)题目87:6,24,48,84,()答案:126(相邻两个数的差依次为18、24、36、42)题目88:1,15,33,57,()答案:87(相邻两个数的差依次为14、18、24、30)题目89:5,23,47,77,()答案:113(相邻两个数的差依次为18、24、30、36)题目90:8,28,52,82,()答案:118(相邻两个数的差依次为20、24、30、36)题目91:3,19,41,69,()答案:105(相邻两个数的差依次为16、22、28、36)题目92:7,27,51,81,()答案:117(相邻两个数的差依次为20、24、30、36)题目93:4,18,38,66,()答案:100(相邻两个数的差依次为14、20、28、34)题目94:6,26,50,80,()答案:116(相邻两个数的差依次为20、24、30、36)题目95:2,16,36,60,()答案:90(相邻两个数的差依次为14、20、24、30)题目96:9,33,63,99,()答案:141(相邻两个数的差依次为24、30、36、42)题目97:8,28,56,92,()答案:136(相邻两个数的差依次为20、28、36、44)题目98:5,21,43,71,()答案:105(相邻两个数的差依次为16、22、28、34)题目99:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目100:7,25,49,79,()答案:115(相邻两个数的差依次为18、24、30、36)。
完整word版小学奥数图形找规律题库学生版

图形找规律.找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;.⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.数量规律板块一.【例 1】请找出下面哪个图形与其他图形不一样观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【例2】【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?.观察下面的图形,按规律在“?”处填上适当的图形】 3【例?)35)(()(4(2))1(观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【例 4】【例 5】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.观察下图中的点群,请回答: 6】【例方框内的点群包含多少个点?(1)个点群中包含多少个点?推测第10(2) 个点群中,所有点的总数是多少?前10(3)观察下面由点组成的图形(点群),请回答:】【例 71)方框内的点群包含多少个点?( 10)个点群中包含多少个点?(2)第( 3)前十个点群中,所有点的总数是多少?(仔细观察后,请回答:下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.【例 8】)五层的“宝塔”的最下层包含多少个小三角形?(1 )整个五层“宝塔”一共包含多少个小三角形?(2旋转、轮换型规律板块二【例 9】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?△☆□○△☆□○○□☆☆○△□△□△□△○☆○☆()()()()()()()().下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形】【例 101)(?组第1组第3组第2(2)?第1组第3组组2第3)(★★★★★?组1第组3第组2第【例 11】观察下图的变化规律,画出丙图.BACABDCD丙乙甲使每一横行和每一竖行.将它们砌在如下图那样的地面上,块【例 12】有六种不同图案的瓷砖,每种各6 你会怎样设计?都没有相同图案的瓷砖.下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画13【例】.出来.. 14【例】观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形她将9她用直尺和圆规在纸上画了幅蝴蝶图,并用剪刀将它们一一剪下来.琪琪特别喜欢蝴蝶,】【例 15只319这只纸蝴蝶摆在桌上,见下图,她发现这些纸蝴蝶排列挺有规律,突然一阵风来,吹走了纸蝴蝶,见下图2.的空缺处吗?3只蝴蝶放入图1的你能找出蝴蝶的排列规律,将图2321465BCA7982图1图.】请观察下图中已有的几个图形,并按规律填出空白处的图形【例 16.17【例】观察下列各组图的变化规律,并在“?”处画出相关的图形 1()?2()?甲乙丙丁.个方格表中阴影的规律,在空白的方格表中也填上相应的阴影3如图,根据图中已知】 18【例)个方格表中阴影部分的小正方形内的几个10【巩固】根据前三个方格表中阴影部分的变化规律,填上第(数之和。
(word完整版)小学奥数图形找规律题库教师版(2021年整理精品文档)

(word完整版)小学奥数图形找规律题库教师版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((word完整版)小学奥数图形找规律题库教师版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(word完整版)小学奥数图形找规律题库教师版的全部内容。
图形找规律找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.板块一数量规律【例 1】请找出下面哪个图形与其他图形不一样。
【例 2】观察图形的变化,想一想,按图形的变化规律,在带“?"的空格处应画什么样的图形?【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变。
因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】 (方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一找规律
1.根据下列各串数的规律,在括号中填入适当的数:
(1)1,4,7,10,( ),16,……
(2)2,3,5,8,13,( ),34,……
(3)1,2,4,8,16,( ),……
(4)2,6,12,2020 ),42,……
2.观察下列各串数的规律,在括号中填入适当的数:
(1)2,3,5,7,11,13,( ),19,……
(2)1,2,2,4,8,32,( ),……
(3)2,5,11,23,47,( ),……
(4)6,7,3,0,3,3,6,9,5,( ),……
3.观察下列各串数的规律,并在每小题的两个括号内填入适当的数:
(1)1,1,2,4,3,9,4,16,( ),25,6,( ),……
(2) 15, 16, 13, 19, 11, 22,( ), 25, 7,( ),……
4.按规律填上第五个数组中的数:
{1,5,10}{2,10,20203,15,30}{4,20200}{ }
5.下面各列算式分别按一定规律排列,请分别求出它们的第40个算式:
(1)1+1,2+3,3+5,1+7,2+9,
3+11,1+13,2+15,
(2)1×3,2×2,1×1,2×3,1×2,2×1,1×3,……
6.下面两张数表中的数的排列存在某种规律,你能找出这个规律,并根据这个规律把括号里的数填上吗?
(1)2 6 7 11 (2)2 3 1
4 4 ( ) 1 3
5 2
3 5 5 6
4 ( ) 3
7.下面各列数中都有一个“与众不同”的数,请将它们找出来:
(1)3,5,7,11,15,19,23,……
(2)6,12,3,27,21,10,15,30,……
(3)2,5,10,16,22,28,32,38,24,……
(4)2,3,5,8,12,16,23,30,……
8.下图所示的两组图形中的数字都有各自的规律,先把规律找出来,再把空缺的数字填上:
(1)
(2)
9.观察下面图形中的数的规律,按照此规律,“?”处是几?
10.根据左下图中数字的规律,在最上面的空格中填上合适的数。
11.观察右上图的规律,然后在括号内填上合适的数。
12◇按数字规律填出下图中空缺的数:
13.下图中有一个圆内四个数字间的关系与另外三个圆不同,请找出这个圆,并修改其中的两个数,使圆内四个数字间的关系与另外三个圆相同。
14.在下面各数阵中,第10行的第3个数分别是几?
15.下面是两个按照一定规律排列的数字三角形,请根据规律填上空缺的数:
(1)
(2)
16.下图中已经画出了三个图,请将第四个图补全。
17.根据下面的图和字母的关系,将ad的图补上。
18.下面的每一个图形都是由△,□,○中的两个构成的。
观察各图形与它下面的数之间的关系,“?”应当是几?
19.左下图中大圆圈内的数字是由它周围的小圆圈里的数字确定的,那么小圆圈里的“?”代表几?
2020上图的数字之间存在着某种关系,请按照这一关系求出数字a 和b。
21.左下图中共有12个小图形,每一个不同的小图形表示1~9中的一个数码,每行的三个图形表示一个三位数,四行表示四个三位数:146,521,658和692。
问第二行表示哪个三位数?
22.右上图中,每个圆代表一个数码,每横行的三个圆从左到右看做一个三位数,四行表示的四个三位数是890, 784,361,256。
那么,。
