4.1.1成比例线段
《成比例线段》教案
（1）在比或a∶b中，a是，b是。
求⑴AB4．1成比例线段4．1．1线段的比，成比例的线段学习目的：1、知道线段的比的概念。
理解成比例线段的概念2、会计算两条线段的比。
3、掌握成比例线段的判定方法。
重点：线段的比与成比例线段的概念。
教学过程：一、自主预习（一）阅读课本，思考并回答下列问题：1、一般地，如果选用量得两条线段AB，CD的长度分别为m,n，那么这两条线段的比就是他们长度的比，即AB∶CD=m:n,或写成ABmCDn,其中，线段AB，CD分别叫做这个线m AB段比的前项和后项.如果把表示成比值k,那么n CDk,或AB k CD。
ab⑵两条线段的要统一。
⑶在同一单位下线段长度的比与选用的无关。
⑷线段的比是一个没有的数。
（二）比例尺1、在地图上或工程图纸上，图上长度与实际长度的比通常称为比例尺。
2、比例尺为1：50000，意思为：。
（三）成比例线段的概念1、一般地，在四条线段中，如果等于的比，那么这四条线段叫做成比例线段。
（举例说明）如：2、四条线段成比例，记作：其中a,d叫比例外项，b,c叫比例内项。
3、四条线段a,b,c,d成比例，有顺序关系。
即a,b,c,d成比例线段，则比例式为：a:b=c:d；a,b,d,c成比例线段，则比例式为：a:b=d:c4、思考：a=12,b=8,c=6,d=4成比例吗？a=12,b=8,c=15,d=10呢？三、例题解析：例1、A、B两地的实际距离AB=250m，画在一张地图上的距离A'B'=5cm,求该地图的比例尺。
例2：已知，在Rt△ABC中，∠C＝90°,∠A＝30°,斜边AB＝2。
AC，⑵BC AB四、巩固练习1、已知某一时刻物体高度与其影长的比值为2：7，某天同一时刻测得一栋楼的影长为30米，则这栋楼的高度为多少？2、某地图上的比例尺为1：1000，甲，乙两地的实际距离为300米，则在地图上甲、乙两地的距离为多少？3、已知线段a,d,b,c是成比例线段，其中a=4,b=5,c=10，求线段d的长。
初中数学北师大版九年级上册《41成比例线段(1)》教学设计
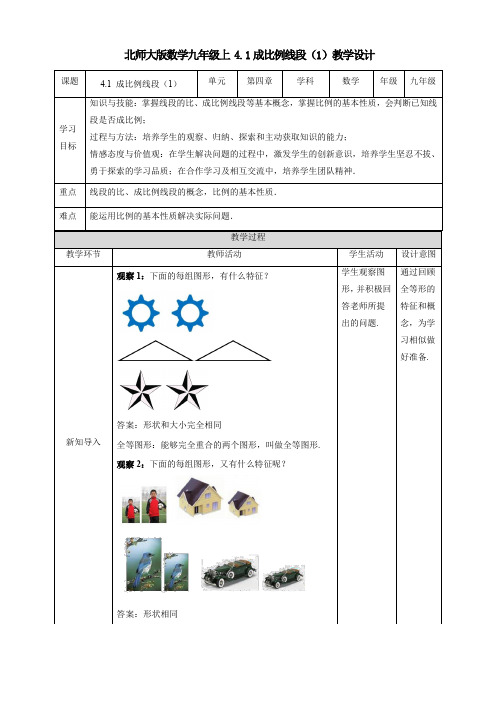
北师大版数学九年级上 4.1成比例线段（1）教学设计观察1：下面的每组图形，有什么特征？答案：形状和大小完全相同全等图形：能够完全重合的两个图形，叫做全等图形.观察2：下面的每组图形，又有什么特征呢？答案：形状相同找一找：你能在下面的图形中找出形状相同的图形吗？答案：追问：这些形状相同的图形有什么不同？答案：大小不同讲解1：对于形状相同而大小不同的两个图形，我们可以用相应线段长度的比来描述它们的大小关系.讲解2：如果选用同一个长度单位得两条线段AB,CD的长度分别是m,n,那么这两条线段的比就是它们长度的比，即AB:CD=m:n或AB mCD n=，其中线段AB,CD分别叫做这个线段比的前项和后项.如：如图，五边形ABCDE与五边形A′B′C′D′E′形状相同，AB=5cm，A′B′=3cm，AB:A′B′=5:3，53就是线段AB与A′B′的比，这个比值刻画了这两个五边形的大小关系.指出：如果把mn表示成比值k,那么ABkCD=，或AB=k·CD,E'D'C'B'A'ABC DE两条线段的比实际上就是两个数的比.引入比值k 的方法是解决比例问题的一种重要方法,以后经常会用到. 做一做：设小方格的边长为1，四边形ABCD 与四边形EFGH 的顶点都在格点上，那么AB ，AD ,EF ,EH 的长度分别是多少？分别计算,,,AB AD DC BCEF EH HG FG的值，你发现了什么？答案：82,4AB EF ==2102,10AD EH == 252,5DC HG ==2172,17BC FG == 即：AB AD DC BCEF EH HG FG===归纳1：四条线段a ,b ,c ,d 中，如果a 与b 的比等于c 与d 的比，即,a cb d =那么这四条线段a ,b ,c ,d 叫作成比例线段，简称比例线段. 如：在AB ADEF EH=中， AB 、EF 、AD 、EH 是成比例线段或者AB 、AD 、EF 、EH 也是成比例线段追问：你还能说出一组成比例线段吗？议一议:如果a ,b ,c ,d 四个数成比例，即,a cb d=，那么ad =bc 吗？反过来,如果ad =bc ，那么a ,b ,c ,d 四个数成比例吗？ 归纳2：比例线段的基本性质如果,a cb d=,那么ad =bc ;如果ad =bc (a ,b ,c ,d 都不等于0)，那么,a cb d=.例：如图，一块矩形绸布的长AB =am ，宽AD =1m ，按照图中所示的方式将它裁成相同的三面矩形彩旗，且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同，即那么a 的值应当是多少？解：根据题意可知，AB =am ，AE =am ，AD =1m .由,AE ADAD AB = 得113,1aa = 即2113a = ∴a 2=3.开平方，得a =3(a =－3舍去).。
九上数学 第13讲 4.1成比例线段
第13讲 《图形的相似》培优训练4.1成比例线段§4.1成比例线段学 习 目 标1.知道两条线段的比的概念并且会计算两条线段的比2.知道成比例线段的定义并会判断四条线段是否成比例3.熟记比例的基本性质并会应用.重点：1、会求两条线段的比 2、知道成比例线段的定义 3、会用比例的性质应用 难点：成比例线段及比例的基本性质的理解与运用。
导学过程：【自主学习，认真准备】小学里已经学过了比例的有关知识，请同学们口答下列问题： 1、若a 与b 的比值和c 与d 的比值相等，应记为： 2、地理中的比例尺是指什么？ 【自主探究、合作交流】任务一：自学课本76页——77页内容，思考并完成下列练习：1、一张桌面的长a=1.25m ，宽b=0.75m ，那么长与宽的比是2、已知线段AB=1.5m ，线段CD=250cm ，那么线段AB 与CD 的比是3、已知A 、B 两地的实际距离是60km,画在地图上其距离A ’B ’是6cm,求这幅地图的比例尺归纳定义：两条线段的比：____________________任务二：完成课本77页“做一做”： 1、计算：=EFAB =EH AD =AD AB =EH EF2、发现： 归纳定义：成比例线段：任务三：完成课本78页“议一议”内容1、结论：归纳：比例的基本性质：如果dcb a ,那么 ；如果ad =bc （a ,b ,c ,d 都不等于0），那么 .还可以写成 形式。
【展示交流】1 、如图，一块矩形绸布的长AB=am,AD=1m ，按照图中所示的方式将它裁成相同的三面矩形彩旗，且使裁出的每面彩旗的长与宽的比与原绸布的长与宽的比相同，即 AD AE = ABAD,那么a 的值应当是多少？,2、已知a=3,b=6,c=9(1)若a,b,c,x 是成比例线段，求x.(2)若a,x,b,c 是成比例线段，求x【当堂练习】1、已知：线段a=5cm ，b=2cm ，则ab= 2、已知a ，b ，m ，n 是成比例线段，其中a=2cm ，b=3cm ，n=9cm ，则m= . 若a=2，b=18，且a ：x=x ：b ，则x=3、把mn=pq （m,n,p,q 都不等于0）写成比例式，写错的是（ ） A ．m q p n = B ．p nm q= C ．q n m p = D ．m p n q =4、如图，△ABC 中，AG DEAH BC=，且DE=12，BC=15，AG=4，求AH ．5、在比例尺是1:8000000的“中国政区”地图上，量得福州与上海之间的距离为 7.5cm ，那么福州与上海之间的实际距离是多少？归纳：比例的基本性质如果b a =dc，那么__________。
4.1.1成比例线段 课件(共16张PPT) 北师大版数学九年级上册
教师讲评
知识点2：成比例线段
四条线段a，b，c，d中，如果a与b的比等于c与d
的比，即
=
，那么这四条
线段a，b，c，d叫做成比例线段，简称比例线段.
四条线段a，b，c，d成比例，有顺序关系，即a，b，c，d是成比例线段，则比
例式为a:b=c:d;a,b,d,c是成比例线段,则比例式为a:b=d:c.
分别叫做这个线段比的前项和后项.如果把 表示成比值k，那么
（1）在 比或a:b中，a是比的前项，b是比的后项；
（2）两条线段的长度单位要统一；
（3）在同一单位下线段的比与选用的长度单位无关；
（4）线段的比是一个没有单位的正数.
= ，其中，线段AB，CD
=k，AB=k∙CD.
+
例 2: 若 − = ,则 : =. ________,
= __________.
例 3: 若
=
= = ,且 + + = ,则 + + 的值为
( B )
A.10
B.4
C.一4
D.一5
【题型三】解决实际问题
例4：已知同一时刻物高与影长成比例，现在有一棵很高的古树，
③成比例线段的基本性质是什么？
Fra bibliotek
（如果 = ，那么bc=ad；如果bc=ad（a，b，c，d都不为0），那么 = ）
1.教材习题：完成课本79页随堂 练习
2.作业本作业：完成对应练习
4.1.1成比例线段PPT课件
注意：
(1)两条线段的长度之比：在同一单位长度下，两
条线段长度的比值叫两条线段的长度之比．
(2)成比例线段是有顺序的,反之，如果说a，b，c， d是成比例线段，那么得到的比例式是 a c，
bd 其中a，d 叫做比例外项，b，c叫做比例内项．
.
12
AB AD2 EH EF
AB,EH,AD,EF是成比例线段
D、2cm, 5dm, 0.2m,10cm
.
18
知识点4：比例的基本性质： a:b=c:d
比例的两个外项之积等于两个内项之积
ac bd
ad=bc （a，b，c，d都不为零）
交叉相乘积相等，内项积等于外项积。
.
19
特别的：
a:b=b:c
b叫做a和c的比例中项
ab bc
b2=ac （b，c都不为零）
如何快（速2地）∵a=将 大0.线 到8,c段 小=从 ）1,d小 的=到 顺2.大序4,b（排=或列3 从， 判断线段是∴a:c计=0算.8第:1一=4和:5第二之比， 否成比例？ d:b第=2三.4和:3第=4四:5之比，看他
课本随堂练习
AB EH2 10 AD EF 5
AB,AD,EH,EF也是成比例线段。
3．a，b，c，d 是成比例线段，其中 a = 3 cm， b = 2 cm，c = 6 cm，求线段 d 的长．
.
13
例1 判断下列线段a、b、c、d是否是成比例线段：
（1）a=4, b=8, c=5, d=10;
计算 AB 、AD、AB 、EH 的值。你发 EH EF AD EF
现了什么？
AB=8，A D226240 21,0EH=4，EF 1232 10
北师大版数学九年 级数学上册4.1：成比例线段与比例的基本性质 课件
第二环节 新课探究
三、比例的基本性质
三、比例的基本性质
小组合作交流三：
如果a、b、c、d 四个数成比例，
即 ac
bd
，那么ad＝bc 吗？反过来，如
果ad＝bc，那么a、b、c、d 四个数成比
例吗？
三、比例的基本性质
如果
a b
c, d
那么
ad
bc
如果 ad bc(a, b, c, d都不等于0），那么 a c bd
巩固练习2
1．判断下列线段是否是成比例线段：
（1）a＝2cm，b＝0.04m，c＝0.3dm，d＝6cm；
（2）a＝0.8，b＝3，c＝1，d＝2.4．
解：（2） a 0.8, c 1, d 2.4,b 3 a 0.8 4 , d 2.4 4 c 1 5b 3 5 a d cb a、c、d、b是成比例线段。
3 题、解决问题能力，培养数学应用意识，体会数学与自然，
社会的密切联系。
2014.10
你能在下面图形中找出形状相同的图形吗？
①
②
③
④
⑤
⑥
⑦
合作交流1：
①
②
③
④ ⑤ ⑥⑦
• 1、图中形状相同的图形有什么不同？ • 2、形状相同的图形其中的一个如何由另一个得到？ • 3、形状相同的图形对应线段如何变化？ • 4、形状相同而大小不同的两个图形，你认为如何描 • 述它们的大小关系？
考考你的眼力
找出这两幅图中四处不同
第一环节 情景引入 在实际生活中，经常会看到许多形状相同的图片
第四章 图形的相似
第1节 成比例线段(一)
4.1.1成比例线段
学习目标
结合现实情境感受学习线段的比的必要性，借助
4.1成比例线段(第一课时)学历案北师大版九年级数学上册
2023学年第一学期九年级数学学历案25班级：_____年级_____班 姓名：__________ 学号：______【课时名称】4.1 成比例线段（第1课时）【课标要求】了解线段的比和成比例线段【学习目标】1.了解线段的比和成比例线段.2.掌握比例的性质及其简单应用 .【评价任务】1.完成任务一（检测目标1）2.完成任务二3.完成任务三（检测目标2）【学习过程】任务一：比例线段1、阅读课本76，说说这些照片的相同之处与不同之处。
2、下面是两个形状相同的五边形，你可以描述它们的大小关系吗？任务二：成比例线段阅读并理解课本77页成比例线段的概念，请找出一组不同于课本的成比例线段。
任务三：比例的性质dc b a =，那如果a,b,c,d 四个数成比例，即么bc ad =吗？你是如何验证的？ 1. 反过来，如果bc ad =，那么a,b,c,d 四个数成比例吗？【检测与作业】一、（检测目标1）1．如图，在Rt △ABC 中，∠C ＝90°，∠A ＝30°，斜边AB ＝2cm ．求：（1）BCAB （2）AB AC 二、（检测目标2）2．已知线段a 、b 、c 、d 满足bc ad =，把它改写成比例式，正确的是（ ）A d ：a =b ：cB a ：d =c ：bC a ：b =c ：dD a ：c =d ：bE D C B A D 'E 'C 'B 'A '3．已知2m =3n ，则mn = ． 4．已知线段a,b,c,d 是成比例线段，其中a =4，b =5，c =10，线段d 的长是___________．5．如图，一块矩形绸布的长AB a =m ，宽2AD =m ，按照图中所示的方式将它裁成相同的三面矩形彩旗，且使裁处的每面彩旗的宽与长的比与原绸布的宽与长的比相同，即AE AD AD AB =，那么a 的值应当是多少？6．已知1x y=，则x y y -的值为 ． 7．如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A ，B ，C 都在横线上．若线段3AB =，则线段BC 的长是( )A ．23B ．1C ．32D ．2【学后反思】。
4.1成比例线段(一)教学设计
第四章图形的相像1．成比率线段 (一)一、学生知识情况剖析相像图形是现实生活中宽泛存在的现象，在小学时学生就接触过比率的知识，在七年级下册时学生已学习了全等图形（其实全等图形就是相像图形的一个特例）。
因此学生已经具备一些知识基础、活动经验基础等，学生在学习线段的比时不会感觉很困难。
二、教课任务剖析（一）教课知识点1、认识相像形、线段的比观点；2、会求两条线段的比 , 应用线段的比解决实质问题。
（二）能力训练要求经过现真相境，进一步发展学生从数学的角度提出问题、剖析问题和解决问题的能力，培养学生的数学应意图识，领会数学与自然、社会的亲密联系。
（三）感情与价值观要求1、相关比率的计算，让学生懂得数学在现实生活中的作用，进而加强学生学好数学的信心；2、经过解答实质问题，激发学生学数学的兴趣，增加社会见解；3、在与别人的共同探究、议论问题的过程中，加强合作沟通的意识。
教课要点：理解线段比的观点及其求解。
教课难点：求线段的比，注意线段长度单位要一致。
教课方法：探究、发现法教课准备：多媒体课件三、教课过程剖析本节课设计了六个教课环节：第一环节：设置情境，引入新课；第二环节：新课解说；第三环节：随堂练习；第四环节：想想；第五环节：回首与思虑；第六环节：部署作业。
第一环节设置情境，引入新课活动内容：经过用幻灯片展现生活的的图片，引入本章的学习内容—相像图形。
活动目的：引起学生思虑相像图形的特点，激发学生的学习兴趣。
实质成效：学生们都很喜悦，对学习充满了好奇心。
第二环节：新课解说 AB AD AB EHEH ,,,活动内容：EF AD EF1.请在下边图形中找出形状同样的图形？你发现这些形状同样的图形有什么不一样？2. 引入线段的比 :假如采纳同一个长度单位量得两条线段 AB,CD 的长度分别是 m ，n,那么就说这两条线段的比 （ratio ）AB:CD=m:n,或写成AB m此中 ,AB,CD 分别叫做这个线段比的前项CDn和后项 .假如把m表示成比值 k,那么ABk ,或 AB=k ·CD.两条线段的比实质上就是两个数的nCD比。
北师大版-数学-九年级上册-教案4.1 成比例线段
4．1 成比例线段第1课时 线段的比和比例的基本性质1．了解线段的比和比例线段的概念．2．掌握比例的基本性质，会求两条线段的比，并应用线段的比解决实际问题．(重点)阅读教材P76～79，完成下列内容：(一)知识探究1．线段的比：如果选用同一个长度单位量得两条线段AB ，CD 的长度分别是m ，n ，那么这两条线段的比(ratio)就是它们________的比，即AB ∶CD ＝m ∶n ，或写成AB CD ＝m n.其中，线段AB ，CD 分别叫做这个线段比的________和________．如果把m n 表示成比值k ，那么AB CD＝k 或AB ＝k ·CD.两条线段的比实际上就是两个数的比．2．四条线段a ，b ，c ，d 中，如果a 与b 的比等于c 与d 的比，即________，那么这四条线段a ，b ，c ，d 叫做成比例线段，简称________．3．比例的基本性质如果a b ＝c d，那么ad ＝________. 如果ad ＝bc(a ，b ，c ，d 都不等于0)，那么a b＝________. (二)自学反馈1．下列各组线段(单位：cm)中，成比例线段是( )A ．1，2，3，4B ．1，2，2，4C ．3，5，9，13D ．1，2，2，32．把mn ＝pq 写成比例式，错误的是( )A.m p ＝q nB.p m ＝n qC.q m ＝n pD.m n ＝p q活动1 小组讨论例 如图，一块矩形绸布的长AB ＝a m ，宽AD ＝1 m ，按照图中所示的方式将它裁成相同的三面矩形彩旗，且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同，即AE AD ＝AD AB，那么a 的值应当是多少？解：根据题意可知，AB ＝a m ，AE ＝13a m ，AD ＝1 m. 由AE AD ＝AD AB，得 13a 1＝1a， 即13a 2＝1. ∴a 2＝3.开平方，得a ＝3(a ＝－3舍去)．本例提供了应用比例基本性质的一个具体情境，应注意阅读和理解题意，然后由比例式得到等积式，再通过计算求得结果．易错提示：开平方后求得的结果，需要检验是否符合题意．活动2 跟踪训练1．等边三角形的一边与这边上的高的比是( )A.3∶2B.3∶1C ．2∶ 3D ．1∶ 32．若四条线段a 、b 、c 、d 成比例，且a ＝3，b ＝4，c ＝6，则d ＝( )A ．2B ．4C ．4.5D ．83．在比例尺为1∶900 000的安徽黄山交通图中，黄山风景区与市政府所在地之间的距离是4 cm ，这两地的实际距离是( )A ．2 250厘米B ．3.6千米C ．2.25千米D ．36千米4．A 、B 两地之间的高速公路为120 km ，在A 、B 间有C 、D 两个收费站，已知AD ∶DB ＝11∶1，AC ∶CD ＝2∶9，则C 、D 间的距离是________km.5．如图，已知AD DB ＝AE EC，AD ＝6.4 cm ，DB ＝4.8 cm ，EC ＝4.2 cm ，求AC 的长． 活动3 课堂小结1．线段的比的概念、表示方法；前项、后项及比值k.2．两条线段的比是有序的；与采用的单位无关，但要选用同一长度单位．3．两条线段的比在实际生活中的应用．【预习导学】(一)知识探究1．长度 前项 后项 2.a b ＝c d 比例线段 3.bc c d(二)自学反馈1．B 2.D【合作探究】活动2 跟踪训练1．C 2.D 3.D 4.905．∵AD DB ＝AE EC ，∴6.44.8＝AE 4.2.解得AE ＝5.6.∴AC ＝AE ＋EC ＝5.6＋4.2＝9.8(cm)．第2课时 等比性质1．理解并掌握等比性质．(重点)2．运用等比性质解决有关问题．(难点)阅读教材P79～80，自学“例2”，完成下列内容：(一)知识探究等比性质：如果a b ＝c d ＝…＝m n (b ＋d ＋…n ≠0)，那么a ＋c ＋…＋m b ＋d ＋…＋n＝________. 注意在运用等比性质时，前提条件是：分母b ＋d ＋…＋n ≠0.(二)自学反馈如果a b ＝c d ＝52(b ＋d ≠0)，那么a ＋c b ＋d＝________.活动1 小组讨论例 在△ABC 与△DEF 中，若AB DE ＝BC EF ＝CA FD ＝34，且△ABC 的周长为18 cm ，求△DEF 的周长． 解：∵AB DE ＝BC EF ＝CA FD ＝34， ∴AB ＋BC ＋CA DE ＋EF ＋FD ＝AB DE ＝34. ∴4(AB ＋BC ＋CA)＝3(DE ＋EF ＋FD)，即DE ＋EF ＋FD ＝43(AB ＋BC ＋CA)． 又∵△ABC 的周长为18 cm ，即AB ＋BC ＋CA ＝18 cm ，∴DE ＋EF ＋FD ＝43(AB ＋BC ＋CA)＝43×18＝24(cm)， 即△DEF 的周长为24 cm.在应用等比性质时，要抓住题目已知条件：三角形ABC 的周长，即三边之和为18 cm.活动2 跟踪训练1．已知a b ＝c d ＝e f＝4，且a ＋c ＋e ＝8，则b ＋d ＋f 等于( ) A ．4 B ．8C ．32D ．22．若a ＋b c ＝b ＋c a ＝c ＋a b＝k ，且a ＋b ＋c ≠0，则k 的值为( ) A ．2 B ．－1C ．2或－1D ．不存在3．已知a b ＝c d ＝e f ＝23，则a ＋e b ＋f＝________. 4．如果a b ＝c d ＝e f＝k(b ＋d ＋f ≠0)，且a ＋c ＋e ＝3(b ＋d ＋f)，那么k ＝________.5．已知a b ＝c d ＝e f ＝23，b ＋2d －3f ≠0，求a ＋2c －3e b ＋2d －3f的值． 活动3 课堂小结等比性质：如果a b ＝c d ＝…＝m n (b ＋d ＋…n ≠0)，那么a ＋c ＋…＋m b ＋d ＋…＋n ＝a b.【预习导学】(一)知识探究 a b(二)自学反馈52【合作探究】活动2 跟踪训练1．D 2.A 3.234.3 5．∵a b ＝c d ＝e f ＝23，b ＋2d －3f ≠0，∴a b ＝2c 2d ＝－3e －3f ＝23.∵b ＋2d －3f ≠0，∴a ＋2c －3e b ＋2d －3f ＝23.。
《成比例线段(1)》教案 2022年北师大版九年级数学上
4.1.1成比例线段（1）【教学目标】知识与技能：知道线段比的概念.会计算两条线段的比. 过程与方法通过计算作图掌握概念：线段的比、成比例线段。
情感、态度与价值观在获得知识的过程中培养学习的自信心． 【教学重难点】教学重点：成比例线段、比例的性质教学难点：会求两条线段的比，注意线段长度的单位要统一. 【导学过程】【创设情景，引入新课】、小学里已经学过了比例的有关知识，下面请同学们口答下列问题： （1）若a 与b 的比值和c 与d 的比值相等，应记为： 。
（2）已知2：3＝4：x ，则：x= 。
【自主探究】(1) 自主学习完成课本60--62页试一试与概括：填写下列空格： （1）、“比例线段”的概念： 。
已知四条线段a 、b 、c 、d,如果dcb a =（或a:b=c:d ），那么a 、b 、c 、d 叫做组成比例的 ， （2）“比例线段”和“线段的比”的区别“比例线段”和“线段的比”这两个概念有什么区别？结论： （3）注意：概念的有序性线段的比有顺序性，a:b 和b:a 通常是不相等的。
比例线段也有顺序性，如dcb a =叫做线段a 、b 、c 、d 成比例，而不能说成是b 、a 、c 、d 成比例。
【课堂探究】例1如图一块矩形的绸布长AB=am ，宽AD=1m ，按照图中所示的方式将它剪裁成相同的三面矩形彩旗，且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同。
即 那么a 的值应当是多少？判断下列线段a 、b 、c 、d 是否是成比例线段： （1）a ＝4，b ＝6，c ＝5，d ＝10；（2）a ＝2，b ＝5，c ＝152，d ＝35． 解：AB ADAD AE =把（1）题中a、b、c、d调换位置可以得到几种情况？哪些情形是成比例线段。
成比例线段在大小排序上有何规律？给你四个数据怎样最快的获取成比例线段排序的最大可能性？总结：如何判断成比例线段，说出你的方法并交流。
【当堂训练】1、已知m、n、p、q是成比例线段，其中m=2cm，n=6cm，q=27cm，则p=_______cm.2、（★★）已知三个数1，2、3，请你再添一个数，使它们构成的四个数成比例关系。
4.1.1线段的比和成比例线段
随
堂
为25 cm，则甲、乙两地间的实际距离是( )
检
A．1 250 km B．125 km C．12.5 km D．1.25 0)，
随
堂
按图可估测杭州在嘉兴的南
检
偏西________度方向上，到
测
嘉兴的实际距离约为_____．
02 PART TWO 成比例线段
堂
检 度，试判断它们是不是成比例线段． 测 (1)a＝16 cm，b＝8 cm，c＝5 cm，d＝10 cm；
(2)a＝8 cm，b＝0.05 cm，c＝0.6 dm，d＝10 cm.
解：(1)因为 a＝16 cm，b＝8 cm，c＝5 cm，d＝10 cm，
ac＝16×5＝80，bd＝8×10＝80，所以 ac＝bd，所以b＝c， ad
n
CD
线段的比实际上就是两个数的比. 说明：AB是CD的 k 倍
知识点 1 两条线段的比
【注意】 单位问题： （1）两条线段的长度 单位 一致时，一般线段的 长度单位可不写； （2）如果给出的线段长度单位不同，则必须化为
统一长度单位 后再求线段的比； （3）两线段的长度比值总是 正数 ，如在运算过程 中出现负数，必须舍去，结果一般化为最简整数比。
解：（1） ∵ a 4 2
b63
c 5 1 d 10 2
，
∴ ac ， bd
∴ 线段a、b、c、d 不是成比例线段．
随 判断下列线段a、b、c、d是否是成比例线段：
堂 （1）a＝4，b＝6，c＝5，d＝10； 检 测 （2）a＝2，b＝ 5 ，c＝ 2 15 ，d＝ 5 3．
解：（2） ∵ a 2 2 5 ，c 2 15 2 5 b 5 5 d 53 5
北师大九年级上册4.1.1 成比例线段 课件
B．2a＝3b
C.
=
D．3a＝2b
4. 生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下
a与全身b的高度比值接近0.618，可以增加视觉美感．若图中b为2 m，则a约为
( A )
A．1.24 m
B．1.38 m
C．1.42 m
D．1.62 m
课堂练习
5.如图，在线段AB上取C，D两点．已知AB＝6 cm，
那么这两条线段的比就是它们长度的比，即AB:CD=m:n，或写成
其中，线段AB,CD分别叫做这个线段比的前项和后项. 如果把
比值k，那么
=
.
表示成
= ，或AB=k×CD.两条线段的比实际上就是两个数的比。
归纳总结
注意:
1.若a:b=k ,说明a是b的 k 倍；
2.两条线段的比与所采用的长度单位无关，但求比时两条线段的长度单位必须
=
，那么
a 的值应当是多少？
典例精析
解：根据题意可知，AB=am，AE= ，AD=1m
由
=
,得
= ，即 =
∴ =
开平方，得 = (a=− 舍去)
课堂练习
1.下列各组中的四条线段成比例的是（ C ）
A.a=1、b=3、c=2、d=4；
是成比例线段。
比例外项
议一议
如果 a,b,c,d 四个数成比例，即 =
，那么 ad = bc 吗？反过来如
北师大版九年级数学上册说课稿：4.1成比例线段
北师大版九年级数学上册说课稿：4.1 成比例线段一. 教材分析北师大版九年级数学上册的“4.1 成比例线段”一节，是在学生已经掌握了比例的性质，以及线段的基本知识的基础上进行的一节内容。
这一节主要向学生介绍成比例线段的定义及其性质，以及如何通过成比例线段来解决一些实际问题。
教材通过生活中的实例，引出成比例线段的定义，接着通过大量的练习，让学生加深对成比例线段的理解。
在这一节的内容中，学生需要掌握成比例线段的定义，以及如何判断两条线段是否成比例，同时，还需要学会如何通过成比例线段来解决实际问题。
二. 学情分析九年级的学生已经具备了一定的数学基础，对于比例的性质和线段的知识有一定的了解。
但是，对于成比例线段的定义及其应用，可能还比较陌生。
因此，在教学过程中，我将会以学生已有的知识为基础，引导学生逐步理解成比例线段的定义，并通过大量的练习，让学生掌握成比例线段的性质和应用。
三. 说教学目标1.知识与技能目标：理解成比例线段的定义，掌握成比例线段的性质，能够判断两条线段是否成比例，并能够运用成比例线段来解决实际问题。
2.过程与方法目标：通过观察、操作、思考、交流等活动，培养学生的逻辑思维能力和解决问题的能力。
3.情感态度与价值观目标：激发学生对数学的兴趣，培养学生的团队合作精神，使学生体验到数学在生活中的应用。
四. 说教学重难点1.教学重点：成比例线段的定义及其性质。
2.教学难点：如何判断两条线段是否成比例，以及如何运用成比例线段来解决实际问题。
五. 说教学方法与手段1.教学方法：采用问题驱动法、案例教学法、小组合作法等，引导学生主动探究，积极参与。
2.教学手段：利用多媒体课件，为学生提供丰富的学习资源，提高教学效果。
六. 说教学过程1.导入：通过生活中的实例，引出成比例线段的定义。
2.新课导入：讲解成比例线段的性质，让学生通过观察、操作、思考，理解并掌握成比例线段的性质。
3.练习巩固：布置一些相关的练习题，让学生通过练习，加深对成比例线段的理解。
4.1-1成比例线段-线段的比
（四）练习巩固：
1.判断下列线段a、b、c、d是否是成比例线段：
（1）a＝4，b＝6，c＝5，d＝10；（2）a＝4cm，b＝2cm，c＝1cm，d＝3cm．
【探究一】：两条线段比的概念:如果选用_______________量得两条线段AB、CD的长分别是m,n，那么这两条线段的比就是它们的长度的比，即AB：CD=_________，或写成______________（注意：线段AB与其长度的位置对应），其中，线段AB，CD分别叫做这个线段比的和。两条线段的比其实就是的比。
（一）自主学习：
观察研究两个几何图形时,我们通常从两个方面来着手,一是观察它们的形状,二是测量它们的图形数据.
1.阅读P76,观察这些图形,首先我们可以通过不同把他们分为三类;对于同一类形状相同的图形,你又是如何区分它们的?说说你的想法.
2.对于形状相同而大小不同的两个平面图形，我们可以用相应线段 _______的_________来描述它们的大小关系。
2.填空：（1）若x是8和4的比例中项，则x的值为。
（2）已知3∶x＝8∶y，求 =（3）已知 ＝ ，求 =
（4）.若 ＝ ，求 =（5）已知 ，则
（6）已知 ，则 （7）如果 ，且 ，那么
（8）线段a=2cm，b=3cm，c=1cm，那么a、b、c的第四比例项d=___________
3.已知: a:b:c=3:5:7且2a+3b-c=28, 求3a-2b+c的值。
归纳：比例的基本性质：
如果 ,那么.如果ad=bc（a,b,c,d都不等于0），那么.
4.1.1成比例线段(教案)
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是“4.1.1成比例线段”这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要判断物体大小比例的情况？”比如，在绘画时，如何按照一定比例缩小或放大物体。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索成比例线段的奥秘。
在教学内容方面，我觉得还可以拓展一些相关知识点，如相似三角形的判定和应用，让学生在学习成比例线段的基础上，进一步拓展知识体系。同时，结合学生的兴趣和实际需求，设计更多有趣、富有挑战性的练习题，提高他们的学习兴趣。
最后，针对学生在课堂上提出的问题，我会在课后进行总结，以后主动提问，及时解决他们的疑惑。
举例解释：例如，在教学过程中，教师可以通过实际例题，如“一个三角形的三边长分别为6cm、8cm、10cm，判断是否为成比例线段”，来强调成比例线段定义的重要性。
2.教学难点
-难点1：成比例线段的判定
-学生可能难以理解如何判断两条线段是否成比例，特别是在涉及多条线段时。
-教师应举例说明，如“线段a=4cm，线段b=6cm，线段c=8cm，线段d=12cm，判断哪些线段成比例”，并引导学生运用交叉相乘法进行判定。
二、核心素养目标
本节课的核心素养目标主要包括以下三个方面：
1.培养学生的几何直观能力：通过观察、分析成比例线段的性质，使学生能够形象地理解比例关系，提高几何直观素养。
2.发展学生的逻辑思维能力：在学习成比例线段的过程中，引导学生运用逻辑推理，分析问题，解决问题，提升逻辑思维素养。
3.培养学生的数学应用意识：将成比例线段知识应用于解决实际问题，让学生体会数学与现实生活的联系，增强数学应用素养。
4.1.1成比例线段
PB·PC
;
②如果CD
EB
DF AD
，那么AD·CD=
EB·DF ;
③如果HF·NF=HE·NK,
那么 HE
NF
HF ； NK
④如果EF·BD=AC·EA, 那么 AC BD . EF EA
2.如果2x 5y.那么 x 5 y2
比例的计算:
一、已知比值
1.若 x y 17 , 则 x 8
变式:已知线段AB=15 mm,CD=3 cm,则线段
AB与CD的比为
；
2.已知线段a,b,c,d成比例，
(1)若a=3㎝,b=2㎝,c=6㎝,则 d= 4 ㎝; (2)若a=5㎝,c=3㎝,d=9㎝,则 b= 15 ㎝;
(3)若a=6㎝,b=1㎝,d=3㎝,则 c= 18 ㎝.
3.若m是2、3、6 的第四比例项,则m= 9 ；
bd 等积式
2.如果ad=bc(a,b,c,d都不等于0),那么
ac bd
由ad＝bc还可以得到哪些比例式？
①两边同时除以cd
ab cd
②两边同时除以bd
ac bd
③两边同时除以ab
d c ba
④两边同时除以ac
d b ca
自学检测2:(2+5+5分钟) 1.完成下列题目：
①如果
PA PB
PPDC ，那么PA·PD=
设比值k
1
.若x 2
y 3
,则
x y
；x x
-
y y
2.已解知：3a设2x
b 4
3y5ck
,求
a b c 及 a b c的值。
c
abc
3.已知
则 a5则2xyxa7b2324kkk,c8by， 3233且ck的3a值 2为b _c_
4.1.1 线段的比和比例的基本性质九年级上册数学北师大版
1a
由 AE AD , 得 3 1 ,即 1 a 2 1.
a
AD
AB
1
3
a 2 3.开平方，得a 3 （a - 3舍去）
.
随堂练习
1.你知道地图比例尺的含义吗？生活中还有哪些
利用线段比的事例？
梯子
黄金分割
2.一条线段的长度是另一条线段长度的5倍，求这
两条线段的比.
5:1
a = c.
么
d
b
例1
如图，一块矩形绸布的长AB = a m, AD =
1m，按照图中所示的方式将它裁成相同的三面矩
形彩旗，且使裁出的每面彩旗的宽与长的比与原
绸布的宽与长的比相同，即
那么 a 的值应当是多少？
AE AD
AD AB
，
解：根据题意可知，AB am，
AE 1 am , AD 1m ,
求AD的长.
解：∵AB=12 ,∴BD=AB-AD=12-AD，
∵AE = 6 cm，EC = 5 cm，且
AD
6
72
,∴
=
,
12−AD5 ∴AD=11 . Nhomakorabea=
AD AE
cm，且 DB = EC
6.如图，将一张矩形纸片沿它的长边对折（EF为折
痕），得到两个全等的小矩形.如果小矩形长边与短
边的比等于原来矩形长边与短边的比，那么原来矩
形的长边与短边的比是多少?
解：设小矩形的长边为x短边为y，则原来矩形的
长边为2y，短边为x.
由题意,得x:y=2y:x,
2
2
即:2 = ,解得 y=
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
情境引入
１、如果a与b的比值和c与d的比值相等，应记
为
。
2、已知2:3=4：x,则x=
。
3、已知a=12cm,b=0.3m，则 a
b
两 条 线 段
。单
位 要 统 一
知识点1 什么叫做两条线段的比呢？
如果选用同一个长度单位量得两条线段AB,CD的
长度分别是m、n；那么这两条线段的比就是两条线
段的长度比。 记作：AB:CD=m:n 或 AB m CD n
C、0.5m, 20cm,10cm, 2.5dm
D、2cm, 5dm, 0.2m,10cm
知识点4：比例的基本性质： a:b=c:d
比例的两个外项之积等于两个内项之积
ac bd
ad=bc （a，b，c，d都不为零）
交叉相乘积相等，内项积等于外项积。
特别的：
a:b=b:c
b叫做a和c的比例中项
ab bc
你能在下面图形中找出形状相同的图形吗？ 你发现这些形状相同的图形有什么不同？
你发现这些形状相同 的图形有什么不同？
• 1、形状相同，大小不同 • 2、图形之间的“放大、缩小” • 3、图形上相应的线段也被“放大、缩小”
• 对于形状相同而大小不同的两个图形，可以用 相应“线段长度的比”来描述图形的大小关系。
其中，AB、CD分别叫做这个线段比的前项、后项。
令 m k （称 k 为比值），则 AB k 或 AB=k﹒CD
n
CD
随堂练习
一条线段的长度是另一条线段的 5 倍，求这两条 线段的比．
注意事项：线段的比
1、求两线段的比时，长度单位必须统一， 若单位不同，先应化为同一长度单位； 2、两线段的比的最后结果应约分、化简； 3、两线段的比是一个没有单位的正数； 4、两线段的比是有顺序的； 5、a:b=k，说明a是b的k倍；
例1 判断下列线段a、b、c、d是否是成比例线段：
（1）a=4, b=8, c=5, d=10;
【解】 b a8 41 2,d c1 5 01 2
ba
c d
,
∴线段a、b、c、d是成比例线段。
（2）a＝2，b＝ 5 ，c＝ 2 15，d＝5 3 ．
解：
∵
a b
2 2 5 55
c 2 152 5 d 53 5
b2=ac （b，c都不为零）
做一做
利用等式性质，能从 a c 能推导出ad=bc吗？Fra bibliotek反过来呢？
bd
练一练
已知ab=cd（ a，b，c，d都不为零）, 请写出有关a,b,c,d成立的比例式.(至少 写4个)
ad cb
d a bc
ac db
ca bd
bd ca
d b ac
bc da
cb ad
想一想
(2)成比例线段是有顺序的,反之，如果说a，b，c，
d是成比例线段，那么得到的比例式是 a c， bd
其中a，d 叫做比例外项，b，c叫做比例内项．
AB AD2 EH EF
AB,EH,AD,EF是成比例线段
课本随堂练习
ABEH2 10 AD EF 5
AB,AD,EH,EF也是成比例线段。
3．a，b，c，d 是成比例线段，其中 a = 3 cm， b = 2 cm，c = 6 cm，求线段 d 的长．
∴a c bd
∴ 线段a、b、c、d是成比例线段．
1．判断下列线段是否是成比例线段： （1）a＝2cm，b＝4cm，c＝3m，d＝6m； （2）a＝0．8，b＝3，c＝1，d＝2．4．
如何快（速2地）∵a=将 大0.线 到8,c段 小=从 ）1,d小 的=到 顺2.大序4,b（排=或列3 从， 判断线段是∴a:c计=0算.8第:1一=4和:5第二之比， 否成比例？ d:b第=2三.4和:3第=4四:5之比，看他
计算 AB 、AD、AB 、EH 的值。你发 EH EF AD EF
现了什么？
AB=8，A D22624 021,0 EH=4，EF 1232 10
AB822 AD 2 102
EH 4 1
EF 10
AB 8 2 10 AD 2 10 5
EH 4 2 10 EF 10 5
知识点2 成比例线段的概念
对于给定的四条线段a、b、c、d，如果其中两条线段
例题1：
五边形 ABCDE与五边形 A’B’C’D’E’形状相同， AB=5cm，A’B’=3cm。 请问：线段AB与线段A’B’ 的比是多少？
注： 1、这个比值刻画了这两个五边形的大小关系。 2、线段的比要统一单位长度。
做一做
如图，设小方格的边长为1，四边形ABCD 与四边形EFGH的顶点都在格点上，那么 AB,AD,EH,EF的长度分别是多少？分别
∴ a,c们,d的,b比成值比是例否线相段同
知识点3 成比例线段判断的步骤
一排： 二算： 三判断：
试一试：
补充练习：1.已知线段a=4cm，b=0.02m， c=6cm，d=0.3dm，试判断它们是否成比 例线段
2.下列能组成比例线段的是（ C ） A、1cm, 2cm,3cm, 4cm
B、2cm, 4cm,8cm,10cm
如何快（速2地）∵a=将 大0.线 到8,c段 小=从 ）1,d小 的=到 顺2.大序4,b（排=或列3 从， 判断线段是∴a:c计=0算.8第:1一=4和:5第二之比， 否成比例？ d:b第=2三.4和:3第=4四:5之比，看他
的长度之比等于另外两条线段的长度之比， 如 a c bd
（或a∶b＝c∶d），那么，这四条线段叫做成比例线段，
简称比例线段．此时也称这四条线段成比例．
比例内项
a:b=c:d
a、b、c的第四比例项
比例式
比例外项
d 叫做 a、b、c的第四比例项.
注意：
(1)两条线段的长度之比：在同一单位长度下，两
条线段长度的比值叫两条线段的长度之比．
a____ b
=
c____ d
a____ b
=
c____ d
a____ b
=
c____ d
ac adbc
bd
ad=bc
a____ b
=
c____ d
ad=bc
ad=bc
…………
1．判断下列线段是否是成比例线段： （1）a＝2cm，b＝4cm，c＝3m，d＝6m； （2）a＝0．8，b＝3，c＝1，d＝2．4．
图形的相似
• 本章学习目标 • 认识图形的相似，进一步积累认识图形性质的经验 • 探索三角形相似的条件，了解相似三角形的性质，进一步发展推理能力 • 能够利用三角形的相似解决一些测量问题 • 了解图形的位似，能利用位似将一个图形放大或缩小
4.1.1 成比例线段
在实际生活中，经常会看到许多形状相同的图片