大学高数课件 8.5 第五节 向量值函数在定向曲面上的积分(第二类曲面积分)

则该点流速为 vi . 法向量为 ni .


o x
y
vi v ( i , i , i )
P ( i , i , i )i Q( i , i , i ) j R( i , i , i )k ,
该点处曲面 Σ 的单位法向量 0
为有向曲面 Σ 上点( x , y , z ) 处的单位法向量 , d S n dS { dydz , dzdx , dxdy } 称 为定 向曲面
n 上的投影 . 元 , An 为向量 A 在
五、计算法
1. 分面投影法
设积分曲面Σ 是由 方程 z z ( x , y ) 所给 出的曲面上侧,Σ 在 xoy面上的投影区域 为 D xy ,函数 z z ( x , y ) 在 D xy 上具 有一阶连续偏导数, 被积函数 R( x , y , z ) 在 Σ 上连续.
n
n
存在条件:
当 P ( x , y , z ), Q ( x , y , z ), R ( x , y , z ) 在有向光滑曲 面Σ 上连续时,对坐标的曲面积分存在.
组合形式:
P ( x, y, z )dydz Q( x, y, z )dzdx R( x, y, z )dxdy

物理意义:

P ( x , y , z )dydz Q( x , y , z )dzdx R( x , y , z )dxdy

性质:
1.
1 2
Pdydz Qdzdx Rdxdy
2
Pdydz Qdzdx Rdxdy Pdydz Qdzdx Rdxdy
lim R( i , i , i )( Si ) xy 存在,
0
i 1 n
则称此极限为函数 R( x , y , z ) 在有向曲面Σ 上对 坐标 x , y 的曲面积分(也称第二类曲面积分)
记作 R( x , y , z )dxdy ,即
R( i , i , i )( Si ) xy R( x, y, z )dxdy lim 0 i 1
xy
若取下侧, cos 0,
R( x , y , z )dxdy R[ x , y , z( x , y )]dxdy D
xy
如果由 x x( y, z )给出, 则有
P ( x , y , z )dydz P[ x( y , z ), y , z ]dydz D
yz
其中的符号当 取前侧时为 , 取后侧时为
如果由 y y( z , x )给出, 则有 Q( x , y, z )dzdx Q[ x , y( z , x ), z ]dzdx
D zx
其中的符号当 取右侧时为 , 取左侧时为
注意: 1. 对坐标的曲面积分,必须注意曲面所取的侧. 2. 如果是垂直于xoy面的柱面时, 其单位法向量
播放
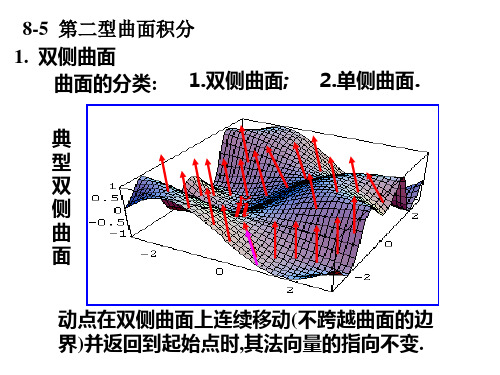
曲面法向量的指向决定曲面的侧.
决定了侧的曲面称为定向曲面.
规定:定向曲面上任一点处的法向量的方向总是指向 曲面取定的一侧.
曲面的投影问题: 在有向曲面Σ 上取一小块
曲面 S , S在xoy面上的投影 ( S ) xy 为
( S ) xy ( ) xy 当 cos 0 时 ( ) xy 当 cos 0 时. 当 cos 0 时 0
P ( x , y , z )dydz Q( x , y , z )dzdx R( x , y , z )dxdy
积分前的符号当 取右侧时为 , 取左侧时为
如果由 x x( y, z )给出, 则有
P ( x , y , z )dydz Q( x , y , z )dzdx R( x , y , z )dxdy P ( x ( y , z ), y , z ) Q( x ( y , z ), y , z ) x y ( y , z ) dydz D yz R( x ( y , z ), y , z ) x z ( y , z ) 积分前的符号当 取前侧时为 , 取后侧时为
2 2
xy
例 2 、 计 算 zxdydz xydzdx yzdxdy ， 其 中 是

x 2 y 2 1，z 1 及三坐标面围成的第一卦限立体曲面
的外侧。
2. 合一投影法
如果由 z z( x , y )给出, 则有
P ( x , y , z )dydz Q( x , y , z )dzdx R( x , y , z )dxdy P ( x , y , z ( x , y )) z x ( x , y ) Q( x , y , z ( x , y )) z y ( x , y ) dxdy D xy R( x , y , z ( x , y )) 积分前的符号当 取上侧时为 , 取下侧时为

( P cos Q cos R cos )dS

向量形式
A dS A ndS

或
A dS A dS
n
其 中 A { P , Q , R }, n {cos , cos , cos }
ds
R( x , y , z )dxdy


o
Dxy
R[ x , y , z ( x , y )]dxdy
D xy
y
x
曲面 Σ 的法向量的方向余弦为
zx cos , 2 2 1 zx zy zy cos , 2 2 1 zx zy 1 cos . 2 2 1 zx zy


n
积分曲面
被积函数
类似可定义

P ( i , i , i )( Si ) yz P ( x, y, z )dydz lim 0 i 1 Q ( i , i , i )( Si ) zx Q( x, y, z )dzdx lim 0 i 1
如果由 y y( z , x )给出, 则有
P ( x , y( z , x ), z ) y x ( z , x ) Q( x , y( z , x ), z ) dzdx D zx R ( x , y ( z , x ), z ) y ( z , x ) z
xyzdxdy xyzdxdy xyzdxdy
2 1
xy 1 x 2 y 2 dxdy xy( 1 x 2 y 2 )dxdy
D xy D xy
2 xy 1 x y dxdy
2 2 D xy
2 2 r sin cos 1 r rdrd . 15 D
(2) 设稳定流动的不可压缩流体(假定密度为 1) 的速度场由
v ( x , y , z ) P ( x , y , z )i Q ( x , y , z ) j R( x , y , z )k
给出,Σ 是速度场中的一片有向曲面,函数
P ( x , y , z ), Q ( x , y , z ), R( x , y , z )
z
z f ( x, y)

o
Dxy
y
x
( s ) xy
1 cos 2 , 2 zx z y 1
若 取上侧, cos 0,
R( x , y , z )dxdy R( x , y , z ) cos dS
R[ x , y , z( x , y )]dxdy D
其中( ) xy 表示投影区域的面积 .
二、概念的引入
实例: 流向曲面一侧的流量. (1) 流速场为常向量v ,有向平面区域 A, 求单位 (假定密度为 1). 时间流过 A 的流体的质量
v
流量

A
0 n
A v cos 0 Av n v A
i 1
n
R( i , i , i ) cos i ]Si
[ P ( i , i , i )( Si ) yz Q ( i , i , i )( Si ) xz
i 1 n
R( i , i , i )( Si ) xy
3.取极限
0 取极限得到流量的精确值.
1
2.
P ( x , y , z )dydz P ( x , y, z )dydz

Q( x , y , z )dzdx Q( x , y, z )dzdx

R( x , y , z )dxdy R( x , y, z )dxdy
都在Σ 上连续, 求在单位 时间内流向Σ 指定侧的流 体的质量 .
x

z
o
y
n 小块si (si 同时也代表 1. 分割 把曲面Σ 分成 第i 小块曲面的面积), v i 在si 上任取一点 z S i ni ( , , ) i i i ( i , i , i ) ,
ni cos i i cos i j cos i k ,
通过si 流向指定侧的流量的近似值为
vi n Si
0 i
(i 1,2,, n).
2. 求和 通过Σ 流向指定侧的流量
0 v n i i Si i 1
n
[ P ( i , i , i ) cos i Q ( i , i , i ) cos i

3. 当由几片定向曲面组成时 , 则应分片计算积分 ,
然后把结果相加 .