二阶巴特沃兹有源滤波器设计与调试
二阶无限增益多路反馈巴特沃斯带通滤波器

二阶无限增益多路反馈巴特沃斯带通滤波器摘要:一、巴特沃斯带通滤波器简介1.滤波器原理2.应用场景二、二阶无限增益多路反馈滤波器设计1.结构特点2.设计方法三、反馈网络构建与分析1.反馈网络拓扑结构2.稳定性分析四、滤波器性能仿真与测试1.仿真软件介绍2.性能指标五、应用实例1.信号处理领域2.通信系统中的应用正文:一、巴特沃斯带通滤波器简介1.滤波器原理巴特沃斯带通滤波器是一种以巴特沃斯函数为传递函数的滤波器,具有频率响应平坦、群延迟均匀的优点。
它能在特定的频率范围内,让信号通过,而阻隔其他频率的信号。
2.应用场景巴特沃斯带通滤波器广泛应用于信号处理、通信系统、音频处理等领域,如滤波、降噪、信号分离等。
二、二阶无限增益多路反馈滤波器设计1.结构特点二阶无限增益多路反馈巴特沃斯带通滤波器,其主要特点是具有多个反馈路径,从而提高滤波器的性能。
这种滤波器的反馈网络由多个运放和电阻、电容组成,形成多路反馈结构。
2.设计方法设计二阶无限增益多路反馈滤波器时,首先需确定滤波器的通带频率、阻带频率和截止频率。
然后,根据这些参数,选取合适的巴特沃斯函数作为滤波器的传递函数,并根据反馈网络的拓扑结构设计电阻、电容的值。
最后,通过仿真软件对滤波器的性能进行仿真和测试。
三、反馈网络构建与分析1.反馈网络拓扑结构二阶无限增益多路反馈滤波器的反馈网络主要包括多个运放、电阻和电容。
根据巴特沃斯函数的特性,设计合适的反馈网络拓扑结构,使滤波器在通带内具有较好的频率响应和群延迟特性。
2.稳定性分析分析滤波器的稳定性,主要看其反馈网络是否产生自激振荡。
通过调整反馈网络的参数,避免不稳定现象的发生,确保滤波器在工作过程中稳定可靠。
四、滤波器性能仿真与测试1.仿真软件介绍使用专业的仿真软件(如Multisim、ADS等),对二阶无限增益多路反馈滤波器进行性能仿真。
这些软件能实时显示出滤波器的频率响应、群延迟等性能指标,便于设计师对滤波器进行优化。
二阶巴特沃斯滤波器的分析与实现电路

二阶巴特沃斯滤波器的分析与实现电路首先,我们需要了解二阶巴特沃斯滤波器的传输函数。
传输函数描述了输入信号与输出信号之间的关系。
二阶巴特沃斯滤波器的传输函数可以写成如下的形式:H(s)=K/(s^2+(ω0/Q)s+ω0^2)其中,s是复频率变量,ω0是滤波器的中心频率,Q是滤波器的品质因数,K是增益系数。
为了实现二阶巴特沃斯滤波器,我们可以使用运算放大器和电容、电阻组成的电路。
具体电路如下所示:其中,R1、R2、C1、C2为电阻和电容元件,OPAMP为运算放大器。
根据传输函数的形式,我们可以将电路分解为三个部分:1.第一个部分是一个非反馈的增益电路,由R1和C1组成。
它起到了对输入信号进行增益的作用,增益大小与R1和C1的取值有关。
2.第二个部分是一个双端口的带通滤波器,由R2、C2和OPAMP组成。
它的作用是滤除输入信号中低频和高频成分,只保留中心频率附近的成分。
中心频率由R2和C2的取值决定。
3.第三个部分是一个反馈网络,由R2和C2组成。
它起到了对输出信号进行反馈的作用,使得滤波器的传输函数满足巴特沃斯滤波器的形式。
根据传输函数的形式,我们可以得到R1、R2、C1、C2的取值公式如下:R1=Q/(K*ω0*C1)R2=1/(K*ω0^2*C2)C1=1/(Q*ω0*R1)C2=1/(K*ω0^2*R2)其中,K可以根据实际需求进行调整,选取适当的增益值。
Q和ω0由滤波器的需求决定,分别代表品质因数和中心频率。
总结起来,二阶巴特沃斯滤波器的分析与实现包括以下几个步骤:1.确定滤波器的中心频率和品质因数,根据传输函数的形式计算出R1、R2、C1、C2的取值。
2.选取合适的电阻和电容元件,连接电路。
3.根据实际需求选择适当的增益值K。
4.搭建电路,并进行测试和调试,确保滤波器的性能符合要求。
二阶巴特沃斯滤波器电路设计

二阶巴特沃斯滤波器电路设计
二阶巴特沃斯滤波器可以通过使用电容器和电感器来实现。
下面是一个常见的二阶巴特沃斯低通滤波器的电路设计:
1. 选择合适的电容和电感。
根据要求的截止频率和阻带衰减率选择合适的电容和电感。
截止频率是滤波器开始衰减的频率,阻带衰减率是滤波器在截止频率之上的衰减量。
2. 设计RC网络。
使用一个电阻和一个电容构建一个RC网络。
这个网络是滤
波器的一部分,用于控制截止频率。
3. 设计RL网络。
使用一个电阻和一个电感构建一个RL网络。
这个网络也是
滤波器的一部分,用于增加滤波器的阻带衰减率。
4. 连接RC和RL网络。
将RC网络和RL网络连接起来,形成一个二阶巴特沃斯低
通滤波器。
5. 使用操作放大器。
如果需要,可以使用操作放大器来增强滤波器的增益和带宽。
6. 测试及调整。
连接信号源和输出设备,对滤波器进行测试,并根据需要调
整电路参数。
需要注意的是,这只是一个基本的二阶巴特沃斯滤波器电路设计步骤的概述。
具体的设计取决于所需的截止频率、阻带衰减率和其他特定需求。
二阶低通滤波器设计报告

二阶低通滤波器设计报告设计目标:设计一个二阶低通滤波器,实现对输入信号的高频成分进行抑制,从而实现信号的平滑处理。
设计原理:二阶低通滤波器是基于巴特沃斯(Butterworth)滤波器的设计方法。
巴特沃斯滤波器是一种特殊的滤波器,其特点是在通带范围内具有最平坦的幅频特性,且在阻带范围内具有最快的衰减。
设计步骤:1. 确定滤波器的通带截止频率和阻带截止频率。
通带截止频率是指在该频率之前的信号成分会通过滤波器,而在截止频率之后的信号成分会被滤波器抑制。
阻带截止频率是指在该频率之后的信号成分会被滤波器抑制。
2. 根据巴特沃斯滤波器的设计表格,可以得到二阶低通滤波器的主要参数:截止频率、通带增益和阻带衰减。
3. 根据所给的截止频率和阻带衰减要求,在设计表格中找到相应的参数值,并得到对应的通带增益。
4. 根据得到的参数值,可以计算出二阶低通滤波器中各个阶段的传递函数和巴特沃斯滤波器的极点位置。
5. 根据所得到的传递函数和极点位置,可以确定滤波器的系统函数。
6. 可以使用系统函数进行滤波器的频率响应仿真和频率响应曲线的绘制。
7. 根据设计需求,可以进行滤波器的进一步优化,如增加滤波器阶数或采用其他滤波器设计方法。
设计结果:根据给定的截止频率和阻带衰减要求,得到了二阶低通滤波器的参数值。
通过系统函数的频率响应仿真和绘制,可以验证滤波器的设计效果。
结论:二阶低通滤波器是一种常用的滤波器设计方法,可以实现对信号的高频成分进行抑制,从而实现信号的平滑处理。
通过合理选择滤波器的参数值,可以得到满足设计要求的滤波器。
在实际应用中,可以根据具体需求对滤波器进行进一步优化,以获得更好的滤波效果。
二阶有源低通滤波器课程设计

二阶有源低通滤波器课程设计引言各种滤波器已经大量的出现在我们的日常生活中,在通信设备、医疗设备、汽车领域等各行各业都存在大量的模拟滤波器。
本文主要研究巴特沃斯低通滤波器,切比雪夫Ⅰ型滤波器,切比雪夫Ⅱ型滤波器,椭圆滤波器等四种滤波器的设计,然后同过比较它们的幅频特性和相位特性,得出性价比最高的滤波器。
由于在现代测控系统中模拟滤波器是不可或缺的一部分,如今模拟滤波器的理论和设计方法已经相当成熟。
有多种典型的滤波器如巴特沃斯滤波器、椭圆滤波器等都有严格的设计公式、归一化低通滤波器的参数,所以我们可以直接选用。
1.通过研究四种滤波器的设计原理加深对四种低通滤波器的学习。
2.通过对四种低通滤波器幅频特性图的观察比较出它们的差别。
2.学习并且掌握四种低通滤波器的MATLAB仿真程序。
1.通过研究滤波器及巴特沃斯低通滤波器,切比雪夫滤波器,椭圆滤波器的性能,有利于加深对课本学习的理解。
2.通过比较四种低通滤波器的性能,有利于我们选择性价比更高的滤波器。
本文研究的是四种低通滤波器的设计及四种低通滤波器的性能比较,具体研究的是在同一参数下比较四种低通滤波器的性能,利用MATLAB程序作出四种低通滤波器的图像,通过比较它们的图像在通带和阻带中图形波纹及过渡带的宽窄,比较出性能最优的低通滤波器。
1实验平台概述1.1滤波器的概述美国在1917年发明了世界上第一台无源滤波器,50年代无源滤波器才逐渐发展,在60年代集成运放获得了迅速地发展,70年代滤波器主要朝着精度高,体积小,稳定等方向发展,90年代主要是各种滤波器的开发和研究。
而我国50年代后才开始使用滤波器,现阶段我国的数字滤波器已使用与各种电信设备,但集成化的滤波器任然需要极大的突破。
滤波器分为有源滤波器和无源滤波器。
经典滤波器和现代滤波器组成了数字滤波器。
经典滤波器的特点是其输入信号中我们需要的信号频率和我们希望屏蔽的信号频率在不同的频带,通过一个合适的滤波器来滤除我们不需要的信号,得到我们所需的纯净信号。
01设计举例有源滤波器设计与制作

01设计举例有源滤波器设计与制作有源滤波器是一种使用有源元件(如晶体管或运算放大器等)的滤波器,它可以增加信号的幅度,改变频率响应,并且具有较低的输出阻抗。
本文将详细介绍一个有源滤波器的设计与制作过程。
首先,我们选择一个二阶巴特沃斯低通滤波器作为设计示例。
第一步是选择适当的滤波器类型。
巴特沃斯滤波器是一种常见的滤波器类型,它具有平坦的通频带响应和陡峭的阻频带响应。
在本例中,我们选择一个截止频率为1kHz的巴特沃斯低通滤波器。
第二步是确定滤波器的阶数。
阶数越高,滤波器的斜率会越陡。
在本例中,我们选择一个二阶滤波器,因为它可以提供足够的滤波效果,并且较为容易实现。
接下来,我们需要进行滤波器的电路设计。
有源滤波器的电路通常由一个有源元件(如晶体管或运算放大器)和被动元件(如电阻、电容和电感)组成。
在本例中,我们选择使用一个运算放大器作为有源元件,并结合电容和电阻来构建滤波器。
通过选择合适的电阻和电容数值,我们可以实现所需的截止频率和增益。
在电路设计中,我们需要考虑各个元件的频率特性以及它们之间的相互影响。
通过使用标准的电路设计工具,如SPICE仿真软件,我们可以模拟电路的频率响应并进行优化。
在滤波器电路设计完成后,我们需要进行电路的布局和连接。
在布局设计中,我们应注意减少元件之间的干扰和交叉耦合。
在连接电路时,我们应选择适当的导线和连接器,并确保电路的正确连接。
完成电路的布局和连接后,我们需要对电路进行测试和调试。
通过使用信号发生器和示波器,我们可以检查滤波器的频率响应和增益,并进行必要的调整。
一旦滤波器的设计和调试都完成了,我们可以进行电路的制作。
我们可以选择将电路制作在芯片上或者使用电路板来制作。
在制作电路板时,我们需要进行电路板的布线和钻孔。
通过使用专业的电路板制作设备,我们可以实现高质量的电路板制作。
完成电路板的制作后,我们可以焊接和安装所有的电子元件。
在焊接过程中,我们应注意避免过热和短路。
二阶RC有源滤波器的设计!!

湖南人文科技学院毕业设计二阶RC有源滤波器的设计摘要:滤波器是一种能够使有用频率信号通过,而同时抑制(或衰减)无用频率信号的电子电路或装置,在工程上常用它来进行信号处理、数据传送或抑制干扰等。
有源滤波器是由集成运放、R、C 组成,其开环电压增益和输入阻抗都很高,输出阻抗又低,构成有源滤波电路后还具有一定的电压放大和缓冲作用,但因受运算放大器频率限制,这种滤波器主要用于低频范围。
本次毕业设计主要是在所学《模拟电子技术基础》、《集成电路》等专业知识的基础上研究和设计几种典型的二阶有源滤波电路:巴特沃斯二阶有源低通滤波器、巴特沃斯二阶有源高通滤波器、二阶有源带通滤波器,研究和设计其电路结构、传递函数,并对有关参数进行计算,再利用multisim 软件进行仿真,组装和调试各种有源滤波器,探究其幅频特性。
经过仿真和调试,本次设计的二阶RC有源滤波器各测量参数均与理论计算值相符,通频带的频率响应曲线平坦,没有起伏,而在阻频带则逐渐下降为零,衰减率可达到|-40Db/10oct|,滤波效果很理想。
关键词:有源滤波器二阶 RC 频率Abstract:Filter is a kind of can make useful frequency signal through,While suppressing ( or attenuation) useless frequency signal electronic circuit or device, commonly used in engineering to signal processing, data transfer or suppression of interference. Active power filter is composed of integrated operational amplifier, R, C composition, its open loop voltage gain and input impedance is very high, and low output impedance, an active filter circuit also has a voltage amplifying and buffering effect, but due to operational amplifier frequency limit, this filter is mainly used in low frequency range.This graduation design is mainly in the" analog electronic technology"," integrated circuit" and other professional knowledge based on research and design of several typical two order active filter circuit: Butterworth two, Butterworth two step active low pass filter active high-pass filter, two step active band-pass filter, research and design of its circuit structure, transfer function, and the related parameters are calculated, then the use of Multisim software simulation, assembly and commissioning of various active filter, explore its amplitude frequency characteristic.After simulation and debugging, the design of the two order active RC filter the measurement parameters and calculation results, the pass band frequency response curve is flat, no ups and downs, and in the stop band is decreased to zero, attenuation rate can reach | - 40dB / 10oct |, filtering effect is very ideal.Key words: Active power filter Two order RC Frequency Signal第一章前言1.1 选题依据近现代,在电子工程、通信工程、自动控制、遥测控制、测量仪器、仪表和计算机等技术领域,滤波器的应用极为广泛,滤波器的优劣直接决定产品的优劣,所以,对滤波器的研究和生产历来为各国所重视。
8-二阶巴特沃什有源滤波器设计
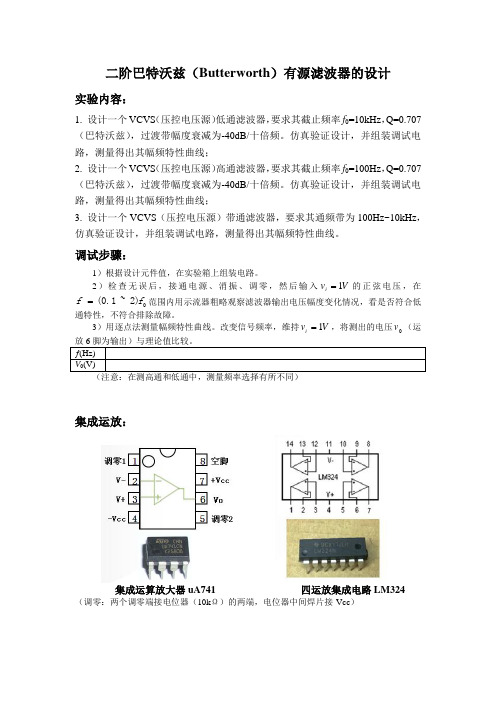
二阶巴特沃兹(Butterworth )有源滤波器的设计 实验内容:
1. 设计一个VCVS (压控电压源)低通滤波器,要求其截止频率f 0=10kHz ,Q=0.707(巴特沃兹),过渡带幅度衰减为-40dB/十倍频。
仿真验证设计,并组装调试电路,测量得出其幅频特性曲线;
2. 设计一个VCVS (压控电压源)高通滤波器,要求其截止频率f 0=100Hz ,Q=0.707(巴特沃兹),过渡带幅度衰减为-40dB/十倍频。
仿真验证设计,并组装调试电路,测量得出其幅频特性曲线;
3. 设计一个VCVS (压控电压源)带通滤波器,要求其通频带为100Hz~10kHz ,仿真验证设计,并组装调试电路,测量得出其幅频特性曲线。
调试步骤:
1)根据设计元件值,在实验箱上组装电路。
2)检查无误后,接通电源、消振、调零,然后输入V v i 1=的正弦电压,在0)2~1.0(f f =范围内用示流器粗略观察滤波器输出电压幅度变化情况,看是否符合低通特性,不符合排除故障。
3)用逐点法测量幅频特性曲线。
改变信号频率,维持V v i 1=,将测出的电压0v (运
集成运放:
集成运算放大器uA741 四运放集成电路LM324 (调零:两个调零端接电位器(10k Ω)的两端,电位器中间焊片接-Vcc )
参考电路:
1.低通滤波电路
2.高通滤波电路:
3.带通滤波电路:。
巴特沃斯有源高通滤波器的设计

昆明理工大学课程设计说明书课题名称:巴特沃斯有源高通滤波器的设计专业名称:电子信息工程学生班级:09级电信三班学生姓名:周剑彪学生学号:200911513339指导老师:王庆平设计时间:2011年6月23日第一部分:题目分析及设计思路(一)、滤波器简介滤波器是一种对信号有处理作用的器件或电路。
主要作用是:让有用信号尽可能无衰减的通过,对无用信号尽可能大的衰减。
滤波器按照所处理的信号,可以分为:模拟滤波器和数字滤波器;按照信号的频段,可以分为:低通、高通、带通和带阻滤波器四种;按照所采用的原件,也可以分为:无源滤波器和有源滤波器。
用来说明滤波器性能的技术指标主要有:中心频率f0,即工作频带的中心;带宽BW;通带衰减,即通带内的最大衰减阻带衰减等。
(二)巴特沃斯滤波器简介巴特沃斯滤波器是电子滤波器的一种。
巴特沃斯滤波器的特点是通频带的频率响应曲线最平滑。
这种滤波器最先由英国工程师斯替芬〃巴特沃斯(Stephen Butterworth)在1930 年发表在英国《无线电工程》期刊的一篇论文中提出的。
一级至五级巴特沃斯低通滤波器的响应如下图所示:巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
在振幅的对数对角频率的波特图上,从某一边界角频率开始,振幅随着角频率的增加而逐步减少,趋向负无穷大。
(三)、巴特沃斯有源高通滤波器优化设计设计目的掌握滤波器的基本概念;掌握滤波器传递函数的描述方法;掌握巴特沃斯滤波器的设计方法;设计一个巴特沃斯滤波器,其技术指标为:(1)阻带截止频率: fc = 1kHz ;(2)通带放大倍数:Aup =2;(3)品质因素:Q = 1;(4)阻带最小衰减率:-25dB。
设计要求:(1)确定传递函数;(2)给出电路结构和元件参数;(运算放大器可以选择)(3)利用PSPICE 软件对电路进行仿真,得到滤波器的幅频响应,是否满足设计指标;第二部分:电路原理分析及基本电路图(一)确定传递参数:二阶高通滤波器的通带增益截止频率,它是二阶高通滤波器通带与阻带的界限频率。
sallen-key 结构的二阶巴特沃斯带通滤波器

sallen-key 结构的二阶巴特沃斯带通滤波器摘要:一、Sallen-Key结构简介1.结构特点2.应用场景二、二阶巴特沃斯带通滤波器原理1.巴特沃斯滤波器特性2.二阶滤波器设计方法三、Sallen-Key结构二阶巴特沃斯带通滤波器设计步骤1.确定滤波器参数2.构建Sallen-Key拓扑结构3.计算滤波器频率响应4.优化滤波器性能四、应用实例与仿真分析1.设计要求2.仿真软件介绍3.滤波器性能验证五、总结与展望1.Sallen-Key结构二阶巴特沃斯带通滤波器优势2.潜在改进方向正文:一、Sallen-Key结构简介1.结构特点Sallen-Key结构是一种常见的无源电子滤波器拓扑结构,具有良好的频率响应特性。
它主要由两个电容和一个电阻组成,形成一个带有放大器的二阶滤波器。
由于其结构简单、性能优越,被广泛应用于各种电子系统中。
2.应用场景Sallen-Key结构适用于需要窄带通、低失真、高抑制比的滤波器设计场景。
例如,在通信、音频处理、传感器信号处理等领域,对信号的滤波处理有着广泛的应用需求。
二、二阶巴特沃斯带通滤波器原理1.巴特沃斯滤波器特性巴特沃斯滤波器是一种最平滑的滤波器,具有零阶截止频率附近波动小的特点。
它能够有效地抑制高频干扰和低频噪声,实现信号的净化。
2.二阶滤波器设计方法二阶滤波器的设计主要依据巴特沃斯滤波器的频率响应特性,通过选取合适的电容和电阻参数来实现。
常见的二阶滤波器类型有Butterworth、Chebyshev、Elliptic等,其中Butterworth滤波器具有频率响应平滑、无纹波等优点。
三、Sallen-Key结构二阶巴特沃斯带通滤波器设计步骤1.确定滤波器参数设计前需确定滤波器的截止频率、通带衰减、阻带衰减等性能指标。
2.构建Sallen-Key拓扑结构根据Sallen-Key结构原理,构建滤波器电路图,包括放大器、电容、电阻等元件。
3.计算滤波器频率响应利用电路仿真软件,如Multisim、LTspice等,对滤波器进行仿真,得到频率响应曲线。
二阶巴特沃兹有源低通滤波器

巴特沃兹有源低通滤波器设计摘要:给出了二阶巴特沃兹有源低通滤波器的设计方法和设计实例,通过multisim 电路仿真试验能够得到一个性能优良的二阶有源低通滤波器。
关键词:有源;低通滤波器;设计 1 概述低通滤波器LPF是滤除噪声用得最多的滤波器。
由于高阶有源低通滤波器的每个滤波节皆由二阶滤波器和一阶滤波器组成。
我们设计一个巴特沃兹二阶有源低通滤波器。
并使用电子电路仿真软件进行性能仿真。
2 设计方法 2.1频率特性巴特沃斯低通滤波器的幅频特性为:ncuou A j A 211)(⎪⎪⎭⎫ ⎝⎛+=ωωω . . . . . . (1)其中Auo 为通带内的电压放大倍数,ωC 为截止角频率,n 称为滤波器的阶。
从(1)式中可知,当ω=0时,(1)式有最大值1;ω=ωC 时,(1)式等于0.707,即Au 衰减了 3dB ;n 取得越大,随着ω的增加,滤波器的输出电压衰减越快,滤波器的幅频特性 越接近于理想特性。
当 ω>>ωC 时,nc uo u A j A ⎪⎪⎭⎫⎝⎛≈ωωω1)( . . . . . . (2) 两边取对数,得:lg20cuo u n A j A ωωωlg 20)(-≈ . . . . . . (3) 此时阻带衰减速率为: -20ndB/十倍频或-6ndB/倍频,该式称为衰减估算式。
任何高阶滤波器都可由一阶和二阶滤波器级联而成。
对于n 为偶数的高阶滤波器,可以由2n 节二阶滤波器级联而成;而n 为奇数的高阶滤波器可以由21-n 节二阶滤波器和一节一阶滤波器级联而成,因此一阶滤波器和二阶滤波器是高阶滤波器的基础。
2.2设计步骤有源滤波器的设计,就是根据所给定的指标要求,确定滤波器的阶数n ,选择具体的电路形式,算出电路中各元件的具体数值,安装电路和调试,使设计的滤波器满足指标要求,以巴特沃斯响应的二阶滤波器的设计为例。
具体步骤如下:1)根据阻带衰减速率要求,确定滤波器的阶数。
二阶巴特沃斯滤波器的分析与实现电路

二阶巴特沃斯滤波器的分析与实现电路一、二阶巴特沃斯滤波器的分析1.二阶巴特沃斯滤波器的传递函数H(s)=K/(s^2+s/Q+1)其中,s是复频率变量,K是增益系数,Q是品质因数。
2.二阶巴特沃斯滤波器的频率响应-通带增益:在通带上的频率响应为平坦的,即各个频率上的增益相同,达到最大的增益,同时增益是线性的。
-阻带增益:在阻带上的频率响应有较大的衰减,一般以-20dB/10倍数进行衰减。
-边缘频率:通带和阻带的分界点被称为边缘频率,可以用截止频率表示。
3.品质因数Q的影响品质因数Q是二阶巴特沃斯滤波器一个重要的参数,它决定了滤波器的响应特性。
-当Q值较大时,滤波器具有较窄的通带和深的阻带,对于截止频率的变化较为敏感。
-当Q值较小时,滤波器具有较宽的通带和浅的阻带,对于截止频率的变化不敏感。
4.构建二阶巴特沃斯滤波器的实现电路构建二阶巴特沃斯滤波器的实现电路有多种方式,其中比较常见的方式是使用运算放大器和电容、电感等元件构成。
二、二阶巴特沃斯滤波器的实现电路1.无源滤波器无源滤波器是利用电容、电感等被动元件构成的滤波器,可以直接用于振荡电路中的滤波。
-RC二阶无源巴特沃斯低通滤波器电路由两个电阻R和两个电容C构成,电容负载在两个分立性电阻之间。
-RL二阶无源巴特沃斯带通滤波器电路由两个电阻R和两个电感L构成,电感负载在两个分立性电阻之间。
2.有源滤波器有源滤波器是利用运算放大器(OP-AMP)和电容、电感等被动元件组成的滤波器,可以增加放大倍数和频率范围。
- Sallen-Key二阶有源巴特沃斯低通滤波器电路由一个运算放大器、两个电阻R1和R2,两个电容C1和C2构成。
- Sallen-Key二阶有源巴特沃斯带通滤波器电路由一个运算放大器、两个电阻R1和R2,两个电容C1和C2构成。
以上是两种常见的二阶巴特沃斯滤波器的实现电路示例,实际构建时还需根据具体的需求进行参数调整和电路优化。
总之,二阶巴特沃斯滤波器是一种常见而有效的模拟滤波器,可以用于对信号进行滤波处理。
二阶有源带通滤波器的设计要点

二阶有源带通滤波器的设计要点1.滤波器类型选择:确定所需的滤波器类型,例如巴特沃斯滤波器、切尔文斯基滤波器等。
每种类型的滤波器都有不同的特性,满足不同的滤波要求。
2.频率范围选择:确定希望滤波器通过的频率范围,这取决于应用的需求。
可以根据信号的频率分析,选择适合的频率范围。
4.滤波器特性:选择滤波器的增益和增益稳定性要求。
对于有源滤波器,可以通过负反馈回路来实现增益调节,并确保稳定性。
5.滤波器的阶数:确定所需的滤波器阶数。
二阶滤波器在频率响应和滤波特性方面通常比一阶滤波器更好。
较高阶数的滤波器可以在抑制带内获得更好的滚降特性。
6.滤波器的增益:确定所需的增益量,以及频率范围内的增益平坦度。
增益可以通过有源放大器的放大倍数调节。
7.模拟滤波器设计:根据滤波器类型和阶数,设计滤波器的模拟电路。
这通常包括选择合适的运算放大器、电容和电阻值,以及设置反馈网络。
8.有源放大器选择:选择适合的有源放大器来放大输出信号。
放大器的选择取决于所需的增益、频率范围和电源电压等因素。
9.噪声和失真:考虑滤波器的噪声级别和失真程度。
噪声和失真可以通过选择合适的放大器和电路设计来最小化。
10.调试和优化:完成滤波器的原理图和PCB设计后,进行调试和优化。
这可能包括电路的频率响应测试、增益平坦度测试和稳定性分析等。
11.参数调整和性能评估:根据实测数据,调整滤波器电路中的元器件数值,以达到所需的滤波特性。
通过频率响应和失真分析,评估滤波器的性能。
12.结果验证和应用:验证滤波器的性能是否满足实际应用的要求。
如果需要,可以进行进一步的调整和优化。
以上是设计二阶有源带通滤波器的一些要点。
设计者应该根据具体的应用需求和电路参数进行适当的调整和优化。
matlabbutterworth带通滤波器_二阶有源带通滤波器设计

matlabbutterworth带通滤波器_⼆阶有源带通滤波器设计⼆阶有源带通滤波器设计1、背景对于微弱的信号的处理⽅式⼀般是:放⼤和滤波,这个过程中就涉及到放⼤电路的选取、滤波器的选择以及偏置电路的设计。
本例以实例的⽅式讲解并附带参数计算、仿真、实物测试三个环节。
假设需要处理⼀个20mV的正弦信号,该信号的频率范围是15~35Hz,经过处理后幅值不超过3.3V,且需要经过带通滤波器滤除杂波。
2、滤波器定义滤波电路⼜称为滤波器,是⼀种选频电路,能够使特定频率范围的信号通过,⽽且其他频率的信号⼤⼤衰减即阻⽌其通过。
按滤波器⼯作频率范围的不同,可分为:低通低通滤波器(Low-pass Filter,LPF)⾼通滤波器(High-pass Filter,HPF)⾼通带通滤波器(Band-pass Filter,BPF)带通带阻带阻滤波器(Band-rejection Filter,BRF)全通滤波器(All-pass Filter,APF)全通有源滤波⽆源滤波器。
如果滤波电路中含有有源元件,如集成运放等,则称为有源滤波仅由电阻、电容、电感这些⽆源器件组成的滤波电路称为⽆源滤波器器。
与⽆源滤波器相⽐,有源滤波器具有效率⾼、带负载能⼒强、频率特性好,⽽且在滤波的同时还可以将有⽤信号放⼤等⼀系列有点⽽得到⼴泛应⽤。
2.1、滤波器种类2.1.1、低通滤波器从f0~f2频率之间,幅频特性平直,它可以使信号中低于f2的频率成分⼏乎不受衰减地通过,⽽⾼于f2的频率成分受到极⼤地衰减。
图 1低通滤波器2.1.2、⾼通滤波器 与低通滤波相反,从频率f1~∞,其幅频特性平直。
它使信号中⾼于f1的频率成分⼏乎不受衰减地通过,⽽低于f1的频率成分将受到极⼤地衰减。
图 2⾼通滤波器2.1.3、带通滤波器 它的通频带在f1~f2之间。
它使信号中⾼于f1⽽低于f2的频率成分可以不受衰减地通过,⽽其它成分受到衰减。
图 3带通滤波器实际上将低通滤波器和⾼通滤波器串联,即可构成带通滤波器,此处需要注意⾼通滤波器的截⽌频率⼀定要⼩于低通滤波器的截⽌频率即fH<fL,否则新构成的滤波器就会变成全频滤波器。
二阶巴特沃斯滤波器的分析与实现电路

巴特沃斯滤波器的分析与实现巴特沃斯滤波器网上没有提供现成的电路和具体参数,此处本文给出几种类型的巴特沃斯滤波器,并给出了参数计算分析。
1、巴特沃斯低通滤波器的定义:巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:其中, n = 滤波器的阶数ωc =截止频率=振幅下降为-3分贝时的频率ωp = 通频带边缘频率1/(1 + ε2) = |H(ω)|2在通频带边缘的数值.2、巴特沃斯滤波器的实现一些常见资料的滤波器的错误有些资料上给出的二阶巴特沃斯滤波器电路图为:图中红线部分为放大电路,其实滤波器为2阶RC滤波器。
其传递函数为:H(s)=11+s(R1C1+R1C2+R2C2)+s2R1R2C1C2下面证明此滤波器不可能为二阶巴特沃斯滤波器:滤波器幅频传递函数为:|H(jw)|=|11+jw(R1C1+R1C2+R2C2)−w2R1C1R2C2|=11+w4(R1R2C1C2)2+w2((R1C1+R1C2+R2C2)2−2R1R2C1C2)若滤波器是巴特沃斯滤波器,则((R1C1+R1C2+R2C2)2−2R1R2C1C2要为0 。
因为(R1C1+R1C2+R2C2)2−2R1R2C1C2始终大于零(R1R2C1C2不取零值,C1或C2为零时为1阶RC滤波器,此时为巴特沃斯滤波器),所以不论R1R2C1C2取何值,都不是二阶巴特沃斯滤波器二阶巴特沃斯滤波器的实现方法本文列举了2种2阶巴特沃斯滤波器的实现方法,并给出了滤波器是巴特沃斯滤波器的参数。
以下详述:方法1:RC压控电压源滤波器传递函数为:H(s)=11+s(R1C1+R1C2+R2C2-A*R1C1)+s2R1R2C1C2(A为放大倍数)下面证明此滤波器在一定情况下可成为为二阶巴特沃斯滤波器:情况1:滤波器幅频传递函数为:|H(jw)|=|A1+jw(R1C1+R1C2+R2C2−A∗R1C1)−w2R1C1R2C2|=A若滤波器是巴特沃斯滤波器,则((R1C1+R1C2+R2C2−A∗R1C1)2−2R1R2C1C2要为0 。
二阶压控压源型巴特沃斯低通滤波器设计教学文案

二阶压控压源型巴特沃斯低通滤波器设计利用VCVS型二阶RC有源网络实现巴特沃斯型低通滤波器的设计一.二阶压控电压源低通滤波器的构成下图所示就是压控压源二阶型滤波网络电路:其传递函数为:与一般低通滤波传输函数相比:可得:截至角频率:增益因子:选择性因子:二阶低通滤波器归一化低通传输函数为:去归一化低通传输函数为:令:得:R2应有实根得:二.各参数的设计由于所需的滤波网络阶次为二阶因为设计指标里通带截至频率规定: f p =100.1KHz,设运放的电压增益为2,而两个电容的值最好相同,则令C C C ==21,带入上式品质因素公式中,可得:因为品质因素在数值上等于截止频率时的滤波网络电压增益和通带电压增益只比,则21=Q则R R R 2212== (1)因为2121121R R C C f p π=(2)则由式(1)(2)可求得RC 110125.16-⨯⨯=由实际电子元器件标称值可以设定:三.结果的验证利用Multisim 对设计的电路进行仿真。
首先搭建整个电路如下:21R R Q =其中XFG1是信号发生器,XBP1是波特仪,而XSC1是示波器。
我们设计的时候所设定的截止频率是100.1K。
所以先选择一个比较低的频率值,看其运放的放大倍数。
所以先设定信号源频率为1K,仿真结果如下:示波器示数:从图中可以看出在低频段时:通道1的峰值为29.98mv,通道2的峰值为62.029mv,滤波网络的放大倍数可以算得A1=2.069。
现在把信号源的频率调到预设截至频率,继续仿真,结果如下:从图中可以看出通道1的峰值为29.974mv,通道2的峰值为43.012mv,则在该频率下的网络放大倍数为A2=1.435。
则在预设截止频率下的放大值与通带下的放大倍数只比为:0.694。
结果约等于0.7。
波特图的结果如下:由图可知,将频率调到100K,衰减幅度为2.714dB,如果频率为100.1K,则结果将非常接近3dB。
二阶巴特沃斯滤波器的分析与实现电路

巴特沃斯滤波器的分析与实现巴特沃斯滤波器网上没有提供现成的电路和具体参数,此处本文给出几种类型的巴特沃斯滤波器,并给出了参数计算分析。
1、巴特沃斯低通滤波器的定义:巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:其中, n = 滤波器的阶数ωc =截止频率=振幅下降为-3分贝时的频率ωp = 通频带边缘频率1/(1 + ε2) = |H(ω)|2在通频带边缘的数值.2、巴特沃斯滤波器的实现2.1 一些常见资料的滤波器的错误有些资料上给出的二阶巴特沃斯滤波器电路图为:图中红线部分为放大电路,其实滤波器为2阶RC滤波器。
其传递函数为:H(s)=11+s(R1C1+R1C2+R2C2)+s2R1R2C1C2下面证明此滤波器不可能为二阶巴特沃斯滤波器:滤波器幅频传递函数为:|H(jw)|=|11+jw(R1C1+R1C2+R2C2)−w2R1C1R2C2|=11+w4(R1R2C1C2)2+w2((R1C1+R1C2+R2C2)2−2R1R2C1C2)若滤波器是巴特沃斯滤波器,则((R1C1+R1C2+R2C2)2−2R1R2C1C2要为0 。
因为(R1C1+R1C2+R2C2)2−2R1R2C1C2始终大于零(R1R2C1C2不取零值,C1或C2为零时为1阶RC滤波器,此时为巴特沃斯滤波器),所以不论R1R2C1C2取何值,都不是二阶巴特沃斯滤波器2.2 二阶巴特沃斯滤波器的实现方法本文列举了2种2阶巴特沃斯滤波器的实现方法,并给出了滤波器是巴特沃斯滤波器的参数。
以下详述:方法1:RC压控电压源滤波器传递函数为:H(s)=11+s(R1C1+R1C2+R2C2-A*R1C1)+s2R1R2C1C2(A为放大倍数)下面证明此滤波器在一定情况下可成为为二阶巴特沃斯滤波器:情况1:滤波器幅频传递函数为:|H(jw)|=|A1+jw(R1C1+R1C2+R2C2−A∗R1C1)−w2R1C1R2C2|=A若滤波器是巴特沃斯滤波器,则((R1C1+R1C2+R2C2−A∗R1C1)2−2R1R2C1C2要为0 。
二阶巴特沃兹滤波器设计
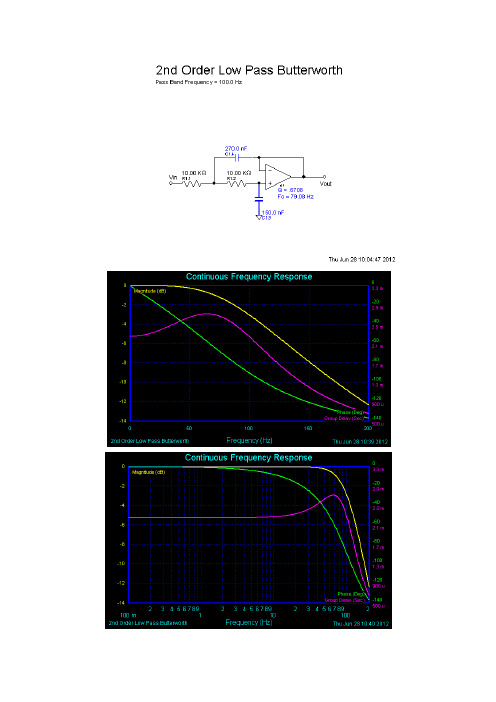
Multisim 仿真验证
频率(Hz)50.182 60.29 69.936 80.065 90.194 100.805 150.001 200.161 250.804 幅值衰减(db)-0.973 -1.664 -2.518 -3.576 -4.744 -8.021 -11.685 -16.381 -20.187 信号衰减倍数0.8940 0.8257 0.7483 0.6625 0.5792 0.3971 0.2604 0.1517 0.0979
输入信号设置为:交流信号发生器输出幅值为5V频率为50HZ的正弦波,另外
一端叠加5V电压。
在电压叠加电路的输出端测量相应的输出电压波形如图1所示。
原始输入信号,叠加5V直流电压,输入幅值为5V周期为50HZ的正弦电压
通过电压叠加电路后的输出波形
由此可见:信号叠加的结果是在5V直流电压的基础上叠加了一个幅值为5V的正弦波。
输出的电压波形是在直流2.5V电压基础上叠加的幅值约0.6V的电压
100HZ叠加输入
150HZ叠加输入
200HZ叠加输入
300HZ叠加输入
400HZ叠加输入
500HZ叠加输入
500HZ叠加输入放大图
100HZ叠加输入放大图
50HZ输入同窗图
滤波电路的特性曲线如下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
200 960
300 1000
(Hz) V0(mV)
500 1000
1000 1000
2000 1000
5000 1000
10000 1000
误差分析:可以看到,在 f=100Hz 是,输出电压 Vo1 =0.704V,在 1kHz 时, 误差大约为 | Vo 2 =1.00V,
Vo1 * 2 Vo 2 在实验误差允许范围内。 | *100%=4.65%, Vo 2
f=100Hz、Vpp=712mV
f=1000Hz、Vpp=1.000V
使用 matlab 处理表格数据得到波特图如下图(九)所示:
图(九) 如图(九)高通幅频波特图可以看到:波形相对比较平滑,当幅度下降 3dB 时 对应的频率大概是 f=100Hz,符合设计预期。
4.3 带通滤波器:
(Hz) V0(mV)
f (0.1 ~ 2) f 0 范围内用示流器粗略观察滤波器输出电压幅度变化情况,看是
否符合低通特性,不符合排除故障。 3)用逐点法测量幅频特性曲线。改变信号频率,维持 vi 1V ,将测出的电 压 v0 与理论值比较。
4.1 低通滤波器:
(Hz)
50 1.0
100 500 700 1k 1.0 1.0 1.0 1.0
10 152
20 240
30 328
50 472
70 592
90 672
100 696
120 752
150 808
180 840
(Hz) V0(mV)
200 880
300 936
400 952
500 960
600 968
700 968
800 976
900 976
1000 976
2000 952
(Hz) V0(mV)
按照该连线,使用 protues 进行仿真,结果如下图(四)所示:
由图可以看到,在频率 f=100Hz 处,曲线相对最大值大概减小了 3dB,说明仿真 符合设计预期,可以按照此连接图进行实际连线。 3.带通滤波器 设计一个 VCVS(压控电压源)带通滤波器,要求其通频带为 100Hz~10kHz,仿 真验证设计,并组装调试电路,测量得出其幅频特性曲线。 带通滤波器, 可以视为一个高通滤波器和另一个低通滤波器组合在一起,由两级 电路来组合成带通滤波器, 但考虑到这两个滤波器之间的互相影响,为了尽可能 减小这种影响, 考虑将前一级电路的输出电阻抗设置得比较低,后一级电路的输 入阻抗设置得非常高, 这样可以将两级滤波器的阻抗之间的互相影响降得非常小 以至于可以忽略。 低通滤波级和高通滤波级电路分别如下图(五)所示:
2. 实验仪器和实验元件
二踪示波器 x1、函数发生器 x1、数字万用表 x1、直流稳压电源 x1 电容电阻若干,集成运算放大器 uA741(如下图)
引脚图
实物图
3. 设计与仿真
1. 低通滤波器: 设计一个 VCVS (压控电压源)低通滤波器,要求其截止频率 f0=10kHz , Q=0.707,过渡带幅度衰减为-40dB/十倍频。仿真验证设计,并组装调试电路, 测量得出其幅频特性曲线; 考虑到巴特沃兹滤波电路可提供过渡带幅度衰减-40dB/十倍频,故采用二阶 巴特沃兹有源低通滤波器。电路图如下图(一)所示:
图(七)
由图可以看出,在频率 f=100Hz 处和 f=10kHz,曲线相对于曲线最大值大概减小 了 3dB, 说明仿真符合设计预期, 说明将后级阻抗设置为前级阻抗的 100 倍之后, 电路两级之间的阻抗影响变得很小, 对电路几乎没有产生影响, 该设计是合理的。
4 . 电路实际连线
1)根据设计元件值,在实验箱上所示电路组装电路。 2)检查无误后,接通电源、消振、调零,然后输入 vi 1V 的正弦电压,在
所以设置后一级电路的 R 2 : R 1 100 : 1 ,因此 R 2 100R 1 16k Ω,由此可得: C2=
1 1 0.001uF=1000pF. wR 2 2fR 2
总体电路连线图如下图(六)所示:
图(六) 按照该连线,使用 protues 进行仿真,结果如下图(七)所示:
高通级 图(五) 对于高通滤波级,计算可得:
低通级
A( jw )
R1 1 R1 jwC1
1- j
1 1 wC1R 1
,当 A( jw ) =
1 时,可得: 2
1 1 1 1 1 ,所以 w 159 Ω ,令 C1=10uF,可得 R 1 wC1 R 1 R 1C1 wC 1 2fC1
f0
0 1 = =10kHz,解得: R 2 R 1 110 Ω 2 2R C1C 2
按照该连线,使用 protues 进行仿真,结果如下图(二)所示:
图(二) 由图可以看到,在频率 f=10kHz 处,曲线相对最大值大概下降了 3dB,说明仿真 符合设计预期,可按照此连接图进行实际连线。 2.高通滤波器 设计一个 VCVS (压控电压源)高通滤波器,要求其截止频率 f0=100Hz , Q=0.707,过渡带幅度衰减为-40dB/十倍频。仿真验证设计,并组装调试电路, 测量得出其幅频特性曲线 原理同低通滤波器的设计,使用 protues 连线如下图(三)所示:
2k 1.0
3k
0.96
4k
0.91
5k
0.87
6k
0.87
7k
0.83
8k
0.79
9k
0.75
V0(V)
(Hz)
10k 11k
12k 13k 14k 15k
16k
17k
18k
19k
20k
V0(V)
0.70
0.69
0.67
0.65
0.61
0.5 5
0.55
0.49
0.47
0.46
0.45
误差分析: 可以看到, 在 f=100Hz 是, 输出电压 Vo1 =1.0V, 在 10kHz 时, Vo 2 =0.70V, 误差大约为 |
图(一)
按照此连线,先取 R 1 R 2 R :
ቤተ መጻሕፍቲ ባይዱ
1 1 1 C1 R C1C2 ,其中 0 ,Q A( s) 2S 1 2 C2 R C1C 2 S2 2 RC1 R C1C2
2
按照设计要求,f0=10kHz,Q=
1 ,取定 C1 2C 2 0.2uF,可得: 2
4.2 高通滤波器:
(Hz) V0(mV)
20 104
30 216
40 224
50 368
60 376
70 464
80 552
90 632
100 704
110 768
(Hz) V0(mV)
120 816
130 848
140 872
150 896
160 920
170 936
180 944
190 952
Vo 2 * 2 Vo1 | *100%=1.01%,在实验误差允许范围内。 Vo1
f=1kHZ、Vpp=1.0V
f=10kHz、Vpp=712mV
借用 matlab 处理数据得到幅频特性图如下图(八)所示:
图(八) 如图(八)低通幅频波特图可以看到:当幅度下降 3dB 时对应的频率大概是 f=10kHz,符合设计要求。
5000 872
8000 776
9000 744
10000
11000
12000
13000
14000
15000
16000
704
652
624
600
568
548
520
(Hz) V0(mV)
18000
19000
20000
30000
40000
50000
100000
480
476
444
324
260
224
128
误差分析:可以看到,在 f=100Hz 是,输出电压 Vo1 =0.696V,在 f=1kHz 时, Vo=0.976V,在 f=10kHz 时, Vo 2 =0.704V,误差大约是:
由于实际电阻没有 159Ω,故使用 R 1 160 Ω
同理,对于低通滤波级,计算可得:
1 1 1 jwC 2 A( jw ) , 当 A( jw ) = 时,可得: 1 1 jwC R 2 2 2 R2 jwC 2
wR 2 C 2 =1, 所以 w
1 , 考虑到为了使得后一级阻抗要远大于前一级的阻抗, R 2C2
(|
Vo1 * 2 Vo V * 2 Vo | | o2 |) / 2 *100%=1.01%,在实验误差允许范围内。 Vo Vo
f=100Hz、Vpp=696mV
f=1000Hz、Vpp=968mV
f=10kHz、Vpp=704mV 使用 matlab 处理表格数据得到波特图如下图(十)所示:
实 验 报 告
实验项目:有源滤波电路的设计与调试 实验人: 黄海进(13348039) 黄淼鑫(13348043) 黄 涛(13348044) 指导老师:郭东亮 实验日期:2014/12/29 日
实验 12 有源滤波电路的设计与调试
1. 实验目的
(1)学会设计有源滤波电路和测量滤波器的幅频特性 (2)掌握电路有关参数对滤波器的影响
图(三) 按照此连线,先取 C1 C 2 C :
A( s) S2 S2 2 1 S R2C R 1R 2 C
,其中 0
1 1 R2 ,Q 2 R1 C R 1R 2
按照设计要求,f0=100Hz,Q=
1 ,取定 C1 C 2 1.0uF,可得: 2
