立体几何公理定理总结
立体几何基本定理与公式

立几基本公式空间直线.1. 空间直线位置分三种:相交、平行、异面.相交直线—共面有且有一个公共点;平行直线—共面没有公共点;异面直线—不同在任一平面内2. 异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)3. 平行公理:平行于同一条直线的两条直线互相平行.4. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如下图).(二面角的取值范围[)οο180,0∈θ) (直线与直线所成角(]οο90,0∈θ) (斜线与平面成角()οο90,0∈θ)(直线与平面所成角[]οο90,0∈θ)(向量与向量所成角])180,0[οο∈θ推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.5. 两异面直线的距离:公垂线的长度. 一、直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种:相交、平行、在平面内.2. 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)3. 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面12方向相同12方向不相同POAa垂直,过一点有且只有一个平面和一条直线垂直.若PA⊥α,a⊥AO,得a⊥PO(三垂线定理),得不出α⊥PO. 因为a⊥PO,但PO不垂直OA.三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.5. ⑴垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上一、平面平行与平面垂直.1. 空间两个平面的位置关系:相交、平行.2. 平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(“线面平行,面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.[注]:一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行,线线平行”)4. 两个平面垂直性质判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直性质判定二:如果一个平面与一条直线垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直,面面垂直”)注:如果两个二面角的平面对应平面互相垂直,则两个二面角没有什么关系.5. 两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面.五、 棱锥、棱柱.1. 棱柱.⑴①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长) ⑵{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱柱}⊃{正方体}. {直四棱柱}⋂{平行六面体}={直平行六面体}.⑶棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全等的矩形...... ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形. (直棱柱定义):棱柱有一条侧棱和底面垂直. ⑷平行六面体:定理一:平行六面体的对角线交于一点.............,并且在交点处互相平分. [注]:四棱柱的对角线不一定相交于一点.定理二:长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和. [注]:①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V S h V ==.正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心.[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)PαβθM AB Oii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. 正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ⑵棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.3. 球:⑴球的截面是一个圆面.①球的表面积公式:24R S π=. ②球的体积公式:334R V π=.②圆锥体积:h r V 231π=(r 为半径,h 为高)③锥形体积:Sh V 31=(S 为底面积,h 为高)六. 空间向量.1(1)共线向量:共线向量亦称平行向量,指空间向量的有向线段所在直线互相平行或重合. (2)共线向量定理:对空间任意两个向量)0(,≠b b a ,a ∥b 的充要条件是存在实数λ(具有唯一性),使λ=.(3)共面向量:若向量a 使之平行于平面α或a 在α内,则a 与α的关系是平行,记作a ∥α. (4)①共面向量定理:如果两个向量b a ,不共线,则向量与向量b a ,共面的充要条件是存在实数对x 、y 使y x +=.②空间任一点...O .和不共线三点......A .、.B .、.C .,则)1(=++++=z y x OC z OB y OA x OP 是PABC 四点共面的充要条件.(简证:→+==++--=AC z AB y AP OC z OB y OA z y OP )1(P 、A 、B 、C 四点共面)注: 是证明四点共面的常用方法.2. 空间向量基本定理:如果三个向量....c b a ,,不共面...,那么对空间任一向量P ,存在一个唯一的有序实数组x 、y 、z ,使c z b y a x p ++=.推论:设O 、A 、B 、C 是不共面的四点,则对空间任一点P , 都存在唯一的有序实数组x 、y 、z使 z y x ++=(这里隐含x +y+z≠1).注:设四面体ABCD 的三条棱,,,,d AD c AC b AB ===其中Q 是△BCD 的重心,则向量)(31c b a AQ ++=用MQ AM AQ +=即证.3. (1)空间向量的坐标:空间直角坐标系的x 轴是横轴(对应为横坐标),y 轴是纵轴(对应为纵轴),z 轴是竖轴(对应为竖坐标). ①令a =(a 1,a 2,a 3),),,(321b b b =,则),,(332211b a b a b a b a ±±±=+))(,,(321R a a a a ∈=λλλλλ332211b a b a b a b a ++=⋅a ∥)(,,332211Rb a b a b a b ∈===⇔λλλλ332211b a b a b a ==⇔ 0332211=++⇔⊥b a b a b a b a222321a a a ++==(a a =⇒⋅=) 232221232221332211||||,cos b b b a a a b a b a b a b a ba b a ++⋅++++=⋅⋅>=<ρρρρρρ②空间两点的距离公式:212212212)()()(z z y y x x d -+-+-=.(2)法向量:若向量a 所在直线垂直于平面α,则称这个向量垂直于平面α,记作α⊥a ,如果α⊥那么向量叫做平面α的法向量. (3)用向量的常用方法:①利用法向量求点到面的距离定理:如图,设n 是平面α的法向量,AB 是平面α的一条射线,其中α∈A ,则点B 到平面α②利用法向量求二面角的平面角定理:设21,n n 分别是二面角βα--l 中平面βα,的法向量,DCBAB则21,n n 所成的角就是所求二面角的平面角或其补角大小(21,n n 方向相同,则为补角,21,n n 反方,则为其夹角).③证直线和平面平行定理:已知直线≠⊄a 平面α,α∈⋅∈⋅D C a B A ,,且CDE 三点不共线,则a ∥α的充要条件是存在有序实数对μλ⋅使CE CD AB μλ+=.(常设CE CD AB μλ+=求解μλ,若μλ,存在即证毕,若μλ,不存在,则直线AB 与平面相交).。
立体几何常考定理总结(八大定理)

立体几何常考定理总结(八大定理)一、线面平行的判定定理:线线平行线面平行文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行、符号语言:关键点:在平面内找一条与平面外的直线平行的线二、线面平行的性质定理:线面平行线线平行文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行、符号语言:关键点:需要借助一个经过已知直线的平面,接着找交线。
三、面面平行的判定定理:线面平行面面平行文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行、符号语言:关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
四、面面平行的性质定理: 面面平行线线平行、面面平行线面平行文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行、符号语言:关键点:找第三个平面与已知平面都相交,则交线平行文字语言:如果两个平面平行,那么其中一个平面内的任意一条直线平行于另一个平面、符号语言:关键:只要是其中一个平面内的直线就行五、线面垂直的判定定理:线线垂直线面垂直文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面、符号语言:关键点:在平面内找两条相交直线与所要证的直线垂直六、线面垂直的性质定理:线面垂直线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意一条直线、符号语言:关键点:往往线面垂直中的线线垂直需要用这个定理推出七、平面与平面垂直的判定定理:线面垂直面面垂直文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直、(如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:关键点:在需要证明的两个平面中找线面垂直八、平面与平面垂直的性质定理:面面垂直线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面、符号语言:关键点:先找交线,再在其中一个面内找与交线垂直的线。
高中数学立体几何判定定理与性质.docx
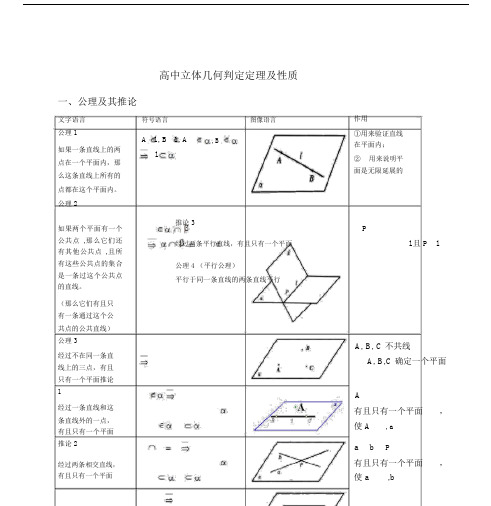
高中立体几何判定定理及性质一、公理及其推论文字语言符号语言图像语言公理 1A l ,B l , A, B如果一条直线上的两l点在一个平面内,那么这条直线上所有的点都在这个平面内。
公理 2作用①用来验证直线在平面内;②用来说明平面是无限延展的如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)公理 3经过不在同一条直线上的三点,有且只有一个平面推论1经过一条直线和这条直线外的一点,有且只有一个平面推论 2经过两条相交直线,有且只有一个平面推论 3经过两条平行直线,有且只有一个平面公理 4 (平行公理)平行于同一条直线的两条直线平行Pl 且 P lA, B, C 不共线A, B,C 确定一个平面A有且只有一个平面,使 A, aa b P有且只有一个平面,使 a,ba ∥ b有且只有一个平面,使 a,ba ∥ ba ∥ cb ∥c ①用来证明两个平面是相交关系;②用来证明多点共线,多线共点。
用来证明多点共面,多线共面用来证明线线平行二、平行关系文字语言(1)公理 4 (平行公理)平行于同一条直线的两条直线平行(2)线面平行的判定定理如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
(3)线面平行的性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(4)面面平行的判定定理如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行 .符号语言图像语言作用a ∥ ba ∥ cb ∥ ca ∥ ba a ∥bb∥b a ∥ baa ∥b ∥a b O∥ab(5)面面平行的判定如果两个平面垂直于同一条直线,那么这两个平面平行。
OOOO∥(6)面面平行的性质定理如果两个∥a a ∥ b平行平面同时和第三b个平面相交 ,那么它们的交线平行。
( 7)面面平行的性∥质如果两个平面平行 , a ∥那么其中一个平面内a的直线平行于另一个平面。
高中数学—立体几何知识点总结(精华版)

立体几何知识点一.基本概念和原理:1.公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线所成的角:范围为( 0°,90° ) esp.空间向量法两异面直线间距离: 公垂线段(有且只有一条) esp.空间向量法2平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)(规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为[0°,90°])斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直。
a和一个平面内的任意一条直线都垂直,就说直线a和平面互相垂直.直线a叫平面的垂线,平面叫做直线a的垂面。
直,那么这条直线垂直于这个平面。
如果两条直线同垂直于一个平面,那么这两条直线平行。
如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
行,那么这条直线和这个平面平行。
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
面,那么这两个平面平行。
如果两个平行平面同时和第三个平面相交,则交线平行。
8.(1)二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
立体几何公理定理总结

判定:一个平面内的两条相交直线与另一个平 面平行,则这两个平面平行.
性质:如果两个平行平面同时和第三个平面相 交,那么它们的交线平行.
整理课件
四.垂直
线线垂直:
平面上的判定 如果直线与平面垂直,则该直线与平面内任意
一条直线垂直.
线面垂直:定义:如果Fra bibliotek条直线垂直于一个平面内的任意 一条直线,那么就说这条直线和这个平面垂直.
线线位置关系:平行、相交、异面. 定理:空间中如果两个角的两边分别对应
平行,那么这两个角相等或互补. 线面位置关系:线在平面内、线与平面相
交、线与平面平行. 面面位置关系:平行、相交.
整理课件
三.平行
线面平行:
判定:平面外一条直线与此平面内的一条直线 平行,则该直线与此平面平行 .
性质:一条直线与一个平面平行,则过这条直 线的任一平面与此平面的交线与该直线平行.
整理课件
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
整理课件
立体几何公理定理总结
整理课件
一.公理
公理1:如果一条直线上两点在一个平面 内,那么这条直线在此平面内.
公理2:过不在一条直线上的三点,有且 只有一个平面.
公理3:如果两个不重合的平面有一个公 共点,那么它们有且只有一条过该点的 公共直线.
公理4:平行于同一条直线的两条直线平 行.
整理课件
二.空间位置关系
判定:一条直线与一个平面内的两条相交直线 都垂直,则该直线与此平面垂直.
性质:垂直于同一个平面的两条直线平行.
整理课件
面面垂直:
定义:两个平面相交,如果它们所成的二面角 是直二面角,就说这两个平面互相垂直.
1.立体几何中基本概念、公理、定理、推论

立体几何中基本概念、公理、定理、推论1. 三个公理和三条推论:(1)公理1:一条直线的两点在一个平面内,那么这条直线上的所有的点都在这个平面内.这是判断直线在平面内的常用方法.(2)公理2:如果两个平面有一个公共点,它们有无数个公共点,而且这无数个公共点都在同一条直线上.这是判断几点共线(证这几点是两个平面的公共点)和三条直线共点(证其中两条直线的交点在第三条直线上)的方法之一.(3)公理3:经过不在同一直线上的三点有且只有一个平面.推论1:经过直线和直线外一点有且只有一个平面.推论2:经过两条相交直线有且只有一个平面.推论3:经过两条平行直线有且只有一个平面.公理3和三个推论是确定平面的依据.2. 直观图的画法(斜二侧画法规则):在画直观图时,要注意:(1)使045x o y '''∠=(或0135),x o y '''所确定的平面表示水平平面.(2)已知图形中平行于x 轴和z 轴的线段,在直观图中保持长度和平行性不变,平行于y 轴的线段平行性不变,但在直观图中其长度为原来的一半.3. 公理4:平行于同一直线的两直线互相平行.(即平行直线的传递性)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. (此定理说明角平移后大小不变) 若无“方向相同”,则这两个角相等或互补.4. 空间直线的位置关系:(1)相交直线――有且只有一个公共点.(2)平行直线――在同一平面内,没有公共点.(3)异面直线――不在同一平面内,也没有公共点.5. 异面直线⑴异面直线定义:不同在任何一个平面内的两条直线叫做异面直线.⑵异面直线的判定:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.⑶异面直线所成的角:已知两条异面直线a 、b ,经过空间任一点O 作直线a '、b ',使//a a '、//b b ',把a '与b '所成的锐角(或直角)叫做异面直线a 、b 所成的角(或夹角).⑷异面直线所成的角的求法:首先要判断两条异面直线是否垂直,若垂直,则它们所成的角为900;若不垂直,则利用平移法求角,一般的步骤是“作(找)—证—算”.注意,异面直线所成角的范围是π0,2⎛⎤⎥⎝⎦;求异面直线所成角的方法:计算异面直线所成角的关键是平移(中点平移,顶点平移以及补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,以便易于发现两条异面直线间的关系)转化为相交两直线的夹角. ⑸两条异面直线的公垂线:①定义:和两条异面直线都垂直且相交的直线,叫做异面直线的公垂线;两条异面直线的公垂线有且只有一条.而和两条异面直线都垂直的直线有无数条,因为空间中,垂直不一定相交.②证明:异面直线公垂线的证明常转化为证明公垂线与两条异面直线分别垂直.⑹两条异面直线的距离:两条异面直线的公垂线在这两条异面直线间的线段的长度.6. 直线与平面的位置关系:(1)直线在平面内;(2)直线与平面相交.其中,如果一条直线和平面内任何一条直线都垂直,那么这条直线和这个平面垂直.注意:任一条直线并不等同于无数条直线;(3)直线与平面平行.其中直线与平面相交、直线与平面平行都叫作直线在平面外.平面与平面的位置关系:(1)平行――没有公共点;(2)相交――有一条公共直线.7.线面平行、面面平行⑴直线与平面平行的判定定理: 如果不在一个平面(α)内的一条直线(l )和平面(α)内的一条直线(m )平行,那么这条直线(l )和这个平面(α)平行.,,////l m l m l ααα⊄⊂⇒ (作用:线线平行⇒线面平行)⑵直线与平面平行的性质定理:如果一条直线(l )和一个平面(α)平行,经过这条直线(l )的平面(β)和这个平面(α)相交(设交线是m ),那么这条直线(l )和交线(m )平行.//,,//l l m l m αβαβ⊂⋂=⇒ (作用: 线面平行⇒线线平行)⑶平面与平面平行的判定定理:如果一个平面(β)内有两条相交直线(,a b )分别平行于另一个平面(α),那么这两个平面(,βα)平行.,,,//,////a b a b P a b ββααβα⊂⊂⋂=⇒ (作用:线面平行⇒面面平行)推论:如果一个平面(β)内有两条相交直线(,a b )分别平行于另一个平面(α)内的两条直线(,a b ''), 那么这两个平面(,βα)平行.,,,,,//,////a b a b P a b a a b b ββααβα''''⊂⊂⋂=⊂⊂⇒(作用: 线线平行⇒面面平行) ⑷平面与平面平行的性质定理:如果两个平行平面(,αβ)同时与第三个平面(γ)相交(设交线分别是,a b ),那么它们的交线(,a b )平行.//,,//a b a b αβαγβγ⋂=⋂=⇒ (作用: 面面平行⇒线线平行)推论:如果两个平面(,αβ)平行,则一个平面(α)内的一条直线(a )平行于另一个平面(β). //,//a a αβαβ⊂⇒ (作用: 面面平行⇒线面平行)8.线线垂直、线面垂直、面面垂直⑴直线与平面垂直的判定定理:如果一条直线(l )和一个平面(α)内的两条相交直线(,m n )都垂直,那么这条直线(l )垂直于这个平面(α).,,,,l m l n m n m n P l ααα⊥⊥⊂⊂⋂=⇒⊥ (作用: 线线垂直⇒线面垂直)⑵直线与平面垂直的性质定理:如果一条直线(l )和一个平面(α)垂直,那么这条直线(l )和这个平面(α)内的任意一条直线(m )垂直.,l m l m αα⊥⊂⇒⊥ .⑶三垂线定理: 其作用是证两直线异面垂直和作二面角的平面角①定理: 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.②逆定理:在平面内的一条直线,如果它和这个平面的一条斜线,那么它也和这条斜线在平面内的射影垂直.(作用: 线线垂直⇒线线垂直)⑷平面与平面垂直的判定定理: 如果一个平面(α)经过另一个平面(β)的一条垂线(l ),那么这两个平面(,αβ)互相垂直.,l l βααβ⊥⊂⇒⊥ (作用: 线面垂直⇒面面垂直)⑸平面与平面垂直的性质定理:如果两个平面(,αβ)垂直,那么在一个平面(α)内垂直于它们交线(m )的直线(l )垂直于另一个平面(β).,,,m l l m l αβαβαβ⊥⋂=⊂⊥⇒⊥ (作用: 面面垂直⇒线面垂直)9. 直线和平面所成的角⑴最小角定理:平面的斜线和它在平面内的射影所成的角,是这条斜线和这个平面内任意一条直线所成的角中最小的角.满足关系式:12cos cos cos θθθ=⋅θ是平面的斜线与平面内的一条直线所成的角;1θ是平面的斜线与斜线在平面内的射影所成的角;2θ是斜线在平面内的射影与平面内的直线所成的角.⑵直线和平面所成的角: 平面的一条斜线和它在平面内的射影所成的锐角,叫这条直线和这个平面所成的角. 范围:[0,90]10.二面角⑴二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,每个半平面叫做二面角的面.棱为l ,两个面分别是α、β的二面角记为l αβ--.二面角的范围:[0,]π⑵二面角的平面角:在二面角的棱上取一点,在二面角的面内分别作两条垂直于棱的射线,这两条射线所成的角叫做二面角的平面角.11.空间距离⑴点到平面的距离:一点到它在一个平面内的正射影的距离.⑵直线到与它平行平面的距离:一条直线上的任一点到与它平行的平面的距离.⑶两个平行平面的距离:两个平行平面的公垂线段的长度.⑷异面直线的距离12. 多面体有关概念:(1)多面体:由若干个平面多边形围成的空间图形叫做多面体.围成多面体的各个多边形叫做多面体的面.多面体的相邻两个面的公共边叫做多面体的棱.(2)多面体的对角线:多面体中连结不在同一面上的两个顶点的线段叫做多面体的对角线.(3)凸多面体:把一个多面体的任一个面伸展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫做凸多面体.13.棱柱⑴棱柱的定义: 有两个面互相平行,其余每相邻两个面的交线互相平行,这样的多面体叫棱柱.两个互相平行的面叫棱柱的底面(简称底);其余各面叫棱柱的侧面;两侧面的公共边叫棱柱的侧棱;两底面所在平面的公垂线段叫棱柱的高(公垂线段长也简称高).⑵棱柱的分类:侧棱不垂直于底面的棱柱叫斜棱柱.侧棱垂直于底面的棱柱叫直棱柱.底面是正多边形的直棱柱叫正棱柱.棱柱的底面可以是三角形、四边形、五边形……这样的棱柱分别叫三棱柱、四棱柱、五棱柱……⑶棱柱的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等,直棱柱的各个侧面都是矩形,正棱柱的各个侧面都是全等的矩形.②与底面平行的截面是与底面对应边互相平行的全等多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.⑷平行六面体、长方体、正方体:底面是平行四边形的四棱柱是平行六面体.侧棱与底面垂直的平行六面体叫直平行六面体,底面是矩形的直平行六面体叫长方体,棱长都相等的长方体叫正方体.⑸①平行六面体的任何一个面都可以作为底面;②平行六面体的对角线交于一点,并且在交点处互相平分;③平行六面体的四条对角线的平方和等于各棱的平方和;④长方体的一条对角线的平方等于一个顶点上三条棱长的平方和.14.棱锥⑴棱锥的定义: 有一个面是多边形,其余各面是有一个公共顶点的三角形,这样的多面体叫棱锥其中有公共顶点的三角形叫棱锥的侧面;多边形叫棱锥的底面或底;各侧面的公共顶点()S ,叫棱锥的顶点,顶点到底面所在平面的垂线段()SO ,叫棱锥的高(垂线段的长也简称高).⑵棱锥的分类:(按底面多边形的边数)分别称底面是三角形,四边形,五边形……的棱锥为三棱锥,四棱锥,五棱锥…… ⑶棱锥的性质:定理:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积比等于顶点到截面的距离与棱锥高的平方比. 中截面:经过棱锥高的中点且平行于底面的截面,叫棱锥的中截面⑷正棱锥:底面是正多边形,顶点在底面上的射影是底面的中心的棱锥叫正棱锥. ⑸正棱锥的性质:①正棱锥的各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高(叫斜高)也相等。
立体几何所有的定理大总结

(4)借助法:两条平行直线,若其中一条垂直于一个平面,则另一条必定也垂直于这个平面。
{}
(5)借助法:一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
{}
“平行”的判定:
(1)定义法:如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
(2)判定法:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。(线线平行线面平行)
相交
共面垂直()
平行()
“异面垂直”的判定:
(1)定义法:如ห้องสมุดไป่ตู้两条异面直线所成的角是直角,那么这两条异面直线互相垂直。
(2)其它法:三垂线逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直。
{}
“共面垂直”的判定:
(1)定义法:如果两条直线所成的角是直角,那么这两条直线互相垂直。
(6) 直二面角:平面角是直角的二面角叫做直二面角。
1.定义:从一条直线出发的两个半平面所组成的图形叫做二面角。
2.表示:如下图,可记作α-AB-β或P-AB-Q
3.范围为【0°,180°】
(5)六种距离
1.点到点的距离:两点之间的线段PQ的长。
2.点到线的距离:过P点作,交于,线段的长。
3.点到面的距离:过P点作,交于,线段的长。
3.经过平面外一点,有且只有一条直线和已知平面垂直。
4.经过平面外一点,有无数个平面和已知平面垂直。
5.经过直线外一点,有且只有一条直线和已知直线平行。
6.经过直线外一点,有无数个平面和已知直线平行。
7.经过直线外一点,有且只有一条直线和已知直线垂直。
8.经过直线外一点,有无数个平面和已知直线垂直。
高中数学—立体几何知识点总结(精华版)

立体几何知识点一.根本概念和原理:1.公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线所成的角:范围为( 0°,90° ) esp.空间向量法两异面直线间距离: 公垂线段(有且只有一条) esp.空间向量法2平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)〔规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为[0°,90°]〕斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直。
a和一个平面内的任意一条直线都垂直,就说直线a和平面互相垂直.直线a叫平面的垂线,平面叫做直线a的垂面。
直,那么这条直线垂直于这个平面。
如果两条直线同垂直于一个平面,那么这两条直线平行。
如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
行,那么这条直线和这个平面平行。
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
面,那么这两个平面平行。
行。
8.〔1〕二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
二面角的取值范围为[0°,180°]〔2〕二面角的平面角:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
立体几何公理定理总结

一.公理
公理1:如果一条直线上两点在一个平面 内,那么这条直线在此平面内.
公理2:过不在一条直线上的三点,有且 只有一个平面.
公理3:如果两个不重合的平面有一个公 共点,那么它们有且只有一条过该点的 公共直线.
公理4:平行于同一条直线的两条直线平 行.
二.空间位置关系
面面平行:
判定:一个平面内的两条相交直线与另一个平 面平行,则这两个平面平行.
性质:如果两个平行平面同时和第三个平面相 交,那么它们的交线平行.
四.垂直
线线垂直:
平面上的判定 如果直线与平面垂直,则该直线与平面内任意
一条直线垂直.
线面垂直:
定义:如果一条直线垂直于一个平面内的任意 一条直线,那பைடு நூலகம்就说这条直线和这个平面垂直.
判定:一条直线与一个平面内的两条相交直线 都垂直,则该直线与此平面垂直.
性质:垂直于同一个平面的两条直线平行.
面面垂直:
定义:两个平面相交,如果它们所成的二面角 是直二面角,就说这两个平面互相垂直.
判定:一个平面经过另一个平面的一条垂线, 则这两个平面垂直.
性质:两个平面互相垂直,则一个平面内垂直 于交线的直线垂直于另一个平面.
线线位置关系:平行、相交、异面. 定理:空间中如果两个角的两边分别对应
平行,那么这两个角相等或互补. 线面位置关系:线在平面内、线与平面相
交、线与平面平行. 面面位置关系:平行、相交.
三.平行
线面平行:
判定:平面外一条直线与此平面内的一条直线 平行,则该直线与此平面平行 .
性质:一条直线与一个平面平行,则过这条直 线的任一平面与此平面的交线与该直线平行.
立体几何中的所有结论

第九章:直线、平面、简单几何体小结一、重要的概念和定理 1.公理和推论公理1.如果一条直线上的两个点在一个平面内,那么这条直线上的所有点都在 这个平面内。
作用:判断直线在平面内的依据。
公理2.如果两个平面有一个公共点,那么它们还有其它公共点,且这些公共点的集合是通过该公共点的一条直线。
作用:判断两个平面相交和共线的依据。
公理3.经过不在同一直线上的三个点,有且只 有一个平面。
推论1.经过一条直线和这条直线外一点,有且 作用:确定平面的依据。
只有一个平面。
推论2.经过两条相交直线,有且只有一个平面。
推论3.经过两条平行直线,有且只有一个平面。
公理4.同平行于一条直线的两条直线互相平行。
作用:判断平行的依据。
2.概念⑴直线与直线 ①异面直线:不在任何一个平面内的两条直线叫做异面直线。
②异面直线所成角:如果a 、b 是异面直线,经过空间任意一点0作a '∥a ,b '∥b ,那么把a '和b '所成的锐角(或直角)叫做异面直线a 和b 所成的角。
如果两条异面直线所成的角是直角,就称这两条异面直线互相垂直。
显然若设异面直线所成角为α,则0<α≤2π。
③异面直线间的距离:和异面直线都垂直相交的直线叫做两条异面直线的公垂线。
两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离。
⑵直线和平面①直线和平面平行:如果一条直线和一个平面没有公共点,那么就说这条直线和这个平面平行。
②直线和平面垂直:如果一条直线和一个平面内的任何一条直线都垂直,那么就说这条直线和这个平面垂直,这条直线叫做平面的垂线,平面叫做直线的垂面。
③射影:自一点P 向平面α引垂线,垂足P ' 叫做点P 在平面α内的正射影(简称射影)。
如果图形F 上的所有点在一平面内射影构成图形F ',则F '叫做图形F 在这个平面内的射影。
过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面上的射影。
立体几何公理、定理推论汇总
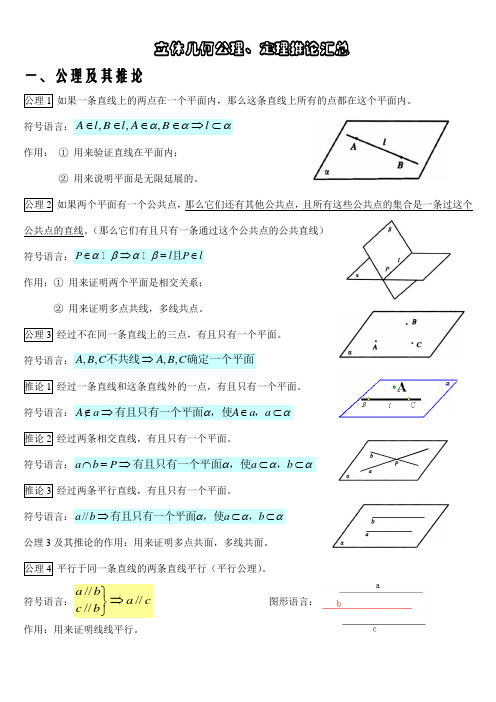
立体几何公理、定理推论汇总一、公理及其推论 公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
符号语言:,,,A l B l A B l ααα∈∈∈∈⇒⊂作用: ① 用来验证直线在平面内;② 用来说明平面是无限延展的。
公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)符号语言:P l P l αβαβ∈⇒=∈I I 且作用:① 用来证明两个平面是相交关系;② 用来证明多点共线,多线共点。
公理3 经过不在同一条直线上的三点,有且只有一个平面。
符号语言:,,,,A B C A B C ⇒不共线确定一个平面推论1 经过一条直线和这条直线外的一点,有且只有一个平面。
符号语言:A a A a a αα∉⇒∈⊂有且只有一个平面,使,推论2 经过两条相交直线,有且只有一个平面。
符号语言:a b P a b ααα⋂=⇒⊂⊂有且只有一个平面,使,推论3 经过两条平行直线,有且只有一个平面。
符号语言://a b a b ααα⇒⊂⊂有且只有一个平面,使,公理3及其推论的作用:用来证明多点共面,多线共面。
公理4 平行于同一条直线的两条直线平行(平行公理)。
符号语言://////a b a c c b ⎫⇒⎬⎭图形语言:作用:用来证明线线平行。
二、平行关系 公理4 平行于同一条直线的两条直线平行(平行公理)。
(1) 符号语言://////a b a c c b ⎫⇒⎬⎭ 图形语言:线面平行的判定定理 如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
(2)符号语言:////a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭ 图形语言:线面平行的性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(3)符号语言:////a b a a b βαβα⎫⎪⊂⇒⎬⎪=⎭I图形语言:面面平行的判定定理 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(4)符号语言://(/,///),a b b b O a a ββαααβ⊂⊂=⎫⎪⇒⎬⎪⎭I 图形语言: 面面平行的判定 如果两个平面垂直于同一条直线,那么这两个平面平行。
立体几何公理定理汇总

立体几何公理定理汇总公理1:对于任意两条不平行的直线,它们在平面上至多有一个交点。
公理2:对于任意一条直线和一点不在该直线上,有且只有一条直线通过该点且与给定直线平行。
公理3:对于任意一条直线,可以在给定直线上任取一点和一个长度,且可以在给定方向上延展。
公理4:对于任意两点之间存在一条线段连接这两个点。
公理5:给定一条线段和一点,可以以该点为中心,线段长度为半径画出一个唯一的圆。
公理6:对于任意两圆上的任意两点,存在且仅存在一条直线通过这两点且与两圆相切。
公理7:对于任意三个不共线的点,存在一条唯一的平面通过这三点。
公理8:对于任意一个平面,存在一个不在该平面上的点,且通过此点的直线与平面的交点至少有两个。
定理1:平行公理的逆定理,若两条直线与第三条直线相交,在同一边的内角和小于两个直角(180度)。
定理2:对于一个未与其他直线平行的直线,若有直线通过它的两点,则直线与此未与其他直线平行的直线相交。
定理3:直线截断定理,若两个交叉相连的线段的两头均与另一直线相交,则两个线段之和大于第三个线段。
定理4:三角形内角和定理,三角形三个内角的和等于一个平角(180度)。
定理5:直角三角形的勾股定理,直角三角形的斜边的平方等于其他两边的平方和。
定理6:正方体对角线的长度等于边长的根号2倍。
定理7:四面体的四个顶点可成一个平面,要求四个面都内含立体。
定理8:正交面定理,两个平面垂直相交的充要条件是它们的法向量互相垂直。
定理9:平行四边形的对角线互相平分。
定理10:球的内切四面体体积公式为:V=(a^3√2)/12,其中a为四面体边长。
这些公理和定理是立体几何学中经常用到的基本准则,通过运用这些准则可以推导出更多的立体几何定理和性质。
在实际应用中,这些定理和公理可以帮助我们解决立体几何问题,从而更好地理解和分析三维空间中的形状和结构。
立体几何八大定理
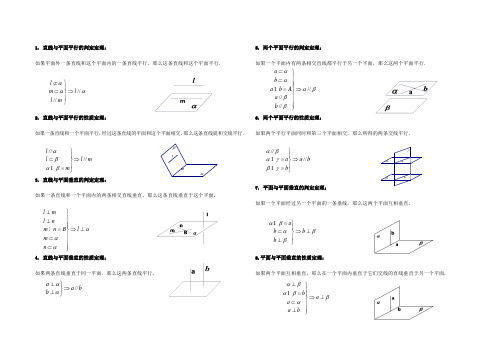
1. 直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.2. 直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.m l m l l ////⇒⎪⎭⎪⎬⎫=⊂βαβα 3. 直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面.l ml n m n B l m n ααα⊥⎫⎪⊥⎪⎪=⇒⊥⎬⎪⊂⎪⊂⎪⎭4. 直线与平面垂直的性质定理:如果两条直线垂直于同一平面,那么这两条直线平行. b a b a //⇒⎭⎬⎫⊥⊥αα5. 两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.6. 两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行.b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα7. 平面与平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.8.平面与平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.βαmlβαββαα//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=⊂⊂b a A b a b aββαβα⊥⇒⎪⎭⎪⎬⎫⊥⊂=b b b a ααα////l m l m l ⇒⎪⎭⎪⎬⎫⊂⊄γbaβαβαβαβα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊥⊂=⊥a b a a b。
立体几何公式定理表

《立体几何》主要公式与定理:
主要公式:(*引申公式)
=
S 直棱柱侧面积
=
S 正棱锥侧 =
=S 正棱台侧 = S =扇形面积 = S =圆柱侧 S =圆锥侧 *S =圆台侧 (找出三者联系)
V =立方体 *=L 立方体对角线长
*=R 立方体外接球 *=R 立方体棱切球 *=R 立方体内切球 (找出三者比例关系)
V =长方体 *=L 长方体对角线长 *=R 长方体外接球
*从长方体对角线的一个端点沿表面到另一个端点的最短距离=
V =柱体 V =锥体 V =台体 (找出三者联系) V =圆柱 V =圆锥 V =圆台 (找出三者联系) S =球 =V 球 (二者有何关系?)
*=h 正四面体 *=S 正四面体 *=V 正四面体 *=R 正四面体内切球 *=R 正四面体外接球 (设正四面体的棱长为a ) 主要定理(立体几何藏宝图):
17、等角定理 18、平行平面截线段成比例定理
19-24、平面的3个基本性质及3个推论(课本35-37页)。
立体几何公式定理大全

立体几何公式定理大全立体几何是研究空间中各种图形的性质和关系的分支学科,其主要研究对象是立体图形的特征、构造和性质。
在立体几何的学习过程中,我们需要掌握一些重要的公式和定理,以便解决与立体图形相关的问题。
下面是一些常用的立体几何公式和定理的详细介绍:1.体积公式:-直角三棱柱的体积公式:体积=底面积×高-正方体的体积公式:体积=边长^3-直角三角柱的体积公式:体积=面积×高-圆柱的体积公式:体积=底面积×高-锥体的体积公式:体积=1/3×底面积×高-球体的体积公式:体积=4/3×π×半径^32.表面积公式:-正方体的表面积公式:表面积=6×边长^2-正方体的棱长公式:棱长=根号下(表面积/6)-正方体的对角线长度:对角线长度=边长×根号下(3)-直角三角柱的表面积公式:表面积=(底面积+两倍底面积的开方)+2×底面积-圆柱的表面积公式:表面积=2×π×半径×高+2×π×半径^2-锥体的表面积公式:表面积=π×半径×斜高+π×半径^2-球体的表面积公式:表面积=4×π×半径^23.空间几何定理:-平行线截立体的定理:如果两组平行线截取同一直线的长度成比例,那么这两组平行线截取的其他直线的长度也成比例。
-空间角平分线的定理:空间中的角可由角平分线平分为两个等角。
-立体的等分线定理:平面将一个立体分为两个等体积的立体时,它将该立体的底面分为两个等面积的底面,并且过底面上的任意一点,以该点为顶点作平行于底面的面将该立体分为两个等体积的立体。
-线与面的关系定理:一条不等于底面的直线与底面所围的锥交于一点,但与底面围成的锥不是等体积的。
-垂直平分面定理:垂直与一条直线的平面把这条直线平分为两段,它把这条直线的平面所围的任一立体分为两个等体积的立体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.公理
ቤተ መጻሕፍቲ ባይዱ
公理1:如果一条直线上两点在一个平面 内,那么这条直线在此平面内. 公理2:过不在一条直线上的三点,有且 只有一个平面. 公理3:如果两个不重合的平面有一个公 共点,那么它们有且只有一条过该点的 公共直线. 公理4:平行于同一条直线的两条直线平 行.
二.空间位置关系
线线位置关系:平行、相交、异面. 定理:空间中如果两个角的两边分别对应 平行,那么这两个角相等或互补. 线面位置关系:线在平面内、线与平面相 交、线与平面平行. 面面位置关系:平行、相交.
三.平行
线面平行:
判定:平面外一条直线与此平面内的一条直线 平行,则该直线与此平面平行 . 性质:一条直线与一个平面平行,则过这条直 线的任一平面与此平面的交线与该直线平行. 判定:一个平面内的两条相交直线与另一个平 面平行,则这两个平面平行. 性质:如果两个平行平面同时和第三个平面相 交,那么它们的交线平行.
面面平行:
四.垂直
线线垂直:
平面上的判定 如果直线与平面垂直,则该直线与平面内任意 一条直线垂直. 定义:如果一条直线垂直于一个平面内的任意 一条直线,那么就说这条直线和这个平面垂直. 判定:一条直线与一个平面内的两条相交直线 都垂直,则该直线与此平面垂直. 性质:垂直于同一个平面的两条直线平行.
线面垂直:
面面垂直:
定义:两个平面相交,如果它们所成的二面角 是直二面角,就说这两个平面互相垂直. 判定:一个平面经过另一个平面的一条垂线, 则这两个平面垂直. 性质:两个平面互相垂直,则一个平面内垂直 于交线的直线垂直于另一个平面.
