《最短路径问题》练习题
(完整版)最短路径习题
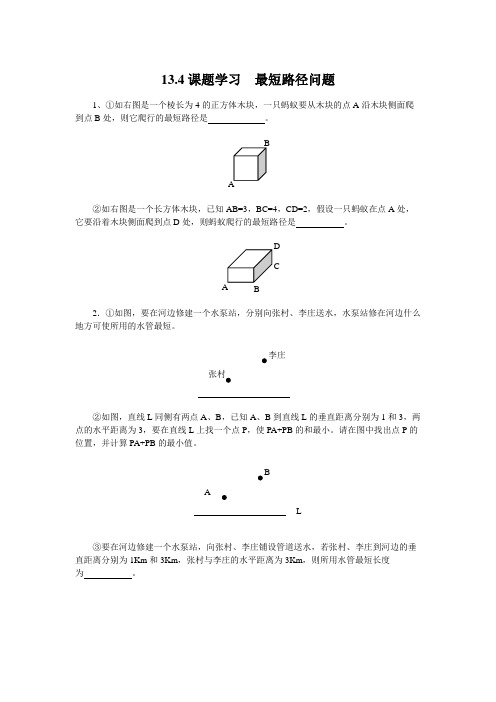
13.4课题学习最短路径问题1、①如右图是一个棱长为4的正方体木块,一只蚂蚁要从木块的点A沿木块侧面爬到点B 处,则它爬行的最短路径是。
BA②如右图是一个长方体木块,已知AB=3,BC=4,CD=2,假设一只蚂蚁在点A处,它要沿着木块侧面爬到点D处,则蚂蚁爬行的最短路径是。
DCA B2.①如图,要在河边修建一个水泵站,分别向张村、李庄送水,水泵站修在河边什么地方可使所用的水管最短。
李庄张村②如图,直线L同侧有两点A、B,已知A、B到直线L的垂直距离分别为1和3,两点的水平距离为3,要在直线L上找一个点P,使PA+PB的和最小。
请在图中找出点P的位置,并计算PA+PB的最小值。
BAL③要在河边修建一个水泵站,向张村、李庄铺设管道送水,若张村、李庄到河边的垂直距离分别为1Km和3Km,张村与李庄的水平距离为3Km,则所用水管最短长度为。
3.如图是一个长方体木块,已知AB=5,BC=3,CD=4,假设一只蚂蚁在点A 处,它要沿着木块侧面爬到点D处,则蚂蚁爬行的最短路径是 。
4.现要在如图所示的圆柱体侧面A 点与B 点之间缠一条金丝带(金丝带的宽度忽略不计),圆柱体高为6cm ,底面圆周长为16cm ,则所缠金丝带长度的最小值为 。
5.如图是一个圆柱体木块,一只蚂蚁要沿圆柱体的表面从A 点爬到点B 处吃到食物,知圆柱体的高为5 cm ,底面圆的周长为24cm ,则蚂蚁爬行的最短路径为 。
6.正方形ABCD 的边长为8,M 在DC 上,且DM =2,N 是AC 上的一动点,DN +MN 的最小值为 。
7.在菱形ABCD 中,AB=2,∠BAD=60°,点E 是AB 的中点,P 是对角线AC 上的一个动点,则PE+PB 的最小值为 。
张村李庄ABCDABAB图(2)8.如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值为____ ___。
13.4轴对称最短路径问题专题练习人教版2024—2025学年八年级上册

13.4轴对称最短路径问题专题练习人教版2024—2025学年八年级上册题型一、两定点一动点作图问题1.如图,A、B是两个居民小区,快递公司准备在公路l上选取点P处建一个服务中心,使P A+PB最短.下面四种选址方案符合要求的是()A.B.C.D.2.如图,直线l是一条河,P,Q是两个村庄,欲在l上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是()A.B.C.D.3.如图,直线l是一条公路,A、B是两个村庄.欲在l上的某点处修建一个车站,直接向A、B两地提供乘车服务.现有如下四种建设方案,图中实线表示铺设的行走道路,则铺设道路最短的方案是()A.B.C.D.4.为了促进A,B两小区居民的阅读交流,区政府准备在街道l上设立一个读书亭C,使其分别到A,B两小区的距离之和最小,则下列作法正确的是()A.B.C.D.5.如图,在正方形网格中有M,N两点,在直线l上求一点P使PM+PN最短,则点P应选在()A.A点B.B点C.C点D.D点题型二、两定点一动点求线段和最小值1.如图,在△ABC中,∠ABC=60°,AD⊥BC于D点,AB=12,.若点E、F分别是线段AD、线段AB上的动点,则BE+EF的最小值是()A.6B.12C.D.2.如图,在△ABC中,AB=AC,BC=4,面积是14,AC的垂直平分线EF分别交AC,AB边于E、F点.若点D为BC边的中点,点M为线段EF上一动点,则CM+DM的最小值为()A.21B.7C.6D.3.53.如图,在△ABC中,∠A=90°,AB=6,AC=8,BC=10,CD平分∠BCA交AB于点D,点P,Q分别是CD,AC上的动点,连接AP,PQ,则AP+PQ的最小值是()A.6B.5C.4.8D.44.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值()A.2.4B.4C.5D.4.85.如图,点N在等边△ABC的边BC上,CN=6,射线BD⊥BC,垂足为点B,点P是射线BD上一动点,点M是线段AC上一动点,当MP+NP的值最小时,CM=7,则AC的长为()A.8B.9C.10D.126.如图,已知等边△ABC的边长为4,点D,E分别在边AB,AC上,AE=2BD.以DE为边向右作等边△DEF,则AF+BF的最小值为()A.4B.4C.4D.47.数形结合是重要的数学思想,借助图形,求解的最小值为.8.如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC,已知线段AB=4,DE=2,BD=8,设CD=x.(1)用含x的代数式表示AC+CE的长;(2)请问点C满足什么条件时,AC+CE最小?最小为多少?(3)根据(2)中的规律和结论,请构图求代数式的最小值.9.如图,A,B两个小镇在河流CD的同侧,到河的距离分别为AC=6千米,BD=14千米,且CD=15千米,现要在河边建一自来水厂,同时向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD上选择水厂的位置M,使铺设水管的费用最省,并求出总费用是多少?题型三、两定点一动点求周长最小值1.如图,在△ABC中,直线m是线段BC的垂直平分线,点P是直线m上的一个动点.若AB=7,AC=4,BC=5,则△APC周长的最小值是()A.12B.11C.9D.72.如图,在△ABC中,AB=AC,BC=4,面积是12,AC的垂直平分线EF分别交AB,AC边于点E,F.若点D为BC边的中点,点P为线段EF上一动点,则△PCD周长的最小值为()A.8B.3C.6D.43.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是()A.(0,3)B.(0,2)C.(0,1)D.(0,0)4.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5,D、E、F分别是AB、BC、AC边上的动点,则△DEF的周长的最小值是()A.2.5B.3.5C.4.8D.65.如图,在△ABC中,∠ACB=90°,以AC为底边在△ABC 外作等腰△ACD,过点D作∠ADC的平分线分别交AB,AC于点E,F.若BC=5,∠CAB=30°,点P是直线DE 上的一个动点,则△PBC周长的最小值为()A.15B.17C.18D.206.如图,在平面直角坐标系中,点P的坐标为(2,3),P A⊥x轴,PB⊥y轴,C是OA的中点,D是OB上的一点,当△PCD的周长最小时,点D的坐标是()A.(0,1)B.C.D.(0,2)7.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为______8.如图,点A(1,﹣1),B(2,﹣3)(1)点A关于x轴的对称点的坐标为.(2)若点P为坐标轴上一点,当△APB的周长最小时,点P的坐标为.三、一定点二动点线段或周长问题1.如图,在五边形中,∠BAE=140°,∠B=∠E=90°,在边BC,DE上分别找一点M,N,连接AM,AN,MN,则当△AMN的周长最小时,求∠AMN+∠ANM的值是()A.100°B.140°C.120°D.80°2.如图,∠AOB=30°,P是∠AOB内的一个定点,OP=12cm,C,D分别是OA,OB上的动点,连接CP,DP,CD,则△CPD周长的最小值为.3.如图,∠AOB=20°,M,N分别为OA,OB上的点,OM=ON=3,P,Q分别为OA,OB上的动点,则MQ+PQ+PN的最小值为.四、一定点二动点角度问题1.如图,在四边形ABCD中,∠C=40°,∠B=∠D =90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为()A.100°B.90°C.70°D.80°2,如图,∠MON=45°,P为∠MON内一点,A 为OM上一点,B为ON上一点,当△P AB的周长取最小值时,∠APB的度数为()A.45°B.90°C.100°D.135°3.如图,点P为∠AOB内一点,点M,N分别是射线OA,OB上一点,当△PMN的周长最小时,∠OPM=50°,则∠AOB的度数是()A.55°B.50°C.40°D.45°4.已知点P在∠MON内.如图1,点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG、OH、OP.(1)若∠MON=50°,求∠GOH的度数;(2)如图2,若OP=6,当△P AB的周长最小值为6时,求∠MON的度数.五、二定点二动点1.如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为()A.10°B.20°C.40°D.60°2.如图,在四边形ABCD中,∠B=90°,AB∥CD,BC=3,DC=4,点E在BC上,且BE=1,F,G为边AB上的两个动点,且FG=1,则四边形DGFE的周长的最小值为.3.如图,锐角∠MON内有一定点A,连结AO,点B、C分别为OM、ON边上的动点,连结AB、BC、CA,设∠MON=α(0°<α<90°),当AB+BC+CA取得最小值时,则∠BAC=.(用含α的代数式表示)4.如图,在平面直角坐标系中,O为原点,点A,C,E的坐标分别为(0,4),(8,0),(8,2),点P,Q是OC边上的两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐标为()A.(2,0)B.(3,0)C.(4,0)D.(5,0)5.已知B,C是平面直角坐标系中与x轴平行且距离x轴1个单位长度的直线上的两个动点(点B在点C左侧),且BC=2,若有点A(0,5)和点D(3,3),则当AB+BC+CD的值最小时,点C的坐标为.6.如图,在平面直角坐标系中,已知点A(0,1),B(4,0),C(m+2,2),D(m,2),当四边形ABCD的周长最小时,m的值是()A.B.C.1D.7.如图,在△ABC中,AB=AC,∠A=90°,点D,E是边AB上的两个定点,点M,N分别是边AC,BC上的两个动点.当四边形DEMN的周长最小时,∠DNM+∠EMN的大小是()A.45°B.90°C.75°D.135°8.如图,∠MON=α,α<30°,点A为ON上一定点,点C为ON上一动点,B,D为OM上两动点,当AB+BC+CD最小时,∠BCD+∠ABC=()A.5αB.6αC.90°﹣αD.180°﹣α9.如图,直线l 1,l 2表示一条河的两岸,且l 1∥l 2.现要在这条河上建一座桥(桥与河的两岸相互垂直),使得从村庄A 经桥过河到村庄B 的路程最短,应该选择路线( )A .B .C .D .10.如图,直线l 1、l 2表示一条河的两岸,且l 1∥l 2,现要在这条河上建一座桥,使得村庄A 经桥过河到村庄B 的路程最短,现两位同学提供了两种设计方案,下列说法正确的是( )方案一:①将点A 向上平移d 得到A ';②连接A 'B 交l 1于点M ;③过点M 作MN ⊥l 1,交l 2于点N ,MN 即桥的位置.方案二:①连接AB 交l 1于点M ;②过点M 作MN ⊥l 1,交l 2于点N .MN 即桥的位置.A .唯方案一可行B .唯方案二可行C .方案一、二均可行D .方案一、二均不可行六、线段差的最大值1.如图,在正方形ABCD 中,AB =8,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且BM =6.P为对角线BD上一点,则PM﹣PN的最大值为()A.2B.3C.D.2.如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,P为CD上的动点,则|P A﹣PB|的最大值为.七、多条线段和的最小值1.如图所示,已知A、B、C、D,请在图中找出一点P,使P A+PB+PC+PD最小.2.如图,在平面直角坐标系中,点E在原点,点D(0,2),点F(1,0),线段DE和EF构成一个“L”形,另有点A(﹣1,5),点B(﹣1,﹣1),点C(6,﹣1),连AD,BE,CF.若将这个“L”形沿y轴上下平移,当AD+DE+BE 的值最小时,E点坐标为;若将这个“L”形沿x轴左右平移,当AD+DE+EF+CF的值最小时,E点坐标为.。
最短路径练习题

最短路径练习题一、选择题:1. 在图论中,最短路径问题是指在加权图中找到两个顶点之间的最短路径,以下哪个算法不是用于解决最短路径问题的?A. Dijkstra算法B. Bellman-Ford算法C. Prim算法D. A*搜索算法2. 以下哪个选项不是Dijkstra算法的前提条件?A. 图必须是有向图B. 所有边的权重必须非负C. 图中不能有负权重边D. 图可以是无向图3. 以下哪个算法可以处理包含负权重边的图?A. Dijkstra算法B. Bellman-Ford算法C. Floyd-Warshall算法D. A*搜索算法4. Floyd-Warshall算法的时间复杂度是:A. O(n^2)B. O(n^3)C. O(nlogn)D. O(n)5. 以下哪个选项是Dijkstra算法的步骤之一?A. 从起点开始,不断扩展最短路径树B. 从终点开始,不断扩展最短路径树C. 从每个顶点开始,计算到其他顶点的最短路径D. 从每个顶点开始,不断扩展最短路径树二、填空题:1. 在Dijkstra算法中,初始时,除了起点的最短路径为0外,其他所有顶点的最短路径都设为________。
2. Dijkstra算法中,当所有顶点都被访问过之后,算法结束,此时得到的距离数组中存储的是从起点到每个顶点的________。
3. Bellman-Ford算法可以处理图中的负权重边,但该算法不能处理图中的________。
4. Floyd-Warshall算法是一种动态规划算法,它可以在O(n^3)的时间复杂度内计算出图中所有顶点对之间的最短路径。
5. A*搜索算法是一种启发式搜索算法,它通过________和实际代价的和来估计从当前顶点到目标顶点的代价。
三、简答题:1. 描述Dijkstra算法的基本思想,并说明其在处理有向图中的最短路径问题时的优势。
2. 说明Bellman-Ford算法如何检测图中是否存在负权重环,并解释其在处理负权重边时的适用性。
最短路径经典练习题

最短路径经典练习题一、基础理论题1. 请简述迪杰斯特拉(Dijkstra)算法的基本原理。
2. 什么是贝尔曼福特(BellmanFord)算法?它适用于哪些类型的图?3. 请解释A搜索算法中启发式函数的作用。
4. 如何判断一个图中是否存在负权环?5. 简述弗洛伊德(Floyd)算法的基本步骤。
二、单选题A. 迪杰斯特拉算法B. 贝尔曼福特算法C. 弗洛伊德算法D. A搜索算法A. 初始化距离表B. 选择当前距离最小的顶点C. 更新相邻顶点的距离D. 重复步骤B和C,直到所有顶点都被访问A. 迪杰斯特拉算法B. 贝尔曼福特算法C. 弗洛伊德算法D. A搜索算法A. 启发式函数B. 起始节点C. 目标节点D. 图的规模三、多选题A. 迪杰斯特拉算法B. 贝尔曼福特算法C. 深度优先搜索算法D. 广度优先搜索算法A. 初始化距离矩阵B. 更新距离矩阵C. 查找负权环D. 输出最短路径A. 图的存储结构B. 顶点的数量C. 边的数量D. 起始顶点四、计算题A (3)>B (2)> D\ | ^ \ | | \(2)\ | (1)/C \|(4)A (1)>B (2)> D\ ^ |\(2)\ | (3)/C \ |(1)A (2)>B (3)> D\ | ^\(3)\ | (1)/C \ |(2)五、应用题1. 假设你是一名地图软件的开发者,请简述如何利用最短路径算法为用户提供导航服务。
2. 在一个网络游戏中,玩家需要从起点到达终点,途中会遇到各种障碍。
请设计一种算法,帮助玩家找到最佳路径。
六、判断题1. 迪杰斯特拉算法只能用于无向图的最短路径问题。
()2. 贝尔曼福特算法可以检测图中是否存在负权环。
()3. 在A搜索算法中,如果启发式函数h(n)始终为0,则算法退化为Dijkstra算法。
()4. 弗洛伊德算法的时间复杂度与图中顶点的数量无关。
()七、填空题1. 迪杰斯特拉算法中,用来存储顶点到源点最短距离的数组称为______。
最短路径练习题

最短路径练习题一、基础理论题1. 请简述迪杰斯特拉(Dijkstra)算法的基本原理。
2. 什么是贝尔曼福特(BellmanFord)算法?它与迪杰斯特拉算法有什么区别?3. 请解释弗洛伊德(Floyd)算法的核心思想。
4. A算法是如何工作的?它相较于其他最短路径算法有什么优势?5. 请列举几种常见的最短路径问题应用场景。
二、单项选择题A. 初始化距离表,将起点到其他点的距离设置为无穷大B. 每次从距离表中找出未确定最短路径的点中距离最小的点C. 更新距离表时,可以出现负权边D. 确定起点到所有点的最短路径后,算法结束A. 图中存在负权边B. 图中存在负权环C. 图中不存在负权环D. 图中存在多条边3. 在弗洛伊德算法中,path[i][j]表示的是?A. 从点i到点j的最短路径长度B. 从点i到点j的最短路径C. 从点j到点i的最短路径长度D. 从点j到点i的最短路径A. 当前点到终点的直线距离B. 当前点到终点的实际路径长度C. 当前点的邻接点数量D. 当前点的父节点三、填空题1. 在迪杰斯特拉算法中,用来存储起点到各点最短距离的数据结构是______。
2. 贝尔曼福特算法的时间复杂度为______。
3. 弗洛伊德算法的核心三重循环分别对应三个变量:______、______和______。
4. A算法的启发式函数f(n) = g(n) + h(n),其中g(n)表示______,h(n)表示______。
四、应用题A 6 B| \ |1 2 3| \ |D 4 CA >B (2)^ || vC <D (1)A >B (4)^ || vC >D (2)4. 请简述如何使用A算法解决迷宫问题,并给出一个示例。
五、编程题1. 编写一个迪杰斯特拉算法的实现,输入为一个带权无向图和起点,输出为起点到其他各顶点的最短路径长度。
2. 编写一个贝尔曼福特算法的实现,输入为一个带权有向图和起点,输出为起点到其他各顶点的最短路径长度及是否存在负权环。
专题3.3 最短路径问题专项训练(30道)(举一反三)(苏科版)(解析版)

专题3.3 最短路径问题专项训练(30道)【苏科版】考卷信息:本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,涵盖了平面直角坐标系中的规律问题所有类型!一.选择题(共12小题)1.(2022春•五华区期末)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )A B.4cm C D.5cm【分析】正方体侧面展开为长方形,确定蚂蚁爬行的起点和终点,根据两点之间线段最短,根据勾股定理可求出最短路径长,【解答】解:如图,它运动的最短路程AB==cm).故选:C.2.(2022春•碑林区校级期末)如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC 上有一点D,且BC=10cm,DC=2cm.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.A.14B.12C.10D.8【分析】首先画出圆柱的侧面展开图,根据底面周长为12cm,求出AB的值;再在Rt△ABD中,根据勾股定理求出AD的长,AD即为所求.【解答】解:圆柱侧面展开图如图所示,∵圆柱的底面周长为12cm,∴AB=6cm.∵BD=8cm,在Rt△ABD中,AD2=AB2+BD2,∴AD10(cm),即蚂蚁从A点出发沿着圆柱体的表面爬行到点D的最短距离是10cm.故选:C.3.(2022春•洛阳期中)如图,圆柱形玻璃杯,高为12cm,底面周长为18cm.在杯内离杯底4cm的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.A.15B C.12D.18【分析】将圆柱沿过A的母线剪开,由题意可知,需在杯口所在的直线上找一点F,使AF+CF最小,则先作出A关于杯口所在直线的对称点A',连接A'C与杯口的交点即为F,此时AF+CF=A'F+CF=A'C,再利用勾股定理求A'C的长即可.【解答】解:如图所示,将圆柱沿过A的母线剪开,由题意可知,需在杯口所在的直线上找一点F,使AF+CF最小,故先作出A关于杯口所在直线的对称点A',连接A'C与杯口的交点即为F,此时AF+CF=A'F+CF=A'C,根据两点之间线段最短,即可得到此时AF+CF最小,并且最小值为A'C的长度,如图所示,延长过C的母线,过A'作A'D垂直于此母线于D,由题意可知,A'D=18÷2=9(cm),CD=12﹣4+4=12(cm),由勾股定理得:A'C=15(cm),故蚂蚁到达蜂蜜的最短距离为15cm,故选:A.4.(2022秋•高州市期末)国庆节期间,茂名市一广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为( )A B C D.5米【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.【解答】解:将圆柱表面切开展开呈长方形,则彩灯带长为2个长方形的对角线长,∵圆柱高3米,底面周长2米,∴AC2=22+1.52=6.25,∴AC=2.5,∴每根柱子所用彩灯带的最短长度为5m.故选:D.5.(2022秋•沈阳期末)如图,长方体的长为3,宽为2,高为4,点B离点C的距离为1,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是( )A B.5C D【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.【解答】解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如图1:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=5;只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图2:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如图3:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=∵5∴蚂蚁爬行的最短距离是5.故选:B.6.(2022春•郾城区期末)如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )cm.A.B.C.120D.130【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【解答】解:如图所示,∵它的每一级的长宽高为20cm,宽30cm,长50cm,∴AB=cm).答:蚂蚁沿着台阶面爬行到点B的最短路程是,故选:B.7.(2022秋•揭阳校级月考)如图,一个棱长为3的正方体,把它分成3×3×3个小正方体,小正方体的棱长都是1.如果一只蚂蚁从点A爬到点B,那么估计A,B间的最短路程d的值为( )A.4B.5C.6D.7【分析】过B作BD⊥AC于D,根据勾股定理即可得到结论.【解答】解:过B作BD⊥AC于D,则AD=4,BD=3,∴A,B间的最短路程d=5,故选:B.8.(2022秋•牡丹区月考)如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘AB=CD=20m.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )(π取3)m.A.30B.28C.25D.22【分析】要求滑行的最短距离,需将该U型池的侧面展开,进而根据“两点之间线段最短”得出结果.【解答】解:其侧面展开图如图:作点C关于AB的对称点F,连接DF,∵中间可供滑行的部分的截面是半径为2.5m的半圆,∴BC=πR=2.5π≈7.5m,AB=CD=20m,∴CF=15m,在Rt△CDF中,DF==25(m),故他滑行的最短距离约为25m.故选:C.9.(2022春•靖西市期中)如图是放在地面上的一个长方体盒子,其中AB=7cm,BC=4cm,BF=6cm,点M在棱AB上,且AM=1cm,点N是FG的中点,一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N,它需要爬行的最短路程为( )A.10cm B.C.D.【分析】利用平面展开图有2种情况,画出图形利用勾股定理求出MN的长即可.【解答】解:如图1中,MN=10(cm),如图2中,MN==10(cm),∴一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N,它需要爬行的最短路程为10cm,故选:A.10.(2022秋•芝罘区期中)某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )A.8cm B.10cm C.12cm D.15cm【分析】画出三棱柱的侧面展开图,利用勾股定理求解即可.【解答】解:将三棱柱沿AA′展开,其展开图如图,则AA′=15(cm).故选:D.11.(2022秋•青岛期末)棱长分别为8cm,6cm的两个正方体如图放置,点A,B,E在同一直线上,顶点G在棱BC上,点P是棱E1F1的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P,它爬行的最短距离是( )A.+10)cm B.C D.+3)cm【分析】求出两种展开图PA的值,比较即可判断.【解答】解:如图,有两种展开方法:方法一:PA=,方法二:PA=..故选:C.12.(2022•广饶县一模)如图,长方体的底面边长分别为2厘米和4厘米,高为5厘米.若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )厘米.A.8B.10C.12D.13【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.【解答】解:如图所示:∵长方体的底面边长分别为2cm和4cm,高为5cm.∴PA=4+2+4+2=12(cm),QA=5cm,∴PQ=13cm.故选:D.二.填空题(共8小题)13.(2022春•德城区期末)如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离是5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是 25 cm.【分析】画出长方体的侧面展开图,根据勾股定理求出AB的长即可.【解答】解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴BD=CD+BC=10+5=15(cm),AD=20cm,在直角三角形ABD中,根据勾股定理得:∴AB=25(cm);只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴BD=CD+BC=20+5=25(cm),AD=10cm,在直角三角形ABD中,根据勾股定理得:∴AB=cm);只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴AC=CD+AD=20+10=30(cm),在直角三角形ABC中,根据勾股定理得:∴AB==cm);∵25<∴蚂蚁爬行的最短距离是25cm.故答案为:25.14.(2022•潍城区一模)云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的,如图左右两幅图分别是公园内云顶滑雪场U型池的实景图和示意图,该场地可以看作是从一个m,其边缘AB=CD=24m,点E在CD 长方体中挖去了半个圆柱而成,它的横截面图中半圆的半径为12π上,CE=4m,一名滑雪爱好者从点A滑到点E,他滑行的最短路线长为.【分析】根据题意可得,AD=12,DE=CD﹣CE=24﹣4=20,线段AE即为滑行的最短路线长.在Rt△ADE中,根据勾股定理即可求出滑行的最短路线长.【解答】解:将半圆面展开可得:AD=12m,DE=DC﹣CE=20m,在Rt△ADE中,AE==m),即滑行的最短路线长为,故答案为:15.(2022春•仁怀市月考)如图,要在河边l上修建一个水泵站,分别向A村和B村送水,已知A村、B 村到河边的距离分别为2km和7km,且AB两村庄相距13km,则铺设水管的最短长度是 15 km.【分析】作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置;利用了轴对称的性质可得AP=A′P,在Rt△AEB中利用勾股定理可以算出AE的长,再在Rt△A′CB中利用勾股定理算出A′B的长,根据两点之间线段最短的性质即可求解.【解答】解:作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置,此时,(PA+PB)的值最小,即所铺设水管最短;过B点作l的垂线,过A′作l的平行线,设这两线交于点C,过A作AE⊥BC于E,则四边形AA′CE和四边形AMNE是矩形,∴EN=AM=2,EC=AA′=2+2=4,A′C=AE,在Rt△ABE中,依题意得:BE=BN﹣EN=7﹣2=5,AB=13,根据勾股定理可得:AE=12,在Rt△B A′C中,BC=BE+EC=5+4=9,A′C=12,根据勾股定理可得:A′B=15,∵PA=PA′,∴PA+PB=A′B=15(km),故答案为:15.16.(2022秋•锦江区校级期末)在一个长4米的长方形草地上,如图堆放着一根三棱柱的木块,它的侧棱长平行且大于场地宽AD,一只蚂蚁从点A处到C处需要走的最短路程是米.【分析】解答此题要将木块展开,然后根据两点之间线段最短解答.【解答】解:由题意可知,将木块展开,相当于是AB+等腰直角三角形的两腰,∴长为2+2﹣10(米);宽为4米.=故答案为:17.(2022秋•高新区校级期末)如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=5米,点P到AD的距离是3米,有一只蚂蚁要从点P爬到点B【分析】可将教室的墙面ADEF与地面ABCD展开,连接P、B,根据两点之间线段最短,利用勾股定理求解即可.【解答】解:如图,过P作PG⊥BF于G,连接PB,∵AG=3米,AP=AB=5米,∴PG=4米,∴BG=8米,∴PB==故这只蚂蚁的最短行程应该是故答案为:18.(2022春•德州期中)如图,点A是正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B【分析】根据题意画出图形,过A作EA⊥CD于E,连接AB,则AB长为最短距离,求出OD=OC,∠DAC=90°,根据直角三角形斜边上中线性质求出AE=DE=EC=1,根据勾股定理求出即可.【解答】解:如图展开:过A作EA⊥CD于E,连接AB,则AB长为最短距离,∵四边形DFGC是正方形,DC=BC=2,∴OD=OC,∠DAC=90°,∴∠ADE=∠ECA=45°,∵AE⊥DC,∴DE=EC,∵∠DAC=90°,DC=1,∴AE=DE=EC=12在△AEB中,∠AEB=90°,BE=1+2=3,EA=1,由勾股定理得:AB19.(2022秋•中原区校级期末)如图,一个三棱柱盒子底面三边长分别为3cm,4cm,5cm,盒子高为9cm,一只蚂蚁想从盒底的点A沿盒子的表面爬行一周到盒顶的点B,蚂蚁要爬行的最短路程是 15 cm.【分析】将三棱柱侧面展开得出矩形,求出矩形对角线的长度即可.【解答】解:如图,右侧为三棱柱的侧面展开图,AA′=3+4+5=12cm,A′B=9cm,∠AA′B=90°,∴AB==15cm,故答案为:15.20.(2022秋•凤城市期中)如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm.在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处吃面包屑.则蚂蚁爬行的最短路线为 100 cm.【分析】作出A关于BC的对称点A′,连接A′G,与BC交于点Q,此时AQ+QG最短;A′G为直角△A′EG的斜边,根据勾股定理求解即可.【解答】解:如图所示作点A关于BC的对称点A′,连接A′G交BC与点Q,小虫沿着A→Q→G的路线爬行时路程最短.在直角△A′EG中,A′E=80cm,EG=60cm,∴AQ+QG=A′Q+QG=A′G=100cm.∴最短路线长为100cm.故答案为:100.三.解答题(共10小题)21.(2022春•宜城市期末)如图,某小区有两个喷泉A,B,两个喷泉的距离长为125m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为60m,BM的长为75m.(1)求供水点M到喷泉A,B需要铺设的管道总长;(2)求喷泉B到小路AC的最短距离.【分析】(1)根据勾股定理解答即可;(2)根据勾股定理的逆定理和垂线段解答即可.【解答】解:(1)在Rt△MNB中,BN==45(m),∴AN=AB﹣BN=125﹣45=80(m),在Rt△AMN中,AM100(m),∴供水点M到喷泉A,B需要铺设的管道总长=100+75=175(m);(2)∵AB=125m,AM=100m,BM=75m,∴AB2=BM2+AM2,∴△ABM是直角三角形,∴BM⊥AC,∴喷泉B到小路AC的最短距离是BM=75m.22.(2022秋•原阳县期末)如图,一个正方体木箱子右边连接一个正方形木板,甲蚂蚁从点A出发,沿a,b,d三个面走最短路径到点B;同时,乙蚂蚁以相同的速度从点B出发,沿d,c两个面走最短路径到点A.请你通过计算判断哪只蚂蚁先到达目的地?【分析】将正方体展开,根据两点之间线段最短,构造出直角三角形,进而求出最短路径的长.【解答】解析展开a,b,c与d在同一平面内,如图所示.由题意可知,甲蚂蚁走的路径为A1B,A1B=cm).乙蚂蚁走的路径为A2B,A2B==cm).所以A1B>A2B,故乙蚂蚁先到达目的地.23.(2022秋•江北区期末)在立方体纸盒的顶点A处有一只蚂蚁,在另一顶点E处有一粒糖,你能为这只蚂蚁设计一条最短路线,使它沿着立方体表面上的这一条路线爬行,最快捷吃到糖吗?以下提供三个方案:①A→B→C→E;②A→C→E;③A→D→E.(1)三种方案①、②、③中爬行路线最短的方案是 ③ ;最长的方案是 ① .(2)请根据数学知识说明理由.【分析】(1)根据“化曲面为平面”,且利用“两点之间线段最短”可知,爬行路线最短的方案是③;最长的方案是①;(2)分别求出三种方案蚂蚁爬行的路程,比较即可求解.【解答】解:(1)三种方案①、②、③中爬行路线最短的方案是③;最长的方案是①.故答案为:③;①;(2)爬行路线最短的方案是③;最长的方案是①.理由如下:‘’设立方体纸盒的棱长为a,则a>0.方案:①A→B→C→E蚂蚁爬行的路程为:AB+BC+CE=a+a+a=3a;方案;②A→C→E蚂蚁爬行的路程为:AC+CE=a+1)a;方案;③A→D→E.1)a<3a,∴爬行路线最短的方案是③;最长的方案是①.24.(2022秋•二道区期末)如图,已知线段BC是圆柱底面的直径,圆柱底面的周长为10,圆柱的高AB=12,在圆柱的侧面上,过点A、C两点嵌有一圈长度最短的金属丝.(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是 C ;(2)求该金属丝的长.【分析】(1)由平面图形的折叠及立体图形的表面展开图的特点解题;(2)要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.【解答】解:(1)因为圆柱的侧面展开面为长方形,AC展开应该是两线段,且有公共点C.故答案为:C;(2)如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.∵圆柱底面的周长为10,圆柱的高AB=12,∴该长度最短的金属丝的长为2AC==26.25.(2022秋•随县期末)如图1所示,长方形是由两个正方形拼成的,正方形的边长为a,对角线为b,长方形对角线为c.一只蚂蚁从A点爬行到C点.(1)求蚂蚁爬行的最短路线长(只能按箭头所示的三条路线走),并说明理由;(2)如果把右边的正方形EFBC沿EF翻转90°得到如图2所示的正方体相邻的两个面(实线表示),则蚂蚁从A点到C点的最短路线长是多少?请在图2中画出路线图,若与图中的线段有交点,则要标明并说明交点的准确位置.(可测量猜想判断)【分析】(1)根据两点之间线段最短求解;(2)把正方体相邻的两个面展开成平面,连接A,C即是最短路线.【解答】解:(1)从A﹣B﹣C路线长:a+a+a=3a,从A﹣D﹣C路线长:a+a+a=3a,从A﹣E﹣C路线长:a+b.(3分)根据两点之间,线段最短.可得AD+DE>AE,即a+a>b,(6分)所以a+a+a>a+b,即3a>a+b(7分)(说明:只要写出理由“两点之间,线段最短”即给6分)故从A到C的最短路线长为a+b;(8分)(2)从A到C的最短路线长为C,(10分)图中的点M为线段EF的中点.(11分)位置如图.(13分)26.(2022秋•罗湖区期中)(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?【分析】(1)利用勾股定理直接求出木棒的最大长度即可.(2)将长方体展开,利用勾股定理解答即可;(3)将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【解答】解:(1)由题意得:该长方体中能放入木棒的最大长度是:=13(cm).(2)分三种情况可得:AG=>AG>AG=,;(3)∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,∴A′D=5cm,BD=12﹣3+AE=12cm,∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B=13(Cm).27.(2022秋•元宝区校级期中)一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,问:丝带共有多长?【分析】根据题意抽象出直角三角形,利用勾股定理求得彩色丝带的长即可.=150cm,答:丝带共有150cm.28.(2022秋•东明县期中)东明县是鲁西南的化工基地,有东明石化集团,洪业化工集团,玉皇化工集团等企业,化学工业越来越成为东明县经济的命脉,化工厂里我们会经常看到如图储存罐,根据需要,在圆柱形罐的外围要安装小梯子,如果油罐的底面半径为6米,高24米,梯子绕罐体半圆到达罐顶,则梯子至少要多长?【分析】把立体图形转化为平面图形,利用勾股定理即可解决问题.【解答】解:如图,根据题意,BC=24m,AB=1•2π•6≈18m,2在Rt△ABC中,AC30m,答:梯子至少要30m.29.(2022秋•福田区期末)如图,是一个圆柱形的饼干盒,在盒子外侧下底面的点A处有甲、乙两只蚂蚁,它们都想要吃到上底面外侧B′处的食物:甲蚂蚁沿A→A′→B′的折线爬行,乙蚂蚁沿圆柱的侧面爬行:若∠AOB=∠A′O′B′=90°(AA′、BB′都与圆柱的中轴线OO′平行),圆柱的底面半径是12cm,高为1cm,则:(1)A′B,甲蚂蚁要吃到食物需爬行的路程长l1+1 cm;(2)乙蚂蚁要吃到食物需爬行的最短路程长l2(π取3);(3)若两只蚂蚁同时出发,且爬行速度相同,在乙蚂蚁采取最佳策略的前提下,哪只蚂蚁先到达食物处?请你通过计算或合理的估算说明理由.(参考数据:π取3≈1.4)【分析】(1)由∠A′O′B′=90°,可知△B′A′O′为等腰直角三角形,故此A′B′=′O ′,然后根据l1=A′B′+AA′求解即可;(2)先求得弧A′B′的长,然后根据勾股定理求得矩形AA′B′B的对角线的长度即可;(3 1.4代入从而可求得l1、l2的近似值,从而可作出判断.【解答】解:(1)∵∠A′O′B′=90°,O′A′=O′B′,∴A′B′=A′B′=′O′=∴l1=A′B′+AA′=1.故答案为:1.=6π=18.(2)A′B′=90°×2π×12360°将圆柱体的侧面展开得到如图1所示矩形AA′B′B.∵A′B′=18,∴A′B′=18.在Rt△ABB′中,AB′=故答案为:(3)∵l1=1≈12×1.4+1=17.8∴l21=316.84.∵l22=2=325,∴l21<l22.∴l1<l2.∴甲蚂蚁先到达食物处.30.(2022秋•安岳县期末)勾股定理是解决直角三角形很重要的数学定理.这个定理的证明的方法很多,也能解决许多数学问题.请按要求作答:(1)选择图1或图2中任一个图形来验证勾股定理;(2)利用勾股定理来解决下列问题:如图3,圆柱形玻璃杯高为12cm,底面周长为16cm,在杯外离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁且与蜂蜜C相对的点A处,点A离杯口3cm.则蚂蚁到达蜂蜜的最短距离为多少?【分析】(1)根据正方形的面积等于四个直角三角形的面积与正方形面积的即可得出结论;(2)蚂蚁实际上是在圆柱的半个侧面上爬行,如果将这半个侧面展开,根据:“两点之间,线段最短“,所求的最短路程就是这一个展开图AC的长.在R t△ABC中,AB=底面周长的一半=8cm,BC=12﹣3﹣3=6cm.,所以由勾股定理得:AC=10cm,所以蚂蚁爬行的最短路程为10cm.ab+c2,【解答】解:(1)若选图1,则由图形可知:(a+b)2=4×12整理得:a2+b2=c2;ab+(b﹣a)2=c2,若选图2,则由图形可知:4×12整理得:a2+b2=c2.(2)如图所示,∵在Rt△ABC中,AB=底面周长的一半=8cm,BC=12﹣3﹣3=6cm,∴由勾股定理得:AC=10cm,∴蚂蚁爬行的最短路程为10cm.。
《最短路径问题》精编练习题(提高)

《最短路径问题》精编练习题(提高)一、解答题1.如图,在平面直角坐标系中.(1)请画出△ABC关于y轴对称的△AB1C1,并写出B1、C1的坐标;(2)直接写出△ABC的面积是_____;(3)在x轴上找到一点P,使PA+PC的值最小,请标出点P在坐标轴上的位置.2.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)画出△ABC关于y轴的对称图形△A1B1C1;(2)在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.3.如图,在Rt△ABC中,∠BAC=30°,∠ACB=90°,AC=3,E为AB的中点,在线段AC上找一点H,使得BH+EH的值最小,并求出该最小值.4.如图,在四边形ABCD中,∠ACB=90°,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一个点M,N,使△AMN的周长最小,求此时∠AMN+∠ANM的度数.5.如图,点M、N在∠AOB的内部,P为射线OA上的一个动点,Q射线OB上的一个动点,求作点P,Q,使得MP+PQ+QN的长最短.6.如图,在等边△ABC中,BD⊥AC于点D,点P,Q分别为线段AB,AD上的两个定点,且QD=15,BP=AQ=20.(1)作点Q关于直线BD对称的点Q'.(2)在BD上有一动点E,求PE+QE的最小值.7.如图,△ABC 是等边三角形,AD 是BC 边上的高,E 是AC 的中点,P 是AD 上的一个动点,当PC+PE 最小时,求∠ACP 的度数.8.如图,在△ABC 中,AB=AC ,∠BAC=90°,BC=a ,点D 是BC 上一动点(不与点B 、C )重合,∠BDE=12∠C ,BE ⊥DE .(1)求∠AFD 的度数;(2)在点D 运动过程中,BEDF 的值是否为定值?说明理由.(3)当CD=13BC 时,连接AD ,△ABD 三边上分别有动点P 、M 、N ,(点P 在BD 上),当△PMN 的周长取最小值时,求AP 的长.9.已知M ,N 分别是∠AOB 的边OA ,OB 上的定点.(1)如图(1),若∠O=∠OMN ,过M 作射线MD ∥OB ,点C 是射线MD 上一动点,∠MNC 的平分线NE 交射线OA 于E 点.试探究∠MEN 与∠MCN 的数量关系.(2)如图(2),若P 是线段ON 上一动点,Q 是射线MA 上一动点.∠AOB=20°,当MP+PQ+QN 取得最小值时,求∠OPM+∠OQN 的值.10.(1)如图①,点A ,B 在直线l 同侧,在直线上找一点P ,使AP+BP 的值最小.作法如下:作点B 关于直线l 的对称点B ',连接AB ',与直线l 的交点就是所求的点P ,线段AB '的长度即为AP+BP 的最小值.(2)如图②,等边△ABC 中,若E 是AB 的中点,P 为高AD 上一点,AD=3,连接BP ,求BP+PE 的最小值.(3)如图②,等边△ABC 中,若P 为高CE 上一点,AD=3,求BP+12CP 的最小值. (4)如图③,∠AOB=30°,P 是四边形OACB 内一定点,Q ,R 分别是OA ,OB 上的动点,当△PQR 周长的最小值为5时,求OP 的长.11.如图1,等边△ABC 三边相等,三个内角都是60°的三角形)的边长为10cm ,动点D 和动点E 同时出发,分别以每秒1cm 的速度由A 向B 和由C 向A 运动,其中一个动点到终点时,另一个也停止运动,设运动时间为ts ,0<t ≤100,DC 和BE 交于点F .(1)在运动过程中,CD 与BE 始终相等吗?请说明理由;(2)连接DE ,求t 为何值时,DE ∥BC ;(3)如图2,若BM ⊥AC 于点M ,点P 为BM 上的点,且使PD+PE 最短.当t=7s 时,PD+PE 的最小值为多少?请直接写出这个最小值,无需说明理由.12.如图,在△ABC 中,∠CAB=30°,∠ACB=90°,AC=4,D 为AB 的中点,E 为线段AC 上任意一点(不与A ,C 两点重合),当点E 在线段AC 上运动时,求DE+12CE 的最小值.。
最短路径问题练习题

13.4最短路径问题练习题班别:姓名:一、单选题.1.已知点A,B是两个居民区的位置,现在准备在墙l边上建立一个垃圾站点P,如图是4位设计师给出的规划图,其中PA+PB距离最短的是( )2.直线l是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )3.A、B是直线l上的两点,P是直线l上的任意一点,要使PA+PB的值最小,那么点P的位置应在( )A.线段AB上B.线段AB的延长线上C.线段AB的反向延长线上D.直线l上4.在如图所示的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最小,则点P应选在( )A.C点B.D点C.E点D.F点5.在△ABC中,AB=AC=5,BC=6,AD⊥BC于D点,且AD=4,若P点在边AC上移动,则BP的最小值是( )A.4.5B.4.6C.4.7D.4.8二、填空题6.如图,在△ABC中,AB=AC,AD,CE是△ABC的两条中线,P是AD上一个动点,则BP+EP的最小值等于线段的长度.7.如图,∠BAC=30°,AB=4,点P是射线AC上的一动点,则线段BP的最小值是______.8.如图,OA、OB分别是线段MC、MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短为.第13题图第13题图9.如图,CD⊥AB,垂足是D,AC=7,BC=5,CD=4,点E是线段AB上的一个动点(包括端点),连接CE,那么CE的范围是.三、作图题10.八年级(1)班同学做游戏,在活动区域边OP放了一些球(如图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?四、解答题11.如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点,若AB=6,AC=4,BC=7,(1)求PA+PB的最小值,并说明理由;(2)求△APC周长的最小值.参考答案1.D.2.D.3.A.4.A.5.D.6.答案为:CE.7.答案为:2.8.答案为:10cm.9.答案为:4≤CE≤7.10.解:如图所示:11.解:(1)PA+PB=AB=6;原因:两点之间,线段最短;(2)∵m是BC的垂直平分线,点P在m上,∴点C关于直线m的对称点是点B,则PB=PC,∵C△ABC=AP+PC+AC,∵AC=4,要使△APC周长最小,即AP+PC最小,当点P是m与AB的交点时,PA+PB最小,即PA+PB=AB,此时C△APC=AB+AC=6+4=10.理由:在OA,OB上取不同于E,F的点E′,F′,连接CE′、E′P′,∵C和P关于直线OA对称,∴PE=CE,CE′=PE′,PF=DF,PF′=DF′,由(2)得知MN+ME+EF+MF<ME′+E′F′+F′D.。
最短路径问题专项练习题(含解析)
故选 .
11.【答案】C
【解答】
解:∵ ,
∴此时 ,
∵点 与点 关于 对称, 平分 ,
∴ ,
在 中, .
即 的最小值为 .
故选 .
12.解:在射线BC上取一点E′,使得BE′=BE.过点A作AH⊥BC于H.
在Rt△ACH中,∵∠AHC=90°,AC=24,∠C=30°,
∴AH= AC=12,
∵BD平分∠ABC,
问题:某正方体盒子,如图左边下方 处有一只蚂蚁,从 处爬行到侧棱 上的中点 点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.
34.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=65°,则∠NMA的度数是度.
(2)若AB=10cm,△MBC的周长是18cm.
(1)如图 为 ,有点 , , ,则线段 的“对称点”是________.(填“ ”" "或" ")
如图 为线段 的“完美对称点”, 为线段 的中点, 为线段 的一个“对称点”,则 的最小值为________.
14.如图,在 中, , ,点 在 边上,且 , ,动点 在 边上,连接 , ,则 的最小值是________.
A. B.
C. D.
3.如图,点 , 在直线 的同侧,若要用尺规在直线 上确定一点 ,使得 最短,则下列作图正确的是()
A. B. C. D .
4.如图,一圆柱高 ,底面半径为 ,一只蚂蚁从点 爬到点 处吃食,要爬行的最短路程是( )
A. B. C. D.
5.如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )
《最短路径问题》精编练习题

《最短路径问题》精编练习题
一、解答题
1.如图,在直线l上分别找出点P,使PA+PB最小.
2.如图,牧童在A处放牛,他的家在B处,l为河流所在直线.晚上回家时要到河边让牛饮一次水,饮水的地点(用点P表示)选在何处,牧童所走的路程最短?
3.如图,A,B在直线l异侧,在直线l上取一点P,使PA+PB最小.
4.如图,点M在∠AOB的内部,P为射线OA上的一个动点,Q为射线OB上的一个动点.求作点P,Q,使得MP+PQ+QM的长最短.
5.已知点A(-2,1),B(2,3).
(1)在坐标系中描出点A,B;
(2)在x轴上找一点P,使PA+PB最小,并写出点P的坐标.
6.如图,(1)画出△ABC关于y轴对称的△A'B'C';
(2)在y轴上找出点P,使得PA+PC最小,并写出点P的坐标.
7.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1),B(4,2),C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)若点M(-4,2)与点N(2,2)关于一条直线成轴对称,请在图中画出这条对称轴;
(3)在x轴上找一点P,使PA+PB最小,则P点的坐标为.
8.如图,在平面直角坐标系中.
(1)请画出△ABC关于y轴对称的△AB1C1,并写出B1、C1的坐标;
(2)直接写出△ABC的面积是______;
(3)在x轴上找到一点P,使PA+PC的值最小,请标出点P在坐标轴上的位置.。
专题02 平面展开-最短路径问题(勾股定理)(专项培优训练)(教师版)

专题02 平面展开-最短路径问题(勾股定理)(专项培优训练)试卷满分:100分考试时间:120分钟难度系数:0.54一、选择题(本大题共10小题,每小题2分,共20分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填写在括号内)1.(2分)(2023•中原区校级开学)如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )A.100cm B.120cm C.130cm D.150cm解:把这个台阶示意图展开为平面图形得图①:在RT△ACB中,∵AC=50,BC=120,∴AB===130,∴一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路AB的长度=130cm.故选:C.2.(2分)(2022秋•新都区期末)一个长方体盒子的长、宽、高分别为15cm,10cm,20cm,点B离点C 的距离是5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到点B,蚂蚁爬行的最短路程是( )A.10cm B.25cm C.5cm D.5cm解:如图所示,将长方体的正面与右侧面展开在同一平面,那么AB==25cm.故选:B.3.(2分)(2023•陇县三模)如图,长方体的底面边长分别为2厘米和4厘米,高为5厘米.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )厘米.A.8B.10C.12D.13解:如图所示:∵长方体的底面边长分别为2cm和4cm,高为5cm.∴PA=4+2+4+2=12(cm),QA=5cm,∴PQ==13cm.故选:D.4.(2分)(2022秋•宛城区校级期末)已知点A,B是两个居民区的位置,现在准备在墙l边上建立一个垃圾站点P,如图是4位设计师给出的规划图,其中PA+PB距离最短的是( )A.B.C.D.解:先作B关于直线l的对称点,连接点A和对称点与l交于点P,此时PA+PB距离最短.故选:D.5.(2分)(2023•十堰模拟)如图.一大楼的外墙面ADEF与地面ABCD垂直,点P在墙面上,若PA=AB=10米,点P到AD的距离是6米,有一只蚂蚁要从点P爬到点B,它的最短行程是( )米.A.16B.8C.15D.14解:如图,将教室的墙面ADEF与地面ABCD展成一个平面,过P作PG⊥BF于G,连接PB,在Rt△APG中,AG=6米,AP=AB=10米,∴PG===8(米),在Rt△BPG中,PG=8米,BG=AG+AB=16米,∴PB==8(米).故这只蚂蚁的最短行程应该是8米.故选:B.6.(2分)(2022秋•蒲城县期末)今年9月23日是第五个中国农民丰收节,小彬用3D打印机制作了一个底面周长为20cm,高为20cm的圆柱粮仓模型.如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )A.20πcm B.40πcm C.D.解:如图,圆柱的侧面展开图为长方形,AC=A'C,且点C为BB'的中点,∵AB=20,BC=20=10,∴装饰带的长度=2AC=2=20(cm),故选:D.7.(2分)(2023•滕州市校级开学)如图一个三级台阶,它的每一级的长宽高分别是5cm,3cm和1cm,A 和B是这个台阶的两个相对的端点,点A上有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B的最短路程长为( )A.10B.11C.12D.13解:如图所示,∵三级台阶平面展开图为长方形,宽为5,长为(3+1)×3=12,∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长,由勾股定理得,则蚂蚁沿着台阶面爬到B点最短路程是13.故选:D.8.(2分)(2022秋•辽阳期末)今年9月23日是第五个中国农民丰收节,小明用3D打印机制作了一个底面周长为12cm,高为8cm的圆柱粮仓模型.如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )A.96πcm B.48cm C.D.20cm解:如图,圆柱的侧面展开图为长方形,AC=A′C,且点C为BB′的中点,∵AB=8,,∴装饰带的长度=,故选:D.9.(2分)(2022秋•辉县市校级期末)如图,圆柱形玻璃杯,高为12cm,底面周长为18cm.在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.A.15B.C.12D.18解:如图所示,将圆柱沿过A的母线剪开,由题意可知,需在杯口所在的直线上找一点F,使AF+CF最小,故先作出A关于杯口所在直线的对称点A',连接A'C与杯口的交点即为F,此时AF+CF=A'F+CF=A'C,根据两点之间线段最短,即可得到此时AF+CF最小,并且最小值为A'C的长度,如图所示,延长过C的母线,过A'作A'D垂直于此母线于D,由题意可知,A'D=18÷2=9(cm),CD=12﹣4+4=12(cm),由勾股定理得:A'C==15(cm),故蚂蚁到达蜂蜜的最短距离为15cm,故选:A.10.(2分)(2023春•五华区校级期中)如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )A.B.C.20cm D.解:将圆柱侧面展开,如图所示,作出A点关于DE的对称点A',过点B作BC⊥CD于点C,∵形容器高为18cm,点A处离杯上沿2cm,点B处离杯底4cm,∴AD=A'D=2cm,CD=18﹣4=14(cm),∴A'C=AD+CD=2+14=16(cm),∵底面周长为24cm,∴,根据勾股定理可得:,故选:C.二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请将正确答案填写在横线上)11.(2分)(2022秋•叙州区期末)如图是一个三级台阶,它的每一级的长、宽、高分别是4米、0.7米、0.3米,A、B是这个台阶上两个相对的顶点,A点处有一只蚂蚁,它想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是 5 米.解:三级台阶平面展开图为长方形,长为4,宽为(0.7+0.3)×3,则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.可设蚂蚁沿台阶面爬行到B点最短路程为x,由勾股定理得:x2=42+[(0.7+0.3)×3]2=25,解得x=5(米),答:蚂蚁沿台阶面爬行到B点最短路程是5米,故答案为:5.12.(2分)(2022秋•安岳县期末)如图所示,ABCD是长方形地面,长AB=10m,宽AD=5m,中间竖有一堵砖墙高MN=1m.一只蚂蚱从A点爬到C点,它必须翻过中间那堵墙,则它至少要走 13 m的路程.解:如图所示,将图展开,图形长度增加2m,原图长度增加2m,则AB=10+2=12m,连接AC,∵四边形ABCD是长方形,AB=12m,宽AD=5m,∴AC===13m,∴蚂蚱从A点爬到C点,它至少要走13m的路程.故答案为:13.13.(2分)(2023春•岚山区期中)如图,圆柱形玻璃杯高为5cm,底面周长为12cm,在杯内壁底的点B 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离是(杯壁厚度不计) 10cm .解:如图,将杯子侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,在直角△A′DB中,由勾股定理得,A′B===10(cm).则蚂蚁从外壁A处到内壁B处的最短距离为10cm,故答案为:10cm.14.(2分)(2022秋•烟台期末)我国古代有这样一道数学问题:“枯木一根直立地上,高三丈,周八尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为3丈,底面周长为8尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 5 丈.解:如图所示:AB表示葛藤的最短长度,由题意可知:BC=3(丈),AC=8×5÷10=4(丈),在Rt△ABC中,(丈).故答案为:5.15.(2分)(2022秋•宛城区期末)如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A 处,则壁虎捕捉蚊子的最短距离为 1m .解:如图:∵高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,∴A′D=0.6m,BD=0.8m,∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B===1(m).故答案为:1m.16.(2分)(2022秋•通许县期末)长方体的长为15cm,宽为10cm,高为20cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是 25cm .解:把左侧面展开到水平面上,连接AB,如图1,AB===5(cm)把右侧面展开到正面上,连接AB,如图2,AB==25(cm);把向上的面展开到正面上,连接AB,如图3,AB===5(cm).∵>>25所以一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离为25cm.故答案为:25cm.17.(2分)(2023春•肇源县月考)如图有一个棱长为9cm的正方体,一只蜜蜂要沿正方体的表面从顶点A爬到C点(C点在一条棱上,距离顶点B 3cm处),需爬行的最短路程是 15 cm.解:∵CD=9cm,AD=(3+9)cm,∴AC===15cm,故答案为:15.18.(2分)(2022秋•榆阳区校级期末)如图所示,已知圆柱的底面周长和高都为8,BC、AD分别为上、下底面的直径,点P在线段AB上,且AP=1,点S为线段CD的中点,若一只蚂蚁从点P出发,沿圆柱的外侧面爬行到点S处,则蚂蚁爬行的最短路程为 5 .解:如图,圆柱侧面展开后连接PS,过点P作PH⊥CD于H.线段PS的长就是蚂蚁爬行的最短路程,因为圆柱的底面周长和高都为8,所以图中AD=×8=4,CD=8,∵AP=1,点S为线段CD的中点,∴HD=1,SD=4,∴SH=4﹣1=3,在Rt△PSH中,由勾股定理得:AC==5,即蚂蚁爬行的最短路程是5.故答案为:5.19.(2分)(2022秋•高新区校级期末)如图,圆柱底面半径为cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一条竖直直线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为 15 cm.解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B 的路线最短;∵圆柱底面半径为cm,∴长方形的宽即是圆柱体的底面周长:2π×=4(cm);又∵圆柱高为9cm,∴小长方形的一条边长是3cm;根据勾股定理求得AC=CD=DB==5(cm);∴AC+CD+DB=15(cm);故答案为:15.20.(2分)(2022秋•沙坪坝区校级期末)如图,一个长方体盒子,其中AB=9,BC=3,M为AB上靠近A 的三等分点,在大长方体盒子上有一个小长方体盒子,EC=6,CG=1,CF=4,一只蚂蚁要沿着长方体盒子的表面从点M爬行到N点,它爬行的最短路程为 10 .解:如图,将面MBCE、面ECGI和面IGNH展开在同一平面内,连接MN,在Rt△MHN中,HN=CE=6,HM=EM+IE+IH=BC+CG+CF=8,∴MN===10,故答案为:10.三、解答题(本大题共8小题,共60分.解答时应写出文字说明、证明过程或演算步骤)21.(6分)(2022秋•宝丰县期中)一只蚂蚁沿图①中立方体的表面从顶点A爬到顶点B,图②是图①立方体的表面展开图,设立方体的棱长为1.(1)在图②中标出点B的位置.(2)求蚂蚁从点A到点B爬行的最短路径长.解:(1)如图所示;(2)连接AB,∵立方体的棱长为1,∴AC=2,BC=1,∴AB==,∴蚂蚁爬行的最短路程是.22.(6分)(2022秋•偃师市期末)如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF =10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?解:如图1,∵AB=18cm,BC=GF=12cm,BF=10cm,∴BM=18﹣6=12(cm),BN=10+6=16(cm),∴MN==20(cm);如图2,∵AB=18cm,BC=GF=12cm,BF=10cm,∴PM=18﹣6+6=18(cm),NP=10(cm),∴MN==2(cm).∴它需要爬行的最短路程是20cm.23.(8分)(2021秋•原阳县期末)如图,一个正方体木箱子右边连接一个正方形木板,甲蚂蚁从点A出发,沿a,b,d三个面走最短路径到点B;同时,乙蚂蚁以相同的速度从点B出发,沿d,c两个面走最短路径到点A.请你通过计算判断哪只蚂蚁先到达目的地?解析展开a,b,c与d在同一平面内,如图所示.由题意可知,甲蚂蚁走的路径为A1B,(cm).乙蚂蚁走的路径为A2B,(cm).因为,所以A1B>A2B,故乙蚂蚁先到达目的地.24.(8分)(2021秋•高青县期末)如图所示是一个三级台阶,它的每一级的长、宽、高分别等于5cm、3cm、1cm,A和B是这两个台阶的两个相对的端点,则一只蚂蚁从点A出发经过台阶爬到点B的最短路线有多长?解:将台阶展开,如图,因为AC=3×3+1×3=12,BC=5,所以AB2=AC2+BC2=169,所以AB=13(cm),所以蚂蚁爬行的最短线路为13cm.答:蚂蚁爬行的最短线路为13cm.25.(8分)(2022秋•沈阳月考)如图,两个一样的长方体礼品盒,其底面是边长为15cm的正方形,高为20cm.现有彩带若干(足够用),数学组的小明和小刚分别采用自己喜欢的方式用彩带装饰两个礼品盒(假设彩带完美贴合长方体礼品盒).(1)如图1,小明从底面点A开始均匀缠绕长方体侧面,刚好缠绕2周到达点B,求所用彩带的长度;(2)如图2,小刚沿着长方体的表面从点C缠绕到点D,点D与点E的距离是5cm,请问小刚所需要的彩带最短是多少?(注:以上两问均要求画出平面展开示意图,再解答)解:(1)如图,将长方体的侧面沿AB展开,取A′B′的中点M,取AB的中点N,连接AM,NB′,则AM+NB′=2AM为所求的彩带长,∵AM2=AA′2+A′M2,AC==10(cm),∴AM+NB′=2AM=20(cm),答:彩带的长度是20cm;(2)当上面的面与前面的面展成一个平面时,如图,此时CD==5(cm);当右边的面与前面的面展成一个平面时,如图,此时CD==20(cm);当上面的面与左边的面展成一个平面时,如图,此时CD==25(cm);由上可知小刚所需要的彩带最短是20cm.26.(8分)(2021秋•景德镇期中)如图,已知圆柱底面的周长为12,圆柱的高为8,在圆柱的侧面上,过点A,C嵌有一圈长度最短的金属丝.(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是 A .(2)如图①,求该长度最短的金属丝的长.(3)如图②,若将金属丝从点B绕四圈到达点A,则所需金属丝最短长度是多少?解:(1)因圆柱的侧面展开面为长方形,AC展开应该是两线段,且有公共点C.故选:A;(2)如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.∵圆柱底面的周长为12,∴BC=12=6,∵圆柱的高AB=8,∴该长度最短的金属丝的长为2AC=2×=20;(3)若将金属丝从点B绕四圈到达点A,则所需金属丝最短长度是=8.27.(8分)(2022春•新市区校级期中)(1)如图1,长方体的底面边长分别为3m和2m,高为1m,在盒子里,可以放入最长为 m的木棒;(2)如图2,在与(1)相同的长方体中,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点C,那么所用细线最短需要 m;(3)如图3,长方体的棱长分别为AB=BC=6cm,AA1=14cm,假设昆虫甲从盒内顶点C1以2厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从盒内顶点A以相同的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉昆虫甲?解:(1)可以放入最长为=(m)的木棒;故答案为:;(2)如图所示:将长方体展开,连接AC,∴AC==(m).故答案为:;(3)因为昆虫是在侧面上爬行,可以看出,下面两图的最短路径相等,设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F,爬行捕捉到昆虫甲需x秒钟,如图1在Rt△ACF中,(2x)2=122+(14﹣2x)2,解得:x=.答:昆虫乙至少需要秒钟才能捕捉到昆虫甲.28.(8分)(2022秋•镇江期中)十九世纪英国赫赫有名的谜题创作者在1903年的英国报纸上发表的“蚂蚁爬行”的问题.问题是:如图1,在一个长、宽、高分别为8m,8m,4m的长方体房间内,一只蚂蚁在右面墙的高度一半位置(即M点处),并且距离前面墙1m,苍蝇正好在左面墙高度一半的位置(即N点处),并且距离后面墙2m,蚂蚁爬到苍蝇处应该怎样爬行所走路程最短,最短路程是多少m?这只蚂蚁在长方体表面爬行的问题,引起了当时很多数学爱好者的研究与讨论,今天我们也一起来研究一下这个当时非常热门的数学问题![基础研究]如图2,在长、宽、高分别为a,b,c(a>b>c)的长方体一个顶点A处有一只蚂蚁,欲从长方体表面爬行去另一个顶点C′处吃食物,探究哪种爬行路径是最短的?(1)观察发现:蚂蚁从A点出发,为了走出最短路线,根据两点之间线段最短的知识,并结合展开与折叠原理,一共有3种不同的爬行路线,即图3、图4、图5所示.填空:图5是由 左 面与 上 面展开得到的平面图形;(填“前”、“后”、“左”、“右”、“上”、“下”)(2)推理验证:如图3,由勾股定理得,.AC′2=(a+b)2+c2=a2+b2+c2+2ab,如图4,由勾股定理得,AC′2=(b+c)2+a2=a2+b2+c2+2bc,如图5,AC′2=(a+c)2+b2=a2+b2+c2+2ac.要使得AC′的值最小,∵a>b>c……,(请补全推理过程)∴ab>ac>bc∴选择如图 4 情况,此时AC′2的值最小,则AC′的值最小,即这种爬行路径是最短的.[简单应用]如图6,长方体的长,宽,高分别为24cm,12cm,40cm,点P是FG的中点,一只蚂蚁要沿着长方体的表面从点A爬到点P,则爬行的最短路程长为 50 cm.[问题回归]最后让我们再回到那道十九世纪英国报纸上发表的“蚂蚁爬行”的问题(如图1),那只蚂蚁所走的最短路程是 13 m.解:(1)将图5上面与左面展开即可得到图5,故答案为:左,上.(2)推理验证∵a>b>c>0,∵a>b,∴ac>bc,∵b>c,∴ab>ac,∴ab>ac>bc.故选图4.[简单应用]∵FP=FG=×12=6cm,根据(2)的推理,爬行最短路径为=50cm.故答案为:50cm.[问题回归]把M、N所在点作为顶点,从房间中切出如图长方体,只能将左、上、右三面展开,得到下面展开图,MN==13m.故答案为:13.。
2022-2023学年人教版八年级数学上册《最短路径问题》专题练习(含答案)
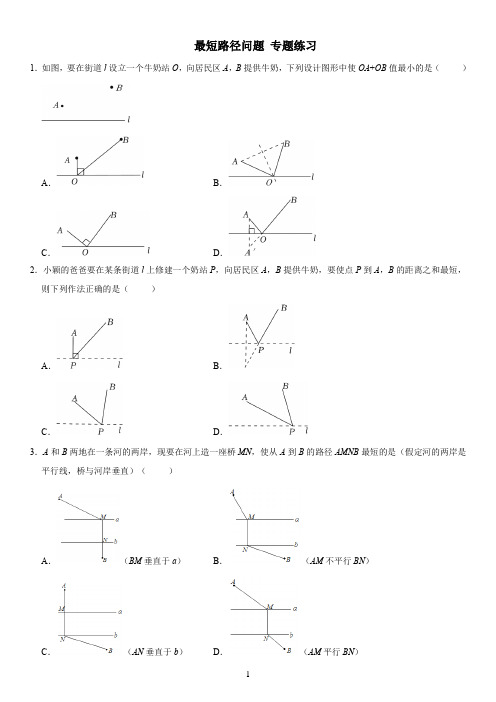
最短路径问题专题练习1.如图,要在街道l设立一个牛奶站O,向居民区A,B提供牛奶,下列设计图形中使OA+OB值最小的是()A.B.C.D.2.小颖的爸爸要在某条街道l上修建一个奶站P,向居民区A,B提供牛奶,要使点P到A,B的距离之和最短,则下列作法正确的是()A.B.C.D.3.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)()A.(BM垂直于a)B.(AM不平行BN)4.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是()A.9.6B.8C.6D.4.85.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则P A+PQ的最小值是()A.1B.2C.3D.46.如图,在△ABC中,AD是△ABC的角平分线,点E、F分别是AD、AB上的动点,若∠BAC=50°,当BE+EF 的值最小时,∠AEB的度数为()A.105°B.115°C.120°D.130°7.如图,四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小时,则∠ANM+∠AMN的度数为()A.80°B.90°C.100°D.130°8.在△ABC中,AB=6,BC=7,AC==4,直线m是△ABC中BC边的垂直平分线,P是直线m.上的一动点,则△APC的周长的最小值为()A.6B.10C.11D.139.如图,Rt △ABC 中,∠ACB =90°,AC =6,BC =8,AB =10,BD 平分∠ABC ,如果点M ,N 分别为BD ,BC上的动点,那么CM +MN 的最小值是( )A .4B .4.8C .5D .610.如图,OE 为∠AOB 的角平分线,∠AOB =30°,OB =6,点P ,C 分别为射线OE ,OB 上的动点,则PC +PB的最小值是( )A .3B .4C .5D .611.如图,△ABC 中,AD ⊥BC ,垂足为D ,AD =BC ,点P 为直线BC 上方的一个动点,△PBC 的面积等于△ABC的面积的12,则当PB +PC 最小时,∠PBD 的度数为( )A .30°B .45°C .60°D .90°12.如图,在锐角三角形ABC 中,AB =4,∠BAC =60°,∠BAC 的平分线交BC 于点D ,M ,N 分别是AD 和AB上的动点,当BM +MN 取得最小值时,AN =( )A .2B .4C .6D .813.如图,△ABC中,AD垂直BC于点D,且AD=BC,BC上方有一动点P满足S△PBC=12S△ABC,则点P到B、C两点距离之和最小时,∠PBC的度数为()A.30°B.45°C.60°D.90°14.如图,在等腰△ABC中,AB=AC,BC=8,作AD⊥BC于点D,AD=12AB,点E为AC边上的中点,点P为BC上一动点,则P A+PE的最小值为.15.如图,点P是∠AOB内任意一点,OP=5cm,点M、N分别是OB、OA边上的点,当△PMN周长的最小值是5cm时,则∠AOB=.16.如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点N,交AB于点M,AB=12cm,△BMC的周长是20cm,若点P在直线MN上,则P A﹣PB的最大值为()A.12cm B.8cm C.6cm D.2cm17.如图,AB=AC=8,∠BAC=110°,AD是∠BAC内的一条射线,且∠BAD=25°,P为AD上一动点,则|PB ﹣PC|的最大值是.思考题1.如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ =α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为()A.10°B.20°C.40°D.60°2.如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN 最小时,∠MBN的度数为()A.15°B.22.5°C.30°D.47.5°最短路径问题专题练习(答案)1.如图,要在街道l设立一个牛奶站O,向居民区A,B提供牛奶,下列设计图形中使OA+OB值最小的是(D)A.B.C.D.2.小颖的爸爸要在某条街道l上修建一个奶站P,向居民区A,B提供牛奶,要使点P到A,B的距离之和最短,则下列作法正确的是(B)A.B.C.D.3.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)(D)A.(BM垂直于a)B.(AM不平行BN)4.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是()A.9.6B.8C.6D.4.8【解答】解:∵AB=AC,AD是∠BAC的平分线,∴AD垂直平分BC,∴BP=CP.过点B作BQ⊥AC于点Q,BQ交AD于点P,则此时PC+PQ取最小值,最小值为BQ的长,如图所示.∵S△ABC=12BC•AD=12AC•BQ,∴BQ=BC⋅ADAC=12×810=9.6.故选:A.5.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则P A+PQ的最小值是()A.1B.2C.3D.4【解答】解:作AH⊥OB于H,交OC于P,作PQ⊥OA于Q,∵∠OAB=∠AOB=15°,∴PH=PQ,∴P A+PQ=P A+PH=AH,∴P A+PQ的最小值为AH,在Rt△ABH中,∵OB=AB=6,∠ABH=30°,∴AH=12AB=3,∴P A+PQ的最小值为3,故选:C.6.如图,在△ABC中,AD是△ABC的角平分线,点E、F分别是AD、AB上的动点,若∠BAC=50°,当BE+EF 的值最小时,∠AEB的度数为()A.105°B.115°C.120°D.130°【解答】解:过点B作BB′⊥AD于点G,交AC于点B′,过点B′作B′F′⊥AB于点F′,与AD交于点E′,连接BE′,如图,此时BE+EF最小.∵AD是△ABC的角平分线,∴∠BAD=∠B′AD=25°,∴∠AE′F′=65°,∵BB′⊥AD,∴∠AGB=∠AGB′=90°,∵AG=AG,∴△ABG≌△AB′G(ASA),∴BG=B′G,∠ABG=∠AB′G,∴AD垂直平分BB′,∴BE=BE′,∴∠E′B′G=∠E′BG,∵∠BAC=50°,∴∠AB′F′=40°,∴∠ABE=40°,∴∠BE′F′=50°,∴∠AE′B=115°.故选:B.7.如图,四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小时,则∠ANM+∠AMN的度数为()A.80°B.90°C.100°D.130°【解答】解:作A点关于CD的对称点F,作A点关于BC的对称点E,连接EF交CD 于N,交BC于M,连接AM、AN,∵∠B=∠D=90°,∴AN=NF,AM=EM,∴△AMN的周长=AM+AN+MN=NF+MN+EM=EF,此时△AMN的周长有最小值,∵∠F AN=∠F,∠E=∠EAM,∴∠E+∠F=180°﹣∠BAD,∵∠BAD=130°,∴∠E+∠F=50°,∴∠BAM+∠F AN=50°,∴∠MAN=130°﹣50°=80°,∴∠ANM+∠AMN=180°﹣∠MAN=100°,故选:C.8.在△ABC中,AB=6,BC=7,AC==4,直线m是△ABC中BC边的垂直平分线,P是直线m.上的一动点,则△APC的周长的最小值为()A.6B.10C.11D.13【解答】解:∵直线m是△ABC中BC边的垂直平分线,∴BP=CP,∴△ACP的周长=AP+PC+AC=BP+AP+AC≥AB+AC,∴当A、B、P三点共线时,△ACP的周长最小,∵AB=6,BC=7,AC=4,∴△ACP的周长6+4=10,∴△ACP的周长最小值为10,故选:B.9.如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,BD平分∠ABC,如果点M,N分别为BD,BC上的动点,那么CM+MN的最小值是()A.4B.4.8C.5D.6【解答】解:如图所示:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于点N,∵BD平分∠ABC,∴ME=MN,∴CM+MN=CM+ME=CE.∵Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,CE⊥AB,∴S△ABC=12•AB•CE=12•AC•BC,∴10CE=6×8,∴CE=4.8.即CM+MN的最小值是4.8,10.如图,OE 为∠AOB 的角平分线,∠AOB =30°,OB =6,点P ,C 分别为射线OE ,OB 上的动点,则PC +PB 的最小值是( )A .3B .4C .5D .6【解答】解:过点B 作BD ⊥OA 交于D 点,交OE 于点P ,过点P 作PC ⊥OB 交于C 点, ∵OE 为∠AOB 的角平分线,∴DP =CP ,∴PB +PC =PD +PB =BD ,此时PC +PB 的值最小,∵∠AOB =30°,OB =6,∴BD =3,故选:A .11.如图,△ABC 中,AD ⊥BC ,垂足为D ,AD =BC ,点P 为直线BC 上方的一个动点,△PBC 的面积等于△ABC 的面积的12,则当PB +PC 最小时,∠PBD 的度数为( )A .30°B .45°C .60°D .90° 【解答】解:∵△PBC 的面积等于△ABC 的面积的12,∴P 在与BC 平行,且到BC 的距离为12AD 的直线l 上,作点B关于直线l的对称点B',连接B'C交l于P,如图所示:则BB'⊥l,PB=PB',此时点P到B、C两点距离之和最小,作PM⊥BC于M,则BB'=2PM=AD,∵AD⊥BC,AD=BC,∴BB'=BC,BB'⊥BC,∴△BB'C是等腰直角三角形,∴∠B'=45°,∵PB=PB',∴∠PBB'=∠B'=45°,∴∠PBC=90°﹣45°=45°;故选:B.12.如图,在锐角三角形ABC中,AB=4,∠BAC=60°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,当BM+MN取得最小值时,AN=()A.2B.4C.6D.8【解答】解:作B点关于AD的对称点E,过E点作EN⊥AB交AB于点N,交AD于CM于点M,连结BM,∵∠BAC=60°,AD平分∠BAC,∴E点在AC上,∵BM+MN=EM+MN=EN,此时BM+MN的值最小,由对称性可知,AE=AB,∵AB=4,在Rt △ABE 中,∠EAN =60°,∴∠AEN =30°,∴AN =2,故选:A .13.如图,△ABC 中,AD 垂直BC 于点D ,且AD =BC ,BC 上方有一动点P 满足S △PBC =12S △ABC,则点P 到B 、C 两点距离之和最小时,∠PBC 的度数为( )A .30°B .45°C .60°D .90° 【解答】解:∵S △PBC =12S △ABC ,∴P 在与BC 平行,且到BC 的距离为12AD 的直线l 上, ∴l ∥BC ,作点B 关于直线l 的对称点B ',连接B 'C 交l 于P ,如图所示:则BB '⊥l ,PB =PB ',此时点P 到B 、C 两点距离之和最小,作PM ⊥BC 于M ,则BB '=2PM =AD ,∵AD ⊥BC ,AD =BC ,∴BB '=BC ,BB '⊥BC ,∴△BB 'C 是等腰直角三角形,∴∠B '=45°,∵PB =PB ',∴∠PBB '=∠B '=45°,∴∠PBC =90°﹣45°=45°;14.如图,在等腰△ABC中,AB=AC,BC=8,作AD⊥BC于点D,AD=12AB,点E为AC边上的中点,点P为BC上一动点,则P A+PE的最小值为4.【解答】解:∵AB=AC,BC=8,AD⊥BC,∴BD=CD=4,延长AD至A',使AD=A'D,连接A'E,交BC于P,此时P A+PE的值最小,就是A'E的长,∵AD=12AB,AA′=2AD,∴AA'=AB=AC,∵AD=A'D,AD⊥CD,∴AC=A'C,∴△AA'C是等边三角形,∵E是AC的中点,∴A'E⊥AC,∴A'E=CD=4,即P A+PE的最小值是4,故答案为:4.15.如图,点P是∠AOB内任意一点,OP=5cm,点M、N分别是OB、OA边上的点,当△PMN周长的最小值是5cm时,则∠AOB=30°.【解答】解:分别作点P关于OA、OB的对称点D、C,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:∵点P关于OA的对称点为D,∴PM=DM,OP=OD,∠DOA=∠POA,∵点P关于OB的对称点为C,∴PN=CN,OP=OC,∠COB=∠POB,∴OC=OP=OD=5,∠AOB=12∠COD,∵△PMN周长的最小值是5cm,∴PM+PN+MN=5,∴DM+CN+MN=5,即CD=5,∴OC=OD=CD,即△OCD是等边三角形,∴∠COD=60°,∴∠AOB=30°;故答案为30°.16.如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点N,交AB于点M,AB=12cm,△BMC的周长是20cm,若点P在直线MN上,则P A﹣PB的最大值为()A.12cm B.8cm C.6cm D.2cm【解答】解:∵MN垂直平分AC,∴MA=MC,又∵C△BMC=BM+MC+BC=20cm,BM+MA=AB=12cm,∴BC=20﹣12=8(cm),在MN上取点P,∵MN垂直平分AC连接P A、PB、PC∴P A=PC∴P A﹣PB=PC﹣PB在△PBC中PC﹣PB<BC当P、B、C共线时,即P运动到与P'重合时,(PC﹣PB)有最大值,此时PC﹣PB=BC=8cm.故选:B.17.如图,AB=AC=8,∠BAC=110°,AD是∠BAC内的一条射线,且∠BAD=25°,P 为AD上一动点,则|PB﹣PC|的最大值是8.【解答】解:如图.作点B关于射线AD的对称点B',连接AB'、CB'.则AB=AB',PB'=PB,∠B'AD=∠BAD=25°,∠B'AC=∠BAC﹣∠BAB'=110°﹣25°﹣25°=60°.∵AB=AC=8,∴AB'=AC=8,∴△AB'C是等边三角形,∴B'C=8,在△PB'C中,|PB'﹣PC|≤B'C,当P、B'、C在同一直线上时,|PB'﹣PC|取最大值B'C,即为8.∴|PB﹣PC|的最大值是8.故答案为:8.思考题1.如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为()A.10°B.20°C.40°D.60°【解答】解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,∴∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,∴∠QPN=12(180°﹣α)=∠AOB+∠MQP=20°+12(180°﹣β),∴180°﹣α=40°+(180°﹣β),∴β﹣α=40°,故选:C.2.如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN的度数为()A.15°B.22.5°C.30°D.47.5°【解答】解:如图1中,作CH⊥BC,使得CH=BC,连接NH,BH.∵△ABC是等边三角形,AD⊥BC,CH⊥BC,∴∠DAC=∠DAB=30°,AD∥CH,∴∠HCN=∠CAD=∠BAM=30°,∵AM=CN,AB=BC=CH,∴△ABM≌△CHN(SAS),∴BM=HN,∵BN+HN≥BH,∴B,N,H共线时,BM+BN=NH+BN的值最小,如图2中,当B,N,H共线时,∵△ABM≌△CHN,∴∠ABM=∠CHB=∠CBH=45°,∵∠ABD=60°,∴∠DBM=15°,∴∠MBN=45°﹣15°=30°,∴当BM+BN的值最小时,∠MBN=30°,故选:C.。
最短路径问题专项练习题

AB最短路径问题专项练习共13页,全面复习与联系最短路径问题一、具体内容包括:蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题;线段(之和)最短问题;二、原理:两点之间,线段最短;垂线段最短。
(构建“对称模型”实现转化)1.最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.为了证明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′,证明AC+CB<AC′+C′B.如下:证明:由作图可知,点B和B′关于直线l对称,所以直线l是线段BB′的垂直平分线.因为点C与C′在直线l上,所以BC=B′C,BC′=B′C′.在△AB′C′中,AB′<AC′+B′C′,所以AC+B′C<AC′+B′C′,所以AC+BC<AC′+C′B.【例1】在图中直线l上找到一点M,使它到A,B两点的距离和最小.分析:先确定其中一个点关于直线l的对称点,然后连接对称点和另一个点,与直线l的交点M即为所求的点.解:如图所示:(1)作点B关于直线l的对称点B′;(2)连接AB′交直线l于点M.(3)则点M即为所求的点.点拨:运用轴对称变换及性质将不在一条直线上的两条线段转化到一条直线上,然后用“两点之间线段最短”解决问题.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点到直线上某点的距离和最小这个核心,所有作法都相同.警误区 利用轴对称解决最值问题应注意题目要求 根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.解决这类最值问题时,要认真审题,不要只注意图形而忽略题意要求,审题不清导致答非所问.3.利用平移确定最短路径选址选址问题的关键是把各条线段转化到一条线段上.如果两点在一条直线的同侧时,过两点的直线与原直线的交点处构成线段的差最大,如果两点在一条直线的异侧时,过两点的直线与原直线的交点处构成的线段的和最小,都可以用三角形三边关系来推理说明,通常根据最大值或最小值的情况取其中一个点的对称点来解决.解决连接河两岸的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.在解决最短路径问题时,我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上,从而作出最短路径的方法来解决问题.【例2】 如图,小河边有两个村庄A ,B ,要在河边建一自来水厂向A 村与B 村供水.(1)若要使厂部到A ,B 村的距离相等,则应选择在哪建厂? (2)若要使厂部到A ,B 两村的水管最短,应建在什么地方?分析:(1)到A ,B 两点距离相等,可联想到“线段垂直平分线上的点到线段两端点的距离相等”,又要在河边,所以作AB 的垂直平分线,与EF 的交点即为符合条件的点.(2)要使厂部到A 村、B 村的距离之和最短,可联想到“两点之间线段最短”,作A (或B )点关于EF 的对称点,连接对称点与B 点,与EF 的交点即为所求.解:(1)如图1,取线段AB 的中点G ,过中点G 画AB 的垂线,交EF 于P ,则P 到A ,B 的距离相等.也可分别以A 、B 为圆心,以大于12AB 为半径画弧,两弧交于两点,过这两点作直线,与EF 的交点P 即为所求.(2)如图2,画出点A 关于河岸EF 的对称点A ′,连接A ′B 交EF 于P ,则P 到A ,B 的距离和最短.【例3】 如图,从A 地到B 地经过一条小河(河岸平行),今欲在河上建一座与两岸垂直的桥,应如何选择桥的位置才能使从A 地到B 地的路程最短?思路导引:从A 到B 要走的路线是A →M →N →B ,如图所示,而MN 是定值,于是要使路程最短,只要AM +BN 最短即可.此时两线段应在同一平行方向上,平移MN 到AC ,从C 到B 应是余下的路程,连接BC的线段即为最短的,此时不难说明点N即为建桥位置,MN即为所建的桥.解:(1)如图2,过点A作AC垂直于河岸,且使AC等于河宽.(2)连接BC与河岸的一边交于点N.(3)过点N作河岸的垂线交另一条河岸于点M.则MN为所建的桥的位置.4.生活中的距离最短问题由两点之间线段最短(或三角形两边之和大于第三边)可知,求距离之和最小问题,就是运用等量代换的方式,把几条线段的和想办法转化在一条线段上,从而解决这个问题,运用轴对称性质,能将两条线段通过类似于镜面反射的方式转化成一条线段,如图,AO+BO=AC的长.所以作已知点关于某直线的对称点是解决这类问题的基本方法.【例4】(实际应用题)茅坪民族中学八(2)班举行文艺晚会,桌子摆成如图a所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短?图a 图b解:如图b.(1)作C点关于OA的对称点C1,作D点关于OB的对称点D1,(2)连接C1D1,分别交OA,OB于P,Q,那么小明沿C→P→Q→D的路线行走,所走的总路程最短.5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键.先做出其中一点关于对称轴的对称点,然后连接对称点和另一个点,所得直线与对称轴的交点,即为所求.根据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值.破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方法.【例5】如图所示,A,B两点在直线l的两侧,在l上找一点C,使点C到点A、B的距离之差最大.分析:此题的突破点是作点A(或B)关于直线l的对称点A′(或B′),作直线A′B(AB′)与直线l交于点C,把问题转化为三角形任意两边之差小于第三边来解决.解:如图所示,以直线l为对称轴,作点A关于直线l的对称点A′,A′B的连线交l于点C,则点C即为所求.理由:在直线l上任找一点C′(异于点C),连接CA,C′A,C′A′,C′B.因为点A,A′关于直线l对称,所以l为线段AA′的垂直平分线,则有CA=CA′,所以CA-CB=CA′-CB=A′B.又因为点C′在l上,所以C′A=C′A′.在△A′BC′中,C′A-C′B =C′A′-C′B<A′B,所以C′A′-C′B<CA-C B.点拨:根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种BC ABLCD方法.三、例题:例1、①如右图是一个棱长为4的正方体木块,一只蚂蚁要从木块的点A沿木块侧面爬到点B处,则它爬行的最短路径是。
最短路径问题练习题

最短路径问题练习题最短路径问题是图论中的一个经典问题,主要研究在加权图中找到两个顶点之间的最短路径。
这个问题在实际生活中有广泛的应用,比如导航系统中的路线规划、网络中的数据传输等。
以下是一些关于最短路径问题的练习题,供同学们练习和思考。
练习题1:Dijkstra算法的应用给定一个包含6个顶点的图,顶点编号为1到6,边的权重如下所示:- 1-2: 7- 1-3: 9- 2-3: 14- 2-4: 10- 3-4: 15- 3-5: 6- 4-5: 11- 5-6: 2- 3-6: 20请使用Dijkstra算法找出从顶点1到顶点6的最短路径。
练习题2:Bellman-Ford算法的应用考虑一个包含5个顶点的图,顶点编号为A、B、C、D、E,边的权重如下所示:- A-B: 5- A-C: 3- B-C: 1- B-D: 2- C-E: 8使用Bellman-Ford算法计算从顶点A到顶点E的最短路径。
练习题3:Floyd-Warshall算法的应用给定一个包含4个顶点的图,顶点编号为1、2、3、4,边的权重如下所示:- 1-2: 4- 1-3: 5- 2-3: 3- 2-4: 7- 3-4: 2使用Floyd-Warshall算法计算所有顶点对之间的最短路径。
练习题4:有向图中的最短路径问题在一个有向图中,有5个顶点,编号为1到5,边的权重如下所示:- 1->2: 2- 1->3: 3- 2->3: 1- 2->4: 4- 3->4: 5- 3->5: 2- 4->5: 1找出从顶点1到顶点5的最短路径。
练习题5:负权重边的最短路径问题考虑一个包含4个顶点的图,顶点编号为1、2、3、4,边的权重如下所示:- 1-2: 10- 2-3: -3- 3-4: 1在这种情况下,使用Bellman-Ford算法找出从顶点1到顶点4的最短路径,并讨论负权重边对最短路径算法的影响。
八年级数学上册最短路径问题专项练习

最短路径问题专项练习一、单选题(共15题)1.如图所示,△ABC 中,AB=AC ,∠EBD =20°,AD=DE=EB ,则∠C 的度数为( )A .70°B .60°C .80°D .65°2.已知点M(-4,2),若点N 是y 轴上一动点,则M ,N 两点之间的距离最小值为( ) A .-4 B .2 C .4 D .-23.如图,直线l 是一条河,P ,Q 两地相距8km ,P ,Q 两地到l 的距离分别为2km ,5km ,欲在l 上的某点M 处修建一个水泵站,向P ,Q 两地供水.现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( ).A .B .C .D .4.如图,在矩形ABCD 中,AB =8,AD =6,动点P 满足PAB S =13S 矩形ABCD ,则点P 到A 、B 两点的距离之和PA+PB 的最小值为( )A .10B .C .D .5.在等腰ABC ∆中,AB AC =,D 、E 分别是BC ,AC 的中点,点P 是线段AD 上的一个动点,当PCE ∆的周长最小时,P 点的位置在ABC ∆的( )A .重心B .内心C .外心D .不能确定6.如图,长宽高分别为3,2,1的长方体木块上有一只小虫从顶点A 出发沿着长方体的外表面亮到现点B ,则它爬行的最短路程是( )AB .C .D .57.如图是放在地面上的一个长方体盒子,其中9,5,6AB BB B C ==''=',在线段AB 的三等分点E (A E=3)处有一只蚂蚁,''B C 中点F 处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )A .10BC .5+D .8.如图,一个长方体盒子紧贴地面,一只蚂蚁由A 出发,在盒子表面上爬到点G ,已知AB =6,BC =5,CG =3,这只蚂蚁爬行的最短路程是( )A .14B .10CD 9.如图,在△ABC 中,AB=AC=10,BC=12,AD=8,AD 是BC 边上的高.若P ,Q 分别是AD 和AC 上的动点,则PC+PQ 的最小值是( ).A .6B .8C .9.6D .1210.在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC 边上的动点,则MN+MC的最小值是().A B.C D.11.如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为()A.(-2012,2)B.(-2012,-2)C.(-2013,-2)D.(-2013,2)12.如图,∠AOB=60°,点P是∠AOB内的定点且M、N分别是射线OA、OB上异于点O 的动点,则△PMN周长的最小值是()A B C.6D.313.如图.在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN 的周长最小时,则∠AMN+∠ANM的度数为()A.84°B.88°C.90°D.96°14.如图,某公司有三个住宅区,A ,B ,C 各区分别住有职工10人,15人,45人,且这三个区在一条大道上(A ,B ,C 三点共线),已知AB =150m ,BC =90m .为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )A .点AB .点BC .点A ,B 之间D .点C15.某开发商的经适房的三个居民小区A 、B 、C 在同一条直线上,位置如图所示.其中小区B 到小区A 、C 的距离分别是70m 和150m ,现在想在小区A 、C 之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )A .小区AB .小区BC .小区CD .AC 的中点16.如图,在△ABC 中,AB =3,AC =4,AB ⊥AC ,EF 垂直平分BC ,点P 为直线EF 上一动点,则△ABP 周长的最小值是( )A .6B .7C .8D .12二、填空题(共6题) 17.如图,在等边ABC ∆中,D 是BC 的中点,E 是AB 的中点,H 是AD 上任意一点.如果10AB AC BC ===,AD =HE HB +的最小值是 .18.如图,在Rt △ABC 中,∠C=90°,∠ABC=30°,点D 是BC 边上的点,CD=1,将△ACD 沿直线AD 翻折,使点C 落在AB 边上的点E 处,若点P 是直线AD 上的动点,则PB+PE 的最小值是________.19.如图,在锐角ABC ∆中,7AC cm =,214ABC S cm ∆=,AD 平分BAC ∠,M ,N 分别是AD 和AB 上的动点,则BM MN +的最小值是_______cm .20.如图,等腰△ABC 底边BC 的长为6cm ,面积是24cm 2,腰AB 的垂直平分线MN 交AB 于点M ,交AC 于点N ,若D 为BC 边上的中点,E 为线段MN 上一动点,则△BDE 的周长最小值为____cm .21.如图,∠AOB=60°,点P 是∠AOB 内的定点且OP=4,若点M 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是_________.三、解答题(共4题)22.如图,在平面直角坐标系中,△ABC 各顶点的坐标分别为:A (﹣2,4),B (﹣4,2),C (﹣3,1),按下列要求作图,保留作图痕迹.(1)画出△ABC 关于x 轴对称的图形△A 1B 1C 1(点A 、C 分布对应A 1、C 1); (2)请在y 轴上找出一点P ,满足线段AP +B 1P 的值最小.23.如图所示,A ,B 是两个村庄,若要在河边l 上修建一个水泵站往两村输水,则水泵站应修在河边的什么位置,才能使铺设的管道最短?请说明理由.24.如图,ABC 三个顶点的坐标分别为()1,1A ,()4,2B ,()3,4C .(1)请画出ABC 关于y 轴对称后得到的111A B C △.(2)请写出点1A 及点1B 点1C 的坐标:1A ( , ),1B ( , )1C ( , ). (3)若P 点在x 轴上,当AP BP +最小时,直接写出AP BP +最小值为 . 25.七年级(1)班同学做游戏,在活动区域边OP 放了一些球(如图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?参考答案1.A2.C3.A4.C5.A6.C7.A8.B9.C10.A11.A12.D13.B14.D15.B 16.B17.18.3.19.4 20.1121.22.略23.作图见解析.24.(1)画图见解析;(2)(−1,1);(−4,2);(−3,4);(3)25.略。
最短路径问题专题练习含答案

·P
O
N
4、在一条河的两岸有两个村庄,现在要在河上建一座小桥,桥的方向于河流垂 直,设河的宽度不变,试问:桥架在何处,才能使从 A 到 B 的距离最短?
·A
·B
参考答案
一、选择题 1、C
二、填空题 2、3
三、解答题 1、作图略,作法:作 P 关于 OM 的对称点 P’,作 P 关于 ON 的对称点 P”,连接 P’P”,分别交 MO,NO 于 Q,R 两点,连接 PQ,PR,则 P’Q=PQ,PR=P”R, 则 Q,R 就是小桥所在的位置 2、作图略,作法:作 BB’垂直于河岸 GH,使 BB’等于河宽,连接 AB’,与河 岸 EF 相交于点 P,作 PD⊥GH,交 GH 于点 D,则 PD//BB’且 PD=BB’。于是四 边形 PDBB’为平行四边形,故 PB’=BD。根据“两点之间线段最短”,知 AB’ 最短,即 AP+BD 最短。因此桥应该建在 PD 上就符合题意了
2、在边长为 2 的正三角形 ABC 中,E,F,G 分别为 AB,AC,BC 的中点,点 P 为线
段 EF 上一个动点,连接 BP,GP,则△BPG 的周长的最小值为( )
三、解答题 3、公园内两条小河 MO,NO 在 O 处汇合,两河形成的半岛上有一处景点 P,现计 划在两条小河上各建一座小桥 Q 和 R,并在半岛上修三段小路连通两座小桥与景 点,这两座小桥应建在何处才能使修路费用最少?
最短路径问题专题练习
一、选择题 1、如图,点 P 为∠AOB 内一点,分别作点 P 关于 OA,OB 的对称点 P1 ,P2 ,连接 P1 P2 ,
交 OA 于 M,交 OB 于 N,若 P1 P2 =6,则△PMN 的周长为( ) A、4 B、5 C、6 D、7
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13.4课题学习最短路径问题
六街中学:罗云膑1.最短路径问题
(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.
如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.
(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.为了证明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′,证明AC+CB<AC′+C′B.如下:
证明:由作图可知,点B和B′关于直线l对称,
所以直线l是线段BB′的垂直平分线.
因为点C与C′在直线l上,
所以BC=B′C,BC′=B′C′.
在△AB′C′中,AB′<AC′+B′C′,
所以AC+B′C<AC′+B′C′,
所以AC+BC<AC′+C′B.
【例1】在图中直线l上找到一点M,使它到A,B两点的距离和最小.
分析:先确定其中一个点关于直线l的对称点,然后连接对称点和另一个点,与直线l 的交点M即为所求的点.
解:如图所示:(1)作点B关于直线l的对称点B′;
(2)连接AB′交直线l于点M.
(3)则点M即为所求的点.
点拨:运用轴对称变换及性质将不在一条直线上的两条线段转化到一条直线上,然后用“两点之间线段最短”解决问题.
2.运用轴对称解决距离最短问题
运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点到直线上某点的距离和最小这个核心,所有作法都相同.
警误区利用轴对称解决最值问题应注意题目要求根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.解决这类最值问题时,要认真审题,不要只注意图形而忽略题意要求,审题不清导致答非所问.
3.利用平移确定最短路径选址
选址问题的关键是把各条线段转化到一条线段上.如果两点在一条直线的同侧时,过两点的直线与原直线的交点处构成线段的差最大,如果两点在一条直线的异侧时,过两点的直线与原直线的交点处构成的线段的和最小,都可以用三角形三边关系来推理说明,通常根据最大值或最小值的情况取其中一个点的对称点来解决.
解决连接河两岸的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.
在解决最短路径问题时,我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上,从而作出最短路径的方法来解决问题.
【例2】如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村与B村供水.
(1)若要使厂部到A,B村的距离相等,则应选择在哪建厂?
(2)若要使厂部到A,B两村的水管最短,应建在什么地方?
分析:(1)到A ,B 两点距离相等,可联想到“线段垂直平分线上的点到线段两端点的距
离相等”,又要在河边,所以作AB 的垂直平分线,与EF 的交点即为符合条件的点.
(2)要使厂部到A 村、B 村的距离之和最短,可联想到“两点之间线段最短”,作A (或
B )点关于EF 的对称点,连接对称点与B 点,与EF 的交点即为所求.
解:(1)如图1,取线段AB 的中点G ,过中点G 画AB 的垂线,交EF 于P ,则P 到A ,
B 的距离相等.也可分别以A 、B 为圆心,以大于12
AB 为半径画弧,两弧交于两点,过这两点作直线,与EF 的交点P 即为所求.
(2)如图2,画出点A 关于河岸EF 的对称点A ′,连接A ′B 交EF 于P ,则P 到A ,B
的距离和最短.
【例3】 如图,从A 地到B 地经过一条小河(河岸平行),今欲在河上建一座与两岸垂
直的桥,应如何选择桥的位置才能使从A 地到B 地的路程最短?
思路导引:从A 到B 要走的路线是A →M →N →B ,如图所示,而MN 是定值,于是要
使路程最短,只要AM +BN 最短即可.此时两线段应在同一平行方向上,平移MN 到AC ,
从C 到B 应是余下的路程,连接BC 的线段即为最短的,此时不难说明点N 即为建桥位置,
MN 即为所建的桥.
解:(1)如图2,过点A 作AC 垂直于河岸,且使AC 等于河宽.
(2)连接BC 与河岸的一边交于点N .
(3)过点N 作河岸的垂线交另一条河岸于点M .
则MN 为所建的桥的位置.
4.生活中的距离最短问题
由两点之间线段最短(或三角形两边之和大于第三边)可知,求距离之和最小问题,就是
运用等量代换的方式,把几条线段的和想办法转化在一条线段上,从而解决这个问题,运用
轴对称性质,能将两条线段通过类似于镜面反射的方式转化成一条线段,如图,AO +BO =
AC 的长.所以作已知点关于某直线的对称点是解决这类问题的基本方法.
【例4】 (实际应用题)茅坪民族中学八(2)班举行文艺晚会,桌子摆成如图a 所示两直排
(图中的AO ,BO ),AO 桌面上摆满了橘子,OB 桌面上摆满了糖果,站在C 处的学生小明先
拿橘子再拿糖果,然后到D 处座位上,请你帮助他设计一条行走路线,使其所走的总路程
最短?
图a
图b
解:如图b.
(1)作C 点关于OA 的对称点C 1,作D 点关于OB 的对称点D 1,(2)连接C 1D 1,分别交
OA ,OB 于P ,Q ,那么小明沿C →P →Q →D 的路线行走,所走的总路程最短.
5.运用轴对称解决距离之差最大问题
利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键.先做出其中一点关
于对称轴的对称点,然后连接对称点和另一个点,所得直线与对称轴的交点,即为所求.根
据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值.
破疑点 解决距离的最值问题的关键 运用轴对称变换及三角形三边关系是解决一些
距离的最值问题的有效方法.
【例5】 如图所示,A ,B 两点在直线l 的两侧,在l 上找一点C ,使点C 到点A 、B
的距离之差最大.
分析:此题的突破点是作点A (或B )关于直线l 的对称点A ′(或B ′),作直线A ′B (AB ′)
与直线l 交于点C ,把问题转化为三角形任意两边之差小于第三边来解决.
解:如图所示,以直线l为对称轴,作点A关于直线l的对称点A′,A′B的连线交l 于点C,则点C即为所求.理由:在直线l上任找一点C′(异于点C),连接CA,C′A,C′A′,C′B.因为点A,A′关于直线l对称,所以l为线段AA′的垂直平分线,则有CA=CA′,所以CA-CB=CA′-CB=A′B.又因为点C′在l上,所以C′A=C′A′.在△A′BC′中,C′A-C′B=C′A′-C′B<A′B,所以C′A′-C′B<CA-C B.
点拨:根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.
仅供个人用于学习、研究;不得用于商业用途。
For personal use only in study and research; not for commercial use.
Nur für den persönlichen für Studien, Forschung, z u kommerziellen Zwecken verwendet werden.
Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.
толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.
以下无正文。
