静力学习题课.
静力学习题课

3-6:对空间任意两个力,一定能找到一根轴,使这两个力在该轴上
的投影分别为零,对否?
正确
精品资料
静力学习题课
3-7:空间任意(rènyì)力系向两个不同的点简化,试问下述情况是 否可能。
(1)主矢相等(xiāngděng) 可能 (,2主)矩主相矢等不(相xiā等n,g主dě矩n相g)等。。 不可能
力2-2偶:吗平?面力偶系向作用面内任一点简化的结果可能是什么?
一个力偶或平衡
2-3:平面任意力系向作用面内任一点简化的结果可能是什么?
一个力、一个力偶、一个力和一个力偶、平衡
2-4:平面平行力系向作用面内任一点简化的结果可能是什么?
一个力、一个力偶、一个力和一个力偶、平衡 2-5:平面任意力系向作用面内任一点简化,一般情况下,主矢和 主矩是否与简化中心的选择有关?
下述三种情况下,物块B、C将发生怎样的运动
?
A.F1<F<F2
B. F2<F<F1 C. F<F2<F1
B和C一起运动 C运动、B不动
B、C均不运动
精品资料
mg θ
F
C
B
A
D.对于任意平面平行力系,一定存在某平面汇交力系与之等效。 错 E.对于任意平面汇交力系,一定存在某平面平行力系与之等效。 对
F.对于任意平面汇交力系,一定存在某平面力偶系与之等效。 错
2-10:图示平面结构,AB//CD,各构件自重不计
F
,在刚体上作用一力偶,试判断下述说法的正误:
M
E
A.这是平面力偶系问题,因为平面力偶系只
的关C系为_______。
M
A θ
P θB
A.FNA=FNB
静力学1-2章习题课

1.压立体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
1.压力体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
2.绘压力体图
p0 A B
pa
1、图算法 2、重力场中流体静压强
的分布规律 3、压力体的绘制
2.答案:
p0 A
B
pa
1、图算法 2、重力场中流体静压强
v 1.075m s
0.4cm
D=12cm L=14cm
牛顿内摩擦定律
第一、第二章 (流体静力学) 习题课
一、流体的主要物理性质 二、重力场中流体静压强的分布规律
z p c
p p0 gh
三、液体的相对平衡 四、液体作用在平面上的总压力 五、液体作用在曲面上的总压力
第一、第二章 (流体静力学) 习题课
8.压立体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
习题: 1.液体的粘滞性只有在流动时才表现出来。( ) 2.在相对静止的同种、连通、均质液体中,等压面就是水平面。 () 3.某点的真空度为65000Pa,当地大气压为0.1MPa,该点的 绝对压强为( )
(a)65000Pa (b)55000Pa (c) 35000Pa (d)165000Pa
5.
1、等压面 2、重力场中流体静压强的分布规律
5.
1、等压面 2、重力场中流体静压强的分布规律
3.计算举例
1.
静止流体中应力的特性
静止流体中应力的特性
2.如图:
已知h1=20mm,
h2=240mm,
h3
h3=220mm, 求水深H。
水银
《理论力学》静力学典型习题+答案
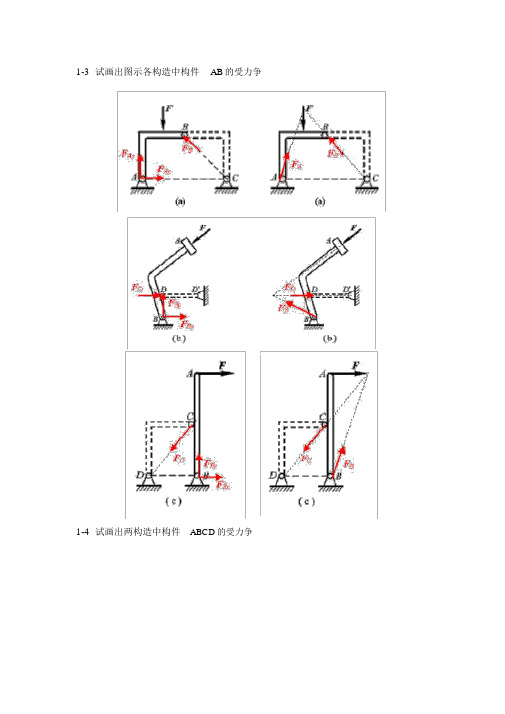
1-3 试画出图示各构造中构件AB的受力争1-4 试画出两构造中构件ABCD的受力争1-5 试画出图 a 和 b 所示刚系统整体各个构件的受力争1-5a1-5b1- 8 在四连杆机构的ABCD的铰链 B 和 C上分别作用有力F1和 F2,机构在图示位置均衡。
试求二力F1和 F2之间的关系。
解:杆 AB,BC, CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法 1( 分析法 )假定各杆受压,分别选用销钉 B 和 C 为研究对象,受力以下图:yyFBCC xB Fo45BCx30o o F60F2CDF AB F1由共点力系均衡方程,对 B 点有:F x0F2F BC cos4500对 C点有:F x0FBC F1 cos3000解以上二个方程可得:F12 6F2 1.63F23解法 2( 几何法 )分别选用销钉 B 和 C 为研究对象,依据汇交力系均衡条件,作用在 B 和C 点上的力构成关闭的力多边形,以下图。
F F2BCF AB o30o45CD60oFF BC F1对 B 点由几何关系可知:F2F BC cos450对 C 点由几何关系可知:F BC F1 cos300解以上两式可得:F1 1.63F22-3 在图示构造中,二曲杆重不计,曲杆AB 上作用有主动力偶 M。
试求 A 和 C 点处的拘束力。
解: BC为二力杆 ( 受力以下图 ) ,故曲杆 AB 在 B 点处遇到拘束力的方向沿BC 两点连线的方向。
曲杆AB遇到主动力偶M的作用, A 点和 B 点处的拘束力一定构成一个力偶才能使曲杆AB保持均衡。
AB受力以下图,由力偶系作用下刚体的均衡方程有(设力偶逆时针为正):M0 F A10a sin(450 )M 0F A0.354Ma此中:tan 1。
对 BC杆有:F C FB F A0.354M 3aA,C两点拘束力的方向以下图。
2-4解:机构中 AB杆为二力杆,点A,B 出的拘束力方向即可确立。
静力学习题课答案

【1】 梁AB 一端为固定端支座,另一端无约束,这样的梁称为悬臂梁。
它承受均布荷载q 和一集中力P 的作用,如图4-9(a )所示。
已知P =10kN , q =2kN/m ,l =4m ,︒=45α,梁的自重不计,求支座A 的反力。
【解】:取梁AB 为研究对象,其受力图如图4-9(b )所示。
支座反力的指向是假定的,梁上所受的荷载和支座反力组成平面一般力系。
在计算中可将线荷载q 用作用其中心的集中力2qlQ =来代替。
选取坐标系,列平衡方程。
)(kN 07.7707.010cos 0cos - 0A A →=⨯====∑ααP X P X X)(kN 07.11707.010242sin 2 0sin 2 0A A ↑=⨯+⨯=+==--=∑ααP ql Y P qlY Y )( m kN 28.404707.0108423sin 83 0sin 422ql 022A A ⋅=⨯⨯+⨯⨯=⋅+==⋅-⎪⎭⎫⎝⎛+-=∑l P ql m l P l l m M A αα力系既然平衡,则力系中各力在任一轴上的投影代数和必然等于零,力系中各力对任一点之矩的代数和也必然为零。
因此,我们可以列出其它的平衡方程,用来校核计算有无错误。
校核028.40407.114424242A A B =+⨯-⨯⨯=+⋅-⨯=∑m l Y l ql M 可见,Y A 和m A 计算无误。
【2】 钢筋混凝土刚架,所受荷载及支承情况如图4-12(a )所示。
已知kN 20 m,kN 2 kN,10 kN/m,4=⋅===Q m P q ,试求支座处的反力。
【解】:取刚架为研究对象,画其受力图如图4-12(b )所示,图中各支座反力指向都是假设的。
本题有一个力偶荷载,由于力偶在任一轴上投影为零,故写投影方程时不必考虑力偶,由于力偶对平面内任一点的矩都等于力偶矩,故写力矩方程时,可直接将力偶矩m 列入。
设坐标系如图4-12(b )所示,列三个平衡方程)(kN 3446106 06 0A A ←-=⨯--=--==++=∑q P X q P X X)(kN 296418220310461834 036346 0B B A ↑=⨯++⨯+⨯=+++==⨯--⨯-⨯-⨯=∑q m Q P Y q m Q P Y M)(kN 92920 00B A B A ↓-=-=-==-+=∑Y Q Y Q Y Y Y校核3462203102)9(6)34(6363266 C=⨯⨯+-⨯+⨯+-⨯--⨯=⨯+-++-=∑qmQPYXMAA说明计算无误。
静力学习题课
工 程 力 学
FCx2
静力学习题课
FCy2
M
F
F
C
( F ) 0,
0,
0,
FBx b FBy a M 0
工 程 力 学
FCx2
x
FBx FCx 2 0
y
FBy FCy 2 0
FCx 2 Pa M 1 qb 2b 2b 4
Pa M 1 FBx qb 2b 2b 4
工 程 力 学
Q 1 q a 2 2
FAx
MA
FBx
把分布力转换成集中力Q´,作用在E´点
1 BE a 3
静力学习题课
再以左半段为研究对象(含铰链B) FBy Q´ E´ FAy
工 程 力 学
FAx
MA
FBx
1 1 M B (F) 0 M A 4 q a 3 a FAy 2a 0
1 FAy FC F q 2a 0 Fy 0 2 1 7 M A (F) 0 M A FC 3a F 2a 2 q 2a 3 a 0
静力学习题课
再以左半段为研究对象(含铰链B)
工 程 力 学
静力学习题课
再以左半段为研究对象(含铰链B) FBy Q´ E´ FAy
解题过程: 起重机
Y A 48.33(kN)
系统整体
梁 CD
x
FAy FBy P 0
FAx FBx qb 0
P M qb 2 FAy 2 2a 4a
P M qb 2 FBy P FAy 2 2a 4a
静力学习题课
2. 再取AC为研究对象,受力分析如图所示。
5静力学习题课

a
a
A
a
a
静定构件
a
20
例5:
一梁由支座A以及BE、CE、DE三杆支撑.
已知:q = 0.5kN/m,a = 2m,梁与支撑杆的重量不计. 求:各杆内力。
寻找二力构件! DE CE BE
整体静定结构
21
1、整体上看,由于DE是二力杆,D的约束反力只
有一个,因此,整体为静定问题。
可求得:
FED
YC 5000 (N)
X 0 XC S FG cos450
整体静定结构
X C 10000 (N)
由m A 0 S DE sin451Q 2 0 S DE 14140 (N)
10
例1 一组合梁ABC 的支承及载荷如图示。已知 F=1 kN,M=0.5 kNm,求固定端A 的约束力。
② 力矩和力偶矩的区别: 力矩:是力对那一点的转矩, 与取矩点有关, 且不能在平面内 任意移动。 力偶矩: 它是在平面内和平行它自身平面内可任意移动,与取矩
点无关。
6
(二) 基本方程
平面
X 0 Y 0
空间
mA 0
X 0,m x ( F ) 0 Y 0,m y ( F ) 0 Z 0,m z ( F ) 0
B
FBy FBx
图(c)
29
整体静定结构
30
1.5m
1.5m
例8 已知 P=1200N,各杆与滑轮 自重不计, 轮的半径为r ; 求 支承A,B处的约束反力及杆 BC的内力
2m
2m
解 整体受力如图,有 XA
X 0, X A T 0 Y 0, YA P YB 0
YA
静力学习题课

解: 在图a和图b中总压力P的大小是相同的,仅作用 方向相反而已。 由于AB是个圆弧面,所以面上各点的静水压 强都沿半径方向通过圆心点,因而总压力P也必 通过圆心。
(1)先求总压力P的水平分力。
铅垂投影面的面积 Ax bh 1 2 2m2 投影面形心点淹没深度 hc h / 2 1m
2
2
(3)闸门上的合力作用中心(对闸门下端之矩)
lc P
b 2
gh1h1
/
s in
1 3
h1
/
s in
b 2
gh2 h2
/
s in
1 3
h2
/ sin
lc
1 P
b 6
g
/ sin 2 (h13
h23 )
lc
1 34.65
1 1 9.8 / sin 2 (45) (33 6
BD
lD
lc
d 2
0.514 m
重力作用线距转动轴B点的距离
l1
d 2
cos60
0.25m
启门力T到B点的距离 l2 2l1 0.5m
由力矩平衡方程 T l2 P BD G l1 解得 T 32.124KN
l1 P
D l2
lC lD
5.平面闸门AB倾斜放置,已知α =45°,门宽b=1m,
1P
y2 h1 h2 e
3
2.45m 0.72m 21.73m 2.45m
1P 3
3 2.11m
1.73m 2.45m 1 P
3
同理, y3 2.72m
静力学习题课

b:一定不 c:不一定
2013-8-15
23
BUAA
习题、例题、思考题
13、如图所示,刚性杆AB的A端用球铰链固定,B端用球铰链
和刚性杆BC连接,考虑杆的粗细。该系统的自由度为
a:2 b:3
。
c:4
d:5
e:6
2013-8-15
24
BUAA
并支撑在铅垂面内,则图
mg
FB
B
2mg mg
2013-8-15
O
tan
3L OC 4 sin 3 sin OB L cos 4 cos
3 f tan f min 4
17
BUAA
题8: 求桁架中杆1、3的内力。
FH
F1
FE
F
x
0
F3 FA
FD
F1 F
问题:若F力铅垂作用于 H点,哪些杆为零力杆?
M M
x
i
y z
( Fi ) 0 ( Fi ) 0
c:不一定是
MO x Fx
i
j y Fy
k z 0 Fz
M Ox yFz zFy 0 M Oy zFx xFz 0 M xF yF 0 y x Oz
26
2013-8-15
BUAA
2013-8-15
。
独立的平衡方程。 D:6个
9
B:4个;
C:5个;
BUAA
能列出几个独立的平衡方程?
B
FBC
FBN
W A
2013-8-15
10
BUAA
习题、例题、思考题
《理论力学》静力学典型习题+答案

1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F = 对C 点由几何关系可知: 0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4FF解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。
静力学习题课

B. F2 F1
C. F1 F2
。
,
自由矢量 C. 定位矢量 D. 滑动矢量
。
,
5
题型二:选择题
3、重 W 80 kN 的物体自由地放在倾角为 30 的斜面上, 若物体与斜面间的静摩擦系数 f 3 4 ,动摩擦系数
f d 0.4 ,则作用在物体上的摩擦力的大小为: C
静力学习题课
1
题型一:判断题
1、力可以沿着作用线移动而不改变它对物体的运动效应。 (×)
2、作用于刚体的力可沿其作用线移动而不改变其对刚体的 运动效应。 (√ )
3、若作用在刚体上的三个力的作用线汇交于同一点,则 该刚体必处于平衡状态。 (×) 4、凡是受到两个力作用的刚体都是二力杆。 (×)
5、用解析法求平面汇交力系的平衡问题时,所建立的坐标 系x,y轴一定要相互垂直。 (× )
A. 27.7kN B. 40kN
。
C. 30kN D. 0
,
6
题型二:选择题
α 4、一重W 的物体置于倾角为 的斜面上,若摩擦因数为f, A 且 tgα < f , 则物体 ;
若增加物体重量,则物体 A ;
若减轻物体重量,则物体
A. 静止不动; B. 向下滑动;
A
。
,
C. 运动与否取决于平衡条件。
7
题型三:填空题
1、沿边长为 a=2m 的正方形各边分别作用有 F1, F 2 , F 3 , F 4 ,
主矢大小为 , 主矩大小为 16 kN· m 。
且 F 1 F 2 F 3 F 4 4kN , 该力系向B点简化的结果为:
0
m 向D点简化的结果是什么? FR=0; MD=16 kN·
习题课-静力学

习题课-静力学
3.图示力偶中等效的是(B)
NEFU- Junkai Lu
(A) a和c (B) a和b (C) b和c (D) b和d
36Fd顺
36Fd顺
36Fd逆
48Fd顺
4.关于力对点之矩的说法,下列哪个是错误的(B)
(A) 互相平衡的两个力,对同一点之矩的代数和等于零。
(B) 力对点之矩与力的大小和方向有关,而与矩心位置无关。
4.关于力对点之矩的说法,下列哪个是错误的( ) (A) 互相平衡的两个力,对同一点之矩的代数和等于零。 (B) 力对点之矩与力的大小和方向有关,而与矩心位置无关。 (C) 力的数值为零、或力的作用线通过矩心时,力矩均为零。 (D) 力对点之矩不会因为力矢沿其作用线移动而改变。
10
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
10. 力系的平衡
平面任意力系
Fx 0
Fy 0
M o 0
Fx 0
M A 0
M B 0
A、B两点 连线不得 与投影轴 x轴垂直
空间任意力系
Fix 0 Fiy 0 Fiz 0
(C) 力的数值为零、或力的作用线通过矩心时,力矩均为零。
(D) 力对点之矩不会因为力矢沿其作用线移动而改变。
力有关,力偶无关
11
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
5.图示正方体顶角上作用着六个大小相等的力,此力系向任一点简化的结 果是( )
D
F3
理论力学 静力学部分习题课

AC 1 MAy 0,FCz AC P 2 2 0, FCz 2 P 2 AC 1 MCy ' 0,( P1 FAz) AC P 2 2 0, FAz P1 2 P 2
Fx 0,F
Ax
FCx 0
(2)杆AB 为研究对象,受力及坐标如图所 示
取曲杆为研究对象受力及坐标如图列平衡方程fxayazazaydzazdyaydxdzdydxayazfxayazdzdydzazdyaydxdzdydxayaz方法二321和bc分别重p1和p2其端点a用球铰固定在水平面上另1端b由球铰链相连接靠在光滑的铅直墙上墙面与ac平行如图的支座约束力以及墙上点b所受的压力
12.图示三铰刚架受力 F 作用,则A支座约束力的大小 为___________,B支座约 束力的大小为__________。
2 F 2
2 F 2
13.正三棱柱的底面为等腰三角形, 已知OA=OB=a,在平面ABED内有 沿对角线AE的一个力,图中,此 力对各坐标轴之矩 M (F ) 0 为: ; 2 M (F ) Fa 。 2
解:AB 和BC 两杆为研究对象,受力及坐标如图所示。 由于未知力较多,尽可能用 轴矩式平衡方程(需保证方 程独立)求解,力求使取矩 轴与较多的未知力相交和平 行,从而使方程中所含未知 量最少。
1 MCz ' ' 0,( FN FAy) AC 0, FAy FN 2 ( P1 P 2)
x
y
结束
题2-46图 (a)所示结构AC、DF、BF及EC四杆组成,其中A、B、 C、D,E及F均为光滑铰链。各杆自重不计。试求支座A、D的 反力及杆BF、EC所受的力。
第I篇 静力学习题课ppt课件

D
F DB F D B
B
FF P
F AB
解:对象:D点;受力:如左图;方程:
Fx 0, F Ec Do sF D B0对象:B点;受力:如右图;方程:
Fy 0, F ED sinF P0 Fx 0, F CsBinF D B 0
FDBtaFn10FP
Fy 0, F Cc B o sFAB 0
F AB tF a D n BF DB 10.F 1 0 P8k 0N#
附录1: 第3章习题解答
补充习题2
补充习题2 图示结构。试求:铅直杆AO上的铰链A、C和O所受的约束力。
a
a
F
F
F'Cy
F FR
F'Cx
C
E
D
FOy
a
a
FOx
FBy O
FBx
解:对象:整体
受力:如图
方程:
M B(F)0, 2aFOy0,
对象:杆CD
受力:如图
FOy 0
# (1)
方程:
M E ( F ) 0 , a F C y a F 0F,CyFFCy#(2)
附录1: 第3章习题解答
3-6
解:对象:图(a)中梁 受力:如图所示 方程:
(b)
FC
FD
O
FB
MO(F)0
6 F C 4 F 1 M 2 F 2 c3 o 0 s 0
FC3.45kN #
MB(F)0
8 F C 6 F 1 M 4 F D s4 i n 2 5 F 2 s3 i n 0 0
M O ( F ) 0 , a F C F x2 a 0FC ,x2FFCx# (3)
附录1: 第3章习题解答
《静力学习题答案》课件

04
力的矩和力矩平衡
力矩的概念和性质
总结词 理解力矩的概念和性质是解决静 力学问题的关键。
力矩的简化表达 在静力学中,通常使用标量表达 力矩,即力矩等于力和垂直于作 用线到转动轴距离的乘积。
力矩的定义 力矩是力和力臂的乘积,表示力 对物体转动作用的量。
静力学基本原理
二力平衡原理
三力平衡定理
一个刚体受两个力作用处于平衡状态 时,这两个力必定大小相等、方向相 反且作用在同一直线上。
一个刚体受三个力作用处于平衡状态 时,这三个力必构成一平面三角形, 且其中任意两个力的合力与第三个力 大小相等、方向相反。
力的可传递性原理
对于通过刚体中心的力,加在刚体上 的力可以沿其作用线移至刚体上任一 点,而不改变该力对刚体的作用效应 。
思维拓展
对于进阶习题,答案解析将不仅局限 于题目的解答,还将进行适当的思维 拓展,引导学生思考更多可能性,培 养其创新思维和解决问题的能力。
进阶习题答案解析
解题技巧
针对进阶习题的特点,答案解析将总结和提炼一些实用的 解题技巧和方法,帮助学生更快更准确地解答题目。
进阶习题答案解析
习题答案
进阶习题答案解析同样将提供完整的 习题答案,并附有详细的解题过程和 思路,方便学生参考和学习。
静力学问题分类
平面问题与空间问题
平面问题是指所有外力都作用在物体某一平面内的问题, 空间问题则是指外力作用在物体三维空间内的问题。
静定问题与静不定问题
静定问题是根据给定的静力平衡条件能够完全确定物体所 有未知力的问题;静不定问题则是不能完全确定未知力的 数量或方向的问题。
刚体问题与变形体问题
刚体问题是指研究刚体的平衡问题,变形体问题则是指研 究物体在受力后发生变形的问题。
理论力学静力学典型习题+答案

1-3试画出图示各结构中构件AB的受力图1-4试画出两结构中构件ABCD勺受力图1-5试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD勺铰链B和C上分别作用有力F i和F2,机构在图示位置平衡。
试求二力F1和F2之间的关系。
解:杆AB BC CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B和C为研究对象,受力如图所示:由共点力系平衡方程,对B点有:F x 0 F2F BC COS45°0对C点有:F x 0 F BC F1COS300 0解以上二个方程可得:F12 6F 1.63F2解法2(几何法)分别选取销钉B和C为研究对象,根据汇交力系平衡条件,作用在B和C点上的力构成封闭的力多边形,如图所示。
对B点由几何关系可知:F2F BC COS450对C点由几何关系可知:F BC F1 COS300解以上两式可得:F1 1.63F22-3在图示结构中,二曲杆重不计,曲杆AB上作用有主动力偶M试求A和C 点处的约束力。
解:BC为二力杆(受力如图所示),故曲杆AB在B点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB受到主动力偶M的作用,A点和B点处的约束力必须构成一个力偶才能使曲杆AB保持平衡。
AB受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):M 0 F A 10a sin(450) M 0 F A 0.354M其中:tan -。
对BC杆有:F C F B F A 0.354M3 aA,C两点约束力的方向如图所示。
2-4解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下 刚体的平衡条件,点 0,C 处的约束力方向也可确定,各杆的受力如图所示。
对1313 -6aFFi FjF 2 FiF 3- F i - —Fj2 222F RFi3Fj M A■-3 Fak F R M A V3 d a F R2Fi24d3 a F X 0 PsinFB X0 F y 0 F By P P cos0 F X 04F A X F B X 0F y 0F AyF By0 M A 0 MA F Byl 0求解以上三式可得:M 1 3N m , F ABF OF C 5N ,方向如图所示Psi nAF BxF AxBC 杆有:M 0对AB 杆有: F B F AF B BC sin300 M 2对OA 杆有:M 0 M i F AOA 0F By , MFA X,FAy, FBX, M A 0 N D aG -cos F l coscos2F y 0 N D cosG F 0N D ,arccosf 2(F (2FG)a 卡G)l ]F Ay F By P(1 COS ) M A P(1 cos )1M y O p eta n F BC cos c F BC sin eta n 0 F BC60.6N 2M x' 0 P 1 aF B c F BC S in2a 0 F B100N F y 0 F Z0F Ay,F A;z M x 0 M DE 0 F2COS4500 F20 M AO 0 F6COS45° a F COS450 COS450 a 0 F6 2 F M BH 02F4COS450 a F6COS450 a 0 F4 2F M AD 02F1 a F6COS450 a F sin450 a 0 £ 1 2 F M CD 02F1 a F3 a F sin45°a 0 F3 1F M BC 02F x 0F3 a F5 a F4COS450 a 0 F50 M 1500N cm Fy 0M O0以下几题可看一看!FA , F NA , FB , F NB ,tan3( f sif s2)FNB 0ta n 6002aM cf s2f si2 3F By 2a 0 F ByM H 0 F D y a Fa 0 F Dy FM BF DX a F 2a 0 F DX2FF y 0F AyF DyF By 0F AyF M A0 FD X a FB X 2aFB XFM BF AX 2aFD Xa0 FA XFM c 0 F D bF XF D-F M A0 F B bF XbF i F 2 (F i2Mpcos45° psin45° F 2)DF N 2 N iF i F 2f s N i f s N 2F i ,N i ,F 2,N 2, f s:s 2p D F e f 2M0 f siF By0.223, f s2 4.49 FB x N iP(i _f s2) _2( i —f ;2)f s%.223450F xF yM AT cosAC sinF N T sinF s T cos pT sin AC cosAB . sin 2FN , F s , T, fsf s 0.646a l . a几F NB a Pcos-Psi n 022 3F NA a P cos-Psin a 小 —— 02 2、3 F AF BPsi nM A 0M B 0 F x 0F A F Bf si F NAS 2F NBS24.49 i2MF D )b F ACAyD 2MF (bF 2x)F B F I F AAa b F A F 3 FxAy F i F 3 cos450F 1M2qa F yF 2aF2 Z M r ( 2qa) F x 0 FAXF 3 cos45(F AX(MaaF AyF 2 F 3si n450 P 4qa 0F AyP 4qa M A F 2 a P 2a 4qa 2a F 3S in450 '3aMM A 24qa 2 Pa M M A0 F By 2a F2a 0 F ByF Ay 2a F 2a 0 F A 『FF x 0 F AXFBx FF 32qa) F 0 F EF2 M C 0 F Bx a F By aV 2(MF AX2q x a) a F E sin450 a 0 F BxM eM BF By FF NDF 3 sin450F yM AM B0F BXM AN 13r P 3rcos60020 N i 6.93(N)F xFA XN 1 sin 60°F AX 6(N) F y 0F AyN 1cos600P 0 F Ay 12.5'(N) FN 1cos300 Tcos300 6.93(N)M A F N 2Lsin2P -cos2 M BF N LsinP Lcos F s Lcos2F S P F SFNtan100 F RC ,F RD F RC , F RD F RC , F RD2 2M A 0 F ND aI 0F ND44M A0F NC a F l 0F NC -FF NDaM O 0 F SC R F SD R 0FNCF X 0sinF — ----------- F----- FS D NCN D1 cos 1 cossin 1 costan —, f SD tanFRC,F2 221 cosF RCSDF NDF SD 0tan — 2 I FaFla cos —2PF RCsi n[180°(1800 2,sin ] ftanFl sinISD (Pa Fl )(1 cos )F yF NDP F SC sin F ND PFl ( (cosasin tan —)2f SD tanFl sin(Pa Fl )(1 cos )F B F ACFBF AC tan1 F3(F ND P) R MDF B \M E (P F NE )1RtanF NDM D M E!FRM DF NDBPL FaM AM EF yF x 4 f sP 4f sP } f s ,1 3f s }F SC%F X0 F NC costa nFl sin (Pa Fl )(1 cos )F NCsinF SC cos F SD 0FNDFSDM E 1FFNE F NE F SD tan2FNDF min{ —P,」 P,R R 3 1 F SD F NE F SE F 02P R M DF SE RF SD 3FFSDf s F ND M FM GF SE;FF SE f s F NEF max 0.362.该系统的位置可通过杆OA 与水平方向的夹角B 完全确定,有一个自由度。
静力学习题课概论

YB
Y 0 YA YD YB 0
YA YD YB P 0 P
∴ X D 2P (→) X A P (←) X B P (←) YD P (↑) YA P ( ↓ ) YB 0
静力学习题课
静力学习题课
静力学习题课
力系
空间力系
平面力系
汇 交 力 系
力 偶 系
平
任
行
意
力
力
系
系
静力学习题课
静力学主要内容
受力分析 力系的等效 力系的简化 力系的平衡
静力学习题课
一 受力分析 1、取研究对象(分离体)——将所要研究的物体 从周围物体中单独拿出来,
2、在其上画出所有的主动力和所有的约束反力。
注意:不论采用哪种 形式的平衡方程,其 独立的平衡方程的个 数只有三个,对一个 物体来讲,只能解三个 未知量,不得多列!
A、B、C 不共线
静力学习题课
平面平行力系的平衡方程
平面平行力系的平衡方程为: Y 0
mO (Fi )0
一矩式
mA (Fi ) 0 二矩式
mB (Fi ) 0
条件:AB连线不能平行 于力的作用线
MA
FAy
AM
FAx a
B
F
F 600
C
C
a
Fx 0
FAx
2、研究BC杆,画受力图
3、再研究整体
FBy
B
F
600
FC
C
FBx a
MB 0
FC
Fy 0
FAy
MA 0
MA
静力学习题课
[例] 已知:构架ABC由AB、AC 、AF三杆组成,受力及尺寸
如图所示。DF杆上的销子E可在 AC
静力学习题课

定研究对象:梁BCD 定问题性质:平面 建立参考坐标系: 受力分析 主动力简化
约束力正向
平衡方程
y
O
F
q C
M D
A
B a a F1 F
x
F2 qa
圆柱铰 动铰支座
a
FOy
FAy
a
FCy
M
未知数与方程个数的分析: 3/3
FOx
a M B ( Fi ) 0, FCy a M F2 0
M=284.9N.m
FAx’
▲ FAy’
方法三:
M
FAy
⑴ 研究 AB 杆与推板 O1C 组成 的局部,受力如图,列平衡方程求 解(间接应用三力平衡汇交定理或二 力平衡公理确定FO 的指向):
1
FAx FO
1
M
K
( F ) 0,
FAy
M FOy FOx
⑵ 研究轮 O
M
( F ) 0, ② M=284.9N.m
M FOy F qa a
力系的平衡/刚体系平衡/解
讨论:
定研究对象:梁BCD
主动力的处理
y
O
F
q C
M D
A
B a a
x
M
a
a
M
F
M
F1 F
M
M
■
14、图所示一结构由AB、BC 与CE 三个构件构成,E 处有一滑轮,细 绳通过该轮悬挂一重为 12 kN 的重 物,A为固定铰支座,B 为滑动铰支 座,C、D 与E 为圆柱铰,AD = BD = l1= 2m,CD = DE = l2= 1.5m,不 计杆件与滑轮的重量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
半径为 a 的的无底薄圆筒置于光滑水平面上,筒内装
有两球,球重均为 P,半径为 r,如图示。问圆筒的重量 Q 多大时圆筒不致翻到?
8
试求图示各桁架上标有数字的各杆的力。
9
棒料重 Q=500N、直径 D=24cm,棒料与 V 型槽面间的摩擦
系数 f =0.2,如图所示。试求转动棒料的最小力偶矩 m。
10
绞车卷筒及制动器的尺寸如图示。若闸瓦与轮
缘间的摩擦系数为 f ,求保持系统平衡时,卷筒轴上 的制动力矩 M 与作用在操纵杆上的力 P 之间的关系。
6
构架的尺寸及载荷如图示,试求G处的反力。
7 在大型水工试验设备中,采用尾门控制下游水位,如图 示。尾门AB在A端用铰链支持,B端系以钢索BE,铰车E可 以调节尾门AB与水平线的夹角,因而也就可以调节下游的 水位。已知=60、=15,设尾门AB长度为a=1.2m、宽 度b=1.0m、重为P=800N。求A端约束力和钢索拉力。
11
梯子重 G、长为 l,上端靠在光滑的墙上,底端与
水平面间的摩擦系数为 f 。(1)已知梯子倾角,为使梯 子保持静止, 问重为 P 的人之活动范围多大?(2)倾角
多大时,不论人在什么位置梯子都保持静止。
Q=60度时,保持平衡所需的液压缸的推力。
AD, B, E 5152
3
静定多跨梁的载荷尺寸如图示,长度单位为 m,
求支座反力和中间铰的压力。
4 组合梁由AC和DC两段铰接构成,起重机放在梁上。已 知起重机重P1 =50KN,重心在铅直线EC上,起重载荷P2 =10KN。不计梁重,求支座A、B和D三处的约束力。
5 在图示结构中,A、E为固定铰支座,B为滚动支座,C、 D为中间铰。已知F及q,试求A、B两处的反力。
