资金的等值计算
第二章第二节资金的等值计算13春

(2)利率
• 概念
简称利率,是一定时期内(一年、半年、 月、季度,即一个计息周期)利息总额与本金 (借贷金额)的比率 。 利率=期利息(I1) *100% 本金(P) 利率是单位本金经过一个计息周期后的增殖额。 (年利率、半年利率、月利率,……)
利息的计算-单利/复利
引入: 现在存入100元,存期3年,每年计息 一次,年利率10%,计算第1年、第2年的 利息。 第一年的利息=100×10%=10 第二年的利息= 已产生的利息 10元是否计息
20 18 16 14 12 10 8 6 4 2 0 0 5 10 15 20 25 30 年数
单利 复利
本利和
6.名义利率和实际利率
(1)名义利率(Nominal Interest Rate) 问题提出 在技术经济分析中,复利计算通常以年为计息 周期。但在实际经济活动中,计息周期有年、半 年、季、月等多种,这样出现了不同计息周期的 利率换算问题。 如:按月计算利息,且其月利率为1%,通常 称为“年利率12%,每月计息一次”。这个年利率 12%称为“名义利率”。
名义年利率:一年的利息额是按单利计算的;
实际年利率:一年的利息额是按复利计算的;
当一年中多次计息时(即m>1时),两者产生差异;
二、资金等值
资金的时间价值引发的问题:
2000
0 1 2 3 4 5
3000
5000
-不能直接比较不同时间点的资金的价值大小。 -需要利用等值换算,将不同时点的资金换算到同 一时点进行比较。
r m i lim (1 ) 1 m m r e 1
若名义年利率为12%,以下各种情况下,实际 年利率等于多少?
按年计息,m=1 按半年计息,m=2 按季度计息,m=4
资金等值计算名词解释

资金等值计算名词解释
资金等值计算
资金等值计算是一种通过计算把一个具体的资金量转换为另外一种资金量的过程,主要用于企业或者个人的财务管理中的计算和决策。
资金等值计算通常是在一个特定的日期上运行,以确定在当下价值上,某一金额所具有的购买力。
历史成本法:历史成本法是按照金钱的历史价值来计算资金等值的方法,即一件收到的物品的历史价值就是一定的资金等值,从而可以以此类推到其他物品的历史价值上。
例如,一家企业在某日的价值1000元,那么在某日之前支出的费用也会按照1000元来计算,而不是按照今日的实际价值计算。
现在价值计算:现在价值计算是按照金钱当前价值来计算资金等值的方法,即一件收到的物品的当前价值就是一定的资金等值,从而可以以此类推到其他物品的现在价值上。
例如,一家企业在某日的价值1000元,那么在某日之前计划支出的费用和其他投资,就可以按照1000元的现在价值来计算它们的经济价值。
风险投资法:风险投资法是按照投资风险来计算资金等值的方法,即把某一风险等级的资金计算为某一数量的资金等值。
例如,对于高风险投资机会来说,可以把3000万元的资金收益计算为200万元的等值资金。
变现价值法:变现价值法是按照金钱未来价值来计算资金等值的方法,即可以把现在的资金计算为将来某一时间点上的资金等
值。
例如,把今天的3000万元,计算为未来三年后可以变现的8000万元的资金等值。
备用:资金等值计算六个公式

资金等值计算公式
2. 等额分付复利公式 (1)等额分付终值公式 0 1 A 2 3 …
F =?
n
F A(1 i ) n 1 A(1 i ) n 2 A(1 i ) A A[1 (1 i ) (1 i ) n 2 (1 i ) n 1 ] 1[1 (1 i ) n ] A 1 (1 i ) (1 i ) n - 1 A i (1 i ) n - 1 其中 称为等额分付终值系数 ,用( F / A, i, n)表示。 i
第2章 资金等值计算/2.2资金等值计算 2.2.2 资金等值计算公式
2. 等额分付复利公式 (2)等额分付偿债基金公式 0 1 2 A=? 3 … F n
(1 i ) n 1 F A i i AF (1 i ) n 1 i 称为偿债基金系数,用 ( A / F , i , n)表示。 n (1 i ) 1
70
解:X = -100(F/P, 0.10, 3)-70(F/P, 0.10, 2) +90(P/F, 0.10, 1)+150(P/F, 0.10, 4) = -100(1.331)-70(1.21)+90(0.9091)+150(0.6830) = -133.1-84.7+81.819+102.45 = -33.531 (万元)
1. 一次支付复利公式 (2)一次支付现值公式 例:某人打算在5年后买100000元的车,已知年利率为10%,那么他现在需 在银行存多少钱? 解: F =100000,i =10%, n =5年 P = F(1+i)-n = F(P/F, i, n) = 62092 (元) 0 P=? 1 2 3 4 5 F=100000
技术经济学_资金等值计算

相关基本概念
资金等值 折现和折现率 现值、终值、年金
资金等值
资金等值是考虑资金时间价值时的 等值。也就是在考虑时间因素的情 况下,不同时点发生的绝对值不等 的资金可能具有相等的价值。
资金等值计算
资金等值有关的基本概念 资金等值计算的基本公式 资金等值计算的三个特例
资金等值有关的基本概念
资金时间价值 利息和利率 单利和复利 名义利率和实际利率
资金时间价值
不同时间发生的等额资金在价值上的 差别
投资收益率 通货膨胀因素 风险因素
利息和利率
利息是指占用资金所付出的代价(或 放弃资金使用价值所得到的补偿) Fn=P+In
Fn=P(1+i) n
名义利率和实际利率
名义利率:通常按月来表示利息, 如年利率为12%,每月计息一次, 年利率12%,成为名义利率
名义利率和实际利率
实际利率:该期间的利息额与本期 初的本金的比值
F=p(1+r/m)m r:名义利率 m:计息次数 r/m:一个计息周期的利率
资金等值计算的基本公式
先付年金的现值公式
先付年金的现值公式 P=A(1+i)(P/A,i,n)
先付年金的现值公式
年金:每期发生的连续不间断的固定数量的现 金流入与流出。
先付年金(Annuity due):于期初发生的年金012源自n-1nA
后付年金:于期末发生的年金
0
1
2
n-1
n
A
永续年金的现值公式
永续年金的现值公式 P=A/i
资金等值计算六个公式 PPT

n
P
A
(1i)n 1 i(1i)n
i(1i)n A P (1i)n 1
i(1i)n 称为 (1i)n 1
资金回收
系数, (A/用P,
i,
n)表示
。
课堂练习
资金等值计算公式
2. 等额分付复利公式 例:某人在未来9年每年年底需向银行存钱, 以供其儿子5年后上大学。已知其儿子每年 需10000元,共4年。那么从现在开始,其 每年年底需向银行存多少钱?已知存款利 率10%。
。已知 i =10%。
x=?
90
150
012 70
100
3 45 67
课堂练习
资金等值计算公式
1. 一次支付复利公式
例:某项目的资金(万元)流动情况如下图所示,求第三期期末的等值资金
。已知 i =10%。
x=?
90
150
012 70
100
3 45 67
解:X = -100(F/P, 0.10, 3)-70(F/P, 0.10, 2) +90(P/F, 0.10, 1)+150(P/F, 0.10, 4)
课堂练习
资金等值计算公式
2. 等额分付复利公式 例:某人在未来9年每年年底需向银行存钱,以供其儿子5年后上大学。已知其 儿子每年需10000元,共4年。那么从现在开始,其每年年底需向银行存多少钱 ?已知存款利率10%。
10000
0 1 2 3 4 56 7 89
A=? 解:第9年A的终值:
F = A(F/A, 0.10, 9) = A(13.5795) 每年10000元,其第9年末的终值: F = 10000(F/A, 0.10, 4) = 10000(4.6410)
资金等值计算的基本概念和原理

资金等值计算的基本概念和原理资金等值计算是财务管理中非常重要的概念,它用于评估不同时间点的现金流量。
本文将介绍资金等值计算的基本概念和原理,帮助读者更好地理解和应用资金等值计算。
一、资金等值计算的概述资金等值计算是一种财务管理工具,用于比较和评估不同时间点的现金流量。
在财务决策中,往往需要对不同时间点的现金流作出评估和比较。
资金等值计算通过将不同时点的现金流量转化为等值现金流量,帮助我们在不同项目或投资选择中做出决策。
二、资金等值计算的原理资金等值计算基于时间价值的原理。
时间价值指的是同一金额的资金在不同时间点的价值是不同的。
基于时间价值的原理,我们需要考虑资金的时间价值,并将不同时期的现金流量进行折现和累积,以便进行有效的比较和评估。
资金等值计算常用的方法有几种,包括现值法、内部收益率法和净现值法。
1. 现值法现值法是资金等值计算中最基本的方法之一,它将不同时期的现金流量转化为当前时间点的等值现金流量。
现值法的计算公式如下:PV = CF / (1+r)^n其中,PV表示现值,CF表示现金流量,r表示折现率,n表示时间。
现值法的计算原理是将未来的现金流量按照折现率的方式减少,使其与当前时间的现金流量进行比较。
如果现值为正,则表示现金流量对投资者是有益的;如果现值为负,则表示现金流量对投资者是不利的。
2. 内部收益率法内部收益率法是另一种常用的资金等值计算方法,它用于确定项目的内部收益率。
内部收益率是指使项目的净现值为零的折现率。
内部收益率法的计算需要通过不同折现率下的净现值计算来确定内部收益率。
内部收益率越高,表示项目所能带来的回报越高。
在资金等值计算中,我们通常会将内部收益率与其他项目的内部收益率进行比较,以判断投资哪个项目更有利。
3. 净现值法净现值法是一种综合考虑现金流量和时间价值的方法,它通过计算项目的净现值来评估项目的价值。
净现值计算公式如下:NPV = CF0 + CF1/(1+r)^1 + CF2/(1+r)^2 + ... + CFn/(1+r)^n其中,NPV表示净现值,CF0表示初始投资,CF1至CFn表示不同时期的现金流量,r表示折现率,n表示时间。
资金等值计算公式
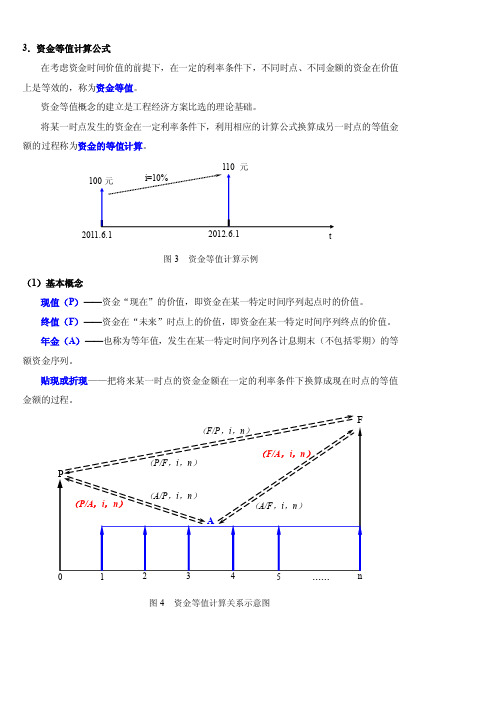
3.资金等值计算公式在考虑资金时间价值的前提下,在一定的利率条件下,不同时点、不同金额的资金在价值上是等效的,称为资金等值。
资金等值概念的建立是工程经济方案比选的理论基础。
将某一时点发生的资金在一定利率条件下,利用相应的计算公式换算成另一时点的等值金额的过程称为资金的等值计算。
(1)基本概念现值(P )——资金“现在”的价值,即资金在某一特定时间序列起点时的价值。
终值(F )——资金在“未来”时点上的价值,即资金在某一特定时间序列终点的价值。
年金(A )——也称为等年值,发生在某一特定时间序列各计息期末(不包括零期)的等额资金序列。
贴现或折现——把将来某一时点的资金金额在一定的利率条件下换算成现在时点的等值金额的过程。
2011.6.1t图3 资金等值计算示例图4 资金等值计算关系示意图(2)资金等值基本计算公式文,wen,从玄从爻。
天地万物的信息产生出来的现象、纹路、轨迹,描绘出了阴阳二气在事物中的运行轨迹和原理。
故文即为符。
上古之时,符文一体。
古者伏羲氏之王天下也,始画八卦,造书契,以代结绳(爻)之政,由是文籍生焉。
--《尚书序》依类象形,故谓之文。
其后形声相益,即谓之字。
--《说文》序》仓颉造书,形立谓之文,声具谓之字。
--《古今通论》(1) 象形。
甲骨文此字象纹理纵横交错形。
"文"是汉字的一个部首。
本义:花纹;纹理。
(2) 同本义[figure;veins]文,英语念为:text、article等,从字面意思上就可以理解为文章、文字,与古今中外的各个文学著作中出现的各种文字字形密不可分。
古有甲骨文、金文、小篆等,今有宋体、楷体等,都在这一方面突出了"文"的重要性。
古今中外,人们对于"文"都有自己不同的认知,从大的方面来讲,它可以用于表示一个民族的文化历史,从小的方面来说它可用于用于表示单独的一个"文"字,可用于表示一段话,也可用于人物的姓氏。
资金等值计算的六个基本公式

资金等值计算的六个基本公式资金等值计算在我们的经济生活中可是有着大用处的,它能帮助我们更好地理解和比较不同时间点上的资金价值。
下面就来给您好好唠唠资金等值计算的六个基本公式。
咱先说说啥叫资金等值。
简单来讲,就是在不同时间点上绝对值不等的资金,如果从资金的时间价值角度来看,它们的价值可能是相等的。
比如说,今天的100 块和一年后的110 块,在一定的利率条件下,就可能是等值的。
这六个基本公式就像是六把神奇的钥匙,能帮我们打开资金等值计算的大门。
第一个公式是一次支付终值公式,F = P(1 + i)^n 。
这里的 P 代表现值,就是现在的资金数额;F 是终值,也就是未来某个时间点的资金数额;i 是利率;n 是计息期数。
举个例子,您现在有 1 万块存在银行,年利率是 5%,存 3 年,那 3 年后您能拿到多少钱呢?用这个公式一算就知道啦,F = 10000×(1 + 5%)^3 = 11576.25 元。
再来说说一次支付现值公式,P = F/(1 + i)^n 。
假如 3 年后您想有 2万块去旅游,还是按照 5%的年利率来算,那您现在得存多少钱呢?用这个公式就能算出来,P = 20000/(1 + 5%)^3 ≈ 17276.75 元。
等额支付终值公式,F = A×[(1 + i)^n - 1]/i 。
这个 A 就是等额支付的金额。
比如说您每个月存 1000 块,年利率还是 5%,存 3 年,那 3年后您一共能有多少钱?算出来 F = 1000×[(1 + 5%)^3 - 1]/5% ≈ 3152.5 元。
等额支付偿债基金公式,A = F×i/[(1 + i)^n - 1] 。
还是刚才那个例子,如果 3 年后您想有 3152.5 元,那每个月得存多少钱呢?A =3152.5×5%/[(1 + 5%)^3 - 1] ≈ 95.3 元。
等额支付现值公式,P = A×[(1 + i)^n - 1]/[i×(1 + i)^n] 。
资金等值计算PPT课件

03
资金等值计算的实例
简单实例:存款与贷款
存款
将资金存入银行,按照一定的利 率获得利息收入。
贷款
向银行借款,需要按照约定的利率 支付利息,并在借款期限结束时偿 还本金。
等值计算
在存款和贷款中,资金等值计算可 以帮助我们确定在未来的某个时间 点,存款和贷款之间的价值相等。
复杂实例:投资决策分析
投资方案
THANKS
感谢观看
金融产品定价
资金等值计算是金融产品定价的基础,如贷款、 债券、保险等,有助于金融机构合理设定产品价 格。
在企业财务管理中的应用
01
02
03
资本预算
企业可以利用资金等值计 算对长期投资项目进行预 算,以确定项目的经济可 行性。
财务规划
资金等值计算可以帮助企 业制定合理的财务规划, 如预测现金流、制定财务 计划等。
折现率与利息
折现率的含义
利息的计算
折现率是指将未来的现金流量折算为 现值所使用的利率,通常用于评估投 资项目的经济价值。
利息的计算通常采用复利或单利方式 进行,复利方式考虑了本金和利息的 共同增长,而单利方式只考虑本金增 长。
折现率的确定
折现率的确定需要考虑投资项目的风 险、通货膨胀率和市场利率等因素, 通常采用加权平均资本成本等方法来 确定。
资金的时间价值
资金时间价值的含义
资金的时间价值是指资金在投资和再投资过程中,由于时 间因素而形成的价值差额。
资金时间价值的产生
资金时间价值的产生是由于资金在投资和再投资过程中, 会面临通货膨胀、风险和收益的不确定性等因素,从而使 得资金的价值随时间发生变化。
资金时间价值的度量
资金时间价值的度量通常采用折现率或利率来计算,折现 率或利率的大小取决于市场条件、风险和收益等因素。
资金等值计算

3.0 资金等值计算
资金等值计算练习3:
计算0.60%月度利率的周、两个月、季度、 半年、年度和两年的名义利率。
3.0 资金等值计算
资金等值计算练习4:
工商银行信用卡透支的利息是每天万分之五, 按复利计息,问年实际利率是多少?
3.0 资金等值计算
5. 连续利率
当企业每天都持续发生大量的现金收、支时,计息次数趋 向于无穷大,即m→∞,我们就可以考虑对这些现金流量连续 计息。此时,实际利率称为连续利率i:
在一定的时期内每年收付等额款项的期末价值是多少? F=? 0 1 100
(1+i)n - 1 F = A (——————) i
2 100
3 100
F = A ( F / A, i, n )
3.0 资金等值计算
资金等值计算练习11:
你未来每年末在银行存入1000元,如存款 利率是年8%,连续3年后按复利计息的本利和 终值是多少?
3.0 资金等值计算
6. 偿债基金值
为在一定时期内聚积一笔预定金额,可运用偿债基 金系数,计算在复利条件下,每年应当提存的相同数额, 如用于设备更新改造或偿还到期债务。计算公式如下:
i A = F n (1 + i ) − 1
A = F ( A / F , i, n )
3.0 资金等值计算
不同计息方式下的利息对比 年份 期初余额 期末利息 年末本利和 年末支付额
小王方案:单利6%/年,期限5年 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 50000 53000 56000 59000 62000 50000 53000 56180 59550.80 63123.85 50000 50000 50000 50000 50000 3000 3000 3000 3000 3000 3000 3180 3370.80 3573.05 3787.43 3000 3000 3000 3000 3000 53000 56000 59000 62000 65000 53000 56180 59550.80 63123.85 66911.28 53000 53000 53000 53000 53000 — — — — 65000 — — — — 66911.28 3000 3000 3000 3000 53000
资金的等值计算

第一节 利息公式 一、利息的种类 1,利息:占用资金一定时间后必须支付的
补偿额或报酬,是资金时间价值的具体体现 2,利率:表示单位资金在单位时间内的利
息 3,计算方式:单利和复利
第二章 资金的等值计算
4,等效值的概念:两个不等额的资金在不同 的时间点上,其价值是相等的,这两个资金就 互为等效值。引入等效值的概念就是为了对经 济活动过程中发生在不同时间点的资金能进行 比较。
i(1+i)n
(1+i)n-1
i(1+i)n
式中: (1+i)n-1
称为等额支付系列的资金恢复系数,也称为资 金回收系数
用(A/P,i,n)表示,则: A=P (A/P,i,n)
第二章 资金的等值计算
例:已知银行利率为10%,为了从第5年开始 直到第10年,每年都能从银行取出10000,问 现在至少应存入银行多少钱?
解:画出这个问题的现金流量图如下:
i=6% F′=?
F=10万元
0
1
23
4
56
78
9
10
A=?
第二章 资金的等值计算
F’=10(P/F,6%,5) 而A=F’(A/F,6%,5) =10(P/F,6%,5)(A/F,6%,5) =10×0.7473×0.1774 =1.3257(万元) 例:从现在开始,连续5年,每年内均存入银行1万
第二章 资金的等值计算
5,当问题包括P与A时,等额系列的第一个A与P 在时间上差一个计息周期,即P发生在期初,第一 个A发生在期末;
6,当问题包括F与A时,F与系列的最后一个A同 时发生;
7,当问题包括P与G时,P发生在第一个G的前两 个计算周期,第一个A1发生在第一个G的前一期, 而如果是F,则F与最后一个G同时发生.
资金的等值计算

资金的等值计算在金融领域,资金的等值计算是一个重要的概念。
它用于衡量不同时期和不同风险水平下的资金价值。
在本文中,我们将介绍资金的等值计算以及其在金融决策中的应用。
一、资金的时间价值资金的时间价值是指不同时间点的资金的价值是不同的。
由于存在通胀、机会成本、利息等因素,同样的金额在不同时间点可能具有不同的购买力。
因此,了解资金的时间价值对于有效进行投资和贷款决策非常重要。
资金的等值计算是基于资金的时间价值概念而进行的。
它可以帮助我们评估不同时间点的现金流量。
通过将不同时期的现金流量进行比较,我们可以确定它们的等价价值,从而做出更明智的决策。
二、资金的等值计算方法资金的等值计算方法有多种,其中常见的包括净现值法、内部收益率法和年金的计算法。
1. 净现值法净现值法是最常用的资金等值计算方法之一。
它通过比较项目的现金流入和现金流出,计算一个项目的净现值。
净现值是指将项目所有未来现金流量带到当前时间点的价值。
如果净现值大于零,则说明项目具有经济效益。
净现值的计算公式如下所示:NV = ∑ (Ct / (1+r)^t) - I其中,NV表示净现值,Ct表示第t期的现金流入,I表示项目的投资成本,r表示折现率。
2. 内部收益率法内部收益率法是另一种常用的资金等值计算方法。
它是指使项目的净现值等于零的折现率。
内部收益率可以帮助我们评估项目的收益率水平,从而判断项目是否值得投资。
计算内部收益率的方法是通过反复尝试不同的折现率,直到找到使净现值等于零的折现率。
这个折现率就是项目的内部收益率。
3. 年金的计算法年金的计算法是一种用于计算等额现金流的资金等值计算方法。
它适用于每期现金流量相等的情况。
通过计算年金的现值或未来值,我们可以得到等额现金流的资金等值。
年金的计算公式如下所示:PV = PMT * [(1 - (1+r)^-n) / r]其中,PV表示现值,PMT表示每期的现金流量,r表示折现率,n 表示期数。
三、资金的等值计算在金融决策中的应用资金的等值计算在金融决策中具有广泛的应用。
如何计算资金等值

如何计算资金等值资金等值是指不同时间点的资金在未来发生的利息或收益下的等值。
计算资金等值是进行投资决策、比较不同投资方案以及评估资产回报率的重要手段。
本文将介绍如何计算资金等值,并通过实例说明应用方法。
一、计算单期资金等值单期资金等值是指同一金额的资金在不同利率下的未来价值。
计算单期资金等值的公式如下:FV = PV × (1 + r)其中,FV代表未来价值,PV代表现值,r代表利率。
例如,假设有一笔投资金额为1万元,投资期限为1年,利率为5%。
根据上述公式,可以计算出未来的资金等值:FV = 10000 × (1 + 0.05) = 10500元在这个例子中,1万元的投资在1年后将变为10500元。
二、计算多期资金等值当资金在多个时间段内产生利息或收益时,需要进行多期资金等值的计算。
假设投资期限为n年,每年的利率分别为r1、r2、r3...rn,资金等值的计算公式如下:FV = PV × (1 + r1) × (1 + r2) × (1 + r3)...× (1 + rn)例如,现有一笔投资金额为1万元,投资期限为3年,第一年的利率为5%,第二年的利率为6%,第三年的利率为7%。
根据上述公式,可以计算出未来的资金等值:FV = 10000 × (1 + 0.05) × (1 + 0.06) × (1 + 0.07) = 11989.38元在这个例子中,1万元的投资在3年后将变为约11989.38元。
三、计算资金等值的应用1. 投资决策:通过计算不同投资方案的资金等值,可以对不同的投资方案进行比较评估,从而做出更明智的投资决策。
2. 资产回报评估:计算资金等值可以帮助评估现有资产的回报情况,判断是否值得继续持有或出售。
4. 贷款决策:对于贷款人来说,计算贷款的资金等值可以帮助其确定是否值得借贷以及还款能力。
2.2资金等值计算(1)

r m ) m
利率
i=
L r = (1 + ) m − 1 P m
2.2资金的等值计算 2.2资金的等值计算——计息制度 资金的等值计算 计息制度
对名义利率一般有两种处理方法: 对名义利率一般有两种处理方法
例 某工程项目需要投资,现在向银行借款100万元(现值),年利率为 10%,借款期5年,一次还清。问5年末一次偿还银行的本利和是多少?
F = P( F / P, i, n) = 100( F / P,10%,5) = 100 × 1.6105 = 161.05 (万元)
2.2资金的等值计算 2.2资金的等值计算——等值计算 资金的等值计算 等值计算
2.2资金的等值计算 2.2资金的等值计算——计息制度 资金的等值计算 计息制度
含义 利息 单利
本金生息,利息不 生息
本利和
F = Ρ (1 + ni )
I = Ρni
n I = Ρ (1 + i ) − 1
复利
本金生息,利息 也生息
F = Ρ(1 + i ) n
I ——利息;F ——本利和或终值; ——本金或现值; ——计息期 n Ρ 数; ——利率; i
偿债基金公式 等额 分付 类型
为了在未来偿还一定数额的债务, 为了在未来偿还一定数额的债务, 而预先准备的年金。 而预先准备的年金。
i A = F ⋅ n (1 + i ) − 1 = F ( A / F , i, n)
偿债基金系数
年金现值公式
在利率为i,复利计息的条件下, 在利率为 ,复利计息的条件下, 求n期内每期期末发生的等额 期内每期期末发生的等额 分付值A的现值 的现值P。 分付值 的现值 。 研究期初借到的一笔资金, 研究期初借到的一笔资金,在每 个计息期末等额偿还本利和, 个计息期末等额偿还本利和, 求每期 期末应偿还的数额。 期末应偿还的数额。
资金等值计算

P
F=A (F/A, i, n) F
A F
等额系列终值公式
(1 + i ) n − 1 F=A i i (1 + i ) n − 1 (1 + i ) n − 1 P=A n i (1 + i )
A=F A=P
F
A 偿债基金公式
A=F (A/F,
i,
n)
A P=A (P/A, i, n) A
A P
等额系列现值公式
P
A 等额系列资本回收公式
i (1 + i ) (1 + i ) n − 1
n
A=P(A/P,
i, n)
0
1
2
3
….
n-1
n
P
等值计算练习
例1.某厂欲积累一笔福利基金用于3年后建造职工 . 俱乐部,此项投资总额为200万元,若金融机构按 6%计算福利,问该厂每年年初至少要存款多少? 例2.某企业预购置设备一台,预计寿命期8年,期 . 末残值为200元,每年可增加收益1500元。若预期 年利率为8%,问该设备投资最高限额是多少?如 果该设备售价为7000元,是否当购买?
资金等值计算 一、资金的时间价值及表现形式 含义:等额资金在不同时间的价值差别。 1、含义:等额资金在不同时间的价值差别。 2、影响因素 资金增值率 通货膨胀因素 风险因素 3、表现形式
银行利率 行业资金利润率
二、资金等值计算及计算公式 概念: 1、概念:把一个时点的资金换算为另一个时点等 值资金的过程。 值资金的过程。
例3.一套运输设备价值3万元,希望在5年内 . 等额收回全部投资。若基准折现率为8%,问 每年至少应回收多少?
资金等值计算六个公式 PPT

资金等值计算公式
1. 一次支付复利公式
(1)一次支付终值公式
例:一位父亲现在把10000元投资于年利率为10%的基金,并计划在1010年
末,帐户里将有多少钱?
P=10000,i=10%,n=10年
F = P(F/P, i, n) = 10000(F/P, 0.10, 10)
= -100(1.331)-70(1.21)+90(0.9091)+150(0.6830) = -133.1-84.7+81.819+102.45 = -33.531 (万元)
资金等值计算公式
F =?
2. 等额分付复利公式
(1)等额分付终值公式
01 2 3 A
…
n
F A(1i)n1 A(1i)n2 A(1i) A A[1 (1i) (1i)n2 (1i)n1] A1[1(1i)n]
。已知 i =10%。
x=?
90
150
012 70
100
3 45 67
课堂练习
资金等值计算公式
1. 一次支付复利公式
例:某项目的资金(万元)流动情况如下图所示,求第三期期末的等值资金
。已知 i =10%。
x=?
90
150
012 70
100
3 45 67
解:X = -100(F/P, 0.10, 3)-70(F/P, 0.10, 2) +90(P/F, 0.10, 1)+150(P/F, 0.10, 4)
123
P
…
n
P
A
(1i)n 1 i(1i)n
i(1i)n A P (1i)n 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
但是,按复利计算,上述“年利率12%,每月 计息一次”的实际年利率则不等于名义利率,应 比12%略大些。
设名义利率为r,一年中计息次数为m,则一个计息周 期的利率应为r/m, 求一年后本利和、年利率?
单利方法: 一年后本利和 F=P(1+i期×m) 利息 P×i期×m 年利率:P×i期×m / P = i期×m = r
复利方法: 一年后本利和 F=P(1+i期) m 利息 P(1+i期) m - P 年利率:i = [ P(1+i期) m —P]/ P = (1+i期) m -1
所以,名义利率与实际利率的换算公式为: i = (1+i期) m –1= (1+r/m) m –1
F=P+I
式中: F——本利和 P——本金 I——利息
利率几个习惯说法的解释: “利率为8%”——指:年利率为8%,一年计息一次。
“利率为8%,半年计息一次”——指:年利率为8%, 每年计息两次,或半年计息一次,每次计息的利率为4%。
计息的方式——单利与复利
1)单利:仅以本金为基数计算利息,利息不 再计息。
当m=1时,名义利率等于实际利率; 当m>1时,实际利率大于名义利率。 当m → ∞时,即按连续复利计算时,i与r的 关系为:
i lim [(1 r / m)m 1] lim [(1 r / m)m/r ]r 1 er 1
m
m
注意: 如果没有特别指出时,通常计算中所给定的利率都是名义利率,而且多数 情况下都是年名义利率。
年份 年初帐面余 年利息 额
年末本利和
1
100
10
110
2
110
11
121
3
121
12.1
133.1
复利计算公式为: 终值F=P(1+ i )n 总利息: I=F-P
通常,商业银行的贷款是按复利计息的。
例 某企业以6%的年利率向银行贷款1000万元,贷 款期5年,分别以单利、复利计算。问5年后企业支 付多少利息?如果贷款期为十年呢?
解: 单利计息法公式:F前3年=P(1+ i n) 复利计息法公式:F后4年=P(1+ i)n
F=10000(1+10%×3)(1+10%)4 =19033元 最后可收回本利和是19033元。
讨论:
▪ 现在存入银行100元,年利率为12%,一年 末一次性可以取出本利和多少?
▪ 若一个月计息一次,则一年末可以取出本利 和多少?
例:住房按揭贷款 名义利率i =5.04%,每年计息12次 计息期利率:r/m=4.2‰ (月息) i =(1+r/m)m - 1
= (1+5.04%/12)12 - 1 =5.158% 实际利率:i=5.158%(年利率)
Hale Waihona Puke 例(P36)现设年名义利率r=6%,则年、半年、季、 月、星期、日的年实际利率如下表所示。
复利法:I=F – P =1000 ×(1+6%)5 – 1000 =338.23万元 单利法:I= F – P = P × i × n =1000×5 ×6%=300万元
从例中可以看到, ①当单利计算和复利计算的利率相等时,资金的复 利值大于单利值,且时间越长,差别越大。
②由于利息是货币时间价值的体现,而时间是连续 不断的,所以利息也是不断地发生的。从这个意义 上来说,复利计算方法比单利计算更能反映货币的 时间价值。因此在技术经济分析中,绝大多数情况 是采用复利计算.
名义利率与实际利率的计算
在复利计算中,利率周期通常以年为单位,计 息周期可以与之相同,也可以不同。当计息周期小 于一年时,一年内计算利息的次数不止一次了,在 复利条件下每计息一次,都要产生一部分新的利息, 因而实际的利率也就不同了(因计息次数而变化)。
假如按月计算利息,且其月利率为1%,通常 称为“年利率12%,每月计息一次”。
▪ 每年计息周期越多,年实际利率和名义利率相差就 越大。
▪ 在技术经济分析中,如果各技术方案的计息期不同, 就不能使用名义利率来评价,而必须换算成实际利 率进行评价,否则会得出不正确的结论。
总结
当利率周期与计息周期不等时,一般有两种 处理方法: (1)将其换算为实际利率后,再进行计算; (2)直接按单位计息周期利率来计算,但计息 期数要作相应调整。
计息期 年
半年 季度
月 星期
日 连续
年计息次数 1 2 4 12 52
365 ∞
计息周期利率(%) 6.0000 3.0000 1.5000 0.5000 0.1154 0.0164 0.0000
年实际利率(%) 6.0000 6.0900 6.1364 6.1678 6.1797 6.1799 6.1837
③
复利
间断复利:计息周期为一定的时 间区间(年、季、月)
连续复利:计息周期无限缩短
间断复利
连续复利
从理论上讲,资金是在不停地运动,每时每刻都通过 生产和流通在增值。但在实际商业活动中,计息周期不可能 无限缩短,因而采用较为简单的间断复利计息。
例:某人把10000元,按利率10%(以单利计息)借 给朋友3年。3年后,改以复利计息,朋友又使用了4 年。最后他从朋友那里收回的本利和F是多少?
例:某年的住房按揭贷款年利率是6.39%,每月计息一次, 则年初借款10万元,则1年末一次性需偿还本利和多少?
年名义利率:6.39%; 月实际利率:6.39%/12=0.5325% 年实际利率:(1+6.39%/12)12 –1=6.58% 10*(1+6.39%/12)12=10.658万 10*(1+6.58%)=10.658万
技术经济学
谭萍
第三章 资金的等值计算
一、利息的计算;名义利率与实际利率的计算。 二、资金时间价值的普通复利计算。(六个公
式的应用) 三、资金时间价值的其他复利计算。(复利周
期与支付周期不等情况下的复利计算)
如果将一笔资金存人银行,这笔资金就称
为本金。经过一段时间之后,储户可在本金之 外再得到一笔利息,这一过程可表示为:
例:本金100元,三年后本利和为 (i=10%,单位:元)
年份 年初帐面余额 年利息
年末本利和
1
100
10
110
2
110
10
120
3
120
10
130
单利计算公式为: F=P(l + i n) 总利息 :I=F - P =P i n
2)复利:以本金与累计利息之和为基数计 算利息,即“利滚利”。
例:本金100元,三年后本利和为 (i=10%,单位:元)
