双曲线第二定义及应用PPT课件
第三讲---双曲线的第二定义

第三讲 双曲线的第二定义知识梳理(一)双曲线的第二定义:平面内一动点 的比为常数 e 到一定点 F (c, 0) 的距离与到一定直线 L : x a2 的距离 cc (e>1) a定点 F (c, 0) 是双曲线的焦点,定直线 L 是双曲线的准线,常数 e 是双曲线的离心率。
(二)焦点三角形的面积公式。
S1 r1r2 sin b 2 tan 2 23.双曲线的方程,图形,渐进线方程,准线方程和焦半径公式: 标准方程 图像 渐进线方程x2 y 2 1(a 0.b 0) a 2 b2b x a a2 x c M 在右支上 r左 =|MF1 |=ex0 a yy 2 x2 1(a 0.b 0) a 2 b2a x b a2 y c y准线方程半径公式r右 =|MF2 |=ex 0 a M 在左支上 r左 =|MF|=-ex 1 0 a r右 =|MF2 |=-ex 0 a典例分析 题型一:与双曲线准线有关的问题 例 1.(1)若双曲线x2 y 2 1 上一点 P 到右焦点的距离等于 13 ,则点 P 到右准线的距离为______ 13 12x2 y 2 1 的离心率为 2,则该双曲线的两条准线间的距离为________ A.若双曲线 m 3练习:已知双曲线的渐进线方程为 3x 2 y 0 ,两条准线间的距离为 解:双曲线渐进线方程为 y 16 13 ,求双曲线的标准方程。
133 x 21所以双曲线方程为x2 y 2 ( 0 )在分 0 时 4 和 0 时。
。
。
4 9题型二:双曲线第二定义及其运用 例 2:设一动点到 F(1,0)和直线 x=5 的距离之比为 3 。
求动点的轨迹方程。
练习:已知双曲线x2 y 2 1(a 0, b 0) 的左右焦点分别为 F1F2 ,点 P 是左支上的一点,P 到左准线的 a 2 b2距离为 d ,若 y 3x 是已知双曲线的一条渐进线,则是否存在这样的 P 点使得 d , | PF1 |,| PF2 | 成为等比 数列?若存在,求出 P 点坐标;若不存在,说明理由。
双曲线课件人教版2

复习:椭圆的定义: 平面内与两个定点F1、F2的距离之和等于常数 (大于|F1F2|) 的点的轨迹是椭圆.
|M 1 | |M F 2 | 2 a F ,( 2 a |F 1 F 2 |)
问题1:平面内与两个定点F1、F2的距离之差等于 常数的点轨迹是什么?
探究一:
在直线l上取两个定点A, B, P是直线l上的动点。在 平面内,取定点F1, F2,
x
F1
方程
x2 a2
by22
1(a0,b0)
y2 a2
bx22
1(a0,b0)
焦点
a.b.c 的关系
双曲线课 件人教 版2(精 品课件 )
F ( ±c, 0)
F(0, ± c)
c2a2b2
双曲线课 件人教 版2(精 品课件 )
双曲线与椭圆之间的区别与联系
定义 方程
椭圆
|MF1|+|MF2|=2a
x2 a2
F1
F2
此时轨迹为线段F1F2的垂直平分线
双曲线课 件人教 版2(精 品课件 )
双曲线课 件人教 版2(精 品课件 )
二.双曲线的标准方程
类比椭圆的方程,如何求
1. 段建F系1F.2的以中F1点,F2为所原在点的建直立线直为角x轴坐这,标优线美的曲线y 的方程? 系
M
2.设点.设M(x , y),双曲线的焦
② |F1F2|=2c ——焦距.
双曲线课 件人教 版2(精 品课件 )
双曲线课 件人教 版2(精 品课件 )
思考1:定义中为什么这个常数要小于|F1F2|?
①若常数=2c,则轨迹是什么?
F1
F2
此时轨迹为以F1或F2为端点的两条射线
人教A版高中数学选修1-1课件双曲线的第二定义

(a,0) y b x
a
e c a
原点
(其中
都对 称
(0,a) y a x c2 a2 b2)
b
例1 点 M (x,y)与定点F (c,0)的距离和它到定直线l : x a2 的 c
距离的比是常数 c (c a 0),求点M的轨迹 .
a
解:设 d是点M到直线 l的距离,则
点 M 的轨迹是实轴、虚轴长分别为 2a、2b的双曲线 .
双曲线的第二定义:
动点 M与一个定点F的距离和它到一条定直线l的距离的比
是常数 e c (e 1),则这个点的轨迹是椭圆 . a
l'
y
定点是双曲线的焦点,定直线叫做双曲线的
l
d .M
准线,常数e是双曲线的离心率 .
对于双曲线
x2 a2
y2 b2
1,
.
.
F’ O
F
x
右焦点F2 (c,0),对应的右准线方程是
x
a2 c
.
左焦点F1(c,0)对应的左准线方程是
x
a2 c
.
焦点在y轴上的双曲线的准线方程是:y a2 c
例2 已知双曲线 x2 - y2 a2 b2
1(a
0,b
0)的焦点F(1 c,0)F2 (c,0),
P(x0, y0 )是双曲线右支上任意点,求证:| PF1 | a ex0 ,
| PF2
| a ex0
其中e为双曲线的离心率。 l'
y
l
证明:双曲线的左准线为x a2
P.
c
由整双理曲得线:的| P第F1二|定ex义0 得a:x|0PF1ac|2
3-2-1双曲线及其标准方程 课件(共67张PPT)

互动 2 在双曲线的定义中,必须要求“常数小于|F1F2|”, 那么“常数等于|F1F2|”“常数大于|F1F2|”或“常数为 0”时,动 点的轨迹是什么?
【解析】 (1)若“常数等于|F1F2|”时,此时动点的轨迹是以 F1,F2 为端点的两条射线 F1A,F2B(包括端点),如图所示.
(2)若“常数大于|F1F2|”,此时动点轨迹不存在. (3)若“常数为 0”,此时动点轨迹为线段 F1F2 的垂直平分线.
互动 3 已知点 P(x,y)的坐标满足下列条件,试判断下列各 条件下点 P 的轨迹是什么图形?
2.关于双曲线应注意的几个问题 (1)双曲线的标准方程与选择的坐标系有关,当且仅当双曲线 的中心在原点,焦点在坐标轴上时,双曲线的方程才具有标准形 式.
(2)如图,设 M(x,y)为双曲线上任意一点,若 M 点在双曲线 的右支上,则|MF1|>|MF2|,|MF1|-|MF2|=2a(0<2a<|F1F2|);若 M 在双曲线的左支上,则|MF1|<|MF2|,|MF1|-|MF2|=-2a,因 此得|MF1|-|MF2|=±2a,这与椭圆不同.
(3)列式:由|MF1|-|MF2|=±2a, 可得 (x+c)2+y2- (x-c)2+y2=±2a.①
(4)化简:移项,平方后可得 (c2-a2)x2-a2y2=a2(c2-a2). 令 c2-a2=b2,得双曲线的标准方程为xa22-yb22=1(a>0,b>0).② (5)从上述过程可以看到,双曲线上任意一点的坐标都满足方 程②;以方程②的解(x,y)为坐标的点到双曲线两个焦点(-c, 0),(c,0)的距离之差的绝对值为 2a,即以方程②的解为坐标的 点都在双曲线上.这样,就把方程②叫作双曲线的标准方程.
双曲线-完整版PPT课件可编辑全文

∴x-32a2+y2=a22.
①
又 P 点在双曲线上,得ax22-by22=1.
②
由①,②消去 y,得
(a2+b2)x2-3a3x+2a4-a2b2=0,
即[(a2+b2)x-(2a3-ab2)](x-a)=0.
当 x=a 时,P 与 A 重合,不符合题意,舍去.
当 x=2aa32-+abb2 2时,满足题意的 P 点存在, 需 x=2aa32-+abb2 2>a, 化简得 a2>2b2, 即 3a2>2c2,ac< 26. 又 e>1,∴离心率 e=ac∈1, 26.
考向三 [149] 双曲线的几何性质
(1)(2014·天津高考)已知双曲线ax22-by22=1(a>0,
b>0)的一条渐近线平行于直线 l:y=2x+10,双曲线的一个
焦点在直线 l 上,则双曲线的方程为( )
A.x52-2y02 =1
B.2x02 -y52=1
C.32x52-130y02 =1
二、双曲线的标准方程和几何性质
标准方程 ax22-by22=1(a>0,b>0)
ay22-bx22=1(a>0, b>0)
图形
范围
x≥a或x≤-a
对称轴: 坐标轴
对称性
对称中心: 原点
y≤-a或y≥a 对称轴: 坐标轴 对称中心: 原点
性 顶点 顶点坐标:
顶点坐标:
质
A1 (-a,0),A2 (a,0) A1 (0,-a,) A2 (0,a)
————————— [1 个对点练] ——————— 过点2,12能作几条与双曲线x42-y2=1 有一个公共点的 直线.
【解】 (1)当斜率不存在时,直线方程为 x=2,显然符 合题意.
第2讲双曲线课件理课件.ppt

【互动探究】
1.设双曲线1x62-9y2=1 上的点 P 到点(5,0)的距离为 15,则 P 点到(-5,0)的距离是( D )
A.7 B.23 C.5 或 23 D.7 或 23 解析:容易知道(5,0)与(-5,0)是给出双曲线的焦点,P 是双 曲线上的点,直接从定义入手.设所求的距离为 d,则由双曲线 的定义可得:|d-15|=2a=8⇒d=7 或 23.
AB 的方程为 y=x+1,
因此 M 点的坐标为12,23, F→M=-32,32. 同理可得F→N=-32,-32. 因此F→M·F→N=-322+32×-32=0 综上F→M·F→N=0,即 FM⊥FN. 故以线段 MN 为直径的圆经过点 F.
的范围变化值需探究;
(3)运用不等式知识转化为 a、b、c 的齐次式是关键.
错源:没有考虑根的判别式 例 5:已知双曲线 x2-y22=1,问过点 A(1,1)是否存在直线 l 与双曲线交于 P、Q 两点,并且 A 为线段 PQ 的中点?若存在求 出直线 l 的方程,若不存在请说明理由.
误解分析:没有考虑根的判别式,导致出错.
y2 9
Hale Waihona Puke -2x72 =1D.以上都不对
3.已知双曲线ax22-by22=1(a>0,b>0)的离心率为 26,则双曲 线的渐近线方程为( C )
A.y=±2x B.y=± 2x
C.y=±
2 2x
D.y=±12x
4.已知双曲线ax22-by22=1(a>0,b>0)的一条渐近线方程为 x
+2y=0,则双曲线的离心率 e 的值为( A )
正解:设符合题意的直线 l 存在,并设 P(x1,y1),Q(x2,y2),
双曲线的第二定义
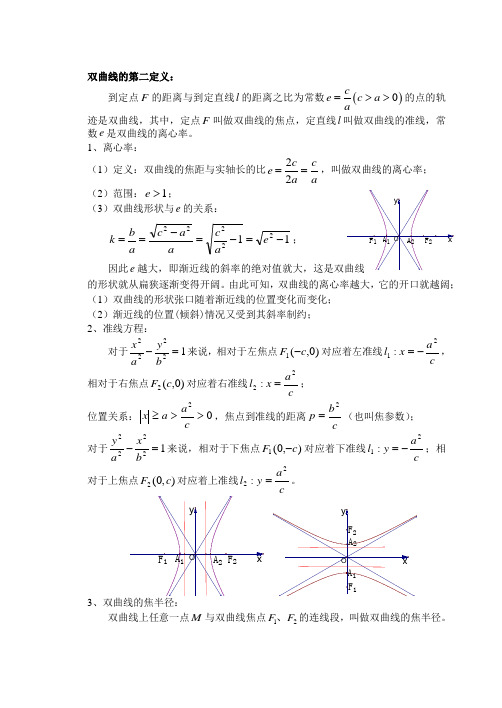
双曲线的第二定义:到定点F 的距离与到定直线l 的距离之比为常数()0ce c a a=>>的点的轨迹是双曲线,其中,定点F 叫做双曲线的焦点,定直线l 叫做双曲线的准线,常数e 是双曲线的离心率。
1、离心率:(1)定义:双曲线的焦距与实轴长的比aca c e ==22,叫做双曲线的离心率; (2)范围:1>e ;(3)双曲线形状与e 的关系:1122222-=-=-==e ac a a c a b k ; 因此e 的形状就从扁狭逐渐变得开阔。
由此可知,双曲线的离心率越大,它的开口就越阔; (1)双曲线的形状张口随着渐近线的位置变化而变化; (2)渐近线的位置(倾斜)情况又受到其斜率制约; 2、准线方程:对于12222=-by a x 来说,相对于左焦点)0,(1c F -对应着左准线c a x l 21:-=,相对于右焦点)0,(2c F 对应着右准线ca x l 22:=;位置关系:02>>≥c a a x ,焦点到准线的距离cb p 2=(也叫焦参数); 对于12222=-bx a y 来说,相对于下焦点),0(1c F -对应着下准线c a y l 21:-=;相对于上焦点),0(2c F 对应着上准线ca y l 22:=。
3双曲线上任意一点M 与双曲线焦点12F F 、的连线段,叫做双曲线的焦半径。
设双曲线)0,0( 12222>>=-b a by a x ,21,F F 是其左右焦点,e d MF =11, ∴e cax MF =+201,∴10MF a ex =+;同理 20MF a ex =-; 即:焦点在x 轴上的双曲线的焦半径公式:1020MF a ex MF a ex ⎧=+⎪⎨=-⎪⎩同理:焦点在y 轴上的双曲线的焦半径公式:1020MF a ey MF a ey ⎧=+⎪⎨=-⎪⎩( 其中12F F 、分别是双曲线的下、上焦点)点评:双曲线焦半径公式与椭圆的焦半径公式的区别在于其带绝对值符号,如果要去绝对值,需要对点的位置进行讨论。
双曲线第二定义及应用优质课件PPT

A(5,0)
5
及定直线
l
:
x
16 5
的
的动点M的轨迹方程。
解:设M(x,y), 4
则| MA| 5 d4
(x 5)2 y2 5
x 16
4
5
化简x2得 y2 1 16 9
练习1:求与定点 距离的比是定值
A(c,0)
5
及定直线
l
:
x
16 5
的
的动点M的轨迹方程。
x
解法 3: xP c,(c2 a2 b2)
P
代入双曲线方 yP程 得 ba2
又 s iP n 1 F 2 F 1 3 得 ta P n 1 F 2 F 2 1 2
F1
0
F2
y |P2F| b2 1
|F1F2| 2ac 2 2
将 b2c2a2代入 ec 得 2 a
Thank you
感谢聆听 批评指导
x a2 c
x a2 c
|M 2 | |M F 1 | 2 a F e 1 a x
焦半径公式:
y
M2(x2,y2)
(一)M1位于双曲线右支
M1(x1,y1)
|M 1F 1|e1x a
|M 1F 2|e1x a
F1
O
F2 x (二)M2位于双曲线左支
|M 2F 1| e2x a
|M 2F 2| e2x a
F A2
22
x
x a2 c
x a2 c
x a 2 a a a
c
c
准线方程 x: a2 c
两条准线比双曲线 的顶点更接近中心
x2 y2 a2 b2 1
双曲线第二定义ppt课件

25 B
2
图2.2 8
x2 a2
y2 b2
1a
0,b
0,
令点C的坐标为13, y,
则点B的坐标为25, y 55.
因为点B,C 在双曲线上,所以
y
252 122
y 552
b2
1,1
132 122
y2 b2
1.
2
C` 13 C
12
x
A` O A
由方程2,
得y
5b 12
负值舍去,
代入方程1,
点M (4, 3) ,求双曲线方程。 法二:巧设方程,运用待定系数法.
解2:双曲线的渐近线方程为x 2 y 0
可设所求双曲线的方程为x2 4 y2 ( 0).
双曲线过点M (4, 3)
42 4( 3 )2 .
4
所求双曲线方程为x2-4y2=4.
变式 1:求与双曲线 x2 y2 1 有共同渐近线,且过点 N(4, 5 ) 4
a2 y
c
y
F
a2
y
cx
o
a2 y
c
F′
15
巩固练习
x2 y2
如果双曲线 13 12 =1 上一点P到右焦点的距离
为 13 ,那么点P到右准线的距离是(A )
A. 13 B.13
C.5
D. 5
5
13
. 变式1:点P到左准线的距离多少? 39 5
F1
o
.P
F2
变式2:若|PF2|=3 13 , 则点P到左准
A′
y
13 C
12
0
Ax
B′
25 B
解 如图2.2 82,建立直
双曲线及其标准方程ppt课件

C.(0,-5),(0,5)
D.(0,- 7),(0, 7)
双曲线的定义
2
1.设 F1,F2 分别是双曲线 x2-24=1 的左、右焦点,P 是双曲线上的一点,且 3|PF1|=4|PF2|, 则△PF1F2 的面积等于 ( )
A.4 2
B.8 3
C.24
D.48
2.已知动点 P(x,y)满足 ( + 2)2 + 2- ( -2)2 + 2=2,则动点 P 的轨迹是 ( )
这两个定点叫做双曲线的焦点. 两焦点的距离叫做双曲线的焦距.
y
M
F1 o F2 x
如何理解绝对值?若去掉绝对值则图像有何变化?
03 双曲线的标准方程
1. 建系:如图建立直角坐标系xOy,使x轴经 过点F1,F2,并且点O与线段F1F2中点重合.
y M
F1 O F2
x
2.设点:设M(x , y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0) 常数=2a
利用定义求轨迹方程
P P127 习题3.2 第5题
如图,圆O的半径为定长 ,A是圆O外一定点,P是圆上任
意一点,线段AP的垂直平分线l和直线OP相交于点Q,当
O
点P在圆O上运动时,点Q的轨迹是什么?为什么?
A Q
P115 习题3.1 第6题 如图,圆O的半径为定长 ,A是圆O内一定点,P是圆上 任意一点,线段AP的垂直平分线l和半径OP相交于点 Q,当点P在圆O上运动时,点Q的轨迹是什么?为什么?
A.椭圆 C.双曲线的左支
B.双曲线 D.双曲线的右支
双曲线的定义
22
【变式练习】
已知
P
是双曲线
双曲线的第二定义课件

MF 1
x 0
a2 c
e
M Faex
1
0
x a2 c
x a2
同理 MF aex
2
0
c
左加右减,下加上减(带绝对值号)
双曲线的第二定义
焦半径公式:
(一)M1位于双曲线右支
y
M2(x2,y2)
|M1F1|ae
x
1
M1(x1,y1) |M1F2|ae1x
F1
O
(二)M2位于双曲线左支
F2 x |M2F1|ae2x
直线 轨迹.
l:x= 1
6 5
的距离的比是常数 5 4
求:点M的
x2 - y2 = 1 16 9
故点M的轨迹为实轴、虚轴长分别为8、6的双曲 线.
双曲线的第二定义
问题: 点M (x,y) 与定点F(c,0)的距离和它到定
直线l: x = a 2
c
的距离的比是常数 c
a
(c>a>0),
求:点M的轨迹.
+3 5
MF
的值最小,并求这个最小值
d min
36 5
M(3 5 ,2) 2
双曲线的第二定义
练习
已 知 点 A(3,2), F(2,0), 在 双 曲 线 x2y 32=1?
上 求 一 点 P, 使 | PA | + 2 1| PF| 的 值 最 小 .
d min
=
3 2
p ( 2 1 ,2 ) 3
双曲线的第二定义
解:设d是点M到直线l的距离,根据题意,所求轨
迹就是集合 P ={M||MF|= c}
da
由此可得: (x c)2 y2 c
双曲线的基本知识点PPT

按方程形式分类
双曲线方程的对称性 双曲线的标准方程是(x-a)²/b² - (y-b)²/a² = 1,其具有中心对称性,即点 (a, b)为中心。 双曲线的焦距与实轴长度的关系 在双曲线中,焦距c与实轴长度2a有固定的数学关系:c² = a² + b²,此 式被称为双曲线的基本性质之一。
T 双曲线关于其轴和中心点均具有对称性,这是由其定义决定的。 双曲线的渐近线性质 双曲线的渐近线是一条直线,该直线与双曲线交于两个无穷远点,这是双 曲线的重要特性之一。
05 双曲线的实际应用
双曲线的实际应用:物理中的应 用
双曲线的几何特性 双曲线是二次曲线的一种,其 双曲线的几何特性 双曲线是二次曲线的一种,其几何特性包括焦点在两个固定点,且所有到两 焦点距离之和为定长的点的集合。 双曲线的方程式 双曲线的标准方程是(x^2)/a^2 - (y^2)/b^2 = 1,其中a, b > 0, a^2 + b^2 = c^2 双曲线在物理中的应用 双曲线广泛应用于物理学中,如电磁场理论、光学、量子力学等,例如,双 曲线的焦散线就是光学中的一条重要概念。 双曲线与实际问题的联系 双曲线的许多性质,如离心率、焦点等,可以用于解决实际问题,如测量物 体的距离、角度等。
双曲线的图形特征:焦点和准线
双曲线定义 双曲线是平面内到两个定点的距离之差的绝对值等于常数的点的轨迹。 焦点性质 双曲线的两个焦点位于实轴两端,距离实轴相等。 准线特征 双曲线有两条互相垂直的准线,分别交坐标轴于原点和渐近线点。
04 双曲线的性质解析
双曲线的性质解析:主要性质
双曲线的焦点特性 双曲线有两焦点位于其对称轴上,距离中心等距。 双曲线的对称性 双曲线具有旋转对称性和平移对称性。 双曲线的渐近线 双曲线有两个渐近线,分别代表双曲线在x轴和y轴上的极限状态。 实数双曲线的面积 实数双曲线的面积是πab/4。
双曲线的第二定义应用

双曲线的第二定义:
动点 M与一个定点F的距离和它到一条定直线l的距离的比 c 是常数 e (e 1),则这个点的轨迹是双曲线 y l ' a 定点是双曲线的焦点, 定直线叫做双曲线的
准线,常数e是双曲线的离心率.
对于双曲线 y x 1, 2 2 a b
2 2
l d .M
双曲线的一渐近线为 y 3x
c2 a 2 b2 b 2 | PF2 | e 2 1 ( ) 4 所以 2 | PF2 | 2 | PF1 | 2 a a a | PF1 |
2
x
x2 y2 例3:已知双曲线 2 2 1的左右焦点分别是 F1 , F2 , 点P a b 是左支上一点,它到左 准线的距离为d,双曲线的一条 渐近线为y 3 x,问是否存在点P使,d , | PF1 |, | PF2 | 成 y 等差数列,若存在,求 出P的坐标。 P . | PF2 | 所以 2 | PF2 | 2 | PF1 | | PF1 |
| AB | | AF2 | | BF2 | 解:圆的半径 r = 2 2
设A, B点到右准线的距离分别 为d1 , d2
r ( d1 d 2 )e 2
F1
y
A .
.
O
. M F .B
2
x
d1 d 2 d 又圆心到右准线的距离 为: 2
e 1
d r
所以圆与右准线相交
由双曲线的第一定义得 :
| PF2 | | PF 1 | 2a
| PF 1 | 2a, | PF 2 | 4a
F1
.
O
.
F2
x
又 | PF 1 |min c a a
3.2.1双曲线及其标准方程(第二课时)课件-高二上学期数学人教A版选择性2

F1P,求F2
3
PF1F2的面积
a 1,b2 24
c2 a2 b2 25
F1
| PF1 | | PF2 | 2,
(| PF1 | | PF2 |)2 4.| PF1 |2 | PF2 |2 -2 | PF1 || PF2 | 4
|
F1F2
|2 |
PF1
F1F2 ,
F1PF2
2 ,求证:tan
n b
作业:
3.如图,圆C的半径为R,A是圆C外一个定点,M是圆C上的任意一点,线段 MA的垂直平分线l与CM相交于点Q,当点M在圆C上运动时,点Q的轨迹是什么?为什么?
M l
o A
小结:
一、焦点三角形中,常用关系:
1)、| MF1 | | MF2 | 2a
PF1 PF2.| PF1 |2 | PF2 |2 | F1F2 |2
F1
| PF1 |2 | PF2 |2 8 又| PF1 | - | PF2 | 2
| PF1 |2 | PF2 |2 -2 | PF1 || PF2 | 4
| PF1 || PF2 | 2
| PF1 | | PF2 | (| PF1 | | PF2 |)2 | PF1 |2 | PF2 |2 2 | PF1 || PF2 |
2 3
P F2
小结:
焦点三角形中,常用关系:
1)、| MF1 | | MF2 | 2a
2)、S F1PF2
1 2
|
MF1
||
MF2
|
SinF1PF2
3)、| F1F2 |2 | MF1 |2 | MF2 |2 2 | MF1 || MF2 | COSF1PF2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
a2 x
c
焦半径公式:
y
(一)M1位于双曲线右支
M 2 (x2, y2 )
F1
O
M1(x1, y1)
x (二)M2位于双曲线左支
F2
| M 2F1 | ex2 a
例1:如图,已知F1,F2为双曲线
1
x a
2 2
y2 b2
1(a
0, b
0)的焦点,
过F2作垂直与x轴的直线交双曲线于点P,且 sin
解法3: xP c, (c2 a2 b2 )
P
代入双曲线方程得yP
b2 a
又
sin
PF1F2
1 得 tan 3
PF1F2
1 22
F1
0
F2
y
| PF2 | b2 1
| F1F2 | 2ac 2 2
将b2 c2 a2代入得e c 2 a
小结
y
F1
练习1:求与定点 A(5,0)
的距离的比是定值
解:设M(x,y),
则 | MA | 5
d
4
( x 5)2 y 2 5
x 16
4
5
化简得 x2 y2 1 16 9
及定直线 的动点M的轨迹方程。
练习1:求与定点 A(c,0)
的距离的比是定值
解:设M(x,y),
则 | MA | 5
o
F2
x
(二)准线方程:x
a2
,
(a
c)
c
(三)焦半径公式的推导及其应用
思考:(1)双曲线
y a
2 2
x2 b2
1的准线方程及焦半径公式?
(2)如何求中心不在原点的双曲线的准线方程?
d
4
( x 5)2 y 2 5
x 16
4
5
化简得 x2 y2 1 16 9
及定直线 的动点M的轨迹方程。
练习1:求与定点 A(c,0)
的距离的比是定值
解:设M(x,y),
则 | MA | 5
d
4
( x 5)2 y 2 5
x 16
4
5
化简得 x2 y2 1
a2
例1:如图,已知F1,F2为双曲线
x a
2 2
y2 b2
1(a
0,b
0)的焦点,
过F2作垂直与x轴的直线交双曲线于点P,且 sin
PF1F2
1. 3
求此双曲线的离心率。
x
P
解法2:由题意xP c
焦半径 | PF1 | ec a,| PF2 | ec a
F1
0
F2
16 9
及定直线 的动点M的轨迹方程。
练习1:求与定点 A(c,0)
的距离的比是定值
及定直线l : x a2 的动点M的轨迹c方程。
解:设M(x,y),
解:设M(x,y),
则 | MA | 5
d
4
则 | MA | c
d
a
( x 5)2 y 2 5
x 16
4
5
化简得 x2 y2 1
1
上的点P到双曲线的
右焦点的距离是8,
那么P到右准线的距
离是 6.4 , P到左
准线的距离是19.2
N1
F1
x a2 c
练习2:求焦半径公式
y
设M(x1, y1),
M(x1,y1)
又|
MN1
|
x1
(
a2 c
)
x1
a2 c
O
x
F2
|
MF1
|
c a
( x1
a2 c
)
ex1
y
sin
PF1F2
| PF2 | PF1
| |
ec ec
a a
1 3
则e c 2 a
3
例1:如图,已知F1,F2为双曲线
x a
2 2
y2 b2
1(a
0, b
0)的焦点,
过F2作垂直与x轴的直线交双曲线于点P,且 sin
PF1F2
1. 3
求此双曲线的离心率。
x
PF1F2
1. 3
求此双曲线的离心率。
x
解法1:| PF1 | | PFቤተ መጻሕፍቲ ባይዱ | 2a 2 | PF2 |
P
又
e
c a
| F1F2 | 2 | PF2 |
1 2
cot
PF1F2
F1
0
F2
y
又
sin
PF1F2
1 3
得 cot
PF1F2
2
2
则e c 1 2 2 2
16 9
(x c)2 y2 c
x a2
a
c
y
F A1 1
O
F A2
x
2
2
x a2 c
a2 x
c
x a2 a a a
c
c
准线方程:x a2 c
两条准线比双曲线的顶点 更接近中心
F1
x a2 c
y
O
F2 x
a2 x
c
练习1:
如果双曲线
x2 y2 64 36
