岳麓区初中生数学实践与应用能力竞赛

合集下载

岳麓区初中生数学实践与应用能力竞赛

岳麓区初中生数学实践与应用能力竞赛获奖名单经过岳麓区中学数学教学专业委员会全体理事集中评卷，初中生数学实践与应用能力竞赛成绩已经揭晓。

本次比赛，各校按在校学生人数的5%选派学生参加全区的竞赛，然后分别按各年级参赛人数的10%、20%、30%确定壹、贰、叁等奖名额，各年级获奖学生名单如下：一、七年级获奖名单壹等奖坪塘镇坪塘中学：徐思旸雨敞坪镇嵇山中学：文祯19中：石星蒋国鹏周志鹏龙红梅28中：柳泽宇曾迈周嘉汇袁野成了师大附中博才实验中学：秦明航谢灵尧文健瞿佳高惟韬张振宇李钊毅王子健韩浩言贰等奖莲花镇五峰中学：谭豪高新区延风中学：张欣荣湘仪学校：许国强苏贵星坪塘镇坪塘中学：饶雅婷虢俊雄坪塘镇白泉学校：戴杰王思彬莲花镇双枫中学：阎妍夏晨懿19中：詹巍李梓鑫陈钰红28中：肖翠婷姚津鑫于润涛林岸潮含浦镇学士中学：阎建民代卫东肖顺海欧婷师大附中博才实验中学：李映波张艺辉文卓张淞陈李赵泽龙唐蔚萱卞俊杰李卓康郑天歌丁谦张曦琳谭泽为刘俊哲洪海涛张重哲李湘龙珺蒋正坤黄竞叁等奖雨敞坪镇嵇山中学：刘敏高新区延风中学：龚明远坪塘镇坪塘中学：黎康何首城坪塘镇白泉学校：谢湘闽谢煦涛含浦镇学士中学：杨飘涂博为莲花镇五峰中学：李迎周静妍雨敞坪镇麻田中学：殷岳佳黄新蓉坪塘镇太平中学：戴聪戴倩吴凡湘仪学校：尹潇锐张杨欧阳杏金含浦镇含浦中学：徐佳王诗菱刘尚凌帅杨思琪28中：余苗郭宇柳宇翔李鑫悦贾正阳田诚怡谭帅程俊华清水塘中学：蒋自力任冬阳胡钰莨曾家欣刘旋黄毅刘冰莹熊国瑜19中：蔡志雄余博涛黄智能戴雨睛陈乐虹刘鹏龚维李赛曹威李浩杰师大附中博才实验中学：张浩钧杨家睿唐博文谭丝何人杰欧万吉缪宗霖蒋坚孙嘉伟张弛胡凯邹怡琳杨红宇刘锦权二、八年级获奖名单壹等奖19中：戴景怡坪塘镇坪塘中学：刘博28中：李异陈章睿含浦镇学士中学：吴斯迪湘仪学校：刘宇刘达之向雨川向思齐唐嘉博杨鸿斌徐旺博艾凌浩王文杰童恺宁任祉燕刘心忱贰等奖雨敞坪镇嵇山中学：吴帅清水塘中学：舒南方莲花镇双枫中学李湘龚聘贤坪塘镇坪塘中学：谢添傲周天傲欧阳宗帅19中：莫明潇唐一平夏子睛张欢李雅丹湘仪学校：刘粲仪唐滢瑾余冠英戴琪贺睿智潘邹林凡邓家欣陈静刘敬28中：江泽星彭盛林徐弘毅谭正豪苏俊杰罗荣达邹紫曦黄茜雯陈学润唐钰铃袁键达叁等奖雨敞坪镇嵇山中学：陈龙坪塘镇太平中学：谢盈雨敞坪镇麻田中学：李尚文李博文含浦镇含浦中学：刘德升童思博坪塘镇坪塘中学：陈正泉吴昀健莫家曦坪塘镇白泉学校：徐炼锋谢煌陈源源含浦镇学士中学：李银芳李俊杰梁佳俊莲花镇双枫中学：李欢颜真唐麓林清水塘中学：刘树力黎琪桂迎杨宇成陈思远李鑫臣28中：黄修永唐奕昕付芊庞吉珊刘灏葭何希贤19中：段仪姿张明山李艳喻巧阳龚乐杨嘉欣李镕昆李陈创马芸芸湘仪学校：匡梦恬言思源李彩黄真李润鑫高瑛刘祎露王欢文雅菲董莳瑶杨菁三、九年级获奖名单壹等奖19中：高阳 28中：刘章倩黄越坪塘镇坪塘中学：吴浪刘作莲花镇双枫中学：李雅倩张蒙杨鹏宁湘龙湘仪学校：黄袆俤李盈王立舒刊余笑嫣贰等奖坪塘镇坪塘中学：周梦婷高新区延风中学：郑飞翔含浦镇学士中学：黄今殊雨敞坪镇嵇山中学：冯楚文雨敞坪镇麻田中学：彭建成含浦镇含浦中学：胡强杨意莲花镇双枫中学：李勇罗知达坪塘镇太平中学：徐馨吴将雄清水塘中学：樊清泉谷翼策杨耀 19中：周陵楚红宇湘仪学校：刘晓旻王紫珏秦旷袁钰坤覃娟28中：谭琳杨振宇代振兴张波魏子明任斯靓叁等奖坪塘镇白泉学校：陈建锌含浦镇学士中学：李鑫佩雨敞坪镇嵇山中学：李尚锋雨敞坪镇嵇山中学：周亚文高新区延风中学：贺蜜张聪湘仪学校：粟茜李旭光清水塘中学：黄维陈康吴吉坪塘镇太平中学：黄晴高琦黄鹂19中：肖凌彭志黄小凤张子剑坪塘镇坪塘中学：李渊龙杨誉周亚周可含浦镇含浦中学：陈剑枫阳权曹亚军戴洁莲花镇双枫中学：黄乐登张新果丁娇宁贺斌彭博周洁28中：于见智蔡艺卓彭阳郭星池罗俊容张益岳麓区中学数学教学专业委员会岳麓区教研室 2010年元月13日。

湖南省长沙市岳麓区湖南师范大学附属中学2024-2025学年高三上学期11月月考数学试题

湖南省长沙市岳麓区湖南师范大学附属中学2024-2025学年高三上学期11月月考数学试题一、单选题1．集合{}0,1,2,3A =的真子集的个数是（）A ．16B ．15C ．8D ．72．“11x -<”是“240x x -<”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．已知角α的终边上有一点P 的坐标是()3,4a a ，其中0a ≠，则sin2α=（）A ．43B ．725C ．2425D ．2425-4．设向量a ，b满足a b += a b -=r r a b ⋅ 等于（）A ．B ．2C ．5D ．85．若无论θ为何值，直线sin cos 10y x θθ⋅+⋅+=与双曲线2215x ym -=总有公共点，则m 的取值范围是（）A ．1m ≥B ．01m <≤C ．05m <<，且1m ≠D ．1m ≥，且5m ≠6．已知函数()2f x 的图象关于原点对称，且满足()()130f x f x ++-=，且当()2,4x ∈时，()()12log 2f x x m =--+，若()()2025112f f -=-，则m 等于（）A ．13B ．23C ．23-D ．13-7．已知正三棱台111ABC A B C -所有顶点均在半径为5的半球球面上，且AB =11A B =）A ．1B ．4C ．7D ．1或78．北宋数学家沈括博学多才、善于观察.据说有一天，他走进一家酒馆，看见一层层垒起的酒坛，不禁想到：“怎么求这些酒坛的总数呢？”经过反复尝试，沈括提出对于上底有ab 个，下底有cd 个，共n 层的堆积物（如图所示），可以用公式()()()2266nn S b d a b d c c a =++++-⎡⎤⎣⎦求出物体的总数，这就是所谓的“隙积术”，相当于求数列ab ，()()()()()()11,22,,11a b a b a n b n cd +++⋅++-+-= 的和.若由小球堆成的上述垛积共7层，小球总个数为238，则该垛积最上层的小球个数为（）A ．2B ．6C ．12D ．20二、多选题9．若2024220240122024(12)x a a x a x a x +=++++ ，则下列正确的是（）A ．02024a =B ．20240120243a a a +++= C ．012320241a a a a a -+-++= D ．12320242320242024a a a a -+--=- 10．对于函数()sin cos f x x x =+和()sin cos 22g x x x ππ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭，下列说法中正确的有（）A ．()f x 与()g x 有相同的零点B ．()f x 与()g x 有相同的最大值点C ．()f x 与()g x 有相同的最小正周期D ．()f x 与()g x 的图象有相同的对称轴11．过点()0,2P 的直线与抛物线2:4C x y =交于()11,A x y ，()22,B x y 两点，抛物线C 在点A 处的切线与直线2y =-交于点N ，作NM AP ⊥交AB 于点M ，则（）A ．5OA OB ⋅=-B ．直线MN 恒过定点C ．点M 的轨迹方程是()22(1)10y x y -+=≠D ．ABMN三、填空题12．已知复数1z ，2z 的模长为1，且21111z z +=，则12z z +=.13．在ABC V 中，角,,A B C 所对的边分别为a ，b ，c 已知5a =，4b =，()31cos 32A B -=，则sin B =.14．若正实数1x 是函数()2e e x f x x x =--的一个零点，2x 是函数()()()3e ln 1e g x x x =---的一个大于e 的零点，则()122e e x x -的值为.四、解答题15．现有某企业计划用10年的时间进行技术革新，有两种方案：贷款利润A 方案一次性向银行贷款10万元第1年利润1万元，以后每年比前一年增加25%的利润B 方案每年初向银行贷款1万元第1年利润1万元，以后每年比前一年增加利润3000元两方案使用期都是10年，贷款10年后一次性还本付息（年末结息），若银行贷款利息均按10%的复利计算.(1)计算10年后，A 方案到期一次性需要付银行多少本息？(2)试比较A 、B 两方案的优劣.（结果精确到万元，参考数据：101.12.594≈，101.259.313≈）16．如图，四棱锥P ABCD -中，底面ABCD 为等腰梯形，222AD AB BC ===.点P 在底面的射影点Q 在线段AC 上.(1)在图中过A 作平面PCD 的垂线段，H 为垂足，并给出严谨的作图过程；(2)若2PA PD ==.求平面PAB 与平面PCD 所成锐二面角的余弦值.17．已知函数()e sin cos x f x x x =+-，()f x '为()f x 的导数.(1)证明：当0x ≥时，()2f x '≥；(2)设()()21g x f x x =--，证明：()g x 有且仅有2个零点.18．在平面直角坐标系xOy 中，已知椭圆2222:1(0)x y C a b a b +=>>的两个焦点为1F 、2F ，P为椭圆C 上一动点，设12F PF θ∠=，当2π3θ=时，12F PF(1)求椭圆C 的标准方程.(2)过点()0,2B 的直线l 与椭圆交于不同的两点M 、N （M 在B ，N 之间），若Q 为椭圆C 上一点，且OQ OM ON =+，①求OBMOBNS S 的取值范围；②求四边形OMQN 的面积.19．飞行棋是大家熟悉的棋类游戏，玩家通过投掷骰子来决定飞机起飞与飞行的步数.当且仅当玩家投掷出6点时，飞机才能起飞.并且掷得6点的游戏者可以连续投掷骰子，直至显示点数不是6点.飞机起飞后，飞行步数即骰子向上的点数.(1)求甲玩家第一轮投掷中，投郑次数X 的均值()()()11lim n n k k E X kP k kP k ∞∞→==⎛⎫== ⎪⎝⎭∑∑）(2)对于两个离散型随机变量ξ、η，我们将其可能出现的结果作为一个有序数对，类似于离散型随机变量的分布列，我们可以用如下表格来表示这个有序数对的概率分布：（记()()()11,mi i ijj p x p x p x y ξ====∑，()()()21,njiij i p y p y p xy η====∑）ξη1x 2x ⋯n x 1y ()11,p x y ()21,p x y ⋯()1,n p x y ()21p y 2y ()12,p x y ()22,p x y L()2,n p x y ()22p y ⋯⋯⋯⋯⋯⋯my ()1,m p x y ()2,m p x y ⋯(),n m p x y ()2m p y ()11p x ()12p x L()1n p x 1若已知i x ξ=，则事件{}j y η=的条件概率为{}{}{}()()1,,j i i j j i i i P y x p x y P y x P x p x ηξηξξ=======.可以发现i x ηξ=依然是一个随机变量，可以对其求期望{}{}()()1111,mmi j j i j i jj i iE x y P y x y p x y p x ηξηξ====⋅===⋅∑∑.（ⅰ）上述期望依旧是一个随机变量（ξ取值不同时，期望也不同），不妨记为{}E ηξ，求{}E E ηξ⎡⎤⎣⎦；（ⅱ）若修改游戏规则，需连续掷出两次6点飞机才能起飞，记0ξ=表示“甲第一次未能掷出6点”，1ξ=表示“甲第一次掷出6点且第二次未能掷出6点”，2ξ=表示“甲第一次第二次均掷出6点”，η为甲首次使得飞机起飞时抛掷骰子的次数，求E η.。

2024年湖南省长沙市部分学校初中学业水平联考数学试题

2024年湖南省长沙市部分学校初中学业水平联考数学试题一、单选题112-， 9，3.14，其中比0小的数是（） AB ．12-C ．9D ．3．14 2．“科技改变世界”．下列与科技最前沿相关的图形中，只是中心对称图形的是（） A ． B ． C ．D ．3．长沙市因地制宜，大力发展新质生产力，眼下长沙跻身“数字经济新一线城市”，数字经济总量达450000000000元，数据450000000000用科学记数法表示为（） A ．120.4510⨯ B ．114.510⨯ C ．104510⨯ D ．104.510⨯ 4．下列计算正确的是（）A ．23a b ab +=B ．()3263a b a b -=C ．()1a b ab a -=-D ．222=- 5．若3，6，x 是某三角形的三边长，则x 可取的最大整数为（）A ．10B ．9C ．8D ．76．下列事件是必然事件的是（）A ．任画一个凸多边形，其外角和是360︒B ．在乒乓球比赛中，世界排名第一的运动员一定打赢排名第二的运动员C ．圆柱无论怎样摆放，它的三视图都是矩形D ．若 a 是实数，则a a >7．如图，直线AB CD ∥，点G 是直线CD 上一点，射线GE ，GF 分别交直线AB 于点H ，N ，若156∠=︒，270∠=︒，则EGF ∠的度数为（）A ．50︒B ．54︒C ．58︒D ．62︒8．如图，AC 是O e 的直径，BC 与O e 相切于点C ，AB 交O e 于点D ，连接OD ，若84COD ∠=︒，则ABC ∠的度数为（）A ．46︒B ．48︒C ．50︒D ．52︒9．龙年春晚的扑克牌魔术激发了小明的兴趣．他抽取了一副扑克牌中的四张：黑桃3，红桃5，梅花7，方片10（黑桃和梅花是黑色，红桃和方片是红色），他将这四张扑克牌充分洗匀，再随机抽取2张，则他抽到的两张扑克牌颜色不同的概率是（）A ．23B ．13C ．14 D ．1610．如图是一张三角形纸片，其中1012AB AC BC ===，，按如下步骤折纸：第一步：将该纸片对折，点B 与点C 重合，折痕为AD ；第二步：展开后，再将该纸片折叠；折痕为BE ，点A 的对称点A '恰好落在AC 上根据以上折纸过程，可以求出折痕BE 的长度为（）A ．10B ．9.8C ．9.7D ．9.6二、填空题11．分解因式：3x 9x -=.12．方程组x y 3{x y 1+=-=的解是．13．安全教育是素质教育的重要内容之一，为增强学生的安全意识，提升学生自我保护能力，某校对学生进行了“中小学生安全知识100条”的讲座和实践活动，为检验学习效果，对学生进行了安全知识测试，并随机抽取了8位学生成绩如下（满分：100分）：98，85，90，88，92，95，82，90，则这一组数据的众数是．14．如图，在Rt PQR △中，90PQR ∠=︒，43PQ RQ ==，，将Rt PQR △绕直线PQ 旋转一周，会得到一个几何体，则这个几何体的侧面积等于．（结果保留π）15．已知一次函数()0y ax a =≠的图象如图所示，则反比例函数a y x=的图象经过第象限．16．如图，正方形ABCD 的边长为4，点E ，F 分别在边AD ，BC 上，点M ，N 分别在边AB ，DC 上，且EF MN ⊥，垂足为点O ，若线段EF 恰好平分正方形ABCD 的面积，1AE =，则22EF MN +=．三、解答题17．计算： 101tan 60202452π-⎛⎫⎛⎫+-︒++ ⎪ ⎪⎝⎭⎝⎭． 18．先化简，后求值：2211121x x x x ⎛⎫+÷ ⎪--+⎝⎭，其中100x =． 19．如图，四边形ABCD 是平行四边形，对角线AC 平分BCD ∠，过点A 作AF CD ⊥交其延长线于点F ，过点F 作FE BC ⊥于点E ．(1)求证：四边形ABCD 是菱形；(2)若60BCD ∠=︒，12AD =，求FE 的值．20．为进一步提高义务教育质量，提升学生的信息素养，湖南中考于2026年将信息科技科目纳入中考范围，2023年入学的七年级新生将于2025年参加信息科技的中考，为了解学生的信息科技课程学习情况，更好地促进课程学习，长沙某校于2023年期末对全校七年级学生进行了信息科技上机测试．学校将测试成绩（满分：100分），收集、整理分组，记得分为x 分，并制作了如下不完整的统计图表．根据上面信息，回答下列问题：(1)该校七年级总人数为____人；a =____；b =____；(2)将频数分布直方图补充完整；(3)若将上述表格转化为扇形统计图，则C 组学生所对应扇形的圆心角的度数为____︒．21．如图，在ABCV中，O是AB边的中点，D是CO上一点，AE∥BD交CO的延长线于点E．(1)求证：AE BD=；(2)若90ACB∠=︒，BDO CAO∠=∠，6AC=，求BD的长．22．为响应国家关于推动各级各类生产设备、服务设备更新和技术改造的号召，某公司计划将办公电脑全部更新为国产某品牌，市场调研发现，A品牌的电脑单价比B品牌电脑的单价少1000元，通过预算得知，用30万元购买A品牌电脑比购买B品牌电脑多10台．(1)试求A，B两种品牌电脑的单价分别是多少元；(2)该公司计划购买A，B两种品牌的电脑一共40台，且购买B品牌电脑的数量不少于A品牌电脑的35，试求出该公司费用最少的购买方案．23．根据以下实践活动项目提供的材料，完成相关任务．【活动主题】怎样确定隧道口车辆通过限行高度？【活动过程】素材1：长沙附近有一条两车道隧道，隧道口有4.5m限高标志，如图1，表示车辆顶部最高处到地面的距离不超过4.5m，否则禁止通行．素材2：李明通过实地测量和查阅有关资料，获得以下信息，如图2：①隧道口上部是一个半圆，下部是一个矩形，矩形的长和半圆的直径相等②矩形的长为10m，高为2m，车道两侧各有1m人行道；③设计部门要求车辆顶部（约定为平顶）与隧道圆拱内部在竖直方向至少有mh的距离．【问题解决】(1)试求隧道口上半圆中点E到路面AB的距离EF；(2)求h 的最小值．24．我们不妨约定：如果抛物线的顶点在直线y x =上，那么我们把这样的抛物线叫做“星链抛物线”．根据约定，解答下列问题：(1)试判断下列抛物线是否为“星链抛物线”，若是，请在括号内画“√”；若不是，请在括号内画“⨯”．①2y x =（）；②221y x x =-+（）；③()2y x h h =--+（）．(2)如图，已知“星链抛物线”()21y x k =--+的顶点为点A ，将该抛物线沿直线y x =向上平移，使点A ，和点B 重合，两条“星链抛物线”的交点为点C ，设点B ，点C 的横坐标分别为m ，(1)n m >．①若AB =②在平移过程中，若45ACB ∠=︒，试求mn 的值．25．如图，过O e 上的动点D 作O e 的切线AD ，在O e 上取点B （异于点D ），使得AB AD =，弦CD AB ∥，连接AC 交O e 于点F ，连接DF 并延长，交AB 于点E ，连接BC ．(1)求证：AB 是O e 的切线；(2)记AEF V ，ADF V ；DCF V 的面积分别为1S ，2S ，3S ，当123S S S +=时，求AF CF的值； (3)设O e 的半径为R ，当DE CB ∥时，求四边形BCDE 的面积．（用含R 的式子表示）。

2021-2022学年湖南省长沙市岳麓区长郡双语实验中学八年级下学期期末数学试卷(解析版)

2021-2022学年湖南省长沙市岳麓区长郡双语实验中学八年级（下）期末数学试卷一、选择题（本题共10个小题，每小题4分，共40分，每小题给出的四个选项中，只有一项是符合题目要求的，请把你认为符合题目要求的选项填在相应的表格内）1．（4分）下列四组线段中，可以构成直角三角形的是（）A．2，3，4B．4，5，6C．1，，3D．1，2，2．（4分）若一个多边形的内角和为1080°，则这个多边形的边数为（）A．6B．7C．8D．93．（4分）已知四边形ABCD是平行四边形，再从①AB＝BC，②∠ABC＝90°，③AC＝BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（）A．选①②B．选②③C．选①③D．选②④4．（4分）已知线段CD是由线段AB平移得到的，点A（﹣1，4）的对应点为C（4，7），则点B（﹣4，﹣1）的对应点D的坐标为（）A．（1，2）B．（2，9）C．（5，3）D．（﹣9，﹣4）5．（4分）一次函数y＝2x+1的图象不经过下列哪个象限（）A．第一象限B．第二象限C．第三象限D．第四象限6．（4分）某棉纺厂为了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x（单位：mm）的数据分布如下表所示，则棉花纤维长度的数据在16≤x＜32这个范围的频率为（）棉花纤维长度x频数0≤x＜818≤x＜16216≤x＜24824≤x＜32632≤x＜403A．0.8B．0.7C．0.4D．0.27．（4分）菱形ABCD中，对角线AC、BD相交于点O，P为AD边中点，菱形ABCD的周长为16，则OP的长等于（）A．2B．4C．6D．88．（4分）图象中所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家．其中x表示时间，y表示张强离家的距离．根据图象提供的信息，以下四个说法错误的是（）A．体育场离张强家2.5千米B．张强在体育场锻炼了15分钟C．体育场离早餐店4千米D．张强从早餐店回家的平均速度是3千米/小时9．（4分）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．等边三角形B．平行四边形C．矩形D．正五边形10．（4分）如图，已知∠AOB＝60°，点P在边OA上，OP＝12，点M，N在边OB上，PM＝PN，若MN＝2，则OM＝（）A．3B．4C．5D．6二、填空题（本题6个小题，每小题5分，共30分）11．（5分）点A（2，3）关于x轴的对称点的坐标是．12．（5分）函数y＝1+中自变量x的取值范围是．13．（5分）已知10个数据：1，1，1，2，2，2，3，3，3，3．其中3出现的频数是．14．（5分）如图，已知△ABC中，∠C＝90°，则．（请写出一条结论）15．（5分）将四根木条钉成的长方形木框变形为平行四边形ABCD的形状，并使其面积为长方形面积的一半（木条宽度忽略不计），则这个平行四边形的最小内角为度．16．（5分）如图，已知△ABC中，∠C＝90°，AB＝10，BC＝6，若点D为AB边上任意一点，则线段CD的取值范围是．三、解答题（本题3个小题，每小题8分，共24分）17．（8分）如图，在△ABC中，AB＝AC＝13cm，D是AC边上的点，DC＝1cm，BD＝5cm，求BC的长．18．（8分）如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE＝DF，连接CE，AF．求证：AF＝CE．19．（8分）在平面直角坐标系中，将坐标为（0，0），（1，3），（2，0），（3，3）的点用线段依次连接起来得到一个图案N．（1）在图（1）中，分别画出图案N关于x轴和y轴对称的图案；（2）在图（2）中，将图案N先向左平移3个单位长度，再向下平移4个单位长度，画出第二次平移后的图案；（3）在图（3）中，以原点为对称中心，画出与图案N成中心对称的图案．四、解答题（本题3个小题，每小题10分，共30分）20．若函数y＝mx+|m|﹣4是正比例函数，且函数值y随自变量x的增大而减小．（1）求该函数的表达式；（2）当函数值为16时，求自变量x的值．21．为了提高学生书写汉字的能力，增强保护汉字的意识，某市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：组别成绩x分频数（人数）第1组25≤x＜304第2组30≤x＜35a第3组35≤x＜4016第4组40≤x＜4512第5组45≤x＜5010（1）求表中a的值；（2）请把频数分布直方图补充完整；（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？22．如图，已知△ABC中，∠C＝90°，AB＝10，BC＝6，若AD为∠ACB的平分线，求AD的长？五、解答题（本题12分）23．（12分）已知水银体温计的读数y（℃）与水银柱的长度x（cm）之间是一次函数关系．现有一支水银体温计，其部分刻度线不清晰（如图），表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度．水银柱的长度x（cm） 4.2…8.29.8体温计的读数y（℃）35.0…40.042.0（1）求y关于x的函数关系式（不需要写出函数的定义域）；（2）用该体温计测体温时，水银柱的长度为6.2cm，求此时体温计的读数．六、解答题（本题14分）24．如图，已知Rt△ABC中，∠ACB＝90°，先把△ABC绕点C顺时针旋转90°至△EDC 后，再把△ABC沿射线BC平移至△GFE，DE、FG相交于点H．（1）判断线段DE、FG的位置关系，并说明理由；（2）连结AG，求证：四边形ACEG是正方形．2021-2022学年湖南省长沙市岳麓区长郡双语实验中学八年级（下）期末数学试卷参考答案与试题解析一、选择题（本题共10个小题，每小题4分，共40分，每小题给出的四个选项中，只有一项是符合题目要求的，请把你认为符合题目要求的选项填在相应的表格内）1．（4分）下列四组线段中，可以构成直角三角形的是（）A．2，3，4B．4，5，6C．1，，3D．1，2，【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个就不是直角三角形，逐一判定即可．解：A、22+32≠42，不符合勾股定理的逆定理，不能构成直角三角形，故本选项不符合题意；B、42+52≠62，不符合勾股定理的逆定理，不能构成直角三角形，故本选项不符合题意；C、12+（）2≠32，不符合勾股定理的逆定理，不能构成直角三角形，故本选项不符合题意；D、12+（）2＝22，符合勾股定理的逆定理，能构成直角三角形，故本选项符合题意．故选：D．【点评】本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．2．（4分）若一个多边形的内角和为1080°，则这个多边形的边数为（）A．6B．7C．8D．9【分析】首先设这个多边形的边数为n，由n边形的内角和等于180°（n﹣2），即可得方程180°（n﹣2）＝1080°，解此方程即可求得答案．解：设这个多边形的边数为n，根据题意得：180°（n﹣2）＝1080°，解得：n＝8．故选：C．【点评】此题考查了多边形的内角和公式．此题比较简单，注意熟记公式是准确求解此题的关键，注意方程思想的应用．3．（4分）已知四边形ABCD是平行四边形，再从①AB＝BC，②∠ABC＝90°，③AC＝BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（）A．选①②B．选②③C．选①③D．选②④【分析】要判定是正方形，则需能判定它既是菱形又是矩形．解：A、由①得有一组邻边相等的平行四边形是菱形，由②得有一个角是直角的平行四边形是矩形，所以平行四边形ABCD是正方形，正确，故本选项不符合题意；B、由②得有一个角是直角的平行四边形是矩形，由③得对角线相等的平行四边形是矩形，所以不能得出平行四边形ABCD是正方形，错误，故本选项符合题意；C、由①得有一组邻边相等的平行四边形是菱形，由③得对角线相等的平行四边形是矩形，所以平行四边形ABCD是正方形，正确，故本选项不符合题意；D、由②得有一个角是直角的平行四边形是矩形，由④得对角线互相垂直的平行四边形是菱形，所以平行四边形ABCD是正方形，正确，故本选项不符合题意．故选：B．【点评】本题考查了正方形的判定方法：①先判定四边形是矩形，再判定这个矩形有一组邻边相等；②先判定四边形是菱形，再判定这个菱形有一个角为直角．③还可以先判定四边形是平行四边形，再用1或2进行判定．4．（4分）已知线段CD是由线段AB平移得到的，点A（﹣1，4）的对应点为C（4，7），则点B（﹣4，﹣1）的对应点D的坐标为（）A．（1，2）B．（2，9）C．（5，3）D．（﹣9，﹣4）【分析】根据点A、C的坐标确定出平移规律，再求出点D的坐标即可．解：∵点A（﹣1，4）的对应点为C（4，7），∴平移规律为向右5个单位，向上3个单位，∵点B（﹣4，﹣1），∴点D的坐标为（1，2）．故选：A．【点评】本题考查了坐标与图形变化﹣平移，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．5．（4分）一次函数y＝2x+1的图象不经过下列哪个象限（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据题目中的函数解析式和一次函数的性质，可以解答本题．解：∵一次函数y＝2x+1，∴该函数经过第一、二、三象限，不经过第四象限，故选：D．【点评】本题考查一次函数的性质，解答本题的关键是明确题意，利用一次函数的性质解答．6．（4分）某棉纺厂为了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x（单位：mm）的数据分布如下表所示，则棉花纤维长度的数据在16≤x＜32这个范围的频率为（）棉花纤维长度x频数0≤x＜818≤x＜16216≤x＜24824≤x＜32632≤x＜403A．0.8B．0.7C．0.4D．0.2【分析】先求得在16≤x＜32这个范围的频数，再根据频率的计算公式即可求解．解：在16≤x＜32这个范围的频数是：8+6＝14，则在16≤x＜32这个范围的频率是：＝0.7．故选：B．【点评】本题考查了频数分布表，用到的知识点是：频率＝频数÷总数．7．（4分）菱形ABCD中，对角线AC、BD相交于点O，P为AD边中点，菱形ABCD的周长为16，则OP的长等于（）A．2B．4C．6D．8【分析】先根据菱形ABCD的周长为16，求出边长AB，然后根据P为AD边中点，可得OP＝AB，即可求解．解：∵菱形ABCD的周长为16，∴AB＝4，∵P为AD边中点，O为BD的中点，∴OP＝AB＝2．故选：A．【点评】本题考查了菱形的性质，解答本题的关键掌握菱形四条边都相等，对角线互相垂直且平分的性质．8．（4分）图象中所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家．其中x表示时间，y表示张强离家的距离．根据图象提供的信息，以下四个说法错误的是（）A．体育场离张强家2.5千米B．张强在体育场锻炼了15分钟C．体育场离早餐店4千米D．张强从早餐店回家的平均速度是3千米/小时【分析】结合图象得出张强从家直接到体育场，故第一段函数图象所对应的y轴的最高点即为体育场离张强家的距离；进而得出锻炼时间以及整个过程所用时间．由图中可以看出，体育场离张强家2.5千米；平均速度＝总路程÷总时间．解：A、由函数图象可知，体育场离张强家2.5千米，故A选项正确；B、由图象可得出张强在体育场锻炼30﹣15＝15（分钟），故B选项正确；C、体育场离张强家2.5千米，体育场离早餐店距离无法确定，因为题目没说体育馆，早餐店和家三者在同一直线上，故C选项错误；D、∵张强从早餐店回家所用时间为95﹣65＝30（分钟），距离为1.5km，∴张强从早餐店回家的平均速度1.5÷0.5＝3（千米/时），故D选项正确．故选：C．【点评】此题主要考查了函数图象与实际问题，根据已知图象得出正确信息是解题关键．9．（4分）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．等边三角形B．平行四边形C．矩形D．正五边形【分析】根据轴对称图形与中心对称图形的概念求解．解：A、等边三角形是轴对称图形，不是中心对称图形．故本选项不合题意；B、平行四边形是中心对称图形，不是轴对称图形．故本选项不合题意；C、矩形既是轴对称图形，又是中心对称图形．故本选项符合题意；D、正五边形是轴对称图形，不是中心对称图形．故本选项不合题意．故选：C．【点评】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形沿着对称轴折叠后两部分可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．10．（4分）如图，已知∠AOB＝60°，点P在边OA上，OP＝12，点M，N在边OB上，PM＝PN，若MN＝2，则OM＝（）A．3B．4C．5D．6【分析】过P作PD⊥OB，交OB于点D，在直角三角形POD中，利用锐角三角函数定义求出OD的长，再由PM＝PN，利用三线合一得到D为MN中点，根据MN求出MD 的长，由OD﹣MD即可求出OM的长．解：过P作PD⊥OB，交OB于点D，在Rt△OPD中，cos60°＝＝，OP＝12，∴OD＝6，∵PM＝PN，PD⊥MN，MN＝2，∴MD＝ND＝MN＝1，∴OM＝OD﹣MD＝6﹣1＝5．故选：C．【点评】此题考查了含30度直角三角形的性质，等腰三角形的性质，熟练掌握直角三角形的性质是解本题的关键．二、填空题（本题6个小题，每小题5分，共30分）11．（5分）点A（2，3）关于x轴的对称点的坐标是（2，﹣3）．【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答．解：点A（2，3）关于x轴的对称点的坐标是（2，﹣3）．故答案为：（2，﹣3）．【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．12．（5分）函数y＝1+中自变量x的取值范围是x≥．【分析】根据二次根式（a≥0），可得2x﹣1≥0，然后进行计算即可解答．解：由题意得：2x﹣1≥0，∴x≥，故答案为：x≥．【点评】本题考查了函数自变量的取值范围，熟练掌握二次根式（a≥0）是解题的关键．13．（5分）已知10个数据：1，1，1，2，2，2，3，3，3，3．其中3出现的频数是4．【分析】根据频数的定义，即可解答．解：已知10个数据：1，1，1，2，2，2，3，3，3，3．其中3出现的频数为：4，故答案为：4．【点评】本题考查了频数与频率，熟练掌握频数的定义是解题的关键．14．（5分）如图，已知△ABC中，∠C＝90°，则∠A+∠B＝90°（答案不唯一）．（请写出一条结论）【分析】根据直角三角形的性质即可求解．解：△ABC中，∠C＝90°，则∠A+∠B＝90°（答案不唯一）．故答案为：∠A+∠B＝90°（答案不唯一）．【点评】本题考查了直角三角形的性质，直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：性质1：直角三角形两直角边的平方和等于斜边的平方（勾股定理）．性质2：在直角三角形中，两个锐角互余．性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点）．性质4：直角三角形的两直角边的乘积等于斜边与斜边上高的乘积．性质5：在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半；在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°．15．（5分）将四根木条钉成的长方形木框变形为平行四边形ABCD的形状，并使其面积为长方形面积的一半（木条宽度忽略不计），则这个平行四边形的最小内角为30度．【分析】根据矩形以及平行四边形的面积求法得出当AE＝AB，则符合要求，进而得出答案．解：过点A作AE⊥BC于点E，∵将四根木条钉成的长方形木框变形为平行四边形ABCD的形状，并使其面积为长方形面积的一半（木条宽度忽略不计），∴当AE＝AB，则符合要求，此时∠B＝30°，即这个平行四边形的最小内角为：30度．故答案为：30．【点评】此题主要考查了矩形的性质和平行四边形面积求法等知识，得出AE＝AB是解题关键．16．（5分）如图，已知△ABC中，∠C＝90°，AB＝10，BC＝6，若点D为AB边上任意一点，则线段CD的取值范围是 4.8≤CD≤8．【分析】过点C作CD′⊥AB于D′，根据勾股定理求出AC，根据三角形的面积公式求出CD′，得到答案．解：过点C作CD′⊥AB于D′，由垂线段最短可知，当CD⊥AB时，CD最短，即点D在点D′的位置时，CD最短，由勾股定理得：AC＝＝＝8，∵S△ABC＝AB×CD′＝AC，∴CD′＝＝4.8，∴4.8≤CD≤8，故答案为：4.8≤CD≤8．【点评】本题考查的是勾股定理、垂线段最短以及三角形的面积计算，根据垂线段最短确定CD的最小值是解题的关键．三、解答题（本题3个小题，每小题8分，共24分）17．（8分）如图，在△ABC中，AB＝AC＝13cm，D是AC边上的点，DC＝1cm，BD＝5cm，求BC的长．【分析】先求出AD的长，再根据勾股定理的逆定理判断△ABD是直角三角形，且∠ADB ＝90°，然后在Rt△BCD中，根据勾股定理求出BC即可．解：∵AC＝13，CD＝1，∴AD＝AC﹣CD＝13﹣1＝12．在△ABD中，∵AB＝13，AD＝12，BD＝5，∴AB2＝132＝169，AD2+BD2＝122+52＝144+25＝169，∴AD2+BD2＝AB2，∴△ABD是直角三角形，且∠ADB＝90°，在Rt△BCD中，∵CD＝1，BD＝5，∴（cm）．即BC的长为cm．【点评】本题考查了勾股定理和勾股定理的逆定理，能熟记勾股定理的逆定理的内容是解此题的关键．18．（8分）如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE＝DF，连接CE，AF．求证：AF＝CE．【分析】根据矩形的性质得出DC∥AB，DC＝AB，求出CF＝AE，CF∥AE，根据平行四边形的判定得出四边形AFCE是平行四边形，即可得出答案．【解答】证明：∵四边形ABCD是矩形，∴DC∥AB，DC＝AB，∴CF∥AE，∵DF＝BE，∴CF＝AE，∴四边形AFCE是平行四边形，∴AF＝CE．【点评】本题考查了平行四边形的性质和判定，矩形的性质的应用，注意：矩形的对边相等且平行，平行四边形的对边相等．19．（8分）在平面直角坐标系中，将坐标为（0，0），（1，3），（2，0），（3，3）的点用线段依次连接起来得到一个图案N．（1）在图（1）中，分别画出图案N关于x轴和y轴对称的图案；（2）在图（2）中，将图案N先向左平移3个单位长度，再向下平移4个单位长度，画出第二次平移后的图案；（3）在图（3）中，以原点为对称中心，画出与图案N成中心对称的图案．【分析】（1）利用轴对称变换的性质作出图形即可；（2）利用平移变换的性质作出图形即可；（3）利用中心对称变换的性质作出图形即可．解：（1）图形如图所示：（2）图形如图所示：（3）图形如图所示．【点评】本题考查利用旋转设计图案，利用平移设计图案，利用轴对称设计图案，解题的关键是掌握轴对称变换，旋转变换，平移变换的性质．四、解答题（本题3个小题，每小题10分，共30分）20．若函数y＝mx+|m|﹣4是正比例函数，且函数值y随自变量x的增大而减小．（1）求该函数的表达式；（2）当函数值为16时，求自变量x的值．【分析】（1）根据题意得出m＜0，|m|﹣4＝0，解得即可；（2）把y＝16代入（1）求得的解析式，解得x＝﹣5．解：（1）∵y＝mx+|m|﹣4是正比例函数，∴|m|﹣4＝0，∴m＝±4，又∵函数值y随自变量x的增大而减小，∴m＜0，∴m＝﹣4，∴该函数的表达式为：y＝﹣4x﹣4；（2）由已知得：16＝﹣4x﹣4，解得：x＝﹣5，∴当函数值为16时，自变量x的值为﹣5．【点评】本题考查了正比例函数的定义，一次函数的性质，一次函数图象上点的坐标特征，熟知一次函数的性质是解题的关键．21．为了提高学生书写汉字的能力，增强保护汉字的意识，某市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：组别成绩x分频数（人数）第1组25≤x＜304第2组30≤x＜35a第3组35≤x＜4016第4组40≤x＜4512第5组45≤x＜5010（1）求表中a的值；（2）请把频数分布直方图补充完整；（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？【分析】（1）用总人数减去第1、2、3、5组的人数，即可求出a的值；（2）根据（1）得出的a的值，补全统计图；（3）用成绩不低于40分的频数乘以总数，即可得出本次测试的优秀率．解：（1）表中a的值是：a＝50﹣4﹣8﹣16﹣10＝12；（2）根据题意画图如下：（3）本次测试的优秀率是＝0.44．答：本次测试的优秀率是0.44．【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．22．如图，已知△ABC中，∠C＝90°，AB＝10，BC＝6，若AD为∠ACB的平分线，求AD的长？【分析】过点D作DE⊥AB于E，根据角平分线的性质得到CD＝DE，根据勾股定理求出AC，根据三角形面积公式求出CD，再根据勾股定理计算，得到答案．解：过点D作DE⊥AB于E，∵AD为∠ACB的平分线，DE⊥AB，∠C＝90°，∴CD＝ED，由勾股定理可得：AC＝＝＝8，设CD＝ED＝x，则×6×8＝×8x+×10x，解得：x＝，即CD＝，由勾股定理可得：AD＝＝＝．【点评】本题考查的是勾股定理、角平分线的性质，根据角平分线的性质得出DC＝DE 是解题的关键．五、解答题（本题12分）23．（12分）已知水银体温计的读数y（℃）与水银柱的长度x（cm）之间是一次函数关系．现有一支水银体温计，其部分刻度线不清晰（如图），表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度．水银柱的长度x（cm） 4.2…8.29.8体温计的读数y（℃）35.0…40.042.0（1）求y关于x的函数关系式（不需要写出函数的定义域）；（2）用该体温计测体温时，水银柱的长度为6.2cm，求此时体温计的读数．【分析】（1）设y关于x的函数关系式为y＝kx+b，由统计表的数据建立方程组求出其解即可；（2）当x＝6.2时，代入（1）的解析式就可以求出y的值．解：（1）设y关于x的函数关系式为y＝kx+b，由题意，得，解得：，∴y＝x+29.75．∴y关于x的函数关系式为：y＝+29.75；（2）当x＝6.2时，y＝×6.2+29.75＝37.5．答：此时体温计的读数为37.5℃．【点评】本题考查了待定系数法求一次函数的解析式的运用，由解析式根据自变量的值求函数值的运用，解答时求出函数的解析式是关键．六、解答题（本题14分）24．如图，已知Rt△ABC中，∠ACB＝90°，先把△ABC绕点C顺时针旋转90°至△EDC 后，再把△ABC沿射线BC平移至△GFE，DE、FG相交于点H．（1）判断线段DE、FG的位置关系，并说明理由；（2）连结AG，求证：四边形ACEG是正方形．【分析】（1）由旋转和平移的性质可得∠BAC＝∠CED，∠ABC＝∠GFE，由余角的性质可得结论；（2）由旋转和平移的性质可得AC＝GE，AC∥GE，AC＝CE，∠ACE＝90°，可得结论．【解答】（1）解：DE⊥FG，理由如下：∵把△ABC绕点C顺时针旋转90°至△EDC，∴∠BAC＝∠CED，∵把△ABC沿射线BC平移至△GFE，∴∠ABC＝∠GFE，∵∠BAC+∠ABC＝90°，∴∠CED+∠GFE＝90°，∴∠FHE＝90°，∴DE⊥GF；（2）∵把△ABC沿射线BC平移至△GFE，∴AC＝GE，AC∥GE，∴四边形ACEG是平行四边形，∵把△ABC绕点C顺时针旋转90°至△EDC，∴AC＝CE，∠ACE＝90°，∴四边形ACEG是正方形．【点评】本题考查了旋转的性质，正方形的判定，平移的性质，掌握旋转和平移的性质是解题的关键．。

湖南省长沙市岳麓区博才小学2024年三上数学期末学业水平测试模拟试题含解析

湖南省长沙市岳麓区博才小学2024年三上数学期末学业水平测试模拟试题请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、认真计算。

1．算一算。

0.70.2+= 4.30.1-= 5.1 4.7+= 30.3-=567⨯+= 8193÷⨯= ()1468+⨯= 90802-÷=2．用竖式计算。

78×7＝ 49÷3＝ 105×4＝3．脱式计算。

（408-385）×4 593-（271+169）（352-289）÷7 二、我会判断。

（对的画√，错的画×）4．1可以看作3个13，也可以看作5个15。

（________） 5．5个小朋友吃一个蛋糕，每个小朋友吃这个蛋糕的15。

（______） 6．502×140的积中间有2个零．（______） 7．下半年的天数一定比上半年的天数多．（______）8．直线行进中的滑雪板的运动属于平移现象。

（______）三、精挑细选。

（把正确答案的序号填在括号里）9．1时50分等于多少分？（）A ．150分B ．110分C ．650分10．妈妈大约带多少元钱去缴费就够了？（）A ．200元B ．400C ．300元11．小明有两套不同颜色的运动装，如果搭配起来穿，一共有( )种不同的穿法．A ．2B ．3C ．412．199×2的积最接近（）。

A ．400B ．500C ．300D ．70013．阳阳晚上9时睡觉，第二天早上6时起床，她一共睡了（）小时。

A．7 B．9 C．8四、快乐填空。

14．学校准备晚上6：30开始“迎中秋”晚会，现在要推迟15分钟开始，晚会开始的时间应该是________，8：00晚会结束，晚会一共开了________小时________分钟。

湖南省长沙市初一数学竞赛卷

湖南省长沙市初一数学竞赛卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共16分)1. （2分）一条船在一条河上的顺流航速是逆流航速的3倍，这条船在静水中的航速与河水的流速之比为（）A . 3：1B . 2：1C . 1:1D . 3:22. （2分） (2018七下·大庆开学考) 如图，已知四边形ABCD中，AD∥BC，AP平分∠DAB，BP平分∠ABC，它们的交点P在线段CD上，下面的结论：①AP⊥BP；②点P到直线AD，BC的距离相等；③PD＝PC．其中正确的结论有（）A . ①②③B . ①②C . ①D . ②3. （2分）不等式2x－6＞0的解集为（）A . x＞3B . x>－3C . x＜3D . x＜－34. （2分） (2019八上·长兴月考) 下列图形中不具有稳定性的是（）A .B .C .D .5. （2分）小华的年龄与爷爷的年龄之和等于爸爸年龄的2倍，爸爸的年龄是小华年龄的3倍，则爷爷的年龄是小华年龄的（）A . 4倍B . 5倍C . 6倍D . 7倍6. （2分）(2017·乐陵模拟) 若函数，则当函数值y=8时，自变量x的值是（）A . ±B . 4C . ± 或4D . 4或﹣7. （1分）规定a※b= ，例如2※3= ，则[2※（-5）]※4=________8. （1分）有八个球编号是①至⑧，其中有六个球一样重，另外两个球都轻1克，为了找出这两个轻球，用天平称了三次，结果如下：第一次①+②比③+④重，第二次⑤+⑥比⑦+⑧轻，第三次①+③+⑤和②+④+⑧一样重．那么，两个轻球的编号是________．9. （1分）科学家最新研究表明，吸烟会导致人的寿命减少，按天计算，平均每天吸一包烟可以导致寿命减少2小时20分，如果一个人一个月有n天每天吸一包烟，则这个月他的寿命减少了________ 天．10. （1分） (2016七上·连城期末) 小虎在写作业时不小心将墨水滴在数轴上，根据图中的数值，判断墨迹盖住的整数之和为________．参考答案一、选择题 (共10题；共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、。

2024年湖南省长沙市初中学业水平考试数学试题(白卷)

2024年湖南省长沙市初中学业水平考试数学试题（白卷）一、单选题1．﹣5的绝对值是（）A ．5B ．﹣5C ．15-D ．152．下列消防安全标识图既是轴对称图形，又是中心对称图形的是（）A ．B ．C ．D ．3．据国家知识产权局消息，截至2023年底，国内高校有效发明专利拥有量达794000件，将数据794000用科学记数法表示为（）A ．479.410⨯B ．57.9410⨯C ．67.9410⨯D ．60.79410⨯ 4．下列运算正确的是（）A ．224a a a +=B ．623a a a ÷=C ．()2211a a -=-D ．()32628a a -=- 5．如图，AB CD ∥，OB OD ⊥，若36ABO ∠=︒，则ODC ∠的度数为（）A ．36︒B ．54︒C ．72°D ．108°6．不等式组26020x x +≥⎧⎨-<⎩的解集在数轴上表示正确的是（） A ． B ．C ．D ．7．某班主任对全班同学关于“最喜欢的球类运动”进行了问卷调查，并绘制了如图所示的条形统计图，则下列说法错误的是（）A ．喜欢排球的人最少B ．喜欢篮球的人数占24%C ．全班共50人D ．喜欢乒乓球人数的频率为0.68．如图，线段AB 与O e 相切于点B ，连接AO 并延长分别交O e 于点C ，D ，点E 是弧CD 上一点，连接CE BE ，，若126ABD ∠=︒，则BEC ∠的度数为（）A ．36︒B ．30︒C ．54︒D ．72︒9．浏阳金桔为湖南省长沙市浏阳市特色地方品种，全国农产品地理标志．某果农种植的金桔在采摘完后，发现大果、中果和小果的产量比为3:5:2，若每斤的售价大果定为12元，中果定为8元，小果定为6元，则该批金桔的平均售价为每斤（）A ．6.5元B ．8.6元C ．8.8元D ．10元10．俗语有云：“一天不练手脚慢，两天不练丢一半，三天不练门外汉，四天不练瞪眼看．”其意思是知识和技艺在学习后，如果不及时复习，那么学习过的东西就会被遗忘．假设每天“遗忘”的百分比是一样的，根据“两天不练丢一半”，则每天“遗忘”的百分比约为（参考数据：1.414）（） A ．20.3% B ．25.2% C ．29.3% D ．50%二、填空题11x 的取值范围是．12．某高校建设的中华优秀传统文化传承基地围绕民族民间音乐、民族民间美术、民族民间舞蹈、戏剧、戏曲、曲艺、传统手工技艺等传统文化项目，李教授了解班上7名学生最喜欢的传统文化项目的个数分别如下：3，5，4，7，5，6，5，则这组数据的众数和中位数分别是和．13．如图，ABC V 是⊙O 的内接三角形，AB AC =，直径CD 垂直于弦AB 于点E ，连接AD ．若2DE =，则AD 的长为．14．某同学在做“小孔成像”实验时，将一支长为3cm 的蜡烛（包括火焰高度）立在小孔前，蜡烛所立位置离小孔的水平距离为6cm ，此时蜡烛火焰通过小孔刚好在小孔另一侧距小孔2cm 处的投影屏上形成了一个“像”，若以小孔为坐标原点，构建如图所示的平面直角坐标系xOy ，设蜡烛火焰顶端A 点处坐标为()6,3-，则A 点对应的“像”的点的坐标为．15．若关于x 的一元二次方程2210mx x +-=有两个实数根，则实数m 的取值范围为． 16．如图，以MAN ∠的顶点A 为圆心，以任意长度为半径画弧，分别与AM AN ，交于点E ，F ．再分别以点E ，F 为圆心，以大于12EF 的长度为半径画弧，两弧相交于点P ，作射线AP ，在射线AC 上取一点C ，分别以点A ，C 为圆心，以大于12AC 的长度为半径画弧，分别相交于G ，Q 两点作直线GQ ，与A M A N A C ，、分别交于点B 、D ，H ．连接，BC CD ，若5AB =，8AC =，则BD =．三、解答题17．计算：()202401452-︒+18．小明和小强一起做游戏，他们面前有大小相同的三张写着分式的卡片，要求组成()B A C -⨯，或B A C ÷+的形式，再进行化简，然后两人均取一个相同的3x =，代入计算分式的值．A ．22441x x x -+- B ．21x x -- C ．2224x x -- (1)小明发现其中有一个分式还可以进行约分，这个分式是______，约分的依据为______．(2)请你帮他们在两个形式中选择一个进行化简求值．19．蚂蚁是一种靠嗅觉寻找食物的生物，它们的嗅觉比较发达，最远能闻出距离几十米处远的食物的味道某天李华同学在户外观察蚂蚁觅食时，发现他所在位置A 点的北偏西66︒方向距A 点60cm 的B 点有一只正在觅食的蚂蚁（如图），A 点北偏东45︒方向距A 点的C 点有一块糖，蚂蚁正沿正东方向朝着C 点处的糖前进．(1)请求出蚂蚁所在位置B 点与糖所在位置C 点之间的距离；(2)若在A 点北偏东75︒方向距A 点40cm 的D 点处刚好有一只蜘蛛，求蚂蚁在找到糖时与蜘蛛的距离．（结果取整数，参数数据：sin 450.707︒≈，cos450.707︒≈，sin 660.914︒≈，cos660.407︒≈，tan 66 2.246︒≈ 1.732≈）20．为了落实教育部提出的普及急救观念、知识和技能，提升校园应急救护能力，某校在全校范围内开展了急救知识普及，并在普及后进行急救知识测试，把成绩（满分100分）分成五个等级，该校为了了解急救知识普及情况，随机抽取部分学生的测试成绩，并根据分析结果绘制了如图所示的不完整的频数分布表和扇形统计图．频数分布表扇形统计图请根据所给信息，解答下列问题：(1)本次一共随机抽取了______名学生的测试成绩，m =______；(2)请计算扇形统计图中“D ”所在扇形的圆心角度数；(3)若学校共有2000名学生，估计该校急救知识测试成绩在80分以上的学生有多少人？(4)学校从A 组中挑选了成绩最好的甲、乙两名男生和丙、丁两名女生，将这四人平均分成两组参加“急救知识”普及宣传，请用画树状图或者列表的方法求出甲和丁恰好在一组的概率．21．如图，在ABC V 中，AB CB =，点D 是边AC 上一点，点E 为ABC V 外的任意一点，连接BD BE DE ，，，其中BE BC =，ABD EBD ∠=∠．(1)求证：ABD EBD △≌△；(2)若CAB DBA ∠=∠，6BE =，8AC =，求BDC V 的周长．22．黄豆是大家比较熟悉的一种食物，它除了可以直接用来做菜以外，还可以做成其他类型的食物，比如水豆腐、豆腐皮、豆浆、豆腐脑等．某豆腐作坊每天都会根据市场需求将黄豆做成水豆腐和豆腐皮进行售卖．根据商家的统计发现：每10斤黄豆能做成30斤水豆腐或者能做成20斤豆腐皮．以下是商家两天对水豆腐和豆腐皮的销售量和销售额的统计情况：(1)求水豆腐和豆腐皮的售价分别为多少？(2)某天商家以1.8元/斤的价格购进30斤黄豆，用于制作水豆腐和豆腐皮，制做完这30斤黄豆需要支付人工费100元，请问这30斤黄豆该如何制做才能使该天的销售利润不低于346元？23．如图，在平行四边形ABCD 中，对角线AC BD ，相交于点O ，且BC OC =．点E 为OB 的中点，过点E 作OC 的平行线，交BC 于点F ．在EF 的延长线上取一点G ，使得FG EF =．连接EC BG CG ，，．(1)求证：四边形ECGB 是矩形；(2)若12BD =，5EG =，求AB 的长．24．如图，AB 是O e 的直径，点C 是»AB 的中点，弦CD CE ，分别交AB 于点F ，G ，且12DCE ACB ∠=∠，连接DE ．(1)设ACD α∠=，用含α的式子表示CDE ∠的度数；(2)求证：222FG AF BG =+；(3)若O e 的半径为1，记A C F B C G C F G ，，V V V 的面积分别为1S ，2S ，S ，设A F a =，BG b =，且满足221121102S S S S S ab +-+⋅=，求a ，b 的值． 25．定义；若当点()1,12a a a ⎛⎫-≠ ⎪⎝⎭在某一函数图象上时，点()11,2a a a ⎛⎫-≠ ⎪⎝⎭也在该函数图象上，则称该函数为“知返函数”，点()1,12a a a ⎛⎫-≠ ⎪⎝⎭称为“知返点”． (1)已知一次函数()0y kx b k =+≠为“知返函数”，求该一次函数的解析式；(2)若反比例函数1k y x=（1k 为整数）的函数图象上存在“知返点”，求1k 的最大值； (3)函数22y x mx =+的图象是由二次函数22y x mx =+的图象x 轴下方的部分沿x 轴翻折到x 轴上方，图象的其余部分保持不变得到的．若函数22y x mx =+的图象与“知返函数”y kx b =+的图象有四个交点，求m 的取值范围．。

2022-2023学年湖南省长沙市岳麓区长郡梅溪湖中学八年级(下)数学试卷+答案解析(附后)

2022-2023学年湖南省长沙市岳麓区长郡梅溪湖中学八年级（下）第一次月考数学试卷1. 下列二次根式中，是最简二次根式的是( )A. B. C. D.2. 如果二次根式有意义，那么实数a的取值范围是( )A. B. C. D.3. 三角形三边长为a，b，c满足，则这个三角形是( )A. 等边三角形B. 钝角三角形C. 锐角三角形D. 直角三角形4. 下列计算正确的是( )A. B.C. D.5. 如图，在中，，，，则AB等于( )A. 2B. 3C.D. 46. 下列说法正确的是( )A. 矩形对角线相互垂直平分B. 对角线相等的菱形是正方形C. 一组邻边相等的四边形是菱形D. 对角线相等的平行四边形是菱形7. 如图，在矩形ABCD中，对角线AC与BD相交于点O，已知，则的大小是( )A. B. C. D.8. 由下列条件不能判定为直角三角形的是( )A. B. a：b：：1：2C. D.9. 如图，数轴上点C所表示的数是( )A. B. C. D.10. 如图，在平行四边形ABCD中，，以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于PQ的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是( )A. B. 1 C. D.11. 《九章算术》中有一道“折竹抵地”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：如图，一根竹子原高一丈丈尺，中部有一处折断，竹梢触地面处离竹根3尺．若设折断处离地面的高度为x尺，则可以列出关于x的方程为( )A.B.C.D.12. 如图，四边形ABCD中，，，且，以AB、BC、DC为边向外作正方形，其面积分别为，，，若，，则的值为( )A. 22B. 24C. 44D. 4813.如图，在中，，，D是AB的中点，则______ .14. 在直角三角形中，两条直角边的长分别为9和12，则斜边的长为______ .15. 如图，，点C、D、E在直线m上，四边形ABED为平行四边形，若的面积为5，则平行四边形ABED的面积是______ .16. 比较大小：______填“>”，“=”，“<”号17. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形较短直角边长为b，若拼成的一个大正方形，设直角三角形较长直角边长为a，，大正方形的面积为16，则小正方形的面积为______ .18. 如图，菱形ABCD的边长为4，E、F分别是AB、AD上的点，连接CE、CF、EF，AC与EF相交于点G，若，，则EF的长为______ .19. 计算：；；；20. 先化简，再求值：，其中21.如图，已知中，，D是AC上一点，且，求证：是直角三角形；求AB的长.22. 如图，已知E、F分别是平行四边形ABCD的边BC、AD上的点，且求证：四边形AECF是平行四边形；在中，若，，，求BC边上的高23. 如图，某渡船从点B处沿着与河岸垂直的路线AB横渡，由于受水流的影响，实际沿着BC航行，上岸地点C与欲到达地点A相距70米，结果发现BC比河宽AB多10米.求该河的宽度AB；两岸可近似看作平行设实际航行时，速度为每秒5米，从C回到A时，速度为每秒4米，求航行总时间.24. 如图，在中，D，E分别是AB，AC的中点，延长DE到点F，使得，连接求证：四边形BCFE是菱形；若，，求菱形BCFE的面积.25. 如图，在四边形ABCD中，，，，，点P从点B出发，沿射线BC方向以每秒4个单位长度的速度运动，同时点Q从点A出发，沿AD以每秒1个单位长度的速度向点D运动，当点Q到达点D时，点P、Q同时停止运动，设点Q的运动的时间为t秒.的长为______ .求PC的长用含t的代数式表示当以点A、C、P、Q为顶点的四边形是平行四边形时，求t的值.直接写出是以CD为腰的等腰三角形时t的值.26. 已知：四边形ABCD是正方形，点E在CD边上，点F在AD边上，且如图1，判断AE与BF有怎样的位置关系？写出你的结果，并加以证明；如图2，对角线AC与BD交于点，AC分别与AE，BF交于点G，点①求证：；②连接OP，若，，求AB的长．答案和解析1.【答案】C【解析】解：，因此不是最简二次根式，故A不符合题意；B.，因此不是最简二次根式，故B不符合题意；C.是最简二次根式，故C符合题意；D.，因此不是最简二次根式，故D不符合题意．故选：根据最简二次根式的定义进行判断即可．本题考查了最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．2.【答案】B【解析】解：由题意得：，，故选：根据二次根式有意义的条件：被开方数为非负数，即可得出a的取值范围．本题考查了二次根式有意义的条件，属于基础题，解答本题的关键是熟练掌握二次根式有意义的条件：被开方数为非负数．3.【答案】D【解析】解：，，，，，，，，，，这个三角形是直角三角形，故选：根据已知条件可得，，，根据勾股定理的逆定理即可判断三角形的形状．本题考查了直角三角形的判定，涉及非负数的性质，勾股定理的逆定理等，求出三角形的三边长是解题的关键．4.【答案】B【解析】解：，无法合并，故此选项不合题意；B.，故此选项符合题意；C.，故此选项不合题意；D.，故此选项不合题意；故选：直接利用二次根式的加减运算法则以及二次根式的除法运算法则、二次根式的性质分别化简，进而判断得出答案．此题主要考查了二次根式的混合运算，正确掌握相关运算法则是解题关键．5.【答案】A【解析】解：在中，，，故选：由的度数及AC的长，结合可求出AB的长，此题得解．本题考查了含30度角的直角三角形以及解直角三角形，通过解直角三角形求出AB的长是解题的关键．6.【答案】B【解析】解：矩形的对角线相等且互相平分，故A原说法错误，不符合题意；B.对角线相等的菱形是正方形，正确，符合题意；C.一组邻边相等的平行四边形是菱形，故C原说法错误，不符合题意；D.对角线相等的平行四边形是矩形，故D原说法错误，不符合题意；故选：根据矩形的性质可得A错误；正方形的判定方法可得B正确；根据菱形的判定可得C错误；根据对角线的关系判定矩形，从而得D错误．本题主要考查了矩形的性质与判定，正方形的判定，菱形的判定，解题的关键在于能够熟练掌握相关知识进行判断求解．7.【答案】C【解析】解：矩形ABCD的对角线AC，BD相交于点O，，，，，，故选：由矩形的性质得，再由等腰三角形的性质得，然后由三角形的外角性质即可得出结论．本题考查了矩形的性质、等腰三角形的性质以及三角形的外角性质，熟练掌握矩形的性质是解题的关键．8.【答案】B【解析】解：A、，，，是直角三角形，不符合题意；B、设，，，，不是直角三角形，符合题意；C、，，，是直角三角形，不符合题意；D、，是直角三角形，不符合题意；故选：根据勾股定理的逆定理和三角形的内角和定理逐个判断即可．本题考查了勾股定理的逆定理和三角形的内角和定理，注意：①如果一个三角形的两边a、b的平方和等于第三边c的平方，那么这个三角形是直角三角形，②三角形的内角和等于9.【答案】D【解析】解：，，，，，故D正确．故选：根据勾股定理求出OB的长，得出，即可得出数轴上点C所表示的数是本题主要考查勾股定理与无理数，掌握定理内容准确计算并利用数形结合思想是解题的关键．10.【答案】B【解析】解：根据题意得，CE是的角平分线，，平行四边形ABCD，，，如图所示，设AD与CE交于点F，，，，是等腰三角形，即，，同理，，且，，是等腰三角形，即，故选：根据题意可求出是等腰三角形，即，是等腰三角形，即，由此即可求解．本题主要考查平行四边形，等腰三角形的综合，掌握平行四边形的性质，等腰三角形的性质是解题的关键．11.【答案】D【解析】解：竹子原高一丈丈尺，折断处离地面的高度为x尺，竹梢到折断处的长度为尺．依题意得：故选：由竹子的原高可得出竹梢到折断处的长度为尺，利用勾股定理，即可得出关于x的一元二次方程，此题得解．本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．12.【答案】C【解析】解：，，，，过A作交BC于E，则，，四边形AECD是平行四边形，，，，，，，，，，故选：根据已知条件得到，，过A作交BC于E，则，根据平行四边形的性质得到，，由已知条件得到，根据勾股定理得到，于是得到结论．本题考查了勾股定理，正方形的性质，平行四边形的判定和性质，正确的作出辅助线是解题的关键．13.【答案】12【解析】解：在中，，D是AB的中点，故答案为：根据直角三角形斜边上的中线等于斜边的一半解答即可．本题主要考查了直角三角形斜边上的中线等于斜边的一半的性质，熟记性质是解题的关键．14.【答案】15【解析】解：在直角三角形中，两条直角边的长分别为9和12，斜边长为：故答案为：根据勾股定理直接求出斜边的长即可．本题主要考查了勾股定理，解题的关键是熟练掌握勾股定理，如果直角三角形的两条直角边长为a、b，斜边长为c，那么15.【答案】10【解析】解：连接BD，，，的面积为5，的面积为5，四边形ABED为平行四边形，平行四边形ABED的面积故答案为：连接BD，由平行线的性质得出，由平行四边形的性质可得出答案．本题考查了平行四边形的性质，平行线的性质，熟练掌握平行四边形的性质是解题的关键．16.【答案】>【解析】解：，，，，故答案为：先把根号外的因式移入根号内，再比较即可．本题考查了实数的大小比较法则和二次根式的性质，能选择适当的方法比较大小是解此题的关键．17.【答案】2【解析】解：由题意可知：每个直角三角形面积为，则四个直角三角形面积为2ab，大正方形面积为，小正方形面积为，，，大正方形的面积为16，，小正方形的面积为，故答案为：观察图形可知，小正方形的面积=大正方形的面积个直角三角形的面积，利用已知，大正方形的面积为16，可以得出直角三角形的面积，进而求出答案．本题主要考查了勾股定理的应用，熟练应用勾股定理解大正方形面积为是解题关键．18.【答案】【解析】解：过点E作于点四边形ABCD是菱形，，，，为等边三角形，，，，≌，，，，是等边三角形，，，，，，，，故答案为：利用全等三角形的性质证明是等边三角形，再利用勾股定理求出EC，可得结论．本题考查菱形的性质，等边三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题．19.【答案】解：；；；【解析】根据二次根式乘法运算法则进行计算即可；根据二次根式除法运算法则进行计算即可；先根据二次根式性质进行化简，然后根据二次根式加减运算法则计算即可；先根据二次根式性质进行化简，然后根据二次根式混合运算法则计算即可．本题主要考查了二次根式的运算，解题的关键是熟练掌握二次根式的性质和运算法则，准确计算．20.【答案】解：原式，当时，原式【解析】本题的关键是对整式化简，然后把给定的值代入求值．本题主要考查整式的运算、平方差公式等基本知识，考查基本的代数计算能力．注意先化简，再代入求值．21.【答案】证明：，，，，，故是直角三角形；解：设，则，，，，解得，故【解析】根据勾股定理的逆定理即可得到结论；设，则，根据勾股定理即可得到结论．本题考查了勾股定理，勾股定理的逆定理，等腰三角形的性质，熟练掌握勾股定理，勾股定理的逆定理是解题的关键．22.【答案】证明：四边形ABCD是平行四边形，，且，，，，四边形AECF是平行四边形；解：，，，，，【解析】本题主要考查了平行四边形的性质与判定，勾股定理，解题的关键是熟练掌握平行四边形的判定方法．利用平行四边形的性质得出，再得出，即可证明四边形AECF是平行四边形；根据勾股定理求出AB的长，然后根据等积法求出BC边上的高AG即可．23.【答案】解：设米，则米，在中，根据勾股定理得：，解得：，答：河宽240米．秒，秒，秒，答：航行总时间为秒．【解析】根据题意可知为直角三角形，根据勾股定理就可求出直角边AB的距离；根据时间=路程速度，求出行驶的时间即可．本题考查勾股定理的应用，熟练掌握勾股定理，列出方程是解题的关键．24.【答案】证明：、E分别是AB、AC的中点，，且又，，，四边形BCFE是平行四边形一组对边平行且相等的四边形是平行四边形又，四边形BCFE是菱形邻边相等的平行四边形是菱形解：在菱形BCFE中，，，是等边三角形．过点E作于点【解析】根据点D和E分别是AB和AC的中点，根据三角形中位线的性质，即可得到，且，再等量代换，根据平行四边形的判定定理，即可得到四边形BCFE是平行四边形，根据邻边的关系，即可得到结论；根据的大小，可判定是等边三角形，再根据等边三角形的性质，可得到边长，作于点G，运用勾股定理，即可得到EG的长，再根据菱形的面积公式，即可得到答案．本题考查菱形判定及菱形面积求解，关键是掌握菱形的判定及性质．25.【答案】5【解析】解：如图，过点D作于E，，，，，，四边形ABED是矩形，，，，，故答案为：5；，，；四边形ACPQ是平行四边形，，，即，，，或，①当时，，解得，或；②当时，则DE垂直平分PC，，即，，综上，是以CD为腰的等腰三角形时t的值为或或过点D作于E，根据题意推出四边形ABED是矩形，根据勾股定理求解即可；根据线段的和差结合绝对值性质求解即可；当四边形ACPQ为平行四边形时，，即，可将t求出；①当时，，据此求解即可；②当时，则DE垂直平分PC，则，即，据此求解即可．本题属于四边形综合题，考查了直角梯形的性质，矩形的判定和性质，平行四边形的判定和性质，等腰三角形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题，学会用分类讨论的思想思考问题．26.【答案】解：理由如下：四边形ABCD是正方形，，，在和中，，≌，，，，，；①证明：四边形ABCD是正方形，，，，已证，，即，在和中，，≌，；②解：如图2，过点O作于M，作于N，≌已证，，在和中，，≌，，四边形OMPN是正方形，，，，，在中，，正方形ABCD的边长【解析】根据正方形的性质可得，，然后利用“边角边”证明和全等，根据全等三角形对应角相等可得，然后求出，再求出，然后根据垂直的定义解答即可；①根据正方形的对角线互相垂直平分可得，，对角线平分一组对角可得，然后求出，再利用“角边角”证明和全等，根据全等三角形对应边相等可得；②过点O作于M，作于N，根据全等三角形对应角相等可得，再利用“角角边”证明和全等，根据全等三角形对应边相等可得，然后判断出四边形OMPN是正方形，根据正方形的性质求出，再求出AM，然后利用勾股定理列式求出OA，再根据正方形的性质求出AB即可．本题是四边形综合题型，主要利用了正方形的性质，全等三角形的判定与性质，②难度较大，作辅助线构造出全等三角形和以OP为对角线的正方形是解题的关键，也是本题的难点．。

初中数学课外知识竞赛

初中数学课外知识竞赛数学知识在初中阶段是非常重要的，而课外知识竞赛则是一种提高学生数学能力的有效途径。

下面将介绍初中数学课外知识竞赛的相关内容，包括参赛要求、竞赛形式和比赛策略。

一、参赛要求1. 年级限制：仅限初中生报名参加。

2. 报名要求：学生需提交个人报名表格，并经过学校老师或指导员的推荐。

3. 基本知识要求：学生参赛前应掌握初中数学基础知识，包括四则运算、代数与方程、几何、概率与统计等。

二、竞赛形式1. 笔试环节：学生将进行一次笔试，题型多样，包括选择题、填空题、计算题等。

2. 实际操作环节：学生需要在规定时间内完成一系列数学问题的实际操作，如测量、几何图形绘制等。

3. 口头答辩环节：学生需回答一系列与数学知识相关的问题，并在一定时间内做出口头答复。

三、比赛策略1. 开展备考计划：根据竞赛的时间安排，制定合理的备考计划，并按部就班地进行学习。

2. 夯实基础知识：复习并巩固初中数学各个章节的基础知识，特别是常见的解题方法和技巧。

3. 练习题目的多样性：做大量的题目练习，涉及各个知识点和难度级别，提高自己的题目处理能力。

4. 增强实际操作能力：进行实际操作的训练，如尺子的使用、几何图形的绘制等，提高自己的实际操作能力。

5. 口语表达练习：平时多进行口头表达练习，增强自己的逻辑思维和口头表达能力。

参加初中数学课外知识竞赛可以帮助学生更好地理解和应用数学知识，提高解决问题的能力和思维灵活性。

通过有趣的比赛形式，学生可以更加主动地去学习数学，积极参与到数学竞赛中来。

此外，竞赛的结果还可以作为学生参加升学考试或申请奖学金的参考依据，对学生的个人发展具有重要意义。

因此，学生们应积极参与初中数学课外知识竞赛，努力学习并提高自己的数学能力。

只有通过实践和不断的努力，才能在数学竞赛中取得优异的成绩，为自己的未来奠定坚实的基础。

希望以上内容对您有所帮助，祝您在初中数学课外知识竞赛中取得好成绩！。

湖南省长沙市岳麓区湖南师范大学附属中学2025届高三第二次模拟考试数学试卷含解析

湖南省长沙市岳麓区湖南师范大学附属中学2025届高三第二次模拟考试数学试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置． 3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效． 5．如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知函数()xe f x ax x=-，(0,)x ∈+∞，当21x x >时，不等式()()1221f x f x x x <恒成立，则实数a 的取值范围为（） A ．(,]e -∞B ．(,)e -∞C ．,2e ⎛⎫-∞ ⎪⎝⎭D ．,2e ⎛⎤-∞ ⎥⎝⎦2．在ABC ∆中，0OA OB OC ++=，2AE EB =，AB AC λ=，若9AB AC AO EC ⋅=⋅，则实数λ=( ) ABCD ．23．已知(2sin,cos),(3cos,2cos)2222xxxxa b ωωωω==，函数()f x a b =·在区间4[0,]3π上恰有3个极值点，则正实数ω的取值范围为（） A ．85[,)52B ．75[,)42C ．57[,)34D ．7(,2]44．已知向量(,1),(3,2)a m b m ==-，则3m =是//a b 的（）A ．充分不必要条件B ．必要不充分条件C ．既不充分也不必要条件D ．充要条件5．在ABC 中，角,,A B C 所对的边分别为,,a b c ，已知23C π=，1c =．当,a b 变化时，若z b a λ=+存在最大值，则正数λ的取值范围为 A ．(0,1)B ．(0,2)C ．1(,2)2D ．(1,3)6．将函数()cos f x x =的图象先向右平移56π个单位长度，在把所得函数图象的横坐标变为原来的1ω(0)>ω倍，纵坐标不变，得到函数()g x 的图象，若函数()g x 在3(,)22ππ上没有零点，则ω的取值范围是（） A ．228(0,][,]939 B ．2(0,]9C ．28(0,][,1]99D ．(0,1]7．若各项均为正数的等比数列{}n a 满足31232a a a =+，则公比q =（） A ．1B ．2C ．3D ．48．某四棱锥的三视图如图所示，记S 为此棱锥所有棱的长度的集合，则（）A ．2223S S ，且B ．2223S S ，且C ．2223S S ，且D ．2223S S ，且9．已知(1)2i ai bi -=+（i 为虚数单位，,a b ∈R ），则ab 等于（） A ．2B ．-2C ．12D ．12-10．复数z 的共轭复数记作z ，已知复数1z 对应复平面上的点()1,1--，复数2z :满足122z z ⋅=-.则2z 等于（） A 2B ．2C 10D ．1011．已知236a b ==，则a ，b 不可能满足的关系是（） A ．a b ab +=B ．4a b +>C ．()()22112a b -+-< D ．228a b +>12．一个袋中放有大小、形状均相同的小球，其中红球1个、黑球2个，现随机等可能取出小球，当有放回依次取出两个小球时，记取出的红球数为1ξ；当无放回依次取出两个小球时，记取出的红球数为2ξ，则（） A ．12E E ξξ<，12D D ξξ< B ．12E E ξξ=，12D D ξξ> C ．12E E ξξ=，12D D ξξ<D ．12E E ξξ>，12D D ξξ>二、填空题：本题共4小题，每小题5分，共20分。

初中数学比赛策划书范文3篇

初中数学比赛策划书范文3篇篇一初中数学比赛策划书范文一、活动名称初中数学比赛二、活动目的1. 提高学生对数学的兴趣和热爱，激发学生学习数学的积极性。

2. 增强学生的数学思维能力和解决问题的能力，提高学生的数学素养。

3. 促进学生之间的交流与合作，培养学生的团队精神和竞争意识。

三、活动时间[具体时间]四、活动地点[具体地点]五、参与人员初中部全体学生六、比赛内容1. 数学知识竞赛：涵盖初中数学的各个知识点，包括代数、几何、概率统计等。

2. 数学解题能力竞赛：通过解决一些具有挑战性的数学问题，考察学生的解题思路和方法。

3. 数学应用能力竞赛：结合实际生活中的问题，考察学生运用数学知识解决实际问题的能力。

七、比赛形式1. 个人赛：每位学生独立完成比赛试题。

2. 团体赛：以班级为单位，组成团队参加比赛，每个团队由[X]名学生组成。

八、比赛规则1. 比赛采用闭卷形式，考试时间为[X]分钟。

2. 参赛学生必须遵守考场纪律，独立完成试题，不得抄袭或作弊。

3. 比赛结束后，将试卷密封，由评委进行评卷。

九、奖项设置1. 个人奖：根据个人赛成绩，评选出一等奖、二等奖、三等奖若干名。

2. 团体奖：根据团体赛成绩，评选出一等奖、二等奖、三等奖若干名。

3. 优秀指导教师奖：对在比赛中表现出色的指导教师进行表彰。

十、活动宣传1. 在学校宣传栏张贴比赛海报，宣传比赛的时间、地点、内容和奖项设置等信息。

2. 利用学校广播、班级群等渠道，向学生宣传比赛的意义和目的，鼓励学生积极参与。

3. 邀请学校领导、数学教师和家长代表参加比赛开幕式，提高比赛的影响力。

十一、活动预算1. 奖品费用：购买奖品、证书等，预计费用为[X]元。

2. 宣传费用：制作海报、宣传单等，预计费用为[X]元。

3. 其他费用：如评委酬金、场地租赁费用等，预计费用为[X]元。

4. 总预算：[X]元。

十二、活动组织与实施1. 成立活动组织委员会：负责比赛的策划、组织和实施。

长沙市“学用杯”初中数学应用与创新能力大赛八年级复赛试题及答案

八年级数学复赛·第1版（共 6 版）八年级数学复赛·第2版（共 6 版）长沙市“学用杯”初中数学应用与创新能力大赛八年级复赛试题（满分：120分）一、选择题（本大题共10小题，每小题4分，共40分）1．一个正整数的算术平方根为，那么它的后一个连续正整数的算术平方根是A ．1+aB ．12+aC ．1+aD ．12+a2．若21-＜m ＜0，且a =21m +，b =21m -，c =m +11，d =m -11，那么a ，b ，c ，d的大小关系是A ．d <b <c <aB ．b <d <a <cC ．d <b <a <cD ．b <d <c <a 3．若112x y-=，则33x xy y x xy y +---的值为A ．35B ．53C ．35-D ．53-4．钝角三角形的三边长是连续整数，那么其三边长必定是 A ．2，3，4 B ．4，5，6 C ．5，6，7 D ．6，7，8 5．等腰三角形一腰上的高与腰长之比为1∶2，则等腰三角形的顶角为 A ．30° B ．60° C ．150° D ．30°或150° 6．如图，四边形ABCD 中，AD ∥BC ，∠B =90°，E 为AB 上一点，分别以ED ，EC 为折痕将两个角（∠A ，∠B ）向内折起，点A ， B 恰好落在CD 边的点F 处．若AD =3，BC =5，则EF 的值是A ．17B ．172C ．15D ．1527．如图，已知BD ，CE 是△ABC 的中线，M ，N 分别是BD ，CE 的中点，那么MN ∶BC 等于 A ．1∶5 B ．1∶4 C ．1∶3 D ．1∶28．在平面直角坐标系中，点A 的坐标为（1，1），点B 的坐标为（11,1），点C 到直线AB 的距离为4，且ABC △是直角三角形，则满足条件的点C 的个数为 A ．5 B ．6 C ．7 D ．89．已知等腰三角形的两边长分別为a 、b ，且a 、b 满足0)1332(5322=-+++-b a b a ，则此等腰三角形的周长为A ．7或8B ．6或10C ．6或7D ．7或1010．在40名同学中调查，每个人至少会玩乒乓球、篮球、排球中的一样，会玩乒乓球的有24人，会玩篮球的有18人，会玩排球的有10人，同时会玩乒乓球和篮球的有6人，同时会玩乒乓球和排球的有4人，三种球都会的只有1人．则同时会打篮球和排球的有 A ．3人 B ．4人 C ．5人 D ．6人二、填空题（本大题共8小题，每小题4分，共32分）11．已知2=+b a ，2=ab ，则代数式22222a b a b ab ++的值为__________． 13．已知方程组⎩⎨⎧=+3135y x 的解是正数，则a 的取值范围是．14．四边形ABCD 中，∠DAB ＝60，∠B ＝∠D ＝90，BC ＝1，CD ＝2，则对角线AC 的长为_________．（第14题）（第15题）（第17题）15. 如图，已知矩形ABCD 的边AB ＝6，BC ＝8，将矩形折叠，使点C 和点A 重合，则折痕EF的长为． 16．若不等式2231x x k k+->+的解是3x >，则k 的值为_________． 17．已知直线x y =1，1312+=x y ，5543+-=x y 的图象如图所示，若无论x 取何值，y 总取1y ，2y ，3y 中的最小值，则y 的最大值为_________．18．已知一个三位数能被11整除，其商是这个三位数的三个数字和．则这个三位数是．学校：姓名：考场：考号：☼……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼……密……☼……封……☼……线……☼三、解答题（本大题共4小题，每小题12分，共48分）19．（本题满分12分）某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A 型和10台B型电脑的利润为3500元．（1)求每台A型电脑和B型电脑的销售利润；（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍。

2024 年长沙市初中学业水平考试模拟试卷数学参考答案1-5

2024年长沙市初中学业水平考试模拟试卷数学（一）参考答案及评分标准一、选择题（本大题共10个小题，每小题3分，共30分）题号12345678910答案A B D D C C A B AB二、填空题（本大题共6个小题，每小题3分，共18分）11．196≥x 12．2(41)a -13．C 14．15．103π16．三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21题每小题8分，第22、23题每小题9分，第24、25题每小题10分，共72分．解答应写出必要的文字说明、证明过程或演算步骤）17．解：原式613=+……………………………………………………………（4分）4=．………………………………………………………………..………………（6分）18．解：原式22221221x x x x x =++-++-4x =．………………………………….……………………………………………（4分）当14x =-时，原式=14(14⨯-=-．……………………..………………………（6分）19．解：（1）如图1，过点A 作AG BC ⊥于点G ，过点D 作DH BC ⊥于点H ．在Rt ABG △中，45B EAB ∠=∠=︒，90AGB ∠=︒，∴400tan 45AGBG ==︒（m ）．在Rt DHC △中，30C FDC ∠=∠=︒，90DHC ∠=︒，∴tan 30DH HC ===︒（m ）．由图易知四边形AGHD 为矩形，∴170GH AD ==（m ），∴4001701250BC BG GH HC =++=++（m ）．答：橘子洲大桥主桥BC 的长约为1250m ；……………………………（3分）（2）如图2，过点Q 作QN BC ⊥于点N，交AD 于点M ．在Rt QDM △中，30QDM FDC ∠=∠=︒，90QMD ∠=︒，∴111)1)22QM QD ==⨯=（m ），∴1)400459.5QN QM MN =+=+≈（m ）．答：该无人机与桥面BC 的距离约为459.5m ．……………………………………………………………………………………….（6分）20．解：（1）30；10；20；…………………………………………………………….………（3分）（2）D 组扇形所对的圆心角的度数为103603620304010︒⨯=︒+++；……（5分）（3）画树状图如下：由图可知，一共有12种等可能的结果，丁同学未被抽中的结果一共有6种，∴丁同学未被抽中的概率为61122P ==．…………………………………（8分）21．（1）证明：∵△ACD 是等边三角形，E 是AC 的中点，∴90DEC ∠=︒，AC DC =，AE EC =．∵2AC BC =，∴BC EC =．在Rt △ABC 和Rt △DEC 中，，，BC EC AC DC =⎧⎨=⎩∴△ABC ≌△DEC （HL ）；………………………………………………（4分）（2）解：如图，连接BD ．在Rt ABC △中，1BC =，∴22AC BC ==．由勾股定理，得AB =．∵ADC △是等边三角形，∴2AD AC ==，60DAC ∠=︒．在△ABC 中，90ABC ∠=︒，2AC BC =，∴30BAC ∠=︒，∴90BAD BAC DAC ∠=∠+∠=︒，∴ABD △是直角三角形，∴BD =．………………………....……（8分）22．解：（1）设第一周到第三周“名师云课堂”收看人数的平均增长率为x ．则224200(1)29282x +=，解得10.110%x ==，2 2.1x =-（舍）．答：第一周到第三周“名师云课堂”收看人数的平均增长率为10%；…………………………………………………………………………………......…（5分）（2）29282(110%)32210⨯+≈（人）．答：估计第四周有32210人收看“名师云课堂”．……………..……（9分）23．（1）证明：如图，连接BF 交AD 于点G ．∵将□ABCD 沿AD 对折，得到□AFED ，∴BF AD ⊥于点G ，BG FG =，AD BC FE ∥∥，由平行线分线段成比例定理得，1BO BG EO FG==，∴BO EO =；…………………………………………………………………（4分）（2）解：由（1）得，若28BC AB ==，60C ∠=︒，BF ⊥AO ，则4AB AF ==，8FE BC ==，∴60BAO FAO C ∠=∠=∠=︒，90AGB AGF ∠=∠=︒，∴cos602AG AB =︒=g ．由（1）得，GO 是BEF △的中位线，∴142GO FE ==，∴246AO AG GO =+=+=．∵sin 60BG AB =︒=g，∴2BF BG ==∴11622AFOB S AO BF ==⨯⨯g 四边形．…………………………（9分）24．（1）证明：在ABC △中，112A ACB ABC ∠∠∠=∶∶∶∶，又∵180A ACB ABC ∠+∠+∠=︒，∴1180454A ACB ∠=∠=︒⨯=︒，2180904ABC ∠=︒⨯=︒，∴AB CB ⊥．∵CB 是O ⊙的直径，∴直线AD 是O ⊙的切线；……………………（3分）（2）解：如图1，连接OG ．由（1）得45ACB ∠=︒，∴90BOG ∠=︒，∴45OCG OGC ∠=∠=︒，90GOB CBD ∠=∠=︒，∴OG BD ∥．又∵OHG BHD ∠=∠，∴△OGH ∽△BDH ．∵CGH △和CDH △在GH 和DH 上的高相等，∴1212S GH S DH ==，∴12OH GH OG BH DH BD ===．设OH a =，则2BH a =，3OB OG a ==，∴26BD OG a ==，∴DH ==∴sin BH BDH DH ∠==；……………….………………………（6分）（3）解：如图2，连接EF ，BG ，BF ．∵BC 是直径，∴90BGC BEC BFC ∠=∠=∠=︒．∵45BCG ∠=︒，∴45CBG BCG ∠=∠=︒，∴GB CG =．由（2）得90CBD ∠=︒，∴90EBD CBE ∠+∠=︒．又∵90ECB CBE ∠+∠=︒，∴EBD ECB BGD ∠=∠=∠．∵EDB BDG ∠=∠，∴DBE DGB △∽△，∴BE DB GB DG=．①∵点C ，F ，E ，G 四点共圆，∴DFE DGC ∠=∠．∵EDF CDG ∠=∠，∴DEF DCG △∽△，∴EF DF CG DG =，②①÷②得，BE DB EF DF =．∵CB m CD n=，∴设CB mk =，CD nk =．（0k ＞）由勾股定理，得BD =．∵90DFB DBC ∠=∠=︒，BDF CDB ∠=∠，∴DBF DCB △∽△，∴DF DB DB DC=，∴222()DB k n m DF DC n-==，∴BE DB EF DF ==．……………（10分）25．解：（1）当自变量x k =时，2122y kx k k k =+=+，22232y kx k k =-=-．∵当自变量x k =时，函数1y ，2y 的图象上恰好是一对“共赢点”，∴2212220y y k k k +=+-=，解得10k =，22k =．∵0k ≠，∴2k =，∴一次函数1y ，2y 的解析式分别为124y x =+，2212y x =-．……（3分）（2）当x a =（0a ≠）时，1m y a =，2n y a =．情形一，若120y y +=，即0m n a a+=，此时0m n +=，∴当0m n +=时，函数1y ，2y 互为“共赢函数”，它们的图象上有无数对“共赢点”，其坐标可以表示为(a ，m a )，(a ，n a )（0a ≠）；情形二，若120y y +≠，即0m n a a+≠，此时0m n +≠，∴当0m n +≠时，函数1y ，2y 不是“共赢函数”，它们的图象上不存在“共赢点”．综上所述，当0m n +=时，函数1y ，2y 互为“共赢函数”，它们图象上有无数对“共赢点”，其坐标可以表示为(a ，m a )，(a ，n a)（0a ≠）；当0m n +≠时，函数1y ，2y 不是“共赢函数”，它们的图象上不存在“共赢点”．…………………………………………..……………………………………（6分）（3）如图，作PE DC ⊥于点E ，PF OB ⊥于点F ．∵22212()y x mx m x m =-+=-，且0m ＞，∴A (0，2m )，C (m ，0)．∵函数2y 与1y 互为“共赢函数”，且当自变量x 取任意实数时，函数1y ，2y 的图象上都存在“共赢点”，∴22222()y x mx m x m =-+-=--，∴B (0，2m -)，∴2OA OB m ==，且DC AB ⊥，∴DC 是经过A ，B ，C 三点的圆的直径，∴90DAC DPC ∠=∠=︒，∴90DAO OAC ∠+∠=︒．又∵AO DC ⊥，∴90DOA AOC ∠=∠=︒，∴90ODA DAO ∠+∠=︒，∴ODA OAC ∠=∠，∴ODA OAC △∽△，∴OD OA OA OC=，∴2OA OD OC =g ，即22()m OD m =g ，∴3OD m =，∴3DC OD OC m m =+=+．∵PF OB ⊥于点F ，∴222PA AF PF =+，222PB BF PF =+，∴222222()()PA PB AF PF BF PF -=+-+22AF BF =-()()AF BF AF BF =+-(2)AB AF BF BF =+-(2)AB AB BF =-(22)AB OB BF =-2()2AB OB BF AB OF =-=g ．∵PE DC ⊥于点E ，∴12PCD S PE DC =g △．∵PE DC ⊥于点E ，PF OB ⊥于点F ，EO BO ⊥于点O ，∴四边形PEOF 是矩形，∴PE OF =，∴2223244881△PCD t PA PB AB OF AB m m f s S PE DC DC m m m -======++g g ，去分母得280fm m f -+=．由26440f ∆=-≥得，216f ≤．∵0m ＞，∴2801m f m =+＞，∴04f ＜≤，∴f 的最大值为4，此时1m =．经检验，符合题意.此时OA OB OC OD ===，AB DC =，且AB CD ⊥，∴四边形ACBD 为正方形．…………………………………………………（10分）数学（二）参考答案及评分标准一、选择题（本大题共10个小题，每小题3分，共30分）题号12345678910答案C C B A D A B A D C二、填空题（本大题共6个小题，每小题3分，共18分）11．12x ≠12．45︒13．215cm π14．415．03x ＜≤16．7三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21题每小题8分，第22、23题每小题9分，第24、25题每小题10分，共72分．解答应写出必要的文字说明、证明过程或演算步骤）17．解：原式1322=-++-⨯…………………………………………….………………（4分）2=．…………………………………………………………………………………（6分）18．解：原式22(1)(1)1(1)x x x x x -+-=-++2111x x x x--=-++11x =-+．…………………………………………………………………………（4分）当1x -时，原式===．……………………（6分）19．（1）证明：∵AB DE ∥，∴B DEF ∠=∠．∵BE CF =，∴BE EC CF EC +=+，∴BC EF =．在△ABC 和△DEF 中，AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩，，，∴△ABC ≌△DEF （SAS ）；………………………………………………（3分）（2）解：∵ABC DEF △△≌，∴60ACB F =∠=∠︒，∴180A B ACB =︒-∠∠-∠1805060=︒-︒-︒70=︒．……………………（6分）20．解：（1）在Rt △ACD 中，45ACD ∠=︒，∴904545CAD ∠=︒-︒=︒，∴ACD CAD ∠=∠，∴8AD CD ==m ，∴AC ==m ．答：点C 到旗杆顶端A 的距离AC为m ；……………………………（4分）（2）在Rt △BCD 中，tan BD BCD CD∠=，∴tan 638 1.96315.704BD CD =︒≈⨯= m ，∴815.70423.7AB AD BD =+=+≈m ，答：学校旗杆的高度AB 约为23.7m ．……………………………………（8分）21．解：（1）本次调查共抽查的学生人数为：1202060360÷=（人）．补全统计图如图所示：……………………….…………………………………（2分）（2）10300050060⨯=（人）．答：每周参加劳动的时间在3小时以上的大约有500人；……………（4分）（3）将这四位同学记为男1，男2，女1，女2，画树状图如下：由图可知，一共有12种等可能结果，其中一男一女的结果有8种，∴所选取的这两名学生恰好是一男一女的概率为82123=．……….…（8分）22.解：（1）设甲型路灯的单价为x 元，乙型路灯的单价为y 元．由题意得300400150000400300144000x y x y +=⎧⎨+=⎩，，解得180240x y =⎧⎨=⎩，．答：甲型路灯的单价为180元，乙型路灯的单价为240元；………（4分）（2）设第三批次购进乙型路灯m 盏．由题意得350180240400000150000144000m ⨯+--≤，解得11796m ≤．∵m 为正整数，∴m 最大为179．答：第三批次最多能购进乙型路灯179盏．………………………………（9分）23．（1）证明：∵DE AB ∥，DF AC ∥，∴四边形AEDF 为平行四边形．由作图可得AD 平分CAB ∠，∴CAD BAD ∠=∠．∵DE AB ∥，∴DAF ADE ∠=∠，∴EAD ADE ∠=∠，∴AE DE =，∴四边形AEDF 为菱形；…………………………………（4分）（2）解：设菱形AEDF 的边长为x ．在Rt ABC △中，10AB =，6BC =，∴8AC ==．∵DE AB ∥，∴EDC ABC △∽△，∴ED AB AC =，∴8108x x -=，∴解得409x =，∴菱形AEDF 的周长为40160499⨯=．在Rt CDE △中，4032899CE =-=，409ED =，∴83CD =，∴4083209327AEDF S AE CD ==⨯=g 菱形．………………………………………（9分）24．解：（1）∵15x ≤≤，15y x=，26y x =-+，∴115y ≤≤，215y ≤≤，∴2y 是1y 的“包容函数”．……………………………………………………（2分）（2）当15x ≤≤时，22(2)1y x =-+，∴2110y ≤≤．①当0k ＞时，1y kx =+的函数值y 随x 的增大而增大，当1x =时，min y 1k =+；当5x =时，max y 51k =+，∴115110k k +⎧⎨+⎩≥，≤，解得905k ≤≤，∴905k ＜≤；②当0k ＜时，1y kx =+的函数值y 随x 的增大而减小，当1x =时，max y 1k =+；当5x =时，min y 51k =+，∴110511k k +⎧⎨+⎩≤，≥，，解得09k ≤≤（舍去）．综上所述，实数k 的取值范围是905k ＜≤．…………………...…………（6分）（3）∵二次函数22y x mx n =-+与一次函数1y x =+互为“包容函数”，∴二次函数22y x mx n =-+与一次函数1y x =+函数值的取值范围相同．∵15x ≤≤，11y x =+，∴126y ≤≤．∵22222()y x mx n x m m n =-+=--+．当1x =时，221y n m =-+；当5x =时，21025y n m =-+；当x m =时，22y n m =-．①当5m ＞时，如图1，∴2102521n m y n m -+-+≤≤，∴10252216n m n m -+=⎧⎨-+=⎩，，解得7212m n ⎧=⎪⎨⎪=⎩，．（舍去）②当35m ≤≤时，如图2，∴2221n m y n m --+≤≤，∴22216n m n m ⎧-=⎨-+=⎩，，解得311m n =⎧⎨=⎩，，或13m n =-⎧⎨=⎩，，（舍去）∴311m n =⎧⎨=⎩，．③当13m ≤＜时，如图3，∴221025n m y n m --+≤≤，∴2210256n m n m ⎧-=⎨-+=⎩，，解得311m n =⎧⎨=⎩，，或751m n =⎧⎨=⎩，．（均舍去）④当1m ＜时，如图4，∴2211025n m y n m -+-+≤≤，∴21210256n m n m -+=⎧⎨-+=⎩，，解得526m n ⎧=⎪⎨⎪=⎩，．（舍去）综上所述，当311m n =⎧⎨=⎩，时，二次函数22y x mx n =-+与一次函数1y x =+互为“包容函数”．…………………………............……（10分）25．（1）证明：如图，连接OC ，∴2POC A ∠=∠．∵1452A P ∠=︒-∠，∴290A P ∠+∠=︒，∴90POC P ∠+∠=︒，∴180()90PCO POC P ∠=︒-∠+∠=︒，∴PC OC ⊥．∵OC 是O ⊙的半径，∴PC 是O ⊙的切线．……………………………（3分）在Rt BCE △中，3BC ===．…（6分）（3）解：①∵AB 是O ⊙的直径，∴90ACB ∠=︒．又∵90OCP ∠=︒，∴ACO PCB ∠=∠．∵OA OC =，∴ACO OAC ∠=∠，∴PCB PAC ∠=∠．在PCB △与PAC △中，∵PCB PAC ∠=∠，P P ∠=∠，∴PCB PAC △∽△，∴PC PB CB PA PC AC ==，∴2(PC PB CB PA PC AC = ，∴2(BC PB AC PA =．在Rt ABC △中，tan BC BAC AC ∠=，∴22tan ()10BC PB x y BAC AC PA x =∠===，数学（三）参考答案及评分标准一、选择题（本大题共10个小题，每小题3分，共30分）题号12345678910答案A A D D B D A A B C二、填空题（本大题共6个小题，每小题3分，共18分）11．3(2)x x -12．3π13．2x ≥14．2315．16．6-三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21题每小题8分，第22、23题每小题9分，第24、25题每小题10分，共72分．解答应写出必要的文字说明、证明过程或演算步骤）17．解：原式141214=--⨯+…………………………………………………………………（4分）54=．…………………………………………………………………………………（6分）18．解：1212326x x x x --⎧⎪⎨⎪+-+⎩≤，①＜，②解不等式①，得1x -≥，解不等式②，得2x ＜，∴该不等式组的解集为12x -≤＜，………………………………………………（4分）∴该不等式组的正整数解为1x =．…………………….……...……………....…（6分）19．解：（1）角平分线；………………..………………………………………………………（2分）（2）由作图可知，OP 平分AOB ∠，∴AON BON ∠=∠．∵OM MN =，∴AON MNO ∠=∠，∴BON MNO ∠=∠，∴MN OB ∥．…..………………………………..…（6分）20．解：（1）随机抽样调查的样本容量是：10025%400÷=，C 所占的百分比是：140100%35%400⨯=，扇形统计图中“B ”所对应的圆心角的度数为：360(125%10%︒⨯--35%)-108=︒．故答案为：400，108；…..…………………………………………………….（3分）（2）选择D 类的人数有：40010%40⨯=（人），选择B 类的人数有：40010014040120---=（人）．补全条形统计图如下：……………..……………………………………………（6分）（3）120800240400⨯=（人）．答：估计该校八年级学生选择“厨艺”劳动课的有240人．………（8分）21．（1）证明：∵四边形ABCD 是菱形，∴AC BD ⊥，12AO OC AC ==，∴90DOC ∠=︒，∵DE AC ∥，12DE AC =，∴DE OC =，DE OC ∥，∴四边形OCED 是平行四边形．又∵90DOC ∠=︒，∴四边形OCED 是矩形；………………………（4分）（2）解：由（1）可知，四边形OCED 是矩形，∴90ECA ∠=︒，122EC OD BD===．由勾股定理可得，6AC ==，∴11641222ABCD S AC BD ==⨯⨯=g 菱形．…………………………………..（8分）22．解：（1）设A 型座椅的单价是x 元，B 型座椅的单价是y 元．根据题意得550028500x y x y +=⎧⎨+=⎩，，解得30002500，x y =⎧⎨=⎩．答：A 型座椅的单价是3000元，B 型座椅的单价是2500元；……（4分）（2）∵A 型座椅数量不少于B 型座椅数量的13，∴1(80)3a a -≥，解得20a ≥．根据题意得30002500(80)500200000w a a a =+-=+．∵5000＞，∴w 随a 的增大而增大，∴20a =时，w 取得最小值，最小值为50020200000210000⨯+=．答：w 关于a 的函数解析式是500200000w a =+，购买两种座椅的总费用最少需要210000元．…………………………………………………………（9分）23．（1）证明：∵BE AB ⊥，∴90ABE ∠=︒．∵点F 是AE 的中点，∴BF AF EF ==．在ACF △和BCF △中，AC BC AF BF CF CF =⎧⎪=⎨⎪=⎩，，，∴ACF BCF △≌△（SSS ）；………………………………………………（4分）（2）解：∵ACF BCF △≌△，∴CBF CAF ∠=∠，∴1tan tan 3CAF CBF ∠=∠=，∴在Rt ACD △中，13CD AC =，即13CD BC =，∴12CD BD =．由（1）可知45ACF BCF ∠=∠=︒．∵AC BC =，∴45CBA ∠=︒，∴45CBE ∠=︒，∴BCF CBE ∠=∠．又∵CDF BDE ∠=∠，∴CFD BED △∽△，∴12CD DF BD DE ==．∵2DF =，∴4DE =，∴6EF =，∴6BF =．………………………（9分）24．（1）证明：如图，作OF AC ⊥于F ，作OG BD ⊥于G ，∴2AC AF =，2BD BG =．∵90OGE AEB OFE ∠=∠=∠=︒，∴四边形OGEF 是矩形．∵ABC BAD ∠=∠，∴ADC BCD =，∴AC BD =，∴AF BG =．连接OB ，OA ．∴Rt AOF △≌Rt BOG △（HL ），∴OF OG =，∴四边形OGEF 是正方形，∴OE 平分AEB ∠；………………………（3分）（2）解：在Rt AOF △中，222AF OA OF =-．同理可得，222BG OB OG =-，∴222222222(2)(2)4()4(AC BD AF BG OA OF OB OG OA +=+=-+-=+222222)4(2)84OB OE r m r m -=-=-．……………………………………（6分）（3=12S S +=．∵121122S S AE DE BE CE =g g g ，341122S S AE BE DE CE =g g g ，∴1234S S S S =，∴12S S +=，∴120S S -=，∴20-=，∴12S S =，∴1323S S S S +=+，∴ABD ABC S S =△△，∴AB CD ∥，∴180BCD ABC ∠+∠=︒．∵180BCD BAD ∠+∠=︒，∴ABC BAD ∠=∠，∴ ADC BCD =，∴AC BD =．……………..…（10分）25．解：（1）反比例函数6y x =是23→上的“民主函数”．理由如下：∵反比例函数6y x=在第一象限，y 随x 的增大而减小，∴当2x =时，3y =，当3x =时，2y =，即图象过(2，3)和(3，2)，满足题意当23x ≤≤时，23y ≤≤，∴反比例函数6y x=是23→上的“民主函数”；…………………………（3分）（2）∵一次函数+y kx b =在m n →上是“民主函数”，由一次函数的图象与性质得，①当0k ＞时，即图象过点(m ，m )和(n ，n )，∴mk b m nk b n +=⎧⎨+=⎩，，解得10k b =⎧⎨=⎩，，∴y x =；②当0k ＜时，即图象过点(m ，n )和(n ，m )，∴mk b n nk b m +=⎧⎨+=⎩，，解得1k b m n =-⎧⎨=+⎩，，∴直线解析式为y x m n =-++．综上所述，当0k ＞时，直线的解析式为y x =，当0k ＜，直线的解析式为y x m n =-++；…………………………………………………………………（6分）（3）抛物线的顶点式为22()24b b y a x c a a =++-，顶点坐标为(2b a -，24b c a -)．∵0a ＞，+0a b ＞，∴122b a -＜，∴抛物线22()24b b y a x c a a=++-在13x ≤≤上y 随x 的增大而增大，∴当1x =时，y 取最小值，当3x =时，y 取最大值，∴14933a b c a a b c ++==⎧⎨++=⎩，，解得14034a b c ⎧=⎪⎪=⎨⎪⎪=⎩，，，∴抛物线的函数解析式为21344y x =+．∵抛物线与直线3y =相交于A ，B 两点，设A (A x ，3)，B (B x ，3)．假设A 点在B 点的左侧，即213344x +=，解得13x =-，23x =，∴在ABC △中，A (3-，3)，B (3，3)，C (0，34)，∴6AB =，154AC =，154BC =．∵外心M 在线段AC 的垂直平分线上，设M (0，t )，则MA MC =，318t =，∴M (0，318)．在ABC △中，根据内心的性质，设内心G 到各边距离为d ，得1916()242ABC S AB BC CA d =⨯⨯=⨯++⨯△，∴1d =．∵ABC △是等腰三角形，y 轴为ACB ∠的角平分线，∴内心G 在y 轴上，∴G (0，2)，∴3115288M G MG y y =-=-=．……………………………………………（10分）数学（四）参考答案及评分标准一、选择题（本大题共10个小题，每小题3分，共30分）题号12345678910答案DC B B CD B AA C 二、填空题（本大题共6个小题，每小题3分，共18分）11．12．(2-，3)-13．1614．48π15．116．三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21题每小题8分，第22、23题每小题9分，第24、25题每小题10分，共72分．解答应写出必要的文字说明、证明过程或演算步骤）17．解：原式324=-+…………………………………………..…………………（4分）0=．…………………………………………………………………...……………（6分）18．解：原式221121a a a a a a --=÷+++21(1)1(1)a a a a a -+=+- 1a a +=．……………………………………………………………………………（4分）当23a =时，原式152a a +==．………………………………………………（6分）19．（1）证明：∵BAD CAB ∠=∠，ADB ABC ∠=∠，∴△ABD ∽△ACB ；…………………………………………………………（3分）（2）解：∵△ABD ∽△ACB ，∴AB AC AD AB =，得686AD =，解得92AD =，∴72CD AC AD =-=．…………………………………………..……………（6分）20．解：（1）根据题意得100.250÷=．故答案为：50．…………………………………………………………………（2分）（2）501641020a =---=，16500.32c =÷=．补全频数分布直方图如图所示：……………………………….…………………………（5分）（3）164120048050+⨯=（人）．答：估计全校学生成绩为“优”等的学生有480人．…………………（8分）21．解：（1）如图，过点B 作BM DD '⊥．∵50AB =cm ，37D AB '∠=︒，BM DD '⊥，∴sin 50sin 37500.6030BM AB BAM =∠=⨯︒≈⨯= （cm ）．答：B 点与支撑柱DD '的距离为30cm ；…………………………...……（4分）（2）∵50=AB cm ，37D AB '∠=︒，BM DD '⊥，∴cos 50cos37500.8040AM AB BAM =∠=⨯︒≈⨯= （cm ）．如图，过点B 作BH DE ⊥于点H ，过点A 作AF BH ⊥于点F ，过点C 作CG BH ⊥于点G ，CE DE ⊥于点E ．∵BM DD '⊥，BH DE ⊥，D D DE '⊥，∴四边形MDHB 为矩形，∴28040320BH DM AD AM ==+=+=（cm ），∴D D BH '∥，∴37ABH D AB '∠=∠=︒．∵72ABC ∠=︒，∴723735CBH ∠=︒-︒=︒，∴cos 700.8257.4BG BC CBH =∠=⨯= （cm ），∴32057.4262.6CE GH BH BG ==-=-=（cm ）．答：路灯C 离地面的距离为262.6cm ．……………………………………（8分）22．解：（1）设葡萄种植基地销售的A ，B 两种葡萄每千克的售价分别是x 元、y 元．根据题意，得24344x y x y =-⎧⎨=+⎩，，解得128x y =⎧⎨=⎩，．答：葡萄种植基地销售的A ，B 两种葡萄每千克的售价分别是12元，8元；…………………………………………………………………………………（4分）（2）设包装A 品种葡萄a 包，则包装B 品种葡萄4002a -包，总利润为w 元．根据题意，得80128(400)3600a a a ⎧⎨+-⎩≥，≤，解得80100≤≤a ．400(18123)(20822)24002a w a a -=--+-⨯-⨯=+．∵20＞，∴w 随a 的增大而增大．∴当100a =时，2100400600w =⨯+=最大．答：当包装A 品种葡萄100包时，所获总利润最大，最大总利润为600元．……………………………………………………………………………….…（9分）23．解：（1）BF AC ⊥．理由：∵四边形ABCD 为矩形，∴AD BC =，90BCD ∠=︒．∵BE AD =，∴BC BE =．在Rt BCF △和Rt BEF △中，BC BE BF BF =⎧⎨=⎩，，∴Rt Rt BCF BEF △≌△（HL ），∴CBF EBF ∠=∠．又∵BE BC =，∴BF AC ⊥；………………………………………...……（4分）（2）∵8AB =，6BC =，∴8AB CD ==，10AC =．∵BF AC ⊥，∴122AB BC AC BG =g g ，∴245AB BC BG AC ==g ，∴185CG =．∵3tan 4AD GF DCA CD CG ∠===，∴33182744510GF CG ==⨯=，∴2427155102BF BG GF =+=+=．…………………………………………（9分）24．解：（1）①在228y x x =--中，令0y =得2280x x --=，解得14x =，22x =-．∵122x x =-，∴此函数是“强基函数”；②在21y x x =++中，令0y =得210x x ++=．∵2141130∆=-⨯⨯=-＜，∴此方程无解，此函数不是“强基函数”；故答案为①．……………………………………………………………..………（2分）（2）∵222)1(y x t x t t =-+++是“强基函数”，令0y =得，22()210x t x t t -+++=，解得11x t =+，2x t =．∴12t t +=-或2(1)t t =-+，解得13t =-或23t =-．当13t =-时，22391y x tx t =+++22x x =-+217()24x =-+，∴函数的对称轴为直线12x =．∵12≤≤x -，10＞a =，∴当1x =-或2x =时，函数最大，此时最大值为：2max 17(1)424y =--+=；当23t =-时，22391y x tx t =+++22x x =-+25(1)4x =-+，∴函数的对称轴为直线1x =．∵12≤≤x -，10＞a =，∴当=1x -时，函数值最大，2max (11)48y =--+=．综上所述，当13t =-时，函数的最大值为4；当23t =-时，函数的最大值为8．………………………………………………………………………………..（6分）（3）①在1+-=x y 中，令0y =得1x =，∴点C 的坐标为(1，0)．由12，，y x y x =-+⎧⎪-⎨=⎪⎩得12，，x y =-⎧⎨=⎩或21，，x y =⎧⎨=-⎩（舍去）∴点A 的坐标为(1-，2)，∴直线AC 的解析式为1y x =-+．∵点B 的坐标为(3-，0)，∴直线AB 的解析式为3y x =+，∵点P 的坐标为(1x ，2x )，且122x x =-，∴点P 在直线2x y =-上．∵点P 位于△ACB 内部，∴123y x y x ⎧=⎪⎨⎪=+⎩，，解得2x =-．在2x y =-中，令0y =得0x =，∴1x 的取值范围是120＜＜x -；…………….…………………………..……（8分）②存在．理由如下：∵1x 为整数，120＜＜x -，∴11-=x ，∴此时221x -=-，解得212=x ，∴12111122b b x x a +=-=-=-+=-，即12b =，12111122c c x x a ===-⨯=- ，∴12c =-，∴该“强基函数”的解析式为21212-+=x x y ．………………………（10分）25．解：（1）如图，连接CO ．∵AC BC =，∴CO AB ⊥．∵CF 是O ⊙的切线，∴∥CE AB ，∴△ABE 和△ABC 同底等高．∵AB 是⊙O 的直径，∴90ACB ∠=︒，∴11111222ABE ABC S S AC BC ===⨯⨯=△△ ，∴△ABE 的面积为12；…………………………………………………………（3分）（2）如图，过点E 作AB EM ⊥于点M ，∴四边形COME 是矩形，∴CO EM =．∵△ABC 是等腰直角三角形，∴AB =，︒=∠45ABC，∴2CO =．∵15CBE ∠=︒，∴︒=︒-︒=∠-∠=∠301545CBE ABC ABE ，∴在△EBM中，22BE EM CO ===…………………….……..…（6分）（3）由（2）知，ABC △为等腰直角三角形，∴AB ==．∵22CH k AB =，∴CH CH k AC BC ==．∵1AC BC ==，∴CH k =，∴1AH AC CH k =-=-，BH =由（1）得∥CE AB ，∴△CEH ∽△ABH ，∴22123()(1)△△CEH ABH S S CH k S S AH k ===-．∵DAH CBH ∠=∠，DHA CHB ∠=∠，∴ADH BCH △∽△，∴2224(S AH SBH ==，∴222222134(1)1S S S S k k k k =+=-g g g ．…………………………...……（10分）数学（五）参考答案及评分标准一、选择题（本大题共10个小题，每小题3分，共30分）题号12345678910答案D A C C D B A A C B二、填空题（本大题共6个小题，每小题3分，共18分）11．2(1)x +12．2413．414．15415．1616．143m ＜＜三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21题每小题8分，第22、23题每小题9分，第24、25题每小题10分，共72分．解答应写出必要的文字说明、证明过程或演算步骤）17．解：原式85=--+（4分）3=--．………………………………………………………………………（6分）18．解：4211223x x x x +-+⎧⎪⎨--⎪⎩＞，①≤，②解不等式①，得1x -＞，解不等式②，得10x ≤，∴原不等式组的解集为110x -＜≤．………………………………………………（6分）19．解：（1）如图111A BC △即为所作；……………………………………………...………（2分）（2）如图，线段1MC 绕点M 顺时针旋转90︒扫过的图形为扇形12C MC ．∵M (1，1)，1C(1-，3)，∴1MC ==，∴线段1MC 在旋转过程中扫过的面积为122902360C MC S =⨯π⨯=π扇形．…………………………………………………………………………….…………（6分）20．解：（1）50(114%24%22%28%)6⨯----=（人）．答：八年级学生中测试成绩为10分的有6人；…………………………（3分）（2）614%724%822%928%1012%8a =⨯+⨯+⨯+⨯+⨯=，9b =，8c =；……………………………………………………………………（6分）（3）两个年级平均数相同，但七年级方差较小，∴七年级的成绩更稳定．…………………………………………..…………（8分）21．（1）证明：∵90ACB ∠=︒，DE AB ⊥，BD 平分ABC ∠，∴BCD BED ∠=∠，CBD EBD ∠=∠．在CBD △和EBD △中，BCD BED CBD EBD BD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩，，，∴CBD EBD △≌△（AAS ），∴BC BE =；……………………………（4分）（2）解：由（1）得CBD EBD △≌△，∴DC DE =．设DC DE x ==．∵9EF =，∴9DF x =-．在Rt CDF △中，222DF CD CF =+，∴222(9)3x x -=+，解得4x =，∴4DC DE ==．………………………………..………………………………（8分）22．解：（1）设甲种树苗每棵的价格是x 元，乙种树苗每棵的价格是y 元．根据题意得1510160010x y x y +=⎧⎨+=⎩，，解得6070x y =⎧⎨=⎩，．答：甲种树苗每棵的价格是60元，乙种树苗每棵的价格是70元；………………………………………………………………………………….（4分）（2）设购买甲种树苗m 棵，则购买乙种树苗（40m -）棵，购买两种树苗共花费w 元．∵购买乙种树苗的数量不少于甲种树苗数量的3倍，∴403m m -≥，解得10m ≤．根据题意得6070(40)102800w m m m =+-=-+．∵100-＜，∴w 随m 的增大而减小，∴当10m =时，w 取得最小值，最小值为101028002700-⨯+=，此时4030m -=．答：购买甲、乙两种树苗至少要花费2700元，此时购买甲种树苗10棵，乙种树苗30棵．………………………..………………………….……………（9分）23．（1）证明：∵四边形ABCD 为矩形，∴AB CD ∥，∴F BAF ∠=∠．由对称可知BAF MAF ∠=∠，∴F MAF ∠=∠，∴AM FM =；…………………………………………（3分）（2）解：由（1）可知ACF △是等腰三角形，AC CF =．在Rt ABC △中，∵3AB =，4BC =，∴5AC =，∴5CF AC ==．∵AB CF ∥，∴ABE FCE △∽△，∴35BE AB CE FC ==．设CE x =，则4BE x =-．∴435x x -=，解得52x =，∴512tan 52CE F CF ∠===；…………………（6分）（3）解：如图，由AB CF ∥可得ABE FCE △∽△，∴53AB BE FC CE ==，即353FC =，∴95CF =．由（1）可知AM FM =．设DM x =，则3MC x =-，则245AM FM x ==-．在Rt ADM △中，222AM AD DM =+，即22224()45x x -=+，解得1115x =，∴2461515AM x =-=．…………………………………………………………（9分）24．（1）解：若□ABCD 是“奇妙四边形”，则□ABCD 是正方形．理由如下：∵四边形ABCD 是平行四边形，∴ABC ADC ∠=∠．∵四边形ABCD 是圆内接四边形，∴180ABC ADC ∠+∠=︒，∴90ABC ADC ∠=∠=︒，∴平行四边形ABCD 是矩形．∵四边形ABCD 是“奇妙四边形”，∴AC BD ⊥，∴□ABCD 是正方形．故答案为：③；……………………………..……………………………………（2分）（2）证明：如图，过点B 作直径BE ，连接AE ．∵BE 是O ⊙的直径，∴90EAB ∠=︒，∴90ABE E ∠+∠=︒．∵AC BD ⊥，∴90DBC ACB ∠+∠=︒．∵E ACB ∠=∠，∴DBC ABE ∠=∠，∴»»DC AE =，∴DC AE =，∴22222AB CD AB AE BE +=+=，∴2222(2)4AB CD R R +==；………………………………………………（6分）（3）解：如图，连接AC ，交PD 于点G ，交BD 于点E ．∵四边形ABCD 是“奇妙四边形”，∴AC BD ⊥．的长度最小值为2．初中学业水平考试数学模拟试卷参考答案及评分标准第21页（共21页）25．解：（1）由题意可得A (12c ，0)，B (c -，0)，C (0，c )，∴2111()()222y x c x c x bx c =-+=++，整理得22211112442x cx c x bx c +-=++，∴21414c b c c ⎧=⎪⎪⎨⎪-=⎪⎩，，解得14b c =-⎧⎨=-⎩，，∴该抛物线的解析式为2142y x x =--；…………………..……..………（3分）（2）当点M 在BC 右侧时，∵ABC BCM ∠=∠，∴∥CM AB ，∴点M 与点C 关于抛物线的对称轴对称，∴M (2，4-)．当点M 在BC 左侧时，∵ABC BCM ∠=∠，∴CM BM =，∴点M 与点O 重合，∴点M 不在抛物线上．综上所述，抛物线上存在点M ，使ABC BCM ∠=∠，点M 的坐标为(2，4-)；……………………………………………………………….…………（6分）（3）设过A ，B ，D 三点的圆为⊙N ，设点N 的坐标为(1，n )，点D 的坐标为(m ，h )，连接AN ，DN ．由题可得2222(21)(0)9AN n n =--+-=+，222(1)()DN m n h =-+-，∴222(1)()9m h n n -+-=+，整理得2282m m n h h---=．∵点D 在抛物线上，∴2142m m h --=，∴2282m m h --=，∴222h n h h-==．∵2()DE h n =-，∴2()22EF h h n n h =--=-=，∴1162622ABE S AB EF ==⨯⨯=△ ．………………………………………（10分）。

湖南省长沙市麓山国际实验学校2024-2025学年八年级上学期第一次月考数学试卷

湖南省长沙市麓山国际实验学校2024-2025学年八年级上学期第一次月考数学试卷一、单选题1．下列各种著名的数学曲线中，不是轴对称图形的是（）A ．B ．C ．D ． 2．在下列图形中，正确画出AC 边上的高的是（）A ．B ．C ．D ．3．一个多边形的每个内角均为120°，则这个多边形是（）A ．五边形B ．六边形C ．七边形D ．八边形． 4．如图，△ABC ≌△DEC ，B 、C 、D 在同一直线上，且CE ＝5，AC ＝7，则BD 长（）A ．12B ．7C ．2D ．145．根据下列已知条件，能画出唯一的ABC V 的是（）A ． 347AB BC AC ===，， B ．4330AB BC A ==∠=︒，，C ．60454A B AC ∠=︒∠=︒=，，D ．6A B AB ∠=∠=，6．下列条件中，不能得到等边三角形的是（）A ．有两个外角相等的等腰三角形B ．三边都相等的三角形C ．有一个角是60︒的等腰三角形D ．有两个内角是60︒的三角形7．一个三角形的两边长为12和7，第三边长为整数，则第三边长的最小值是（） A ．5 B ．6 C ．7 D ．88．如图，是一块三角形的草坪，现要在草坪上建一凉亭，要使凉亭到草坪三个顶点的距离相等，凉亭应选的位置是（）A ．ABC V 的三条中线的交点B ．ABC V 三条角平分线的交点 C ．ABC V 三边的垂直平分线的交点D ．ABC V 三条高所在直线的交点9．如图，在ABC V 中， 90,BAC AD ∠=︒是高， BE 是中线， CF 是角平分线， CF 交AD 于点G ，交BE 于点H ，下面说法正确的是（）①ABE V 的面积BCE =△的面积 ②AFG AGF ∠=∠； ③2FAG ACF ∠=∠ ④AF FB =． A ．①②③④ B ．①②④ C ．①②③ D ．③④10．如图，先将正方形纸片对着，折痕为MN ，再把B 点折叠在折痕MN 上，折痕为AE ，点B 在MN 上的对应点为H ，沿AH 和DH 剪下得到△ADH ，则下列选项正确的个数为（） ①AE 垂直平分HB ；②∠HBN =15°；③DH =DC ；④△ADH 是一个等边三角形．A ．1个B ．2个C ．3个D ．4个二、填空题11．点(1,2)P -关于y 轴对称的点的坐标为．12．在Rt ABC △中，=90C ∠︒，30A ∠=︒，6cm AB =，则BC =．13．如图，ACD ∠是ABC V 的外角，若35A ∠=︒，40B ∠=︒，则1∠的度数为︒．14．如图，三角形纸片中，8cm AB =，6cm BC =，5cm AC =．沿过点B 的直线折叠这个三角形，使点C 落在AB 边上的点E 处，折痕为BD ，ADE V 的周长为cm ．15．如图，ABC V 的边BC AC ，的垂直平分线12l l ，相交于点O ．若110A ∠=︒，则B O C ∠=°．16．若等腰三角形的两条高所在直线形成的角中有一个为45︒，则其顶角的度数为．三、解答题17．计算：2024012(3)π---18．如图，网格中的ABC V 和DEF V 是轴对称图形．(1)利用网格线，作出ABC V 和DEF V 的对称轴l ；(2)如果每个小正方形的边长为1，则ABC V 的面积为__________．19．如图，点E 、F 在BC 上，BE ＝CF ，AB ＝DC ，∠B ＝∠C ．求证：∠A ＝∠D ．20．用一条长为20cm 的细绳围成一个等腰三角形．(1)若腰长比底边长短2cm ，求它的三边长；(2)能围成有一边的长是4cm 的等腰三角形吗﹖若能，请求出它的另两边，若不能，请说明理由．21．如图，AB AC =，AD BC =，AB 的垂直平分线MN 交AC 于点D ，求DBC ∠的度数．22．如图，过等边△ABC 的顶点A ，B ，C 依次作AB ，BC ，CA 的垂线MG ，MN ，NG ，三条垂线围成△MNG ．求证：△MNG 是等边三角形．23．（1）如图1，在ABC V 中，AB AC =，90BAC ∠=︒，CD 平分ACB ∠，BE CD ⊥，垂足为E ，试探究线段BE 和CD 之间的数量关系，并写出你的理由．（2）如图2，把条件改为：“在ABC V 中，AB AC =，90BAC ∠=︒，点D 在BC 上，12EDB C ∠=∠，BE ED ⊥，DE 与AB 相交于F 点，则线段BE 和FD 之间的数量关系如何?并证明你的结论．”24．如图，点A a ,0 ，()0,B b ，满足()21220a b -+-=，若点P 为射线OA 上异于原点O 和点A 的一个动点．(1)如图1，①直接写出点A 的坐标为，点B 的坐标为；②当点P 位于点O 与点A 之间时，连接PB ，以线段PB 为边作等腰直角BPE V （P 为直角顶点，B ，P ，E 按逆时针方向排列），连接AE ．求证：AB AE ⊥；(2)点D 是直线AB 上异于点A 与点B 的一点，使得BPO APD ∠∠=，过点D 作DF BP ⊥交y 轴于点F ，探究BP ，DP ，DF 之间的数量关系，并证明．25．（1）如图1，学习了等腰三角形，我们知道：在一个三角形中，等边所对的角相等；反过来，等角所对的边也相等．如果在一个三角形中，两个角不等，那么它们所对的边有什么大小关系呢？猜想：在ABC V 中，如果AB AC >，则C ∠B ∠（填写“＞”“＜”或“＝”），请证明你的猜想；（2）如图2，在ABC V 中()AB BC >，BP 平分ABC ∠交AC 于点D ，连接AP ，CP ．判断AB BC -与PC PA -的大小关系，并证明；（3）如图3，在ABC V 中，60A ∠=︒，ABC V 的角平分线BF ，CE 交于点D ，若57DE CD =，则BDCD．。

湖南省长沙市岳麓区湖南师范大学附属中学2024-2025学年九年级上学期第一次调研考试数学试题

湖南省长沙市岳麓区湖南师范大学附属中学2024－2025学年九年级上学期第一次调研考试数学试题一、单选题1．下列函数中，二次函数是（） A ．28y x =B ．81y x =+C ．8y x =-D ．8y x=-2 ）A BC D 3．下列长度的三条线段能组成直角三角形的是（） A ．5，11，12B ．2，3，4C ．4，6，7D ．3，4，54．如图，在Rt ABC V 中，30A ∠=︒，点D 、E 分别是直角边AC 、BC 的中点，连接DE ，则CED ∠度数是（）A ．70°B ．60°C ．30°D ．20°5．为评估一种水稻的种植效果，选了10块地作试验田．这10块地的亩产量（单位：kg ）分别为1210,,,x x x ⋯，下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是（） A ．这组数据的平均数 B ．这组数据的方差 C ．这组数据的众数D ．这组数据的中位数6．如图，在ABCD Y 中，13AB =，5AD =，AC BC ⊥，则ABCD Y 的面积为（）A ．30B ．60C ．65D ．6527．下列说法不正确．．．的是（） A ．一组邻边相等的矩形是正方形B ．对角线互相垂直且相等的四边形是正方形C ．正方形是轴对称图形，且有四条对称轴D ．正方形的对角线平分一组对角8．抛物线2y ax bx c =++上部分点的横坐标x 、纵坐标y 的对应值如表所示：从上表可知，4x =时，y 的值为（） A ．3B ．4C ．5D ．69．某公司今年销售一种产品，一月份获得利润5万元，由于产品畅销，利润逐月增加，一月份到二月份的增长率为x ，二月份到三月份的增长率是1.5x ，若三月份获得利润为7.8万元，则可列出方程为（） A ．()51 1.57.8x x ++= B ．()51 1.57.8x x +⨯= C ．()()7.811 1.55x x --=D ．()()511 1.57.8x x ++=10．二次函数2y ax bx c =++的最大值为a b c -+，且()()()()()4,,3,,1,,2,,3,1M c N m P m Q n R n --+中只有两点不在该二次函数图象上，下列关于这两点的说法正确的是（）A ．这两点一定是M 和NB ．这两点一定是Q 和RC ．这两点可能是M 和QD ．这两点可能是P 和Q二、填空题11．一组数据：1、1、1、2、5、6，它们的众数为．12x 的取值范围是.13．若关于x 的方程2120x kx --=的一个根为3，则k 的值为．14．如图，函数y kx =和4y ax =+的图象相交于点()2,5A ，则不等式4kx ax <+的解集为．15．如图，若被击打的小球飞行高度h （单位：m ）与飞行时间t （单位：s ）之间具有的关系为2205h t t =-，则小球从飞出到落地所用的时间为s ．16．如图，ABC V 中90C ∠=︒，8AC =，6BC =，线段DE 的两个端点D 、E 分别在边AC ，BC 上滑动，且4DE =，若点M 、N 分别是DE 、AB 的中点，则MN 的最小值．三、解答题17．计算：011(2024)42-⎛⎫-⨯- ⎪⎝⎭．18．如图，已知线段AB ，用直尺和圆规作菱形ABCD ：①以A 为顶点，任意作一条射线AP ；②以A 为圆心，AB 长为半径画弧交射线AP 于点D ；③分别以B ，D 为圆心，AB 长为半径画弧，两弧相交于点C ，连接BC ，DC ．根据作图步骤及痕迹回答下列问题：(1)能得到四边形ABCD 是菱形的依据是（）A ．一组邻边相等的四边形是菱形B ．四边相等的四边形是菱形C ．对角线互相垂直的平行四边形是菱形D ．每条对角线平分一组对角的平行四边形是菱形(2)连接BD ，若50BCD ∠=︒，求ABD ∠的度数．19．如图，沿AC 方向开山修路．为了加快施工进度，要在小山的另一边同时施工，从AC 上的一点B 取∠ABD=120°，BD=520m ，∠D=30°．那么另一边开挖点E 离D 多远正好使A ，C ，E 三点在一直线上1.732，结果取整数）？20．某企业生产了2000个充电宝，为了解这批充电宝的使用寿命（完全充放电次数），从中随机抽取了20个进行检测，数据整理如下：(1)表中a 的值为__________，本次检测采用的是__________调查（填“全面”或“抽样”）； (2)根据上述信息，下列说法中正确的是__________（写出所有正确说法的序号）； ①这20个充电宝的完全充放电次数都不低于300次；②这20个充电宝的完全充放电次数t 的中位数满足500600t ≤<； ③这20个充电宝的完全充放电次数t 的平均数满足300400t ≤<． (3)估计这批充电宝中完全充放电次数在600次及以上的数量． 21．已知关于x 的方程21204x kx k ---=． (1)当1k =时，解这个方程；(2)若方程有两个实数根1x ，2x ，且12x x =，求k 的值．22．某次气象探测活动中，在一广场上同时释放两个探测气球．1号探测气球从距离地面5米处出发，以1米/分的速度上升，2号探测气球距离地面的高度y （单位：米）与上升时间x （单位：分）满足一次函数关系，其图象如图所示．(1)求y 关于x 的函数解析式；(2)探测气球上升多长时间时，两个气球位于同一高度？此时它们距离地面多少米？ 23．如图，矩形ABCD 中，BCD ∠的角平分线交AD 于点E ，F 是AB 延长线上一点，满足BF AE =，连接EF ，CF ．(1)求证：EF CF =； (2)当60EFC ∠=︒时，求ADAB的值． 24．我们约定：平面直角坐标系xOy 中，点()11,A x y ，()22,B x y 满足12x x ≠，12y y =，则称A ，B 为一对“等值点”．根据约定，解决下列问题：(1)若点()1012,P p 和点(),1013Q q 为函数y mx =图象上的一对“等值点” (2)关于x 的函数y kx b =+（k ，b 为常数）的图象上是否存在“等值点”？如果存在，请指出它有多少对“等值点”，如果不是，请说明理由；(3)已知二次函数2y ax bx c =++（a ，b ，c 是常数，0a ≠）的图象与x 轴交于 C ，D 两点，点()11,E x y 和()22,F x y ，点()33,G x y 和()44,H x y 是该函数图象上的两对“等值点”，且满足()2221313220a a y y y y +-++=．若以CD ，EF ，GH 这三条线段的长为边长的三角形是直角三角形，试求该直角三角形的周长．25．已知抛物线()2y x n n =-+（n 为常数）的顶点为P ．(1)求证：当0n >时，抛物线与x 轴无交点；(2)若x t ≤时，y 有最小值7，x t >时，y 有最小值3，求t 的值；(3)如图，抛物线与直线2y x =+交于A ，B 两点，记PAB V 的面积为S ，OAB △的周长为l ，当n 取不同实数时，求Sl的最大值．。

初中生数学竞赛活动方案精选四篇

初中生数学竞赛活动方案精选四篇活动方案指的是为某一次活动所指定的书面安排，详细行动实施方法细则，步骤等。

对详细将要进行的活动进行书面的安排，对每个步骤的具体分析，探讨，以确定活动的顺当，圆满进行。

以下是我整理的初中生数学竞赛活动方案精选四篇，仅供参考，希望能够帮助到大家。

初中生数学竞赛活动方案1为增加我校学生的数学学习爱好，培育学生竞争意识，也为了履行本学期初的教务工作安排，我数学教研组特定于5月25日下午其次节课在全校七、八年级学生中实行一次数学竞赛，详细竞赛方案如下：一、竞赛组织老师：七年级组：×××、×××、×××（出卷：×××；监考：×××；改卷：×××）八年级组：×××、×××、×××（出卷：×××；监考：×××；改卷：×××）由于九年级接近中考故不参与，九年级老师做好复习迎考工作。

二、参赛人员：由七、八年级各数学老师或班主任以从班上抽选或组织学生自愿报名的形式每班至少抽取5名学生参与竞赛。

三、奖项设置：每年级组设置一等奖1名，二等奖2名，三等奖3名，组织奖每班一名，分别嘉奖80元、60元、40元的奖金或等价值奖品。

20XX年5月25日（星期二）下午2:55—4:55五、考场支配：七年级组考场设置在老师会议室，实行单人单桌考试制度；八年级组考场设置在多媒体教室，实行单人单桌考试制度。

监考老师务必从严监杜绝舞弊现象。

改卷老师务必做到公正、公允5月25日下午7点前各评卷老师将竞赛试卷交于教务处，请教务处的同志支配发奖事项。

×××中学数学教研组初中生数学竞赛活动方案2为增加我校九年级学生的数学学习爱好，培育学生竞争意识，也为了履行本学期初的教务工作安排，九年级数学组特定于11月19日下午其次节课实行一次数学竞赛，详细竞赛方案如下：一、竞赛组织老师：九年级全体数学老师二、参赛人员：九年级各数学老师或班主任以从班上抽选或组织学生自愿报名的形式每班至少抽取5名学生参与竞赛。

湖南省长沙市岳麓区湖南师范大学附属中学2025届高考冲刺数学模拟试题含解析

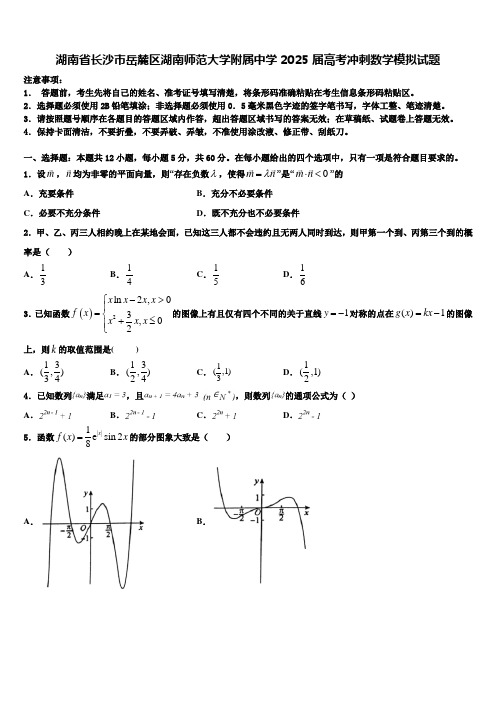
湖南省长沙市岳麓区湖南师范大学附属中学2025届高考冲刺数学模拟试题注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B 铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设m ，n 均为非零的平面向量，则“存在负数λ，使得m n λ=”是“0m n ⋅<”的 A ．充要条件 B ．充分不必要条件 C ．必要不充分条件D ．既不充分也不必要条件2．甲、乙、丙三人相约晚上在某地会面，已知这三人都不会违约且无两人同时到达，则甲第一个到、丙第三个到的概率是（） A ．13B ．14C ．15D ．163．已知函数()2ln 2,03,02x x x x f x x x x ->⎧⎪=⎨+≤⎪⎩的图像上有且仅有四个不同的关于直线1y =-对称的点在()1g x kx =-的图像上，则k 的取值范围是( ) A ．13(,)34B ．13(,)24C ．1(,1)3D ．1(,1)24．已知数列满足，且，则数列的通项公式为（） A ．B ．C ．D ．5．函数||1()e sin 28x f x x =的部分图象大致是（） A ． B ．C ．D ．6．设x ，y 满足24122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩，则z x y =+的取值范围是（）A ．[]5,3-B ．[]2,3C ．[)2,+∞D ．(],3-∞7．以下四个命题：①两个随机变量的线性相关性越强，相关系数的绝对值越接近1；②在回归分析中，可用相关指数2R 的值判断拟合效果，2R 越小，模型的拟合效果越好； ③若数据123,,,,n x x x x 的方差为1，则1232+1,2+1,2+1,,2+1n x x x x 的方差为4；④已知一组具有线性相关关系的数据()()()11221010,,,,,,x y x y x y ，其线性回归方程ˆˆˆy bx a =+，则“()00,x y 满足线性回归方程ˆˆˆybx a =+”是“1210010x x x x +++= ，1210010y y y y ++=”的充要条件；其中真命题的个数为( ) A ．4B ．3C ．2D ．18．已知正三角形ABC 的边长为2，D 为边BC 的中点，E 、F 分别为边AB 、AC 上的动点，并满足2AE CF =，则DE DF ⋅的取值范围是（） A ．11[,]216- B ．1(,]16-∞ C ．1[,0]2-D ．(,0]-∞9．设O 为坐标原点，P 是以F 为焦点的抛物线24y x =上任意一点，M 是线段PF 上的点，且PM MF =，则直线OM 的斜率的最大值为（）A ．1B ．12C ．22D 5 10．使得()3nx n N x x +⎛+∈ ⎝的展开式中含有常数项的最小的n 为( )A ．4B ．5C ．6D ．711．已知函数()f x 的定义域为()0,∞+，且()()2224m f m f f n n ⎛⎫⎪⎝⎭⋅=，当01x <<时，()0f x <.若()42f =，则函数()f x在[]1,16上的最大值为（） A ．4B ．6C ．3D ．812．已知函数()[]010x x f x x x ⎧≥⎪=⎨⎪⎩，，＜（[]x 表示不超过x 的最大整数），若()0f x ax -=有且仅有3个零点，则实数a的取值范围是（）A ．12,23⎛⎤ ⎥⎝⎦B ．12,23⎡⎫⎪⎢⎣⎭C ．23,34⎡⎫⎪⎢⎣⎭D ．23,34⎛⎤ ⎥⎝⎦二、填空题：本题共4小题，每小题5分，共20分。

湖南省长沙市岳麓区湖南师大附中博才实验中学2023-2024学年八年级上学期期中数学试题(解析版)

湖南师大附中博才实验中学2023—2024学年度第一学期八年级期中考试试题卷·数学时间：120分钟满分：120分一、选择题（共10小题，每小题3分，共30分）1.第19届杭州亚运会刚刚落下帷幕，在以下给出的运动图片中，属于轴对称图形的是（）A. B. C. D.【答案】D【解析】【分析】此题考查了轴对称图形即沿着某条直线折叠，直线两旁的部分完全重合，熟练掌握定义是解题的关键，根据定义逐项判断即可．【详解】A 、此选项不是轴对称图形，不符合题意；B 、此选项不是轴对称图形，不符合题意；C 、此选项不是轴对称图形，不符合题意；D 、此选项是轴对称图形，符合题意；故选：D ．2.下列计算正确的是（）A.235a a a⋅= B.()235a a = C.33()ab ab = D.223a a a +=【答案】A【解析】【分析】根据同底数幂的乘法，幂的乘方，积的乘方，合并同类项，逐项分析判断即可求解．【详解】解：A.235a a a ⋅=，故该选项正确，符合题意；B.()236a a =，故该选项不正确，不符合题意；C.333()ab a b =，故该选项不正确，不符合题意；D.23a a a +=，故该选项不正确，不符合题意；故选：A ．【点睛】本题考查了同底数幂的乘法，幂的乘方，积的乘方，合并同类项，熟练掌握以上运算法则是解题的关键．3.如图，△ABC ≌△DEC ，B 、C 、D 在同一直线上，且CE ＝5，AC ＝7，则BD 长（）A.12B.7C.2D.14【答案】A【解析】【分析】由题意易得BC=EC ，AC=DC ，然后由CE ＝5，AC ＝7可求解．【详解】解： △ABC ≌△DEC ，∴BC=EC ，AC=DC ，CE ＝5，AC ＝7，∴BD=BC+CD=CE+AC=5+7=12；故选A ．【点睛】本题主要考查全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．4.如图，在Rt ABC 与Rt DCB △中，已知90A D ∠=∠=︒，添加一个条件，不能使得≌Rt ABC Rt DCB 的是（）A.AB DC= B.AC DB = C.ABC DCB ∠=∠ D.BC BD=【答案】D【解析】【分析】要证明 ≌Rt ABC Rt DCB ，由已知条件90A D ∠=∠=︒，BC BC =，再加一个条件，可以根据HL ，AAS 来判断．【详解】解：根据三角形全等的判定定理，A ，90A D ∠=∠=︒，AB DC =，BC BC =，符合HL ，能使得 ≌Rt ABC Rt DCB 成立，不符合题意；B ，90AD ∠=∠=︒，AC DB =，BC BC =，符合HL ，能使得 ≌Rt ABC Rt DCB 成立，不符合题意；C ，90AD ∠=∠=︒，ABC DCB ∠=∠，BC BC =，符合AAS ，能使得 ≌Rt ABC Rt DCB 成立，不符合题意；D ，90A D ∠=∠=︒，BC BD =，BC BC =，不能使得 ≌Rt ABC Rt DCB 成立，符合题意；故选：D ．【点睛】本题考查了证明三角形全等的判断定理，解题的关键是：熟练应用三角形全等的判定定理：,,,,SSS SAS ASA AAS HL ．5.下面说法错误的是（）A.两个全等三角形的面积相等B.两角和一边对应相等的两个三角形全等C.三角形三条角平分线的交点到三个顶点的距离相等D.线段是轴对称图形【答案】C【解析】【分析】利用角平分线的性质、全等三角形的性质与判定、轴对称定义知识逐项判断即可．【详解】A 、两个全等三角形的面积相等，原说法正确，本选项不符合题意；B 、两角和一边对应相等的两个三角形全等，原说法正确，本选项不符合题意；C 、三角形三条角平分线的交点到角的两边的距离相等，原说法错误，本选项符合题意；D 、线段是轴对称图形，原说法正确，本选项不符合题意；故选：C ．【点睛】此题考查了角平分线的性质、全等三角形的性质与判定、轴对称定义，熟练掌握三角形角平分线的性质和全等三角形的性质与判定是解题的关键．6.如图，ABC 中，90C ∠=︒，AD 平分CAB ∠交BC 于D ，DE AB ⊥于点E ，且6cm CD =，则DE 等于（）A.4cmB.5cmC.6cmD.7cm【答案】C【解析】【分析】根据角平分线的性质，可得DE CD =，即可求解．【详解】解：∵90C ∠=︒，AD 平分CAB ∠交BC 于D ，DE AB ⊥，∴DE CD =，∵6cm CD =，∴6cm DE =．故选：C【点睛】本题主要考查了角平分线的性质，熟练掌握角平分线上点到角两边的距离相等是解题的关键．7.已知：如图，AC CD =，90B E ∠=∠=︒，AC CD ⊥，则正确的结论是（）A.A D∠=∠ B.2A ∠=∠ C.AB ED = D.12∠=∠【答案】B【解析】【分析】此题考查了全等三角形的性质和判定，利用同角的余角相等求出2A ∠=∠，再利用“AAS ”证明ABC CED △≌△，根据全等三角形对应边相等，对应角相等，即可解答．【详解】解：∵AC CD ⊥，∴=90ACD ∠︒，∴1290∠+∠=︒，则D 错误；∵90B E ∠=∠=︒，∴190A ∠+∠=︒，∴2A ∠=∠，则B 正确；在ABC 和CED 中，2B E A AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AAS ABC CED V V ≌，∴1D ∠=∠，AB CE =，BC DE =，则A 、C 错误；故选：B ．8.已知等腰三角形的一边长为4cm ，周长是18cm ，则它的腰长是（）A.4cmB.7cmC.10cmD.4cm 或7cm【答案】B【解析】【分析】分4cm 为等腰三角形的腰长和底边长两种情况，结合三角形的三边关系解答即可．【详解】解：若4cm 为等腰三角形的腰长，则底边长=18－4－4=10cm ，由于4+4＜10，此时不能构成三角形，故此种情况须舍去；若4cm 为等腰三角形的底边长，则腰长=（18－4）÷2=7cm ，此时三角形的三边长分别为7cm 、7cm 、4cm ，能构成三角形．故选：B ．【点睛】本题考查了等腰三角形的定义和三角形的三边关系，属于基础题型，正确分类、熟练掌握基本知识是解题关键．9.如图，ABC 中，分别以点A 和点B 为圆心，大于12AB 的长为半径作弧，两弧相交于M 、N 两点，作直线MN ，交BC 于点D ，连接AD ．若10AD =，5CD =，则CB 长为（）A.5B.10C.15D.20【答案】C【解析】【分析】此题考查了基本作图以及线段垂直平分线的性质，由作法得MN 垂直平分AB ，根据线段垂直平分线的性质得到AD BD =，然后根据线段和差即可求解．【详解】解：由作图可知：MN 垂直平分AB ，∴5AD BD ==，∴51015CB CD BD CD AD =+=+=+=，故选：C ．10.规定22a b a b =⨯※，例如：123122228=⨯==※；若()2132x +=※，则x 的值为（）A.29B.4C.3D.2【答案】D【解析】【分析】根据定义新运算列出相应的等式，然后利用同底数幂的乘法法则进行计算求解．【详解】解：∵()2132x +=※，由题意可得：212232x +⨯=∴352322x +==∴35x +=，解得2x =故选：D ．【点睛】本题考查定义新运算及同底数幂的乘法运算，理解题意列出等式，并掌握同底数幂的乘法法则准确计算是解题关键．二、填空题（共6小题，每小题3分，共18分）11.点()2,3P -关于x 轴对称点的坐标为______．【答案】()2,3【解析】【分析】关于x P （2，-3）关于x 轴对称的点的坐标是（2，3）．【详解】解：∵点P 的坐标为(2，-3)，∴点P 关于x 轴的对称点的坐标是(2，3)．故答案为：(2，3)．【点睛】此题主要考查了关于x 轴对称点的性质，正确掌握关于x 轴对称点的性质是解题关键．12.计算：()223x x ⋅=___________．【答案】49x 【解析】【分析】根据积的乘方、同底数幂的乘法法则计算即可．【详解】解：()22224399x x x x x ⋅=⋅=．故答案为：49x ．【点睛】本题主要考查了积的乘方，同底数幂的乘法，熟练掌握幂的运算法则是解答本题的关键．13.在Rt ABC 中，∠C=90°，∠A=30°，BC=4，则AB=_______．【答案】8【解析】【分析】根据直角三角形的性质30°所对的直角边等于斜边的一半求解即可．【详解】∵在Rt △ABC 中，∠A=90°，∠C=30°，∴12BC AB =，∵BC=4，∴AB=8．故答案为：8．考点：含30度角的直角三角形．14.如图，AD DC ⊥，AB BC ⊥，若AB AD =，120DAB ∠=︒，则ACB =∠______︒．【答案】30【解析】【分析】本题主要考查了全等三角形的性质和判定，先根据HL 证明ACD ≌ACB △，得出CAD CAB ∠=∠，即可得出答案.【详解】在Rt ACD △和Rt ACB △中，AC AC AB AD=⎧⎨=⎩，∴Rt ACD △≌Rt ACB △，∴1==602CAD CAB DAB ∠=∠∠︒，∴=90=30ACB BAC ∠︒-∠︒.故答案为：30.15.如图，边长为5cm 的正三角形ABC 向右平移1cm ，得到正三角形A B C '''，此时阴影部分的周长为______cm ．【答案】12【解析】【分析】此题考查了等边三角形的性质和判定，平移的性质，利用等边三角形的性质得到5cm AB BC ==，60B ACB ∠=∠=︒，再根据平移的性质得到60A B C B '''∠=∠=︒，1cm BB '=，4cm B C '=，于是可判断阴影部分为等边三角形，从而得到阴影部分的周长．【详解】解：∵ABC 为等边三角形，∴5cm AB BC ==，60B ACB ∠=∠=︒，∵等边ABC 向右平移1cm 得到A B C ''' ，∴60A B C B '''∠=∠=︒，1cm BB '=，∴60A B C ACB '''∠=∠=︒，514cm B C BC BB ''=-=-=，∴阴影部分为等边三角形，∴阴影部分的周长为()3412cm ⨯=，故答案为：1216.如图，在ABC 中，10AB AC ==，12BC =，8AD =，AD 是BC 边上的高，若P ，Q 分别是AD 和AC 上的动点，则PC PQ +的最小值是_____【答案】9.6【解析】【分析】由等腰三角形的三线合一可得出AD 垂直平分BC ，过点B 作BQ AC ⊥于点Q ，BQ 交AD 于点P ，则此时PC PQ +取最小值，最小值为BQ 的长，在ABC 中，利用面积法可求出BQ 的长度，此题得解．【详解】解：∵AB AC =，AD 是BC 边上的高，∴AD 垂直平分BC ，∴BP CP =，过点B 作BQ AC ⊥于点Q ，BQ 交AD 于点P ，则此时PC PQ +取最小值，最小值为BQ 的长，如图所示．∵1122ABC S BC AD AC BQ =⋅=⋅ ，∴1289.610BC AD BQ AC ⋅⨯===．故答案为：9.6．【点睛】本题考查了线段垂直平分线的性质、垂线段最短、等腰三角形的性质以及三角形的面积，利用点到直线垂直线段最短找出PC PQ +的最小值为BQ 是解题的关键．三、解答题（共9小题，其中每小题6分，20-21每小题8分，22-23每小题9分，24-25每小题10分，共72分）17.计算：2(2)|2|-+-+．【答案】6【解析】【分析】本题考查了实数的混合运算，根据有理数的乘方，化简绝对值，求一个数的算术平方根，立方根，即可求解．【详解】解：2(2)|2|-+-+4233=++6=-18.先化简，再求值：(31)(3)4(21)x x x +-+-，其中2x =．【答案】237x -，5．【解析】【分析】此题考查了整式的化简求值，熟练掌握整式的乘法运算和合并同类项法则是解题的关键．利用多项式乘以多项式法则计算，去括号合并得到最简结果，把x 的值代入计算即可求出值．【详解】原式239384x x x x =-+-+-，237x =-，当2x =时，原式2327=⨯-，127=-，5=．19.ABC 在平面直角坐标系中的位置如图所示，按下列要求解答：（1）画出ABC 关于y 轴对称的图形111A B C △；（2）写出1A 、1B 、1C 三个点的坐标．【答案】（1）见解析（2）()()()111,5,3,0,4,3A B C 【解析】【分析】本题考查了坐标与图形，画轴对称图形；（1）利用轴对称变换的性质分别作出A ，B ，C 的对应点1A ，1B ，1C 即可；（2）根据坐标系写出1A ，1B ，1C 即可．【小问1详解】解：如图所示，【小问2详解】解：()()()111,5,3,0,4,3A B C 20.如图，点B E C F 、、、在一条直线上，,,AB DE AC DF BE CF ===．（1）求证：ABC DEF ≌△△；（2）若45D ∠=︒，求EGC ∠的大小．【答案】（1）见解析（2）45︒【解析】【分析】（1）先证明BC EF =，即可根据“SSS ”证明；（2）根据（1）的结论可得ACB F ∠=∠，即有AC DF ∥，则D EGC ∠=∠，问题得解．【小问1详解】证明：BE CF = ，BE EC CF EC ∴+=+，BC EF ∴=，在ABC 和DEF 中，AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩()SSS ABC DEF ∴△≌△；【小问2详解】解：ABC DEF ≌，ACB F ∴∠=∠，AC DF \∥，45EGC D ∴∠=∠=︒．【点睛】本题主要考查了平行线的判定与性质，全等三角形的判定与性质等知识，掌握全等三角形的判定与性质，平行线的判定与性质，是解答本题的关键．21.如图，把四边形纸片ABCD 沿AC 折叠，点B 落在点E 处，CE 与AD 相交于点O ．已知在四边形纸片ABCD 中，AD BC ∥．（1）求证：AOC 是等腰三角形；（2）若BC CD ⊥于点C ，30OCD ∠=︒，CD =，2OD =，求AOC 的面积．【答案】（1）见解析；（2）【解析】【分析】（1）根据翻折的性质可得BCA ECA ∠=∠，由AD BC ∥得出BCA OAC ∠=∠，从而即可证明；（2）由BC CD ⊥求出90BCD ∠=︒，根据平行线的性质得出90D Ð=°，再通过勾股定理得4OA OC ==，然后利用三角形的面积公式列式计算即可得解．【小问1详解】由折叠性质可知：BCA ECA ∠=∠，∵AD BC ∥，∴BCA OAC ∠=∠，∴OAC ECA ∠=∠，∴OA OC =，∴AOC 是等腰三角形；【小问2详解】∵BC CD ⊥，∴90BCD ∠=︒，∵AD BC ∥，∴180BCD D ∠+∠=︒，∴90D Ð=°，在Rt OCD △中，由勾股定理得：4OC ==，由（1）得：4OA OC ==，∴AOC 的面积为11·422OA CD =⨯⨯=．【点睛】此题考查了翻折变换的性质，等腰三角形的判定，平行线的性质和勾股定理，熟练掌握以上知识的应用是解题的关键．22.如图，某校有一块长()3a b +米，宽()2a b +米的长方形地块，后勤部门计划将阴影部分进行绿化，在中间正方形空白处修建一座孔子雕像．（1）计算绿化地块的面积；（2）当3a =， 1b =时，绿化地块的面积是多少平方米？【答案】（1）()2253ma ab +（2）254m 【解析】【分析】本题考查的是列代数式，求代数式的值，整式的乘法与完全平方公式的实际应用．（1）由长方形的面积减去正方形的面积，再列式计算即可；（2）把2a =，1b =代入（1）中的代数式计算即可．【小问1详解】解：绿化面积2(3)(2)()=++-+a b a b a b ()22226322a ab ab b a ab b =+++-++253a ab =+．∴绿化的面积为22(53)m a ab +；【小问2详解】当3a =，1b =时，绿化的面积25333154=⨯+⨯⨯=．∴当3a =，1b =时，绿化的面积是254m ．23.如图，在四边形ABCD 中，AB AD =，CB CD =，60A ∠=︒，E 为AD 上一点，连接BD ，CE 交于点F ，且CE BA ∥．（1）连接AC ，求证：直线AC BD 的垂直平分线；（2）求证： EDF △是等边三角形；（3）若12AD =，8CE =，求CF 的长．【答案】（1）见解析（2）见解析（3）4【解析】【分析】（1）连接AC ，根据垂直平分线的判定定理，直接可得结论；（2）证明ABD 是等边三角形，可得60ADB ∠=︒，再由平行线的性质可得60CED EDF DFE ∠=∠=∠=︒，则结论得证；（3）连接AC 交BD 于点O ，由题意可证AC 垂直平分BD ，由ABD 是等边三角形，可得30BAO DAO ∠=∠=︒，12AB AD ==，由（2）中EDF 是等边三角形，可得4EF DE ==，可得CF 的长．【小问1详解】证明：连接AC ，∵AB AD =，CB CD =，∴直线AC 是线段BD 的垂直平分线；【小问2详解】证明：AB AD = ，60A ∠=︒，ABD ∴ 是等边三角形．60ABD ADB ∴∠=∠=︒．CE BA ∥，60CED A ∴∠=∠=︒，60DFE ABD ∠=∠=︒，CED ADB DFE ∴∠=∠=∠，DEF ∴ 是等边三角形；【小问3详解】解：如图所示，AB AD = ，CB CD =，AC ∴是BD 的垂直平分线，即AC BD ⊥．AB AD = ，60BAD ∠=︒，30BAC DAC ∴∠=∠=︒．CE BA ∥，30BAC ACE CAD ∴∠=∠=∠=︒，8AE CE ∴==，1284DE AD AE ∴=-=-=．DEF 是等边三角形，4EF DE ∴==，844CF CE EF ∴=-=-=．【点睛】本题考查了平行线的性质，线段垂直平分线的性质与判定定理，等边三角形的性质和判定等知识，熟练运用等边三角形的判定是本题的关键．24.阅读以下材料：己知两个两位数，将它们各自的十位数字和个位数字交换位置后，得到两个与原两个两位数均不同的新数，若这两个两位数的乘积与交换位置后两个新两位数的乘积相等，则称这样的两个两位数为“幸福数对”，例如436834862924⨯=⨯=，所以43和68与34和86都是“幸福数对”.解决如下问题：（1）请判断24与63是否是“幸福数对”？并说明理由：（2）为探究“幸福数对”的本质，可设“幸福数对”中一个数的十位数字为a ，个位数字为b ，且a b ¹；另一个数的十位数字为c ，个位数字为d ，且c d ≠，试说明a ，b ，c ，d 之间满足怎样的数量关系，并写出证明过程；（3）若有一个两位数，十位数字为()21++x x ，个位数字为()223x x ++；另一个两位数，十位数字为()225x x ++，个位数字为()22x x ++．若这两个数为“幸福数对”，求出这两个两位数．【答案】（1）24与63是“幸福数对”，理由见解析（2）ac bd =；证明见解析（3）36和84【解析】【分析】本题考查了多项式乘以多项式和新定义“幸福数对”，根据多项式乘以多项式进行计算即可求解．（1）根据定义即可得到答案；（2）根据定义得：()()()()10101010a b c d b a d c ++=++，化简得ac bd =；（3）根据定义列等式，化简解方程可得x 的值，从而得出答案．【小问1详解】解：∵24631512⨯=，42361512⨯=，∴24634236⨯=⨯，∴24与63是“幸福数对”【小问2详解】解：ac bd=理由如下，依题意，()()10101001010a b c d ac ad bc bd ++=+++，()()10101001010b a d c bd bc ad ac ++=+++，()()100101010010100ac ad bc bd bd bc ad ac +++-+++=，99990ac bd -=，()990ac bd -=，∴0-=ac bd ．即ac bd=【小问3详解】解：由（2）可得()21++x x ()225x x ++=()223x x ++()22x x ++即4324322386523856x x x x x x x x ++++=++++∴6556x x +=+解得：1x =，则()21++x x 3=，()223x x ++2136=++=；()225x x ++2158=++=，()22x x ++1124=++=∴这两个两位数分别为：36和84．25.平面直角坐标系中，点(),0A a ，()0,B b ，且a 、b ()23b =--，点A 、C 关于y 轴对称，点F 为x 轴上一动点．（1）求点A 、B 两点的坐标；（2）如图1，若BC CD ⊥，BA EA ⊥，且BD BE =，连接ED 交x 轴于点M ，求证：DM ME =；（3）如图2，若BC CD ⊥，且BC CD =，直线BC 上存在某点(),33G m m +，使DFG 为等腰直角三角形（点D 、F 、G 按逆时针方向排列），请直接写出点F 的坐标．【答案】（1）(1,0),(0,3)A B （2）见详解（3）(1,0)-或(4,0)或(11,0)-【解析】【分析】（1）由()23b =--2(3)0b -=，再由非负数的性质列出方程求出a 、b 的值即可；（2）作EN CD ∥，交x 轴于点N ，先证明Rt BCD Rt BAE ≌，再证明CMD NME ≌，即可证明DM ME =；（3）过点D 作DL x ⊥轴于点L ，先证明BCD △为等腰直角三角形，再证明BOC CLD ≌，则(4,0),(4,1)L D --，再按点F 与点C 重合、DG GF =且90DGF ∠=︒、DF GD =且90FDG ∠=︒三种情况，分别求出相应的m 的值，然后确定点F 的坐标即可．【小问1详解】()23b =--2(3)0b -=，20,(3)0b ≥-≥，∴10,30a b -=-=，解得1,3a b ==，∴(1,0),(0,3)A B ；【小问2详解】证明：如图3，作EN CD ∥，交x 轴于点N ，则DCM ENM =∠∠，∵,BC CD BA EA ⊥⊥，∴90BCD BAE ∠=∠=︒，∵点A 、C 关于y 轴对称，∴点(1,0)C -，y 轴是线段AC 的垂直平分线，∴CB AB =，∵BD BE =，∴()Rt BCD Rt BAE HL ≌，∴CD AE =；∵90,90DCM BCA EAC BAC +=︒+=︒∠∠∠∠，且BCA BAC ∠=∠，∴DCM EAC =∠∠，∴ENM EAC ∠=∠，∴AE NE =，∴CD NE =，∵CMD NME =∠∠，∴()CMD NME AAS ≌，∴DM ME =；【小问3详解】解：如图4，∵BC CD ⊥，∴90BCD ∠=︒，∵BC CD =，∴BCD △为等腰直角三角形，当点F 与点C 重合、点G 与点B 重合时，则DFG 为等腰直角三角形，∴(1,0)F -，过点D 作DL x ⊥轴于点L ，则90BOC CLD ==︒∠∠，∵90,CBO OCB DCL BC CD =︒-==∠∠∠，∴()BOC CLD AAS ≌，∴3,1BO CL OC LD ====，∴134OL OC CL =+=+=，∴(4,0),(4,1)L D --．如图5，若,90DG GF DGF ==︒∠，由题意可得，(,33)G m m +，过点G 作QR x ∥轴交y 轴于点K ，作DR QR ⊥于点R ，FQ QR ⊥于点Q ，则90R Q ==︒∠∠，∴90DGR QGF GFQ =︒-=∠∠∠，∴()DGR GFQ AAS ≌，∴33RG QF m ==+，∴(4,33)R m -+，由4RK =可得，334m m +-=，解得12m =，∴1733133122GQ DR m ==+-=⨯+-=，∵OF KQ =，∴17422F x =+=，∴(4,0)F ；如图6，若,90DF GD FDG ==︒∠，作GH x ∥轴，作DH x ⊥轴于点P ，交GH 于点H ，∵90DPF H ==︒∠∠，∴90FDP GDH DGH =︒-=∠∠∠，∴()DPF GHD AAS ≌，∴1DP GH ==，∴41=3m =-+-，∴(3,6)G --，∴1(6)7PF HD ==--=，∵(4,0)P -，∴4711F x =--=-，∴(11,0)F -，综上所述，点F 的坐标为(1,0)-或(4,0)或(11,0)-．【点睛】本题主要考查了非负数的性质、全等三角形的判定与性质、等腰三角形的判定与性质、坐标与图形、轴对称的性质等知识，解题的关键是正确作出辅助线，构造全等三角形，并运用分类讨论的思想分析问题．。

长郡外国语实验中学2024-2025学年七年级上学期第一次月考数学试题(解析版)

七年级数学素养能力初赛一、单选题（每题3分，共30分）1. 龙年春晚分会场，“长沙元素”吸引八方来客，春节假日接待旅游人数278.94万人次，同比增长109.25%，其中数据278.94万用科学记数法表示为（）A. 62.789410×B. 70.2789410×C. 72.789410×D. 527.89410× 【答案】A【解析】【分析】此题考查科学记数法的表示方法．科学记数法的表示形式为10n a ×的形式，其中1||10a ≤<，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值10≥时，n 是正整数；当原数的绝对值1<时，n 是负整数．【详解】解：278.94万62789400 2.789410=×，故选：A ．2. 刘徽在《九章算术注》中有“今两算得失相反，要令正负以名之．”可翻译为“今有两数若其意义相反，则分别叫做正数和负数．”如果气温为“零上20℃”记作20+℃，那么气温为“零下10℃”应表示为（） A. 20℃B. 10℃C. 10−℃D. 20−℃【答案】C【解析】【分析】此题主要用正负数来表示具有意义相反的两种量：零上温度记作“+”，零下温度记作“−”，由此求解．【详解】解：气温为“零上20℃”记作20+℃，那么气温为“零下10℃”应表示为10−℃，故选：C ．3. 0.8，()4−−， 1.5−−，20%，0，()26−，26−，()24−−这八个数中，非负数有（） A. 7个B. 6个C. 5个D. 4个【答案】C【解析】【分析】本题主要考查了有理数的分类．解题的关键是熟练掌握绝对值的化简，符号化简，乘方运算法则，有理数的分类．化简符号，根据有理数的分类进行解答即可．【详解】解：∵()44−−=， 1.5 1.5−−=−，()2636−=，2636−=−，()2416−−−，∴这八个数中，非负数有：0.8，()4−−，20%，0，()26−，共5个．故答案为：C ．4. 备受瞩目的郡外篮球社团即将开始招新，为保证后续社团活动的顺利开展，该社团负责人采购了一批篮球备用，现随机检测了4个篮球，其中质量超过标准的克数记为正数，不足的克数记为负数，从轻重的角度看，最接近标准的篮球是（）A. B. C. D.【答案】D【解析】【分析】本题考查了绝对值的意义和性质，先计算各选项的绝对值，然后比较即可，熟练掌握绝对值的意义是解题的关键．【详解】解：∵1010+=，1212−=，+88=，55−=， ∴581012<<<，∴最接近标准的篮球是标记5g −球，故选：D ．5. 有理数a 、b 在数轴上的位置如图所示，则下列各式的符号为正的是（）A. a b +B. a bC. abD. a b −【答案】D【解析】【分析】本题主要考查了有理数与数轴，有理数的四则运算，先根据数轴得到0b a <<，b a >，再根据有理数的四则运算法则求解即可．【详解】解；由题意得，0b a <<，b a >，∴0000aa b ab a b b+<<<−>，，，，∴四个选项中只有D 选项中式子符号为正，故选：D ．6. 现规定一种新运算“*”：1*a b b a =−，如145*1155=−=−，计算(2)*3−=（） A. 5−B. 1−C. 72−D. 52【答案】C【解析】【分析】此题考查了新定义运算，有理数的减法，根据新定义运算列式求解即可．【详解】17(2)*3322−=−−=−．故选：C ． 7. 下列说法中，正确的有（）①任何数乘以0，其积为零；②0除以任何一个数，其商为零；③任何有理数的绝对值都是正数；④两个有理数相比较，绝对值大的反而小．A. 2个B. 3个C. 4个D. 1个【答案】D【解析】【分析】有理数的除法法则，绝对值的性质，有理数的大小比较法则等知识点，能熟记知识点是解此题的关键，①0乘以任何数都等于0，0除以任何一个不等于0的数都得0，③两个负数比较大小，其绝对值大的反而小，④正数的绝对值等于它本身，负数的绝对值等于它的相反数，0的绝对值等于0.根据有理数的乘法法则即可判断①；根据有理数的除法法则即可判断②；根据绝对值的性质即可判断③；根据有理数的大小比较法则即可判断④．【详解】解：任何数乘以0，其积为零，故①正确；0除以任何一个不等于0的数，其商为零，故②错误；0的绝对值是0，不是正数，故③错误；如2200||==，， ∵20>，∴20>，即两个有理数比较大小，绝对值大的反而小不对，故④错误；所以正确的有1个，故选：D的8. 若9,4x y ==，且0x y +<，那么x y −的值是（） A. 5或1B. 5或13−C. 5−或13D. 5−或13−【答案】D【解析】【分析】本题考查了绝对值的化简计算，有理数的加减运算；根据9x =，4y =，且0x y +<，得到9x =−，4y =±，代入计算即可．【详解】∵9x =，4y =，且0x y +<，∴9x =−，4y =±，∴9413x y −=−−=−或()945x y −=−−−=− 故选D ．9. 已知非零实数a ，b ，c ，满足1b a c a b c ++=−，则||abc abc等于（） A. ±1B. ﹣1C. 0D. 1 【答案】D【解析】【详解】1b a c a b c++=− ,∴a,b,c 两个是负数，一个是正数,0abc ∴>, 1abcabc ∴=.选D.点睛：（1）b a c a b c++需要分类讨论，a,b,c 同正，同负，两正一负，两负一正. （2）化简绝对值公式：|x |,0,0x x x x −< = ≥ . 10. 如图，圆的周长为4个单位长度，在该圆的4等分点处分别标上0，1，2，3，先让圆周上表示数字0的点与数轴上表示1−的点重合，再将圆沿着数轴向右滚动，则数轴上表示100的点与圆周上表示（）的点重合．A. 0B. 1C. 2D. 3【答案】B【解析】【分析】本题考查数轴，有理数的减法与除法，圆周上表示数字0的点与数轴上表示1−的点重合，滚动到100时，滚动了101个单位长度，用101除以4，余数即为重合点．【详解】解：圆周上表示数字0的点与数轴上表示1−的点重合，()1001101−−=，1014251÷= ，∴数轴上表示100的点与圆周上表示1的点重合．故选：B二、填空题（每题3分，共18分）11. 比较大小：23−____34−（填“>”“<”或“=”）【答案】>【解析】【分析】本题考查了有理数的大小比较，根据两个负数，绝对值大的反而小即可判断求解，掌握有理数的大小比较法则是解题的关键．【详解】解：2233−=，3344−=， ∵2334<， ∴2334−>−，故答案为：>．12. a 的相反数是23−，则a 的倒数是______．【答案】32【解析】【分析】本题考查了相反数和倒数的概念，先根据相反数的概念求出a 的值，再求倒数即可．熟练掌握概念是解题的关键．【详解】解： a 的相反数是23−， 23a ∴=，a ∴的倒数是32．故答案为：32． 13. 近似数46.1510×精确到______位．【答案】百【解析】【分析】本题考查了近似数，将数字46.1510×进行还原，然后再判断精确到的位数即可求解，正确还原数字是解题的关键．【详解】解：∵46.151061500×=，∴近似数46.1510×精确到百位，故答案为：百．14. 在－1，2，－3，0，5这五个数中，任取两个数相除，其中商最小是________．【答案】－5【解析】【分析】所给的五个数中,最大的数是5,绝对值最小的负数是-1,所以取两个相除,其中商最小的是:5÷（-1）=-5.【详解】∵-3<-1<0<2<5,所给的五个数中,最大的数是5,绝对值最小的负数是-1,∴任取两个相除,其中商最小的是:5÷（-1）=-5,故答案为:-5．【点睛】本题主要考查有理数的大小比较和有理数除法,解决本题的关键是要熟练掌握有理数大小比较和有理数除法法则.15. 在(-1)3，(-1)2，-22，(-2)3这四个数中,最大的数与最小的数的和等于_________.【答案】-7【解析】【详解】解：(-1)3=-1，(-1)2=1，-22=-4，(-2)3=-8，最大的数为1，最小的数为-8，故最大的数与最小的数的和=1+（-8）=-7．故答案为-7．16. 已知满足2a 3(ab 5)0−+−−=，则a b =________．【答案】-8【分析】根据偶次幂具有非负性，绝对值具有非负性可得a -3=0，a -b -5=0，再解即可．【详解】解：由题意得：a -3=0，a -b -5=0，解得：a =3，b =-2，b a =-8，故答案为：-8．【点睛】此题主要考查了非负数的性质，关键是掌握偶次幂和绝对值具有非负性．三、解答题17. 计算：（1）()()()()7192315++−+++−；（2）313217524528−−+−+−；（3）111135532114×−×÷ ；（4）753719641836 −+−÷．【答案】（1）4−（2）98−（3）225− （4）11【解析】【分析】本题考查了有理数的四则混合运算，有理数的乘法简便运算，掌握有理数的运算法则与运算律是解题的关键．（1）根据有理数的加减混合运算进行计算即可；（2）根据有理数的加减混合运算进行计算即可；（3）根据有理数的四则混合运算进行计算即可；（4）根据有理数的乘法分配律进行简便运算．【小问1详解】解：原式7192315=−+−7231519=+−−【小问2详解】解：原式323711554822=−−+−−+ 118=−− 98=−；【小问3详解】解：原式1113456115=−××× 225=−；【小问4详解】解：原式75373696418 −+−× 75373636363696418=×−×+×−× 28302714=−+−11=．18（6分）．已知m 的绝对值为1，a 和b 互为倒数，c 和d 互为相反数，求()()202450ab c d m −++−的值．18. 如图，数轴上每个刻度为1个单位长度上点A 表示的数是3−．（1）在数轴上标出原点，并指出点B 所表示的数是；（2）在数轴上找一点C ，使它与点B 的距离为2个单位长度，那么点C 表示的数为；（3）在数轴上表示下列各数，并用“＜”号把这些数按从小到大连接起来．2.5，4−，152，122−，| 1.5|−，( 1.6)−+．【答案】（1）见解析，4 （2）2或6 （3）数轴表示见解析，()11421.6 1.52.5522−<−<−+<−<< 【解析】【分析】本题主要考查了在数轴上表示有理数以及有理数的比较大小：（1）根据点A 表示3−即可得原点位置，进一步得到点B 所表示的数；（2）分两种情况讨论即可求解；（3）首先在数轴上确定表示各数的点的位置，再根据在数轴上表示的有理数，右边的数总比左边的数大用“＜”号把这些数连接起来即可．【小问1详解】如图，O 为原点，点B 所表示的数是4，故答案为：4；【小问2详解】点C 表示的数为422−=或426+=．故答案为：2或6；【小问3详解】| 1.5| 1.5 ，()1.6 1.6−+=−，在数轴上表示，如图所示：由数轴可知：()1142 1.6 1.5 2.5522−<−<−+<−<< 19. 今年“十•一”黄金周是7天的长假，梅花山虎园在7天假期中每天旅游人数变化如表（正号表示人数比前一天多，负号表示比前一天少）日期 1日2日3日 4日 5日 6日 7日人数变化单位：万人 +1.8﹣0.6 +0.2 ﹣07 ﹣0.3 +0.5 ﹣0.7若9月30日的游客人数为0.2万人，问：（1）10月4日的旅客人数为万人；（2）七天中旅客人数最多的一天比最少的一天多万人？（3）如果每万人带来的经济收入约为150万元，则黄金周七天的旅游总收入约为多少万元？【答案】(1)0.9；(2)1.6；(3)1200万元.【解析】的.【分析】（1）根据题意列得算式，计算即可得到结果；（2）根据表格找出旅客人数最多的与最少的，相减计算即可得到结果；（3）根据表格得出1日到7日每天的人数，相加后再乘以100即可得到结果．【详解】解：（1）根据题意列得：0.2+（+1.8﹣0.6+0.2﹣0.7）=0.9；故答案是：0.9；（2）根据表格得：7天中旅客最多的是1日为2万人，最少的是7日为0.4万人，则七天中旅客人数最多的一天比最少的一天多2﹣0.4=1.6（万人）；故答案是：1.6；（3）10月1日有游客：0.2+1.8=2 （万）；10月2日有游客：2﹣0.6=1.4（万）；10月3日有游客：1.4+0.2=1.6（万）；10月4日有游客：1.6﹣0.7=0.9 （万）；10月5日有游客：0.9﹣0.3=0.6 （万）；10月6日有游客：0.6+0.5=1.1 （万）；10月7日有游客：1.1﹣0.7=0.4 （万）；黄金周七天游客：2+1.4+1.6+0.9+0.6+1.1+0.4=8（万），8×150=1200（万元），答：黄金周七天旅游总收入约为1200万元．【点睛】此题考查了有理数的混合运算的应用，弄清题意是解本题的关键．20. 观察下列三列数：1−、3+、5−、+7、9−、11+、…①-3、1+、7−、5+、11−、9+、…②3+、9−、15+、21−、27+、33−、…③（1）第①行第10个数是，第②行第15个数是；（2）在②行中，是否存在三个连续数，其和为1001？若存在，求这三个数；若不存在，说明理由；（3）若在每行取第k 个数，这三个数的和正好为599，求k 的值．【答案】（1）19+，31−（2）不存在，见解析（3）301k =【解析】【分析】本题主要考查了数字规律，一元一次方程的应用，关键是找出数字规律．（1）根据规律进行计算即可；（2）设三个连续整数为()()11232n n −−−−，()()1212n n −−−，()()11212n n +−+−，根据题意分n 为奇数和偶数分别列出方程，根据方程的解的情况进行判断即可；的（3）分k 为奇数和偶数，分别列出方程，解方程即可求解．【小问1详解】解：根据规律可得，第①行第10个数是210119×−=；第②行第15个数是()215131−×+=−；故答案为：19+；31−．【小问2详解】解：不存在．理由如下：由（1）可知，第②行数的第n 个数是()()1212n n −−−，设三个连续整数为()()11232n n −−−−，()()1212n n −−−，()()11212n n +−+−，当n 为奇数时，则2322122121001n n n −−−+−++−=，化简得，271001n −=，解得，504n =（舍）当n 为偶数时，则()()()2322122121001n n n −−−+−−−+−=，化简得，251001n −−=，解得，503n =−（不合题意，舍去），综上，不存在三个连续数，其和为1001．【小问3详解】解：当k 为奇数时，根据题意得，()()()2121321599k k k −−−++×−=，解得，301k =，当k 为偶数时，根据题意得，()()()2123321599k k k ++−−−=，解得，299k =−（舍去），综上，301k =．21. 【概念学习】定义新运算：求若干个相同的有理数（均不等于0）的商的运算叫做除方、比加222÷÷，()()()()3333−÷−÷−÷−等，类比有理数的乘方，我们把222÷÷写作2③，读作“2的圈3次方”，()()()()3333−÷−÷−÷−写作()3−④，读作“()3−的圈4次方”．一般地，把n aa a a a÷÷÷ 个记作：a ⓝ，读作“a 的n 次方”，特别地，规定：a a =①．【初步探究】（1）直接写出计算结果：2023=②______；（2）若n 为任意正整数，下列关于除方的说法中，正确的有______：（横线上填写序号）A ．任何非零数的圈2次方都等于1B ．任何非零数的圈3次方都等于它的倒数C ．圈n 次方等于它本身的数是1或1−D ．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数【深入思考】我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？（3）请把有理数(0)a a ≠的圈()3n n ≥次方写成幂的形式：a =ⓝ______；（4）计算：()2111472 −−÷−×− ④⑧⑨．【答案】（1）1；（2）ABD ；（3）21n a − ；（4）24022401− 【解析】【分析】本题考查有理数的混合运算、新定义，解答本题的关键是明确新定义的内容，计算出所求式子的值．（1）根据题意，计算出所求式子的值即可；（2）根据题意，可以分别判断各个选项中的说法是否正确，从而可以解答本题；（3）根据题意，可以计算出所求式子的值．（4）根据题意，可以计算出所求式子的值．【详解】解：（1）由题意可得，2023202320231=÷=②，故答案为：1；（2）A ．因为()10aa a a =÷=≠②，所以任何非零数的圈2次方都等于1，正确； B ．因为()10a a a a a a =÷÷=≠③，所以任何非零数的圈3次方都等于它的倒数，正确； C ．如()11−=②，则圈n 次方等于它本身的数是1或1−，说法错误；D ．根据新定义以及有理数的乘除法法则可知，负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数，正确；故答案为：ABD ；（3）21111n a a a a a a a a a a − =÷÷÷÷=⋅⋅= ⓝ，故答案为：21n a −；（4）解：()2111472 −−÷−×− ④⑧⑨ ()()()()918711111111967772222− =−÷÷⋅⋅⋅÷−÷−÷−÷−÷−×−÷−÷⋅⋅⋅÷−个个 61119647=−−÷× 112401=−− 24022401=−． 22. 定义：若A ，B ，C 为数轴上三点，若点C 到点A 的距离是点C 到点B 的距离2倍，我们就称点C 是[],A B 的美好点．例如；如图1，点A 表示数为1−，点B 表示的数为2，表示1的点C 到点A 的距离是2，到点B 的距离是1，那么点C 是[],A B 的美好点；又如，表示0的点D 到点A 的距离是1，到点B 的距离是2，那么点D 就不是[],A B 的美好点，但点D 是[],B A 的美好点．如图2，M ，N 为数轴上两点，点M 所表示的数为7−，点N 所表示的数为2．（1）点E ，F ，G 表示的数分别是3−，6.5，11，其中是[],M N 美好点的是________；写出[],N M 美好点H 所表示的数是___________．（2）现有一只电子蚂蚁P 从点N 开始出发，以2个单位每秒的速度向左运动．当t 为何值时，点P 恰好为M 和N 的美好点？【答案】（1）G ，4−或16−（2）1.5或3或9【解析】的【分析】（1）根据美好点的定义即可求解；（2）根据美好点的定义，分三种情况分别确定P 点的位置，进而可确定t 的值．【小问1详解】解：根据题意得∶()()()374,235EM EN =−−−==−−=，此时2EM EN ≠，故点E 不是[,]M N 美好点；()6.5713.5, 6.52 4.5FM FN =−−==−=，此时2FM FN ≠，故点F 不是[,]M N 美好点；()11718,1129GM GN =−−==−=，此时2GM GN =，故点G 是[,]M N 美好点；故答案是：G ．设点H 所表示的数是x ，则7,2HM x HN x =+=−， ∵点H 为[],N M 美好点，∴2HN HM =， ∴227x x −=+，解得：4x =−或16−；故答案是：4−或16−．【小问2详解】解：第一情况：当P 为[],M N 的美好点，点P 在M ，N 之间，如图1，∵2MP PN =，()279MN =−−=，∴3PN =， ∴3 1.52t ==秒；第二种情况，当P 为[],N M 的美好点，点P 在M ，N 之间，如图2，∵2PM PN =，()279MN =−−=，∴6PN =， ∴632t ==秒；第三种情况，P 为[],N M 的美好点，点P 在M 左侧，如图3，∵22PN PM MN ==，()279MN =−−=，∴18PN =， ∴1892t ==秒；综上所述，t 的值为：1.5或3或9．【点睛】本题考查实数与数轴、美好点的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考创新题目．。