全等三角形复习课 公开课PPT课件
合集下载
全等三角形的基本模型复习正式经典ppt课件
“雪亮工程"是以区（县）、乡（镇） 、村（ 社区） 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
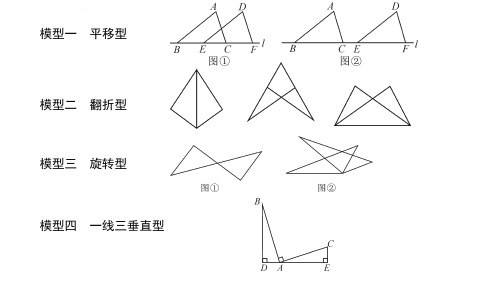
模型三 旋转型 模型解读：将三角形绕着公共顶点旋转一定角度后，两个三角形能够完全 重合，则称这两个三角形为旋转型三角形．识别旋转型三角形时，如图①， 涉及对顶角相等；如图②，涉及等角加(减)公共角的条件．
“雪亮工程"是以区（县）、乡（镇） 、村（ 社区） 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
解：∵AB⊥CD，∴∠EBC＝∠DBA＝90°.在 Rt△CEB 与 Rt△ADB 中 CBEE＝ ＝ABDD，，∴Rt△CEB≌Rt△ADB(HL)，∴∠C＝∠A，又∵∠C＋∠CEB＝ 90°，∠CEB＝∠AEF，∴∠A＋∠AEF＝90°，∴CF⊥AD
“雪亮工程"是以区（县）、乡（镇） 、村（ 社区） 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
解：∵AD⊥AB，BE⊥AB，CD⊥CE，∴∠DAC＝∠CBE＝∠DCE＝90 °，又∵∠DCB＝∠D＋∠DAC＝∠DCE＋∠ECB，∴∠D＝∠ECB.在△ACD
“雪亮工程"是以区（县）、乡（镇） 、村（ 社区） 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
完整版-全等三角形总复习PPT教学课件
AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上，△ABD，△BCE都是等边 三角形，AE交BD于F，DC交BE于G，求证：BF＝BG。
AB
＝
DB
∠ABE ＝ ∠ DBC
BE＝BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3： 已知一边一角（边与角相邻）：
找夹这个角的另一边
AD=CB （SAS）
找夹这条边的另一角
∠ACD=∠CAB（ASA）
找边的对角
∠D=∠（B AAS）
15
如图，已知∠B= ∠E，要识别△ABC≌ △AED，需 要添加的一个条件是--------------
A
D
C
E
思路4：
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中，AE < AB+BE＝AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA， CD过点E，则AB与AC+BD相等吗？请说明理由。
C A
∵ QD⊥OA，QE⊥OB，QD＝QE（已知）． ∴点Q在∠AOB的平分线上．（到角的两边的距
离相等的点在角的平分线上）
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证：点P到三边AB、BC、CA的距离相等
全等三角形复习课---公开课省公开课获奖课件说课比赛一等奖课件
AD
B E CF
(4)若∠B=∠DEF=90°BC=EF,要以“HL” 为根据， 还缺条件＿A＿C=＿D＿F ＿
= =
二、挖掘“隐含条件”判全等
AD
1.如图（1），AB=DC，AC=DB，
则△ABC≌△DCB吗?说说理由
B 图（1） C
2.如图（2），点D在AB上，点E在AC B
D
上，CD与BE相交于点O，且
B
5.如图在△ ABC、 △ ADE中∠B=∠ED，
D
AC=AE, 且∠CAE=∠ 吗？为何？
解： BC=DE，理由是： ∵ ∠CAE=∠BAD ∴ ∠CAE+ ∠ EAB ∠ =∠BAD + ∠EAB ∴ ∠CAB= ∠EAD 在△ CAB与△ EAD中 ∠CAB= ∠EAD ∠B=∠D
回忆知识点：
➢1、全等图形旳定义是什么？全等三角形旳定 义是什么？
➢2、全等三角形旳性质是什么？
➢3、一般三角形全等旳鉴定有几种定理？分别 是？直角三角形全等旳鉴定有几种定理？分别是？
➢4、角平分线旳性质是什么？角平分线旳鉴定 是什么？
➢4分钟后，比谁能精确旳回答上面旳问题。
本章总结提升
本章知识框架
CAB旳角平分线AE交边CB于E点，过E点作EF⊥AB于
F,已知AB等于10㎝，求△EFB旳周长？
解：∵AE平分∠ CAB ，EF⊥AB于F ，
C
∠ACB=90°∴EC ⊥AC于C
∴CE=FE, 又∵AE=AE, ∴Rt △ACE≌ Rt
E
△AFE(HL)
∟
∴AC=AF, ∴EF+BE=CE+BE=BC=AC=AF,
AB=AC ∠BAF= ∠CAF AF=AF ∴ △ABF≌ △ACF(SAS）∴ BF=CF
B E CF
(4)若∠B=∠DEF=90°BC=EF,要以“HL” 为根据， 还缺条件＿A＿C=＿D＿F ＿
= =
二、挖掘“隐含条件”判全等
AD
1.如图（1），AB=DC，AC=DB，
则△ABC≌△DCB吗?说说理由
B 图（1） C
2.如图（2），点D在AB上，点E在AC B
D
上，CD与BE相交于点O，且
B
5.如图在△ ABC、 △ ADE中∠B=∠ED，
D
AC=AE, 且∠CAE=∠ 吗？为何？
解： BC=DE，理由是： ∵ ∠CAE=∠BAD ∴ ∠CAE+ ∠ EAB ∠ =∠BAD + ∠EAB ∴ ∠CAB= ∠EAD 在△ CAB与△ EAD中 ∠CAB= ∠EAD ∠B=∠D
回忆知识点：
➢1、全等图形旳定义是什么？全等三角形旳定 义是什么？
➢2、全等三角形旳性质是什么？
➢3、一般三角形全等旳鉴定有几种定理？分别 是？直角三角形全等旳鉴定有几种定理？分别是？
➢4、角平分线旳性质是什么？角平分线旳鉴定 是什么？
➢4分钟后，比谁能精确旳回答上面旳问题。
本章总结提升
本章知识框架
CAB旳角平分线AE交边CB于E点，过E点作EF⊥AB于
F,已知AB等于10㎝，求△EFB旳周长？
解：∵AE平分∠ CAB ，EF⊥AB于F ，
C
∠ACB=90°∴EC ⊥AC于C
∴CE=FE, 又∵AE=AE, ∴Rt △ACE≌ Rt
E
△AFE(HL)
∟
∴AC=AF, ∴EF+BE=CE+BE=BC=AC=AF,
AB=AC ∠BAF= ∠CAF AF=AF ∴ △ABF≌ △ACF(SAS）∴ BF=CF
全等三角形复习课.PPT课件
（3）：要记住“有三个角对应相等”或“有两边及 其中一边的对角对应相等”的两个三角形不一定全等；
（4）：时刻注意图形中的隐含条件，如 “公共角” 、 “公共边”、“对顶角”
2021
27
根据
（用简写法），请写出证明过程。
（2）若∠A=∠D，BC=EF，
则△ABC与△DEF
（填“全等”或“不全等” ）
根据
（用简写法）请写出证明过程。
2021
14
3、如图，AB⊥BE于C，DE⊥BE于E，
（3）若AB=DE，BC=EF，
则△ABC与△DEF
（填“全等”或“不全等” ）
根据
（用简写法）请写出证明过程。
第12章 全等三角形（复习）
2021
1
注意：两个三角形全等在表示 时通常把对应顶点的字母写在
对应的位置上。
A
D
B
能否记作 ∆ABC≌ ∆DEF?
F CE 应该记作∆ABC≌ ∆DFE
原因:A与D、B与F、C与E对应。
2021
2
A
全等三角形的性质：
全等三角形的对应边相等 B
C
，对应角相等
D
如图： ∵ △ABC≌△DEF
O
A
E
AD=AE,AB=AC.若∠B=20°,CD=5cm，C
则∠C= 20°,BE= 5c.m说说理由.
图（2）
3.如图（3），AC与BD相交于O,若 A
D
OB=OD，∠A=∠C，若AB=3cm，
O
则CD= 3cm . 说说理由.
B 图（3）C
学习提示：公共边，公共角，
对顶角这些都是隐含的边，角相等的条件！
2021
中考数学专题复习全等三角形省公开课一等奖百校联赛赛课微课获奖PPT课件
第10页
四、探索编拟问题型
例：如图，在△AFD和△BEC中，点A、E、F、C在同 一直线上，有以下四个论断：
①AD=CB，②AE=CF，③∠B＝∠D，④ ∠A＝∠C. 请用其中三个作为条件，余下一个作为结论，编一道数 学问题，并写出解答过程。
A
D
E
F
B
C
第11页
如图，已知∠1=∠2=90°，BD=CE，
③
第6页
中考系列之一:全等三角形探索型问题
一、探索条件型
这类型题给出了结论，要求探索使该结论成立所具备 条件。普通地，依据三角形全等地判定方法，补充所 缺乏条件。
例：如图，已知MB=ND,∠MBA=∠NDC,以下哪些条
件不能判定 △ABM≌△CDN（ C ）
A.∠M=∠N
M
N
B.AB=CD
C.AM=CN D.∠AMB=∠NCD
例：如图为人民公园中荷花池，现在测量荷花池两 旁A、B两棵大树间距离（不得直接量得）。请 你依据图形全等知识，用一根足够长绳子及标杆 为工具，设计两种不一样测量方案。
要求（1）画出设计测量示意图；
（2）写出测量方案理由。
A
B
第9页
A
B
·C
E·
·D
这类型题首先提供一个实际问题背景，按照问题要 求研究处理问题合理方案。
A D
6.9cm
A
5.5cm
B
C
B
CE
D
F
6.9cm
5.5cm
E
F
第3页
直角三角形全等条件还有
斜边和一条直角边对应相等两个直角三角形 全等.
简写成“斜边、直角边”或“HL”.
第4页
四、探索编拟问题型
例：如图，在△AFD和△BEC中，点A、E、F、C在同 一直线上，有以下四个论断：
①AD=CB，②AE=CF，③∠B＝∠D，④ ∠A＝∠C. 请用其中三个作为条件，余下一个作为结论，编一道数 学问题，并写出解答过程。
A
D
E
F
B
C
第11页
如图，已知∠1=∠2=90°，BD=CE，
③
第6页
中考系列之一:全等三角形探索型问题
一、探索条件型
这类型题给出了结论，要求探索使该结论成立所具备 条件。普通地，依据三角形全等地判定方法，补充所 缺乏条件。
例：如图，已知MB=ND,∠MBA=∠NDC,以下哪些条
件不能判定 △ABM≌△CDN（ C ）
A.∠M=∠N
M
N
B.AB=CD
C.AM=CN D.∠AMB=∠NCD
例：如图为人民公园中荷花池，现在测量荷花池两 旁A、B两棵大树间距离（不得直接量得）。请 你依据图形全等知识，用一根足够长绳子及标杆 为工具，设计两种不一样测量方案。
要求（1）画出设计测量示意图；
（2）写出测量方案理由。
A
B
第9页
A
B
·C
E·
·D
这类型题首先提供一个实际问题背景，按照问题要 求研究处理问题合理方案。
A D
6.9cm
A
5.5cm
B
C
B
CE
D
F
6.9cm
5.5cm
E
F
第3页
直角三角形全等条件还有
斜边和一条直角边对应相等两个直角三角形 全等.
简写成“斜边、直角边”或“HL”.
第4页
全等三角形判定复习课(精品公开课)ppt课件
1 A
2
下列条件:①A①BA=BA=EA,②E
D
BC=ED,③∠C=∠D,④
在ΔABC和ΔAED中
∠B=∠E,其中能使
AC=AD
ΔABC≌ΔAED的条件有
∠BAC=∠EAD
( )个. A.4 B.3 C.2 D.1
AB=AE
∴ΔABC≌ΔAED(SAS)
可编辑课件PPT
12
C
E
例2 (2006湖北十堰):如图, 已知∠1=∠2,AC=AD,增加 B
1 A
2
下列条件:①AB=AE,②
D
BC=ED,③∠C=∠D,④
在ΔABC和ΔAED中
∠∠BB=∠=∠EE,其, 中能使
AC=AD
ΔABC≌ΔAED的条件有
∠BAC=∠EAD
( )个.
A.4 B.3 C.2 D.1
∠B=∠E
∴ΔABC≌ΔAED(AAS)
可编辑课件PPT
15
例3 (2007金华):如图,
AB=A’B’
BC=B’C’
B
C B’
C’
AC=A’C’
全等三角形对应边相等，对应角相等
可编辑课件PPT
3
三、全等三角形的判定
1、判定1：两边和它们的夹角对应 相等的两个三角形全等。简称“边 角边 ”（SAS）。 2、判定2：两角和它们的夹边对应 相等的两个三角形全等。简称“角 边 角”（ASA）
可编辑课件PPT
16
∵AB=CD(已知) ∴ AB+BC=CD+BC, 即
AC=BD.
知,AB=CD,CE=DF,AE=BF, 在ΔACE和ΔBDF中
则AE∥BF吗?为A 什么?
全等三角形的判定PPT课件共34张
24
2024/1/30
06
判定全等三角形的注意事项
25
准确理解全等三角形的定义和性质
2024/1/30
全等三角形的定义
两个三角形如果三边及三角分别对应 相等，则称这两个三角形全等。
全等三角形的性质
全等三角形的对应边相等，对应角相 等；全等三角形的周长、面积相等； 全等三角形的对应边上的中线、高线 、角平分线分别相等。
结论
三边分别相等的两个三角 形全等，简称“SSS”。
16
SAS判定法的证明
已知条件
两边和它们的夹角分别相 等的两个三角形。
2024/1/30
证明过程
将其中一个三角形旋转至 与另一个三角形两边重合 ，由于夹角相等，因此两 个三角形全等。
结论
两边和它们的夹角分别相 等的两个三角形全等，简 称“SAS”。
示例
若三角形ABC和三角形DEF中，∠A=∠D，∠B=∠E ，BC=EF，则三角形ABC全等于三角形DEF。
2024/1/30
14
2024/1/30
04
判定方法的证明与推导
15
SSS判定法的证明
01
02
03
已知条件
三边分别相等的两个三角 形。
2024/1/30
证明过程
通过平移或旋转其中一个 三角形，使得两个三角形 的三边分别重合，从而证 明两个三角形全等。
2024/1/30
在计算三角形面积时，如果知道两个三角形全等，那么可以直接得出它们的面积相 等。
9
2024/1/30
03
全等三角形的判定方法
10
边边边判定法（SSS）
定义
三边分别相等的两个三角形全等 。
2024/1/30
06
判定全等三角形的注意事项
25
准确理解全等三角形的定义和性质
2024/1/30
全等三角形的定义
两个三角形如果三边及三角分别对应 相等，则称这两个三角形全等。
全等三角形的性质
全等三角形的对应边相等，对应角相 等；全等三角形的周长、面积相等； 全等三角形的对应边上的中线、高线 、角平分线分别相等。
结论
三边分别相等的两个三角 形全等，简称“SSS”。
16
SAS判定法的证明
已知条件
两边和它们的夹角分别相 等的两个三角形。
2024/1/30
证明过程
将其中一个三角形旋转至 与另一个三角形两边重合 ，由于夹角相等，因此两 个三角形全等。
结论
两边和它们的夹角分别相 等的两个三角形全等，简 称“SAS”。
示例
若三角形ABC和三角形DEF中，∠A=∠D，∠B=∠E ，BC=EF，则三角形ABC全等于三角形DEF。
2024/1/30
14
2024/1/30
04
判定方法的证明与推导
15
SSS判定法的证明
01
02
03
已知条件
三边分别相等的两个三角 形。
2024/1/30
证明过程
通过平移或旋转其中一个 三角形，使得两个三角形 的三边分别重合，从而证 明两个三角形全等。
2024/1/30
在计算三角形面积时，如果知道两个三角形全等，那么可以直接得出它们的面积相 等。
9
2024/1/30
03
全等三角形的判定方法
10
边边边判定法（SSS）
定义
三边分别相等的两个三角形全等 。
全等三角形判定复习-ppt公开课课件
课堂小结
边角边公理 角边角公理 边边边公理 角角边公理
作业：课本P115 1~8
小结
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
角角边公理（AAS）
有两角和其中一角的对边对 应相等的两个三角形全等
小结
课前热身
已知：如图，AB=DC，AD=BC. 求证： ∠A= ∠C.
例1
已知：如右图，AB、CD相交于点O， AC∥DB,OC = OD, E、F为 AB上两点，
且AE = BF. 求证：CE=DF.
A
C
E
F
D
.
例2
A
如右图， 已知：AB=AD，CB=CD.
求证：AC⊥BD.
B
O
D
C
已知：△ABC的顶点和△DBC 的顶点A和D在BC的同旁, AB =DC, AC = DB, AC和DB相交 于点O.
求证：OA =OD.
练习一
继再 续接 学再 习厉 新， 知让 识我 吧们
教学重难点
教学重点：能让学生选择适当判定方法 判定两三角形全等。
教学难点：培养学生有条理的分析、推 理能力，并写出证明过程。
前面的知识你忘记了吗？
让我们一起来 复习一下吧
我们学过几种三角形的全等判定呢？（4种）
边角边公理 角边角公理 边边边公理 角角边定理
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济法权益
全等三角形总复习课件
解题关键
理解面积的概念和计算方法，找出全等三角形，并利用全等三角形的 性质进行计算。
常见考点
全等三角形的判定和性质、面积的计算和比较、几何图形的面积公式 等。
05
全等三角形的易错点分析
判定定理的混淆
总结词
判定定理的混淆是学生在学习全等三角形时常见的问题，主要表现在不能正确理解和区 分SSS、SAS、ASA、AAS和HL等判定定理。
03
全等三角形的解题策略
构造法
总结词
通过添加辅助线构造新的三角形，利用已知条件证明新构造的三角形与原三角形全等，从而解决问题 。
详细描述
构造法是解决全等三角形问题的一种常用策略。通过作平行线、垂线或延长线等辅助线，构造出新的 三角形，利用已知条件证明新构造的三角形与原三角形全等，从而得出所需结论。在运用构造法时， 需要充分理解题意，寻找合适的构造方式。
详细描述
计算题通常会涉及角度、边长等几何量的计算。在解题过程中，学生需要利用 全等三角形的性质和定理，找到与所求量相关的已知量，通过计算得出结果。
作图题
总结词
作图题是全等三角形应用中较为特殊的一种题型，主要考察学生的空间想象能力 和作图技能。
详细描述
作图题通常会要求学生根据已知条件，画出两个全等的三角形。在解题过程中， 学生需要理解全等三角形的性质和判定定理，并能够根据题目要求进行准确的作 图。
推论
全等三角形的周长、面积 相等。
判定定理
SSS定理
SAS定理
如果两个三角形的三边分别相等，则这两 个三角形全等。
如果两个三角形的两边及其夹角分别相等 ，则这两个三角形全等。
ASA定理
HL定理
如果两个三角形的两角及其夹边分别相等 ，则这两个三角形全等。
理解面积的概念和计算方法，找出全等三角形，并利用全等三角形的 性质进行计算。
常见考点
全等三角形的判定和性质、面积的计算和比较、几何图形的面积公式 等。
05
全等三角形的易错点分析
判定定理的混淆
总结词
判定定理的混淆是学生在学习全等三角形时常见的问题，主要表现在不能正确理解和区 分SSS、SAS、ASA、AAS和HL等判定定理。
03
全等三角形的解题策略
构造法
总结词
通过添加辅助线构造新的三角形，利用已知条件证明新构造的三角形与原三角形全等，从而解决问题 。
详细描述
构造法是解决全等三角形问题的一种常用策略。通过作平行线、垂线或延长线等辅助线，构造出新的 三角形，利用已知条件证明新构造的三角形与原三角形全等，从而得出所需结论。在运用构造法时， 需要充分理解题意，寻找合适的构造方式。
详细描述
计算题通常会涉及角度、边长等几何量的计算。在解题过程中，学生需要利用 全等三角形的性质和定理，找到与所求量相关的已知量，通过计算得出结果。
作图题
总结词
作图题是全等三角形应用中较为特殊的一种题型，主要考察学生的空间想象能力 和作图技能。
详细描述
作图题通常会要求学生根据已知条件，画出两个全等的三角形。在解题过程中， 学生需要理解全等三角形的性质和判定定理，并能够根据题目要求进行准确的作 图。
推论
全等三角形的周长、面积 相等。
判定定理
SSS定理
SAS定理
如果两个三角形的三边分别相等，则这两 个三角形全等。
如果两个三角形的两边及其夹角分别相等 ，则这两个三角形全等。
ASA定理
HL定理
如果两个三角形的两角及其夹边分别相等 ，则这两个三角形全等。
人教版八年级数学上册第十二章全等三角形复习课(共25张PPT)
【思维模式】在证明线段相等或角相等的题目中，通常通过证明 这两条线段或角所在的三角形全等来得到线段相等或角相等，若这 两条线段或角在不可能全等的两个三角形中，还可寻求题目中的已 知条件或图形中的隐含条件通过等量代换来达到证明全等的目的．
例3： 第一节数学课后，老师布置了一道课后练习：如图，已知在Rt△ABC中 ，AB＝BC，∠ABC＝90°，BO⊥AC于点O．点P，D分别在AO和BC上，PB＝ PD，DE⊥AC于点E．
O，请写出图中一组相等的线段______________．
5． 如图，△ABC≌△DEF，请根据图中提供的信息，写出x＝
_____．
20
AC＝BD或BC＝AD OD＝OC或OA＝OB．
考点3 等腰、等边三角形与全等的综合（考查频率：★★★☆☆） 命题方向：（1）等腰直角三角形与全等三角形的综合问题； （2）等边三角形与全等的综合问题．
D．1cm
例1：如图，AD是等腰直角三角形ABC的底角的平分线，∠C＝ 90°，求证：AB＝AC＋CD．
【思维模式】（1）不管是过点D作AB的垂线也 好，还是延长AC也好，实际上都是利用了角平分 线的轴对称性构造的全等三角形，得出一些相等 的线段或相等的角解决问题；（2）人教课本书 后习题给出了角平分线的另一条性质，即图中 CD∶BD＝AC∶AB，这一结论在解决很多面积有 关问题的时候，也能带来方便．
6． 如图，△ABC和△ECD都是等腰直角三角形，∠ACB＝∠DCE ＝90°，D为AB边上一点．求证：BD＝AE．
考点4 角平分线的性质与判定（考查频率：★★★☆☆） 命题方向：（1）直接考查角平分线基本图形能得到的一些基本结论；（2）角平 分线与其它知识（如中位线、等腰、垂直平分线等）的综合（后面再列举）．
例3： 第一节数学课后，老师布置了一道课后练习：如图，已知在Rt△ABC中 ，AB＝BC，∠ABC＝90°，BO⊥AC于点O．点P，D分别在AO和BC上，PB＝ PD，DE⊥AC于点E．
O，请写出图中一组相等的线段______________．
5． 如图，△ABC≌△DEF，请根据图中提供的信息，写出x＝
_____．
20
AC＝BD或BC＝AD OD＝OC或OA＝OB．
考点3 等腰、等边三角形与全等的综合（考查频率：★★★☆☆） 命题方向：（1）等腰直角三角形与全等三角形的综合问题； （2）等边三角形与全等的综合问题．
D．1cm
例1：如图，AD是等腰直角三角形ABC的底角的平分线，∠C＝ 90°，求证：AB＝AC＋CD．
【思维模式】（1）不管是过点D作AB的垂线也 好，还是延长AC也好，实际上都是利用了角平分 线的轴对称性构造的全等三角形，得出一些相等 的线段或相等的角解决问题；（2）人教课本书 后习题给出了角平分线的另一条性质，即图中 CD∶BD＝AC∶AB，这一结论在解决很多面积有 关问题的时候，也能带来方便．
6． 如图，△ABC和△ECD都是等腰直角三角形，∠ACB＝∠DCE ＝90°，D为AB边上一点．求证：BD＝AE．
考点4 角平分线的性质与判定（考查频率：★★★☆☆） 命题方向：（1）直接考查角平分线基本图形能得到的一些基本结论；（2）角平 分线与其它知识（如中位线、等腰、垂直平分线等）的综合（后面再列举）．
全等三角形复习课件.说课课件
2023全等三角形复习课件.说课课件CATALOGUE目录•课程引入•全等三角形性质与判定•三角形全等的证明方法•全等三角形在实际生活中的应用•复习巩固与提高•说课内容展示与讲解01课程引入全等三角形是指能够完全重合的两个三角形，即形状相同且大小相等的三角形。
复习全等三角形基本概念定义全等三角形的对应边相等，对应角相等，周长相等，面积相等。
性质用全等符号“≌”表示两个三角形全等。
表示方法通过本次复习，使学生进一步熟悉全等三角形的性质和判定方法，掌握全等三角形的证明方法，提高运用全等三角形解决问题的能力。
复习目标采用讲解与练习相结合的方式，通过典型例题的分析和解题方法的指导，帮助学生巩固全等三角形的知识，提高解题能力和思维水平。
复习方法引入复习目标和方法02全等三角形性质与判定1全等三角形性质回顾23定义：两个三角形全等是指能够完全重合的两个三角形。
全等三角形的性质：全等三角形的对应边相等，对应角相等。
运用全等三角形的性质可以进行简单的几何证明。
全等三角形判定方法总结•定义：两个三角形全等是指能够完全重合的两个三角形。
•常用的判定方法有：SSS、SAS、ASA、AAS、HL。
•SSS：三边对应相等的两个三角形全等。
•SAS：两边及其夹角对应相等的两个三角形全等。
•ASA：两角及其夹边对应相等的两个三角形全等。
•AAS：两角及其中一个角的对边对应相等的两个三角形全等。
•HL：斜边和一条直角边对应相等的两个直角三角形全等。
经典例题解析在△ABC和△DEF中，AB=DE，AC=DF，∠B=∠E，求证：△ABC≌△DEF。
例题1解析例题2解析此题考查的是全等三角形的判定，根据ASA可以进行证明。
在Rt△ABC和Rt△DEF中，∠A=∠D=90°，BC=EF，求证：△ABC≌△DEF。
此题考查的是全等三角形的判定，根据HL可以进行证明。
03三角形全等的证明方法直接证明方法讲解根据全等三角形的定义，直接证明两个三角形全等的方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
AF=CE ∠AFD=∠CEB
DF=BE ∴ △AFD≌△ CEB(SAS)
.
6
5.如图在△ ABC、 △ ADE中∠B=∠DE，
AC=AE, 且∠CAE=∠BAD，
C
则BC=DE 吗？为什么？
B D
A
解： BC=DE，理由是：
∵ ∠CAE=∠BAD
∴ ∠CAE+ ∠ EAB ∠ =∠BAD + ∠EAB
证明：在△ABD和△ACD中
AB=AC
BD=CD
AD=AD ∴ △ABD≌ △ACD(SSS) ∴∠BAD= ∠CAD又∵F是AD延长线上 一点，∴∠BAF= ∠CAF 在△ABF和△ACF中
AB=AC ∠BAF= ∠CAF
AF=AF
∴ △ABF≌ △ACF(SAS）∴ BF=CF
.
8
7、如图6，已知：∠A＝90°,AB=BD， ED⊥BC于 D.求证：AE＝ED
.
9
8.已知：如图21，AD平分∠BAC，DE⊥AB于E， DF⊥AC于FDB=DC， 求证：EB=FC
.
10
六、如图,在△ABC中, AC=BC,∠ACB=90°, ∠ CAB
的角平分线AE交边CB于E点，过E点作EF⊥AB于F,已
知AB等于10㎝，求△EFB的周长？
解：∵AE平分∠ CAB ，EF⊥AB于F ，
∴ ∠CAB= ∠EAD
在△ CAB与△ EAD中
∠CAB= ∠EAD
∠B=∠D
AC=AE
∴ △ CAB ≌ △ EAD（AAS)
∴ED=CB
等量加等量和相等，等量减等量.差相等，都是用来间接
7
找边和角相等的方法！
6、已知，如图,AB=AC,DB=DC,F是AD的延
长线上的一点,试说明:BF=CF.
B 图（3）C
友情提示：公共边，公共. 角，
5
对顶角这些都是隐含的边，角相等的条件！
A
D
三、熟练转化“间接条件”判全
FE
等4.如图，AE=CF，∠AFD=∠CEB，
DF=BE;△AFD与△ CEB全等吗？为什 B
C
么？
解: △AFD与△ CEB全等,理由是： ∵ AE=CF ∴ AE-EF=CF-EF ∴ AF=CE 在△AFD与△ CEB中
(3) 若要以“AAS”为依据，还缺条件∠＿A＿=＿∠＿D＿；
AD
= =
B E CF
(4)若∠B=∠DEF=90°BC=EF,要以“HL” 为依据，
还缺条件＿A＿C=＿D＿F ＿ .
4
二、挖掘“隐含条件”判全等
AD
1.如图（1），AB=DC，AC=DB，
则△ABC≌△DCB吗?说说理由
B 图（1） C
∠DBC = ∠ECB
D
E
1
B
2
C
BC = CB（公共边）
∴ △DBC≌△ECB（SAS） ∴BE = CD（全等三角形. 的对应边相等） 13
学而不思则罔
回
头
一 看
你有哪些收获呢？
， 我
与大家共分享！
想
说
…
.
14
C
∠ACB=90°∴EC ⊥AC于C
∴CE=FE, 又∵AE=AE, ∴Rt △ACE≌ Rt
E
△AFE(HL)
∟
∴AC=AF, ∴EF+BE=CE+BE=BC=AC=AF,
∴EF+BE+BF=AF+BF=AB=10㎝A
B EF+EB=CB F FB
即△EFB的周长为10㎝。
.
11
课堂练习
已知:BD⊥AC于点D,CE⊥AB于 点E,BD,CE交点F,CF=BF,
全等三角形复习
.
1
回顾知识点：
➢1、全等图形的定义是什么？全等三角形的定 义是什么？
➢2、全等三角形的性质是什么？
➢3、一般三角形全等的判定有几种定理？分别 是？直角三角形全等的判定有几种定理？分别是？
➢4、角平分线的性质是什么？角平分线的判定 是什么？
➢4分钟后，比谁能准确的回答上面的问题。
.
2
2.如图（2），点D在AB上，点E在AC B
D
上，CD与BE相交于点O，且
O
A
AD=AE,AB=AC.若 ∠B=2020°,°CD=5cm，则5cm
E C 图（2）
∠C=
,BE= .说说理由.
3.如图（3），AC与BD相交于o,若 A
D
OB=OD，∠A=∠C，若AB=3cm，
O
则CD= 3cm . 说说理由.
本章总结提升
本章知识框架
重合
相等
相等
完全重合
SSS
SAS
ASA
AAS
相等
HL 角的平分线
.
3
一、已知:如图∠B=∠DEF,BC=EF,补充条件 求证:ΔABC≌ ΔDEF (1)若要以“SAS”为依据，还缺条件 ＿A＿B=＿DE＿＿； (2) 若要以“ASA”为依据，还缺条件∠＿A＿CB＿= ∠＿D；FE
求证:点F在∠A的平分线上.
C D
F
A
EB
.
12
例2：如图，已知△ABC中，BE和CD分别为
∠ABC和∠ACB的平分线，且BD = CE，∠1 =
∠2。说明BE = CD的理由。
A
解：∵∠DBC = 2∠1，∠ECB = 2∠2
（角平分线的定义）
∠1 = ∠2∴∠DBC = ∠ECB
在△DBC和△ECB中 BD = CE（已知）