结构力学第2阶段练习题
结构力学2-4章练习题

题1
2.计算图示体系的自由度,试分析其体系的几何组成。
题2
3.图示静定桁架结构,杆 1、杆 2、杆 3 的轴力性质分别是
、
、
。
1 3
2
题3
4.计算下列静定结构内力并绘制其弯矩图。
10kN
A
B
2m
2m
题 4-1
ห้องสมุดไป่ตู้
4m
FG 2m
题6
3m 4m
7.作图示结构的弯矩、剪力和轴力图。
24kN
A
D
E
B
C F
4m
4m
4m
4m
题7
8.作图示桁架杆件 1 当单位荷载分别在下弦杆和上弦杆移动时的内力影响线。
F
G
H
I
1
A
B
C
D
E
P=1
8×3m
题8
9.用机动法作图示多跨静定梁中指定量值的影响线。
1kN
A
B CH DE
FG
3m
1m 1m 1m 1m
100kN·m
B
C
100kN E
20kN·m
A
D
F
2m
2m
2m
2m
题 4-2
4m
5.图示静定桁架在荷载作用下,计算该桁架指定杆件 1、杆件 2 的轴力。
60kN 1
2
4m
3m
3m
3m
题5
2m
6.计算图示静定结构,并绘制其弯矩图、剪力图。
6kN
A B
2m 2m 2m
结构力学2习题集同济版

南华大学《结构力学II》习题集(适合于大土木工程各专业方向)组编:刘华良班级:姓名:学号:建筑工程与资源环境学院道路桥梁工程教研室衡阳 2005年前言本习题集取材于第九章位移法9-l 确定下列各结构的位移法未知数目,并绘出基本结构。
9-2~9-3 用位移法计算下列结构内力.并绘出其弯矩图、剪力图和轴力图。
题9-2图题9-3图9-4~9-11 用位移法绘制下列结构弯矩图。
题9-4图题9-5图题9-6图题9-7图题9-8图题9-9图题9-10图题9-11图9-12~9-15 用位移法绘制下列具有斜杆的刚架的弯矩图。
题9-12图题9-13图题9-14图题9-15图9-16~9-17 列出下列结构的位移法典型方程式,并求出所有系数和自由项。
题9-16图题9-17图9-18~9-23 用位移法绘制下列具有无限刚性杆结构的M图。
题9-18图题9-19图题9-20图题9-21图题9-22图题9-23图9-24~9-26 用位移法绘制下列刚架M图。
题9-24图题9-25图题9-26图9-27 用位移法绘制图9-27所示结构弯矩图,并求桁架杆的轴向力。
题9-27图9-28 用位移法求图9-28所示桁架各杆轴向力。
题9-28图9-29 图9-29所示为一个三角形刚架,考虑杆件的轴向变形,试写出位移法的典型方程,并求出所有系数和自由项。
题9-29图9-30~9-31 用位移法计算图示有剪力静定杆组成的刚架的M图。
题9-30图题9-31图9-32~9-41 利用对称性,用位移法求作下列结构的M图。
题9-32图题9-33图题9-34图题9-35图题9-36图题9-37图题9-38图题9-39图题9-40图题9-41图9-42~9-48 试直接按平衡条件建立位移法方程计算题9-2、9-5、9-8、9-11、9-12、9-24、9-35,并绘出M图。
题9-42图题9-43图题9-44图题9-46图题9-47图题9-48图9-49~9-52 试用位移法求作下列结构由于支座位移产生的M图。
结构力学2考试题和答案

结构力学2考试题和答案一、单项选择题(每题2分,共20分)1. 在结构力学中,下列哪一项不是结构分析的基本假设?A. 平面假设B. 小变形假设C. 材料均匀性假设D. 材料非线性假设答案:D2. 确定结构的内力时,通常采用哪种分析方法?A. 能量法B. 弯矩分配法C. 弯矩图法D. 极限平衡法答案:C3. 在结构力学中,以下哪种类型的结构是超静定结构?A. 简支梁B. 悬臂梁C. 连续梁D. 刚架答案:C4. 梁的剪力图和弯矩图的零点位置关系是什么?A. 剪力图的零点与弯矩图的极值点重合B. 弯矩图的零点与剪力图的极值点重合C. 剪力图的零点与弯矩图的零点重合D. 剪力图的极值点与弯矩图的零点重合答案:A5. 以下哪种情况下,结构的稳定性分析是必要的?A. 荷载较小B. 荷载较大C. 荷载恒定D. 荷载变化答案:B6. 确定结构的位移时,通常采用哪种方法?A. 弯矩分配法B. 弯矩图法C. 虚拟力法D. 能量法答案:C7. 在结构力学中,以下哪种结构是静定结构?A. 三铰拱B. 刚架C. 连续梁D. 悬臂梁答案:D8. 以下哪种方法可以用来求解超静定结构?A. 弯矩分配法B. 弯矩图法C. 能量法D. 所有以上方法答案:D9. 结构力学中,以下哪种荷载属于分布荷载?A. 集中荷载B. 均布荷载C. 点荷载D. 线荷载答案:B10. 在结构力学中,以下哪种情况下结构会发生屈曲?A. 荷载较小B. 荷载较大C. 荷载恒定D. 荷载变化答案:B二、填空题(每题2分,共20分)1. 结构力学中,结构的内力包括______、______和______。
答案:轴力、剪力、弯矩2. 梁的挠度计算中,通常采用的两种方法是______和______。
答案:弯矩分配法、能量法3. 结构的稳定性分析中,______是衡量结构稳定性的一个重要参数。
答案:屈曲荷载因子4. 在结构力学中,______是结构分析的基本假设之一。
(整理)结构力学二

精品文档【题型:计算】【分数:8分】 得分:0分[1] 绘制图示多跨静定梁 C 截面弯矩影响线。
答题说明:按你的分析结果给出2、C、D、E、F 五个控制截面的影响量及正负。
答: 答 案:【题型:单选】【分数:2分】 得分:0分[2] 一般单元的单元刚度矩阵的行列式的值是什么? A 大于零 B 小于零 C 等于零 D 不等于零答: 答案: C 【题型:分析】【分数:12分】 得分:0分 [3] 左下图示为一超静定刚架,梁和柱的截面惯性矩分别是 I1和 I2,I1﹕I2=2﹕1。
横梁承受均布荷载 q=10kN/m 作用,试用右下图所示基本体系计算。
答题说明:给出系数和自由项和 D 截面弯矩(保留一位小数)。
答: 精品文档精品文档答 案:252|-1080|25.7【题型:填空】【分数:2分】 得分:0分[4] 能作为建筑结构使用的是( )体系。
答:答案: 无多余约束的几何不变体系和有多余约束的几何不变体系【题型:计算】【分数:8分】 得分:0分[5] 绘制图示静定刚架的弯矩图。
答题说明:按你的分析结果给出 A、C、DC、BA 四个控制截面的弯矩及受拉侧。
答: 答 案:【题型:分析】【分数:12分】 得分:0分[6] 求体系的自振频率和主振型。
已知 a=2m。
答题说明:给出体系柔度系数、主振型。
精品文档精品文档答:答 案:8/EI|2/EI|8/(6EI)|1/0.277|-1/3.610【题型:单选】【分数:2分】 得分:0分[7] 由主从结构的受力特点可知:附属部分的内力影响线在基本部分上 A 全为零 B 全为正 C 全为负 D 可正可负答:答案: A【题型:填空】【分数:2分】 得分:0分[8] 三铰拱的水平推力与( )、跨度、荷载有关。
答:答 案:三铰拱的水平推力与矢高、跨度、荷载有关,与拱轴线形状无关与刚度无关。
【题型:计算】【分数:8分】 得分:0分[9] 作图示刚架弯矩图。
答题说明:按你的分析结果给出 A、BA、BC、D、E 五个控制截面的弯矩及受拉侧。
《结构力学(2)》试题-2012-A-参考答案

M A = 350 × 3+300 × 1 = 1350kN.m (4)综上, M A,max = 1475kN.m ,下侧受拉。
《结构力学(2) 》试卷 A 卷
第 2 页 共 6 页
题 4 解:
EI
1) 自由度 (如图) : (5 分) 2)δ11 计算(5 分)
δ 11 = 1 1 a3 5a 3 2 × × (0.5a ) × a + = EI 3 48 EI 48 EI
M2
1
1
第二振型
题 7 解: 1)2 个自由度如图: (5 分) m1 = 2m 2)建立运动方程: (5 分)
δ 11 = 1 1 1 a 2 3 (a ) 2a + (a ) = 3 EI 3 EI a3 4 EI
3
y1
m2 = m
m
P(t ) = P0 sinθt
A
m
C
y2
3m
专业
3m
M A 影响线
tan α1 = -1 , tan α 2 = 1 , tan α 3 = -1 (2)将各个集中荷载依次移动到 B 点,求解最大负弯矩 ----------(5 分) P4 作用在 B 点时,P P2 不在结构上: 左移, 右移, ∑ Pi tan α i <0 ; ∑ Pi tan α i = -50<0 , 1、 不是临界位置。 P3 作 用 在 B 点 时 , P 1 不 在 结 构 上 : 左 移,
( 32 − λ ) A3 +8 A4 = 0 16 A3 + ( 5 − λ ) A4 = 0
特征方程为 32 − λ 8 =0 16 5−λ 解得: λ1 = 36.11 , λ2 = 0.886 ,即 ω1 = 24 EI EI 24 EI EI = 0.815 , ω2 = = 5.20 。代入振型方 3 3 3 λ1ma ma λ2 ma ma3
结构力学第2章习题及参考答案
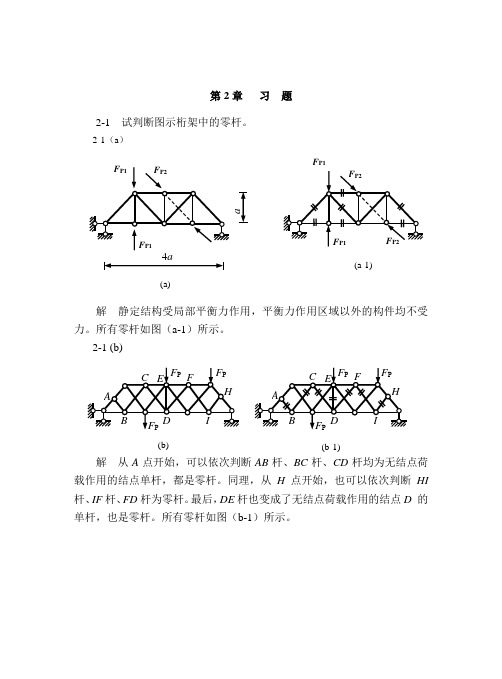
解悬臂刚架,梁部分先求杆端控制弯矩,再区段叠加。柱剪力为零,弯矩图为常数。
2-21(b)
解两刚片三支杆组成单体刚架,先求支座反力,再作弯矩图。注意二杆结点有外力偶作用时,杆端弯矩将产生突变,突变值等于力偶值。
2-21(c)
解(1)铰附近截面作用有集中力偶时,弯矩值等于力偶值,据此,可知顶铰左右两侧截面的弯矩为M,上侧受拉。又因为横梁上没有竖向集中力作用,弯矩图应是一条直线。考虑本题结构对称,荷载也对称,则横梁上的弯矩图为一条水平线。
2-14试作图示多跨静定梁内力图。
解:(1)确定求解顺序:EF→CDE→ABC
(2)求支座反力及各部分之间的相互作用力。结果如图(b)所示。
(3)分别画出每一部分的内力图,组合在一起就是原结构的内力图,如图(c)和(d)所示。
2-15试作图示多跨静定梁弯矩图。
解:(1)确定求解顺序。DEF→DCB→AB。
(2)二杆刚结点上,若无集中力偶作用时,则两个杆的杆端弯矩应该相等,且同时外侧受拉。这样就可以画出两个柱子的弯矩图了。
2-21(d)
解本题为基——附型结构,先算上部、后算下部。两个部分均三铰刚架,分别求解即可。
2-21(e)
2-22试作图示组合结构的弯矩图和轴力图。
FN12= -75kN,FN34=75kN
100kn100kn50kn2520251875knm202550kn截面内力5mcos3025sincos187525295kncossin5050188knsincos5050683kn5m305m5m213求图示三铰拱结构的支座反力链杆轴力并求指定截面k1求支座反力10kn10kn取ceb部分为隔离体截面的弯矩取kad部分为隔离体40knayed20kn4m4m4m4m214试作图示多跨静定梁内力图
结构力学二考试题和答案

结构力学二考试题和答案****一、单项选择题(每题2分,共10分)1. 梁在弯曲时,其截面上的正应力分布规律是()。
A. 线性分布B. 抛物线分布C. 正弦分布D. 指数分布答案:B2. 以下哪一项不是结构力学中的基本假设?()。
A. 平面截面假设B. 均匀材料假设C. 各向同性假设D. 材料非线性假设答案:D3. 在结构力学中,以下哪种力是内力?()。
A. 外力B. 支持力C. 弯矩D. 剪力答案:C4. 根据欧拉公式,临界载荷与构件的()有关。
A. 长度B. 截面惯性矩C. 材料的弹性模量D. 所有以上因素答案:D5. 梁的剪力图和弯矩图之间的关系是()。
A. 线性关系B. 抛物线关系C. 正比关系D. 微分关系答案:D二、填空题(每空1分,共10分)6. 结构力学中,结构的稳定性分析主要考虑的是结构在__________作用下的变形和破坏。
答案:荷载7. 梁在纯弯矩作用下,其截面上的正应力分布规律是__________分布。
答案:线性8. 根据弯矩图,梁的最大弯矩通常出现在__________。
答案:支座附近9. 梁的剪力图和弯矩图之间的关系可以通过__________得到。
答案:微分10. 欧拉临界载荷公式适用于__________。
答案:理想柱三、简答题(每题5分,共20分)11. 简述结构力学中“虚功原理”的基本思想。
内力分布的一种方法。
它基于这样一个假设:在平衡状态下,任何虚位移所做的虚功等于外力在这些虚位移上所做的功。
通过计算虚功,可以推导出结构的平衡方程和内力分布。
12. 描述梁的剪力和弯矩之间的关系,并给出相应的公式。
答案:梁的剪力和弯矩之间存在微分关系。
弯矩是剪力对梁长积分的结果,而剪力是弯矩对梁长的导数。
具体公式为:M =∫Vdx 和 V = dM/dx,其中M表示弯矩,V表示剪力。
13. 解释什么是结构的稳定性,并给出一个实际工程中的例子。
答案:结构的稳定性是指结构在受到荷载作用时,保持其原有形状和位置的能力。
结构力学第2阶段测试题

第二阶段测试卷考试科目:《结构力学》第五章(总分100分)时间:90分钟学习中心(教学点)批次:层次:专业:学号:身份证号:姓名:得分:一、单项选择题(本题共5小题,每题2分,共10分)1、对于理想线弹性体系,下面描述正确的是()A、荷载与位移成正比B、计算位移不可用叠加原理C、应力应变非线性D、只发生刚体体系位移2、静定结构由于支座移动,结构将()A、有内力,有应变,有位移B、有内力,无应变,有位移;C、无内力,有应变,有位移D、无内力,无应变,有位移;3、下图所示单位荷载设法是求()A、求自由端截面的转角B、求自由端水平位移C、求自由端竖向位移D、不能求位移4、下图所示单位荷载设法是求()A、求A点的相对位移B、求B点的相对位移C、求AB两点的水平位移D、求AB两点的相对位移5、下图结构位移描述正确的是()aaAB CA 、结构无变形B 、结构发生刚体位移C 、A 点无位移D 、自由端点无位移二、多项选择题(本题共5小题,每小题3分,共15分。
在每小题列出的四个选项中有2至4个选项是符合题目要求的,请将正确选项前的字母填在括号内。
多选、少选、错选均无分。
) 1、产生位移的机理描述正确的是:( ) A 、荷载作用:(外力→内力→变形→位移)B 、温度改变:(材料自由胀缩→无应力→有应变→结构变形)C 、支座移动:(无应力→无应变→几何位置变化的刚体位移)D 、支座移动:(有应力→有应变→几何位置变化的刚体位移) 2、根据结构是否变形,位移分为( )。
A 、线位移B 、刚体位移C 、相对角位移D 、变形体位移 3、对于∑⎰=∆ds EI M M P,说法正确的是( )A 、M 是虚设荷载的弯矩B 、P M 实际荷载引起的弯矩C 、EI 是抗弯刚度D 、M 、P M 同号为负 4、图乘法说法正确的是( )。
A 、如两个弯矩图形均是直线,则标距y 0可取自其中任一图形;B 、如一个为曲线,另一个是几段直线组成的折线,则分段叠加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江南大学现代远程教育第二阶段练习题及答案考试科目:《结构力学》第五章(总分100分)
学习中心(教学点)批次:层次:
专业:学号:身份证号:姓名:得分:
一、单项选择题(本题共5小题,每题2分,共10分)
1、对于理想线弹性体系,下面描述正确的是()
A、荷载与位移成正比
B、计算位移不可用叠加原理
C、应力应变非线性
D、只发生刚体体系位移
2、静定结构由于支座移动,结构将()
A、有内力,有应变,有位移
B、有内力,无应变,有位移;
C、无内力,有应变,有位移
D、无内力,无应变,有位移;
3、下图所示单位荷载设法是求()
A、求自由端截面的转角
B、求自由端水平位移
C、求自由端竖向位移
D、不能求位移
4、下图所示单位荷载设法是求()
A、求A点的相对位移
B、求B点的相对位移
C、求AB两点的水平位移
D、求AB两点的相对位移
5、下图结构位移描述正确的是()
A 、结构无变形
B 、结构发生刚体位移
C 、A 点无位移
D 、自由端点无位移
二、多项选择题(本题共5小题,每小题3分,共15分。
在每小题列出的四个选项中有2至4个选项是符合题目要求的,请将正确选项前的字母填在括号内。
多选、少选、错选均无分。
) 1、产生位移的机理描述正确的是:( ) A 、荷载作用:(外力→内力→变形→位移)
B 、温度改变:(材料自由胀缩→无应力→有应变→结构变形)
C 、支座移动:(无应力→无应变→几何位置变化的刚体位移)
D 、支座移动:(有应力→有应变→几何位置变化的刚体位移) 2、根据结构是否变形,位移分为( )。
A 、线位移
B 、刚体位移
C 、相对角位移
D 、变形体位移 3、对于∑⎰=
∆ds EI M M P
,说法正确的是( )
A 、M 是虚设荷载的弯矩
B 、P M 实际荷载引起的弯矩
C 、EI 是抗弯刚度
D 、M 、P M 同号为负 4、图乘法说法正确的是( )。
A 、如两个弯矩图形均是直线,则标距y 0可取自其中任一图形;
B 、如一个为曲线,另一个是几段直线组成的折线,则分段叠加。
C 、两个梯形不能图乘
D 、均布荷载作用区段,弯矩竖标叠加而非图形叠加。
5、下图结构发生的位移有( )
A 、杆件的角位移
B 、两截面相对角位移: C
、两杆件相对角位移 D 、截面角位移
三、判断题(本题共10小题,每小题1分,共10分。
请在你认为对的题后括号内打一个“√”,
认为错的题后括号内打一个“×”,不需要改错。
)
1、下图图乘结果为0Ay .( )
2、下图图乘结果为0Ay .( )
S=A y 0(
)A
y 0
③S=A
y 0()
⑤S=A
y 0()A
y 0
⑥S=A
y 0()
3、计算位移主要是为验算结构的刚度。
( )
4、图乘法可以应用任何结构。
( )
5、对称弯矩图与反对称弯矩图的图乘结果为零。
(
)
6、静定结构由于支座移动,将发生变形体位移。
( )
7、单位荷载法关键步骤是在待求位移方向虚加一个独立的单位荷载。
( )
8、位移的量纲都为长度。
( )
9、全二次抛物线,面积w=lh/2,形心l/2( ) 10、广义力和广义位移一一对应。
( )
四、简答题(本题共1小题,共10分) 1、阐述图乘法的应用条件.
五、绘图题(本题共1小题,共10分)
1、绘制结构大致的变形图像。
六、计算题(本题共3小题,每小题15分,共45分) 1、下图已知A 支座向上移动A c ,求C 点的竖向位移。
A
2、试用图乘法求图示结构C铰两侧截面的相对转角位移。
各杆EI均为常数。
3、求简支梁B端转角,EI为常数。
附:参考答案
一、单项选择题(本题共5小题,每小题2分,共10分)
1、A
2、D
3、A
4、D
5、C
二、多项选择题(本题共5小题,每小题3分,共15分。
)
1、A.B.C
2、B.D.
3、A.B.C
4、A.B.D
5、B.D
三、判断题(本题共10小题,每小题1分,共10分。
)
1、×
2、×
3、√
4、×
5、√
6、×
7、√
8、×
9、× 10、√
四、简答题(本题共1小题,共10分)
1、答:结构可分为等截面直杆段;单位弯矩图或荷载弯矩图其中之一可分为直线段。
五、绘图题(本题共1小题,共10分)
1、
六、计算题(本题共3小题,每小题15分,共45分) 1、解:
()
1
110
3c A c ⋅∆-⋅=A c c 3
1
=∆()
2、解:
3、解:
(逆时针)
P l /4
1/2
y 1=1 y 2=1
EI Pl
l Pl EI B 162142112
-
=∙-=ϕ。
