《幂的乘方与积的乘方》PPT课件
合集下载
北师大版数学七年级下册幂的乘方与积的乘方——幂的乘方课件(第一课时20张)

拓展与延伸
已知16m=4×22n-2,27n=9×3m+3 ,求 m,n 的值.
解:因为16m=4×22n-2,所以24m =22×22n-2 . 所以24m=22n,即4m=2n,2m=n. ① 因为 27n=9×3m+3 ,所以(33)n=32×3m+3 . 所以33n=3m+5,即3n=m+5. ② 由①②得,m=1,n=2.
解:a4n-a6n = (a2n)2- (a2n)3 = 32-33 = -18 .
把指数是积的情势的幂写成幂的乘方,amn=(am)n (m,n都是正整数),然后整体代入,求出式子的值.
课堂小结
幂 的 乘 方
性质:幂的乘方,底数不变, 指数相乘.
(am)n=amn (m,n为正整数)
当堂小练
1.计算(x3)3的结果是( D )
新课导入
视察计算结果,你能发现什么规律? (1) (x2)2 = x2∙x2 = x2+2= x4 ;
(2) (x2)3 = x2∙x2∙x2 = x2+2+2= x6 .
结 论 (1) (x2)2 = x2∙2= x4 ; (2) (x2)3 = x2∙3= x6 .
新课导入
视察计算结果,你能发现什么规律?(m,n为正整数)
A. x5
B. x6
C. x8
D. x9
2. 下列运算正确的是( B )
A. a2·a3=a6 a5
B. (a2)3=a6
C. a5·a5=a25 a10
D. (3x)3=3x3 27x3
当堂小练
3. (1)若2x+y=3,则4x·2y= 8 . (2)已知3m·9m·27m·81m=330,求m的值. 解:3m·32m·33m·34m=330 310m=330 m=3
课件114幂的乘方与积的乘方.ppt
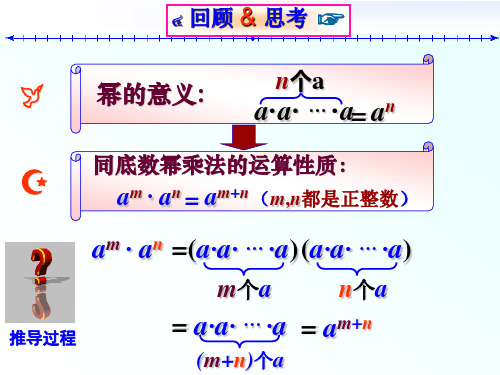
证 明
=am+m+ … +m (同底数幂的乘法性质)
=amn (乘法的意义)
幂 的 乘 方 法则
(am)n=amn (m,n都是正整数)
幂的乘方,底数 不变 , 指数 相乘.
阅读 体验 ☞例题解析
【例1】计算:
(1) (102)3 ;
(2) (b5)5 ;
(4) -(x2)m ; (5) (y2)3 ·y ;
V球
4 3
R3
甲球的半径是乙球的10倍,则 甲球的体积V甲= 36000 cm3 .
V甲 是 V乙 的 1000 倍
即 103 倍
如果甲球的半径是乙球的n 倍,那么甲球体积是乙球体积的 n3倍。
地球、木星、太阳可以近似地看作球体 。木星、太阳
的半径分别约是地球的10倍和102倍,它们的体积分别约
是地球的 103 倍和 106 倍. (102)3=106,为什么?
底数 不变 , 指数 相加 .
作作业业
(6) 2(a2)6 – (a3)4 =2a2×6 - a3×4 =2a12-a12 =a12.
随随堂堂练练习习
1、计算: (1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 ·x2 ; (4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 ·x3 .
解:(1) (62)4 = 62·62·62·62=62+2+2+2 =68 =62×4 ;
(2) (a2)3 = a2·a2·a2 =a2+2+2 =a6 =a2×3 ;
(3) (amm)22=am·am =am+m=a2m ;
初中数学北师大版七年级下册《幂的乘方与积的乘方(第2课时)》课件

(2)-(-2x3y4)3 =-(-2)3(x3)3(y4)3 =-(-8)x9y12 =8x9y12
4.计算:
(1)a2·(-a)3·(-a2)4; (2)(3x4y2)2+(-2x2y)4;
=a2·(-a3)·a8 =-a2·a3·a8 =-a13
=9x8y4+16x8y4 =25x8y4
(3)
探究新知 (1)(3×5)4=(3×5)×(3×5)×(3×5)×(3×5)×=(3×3×3×3) ×(5×5×5×5)=3( ) ×5( );
4
4
(2)(ab)4=
=
=a( )b( );
(3)(ab)n=
=
=a( )b( ).
解:(2)(ab)4=(ab)·(ab)·(ab)·(ab)=(a·a·a·a)·(b·b·b·b)=a4b4;
1.2
幂的乘方与 积的乘方
数学北师大版 七年级下
学习目标 1.掌握积的乘方的运算法则,并能利用法则进行计算和解决一些实际问题.
2.探索积的乘方的法则,进一步体会幂的意义,发展推理能力和有条理的表达 能力,培养从特殊到一般,从具体到抽象的逐步概括抽象的认识能力.
1.同底数幂的乘法的运算性质: 同底数幂相乘,底数不变,指数相加. 2.幂的乘方的运算性质: 幂的乘方,底数不变,指数相乘.
( n )个ab
(ab)n (ab) (ab) (ab)
( n )个a
( n )个b
aa abb b
a( n )b( n );
(ab)n =a( n )b( n () n是正整数).
2.把你发现的规律用文字语言表述,再用符号语言表达. 积的乘方的结果是把积的每一个因式分别乘方,再把所得的
=-8a6·a3+16a2·a7-125a9
人教版八年级上册课件 14.1.2 幂的乘方和积的乘方 (共48张PPT)

2018/8/1
温故知新
1.幂的乘方的法则 语言叙述 幂的乘方,底数不变,指数相乘.
符号叙述 ( a ) a
m n
m n
(m、n都是正整数) .
公式中的a可表示一 个数、字母、式子等 .
2.幂的乘方的法则可以逆用.即
a
mn
(a ) (a )
m n
n m
3.多重乘方也具有这一性质.如
[(a ) ] a
已知:am=2, an=3.
m+n 求a
= ?.
=2 × 3=6
解: am+n = am · an
2018/8/1
1.( x) ( -x) ( x)
6 5
2.( y x) ( x-y)
3 4
2018/8/1
判断下面计算是否正确,如有错误请改正。
a +a a
6 6
12
(×)
2018/8/1
(3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4Χ3 = - x12 .
计算: (1) (103)3; (2) (x3)2;
(3) - ( xm )5 ; ⑸ ( y 3 )2
(4) (a2 )3∙ a5;
⑹
[(a b) 3 ]4
幂的乘方法则(重点) 例 2:计算: (1)(x2)3; (3)(a3)2-(a2)3; (2)-(x9)8; (4)(a2)3· a5.
a
6
a a
6
2a
2018/8/1
6
2、
(1) [(x y) ]
3 4
⑵ (a-b)3[(a-b)3]2
⑶[(x-y)2]2[(y-x)2]3
温故知新
1.幂的乘方的法则 语言叙述 幂的乘方,底数不变,指数相乘.
符号叙述 ( a ) a
m n
m n
(m、n都是正整数) .
公式中的a可表示一 个数、字母、式子等 .
2.幂的乘方的法则可以逆用.即
a
mn
(a ) (a )
m n
n m
3.多重乘方也具有这一性质.如
[(a ) ] a
已知:am=2, an=3.
m+n 求a
= ?.
=2 × 3=6
解: am+n = am · an
2018/8/1
1.( x) ( -x) ( x)
6 5
2.( y x) ( x-y)
3 4
2018/8/1
判断下面计算是否正确,如有错误请改正。
a +a a
6 6
12
(×)
2018/8/1
(3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4Χ3 = - x12 .
计算: (1) (103)3; (2) (x3)2;
(3) - ( xm )5 ; ⑸ ( y 3 )2
(4) (a2 )3∙ a5;
⑹
[(a b) 3 ]4
幂的乘方法则(重点) 例 2:计算: (1)(x2)3; (3)(a3)2-(a2)3; (2)-(x9)8; (4)(a2)3· a5.
a
6
a a
6
2a
2018/8/1
6
2、
(1) [(x y) ]
3 4
⑵ (a-b)3[(a-b)3]2
⑶[(x-y)2]2[(y-x)2]3
幂的乘方与积的乘方PPT课件

知识回顾
1、同底数的幂相乘 法则:同底数的幂相乘,底数不变,指数相加。
数学符号表示: am • an amn
(其中m、n为正整数)
练习:判断下列各式是否正确。
a3 • a3 2a3,b4 b4 b8, m2 m2 2m2 (x)3 • (x)2 • (x) (x)6 x6
2、幂的乘方 法则:幂的乘方,底数不变,指数相乘。
c ·c3 = c4
y5 ·y5 =y10 (6)m + m3 = m4 (×)
m + m3 = m + m3
基础演练
(1) a ·a7- a4 ·a4 = 0
;
(2)(1/10)5 ×(1/10)3 = (1/10)8 ; (3)(-2 x2 y3)2 = 4x4y6 ;
(4)(-2 x2 )3 = -8x6 ;
(5)求代数式的值 1、已知10m=4,10n=5. 求103m+2n+1的值.
2、已知162×43×26=22a+1, (102)b=1012,求a+b的值。
能力挑战:
若xm3 x2 x7则m的值为 ___2__
已知2x 2 y 25 , 则正整数 x, y 的值有(D)
(A)1对 (B)2对 (C)3对 (D)4对
)
=p6+10 ( 同底数幂的乘法法则 )
=p16
例、木星是太阳系九大行星中最大的一 颗,木星可以近似地看作球体.已知木星 的半径大约是7×104km,木星的体积大约 是多少km3(∏取3.14)?
分析:球体体积公式 v 4 R3 解: v 4 (7 104 )3 3
3
4 73 1012
数学符号表示: (a m )n a mn
1、同底数的幂相乘 法则:同底数的幂相乘,底数不变,指数相加。
数学符号表示: am • an amn
(其中m、n为正整数)
练习:判断下列各式是否正确。
a3 • a3 2a3,b4 b4 b8, m2 m2 2m2 (x)3 • (x)2 • (x) (x)6 x6
2、幂的乘方 法则:幂的乘方,底数不变,指数相乘。
c ·c3 = c4
y5 ·y5 =y10 (6)m + m3 = m4 (×)
m + m3 = m + m3
基础演练
(1) a ·a7- a4 ·a4 = 0
;
(2)(1/10)5 ×(1/10)3 = (1/10)8 ; (3)(-2 x2 y3)2 = 4x4y6 ;
(4)(-2 x2 )3 = -8x6 ;
(5)求代数式的值 1、已知10m=4,10n=5. 求103m+2n+1的值.
2、已知162×43×26=22a+1, (102)b=1012,求a+b的值。
能力挑战:
若xm3 x2 x7则m的值为 ___2__
已知2x 2 y 25 , 则正整数 x, y 的值有(D)
(A)1对 (B)2对 (C)3对 (D)4对
)
=p6+10 ( 同底数幂的乘法法则 )
=p16
例、木星是太阳系九大行星中最大的一 颗,木星可以近似地看作球体.已知木星 的半径大约是7×104km,木星的体积大约 是多少km3(∏取3.14)?
分析:球体体积公式 v 4 R3 解: v 4 (7 104 )3 3
3
4 73 1012
数学符号表示: (a m )n a mn
北师大版七年级数学下册课件:1.2 幂的乘方与积的乘方(共25张PPT)

(1) (ab4)4 = ab8 ;
(2) (-3pq)2 = –6p2q2
解:(1)错误,结果应为a4b16; (2)错误,结果应为9p2q2
2. 计算:
(1) (- 3n)3 ; (2) (5xy)3 ; (3) –a3 +(–4a)2 a
解 (1)(-3n)3=(-3)3n3=-27n3; (2)(5xy)3=53x3y3=125x3y3; (3)–a3 +(–4a)2 a=–a3+16a2a=–a3+16a3=15a3
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式
都要“乘方”;注意结果的符号、幂指数及 其逆向运用(混合运算要注意运算顺序)
n个a m
=am+m+…+m
n个m
同底数幂的乘法法则
=amn
乘法的定义
幂的乘方的计算公式:
(am)n=amn(m,n都是正整数)
幂的乘方,底数_不__变___,指数__相__乘____.
例1 计算:
(1) (102)3; (2) (b5) 5 ; (3) (an) 3
(4) -(x2)m;(5) (y2)3 • y ; (6)2 (a2)6 - ( a3) 4
3
3
那么,(6×103)3=?这种运算有什么特征?
填空,看看运算过程用到哪些运算律,从运算结果 看能发现什么规律? (1)(ab)2=(ab)·(ab)=(a·a)·(b·b) =a(2)b(2 ). (2)(ab)3=(__a_b_)__·(__a_b_)__·_(__ab)
=(_a_a_a_)__·(_b_b_b_)_ =a( 3 )b( 3 ) .
解:(1) (102)3= 102×3 = 106; (2) (b5)5 = b5×5 = b25 ; (3) (an) 3 = an×3 = a3n ; (4) -(x2)m = -x2×m = -x2m ; (5) (y2)3 • y = y2×3 • y = y7 ;
幂的乘方与积的乘方课件

04
THANKS
[ 感谢观看 ]
注意处理负指数和分数指数
在进行积的乘方运算时,应注意处理负指数和分 数指数的情况,如 $a^{-m} = frac{1}{a^m}$, $a^{frac{1}{n}} = sqrt[n]{a}$。
CHAPTER 03
幂的乘方与积的乘方的关系
幂的乘方与积的乘方的相同点
两者都是基于乘法的运算性质
幂的乘方和积的乘方都是基于乘法运算的性质进行推导的,是数学中指数运算 的一部分。
CHAPTER 04
幂的乘方与积的乘方的练习题
基础练习题
1. $(a^m)^n = ?$
总结词:考察基本概念和运 算规则
பைடு நூலகம்
01
02
03
2. $a^{m times n} = ?$
3. $(ab)^n = ?$
04
05
4. $a^m times a^n = ?$
进阶练习题
总结词:增加难度,考察 理解和应用能力
幂的乘方与积的乘方课 件
CONTENTS 目录
• 幂的乘方 • 积的乘方 • 幂的乘方与积的乘方的关系 • 幂的乘方与积的乘方的练习题
CHAPTER 01
幂的乘方
幂的乘方运算规则
幂的乘方运算法则
$(a^m)^n = a^{m times n}$
运算步骤
先计算指数的乘积,再对底数进行幂运算。
注意事项
两者都涉及到指数的运算
无论是幂的乘方还是积的乘方,都涉及到指数的运算,这是理解两者关系的基 础。
幂的乘方与积的乘方的不同点
定义不同
幂的乘方是指数相乘,底数不变 ;而积的乘方是将几个相同的因 式相乘,每个因式的指数相加。
幂的乘方与积的乘方(第1课时)PPT课件

C.3个 D.2个
解析: (x5)2=x10,所以①②错;x5·x2=x7,所以 ④错;因为x5与x2不是同类项,所以不能合并, 所以⑤错.故选B.
3.若(54)x=512,则x= 3
.
解析: (54)x=54x=512,所以4x=12,所 以x=3.故填3.
4.计算. (1)(-xm)3; 解:原式=-xm·3=x3m.
观察上面各式中幂指数之间的关系,猜想:若m,n
是正整数,则(am)n = amn
.
根据乘方的意义及同底数幂乘法的性质,对于正整数m,n, 有:
n个am
(am)n =( am ×am×··· × am )
n个m
= am +m+m+··· +m
=a mn.
(am)n =amn(m,n是正整数).
幂的乘方,底数不变,指数相乘.
1.计算a2)3的结果是 C (
A.3a2
B.a5
) 检测反馈
C.a6
D.a3
解析:根据幂的乘方的法则,(a2)3=a2×3=a6. 故选C.
2.下列计算:
①(x5)2=x7;②(x5)2=x25;③x5·x2=x7;④x5·x2=x10;
⑤x5+x2=2x5.其中错误的有B ( )
A.5个 B.4个
七年级数学·下 新课标[冀教]
第八章 整式的乘法
8.2 幂的乘方与积的乘方 (第1课时)
问题思考
学习新知
(1)有甲乙两个球,如果甲球的半径是乙球半径
的n倍,那么甲球的体积是乙球体积的多少倍?
(2)学生计算.
(102)3=
(102)3=106.
,怎样计算?
活动1 探究幂的乘法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) a ·a7- a4 ·a4 = 0 ; (2)(1/10)5 ×(1/10)3 = (1/10)8 ; (3)(-2 x2 y3)2 = 4x4y6 ; (4)(-2 x2 )3 = -8x6 ;
想一想:
1.下面的计算对吗? 错的请改正:
(1) (43)5=48 ×, 415(2) (-28)3=(-2)24 ×, 224
幂的乘方与积的乘方
1
知识回顾
1、同底数的幂相乘 法则:同底数的幂相乘,底数不变,指数相加。
数学符号表示: am•anamn
(其中m、n为正整数)
练习:判断下列各式是否正确。
a3•a32a3,b4b4b8,m2m22m2 (x)3•(x)2•(x)(x)6x6
2、幂的乘方 法则:幂的乘方,底数不变,指数相乘。
即 am·an=am+n (m、n都是正整数)
b.幂的乘方法则:
幂的乘方,底数不变,指数相乘.
即 (am)n=amn (m、n都是正整数)
c.积的乘方法则 积的乘方,等于把积的每一个因式分别乘方,再把所得 的幂相乘.
即(ab)n= anbn (n为正整数)
(3) [(-3)5]3=-315 √ (并将它们填入括号内:
(p2)3.(p5)2
=p6.p10 ( 幂的乘方法则
)
=p6+10 ( 同底数幂的乘法法则 )
=p16
例、木星是太阳系九大行星中最大的一 颗,木星可以近似地看作球体.已知木星 的半径大约是7×104km,木星的体积大约 是多少km3(∏取3.14)?
2.注意幂的性质的混淆和错误
(a5)2=a7, a5·a2=a10. am+n=am+an
3、注意幂的运算法则逆用
am·an=am+n (a≠0,m、n为正整数), (am)n=amn, (ab)n=anbn
(1)用于实数计算
计算: 1、(-4)2007×0.252008 2、22006-22005-22004-…-2-1
能力挑战:
若 x m 3 x 2 x 7 则 m 的 值 为 _ _ _ 2 _ _
已知2x 2y 25, 则正整数 x , y 的值有(D )
(A)1对 (B)2对 (C)3对 (D)4对
已知2x 8,2y 16, 则 2xy _1_2_8__
能力挑战:
1.比较大小:
(-2) ×(-2)2× (-2)3×…× (-2)9× (-2)10 < 0.
(ab)n anbn,(其中 n为正整),数 (ab)cn anbncn(其中 n为正整) 数
练习:计算下列各式。
(2 x) y 4,(z 1a 2 b )3,( 2 x2y )3,( a 3 b 2)3 2
基础演练
➢下面的计算对不对?如果不对,怎样改正?
(1)b5 ·b5= 2b5 (×) (2)b5 + b5 = b10 (×)
分析:球体体积公式 v 4 R3 解: v 4 ( 7 10 4 ) 3 3
3 4 7 3 10 12
3 4 3 .14 343 10 12
3 1436 10 12 1 .44 10 15
答:木星的体积大约是1.44×1015km3.
能力挑战 你能用简便的方法计算下列各题:
2.已知,数a=2×103 , b=3×104 , c=5×105.
那么a·b·c的值中,整数部分有 14 位.
3.若10n×10m×10=1000,则n+m= 2
.
动手合作:
在数学活动中,小明为了
求 12212 213 21n 的值,
设计如图(1)所示的几何图形。
(1)请你利用这个几何图形求
的值为
。
1 1 1 1
2 22 23
2n
1
1 22
2
1 23
图(1)
(2)请你利用图(2),再设计一个能求
1 1 1 1的值的几何图形。
2 22 23
2n
(2)
(3)请仿照上述方法计算下列式子:
23322 323 32n
知识要点
a.同底数幂的乘法法则: 同底数的幂相乘,底数不变,指数相加.
(2)求整数的位数
求N=212×58是几位整数.
(3)确定幂的末尾数字 求7100-1的末尾数字. (4)比较实数的大小 比较750与4825的大小.
(5)求代数式的值 1、已知10m=4,10n=5. 求103m+2n+1的值.
2、已知162×43×26=22a+1, (102)b=1012,求a+b的值。
数学符号表示: (am)n amn
(其中m、n为正整数)
[(am)n]p amn(p其中m、n、P为正整数)
练习:判断下列各式是否正确。
(a4)4a44a8, [b(2)3]4b234b24 (x2)2n1x4n2, (a4)m(am)4(a2m)2
3、积的乘方
法则:积的乘方,先把积中各因式分别乘方,再把 所得的幂相乘。(即等于积中各因式乘方的积。) 符号表示:
b5 ·b5= b10
b5 + b5 = 2b5
(3)x5 ·x5 = x25 (×) (4)y5 ·y5 = 2y10 (×)
x5 ·x5 = x10 (5)c ·c3 = c3 (×)
c ·c3 = c4
y5 ·y5 =y10 (6)m + m3 = m4 (×)
m + m3 = m + m3
基础演练
(1) 24 54
(2) 2.5948
(3) (24)5 2115
(4) 若Xa=2, yb=3, 求(x3a+2b)2的值.
1.注意符号问题
例1 判断下列等式是否成立:
① (-x)2=-x2,
② (-x)3=-x3, √ ③ (x-y)2=(y-x)2,√
④ (x-y)3=(y-x)3,
⑤ x-a-b=x-(a+b),√ ⑥ x+a-b=x-(b-a).√
想一想:
1.下面的计算对吗? 错的请改正:
(1) (43)5=48 ×, 415(2) (-28)3=(-2)24 ×, 224
幂的乘方与积的乘方
1
知识回顾
1、同底数的幂相乘 法则:同底数的幂相乘,底数不变,指数相加。
数学符号表示: am•anamn
(其中m、n为正整数)
练习:判断下列各式是否正确。
a3•a32a3,b4b4b8,m2m22m2 (x)3•(x)2•(x)(x)6x6
2、幂的乘方 法则:幂的乘方,底数不变,指数相乘。
即 am·an=am+n (m、n都是正整数)
b.幂的乘方法则:
幂的乘方,底数不变,指数相乘.
即 (am)n=amn (m、n都是正整数)
c.积的乘方法则 积的乘方,等于把积的每一个因式分别乘方,再把所得 的幂相乘.
即(ab)n= anbn (n为正整数)
(3) [(-3)5]3=-315 √ (并将它们填入括号内:
(p2)3.(p5)2
=p6.p10 ( 幂的乘方法则
)
=p6+10 ( 同底数幂的乘法法则 )
=p16
例、木星是太阳系九大行星中最大的一 颗,木星可以近似地看作球体.已知木星 的半径大约是7×104km,木星的体积大约 是多少km3(∏取3.14)?
2.注意幂的性质的混淆和错误
(a5)2=a7, a5·a2=a10. am+n=am+an
3、注意幂的运算法则逆用
am·an=am+n (a≠0,m、n为正整数), (am)n=amn, (ab)n=anbn
(1)用于实数计算
计算: 1、(-4)2007×0.252008 2、22006-22005-22004-…-2-1
能力挑战:
若 x m 3 x 2 x 7 则 m 的 值 为 _ _ _ 2 _ _
已知2x 2y 25, 则正整数 x , y 的值有(D )
(A)1对 (B)2对 (C)3对 (D)4对
已知2x 8,2y 16, 则 2xy _1_2_8__
能力挑战:
1.比较大小:
(-2) ×(-2)2× (-2)3×…× (-2)9× (-2)10 < 0.
(ab)n anbn,(其中 n为正整),数 (ab)cn anbncn(其中 n为正整) 数
练习:计算下列各式。
(2 x) y 4,(z 1a 2 b )3,( 2 x2y )3,( a 3 b 2)3 2
基础演练
➢下面的计算对不对?如果不对,怎样改正?
(1)b5 ·b5= 2b5 (×) (2)b5 + b5 = b10 (×)
分析:球体体积公式 v 4 R3 解: v 4 ( 7 10 4 ) 3 3
3 4 7 3 10 12
3 4 3 .14 343 10 12
3 1436 10 12 1 .44 10 15
答:木星的体积大约是1.44×1015km3.
能力挑战 你能用简便的方法计算下列各题:
2.已知,数a=2×103 , b=3×104 , c=5×105.
那么a·b·c的值中,整数部分有 14 位.
3.若10n×10m×10=1000,则n+m= 2
.
动手合作:
在数学活动中,小明为了
求 12212 213 21n 的值,
设计如图(1)所示的几何图形。
(1)请你利用这个几何图形求
的值为
。
1 1 1 1
2 22 23
2n
1
1 22
2
1 23
图(1)
(2)请你利用图(2),再设计一个能求
1 1 1 1的值的几何图形。
2 22 23
2n
(2)
(3)请仿照上述方法计算下列式子:
23322 323 32n
知识要点
a.同底数幂的乘法法则: 同底数的幂相乘,底数不变,指数相加.
(2)求整数的位数
求N=212×58是几位整数.
(3)确定幂的末尾数字 求7100-1的末尾数字. (4)比较实数的大小 比较750与4825的大小.
(5)求代数式的值 1、已知10m=4,10n=5. 求103m+2n+1的值.
2、已知162×43×26=22a+1, (102)b=1012,求a+b的值。
数学符号表示: (am)n amn
(其中m、n为正整数)
[(am)n]p amn(p其中m、n、P为正整数)
练习:判断下列各式是否正确。
(a4)4a44a8, [b(2)3]4b234b24 (x2)2n1x4n2, (a4)m(am)4(a2m)2
3、积的乘方
法则:积的乘方,先把积中各因式分别乘方,再把 所得的幂相乘。(即等于积中各因式乘方的积。) 符号表示:
b5 ·b5= b10
b5 + b5 = 2b5
(3)x5 ·x5 = x25 (×) (4)y5 ·y5 = 2y10 (×)
x5 ·x5 = x10 (5)c ·c3 = c3 (×)
c ·c3 = c4
y5 ·y5 =y10 (6)m + m3 = m4 (×)
m + m3 = m + m3
基础演练
(1) 24 54
(2) 2.5948
(3) (24)5 2115
(4) 若Xa=2, yb=3, 求(x3a+2b)2的值.
1.注意符号问题
例1 判断下列等式是否成立:
① (-x)2=-x2,
② (-x)3=-x3, √ ③ (x-y)2=(y-x)2,√
④ (x-y)3=(y-x)3,
⑤ x-a-b=x-(a+b),√ ⑥ x+a-b=x-(b-a).√
