用迭代法球a的平方根
牛顿迭代法求平方根

⽜顿迭代法求平⽅根迭代是数值分析中通过从⼀个初始估计出发寻找⼀系列近似解来解决问题(⼀般是解⽅程或者⽅程组)的过程,为实现这⼀过程所使⽤的⽅法统称为迭代法(Iterative Method)。
⼀般可以做如下定义:对于给定的线性⽅程组x=Bx+f(这⾥的x、B、f同为矩阵,任意线性⽅程组都可以变换成此形式),⽤公式x(k+1)=Bx(k)+f(括号中为上标,代表迭代k次得到的x,初始时k=0)逐步带⼊求近似解的⽅法称为迭代法(或称⼀阶定常迭代法)。
如果k 趋向⽆穷⼤时limt(k)存在,记为x*,称此迭代法收敛。
显然x*就是此⽅程组的解,否则称为迭代法发散。
跟迭代法相对应的是直接法(或者称为⼀次解法),即⼀次性的快速解决问题,例如通过开⽅解决⽅程x +3= 4。
⼀般如果可能,直接解法总是优先考虑的。
但当遇到复杂问题时,特别是在未知量很多,⽅程为⾮线性时,我们⽆法找到直接解法(例如五次以及更⾼次的代数⽅程没有解析解,参见阿贝⽿定理),这时候或许可以通过迭代法寻求⽅程(组)的近似解。
最常见的迭代法是⽜顿法。
其他还包括最速下降法、共轭迭代法、变尺度迭代法、最⼩⼆乘法、线性规划、⾮线性规划、单纯型法、惩罚函数法、斜率投影法、遗传算法、模拟退⽕等等。
利⽤迭代算法解决问题,需要做好以下三个⽅⾯的⼯作:确定迭代变量 在可以⽤迭代算法解决的问题中,⾄少存在⼀个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
建⽴迭代关系式 所谓迭代关系式,指如何从变量的前⼀个值推出其下⼀个值的公式(或关系)。
迭代关系式的建⽴是解决迭代问题的关键,通常可以顺推或倒推的⽅法来完成。
对迭代过程进⾏控制 在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。
不能让迭代过程⽆休⽌地重复执⾏下去。
迭代过程的控制通常可分为两种情况:⼀种是所需的迭代次数是个确定的值,可以计算出来;另⼀种是所需的迭代次数⽆法确定。
对于前⼀种情况,可以构建⼀个固定次数的循环来实现对迭代过程的控制;对于后⼀种情况,需要进⼀步分析出⽤来结束迭代过程的条件。
解平方根的常见方法与技巧

解平方根的常见方法与技巧在数学中,平方根是一种常见的运算,求解平方根的方法与技巧是非常重要的数学基础知识。
本文将介绍一些常见的方法与技巧,以帮助读者更好地理解和运用平方根的概念。
1. 直接开平方直接开平方是最常见的方法之一,简单直接。
对于一个正实数a,其平方根记作√a,即a的平方根等于b。
举个例子,√25=5,因为5的平方等于25。
2. 分解质因数法当我们需要求解非完全平方数的平方根时,可以运用分解质因数的方法。
首先,将原数分解成质因数的乘积形式,并对每个质因数的指数进行除2操作。
最后将所得的结果相乘,并开方,即可得到原数的平方根。
例如,对于数100,先将其分解成2^2乘以5^2,然后进行除2操作,结果为2乘以5,即10,最后开方得到√100=10。
3. 二分查找法二分查找法是一种高效的找根方法,特别适用于近似解的求解过程。
该方法基于数值的中间值,通过不断缩小范围来逼近平方根的值。
具体步骤如下:- 确定平方根的上下限,例如对于求解根号2,可以将上限a设置为2,下限b设置为1。
- 求取平方根的中间值c,即(a+b)/2。
- 判断中间值的平方是否接近原数,若平方值大于目标数,将上限a 设置为c,若平方值小于目标数,将下限b设置为c。
- 重复以上步骤,不断缩小范围直至所求的平方根满足要求。
4. 迭代法迭代法是一种逐步逼近平方根的方法,通过不断迭代优化来达到精确解。
该方法使用下面的迭代公式:(x + a / x) / 2,其中x为初始近似解,a为原数。
通过不断迭代,不断更新x的值,最终得到原数的平方根。
迭代法适用于对较大的正实数进行近似求根。
5. 牛顿迭代法牛顿迭代法是一种数值分析中常用的方法,也适合用来解决平方根的问题。
其基本思想是通过切线逼近曲线来求解函数的根。
对于求解根号a,可以选取初始近似解x,然后通过不断迭代优化来逼近平方根。
具体迭代公式如下:x = (x + a / x) /2。
不断迭代,直到满足精度要求。
平方根的计算方法

平方根的计算方法导言:平方根(square root)是数学中常见的运算,用于求一个数的平方根。
计算平方根可以帮助我们解决很多实际问题,例如在几何学、物理学和工程学中的应用。
本文将介绍几种计算平方根的方法,并探讨它们的优缺点。
一、牛顿法(Newton's Method)牛顿法是一种迭代法,通过不断逼近平方根的值来得到更加精确的结果。
该方法基于牛顿-拉夫逊法则,其迭代公式如下:x_(x+1) = x_x - (x_x^2 - x)/(2x_x)其中,x为需要求平方根的数,x为迭代次数,x_x为迭代过程中的近似值。
通过迭代计算,x_x将逐渐逼近平方根。
牛顿法的优点是收敛速度快、迭代次数较少,适用于求解大部分整数和实数的平方根。
但是,牛顿法需要选择一个合适的初始值,否则可能导致结果偏离真实值。
二、二分法(Bisection Method)二分法是一种基于区间划分的方法,通过不断将区间缩小,逐渐逼近平方根的值。
该方法的思路是,如果一个数的平方大于待求平方根的数,那么这个数的平方根必然在该数左侧;反之,如果一个数的平方小于待求平方根的数,那么这个数的平方根必然在该数右侧。
通过不断将区间一分为二,可以逐步缩小范围。
二分法的优点是简单易实现,并且收敛性较好。
然而,与牛顿法相比,二分法的收敛速度较慢,需要更多的迭代次数。
三、连分数(Continued Fraction)法连分数法是一种将平方根表示为连分数的方法,通过截断连分数的展开式,可以近似计算平方根的值。
以求解正整数的平方根为例,设平方根为一个无限连分数:√x = x_0 + 1/(x_1 + 1/(x_2 + 1/(x_3 + 1/(x_4 + ...))))其中,x_x为连分数的系数。
通过不断截断、逼近连分数的展开,可以得到近似的平方根。
连分数法的优点是可以提供较为准确的结果,并且在计算机实现时能够保持高精度。
然而,连分数法的计算步骤繁琐,对于非整数的平方根计算较为复杂。
用迭代法求a的平方根的原理

用迭代法求a的平方根的原理
迭代法是一种通过反复逐步逼近的方法,用于求解一个方程的近似解。
对于求平方根的问题,迭代法的原理可以描述如下:
1. 假设我们要求一个数a 的平方根,我们可以猜测一个初始的近似解x0。
2. 我们利用这个近似解x0 来更新我们的猜测,并得到一个更好的近似解x1。
这个更新的过程可以使用如下的迭代公式来进行:
x_{k+1} = (x_k + a / x_k) / 2
其中,x_{k+1} 表示新的近似解,x_k 表示上一次的近似解。
3. 我们不断地重复上述的更新过程,直到我们得到一个满足我们要求的精度或近似解为止。
可以通过设定一个迭代次数或者定义一个收敛准则来判断何时停止迭代。
4. 当满足停止条件后,我们得到的近似解x_k 可以作为a 的平方根的近似值。
迭代法的原理在不断逼近的过程中,通过近似解的不断更新,逐渐靠近真实解。
这样的方法常用于求解无法直接求解的方程或函数,包括求解平方根、方程根、最优解等,并且具有广泛的应用。
如何利用心算技巧快速计算平方根

如何利用心算技巧快速计算平方根心算技巧是一种利用脑力进行计算的方法,可以帮助我们在没有计算器的情况下快速求解数学问题。
计算平方根是数学中常见的运算,下面将介绍一些利用心算技巧来快速计算平方根的方法。
1. 近似法:近似法是一种简单但有效的心算技巧,可以帮助我们快速计算平方根。
首先,我们需要找到和待求平方根最接近的两个完全平方数。
以待求平方根为例,假设它介于两个完全平方数之间,分别为a和b,其中a<b。
接下来,我们可以使用下面的公式进行近似计算:平方根≈ (待求平方根- a) / (b - a)通过这个公式,我们可以快速得到一个近似值。
2. 数学公式法:利用数学公式是另一种快速计算平方根的方法。
其中,牛顿法是一种常用的数学公式,可以大大简化计算过程。
牛顿法的公式如下:平方根≈ (平方根 + 待求平方根/平方根) / 2通过反复迭代计算,我们可以逐渐逼近平方根的准确值。
3. 分解法:分解法是一种直观且易于理解的心算技巧。
首先,我们将待求平方根进行分解,例如将√x 分解为√(a * b),其中 a 和 b 为两个因数。
然后,我们找到 a 和 b 之中那个较接近 x 的数,将其作为待求平方根的近似值。
通过反复调整 a 和 b 的取值,我们可以逐渐逼近平方根的准确值。
4. 迭代法:迭代法是一种基于逐步逼近的心算技巧。
我们首先猜测一个平方根的近似值,并将其作为起始点。
然后,我们通过迭代计算来逐步逼近准确值,直到所得值的误差足够小。
通过以上几种方法,我们可以利用心算技巧来快速计算平方根。
不同的方法适用于不同的场景,我们可以根据具体的题目选择合适的方法。
需要注意的是,心算技巧虽然可以提高计算速度,但并不保证完全准确,因此在进行计算时要注意防止精度误差的积累。
总结起来,利用心算技巧快速计算平方根的方法有近似法、数学公式法、分解法和迭代法等。
根据具体情况选择合适的方法,可以帮助我们在没有计算器的情况下快速求解数学问题。
迭代法求平方根公式

迭代法求平方根公式
平方根是在数学中经常使用的基本概念,而求平方根的方法也有很多种。
其中一种较为常用的方法是迭代法。
迭代法求平方根的公式如下:
设一个数a的平方根为x,则可以得到以下迭代公式:
x1 = (x0 + a/x0)/2
x2 = (x1 + a/x1)/2
……
xn+1 = (xn + a/xn)/2
通过迭代,取得的值逐渐逼近平方根的实际值。
当取得的值与实际值相差足够小时,即可停止迭代,得到近似值。
这种方法的优点在于简单易实现,同时可以通过迭代次数来控制精度。
当然,迭代法求平方根也存在一些缺点,比如可能会出现无限循环或者收敛速度较慢等问题。
因此,在具体使用时需要结合实际情况进行判断和调整。
使用牛顿迭代法求解平方根

使用牛顿迭代法求解平方根引言:平方根是数学中常见的概念,它表示一个数的平方根。
求解平方根在科学计算和工程领域中经常用到。
牛顿迭代法是一种常见的数值计算方法,它可以用来求解方程的近似解。
本文将介绍如何使用牛顿迭代法来求解平方根。
一、平方根的定义:平方根是指一个数的平方等于该数的非负实数解。
例如,数学中常见的平方根有2的平方根为√2,3的平方根为√3等。
二、牛顿迭代法的原理:牛顿迭代法是一种通过不断逼近来求解方程近似解的方法。
它的基本思想是:假设我们要求解方程f(x)=0的根,首先选取一个初始近似解x0,然后通过迭代公式x_(n+1)=x_n-f(x_n)/f'(x_n)来不断逼近真实解。
其中f'(x)表示函数f(x)的导数。
三、使用牛顿迭代法求解平方根的步骤:1. 确定要求解平方根的数为a,设定初始近似解x0为a/2。
2. 根据迭代公式x_(n+1)=(x_n+a/x_n)/2来计算下一个近似解x_(n+1)。
3. 判断迭代结果是否满足精度要求,如果满足则停止迭代,输出结果;如果不满足,则继续迭代。
四、使用牛顿迭代法求解平方根的例子:我们以求解2的平方根为例来演示使用牛顿迭代法的过程。
1. 确定要求解平方根的数为2,设定初始近似解x0为2/2=1。
2. 根据迭代公式x_(n+1)=(x_n+2/x_n)/2来计算下一个近似解x1: x1=(1+(2/1))/2=1.53. 判断迭代结果是否满足精度要求,如果满足则停止迭代,输出结果;如果不满足,则继续迭代。
继续迭代,计算x2:x2=(1.5+(2/1.5))/2=1.4167继续迭代,计算x3:x3=(1.4167+(2/1.4167))/2=1.41424. 判断迭代结果是否满足精度要求,如果满足则停止迭代,输出结果;如果不满足,则继续迭代。
继续迭代,计算x4:x4=(1.4142+(2/1.4142))/2=1.4142迭代结果满足精度要求,停止迭代,输出结果x=1.4142。
平方根与立方根的运算

平方根与立方根的运算平方根与立方根是数学中常见的运算概念,用于求一个数的平方根或立方根。
在实际应用中,平方根与立方根的运算常常用于数值计算、统计分析和科学研究等领域。
本文将对平方根与立方根的运算方法进行详细介绍和分析。
一、平方根的运算1. 定义平方根是指一个数的平方等于这个数本身的非负实数解。
通常用符号√a表示,其中a为被开方数。
例如,√9 = 3,因为3 × 3 = 9。
2. 平方根的计算方法平方根的计算可以使用手算方法或计算器等工具进行。
以下是手算平方根的一种常见方法——牛顿迭代法:(1) 选择一个近似值x0,通常可以选择被开方数a的正平方根的整数部分作为近似值,即x0 = int(√a)。
(2) 计算下一个近似值xn+1 = (xn + a / xn) / 2,直到满足精度要求。
(3) 当xn+1和xn的差值小到满足精度要求时,xn+1即为被开方数a 的平方根。
3. 示例(1) 选择近似值x0 = int(√8) = 2;(2) 计算下一个近似值 x1 = (x0 + 8 / x0) / 2 = (2 + 8 / 2) / 2 = 2.5;(3) 当 x1 和 x0 的差值满足精度要求时,结束计算,√8 ≈ 2.5。
二、立方根的运算1. 定义立方根是指一个数的立方等于这个数本身的实数解。
通常用符号³√a 表示,其中a为被开方数。
例如,³√8 = 2,因为2 × 2 × 2 = 8。
2. 立方根的计算方法立方根的计算方法与平方根类似,可以使用手算方法或计算器等工具进行。
以下是手算立方根的一种常见方法——二分逼近法:(1) 选择两个数x1和x2,使得x1³ < a < x2³,并计算它们的平均值mid = (x1 + x2) / 2。
(2) 判断mid³与a的大小关系,若mid³ > a,则将x2替换为mid;若mid³ < a,则将x1替换为mid。
平方根的运算定律

平方根的运算定律平方根(square root)是数学中常见的一个运算,用于求一个数的平方根。
平方根的运算定律包括主要的两个方面:平方根的性质和平方根的计算方法。
本文将对平方根的运算定律进行详细的论述。
一、平方根的性质1. 非负数的平方根是唯一的:对于任意一个非负数a,它的平方根是唯一确定的。
即如果b和c都是a的平方根,则b=c。
这个性质可以通过数学证明得到。
2. 负数的平方根是虚数:对于任意一个负数a,它的平方根是虚数。
虚数是指实部为0的复数,通常用i来表示。
例如,-1的平方根为i。
3. 零的平方根是零:零的平方根是零本身。
即0的平方根为0。
二、平方根的计算方法1. 开方法:开方法是一种常见的计算平方根的方法。
它的基本思想是通过逼近来求得一个数的平方根。
例如求解√a,可以选择一个近似值x0,然后通过迭代的方式不断逼近真实的平方根。
2. 牛顿迭代法:牛顿迭代法也是一种常用的计算平方根的方法。
它的基本思想是通过不断逼近零点来求得方程的解。
对于求解√a,可以将其转化为求解f(x) = x^2 - a = 0的解。
然后使用牛顿迭代法进行迭代计算,直到满足精度要求为止。
3. 二分法:二分法也是计算平方根的一种常见方法。
它的基本思想是通过不断折半查找来逼近平方根。
对于一个非负数a,假设它的平方根在区间[0, a]之间,那么可以将该区间一分为二,然后判断平方根是否在左边的子区间还是右边的子区间。
通过不断迭代这个过程,最终可以得到平方根的近似值。
总结:平方根的运算定律包括平方根的性质和计算方法两个方面。
平方根的性质包括非负数的平方根是唯一的、负数的平方根是虚数以及零的平方根是零。
计算平方根可以通过开方法、牛顿迭代法和二分法等方法来实现。
这些方法都是基于数学原理和数值计算的基础上得出的,可以在实际问题中应用。
通过了解平方根的运算定律,我们可以更好地理解和应用平方根的概念,提高数学运算的效率和准确性。
在实际问题中,平方根的运算定律也具有重要的应用价值,例如在物理学、工程学和金融学等领域中经常需要用到平方根的运算。
平方根计算方法

平方根计算方法平方根是数学中常用的一个概念,求一个数的平方根可以帮助我们理解数的大小关系以及解决一些实际问题。
在计算平方根的过程中,我们常常用到各种不同的方法和公式。
本文将介绍几种常用的平方根计算方法。
一、牛顿迭代法牛顿迭代法是一种求函数零点的数值逼近方法,也可以用来计算平方根。
以下是使用牛顿迭代法计算平方根的步骤:1. 我们要求解的平方根是x,我们先随意猜测一个近似值y。
2. 计算出y的平方,如果y的平方接近于x,那么y就是x的平方根。
3. 如果y的平方与x相差较大,我们可以利用牛顿迭代法进行改进。
a. 我们可以通过求函数f(y)=y^2-x的导数f'(y)来得到曲线的切线斜率。
b. 曲线上的一点(x, f(x))和曲线的切线交点(x', f(x'))可以近似地代表函数f(y)的零点。
c. 利用切线和x轴的交点求出新的近似值,再通过重复步骤3,直到y的平方接近于x。
牛顿迭代法是一种快速高效的平方根计算方法,但在实际应用中可能会出现收敛性问题。
因此,当使用牛顿迭代法时,我们需要注意收敛性的检验。
二、二分法二分法是一种基于区间逼近的方法,也可以用来计算平方根。
以下是使用二分法计算平方根的步骤:1. 我们要求解的平方根是x,我们先确定一个范围[a, b],其中a为x的下界,b为x的上界。
2. 计算出区间的中点c,即c=(a+b)/2。
3. 如果c的平方接近于x,那么c就是x的平方根。
4. 如果c的平方大于x,说明平方根落在区间[a, c]内,那么我们将b更新为c。
5. 如果c的平方小于x,说明平方根落在区间[c, b]内,那么我们将a更新为c。
6. 重复步骤2到5,直到区间的长度足够小或满足精度要求。
三、连分数法连分数法是一种用连分数表示平方根的方法,每一项都是一个有理数。
以下是使用连分数法计算平方根的步骤:1. 将待求的平方根表示为一个连分数形式:√x = a0 + 1/(a1 + 1/(a2 + 1/(a3 + ...)))。
平方根与立方根的计算

平方根与立方根的计算在数学中,平方根和立方根是非常常见的运算。
平方根是指一个数的平方等于该数时所求得的值,用符号√表示;而立方根是指一个数的立方等于该数时所求得的值,用符号^3√表示。
本文将详细介绍平方根和立方根的计算方法及其应用。
一、平方根的计算计算一个数的平方根是求解一个方程的过程。
设某数的平方根为x,那么根据平方根的定义可得 x^2 = a,其中a为待求的数。
要计算a的平方根,可以使用牛顿迭代法或二分法等数值方法进行逼近求解,或者使用计算器或电脑软件进行计算。
以牛顿迭代法为例,假设要计算一个数a的平方根,首先先猜测一个初始解x0,然后利用迭代公式进行迭代计算,直到收敛为止。
迭代公式如下:x(n+1) = (x(n) + a/x(n)) / 2其中,n表示迭代次数,x(n)表示第n次迭代得到的近似解。
二、立方根的计算计算一个数的立方根与计算平方根类似,同样是求解一个方程。
设某数的立方根为x,那么根据立方根的定义可得 x^3 = a,其中a为待求的数。
立方根的计算方法也可以使用牛顿迭代法或二分法等数值方法进行逼近求解,或者使用计算器或电脑软件进行计算。
以牛顿迭代法为例,假设要计算一个数a的立方根,先猜测一个初始解x0,然后利用迭代公式进行迭代计算,直到收敛为止。
迭代公式如下:x(n+1) = (2*x(n) + a / (x(n)^2)) / 3其中,n表示迭代次数,x(n)表示第n次迭代得到的近似解。
三、平方根与立方根的应用平方根和立方根在生活中有着广泛的应用。
比如,在几何学中,平方根用于计算图形的边长、面积和体积;在物理学中,平方根用于计算速度、加速度等;在工程学中,平方根用于计算电路中的电流、电压和功率等。
而立方根则在物理学和工程学中更为常见。
比如,在物理学中,立方根用于计算物体的体积、密度和各种物理量的单位转换;在工程学中,立方根用于计算水流、气流和声音等的流量和能量。
总之,平方根和立方根的计算是数学中的常见问题。
根号基本算法公式

根号基本算法公式根号是数学中常见的运算符号,表示对一个数的平方根的运算。
在数学中,求根号的基本算法公式有以下几种:1.牛顿迭代法:牛顿迭代法是一种数值计算方法,用来寻找方程的根。
对于求平方根而言,可以使用牛顿迭代法来逼近平方根的值。
其基本思想是通过迭代来不断逼近平方根的实际值。
牛顿迭代法的算法公式如下:$x_{n+1} = \\frac{1}{2} \\left( x_n + \\frac{a}{x_n} \\right)$其中,x n+1表示迭代后的值,x n表示当前迭代的值,a表示要求平方根的数。
通过不断迭代计算,可以得到数a的平方根的逼近值。
2.二分查找法:二分查找法是一种用于在有序数组中查找特定元素的算法。
在求平方根时,我们可以利用二分查找法来逼近平方根的值。
其算法流程如下:–首先确定一个范围,左边界为0,右边界为a;–在这个范围内不断进行二分查找,直到找到一个数b,使得b2与a的差足够小;–最终b就是a的平方根的近似值。
3.牛顿拉夫逊迭代法:牛顿拉夫逊迭代法是求解非线性方程组的一种常用方法,也可以用来求平方根。
其迭代公式如下:$x_{n+1} = \\frac{1}{2} \\left( x_n + \\frac{a}{x_n} \\right)$与牛顿迭代法相似,不同之处在于牛顿拉夫逊迭代法是对一阶导数根据牛顿法进行迭代计算,通常可以更快地收敛到平方根的实际值。
以上是几种求根号的基本算法公式,通过这些算法,我们可以快速有效地求解各种数的平方根。
在实际应用中,可以根据计算需求和精度要求选择合适的算法来求解平方根。
初中数学平方根的计算公式怎么算更简洁

初中数学平方根的计算公式怎么算更简洁平方根是数学中的一个重要概念,经常在初中数学学习中出现。
在计算平方根时,可以使用不同的方法和公式。
下面我将向你介绍几种简洁计算平方根的方法。
1. 通用方法:用长除法的思想来计算平方根。
以√a为例,首先将a 分为一组两位数,最高位单独一组;然后从左向右依次进行计算。
对于每一组,找出一个数x,使得xx<=该组的数,但(x+1)(x+1)>该组的数。
将x带入计算,并将余数带入下一组的计算,依此类推。
最后将所有组的计算结果合并,即为所求的平方根。
这种方法的优点是适用于任意数字的平方根计算,但缺点是需要进行一系列的繁琐计算,所以不适用于大数的平方根计算。
2.牛顿迭代法:这是一种迭代逼近的方法。
对于求解√a,首先猜测一个近似值x,然后计算f(x)=x²-a,然后根据切线的斜率计算出新的近似值x'。
重复这个过程直到两次近似值的差值小于预设的精度要求。
最终得到的近似值即为所求的平方根。
这种方法的优点是不需要进行复杂的计算,收敛速度较快,但缺点是需要预设一个精度要求。
3.二分法:这是一种迭代逼近的方法。
对于求解√a,找出一个左边界和右边界,使得左边界的平方小于a,右边界的平方大于a。
然后每次取中点的平方,判断与a的大小关系,更新边界。
重复这个过程直到两个边界的差值小于预设的精度要求。
最终得到的近似值即为所求的平方根。
这种方法的优点是简单易懂,但需要进行多次计算,收敛速度较慢。
4.公式法:对于一些特殊的数,可以使用一些平方根公式来计算。
例如,对于完全平方数,其平方根即为其本身;对于形如√(a²+b²)的数,可以使用勾股定理来计算。
这些公式可以简化计算过程,但只适用于特定的数。
综上所述,计算平方根并没有一种万能的方法,不同的方法适用于不同的场景。
在实际应用中,可以根据需要选择合适的方法来计算平方根,以达到更简洁的计算效果。
手算平方根

开平方根方法一:迭代法⑴先假设a的平方根为x,⑵计算(a/x+x)/2⑶把得到的数当成x⑷同样计算(a/x+x)/2.比如计算√3,我假设是1.5 ,代入上面公式,(3/1.5+1.5)/2=1.75,我再计算一遍(3/1.75+1.75)/2=1.732, 我继续计算(3/1.732+1.732)/2=1.732, 两个一样了,那保留三位小数就是1.732,你按计算器得到的是1.732050807568.方法二:竖式法1.从个位起向左每隔两位为一节,若带有小数从小数点起向右每隔两位一节,用“,”号将各节分开;2.求不大于左边第一节数的平方根,为平方根最高上的数;3.从左边第一节数里减去求得的最高位上的数的平方,在它们的差的右边写上第二节数作为第一个余数;4.把商的最高位上的数乘20去试除第一个余数,所得的是整数作试商(如果这个最大整数大于或等于10,就用9或8作试商);5.用最高位的数乘以20加上试商再乘以试商.如果所得的积小于或等于余数,这个试商就是平方根的第二位数;如果所得的积大于余数,就把试商逐次减小再试,直到积小于或等于余数为止;6.用同样的方法,继续求平方根的其他各位上的数.例题1:3的平方根怎么算1.7^2<3<1.8^2设√3=1.7+x3=(1.7+x)^2=1.7^2+3.4x+x^2x^2太小,近似计算时可以忽略不计1.7^2+3.4x≈3x≈(3-1.7^2)/3.4=3/3.4-1.7/2≈0.03235 √3≈1.7+x≈1.732例题2:17的平方根怎么算4^2<17<4.2^2设√17=4+x17=(4+x)^2=4^2+8x+x^2x^2太小,近似计算时可以忽略不计4^2+8x≈17x≈(17-4^2)/8=0.125√17≈4+x≈4.125√17≈4.125。
牛顿迭代法快速寻找平方根
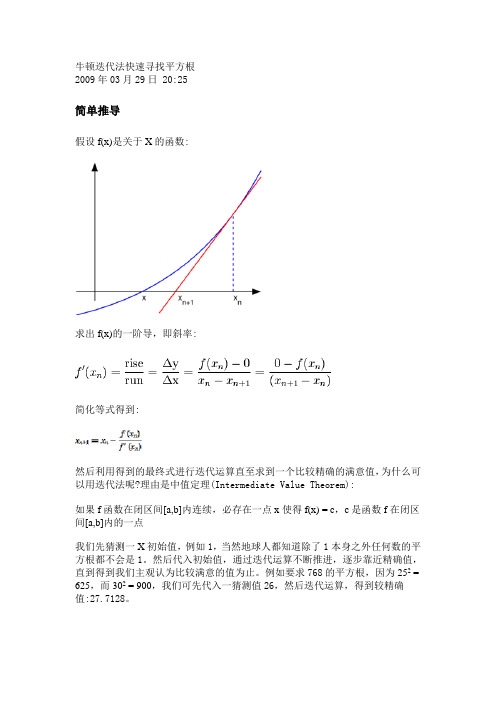
牛顿迭代法快速寻找平方根2009年03月29日 20:25简单推导假设f(x)是关于X的函数:求出f(x)的一阶导,即斜率:简化等式得到:然后利用得到的最终式进行迭代运算直至求到一个比较精确的满意值,为什么可以用迭代法呢?理由是中值定理(Intermediate Value Theorem):如果f函数在闭区间[a,b]内连续,必存在一点x使得f(x) = c,c是函数f在闭区间[a,b]内的一点我们先猜测一X初始值,例如1,当然地球人都知道除了1本身之外任何数的平方根都不会是1。
然后代入初始值,通过迭代运算不断推进,逐步靠近精确值,直到得到我们主观认为比较满意的值为止。
例如要求768的平方根,因为252 = 625,而302 = 900,我们可先代入一猜测值26,然后迭代运算,得到较精确值:27.7128。
回到我们最开始的那个”莫名其妙”的公式,我们要求的是N的平方根,令x2 = n,假设一关于X的函数f(x)为:f(X) = X2 - n求f(X)的一阶导为:f'(X) = 2X代入前面求到的最终式中:X k+1 = X k - (X k2 - n)/2X k化简即得到我们最初提到的那个求平方根的神奇公式了:这种算法的原理很简单,我们仅仅是不断用(x,f(x))的切线来逼近方程x^2-a=0的根。
根号a实际上就是x^2-a=0的一个正实根,这个函数的导数是2x。
也就是说,函数上任一点(x,f(x))处的切线斜率是2x,如图,x(n+1)比x(n)更接近x。
那么,x-f(x)/(2x)就是一个比x更接近的近似值。
代入f(x)=x^2-a得到x-(x^2-a)/(2x),也就是(x+a/x)/2。
用泰勒公式推导我之前介绍过在The Art and Science of C一书中有用到泰勒公式求平方根的算法,其实牛顿迭代法也可以看作是泰勒公式(Taylor Series)的简化,先回顾下泰勒公式:仅保留等式右边前两项:令f(X0+ε) = 0,得到:再令X1 = X0+ ε0,得到ε1…依此类推可知:转化为:引申从推导来看,其实牛顿迭代法不仅可以用来求平方根,还可以求立方根,甚至更复杂的运算。
平方根的算法

平方根的算法平方根是数学中常见的运算之一,它的意义是求一个数的正平方根。
在日常生活中,我们经常需要计算平方根,比如计算房间的面积、计算某些物品的长度等等。
而计算平方根的方法也有很多种,下面介绍几种常见的算法。
1.牛顿迭代法牛顿迭代法是一种求函数零点的方法,它可以用来计算平方根。
该方法的基本思路是:从一个初始值开始,不断迭代,直到满足精度要求为止。
具体实现步骤如下:假设要求一个数x的平方根,先猜测一个初值y;计算y的平方与x之间的差值,记作d=y^2-x;如果d的绝对值小于某个精度要求,则停止迭代,返回y;否则,更新y的值为y-d/(2*y),然后回到第二步,继续迭代。
2.二分法二分法是一种比较简单的求平方根的方法,它的基本思路是:对于一个非负实数x,它的平方根y满足0<=y<=x。
因此可以将y的取值范围二分,然后逐步缩小,直到满足精度要求为止。
具体实现步骤如下:假设要求一个数x的平方根,先确定两个值low=0和high=x;计算mid=(low+high)/2,然后计算mid的平方与x之间的差值d=mid^2-x;如果d的绝对值小于某个精度要求,则停止迭代,返回mid;否则,如果d>0,则说明mid的平方大于x,因此将high更新为mid,然后回到第二步;否则,如果d<0,则说明mid的平方小于x,因此将low更新为mid,然后回到第二步。
3.近似公式除了上述两种算法之外,还有一些近似公式可以用来计算平方根。
其中比较常见的是以下两种公式:y=(x+a/x)/2,其中a是一个常数,通常取1;y=x/2+(a/x)/2,其中a是一个常数,通常取1。
以上是几种常见的求平方根的算法,不同的算法各有优缺点,选取合适的算法需要根据具体情况来决定。
同时,在进行计算时还需要注意精度问题,避免出现误差过大的情况。
单片机开根号的算法

单片机开根号的算法全文共四篇示例,供读者参考第一篇示例:单片机是一种小型的计算机集成电路,在很多嵌入式系统中被广泛应用。
在实际的应用中,我们经常会遇到需要进行开根号运算的情况。
虽然单片机的计算能力有限,但是我们可以通过一些算法来实现开根号运算,从而满足实际需求。
一般情况下,我们可以通过数学函数库提供的开根号函数来实现开根号运算,但是在一些特殊的应用场景中,我们需要自己设计开根号算法。
本文将介绍一种比较常见的单片机上的开根号算法——牛顿迭代法。
牛顿迭代法是一种通过迭代逼近某一函数的根的方法,它的基本思想是:从一个初始猜测值开始,通过不断迭代,逐渐逼近函数的根。
对于开根号运算来说,我们可以将其转化为求解方程f(x) = x^2 - a = 0的根问题,其中a是待开方的数。
牛顿迭代法的迭代公式为:x_(n+1) = x_n - f(x_n) / f'(x_n),其中x_n为第n次迭代的值,f'(x_n)为函数f在点x_n处的导数。
对于求解方程f(x) = x^2 - a = 0的根的问题,迭代公式可以简化为:x_(n+1) = (x_n + a / x_n) / 2。
下面我们以求解a的平方根为例,来演示牛顿迭代法在单片机上的实现。
```c#include <stdio.h>float sqrt_newton(float a) {float x0 = a;float x1 = (x0 + a / x0) / 2;while (fabs(x1 - x0) > 0.0001) {x0 = x1;x1 = (x0 + a / x0) / 2;}return x1;}在这段代码中,我们首先定义了一个函数sqrt_newton,用于实现牛顿迭代法。
在主函数中,我们以25.0作为待开方的数,调用sqrt_newton函数来计算其平方根,并输出计算结果。
需要注意的是,牛顿迭代法的收敛性取决于初始猜测值的选取,如果初始猜测值离真实值较远,可能会导致算法收敛速度较慢甚至无法收敛。
迭代法

迭代法迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法(或者称为一次解法),即一次性解决问题。
迭代法又分为精确迭代和近似迭代。
“二分法”和“牛顿迭代法”属于近似迭代法。
迭代算法是用计算机解决问题的一种基本方法。
它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
利用迭代算法解决问题,需要做好以下三个方面的工作:一、确定迭代变量。
在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
二、建立迭代关系式。
所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。
迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成。
三、对迭代过程进行控制。
在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。
不能让迭代过程无休止地重复执行下去。
迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。
对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件。
例 1 :一个饲养场引进一只刚出生的新品种兔子,这种兔子从出生的下一个月开始,每月新生一只兔子,新生的兔子也如此繁殖。
如果所有的兔子都不死去,问到第 12 个月时,该饲养场共有兔子多少只?分析:这是一个典型的递推问题。
我们不妨假设第 1 个月时兔子的只数为u 1 ,第 2 个月时兔子的只数为 u 2 ,第 3 个月时兔子的只数为 u 3 ,……根据题意,“这种兔子从出生的下一个月开始,每月新生一只兔子”,则有u 1 = 1 , u 2 = u 1 +u 1 × 1 = 2 , u 3 = u 2 +u 2 × 1 =4 ,……根据这个规律,可以归纳出下面的递推公式:u n = u n - 1 × 2 (n ≥ 2)对应 u n 和 u n - 1 ,定义两个迭代变量 y 和 x ,可将上面的递推公式转换成如下迭代关系:y=x*2x=y让计算机对这个迭代关系重复执行 11 次,就可以算出第 12 个月时的兔子数。
牛顿迭代公式求平方根

牛顿迭代公式求平方根好嘞,今天咱们聊聊牛顿迭代公式,顺便求个平方根。
听上去好像挺复杂的,其实呢,简单得很,就像学会骑自行车一样,起初觉得难,熟练之后就觉得小菜一碟。
大家都知道,平方根就是一个数的平方等于另一个数,那比如说,咱们想求个数字的平方根,得想办法让这个问题简单化,不然就像在迷宫里转圈圈,出不去。
牛顿大叔可真是个聪明人,他想出了个好办法,咱们今天就来聊聊他的绝招。
牛顿的办法其实就像是先估算一个答案,然后慢慢调整。
就像你去买衣服,第一次试的可能不合身,但你再换一件,试试不同的风格,最后总能找到适合自己的。
假设你想找的是一个数字x的平方根,咱们可以先随便找个数字y,可能它离x的平方根有点远,没关系,牛顿的公式会帮咱们慢慢接近。
牛顿大叔教我们,新的y等于老的y加上x除以老的y,再除以2。
这个看似复杂的公式,其实就是在说,别急,慢慢来,调整一下就好。
这个方法听起来是不是有点神奇?就像在拍照时,先对焦,再微调一下角度,完美的瞬间就来了。
让我们拿个具体的例子来试试,假如咱们要找16的平方根。
第一步,找个估算的值,可能选个4。
然后我们把这个4带入公式,哎呀,牛顿真是个聪明蛋,4加上16除以4,得到了8,再除以2,咱们的新的y变成了6。
虽然6离4还有点远,但没事,咱们再来一次。
再把6放进去,结果是5,继续调,最后几次下来,咱们就能接近4,嘿,平方根就是4。
再说说这牛顿迭代的乐趣,简直就像打游戏,一关一关地打,越打越顺,成就感满满。
每次调整的时候,你会觉得自己离目标越来越近,心中不禁默念:“我行,我能!”这就跟生活中的追求一样,不论是工作,还是学习,总是要一步一步来。
可能前几次会有点偏差,心里想着:“哎呀,我怎么这么笨?”其实根本不是,调整过后,慢慢就能找到那个答案,成功的感觉简直不要太棒。
说到这里,牛顿迭代法的美妙之处不仅在于它的数学精髓,更在于它教会我们的道理。
生活中,很多事情不也是这样吗?找工作、谈恋爱、甚至买房,都是在不断尝试中调整方向,最终找到合适自己的那一个。
676的平方根计算过程

676的平方根计算过程在数学中,计算一个数的平方根是一个常见的问题。
今天我们来计算一下676的平方根。
首先,我们可以使用数学公式来计算一个数的平方根。
对于任意正数a,它的平方根可以通过不断逼近的方法来计算。
这种方法被称为开平方的迭代法。
具体来说,我们可以使用牛顿迭代法来计算平方根。
这个方法的基本思想是通过不断逼近来找到一个数的平方根。
对于一个数x,它的平方根可以通过以下公式来计算:\[x_{n+1} = \frac{1}{2}(x_n + \frac{a}{x_n})\]其中,\(x_n\)是第n次迭代的结果,\(x_{n+1}\)是下一次迭代的结果,a是要计算平方根的数。
现在,让我们来计算676的平方根。
首先,我们可以随便猜测一个初始值,比如10。
然后,我们可以使用上面的公式来进行迭代计算。
初始值,\(x_0 = 10\)。
第一次迭代,\(x_1 = \frac{1}{2}(10 + \frac{676}{10}) =\frac{1}{2}(10 + 67.6) = \frac{1}{2}(77.6) = 38.8\)。
第二次迭代,\(x_2 = \frac{1}{2}(38.8 + \frac{676}{38.8}) = \frac{1}{2}(38.8 + 17.4) = \frac{1}{2}(56.2) = 28.1\)。
继续迭代下去,直到结果收敛。
在实际计算中,可以根据精度要求进行迭代次数的控制。
通过这种方法,我们可以计算出676的平方根约为26.。
这就是使用迭代法计算676的平方根的过程。
总之,计算一个数的平方根是一个有趣的数学问题,而迭代法是一种常用的方法。
希望通过这篇文章,你能更好地理解计算平方根的过程。
