专题训练(七) 圆中常见辅助线归类
圆中常作哪些辅助线

圆中常作哪些辅助线?通过作辅助线能使复杂问题简单化,圆问题中常用的辅助线是哪些呢?现把一些规律总结如下:弦与弦心距,密切紧相连直径对直角,圆心作半径已知有两圆,常画连心线遇到相交圆,连接公共弦遇到相切圆,作条公切线“有点连圆心,无点作垂线.”切线证明法,规律记心间一、作弦心距.在解决有关弦的问题时,常常作弦心距,以利用垂经定理或圆心角、弦、弦心距之间的关系定理及推论.因此“弦与弦心距,密切紧相连例1.如图,AB是O O的直径,P0丄AB交O O于P点, 弦PN与AB相交于点M,求B 证:PM?PN=2PO 2分析:要证明PM?PN=2PO12,即证明PM ?—PN =PO 2 ,2过O点作OC丄PN于C,根据垂经定理-PN =PC,只需证明2爭、。
…企M0PM ?PC=PO 2,由PO_PM亠,“三点定型”法可判断需证。
_。
丈Z企OCPC PO明Rt △^OC s Rt△^MO.证明:过圆心O作OC丄PN于C,.・.PC= — PN2 •••PO 丄AB, OC 丄PN ,•••/"OP= /OCP=90 0又V/0PC= /MPO APOCsRt△PMO.PO PM 2•——=——,即•P02= PM ?PC.PC PO1•••PO 2= PM ?—PN ,.・.PM?PN=2PO 22二、连结半径与切线相互垂直”都与圆的半径有关 .连结半径是常用的方法之一例2 .已知:△KBC 中,/ B=90 0, O 是AB 上一点,以 0为圆心,以 0B 为半径的圆 切AC 与D 点,交AB 与E 点,AD=2 , AE=1.求证:CD 的长.分析:D 为切点,连结 DO ,/ODA=90 0.根据切线长定理A CD=CB.DO=EO= 半径r ,在Rt △ADO 中根据勾股定理或 Rt △ADO- Rt △KBC ,求出 CD.证明:连结DO••QD 丄 AC 于 D, •••JOCP=90 0 ••AB 过 O 点,/B=90 0.•••BC 为O O 的切线,•••CD=CB 设 CD=CB=x,DO=EO=y 在 Rt △KDO 中,AO 2 =AD 2+ DO 2, AD=2 , AE=1 3 .•(1+y) 2=2 2+y 2, • y= 一2在 Rt △KBC 中,AC 2=AB 2+ BC 2,即(2+x) 2=(1 +•••CD=3. 三、连结公共弦第2页共9页 二_圆的半径是圆的重要元素,圆中的许多性质如:“同圆的半径相等”和“过切点的半径3+3)2+x 2,.・.X=32 2在处理有关两圆相交的问题时,公共弦像一把A“钥匙”,常常可以打开相应的“锁”,因此“遇到相交圆,连接公共弦例3 .已知:如图,O O i和O 02相交于点A和B,0201的延长线交O 0i于点C, CA、CB的延长线分别和O 02相交于点D、E,求证:AD=BE.分析:O 01和O 02是相交的两圆,作公共弦AB为辅助线.证明:连结AB交0201于P点,•••01 02丄A B且01 02的平分AB•••CA=CB•••ZAC P= /BC P•••点02到线段AD、CE的距离相等•••AD=BE.四、作连心线两圆相交,连心线垂直平分两圆的公共弦;两圆相切,连心线必过切点.通过作两圆的连心线,可沟通圆心距、公共弦、两圆半径之间的关系.因此,“已知有两圆,常画连心线.”例4 .已知:如图,O A和O B外切于P点, O A的半径为r和O B的半径为3r, CD为O A、••AC 丄CD , BD 丄CD第3页共9页•••/BAC= 90 0•••AB 丄 A C .O B 的外公切线,C 、D 为切点,求:(1 ) CD与弧PD 及弧PC 所围成的阴影部分的面积解:连结AB 、AC 、BD• O A 和O B 外切于P 点,••• AB 过P 点 •••CD 为O A 、O B 的外公切线,C 、D 为切点,过A 点作AE 丄BD 于E ,则四边形 ACDE 为矩形.的长;(2)•••/BAC= 90 0•••AB 丄 A C .题中,所作的内公切线 MN 起到沟通两圆的作用.因此,相切两圆过切点的公切线是常用辅 助线.例5 .已知:O O i 和O O 2外切于点A , BC 是O 求证:AB 丄A C证明:过切点A 作公切线MN 交BC 于P 点,•••BC 是O 01和O 02外公切线,.•.PB = PA=PC•••/PBA= /PAB ,/P AC= /PCA •//PBA+ /P AB+ /P AC+ /P CA= 180 0•••DE=AC= r , BE=BD-DE=3r-r=2r 在 Rt △AEB 中,AB=AP+PB=r+3r=4r ,BE=2r••AE= J AB 2 - BE 2 = J16r 2 -4r 2 =273r .•••CD=2 J 3 r .•••COSB=匹卫」,•/B=60 0.AB 4r 2•••2CAB= /CAE+ /BAE=90 0+3O 0=120 0•S 阴影=S 梯形ABDC -S 扇形BPD -S 扇形ACP_ 3 1— =4 V 3 r 2 -------- n r 2 ------- 冗r 2 = (4 J 3 —2 311—n) r 2.6五、作公切线分析:相切两圆过切点有一条公切线,这条公切线在解题时起着非常重要的作用,如本01和O 02外公切线,B 、C 为切点 N六、切线判定分两种:公共点未知作垂线、公共点已知作半径切线的判定定理是:“经过半径的外端,并且垂直于这条半径的直线是圆的切线.”就是说, 要判定一条直线是否是切线,应同时满足这样的两条: (1 )直线经过半径的外端,(2)直线垂直于这条半径,所以,在证明直线是切线时,往往需要通过作恰当的辅助线,才能顺利地解决问题•下面是添辅助线的小规律1 .无点作垂线需证明的切线,条件中未告之与圆有交点,则联想切线的定义,过圆心作该直线的垂线, 证明垂足到圆心的距离等于半径D例6 .已知:如图,AB是半圆的直径,AD丄AB于A , BC丄AB于B,若/DOC= 90 0.求证:DC是半圆的切线.A分析:DC与O O没有交点,“无点作垂线”,过圆心O作OE丄DC,只需证0E等于圆的半径•因为AO为半径,若能证OE=OA即可•而0E、0A 在MEO、8AO 中,如何证明ADEO空DAO呢?证明:作OE丄DC于E点,取DC的中点F,连结OF.又•••/DOC= 90 0••• FO=FD••AD 丄AB , BC 丄AB,••• /2= /3.•••OF为梯形的中位线.•••OF /AD .•••DO是/ADE的角平分线.••OA 丄DA , OE 丄DC ,•••OA=OE=圆的半径.• DC是半圆的切线.2 .有点连圆心.当直线和圆的公共点已知时,联想切线的判定定理,只要将该点与圆心连结,再证明该半径与直线垂直例7 . AB为O O的直径,BC为O O的切线,切点为B, OC平行于弦AD,求证:CD是O O的切线.分析:D在O O上,“有点连圆心”,连结DO,证明DO丄DC即可.证明:连结DO , V OC //AD •••/DAO= /COB , /DAO= /DOC •••JDOC= /COB,又OC=OC , DO=BO •••△DOC ^^BOC •••/ODC= /OBC ,•••BC为O O的切线,切点为B •••/OBC=90 0[课后冲浪]•••/ODC=90 0,又 D 在O O 上,•••CD是O O的切线.一、证明解答题且AB=CD.求证:P0平分/BPD .0相切.19 •如图,学校 A 附近有一公路 MN ,—拖拉机从 P 点出发向PN 方向行驶,已知/ NPA=30 °,AP=160米,假使拖拉机行使时,A 周围100米以内受到噪音影响,问:当拖拉机向PN 方向行驶时,学校是否会受到噪音影响?请说明理由.如果拖拉机速度为 18千米/小时,则受噪音影响的时间是多少秒?20 .如图,A 是半径为1的圆0外的一点,0A=2 切线,B 是切点,弦BC//0A ,连结AC ,求阴影部分的面积.16 .已知:P 是O O 外一点,PB , 17 .如图,A ABC 中,/C=90 圆0分别与AC 、BC 相切于 M 、N ,如果 A0=15 cm, BO=10 cm,求圆 O18 .已知:CABCD 的对角线 AC 、BD 交于0点,BC 切O 0于E 点.求证:AD 也和OPPD 分别交O 0于A 、B 和C 、_■CD 是弦,AE 丄CD ,垂足为 E,BF 丄CD ,垂足为02为圆心,0i 02为半径作一个圆交O 01于C ,AF.求证:DE=CF.D .直线0i 02分别交O 0i 于延长线和O 结AC , BC .⑴求证:AC=BC ;⑵设O 0i 连AD , BD ,求证:四边形ADBC 是菱形;0i , O 02于点A 与点B .连的面积. 23 .已知:如图, AB 是O 0的直径,BC 是O 0的切线,连 AC 交O 0 21 .如图,已知 AB 是O O 的直径,22 .如图,02是O O i 上的一点,以于D ,过D 作O O 的切线EF ,交BC 于E 点.求证:OE //AC.二、探索题BC 是O O 的切线,切点为B , OC 平行于弦 AD .求察P 点在DE 的什么位置?并说明理由B24 .已知:图a, AB 是O O 的直径, 证:(1) DC 是O O 的切线,(2 )过D 点作DE 丄AB ,图b 所示,交AC 于P 点,请考。
圆中常用的作辅助线的八种方法

证明:1 如图;过点D作⊙O的直径DE;连接AE;EC;AC ∵DE是⊙O的直径; ∴∠ECD=∠EAD=90° 又∵CD⊥AB;∴EC∥AB ∴∠BAC=∠ACE ∴B︵C=A︵E ∴BC=AE 在Rt△AED中;AD2+AE2=DE2; ∴AD2+BC2=4R2
2若弦AD;BC的长是方程x26x+5=0的两个根 AD>BC;求⊙O的半径及点O到AD的距离
1求证:PB是⊙O的切线; 证明:1 如图;连接OB;∵OA=OB;
∴∠OAB=∠OBA ∵PA=PB; ∴∠PAB=∠PBA ∴∠OAB+∠PAB=∠OBA+∠PBA
即∠PAO=∠PBO 又∵PA是⊙O的切线;∴∠PAO=90° ∴∠PBO=90° ∴OB⊥PB 又∵OB是⊙O的半径; ∴PB是⊙O的切线
︵ 2求由弦CD;BD与BC所围成的阴影部分的面积
结果保留π
解:2∵OE⊥DB;∴EB=
D1 B=3 2
c3m
在Rt△EOB中;∵∠OBD=30°;
∴OE=
1 2
OB
∵EB=3 3 cm;
∴由勾股定理可求得OB=6 cm
又∵∠CDB=∠DBO;DE=BE;
∠CED=∠OEB;
∴△CDE≌△OBE
方法 8 巧添辅助线计算阴影部分的面积
9 中考·自贡如图所示;点B;C;D都在⊙O上; 过点C作AC∥BD交OB的延长线于点A;连接CD; 且∠CDB=∠OBD=30°;DB=6 3cm
1求证:AC是⊙O的切线;
证明:1如图;连接CO;交DB于点E; ∴∠O=2∠CDB=60° 又∵∠OBE=30°; ∴∠BEO=180°60°30°=90° ∵AC∥BD;∴∠ACO=∠BEO=90° 即OC⊥AC 又∵点C在⊙O上; ∴AC是⊙O的切线
(完整版)初中几何辅助线——圆常用辅助线

初中几何辅助线——圆常用辅助线题型 1.圆中解决有关弦的问题时,常常需要作出圆心到弦的垂线段(即弦心距)这一辅助线,一是利用垂径定理得到平分弦的条件,二是构造直角三角形,利用勾股定理解题.例1如图,在以O 为圆心的两个同心圆中,大圆的弦AB 交小圆于C 、D 二点.求证:AC = BD证明:过O 作OE ⊥AB 于E∵O 为圆心,OE ⊥AB∴AE = BE CE = DE ∴AC = BD练习:如图,AB 为⊙O 的弦,P 是AB 上的一点,AB = 10cm ,P A = 4cm .求⊙O 的半径.题型2.有等弧或证弧等时常连等弧所对的弦或作等弧所对的圆心角.例2如图,已知AB 是⊙O 的直径,M 、N 分别是AO 、BO 的中点,CM ⊥AB ,DN ⊥AB ,求证:证明:(一)连结OC 、OD∵M 、N 分别是AO 、BO 的中点∴OM =12AO 、ON = 12BO ∵OA = OB∴OM = ON∵CM ⊥OA 、DN ⊥OB 、OC = OD ∴Rt △COM ≌Rt △DON ∴∠COA = ∠DOB ∴(二)连结AC 、OC 、OD 、BD∵M 、N 分别是AO 、BO 的中点 ∴AC = OC BD = OD ∵OC = OD ∴AC = BD∴题型3.有弦中点时常连弦心距例3如图,已知M 、N 分别是⊙O 的弦AB 、CD 的中点,AB = CD ,求证:∠AMN = ∠CNM证明:连结OM 、ON∵O 为圆心,M 、N 分别是弦AB 、CD 的中点 ∴OM ⊥AB ON ⊥CD ∵AB = CD ∴OM = ON∴∠OMN = ∠ONM∵∠AMN = 90o -∠OMN ∠CNM = 90o-∠ONM ∴∠AMN =∠CNM题型4.证明弦相等或已知弦相等时常作弦心距.例4如图,已知⊙O 1与⊙O 2为等圆,P 为O 1、O 2的中点,过P 的直线分别交⊙O 1、⊙O 2于A 、C 、D 、B .求证:AC = BD证明:过O 1作O 1M ⊥AB 于M ,过O 2作O 2N ⊥AB 于N ,则O 1M ∥O 2N∴1122O M O PO N O P= ∵O 1P = O 2P ∴O 1M = O 2N ∴AC = BD题型5.有弧中点(或证明是弧中点)时,常有以下几种引辅助线的方法:⑴连结过弧中点的半径 ⑵连结等弧所对的弦 ⑶连结等弧所对的圆心角例5如图,已知D 、E 分别为半径OA 、OB 的中点,C 为弧AB 的 中点,求证:CD = CE证明:连结OC∵C 为弧AB 的中点∴»»AB BC = ∴∠AOC =∠BOC∵D 、E 分别为OA 、OB 的中点,且AO = BO∴OD = OE = 12AO = 12BO又∵OC = OC∴△ODC ≌△OEC ∴CD = CE结论1.圆内角的度数等于它所对的弧与它对顶角所对的弧的度数之和的一半. 结论2.圆外角的度数等于它所截两条弧的度数之差的一半.结论3.有直径时常作直径所对的圆周角,再利用直径所对的圆周角为直角证题.例6如图,AB为⊙O的直径,AC为弦,P为AC延长线上一点,且AC = PC,PB的延长线交⊙O于D,求证:AC = DC 证明:连结AD∵AB为⊙O的直径∴∠ADP = 90o∵AC = PC∴AC = CD =12 AP练习:如图,在Rt△ABC中,∠BCA = 90o ,以BC为直径的⊙O交AB于E,D为AC中点,连结BD交⊙O于F.求证:BC CF BE EF=题型6.有垂直弦时也常作直径所对的圆周角.题型7.有等弧时常作辅助线有以下几种:⑴作等弧所对的弦⑵作等弧所对的圆心角⑶作等弧所对的圆周角练习:1.如图,⊙O的直径AB垂直于弦CD,交点为E,F为DC延长线上一点,连结AF交⊙O于M.求证:∠AMD =∠FMC(提示:连结BM)2.如图,△ABC内接于⊙O,D、E在BC边上,且BD = CE,∠1 =∠2,求证:AB = AC(提示如图)题型8.有弦中点时,常构造三角形中位线例7已知,如图,在⊙O中,AB⊥CD,OE⊥BC于E,求证:OE =12 AD证明:作直径CF,连结DF、BF ∵CF为⊙O的直径∴CD⊥FD又∵CD⊥AB∴AB∥DF∴»»AD BF=∴AD = BF∵OE⊥BC O为圆心CO = FO ∴CE = BE∴OE =12 BF∴OE =12ADP2题图A1题图BA题型9.圆上有四点时,常构造圆内接四边形.例8如图,△ABC 内接于⊙O ,直线AD 平分∠F AC ,交⊙O 于E ,交BC 的延长线于D ,求证:AB ·AC= AD ·AE证明:连结BE ∵∠1 =∠3 ∠2 =∠1 ∴∠3 =∠2∵四边形ACBE 为圆内接四边形 ∴∠ACD =∠E ∴△ABE ∽△ADC∴AE AB AC AD∴AB ·AC = AD ·AE题型10.两圆相交时,常连结两圆的公共弦例9如图,⊙O 1与⊙O 2相交于A 、B ,过A 的直线分别交⊙O 1、⊙O 2于C 、D ,过B 的直线分别交⊙O 1、⊙O 2于E 、F .求证:CE ∥DF证明:连结AB∵四边形为圆内接四边形∴∠ABF =∠C同理可证:∠ABE =∠D∵∠ABF +∠ABE = 180o ∴∠C +∠D = 180o ∴CE ∥DF题型11.在证明直线和圆相切时,常有以下两种引辅助线方法:⑴当已知直线经过圆上的一点,那么连结这点和圆心,得到辅助半径,再证明所作半径与这条直线垂直即可.⑵如果不知直线与圆是否有交点时,那么过圆心作直线的垂线段,再证明垂线段的长度等于半径的长即可.例10如图,P 为⊙O 外一点,以OP 为直径作圆交⊙O 于A 、B 两点,连结P A 、PB .求证:P A 、PB 为⊙O 的切线 证明:连结OA ∵PO 为直径∴∠P AO = 90o ∴OA ⊥P A∵OA 为⊙O 的半径 ∴P A 为⊙O 的切线同理:PB 也为⊙O 的切线例11如图,同心圆O ,大圆的弦AB = CD ,且AB 是小圆的切线,切点为E ,求证:CD 是小圆的切线证明:连结OE ,过O 作OF ⊥CD 于F ∵OE 为半径,AB 为小圆的切线∴OE ⊥AB ∵OF ⊥CD , AB = CD∴OF = OE ∴CD 为小圆的切线P练习:如图,等腰△ABC ,以腰AB 为直径作⊙O 交底边BC 于P ,PE ⊥AC 于E , 求证:PE 是⊙O 的切线题型12.当已知条件中有切线时,常作过切点的半径,利用切线的性质定理证题.例12如图,在Rt △ABC 中,∠C = 90o ,AC = 12,BC = 9,D 是AB 上一点,以BD 为直径的⊙O 切AC 于E ,求AD 长.解:连结OE ,则OE ⊥AC∵BC ⊥AC ∴OE ∥BC∴OE AOBC AB=在Rt △ABC 中,AB= 15==∴15915OE AB OB OEAB --==∴OE = OB = 458∴BD = 2OB = 454∴AD = AB -DB = 15-454= 154答:AD 的长为154.练习:如图,⊙O 的半径OA ⊥OB ,点P 在OB 的延长线上,连结AP 交⊙O 于D ,过D 作⊙O 的切线CE 交OP 于C ,求证:PC = CDCC AE。
2017年中考数学专题汇编:圆中常用的作辅助线的八种方法

专训2圆中常用的作辅助线的八种方法名师点金:在解决有关圆的计算或证明题时,往往需要添加辅助线,根据题目特点选择恰当的辅助线至关重要.圆中常用的辅助线作法有:作半径,巧用同圆的半径相等;连接圆上两点,巧用同弧所对的圆周角相等;作直径,巧用直径所对的圆周角是直角;证切线时“连半径,证垂直”以及“作垂直,证半径”等.作半径,巧用同圆的半径相等1.如图,两正方形彼此相邻,且大正方形ABCD的顶点A,D在半圆O上,顶点B,C在半圆O的直径上;小正方形BEFG的顶点F在半圆O上,E点在半圆O的直径上,点G在大正方形的边AB上.若小正方形的边长为 4 cm,求该半圆的半径.(第1题)[来源学科网Z,X,X,K]连接圆上两点,巧用同弧所对的圆周角相等2.如图,圆内接三角形ABC的外角∠ACM的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BM,垂足为H.求证:AP=BH.(第2题)作直径,巧用直径所对的圆周角是直角3.如图,⊙O的半径为R,弦AB,CD互相垂直,连接AD,BC.(1)求证:AD2+BC2=4R2;(2)若弦AD,BC的长是方程x2-6x+5=0的两个根(AD>BC),求⊙O的半径及点O到AD的距离.(第3题)证切线时辅助线作法的应用4.如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点 D.判断CD 与⊙O的位置关系,并说明理由.(第4题)遇弦加弦心距或半径5.如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为()A.3 B.4 C.3 2 D.4 2(第5题)(第6题)6.【中考·贵港】如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB =23,OH=1,则∠APB=________.遇直径巧加直径所对的圆周角7.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点.(1)求证:△ABC为等边三角形;(2)求DE的长.(第7题)遇切线巧作过切点的半径8.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.(1)求证:PB是⊙O的切线;(2)已知PA=3,∠ACB=60°,求⊙O的半径.(第8题)巧添辅助线计算阴影部分的面积9.【中考·自贡】如图,点B ,C ,D 都在⊙O 上,过点C 作AC ∥BD 交OB 的延长线于点A ,连接CD ,且∠CDB =∠OBD =30°,DB =6 3 cm.(1)求证:AC 是⊙O 的切线;(2)求由弦CD ,BD 与BC ︵所围成的阴影部分的面积(结果保留π).(第9题)[来源:学_科_网Z_X_X_K]答案1.解:如图,连接OA ,OF.设OA =OF =r cm ,AB =a cm.(第1题)在Rt △OAB 中,r 2=a 22+a 2,在Rt △OEF 中,r 2=42+4+a 22,∴a 24+a 2=16+16+4a +a 24. 解得a 1=8,a 2=-4(舍去).∴r 2=822+82=80.∴r 1=45,r 2=-45(舍去).即该半圆的半径为4 5 cm.点拨:在有关圆的计算题中,求角度或边长时,常连接半径构造等腰三角形或直角三角形,利用特殊三角形的性质来解决问题.2.证明:如图,连接AD ,BD.(第2题)∵∠DAC ,∠DBC 都是DC ︵所对的圆周角.∴∠DAC =∠DBC.∵CD 平分∠ACM ,DP ⊥AC ,DH ⊥CM ,∴DP =DH.在△ADP 和△BDH 中,∠DAP =∠DBH ,∠DPA =∠DHB =90°,DP =DH.∴△ADP ≌△BDH.∴AP =BH.点拨:本题通过作辅助线构造圆周角,然后利用“同弧所对的圆周角相等”得到∠DAC =∠DBC ,为证两三角形全等创造了条件.3.(1)证明:如图,过点D 作⊙O 的直径DE ,连接AE ,EC ,AC.(第3题)∵DE 是⊙O 的直径,∴∠ECD =∠EAD =90°. 又∵CD ⊥AB ,∴EC ∥AB. ∴∠BAC =∠ACE. ∴BC ︵=AE ︵.∴BC =AE.在Rt △AED 中,AD 2+AE 2=DE 2,∴AD 2+BC 2=4R 2.(2)解:如图,过点O 作OF ⊥AD 于点 F.∵弦AD ,BC 的长是方程x 2-6x +5=0的两个根(AD>BC),[来源:]∴AD =5,BC =1.由(1)知,AD 2+BC 2=4R 2,∴52+12=4R 2.∴R =262. ∵∠EAD =90°,OF ⊥AD ,∴OF ∥EA.又∵O 为DE 的中点,∴OF =12AE =12BC =12,即点O 到AD 的距离为12.点拨:本题作出直径DE ,利用“直径所对的圆周角是直角”构造了两个直角三角形,给解题带来了方便.4.解:CD 与⊙O 相切,理由如下:如图,作⊙O 的直径CE ,连接AE.(第4题)∵CE是⊙O的直径,∴∠EAC=90°.∴∠E+∠ACE=90°.∵CA=CB,∴∠B=∠CAB.∵AB∥CD,∴∠ACD=∠CAB.∴∠B=∠ACD.又∵∠B=∠E,∴∠ACD=∠E.∴∠ACE+∠ACD=90°,即OC⊥DC.又∵OC为⊙O的半径,∴CD与⊙O相切.5.C 6.60°(第7题) 7.(1)证明:如图,连接AD,∵AB是⊙O的直径,∴∠ADB=90°.∵点D是BC的中点,∴AD是线段BC的垂直平分线.∴AB=AC.又∵AB=BC,∴AB=BC=AC.∴△ABC为等边三角形.(2)解:如图,连接BE.∵AB是⊙O的直径,∴∠AEB=90°.∴BE⊥AC.[来源学科网]∵△ABC是等边三角形,∴AE=EC,即E为AC的中点.又∵D是BC的中点,故DE为△ABC的中位线.∴DE=12AB=12×2=1.8.(1)证明:如图,连接OB,∵OA=OB,(第8题)∴∠OAB=∠OBA.∵PA=PB,∴∠PAB=∠PBA.∴∠OAB+∠PAB=∠OBA+∠PBA,即∠PAO=∠PBO.又∵PA是⊙O的切线,∴∠PAO=90°.∴∠PBO=90°.∴OB⊥PB.又∵OB是⊙O的半径,∴PB是⊙O的切线.(2)解:如图,连接OP,∵PA=PB,∴点P在线段AB的垂直平分线上.∵OA=OB,∴点O在线段AB的垂直平分线上.∴OP为线段AB的垂直平分线.又∵BC⊥AB,∴PO∥BC.∴∠AOP=∠ACB=60°.由(1)知∠PAO=90°.∴∠APO=30°.∴PO=2AO.∵在Rt△APO中,AO2+PA2=PO2,∴AO2+3=(2AO)2.又∵AO>0,∴AO=1.∴⊙O的半径为 1.(第9题)9.(1)证明:如图,连接CO,交DB于点E,∴∠O=2∠CDB=60°. 又∵∠OBE=30°,∴∠BEO=180°-60°-30°=90°.∵AC∥BD,∴∠ACO=∠BEO=90°,即OC⊥AC.又∵点C在⊙O上,∴AC是⊙O的切线.(2)解:∵OE⊥DB,∴EB=12DB=3 3 cm.在Rt△EOB中,∵∠OBE=30°,∴OE=12 OB.∵EB=3 3 cm,∴由勾股定理可求得OB=6 cm.∵∠CDB=∠DBO,DE=BE,∠CED=∠OEB,∴△CDE≌△OBE.∴S△CDE=S△OBE.∴S阴影=S扇形COB=60360π·62=6π(cm2).[来源:Z&xx&]。
专题课堂3--圆的常用辅助线

• (2)当△ABC为正三角形时,点E是否AC的中点?为什么?
解:(1)AB=AC, 连接AD,
∵AB是⊙O的直径, ∴∠ADB=90°, 即AD⊥BC, ∵BD=DC, ∴AB=AC
类型二 遇直径添加直径所对的圆周角是直角
• 【例3】如图,点A,B,D,E在⊙O上,弦AE,BD的延长 线相交于点C.若AB是⊙O的直径,D是BC的中点. • (1)试判断AB,AC之间的大小关系,并给出证明; • (2)当△ABC为正三角形时,点E是否AC的中点?为什么?
北师版
梦 境
专题课堂3 圆中常见的辅助线归类
类型一 遇弦加弦心距或半径
【例1】已知:如图,OA=OB,AB交⊙O于C,D两点, 求证:AC=BD.
证明:过点O作OE⊥AB, ∵OA=OB, ∴AE=BE, 又∵OC=OD, ∴CE=DE,
E ∴AC=BD
[例 2] 如图,在 Rt△ABC 中,∠ACB=90°,AC=3,BC=4, 以点 C 为圆心,CA 为半径的圆与 AB 交于点 D,则 AD 的长为 __________.
对应练习
E
类型三 遇切线添加过切点的半径
例 4.如图,BD 是⊙O 的直径,BA 是⊙O 的弦,过点 A 的切线交 BD 延长线于点 C,OE⊥AB 于 E,且 AB=AC,若 CD=2 2,则 OE 的长为 ______2______.
类型三 遇切线添加过切点的半径
E
提升训练1:
已知:如图,⊙O是△ABC的外接圆,AB为⊙O
直径,BC=6,AC=8,OE⊥AE,垂足为E,交⊙O
于点P,连接BP交AC于D.
(1)求PE的长;
(完整版)圆中常见辅助线作法分类大全

1.碰到弦时(解决相关弦的问题时)经常增添弦心距,或许作垂直于弦的半径(或直径)或再连结过弦的端点的半径。
或许连结圆心和弦的两个端点,构成等腰三角形,还可连结圆周上一点和弦的两个端点。
作用: 1 、利用垂径定理;2、利用圆心角及其所对的弧、弦和弦心距之间的关系;3、利用弦的一半、弦心距和半径构成直角三角形,依据勾股定理求相关量。
4、可得等腰三角形;5、据圆周角的性质可得相等的圆周角。
例:如图,AB是⊙ O 的直径 ,PO⊥ AB 交⊙ O 于 P 点,弦 PN 与 AB 订交于点 M ,求证:PM ?PN=2PO 2.剖析:要证明PM?PN=2PO2,即证明 PM ?PC =PO 2,过 O 点作 OC⊥PN 于 C,依据垂经定理 NC=PC ,只需证明PM?PC=PO2,要证明 PM?PC=PO2只需证明 Rt△ POC∽Rt △ PMO.1证明 : 过圆心 O 作 OC⊥ PN 于 C,∴ PC=PN2∵PO⊥ AB, OC ⊥PN ,∴∠ MOP= ∠ OCP=90° .又∵∠ OPC=∠ MPO ,∴ Rt△POC∽ Rt△PMO.∴ PO PC即∴ PO2 = PM?PC.∴ PO2= PM ?1PN,∴ PM ?PN=2PO2.PM PO2【例 1】如图,已知△ ABC内接于⊙ O,∠ A=45°, BC=2,求⊙ O的面积。
AOB C【例 2】如图,⊙ O的直径为10,弦 AB=8, P 是弦 AB 上一个动点,那么 OP的长的取值范围是 _________ .【例 3】如图,弦AB的长等于⊙ O的半径,点 C 在弧 AMB上,则∠ C的度数是 ________.2. 碰到有直径时经常增添(画)直径所对的圆周角。
作用:利用圆周角的性质,获得直角或直角三角形。
例 如图,在△ ABC 中,∠ C=90°,以 BC 上一点 O 为圆心,以 OB 为半径的圆交 AB 于点 M ,交 BC 于点 N .( 1) 求证: BA · BM=BC · BN ;( 2) 假如 CM 是⊙ O 的切线, N 为 OC 的中点,当 AC=3 时,求 AB 的值.剖析:要证 BA · BM=BC · BN ,需证△ ACB ∽△ NMB ,而∠ C=90°,因此需要△ NMB 中有个直角,而BN 是圆 O 的直径,因此连结 MN 可得∠ BMN=90 °。
初中数学圆的辅助线八种作法

中考数学圆的辅助线在平面几何中,与圆有关的许多题目需要添加辅助线来解决。
百思不得其解的题目,添上合适的辅助线,问题就会迎刃而解,思路畅通,从而有效地培养学生的创造性思维。
添加辅助线的方法有很多,本文只通过分析探索归纳几种圆中常见的辅助线的作法。
下面以几道题目为例加以说明。
1.有弦,可作弦心距在解决与弦、弧有关的问题时,常常需要作出弦心距、半径等辅助线,以便应用于垂径定理和勾股定理解决问题。
例1 如图1, ⊙O 的弦AB 、CD 相交于点P , 且AC=BD 。
求证:PO 平分∠APD 。
分析1:由等弦AC=BD 可得出等弧 = 进一步得出 = ,从而可证等弦AB=CD ,由同圆中 等弦上的弦心距相等且分别垂直于它们所对应的弦,因此可作辅助线OE ⊥AB ,OF ⊥CD ,易证△OPE ≌△OPF ,得出PO 平分∠APD 。
证法1:作OE ⊥AB 于E ,OF ⊥CD 于FAC=BD => = => ==> AB=CD => OE=OF∠OEP=∠OFP=90° => △OPE ≌△OPF0OP=OP=>∠OPE=∠OPF => PO 平分∠APD 分析2:如图1-1,欲证PO 平分∠APD ,即证AB(BD , (CD (D 图 1AC(AC (BD (AB (CD(∠OPA=∠OPD ,可把∠OPA 与∠OPD 构造在两个 三角形中,证三角形全等,于是不妨作辅助线即半径OA ,OD ,因此易证△ACP ≌△DBP ,得AP=DP ,从而易证△OPA ≌△OPD 。
证法2:连结OA ,OD 。
∠CAP=∠BDP∠APC=∠DPB =>△ACP ≌△DBP AC=BD=>AP=DPOA=OD =>△OPA ≌△OPD =>∠OPA=∠OPD =>PO 平分∠APD OP=OP2.有直径,可作直径上的圆周角对于关系到直径的有关问题时,可作直径上的圆周角,以便利用直径所对的圆周角是直角这个性质。
九数培训---圆中常用辅助线
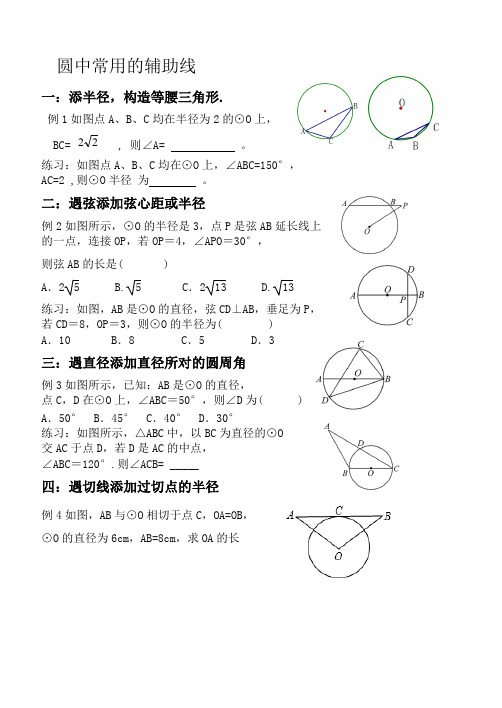
圆中常用的辅助线一:添半径,构造等腰三角形.例1如图点A、B、C均在半径为2的⊙O上,2 , 则∠A= 。
BC= 2练习:如图点A、B、C均在⊙O上,∠ABC=150°,AC=2 ,则⊙O半径为。
二:遇弦添加弦心距或半径例2如图所示,⊙O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长是( )A.2 5 B. 5 C.213 D.13练习:如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=3,则⊙O的半径为( )A.10 B.8 C.5 D.3三:遇直径添加直径所对的圆周角例3如图所示,已知:AB是⊙O的直径,点C,D在⊙O上,∠ABC=50°,则∠D为( ) A.50° B.45° C.40° D.30°练习:如图所示,△ABC中,以BC为直径的⊙O交AC于点D,若D是AC的中点,∠ABC=120°.则∠ACB= _____四:遇切线添加过切点的半径例4如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为6cm,AB=8cm,求OA的长练习:如图,PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,若∠APB=40°,则∠ACB= .五.添加辅助线计算阴影部分面积例5如图,扇形AOB的圆心角为90°,四边形OCDE是边长为1的正方形,点C、E、D分别在OA、OB、弧AB上,过A作AF⊥ED交ED的延长线于点F,那么图中阴影部分的面积为______ .练习:已知:PA、PB与⊙O相切于A点、B点,OA=1,PA= 3,则图中阴影部分的面积是______六:切线的判定方法(1)当明确指出直线与圆有公共点时, “连半径,证垂直”。
(2) 当没有明确直线与圆有公共点时, “作垂直,证相等”。
例6如图点A是⊙O外的一点,AO的延长线交⊙O于C,直线AB经过⊙O上一点B,且 AB=BC,∠C=30°求证:直线AB是⊙O的切线练习:如图:在同心圆中,大圆的半径是8,小圆的直径是8,弦AB=8 3求证:直线AB是小⊙O的切线圆的综合题(2016•福州)如图,正方形ABCD内接于⊙O,M为中点,连接BM,CM.(1)求证:BM=CM;(2)当⊙O的半径为2时,求的长(2016龙岩)如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.(1)求证:CD是⊙O的切线;(2)若AD=1,OA=2,求AC的值。
圆中常用辅助线的作法【八大题型】(解析版)-初中数学

圆中常用辅助线的作法【八大题型】【题型1遇弦连半径构造三角形】 1【题型2遇弦作弦心距解决有关弦长的问题】 5【题型3遇直径作直径所对的圆周角】 8【题型4遇切线作过切点的半径】 11【题型5遇90°的圆周角连直径】 16【题型6转移线段】 19【题型7构造相似三角形】 23【题型8四点共圆】 30【题型1遇弦连半径构造三角形】1.(2024·陕西渭南·三模)如图,△ABC内接于⊙O,AB为⊙O的直径,点D在⊙O上,连接CD、BD,BD =BC,延长DB到点E,使得BE=BD,连接CE.(1)求证:∠A+∠E=90°;(2)若⊙O的半径为256,BC=5,求CE的长.【答案】(1)见解析(2)6【分析】本题考查了圆综合,其中涉及到了等腰三角形的性质,三角形的中位线定理,勾股定理解三角形,圆周角定理及推论等知识点,熟练掌握这些知识点是解题的关键.(1)利于等边对等角的性质得到∠BCE=∠E,∠BCD=∠D,利用三角形的内角和得到∠BCE+∠E+∠BCD+∠D=180°,即可得到∠E+∠D=90°,再由圆周角的性质等量代换即可;(2)连接OC,由垂径定理推出OB⊥CD,CF=DF,利用勾股定理建立式子运算出BF的长,再利用中位线定理即可推出CE的长.【详解】(1)证明:∵BD=BC,BE=BD,∴BC=BE,∴∠BCE=∠E,∠BCD=∠D,∵∠BCE+∠E+∠BCD+∠D=180°,∴∠E +∠D =12×180°=90°,∵∠A =∠D ,∴∠A +∠E =90°;(2)解:连接OC ,则OC =OB =256,如图所示:∵BC =BD ,∴BC =BD ,∴OB ⊥CD ,CF =DF ,在Rt △OCF 中,CF 2=OC 2-OF 2=2562-256-BF 2,在Rt △BCF 中,CF 2=BC 2-BF 2=52-BF 2,∴256 2-256-BF 2=52-BF 2,解得BF =3,∵BD =BE ,DF =CF ,∴BF 为△DCE 的中位线,∴CE =2BF =6.2.(23-24九年级上·重庆大足·期末)如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为点P ,若CD =8,OP =3,则⊙O 的直径为()A.10B.8C.5D.3【答案】A 【分析】连接OC ,由垂径定理可得CP =PD =4,然后再根据勾股定理可得OC ,进而问题可求解.【详解】解:连接OC ,如图所示:∵CD ⊥AB ,CD =8,∴CP =PD =4,∵OP =3,∴在Rt △CPO 中,OC =CP 2+OP 2=5,∴⊙O 的直径为10;故选A .【点睛】本题主要考查垂径定理,熟练掌握垂径定理是解题的关键.3.(2024·贵州黔东南·二模)如图,⊙O 是△ABC 的外接圆,且AC =BC ,过点B 作BE ⊥AC ,垂足为点E ,延长BE 交⊙O 于点D ,连接AD ,CD ,CO ,并延长CO 交BD 于点F .(1)写出图中一个与∠ACD相等的角∶;(2)求证∶CD=CF;(3)若BC=10,BE=6,求⊙O的半径.【答案】(1)∠ACD=∠ABD(答案不唯一)(2)见解析(3)⊙O的半径为5103【分析】本题考查圆周角定理,垂径定理及其推论,相似三角形的判定与性质;(1)根据圆周角可得∠ACD=∠ABD;(2)延长CF交AB于M,根据垂径定理的推论可得∠ACF=∠BCF,CM⊥AB,即可由BE⊥AC得到∠ACF=∠ABD,进而得到∠ACD=∠ABD=∠ACF=∠BCF,由三线合一即可得到CD=CF;(3)连OA,由勾股定理求得CE=8,进而依次得到AE=2,AB=210,AM=1AB=10,再求出CM,最2后在Rt△AOM中利用勾股定理求半径即可.【详解】(1)由圆周角可得:∠ACD=∠ABD,故答案为:∠ABD(答案不唯一);(2)延长CF交AB于M,∵AC=BC,延长CO交BD于点FAB∴∠ACF=∠BCF,CM⊥AB,AM=12∵BE⊥AC,∴∠BEC=∠AMC=90°,∴∠ACF=∠ABD=90°-∠CAB,∴∠ACD=∠ABD=∠ACF=∠BCF,∵BE⊥AC,∴∠CED=∠CEF=90°,∴△CED≌△CEF,∴CD=CF;(3)连OA,∵BC=10,BE=6,∴CE=BC2-CE2=8,AC=BC=10∴AE=AC-CE=2,∴AB=AE2+BE2=210,AB=10∴AM=12∴CM=AC2-AM2=310,∴OM=CM-OA=310-OA222∴310-OA2+102=OA2解得OA=510 3,∴⊙O的半径为5103.4.(2024·陕西咸阳·模拟预测)如图,在Rt△ABC中,∠ACB=90°,BC是⊙O的直径,⊙O与边AB交于点D,E为BD的中点,连接CE,与AB交于点F.(1)求证:AC=AF.(2)当F为AB的中点时,求证:FC=2EF.【答案】(1)见详解(2)见详解【分析】(1)连接EO,交BD于点N,根据E为BD的中点,可得OE⊥BD,即有∠NEF+∠EFN=90°,再根据EO=OC,可得∠OEC=∠OCE,进而可得∠ACF=∠AFC,即可证明;(2)连接EB,在Rt△ABC中,有BF=AF=FC=12AB,即∠ABC=∠FCB,再由E为BD的中点,可得∠EBD=∠FCB,进而可得∠EBD=∠ABC,即可证明△EBF∽△CBA,问题随之得证.【详解】(1)连接EO,交BD于点N,如图,∵E为BD的中点,∴OE⊥BD,∴∠ENF=90°,∴∠NEF+∠EFN=90°,∴∠NEF+∠AFC=90°,∵EO=OC,∴∠OEC=∠OCE,∵∠ACB=90°,∴∠ACF+∠OCE=90°,∴∠ACF+∠OEC=90°,∵∠NEF+∠AFC=90°,∴∠ACF=∠AFC,∴AC=AF;(2)连接EB,如图,∵在Rt△ABC中,F为AB的中点,∴BF=AF=FC=12AB,∵E 为BD 的中点,∴DE =BE ,∴∠EBD =∠FCB ,∴∠EBD =∠ABC ,∵BC 是⊙O 的直径,∴∠BEC =90°,∴∠BEC =∠ACB ,又∵∠EBD =∠ABC ,∴△EBF ∽△CBA ,∴EF AC =BF AB ,即EF AC =BF AB=12,∴2EF =AC ,∵AF =FC ,且在(1)已证明AC =AF ,即FC =2EF .【点睛】本题主要考查了垂径定理,圆周角定理,相似三角形的判定与性质,等角对等边等知识,作出合理的辅助线,掌握垂径定理是解答本题的关键.【题型2遇弦作弦心距解决有关弦长的问题】5.(23-24九年级上·云南昆明·期末)如图,半径为5的⊙O 中,有两条互相垂直的弦AB 、CD ,垂足为点E ,且AB =CD =8,则OE 的长为()A.3B.3C.23D.32【答案】D 【分析】作OM ⊥AB 于M ,ON ⊥CB 于N ,连接OA ,OC ,根据垂径定理得出BM =AM =4,DN =CN =4,根据勾股定理求出OM 和ON 证明四边形OMEN 是正方形,即可解决问题.【详解】解:如图,作OM ⊥AB 于M ,ON ⊥CB 于N ,连接OA ,OC .∴AM =BM =4,CN =DN =4,∵OA =OC =5,∴OM =OA 2-AM 2=52-42=3,ON =OC 2-CN 2=52-42=3∴OM =ON ,∵AB ⊥CD ,∴∠OME =∠ONE =∠MEN =90°,∴四边形OMEN 是矩形,∵OM =ON ,∴四边形OMEN 是正方形,故选:D.【点睛】本题主要考查圆的垂径定理和正方形的判定,关键在于作出辅助线,利用垂径定理得到证明.6.(23-24九年级上·山东潍坊·期末)如图,⊙O的半径是4,点P是弦AB延长线上的一点,连接OP,若OP=6,∠APO=30°,则弦AB的长为()A.27B.7C.5D.52【答案】A【分析】本题主要考查垂径定理,勾股定理,含30°的直角三角形,连接OA,则OA=4,过点O作OD⊥AB交AB于点D,则可计算出OD,利用勾股定理求出AD,进一步利用垂径定理即可求出弦AB的长.【详解】解:连接OA,则OA=4,过点O作OD⊥AB交AB于点D,∵若OP=6,∠APO=30°∴OD=OP÷2=6÷2=3,则AD=OA2-OD2=42-32=7=7∴AB=2AD=27.故选:A.7.(23-24九年级下·上海·阶段练习)如图,⊙O1和⊙O2相交于A和B,过点A作O1O2的平行线交两圆于C、D,已知O1O2=20cm,则CD=cm.【答案】40【分析】本题考查了矩形的性质和判定,垂径定理的应用,作O1E⊥CD于点E,O2F⊥CD于点F,利用垂径定理得到AE=CE,AF=DF,且易得四边形O1O2FE为矩形,进而得到EF=O1O2=20cm,再利用等量代换即可得到CD.E⊥CD于点E,O2F⊥CD于点F,【详解】解:作O∴O1E∥O2F,AE=CE,AF=DF,∵O1O2∥CD,易得四边形O1O2FE为矩形,∵O1O2=20cm,∴EF=O1O2=20cm,∴CD=CE+AE+AF+DF=2AE+AF=2EF=40cm,故答案为:40.8.(23-24九年级上·福建厦门·期末)关于x的一元二次方程2ax2+2cx+2b=0,如果a、b、c满足a2 +b2=c2且c≠0,那么我们把这样的方程称为“勾系方程”,请解决下列问题:(1)求证:关于x的“勾系方程”2ax2+2cx+2b=0必有实数根.(2)如图,已知AB、CD是半径为5的⊙O的两条平行弦,AB=2a,CD=2b,且关于x的方程2ax2+ 10x+2b=0是“勾系方程”.①求∠BDC的度数,②直接写出BD的长:(用含a、b的式子表示).【答案】(1)见解析(2)①∠BDC=45°;②2a+b【分析】(1)根据一元二次方程根的判别式即可判断;(2)①由勾股定理,圆周角定理,垂径定理即可求解.②过点D作AB的垂线,垂足为G,则四边形DGEF是矩形,根据AB∥CD,得出∠GBD=∠BDC=45°,进而勾股定理,即可求解.【详解】(1)证明:∵关于x的一元二次方程2ax2+2cx+2b=0是“勾系方程”,∴a2+b2=c2且c≠0,a≠0,Δ=2c2-4⋅2a⋅2b=4c2-8ab=4a2+b2-8ab=4a2+b2-2ab=4a-b2,∵a-b2≥0,∴Δ≥0,∴方程必有实数根;(2)解:①∠BDC=45°,理由如下:作OE⊥AB于E,延长EO交CD于F,连接OB,OC,∵DC∥AB,∴EF⊥CD,∴AE=BE=a,CF=DF=b,∵BE2+OE2=OB2,∴a2+OE2=52,∵2ax2+10x+2b=0是“勾系方程”,∴a2+b2=52,∴OE=b=CF;∵OB=OC,∴Rt△BOE≌Rt△OCF HL;∴∠FOC=∠OBE,∵∠OBE+∠EOB=90°,∴∠FOC+∠EOB=90°,∴∠COB=90°,∠BOC=45°.∴∠BDC=12②如图所示,过点D作AB的垂线,垂足为G,则四边形DGEF是矩形,∴DG=EF=a+b,∵AB∥CD,则∠GBD=∠BDC=45°∴DB=2DG=2a+b故答案为:2a+b.【点睛】本题考查了“勾系方程”的概念,一元二次方程根的判别式,勾股定理,圆周角定理,垂径定理,三角形全等,解题的关键是明白“勾系方程”的定义.【题型3遇直径作直径所对的圆周角】9.(2024·安徽合肥·一模)如图,AB是⊙O的直径,CD是⊙O的一条弦,AB⊥CD于点M,连接OD.(1)若∠ODB=54°,求∠BAC的度数;(2)AC,DB的延长线相交于点F,CE是⊙O的切线,交BF于点E,若CE⊥DF,求证:AC=CD.【答案】(1)36°(2)见详解【分析】(1)根据等腰三角形的性质得到∠ODB=∠OBD=54°,求得∠DOB=180°-∠OBD-∠ODB=72°,根据垂径定理得到BC=BD,于是得到结论;(2)连接OC,BC,根据切线的性质得到OC⊥CE,根据平行线的性质得到∠ACO=∠F,根据等腰三角形的性质得到∠A=∠ACO,求得AB=BF,根据等腰三角形的性质得到AC=CF,等量代换得到结论.本题考查了切线的性质,等腰三角形的判定和性质,平行线的判定和性质,圆周角定理,正确地作出辅助线是解题的关键.【详解】(1)解:∵OD=OB,∴∠ODB=∠OBD=54°,∴∠DOB=180°-∠OBD-∠ODB=72°,∵AB是⊙O的直径,AB⊥CD,∴BC=BD,∠BOD=36°,∴∠BAC=12故∠BAC的度数为36°;(2)证明:连接OC,BC,∵CE是⊙O的切线,∵CE⊥DF,∴OC∥DF,∴∠ACO=∠F,∵OA=OC,∴∠A=∠ACO,∴∠A=∠F,∴AB=BF,∵AB是⊙O的直径,∴BC⊥AF,∴AC=CF,∵∠A=∠CDB,∴∠CDB=∠F,∴CD=CF,∴AC=CD.10.(2024九年级上·湖北武汉·期中)如图,AB为⊙O的直径,点C为BE的中点,CD⊥AE交直线AE于D点.(1)求证:OC∥AD;(2)若DE=1,CD=2,求⊙O的直径.【答案】(1)见解析(2)5【分析】(1)证明OC⊥EB,AD⊥BE即可得出结论;(2)设BE交OC于点T,证明四边形DETC是矩形,设OB=OC=r,利用勾股定理即可求解.【详解】(1)证明:连接BE,如图,∵AB为⊙O的直径,∴∠AEB=90°,即AD⊥BE,∵点C为BE的中点,∴EC=CB,∴OC⊥EB,∴OC∥AD;(2)解:设BE交OC于点T,如图,∵CD⊥AD,∴∠D=∠DET=∠CTE=90°,∴四边形DETC是矩形,∴CD=ET=2,DE=CT=1,∴BT =TE =2,设OB =OC =r ,则r 2=r -1 2+22,∴r =52,∴AB =2r =5,即⊙O 的直径为5;【点睛】本题考查圆周角定理,垂径定理,矩形的判定和性质,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题.11.(2024·浙江温州·三模)如图,已知△ABC 中,∠ACB =90°,AB =4,AC =3,点E 是AC 边上的动点,以CE 为直径作⊙F ,连接BE 交⊙F 于点D ,则AD 的最小值为.【答案】43-72【分析】连接DC ,由以CE 为直径作⊙F ,得∠CDE =90°,∠CDB =90°,即可得动点D 在以BC 为直径的圆上运动,当A ,D ,O 在一直线上时,根据AD ≥AO -OD ,即可求解.【详解】解:△ABC 中,∠ACB =90°,AB =4,AC =3,∴BC =AB 2-AC 2=42-32=7连接DC ,由以CE 为直径作⊙F ,BC =4,AC =5,∴∠CDE =90°,∠CDB =90°,∴动点D 在以BC 为直径的圆上运动,O 为圆心,当A ,D ,O 在一直线上时,AO =32+72 2=432∴AD ≥AO -OD =432-72=43-72即AD 的最小值为43-72故答案为:43-72.12.(23-24九年级上·福建莆田·期中)如图,AB 是半圆O 的直径,AB =10,点D 在半圆O 上,AD =6,C是弧BD 上的一个动点,连接AC ,过D 点作DH ⊥AC 于H ,连接BH ,在点C 移动的过程中,BH 的最小值是.【答案】73-3/-3+73【分析】连接BD,取AD的中点E,连接BE,由题意先判断出点H在以点E为圆心,AE为半径的圆上,当B、H、E三点共线时,BH取得最小值,然后利用勾股定理,求出BD的长,再利用勾股定理,求出BE的长,再利用直角三角形中,斜边上的中线等于斜边的一半,求出EH的长,再由BH=BE-EH,即可算出BH的长.【详解】解:如图,连接BD,取AD的中点E,连接BE,∵DH⊥AC,∴点H在以点E为圆心,AE为半径的圆上,当B、H、E三点共线时,BH取得最小值,∵AB是直径,∴∠BDA=90°,在Rt△BDA中,∵AB=10,AD=6,∴由勾股定理得:BD=AB2-AD2=100-36=8,∵E为AD的中点,AD=3,∴DE=12在Rt△BDE中,∵BD=8,DE=3,∴由勾股定理得:BE=DE2+BD2=9+64=73,又∵DH⊥AC,且点E为AD的中点,AD=3,∴EH=12∴BH=BE-EH=73-3.故答案为:73-3.【点睛】本题考查了勾股定理解三角形,直径所对的圆周角为直角,直角三角形斜边上的中线等于斜边的一半,能够判断出动点的运动轨迹是解本题的关键.【题型4遇切线作过切点的半径】13.(2024·贵州·模拟预测)如图,在Rt△ABC中,∠ACB=90°,点P为边BC上一点,连接AP,分别以点A,P为圆心,大于是1AP的长为半径画弧,两弧交于点E,F,EF交AB于点D,再以点D为圆心,DA长2为半径作圆,交AB于点M,BC恰好是⊙D的切线.若∠B=30°,AC=3,则BM的长为()A.233B.33C.34D.3【答案】A【分析】本题考查的是切线的性质、含30°角的直角三角形的性质,相似三角形的判定与性质,掌握圆的切线垂直于经过切点的半径是解题的关键.连接DP ,由线段垂直平分线的性质可得AD =DP ,再由直角三角形性质求得AB =23,根据切线的性质得到∠DPB =90°,再证明△BPD ∽△BCE ,再列出方程求解即可.【详解】解:连接DP ,由题意可得,EF 是AP 的垂直平分线,∴AD =DP ,设AD =DP =r ,∵∠B =30°,AC =3,∴AB =23,∵BC 是⊙O 的切线,∴∠DPB =90°,∵∠ACB =90°,∴∠DPB =∠ACB =90°,∴DP ∥AC ,∴△BPD ∽△BCE ,∴BD AB =DP AC ,∴23-r 23=r 3,∴r =233,∴AD =233,∴AM =433,∴BM =AB -AM =23-433=233,故选:A 14.(2024·辽宁大连·一模)如图,△ABC 内接于⊙O ,AD 是⊙O 的直径与BC 交于点F ,∠CAD =45°,过B 点的切线交AD 的延长线于点E .(1)若∠C=64°,求∠E的度数;(2)⊙O的半径是3,OF=1,求BE的长.【答案】(1)38°(2)BE的长为4【分析】此题考查了切线的性质、勾股定理、圆周角定理等知识.(1)连接OB,由切线的性质得到∠OBE=90°,由圆周角定理得到∠AOB=2∠C,又由∠C=64°得到∠AOB =128°,则∠BOE=180°-128°=52°,利用直角三角形性质即可得到答案;(2)连接OC,OB,由圆周角定理得到∠COD=2∠CAD=2×45°=90°,再证明EF=BE,在Rt△OBE中,根据勾股定理得,OE2=OB2+BE2,设BE=EF=x,得到x+12=32+x2,解方程即可得到答案.【详解】(1)解:连接OB,∵BE是⊙O的切线∴OB⊥BE∴∠OBE=90°∵AB=AB∴∠AOB=2∠C∵∠C=64°∴∠AOB=128°∴∠BOE=180°-128°=52°∴∠E=90°-52°=38°(2)解:连接OC,OB,∵CD=CD∴∠COD=2∠CAD=2×45°=90°∴∠1+∠3=90°∵OC=OB∴∠1=∠2∵∠OBE=90°∴∠2+∠4=90°∴∠3=∠4∵∠3=∠5∴∠4=∠5∴EF=BE在Rt△OBE中,∠OBE=90°,根据勾股定理得,OE2=OB2+BE2设BE=EF=x,由OB=3,OF=1得,x+12=32+x2∴BE 的长为4.15.(2024·福建泉州·模拟预测)已知AB 与⊙O 相切于点B ,直线AO 与⊙O 相交于C ,D 两点(AO >AC ),E 为BD 的中点,连接OE 并延长,交AB 的延长线于点F .(1)如图①,若E 为OF 的中点,求∠A 的大小;(2)如图②,连接BD 与OF 相交于点G ,求证:∠D =∠F .【答案】(1)30°(2)见解答【分析】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理和圆周角定理.(1)连接OB ,如图①,先根据切线的性质得到∠OBF =90°,再利用余弦的定义求出∠BOF =60°,接着根据圆心角、弧、弦的关系得到∠DOE =∠BOE =60°,所以∠AOB =60°,然后利用互余得到∠A 的度数;(2)连接OB ,如图②,根据垂径定理得到OE ⊥BD ,再利用等角的余角相等得到∠OBD =∠F ,加上∠OBD =∠D ,从而得到∠D =∠F .【详解】(1)解:连接OB ,如图①,∵AB 与⊙O 相切于点B ,∴OB ⊥AF ,∴∠OBF =90°,∵E 为OF 的中点,∴OE =EF ,∴OF =2OB ,在Rt △OBF 中,∵cos ∠BOF =OB OF =12,∴∠BOF =60°,∵点E 为BD 的中点,∴∠DOE =∠BOE =60°,∴∠AOB =60°,∴∠A =90°-60°=30°;(2)证明:连接OB ,如图②,∵点E 为BD 的中点,∴OE ⊥BD ,∴∠OGB =90°,∵∠OBD +∠BOF =90°,∠BOF +∠F =90°,∴∠OBD =∠F ,∵OB =OD ,∴∠OBD =∠D ,∴∠D =∠F .16.(23-24九年级上·北京西城·期中)如图,AB 为⊙O 的直径,CB ,CD 分别切⊙O 于点B ,D ,CD 交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.若BC=6,DE=4.(1)求证:∠FEB=∠ECF;(2)求⊙O的半径长.(3)求线段EF的长.【答案】(1)证明见解析(2)3(3)25【分析】(1)根据切线的性质及SAS证得△COD≌△COB,可证∠OCD=∠OCB,再利用角的等量代换即可求证结论;(2)设OD=x,则OB=x,OE=8-x,在Rt△BCE和Rt△OED中,分别利用勾股定理即可求解;(3)在Rt△OED和Rt△OCD中,利用勾股定理得OE=5,OC=35,再利用相似三角形的判定及性质即可求解;【详解】(1)证明:连接OD,∵CB,CD是⊙O的切线,∴CB=CD,∠ODC=∠OBC=90°,在△COD和△COB中,OD=OB∠CDO=∠CBO CD=CB,∴△COD≌△COB(SAS),∴∠OCD=∠OCB,∵EF⊥OG,∴∠OEF+∠EOF=90°,∵∠BOC+∠BCO=90°,∠EOF=∠BOC,∴∠FEB=∠OCB,∴∠FEB=∠ECF.(2)解:由(1)得:CD=CB=6,∵DE=4,∴CE=CD+DE=10,在Rt△BCE中,根据勾股定理得:∴BE=EC2-BC2=102-62=8,在Rt△OED中,设OD=x,则OB=x,OE=8-x,由勾股定理得:DE2+OD2=OE2,即:42+x2=8-x2,解得:x=3,∴OD=3,即⊙O的半径为3.(3)解:在Rt△OED和Rt△OCD中,根据勾股定理得:OE=OD2+DE2=32+42=5,OC=OD2+CD2=32+62=35,∵∠FEO=∠DCO,∠EFO=∠CDO=90°,∴△EOF∽△COD,∴EF CD =OEOC,即:EF6=535,∴EF=25.【点睛】本题考查了切线的性质、全等三角形的判定及性质、勾股定理及相似三角形的判定及性质:作出合适的辅助线是解本题的关键.【题型5遇90°的圆周角连直径】17.(2024·安徽合肥·一模)如图,四边形ABCD内接于⊙O,∠BAD=90°,BC=CD,过点C作CE,使得CD=CE,交AD的延长线于点E.(1)求证:AB=AE.(2)若AD=DE=2,求CD的长.【答案】(1)见解析(2)10【分析】(1)如图,连接AC,根据BC=CD推出∠BAC=∠EAC,再证明BC=CE,∠B=∠E,进而证明△ABC≌△AEC AAS,即可证明AB=AE.(2)先证明BD是⊙O的直径,得到∠BCD=90°.由(1)可得AB=4.在Rt△ABD中求出BD=25;在Rt△BCD中,CD=BC=22BD=10.【详解】(1)证明:如图,连接AC.∵BC=CD,∴BC=CD,∴∠BAC=∠EAC.∵CD=CE,∴∠E=∠CDE,BC=CE.∵∠B+∠ADC=180°,∠CDE+∠ADC=180°,∴∠B=∠CDE,∴∠B=∠E.在△ABC 与△AEC 中,∠BAC =∠EAC ,∠B =∠E ,BC =CE ,∴△ABC ≌△AEC AAS ,∴AB =AE .(2)解:如图,连接BD .∵∠BAD =90°,∴BD 是⊙O 的直径,∴∠BCD =90°.由(1)可得AB =AE .∵AD =DE =2,∴AB =4.在Rt △ABD 中,BD =AB 2+AD 2=25;在Rt △BCD 中,CD =BC =22BD =10.【点睛】本题主要考查了弧,弦,圆周角之间的关系,圆内接四边形的性质,等边对等角,勾股定理,90度圆周角所对的弦是直径,直径所对的圆周角是直角,全等三角形的性质与判定等等,正确作出辅助线构造全等三角形和直角三角形是解题的关键.18.(2024·浙江嘉兴·模拟预测)如图,矩形ABCD 内接于⊙O ,AB =2,BC =23,则AB ⏜的长为()A.13πB.23πC.33πD.233π【答案】B【分析】本题考查了圆的基础知识,如图,连接AC ,BD ,根据内接矩形的性质可得AB ,CD 是直径,根据直角三角形斜边中线等于斜边上的高,可得OA =OB =2,可得△AOB 是等边三角形,再根据弧长的计算方法即可求解,掌握矩形的性质,圆的基础值,弧长计算公式是解题的关键.【详解】解:如图所示,连接AC ,BD ,∵四边形ABCD 是矩形,∴∠BAD =∠ABC =90°,∴AC ,BD 是直径,点O 是线段AC 的中点,∴在Rt △ABC 中,AC =AB 2+BC 2=22+23 2=4,∴OB =12AC =2=OA ,∴OA =OB =AB =2,∴△AOB 是等边三角形,∴∠AOB =60°,∴l AB ⏜=n πr 180=60π×2180=23π故选:B.19.(23-24九年级下·四川成都·开学考试)《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的边长为2.以它的对角线的交点为位似中心,作它的位似图形A B C D ,若A B :AB=2:1,则四边形A B C D 的外接圆半径为.【答案】22【分析】本题考查位似图形的性质,根据正方形ABCD的边长为2和位似比求出A B =4,进而即可求解.解题关键求出正方形的边长.【详解】解:如图,连接A C ,∵正方形ABCD与四边形A B C D 是位似图形,∴四边形A B C D 是正方形,∴∠A B C =90°∴A C 是四边形A B C D 的外接圆直径,∵正方形ABCD的边长为2,A B :AB=2:1∴A B =4∴AC =42+42=42∴四边形A B C D 的外接圆半径为22,故答案为:22.20.(2024·江西景德镇·三模)如图,在平面直角坐标系xOy中,⊙P经过点O,与y轴交于点A0,6,与x轴交于点B8,0,则OP的长为.【答案】5【分析】本题考查了90度圆周角所对的弦为直径,勾股定理,连接AB,通过题意判断出AB为直径,圆心P在AB上,根据勾股定理计算出AB的长,从而得出结果.【详解】解:如图,连接AB,∵∠AOB为直角,且点A,B,O都在圆上,∴AB为直径,圆心P在AB上,∵A 0,6 ,B 8,0 ,∴OA =6,OB =8,∴AB =OA 2+OB 2=10,∴OP =12AB =5,故答案为:5.【题型6转移线段】21.(23-24九年级上·四川泸州·阶段练习)如图,⊙O 的直径AB =8,弦CD =3,且弦CD 在圆上滑动(CD 的长度不变,点C 、D 与点A 、B 不重合),过点C 作CP ⊥AB 于点P ,若M 是CD 的中点,则PM 的最大值是.【答案】4【分析】本题考查垂径定理、三角形中位线定理,延长CP 交⊙O 于点K ,连接DK ,根据垂径定理可得CP =PK ,再根据三角形中位线定理可得PM =12KD ,进而可得当KD 最大时,PM 的值最大,即即当KD 为直径时,KD 的值最大,即可求解.【详解】解:延长CP 交⊙O 于点K ,连接DK ,∵AB ⊥CK ,∴CP =PK ,∵M 是CD 的中点,∴PM 是△CKD 的中位线,∴PM =12KD ,∴当KD 最大时,PM 的值最大,即当KD 为直径时,KD 的值最大,∵⊙O 的直径AB =8,∴PM =12KD =12AB =4,故答案为:4.22.(2024九年级上·浙江台州·期中)如图,在△ABC 中,AB =5,AC =4,BC =3,经过点C 且与边AB 相切的动圆与CA 、CB 分别相交于点P 、Q ,则线段PQ 长度的最小值是.【答案】125/2.4/225【分析】设圆心为点F ,圆F 与AB 的切点为D ,连接FD 、CF 、CD ,则有FD ⊥AB ,由勾股定理的逆定理可得△∠ACB =90°,再由直角三角形的性质可得FC +FD =QP ,又由FC +FD ≥CD ,PQ 为圆F 的直径,可得点F 在直角三角形ABC 的斜边AB 的高CD 上时,PQ =CD 有最小值,即CD 为圆F 的直径,再利用△ABC 的面积即可求解.【详解】解:如图,设圆心为点F ,圆F 与AB 的切点为D ,连接FD 、CF 、CD ,∵圆F 与AB 相切,∴FD ⊥AB ,∵在△ABC 中,32+42=52,即BC 2+AC 2=AB 2,∴△∠ACB =90°,∴CF =12QP ,又∵CF =FD ,∴FC +FD =QP ,∵FC +FD ≥CD ,PQ 为圆F 的直径,∴当点F 在直角三角形ABC 的斜边AB 的高CD 上时,PQ =CD 有最小值,即CD 为圆F 的直径,∵S △ABC =12BC ⋅AC =12AB ⋅CD ,∴12×4×3=12×5×CD ,∴CD =125,故答案为:125.【点睛】本题考查切线的性质、直角三角形的性质、勾股定理的定理、三角形的三边关系及三角形的面积公式,根据题意可知当点F 在直角三角形ABC 的斜边AB 的高CD 上时,PQ =CD 有最小值是解题的关键.23.(2024·江苏徐州·三模)【问题情境】如图1,P 是⊙O 外的一点,直线PO 分别交⊙O 于点A 、B .小明认为线段P A 是点P 到⊙O 上各点的距离中最短的线段,他是这样考虑的:在⊙O 上任意取一个不同于点A 的点C ,连接OC 、CP ,则有OP <OC +PC ,即OP -OC <PC ,由OA =OC 得OP -OA <PC ,即P A <PC ,从而得出线段P A 是点P 到⊙O 上各点的距离中最短的线段.小红认为在图1中,线段PB 是点P 到⊙O 上各点的距离中最长的线段,你认为小红的说法正确吗?请说明理由.【直接运用】如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是CD上的一个动点,连接AP,则AP的最小值是;【构造运用】如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A MN,连接A C,请求出A C长度的最小值.【深度运用】如图5,已知点C在以AB为直径,O为圆心的半圆上,AB=4,以BC为边作等边△BCD,则AD的最大值是.【答案】问题情境:正确,理由见解析;直接运用:5-1;构造运用:7-1;深度运用:23+2【分析】问题情境∶根据三角形的任意两边之和大于第三边即可得解;直接运用∶取半圆的圆心O,连接OA交半圆于点M,则当P与点M重合时,P A最小,由勾股定理得OA= 22+12=5,从而即得解;构造运用:由折叠知A M=AM,进而得点A ,A,D都在以AD为直径的圆上.如图3,以点M为圆心,MA 为半径画⊙M,连接MC.当A C长度取最小值时,点A 在MC上,过点M作MH⊥DC于点F,根据菱形的性质及勾股定理即可得解;深度运用:如图,在AB的上方作等边△ABH,连接DH,取BH的中点G连接DG,证明△ABC≌△HBD,得∠BDH=∠ACB=90°,点D在以BH为直径的半圆上,进而利用勾股定理及三角形的两边之和大于第三边即可得解.【详解】解:问题情境∶小红的说法正确,在圆О上任意取一个不同于点B的点C,连接OC、OP,∵在△POC 中,OP +OC >PC .OB =OC ,∴OP +OB >PC ,即PB >PC .∴线段PB 是点Р到圆О上各点的距离中最长的线段.∴小红的说法正确;直接运用∶取半圆的圆心O ,连接OA 交半圆于点M ,则当P 与点M 重合时,P A 最小,∵∠ACB =90°,AC =BC =2,∴OC =1,OC 2+AC 2=OA 2,∴OA =22+12=5,∴P A 的最小值为OA -AM =5-1故答案为:5-1.构造运用:由折叠知A M =AM ,∵M 是AD 的中点,∴MA =MA =MD ,∴点A ,A ,D 都在以AD 为直径的圆上.如图3,以点M 为圆心,MA 为半径画⊙M ,连接MC .当A C 长度取最小值时,点A 在MC 上,过点M 作MH ⊥DC 于点F ,∵在边长为6的菱形ABCD 中,∠A =60°,M 为AD 中点,∴2MD =AD =CD =2,∠HDM =60°,∴∠HMD =30°,∴HD =12MD =12.∴HM =DM ×cos30°=32,HC =52,∴MC =HM 2+HC 2=7,∴A C =MC -MA =7-1;深度运用:如图,在AB 的上方作等边△ABH ,连接DH ,取BH 的中点G 连接DG ,∵AB 是半圆的直径,∴∠ACB =90°,∵△ABH 和△BCD 都是等边三角形,∴AB =BH =AH =4,BD =BC =DC ,∠ABH =∠CBD =60°即∠ABC +∠CBH =∠CBH +∠HBD ,∴∠ABC =∠HBD ,∴△ABC ≌△HBD ,∴∠BDH =∠ACB =90°,∴点D 在以BH 为直径的半圆上,∵G 是BH 的中点,AB =AH =BH =4,∴AG ⊥BH ,BG =DG =HG =2,∴AG =AB 2-BG 2=42-22=23,∴根据三角形的两边之和大于第三边可得AD 的最大值为AG +DG =23+2,故答案为:23+2.【点睛】本题主要考查了全等三角形的判定,勾股定理,等边三角形的性质,圆周角定理的推论以及三角形的三24.(23-24九年级上·河南开封·阶段练习)如图,以G(0,3)为圆心,半径为6的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为⊙G上一动点,CF⊥AE于F,点E在G的运动过程中,线段FG的长度的最小值为.【答案】33-3/-3+33【分析】本题主要考查垂径定理,圆周角定理,直角三角形30度角的判定和性质,熟练掌握性质定理,构造直角三角形是解题的关键.过点G作GM⊥AC于点F,连接AG.得到点F在MG的延长线上时,FG的长度的最小,最小值=FM-GM,即可得到答案.【详解】解:过点G作GM⊥AC于点F,连接AG,∵GO⊥AB,∴OA=OB,∵G(0,3),∴OG=3,在Rt△AGO中,AG=6,OG=3,∴OA=AG2-GO2=33,∴∠GAO=30°,AB=2AO=63,∴∠AGO=60°,∵GC=GA=6,∴∠GCA=∠GAC,∵∠AGO=∠GCA+∠GAC,∴∠AGO=∠GAC=30°,∴AC=2OA=63,MG=1CG=3,2∵∠AFC=90°,∴点F在以AC为直径的⊙M上,∴MF=AC=33,2点F在MG的延长线上时,FG的长度的最小,最小值=FM-GM=33-3,故答案为:33-3.【题型7构造相似三角形】25.(2024·贵州六盘水·二模)如图,四边形ABCD内接于⊙O,AD为直径,DB平分∠ADC,CA=CD,DB与CA交于点E,延长AB,DC交于点F.(1)直接写出线段AB 与线段BC 的数量关系;(2)求证:△AFC ≌△DEC ;(3)设△ABD 的面积为S 1,△BCD 的面积为S 2,求S 1S 2的值.【答案】(1)AB =BC(2)见解析(3)2【分析】(1)根据等角,等弧,等弦,即可得出结论;(2)根据同弧所对的圆周角相等,利用ASA 证明△AFC ≌△DEC 即可;(3)过点C 作CH ⊥DE ,圆周角定理得到∠ACD =∠ABD =90°,勾股定理得到AD =CA 2+CD 2=2CD ,证明△ABD ∽△CHD ,得到AB CH =AD CD=2,根据同底三角形的面积比等于高线比,即可得出结果.【详解】(1)解:连接OB ,OC ,则:∠AOB =2∠ADB ,∠BOC =2∠CDB ,∵DB 平分∠ADC ,∴∠ADB =∠CDB ,∴∠AOB =∠BOC ,∴AB =BC ,∴AB =BC ;(2)∵AD 为直径,∴∠ACD =90°,∴∠ACF =90°=∠ACD ,又∵∠BAC =∠CDB ,CA =CD ,∴△AFC ≌△DEC ;(3)过点C 作CH ⊥DE ,则∠CHD =90°∵AD 为直径,∴∠ACD =∠ABD =90°,∵CA =CD ,∴AD =CA 2+CD 2=2CD ,∵∠ABD =∠CHD =90°,∠ADB =∠CDB ,∴△ABD ∽△CHD ,∴AB CH =AD CD =2,∴S 1S 2=12AB ⋅BD 12CH ⋅BD =AB CH =2.【点睛】本题考查圆周角定理,弧,弦,角之间的关系,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识点,熟练掌握相关知识点,并灵活运用,是解题的关键.线上.且AD =2.过点A 另一条直线交⊙O 于B 、C .(1)如图1,当AC =5时,研究发现:连接CE 、BD 可以得到△ABD ∽△AEC ,继而可以求AB 长.请写出完整的解答过程.(2)如图2,当B 、C 重合于一点时,AC =.(3)如图3,当OB 平分∠AOC 时,AC =.【答案】(1)AB =165;过程见解析(2)4(3)8105【分析】(1)连接BD 、CE ,证明△ABD ∽△AEC ,得出AD AC =AB AE,求出AB =165.(2)连接OC ,根据当B 、C 重合于一点时,AC 与⊙O 相切于点C ,得出∠ACO =90°,求出AC =AO 2-OC 2=52-32=4.(3)连接BD ,根据角平分线定义得出∠AOB =∠COB =12∠AOC ,证明DB =BC ,△ABD ∽△AOB ,得出AB AO =AD AB =BD OB ,即AB 5=2AB=BD 3,求出AB =10,BD =3105,即可求出结果.【详解】(1)解:连接BD 、CE ,如图所示:∵DE =6,AD =2,∴AE =AD +DE =2+6=8,∵∠ABD +∠CBD =180°,∠CBD +∠E =180°,∴∠ABD =∠E ,∵∠BAD =∠EAC ,∴△ABD ∽△AEC ,∴AD AC =AB AE ,∴25=AB 8,解得:AB =165.(2)解:连接OC ,如图所示:∵当B 、C 重合于一点时,AC 与⊙O 相切于点C ,∴∠ACO =90°,∵DE =6,∴OC =OD =OE =3,∴AO =AD +DO =2+3=5,∴AC =AO 2-OC 2=52-32=4.∵OB 平分∠AOC ,∴∠AOB =∠COB =12∠AOC ,∴DB =BC ,∵OC =OE ,∴∠OCE =∠OEC ,∵∠AOC =∠OCE +∠OEC ,∴∠OCE =∠OEC =12∠AOC ,∴∠DOB =∠OEC ,根据解析(1)可知:∠ABD =∠AEC ,∴∠ABD =∠AOB ,∵∠DAB =∠OAB ,∴△ABD ∽△AOB ,∴AB AO =AD AB =BD OB ,即AB 5=2AB=BD 3,解得:AB =10,BD =3105,∴AC =AB +BC =AB +BD =10+3105=8105.【点睛】本题主要考查了相似三角形的判定和性质,勾股定理,圆内接四边形的性质,等腰三角形的性质,切线的性质,解题的关键是作出辅助线,熟练掌握相关的判定和性质.27.(23-24九年级下·福建厦门·阶段练习)如图,以AB 为直径的⊙O 与AH 相切于点A ,点C 在AB 左侧圆弧上,弦CD ⊥AB 交⊙O 于点D ,连接AC ,AD ,点A 关于CD 的对称点为E ,直线CE 交⊙O 于点F ,交AH 于点G .(1)求证:∠CAG =∠AGC ;(2)当点E 在AB 上,连接AF 交CD 于点P ,若EF CE =25,求DP CP的值;(3)当点E 在射线AB 上,AB =2,四边形ACOF 中有一组对边平行时,求AE 的长.【答案】(1)见解析(2)57(3)2-2或3-52【分析】(1)设AB 与CD 相交于点M ,由⊙O 与AH 相切于点A ,得到∠BAG =90°,由CD ⊥AB ,得到∠AMC =90°,进而得到AG ∥CD ,由平行线的性质推导得,∠CAG =∠ACD ,∠AGC =∠FCD ,最后由点A关于CD 的对称点为E 得到∠FCD =∠ACD 即可证明.(2)过F 点作FK ⊥AB 于点K ,设AB 与CD 交于点N ,连接DF ,证明∠FAD =∠ADC 得到DP =AP ,再证明△CP A ≌△FPD 得到PF =PC ;最后根据△KEF ∽△NEC 及△APN ∽△AFK 得到KE EN =EF CE =25和P A AF =AN AK=512,最后根据平行线分线段成比例求解.(3)分两种情形:当OC ∥AF 时,当AC ∥OF 时,分别求解即可.【详解】(1)证明:如图,设AB 与CD 相交于点M ,∵⊙O 与AH 相切于点A ,∴∠BAG =90°,∵CD ⊥AB ,∴∠AMC =90°,∴AG ∥CD ,∴∠CAG =∠ACD ,∠AGC =∠FCD ,∵点A 关于CD 的对称点为E ,∴∠FCD =∠ACD ,∴∠CAG =∠AGC .(2)解:过F 点作FK ⊥AB 于点K ,设AB 与CD 交于点N ,连接DF ,如下图所示:由同弧所对的圆周角相等可知:∠FCD =∠FAD ,∵AB 为⊙O 的直径,且CD ⊥AB ,由垂径定理得:AC =AD ,∴∠ACD =∠ADC ,∵点A 关于CD 的对称点为E ,∴∠FCD =∠ACD ,∴∠FAD =∠FCD =∠ACD =∠ADC ,即∠FAD =∠ADC ,∴DP =AP ,由同弧所对的圆周角相等得:∠ACP =∠DFP ,且∠CP A =∠FPD ,∴△CP A ≌△FPD ,∴PC =PF ,∵FK ⊥AB ,AB 与CD 交于点N ,∴∠FKE =∠CNE =90°.∵∠KEF =∠NEC ,∠FKE =∠CNE =90°,∴△KEF ∽△NEC ,∴KE EN =EF CE=25,设KE =2x ,EN =5x ,∵点A 关于CD 的对称点为E ,∴AN =EN =5x ,AE =AN +NE =10x ,AK =AE +KE =12x ,又FK ∥PN ,∴△APN ∽△AFK ,∴P A AF =AN AK=5x 12x =512.∵∠FCD =∠CDA ,∴CF ∥AD ,∴DP =AP =AP =5;。
小专题圆中常见的辅助线归类-北师大版九年级数学下册习题课件

小专题(六) 圆中常见的辅助线归类
-12-
8.如图,在△ABC 中,BC=3,以 BC 为直径的☉O 交 AC 于点 D.若 D
是 AC 的中点,∠ABC=120°.
(1)求∠ACB 的大小;
(2)求点 A 到直线 BC 的距离.
小专题(六) 圆中常见的辅助线归类
解:(1)连接BD.∵BC为☉O的直径,
形,以便利用直角三角形的知识求解;(2)若已知圆的直径解答有关问题时,一般需构造直径所对的圆周角,以便利用直角三角形的知识解答问题;(3)如果已知圆与直线相切,一般添加过切点
的半径,以便利用切线的性质构造直角三角形;如果已知直线与圆的交点,要判断该直线是圆的切线时,只需连接过交点的半径,证明此半径垂直于直线即可.
半径为( C
A.3 cm
)
B.4 cm
C.5 cm
D.6 cm
小专题(六) 圆中常见的辅助线归类
-5-
3.☉O 的半径为 6 cm,P 是☉O 内一点,OP=2 cm,那么过点 P 的最
短弦的长等于(
B )
A.12 cm
B.8 cm
C.6 cm
D.4 cm
小专题(六) 圆中常见的辅助线归类
又∵OC=OB,∴∠BCO=∠ABC,
如图是某圆柱形输水管的横截面,阴影部分为有水部分.
4.如图,☉O 的直径 AB 和弦 CD 相交于点 E,已知 AE=6 cm,BE=2
cm,∠CEA=30°,求 CD 的长.
小专题(六) 圆中常见的辅助线归类
解:过点 O 作 OP⊥CD 于点 P,连接 OC.∴CD=2CP.
点 C,过点 B 作 BD⊥MN 于点 D.
(1)求证:∠ABC=∠CBD;
初中几何辅助线——圆常用辅助线

习 求证:
习
学
学C
D
分证明:(一)连结 OC、OD
分A
满 满 ∵M、N 分别是 AO、BO 的中点 ∴OM = 1 AO、ON = 1 BO
MO N
B
2
2
习 学 分 满
∵OA = OB
习
习
关注公众号:满分学习,每天查看更过干货资料!
习
分 满 ∴OM = ON
分 关注公众号:满分学习,每天查看更过干货资料! 满
CD = CE
证明:连结 OC
习 ∵C 为弧 AB 的中点
习O
学 ∴ AB BC
学D E
分∴∠AOC =∠BOC
分A
B
C
满
满 ∵D、E 分别为 OA、OB 的中点,且 AO = BO
∴OD = OE = 1 AO = 1 BO
2
2Leabharlann 又∵OC = OC习 学 分 满
∴△ODC≌△OEC
习 习 ∴CD = CE 学 学 结论 1.圆内角的度数等于它所对的弧与它对顶角所对的弧的度数之和的一半.
分
满
满
习 学 分 满
例 3 如图,已知 M、N 分别是⊙O 的弦 AB、CD 的中点,AB = CD,求证:∠AMN
= ∠CNM
习 证明:连结 OM、ON
习A
C
习
学 学 ∵O 为圆心,M、N 分别是弦 AB、CD 的中点
M
N
学
分∴OM⊥AB
ON⊥CD
分 分 O
B
D
满 ∵AB = CD
满
满
∴OM = ON
分 满
∵CM⊥OA、DN⊥OB、OC = OD
九年级数学中考几何微专题:圆中的辅助线
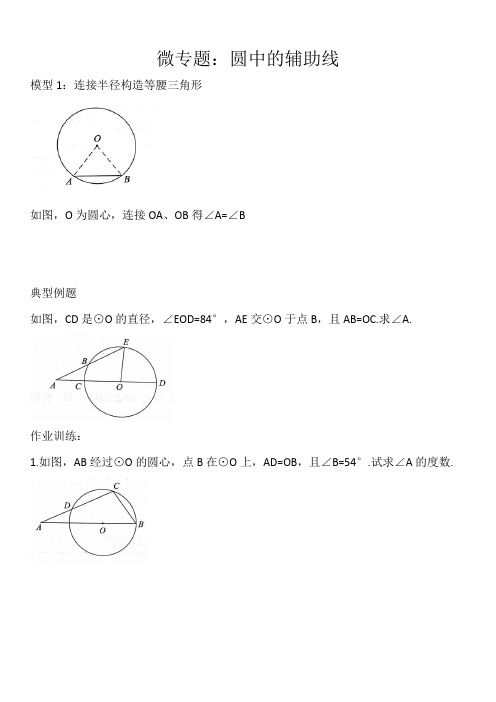
微专题:圆中的辅助线模型1:连接半径构造等腰三角形如图,O为圆心,连接OA、OB得∠A=∠B典型例题如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC.求∠A.作业训练:1.如图,AB经过⊙O的圆心,点B在⊙O上,AD=OB,且∠B=54°.试求∠A的度数.2.如图,AB 是⊙O 的直径,弦PQ 交AB 于点M ,且PM=MO.求证:.31⌒⌒BQ AP =模型2:构造直角三角形如图①,已知AB 是⊙O 的直径,点C 是圆上一点,连接AC 、BC ,则∠ACB=90°.如图②,已知AB 是⊙O 的一条弦,过点O 作OE ⊥AB ,则222OA AE OE =+.典型例题:例1:已知⊙O 的直径AB 和弦 CD 相交于点E ,AE=2,BE=6,∠DEB=60°.求CD 的长.例2:如图,AB 是⊙O 的直径,AB=AC ,BC 交⊙O 于点D ,AC 交⊙O 与点E ,∠BAC=45°.(1)求∠EBC 的度数;(2)求证:BD=CD.作业训练1.如图,⊙O 的弦AB 、CD 互相垂直,垂足为E ,且AE=5,BE=13,点O 到AB 的距离为102.求点O 带CD 的距离,线段OE 的半径的长及⊙O 的半径.2.如图,已知AB 和CD 是⊙O 的两条弦,且AB ⊥CD 与点H ,连接BC 、AD ,作OE ⊥AD 于点E.求证:.21BC OE3.如图,直径AB=2,AB 、CD 交于点E 且夹角为45°,则=+22DE CE .模型3:与圆的切线有关的辅助线.典型例题:例1:如图,OA 、OB 是⊙O 的半径,且OA ⊥OB ,P 是OA 上任意一点,BP 的延长线交⊙O 于Q 点,过Q 点的切线交OA 的延长线于R 点.求证:RP=RQ.例2:如图,△ABC内接于⊙O,过点A作直线DE,当∠BAE=∠C时,试确定直线DE 与⊙O的位置关系,并证明你的结论.作业训练:1.如图,在△ABC中,以AB为直径的⊙O分别于BC、AC相交于点D、E,BD=CD,过点D作⊙O的切线交AC于点F.求证:.DFAC2.如图,AB是⊙O的直径,AC是它的切线,CO平分∠ACD.求证:CD是⊙O的切线.3.如图,直线AC与⊙O相交于B、C两点,E是⌒BC的中点,D是⊙O上一点,若∠EDA=∠AMD.求证:AD是⊙O的切线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类型之四 添加辅助线计算阴影面积
(2)∵OE⊥DB,∴EB=12DB=3 3.在 Rt△EOB 中,∵EB=3 3, 由勾股定理可得 OB=6.又∵∠D=∠DBO,DE=BE,∠CED=∠OEB, ∴△CDE≌△OBE.∴S△CDE=S△OBE.
D.4 2
4.如图所示,AB 是⊙O 的弦,OH⊥AB 于点 H,点 P 是优弧上一
点,若 AB=2 3,OH=1,则∠APB 的度数是__6_0_°__.
第3题图
第4题图
类型之二 遇直径添加直径所对的圆周角
5.如图所示,已知:AB是⊙O的直径,点C,D在⊙O上,∠ABC= 50°,则∠D为( C ) A.50° B.45° C.40° D.30°
接 OP,若 OP=4,∠APO=30°,则弦 AB 的长是( A )
A.2 5
B. 5
C.2 13
D. 13
第1题图
第2题图
类型之一 遇弦加弦心距或半径
3.如图所示,在半径为 5 的⊙O 中,AB,CD 是互相垂直的两条弦,
垂足为 P,且 AB=CD=8,则 OP 的长为( C )
A.3
B.4
C.3 2
∴S 阴影=S 扇形 OCB=36600π·62=6π(cm2)
(3)存在点P使△PBD≌△AED.由(1)(2)知,BD=ED, ∵ ∠ BAC = 60° , DE∥AB , ∴ ∠ AED = 120°.∵∠ABC = 60° , ∴∠PBD=120°,∴∠PBD=∠AED.要使△PBD≌△AED, 只需PB=AE=1
类型之三 遇切线添加过切点的半径
9.如图所示,已知 MN 是⊙O 的直径,直线 PQ 与⊙O 相切于 P 点, NP 平分∠MNQ. (1)求证:NQ⊥PQ; (2)若⊙O 的半径 R=3,NP=3 3,求 NQ 的长. 解:(1)证明:连接OP.∵直线PQ与⊙O相切于P点,MN 是 ⊙ O 的 直 径 , ∴ OP⊥PQ. 又 ∵ NP 平 分 ∠ MNQ , ∴∠MNP =∠QNP ,又 ∠OPN=∠ MNP =∠QNP , ∴OP∥NQ,∴NQ⊥PQ
类型之四 添加辅助线计算阴影面积
11.如图所示,以 AD 为直径的半圆 O 经过 Rt△ABC 斜边 AB 的两个
端点,交直角边 AC 于点 E,B,E 是半圆弧的三等分点,B︵
π
A. 9
3π
B. 9
3 C. 2
3-32π
3 D.
2
3-23π
1中2阴.影如部图分所的示面,积AB是是__⊙4_π_O_-_3的_3_直__3径__,_.弦 AC=2,∠ABC=30°,则图
类型之二 遇直径添加直径所对的圆周角
8.如图所示,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交 BC,AC于点D,E,且点D为BC的中点. (1)求证:△ABC为等边三角形; (2)求DE的长; (3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在, 请求出PB的长;若不存在,请说明理由.
(2)连接BF.∵∠AEF为Rt△ADE的一个外角,∠DAE=18°,∴∠AEF =∠ADE+∠DAE=90°+18°=108°.在⊙O中, 四边形ABFE是圆内接四边形,有∠AEF+∠B=180°, ∴∠B=180°-108°=72°.由AB是⊙O的直径, 得∠AFB=90°.∴∠BAF=90°-∠B=18°
(2)连接 MP,在 Rt△MNP 中,∵MN=2R=6,NP=3 3, ∴MP= MN2-PN2=3,则∠MNP=30°,∴∠QNP=30°.
∴PQ=32 3.故 NQ= PN2-PQ2=92
类型之三 遇切线添加过切点的半径
10.已知直线l与⊙O相切,AB是⊙O的直径,AD⊥l于点D. (1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC 的大小; (2) 如 图 ② , 当 直 线 l 与 ⊙ O 相 交 于 点 E , F 时 , 若 ∠ DAE = 18° , 求 ∠BAF的大小.
第11题图
第12题图
类型之四 添加辅助线计算阴影面积
13.如图所示,点 B,C,D 都在⊙O 上,过点 C 作 AC∥BD 交 OB 延长线于点 A,连接 CD,且∠CDB=∠OBD=30°,DB=6 3cm.
(1)求证:AC 是⊙O 的切线;
(2)求由弦 CD,BD 与B︵C所围成的阴影部分的面积(结果保留π).
6.如图所示,点A,B,C,D分别是⊙O上四点,∠ABD=20°, BD是直径,则∠ACB=_7_0_°___.
第5题图
第6题图
第7题图
7.如图所示,△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若 D是AC的中点,∠ABC=120°. (1)求∠ACB的大小; (2)求点A到直线BC的距离.
类型之三 遇切线添加过切点的半径
解:(1)连接OC,∵直线l与⊙O相切于点C时,∴OC⊥l, 得∠OCD=90°.由AD ⊥l,得∠ADC=90°.∴AD∥OC, ∴ ∠ ACO = ∠ DAC. 在 ⊙ O 中 , 由 OA = OC , 得 ∠ BAC = ∠ ACO , ∴∠BAC=∠DAC=30°
解:(1)证明:连接AD,∵AB是⊙O的直径,∴∠ADB=90°. ∵点D是BC的中点,∴AD是线段BC的垂直平分线,∴AB=AC. ∵AB=BC,∴AB=BC=AC.∴△ABC为等边三角形
类型之二 遇直径添加直径所对的圆周角
(2)连接 BE.∵AB 是直径,∴∠AEB=90°,∴BE⊥AC. ∵△ABC 是等边三角形,∴AE=EC,即 E 为 AC 的中点. ∵D 是 BC 的中点, 故 DE 为△ABC 的中位线,∴DE=12AB=12×2=1
类型之二 遇直径添加直径所对的圆周角
解:(1)连接BD,∵以BC为直径的⊙O交AC于点D, ∴∠BDC=90°.∵D是AC的中点,∴BD是AC的垂直平分线. ∴AB=BC,∴∠A=∠C.∵∠ABC=120°,∴∠A=∠C=30°,
即∠ACB=30° (2)过点 A 作 AE⊥BC 交 CB 的延长线于点 E,∵BC=3, ∠ACB=30°,∠BDC=90°,∴BD=32.在 Rt△BCD 中, 由勾股定理可得 CD= BC2-BD2=32 3.∵AD=CD,∴AC=3 3. ∵在 Rt△AEC 中,∠ACE=30°,∴AE=12AC=12×3 3=3 2 3, 即点 A 到直线 BC 的距离为32 3
九年级数学上册(人教版)
第二十四章 圆 专题训练(七) 圆中常见辅助线归类
类型之一 遇弦加弦心距或半径
1.如图,AB 是⊙O 的直径,弦 CD⊥AB,垂足为 P,若 CD=8,
OP=3,则⊙O 的半径为( C )
A.10
B.8
C.5
D.3
2.如图所示,⊙O 的半径是 3,点 P 是弦 AB 延长线上的一点,连
