高等数学-曲率
同济大学 高等数学 课件 2.11

.
例3 求 y ln x 在任意点处的曲率. 解 因
1 1 y , y 2 , x x
由计算公式得曲线在任一点处的曲率为
K
y
1 y
x 0
2 3/ 2
1/ x 2
1 1/ x
2 3/ 2
x
1 x
2 3/ 2
,
注意到, lim K
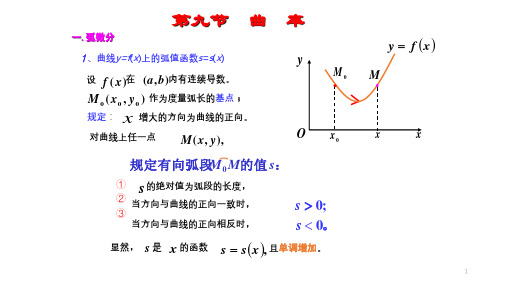
y f x M M0 s M +
o a b
x
而线段 MM 的长度为
MM
并注意到
x 0
x
s MM
2
y ,
2
lim
1,
(此式将在定积分中证明) 因
s MM lim lim lim x 0 x x 0 MM x x 0 s
K
2a
3/ 2
,
曲率圆与曲率半径 设曲线 C 在点 M 点 D, 使
x, y 处的曲率为K K 0 , 作出
y
D
1 K
点 M 处曲线 C 的法线,并且在曲线凹向一侧的法线上取
1 MD . K 以 D为圆心, 为半径作圆,
称该圆为曲线 C 在点 M 的曲率 圆, 为曲线 C 在 M 处的率的极限存在,则称此极限为 曲线 C 在点 M 处的曲率,记为K ,即
K lim . M M s
⑴
例1 对直线而言,动点从 M 到 M 相应的切线的转角 为 0, 则
K 0, s
从而曲率
K lim 0. M M s
x3 , 并设OA 的方程为 y aRl
的长度,a是待定常数.
《高等数学曲率》课件

曲率与生物形态
在自然界中,许多生物形态都呈现出 曲率的特点。例如,鸟类的飞行轨迹 、河流的流向、植物的生长方式等都 与曲率密切相关。通过研究这些生物 形态的曲率特点,可以更好地理解自 然界的规律和原理。
VS
曲率在生物形态中的应用还体现在仿 生学领域。通过模仿自然界中生物的 形态和运动方式,可以创造出更加高 效、环保和可持续的交通工具、建筑 材料等。例如,仿生学中的“蜂巢” 结构就是利用了曲率的特点,具有很 好的抗压和抗震性能。
曲率与建筑设计
在建筑设计中,曲率也被广泛应用。通过合理利用曲率,可以创造出更加美观、舒适和功能性的建筑。例如,在建筑设计时 可以利用曲率来优化建筑的外观和结构,提高建筑的稳定性和安全性。
曲率还可以用于建筑内部的布局和空间设计。例如,利用曲率可以将建筑的内部空间划分为不同的区域,提高建筑的实用性 和舒适性。
曲率研究展望
曲率与几何拓扑关系
未来研究可以探索曲率与几何拓扑之间的关系,例如研究 曲率在曲面分类中的作用,以及曲率在流形学习等方面的 应用。
高维空间曲率研究
随着高维几何的发展,对高维空间中曲率的研究也日益重 要,未来可以进一步探讨高维空间中曲率的性质和计算方 法。
数值计算与模拟
随着计算机技术的发展,数值计算和模拟已经成为研究曲 率的重要手段,未来可以借助更先进的计算方法和模拟技 术,对曲率进行更精确和深入的研究。
03
曲率应用
曲率在几何学中的应用
曲率在几何学中有着广泛的应用,它描述了曲线在某一点的 弯曲程度。在平面几何中,曲率用于描述曲线在某一点的弯 曲程度,而在球面几何中,曲率则用于描述曲面在某一点的 弯曲程度。
在几何学中,曲率的概念可以帮助我们更好地理解空间中的 几何形状,以及它们之间的相互关系。例如,在研究行星运 动时,曲率的概念可以帮助我们理解行星轨道的形状和大小 。
3-7 曲率(高等数学)

§3.7 曲率教学内容:一.弧微分1.光滑曲线:设函数)(x f y =在区间(,)a b 内具有连续导数,则曲线)(x f y =在(,)a b 内的每点处有能连续转动的切线,称曲线)(x f y =为光滑曲线.2. 弧微分:函数()s x 关于x的微分d s x =,或者d s =.二.曲率1.定义:0lim →∆s s ∆∆α称为曲线在点M 处的曲率,即K =0lim →∆s s ∆∆α=d d sα.2. 计算公式:设曲线的方程为)(x y y =,且()y x 具有二阶导数,322d d (1')y K s y α''===+.三.曲率半径与曲率圆1. 曲率圆与曲率半径的定义:设曲线)(x f y =在点(,)M x y 处的曲率0K ≠(即0y ''≠),在点M 处作曲线的法线,法线指向曲线凹的一侧.在此侧的法线上取一点D ,使1MD Kρ==,以D 为圆心,ρ为半径作圆,称这个圆为曲线在点M 处的曲率圆,它的半径1Kρ=称为曲率半径,圆心D 称为曲率中心.图3.212.曲率圆与曲线在点M 处有相同的切线与曲率,且在点M 的邻近有相同的弯曲方向,从而曲率圆与曲线所对应的函数在点M 有相同的函数值、一阶导数值和二阶导数值.3.在工程设计中,一般可用曲率圆在点M 附近的一段弧来近似代替曲线弧.四.例题讲解例1.求直线b ax y +=的曲率.例2.求半径为R 的圆的曲率.例3.求曲线122--=x x y 在极小值点处的曲率.例4.在车床加工中,用圆柱形铣刀加工一弧长不大的椭圆形工件,该段弧的中点为椭圆长轴的顶点,其方程为222214050x y +=(单位:mm ),应选用多大直径的铣刀,可得较好的近似效果.。
高等数学上3.7平面曲线的曲率PPT

Q 70(千克力) 571.4(千克力),
641.5(千克力).
即:飞行员对座椅的压力为641.5千克力.
首页
上页
返回 第11页,共26页。
下页
结束
小结
运用微分学的理论,研究曲线和曲面的性质的数学分支—
—微分几何学.
1. 弧长微分 ds 1 y2 dx 或 ds (dx)2 (dy)2
3
要使 k最大, 必有 (4 5cos2 t )2 最小,
t , 3 此时 k最大,
22
首页
上页
返回 第13页,共26页。
下页
结束
补充:参数方程曲率公式
设
x y
(t ), (t ),
二阶可导,
dy dx
(t ) (t )
,
d2y dx 2
(t)
(t) (t) 3(t)
(t) .
高等数学上3.7平面曲线的曲率
首页
上页
返回 第1页,共26页。
下页
结束
一、 弧微分
设
在(a , b)内有连续导数, 其图形为 AB,
弧长 s AM s(x)
s M M M M x M M x
M M (x)2 (y)2
MM
x
y
y
f (x) M
B
A M y
x
oa x
bx
x x
M M 1 (y)2
的凹向一侧法线上取点 D 使
CR
T
M (x, y)
DM R 1
o
x
K
把以 D 为中心, R 为半径的圆叫做曲线在点 M 处的
曲率圆 ( 密切圆 ) , R 叫做曲率半径, D 叫做 曲率中心.
高等数学高数07第七节曲率

第七节 曲率在生产实践和工程技术中,常常需要研究曲线的弯曲程度,例如,设计铁路、高速公路的弯道时,就需要根据最高限速来确定弯道的弯曲程度. 为此,本节我们介绍曲率的概念及曲率的计算公式.分布图示★ 弧微分★ 曲率的定义 ★ 曲率的计算公式★ 直线与圆的曲率 ★ 例1 ★ 例2★ 曲率圆与曲率半径 ★ 例3★ 例4 ★ 例5 ★ 例6★ 内容小结 ★ 课堂练习★ 习题3-7 ★ 返回内容要点一、弧微分22)()(dy dx ds +=二、曲率及其计算公式.)1(232y y K '+''=三、曲率圆 曲率半径 曲率中心;例题选讲曲率的计算与应用例1 (E01) 抛物线c bx ax y ++=2上哪一点的曲率最大? 解 ,2b ax y +=',2a y =''∴.])2(1[|2|232b ax a K ++=显然,当abx 2-=时,K 最大. 又 ⎪⎪⎭⎫⎝⎛---a ac b a b 44,22为抛物线的顶点,故抛物线在顶点处的曲率最大.例2(E02) 在修筑铁路时,常需根据地形的特点和最高限速的要求来设计铁轨的圆弧弯道. 铁轨由直道转入圆弧弯道时, 若接头处的曲率突然改变, 容易发生事故, 为了行使平稳,往往在直道和圆弧弯道之间接入一段缓冲段A O(图3-7-7), 使轨道曲线的曲率由零连续地过渡到圆弧的曲率R 1, 其中R 为圆弧轨道的半径.证 根据分析,在缓冲段OA 上,,212x Rl y ='.1x Rly ='' 故在缓冲段始端0=x 处的曲率为.00=K )0,0(=''='y y 题意实际要求,0x l ≈,1⎪⎭⎫⎝⎛<<R l 故 0x x y ='Rl x 220=Rl l 22≈,2Rl =0x x y =''Rl x 0=Rl l ≈.1R= 故在终端A 的曲率为A K ()2321||x x y y ='+''=2322411⎪⎪⎭⎫ ⎝⎛+≈R l R ,1R≈).1(<<R l例3 (E03) 求曲线x y tan =在点)1,4(π处的曲率与曲率半径.解 ,sec 2x y ='x x y tan sec 22='',cos sin 23xx=曲率K 及曲率半径R 分别为 K ,)1(||2/32y y '+''=R K 1=.||)1(2/32y y '''+= 由24/='=πx y 及,44/=''=πx y 得点⎪⎭⎫⎝⎛1,4π处的曲率与曲率半径分别为 ,2554=K .455=R例4 求椭圆⎩⎨⎧==t b y ta x sin cos 在),0(b 点处的曲率及曲率半径.解 点),0(b 对应的参数,2π=t 由于,sin )(t a dtdxt -=='ϕ,cos )(t a t -=''ϕ ,cos )(t b dtdyt =='ψt b t sin )(-=''ψ 故将2π=t 代入得 ,2a dt dx -==⎪⎭⎫ ⎝⎛'πϕ,02=⎪⎭⎫ ⎝⎛''πϕ ,02==⎪⎭⎫ ⎝⎛'dtdy πψ,2b -=⎪⎭⎫ ⎝⎛''πψ由曲率公式, 有2/2/322)]()([|)()()()(|πψϕψϕψϕ='+''''-'''=t t t t t t t K 2a b =所求曲率半径为.2ba R =例5 (E04) 飞机沿抛物线4000/2x y =(单位为米)俯冲飞行, 在原点处速度为,/400秒米=v 飞行员体重70千克. 求俯冲到原点时,飞行员对座椅的压力.解 飞行员对座椅的压力(kg) ,P F Q += 其中飞行员的体重70=P (kg),离心力,2ρmv F =由40002x y =⇒0='x y 02000==x x ,0=0=''x y .20001=则曲线在原点处曲率为.20001=K 曲率半径为2000=ρ米. F ∴2000400702⨯=)(5600牛=),(4.571千克≈Q ∴)(4.571)(70千克力千克力+=).(4.641千克力=即:飞行员对座椅的压力为 641.4 千克力.例6 设)(x f y =为过原点的一条曲线, )0(),0(f f '''存在, 又知有一条抛物线)(x g y =与曲线)(x f y =在原点相切, 在该点处有相同的曲率, 且在该点附近此二曲线有相同的凹向, 求).(x g解 设.)(2c bx ax x g ++=依题可得),0()0(f g =),0()0(f g '=').0()0(f g ''='' 由0)0()0(==f g ⇒,0=c 由)0()0(f g '='⇒),0(f b '= 由)0()0(f g ''=''⇒),0(2f a ''=即),0(21f a ''= 因此所求函数为.)0()0(21)(2x f x f x g '+''=课堂练习1. 椭圆t x cos 2=, t y sin 3=上哪些点处曲率最大?。
高等数学 第3章 第九节 曲率
曲线的弯曲程度与下列两个量有关:
(1)切线转过的角度; (2)弧段的长度。 曲率:单位弧长上切线所转过的角度。
M1M2 N1N2
1 2
3
设 MM'的长度为
切线转过的角度为
平均曲率:
s , .
s
MM '的平均弯曲程度
K
s
y
M
•
s
M
M0
•
•
O
x
曲线在点M处的曲率:
K lim s0 s
x,
y
相应的有向弧段的值
s有增量 s,
s M 0 M M 0 M MM
s ?
x
y f x
M •
M0
y
• M•
x
s s MM MM MM o
x x x MM x
MM
MM
xs2与x2x总y是2 同号MM的MM
1 y 2 x
ds
lim
s
lim
MM
1
y
2
dx x0 x x0 MM
ds y
dx
3
1 y2 2
ds 1 y2 dx
d ?
dx
6
设曲线的参数方程为
x (t)
y
(t
)
't "t "t 't
K
'2 t '2 t 3/ 2
例1 计算 xy 1 在点 1,1 处的曲率。
解
y 1, x
y
1 x2
,
y
2 x3
.
y 1, y 2.
平均曲率的极限
若 lim 存在,则
高等数学曲率

yxddyxcRss2cin dd
1
R sin3
K
y
3
R
1 sin
3
3
(1 y2 )2 ( 1 cot 2 ) 2
1 csc 2
R
3
(csc 2 ) 2
1 . R
12
例3 抛物y线 ax2bxc上哪一点的曲 ? 率
解 y2a xb, y2a,
D
1
k
yf(x)
在凹的一侧取一点D,使
DM 1 , 以D为圆心, o
K
M
x
为半径作圆(如图),称此圆为曲线在点M处的曲率圆.
D曲率中 , 心 曲率半. 径
15
注意: 1.曲线上一点处的曲率半径与曲线在该点处的
曲率互为倒数.
即
1 K
,K
1
.
2.曲线上一点处的曲率半径越大,曲线在该点
复习
1.判定凹凸性的方法:
如果 f (x) 在 (a,b)内具有二阶导数,若在(a,b)内 (1) f(x)0,则曲线 f (x)在(a,b)内是凹的. (2) f(x)0,则曲线 f (x) 在 (a,b)内是凸的.
说明:拐点的横坐标可能是 y 0的根, 也可能是 y不存在的点.
弧微分公式
4
ds 1 y2dx
y
变形 ds
1
( dy)2 (d x)2
dx
(dx)2(dy)2
M
M0
ds
M
Tdy
R
dx
o
则有 (ds)2(dx)2(dy)2.
x0
x
xx x
弧微分的几何意义:ds 就是曲线 y f(x)上点M(x, y)
高等数学导数应用(三)曲率PPT课件

目录
• 曲率定义与计算 • 导数与曲率的关系 • 曲率在实际问题中的应用 • 曲率的应用案例分析 • 总结与展望
01
曲率定义与计算
曲率的定义
曲率是描述曲线在某一点弯曲程 度的量,定义为曲线在该点处切
线的斜率的变化率。
在二维平面上,曲线的曲率等于 其上任一点处切线的斜率的导数。
导数的性质
导数具有连续性、可导性、可积性等 性质,这些性质在研究函数的形态、 单调性、极值等问题中具有重要作用。
导数与曲率的关系
导数与曲率的关系
曲率是描述曲线在某一点弯曲程度的 量,与函数在该点的导数密切相关。 曲率等于函数在该点的导数的绝对值 。
导数与曲率的几何意义
在几何上,导数表示曲线在某一点的 切线斜率,而曲率表示该点附近曲线 的弯曲程度。因此,导数和曲率共同 决定了曲线在该点的形态。
在几何图形中,曲率的应用非常广泛,如圆、椭圆、 抛物线、双曲线等。
曲率决定了图形的形状和性质,如圆的曲率处处相等 且为常数,而抛物线的曲率只在顶点处为0。
在工程和科学研究中,曲率的应用也非常重要,如分 析机械零件的应力分布、研究光的传播路径等。
的定义
导数是函数在某一点的变化率,表示 函数在该点的切线斜率。
05
总结与展望
总结高等数学导数应用(三)曲率的主要内容
曲率的概念
曲率是描述曲线弯曲程度的量,对于二维平面上的曲 线,曲率等于切线方向的转动角速度。
导数与曲率的关系
曲率是函数二阶导数的几何意义,即曲率等于函数二 阶导数的值。
曲率的应用
曲率在几何、物理、工程等领域有着广泛的应用,如 分析机械零件的应力分布、预测股价波动等。
高等数学:第六节 曲率

四、作业
作业19
30
21
例4 求曲线y ln x与x轴交点处的曲率半径.
解 曲线y ln x与x轴的交点为M (1, 0). 在交点M处
的曲率为
| y'' |
1
k( x) [1 ( y' )2 ]3/ 2 2
. 2
曲率半径为R 1 2 2. k
22
三、小结
平均曲率 单位弧长的弧段上的切线转角, 即
k .
基点,
点M
是C
上某定点M
的
0
M
•
临近点. 又设M0、M处对应的弧长
M0
C P0 •
和倾斜角分别为s、s s和、 O
x
.
当点M沿曲线C趋于点M0时(此时s 0), 若平均曲率k
的极限存在, 则称此极限为曲线C在M0处的曲率, 记做k, 即
k= lim k lim d .
x0
MM0 s
当曲线y f ( x)在点M( x, y)处的曲率为k(k 0)时, 就可以通过半径为1/ k的圆, 将弯曲程度形象的表示 出来.
20
设曲线y f ( x)在点M(x,y)处的曲率为k(k 0), 在点M处的法线上取线段MC,使 MC =1 / k R. 以C为圆心,R为半径作圆,此圆称为曲线y f ( x) 在点M处的曲率圆. C称为曲线y f ( x)在点M处 的曲率中心. 曲率圆的半径R 1 / k称为曲线y f ( x) 在点M处的曲率半径.
dx
d
y''
y''
dx 1 tan2 1 ( y' )2 ,
转角的微分为d
y'' 1 ( y')2
高等数学课件3-5曲率

高等数学课件3-5曲率
汇报人:
目录
01 02 03 04 05 06
添加目录项标题
曲率的概念
曲率在高等数学中的意义
高等数学课件3-5曲率的讲解重点 如何理解高等数学课件3-5曲率的
意义 如何应用高等数学课件3-5曲率解
决实际问题
01
添加目录项标题
02
曲率的概念
曲率的定义
曲率是描述曲线 弯曲程度的量
曲率越大,曲线 弯曲程度越大
曲率是曲线在某 一点的切线方向 与该点处曲线的 法线方向之间的 夹角
曲率是曲线在某 一点的切线方向 与该点处曲线的 法线方向之间的 夹角
曲率的计算方法
曲率公式:k = 1/r,其中k为曲率,r 为半径
曲率圆:曲率半径的圆,曲率中心为 圆心,曲率半径为半径
曲率半径:r = 1/k,其中k为曲率
曲率在曲线和曲面中的应用
曲率是描述曲 线或曲面弯曲
程度的量
曲率越大,曲 线或曲面的弯
曲程度越大
曲率在微分几 何、拓扑学、 物理等领域有
广泛应用
曲率可以帮助 我们理解和分 析曲线和曲面 的性质,如长 度、面积、体
积等
曲率在微积分学中的应用
曲率是描述曲线弯曲程度的重要 参数
曲率在微积分学中用于求解曲线 的弧长、面积等问题
利用曲率进行创新和设计
曲率在工程设计中的应用:如 桥梁、建筑、机械等
曲率在艺术设计中的应用:如 雕塑、绘画、平面设计等
曲率在科学研究中的应用:如 物理、化学、生物等
曲率在商业设计中的应用:如 产品包装、广告设计等
感谢观看
汇报人:
添加标题
添加标题
高教社2024高等数学第五版教学课件-3.5 曲率

设, 是曲线 = ()的两个点,假如曲线在点和
点的切线与轴的夹角分别为和 + ,那么当点沿
曲线 = ()变到时,角度改变了,而改变这个角
度经过的路程则是弧长 = ,就用比值
来刻画
曲线段的弯曲程度,称为平均曲率。为了刻画曲线
在某点处的曲率,有下面的定义:
来向北最后拐向东了,即方向改变了90 ;另一方面是指在多远的路程上
改变了这个角度,如果两个弯都改变了90 ,但一个是在10m内改变的,另
一个是在1000m内改变的,当然前者比后者弯曲得厉害。由此可见,弯曲
程度是由方向改变的大小及在多长一段路程上改变的这两个因素所决定的,
并且弯曲程度与方向改变的大小成正比,与改变这个方向所经过的路程成
=
| ″ |
(1+ ′2 )3Τ2
=
2
(1+(−1)2 )3Τ2
=
12ຫໍສະໝຸດ =22
例4
抛物线 = 2 + + 上哪一点处的曲率最大?
′
″
解 由于 = 2 + = 2由曲率公式 得 =
显然 当2 + = 0即 = −
|2|
[1+(2+)2 ]3Τ2
第三章 导数的应用
第五节 曲率
在现实生活中,许多问题都要考虑曲线的弯曲程度,如修建铁
路时,铁路线的弯曲程度必须合适,否则容易造成火车出轨。数学
上常用“曲率”这一概念来描述曲线的弯曲程度。
一、 曲率的概念
人们坐汽车时,公路弯曲程度在车上是有感觉的。人们说这个弯大,
那个弯小,通常是从两个方面来说的:一是指公路方向改变的大小,如原
曲率的计算_高等数学(上册)_[共2页]
![曲率的计算_高等数学(上册)_[共2页]](https://img.taocdn.com/s3/m/53337ae0f111f18582d05a64.png)
然弧 s 是 x 的函数,记为 s = s ( x) ,且 s ( x) 是 x 的单调增加函数. 下面来求 s = s ( x) 的导数与微分. 如图 3-7-2 所示,设 x, x + Δx 为 (a,b) 内两个邻近的点,它们分别对应曲线 y = f ( x) 上两点
MM ′ MM ′
⎞2 ⎟⎟⎠
⋅
⎡ ⎢1 ⎢⎣
+
⎛ ⎜⎝
Δy Δx
⎞2 ⎟⎠
⎤ ⎥ ⎥⎦
.
因为当 Δx → 0 时, M ′ → M ,所以
从而
⎛
lim
M ′→M
⎜⎜⎝
MM ′ MM ′
⎞2 ⎟⎟⎠
=1,
即有
⎛ ⎜⎝
ds dx
⎞2 ⎟⎠
=
lim
Δx → 0
⎛ ⎜⎝
Δs Δx
ห้องสมุดไป่ตู้⎞2 ⎟⎠
=
1
+
⎛ ⎜⎝
dy dx
⎞2 ⎟⎠
,
ds = ± dx
1+
⎛ ⎜⎝
dy dx
⎞2 ⎟⎠
.
由于 s = s ( x) 是单调增加函数,故根号前应取正号,所以
ds = 1+ y′2 dx 或 ds = (dx)2 + (dy)2 , 称之为弧 s ( x) 关于 x 的弧微分.
130
3.7.2 曲率的计算
为了计算曲率,首先介绍弧微分的概念.
设函数 y = f ( x) 在 (a,b) 内具有连续导数,在曲线 y = f ( x) 上任取一固定点 M 0 ( x0 , y0 ) 作为度量
高等数学《曲率》

为零,并且当 l 很小 R
( l 1) 时,在终端 R A的曲率近似为 1 .
R
y
B
R
l
A( x0 , y0 )
o
C( x0 ,0)
x
证 如图
y
B
x的负半轴表示直道,
OA是缓冲段, AB是圆弧轨道.
在缓冲段上,
y 1 x2 , y 1 x.
2Rl
Rl
R
l
A( x0 , y0 )
o
C( x0 ,0)
o
C( x0 ,0)
x
l 1, R
略去二次项 l2 4R2
,
得
kA
1. R
三、曲率圆与曲率半径
定义 设曲线 y f ( x) 在点 y
M( x, y) 处的曲率为k(k 0). 在点 M 处的曲线的法线上,
D 1
k
y f (x)
在凹的一侧取一点D, 使 DM
o
1 .以 D 为圆心, 为半径
二、k cos x , sec x .
三、k 2 . 3a sin 2t0
五、( ,1)处曲率半径有最小值 1. 2
六. ( 1 ln 2, 1 ), 3 3 .
2
2
2
3、0.
的曲率突然改变,容易发生事故,为了行驶平 稳,往往在直道和
弯道之间接入一段
缓冲段(如图),使曲 率连续地由零过渡
到 1 (R为圆弧轨道 R
的半径).
点击图片任意处播放\暂停
通常用三次抛物线
y
1 6Rl
x 3,x
[0,
x0
].作为
缓冲段 OA,其中 l 为 OA的长度,验证缓冲段
曲率及其计算方法

曲率及其计算方法曲率是求解曲线弯曲程度的一种数学概念,可以十分精确地描述曲线的形态。
在物理、工程、制图等领域中,曲率的计算十分重要,可以用来精确描述曲线的性质和特征。
这篇文章将介绍曲率的概念、定义和计算方法,并通过实例来说明它对于现实问题的应用。
一、曲率的概念和定义在平面或者空间中,曲线上的每一个点都可以定义一个曲率。
曲率是该点所在曲线的弯曲程度的度量。
在数学中,曲率的定义如下:(1) 平面曲线上一点的曲率:曲率k是切线方向上一阶导数 |v'(t)| 与切向量方向上一阶导数|v(t)| 之比的绝对值:k = |v'(t)| / |v(t)|其中v(t)是曲线的弧长参数表示,v'(t)是v(t)关于t的一阶导数。
曲率k的单位是1/长度。
(2) 空间曲线上一点的曲率:空间曲线上一点的曲率是该点在曲线切平面中切向量的曲率。
二、曲率的计算方法有了前面的曲率概念和定义的基础,接下来我们将介绍如何计算曲线的曲率。
首先,我们需要了解两个概念:弧长和参数式。
(1) 弧长弧长是曲线长度的测量量。
对于参数式 r(t) = (x(t),y(t)), t∈[a,b]的曲线,它的弧长可以通过下式计算:s = ∫(a,b) |r'(t)| dt其中 |r'(t)| 表示 r(t) 的变化率,s 为曲线长度。
通过弧长可以确定曲线上每一点的位置以及曲线围成面积的大小。
(2) 参数式对于平面曲线,我们可以用参数式来表示曲线上的点,即x(t) = x,y(t) = y其中t作为参数。
通过变化t的值,我们可以确定曲线上的每一个点。
同理,对于空间曲线,我们也可以用参数式来表示曲线上的每一个点。
现在我们已经具备了曲率计算的前置知识,接下来我们将详细介绍两种曲率的计算方法。
(1) 弧长参数曲率计算法对于参数式表示的曲线,我们可以通过弧长参数求解其曲率,具体计算方法如下:1. 计算弧长s:s = ∫(a,t) |r'(t)| dt其中r'(t)为r(t)的一阶导数。
高等数学 第七节 曲率完美版PPT资料

ds dx
lim
x 0
s lim x2 y2 x0
x2 y2 x
,
其中 lim s 1 , x0 x2 y2
lx i0m x 2 x y 2 lx i0m 1 x y2
1
dy dx
2
1y2 ,
ds dy
dx
ds1y2, dx
ds2 dx2 d y2
时, F发生跳变而震动 , 只有k当 连续,时 火车运行才能 .
因此 , f(x)应当满:足 1. f(0)0, 2. f(0)0, 与 BO 方向一致
3. f(0)0, 即 k 0与 BO 段曲率相同 4. f(2)2. 火车过 A点
如 f ( x 果 ) a 3 x 3 a 2 选 x 2 a 1 x a 0 根据前述,确 四定 f个 (x)的 条四 件个 ,得 :系数
按 . 曲率越大 , 弯曲越厉害 . 直线曲率 k 0 .
例 1 .y a 2 x 2 . ( a x a )
半径为 a 的上半圆方程 .
y x , a2 x2
y
a2 a2 x2
3
,
a2
曲率k
y 1y2
3 2
a2 x2 3
1
a
x2 2x
2
3
2
1 a
.
结论:
半径为 a 的圆之圆弧曲率处处为
*曲率中(心 曲率圆的)圆x心 弧微分 .
弧 d 1 微 s y 2 d d x 分 2 d x 2 y x 2 y 2 d t .
曲率k
y
1y2
3 2
.
圆的曲率
1 R
,
R圆半径.
曲率半 k 1径 1yy2
高等数学曲率

例2. 我国铁路常用立方抛物线 y 1 x3 作缓和曲线, 6Rl
其中R是圆弧弯道的半径, l 是缓和曲线的长度, 且 l << R.
求此缓和曲线在其两个端点 O(0, 0), B(l , l2 ) 处的曲率.
解: 当 x [0,l ]时,
6R y
y 1 x2 l 0 2 Rl 2 R
R
y 1 x Rl
K y 1 x Rl
显然
K x0 0;
K
xl
1 R
B
ol
x
y 1 x3 6Rl
机动 目录 上页 下页 返回 结束
例3.
求椭圆
xy
a cos t bsin t
(0 t 2 ) 在何处曲率最大?
解: x asin t ; y bcos t ;
x a cos t y bsin t
机动 目录 上页 下页 返回 结束
设一工件内表面的截痕为一椭圆, 现要用砂轮磨
机动 目录 上页 下页 返回 结束
K 的曲率半径 R , 并分析何处 R 最小?
我国铁路常用立方抛物线
s
机动 目录 上页 下页 返回 结束
我国铁路常用立方抛物线
点 M 处的曲率 把以 D 为中心, R 为半径的圆叫做曲线在点 M 处的
ds
ds
T
M dy
dx
o x x dx x
机动 目录 上页 下页 返回 结束
二、曲率及其计算公式 在(a , b)内有连续导数,
摆线 目录 上页 下页 返回 结束
s , 在光滑弧上自点 M 开始取弧段, 其长为 曲线 C 称为曲线 G 的渐伸线 .
注意: 直线上任意点处的曲率为 0 !
对应切线
高等数学(上)课件:3_7曲率

b
这说明椭圆在点( a, 0) 处曲率 a
ax
最大.
b
例4. 设一工件内表面的截痕为一椭圆, 现要用砂轮磨 削其内表面 , 问选择多大的砂轮比较合适?
解: 有上述可知
椭圆在
处曲率最大 ,
y
即曲率半径最小, 且为
R
(a2 sin2 t
b2
cos2
t
)
3 2
ab
t0
o
x
显然, 砂轮半径不超过 时, 才不会产生过量磨损 , 或有的地方磨不到的问题.
3.曲线上一点处的曲率圆弧可近似代替该点附 近曲线弧(称为曲线在该点附近的二次近似).
例4. 设一工件内表面的截痕为一椭圆, 现要用砂轮磨 削其内表面 , 问选择多大的砂轮比较合适?
解: 设椭圆方程为
x asin t ;
x acost
x 表示对参
y bcost ;
y bsin t
数 t 的导数
显然
K x0 0;
K
xl
1 R
y
R
B
ol
x
y 1 x3 6Rl
主要内容
1 弧微分 2 曲率及其计算公式 3 曲率圆与曲率半径
曲率圆和曲率半径
设曲线y f ( x)在点 y
M ( x, y)处的曲率为K (K
y f (x)
0).在点 M 处的曲线的
D
法 线 上, 在 凹 的 一 侧 取 一
高等数学(上) 3.7节 曲率
主要内容
1 弧微分 2 曲率及其计算公式 3 曲率圆与曲率半径
弧微分
设
在(a , b)内有连续导数, 其图形为 AB,
弧长 s AM s(x)
高等数学(上册)-第3章第6讲(弧微分与曲率)[19页]
![高等数学(上册)-第3章第6讲(弧微分与曲率)[19页]](https://img.taocdn.com/s3/m/9fb41ee71a37f111f0855b33.png)
18
高等数学(上册)(慕课版)
学海无涯,祝你成功!
主讲教师 |
O
x0
y f (x)
M
•
x
x
4
一、弧微分
弧微分公式 ds ? ds s(x)dx 先求s s(x)的导数 d s lim s
d x x0 x
s ? x
在x处给自变量x一增量x,
相应的有向弧段的值s有增量s,
s M0M M0M MM
s s MM MM MM x x x MM x
解 根据摆线方程可得x(t) a a cos t,y(t) a sin t,故
y(x) d y y(t) sin t cot t ,
d x x(t) 1 cos t
2
y(x)
d2 y d x2
d dt
cot
t 2
1 x(t)
1 2 sin2
t
1 a(1 cos t)
a(1
1 cos
y
K
y
3
(1 y2 )2
分析
K
d
ds
s s(x), (x)
d
ds
d?dx
ds dx
M
•
s
M
M •
0
•
O
x
ds dx
1 y2
d
dx
?
12
二、曲率
证明
tan y,
sec2 d y.
dx
d
dx
y
sec2
y
1 tan2
y 1 y2
.
又 d s 1 y2 dx
高等数学 曲率半径的正负判断

高等数学曲率半径的正负判断
在高等数学中,曲率半径是一个重要的概念。
曲率半径是曲线在某一点处的曲率半径的倒数,用R表示。
当R>0时,曲线在该点处的曲率方向与曲线的切线方向一致;当R<0时,曲线在该点处的曲率方向与曲线的切线方向相反。
为了判断曲线在某一点处的曲率半径的正负,我们需要计算曲线在该点处的曲率。
曲率可以通过求解曲线的二阶导数来得到。
如果二阶导数为正,则曲线在该点处的曲率为正;如果二阶导数为负,则曲线在该点处的曲率为负。
根据曲线在该点处的曲率符号,我们可以得到曲线在该点处的曲率半径的正负。
需要注意的是,如果曲线在某一点处的曲率为0,则曲率半径不存在。
这种情况通常出现在曲线的拐点处。
此外,曲线在某一点处的曲率半径的正负还与曲线在该点处的方向有关。
如果曲线在该点处的方向与曲率方向相同,则曲率半径为正;如果曲线在该点处的方向与曲率方向相反,则曲率半径为负。
综上所述,判断曲线在某一点处的曲率半径的正负需要计算曲线在该点处的曲率,并考虑曲线在该点处的方向与曲率方向的关系。
这是高等数学中曲率半径的重要知识点,也是应用数学中很多问题的关键。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y d 2. 曲率公式 K 3 2 ds (1 y ) 2 3. 曲率圆 2 32 1 (1 y ) 曲率半径 R y K 2 y (1 y ) x y 曲率中心 2 1 y y y
目录 上页 下页 返回 结束
思考与练习
K s
点 M 处的曲率
M
M s
d K lim s 0 s ds
注意: 直线上任意点处的曲率为 0 !
目录 上页 下页 返回 结束
例1. 求半径为R 的圆上任意点处的曲率 .
解: 如图所示 ,
s R
1 K lim s 0 s R
1) 2 2 x
3
O 1
x
2
显然 R
x 1
2 为最小值 .
利用 a 2 b 2 2 ab
目录 上页 下页 返回 结束
d K ds
d (arctan y) d x
又 故曲率计算公式为
K
y (1 y )
2 32
当 y 1 时 , 有曲率近似计算公式 K y
目录 上页 下页 返回 结束
说明:
x x(t ) 给出, 则 (1) 若曲线由参数方程 y y (t ) x y x y K 2 2 32 (x y )
目录 上页 下页 返回 结束
f (t ) (a 2 b 2 ) sin 2 t
三、 曲率圆与曲率半径
设 M 为曲线 C 上任一点 , 在点 M 处作曲线的切线和法线, 在曲线 的凹向一侧法线上取点 D 使
y
D( , )
C
R
M ( x, y )
T
1 x O DM R K 把以 D 为中心, R 为半径的圆叫做曲线在点 M 处的
由此可得曲率中心公式
2 y (1 y ) x y 1 y2 y y
y
D( , )
C
O
R
M ( x, y)
T
x
(注意 y 与 y 异号 )
当点 M (x , y) 沿曲线
移动时, 相应的曲率中心
的轨迹 G 称为曲线 C 的渐屈线 , 曲线 G 的渐伸线 . 满足方程组 ,C 称为曲线 2 2 2 ( M ( x , y ) 在曲率圆上 ) 曲率中心公式可看成渐 ( x ) ( y ) R x 屈线的参数方程 (参数为x). ( DM MT ) y y 点击图中任意点动画开始或暂停
第七节 平面曲线的曲率
曲线的弯 与切线的转角有关 曲程度 与曲线的弧长有关 主要内容: 一、 弧微分 二、 曲率及其计算公式 三、 曲率圆与曲率半径
目录 上页
第三章
M
M M
下页
返回
结束
一、 弧微分
设 在(a , b)内有连续导数, 其图形为 AB, 弧长 s AM s( x)
1 a (1 cos t ) 2
y(1 y2 ) x y 1 y2 y y
摆线
a ( sin ) a (1 cos )
( 仍为摆线 )
O
摆线 目录 上页 下页 返回 结束
内容小结
2 2 d s (d x ) (d y ) 1. 弧长微分 ds 1 y dx 或 2
目录 上页 下页 返回 结束
例4. 设一工件内表面的截痕为一椭圆, 现要用砂轮磨
削其内表面 , 问选择多大的砂轮比较合适? 解: 设椭圆方程为 由例3可知, 椭圆在 处曲率最大,
2 2
3
例3
y O
即曲率半径最小, 且为
x
(a sin t b cos t ) R ab
显然, 砂轮半径不超过
或有的地方磨不到的问题.
求此缓和曲线在其两个端点 解: 当 x [ 0 , l ] 时, 1 2 l 0 y x 2 Rl 2R 1 y x Rl 1 x K y Rl 1 显然 K x 0 0 ; K x l
处的曲率.
y
R B
O
l
1 3 y x 6 Rl
x
R
目录
上页
t
f (t )
0
b
2
π 2
π
2
3π 2
2π
b
2
a
b
2
a
2
设 0 b a , 则t 0 , π , 2 π时
y b
f (t ) 取最小值 , 从而 K 取最大值 .
这说明椭圆在点 ( a , 0 ) 处曲率
a
O
b
a x
最大.
K 最大
f (t ) a 2 sin 2 t b 2 cos 2 t 最小
1. 曲线在一点处的曲率圆与曲线有何密切关系?
答: 有公切线 ;
2. 求双曲线
凹向一致 ;
曲率相同.
的曲率半径 R , 并分析何处 R 最小? y 1 2 解: y 2 , y 3 , 则 x x 1
2
3 2
(1 y ) R y
(1
2
1) 2 x4
3
x3
1 ( x2 2
(2) 若曲线方程为 x ( y ) , 则
K
x ( 1 x )
2
3 2
K
y (1 y )
上页 下页 返回
2
3
2
目录
结束
1 3 x 作缓和曲线, 例2. 我国铁路常用立方抛物线 y 6 Rl 其中R是圆弧弯道的半径, l 是缓和曲线的长度, 且 l << R.
下页
返回
结束
例3. 求椭圆 解: x a sin t ;
在何处曲率最大?
y b cos t ;
故曲率为
x a cos t y b sin t
2
K
x y x y (x y )
2 2
3
ab
(a sin t b cos t )
y
s M M M M x M M x
M M (x) 2 (y ) 2 MM x MM y 2 1 ( ) MM x s s( x) lim 1 ( y) 2 x0 x
y f ( x) B M A M y x
求此缓和曲线在其两个端点 说明:
处的曲率.
铁路转弯时为保证行车 平稳安全, 离心力必须
连续变化 , 因此铁道的 曲率应连续变化 .
点击图片任意处播放\暂停
目录 上页 下页 返回 结束
1 3 x 作缓和曲线, 例2. 我国铁路常用立方抛物线 y 6 Rl 其中R是圆弧弯道的半径, l 是缓和曲线的长度, 且 l << R.
O a
x
x x
b x
MM lim 1 x0 M M
目录
上页
下页
返回
结束
2 2 或 d s (d x ) (d y ) ds 1 ( y) dx 2
x x(t ) 若曲线由参数方程表示: y y (t )
则弧长微分公式为
几何意义:
ds x 2 y 2 dt
2
2
2
t 0
才不会产生过量磨损 ,
目录
上页
下页
返回
结束
例5. 求摆线
的渐屈线方程 . 摆线
d ( y ) dt
sin t y , 解: y y x 1 cos t x 代入曲率中心公式, 得渐屈线方程 a (t sin t ) a (cos t 1)
x 表示对参 数 t 的导数
y
ds M T
dy sin dsΒιβλιοθήκη dx cos ; ds
d x O x x dx x
目录 上页 下页 返回 结束
M
T dy
二、曲率及其计算公式
在光滑弧上自点 M 开始取弧段, 其长为 s , 对应切线 转角为 , 定义 弧段 s 上的平均曲率
曲率圆 ( 密切圆 ) , R 叫做曲率半径, D 叫做 曲率中心. 在点M 处曲率圆与曲线有下列密切关系: (1) 有公切线; (2) 凹向一致; (3) 曲率相同 .
目录 上页 下页 返回 结束
设曲线方程为 曲率半径及曲率中心
且
求曲线上点M 处的 的坐标公式 .
设点M 处的曲率圆方程为
y
故曲率半径公式为
M s R M
可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ;
R 愈大, 则K 愈小 , 圆弧弯曲得愈小 .
目录
上页
下页
返回
结束
曲率K 的计算公式 设曲线弧 y f ( x) 二阶可导, 则由
得
π π tan y ( 设 ) 2 2 arctan y
2 1 (1 y ) R K y
3 2
D( , )
C
O
R
M ( x, y )
T
x
, 满足方程组
2 2 2 ( x ) ( y ) R x y y
( M ( x , y ) 在曲率圆上 )
( DM MT )
目录 上页 下页 返回 结束
2 2 2 2
3 2
K 最大
求驻点:
f (t ) a 2 sin 2 t b 2 cos 2 t 最小
f (t ) 2a 2 sin t cos t 2b2 cos t sin t (a 2 b 2 ) sin 2 t
