第五章_系统的稳定性
机械工程控制基础第五章系统稳定性分析

9/88
5.3 代数稳定性判据 劳斯判据
Logo
同时,如果劳斯阵列中第一 列所有项均为正号,则系统 一定稳定。
劳斯阵列为
sn a0 a2 a4 a6 s n1 a1 a3 a5 a7 s n2 b1 b2 b3 b4 s n3 c1 c2 c3 c4
由劳斯阵列的第一列看出:第一列中系数符号全为正
值,所以控制系统稳定。
16/88
Logo
5.3 代数稳定性判据 劳斯判据
例2 设控制系统的特征方程式为
s4 2s3 3s2 4s 3 0
试应用劳斯稳定判据判断系统的稳定性。
解:首先,由方程系数可知已满足稳定的必要条件。其次,排劳
阵列
s4 1 3 3
2/88
5.1 系统稳定性的基本概念
d
o
F
Logo
b
c
M
o
稳定性的定义:若控制系统在任何足够小的初始偏差的 作用下,其过渡过程随着时间的推移,逐渐衰减并趋于 零,具有恢复到原来状态的性能,则该系统是稳定的, 否则,该系统为不稳定。
3/88
Logo
5.2 系统稳定的充要条件
N(s)
X i s
+
G1 s
➢ 劳斯判据还说明:实部为正的特征 根数,等于劳斯阵列中第一列的系 数符号改变的次数。
12/88
5.3 代数稳定性判据 劳斯判据
Logo
劳斯判据的表述:
1.系统闭环传递函数特征方程式的系数没有为0的, 同时都是正数。(必要条件,要想系统稳定必 须满足这个条件)
2.劳斯阵列的第一列全部为正。(充分条件)
机械工程控制基础课件第5章

n
(s s1 )( s s2 )(s sn ) sn ( si )sn1 ( si s j )sn2 (1)n si
i 1
i j
i 1
i1, j2
11
比较系数,得出根与系数的关系:
an1
an
n
i 1
si ,
an3
an
n
si s j sk ,
i jk
i 1, j 2,k 3
自由响应
强迫响应
n
n
xo(t )
A1i e si t
A2i e si t B(t )
i 1
i 1
初态引起的 输入引起的自由响
自由响应
应
si:系统的特征根
5
1) 当系统所有的特征根si(i=1,2,…,n)均具有负实部 (位于[s]复平面的左半平面)
ltim
n i 1
A1i e si t
a2>0, a1>0, a0>0 三阶系统(n=3)稳定的充要条件: a3>0, a2>0, a1>0,a0>0, a1a2-a0a3>0
17
【例2】已知=0.2,n=86.6,K取何值时,系统能稳定?
系统开环传递函数:
GK (s)
Xo( s ) E(s)
2 n
(
s
K
)
s2 (s 2 n )
系统闭环传递函数:
对其求导得零行系数。 继续计算Routh表的其余各元。
劳斯表出现零行系统一定不稳定
24
【例5】系统特征方程 D(s)=s5+2s4+24S3+48s2-25s-50=0 试用Routh表判别系统的稳定性。
第五章_控制系统的稳定性分析

, c2
b1a5 a1b3 b1
, c3
b1a7 a1b4 b1
f1
e1d 2
e1
d1e2
这样可求得n+1行系数
14
这种过程需一直进行到第n行被算完为止,系数 的完整阵列呈现一个倒三角形。
注意:
为简化计算,可用一个正整数去除或乘某一整个 行,并不改变稳定性结论。
15
劳斯稳定判据
劳斯稳定判据是根据所列劳斯表第一列系数符 号的变化,去判别特征方程式根在S平面上的具体 分布,过程如下:
27
5.3.4劳斯-赫尔维茨稳定性判据的应用
判定控制系统的稳定性
[例5-7] 系统的特征方程为:s4 2s3 3s2 4s 5 0 ,判断系统的稳定性。
[解]:排列劳斯阵如下:
s4 1 3 5 s3 2 4 0
因阵第为一,a列i 不0全, (为i 正0,~所4)以,,且系劳统斯
不稳定。
8
0
3
j 2 , j2
S0
16
显然这个系统处于临界稳定状态。
22
5.3.2 劳斯判据的应用
稳定判据只回答特征方程式的根在S平面上的分布 情况,而不能确定根的具体数据。也即也不能保证系 统具备满意的动态性能。换句话说,劳斯判据不能表 明系统特征根在S平面上相对于虚轴的距离。但能判断 是否所有特征根都落在虚轴的左半平面.若用S=Z-1带 入特征方程中,求出的根的实部即为特征根距S=-1垂线 的距离.可判断稳定程度.
s2 1 5 0 由于劳斯阵第一列有两次符号变
2
如果系统不稳定,就会在任何微小的扰动作用下偏离原 来的平衡状态,并随时间的推移而发散。
因此,如何分析系统的稳定性并提出保证系统稳定的措施, 是自动控制理论的基本任务之一。
第五章_系统的稳定性修改

第五章 系统的稳定性本章主要介绍了稳定性的基本概念,判断线性系统稳定性的基本出发点,着重介绍了Routh 稳定判据、Nyquist 稳定判据及Bode 判据的基本原理和方法,并在此基础上讨论系统的相对稳定性及最小相位系统和非最小相位系统的概念。
这些内容,对于分析和设计系统是十分重要的。
系统的稳定性是保证控制系统正常工作的首要条件,也是控制系统的重要性能指标之一。
因此,分析系统的稳定性并求出保证系统稳定的条件,是控制理论的重要组成部分。
5.1 系统稳定性的基本概念控制系统在外来干扰的作用下,被控量会偏离平衡状态产生偏差,一旦干扰消失后,经过足够长的时间,系统又能够逐渐恢复到原来的状态,则系统是稳定的;否则,系统就是不稳定的。
如图5-1所示的小球,当小球处于图中a 点时,如果有适当的外力作用在小球上,将小球带离a 点,如带到d 点,外力去掉,小球会在d 、e 之间来回滚动,经过一段时间后,最后会停在a 点,说明小球处于a 点是稳定的。
当小球处于b 、c 点时,只要有外力作用在小球上将小球带离b 、c 点,外力去掉后,小球便不会回到原来的位置上,说明小球在b 、c 时是不稳定的。
小球运动的过渡过程曲线如图5-2中a 、b 所示。
t(a)t(b)图5-2 小球运动的过渡过程曲线由上例可知,如果一个系统在干扰消失后,随着时间的推移,系统能恢复到原平衡位置或达到一个新的平衡位置,说明此系统是稳定的。
否则,称该系统是不稳定的。
系统的稳定性是系统本身的一种固有特性,它只决定于系统本身的结构和参数匹配,而与外作用无关。
不稳定的系统不但不能正常工作,有时甚至会使系统本身遭受严重破坏。
5.1.1 判断线性系统稳定性的基本出发点一般的线性定常系统的过渡过程特性,可用高阶线性微分方程来描述:110101()()()()()()n n m m n m a y t a y t a y t b x t b x t b x t --+++=+++ (5-1)式中, ()x t 为系统的输入,()y t 为系统的输出,00,n m a a b b 是由系统结构所决定的常数,研究此微分方程的解,就可研究所描述系统的稳定性。
第5章 系统的稳定性

s5 s4 s s
3
1
24
48
0
96
25
50 0
F (s) 2s 4 48s 2 50 0
取F(s)对s的导数得新方程:
2
0
8
24
0
F (s) 8s3 96s 0
用上式中的系数8和96代替0元 行,继续进行运算。
2
50
0
0
s1 s0
112 .7
50
改变符号一次
武汉理工大学材料学院 当解析点s按顺时针方向沿Ls变化一周时,向量F(s)将按顺时针方 向旋转N 周,即F(s)以原点为中心顺时针旋转N 周,这就等于曲线LF 顺时针包围原点N 次。若令Z 为包围于Ls内的F(s)的零点数,P 为包 围于Ls 内的F(s)的极点数,则有 N =Z-P
j
Im
(5.3.2)
武汉理工大学材料学院
(2)令s=z-1,代入特征方程得:
( z 1)3 14( z 1)s 2 40( z 1) 40K 0
即
z 3 11z 2 15z 40K 27 0
由Routh表和Routh判据得:
列Routh表如下:
s3
1
11
15
s2
40 K 27
4 2
解此辅助多项式可得:
s 1; s j5
这两对复根是原特征方程的根的一部分。
武汉理工大学材料学院
四、相对稳定性的检验
对于稳定的系统,应用Routh判据还可以检验系统 的相对稳定性。方法如下: (1)将s平面的虚轴向左移动某个数值,即令s=z- σ (σ 为正实数),代入系统特征方程,则得到关于z的特 征方程。
控制工程基础:第五章系统稳定性

∆2 = a1 a0 a3 a2 = a 1a 2 − a 0 a 3 > 0
∆n
L L L 0 0 0 M 0 an
a5 L
a4 L a3 L M O M 0
a1 ∆3 = a 0 0
a3 a2 a1
0 2 2 a 4 = a 1a 2 a 3 − a 4 a 1 − a 0 a 3 > 0 a3
− c2 =
劳斯表的列法
前两行为特征方程的系数,右移一位降两阶; 前两行为特征方程的系数,右移一位降两阶; 第三行起元素的计算为: 第三行起元素的计算为:分母为上一行第一 个元素; 个元素; 分子为一行列式,第一列为上两行的第一列, 分子为一行列式,第一列为上两行的第一列, 第二列为所计算元素右肩上元素。 第二列为所计算元素右肩上元素。次对角线 减主对角线元素。 减主对角线元素。 一行可同乘以或同除以某正数
c( t ) = ∑ c i e
i =1
k
pi t
+ ∑ e (A j cos ω j t + B j in ω j t )
j=1
r
σ jt
由上式知: 如果p 均为负值, 如果 i 和 σ i 均为负值 , 当 t
∞ 时 , c(t)
0。 。
自动控制系统稳定的充分必要条件: 系统特征方程的根全部具有负实部, 系统特征方程的根全部具有负实部, 闭环系统的极点全部在S平面左半部。 即:闭环系统的极点全部在S平面左半部。 系统特征方程
a4 a5 b3 c3 …
a6 a7 b4 c4 …
… … … …
a1 a5 a1a4 − a0 a5 = a1 a1 a1 a3 b1 b2 b1a3 − a1b2 = b1 b1 a1 a5 b1 b3 b1a5 − a1b3 = b1 b1
第五章第五节 生态系统的稳定性

恢复力稳定性高的生态系统特征:
① 生物种类较少,物种扩张受到的制约较小。
恢复力强
恢复力弱
恢复力稳定性高的生态系统特征:
②、生物个体小,繁殖快。能以休眠方式渡 过不利时期或产生适应新环境的变异。
6、在草原上人工种草,为了防止鸟把草籽吃掉, 用网把试验区罩上,后来发现,草的叶子几乎被 虫吃光,而没加网罩的草地反而长得较好。造成 这种现象的原因是( C ) A.植被破坏 B.环境污染 C.食物链被破坏 D.缺水干旱 7、生态系统能够保持稳定的原因主要是( A.相对稳定的物质循环 B.缺水干旱 C.自动调节能力 D.食物链被破坏
丁 甲 乙 丙 甲 乙
丙
甲 乙 丁
丙 甲
丁
乙 丁 丙
A
B
C
D
6、某生态学家以“保护和利用草原生态系统”为课题, 对某草原进行了几项专题研究,并绘制了如下两图。其 中:甲图表示一个鼠群迁入一个新的生态系统后的种群 增长曲线;乙图表示单位面积的放牧量与生产者的净生 产量的关系,图中的虚线代表未放牧时,草原中生产者 的净生产量,请据图分析并回答下列问题:
负反馈调节 兔与植物的关系
兔的数量增加 兔吃大量植物 兔因饥饿死亡
兔吃少量植物 植物减少
兔的食物增加
植物增加
结果:抑制或减弱了最初发生的变化,使 生态系统达到或保持稳定。 范围:生物群落内部、 生物群落与无机环境之间
正反馈
生态系统中某一成分 的变化所引起的其它 一系列的变化,反过 来加速最初发生变化 的成分所发生的变化。
恢复力强
恢复力较弱
3、抵抗力稳定性与恢复力稳定性的关系
第五章系统的稳定性-机械工程控制基础-教案

Chp.5系统稳定性基本要求1.了解系统稳定性的定义、系统稳定的条件;2.掌握Routh判据的必要条件和充要条件,学会应用Routh判据判定系统是否稳定,对于不稳定系统,能够指出系统包含不稳定的特征根的个数;3.掌握Nyquist 判据;4.理解Nyquist 图和Bode 图之间的关系;5.掌握Bode 判据;6.理解系统相对稳定性的概念,会求相位裕度和幅值裕度,并能够在Nyquist 图和Bode 图上加以表示。
重点与难点本章重点1.Routh 判据、Nyquist 判据和Bode 判据的应用;2.系统相对稳定性;相位裕度和幅值裕度求法及其在Nyquist图和Bode 图的表示法。
本章难点Nyquist 判据及其应用。
§1 概念示例:振摆1、稳定性定义:若系统在初始条件影响下,其过渡过程随时间的推移逐渐衰减并趋于0,则系统稳定;反之,系统过渡过程随时间的推移而发散,则系统不稳定。
(图5.1.2)讨论:①线性系统稳定性只取决于系统内部结构和参数,是一种自身恢复能力。
与输入量种类、性质无关。
②系统不稳定必伴有反馈作用。
(图5.1.3)若x0(t)收敛,系统稳定;若x0(t)发散,则系统不稳定。
将X0(s)反馈到输入端,若反馈削弱E(s) →稳定若反馈加强E(s) →不稳定③稳定性是自由振荡下的定义。
即x i(t)=0时,仅存在x i(0-)或x i(0+)在x i(t)作用下的强迫运动而系统是否稳定不属于讨论范围。
2、系统稳定的条件:对[a n p n+a n-1p n-1+…a1p+a0]x0(t)=[b m p m+b m-1p m-1+…b1p+b0]x i(t)令B(s)= a n p n+a n-1p n-1+…a1p+a0 A(s)= b m p m+b m-1p m-1+…b1p+b0初始条件:B0(s) A0(s)则B(s)X0(s)- B0(s)= A(s)X i(s)- B0(s)X i(s)=0,由初始条件引起的输出:L-1变换根据稳定性定义,若系统稳定须满足,即z i为负值。
《自动控制原理》第五章:系统稳定性

5.2 稳定的条件
当σi和λi均为负数,即特征根的 σi和λi均为负数, 均为负数 实部为负数,系统是稳定的; 实部为负数,系统是稳定的; 或极点均在左平面。 或极点均在左平面。
5.3 代数稳定性判据
定常线性系统稳定的充要条件 定常线性系统稳定的充要条件是特征方程的根具有负 充要条件是特征方程的根具有负 实部。因此,判别其稳定性,要解系统特征方程的根。为 实部。因此,判别其稳定性,要解系统特征方程的根。 避开对特征方程的直接求解,可讨论特征根的分布, 避开对特征方程的直接求解,可讨论特征根的分布,看其 是否全部具有负实部,并以此来判别系统的稳定性,这样 是否全部具有负实部,并以此来判别系统的稳定性, 也就产生了一系列稳定性判据。 也就产生了一系列稳定性判据。 其中最主要是E.J.Routh(1877 )h和Hurwitz( 其中最主要是E.J.Routh(1877年)h和Hurwitz(1895 E.J.Routh(1877年 年)分别提出的代数判据。 分别提出的代数判据 代数判据。
习题讲解: 习题讲解:
µ
G1
Q21
G1
h2
k1 k1 G1 ( s ) = , G1 ( s ) = (T1s + 1) (T1s + 1) k1k 2 G0 ( s ) = (T1s + 1)(T2 s + 1)
kp
G0 ( s ) G(s) = 1 + G0 ( s ) K p
5.4 Nyquist稳定性判据 Nyquist稳定性判据
系统稳定的条件? 系统稳定的条件?
5.2 稳定的条件
d n y (t ) d ( n −1) y (t ) dy (t ) 线性系统微分方程: 线性系统微分方程: n a + an −1 + L + a1 + a0 y (t ) n ( n −1) dt dt dt d m x(t ) d ( m −1) x(t ) dx(t ) = bm + bm−1 + L + b1 + b0 x(t ) m ( m −1) dt dt dt d n y (t ) d ( n −1) y (t ) dy (t ) + a( n −1) + L + a1 + a0 y (t ) = 0 齐次微分方程: 齐次微分方程: an n ( n −1) dt dt dt an s n + an −1s n −1 + L + a1s + a0 = 0 设系统k 设系统k个实根
机械工程控制基础(第5章_系统的稳定性)

(5.2.3)
武科大城市学院
机电学部
比较式(5.2.2)与式(5.2.3)可看出根与系数有如下的关系:
n an1 si an i 1
n a n2 si s j an i j
i 1, j 2
an3 an
i jk
s s s
i
n
j k
(5.2.4)
i 1, j 2 , k 3
n a0 n 1 si i 1 an
武科大城市学院
机电学部
从式(5.2.4)可知,要使全部特征根 s1 , s2 , , sn 均具有负实部,就必 须满足以下两个条件,即系统稳定的必要条件: (1)特征方程的各项系数 ai (i 0,1, 2,, n 1, n) 都不等于零,因为若有一 系数为零,则必出现实部为零的特征根或实部有正有负的特征根,才 能满足式(5.2.4)中各式。 (2)特征方程的各项系数 ai的符号都相同,这样才能满足式(5.2.4)中各式。 按习惯,一般取 ai 为正值,因此,上述两个条件可归结为系统稳定 的一个必要条件,即
E 来越小,系统最终趋于稳定; ( s )
若反馈的结果,加强了E(s)的作用(即正反馈),则使 Xo(s) 越来越 大,此时,此闭环系统是否稳定,则视 Xo( s ) 是收敛还是发散而定。
武科大城市学院
机电学部
第三,控制理论中所讨论的稳定性其实都是指自由振荡下的稳定性。
即讨论输入为零,系统仅存在有初始状态不为零时的稳定性,即
武科大城市学院
机电学部
5.2.2 系统稳定的充要条件
1. Routh表
(1)将系统的特征方程式(5.2.1)的系数按下列形式排成两行:
an
an1ห้องสมุดไป่ตู้
机械控制工程基础-自动控制原理 第五章-系统的稳定性

二、系统稳定的条件
第五章 系统的稳定性
线性定常系统的微分方程一般式为:
a0
dn dt n
xo
(t)
a1
d n1 dt n1
xo (t)
an1
d dt
xo (t) an xo (t)
dm
d m1
d
b0 dt m xi (t) b1 dt m1 xi (t) bm1 dt xi (t) bm xi (t)
劳斯表的构造:
D(s) a0sn a1sn1 a2sn2 an1s an 0
sn a0 a2 a4 … sn−1 a1 a3 a5 … sn−2 b1 b2 b3 … ┋┋ s1 …
s0 g1
b1
a1a2 a0a3 a1
b2
a1a4 a0a5 a1
自动控制原理
1
第五章 系统的稳定性
第一节 稳定性的基本概念 第二节 Routh(劳斯)稳定判据 第三节 Nyquist稳定判据 第四节 系统的相对稳定性
第五章 系统的稳定性
第一节 稳定性的基本概念
一、稳定性的概念
系统受到扰动作用时,输出偏离平衡状态,当扰动消 除后,若系统在足够长的时间内能恢复其原来的平衡状态 或趋于一个给定的新平衡状态,则该系统是稳定的。反之, 如果系统对于干扰的瞬态响应随时间的推移而不断扩大或 发生持续振荡,则系统是不稳定的。
表中:1)最左一列元素按s 的幂次排列,由高到低,只起标识作
用,不参与计算。 2)第一,二行元素,直接用特征方程式的元素填入。 3)从第三行起各元素,是根据前二行的元素计算得到。
第五章 系统的稳定性PDF

第五章系统的稳定性讲授内容5.1系统稳定的初步概念一、稳定性的定义系统稳定性是指系统在干扰作用下偏离平衡位置,当干扰撤除后,系统自动回到平衡位置的能力。
若系统在初始状态的影响下,由它所引起的系统的时间响应随着时间的推移,逐渐衰减并趋向于零(即回到平衡位置),则称系统为稳定的;反之,由它所引起的系统的时间响应随着时间的推移而发散(即偏离平衡位置越来越远),则称系统为不稳定的。
线性系统的稳定性是系统的固有特性,仅与系统的结构及参数有关;而非线性系统的稳定性不仅与系统的结构及参数有关,而且还与系统的输入有关。
二、系统稳定的充要条件系统稳定的充要条件是的系统所有特征根的实部全都小于零,或系统传递函数的所有极点均分布在s平面的左半平面内。
若系统传递函数的所有极点中,只有一个位于虚轴上,而其它极点均分布在s平面的左半平面内,则系统临界稳定。
而临界稳定的系统极易因为系统的结构或参数的细微变化而变成不稳定的系统。
因此,临界稳定往往也归结为不稳定的一种。
5.2 (劳斯)稳定判据Routh Routh 判据是判别系统特征根分布的一个代数判据。
一、系统稳定的必要条件要使系统稳定,即系统全部特征根均具有负实部,就必须满足以下两个条件:1)特征方程的各项系数都不等于零。
2)特征方程的各项系数的符号都相同。
此即系统稳定的必要条件。
按习惯,一般取最高阶次项的系数为正,上述两个条件可以归结为一个必要条件,即系统特征方程的各项系数全大于零,且不能为零。
二、系统稳定的充要条件系统稳定的充要条件是表的第一列元素全部大于零,且不能等于零。
Routh 运用判据还可以判定一个不稳定系统所包含的具有正实部的特征根的个数为表第一列元素中符号改变的次数。
Routh Routh 运用判据的关键在于建立表。
建立表的方法请参阅相关的例题或教材。
运用判据判定系统的稳定性,需要知道系统闭环传递函数或系统的特征方程。
Routh Routh Routh Routh 在应用判据还应注意以下两种特殊的情况:Routh 1.如果在表中任意一行的第一个元素为0,而其后各元不全为0,则在计算下一行的第一个元时,该元将趋于无穷大。
第五章 控制系统的稳定性

例 5 - 2. 设有下列特征方程 s 4 + 2s 3 + 3s 2 + 4s + 5 = 0
试用Routh判据判别该特征方程正实部根的个数。 判据判别该特征方程正实部根的个数。 试用 判据判别该特征方程正实部根的个数
解 : 列写 劳斯 阵列 : s4 s3 s2 s s
1 0
1 2
2× 3 - 4 2
s3 s2 s s0
1 0≈ε
- 3ε - 2
-3 2 0
改变一次
ε
2
改变一次
∴ 有两实部为正的根。
b.劳斯表某行全为零 说明特征方程中存在一些大小相等,但方向相反的 根。 可用全零行的前一行数值组成辅助方程 A' ( s ),并用 dA' ( s ) / ds 的系数代替全零行的各项,完成劳斯表 ,利用 的系数代替全零行的各项,完成劳斯表, 可解得那些对称根。 辅助方程 A' ( s )可解得那些对称根。
一幅 原 . 角 理 设 (S)是 变 的 项 之 ,除 S平 的 限 奇 复 量 多 式 比 在 面 有 个 F 点 ,为 值 续 则 数又 P为 (S)极 数 , Z为 (S) 外 单 连 正 函 . 设 F 点 目 F 的 点 目 其 包 重 点 重 点 目 以 F(S)的 零 数 , 中 括 极 与 零 数 , 及 全 部 点 零 均 布 S平 的 闭 线 S内 而 S不 过 极 与 点 分 在 面 封 轨 Γ , Γ 通 F(S)的 何 点 零 . 在 种 况 , 当 S以 时 方 任 极 与 点 这 情 下 点 顺 针 向 沿 S 运 , ΓS在 F(S)]平 上 映 ΓF按 时 方 包 原 Γ 动 [ 面 的 射 顺 针 向 围 点 次 的 数 N = Z- P N>0 N<0 N =0 表 ΓF顺 针 围 点 次 示 时 包 原 N 表 ΓF逆 针 围 点 次 示 时 包 原 N 表 ΓF不 围 点 示 包 原
现代机械控制工程 第五章 系统的稳定性

其中,ai>0 (i=0,1,2,…,n),即满足系统稳定的 必要条件。
劳斯稳定判据的判别过程如下:
n列出劳斯阵列 s a0 a2 sn-1 a1 a3 sn-2 b1 b2 sn-3 c1 c2 sn-4 d1 d2 …… s2 e1 e2 s1 f1 s0 g1
a1a2 a0a3 b1 a1 b2
K 0 6 5 K 0
即:当0<K<30时系统稳定。
例2:单位反馈系统的开环传递函数为:
K ( s 1) G( s) s(Ts 1)(5s 1)
求系统稳定时K和T的取值范围。 解:系统闭环特征方程为:
5Ts3 (5 T )s 2 (1 K )s K 0
系统稳定条件为:
T 0 K 0 (5 T )(1 K ) 5TK 0
T 0 5T 0 K 4T 5
劳斯阵列的特殊情况 劳斯阵列表某一行中的第一列元素等于 零,但其余各项不等于零或不全为零。 处理方法:用一个很小的正数 代替该行第 一列的零,并据此计算出阵列中的其余 各项。然后令 0,按前述方法进行判别。 如果零( )上下两项的符号相同,则系统存在 一对虚根,处于临界稳定状态;如果零 ( )上 下两项的符号不同,则表明有一 个符号变化,系统不稳定。
e t (a1 a2t ar t r 1)
当- < 0时,该输出分量指数单调衰减。 当- > 0时,该输出分量指数单调递增。 当- = 0时,该输出分量多项式递增。 对于一对r重复根-+j,相应的时域分量为:
e t (b1 b2t br t r 1 ) cos t (c1 c2t cr t r 1 ) sin t e t
第五章 控制系统的稳定性分析

第五章 控制系统的稳定性分析
5-2 控制系统稳定性判据 例 已知一调速系统的特征方程式为
试用劳斯判据判别系统的稳定性:S 3 + 41.5S 2 + 517 S + 2.3 × 10 4 = 0 解:列劳斯表
S3 S2 S1 S0 1 41.5 − 38.5 2.3 × 10 4 517 2.3 × 10 4 0 0
a n s n + a n −1 s n −1 + ⋯ + a 0 = 0 通过因式分解,总 对于特征方程: 通过因式分解, 对于特征方程:
第五章 控制系统的稳定性分析
5-2 控制系统稳定性判据
1) 列写罗斯计算表:任意一行的各项同时乘以一个正数,结果不变 列写罗斯计算表:任意一行的各项同时乘以一个正数, 。
第五章 控制系统的稳定性分析
5-2 控制系统稳定性判据 一.代数稳定判据
不必求解系统的特征方程, 不必求解系统的特征方程 ,通过对特征方程的系数进行分析来判 断系统的稳定性的方法。 断系统的稳定性的方法。
可 以 分 解 为 一 次 因 子 和 二 次 因 子 的 乘 积 的 形 式 , 即 : (s+a) 和 (s2+bs+c)相乘的形式。只有 、b、c都是非零的正值时,才能得到负 相乘的形式。 都是非零的正值时, 相乘的形式 只有a、 、 都是非零的正值时 实根或具有负实部的共轭复根。所以ai>0是判定系统稳定的必要条 实根或具有负实部的共轭复根 。 所以 是判定系统稳定的必要条 但非充分条件。罗斯-赫尔维茨稳定判据即是检验系统稳定的充 件,但非充分条件。罗斯 赫尔维茨稳定判据即是检验系统稳定的充 要条件。 要条件。 1、罗斯(Routh)稳定判据: 、罗斯( )稳定判据:
控制工程第五章_系统的稳定性

本 章 难 点Nyquist判剧及其应用。
5.1
1摆小球的稳定性2.系统稳定的定义
若系统零输入响应随时间的推移,逐渐衰减并趋向于零(回到平衡位置),则称该系统是稳定的;反之,若系统的零输入响应发散,则系统是不稳定的。
基本要求1.了解系统稳定性的定义、系统稳定的条件。
2.掌握系统稳定性代数判据的必要条件和充要条件,学会应用代数判
据判定系统是否稳定。3.掌握Nyquist判据。 4.掌握Bode判据。
5.理解系统相对稳定性概念,能够在Nyquist图和Bode图上加以应用。
本章重点1.代数判剧、Nyquist判剧和Bode判剧的应用。
3.稳定性条件
对于线性微分方程
(anp
an1
pn1a
pa0
)xo
(t)
xi(t)
闭环传递函数为:
G(s)G(s)
B1G(s)H(s)
est
第5章系统的稳定性

经典控制论中,系统稳定性判据
代数判据
Routh(劳斯)判据 Hurwitz(古尔维茨)判据 Nyquist判据 Bode判据
几何判据
5.2 Routh(劳斯)稳定判据
Routh稳定判据
不求解特征方程的根,直接根据特征方程的系 数,判断系统的稳定性,回避了求解高次方程根 的困难。
【例】D(s) s 4 3s3 4s 2 12s 16
【解】:Routh表为: s4 s3 s2 s1 s0 1 3 4 16 12
12 48 48
0( ) 16 12 48 0
很小时,
12
0
16
【结论】:系统不稳定,并有两个正实部根。
【情况2】:
n n n an1 an2 an3 si, si s j, an an an i 1 i j i j k i 1, j 2
(1)
n
s
i 1
n
i
si s j sk,
i 1, j 2, k 3
n a0 n , (1) si an i 1
系统稳定的必要条件:特征方程中所有项的系数均大 于0,只要有一项等于或小于0,则为不稳定系统。 充分必要条件:Routh表第一列元素均大于0。
必要条件证明
D(s) an s n an1s n1 an1 n1 得:s s an 再展开,得
n
a1s a0 0,两端同除以an,并分解因式, (s sn )
其中N+为:正穿越与半次正穿越次数的和。 其中N-为:负穿越与半次负穿越次数的和。
系统的稳定性

L L L L M
a1
0 0 0 0 0 ao
∆n =
M
0 0
M L
M L
a2
第五章 系统的稳定性
∆1=an-1>0
an-1 ∆2 = an an-3 >0 an-2 an-1 an-3 an-5 ∆3 = an-2 an-4 an-6 >0 0 an-1 an-3
∆n>0
Hurwitz行列式直接由系数排列,规律简单 行列式直接由系数排列, 行列式直接由系数排列 而明确,因此,比列Routh表要简单些,使用也 表要简单些, 而明确,因此,比列 表要简单些 较为方便,但对六阶以上的系统, 较为方便,但对六阶以上的系统,由于行列式 计算麻烦,故应用较少。对于简单形式: 计算麻烦,故应用较少。对于简单形式:
第五章 系统的稳定性
补充: 补充: 映射定理:设复变函数 映射定理:设复变函数F(s)有p 有 个极点和Z个零点被 平面内某一封 个极点和 个零点被s平面内某一封 个零点被 闭曲线所包围, 闭曲线所包围,并且这一封闭曲线 不经过F(s)的任何极点或零点。当 的任何极点或零点。 不经过 的任何极点或零点 复变量s顺时针方向沿此封闭曲线 复变量 顺时针方向沿此封闭曲线 移动一周时, 移动一周时,在F(s)平面内的映射 平面内的映射 曲线将顺时针方向包围坐标原点
a n-2 a n-3
… …
每一行元素可以同时乘以或除以相同数 2)列出Routh表 列出 表 3)由稳定判据判断稳定性 ) 第一列符号无改变, 第一列符号无改变,系统无实部为正的 特征根→ 特征根→稳定 第一列符号改变n 则有n 第一列符号改变n次,则有n个实部为正 的特征根→ 的特征根→不稳定
第五章 系统的稳定性
第5章系统的稳定性
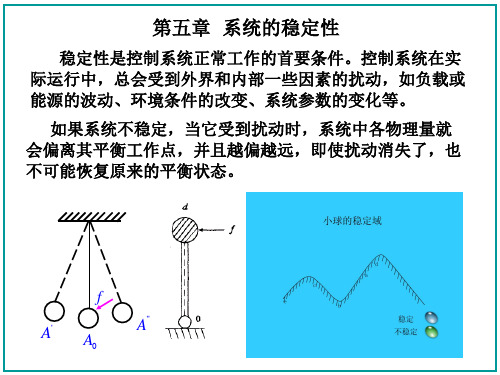
稳定性是控制系统正常工作的首要条件。 稳定性是控制系统正常工作的首要条件。控制系统在实 际运行中,总会受到外界和内部一些因素的扰动, 际运行中,总会受到外界和内部一些因素的扰动,如负载或 能源的波动、环境条件的改变、系统参数的变化等。 能源的波动、环境条件的改变、系统参数的变化等。 如果系统不稳定,当它受到扰动时, 如果系统不稳定,当它受到扰动时,系统中各物理量就 会偏离其平衡工作点,并且越偏越远,即使扰动消失了,也 会偏离其平衡工作点,并且越偏越远,即使扰动消失了, 不可能恢复原来的平衡状态。 不可能恢复原来的平衡状态。
例
系统特征方程 D( s ) = s 6 + 2s 5 + 8s 4 + 12s 3 + 20s 2 + 16s + 16 = 0, 试用劳斯判据判别系统的稳定性。 试用劳斯判据判别系统的稳定性。
解: (1)特征方程的所有系数均为正实数,满足系统稳定 )特征方程的所有系数均为正实数, 的必要条件。 的必要条件。 (2)列劳斯数列表 )
得系统的脉冲响应函数
A C(s) = φ(s) = ∑ i i=1 s − si
n sit i=1
n
g(t) = c(t) = ∑Ae i
若系统稳定
n sit t →∞ t →∞ i=1
lim g(t) = lim∑Ae = 0 i
si (2)若 (2)若 s 为复数 i
(1)若 (1)若 为实数
t →∞
例
已知系统特征方程 D( s ) = s 5 + 3s 4 + 3s 3 + 9s 2 − 4s − 12 = 0 , 试用劳斯判据判别系统的稳定性。 试用劳斯判据判别系统的稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
46
5.4 Bode(伯德)稳定判据
一、nyquist图和bode图的对应关系
47
5.4 Bode(伯德)稳定判据
ωc
:开环频率特性幅值为1时所对应的角频率为幅值穿越频率或
剪切频率Wc。 在极坐标平面上,开环nyquist图穿越单位圆的点所对应的角 频率就是幅值穿越频率Wc。 在bode图上,开环幅频特性穿越0dB线的点所对应的角频率 就是幅值穿越频率Wc。
即:s 4 6 s 2 8 0
( s 2 2)( s 2 4) 0 s1, 2 j 2 s3, 4 j 2
结论:系统是不稳定的(本题是临界稳定)。 由辅助方程式可以求得系统对称于原点的 根:
这两对根是原方程的 根的一部分。
19
5.2 Routh(劳斯)稳定判据
15
5.2 Routh(劳斯)稳定判据
三、Routh判据的特殊情况 1)劳斯表第一列出现系数为零。
4 3 3 例5-5:设线性系统特征方程式为: D( s) s 2s 2s 4s 5 0 试判断系统的稳定性。
解:建立劳斯表:
s s s s
4 3 2
1 2 0
2 4 5
5 0
围(-1,j0)点两 圈,N=2。 而p=0,所以闭环 不稳定。
40
5.3 Nyquist(乃奎斯特)稳定判据
41
5.3 Nyquist(乃奎斯特)稳定判据
42
5.3 Nyquist(乃奎斯特)稳定判据
43
5.3 Nyquist(乃奎斯特)稳定判据
44
5.3 Nyquist(乃奎斯特)稳定判据
D( s) s 6 2s 5 8s 4 12 s 3 20 s 2 16 s 16 0
试判断系统的稳定性。 解:建立劳斯表:
s6 s5 s4 s3 s2
1
8
20 16 0
2 12 16 2 12 16 0 0
17
5.2 Routh(劳斯)稳定判据
Routh表中出现某行系数全为零,这是因为在系统的特征方程中出 现了对称于原点的根(如大小相等,符号相反的实数根;一对共轭纯虚 根;对称于原点的两对共轭复数根)。 解决的办法:
系统的特征方程
45
5.4 Bode(伯德)稳定判据
Nyquist稳定判据是利用开环频率特性Gk(jw)的极坐标图
(nyquist图)来判定闭环系统的稳定性。
如果将开环极坐标图改画为开环对数坐标图,即bode图,同样 可以利用它来判定系统的稳定性。这种方法称为对数频率特性判据,
简称为对数判据或伯德判据。
例5.7:设线性系统特征方程式为:
D( s) s 6 s 5 2s 4 3s 3 7 s 2 4s 4 0
试判断系统的稳定性。 解:建立劳斯表:
s6 s5 s4 s3 s2 s
1
1 1 1 4 6
2 3 3 6
7 4 4
4 0
s 4 3s 2 4 4s 3 6s
对称于原点的根可由全零行上面一行的系数构造一个辅助方程式
F(s)=0求得,而全零行的系数则由全零行上面一行的系数构造一个辅 助多项式F(s)对s求导后所得的多项式系数来代替,劳斯表可以继续计
算下去。(s的次数为偶数)
结论:一旦劳斯表中出现某行系数全为零,则系统的特征方程中出现 了对称于原点的根,系统必是不稳定的。劳斯表中第一列系数符号改 变的次数等于系统特征方程式根中位于右半s平面的根的数目。 这些数值相同、符号相异的成对的特征根,可通过解由辅助多项式构
(b)图包围(-1,j0)点, 故相应的闭环系统不稳定。
37
5.3 Nyquist(乃奎斯特)稳定判据
例5-5 下图为某系统的开环nyquist图,其开环传递函数为:
因为G(S)H(S)在[s]平面的 右半平面有一个极点,为s =1/T2,所以p=1 当w由-∞至+∞时,由于
开环nyquist轨迹逆时针包
ωg
:开环频率特性的相位等于-180°时,所对应的角频率称
为相位穿越频率,记为Wg。
48
5
5.1系统稳定性额初步概念
二、稳定的定义
6
5.1系统稳定性额初步概念
7
5.1系统稳定性额初步概念
8
5.1系统稳定性额初步概念
j
稳 定 区 不 稳 定 区 不 稳 定 区 s平面
所以:
稳 定 区 临界 稳定
9
5.1系统稳定性额初步概念(系统稳定的判别方法)
10
5.2 Routh(劳斯)稳定判据
围(-1,j0)点一圈,所 以闭环系统仍然是稳定的。
38
5.3 Nyquist(乃奎斯特)稳定判据
39
5.3 Nyquist(乃奎斯特)稳定判据
首先画出开环系统的 Nyquist图, 然后,根据两个积分环 节按顺时针从π到-π转 过半径为无穷大的圆弧。
当w由-∞到+∞时,开
环nyquist轨迹顺时针包
根据Routh表,由系统稳定的充要条件,有: ( )+1 0,即 1; 1 (2) ( ) 0,即 0, ; (3) 1 0, 即 1。 所以,使系统稳定的、的取值范围为:
0及 1。
参考教材P163 图5.2.2
系统是不稳定的。特征方程共有6个根:
16
100 16
s0
s1, 2 2 s3, 4 j s5,6
1 j 3 2
20
5.3 Nyquist(乃奎斯特)稳定判据
前面介绍了判断系统稳定性的方法。代数判据法根据特征方程 根和系数的关系判断系统的稳定性。 本节介绍另一种重要并且实用的方法——乃奎斯特稳定判据。 这种方法可以根据系统的开环频率特性,来判断闭环系统的稳定性, 并能确定系统的相对稳定性。是频域分析法的重要成果。
由上式可见,复变函数F(s)的 零点为系统特征方程的根(闭环 极点)s1、s2 、…sn, 而F(s)的极点则为系统的开环 极点p1、 p2 、… pn。
22
5.3 Nyquist(乃奎斯特)稳定判据
(一)s平面与F(S)平面的映射关系
23
5.3 Nyquist(乃奎斯特)稳定判据
24
5.3 Nyquist(乃奎斯特)稳定判据
21
5.3 nyquist(乃奎斯特)稳定判据
一、幅角定理(又称映射定理) 它是建立在复变函数理论基础上的。 下面简要介绍幅角定理: 如图所示的闭环系统,设其开环传递函数为:
K (s z1 )( s z 2 )(s z m ) G( s) H ( s) (s p1 )( s p2 )(s pn )
4.根据辐角原理确定z是否为零。如果z=0,表示闭环系统稳定。Z≠0, 表示该闭环系统不稳定。Z的数值反映了闭环特征方程式的根在s 右半面上的个数。
36
5.3 Nyquist(乃奎斯特)稳定判据
下面两图为当P=0时,系统的开环nyquist图,求系统 的闭环稳定性。
(a)图不包围(-1,j0)点, 故相应的闭环系统稳定。
二、基于辅助函数F(S)的奈氏判据
乃奎斯特轨迹由两部分组成:
一部分是沿着虚轴由下向上移动的直线
段L1,在此线段上s=jω,ω由-∞变到+∞。 另一部分是半径为无穷大的半圆L2。如
此定义的封闭曲线肯定包围了F(s)的位于右
半部的所有零点和极点。
32
5.3 Nyquist(乃奎斯特)稳定判据
33
5.3 Nyquist(乃奎斯特)稳定判据
3
5.1系统稳定性额初步概念
4
5.1系统稳定性额初步概念
上例中,系统是在输入撤销后,从偏离平衡位置所处得初 始状态出发,因系统本身的固有特性而产生振动的,故线性系 统的稳定性只取决于系统本身的结构与参数,而与输入无关。
分析P155 单位反馈系统 控制理论中所讨论的稳定性其实都是指自由振荡下的稳定 性,也就是说,是讨论输入为零,系统仅存在有初始状态不为 零时的稳定性,即讨论系统自由振荡是收敛的还是发散的。
系统的闭环传递函数: 系统的特征方程为: F(s)=1+G(s)H(s)=0 可得: F ( s) 1
K (s z1 )( s z 2 )(s z m ) (s s1 )( s s 2 )(s s m ) (s p1 )( s p2 )(s pn ) (s p1 )( s p2 )(s pn )
13
5.2 Routh(劳斯)稳定判据(判断系统稳定性)
14
5.2 Routh(劳斯)稳定判据(判断系统稳定性)
例5.4:设某系统的特征方程
D( s ) s 3 ( 1) s 2 ( 1) s 1 0 试确定待定参数及,以便使系统稳定。
解:根据特征方程的各项系数,列出Routh表:
35
5.3 Nyquist(乃奎斯特)稳定判据
应用奈氏判据判别闭环系统的稳定性步骤: 1.作出开环系统的奈氏曲线G(jw)H(jw). 2.计算奈氏曲线G(jw)H(jw)对点(-1,j0)按顺时针方向的包围圈 数N. 3.确定开环系统是否稳定,若不稳定,则确定开环系统在右半s平 面上的极点数P。
25
5.3 Nyquist(乃奎斯特)稳定判据
26
5.3 Nyquist(乃奎斯特)稳定判据
27
5.3 Nyquist(乃奎斯特)稳定判据
28
5.3 Nyquist(乃奎斯特)稳定判据
29
5.3 Nyquist(乃奎斯特)稳定判据
30
5.3 Nyquist(乃奎斯特)稳定判据
31
5.3 Nyquist(乃奎斯特)稳定判据
Routh判据是基于方程式根与系数的关系建立的,通过对系统特 征方程式的各项系统进行代数运算,得出全部根具有负实部的条件, 从而判断系统的稳定性。
