弹性力学轴对称问题

河南理工弹性力学- 轴对称应力问题

4.5 轴对称应力问题
u 1 A (1 ) 2 (1 3)B 2(1 )B ln 2(1 )C E
1 u u 1 A (1 ) 2 (3 )B 2(1 )B ln 2(1 )C E
其中，H、I、K 是新引入的积分常数。
6
4.5 轴对称应力问题
1 A u (1 ) 2(1 )B (ln 1) (1 3)B 2(1 )C E I cos K sin 4B u H I sin K cos E
E E , . 1 1 2
8
u 当 H 0 时， u
cos sin I ，说明 I、K sin cos K H , I u 0 , K v 0 .
其中，A、B、C、D 是待定的积分常数。
1 d A B(1 2 ln ) 2C 2 d 2 d A B(3 2 ln ) 2C 2 d 2 0
()
1 d d 2 d d 2 0
Laplace 算子
2 1 1 2 2 2 2
2
()
1 d d d2 1 d d d 2 d d
B

d
d

C

d

y
d
③ 切应力

第10章弹性力学轴对称问题的有限元法简介

第10章弹性力学轴对称问题的有限元法简介
一、轴对称问题的定义 (1)几何形状轴对称：要求结构是相对对称轴的受到的载荷和位移约束条件具有轴对称性。 (3)材料轴对称要求：结构的材料特性具有轴对称性。
二、轴对称问题基本方程
轴对称问题的特点是结构的位移、应变和应力都呈轴对称分布。 (l) 柱坐标系(r, θ, z) (u, v, w) 有许多实际工程问题，其几何形状、约束条件以及载荷都对称于某一固定轴，这类问题为轴对称问题。 (2)基本变量对于轴对称问题，在柱坐标中的三大类力学变量为: 位移: ur , wz , (vθ=0)
(下标i, j, m轮换)
用矩阵表示的单元位移为
u Ni w 0
0 Ni
Nj 0
0 Nj
Nm 0
ui w i 0 u j N m w j um wm
四、三结点单元刚度矩阵
轴对称问题的几何方程：
u a1 a 2 r a 3 z w a4 a5 r a6 z
该模式与平面问题三节点三角形单元相同，由节点条件可以推出相同的形状函数矩阵，即
Ni N 0
定义形态函数为
Ni
0 Ni
Nj 0
0 Nj
Nm 0
0 Nm
1 (ai bi r ci z ) 2
bj 0 fj 0 0 cj cj bj
式中
ai ci z f i bi r r
{ } [ B] { }e
(i , j, m )
B B( r , z )
用几何矩阵表示单元的应变
[ B] [ Bi
Bj
Bm ]
bi 1 fi [ Bi ] 2 0 ci

弹性力学13-轴对称应力和相应的位移

df1 ( r ) df (j ) f1 ( r ) r = f (j )dj dr dj
上式等号两边分别只是单独 r 和单独 j 的函数式，要使该式成立，两边须为同一常数，因此有： df1 ( r ) f1 ( r ) r =F (d) dr df (j ) f (j )dj = F (e) dj
第四章平面问题的极坐标解答 4.5 轴对称应力和相应的位移
得到轴对称问题在极坐标（ r ，j ）下的：
应力分量的通用表达式（含待定系数）
位移分量的通用表达式（含待定系数）
第四章平面问题的极坐标解答 4.5 轴对称应力和相应的位移
轴对称问题：物体的形状或物理量是绕一轴对称的，凡通过对称轴的任何面均是对称面。即，在对称面两边对应点的物理量必须满足如下两个条件：（1）数值必须相等：在极坐标下，任一环向线上的各点的应力分量的数值相同。因此，它只能是径向坐标 r 的函数，不随环向坐标 f 改变，即与 f 无关。由此可见，凡是轴对称问题，总是使自变量减少一维。（2）方向必须对称，即方向对称于z轴，方向不对称的物理量不能存在：trj= tjr=0 。
r =r r =R
在内外边界面上，分别有应力边界条
= q1 , t rj = q 2 , t rj
r
r =r r =R
=0 =0
由于轴对称，关于切应力的两个条件是自然满足的。将应力分量表达式代入应力边界条件，得到 2 个方程，显然不能确定 3 个待定常数A、B、C。
A B 1 2 ln r 2C = q1 2 r A B 1 2 ln R 2C = q2 2 R
当外半径趋于无限大时，由上式可得到具
有圆孔的无限大薄板或具有圆孔的无限大弹性体的应力解答： r2 r2

《弹塑性力学》第九章空间轴对称问题

80%
物理方程
描述了材料在不同应力状态下表现出的物理性质。
塑性力学的基本方程
流动法则
描述了塑性应变与应力之间的关系。
屈服准则
描述了材料屈服的条件，即应力达到屈服点时的状态。
强化准则
描述了材料在塑性变形过程中的应力增强机制。
空间轴对称问题的边界条件和初始条件
边界条件
描述了物体在边界上的受力状态和位移约束。
如旋转机械、航空航天器等的设计和分析。
土木工程
如桥梁、高层建筑等大型结构的分析。
石油工程
如油藏模拟、油气管道设计等。
核工程
如核反应堆、核废料处理设施等安全评估。
02
空间轴对称问题的数学模型
弹性力学的基本方程
80%
平衡方程
描述了物体内部各点的受力平衡状态。
100%
几何方程
描述了物体在受力后产生的形变和位移。
近原问题的解。
在处理空间轴对称问题时，有限元法能够将复杂的空间几何形状和边界条件简化为易于处理和计算的离散模型，从而
提高求解效率。
有限元法在空间轴对称问题中广泛应用于弹性力学、塑性力学等领域，能够得
到高精度的数值解。
有限差分法在空间轴对称问题中的应用
有限差分法是一种将偏微分方程离散化为差分方程的方法，通过求解差分方程来逼近原问题
目
CONTENCT
录
• 空间轴对称问题的基本概念 • 空间轴对称问题的数学模型 • 空间轴对称问题的解析解法 • 空间轴对称问题的数值解法 • 空间轴对称问题的实验研究
01
空间轴对称问题的基本概念
定义与特性
定义
空间轴对称问题是指物体在空间中关于某一直线或平面对称分布的问题。

弹塑性力学讲义第九章空间轴对称问题

的取值范围：由 0 1 的取值范围：0
r sin 1 a a sin

2
w
4(1 2 )q 2 2 a a 2 sin 2 0 E
a cos d a2 r 1 2 sin 2 r

4(1 2 )q a 2 cos 2 d E a2 r 1 2 sin 2 r
r R z z
当 R 时 R=(r +z ) ，应力、位移 0；当 R 0 时，应力奇异。 Boussinesq 采取 Love 函数求解，

x
y
(r,z)为重调和函数，由(r,z)的三次微分导出应力。
选
(r,z) 为 r 和 z 的正一次幂式: (r,z) = A1R+ A2[R - zln(R+z)] ——为双调和函数 (r,z) 自然满足 4=0 。代入位移、应力计算式
其中
2 1 2 2 r r z 2 r
2
7．按位移法解 a．基本未知函数： ur 和 w
基本方程两个：
( G )
u e G( 2 u r r ) f r 0 r r
( G )
e G 2 w f z 0 z
并考虑适当的边界条件。 b. 引入 Love（拉甫、勒夫）位移函数（当无体力作用时）对于位移法的基本方程的解可由考虑体力的一个特解加上齐次方程的通解。轴对称问题齐次拉梅方程的通解可以引入一个 Love 位移函数
(1 ) P (1 2 ) P w 2Gr Er
圆面积均布荷载 q 对圆外 M 点竖向位移影响可取一个微面元，距 M 点为 s，角度为处，dA=sdds ，dA 上 q 对 M 点影响：

弹性力学13-轴对称应力和相应的位移

1. 压力隧洞问题特点：（1）接触问题：因为不符合均匀性假定，所以不能用一个表达式同时表述两个问题的未知量分布。因此本题是两个圆筒的接触问题，要考虑两个物体接触面上的接触条件。
第四章平面问题的极坐标解答 4.7 压力隧洞
（2）两个问题均为轴对称问题，是平面应变问题。外围无限大弹性体可看成内半径为
1 ur uj uj = rj = 0 r r r
（4）位移分量对第一式径向应变积分：
ur = 1 A (1 ) (1 3 ) B r 2(1 ) B r (ln r 1) 2(1 ) C r f (j ) E r
R2
r =
r
2 2
1 q1 , j =
R2
r
2 2
1 q1
R 1 2 r
R 1 2 r
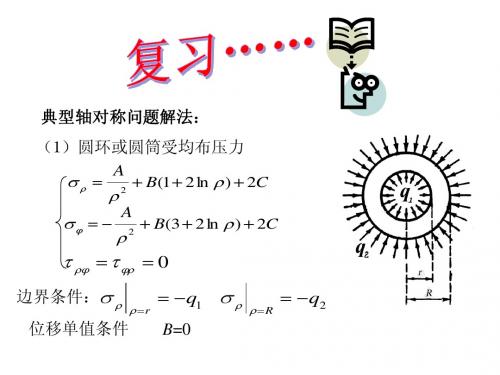
第四章平面问题的极坐标解答 4.6 圆环或圆筒受均布压力
R
2 2
r =
r2
2
1 q1 , j =
R
r2
R2 r2
R 1 2 r
显然，由应力公式可知，径向 1 正应力总为负值，即为压应力 q1；环向正应力总为正值，即为 1 拉应力。应力分布大致如图所示。最大值发生在内壁处。
第四章平面问题的极坐标解答 4.5 轴对称应力和相应的位移
得到轴对称问题在极坐标（ r ，j ）下的：
应力分量的通用表达式（含待定系数）
位移分量的通用表达式（含待定系数）
第四章平面问题的极坐标解答 4.5 轴对称应力和相应的位移
轴对称问题：物体的形状或物理量是绕一轴对称的，凡通过对称轴的任何面均是对称面。即，在对称面两边对应点的物理量必须满足如下两个条件：（1）数值必须相等：在极坐标下，任一环向线上的各点的应力分量的数值相同。因此，它只能是径向坐标 r 的函数，不随环向坐标 f 改变，即与 f 无关。由此可见，凡是轴对称问题，总是使自变量减少一维。（2）方向必须对称，即方向对称于z轴，方向不对称的物理量不能存在：trj= tjr=0 。

弹性力学空间轴对称问题有限元法

轴对称问题是空间问题的一种特殊情况，在实际工程中存在大量的轴对称问题，如飞轮、回转类的压力容器、发动机汽缸套、烟囱及受内压的球壳等，无限大、半无限大的弹性体受集中载荷作用时也可以处理为轴对称问题。
7.1 弹性力学空间轴对称问题的描述
一、柱坐标系
由于轴对称性质，采用柱坐标系（ r、θ、z ）分析轴对称问题
w r
u z
• 尽管点的位移发生在平面内，但是，对于垂直于平面的线元素却存在着伸缩的可能，因此，轴对称问题的环向应变不为零。
2）几何方程
• 对于周向应变，尽管不存在周向位移，但由于A点发生径向位移后，它与轴的距离变为，从而导致产生周向的变形，如图所示，则产生周向应变为
(r u)d rd rd
Ke
B
eT
e
DB
dv
Ve
Fbe NeTf dv
Ve
Fqe NeT f dS Se
Fe 0
BeT0 dv
Ve
Fe 0
BeTD0 dv
Ve
Ke 2
BeT
e
DB
rdrdz
e
Fbe 2 NeTf rdrdz e
Fqe 2 NeT f rds Se
Fe 0
2
BeT0 rdrdz
u r
u
r
z
r u r w
rz
z
w
u
r z
7.1 弹性力学空间轴对称问题的描述三、基本方程
（2）应力应变关系 —物理方程
1
1 1
0
r
σ
z rz
E 1 1 1
2
1 1
1
1
1
1

弹性力学问题的有限元法轴对称问题

drdz
Ri e
πA
6 2ri
0 rj
rm
(i, j,m)
当
rc ri rj rm, 则有
Wi
Wj
Wm
1 3
2πArc
2020/5/7
13
面积力沿单元的jm面
q L0j q
Re
2π
A
Ni
0
0 Ni
Nj 0
0 Nj
Nm 0
0 Nm
T
L0jqrdS
z
m
q j i
r
2020/5/7
πrc A3 2A
brbs
fr fs A1 br fs frbs A1cr bs fs A2brbs
A2cr cs
(r, s i, j,m)
A1cs br fr A2crbs
crcs A2brbs
其中
A1
1
A2
1 2 2(1 )
A3
E(1 ) (1 )(1 2)
ci z
(i, j, m)
1 ri zi
面积 A 1 rj z j
1 rm zm
常数
abii
rj zm zj
rm z j zm
c j rj rm
(i, j,m)
f
u w
N
e
Ni I 2
N jI2
Nm I2 e
备注:
平面三角形单元
x, y
轴对称三角形单元
r, z
2020/5/7
4
2. 确定应力-应变、应变-位移
(i, j, m)
应变 r , z , rz是常量, 是单元中r和z的函数;
Be Bi Bj Bm e

弹性力学轴对称问题的有限元法

4. 弹性力学轴对称问题的有限元法本章包括以下内容：4.1用虚功方程建立有限元方程 4.2三结点单元位移函数 4.3三结点单元刚度矩阵 4.4载荷移置4.5轴对称分析举例4.1用虚功方程建立有限元方程物体的几何形状、约束情况及所受的外力都对称于空间的某一根轴，因此在物体中通过该轴的任何平面都是对称面，所有应力、应变和位移也对称于该轴，这类问题称为轴对称问题。

研究轴对称问题时通常采用圆柱坐标系（r ，θ，z ），以z 轴为对称轴。

图4.1受均布内压作用的长圆筒如图4.1所示的受均布内压作用的长圆筒，通过Z 轴的一个纵截面就是对称面。

由于对称性，轴对问题共有4个应力分量：⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=zr z r τσσσσθ}{（4-1）其中r σ表示沿半径方向的正应力，称为径向应力；θσ表示沿θ方向的正应力，称为环向应力或切向应力；z σ表示沿z 方向的正应力，称为轴向应力；zr τ表示在圆柱面上沿z 方向作用的剪应力。

同样，轴对称问题共有4个应变分量：⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=zr z r γεεεεθ}{（4-2）其中r ε表示沿半径方向的正应变，称为径向正应变；θε表示沿θ方向的正应变，称为环向正应变或切向正应变；z ε表示沿z 方向的正应变，称为轴向正应变；zr γ表示沿r 和z 方向的剪应变。

在轴对称问题中，弹性体内任意一点上，不存在切向位移，只存在径向位移u 和轴向位移w ，两个位移分量表示为，⎭⎬⎫⎩⎨⎧=w u f }{（4-3）在讨论弹性力学平面问题的有限元法时，我们先由将弹性体划分为有限个单元的组合体，由虚功方程得到单元刚度矩阵，集成后得到整体刚度矩阵。

在这里，我们用虚功方程直接得到轴对称问题的有限元列式。

由虚功方程可得，外力虚功等于内力虚功或虚应变能， ds p f dxdydz F f dxdydz T sT T }{}{}{}{}{}{***⎰⎰⎰⎰⎰⎰⎰⎰+=σε（4-4）其中{F}为体力，{p}为面力。

2014-计算力学-4-轴对称问题有限元

e
Nj 0
0 Nj
Nm 0
e

N m I

0 i j Nm m
(4-11)
N
其中：[I]为二阶单位矩阵
1 0 I 0 1
因此，形函数矩阵的表达式为
Ni N 0 0 Ni Nj 0 0 Nj Nm 0 0 Nm
bi A1 f i 2 A3 A1 bi f i Si A b f 1 i i A2 ci A1ci ci A1ci A2 bi
i, j, m
单元分析
其中
u A1 1 u ， 1 2u A2 21 u
rr
于是
1 ri r j rm 3 1 z z zi z j z m 3
fi fi ai cz bi i r r

i, j, m
有限元网格确定后，各单元的就是定值。这样就可以把轴对称问题的各单元看成是常应变矩阵，所求得的应变是形心处的应变值。当轴对称结构的单元划分比较小时，这种近似所引起的误差是很小的。特别当结构上各单元的形心离 Z 轴较远时，产生的误差就更小了。
u N i ui N j u j N m um w N i wi N j w j N m wm
（4-5）
单元分析
其中形函数
Ni
a
i
bi r ci z
2
i,
j, m
（4-6）（4-7）
而

1 1 rj 2 1 rm
1 ri
zi zj zm
ai
rj rm
zj zm

第八章弹性力学问题一般解·空间轴对称问题

(8 6)
因为 F x F y 0 其第三式为
只与z有关。
又 Fz q
将式(3)代入式(4)得
，再代回式(3)，得
为了确定常数B，可以将无限的边界条件转化为有限的，即假定半空间体在距平面边界h足够远处已经很小而可以忽略，即，则由式(5)得

于是，式(3)给出的位移为
E E G (1 )(1 2 ) 2(1 )
利用式(4-5)，式(1)中简化后得
，
由式(i)并将下标符号i改为k可得
于是有
由
，式(8-10)可写成
其展开式为（用应力表示的协调方程）6个方程可以解6个应力分量）
x y z
当不计体力时，有
式(8—12)和式(8—13)称为Beltrami—Michell(贝尔特拉米—米歇尔)方程，也即应力协调方程。由此，用应力法解弹性力学问题归结为按给定边界条件满足平衡微分方程(4-1)和协调方程。注意到：Beltrami—Michell方程是以应力形式表示的变形协调方程，并且在推导中虽然用到了平衡方程(此处引用Lame方程推出)，但推导中进行了对平衡方程的求导[见式(f)]已不能代表平衡方程本身了，故而要重新考虑平衡方程，于是得出上述应力法求解的结论。下一节我们举等截面悬臂梁的弯曲为空间问题按应力求解的实例。现在我们来讨论两种求解方法的特点：按位移法求解弹性力学问题时，未知函数的个数比较少，仅有三个未知量 u 、v 、 w 。但必须求解三个联立的二阶偏微分方程。
(8 1)
如物体内质点处于运动状态，式(8-1)也可写为
式(8-2)Biblioteka (用位移表示的）平衡(运动)微分方程的展开式为
e 2u 2 ( G ) x G u Fx 0( t 2 ) e 2v 2 G v Fy 0( 2 ) ( G ) y t e 2w 2 G w Fz 0( ) ( G ) 2 z t

弹性力学第四章_4

典型轴对称问题解法：典型轴对称问题解法：（1）圆环或圆筒受均布压力
σρ =
A
ρ
2
+ B(1+ 2ln ρ) + 2C
2
σϕ = −
A
τρϕ =τϕρ = 0
边界条件：σρ 位移单值条件
ρ=r
ρ
+ B(3+ 2ln ρ) + 2C
= −q1 σρ ρ=R = −q2
B=0
（2）压力隧洞
+ B(1+ 2ln ρ) + 2C ρ A σϕ = − 2 + B(3+ 2ln ρ) + 2C
（2) y 轴
(φ= 90 o )
上应力，上应力，
2 4
1r 3r σx =σϕ =q(1+ 2 + 4 )。 2ρ 2ρ ρ = r 2r 3r 4r 远处 σx = 3q 1.22q 1.07q 1.04q q
可见，距孔边1.5D处可见，距孔边1.5D处 (ρ=4r) ， 1.5D 由于孔口引起的应力扰动<5% <5%。由于孔口引起的应力扰动<5%。
f (t) = C e4t +C2e2t +C3 +C4e−2t 1
f (ρ) = Aρ + Bρ +C + D
4 2
r ±ωi
对应解的两项：对应解的两项：
1
பைடு நூலகம்ρ2
第四章平面问题的极坐标解答
代入 Φ = f (ρ) cos 2ϕ 得应力函数 4 D 2 Φ = cos 2ϕ Aρ + Bρ +C + 2 ρ 代入(4-5) 代入 1 ∂Φ 1 ∂2Φ ∂2Φ + 2 2 σρ = σϕ = 2 ρ ∂ρ ρ ∂ϕ ∂ρ

ANSYS_轴对称问题

关于 ANSYS 轴对称应力问题1. 什么是轴对称应力问题弹性力学中将廻转体对称于转轴而变形的问题定义为轴对称问题。

根据铁摩辛柯《弹性理论》一书，公式 (169)(P.322) 与 (178) (P.360)可以看到，在轴对称情况，只有径向和轴向位移，不能有周向位移。

轴对称分析要求，除了结构是轴对称的外，载荷和约束也必须是轴对称的。

由上面的说明可见，在轴对称分析中不能有周向变形，因而也不能有周向的载荷。

即不能有扭矩之类的载荷和扭转变形。

对于轴对称结构，如果承受轴对称约束，而载荷是非轴对称的，但该载荷可以分解为旋转角θ的三角函数，可以使用“轴对称谐波单元–Plane25，Shell61，Plane75，Plane78，Plane83，Shell208, Shell209 等”进行求解，不过本文不涉及。

2. ANSYS 对轴对称模型的基本要求在 ANSYS 中分析轴对称问题时，要求：(1) 分析模型 (轴对称) 必须位于整体坐标系的 X-Y 平面中，Y 轴为旋转轴，模型中的所有实体 (Keypoint,Line,Area,Volume,Node, Element等) 都必须位于 X >= 0 的范围中。

(2) 所有的载荷、约束都必须是轴对称的。

为此：a. 只能施加 XY 平面内的载荷和约束，不能施加垂直于 XY 平面的载荷 (如扭矩，会产生法向的位移，对于轴对称单元不存在该位移，故不能施加)；b. 根据轴对称理论，在旋转轴上 (X=0) 应该有 Ux ＝0，因此在旋转轴上不能施加非零的径向 (X 方向) 位移约束，也不能施加径向的载荷 (否则会破坏结构 Ux ＝0 的条件)。

3.ANSYS 中如何施加轴对称载荷对于约束、面载荷、体载荷、Y 方向的加速度、X 方向的角速度等，定义方式与非轴对称结构相同；对集中力载荷则有所不同。

对于集中力，要求输入载荷作用点处，360 度圆周上的合力。

例如：在实际结构直径 d = 10 mm 的圆周上作用 p = 1500 N/mm 的 Y 向载荷，则应输入为 (见图 1)：F,n,Y,-47214 ! n –加载点的节点编号其中： 47214 ＝π * d * p = 3.1416 * 10 * 1500图 1 轴对称结构施加集中力同样，轴对称分析结果的表述方式也和载荷相同，即节点反力是该节点所在圆周上的全部反力的合力。

弹性力学课件08第八章空间问题的解答

将应力表达式代入
∞
σ ρ = A2 σϕ =
A2 , R( R + z ) Az Aρ σ z = − 23 , τ zρ = − 2 3 , R R
∫
0
(2πρ d ρ)σ z + F = 0
第三节
半空间体在边界上受法向集中力
F (1 − 2ν ) R 3ρ 2 z − 3 σρ = 2 2πR R + z R (1 − 2ν ) F z R − σϕ = 2πR 2 R R + z
∇ 2ϕ = 0
第三节
半空间体在边界上受法向集中力根据位移分量和应力分量与位移函数的关系：
1 ∂ 2ζ 1 ∂2 u=− ,ω = 2(1 −ν )∇ 2 − 2 ζ ∂z 2G ∂ρ∂z 2G ∂ 2 ∂2 σ ρ = ν∇ − 2 ζ ∂ρ ∂z
半空间体，体力不计，坐标系如图。通过量纲分析，位移函数应是F乘以R、 z、ρ等长度坐标的正一次幂，试算后，取设位移函数为
化简后得到
∂σ ρ
τ ρz + + + Fb z = 0 ∂z ∂ρ ρ
∂τ ρz
第二节空间轴对称问题这样，空间轴对称问题的平迭加得到几何方程衡方程为 ∂σ ρ ∂τ zρ σ ρ − σ ϕ ∂u u + + + Fb ρ = 0 ε ρ = , εϕ = ρ ∂ρ ∂z ∂ρ ρ ∂σ z ∂τ ρz τ ρz ∂u ∂w ∂w + + + Fb z = 0 + , γ zρ = εz = ∂z ∂ρ ρ ∂z ∂ρ ∂z 由于对称，各点环向位移为零，这里的物理方程是由径向位移产生的应变为 1 ∂u u ∂u ε ρ = [σ ρ −ν (σ φ + σ z )] ερ = , ε ϕ = , γ zρ = E ∂ρ ρ ∂z 1 ε ϕ = [σ ϕ −ν (σ z + σ ρ )] E 由轴向位移w产生的应变为

弹性力学第四章 (5)轴对称问题

A 2 BC (1 2 ln ) 2C A 2 B (3 2 ln ) 2C 0
（4—11）
三、位移分量：
（4-11）代（4-3）代（4-2）
1 1 A ( ) (1 ) 2 B[(1 3 ) E E
1 1 A ( ) (1 ) 2 B[(3 ) 2(1 ) ln ] E E
2(1 ) ln ] 2(1 )C

2(1 )C

令 e
t
则由几何方程得：
ln t d et dt
d 2 f ( ) f ( ) 0 2 d
将(g) 带入 (b): 1 A u [(1 ) 2(1 ) B (ln 1) (1 3 ) B E
2(1 ) B 2(1 )C ]
I cos K sin
2
2
二、轴对称问题应力分量： 1、解出方程（A）,求

4 3 2 d d d d 3 2 （A）式写为： 4 2 0 4 3 2 d d d d
方程为（欧拉型）四阶.变系数.齐次.线性.常微分方程：
引入代换：
e (t ln ) （a）
ln d te dt
t
分步积分
te e (ln 1)
t t

u

1 E
A ( 1 ) B [( 1 3 ) 2 ( 1 ) ln ] 2 ( 1 ) C 2

1 2 2 0

02弹性力学中的几个问题

( ) 其几何方程也与平面应力问题的几何方程一样。但是，由于 ε z = 0 ，即σ z = µ σ x + σ y ，因而平
面应变问题的物理方程与平面应力问题的物理方程是不同的，即
[ ] ε x
= 1+ µ E
(1 − µ )σ x
− µσ y
[ ] ε y
= 1+ µ E
(1 − µ )σ y
− µσ x
在平面应力状态下，由于σ z = τ zx = τ zy = 0 ，所以根据式(0.1.4)可以很容易得到平面应力问
题的平衡方程，即 Navier 方程在平面问题中的简化形式，由式(0.1.7)可得到平面应力问题的几何方程，即 Cauchy 方程在平面问题中的简化形式，
∂σ x ∂x
+
∂τ yx ∂y
对于轴对称问题，采用圆柱坐标 r ,θ , z 比采用直角坐标 x，y，z 方便得多。这是因为，当以弹
性体的对称轴为 z 轴时(如图 0.2.3 所示)，则所有的应力分量、应变分量和位移分量都将只是 r 和
z 的函数，而与θ 无关(即不随θ 变化)。为推得轴对称问题的平衡微分方程，可取 z 轴垂直向上，用间距为 dr 的两个圆柱面，且互成 dθ
从弹性力学角度讲，不论是平面应力问题还是平面应变问题，只要材料是各向同性弹性体，体积力又只是重力，那么其应力函数则都由同一个基本方程来决定(推导省略)。两者的区别仅在于，当求得应力分量之后如何确定应变分量。
0.2.2 轴对称问题
在空间问题中，如果弹性体的几何形状、约束状态，以及其他外在因素都是对称于某一根轴(过该轴的任一平面都是对称面)，那么弹性体的所有应力、应变和位移也就都对称于这根轴。这类问题通常称为空间轴对称问题。

5_轴对称问题有限元分析

<<结构分析中的有限单元法>>
By Xiaojun Wang
13 /54
单元刚度矩阵
同平面问题一样，同平面问题一样，用虚位移原理推导单元刚度矩在轴对称情况下，单元的虚阵。在轴对称情况下，单元的虚位移方程为
(u ) F = ∫∫∫ (ε ) σ rdrdθ dz
e* T e *
T
(5.17)
0 0 cm bm
( m = i, j , k )
(5.12)<<构分析中的有限单元法>>
By Xiaojun Wang
8 /54
单元应变与应力
由此可见，轴对称问题的几何方程式(5.11)，由此可见，轴对称问题的几何方程式，在形式上和平面问题是一样的，和平面问题是一样的，但是轴对称问题中的 B 和 ε 并不完全是常量元素，的函数，全是常量元素，其中各点的应变将随 r 、z 的函数，故 B 是的函数。 r 、 z 的函数。由于 B 是 r 、z 的函数，的函数，所以单元中各点的应变将随 r 、而变化，即单元中各点的应变不同。为了简化计算， z 而变化，即单元中各点的应变不同。为了简化计算，通常用单元形心坐标 ( z , r ) 近似代替 f i 中的 r 、 z 值，即用单处的应变作为单元的平均应变，元形心 ( z , r ) 处的应变作为单元的平均应变，变成常应变单元，单元，即
<<结构分析中的有限单元法>>
By Xiaojun Wang 9 /54
单元应变与应力
1 z ≈ z = ( zi + z j + zk ) 3 1 r ≈ r = ( ri + rj + rk ) 3 am cm z fm ≈ fm = + bm + r r

弹性力学轴对称问题

河南理工弹性力学- 轴对称应力问题

第10章 弹性力学轴对称问题的有限元法简介

弹性力学13-轴对称应力和相应的位移

《弹塑性力学》第九章空间轴对称问题

弹塑性力学讲义 第九章空间轴对称问题

弹性力学13-轴对称应力和相应的位移

弹性力学空间轴对称问题有限元法

弹性力学问题的有限元法轴对称问题

弹性力学轴对称问题的有限元法

2014-计算力学-4-轴对称问题有限元

第八章弹性力学问题一般解·空间轴对称问题

弹性力学 第四章_4

ANSYS_轴对称问题

弹性力学课件08第八章 空间问题的解答

弹性力学第四章 (5)轴对称问题

02弹性力学中的几个问题

5_轴对称问题有限元分析

第10章弹性力学轴对称问题的有限元法简介

弹塑性力学讲义第九章空间轴对称问题

弹性力学第四章_4

弹性力学课件08第八章空间问题的解答