七年级数学上册 第5课时 绝对值与相反数(一)人教版
人教版数学七年级上册绝对值完美课件
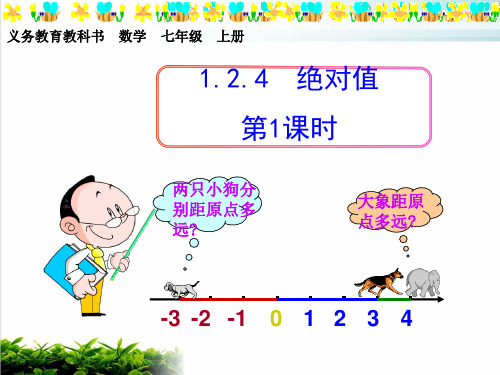
2 的绝对值是 2,即| 2|= 2;
3
3
33
0的绝对值是0,即|0|=0;
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
-2.3的绝对值是2.3,即|-2.3|=2.3;
+0.56的绝对值是0.56,即|+0.56|=0.56;
-6的绝对值是6,即|-6|=6;
+6的绝对值是6 ,即|+6|=6;
21 的绝对值是 21,即| 21|=
2
2
2
21.
2
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
1.字母 a 表示一个数,-a 表示什 么?-a一定是负数吗?
2 , 2 , 0. 55 20 2
55
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
3.化简 5 _5__
5 _-_5_
21
2 1 __4_
4
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
绝对值的表示 数a的绝对值,记作:|a|.
│-5│=5
A
│4│=4
B
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
在数轴上表示-5的点与原点的距离是5, 即-5的绝对值是5,记作:|-5|=5.
11 3
的绝对值是1 1 3
人教版七年级数学上册1.2.4《绝对值》课件 (13张PPT)

1.2.4(1) 绝对值
1、数轴三要素
2、什么是互为相反数
谁离乒乓球网架远呢?
20 20
-20 -15 -10 -5 5 10 0 15 20 -20与+20在数轴上所表示的点到原点的距离都是 20个单位,距离20是-20和20的绝对值.
-20的绝对值表示-20的点到原点的距离,它的绝对值是20. -3的绝对值表示什么呢?它的绝对值是多少呢?
数轴原点表示的是0,0绝对值是0
绝对值性质:对于任意一个有理数a都有, 1、当a>0 时, |a|= _____ a ;
0 ; 2、当a=0 时, |a|= _____
3、当a<0 时, |a|= _____. -a
绝对值的代 数意义
1.填空:
1.7 |-1.7|_____ ; -4 ; -|-4|=____
-7 7
绝 对 值 发 生 器
7 7
、数轴原点右边表示的是什么数?该数的绝对值与这个数有什 么关系?
数轴原点右边表示的是正数,正数的绝对值是它本身
、数轴原点左边表示的是什么数?该数的绝对值与这个数有 什么关系?
数轴原点左边表示的是负数,负数的绝对值是它的相反数
、数轴原点表示的是什么数?该数的绝对值是多少?
1、绝对值的几何意义及表示方法 2、绝对值的代数意义 (1)一个正数的绝对值是它本身;
(2)零的绝对值是零;
(3)一个负数的绝对值是它的相反数;
1、必做题:习题1.2 第5、8题 2、选做题:绝对值评测训练
2的绝对值表示什么呢?它的绝对值是多少呢? 2 3 的绝对值表示什么呢?它的绝对值是多少呢?
2 3
-3 -2 -1
0
人教版七年级数学上册《有理数——绝对值》教学PPT课件(3篇)

非__正__数__的绝对值是它的相反数.
1
2.|- 1 |的相反数是
3
-3
;若| a |=2,则
a= _±__2__.
3.化简: | 0.2 |= 0.2
-273 =
27 3
| b |= -b (b<0)
| a – b | = a-b (a>b)
课堂总结
1.绝对值的定义:数轴上表示数a的点与原点的距离叫做数a
同类型题检测:学案课堂练习第2题
活动形式:1、学生独立思考 2、小组讨论,每一组拍一份答案上传 3、展示小组讨论结果,互评评优,找到问题所在,有针对性的点评讲解
同类型题检测:
已知|a -1|+|b+2|=0,求a+b的值
巩固练习:学案课堂练习第4题 4.正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超 过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下:
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
知识点二:运用法则比较有理数的大小
学生自学问题展示:
展示学案对应部分学生的典型问题
知识点二:运用法则比较有理数的大小
同桌讨论:两个负数之间如何比较大小? 要点梳理: (1)正数大于0,负数小于0,正数大于负数; (2)两个负数,绝对值大的反而小.
活动形式:1、学生独立完成,拍照上传, 2、老师给出标准答案,互评 3、展示互评结果,找到问题所在,有针对性的点评讲解
学生自学问题展示:学案课前自主学习任务第7题
同类题检测:
(1)绝对值等于2的数是 2或-2 ,
(2)绝对值等于0的数是 0
七年级数学上册绝对值知识梳理人教版

1 / 2绝对值【知识梳理】1、什么叫绝对值?在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值.例如+5的绝对值等于5,记作|+5|=5;-3的绝对值等于3,记作|-3|=3.2、绝对值的特点有哪些?(1)一个正数的绝对值是它本身;例如,|4|=4 , |+7.1| = 7.1 (2)一个负数的绝对值是它的相反数;例如,|-2|=2,|-5.2|=5.2 (3)0的绝对值是0.容易看出,两个互为相反数的数的绝对值相等.如|-5|=|+5|=5.若用a 表示一个数,当a 是正数时可以表示成a >0,当a 是负数时可以表示成a <0,这样,上面的绝对值的特点可用用符号语言可表示为:(1) 如果a >0,那么|a|=a ; (2) 如果a <0,那么|a|=-a ; (3) 如果a =0,那么|a|=0。
3、绝对值在本节课中的应用――比较两个负数的大小由于绝对值是表示数的点到原点的距离,则离原点越远的点表示的数的绝对值越大.负数的绝对值越大,表示这个数的点就越靠左边,因此,两个负数比较,绝对值大的反而小.【重点难点】重点:(1)绝对值的概念; (2)化简;(3)用绝对值比较两个负数的大小。
难点:绝对值的化简;用绝对值比较两个负数的大小。
【典例解析】例1 、已知|x |=5,求x 的值。
解:因为|x |=5,所以x =5或x =-5。
﹡拓展:|x -3|=5,求x 的值.解:因为|x -3|=5所以x -3=5或x -3=-5,则x=8或x=-2 例2、绝对值小于5的整数有哪些?解:有4+,4-,3+,3-,2+,2-,1+,1-,0。
例3、 比较87-和76-的大小. 分析 比较两个负数的大小,应先比较它们绝对值的大小,再根据“两个负数,绝对值大的反而小”来判断它们的大小.解 564987|87|==-,564876|76|==-, 56485649>,所以87-<76- 【过关试题】1、下列说法中正确的有( )① 互为相反数的两个数的绝对值相等;②正数和零的绝对值都等于它本身;③只有负数的绝对值是它的相反数;④一个数的绝对值相反数一定是负数。
人教版七年级上册数学绝对值ppt课堂课件

人教版七年级上册数学课件:1.2.4绝 对值
人教版七年级上册数学课件:1.2.4绝 对值
2.若|a|+ |b-3| =0.则a =__0___,
b= __3___. 3.如果一个数的绝对值等于4.53 ,
则这个数是__4_._5_3或__-__4_.5_3____. 4.如果|x-1|=2,则x=___3或__-__1___. 5.如果a 的相反数是-0.86,那么|a|
东、西方向行驶10km,到达A、B两处(图
1.2-5)。
方向不同, (正负性)
(1)它们的行驶路线的方向相同吗?距(不离。管相方同向,)
(2)它们行驶路程的距离(线段OA、OB的长 度)相同吗?
A
10
-10
O
10
B
0
10
人教版七年级上册数学课件:1.2.4绝 对值
人教版七年级上册数学课件:1.2.4绝 对值
人教版七年级上册数学课件:1.2.4绝 对值
1.2.4
人教版七年级上册数学课件:1.2.4绝 对值
人教版七年级上册数学课件:1.2.4绝 对值
学习目标
1. 初步理解绝对值的概念,能求一个
数的绝对值. 2.通过应用绝对值解决相关问题,体 会绝对值的意义和作用.
人教版七年级上册数学课件:1.2.4绝 对值
❖
6本课的突出特点是拟人手法的运用, 把植物 和种子 分别当 作“妈 妈”和 “孩子 ”来写 。“妈 妈孩子 ”这样 的关联 ,易触 动儿童 的情感 世界, 易激发 想象、 引发思 考,读 起来亲 切、有 趣,易 于调动 小读者 的阅读 兴趣。
❖
7学习这篇课文,应该重点引导学生运 用探究 式的学 习方式 ,注意 激发学 生了解 植物知 识、探 究大自 然奥秘 的兴趣 ,把向 书本学 习和向 大自然 学习结 合起来 ,引导 学生养 成留心 身边的 事物、 认真观 察的好 习惯。
第一讲正数负数相反数绝对值(教案)

(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“正数负数相反数绝对值在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
(3)绝对值的定义及性质:理解绝对值的概念,掌握绝对值的性质,如非负性、对称性等。
举例:数字-3的绝对值为3,绝对值表示数与原点的距离。
(4)正数、负数、相反数、绝对值之间的相互关系和运算:熟练掌握这些概念之间的联系,能正确进行运算。
举例:计算两个相反数的和为0,两个相同绝对值的负数的差等于它们的绝对值。
3.重点难点解析:在讲授过程中,我会特别强调正数、负数、相反数和绝对值这两个重点。对于难点部分,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与正数负数相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《正数负数相反数绝对值》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过表示相反意义的量,比如温度、海拔等?”这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索正数负数的奥秘。
1.2相反数的定义,如何找到一个数的相反数;
1.3绝对值的定义,如何计算一个数的绝对值;
1.4通过实例和练习,让学生掌握正数、负数、相反数、绝对值在实际问题中的应用。
新版人教版七年级数学上册《绝对值》课件(17张)
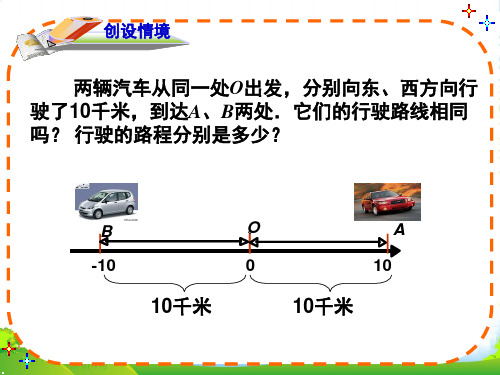
两辆汽车从同一处O出发,分别向东、西方向行 驶了10千米,到达A、B两处.它们的行驶路线相同 吗? 行驶的路程分别是多少?
B
O
A
-10
0
10
10千米
10千米
做游戏
请两位同学分别站在老师的左右两边,两位同学 同时向东、西相反的方向走1米,把这两位同学所 站位置用数轴上的点表示出来.
距
距
离
离
是1
学生活动 2.互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们 到原点的距离是相等的.所以互为相反数的两 个数的绝对值相等.
7 图1.2-7
学生活动
你能把14个气温从低到高排列吗?能把这14个数 用数轴上的点表示出来吗?观察这些点在数轴上的位 置,思考它们与温度的高低之间的关系,你觉得两个 有理数可以比较大小吗?
(B )
A.可以是负数 B.不可能是负数
C.必是正数
D.可以是正数也可以是负数
温馨提示: 认真完成作业是巩固知识的有效方法!!
12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/5/52022/5/5May 5, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。
练习2:|-13 |的相反数是 ;若|a|=2,则a=±2 .
练习3:绝对值小于3.5的整数是-3,-2,-1,0,1,2,3 . 练习4:已知:x342y0,则x= -3 ,y= 2 .
课堂练习
人教版七年级数学上册.3相反数课件

第5课时 课题:1.2.3 相反数
新课准备
1、数轴的三要素 是: 原点 、 正方向、单位长度;
2、填空:数轴上与原点的距离是2的点 有 2 个,这些点表示的数是 2或-2 ; 与原点的距离是5的点有 2 个,这些点 表示的数是5或-5 。
新课导入 视察下列各数:2与-2,5与-5,
1 2
与
1,3
22
.2
31 2
.
31
1 0 1
2
31 2
新课探究 1、分别在下面的数轴上描出表示
2与-2,5与-5,1 与 1,3 1 与 3 1
2 22
2
这四对数的对应点:
2、视察上面四对数在数轴上的对应点的 位置,发现,它们都位于原点的 两侧, 且到原点的距离相等。
新课探究 知识点:相反数的概念
像上面,2与-2,5与-5,
2(2) 若 (x y)是负数,
则x+y < 0.
总结反思,归纳升华
通过本节课的学习,你有哪些感悟和 收获,与同学交流一下: ①学到了哪些知识? ②获得了哪些学习方法和学习经验? ③与同学的合作交流中,你对自己满意 吗? ④在学习中,你受到的启示是什么?你 认为应该注意的问题是什么?
课后提练,拓展空间
1、想一想:当+6前面有2013个正号时, 化简结果为 ; 当+6前面有2013个负号时,化简结果 为; 当+6前面有2014个负号时,化简结果 为。
2、在数轴上点A表示7,点B、C表示互为相 反数的两个数,且C与A间的距离为2,则B 对应的数为 ,C对应的数为 。
七年级数学基础巩固与拓展提优:第二章 第5课时 绝对值与相反数(1)

第5课时绝对值与相反数(1)(附答案)【基础巩固】1.在数轴上离原点距离是3的数是________.2.绝对值等于本身的数是________,绝对值小于2的整数是________.3.数轴上与表示1的点的距离是2的点所表示的数有________.4.+6的符号是________,绝对值是________,56-的符号是_______,绝对值是_______.5.计算:2 3.6 1.6-+--=_______.6.绝对值等于10的数是________.7.下列说法中,错误的是 ( )A.+5的绝对值等于5 B.绝对值等于5的数是5 C.-5的绝对值是5 D.+5、-5的绝对值相等8.绝对值最小的有理数是 ( )A.1 B.0 C.-1 D.不存在9.绝对值等于本身的数有 ( )A.1个 B.2个C.4个 D.无数个10.绝对值小于3的负数有 ( )A.2个 B.3个 C.4个 D.无数个11.化简3--等于 ( )A.-3 B.-13C.13D.312.求下列数的绝对值,并用“<”号把这些绝对值连接起来.-1.5,-3.5,2,1.5,-2. 75.13.正式足球比赛时所用足球的质量有严格的规定,下面是6个足球的质量检测结果,用正数记超过规定质量的克数,用负数记不足规定质量的克数,检测结果:-25、+10、-20、+30、+15、-40.请指出哪个足球的质量好一些,并用绝对值的知识进行说明.【拓展提优】14.在数轴上表示-2的点离开原点的距离等于 ( )A.2 B.-2 C.±2 D.415.下列各式中,正确的是 ( )A.若a=b,则a=b B.若a>b,则a>bC.若a<b,则a<b D.若a=b,则a=±b16.如图,数轴上A、B两点分别对应实数a、b,则下列结论正确的是 ( )A.a+b>0 B.ab>0 C.a-b>0 D.->017.实数a、b在数轴上的位置如图所示,则a、b的大小关系是_______.18.大家知道550=-,它在数轴上的意义是表示5的点与原点(即表示0的点)之间的距离,又如式子,它在数轴上的意义是表示6的点与表示3的点之间的距离.类似地,式子5a+在数轴上的意义是________.19.已知a=5,b=8,且a<b,则a+b=_______.20.计算:1111111122334910-+-+-++-.21.阅读下面的例题:解方程:15x-=.解:由绝对值的定义,得 x-1=5或x-1=-5.所以x=6或x=-4.仿照上面的思路,解下列方程:(1)3x=6;(2)17x+=22.若x<0,y>0,求x y xyx y xy++的值.23.(1)比较下列各式的大小(用“>”“=”或“<”连接).23_______23-+-+;35_______35+--;1111_______2323-+---;05_______05+--;……(2)通过(1)的比较,请你分析,归纳出当a、b为有理数时,a+b与a b+的大小关系.(3)根据(2)中你得出的结论,当x+2012=2012x-时,求x的取值范围.24.数形相伴.(1)如图,点A 、B 所代表的数分别为-1,2,在数轴上画出与A 、B 两点的距离和为5的点(并标上字母).(2)若数轴上点A 、B 所代表的数分别为a 、b ,则A 、B 两点之间的距离可表示为AB =a b -,那么,12x x ++-=7时,当=7时,x =_______;当12x x ++->5时,数x 所对应的点在数轴上的位置是在_______.参考答案【基础巩固】1.±3 2.非负数±1,0 3.3,-1 4.正号 6 负号565.4 6.±107.B 8.B 9.D 10.D 11.A 12. 1.52 2.75 3.5±<<--13.+10的绝对值最小,质量好些【拓展提优】14.A 15.D 16.C 17.a b> 18.表示a的点与表示-5的点之间的距离 19.13或3 20.91021.(1)x=±2 (2)x=6或x=-8 22.-1 23.(1)> > ==(2)a b a b+≥+ (3)x≤024.(1)如图,C、D两点即为所求. (2)-3或4点C的左边或点D的右边。
人教版七年级数学上册《有理数(第5课时)》示范教学课件

a=b=0
|a|≥0
我们已经知道两个正数(或0)是怎样比较大小的,例如
任意两个有理数(例如-4和-3,-2和0,-1和1)怎样比较大小呢?
0<1,1<2,2<3,….
问题
右图给出了未来一周中每天的最高气温和最低气温,其中最低气温是____℃,最高气温是____℃.你能将这七天中每天的最低气温按从低到高的顺序排列吗?
|a|
负数
0
相等
相等或者互为相反数
3.一个正数的绝对值是________;一个负数的绝对值是____________;0的绝对值是____.即(1)如果a>0,那么_______;(2)如果a=0,那么_______;(3)如果a<0,那么_________.
它本身
它的相反数
0
|a|=a
|a|=-a
解:
解:
解:
异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
例2 有理数a,b满足a>0,b<0,|a|<|b|,试利用数轴判断a,b,-a,-b之间的大小关系.
分析:此类题目需要先画出数轴,把各数标在数轴上,再借助用数轴比较有理数大小的方法进行判断.
在对多个数进行大小比较时,运用数轴比较法比较合适.
|a|=0
5.求一个数的绝对值的两种方法:方法1:求某个数的绝对值,首先要确定这个数的_______,然后根据______________进行求值.方法2:根据___________________进行求解.
Байду номын сангаас绝对值的性质
符号
绝对值的几何意义
4.绝对值的非负性:任何一个有理数的绝对值总是________.即对任意有理数a,总有______.若|a|+|b|=0,则必有_________.
人教版七年级数学上册1.2.3《相反数》说课稿

人教版七年级数学上册1.2.3《相反数》说课稿一. 教材分析《人教版七年级数学上册》第一章第二节第三小节《相反数》是整个初中数学基础知识的重要组成部分。
它不仅为学习绝对值、有理数乘法等知识打下基础,而且也培养学生的抽象思维能力。
本节内容主要让学生理解相反数的含义,掌握求一个数的相反数的方法,以及了解相反数在实际问题中的应用。
二. 学情分析面对刚从小学升入初中的学生,他们的思维方式正在从具体形象思维向抽象逻辑思维过渡。
在这个阶段,学生对新鲜事物充满好奇,善于发现和探索。
但同时,他们也可能因为缺乏实际操作经验,对抽象概念的理解存在一定的困难。
因此,在教学过程中,我们需要结合学生的认知特点,采用生动、形象的教学手段,帮助他们理解和掌握相反数的概念。
三. 说教学目标1.知识与技能目标:让学生理解相反数的含义,掌握求一个数的相反数的方法,能运用相反数解决实际问题。
2.过程与方法目标:通过观察、分析、归纳等方法,培养学生抽象思维能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养他们积极思考、合作探究的良好学习习惯。
四. 说教学重难点1.教学重点:相反数的定义及其求法。
2.教学难点:相反数在实际问题中的应用,以及学生对相反数概念的理解。
五. 说教学方法与手段1.采用问题驱动法,引导学生主动探究相反数的含义。
2.利用多媒体演示,帮助学生形象地理解相反数的概念。
3.运用合作学习法,让学生在小组讨论中共同解决问题,提高他们的团队协作能力。
4.通过课后实践,让学生将所学知识应用于实际问题,巩固所学内容。
六. 说教学过程1.导入新课:利用生活实例,如电梯上升和下降,引出相反数的概念。
2.自主学习:让学生阅读教材,理解相反数的定义。
3.课堂讲解:详细讲解相反数的含义,以及如何求一个数的相反数。
4.互动环节:学生提问,教师解答;学生上台演示,加深对相反数概念的理解。
5.巩固练习:设置适量习题,让学生独立完成,检查他们对相反数的掌握程度。
数学人教版(2024)七年级上册 第一章 有理数 第5课时 相反数

相反数等于它本身的数是0;-a是a的相反数,-a不一定是 负数,可以是正数、负数和0.
领跑作业本 ·数学(七年级上册RJ)
第5课时 相反数
返回目录
5.如图,数轴上A,B两点表示的数互为相反数,且点A与点B 之间的距离为4个单位长度,则点A表示的数是_-__2_____.
第5题图
领跑作业本 ·数学(七年级上册RJ)
第5课时 相反数
返回目录
6.【数形结合】写出下列各数的相反数,并将这些数连同它们的相反 数在如图所示的数轴上表示出来:-4.5,6,-130 ,0,-(+2),--12 .
第6题图 第6题答图 解:这些数的相反数分别为 4.5,-6,130 ,0,2,-12 . 这些数及它们的相反数在数轴上的表示如答图所示.
1 =_____2_____.
领跑作业本 ·数学(七年级上册RJ)
C.+(-9)=9
D.+(+5)=-5
返回目录
领跑作业本 ·数学(七年级上册RJ)
综合提升
返回目录
第5课时 相反数
返回目录
4.(1)如果a=-a,那么a表示的数是____0____. (2)若a为正数,则-a为__负__数___;若a为负数,则-a为__正__数____;
若a=0,则-a=____0____.(填“正数”“负数”或“0”)
返回目录
2.如图,数轴上点A表示的数为a,则a的相反数为( B )
A.-2 B.2 C.-12 D.12
第2题图
领跑作业本 ·数学(七年级上册RJ)
第5课时 相反数
返回目录
3.化简: (1)+(-6)=___-__6_____;(2)-(+15)=___-__1_5____;
(3)--73
相反数课件人教版七年级数学上册

第5课时 相反数
1.(2022新课标)借助数轴理解相反数的意义,掌握求有理数 的相反数的方法. 2.体验数形结合思想.
知识点一:相反数的概念 (1)定义: 只有符号 不同的两个数叫做互为相反数.特别 地,0的相反数是0. (2)相反数是 成对 出现的,单独的一个数不能说是相反 数.除 0 外互为相反数的两个数都是一正一负.
(2)若数c与-c表示的点相距10个单位长度,则c与-c表示的 数分别是什么? 解:(1)画表示-a,-b的点,图略. (2)c表示5,-c表示-5或c表示-5,-c表示5. 小结:作图依据是相反数的几何意义.
-100 3.9
-2
B
7 -12
5
★12.(创新题)如图,数轴的1个单位长度为1.
A
(2)下列说法是正确的是( D ) A.-2是相反数 B.-2与+3是相反数 C.-2与-3是相反数 D.-2与2是相反数
(3)(2022湖北一模)相反数等于它本身的数是 0 .
知识点二:相反数的几何意义 互为相反数的两个数表示的点在数轴上,分别位于原点的 两旁 ,并且到原点的距离 相等 .
知识点四:多重符号的化简
(1)方法1:由相反数定义由内向外化简. (2)方法2:多重符号化简的结果是由 - 号的个数决定的, 与 + 号无关.如果“-”号的个数是 奇 数,那么结果 为“-”;如果“-”号的个数是 偶 数,那么结果为 “+”;简称:“ 奇 负 偶 正”.
6 -6 -6 6 1
-7
-6 8
0 小结:只有符号不同的两个数是互为相反数的.特别地,0的相 反数是0.
√ √
√ × 小结:根据互为相反数的定义去判断对与错.
68 -
- 小结:方法一,根据相反数的概念;方法二,按负号个数的奇偶 判断结果的符号,即“奇负偶正”.
人教版福建初一数学七年级上册第一章 第5课时1-2-4绝对值(1)

第5课时1.2.4 绝对值(1)1.绝对值的定义及记法(1)定义:数轴上表示数a 的点与__原点__的距离. (2)记法:数a 的绝对值记作__|a|__.2.有理数的绝对值(1)语言描述:一个正数的绝对值是它__本身__;一个负数的绝对值是它的__相反数__;0的绝对值是__0__.(2)符号表示:|a|=__±a __.3.绝对值非负性(1)语言叙述:任何一个数的绝对值都是__非负数__.(2)字母表示:__|a|≥0__.(2020·青岛中考)-4的绝对值是( A )A .4B .-4C .14D .-14求下列各数的绝对值.-3.1,12,0,-100,3,+0.1. 【解析】|-3.1|=3.1,⎪⎪⎪⎪⎪⎪12 =12 ,|0|=0,|-100|=100,|3|=3,|+0.1|=0.1.一个有理数的绝对值是( D )A.正数B.负数C.非正数D.非负数如果一个有理数的绝对值是正数,那么这个数必定( B )A.是正数 B.不是0C.是负数 D.以上答案都不对(2021·周口期末)某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负.某天自A地出发到收工时,所走路程(单位:千米)为:+10,-3,+4,+2,-8,+13,-2,+12,+8,+5(1)问收工时距A地多远?(2)若每千米耗油0.2升,问从A地出发到收工时共耗油多少升?【解析】(1)10+(-3)+(+4)+(+2)+(-8)+(+13)+(-2)+(+12)+(+8)+(+5)=41千米.所以收工时距A地41千米;(2)从A地出发到收工时共耗油量为(10+3+4+2+8+13+2+12+8+5)×0.2=13.4升.某车间生产一种机器零件,从中抽取5件进行检查,比规定直径长的毫米数记为正数,比规定直径短的毫米数记为负数,检查结果如表所示(单位:毫米).1 2 3 4 5+0.16 -0.08 +0.14 -0.10 +0.06指出哪一个零件更符合规定?你能用绝对值的知识说明你是怎样判断的吗?【解析】第5个零件更符合规定,因为它的绝对值最小.1.(2021·兰州期末)5的相反数和绝对值分别是( B )A .-5;-5B .-5;5C .5;-5D .5;52.下列说法中正确的是( C )A .有理数的绝对值一定是正数B .如果两个数的绝对值相等,那么这两个数相等C .如果一个数是正数,那么这个数的绝对值是它本身D .如果一个数的绝对值是它本身,那么这个数是正数3.(2020·呼伦贝尔中考)-2 020的绝对值是( B )A .-2 020B .2 020C .-12 020D .12 0204.(2020·烟台中考)实数a ,b ,c 在数轴上的对应点的位置如图所示,那么这三个数中绝对值最大的是( A )A .aB .bC .cD .无法确定5.若||x =5,则x =__±5__,|x|=|-4|,则x =__±4__.6.计算下列各式的值.(1)-||-3 ;(2)-(-3);(3)⎪⎪⎪⎪⎪⎪-32 +||-5 ;(4)⎪⎪⎪⎪⎪⎪-32 ×||+5 ; (5)||-3 ÷⎪⎪⎪⎪⎪⎪-23 ; (6)-(-2)-|-3|.【解析】(1)-||-3 =-3;(2)-(-3)=3;(3)⎪⎪⎪⎪⎪⎪-32 +||-5 =32 +5=132 ; (4)⎪⎪⎪⎪⎪⎪-32 ×||+5 =32 ×5=152 ; (5)||-3 ÷⎪⎪⎪⎪⎪⎪-23 =3÷23 =3×32 =92 ; (6)-(-2)-||-3 =2-3=-1.1.已知|a +3|+|b -1|=0,则a +b =__-2__.2.若x 为整数,且|x|<2,则x 为__1,0,-1__.3.在数轴上与3的距离为5个单位长度的点表示的数是__-2或8__.4.(2021·酒泉期末)在一条不完整的数轴上从左到右有点A ,B ,D ,C ,其中AB =2,BD =3,DC =1,如图所示,设点A ,B ,D ,C 所对应数的和是p.(1)若以B 为原点,写出点A ,D ,C 所对应的数,并计算p 的值;(2)若原点O 在图中数轴上点C 的右边,且CO =1,求p 的值.【解析】(1)若以B 为原点,因为AB =2,BD =3,DC =1所以点A,D,C所对应的数分别为:-2,3,4;p=3+4-2=5;(2)若原点O在题图中数轴上点C的右边,且CO=1,则p=-7-5-2-1=-15.。
人教版七年级数学上册教学课件-1.2.4绝对值(1)

教学过程 ∣+24∣= ____,|5|=_____
2、由上面新课引入知,课本11页A,B两点分别表示10和-10,它们与原点的距离都是 个单位长度. 解:一个数的绝对值不可能小于它本身.
解:a可能是正数,可能是零,不可能是负数.
(2)如果数 a 的绝对值大于 a ,那么 a 可能是正 数吗?可能是零吗?可能是负数吗?
解:a 不可能是正数,不可能是零,一定是负数. (3)一个数 的绝对值可能小于 它本身吗?
解:一个数的绝对值不可能小于它本身.
归纳
(2)如果数 a 的绝对值大于 a ,那么 a 可能是正数吗?可能是零吗?可能是负数吗? 2、由上面新课引入知,课本11页A,B两点分别表示10和-10,它们与原点的距离都是 个单位长度. 让感受到数学与生活的联系,通过数形结合理解绝对值的意义,进一步渗透数形结合的思想。
2、对任意有理数a,总有|a|≥0.因此可知绝对 (2)-8的绝对值是________,
1、一般地,数轴上表示数a的点与 1、写出下列各数的绝对值:
值等于它本身的数是正数或零,绝对值等于它 (1)借助数轴初步理解绝对值的概念。
(7)0的绝对值是___________.
的相反数的数是负数或零。 认真阅读课本第11页的内容,完成下面练习并体验知识点的形成过程.
让感受到数学与生活的联系,通过数形结合理 解绝对值的意义,进一步渗透数形结合的思想。
四、教学重难点
1、重点:绝对值概念,能求出一个 数的绝对值
七年级(上)第二章 有理数 第5课时 绝对值与相反数(1)(附答案)

第5课时绝对值与相反数(1)预学目标1.通过课本中“家与学校的距离”问题,了解距离与数轴上的单位长度之间的关系.2.了解绝对值的概念,尝试理解绝对值与距离的关系(即绝对值的几何意义).3.了解绝对值的表示方法.4.了解绝对值的大小比较.知识梳理1.绝对值的概念(1)观察图1,点A、B、C、D到原点的单位长度分别为________、________、________、_______,即它们到原点的距离为_______、________、________、_______.(2)点A、B、C、D所表示的数的绝对值为_______、________、________、________.归纳:数轴上表示一个数的点到_____________________,叫做这个数的绝对值.2.绝对值的表示与比较-5的绝对值为______,记为:5-=______;-212的绝对值为_______,记为:______;3.2的绝对值为_______,记为:_______.我们容易看出:_____<_____<_____.例题精讲例l 求下列各数的绝对值:-112,5,0,-1,4.5.提示:求一个数的绝对值的问题,其实就是处理符号的问题.解答:112-=l12,5-=5,0=0,1-=1,4.5=4.5.点评:理解一个数的绝对值,我们可以借助于数轴,先在数轴上画出表示这个数的点,再求出它到原点的距离,这个距离就是这个数的绝对值.例2 某工厂生产一批零件,根据零件的质量要求(零件长度可以有0.2 cm的误差),现检查6个零件,检查数据如下(超过规定长度的厘米数记作正数,反之记作负数):以上6个零件中,( )号零件符号要求,其中质量最好的一个是( )号.提示:我们可以分别求出每一个数的绝对值,将所求值与误差作比较.小于或等于0.2的为合格产品,绝对值越小的质量越好.解答:①③④⑤;④.点评:一个数的绝对值越小,表示这个数距离原点越近;一个数的绝对值越大,表示这个数距离原点越远.热身练习1.在数轴上表示-12的点与原点的距离是 ( ) A .-12 B .12C .-2D .2 2.-14的绝对值是 ( ) A .14 B .4 C .-14D .-4 3.-23的绝对值是_______,23的绝对值是_______. 4.12+=_______;0=_______; 2.1-=_______;9--5=________.5.在数轴上分别画出表示-4、3、-2.5的点A 、B 、C ,然后填空:(1)点A 、B 、C 到原点的距离分别是_______、_______、_______.(2)4、3、-2.5的绝对值分别是_______、_______、________.6.用“>”、“<”或“=”填空:(1)3- _______2.7; (2) 5.5______7.2-- .7.在数轴上表示下列各数,并将它们的绝对值用“<”号连接起来.0,-3,2,-14,5.8.正式的排球比赛对所用排球的重量有严格的规定.检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下(单位:克):+12,-14,+23,-16,-7.请运用学过的绝对值知识说明哪个排球的质量最好.参考答案1.B 2.A 3.23234.12 0 2.1 4 5.图略(1)4 3 2.5 (2)4 3 2.56.(1)> (2)< 7.图略0<14-<2<3-<58.离规定重量的克数为-7克的排球最好理由:因为它离规定重量的克数的绝对值最小.。
2023-2024学年人教版数学七年级上册1

三种说法:5是-5的相反数,5的相反数是-5;5与-5互为相反数
讲授新课
练一练
一、填空: (1)-9是______的相反数; (2) 14的相反数是________; (3)10和_________互为相反数. (4)如果m=-6,则-m=________.
讲授新课
二、判断题,看谁回答的又对又快! (1)10是-1的相反数。 ( )
a a>0 |a| = 0 a=0
-a a<0
|a| ≥0,即 任何一个有理数的绝对值都是非负数
讲授新课 做一做
(1)绝对值是7的数是 (2)绝对值是-2的数是 (3)绝对值是0的数是 (4)绝对值小于3的整数是
. .
. .
讲授新课
三 比较两个负数的大小 (1)在数轴上表示-1.5,-3,-1,-5,并比较它们的大小;
【归纳】 几个非负数的和为0,则这几个数都为0.
当堂检测
1.任何一个有理数的绝对值一定( D )
A.大于0
B.小于0
C.小于或等于0 D.大于或等于0
2. A,B是数轴上两点,线段AB上的点表示的数中,有互为相反数
的是( B )
A.
B.
C.
D.
当堂检测
3.已知│a│=3,│b│=2,│c│=2,有理数a,b,c在数轴上的位 置如图所示,则a=____;b=_____;c=____.
讲授新课
例 已知|x|=2,|y|=3,且x<y,求x,y. [解析] 由绝对值的定义知x=±2,y=±3, 再由x<y决定x,y的值.
解:因为|x|=2,|y|=3, 所以x=±2,y=±3. 又因为x<y, 所以x=2,y=3或x=-2,y=ห้องสมุดไป่ตู้.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5课时 绝对值与相反数(一)
班级 姓名
1.在数轴上,表示-
12
的点与原点的距离是 ( ) A .-12 B .12
C .-2
D .2 2.-14
的绝对值是 ( ) A .14 B .4 C .-14 D .-4 3.12+=___________;0=___________; 2.1-=_________.
4.95--=__________.
5.___________的绝对值是其本身.
6.-23的绝对值是_________,23
的绝对值是_________. 7.绝对值是6的整数是___________,绝对值小于3的整数有__________. 8.35-
=__________;8--=_________;1532-=_________;53-++=_________. 9.用“>”、“<”或“=”填空:
3-__________2.7; 5.5-_________7.2-.
10.在数轴上分别画出表示-4、3、-2.5的点A 、B 、C ,然后填空:
(1)点A 、B 、C 到原点的距离分别是_________、___________、_________;
(2)4、3、-2.5的绝对值分别是__________、__________、__________.
11.求下列各数的绝对值: -
12,4,0,-143
12.在数轴上表示下列各数:-
12,-13,14,并用“<”号将它们的绝对值连接起来.
13.求下列各数的绝对值:
-5,4.5,-0.5,+1,0,π-3.
14.在数轴上表示下列各数:0,-3,2,-1
4
,5.并将上述各数的绝对值用“<”号连接
起来.
15.正式的排球比赛对所用排球的重量有严格的规定.检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下(单位:克):+12,-14,+23,-16,-7.请用学过的绝对值的知识来说明哪个排球的质量最好.
16.如图,按下列方法将数轴的正半轴绕在一个圆上(该圆的周长为3个单位长度,且在圆周的三等分点处分别标上了数字0、1、2).先让原点与圆周上0所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1,2,3,4……所对应的点分别与圆周上1,2,0,1……所对应的点重合.这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
(1)若圆周上的数字以与数轴上的数5对应,则a=________.
(2)若数轴绕过圆周n圈(n为正整数)后,数轴上的一个整数点,刚好落在圆周上数字l
所对应的位置,则这个整数是___________(用含托的代数式表示).
第5课时绝对值与相反数(一)
参考答案
1.B 2.A 3.12 0 2.1 4.4 5.0和正数
6.2
3
2
3
7.±6 0,±1,±2
8.3
5
-8
3
2
8
9.> <
10.(1)4 3 2.5 (2)4 3 2.5
11.1
2
,4,0,
1
4
3
12.图略,111 432 <-<-
13.5,4.5,0.5,1,0,π-3
14.图略
1
0235
4
<-<<-<
15.最后一个排球质量最好,因为231614127
+>->->+>-16.(1)2 (2)3n+1。
