lagrange插值分段线性插值matlab代码
用MATLAB实现拉格朗日插值和分段线性插值

用MATLAB真止推格朗日插值战分段线性插值之阳早格格创做1、真验真质:用MATLAB真止推格朗日插值战分段线性插值.2、真验手段:1)教会使用MATLAB硬件;2)会使用MATLAB硬件举止推格朗日插值算法战分段线性好值算法;3、真验本理:利用推格朗日插值要领举止多项式插值,并将图形隐式出去.4、真验步调及运止截止(1)真止lagrange插值1)定义函数:f = 1/(x^2+1) 将其保存正在f.m 文献中,简直步调如下:function y = f1(x)y = 1./(x.^2+1);2)定义推格朗日插值函数:将其保存正在lagrange.m 文献中,简直真止步调编程如下:function y = lagrange(x0,y0,x)m = length(x); /区间少度/n = length(x0);for i = 1:nl(i) = 1;endfor i = 1:mfor j = 1:nfor k = 1:nif j == kcontinue;endl(j) = ( x(i) -x0(k))/( x0(j) - x0(k) )*l(j);endendendy = 0;for i = 1:ny = y0(i) * l(i) + y;end3)修坐尝试步调,保存正在text.m文献中,真止绘图:x=-5:0.001:5;y=(1+x.^2).^-1;p=polyfit(x,y,n);py=vpa(poly2sym(p),10)plot_x=-5:0.001:5;f1=polyval(p,plot_x);figureplot(x,y,‘r',plot_x,f1)输进n=6,出现底下的图形:通过上图不妨瞅到当n=6是不很佳的模拟.于是沉新运止text.M并采用n=11由此可睹n=11时的图像是不妨很佳的真止模拟(2)分段线性插值:修坐div_linear.m文献.简直编程如下/*分段线性插值函数:div_linear.m 文献*/function y = div_linear(x0,y0,x,n)%for j = 1:length(x)for i = 1:n-1if (x >= x0(i)) && (x <= x0(i+1))y = (x - x0(i+1))/(x0(i) - x0(i+1))*y0(i) + ( x - x0(i))/(x0(i+1) - x0(i))*y0(i+1);elsecontinue;endend%end尝试步调(text2.m):n = input(‘输进n =:’);x0 = linspace( -5,5,n);for x = -5:0.01:5y = div_linear(x0,f(x0),x,n);hold on;plot(x,y,'r');plot(x,f(x),'b');end2)运止尝试步调,那是会出现:输进n=:2)输进n=6,并按Enter键,出现:4)闭掉图形界里后,沉新运止步调,输进n=11,并按enter键后出现:5)再次闭掉图形界里,输进n=100,并按enter键,出现:此时.图形将于本函数图形基础符合,证明分隔区间越多,图像交近真正在的图像.(3)用lagrange插值瞅察y = |si n(k*π*x)|的缺点分解:1)编写函数文献,保存正在f2.m 中x=0:0.01:1;k= input('输进k:')n= input('输进n:');y=abs(sin(k*pi*x));p=polyfit(x,y,n-1);py=vpa(poly2sym(p),8);plot_x=0:0.01:1;f1=polyval(p,plot_x);plot(x,y,plot_x,f1);2)运止该步调:输进k=:1输进n=:2出现如下图形界里:闭掉图形界里后沉新运止f2.m,输进k=:1,n=:3出现如下界里:再次闭掉图形界里,输进k=:1,n=:6 后出现:此时图形基础符合.类推,输进k=2,n=3后出现:k =2, n =11,出现如下图形:k =2,n =15,那时出现:k =2,n =19,出现:当k=2,n=21时,图形如下:此时基础符合.5、真验归纳:通过本次课程安排,尔发端掌握了MATLAB使用,加深了对付于百般线性插值的明白;培植了独力处事本领战创制力;概括使用博业及前提知识,办理本质数教问题的本领;正在本次课程安排中,正在教授的粗心指挥下,支益匪浅.共时对付数教的钻研有了更深进的认识.。
matlab实现拉格朗日插值,多项式插值,邻近插值,线性插值 程序

题 7:一维函数插值算法课题内容:课题 7:一维函数插值算法课题内容:对函数||e-y x=,取[-5,5]之间步长为 1 的值*10作为粗值,以步长0.1 作为细值,编写程序实现插值算法:最邻近插值算法,线性插值算法和三次多项式函数插值算法,并对比插值效果。
课题要求:1、设计良好的人机交互 GUI 界面。
2、自己编写实现插值算法。
3、在同一个图形窗口显示对比最后的插值效果。
附录一、界面设计二、图像结果三、程序设计1、线性插值function pushbutton1_Callback(hObject, eventdata, handles) x=-5:5;y=10*exp(-abs(x));f1=[];for x1=-5:0.1:5a=(x1-floor(x1));%请读者认真逐一带入推导if x1==floor(x1)f1=[f1,y(floor(x1)+6)];elsef1=[f1,y(floor(x1)+6)+a*(y(floor(x1)+7)-y(floor(x1)+6))]; endendm=-5:0.1:5plot(m,f1,'-r',x,y,'+')axis([-5 5 0 10])legend('liner插值','原函数');xlabel('X');ylabel('Y');title('liner插值与原函数的对比');grid2、多项式插值x0=-5:1:-3;y0=10*exp(-abs(x0));x=-5:0.1:-3;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=-3:1:-1;y0=10*exp(-abs(x0));x=-3:0.1:-1;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=-1:1:1;y0=10*exp(-abs(x0));x=-1:0.1:1;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=1:1:3;y0=10*exp(-abs(x0));x=1:0.1:3;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=3:1:5;y0=10*exp(-abs(x0));x=3:0.1:5;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');grid3、最邻近插值function pushbutton3_Callback(hObject, eventdata, handles) x=-5:5;y=10*exp(-abs(x));f2=[];for x1=-5:0.1:5if abs(x1-floor(x1))<0.5f2=[f2,y(floor(x1)+6)];elsef2=[f2,y(floor(x1)+7)];endendm=[-5:0.1:5];f4=10*exp(-abs(m));plot(m,f2,'-r',x,y,'+')axis([-5 5 0 10])legend('nearest插值','原函数');xlabel('X');ylabel('Y');title('nearest插值与原函数的对比');grid。
lagrange插值作业

给定函数211)(x x f +=,现考察在区间【-5,5】上)(x f 上的等距插值问题。
1. 利用matlab 可以得到211)(x x f +=的图形如下图所示: x=-5:0.1:5;y=1./(1+x.^2);plot(x,y)2. 作)(x f 的20个节点的分段线性插值)(20x lin ,其实现代码及图形如下:x=-5:0.1:5;y=1./(1+x.^2);x1=linspace(-5,5,20);y1=interp1(x,y,x1,'linear');plot(x,y,’r ’,x1,y1,’b ’)所得图形如下:其中兰线我分段线性插值函数)(20x lin 的曲线此处需说明由于此处利用的PLOT 函数其绘制曲线的原理既是描点,连线,其所得图形是折线。
所以通过plot 函数绘制)(x f 函数时,如果取点不够多,且恰好去20个等距节点时,其所得的图形和通过分段线性插值所得的)(20x lin 图形是一样,即若运行下列代码会得到下面图形:x=linspace(-5,5,20);y=1./(1+x.^2);plot(x,y)即其和通过分段线性插值所得的函数)(20x lin 的曲线是重合的。
3. 作)(x f 的21个等距节点的20次lagrange 插值函数)(20x l 。
此处由于matlab 中没有固定的lagrange 插值函数,所以定义lagrange 函数如下,并将其放入matlab 可搜索到的工作目录中:\\....\matlab7.0\work 中。
所定义的lagrange 函数如下:(此处参考:Numerical Computing with MATLAB 【M 】 Cleve Moler, 并下载其附带的lagrange 函数)% textbook page 35function yh = lagrange(x,y,xh)n = length(x);m = length(xh);x = reshape(x,n,1); % x = x(:);y = reshape(y,n,1); % y = y(:);xh = reshape(xh,m,1); % xh = xh(:);yh = zeros(m,1);c1 = ones(1,n-1);c2 = ones(m,1);for i=1:n,xp = x([1:i-1,i+1:n]);yh = yh + y(i) * prod((xh*c1-c2*xp')./(c2*(x(i)*c1-xp')),2);end然后运行下列代码:x=linspace(-5,5,21)y=1./(1+x.^2)x1=linspace(-5,5,23)y1=lagrange(x,y,x1)plot(x,y,'r',x1,y1,'b')可得到如下图形;这里需说明用plot 函数所得的被插值函数)(x f 与20次lagrange 插值函数的曲线都不是其精确值,由于在绘制)(x f 曲线时,只取了【-5,5】上的21个点,而绘制)(20x l 函数时只取了【-5,5】上的23个点。
lagrange插值分段线性插值matlab代码

Lagrange插值:x=0:3;y=[-5,-6,-1,16];n=length(x);syms q;for k=1:nfenmu=1;p=1;for j=1:nif(j~=k)fenmu=fenmu*(x(k)-x(j))p=conv(p,poly(x(j)))endendc(k,:)=p*y(k)/fenmuenda=zeros(1,n);for i=1:nfor j=1:na(i)=a(i)+c(j,i)endend输出结果:fenmu =-1p =1 -1fenmu =2p =1 -3 2fenmu =-6p =1 -6 11 -6c =0.8333 -5.0000 9.1667 -5.0000 fenmu =1p =1 0fenmu =-1p =1 -2 0fenmu =2p =1 -5 6 0c =0.8333 -5.0000 9.1667 -5.0000-3.0000 15.0000 -18.0000 0 fenmu =2p =1 0fenmu =2p =1 -1 0fenmu =-2p =1 -4 3 0c =0.8333 -5.0000 9.1667 -5.0000-3.0000 15.0000 -18.0000 00.5000 -2.0000 1.5000 0 fenmu =3p =1 0fenmu =6p =1 -1 0fenmu =6p =1 -32 0c =0.8333 -5.0000 9.1667 -5.0000-3.0000 15.0000 -18.0000 00.5000 -2.0000 1.5000 02.6667 -8.0000 5.3333 0a =0.8333 0 0 0a =-2.1667 0 0 0 a =-1.6667 0 0 0a =1 0 0 0a =1 -5 0 0a =1 10 0 0a =1 8 0 0a =1 0 0 0a =1.0000 0 9.1667 0a =1.0000 0 -8.8333 0a =1.0000 0 -7.3333 0a =1.0000 0 -2.0000 0a =1.0000 0 -2.0000 -5.0000a =1.0000 0 -2.0000 -5.0000a =1.0000 0 -2.0000 -5.0000a =1.0000 0 -2.0000 -5.0000 分段线性插值:先保存M文件:x=1:6;y=[7 16 8 25 12 24];u=5.3;delta=diff(y)./diff(x);n=length(x);for j=2:(n-1)if x(j)<uk=j;endend在command window中输入:s=u-x(k);v=y(k)+s.*delta(k)输出结果:v =15.6000解:第一种做法,用spline,共55个点,其中,54个有效首先保存你一个M文件:figure('position',get(0,'screensize'))axes('position',[0 0 1 1])[x,y] = ginput;然后在command window里输入以下内容:n = length(x);s = (1:n)';t = (1:.05:n)';u = spline(s,x,t);v = spline(s,y,t);clf resetplot(x,y,'.',u,v,'-');对应的x、y值:0.3572917 0.25361450.3572917 0.29096390.3503472 0.34036140.3461806 0.42590360.3427083 0.52710840.3253472 0.61626510.3065972 0.68734940.290625 0.75240960.2892361 0.79337350.2954861 0.7969880.3225694 0.75481930.340625 0.68493980.3690972 0.6150602 0.3864583 0.6126506 0.3899306 0.7259036 0.3927083 0.8066265 0.3920139 0.8993976 0.4024306 0.9295181 0.4239583 0.8933735 0.4239583 0.8078313 0.4295139 0.7343373 0.4315972 0.6451807 0.4440972 0.6439759 0.4565972 0.7439759 0.4704861 0.8451807 0.4767361 0.9054217 0.4961806 0.9463855 0.5086806 0.876506 0.5045139 0.8186747 0.5010417 0.7524096 0.4892361 0.6403614 0.503125 0.6295181 0.5052083 0.6271084 0.5322917 0.7090361 0.5510417 0.763253 0.5739583 0.8355422 0.5961806 0.8572289 0.5947917 0.7837349 0.5753472 0.7090361 0.5579861 0.6391566 0.5357639 0.5668675 0.5322917 0.5283133 0.5350694 0.4789157 0.565625 0.536747 0.5947917 0.5933735 0.6253472 0.610241 0.6322917 0.5728916 0.615625 0.5331325 0.6003472 0.4993976 0.5788194 0.4415663 0.559375 0.3716867 0.5295139 0.2957831 0.4975694 0.2403614 0.4711806 0.2018072 0.6607639 0.3090361第二种做法,用pchip,共52个点,全部有效首先保存一个M文件:figure('position',get(0,'screensize'))axes('position',[0 0 1 1])[x,y] = ginput;然后在command window里输入以下内容:n = length(x);s = (1:n)';t = (1:.05:n)';u = pchip (s,x,t);v = pchip (s,y,t);clf resetplot(x,y,'.',u,v,'-');对应的x、y值:0.5190972 0.84879520.5052083 0.75120480.4947917 0.67891570.5100694 0.66927710.5399306 0.73554220.5753472 0.81746990.596875 0.86204820.6190972 0.87771080.6149306 0.81385540.5878472 0.74277110.5878472 0.74277110.5635417 0.67168670.5350694 0.6030120.528125 0.5632530.528125 0.52590360.565625 0.58012050.6052083 0.62710840.634375 0.61867470.6190972 0.57168670.5878472 0.5234940.5364583 0.41265060.4961806 0.32108430.459375 0.2753012我更喜欢第一种,用spline的,这个能将之间画出弧度,而pchip更像是直接用线段将点依次连接得到的。
用MATLAB实现拉格朗日插值和分段线性插值.

用MATLAB实现拉格朗日插值和分段线性插值1、实验内容:用MATLAB实现拉格朗日插值和分段线性插值。
2、实验目的:1学会使用MATLAB软件;2会使用MATLAB软件进行拉格朗日插值算法和分段线性差值算法;3、实验原理:利用拉格朗日插值方法进行多项式插值,并将图形显式出来。
4、实验步骤及运行结果(1实现lagrange插值1定义函数:f = 1/(x^2+1 将其保存在 f.m 文件中,具体程序如下:function y = f1(xy = 1./(x.^2+1;2定义拉格朗日插值函数:将其保存在lagrange.m 文件中,具体实现程序编程如下:function y = lagrange(x0,y0,xm = length(x; /区间长度/n = length(x0;for i = 1:nl(i = 1;endfor i = 1:mfor j = 1:nfor k = 1:nif j == kcontinue;endl(j = ( x(i -x0(k/( x0(j - x0(k *l(j;endendendy = 0;for i = 1:ny = y0(i * l(i + y;end3建立测试程序,保存在text.m文件中,实现画图:x=-5:0.001:5;y=(1+x.^2.^-1;p=polyfit(x,y,n;py=vpa(poly2sym(p,10plot_x=-5:0.001:5;f1=polyval(p,plot_x;figureplo t(x,y,‘r',plot_x,f1输入n=6,出现下面的图形:通过上图可以看到当n=6是没有很好的模拟。
于是重新运行text.M并选择n=11由此可见n=11时的图像是可以很好的实现模拟(2分段线性插值:建立div_linear.m文件。
具体编程如下/*分段线性插值函数:div_linear.m 文件*/ function y = div_linear(x0,y0,x,n%for j = 1:length(xfor i = 1:n-1if (x >= x0(i && (x <= x0(i+1y = (x - x0(i+1/(x0(i - x0(i+1*y0(i + ( x - x0(i/(x0(i+1 - x0(i*y0(i+1;elsecontinue;endend%end测试程序(text2.m:输入n =:’;n = input(‘x0 = linspace( -5,5,n;for x = -5:0.01:5y = div_linear(x0,f(x0,x,n;hold on;plot(x,y,'r';plot(x,f(x,'b';end2运行测试程序,这是会出现:输入n=:2输入n=6,并按Enter键,出现:4关掉图形界面后,重新运行程序,输入n=11,并按enter键后出现:5再次关掉图形界面,输入n=100,并按enter键,出现:此时。
Langrage和Newton插值法的matlab实现

仅供参考1.已知数据如下:(1)用MATLAB语言编写按Langrage插值法和Newton插值法计算插值的程序,对以上数据进行插值;(2)利用MATLAB在第一个图中画出离散数据及插值函数曲线。
(1.1)langrage插值法编程实现syms xx0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];for i=1:5a=1;for j=1:5if j~=ia=expand(a*(x-x0(j)));endendb=1;for k=1:5if k~=ib=b*(x0(i)-x0(k));endendA(i)=expand(a/b);endL=0;for p=1:5L=L+y0(p)*A(p);endLL =-25/48*x^4+5/6*x^3-53/48*x^2+23/120*x+49/50(1.2)Newton插值程序实现clear allclcsyms xx0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];for k=1:5for i=1:ka=1;b=0;for j=1:kif j~=ia=a*(x0(i)-x0(j));endendb=b+y0(i)/a;endA(k)=b;endB=[1,(x-x0(1)),(x-x0(1))*(x-x0(2)),(x-x0(1))*(x-x0(2))*(x-x0(3)),(x-x 0(1))*(x-x0(2))*(x-x0(3))*(x-x0(4))];L1=A.*B;l=0;for m=1:5l=l+L1(m);endL=expand(l)L =61/100+13/30*x+383/48*x^2-155/24*x^3+475/48*x^4(2)画图x0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];subplot(1,2,1);plot(x0(1),y0(1),'+r',x0(2),y0(2),'+r',x0(3),y0(3),'+r',x0(4),y0(4),' +r',x0(5),y0(5),'+r')x=0:0.05:1;y=-25/48.*x.^4+5/6.*x.^3-53/48.*x.^2+23/120.*x+49/50;subplot(1,2,2);plot(x,y)2.给定函数21(),[1,1]125f x x x ,利用上题编好的Langrage 插值程序(或Newton 插值程序),分别取3个,5个、9个、11个等距节点作多项式插值,分别画出插值函数及原函数()f x 的图形,以验证Runge 现象、分析插值多项式的收敛性。
拉格朗日插值法matlab

2.五次拉格朗日
clc
x=[-3.15-1 0.01 1.02 2.03 3.25];
y=[37.037.24 1.05 2.03 17.06 23.05];二次拉格朗日插值的误差为:R
L0=poly([x(2) x(3) x(4) x(5)
x(5)
x(5)
x(5)
x(4)
x(4) x(6)])/((x(1)-x(2))*(x(1)-x(3))*(x(1)-x(4))*(x(1)-x(5))*(x(1)-x(6)));
L1=poly([x(1) x(3) x(4) x(6)])/((x(2)-x(1))*(x(2)-x(3))*(x(2)-x(4))*(x(2)- x(5))*(x(2)-x(6))); L2=poly([x(1) x(2) x(4) x(6)])/((x(3)-x(1))*(x(3)- x(2))*(x(3)-x(4))*(x(3)-x(5))*(x(3)-x(6))); L3=poly([x(1) x(2) x(3) x(6)])/((x(4)-x(1))*(x(4)-x(2))*(x(4)-x(3))*(x(4)-x(5))*(x(4)-x(6)));
拉格朗日插值法
实验题目 拉格朗日插值法
一、实验目的及要求
利用Matlab学习拉格朗日插值法
二、研究、解答以下问题
问题:1、已知一‘⑪4;CUM辺汕,_'仏环0.爪以1字,「丄幻0. 510H26,
分别用线性插值法和二次拉格朗日插值法分别计算f(0.54),并且说明哪个结果误差更小。
2、给出节点,「:LOU.;「到,L〔)•皿,
b = -0.6153
误差:
function [R]=wucha(M,x,X) n=length(X);
matlab实现lagrange插值和分段线性插值
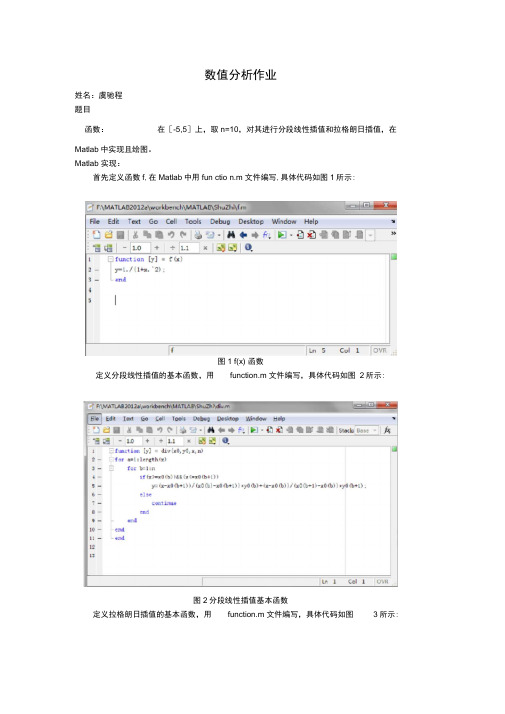
数值分析作业姓名:虞驰程题目函数:在[-5,5]上,取n=10,对其进行分段线性插值和拉格朗日插值,在Matlab中实现且绘图。
Matlab 实现:首先定义函数f,在Matlab中用fun ctio n.m 文件编写,具体代码如图1所示:图1 f(x) 函数定义分段线性插值的基本函数,用function.m 文件编写,具体代码如图2所示:图2分段线性插值基本函数定义拉格朗日插值的基本函数,用function.m 文件编写,具体代码如图3所示:图3拉格朗日插值的基本函数进行分段线性插值并绘图和原函数进行对比的Matlab实现代码如图4所示:图4分段线性插值函数绘制其结果如图5所示,其中红色代表分段线性插值结果,蓝色代表原函数:图5分段线性插值和原函数对比同理可以进行拉格朗日插值并绘图,其Matlab实现代码如图6所示,其结果如图Ffe Edit Tesrt Go C«ll TooU D«bug Oesktop Wind Help *1 D 已■ | $ ■•勺◊Qi 勺-it • * F;iL ・昌电T・• ■ ■ ■ | MadgJBmr ■血*S肓匸1必」•* _U■「鬲迢[0 _L 1- IWEU I1『inpirt ftji')2 - ■Elinus:""卜氐£11*1〕3 - \-\t^£ 15* —yslftErflnfeiwQpiftrtl,!!) ■5 —told An:ft - plfft <45- r* * E X).7 - jlflrt(i p fCx)/lb J kE — d.isp(-x):9 - -end2 u"含m al=n' taufwi图6拉格朗日插值函数绘制图7拉格朗日插值和原函数对比7所示:最后我们可以将分段线性插值、拉格朗日插值和原函数进行对比,其实现代码如图8所示,最终结果如图9所示(黑色代表原函数,蓝色是分段线性插值,红色是拉格朗日插值)图8两种插值方法和原函数对比实现图9两种插值方法和原函数对比。
拉格朗日插值法matlab程序代码

拉格朗日插值法matlab程序代码文章开始:拉格朗日插值法是一种常用的数值计算方法,用于在已知的数据点上构造一个多项式,以逼近未知的函数值。
其主要思想是通过构造一个经过已知数据点的多项式,从而在未知点上近似函数的值。
在本文中,我将通过MATLAB编程来实现拉格朗日插值法,并给出相应的程序代码和解释。
在开始编写程序之前,让我们首先了解一下拉格朗日插值法的基本原理。
给定一组已知数据点(x0, y0), (x1, y1), ..., (xn, yn),其中xi为自变量,yi为因变量。
我们的目标是构造一个多项式P(x),使得对于任意的x,P(x)可以近似地表示未知函数f(x)的值。
首先,我们需要定义Lagrange基函数Li(x)。
每个基函数都满足以下两个性质:Li(xi) = 1Li(xj) = 0,其中i ≠ j基于这些性质,Li(x)可以通过以下公式计算:Li(x) = Π(j=0 to n, j ≠ i) ((x - xj) / (xi - xj))接下来,我们将利用这些基函数和已知数据点的因变量yi来构造拉格朗日插值多项式P(x):P(x) = Σ(i=0 to n) (yi * Li(x))有了这个多项式,我们可以使用它来近似未知函数f(x)在任意点x的值。
现在,让我们来实现这个算法,并给出MATLAB代码。
``` MATLABfunction P = lagrange_interpolation(x, y, x_val)% x: 已知数据点的自变量% y: 已知数据点的因变量% x_val: 需要插值的自变量n = length(x) - 1; % 数据点的数量P = zeros(size(x_val)); % 初始化插值多项式的值for i = 1:n+1% 计算基函数L = ones(size(x_val));for j = 1:n+1if j ~= iL = L .* (x_val - x(j)) / (x(i) - x(j));endend% 更新插值多项式的值P = P + y(i) * L;endend```上面的代码实现了拉格朗日插值法的核心算法。
拉格朗日插值matlab程序例题

拉格朗日插值是一种常用的数据拟合方法,它可以通过已知数据点来估计出未知数据点的值。
在数学和工程领域中,拉格朗日插值经常被用来进行数据的近似和预测。
在本文中,我们将深入探讨拉格朗日插值的原理和应用,并以Matlab程序例题来展示其实际运用。
1. 拉格朗日插值的原理拉格朗日插值是利用已知数据点来构造一个多项式,通过这个多项式来拟合数据并进行预测。
它的原理基于拉格朗日多项式的概念,即通过已知的n个点来构造一个n-1次的拉格朗日多项式,利用这个多项式来估计其他点的数值。
2. 拉格朗日插值的公式假设有n个已知的数据点(x1, y1), (x2, y2), …, (xn, yn),则拉格朗日插值多项式可以表示为:L(x) = Σ(yi * li(x)), i=1 to n其中li(x)是拉格朗日基函数,定义为:li(x) = Π((x - xj) / (xi - xj)), j=1 to n, j≠i利用这个公式,我们可以得到拉格朗日插值多项式,进而进行数据的拟合和预测。
3. 拉格朗日插值的Matlab程序实现下面我们将以一个具体的例题来展示如何使用Matlab来实现拉格朗日插值。
假设有如下数据点:y = [10, 5, 8, 3, 6];我们希望利用这些数据点来构造拉格朗日插值多项式,并使用这个多项式来估计x=3.5处的数值。
我们可以编写Matlab程序来实现拉格朗日插值。
代码如下:```matlabfunction result = lagrange_interpolation(x, y, xx)n = length(x);result = 0;for i = 1:ntemp = y(i);for j = 1:nif i ~= jtemp = temp * (xx - x(j)) / (x(i) - x(j));endendresult = result + temp;endend```我们可以调用这个函数来进行插值计算:```matlaby = [10, 5, 8, 3, 6];xx = 3.5;result = lagrange_interpolation(x, y, xx)disp(result);```通过这段程序,我们可以得到x=3.5处的插值结果为6.75。
用matlab编写拉格朗日插值算法的程序

用matlab编写拉格朗日插值算法的程序10[ 标签:matlab,插值算法,程序]用matlab编写拉格朗日插值算法的程序,并以下面给出的函数表为数据基础,在整个插值区间上采用拉格朗日插值法计算f(),写出程序源代码,输出计算结果xy匿名回答:1 人气:6 解决时间:2011-05-24 19:58满意答案好评率:83%做了一个测试,希望有所帮助。
代码:% 用matlab编写拉格朗日插值算法的程序,并以下面给出的函数表为数据基础,% 在整个插值区间上采用拉格朗日插值法计算f(),写出程序源代码,输出计算结果% x% yfunction main()clc;x = [ ]; y = [ ];x0 = ;f = Language(x,y,x0)function f = Language(x,y,x0)%求已知数据点的拉格朗日插值多项式%已知数据点的x坐标向量: x%已知数据点的y坐标向量: y%插值点的x坐标: x0%求得的拉格朗日插值多项式或在x0处的插值: f syms t l;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return; %检错endh=sym(0);for (i=1:n)l=sym(y(i));for(j=1:i-1)l=l*(t-x(j))/(x(i)-x(j));end;for(j=i+1:n)l=l*(t-x(j))/(x(i)-x(j));end;h=h+l;endsimplify(h);if(nargin == 3)f = subs (h,'t',x0); %计算插值点的函数值elsef=collect(h);f = vpa(f,6); %将插值多项式的系数化成6位精度的小数end结果:f =>>如何用MATLAB编写的拉格朗日插值算法的程序、二阶龙格-库塔方法的程序和SOR迭代法的程序,要能运行的∮初夏戀雨¢回答:2 人气:29 解决时间:2009-12-08 19:04满意答案好评率:100%拉格朗日function y=lagrange(x0,y0,x) n=length(x0);m=length(x);for i=1:mz=x(i);s=;for k=1:np=;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j)); endends=p*y0(k)+s;endy(i)=s;endSOR迭代法的Matlab程序function [x]=SOR_iterative(A,b)% 用SOR迭代求解线性方程组,矩阵A是方阵x0=zeros(1,length(b)); % 赋初值tol=10^(-2); % 给定误差界N=1000; % 给定最大迭代次数[n,n]=size(A); % 确定矩阵A的阶w=1; % 给定松弛因子k=1;% 迭代过程while k<=Nx(1)=(b(1)-A(1,2:n)*x0(2:n)')/A(1,1);for i=2:nx(i)=(1-w)*x0(i)+w*(b(i)-A(i,1:i-1)*x(1:i-1)'-A(i,i+1:n)*x0(i+1:n)')/ A(i,i);endif max(abs(x-x0))<=tolfid = fopen('', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'x的值\n\n');fprintf(fid, '% \n', x);break;endk=k+1;x0=x;endif k==N+1fid = fopen('', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'超过最大迭代次数,求解失败!');fclose(fid);endMatlab中龙格-库塔(Runge-Kutta)方法原理及实现龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
数值分析分段线性插值样条插值Runge函数Newton-Lagrange-Chebyshev插值多项式Runge现象matlab源程序代码
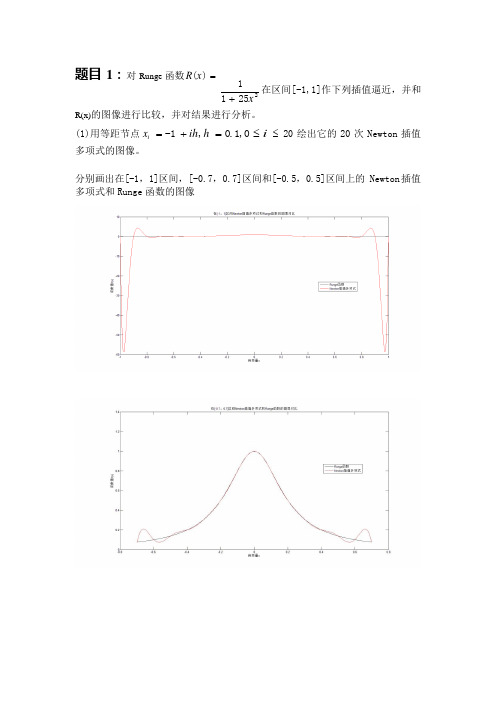
题目1:对Runge 函数R(x ) =1在区间[-1,1]作下列插值逼近,并和1 + 25x 2R(x)的图像进行比较,并对结果进行分析。
= -1 + ih,h= 0.1,0 ≤ i≤ 20 绘出它的20 次Newton 插值(1)用等距节点xi多项式的图像。
分别画出在[-1,1]区间,[-0.7,0.7]区间和[-0.5,0.5]区间上的 Newton 插值多项式和Runge 函数的图像从图中可以看出: 1)在[-0.5,0.5]区间 Newton 插值多项式和 Runge 函数的图像偏差较小,这说 明 Newton 插值多项式在此区间上可以较好的逼近 Runge 函数; 2)在边界(自变量 x=-1 和 x=1)附近,Newton 插值多项式和 Runge 函数的图像 偏差很大,Newton 插值多项式出现了剧烈的震荡。
(Runge 现象) (2)用节点 x = cos(2i + 1π)(, i = 0,1,2,⋅ ⋅ ⋅ ,20),绘出它的 20 次 Lagrangei 42 插值多项式的图像。
画出在[-1,1]区间上的 Lagrange 插值多项式和 Runge 函数的图像从图中可以看出:使用 Chebyshev 多项式零点构造的 Lagrange 插值多项式和 Runge 函数的图 像偏差较小,没有出现 Runge 现象。
(3)用等距节点 x i 的图像。
= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的分段线性插值函数画出在[-1,1]区间上分段线性插值函数和 Runge 函数的图像从图中可以看出:使用分段线性插值函数和 Runge 函数的图像偏差较小,也没有出现 Runge 现象,只在自变量 x=0 处有稍许偏差。
(4)用等距节点 x i 函数的图像。
= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的三次自然样条插值画出在[-1,1]区间上三次自然样条插值函数和 Runge 函数的图像从图中可以看出:使用三次自然样条插值函数和 Runge 函数的图像偏差较小,也没有出现 Runge 现象。
matlab计算拉格朗日牛顿及分段线性插值的程序

end %检错 for k=1:n-1 if (x(k)<=x0&x0<=x(k+1)) temp=x(k)-x(k+1); f=(x0-x(k+1))/temp*y(k)+(x0x(k))/(-temp)*y(k+1); end; end
return;
四.程序运行结果 1.拉格朗日插值法 >> x=[0 3 5 7 9 11 12 13 14 15]; >> y=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6]; >> xi=0.5:0.5:14.5; >> yi=lang(x,y,xi) yi = Columns 1 through 8 -15.4117 -15.9238 -10.9898 -5.4272 -1.2253 1.2000 2.1765 2.2666 Columns 9 through 16 1.9894 1.7000 1.5703 1.6249 1.7995 2.0000 2.1477 2.2040 Columns 17 through 24 2.1752 2.1000 2.0269 1.9904 1.9928 2.0000 1.9537 1.8000 Columns 25 through 29 1.5272 1.2000 0.9656 1.0000 1.3480 >> plot(x,y,'b:',xi,yi) 2.牛顿插值法 >> yi=newdun(x,y,xi) yi = Columns 1 through 8 -15.4117 -15.9238 -10.9898 -1.2253 1.2000 2.1765 Columns 9 through 16 1.9894 1.7000 1.5703 1.7995 2.0000 2.1477 Columns 17 through 24 2.1752 2.1000 2.0269 1.9928 2.0000 1.9537 Columns 25 through 29 1.5272 1.2000 0.9656 1.3480 >> plot(x,y,xi,yi,'g+')
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 8 0 0
a =
1 0 0 0
a =
1.0000 0 9.1667 0
a =
1.0000 0 -8.8333 0
a =
1.0000 0 -7.3333 0
a =
1.0000 0 -2.0000 0
a =
1.0000 0 -2.0000 -5.0000
a =
1.0000 0 -2.0000 -5.0000
end
end
c(k,:)=p*y(k)/fenmu;
end
a=zeros(1,n);
fori=1:n
forj=1:n
a(i)=a(i)+c(j,i);
end
end
然后在command window里输入以下内容:
plot(x,y,'*');
hold on;
plot(x,y,'*');
hold on;
0.3089 -0.1531 0.8872
-0.1848 -0.8184 0.2754
0.6400 -0.4671 0.9154
0.4367 -0.6927 -0.5186
0.9373 -0.4380 0.3522
0.0627 -0.1198 -0.4219
-0.3497 0.0543 0.3436
end
a=zeros(1,n);
fori=1:n
forj=1:n
a(i)=a(i)+c(j,i)
end
end
输出结果:
fenmu =
-1
p =
1 -1
fenmu =
2
p =
1 -3 2
fenmu =
-6
p =
1 -6 11 -6
c =
0.8333 -5.0000 9.1667 -5.0000
fenmu =
end
c(k,:)=p*y(k)/fenmu;
end
a=zeros(1,n);
fori=1:n
forj=1:n
a(i)=a(i)+c(j,i);
end
end
输出结果:
x =
0.9150 -0.6848
0.9298 0.9412
然后在command window里输入:
plot(x,y,'*');
hold on;
0.559375
0.3716867
0.5295139
0.2957831
0.4975694
0.2403614
0.4711806
0.2018072
0.6607639
0.3090361
第二种做法,用pchip,共52个点,全部有效
首先保存一个M文件:
figure('position',get(0,'screensize'))
0.6190972
0.8777108
0.6149306
0.8138554
0.5878472
0.7427711
0.5878472
0.7427711
0.5635417
0.6716867
0.5350694
0.603012
0.528125
0.563253
0.528125
0.5259036
0.565625
0.5801205
-0.4462 0.6469 0.9004
n=10时,
x =
Columns 1 through 7
-0.3210 0.9661 -0.6578 0.7110 0.1660 -0.7845 -0.6425
0.9033 -0.3971 -0.9348 0.2895 -0.4964 0.8126 -0.1542
k=j;
end
end
在command window中输入:
s=u-x(k);
v=y(k)+s.*delta(k)
输出结果:
v =
15.6000
解:
第一种做法,用spline,共55个点,其中,54个有效
首先保存你一个M文件:
figure('position',get(0,'screensize'))
(b)
先保存M文件:
n=2;
x=2.*rand(n)-1
y=1./(1+25.*x.*x);
n=n^2;
%lagrangc?????¡§
fork=1:n
fenmu=1;
p=1;
forj=1:n
if(j~=k)
fenmu=fenmu*(x(k)-x(j));
p=conv(p,poly(x(j)));
end
0.6052083
0.6271084
0.634375
0.6186747
0.6190972
0.5716867
0.5878472
0.523494
0.5364583
0.4126506
0.4961806
0.3210843
0.459375
0.2753012
我更喜欢第一种,用spline的,这个能将之间画出弧度,而pchip更像是直接用线段将点依次连接得到的。
1
p =
1 0
fenmu =
-1
p =
1 -2 0
fenmu =
2
p =
1 -5 6 0
c =
0.8333 -5.0000 9.1667 -5.0000
-3.0000 15.0000 -18.0000 0
fenmu =
2
p =
1 0
fenmu =
2
p =
1 -1 0
fenmu =
-2
p =
1 -4 3 0
x1=-1:0.01:1;
y1=0;
for i=1:n
y1=y1.*x1+a(i)
end
y2=1./(1+25.*x1.*x1);
plot(x1,y1,'b');
hold on;
plot(x1,y2,'g');
得到以下几幅图:
n=3时,
x =
0.4121 -0.9077 0.3897
-0.9363 -0.8057 -0.3658
0.6271084
0.5322917
0.7090361
0.5510417
0.763253
0.5739583
0.8355422
0.5961806
0.8572289
0.5947917
0.7837349
0.5753472
0.7090361
0.5579861
0.6391566
0.5357639
0.5668675
0.4704861
0.8451807
0.4767361
0.9054217
0.4961806
0.9463855
0.5086806
0.876506
0.5045139
0.8186747
0.5010417
0.7524096
0.4892361
0.6403614
0.503125
0.6295181
0.5052083
使用的是splinetx。
解:
(a)
首先保存一个M文件:
n=3;
xishu=2/(n-1);
x=-1:xishu:1;
y=1./(1+25.*x.*x);
fork=1:n
fenmu=1;
p=1;
forj=1:n
if(j~=k)
fenmu=fenmu*(x(k)-x(j));
p=conv(p,poly(x(j)));
0.8407 0.4022 0.1224 -0.2475 -0.4191 0.7593 -0.8115
-0.8946 0.3327 0.7637 -0.6182 0.2342 0.6355 0.1970
0.4757 0.0783 0.3384 -0.1435 -0.4694 -0.4785 -0.0582
-0.7887 -0.0852 0.3903
n=10时,数据太大,没运行出来。
可以看出,将[-1,1]做n-1等分的n个插值点,在[-0.92,0.92]的区间内,随着n趋近于 时 趋近于f(x)。
解:
(a)
t = 1900:10:2000
V = vander(t)
输出结果:
t =
a =
1.0000 0 -2.0000 -5.0000
a =
1.0000 0 -2.0000 -5.0000
分段线性插值:
先保存M文件:
x=1:6;
y=[7168251224];
u=5.3;
delta=diff(y)./diff(x);
n=length(x);
forj=2:(n-1)
ifx(j)<u
-3.0000 15.0000 -18.0000 0
0.5000 -2.0000 1.5000 0
2.6667 -8.0000 5.3333 0
a =
0.8333 0 0 0
a =
-2.1667 0 0 0
a =
-1.6667 0 0 0
a =
1 0 0 0
a =
1 -5 0 0
a =
1 10 0 0
Lagrange插值:
x=0:3;
y=[-5,-6,-1,16];
