第八章--图与网络
运筹学8图与网络分析

e3 。在剩下的图中,再取一个圈
定理8.7充分性的证明,提供了一个 寻找连通图支撑树的方法叫做“破圈法”。 就是从图中任取一个圈,去掉一条边。再 对剩下的图重复以上步骤,直到不含圈时 为止,这样就得到一个支撑树。
例8.4 用破圈法求出图8-11的一个支
撑树。
v2
e1
e7 e4
v1
e3 v4
e8
v5
e2
e5
v3
e6
图8-11
取一个圈(v1,v2,v3,v1),在一个圈中去掉边
3
4
初等链:链中所含的 点均不相同, 也称通 路;
5
6
为闭链或回路或圈;
简单圈:如果在一个圈中所含的边均不相同 初等圈:除起点和终点外链中所含的点 均
不相同的圈;
连通图:图中任意两点之间均
至少有一条通路,否则 v1
v4 v5 v8
称为不连通图。
v2
初等链: (v1 , v2 , v3 , v6 ,
图的连通性:
简单链:链中所含的 边均不相同;
圈:若 v0 ≠ vn 则称该链为开链,否 则称
1
2
链:由两两相邻的点及其相 关联的边构成的点边序列。 如:v0 ,e1 ,v1 ,e2 ,v2,e3 ,v3 ,…,vn1 , en , vn ; v0 ,vn 分别为链的起点和终点 。记 作( v0 ,v1 , v2, ,v3 , …, vn-1 , vn )
v5
v7
(v5
,v1v6),(v6
(v4 ,v6),(v5 ,v7)}
,v3),(v5
v6
,v4),
v2
v4
图8.5
下面介绍一些常用的名词:
运筹学 填空题 及基础知识

8.若X﹡和Y﹡分别是线性规划的原问题和对偶问题的最优解,则有CX﹡= Y﹡b。
9.若X、Y分别是线性规划的原问题和对偶问题的可行解,则有CX≤Yb。
10.若X﹡和Y﹡分别是线性规划的原问题和对偶问题的最优解,则有CX﹡=Y*b。
6.若线性规划问题有最优解,则最优解一定可以在可行域的顶点(极点)达到。
7.线性规划问题有可行解,则必有基可行解。
8.如果线性规划问题存在目标函数为有限值的最优解,求解时只需在其基可行解_的集合中进行搜索即可得到最优解。
9.满足非负条件的基本解称为基本可行解。
10.在将线性规划问题的一般形式转化为标准形式时,引入的松驰数量在目标函数中的系数为零。
14.(单纯形法解基的形成来源共有三 种
15.在大M法中,M表示充分大正数。
七、用大M法求解下列线性规划问题。并指出问题的解属于哪一类。
第四章 线性规划的对偶理论
一、填空题
1.线性规划问题具有对偶性,即对于任何一个求最大值的线性规划问题,都有一个求最小值/极小值的线性规划问题与之对应,反之亦然。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。运筹学研究和解决问题的效果具有连续性。
6.运筹学用系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用特性。
8.运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9.运筹学解决问题时首先要观察待决策问题所处的环境。
第五章 线性规划的灵敏度分析
一、填空题
1、灵敏度分析研究的是线性规划模型的原始、最优解数据变化对产生的影响。
最大流最小割

计算结果: — — 为最短路,路长为49。
即:在第一年、第三年初各购买一台新设备为最优决策。这时5年的总费用为49。
例13已知某地区的交通网络如图8-37所示,其中点代表居民小区,边代表公路, 为小区间公路距离,问区中心医院应建在哪个小区,可使离医院最远的小区居民就诊时所走的路程最近?
={59,…19+30,…12+20,…}=28,
给 标号(28),( , )加粗线。
5) min{( ), , , ,( ), , , }
={40,…41, 40,… 43, …}=40,对应两个边:
给 标号(40),( , )加粗线,( , )加粗线。
6)min{ , ,( ), , }= min{59,53,49,50,55}=49
边( , )表示第i年购进的设备一直使用到第j年初(即第j-1年底)。
边( , )上的数字表示第i年初购进设备,一直使用到第j年初所需支付的购买费、维修的全部费用(可由表8-2计算得到)。例如:( , )边上的28是第一年初的购买费11加上三年的维修费5,6,8,减去3年役龄机器的残值2;( , )边上的20是第二年初购买费12减去机器残值3与使用二年维修费5,6之和,见下图:
Min{( ), , }=min{6,9,8}=6
给 标号(6):表明从第二个圈出来最近的一站是 ,总长度是6。
给( , )划成粗线。
划第三个圈。
表明:圈内的点已完成考察。
4)现已走出第三个圈,向 奔。有四条路可走,最优路线在何方?即:
Min{ ,( ), , }=min{9,8,10,13}=8
给 标号(8):表明从第三个圈出来后最近的一站是 ,总长度是8。
第八章 图与网络分析

16
赋权图 网络
赋权图:设图G=(V,E),对G的每一条边(vi,vj)相应赋 予数量指标 wij , wij 称为边 (vi,vj) 的权 , 赋予权的图 G 称 为赋权图。赋权图中的权可以代表距离、费用、通 过能力(容量)等等。 网络:若G=(V,E)为一赋权图,并在其顶点集合V中 指定了起点和终点,其余的点为中间点,这样的赋 权图称为网络图(简称网络)。
v2 9 v1 20
10
v3
15 7 v4 14 6 19 25
v5
v6
子图,支撑子图
图G1={V1、E1}和图G2={V2,E2},如果有
V1 V2和E1 E2 称G1是G2的一个子图。
若有 V1=V2,E1 E2 ,则称G1是G2的一个 支撑子图。 v2
v1 e4 e3 v3 e6 e8 e6 e2
第8章 图与网络优化
8.1 8.2 8.3 8.4 8.5 8.6 图的基本概念 树 最短路问题 网络最大流 最小费用最大流问题 中国邮递员问题
图论起源——哥尼斯堡七桥问题
A C B
问题:一个散步者能否从任一 块陆地出发,走过七座桥,且 每座桥只走过一次,最后回到 出发点?
A
D
C
B 欧拉证明了上述图形一笔画 是不可能的,因为图中每一个 点都只和奇数条线相关联. 他的结论是:图形能一笔画 的充要条件是图形的奇顶点 (连接奇数条线的顶点)的个 数为零
图的基本性质:
定理1 图G=(V,E),顶点次数之和等于所有边数的2 倍。
证明:由于每条边必与两个顶点关联,在计算点的次时,每 条边均被计算了两次,所以顶点次数的总和等于边数的2倍。
定理2 任何图中,次为奇数的顶点必为偶数个。
第8章远程管理与网络拓扑图绘制.doc

第8章远程管理与网络拓扑图绘制作为一个网络管理员,管理工具(如远程控制工具、网络拓扑设计的工具)是必不可少的,掌握这些工具的使用方法,可以使你的网络管理工作获得事半功倍的效果。
学习目的与内容领会远程管理的原理、网络拓扑设计的内容与要求;了解相关技术和软件的使用;掌握pcAnywhere的使用方法、网络拓扑设计图的内容与要求;学习完毕,能够绘制网络拓扑结构图、能够运用远程管理解决实际问题。
学习要求与方法远程控制的原理及pcAnywhere的使用、拓扑结构图的内容与要求、V isio的使用是本章的重点;在本章学习过程中,建议你经常上网查询相关资料;本章学习完毕,建议你根据本章的学习内容多做实验。
8.1 远程控制作为网络管理员,如果你的服务器托管在ISP机房,对服务器配置时,你需要到ISP机房去。
如果你使用远程控制软件来完成上述工作,就不必每次都到ISP机房去了。
8.1.1 远程控制的原理运行着远程控制软件的PC机,通过TCP/IP协议去控制运行着远程控制服务的主机。
PC机将键盘和鼠标的指令传送给远程被控端主机,同时通过TCP/IP协议将被控端计算机的屏幕传回来,显示在主控端PC机屏幕上。
8.1.2 pcAnywhere的使用在各种远程控制软件中,pcAnywhere是一款易于使用且很受欢迎的远程控制软件。
1. 服务器端(被控端)的配置(1)在服务器上运行pcAnywhere,在“pcAnywhere Manager”窗口的菜单栏上点击“Host”按钮,会看见下面的窗口中有4个图标,如图8-1。
图8-1 pcAnywhere Manager窗口Add Host:添加并配置主机,使其变成被控制端,以随时接受主控端发出的控制指令;DIRECT:直接用并口/串口连接,意思是指直接通过电缆相连,但现在较少采用;MODEM:指的是拨号访问,可以通过电话线调制解调器与远程计算机连接;NETWORK,CABLE,DSL:指的是通过网络访问和连接。
运筹学课件 第八章 图与网络分析

运筹学教程
例:哥尼斯堡七桥问题 哥尼斯堡(现名加里宁格勒)是欧洲一
个城市,Pregei河把该城分成两部分,河中 有两个小岛,十八世纪时,河两边及小岛之 间共有七座桥,当时人们提出这样的问题: 有没有办法从某处(如A)出发,经过各桥 一次且仅一次最后回到原地呢?
A C
B
运筹学教程
D
运筹学教程
最后,数学家Euler在1736年巧妙地给出 了这个问题的答案,并因此奠定了图论的基 础,Euler把A、B、C、D四块陆地分别收缩 成四个顶点,把桥表示成连接对应顶点之间 的边,问题转化为从任意一点出发,能不能 经过各边一次且仅一次,最后返回该点。这 就是著名的Euler问题。
第二阶段是从十九世纪中叶到二十世纪 中叶,这时,图论问题大量出现,如 Hamilton问题,地图染色的四色问题以 及可平面性问题等,这时,也出现用图 解 决 实 际 问 题 , 如 Cayley 把 树 应 用 于 化 学领域,Kirchhoff用树去研究电网络等.
运筹学教程
第三阶段是二十世纪中叶以后,由生产管 理、军事、交通、运输、计算机网络等方 面提出实际问题,以及大型计算机使大规 模问题的求解成为可能,特别是以Ford和 Fulkerson建立的网络流理论,与线性规划、 动态规划等优化理论和方法相互渗透,促 进了图论对实际问题的应用。
e5
运筹学教程
v2
v3
e2
e6
v4
v5
e8
运筹学教程
二、连通图
定义8:如果图中的某些点、边可以排列成点和边的交错序列 (v0 ,e1 ,v1 ,e2 ,v2,e3 ,v3 ,…,vn-1 , en , vn ) ,ei=(vi-1,vi),则称 此为一条链。 由两两相邻的点及其相关联边构成的点边序列。 初等链:链中无重复的点和边; 定义9:无向图中,如一条链中起点和终点重合,则称此链为 圈。 初等圈:圈中无重复的点和边; 有向图中,当链(圈)上的边方向相同时,为道路(回路)。
运筹学 第八章 图论 - 全

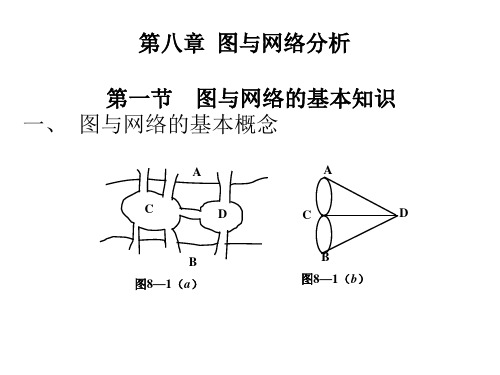
(a)明显为二部图,(b)也是二部图,但不明显,改画为(c) 时即可看出。
2017/7/13 11
图与网络的基本知识
次,奇点,偶点,孤立点 与某一个点vi相关联的边的数目称为 点vi的次(也叫做度),记作d(vi)。 右图中d(v1)=4,d(v3)=5,d(v5)=1。次 为奇数的点称作奇点,次为偶数的
2017/7/13
18
图与网络的基本知识
有向图 无向图
道路
回路
链
圈
道路(边的方向一致)
2017/7/13 19
图与网络的基本知识
连通图
定义10 一个图中任意两点间至少有一条链相连,则称此图为 连通图。任何一个不连通图总可以分为若干个连通子图,每 一个称为原图的一个分图(连通分支)。
连通图
2017/7/13
边,对余下的图重复这个步骤,直至无圈为止。
2、避圈法:每次增加一条边,且与已有边不构成圈,直至恰 有n-1条边为止。
2017/7/13
24
树
例1、下图是某建筑物的平面图,要求在其内部从每一房间都能走到 别的所有的房间,问至少要在墙上开多少门? 试给出一个开门的方案。
三
七
Байду номын сангаас
三 八 一 四 二 五
七 八 九 六
无向图
2017/7/13
有向图
8
图与网络的基本知识
环, 多重边, 简单图 如果边e的两个端点相重,称该边为 环。如右图中边e1为环。如果两个点 之间边多于一条,称为多重边,如右
v2 e5
多重边
e2
e1 v1
环
e3 v3
e4
图中的e4和e5,对无环、无多重边的
运筹学第八章--图与网络分析-胡运权

赵明霞山西大学经济与管理学院
2
第八章 图与网络分析
图与网络的基本概念 树 最短路问题 最大流问题 最小费用最大流问题
3
柯尼斯堡七桥问题
欧拉回路:经过每边且仅一次 厄尼斯堡七桥问题、邮路问题哈密尔顿回路:经过每点且仅一次 货郎担问题、快递送货问题
例8-9
28
基本步骤标号T(j)→P(j)
29
2017/10/26
30
最长路问题例8-10(7-9)设某台新设备的年效益及年均维修费、更新净费用如表。试确定今后5年内的更新策略,使总收益最大。
役龄项目
0
1
2
3
4
5
效益vk(t)
5
4.5
4
3.75
3
2.5
14
15
柯尼斯堡七桥问题
欧拉回路:经过每边且仅一次 厄尼斯堡七桥问题、邮路问题 充要条件:无向图中无奇点,有向图每个顶点出次等于入次
16
第二节 树
树是图论中的重要概念,所谓树就是一个无圈的连通图。
图8-4中,(a)就是一个树,而(b)因为图中有圈所以就不是树, (c)因为不连通所以也不是树。
7
G=(V,E)关联边(m):ei端(顶)点(n):vi, vj点相邻(同一条边): v1, v3边相邻(同一个端点):e2, e3环:e1多重边: e4, e5
8
简单图:无环无多重边
多重图:多重边
9
完全图:每一对顶点间都有边(弧)相连的简单图
10
次(d):结点的关联边数目d(v3)=4,偶点d(v2)=3,奇点d(v1)=4d(v4)=1,悬挂点e6, 悬挂边d(v5)=0,孤立点
(一)线性(整数)规划法
主题班会第八章第一节《正确使用网络》心理健康教育通用PPT课件

(4)出现不道德行为。 (5)染上网络成瘾症。 (6)有的学生为了支付上网费铤而走险,以偷窃或抢劫的方式获取金钱;有 的学生将网络游戏中的暴力行为应用到了现实中;有些学生陷入虚幻的网恋之 中而不能自拔。
在全班选出 8 名同学分成两组,就“网络是天使”还是“网络是魔鬼”进行辩 论。
正方:网络是天使;反方:网络是魔鬼。 全班投票选出“最佳辩论小组”和“最佳辩手”。
思考:原本乖巧的张某沉迷网络后发生了怎样的变化?最终将会导致什么样 的后果呢?
在当今信息高度发达的社会,几乎每个人的生活都离不开网络,那么网络 具有什么特点和作用呢?
一、网络的特点 (1)新异性。在网络上,一个广阔的大千世界呈现在人们面前,从中大家可以 了解到现实生活中所不可能接触到的五花八门的新奇事物。 (2)自由性。网络是一个自由的世界,在这里人们可以讨论自己最感兴趣的 话题,欣赏自己最喜欢的艺术品,听自己最爱听的音乐,说自己最想说的话。这 里是一个无拘无束的自由天地。
2.消极的作用 (1)“吞噬”大量的学习时间,影响学习和健康。 神奇的互联网充满了诱惑,当我们将大量的时间和精力投入网络这个虚拟 世界时,学习必然会受到严重影响。不仅如此,网络也打破了我们正常的生活规 律:一些同学为了上网,饭可以不吃,觉可以不睡。青少年正处于成长时期,正常 的生活规律被打破无疑会危害自己的身体健康,影响自己的成长。
小萍最终没有告诉他。从那以后,小萍上网更频繁了。由于上网时间过长,她的视力开 始下降。同时由于睡眠不足,上课时精神恍惚,班主任开始找她谈话。小萍在苦恼中迎来了期 中考试,她的各科成绩全部下滑,数学更是不及格,小萍怎样才能摆脱困扰呢?
讨论:大家一起来给小萍出出主意吧。
张某原是一名乖巧的初中生,由于中考失利,进入了一所中职学校就读。受 周围同学的影响,他开始迷上了网络游戏,视力迅速下降,由 1.2 变成了 0.2。起 初在网吧只待一两个小时,越到后面越不可收拾:为了上网,不惜旷课,装病请 假,甚至演变到瞒着父母半夜偷偷溜出外面,整晚泡在网吧。张某无心上学,成 绩一落千丈,他陷入虚拟的网络世界无法自拔。随着上网的次数不断增加,他的 零花钱像流水般不断流向网吧,甚至连伙食费也拿去上网了。最后,为了钱财, 他开始撒谎找各种理由向父母要钱,向亲朋好友借钱,甚至到周边的小学去勒 索小学生的钱……
运筹学习题答案(1)

第一章 线性规划及单纯形法(作业)1.4 分别用图解法和单纯型法求解下列线性规划问题,并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。
(1)Max z=2x 1+x 2St.⎪⎩⎪⎨⎧≥≤+≤+0,24261553212121x x x x x x 解:①图解法:由作图知,目标函数等值线越往右上移动,目标函数越大,故c 点为对应的最优解,最优解为直线⎩⎨⎧=+=+242615532121x x x x 的交点,解之得X=(15/4,3/4)T 。
Max z =33/4. ② 单纯形法:将上述问题化成标准形式有: Max z=2x 1+x 2+0x 3+0x 4St. ⎪⎩⎪⎨⎧≥≤++≤++0,,,242615535421421321x x x x x x x x x x其约束条件系数矩阵增广矩阵为:P 1 P 2 P 3 P 4⎥⎦⎤⎢⎣⎡241026150153 P 3,P 4为单位矩阵,构成一个基,对应变量向,x 3,x 4为基变量,令非基变量x 1,x 2为零,找到T 优解,代入目标函数得Max z=33/4.1.7 分别用单纯形法中的大M 法和两阶段法求解下列线性规划问题,并指出属哪一类。
(3)Min z=4x 1+x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 解:这种情况化为标准形式: Max z '=-4x 1-x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 添加人工变量y1,y2Max z '=-4x 1-x 2+0x 3+0x 4-My 1-My 2⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x(2) 两阶段法: Min ω=y 1+y 2St.⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x第二阶段,将表中y 1,y 2去掉,目标函数回归到Max z '=-4x 1-x 2+0x 3+0x 4第二章 线性规划的对偶理论与灵敏度分析(作业)2.7给出线性规划问题:Max z=2x 1+4x 2+x 3+x 4⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤++≤++≤+≤++)4,3,2,1(096628332143221421j x x x x x x x x x x x x j要求:(1)写出其对偶问题;(2)已知原问题最优解为X *=(2,2,4,0),试根据对偶理论,直接求出对偶问题的最优解。
8.1__图与网络分析基本概念

• 不连通图中的每个连通的部分,称为原图的连通分图. 链、圈、路、回路都是原图的连通分图.
16
5、连通图、连通分图、子图
• 给定图 G
(V , E )
,如果有 (V , E ),使得 V V,E E , G 为 则称 G 为 G 的一个子图.当 V V 时, 则称 G G 的一个
而 e i 是 v i , v j的关联边. • 同一条边的两个端点称为相邻顶点.具有共同端点的边 称为相邻边. • 一条边的两个端点相同,称为环.具有两个共同端点的
两条边称为多重边. • 既没有环也没有多重边的图称为简单图.
9
3、端点、关联边、相邻、次
• 一个没有环,但允许有多重边的图称为多重图. 今后若不加特别说明,所研究的图均为简单图. • 在无向图中,以顶点 v 为端点的边的数目,称为该顶点 的次,记作 d ( v ) . 次为1的点称为悬挂点,连接悬挂点的边称为悬挂边. 次为0的点称为孤立点. 仅有孤立点的图为零图. 次为奇数的点称为奇点,次为偶数的点称为偶点. 图中顶点均为偶点的图称为偶图.
链中没有重复点和重复边的链称为初等链. • 链 ( v i , v i , v i ) 中,若 v i v i ,则称此链为圈.
1 1 k
1
k
没有重复点和重复边的圈称为初等圈.
14
4、链、圈、路、回路
• 设D是一个有向图, G是它的基础图.若 ( v i , e i , ...., e i , v i )
6
无向图
有向图
混合图
• 图G或D的边数记作 m ( G ) 或 m ( D ) , 顶点个数记作n ( G ) 或 n ( D ) .在不引起混淆情况下,也简记为m , n .
北交大交通运输学院《管理运筹学》知识点总结与例题讲解第8章 图与网络分析

(a)
(b)
(c)
图 8-9 图、子图、支撑子图
(4)图的同构 设 G1 与 G2 是两个同阶图,若顶点集合 V1 和 V2 以及边集 E1 和 E2 之间在保持关联性
质条件下的一一对应,则称图 G1 和图 G2 同构。 例如:图 8-10(a)和图 8-10(b)就为同构。
(a)
(b)
图 8-10 同构图
(10)定理 8.1 对于图 G=(V ,E) ,其中 V = n , E = m ,则有:
∑d (v) = 2m
(8-2)
v∈V
证明:每条边都有两个端点,在计算顶点的次时,每个端点都要计算对应边次,故共有
2m 次。
通俗地讲,就是线有两头,共有 2m 个线头的意思。
(11)定理 8.2 奇次顶的总数是偶数。
第八章 图与网络分析
8.1 图与网络的基本知识
8.1.1 图与网络的基本概念 8.1.1.1 图的定义 自然界和人类社会中,大量的事物以及事物之间的关系,常可以用图形来描述。例如: 图 8-4 所示的我国北京、上海等十个城市间的交通图反映了这十个城市间铁路
分布情况。这里用点代表城市,用点和点之间的连线代表这两个城市之间有直通铁路。
图 8-7 一个无向图
G = (V, E) V= {v1, v2 ,v3 , v4} E={e1, e2 ,e3 , e4 ,e5 , e6 , e7}
其中
e1 = [v1 ,v2 ] , e2 = [v1 ,v2 ] , e3 = [v2 ,v3 ] , e4 = [v3 ,v4 ] ,
图 8-8 是一个有向图。该图可以表示为:
图 8-4 十个城市间铁路分布图
又如某单位储存五种化学药品,其中,某些药品是不能放在同一库房里的,为了反映这 种情况,可以用点 v1 、 v2 、 v3 、 v4 、 v5 分别代表这五种药品,若药品 vi 和药品 v j 是不能存 放在同一库房的,则在 vi 和 v j 之间连一条线,如图 8-5 所示。如果问题归结为寻求存放这种 化学药品的最少库房个数,则该问题就是染色问题。事实上,至少需要三个库房来存放这些 药品,即 v1 和 v5 、 v2 和 v4 、 v3 各存放在一个库房里。
运筹学—第八章 图与网络分析
v5 1 v6 7 1 v7 -5 -3
e1 {v1 , v2 }
e3 {v2 , v3 }
e2 {v1 , v2 }
e4 {v3 , v4 } e6 {v3 , v5 } e8 {v5 , v6 } e10 {v1 , v6 }
e5 {v1 , v3 }
e7 {v3 , v5 } e9 {v6 , v6 }
v1
第二节 树 一、 树的概念和性质 例8.3 已知有六个城市,它们之间 要架设电话线,要求 任意两个城市均可以互相通话,并且电话线的总长度最短。
v1 v6 v5 v2
v3
v4
定义9 一个连通的无圈的无向图叫做树。
作为树T的定义,下列定义是等价的: (1)T是一个树。(设其顶点数为n ,边数为 m ) (2)T无圈,且m=n-1。 (3)T连通,且m=n-1 。 (4)T无圈,但在树中不相邻的两个点之间加上一条边, 那么恰好得到一个圈。 (5)T中任意两个顶点之间有且仅有一条链。 (6)T连通,但去掉T的任一条边,T就不连通。
( vi , v j )
一、 狄克斯屈拉(Dijkstra)算法 适用于wij≥0,给出了从vs到任意一个点vj的最短路。
算法步骤: 1.给始点vs以P标号 P(vs ) 0 ,这表示从vs到 vs的最短距离 T 为0,其余节点均给T标号, (vi ) (i 2 , 3,, n) 。 2.设节点 vi 为刚得到P标号的点,考虑点vj,其中 (vi , v j ) E ,且vj为T标号。对vj的T标号进行如下修改:
e1 v1
e2 e5
e8 v5
v2
d(v1)= 4,d(v6)= 4
e10 v6 e9
e3 e v4 4 e6 e7 v3
《运筹学》 第八章图与网络分析习题及 答案

《运筹学》第八章图与网络分析习题1.思考题(1)解释下列名词,并说明相互之间的区别与联系:①顶点,相邻,关联边;②环,多重边,简单图;③链,初等链;④圈,初等圈,简单拳;⑤ 回 路,初等路;⑥节点的次,悬挂点,孤立点;⑦)连通图,连同分图, 支 撑子图;⑧有向图,基础图,赋权图。
⑨子图,部分图,真子图.(2)通常用记号G=(V,E)表示一个图,解释V及E的涵义及这个表达式 的涵义.(3)通常用记号D=(V,A)表示一个有向图,解释V及A的涵义及这个表 达式的涵义.(4) 图论中的图与一般几何图形的主要区别是什么? (5) 试述树与图的区别与联系.(6) 试述 求最短路问题的Dijkstra 算法的基本思想及其计算步骤. (7) 试述寻求最大流的标号法的步骤与方法.(8) 简述最小费用最大流的概念及其求解的基本思想和方法.(9) 通常用记号N=(V,A,C)表示一个网络,试解释这个表达式的涵义. (10) 在最大流问题中,为什么当存在增广链时,可行流不是最大流? (11) 试叙述最小支撑树、最大流、最短路等问题能解决那些实际问题。
2.判断下列说法是否正确(1) 图论中的图是为了研究问题中有哪些对象及对象之间的关系,它与图的几何形状无关。
(2) 一个图G 是树的充分必要条件是边数最少的无孤立点的图。
(3) 如果一个图G 从V 1到各点的最短路是唯一的,则连接V 1到各点的最短路,再去掉重复边,得到的图即为最小支撑树。
(4 )图G 的最小支撑树中从V 1到V n 的通路一定是图G 从V 1到V n 的最短路。
(5) {f ij =0}总是最大流问题的一个可行流。
(6 )无孤立点的图一定是连通图。
(7) 图中任意两点之间都有一条简单链,则该图是一棵树。
(8) 求网络最大流的问题总可以归结为求解一个线性规划问题。
(9)在图中求一点V1到另一点Vn 的最短路问题总可以归结为一个整数规划问题 (10) 图G 中的一个点V 1总可以看成是G 的一个子图。
《应用数学基础》(陈冲)教学课件 第八章 图 论

第八章 图 论
目录
ONTENTS
1 图的基本概念 2 图的矩阵表示 3 图的连通性
01 图的基本 概念
1.1 图的定义
在某计算机网络中,两台计算机之间通过网络线连接起来,如图 8-1 所示.顶点表示每台计 算机的位置,边表示网络连线.这类图在绘制时,可用圆圈(或实心点)来表示顶点,对图的 所有顶点标以名称:v1 ,v2 ,v3 ,v4 ;用直线或曲线来表示边,同时对图的所有边标以名称:e1 , e2 , e3 , e4 , e5 ,如图 8-2 所示.
该定理之所以称为握手定理,因为它有非常直观而形象的解释:假定有若干个人握手,每握
一次手,需要 2 只手来完成.此时有人用自己的右手握自己的左手,也算一次握手.参加握手的 手的总数目(包含重复的)恰好等于握手次数的 2 倍.这里用到了图论模型解决实际问题:把每 个人看成一个顶点,某两人握一次手,则在相应顶点之间连上一条边;如果某人与自己握手,则
设 G (V ,E) 是有向图, v V ,称以 v 为终点的边数为 v 的入度,记为 d (v) ;称以 v 为起 点的边数为 v 的出度,记为 d (v) .
若 d(v) 是奇数,就称 v 为奇点;若 d(v) 是偶数,就称 v 为偶点.度为 1 的点称为悬和是边数的 2 倍,这是图的一般性质.下面给出的定理是 Euler 在 1936 年提出 的,常称为握手定理,是图论中的基本定理.
定理 1(握手定理) 设 G (V ,E) 是图,G 中所有顶点度数之和 d (v) 等于 G 中边数 m 的 vV
两倍,即
d(v) 2m .
vV
1.2 顶点的度
在图 8-3 中,由于 e3 (v2 ,v3 ) ,则点 v2 与点 v3 邻接,点 v2 与边 e3 关联,点 v3 与边 e3 关联; 由于边 e1 和边 e3 有共同的顶点 v2 ,则边 e1 和边 e3 邻接; v5 为孤立点.
运筹学教学大纲

《运筹学》课程教学大纲一、教学对象本课程大纲适用于工商企业管理专业三年制高职学生。
二、学分与学时本课程共68学时三、课程模块类别及课程属性课程模块:专业课课程属性:必修课四、课程性质、任务和目的性质:《运筹学》是工商企业管理专业的专业基础课程,它广泛应用现有的科学技术知识和数学方法,解决实际工作中提出的专门问题,为决策者选择满意方案提供定量依据。
任务:使学生获得系统最优化的基本知识、必要的基础理论和常用的思维方式及运算方法,培养学生的分析思维能力和比较熟练的运算能力,为提高学生的基本素质和后继课程的学习以及进一步扩大应用数学知识解决实际问题奠定良好的基础。
目的:通过这门课程的学习,使学生掌握整体优化的基本思想,培养学生的逻辑思维能力和创新素质;使学生掌握运筹学的工作步骤,培养学生运用模型和算法并借助计算机手段解决实际问题的能力;使学生了解本领域的发展动态。
五、主要先修与后续课程先修课程:高等数学、概率论与数理统计、管理学后续课程:生产运作与管理、人力资源管理、采购管理、管理会计六、教学目的要求和主要内容第一章线性规划与单纯形法【目的要求】1.掌握线性规划数学模型的基本特征和标准形式,以及线性规划问题数学模型的建立方法,学会用图解法求解简单的线性规划问题;掌握运用单纯形法求解线性规划问题;2.熟悉线性规划问题的解的概念;3.了解线性规划的基本理论,了解单纯形表的构成。
【主要内容】●讲授内容1.问题的提出2.图解法3.线性规划问题解的标准形式4.线性规划问题解的概念5.单纯形法的解题思路6.单纯形表7.线性规划应用举例●自学内容1.初始可行基的求法---人工变量法第二章对偶理论与灵敏度分析(自学)【目的要求】1.掌握原问题与对偶问题的关系;掌握运用对偶单纯形法求解线性规划问题;2.熟悉对偶单纯形法的计算步骤;3.了解线性规划的对偶理论【主要内容】1.单纯形法的矩阵描述2.对偶问题的概念3.对偶问题的基本性质4.影子价格5.对偶单纯形法6.灵敏度分析第三章运输问题【目的要求】1.掌握运输问题表上作业法,产销不平衡的运输问题及其求解方法;2.熟悉表上作业法的理论依据;3.了解运输问题的经济含义,表上作业法与单纯形法的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B A
G 端点
H
边
C D
G=(V,E)
N
F 端点 M
V={A,B,C,D,N,F,G,H,M}
E={[A,A],[A,B],[A,C],…,[H,M]}
m(G)=12;n(G)=9
G 始点
弧
M N
D=(V,A)
终点 F
V={M,N,F,G}
A={[M,G],[G,F],[M,N],[N,F]}
2、如果一条边的两端点相同,此边称为环, 两点之间多于一条边的,称为多重边。
v2
v5
v6
v3
v1 v4
v2
v5 v6
v4
v3
v1
v4
v5
v2
v3
v1
v4
v5
v2
二、最小生成树的算法
(1)避圈法——每步从未选的边中选取e,使 它与已选边不构成圈,且e是未选边中的最小权 边,直到选够(n-1)条边为止。
(2)破圈法——每步从未破掉的圈中任选一个 圈,将该圈的边中权最大的一条边e去掉,直到 图中无圈为止。
v5
v4
v6
v7
v3
v1
v2
7、连通图:图G=(V,E)中任意两点间至少有一 条链。 子图: G′=(V′,E′),其中 V′V ,E′ E。
B
G
H
G
D N
FM
N
F
支撑(生成)子图:对于子图G′=(V′,E′),当 V′=V时,且与图G=(V,E)的连通性相同的子 图称为支撑子图,或生成子图。
B
G G
10 20
D N
D 40
F
N
30 F
10、图的矩阵表示:邻接矩阵与权矩阵
(1)邻接矩阵:图G=(V,E),│V│=n,构造一 个矩阵——邻接矩阵A=(aij)n×n,其中
1
aij
0
(vi , v j ) E 其它
(2)权矩阵:图G=(V,E),│V│=n,边(vi, vj) 有权ωij,构造矩阵——权矩阵B=(bij)n×n,其中
第八章 图与网络分析
教学目的:让学生了解图论的基本知识,掌握用网络 表示所研究问题、对象的基本属性及其解决方法。 教学内容:基本概念、树、最短路、最大流、最小费 用最大流等。 教学难点:建立网络图的技巧和各种方法产生的思路。 学时安排:8~10学时。
第一节 图与网络的基本知识
北京 郑州 武汉
天津 济南 徐州 南京
青岛 上海
一、图论形成的历史回顾
1、18世纪哥尼斯堡城中普雷•格尔河中有两个小岛C、 D,它们之间与两岸A、B共有七座桥相连。
A
C
D
B
当地人热衷于这样的游戏:一个人怎样才能一次连续 走过七桥且每桥只走一次,再回到出发点。
1736年,著名数学家欧拉把此问题简化为图,并 发表了论文:“依据几何位置的解题方法”。
N
M
5、 圈:链上首、尾节点是同一节点时,称为圈; 简单圈:圈中没有重复的边;(A,B,G,B,D,C,A) 初等圈:既无重复点,也无重复边;(A,B,D,C,A)
B A
G
H
C D
N
M
F
路:链上边方向一致时,称为路; 回路:路上首、尾节点是同一节点时, 称为回路。
G
D N F
6、顶点的次:以点vi为端点的边数,记为d(vi )。
一个邮递员如何选择一条道路,是他能从邮局出发,走遍他负责 送信的所有街道,最后回到邮局,并且所走的路程为最短。
给定一个连通图G,每边有非负权l(e),要求一条回路过每边至 少一次,且满足总权最小。
中国邮路问题可用于邮政部门、扫雪车路线、洒水车路线、警车 巡逻路线、(计算机绘图)如何节约画笔的空走问题、(计算机制造 工业)如何将激光刻制用于集成电路加工的模具等。
G
d(G)=2; d(D)=2;
d(N)=2;d(F)=2;
D N F
定理2 任何图中,次为奇数的顶点必为偶数个。 次为奇数的点为奇点,次为偶数的点为偶点。 奇点的集合可记为V1,偶点的集合记为V2。
d(v) d(v) d(v) 2m
vV1
vV2
vV
B
G
D
N
F
四、欧拉回路与道路
定义:连通图G中,若存在一条道路,经过每 边一次且仅一次,则称这条路为欧拉道路。若 存在一条回路,经过每边一次且仅一次,则称 这条回路为欧拉回路。 具有欧拉回路的图称为欧拉图(E图)。
而未得到P标号的点,赋予试探性(临时性标号)标号—— T(tentative label)标号,表示从vs 到vk 点的最短路长的上界。
T(v2 )=3 v2 5
v1
3
11
P (v1 ) =0
2
v3
v4
T(v4 6
)=8
v6 T(v6 )=14
v5 3
2、算法的步骤
(1)给vs以P标号,P(vs)=0,其余各点均给T类标号, T(vi)=+∞
序列{v1, v4,v5 }是从v1 至 vn 的一个最短路 则序列{v1, v4}是从v1 至 v4 的一个最短路
v2 6 v4
65
v1
7
2
10 v5 v3
(3)标记:
从vs出发,给从vs 到 vk 最短路长的点 vk 赋予固定标号— —P(permanent label)标号,并记下相应的最短路长(真实的 长度);
v1
v4
v1
v4
v2
v3
v2
v3
该定理的证明给出了求生成树的方法:每步选出
一条边,使它与已经选出的边不形成圈,直至选
出(n-1)条边为止。
(1)支撑树的求法:破圈法 v33
v3
v5
v1
v1 v2
v6 v22
v4
v55 v6
v4
v3 v1
vv22
vv55
v6
v3
v1 vv44
v2
v5 v6
v4
v3 v1
bij
ij
0
(vi,vj ) E 其它
10
D 40 N
DN FG
G
D 0 1 0 1 N 1 0 1 0
20
F 0 1 0 1 G 1 0 1 0
DN FG
30
D 0 40 0 10
F N 40
0
30
0
F 0 30 0 20
G 10
0
20
0
三、基本理论
定理1 任何图中,顶点次的总和等于边数的2倍。
v1
4
v2
5
5
3
2
v8
2
8 v9
3
6 7
6 4
1
7
v7
v6
v3 8
v4 6
v5
第三节 最短路问题
一、问题的提出
v3 5
v5
32
2
v1
v6
67
5
4
v2 1
v4
二、最短路的定义
设D =(V,A)为一个赋权有向图,图中各弧(vi ,vj) 有权lij≥0, vs、vt为图中任意两点,求一条路P0,它是从 vs 到 vt的所有路P中总权最小的路。
3、简单图:无多重边和环的图; 多重图:有多重边,无环的图。
B A
G
H
C D
N
M
F
4、链:点、边交替的序列(V1,e1, V2,e2, …,Vi,ei) ; 简单链: 边不重复, {A, C, D, B, G,D,N}; 初等链: 点、边不重复, {A, B, G, F, N}; 。
B A
G
H
C D
CCCC
C
C
C
C
5、1857年,英国数学家哈密尔顿发明了一个 游戏,他用一个实心正12面体象征地球,正12面 体的20个顶点分别表示世界上的20个城市,要求
寻找一条路径:由某个城市出发每城市仅去一次, 最终回到出发点。
二、图与网络的基本概念
一个图是由点集V={vi}和V中元素(顶点)之 间的连线所组成。
例8—2 一个乡有9个自然村,其间道路及 各道路长度如下图所示,各边上的权表示距离, 问如何拉电缆线才能使用线总长度最短。
解:这是一个最小生成树问题。具体解法如下:
v1
4
v2
5
v3
5
3
2
v8
2
8 v9
3
6 7
6 4
8 v4
6
1
7
v5
v7
v6
最小树权值为W(T) =5+2+3+2+3+4+6+1=26。
v3 树枝 v5
v3
v5
树枝
弦
v1
弦 弦 树枝
v6 v1
树枝
树枝
弦
v2
v4
v2
v6 v4
3.最小生成树——连通图G=( V,E ),每条边上 有非负权L( e )。一棵生成树所有树枝上权的总和 称为这棵生成树的权。具有最小权的生成树称为 最小生成树(最小支撑树),简称最小树。
v3 2
v5
v3 2
v5
C
能否从某一点
开始不重复地
一笔画出这个 A
图形,最终回
B
到原点?
D
2、1847年,物理学家基尔霍夫为解决有关线 性方程组而发展了“树”的理论。他将网络中的 电感、电容、电阻等抽象为点和线,得到一简单 的组合结构。这种结构便于运算,不必指明为何 种元素。
3、1857年,凯莱研究饱和烃链CnH2n+2的同分 异构体时,又一次引入树状结构,例如, C4H10 。
