椭圆方程式知识点总结

椭圆总结(全)

椭圆总结一、椭圆的定义：（隐含条件）平面内与两定点F 1，F 2的距离的和等于定长()2122F F a a >的动点P 的轨迹，即点集M={P| |PF 1|+|PF 2|=2a ，2a ＞|F 1F 2|}；（212F F a =时为线段21F F ，212F F a <无轨迹）。

其中两定点F 1，F 2叫焦点，定点间的距离叫焦距。

二、方程1、标准方程：（1）焦点在x 轴上，中心在原点：12222=+by a x （a ＞b ＞0）；焦点F 1（－c ，0）， F 2（c ，0）。

其中22b a c -=（一个Rt 三角形）（2）焦点在y 轴上，中心在原点：12222=+bx a y （a ＞b ＞0）；焦点F 1（0，－c ），F 2（0，c ）。

其中22b a c -=2、一般方程：)0,0(122>>=+B A By Ax Ax 2+By 2=1 （A ＞0，B ＞0，A ≠B ），当A ＜B 时，椭圆的焦点在x 轴上，A ＞B 时焦点在y 轴上。

要求能熟练的把一般方程转化成标准方程，并找出a,b,c.三、性质：对于焦点在x 轴上，中心在原点：12222=+b y a x （a ＞b ＞0）有以下性质：1、范围：|x|≤a ，|y|≤b ；[][]22121212,*,0PF a c a c PF PF b a F PF F BF ∈-+⎡⎤∈⎣⎦∈角，2、对称性：对称轴方程为x=0，y=0，对称中心为O （0，0）；3、顶点：A 1（-a ，0），A 2（a ，0），B 1（0，-b ），B 2（0，b ），长轴|A 1A 2|=2a ，短轴|B 1B 2|=2b ；（a 半长轴长，b 半短轴长）；4、通径：过椭圆的焦点与椭圆的长轴垂直的直线被椭圆所截得的线段称为椭圆通径，通径最短=ab 225、离心率：e=ca==（焦距与长轴长之比）()1,0∈；e 越大越扁，0=e 是圆。

椭圆知识点详细总结优选版

椭圆知识点详细总结优选版椭圆方程式知识点总结1. 椭圆方程的第一定义：⑴①椭圆的标准方程：i. 中心在原点，焦点在x轴上：. ii. 中心在原点，焦点在轴上：.②一般方程：.③椭圆的标准参数方程：的参数方程为（一象限应是属于）.⑵①顶点：或.②轴：对称轴：x轴，轴；长轴长，短轴长.③焦点：或.④焦距：.⑤准线：或.⑥离心率：.⑦焦点半径：i.设为椭圆上的一点，为左、右焦点，则由椭圆方程的第二定义可以推出.为椭圆上的一点，为上、下焦点，则由椭圆方程的第二定义可以推出.由椭圆第二定义可知：归结起来为“左加右减”. 注意：椭圆参数方程的推导：得方程的轨迹为椭圆.⑧通径：垂直于x轴且过焦点的弦叫做通经.坐标：和⑶共离心率的椭圆系的方程：椭圆的离心率是，方程是大于0的参数，的离心率也是我们称此方程为共离心率的椭圆系方程.⑸若P是椭圆：上的点.为焦点，若，则的面积为（用余弦定理与可得）. 若是双曲线，则面积为.椭圆的简单几何性质常见考法在段考中，多以选择题、填空题和解答题的形式考查椭圆的简单几何性质。

选择题和填空题一般属于容易题，解答题一般属于难题。

在高考中，一般以解答题的形式融合其它圆锥曲线联合考查椭圆的几何性质，难度较大。

误区提醒求椭圆的方程，用待定系数法，先定位，后定量。

如果不能确定，要分类讨论。

【典型例题】椭圆知识点知识点一：椭圆的定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距.注意：若2121F F PF PF =+，则动点P 的轨迹为线段21F F ；若2121F F PF PF <+，则动点P 的轨迹无图形.知识点二：椭圆的简单几何性质椭圆：12222=+b y a x )0(>>b a 与 12222=+bx a y )0(>>b a 的简单几何性质标准方程 12222=+b y a x )0(>>b a 12222=+b x a y )0(>>b a 图形性质焦点)0,(1c F -，)0,(2c F ),0(1c F -，),0(2c F 焦距c F F 221= c F F 221= 范围a x ≤，b y ≤ b x ≤，a y ≤ 对称性关于x 轴、y 轴和原点对称顶点)0,(a ±，),0(b ± ),0(a ±，)0,(b ± 轴长长轴长=a 2，短轴长=b 2 离心率 )10(<<=e ac e c a F A F A -==2211；c a F A F A +==1221；c a PF c a +≤≤-1；(p 是椭圆上一点)1．椭圆标准方程中的三个量c b a ,,的几何意义222c b a +=2.通径:过焦点且垂直于长轴的弦,其长a b 223.最大角:p 是椭圆上一点，当p 是椭圆的短轴端点时，21PF F ∠ 为最大角。

初中椭圆方程知识点总结

初中椭圆方程知识点总结椭圆是平面上一个固定点F到平面上任意一点P的距离之和等于常数2a的轨迹。

椭圆的方程可以用于描述椭圆的形状和位置。

在初中数学课程中，学生通常会学习如何识别和使用椭圆方程。

本文将总结初中阶段涉及的椭圆方程的知识点。

一、椭圆的定义在讨论椭圆的方程之前，我们首先来了解一下椭圆的定义。

椭圆是平面上一个固定点F到平面上任意一点P的距离之和等于常数2a的轨迹。

这个固定点F叫做焦点，称为F1和F2。

椭圆上任意一点P到两个焦点的距离之和是常数2a。

二、椭圆的标准方程椭圆的标准方程可以写成(x-h)²/a² + (y-k)²/b² = 1，其中(h, k)是椭圆的中心坐标，a和b分别是x轴和y轴上的半径。

当椭圆的中心在原点时，标准方程变为x²/a² + y²/b² = 1。

三、椭圆的参数方程椭圆还可以用参数方程表示：x = h + a*cos(θ)，y = k + b*sin(θ)。

这里θ是参数，通常取值在[0,2π]之间。

使用参数方程可以方便地描述椭圆上的点，但在初中阶段，学生一般不需要深入研究参数方程。

四、椭圆的一般方程椭圆的一般方程可以写成Ax² + By² + Cx + Dy + E = 0，其中A、B、C、D、E都是常数。

一般方程描述了椭圆的所有可能形状和方位，但通常需要将一般方程转化为标准方程才能进行具体的计算和分析。

五、椭圆的性质对于初中生而言，了解椭圆的一些基本性质是很重要的。

例如，椭圆的离心率e满足0 <e < 1，椭圆的长轴长度是2a，短轴长度是2b，焦点到中心的距离是c，有关椭圆的这些性质可以帮助学生理解椭圆方程的意义和应用。

六、椭圆的图像学生需要掌握如何根据椭圆的方程画出椭圆的图像。

对于标准方程x²/a²+ y²/b²= 1而言，椭圆的图像在x轴和y轴上分别展开a个单位和b个单位。

高三数学椭圆方程式知识点归纳

高三数学椭圆方程式知识点归纳数学是学习生涯的关键阶段，为了能够使同学们在数学方面有所建树，小编特此整理了高三数学椭圆方程式知识点归纳，以供大家参考。

1. 椭圆方程的第一定义：
⑴①椭圆的标准方程：
i. 中心在原点，焦点在x轴上：
. ii. 中心在原点，焦点在
轴上：
②一般方程：
.③椭圆的标准参数方程：
的参数方程为
(一象限
应是属于
⑵①顶点：
或
.②轴：对称轴：x轴，
轴;长轴长
，短轴长
.③焦点：
或
.④焦距：
.⑤准线：
或
.⑥离心率：
.⑦焦点半径：
i.
设
为椭圆
上的一点，
为左、右焦点，则
由椭圆方程的第二定义可以推出.
ii.设
为椭圆
上的一点，
为上、下焦点，则
由椭圆方程的第二定义可以推出.
由椭圆第二定义可知：
归结起来为左加右减.
注意：椭圆参数方程的推导：得
方程的轨迹为椭圆.
⑧通径：垂直于x轴且过焦点的弦叫做通经.坐标：和
⑶共离心率的椭圆系的方程：椭圆
的离心率是
，方程
是大于0的参数，
的离心率也是
我们称此方程为共离心率的椭圆系方程.
⑸若P是椭圆：
上的点.
为焦点，若
，则
的面积为
(用余弦定理与
可得). 若是双曲线，则面积为。

(完整word版)椭圆总结(全),推荐文档

椭圆一．知识清单1.椭圆的两种定义：①平面内与两定点F1，F2的距离的和等于定长2a 2a F1 F2的动点P 的轨迹，即点集M={P||PF|+|PF |=2a ， 2a＞ |F F |} ；（2a F1 F2时为线段 F1F2，2a F1F2无轨迹）。

此中两定1212点 F1， F2叫焦点，定点间的距离叫焦距。

②平面内一动点到一个定点和必定直线的距离的比是小于 1 的正常数的点的轨迹，即点集M={P|PF e， 0＜ e＜ 1 的常数。

（ e1为抛物线； e1为双曲线）d（利用第二定义 , 能够实现椭圆上的动点到焦点的距离与到相应准线的距离相互转变，定点为焦点，定直线为准线） .2 标准方程：（ 1）焦点在 x 轴上，中心在原点：x2y 21 （a＞b＞0）；a2 b 2焦点 F （－ c， 0）， F（ c，0）。

此中c a2b2（一个 Rt 三角形）12（ 2）焦点在 y 轴上，中心在原点：y 2x 21（a＞b＞0）；a2b2焦点 F1（ 0，－ c）， F2（ 0， c）。

此中c a 2 b 2注意：①在两种标准方程中，总有a＞ b＞ 0，c a 2b2而且椭圆的焦点总在长轴上；②两种标准方程可用一般形式表示：Ax2+By2=1 （A＞ 0，B＞ 0，A≠ B），当 A＜ B 时，椭圆的焦点在 x 轴上， A＞ B 时焦点在 y 轴上。

3 参数方程：焦点在 x 轴，x a cos（为参数）y b sin4 一般方程：Ax2By 21( A0,B 0)5. 性质：对于焦点在 x 轴上，中心在原点：x2y21（ a＞ b＞ 0）有以下性质：a2b2坐标系下的性质：①范围： |x|≤a， |y|≤b；② 对称性：对称轴方程为x=0， y=0，对称中心为O（0， 0）；③极点：A1（-a，0），A2（a，0），B1（0，-b），B2（0，b），长轴|A1A2|=2a，短轴|B1B2|=2b；（ a 半长轴长，b半短轴长）；④ 椭圆的准线方程：对于 x2y 21，左准线 l 1 : x a 2；右准线 l 2 : x a2a 2b 2c c对于 y 2x 21，下准线 l1 : y a 2；上准线 l 2 : y a 2a 2b 2c c焦点到准线的距离 pa 2 a 2 c 2b 2 cc（焦参数）cc椭圆的准线方程有两条，这两条准线在椭圆外面，与短轴平行，且对于短轴对称⑤ 焦半径公式： P （ x 0，y 0）为椭圆上任一点。

高中数学知识点总结：椭圆方程式

高中数学知识点总结：椭圆方程式数学网整理高中数学知识点总结：包括有关函数、数列、平面解析几何、立体几何等知识点的整理。

数学网各科复习资料：://gaokao.xdf/list_1019_1.html椭圆方程式知识点总结1. 椭圆方程的第一定义：⑴①椭圆的标准方程：i. 中心在原点，焦点在x轴上：ii. 中心在原点，焦点在轴上：②一样方程：.③椭圆的标准参数方程：的参数方程为(一象限应是属于).⑵①顶点：或.②轴：对称轴：x轴，轴;长轴长，短轴长.③焦点：或.④焦距：.⑤准线：或⑥离心率：⑦焦点半径：i. 设为椭圆上的一点，为左、右焦点，则由椭圆方程的第二定义能够推出.ii.设为椭圆上的一点，为上、下焦点，则由椭圆方程的第二定义能够推出.由椭圆第二定义可知：归结起来为“左加右减”.注意：椭圆参数方程的推导：得方程的轨迹为椭圆.⑧通径：垂直于x轴且过焦点的弦叫做通经.坐标：和死记硬背是一种传统的教学方式,在我国有悠久的历史。

但随着素养教育的开展,死记硬背被作为一种僵化的、阻碍学生能力进展的教学方式,慢慢为人们所摒弃;而另一方面,老师们又为提高学生的语文素养煞费苦心。

事实上,只要应用得当,“死记硬背”与提高学生素养并不矛盾。

相反,它恰是提高学生语文水平的重要前提和基础。

与当今“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。

金代元好问《示侄孙伯安》诗云：“伯安入小学，颖悟专门貌，属句有夙性，说字惊老师。

”因此看，宋元时期小学教师被称为“老师”有案可稽。

清代称主考官也为“老师”，而一样学堂里的先生则称为“教师”或“教习”。

可见，“教师”一说是比较晚的事了。

现在体会，“教师”的含义比之“老师”一说，具有资历和学识程度上较低一些的差别。

辛亥革命后，教师与其他官员一样依法令任命，故又称“教师”为“教员”。

⑶共离心率的椭圆系的方程：椭圆的离心率是，方程是大于0的参数，的离心率也是我们称此方程为共离心率的椭圆系方程.⑸若P是椭圆：上的点.为焦点，若，则的面积为(用余弦定理与可得). 若是双曲线，则面积为.。

椭圆知识点汇总

椭圆知识点汇总一、椭圆的定义平面内与两个定点 F₁、F₂的距离之和等于常数（大于|F₁F₂|）的点的轨迹叫做椭圆。

这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。

若 M 为椭圆上任意一点，F₁、F₂为椭圆的焦点，则有|MF₁| ＋｜MF₂| ＝ 2a（2a ＞ 2c，其中 2c 为焦距）。

二、椭圆的标准方程1、焦点在 x 轴上的椭圆标准方程：＼（＼frac{x^2}｛a^2} ＋＼frac{y^2}｛b^2} ＝ 1\）（＼（a ＞ b ＞ 0\）），其中\（a\）为椭圆的长半轴长，＼（b\）为椭圆的短半轴长，＼（c\）满足\（c^2 ＝ a^2b^2\），焦点坐标为\（（＼pm c, 0)＼）。

2、焦点在 y 轴上的椭圆标准方程：＼（＼frac{y^2}｛a^2} ＋＼frac{x^2}｛b^2} ＝ 1\）（＼（a ＞ b ＞ 0\）），焦点坐标为\（（0, ＼pm c)＼）。

三、椭圆的性质1、对称性椭圆关于 x 轴、y 轴和原点都是对称的。

2、范围对于焦点在 x 轴上的椭圆\（＼frac{x^2}｛a^2} ＋＼frac{y^2}｛b^2} ＝ 1\），有\（a ＼leq x ＼leq a\），＼（b ＼leq y ＼leq b\）；对于焦点在 y 轴上的椭圆\（＼frac{y^2}｛a^2} ＋＼frac{x^2}｛b^2} ＝ 1\），有\（b ＼leq x ＼leq b\），＼（a ＼leq y ＼leq a\）。

3、顶点焦点在 x 轴上的椭圆顶点坐标为\（（＼pm a, 0)＼），＼（（0, ＼pm b)＼）；焦点在 y 轴上的椭圆顶点坐标为\（（0, ＼pm a)＼），＼（（＼pm b, 0)＼）。

4、离心率椭圆的离心率\（e ＝＼frac{c}｛a}＼）（＼（0 ＜ e ＜ 1\）），它反映了椭圆的扁平程度。

＼（e\）越接近0，椭圆越接近于圆；＼（e\）越接近 1，椭圆越扁。

椭圆知识点总结

椭圆知识点总结一、椭圆的方程椭圆的标准方程是x^2/a^2 + y^2/b^2 = 1，其中a和b分别代表椭圆长轴和短轴的一半。

椭圆的焦点到中心的距离是c，满足c^2 = a^2 - b^2。

二、椭圆的性质1. 椭圆对称性：椭圆关于x轴和y轴对称。

2. 焦点性质：椭圆上任意一点到两个焦点的距离之和等于常数2a。

3. 长短轴性质：椭圆的长轴和短轴互相垂直，长轴的长度是2a，短轴的长度是2b。

4. 离心率：椭圆的离心率e定义为c/a，表示椭圆拉伸的程度，离心率介于0到1之间。

5. 参数方程：椭圆的参数方程为x = a*cos(t)，y = b*sin(t)，其中t为参数。

6. 弦长：椭圆上任意一点到两个焦点的距离之和等于常数2a，因此椭圆上任意一条弦的长度小于或等于2a。

7. 焦准线性质：椭圆上任意一点到两个准线的距离之差等于常数2a。

三、椭圆与圆的关系1. 圆是椭圆的特殊情况：当椭圆的长轴和短轴相等时，椭圆就变成了圆。

2. 椭圆的离心率介于0到1之间，当离心率等于0时，椭圆就是一个圆。

因此，椭圆和圆可以看作是同一种几何图形的不同特例。

四、椭圆的应用1. 天体运动：椭圆轨道是描述天体运动的重要数学工具，如行星绕太阳运动、卫星绕地球运动等。

2. 光学：椭圆镜片和椭圆抛物面反射器是光学领域常用的元件，用于聚焦和成像。

3. 工程设计：椭圆的性质在设计椭圆形建筑、椭圆形机械零件、椭圆形轨迹等方面有重要应用。

4. 地理测量：椭圆在地图投影和地理测量中有广泛应用，如椭球面测量、椭圆地图投影等。

五、椭圆的求解1. 椭圆的参数方程可以通过消除参数t来得到椭圆的标准方程。

2. 根据椭圆的焦点性质和准线性质，可以求解椭圆的焦点和准线方程。

3. 椭圆的面积可以通过积分求解，面积公式为S = πab。

4. 椭圆的周长可以通过椭圆的参数方程求解，周长公式为L = 4aE(e)，其中E(e)为椭圆的第二类完全椭圆积分。

六、椭圆的变换1. 平移变换：椭圆的平移变换可以用矩阵形式表示，通过平移变换可以将椭圆移动到任意位置。

(完整版)椭圆的基本知识

椭圆的基本知识一、基本知识点知识点一：椭圆的定义：椭圆三定义，简称和比积1、定义1:（和）到两定点的距离之和为定值的点的轨迹叫做椭圆。

这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距,定值为_______________________ .2、定义2：（比）到定点和定直线的距离之比是定值的点的轨迹叫做椭圆。

定点为焦点，定直线为准线，定值为。

3、定义3：（积）到两定点连线的斜率之积为定值的点的轨迹是椭圆.两定点是长轴端点,定值为m = e 2 —1（-1< m <0）.知识点二：椭圆的标准方程1、当焦点在％轴上时，椭圆的标准方程为，其中C2 = a2 -b2。

2、当焦点在y轴上时，椭圆的标准方程为，其中c 2 = a 2 - b 2.知识点三:椭圆的参数方程兰+2=1（a > b >0）的参数方程为___________________ 。

a2 b2知识点四：椭圆的一些重要性质（1）对称性：椭圆的标准方程是以％轴、y轴为对称轴的轴对称图形，并且是以原点为对称中心的中心对称图形，这个对称中心就是椭圆的中心。

（2）范围：椭圆上所有的点都位于直线x = ±a和y= ±b所围成的矩形内，所以椭圆上点的坐标满足凶 < a,| y| < b。

（3）顶点：①椭圆的对称轴与椭圆的交点为椭圆的顶点；②椭圆土+二=1（a > b >0）与坐标轴的四个顶点分别为________________________________ 。

a2 b2③椭圆的长轴和短轴.2c c（4）离心率：①椭圆的焦距与长轴长度的比叫做椭圆的离心率，用e表示，记作e = 一二—。

2a a②因为a>c>0,所以e的取值范围是0V e<1.（5）焦半径：椭圆上任一点P（x ,y）到焦点的连线段叫做焦半径.对于焦点在x轴上的椭圆，左焦半径00r - a + ex，右焦半径r = a - ex .10 20（6）准线方程：x二士一c（7）焦准距：焦点到准线的距离，用p表示，记作p二一。

椭圆的方程所有知识点总结

椭圆的方程所有知识点总结第一部分：椭圆的基本概念1.1 椭圆的定义椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点P的轨迹。

这两个定点称为焦点，常数2a称为椭圆的主轴长度。

椭圆还具有第三个重要的参数b，b称为次轴长度，椭圆的离心率e和焦点之间的距离c与主轴长度和次轴长度有关。

1.2 椭圆的几何性质椭圆有许多重要的几何性质，例如椭圆的中心、焦点、顶点、边界等。

椭圆还具有许多特殊的对称性质，以及与其他图形的关系，如与圆的关系和与双曲线的关系等。

第二部分：椭圆的方程2.1 椭圆的一般方程椭圆的一般方程是x²/a² + y²/b² = 1，其中a和b分别是椭圆的主轴长度和次轴长度。

这个方程描述了椭圆的形状和位置，可以用来解决各种与椭圆相关的数学问题。

2.2 标准方程和一般方程的相互转换标准方程是描述椭圆的一种特殊形式的方程，可以使用平移和旋转变换将一般方程转换为标准方程。

这样做可以简化椭圆的分析和计算过程，使问题的求解更加方便和直观。

2.3 椭圆的参数方程椭圆还可以通过参数方程进行描述，参数方程可以更加直观地描述椭圆的形状和位置，同时也方便进行相关计算和分析。

第三部分：椭圆的性质和应用3.1 椭圆的焦点和离心率椭圆的焦点是描述椭圆形状的一个重要参数，可以通过椭圆的方程确定焦点的位置。

离心率是描述椭圆形状的另一个重要参数，可以用来衡量椭圆形状的扁平程度。

3.2 椭圆的面积和周长椭圆的面积和周长是椭圆的重要特征，可以通过椭圆的参数方程和一般方程计算得到。

对于不同类型的椭圆，面积和周长的计算方法也有所不同。

3.3 椭圆的应用椭圆在许多领域中都有广泛的应用，如天文学、工程学、几何光学、计算机图形学等。

椭圆方程可以用来描述行星运动、天体轨迹、光学成像等现象，对于解决相关问题具有重要的作用。

第四部分：椭圆的相关证明和推导4.1 椭圆的焦点和离心率的证明椭圆的焦点和离心率是椭圆的重要性质，可以通过椭圆的方程和参数方程进行证明。

高一椭圆知识点公式大全

高一椭圆知识点公式大全椭圆是我们在高中数学中学习的一类二次曲线，具有许多重要的性质和应用。

在本文中，我们将详细介绍高一阶段学习椭圆所需掌握的知识点和相关公式，以便帮助同学们更好地理解和应用椭圆。

一、椭圆的定义与性质椭圆可以通过以下定义来理解：在平面上给定两点 F1 和 F2（称为焦点），和一个准确的正实数 2a（称为长轴的长度），满足任意一点 P 到 F1 的距离加上到 F2 的距离等于 2a（即 PF1 + PF2 = 2a），则点 P 的轨迹就是一个椭圆。

根据这个定义，我们可以得出椭圆的几个重要性质：1. 椭圆的离心率 e 满足 0 < e < 1。

2. 长轴的长度为 2a，短轴的长度为 2b，其中 a、b 为焦点到椭圆中心距离。

3. 椭圆的中心为焦点连线的中点。

4. 焦点到椭圆上一点的距离和焦半径（即焦点到椭圆的任意切线的距离）之积为常数。

二、椭圆的标准方程与参数方程椭圆的标准方程为 x^2/a^2 + y^2/b^2 = 1 或者 y^2/a^2 + x^2/b^2 = 1，其中 a 和 b 分别代表长轴和短轴的长度。

对于椭圆的参数方程，我们可以表示为：x = a*cosθy = b*sinθ其中θ 为参数，取值范围为0 ≤ θ ≤ 2π。

三、椭圆的焦点与直径椭圆的焦点是椭圆的重要特征之一。

根据椭圆的定义，焦点到椭圆中心的距离为 c。

我们可以通过以下公式来计算焦点的坐标：F1: (-c, 0)F2: (c, 0)椭圆的直径是指椭圆上两个相对的点，且经过椭圆的中心。

直径的长度为 2a。

四、椭圆的离心率与焦半径公式椭圆的离心率 e 可以通过以下公式计算：e = c/a其中 c 为焦点到椭圆中心的距离，a 为长轴的长度。

而焦半径 r 可以通过以下公式计算：r = a*(1 - e^2)其中 e 为离心率。

五、椭圆的周长与面积公式椭圆的周长和面积公式如下：周长 C = 4a*E(e)面积A = π*a*b其中 E(e) 为椭圆的第二类椭圆积分，具体计算过程较为复杂，可通过数学软件或查表获得具体值。

椭圆公式知识点总结

椭圆公式知识点总结一、椭圆的定义：椭圆可以通过焦点和准线来定义。

给定两个点F1和F2（焦点），定义椭圆E为平面上到这两个焦点的距离之和等于常数2a的点的集合。

即对于椭圆E上的任意一点P，有PF1 + PF2 = 2a。

该常数2a称为椭圆的长轴长度。

二、椭圆的标准方程：椭圆的标准方程为(x-h)²/a² + (y-k)²/b² = 1，其中(h,k)为椭圆的中心，a为长轴的长度的一半，b为短轴的长度的一半。

该方程中的参数可以通过椭圆的焦点和准线的位置确定。

三、半通径和离心率：对于椭圆E，定义半通径r为椭圆上任意一点P到椭圆中心O的距离，即OP=r。

另外，椭圆的离心率e定义为焦点到中心的距离除以长轴的长度，即e=√(a²-b²)/a。

离心率可以描述椭圆的瘦胖程度，当离心率接近于0时，椭圆趋近于圆形；当离心率接近于1时，椭圆变得更加扁平。

四、焦点和准线属性：椭圆的焦点F1和F2具有一些特殊的性质。

首先，椭圆上的任意一点到两个焦点的距离之和等于椭圆的长轴长度。

其次，椭圆上任意一点到准线的距离之和等于椭圆的长轴长度。

这些性质可以通过椭圆的几何构造得到。

五、参数方程和极坐标方程：椭圆也可以通过参数方程和极坐标方程进行描述。

参数方程为x = a*cos(t)，y = b*sin(t)，其中t为参数。

极坐标方程为r = a*(1-e*cos(θ))，其中θ为极角。

这些方程可以将椭圆与圆和其他曲线进行对比，从而更好地理解椭圆的性质。

六、旋转椭圆：椭圆可以通过旋转来获得不同的形态。

当椭圆沿着坐标轴旋转θ角度时，可以得到旋转椭圆。

旋转椭圆的标准方程可以通过坐标变换得到。

旋转椭圆的性质与普通椭圆类似，但是在计算和解析过程中需要考虑坐标轴的旋转。

七、椭圆的应用：椭圆具有广泛的应用。

在几何学中，椭圆可以描述行星的轨道和天体的运动。

在工程学和物理学中，椭圆可以用来描述光学系统的成像和传输特性。

椭圆与方程知识点总结

椭圆与方程知识点总结椭圆的定义首先，让我们来回顾一下椭圆的定义。

椭圆是平面上的一条闭合曲线，其定义为到两个定点的距离之和等于常数的点的轨迹。

这两个定点通常被称为焦点，常数称为椭圆的得以。

椭圆还有一个重要的性质，即椭圆上任意一点到两个焦点的距离之和是常数。

这个性质决定了椭圆的形状，使得椭圆在数学和工程中都具有着重要的应用价值。

椭圆的方程下面让我们来看一下椭圆的方程。

一般来说，椭圆的标准方程为：x^2/a^2 + y^2/b^2 = 1这里a和b分别是椭圆在x轴和y轴上的半轴长。

当椭圆的中心在原点时，椭圆的方程可以简化为：x^2/a^2 + y^2/b^2 = 1如果中心不在原点，可以通过平移变换将椭圆的方程转化为标准方程。

这样，我们就可以用标准方程来描述任意位置的椭圆。

椭圆的性质在椭圆的研究中，我们需要了解一些椭圆的重要性质。

下面是一些关于椭圆性质的总结：1. 椭圆的离心率离心率是描述椭圆形状的一个重要参数，它的定义为e=c/a，其中c是焦点到中心的距离，a是椭圆的半长轴。

离心率越大，椭圆的形状越扁平；离心率越小，椭圆的形状越圆。

2. 椭圆的焦点和直径椭圆上的两个焦点是椭圆的重要特征点，它们决定了椭圆的形状。

此外，椭圆上的任意两个焦点之间的距离等于椭圆的长轴长度。

这个性质可以帮助我们更好地理解椭圆的形状。

3. 椭圆的对称性椭圆具有很强的对称性，它在x轴和y轴上均有镜像对称性。

这个性质使得我们可以通过椭圆的一部分来推断出整个椭圆的形状。

4. 椭圆的参数方程椭圆还可以用参数方程来描述，它的参数方程为：x=a*cos(t)y=b*sin(t)这里，t是参数，a和b分别是椭圆在x轴和y轴上的半轴长。

参数方程的形式可以更好地描述椭圆的轨迹，对于一些特定的问题有着重要的应用价值。

椭圆的周长和面积最后，让我们来看一下椭圆的周长和面积。

椭圆的周长可以用椭圆的第一类完全椭圆积分来表示，它的计算公式为：C=4a*E(e)这里，a是椭圆的长轴长度，E(e)是椭圆的第一类完全椭圆积分，e是椭圆的离心率。

椭圆方程知识点总结

椭圆方程知识点总结椭圆方程是高等数学中的一个重要内容，它涵盖了多个学科领域，包括微积分、复变、偏微分方程等。

本文将从椭圆方程的定义、性质、求解方法等多个方面进行详细讲解和总结，以期让读者对该内容有更加深入的了解。

一、椭圆方程的定义椭圆方程是指形如$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$这样的方程，其中$a$和$b$都是正实数，且$a>b$。

这个方程描述了一个平面上的椭圆，其中$a$和$b$称为椭圆的半轴长度，椭圆的中心位于坐标原点。

在三维空间中，类似的方程也可以描述一个椭球。

椭球的半轴长度分别对应方程中$x$、$y$、$z$三个变量的系数，即$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$，其中$a>b>c$。

二、椭圆方程的性质1. 椭圆方程所描述的图形为平面上的椭圆。

2. 椭圆方程满足反对称性质，即交换$x$和$y$的值，方程的解不会发生变化。

3. 在坐标系中，椭圆具有x轴和y轴的对称性，即椭圆关于x 轴和y轴对称。

4. 直线$y=kx$与椭圆相交时，只有两个交点或没有交点。

若有两个交点，则交点的$x$坐标满足$a^2k^2+b^2=x^2$，解得$x=\pm\frac{ab}{\sqrt{a^2k^2+b^2}}$。

5. 椭圆方程在$(\pm a,0)$和$(0,\pm b)$四点处有拐点，即曲率半径为无穷大。

而在椭圆上任意一点的曲率半径为$\rho=\frac{ab}{\sqrt{(b^2x^2+a^2y^2)^3}}$。

6. 椭圆方程的面积为$S=\pi ab$，周长为$C=4aE(e)$，其中$E(e)$为第二类椭圆积分，$e=\sqrt{1-\frac{b^2}{a^2}}$为椭圆的离心率。

三、椭圆方程的求解方法1. 标准形式化简法将椭圆方程化为标准形式：$\frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1$。

椭圆标准方程及其性质知识点大全

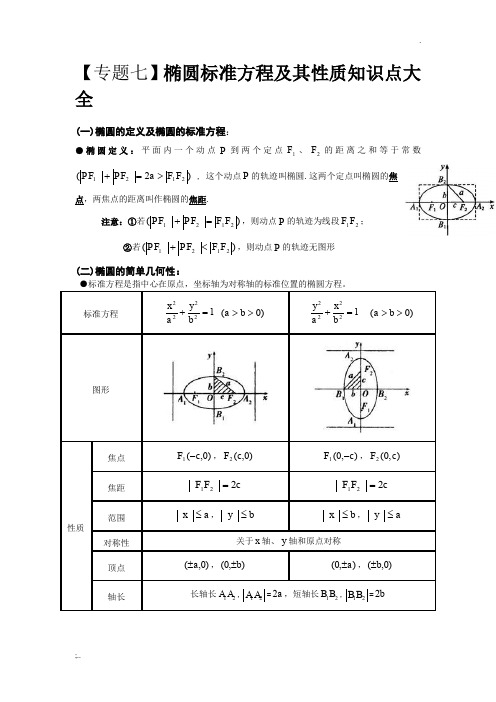
【专题七】椭圆标准方程及其性质知识点大全(一)椭圆的定义及椭圆的标准方程：●椭圆定义：平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ , 这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距. 注意：①若)(2121F F PF PF =+，则动点P 的轨迹为线段21F F ； ②若)(2121F F PF PF <+，则动点P 的轨迹无图形(二)椭圆的简单几何性：●标准方程是指中心在原点，坐标轴为对称轴的标准位置的椭圆方程。

标准方程12222=+b y a x )0(>>b a 12222=+b x a y )0(>>b a 图形性质焦点 )0,(1c F -，)0,(2c F ),0(1c F -，),0(2c F焦距 c F F 221= c F F 221= 范围a x ≤，b y ≤b x ≤，a y ≤对称性关于x 轴、y 轴和原点对称顶点 )0,(a ±，),0(b ± ),0(a ±，)0,(b ±轴长长轴长12A A ,12A A =a 2，短轴长12B B ,12B B =b 2离心率①(01)c e e a =<< ，②21()b e a=-③222b a c -=（离心率越大，椭圆越扁）【说明】：1.方程中的两个参数a 与b ，确定椭圆的形状和大小，是椭圆的定型条件，焦点F 1，F 2的位置，是椭圆的定位条件，它决定椭圆标准方程的类型，常数a ，b ，c 都大于零，其中a 最大且a 2=b 2+c 2.2. 方程22Ax By C +=表示椭圆的充要条件是：ABC ≠0，且A ，B ，C 同号，A≠B 。

A ＞B 时，焦点在y 轴上，A ＜B 时，焦点在x 轴上。

(三)焦点三角形的面积公式：122tan2PF F S b θ∆=如图：●椭圆标准方程为:12222=+by a x )0(>>b a ，椭圆焦点三角形：设P 为椭圆上任意一点，12,F F 为焦点且∠12F PF θ=，则△12F PF 为焦点三角形，其面积为122tan2PF F S b θ∆=。

高中数学椭圆及其标准方程知识点

椭圆知识点知识要点小结：知识点一：椭圆的定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距. 注意：若)(2121F F PF PF =+，则动点P 的轨迹为线段21F F ；若)(2121F F PF PF <+，则动点P 的轨迹无图形.知识点二：椭圆的标准方程1．当焦点在x 轴上时，椭圆的标准方程：12222=+by a x )0(>>b a ，其中222b a c -=2．当焦点在y 轴上时，椭圆的标准方程：12222=+bx a y )0(>>b a ，其中222b a c -=；注意：1．只有当椭圆的中心为坐标原点，对称轴为坐标轴建立直角坐标系时，才能得到椭圆的标准方程；2．在椭圆的两种标准方程中，都有)0(>>b a 和222b a c -=； 3．椭圆的焦点总在长轴上.当焦点在x 轴上时，椭圆的焦点坐标为)0,(c ，)0,(c -；当焦点在y 轴上时，椭圆的焦点坐标为),0(c ，),0(c - 知识点三：椭圆的简单几何性质椭圆：12222=+by a x )0(>>b a 的简单几何性质（1）对称性：对于椭圆标准方程12222=+b y a x )0(>>b a ：说明：把x 换成x -、或把y 换成y -、或把x 、y 同时换成x -、y -、原方程都不变，所以椭圆12222=+by a x 是以x 轴、y 轴为对称轴的轴对称图形，并且是以原点为对称中心的中心对称图形，这个对称中心称为椭圆的中心。

（2）范围：椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内，所以椭圆上点的坐标满足a x ≤，b y ≤。

（3）顶点：①椭圆的对称轴与椭圆的交点称为椭圆的顶点。