将军饮马问题(讲)

合集下载

八年级将军饮马问题例题讲解

八年级将军饮马问题例题讲解哎呀，今天咱们聊聊八年级的将军饮马问题，听名字就觉得特别有意思，对吧？咱们先来个开门见山，将军带着他的军队，经过一条河，得给马喝水。

这问题看似简单，但其实里面藏着不少小玄机，真的是个大考验，脑袋瓜得动一动。

想象一下，这将军带着一帮士兵，行军走到河边，嗨，口渴得不行，马儿们更是想喝水。

可是，问题来了，河边的水不深，能让马儿们喝到，但不让它们掉进水里。

将军一边心急如焚，一边得想办法。

怎么让这些马儿在喝水的时候不掉进河里呢？这时候就得用到一些小技巧了。

咱们可以想象一下，马儿们得排队，得一个一个地喝水。

将军心里想着，得控制好马儿的喝水速度，别让它们都挤在一起，这样容易出事。

也许能用一些方法，比如说把马儿们牵得远一些，慢慢地让它们喝，像是在参加比赛一样，嘿嘿，真是有意思的场景。

想想马儿们排成一队，乖乖的，一个个慢慢走过来喝水，真是可爱。

这时候就得算一算了，马儿们得喝多少水，每匹马喝水的速度又有多快。

嘿，可能是三两口就满足了，也可能是急着想喝个痛快，一口气喝个干净。

将军得根据情况来调整策略，真是够麻烦的。

不过，思来想去，最好的办法还是得让马儿们分批来，排着队，井然有序。

然后，咱们再来想象一下，如果马儿们不听话，乱跑，那可就麻烦了。

想象一下将军那个急得直挠头的样子，心里想着：这马儿也太不听话了！要不就得用点小办法，比如说放一块香饽饽在河边，吸引它们过来，嘿嘿，果然，马儿们就乖乖走过来喝水了。

就像小朋友看到喜欢的玩具一样，立马就冲过去了，真是太可爱了。

接着咱们来讨论一下，假设这条河不宽，马儿们很快就能喝到水，那将军得加快速度，不能让马儿们等太久。

想想那画面，马儿们都急得不行，口水都快流下来了，哈哈，真是个搞笑的场景。

将军这时候就得使出浑身解数，调整路线，确保马儿们能尽快喝水。

但是，事情总是没那么简单。

马儿喝水喝得急，可能还会打架，踩到脚，这可就不好了。

所以，将军得一边指挥，一边安抚，真是一场心力交瘁的战斗。

初中数学58种模型之12、“将军饮马”三种模型详解

当两淀点A 、R 在克罐/何侧时，在亞线』上携一点几便|阳一户创最大°将军饮马”三种模型"将军饮马"问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

晋两定点A.U 在点线F 异創时-在肖践f 上找一点Pt 使PA+PB 锻小*述接也交h 纱/于点P.点卩閒为所求作的点.肖两远点上B 在直雜I 同测时,在直刻上拥一点P,使PA+PB 最小'作庖U 芸于宜线F 的对称点V ■连楼AB'交直线于点P.点P 即为用求作的点"―二I \PA-P^\荊卩址大值洵丽。

连接班并延长交直戦』十点几点卩即为所求作的点。

当两定点仏k 在直找门司侧时，在直线』上找一点人使PA-PB\^扎作点B 关于直统』的对称点B'h 谨接恋’井延快交宜鏡于点巴点F 即为所求作的点。

皓论PAPI1的颯小°PA-PB 的盘小值为AB'□冋-卿的最大值为上的动点，则户创的圮大值是多少？A ■B ■\A\PA-PB\的 1当两定点限廿在宜线/同删时，在直线丿上找--点片使f4-砂|最小“ 叫连接馭作■-朋的垂直平分钱交直线f 于点P ，点卩即沟所求作的点-最小值为叽模型实例例1一如图"止厅形的面积是1氛是等边三博形，点E 在止方刑ABCI ）内“在对角纯蚯上有一点卩*则PD+FE 的艮小值为°^12.如圜已S11AABC 为辱展宜角匸角形…怔-氏=4”ZBCD 15".P 拘匚D热搜掃练I.如虱^AABC 中「ZACB-fJO 3，乃是就边的中点，II 是屈边b -动直+则LCIED 的最小悄是°])2・如图.点C的坐标为（3,y）,当△ABC的周长最短时，求丿的值。

3.如图.正方形ABCD中,AB-7,M是DCI：的一点，且DM-3,N是AC上的一动点.求|DN-MN|的嚴小值与战大值.△PCD 周氏最小为点P 在ZAOB 的内部，在0B 上找点D,在0A 上找点C,使得△PCD 周长最小。

将军饮马问题(讲)

类型一、基本模式类型二、轴对称变换的应用（将军饮马问题）2、如图所示，如果将军从马棚上的某一位置 Q ,然后立即返回校场Q ）,使得总路程 MP +PQ + QN 最短.OB 上的某一位置 Q .请为将军设计一条路线（即选择点P 和Q ）,使得总路程 MP +PQ 最短.3、将军要检阅一队士兵，要求（如图所示）：队伍长为a ,沿河0B 排开（从点P 到点Q ）;将军从马棚M 出发到达队头P,从P 至Q 检阅队伍后再赶到校场 N .请问：在什么位置列队（即将军饮马问题flM 出发，先赶到河 0A 上的某一位置 P ,再马上赶到河 0BN .请为将军重新设计一条路线（即选择点P 和【变式】如图所示，将军希望从马棚 M 出发, 先赶到河OA 上的某一位置P ,再马上赶到河AOA 边的距离之和最小P 到练习1、已知点A 在直线直线I 上运动时，点请说明理由.I 外，点P 为直线I 上的一个动点，探究是否存在一个定点B ，当点P 在 P 与A 、B 两点的距离总相等，如果存在，请作出定点 B ;若不存在，5已知/ MON 内有一点P , P 关于OM , ON 的对称点分别是百和均,分别交OM, ON于点A 、B,已知耳时=15,则^ PAB 的周长为（6. 已知/ AOB ,试在/ AOB 内确定一点 P ,如图，使 P 到OA 、OB 的距离相等，并且到 N 两点的距离也相等.7、已知/ MON = 40°, P 为/ MON 内一定点，OM 上有一点 A , ON 上有一点B ,当△ PAB 的周长取最小值时，A. 15B 7.5 C. 10D. 24求/ APB 的度数.8.如图，在四边形 ABCD 中，/ A = 90°, AD = 4,连接 BD , BD 丄 CD,/ ADB =/ C 若 P 是BC 边上一动点，则 DP 长的最小值为5、如图，已知/ AOB 内有一点P ,试分别在边 OA 和0B 上各找一点 E 、F ,使得△ PEF 的周长最小。

将军饮马(最完整讲义)

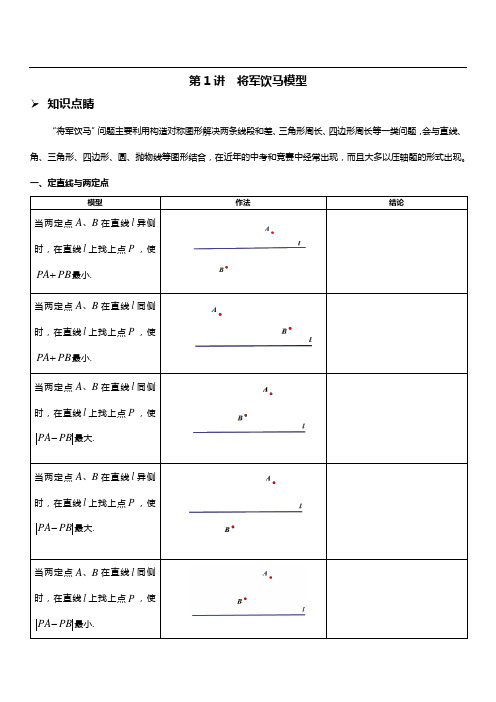
第1讲将军饮马模型➢知识点睛“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。

一、定直线与两定点模型作法结论A、在直线l异侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l异侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最小.PB二、角到定点模型作法结论点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得PCD ∆周长最小.点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得MN PN +最小.点Q P 、在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得四边形PMNQ 周长最小.点M 在AOB ∠的外部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点M 在AOB ∠的内部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点Q P 、分别在AOB ∠的边OB OA 、是，在OA 上找一点M ，在OB 上找一点N ,使得MQ MN PN ++最小.二、两定点一定长模型作法结论如图在直线l 上找上两点N M 、（M 在左），使NB MN AM ++最小,且d MN =.如图，21//l l ，21l l 、之间的距离为d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，且NB MN AM ++最小.如图，21//l l ，43//l l ,21l l 、之间的距离为1d ，43//l l 之间的距离为2d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，在43l l 、上分别找Q P 、两点，使3l PQ ⊥且QB PQ NP MN AM ++++最小.如图，在⊙O 上找一点N ，在直线l 找一点M ,使得MN AM +最小.➢ 精讲精练例1：如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值．P OBAMN例2：如图，正方形ABCD 的边长是4，M 在DC 上，且DM =1， N 是AC 边上的一动点，则△DMN 周长的最小值．例3：如图，在Rt △ABO 中，∠OBA =90°，A （4,4），点C 在边AB 上，且AC :CB =1:3，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为( )A ．(2,2)B ．5(2，5)2C ．8(3，8)3D ．(3,3)第3题图第4题图第5题图例4：如图，在△ABC 中，AC =BC ，∠ACB =90°，点D 在BC 上，BD =3，DC =1，点P 是AB 上的动点，则PC +PD 的最小值为( ) A ．4B ．5C ．6D ．7例5：如图，在等边△ABC 中，AB =6， N 为AB 上一点且BN =2AN ， BC 的高线AD 交BC 于点D ，M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________． PDCBAA BCDMNNMDCBA例6：如图，在Rt △ABD 中，AB =6，∠BAD =30°，∠D =90°，N 为AB 上一点且BN =2AN ， M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值．例7：如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为( ) A ．3 B ．4 C ． D ．第7题图第8题图第9题图例8：如图，在锐角三角形ABC 中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是( ) A B ．2 C ．D ．4例9：如图，在菱形ABCD 中，AC =BD =6，E 是BC 的中点，P 、M 分别是AC 、AB 上的动点，连接PE 、PM ，则PE +PM 的最小值是( ) A ．6B ．C ．D ．4.5NMDBA E AFCDBNM DCBAEPDCBAM例10：如图，矩形ABOC 的顶点A 的坐标为（-4,5），D 是OB 的中点，E 是OC 上的一点，当△ADE 的周长最小时，点E 的坐标是( ) A ．4(0,)3B ．5(0,)3C ．(0,2)D ．10(0,)3第10题图第11题图第12题图例11：如图，在矩形ABCD 中，AB =6，AD =3，动点P 满足13PAB ABCD S S ∆=矩形，则点P 到A 、B 两点距离之和PA +PB 的最小值为( ) A ．B ．C ．D 例12：如图，矩形ABCD 中，AB =10，BC =5，点E 、F 、G 、H 分别在矩形ABCD 各边上，且AE =CG ，BF =DH ，则四边形EFGH 周长的最小值为( )A ．B ．C ．D ．例13：如图，∠AOB =60°，点P 是∠AOB 内的定点且OP M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是( )A B C ．6D ．3第13题图第14题图 CBH FGEDCB AA BMOPN例14：如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N （3,0）是OB 上的一定点，点M 是ON 的中点，∠AOB =30°，要使PM +PN 最小，则点P 的坐标为．例15：如图，已知正比例函数y =kx （k >0）的图像与x 轴相交所成的锐角为70°，定点A 的坐标为（0，4），P 为y 轴上的一个动点，M 、N 为函数y =kx （k >0）的图像上的两个动点，则AM +MP +PN 的最小值为___________．第15题图例16：如图，在平面直角坐标系中，矩形ABCD 的顶点B 在原点，点A 、C 在坐标轴上，点D 的坐标为（6，4），E 为CD 的中点，点P 、Q 为BC 边上两个动点，且PQ =2，要使四边形APQE 的周长最小，则点P 的坐示应为______________．例17：如图，矩形ABCD 中，AD =2，AB =4，AC 为对角线，E 、F 分别为边AB 、CD 上的动点，且EF ⊥AC 于点M ，连接AF 、CE ，求AF +CE 的最小值．AB CD EFMx例18：如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，求PD+PE 的最小值。

将军饮马(最完整讲义)

第1讲将军饮马模型➢知识点睛一、“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题, 会与直线、角、三角形、四边形、圆、抛物线等图形结合, 在近年的中考和竞赛中经常出现, 而且大多以压轴题的形式出现。

二、定直线与两定点模型作法结论当两定点在直线异侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最大.当两定点在直线异侧时, 在直线上找上点, 使最大.当两定点在直线同侧时, 在直线上找上点, 使最小.二、角到定点模型作法结论点在的内部, 在上找一点, 在上找一点,使得周长最小.点在的内部, 在上找一点, 在上找一点,使得最小.点在的内部, 在上找一点, 在上找一点,使得四边形周长最小.点在的外部, 在射线上找一点, 使与点到射线的距离和最小.点在的内部, 在射线上找一点, 使与点到射线的距离和最小.点分别在的边是, 在上找一点, 在上找一点,使得最小.三、两定点一定长模型作法结论如图在直线上找上两点（在左）, 使最小,且.如图, , 之间的距离为, 在上分别找两点, 使, 且最小.如图, , ,之间的距离为, 之间的距离为, 在上分别找两点, 使, 在上分别找两点, 使且最小.如图, 在⊙上找一点, 在直线找一点,使得最小.➢精讲精练例1: 如图, 点P是∠AOB内任意一点, ∠AOB=30°, OP=8, 点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值.例2: 如图, 正方形ABCD 的边长是4, M 在DC 上, 且DM=1, N 是AC 边上的一动点, 则△DMN 周长的最小值.A ．例3: 如图, 在Rt △ABO 中, ∠OBA=90°, A （4,4）, 点C 在边AB 上, 且AC:CB=1:3, 点D 为OB 的中点, 点P 为边OA 上的动点, 当点P 在OA 上移动时, 使四边形PDBC 周长最小的点P 的坐标为 B. ,C ．,D ．第3题图第4题图第5题图例4: 如图, 在△ABC 中, AC=BC, ∠ACB=90°, 点D 在BC 上, BD=3, DC=1, 点P 是AB 上的动点, 则PC+PD 的最小值为 A. 4 B. 5 C. 6 D. 7例5：如图, 在等边△ABC 中, AB=6, N 为AB 上一点且BN=2AN, BC 的高线AD 交BC 于点D, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值是___________．A BCDMN例6: 如图, 在Rt △ABD 中, AB=6, ∠BAD=30°, ∠D=90°, N 为AB 上一点且BN=2AN, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值.例7: 如图, 在Rt △ABC 中, ∠ACB=90°, AC=6. AB=12, AD 平分∠CAB, 点F 是AC 的中点, 点E 是AD 上的动点, 则CE+EF 的最小值为 A. 3 B. 4 C.D.第7题图第8题图第9题图A ．例8: 如图, 在锐角三角形ABC 中, BC=4, ∠ABC=60°, BD 平分∠ABC, 交AC 于点D, M 、N 分别是BD, BC 上的动点, 则CM+MN 的最小值是B. 2C.D. 4例9: 如图, 在菱形ABCD 中, AC=, BD=6, E 是BC 的中点, P 、M 分别是AC.AB 上的动点, 连接PE 、PM, 则PE+PM 的最小值是A. 6B.C.D. 4.5E AFCDBNM DCBAEPDCBAMA ．例10: 如图, 矩形ABOC 的顶点A 的坐标为（-4,5）, D 是OB 的中点, E 是OC 上的一点, 当△ADE 的周长最小时, 点E 的坐标是B. C. D.第10题图第11题图第12题图例11: 如图, 在矩形ABCD 中, AB=6, AD=3, 动点P 满足, 则点P 到A.B 两点距离之和PA+PB 的最小值为A. B. C. D.例12: 如图, 矩形ABCD 中, AB=10, BC=5, 点E 、F 、G 、H 分别在矩形ABCD 各边上, 且AE=CG, BF=DH, 则四边形EFGH 周长的最小值为A. B. C. D.例13: 如图, ∠AOB=60°, 点P 是∠AOB 内的定点且OP=, 若点M 、N 分别是射线OA.OB 上异于点O 的动点, 则△PMN 周长的最小值是A. B. C. 6 D. 3第13题图第14题图CBH FGEDCB AABMOPN例14: 如图, ∠AOB 的边OB 与x 轴正半轴重合, 点P 是OA 上的一动点, 点N （3,0）是OB 上的一定点, 点M 是ON 的中点, ∠AOB=30°, 要使PM+PN 最小, 则点P 的坐标为 .例15：如图, 已知正比例函数y=kx （k>0）的图像与x 轴相交所成的锐角为70°, 定点A 的坐标为（0, 4）, P 为y 轴上的一个动点, M 、N 为函数y=kx （k>0）的图像上的两个动点, 则AM+MP+PN 的最小值为___________．第15题图例16: 如图, 在平面直角坐标系中, 矩形ABCD 的顶点B 在原点, 点A.C 在坐标轴上, 点D 的坐标为（6, 4）, E 为CD 的中点, 点P 、Q 为BC 边上两个动点, 且PQ=2, 要使四边形APQE 的周长最小, 则点P 的坐示应为______________.例17：如图, 矩形ABCD 中, AD=2, AB=4, AC 为对角线, E 、F 分别为边AB 、CD 上的动点, 且EF ⊥AC 于点M,连接AF 、CE, 求AF+CE 的最小值．x例18: 如图, 正方形ABCD的面积是12, △ABE是等边三角形, 点E在正方形ABCD内, 在对角线AC上有一点P, 求PD+PE的最小值。

第11讲 “将军饮马”问题探究(学生版)

知识导航
①作定点关于动点所在直线的对称点，构造轴对称图形
②等腰三角形、角分线模型是天然的轴对称模型
经典例题
1
三角板、刻度尺作图，保留作图痕迹，不写作法．
2
如图，正方形3
如图，正方形4
在
1
三角板、刻度尺作图，保留作图痕迹，不写作法：2
如图，在
3
如图，在
知识导航
经典例题1
如图，直线2
如图，
知识导航
经典例题
1
如图，在一组平行线2
如图，直线
3
如图，在正方形
设汽车行驶到公路上点的位置时，距离村庄最近，行驶到点的位置时，距离村庄上分别画出、的位置；
行驶时，在公路的哪一段上距离、两村都越来越近？在哪一段
巩固2
如图，、为的边、上的两个定点，在上求一点，使的周长最短．
巩固3
如图，，角内有点，在角的两边有两点、(均不同于点)，求作、，使得的周长的最小．
巩固4
如图，在中，若在，上各取一点，，使的值最小，试在图中画出，的位置．
巩固5
如图（1），、两单位分别位于一条封闭街道两旁（直线、是街道两边沿），现准备合作修建一座过街人行天桥．天桥应建在何处才能使由经过天桥走到的路程最短？在图（2）中作
如图，四边形中，，，在、上分别找一点、，使周长最小，求此时的度数以及的度数．。

将军饮马课件ppt

05
将军饮马问题的扩展和挑战
变种问题
01
02
03
04
障碍物问题
在路径上设置障碍物，求最短路径时需要避开障碍物。
多点折返问题
在路径上设置多个折返点，求最短路径时需要多次折返。
限制条件问题
在求最短路径时加入限制条件，如步数限制、时间限制等。
动态变化问题
路径长度会随时间或其他因素变化，需要求最短路径时考虑
这些变化。
计算复杂度
最坏情况下的时间复杂度
在最坏情况下，算法的时间复杂度可能较高，需要优化算法以降低时间复杂度。
空间复杂度
并行计算
为了提高算法的效率，可以考虑使用并行计算来加速计算过程。
算法的空间复杂度也需要考虑，以评估算法的内存消耗。
实际应用中的限制和优化
数据精度
在实际应用中，需要考虑数据精度对算法的影响，以避免误差累积导致结果不准确。
在车辆调度方面，将军饮马问题同样适用。通过优化车辆的出发时间和行驶路线，物流公司可以最大化利用车辆资源，提高运输效率。
计算机算法
图论算法
将军饮马问题作为图论中的经典问题，可以应用于计算机算法领域。通过解决将军饮马问题，可以开发出更高效的图论算法，用于解决其他相关问题。
最短路径算法
最短路径算法是计算机算法中的重要组成部分。将军饮马问题可以作为最短路径算法的参考模型，帮助开发人员找到图中两点之间的最短路径。
03
04
几何法是利用几何知识解决将军饮马问题的方法。
它通过将问题转化为几何图形，利用几何定理和性质来找到
最短路径。
几何法适பைடு நூலகம்于具有明显几何特征的问题，如两点之间的最短距离、三角形中的最短路径等

专题07 最值模型之将军饮马精讲练(11大模型)(解析版)

专题07最值模型之将军饮马精讲练（11大模型）学校:___________姓名：___________班级：___________考号：___________模型背景【模型来历】早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．【考点】两点之间线段最短，垂线段最短；三角形两边三边关系；轴对称；平行四边形--平移；【解题思路】学会化归，移花接木，化折为直【核心思想】共线与垂线段最短。

模型精讲一、两动一定型（2种模型）：两定点到直线上一动点的距离和最小。

例1-1：如图1-1在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB最小.【证明】图1-2。

PA+PB的最小值即为线段AB的长度理由：在l上任取异于点P的一点P´，连接AP´、BP´，在△ABP’中，AP´+BP´>AB，即AP´+BP´>AP+BP ∴P为直线AB与直线l的交点时，PA+PB最小.图1-2lPABP'lAB图1-1反思：解决本题很简单，但却点明了将军饮马的解题思路。

【变式】例1-2 如图1-3，如图，定点A 和定点B 在定直线l 的同侧要求：在直线l 上找一点P ，使得PA+PB 值最小。

作法：图1-41.作A 关于直线CD 对称点A’。

2.连A’B 。

3.交点P 就是要求点。

连线长A’B 就是PA+PB 最小值。

【证明】：图1-5在l 上任取异于点P 的一点P´，连接AP´、BP´，在△ABP’中，AP´+BP´>AB ，即AP´+BP´>AP+BP ∴P 为直线AB 与直线l 的交点时，PA+PB 最小.二、造桥选址，移花接木。

华东师大版八年级数学下册“将军饮马模型”专题讲义及解析

华东师大版八年级数学下册“将军饮马模型”专题讲义及解析华东师大版八年级数学下册“将军饮马模型”专题讲义及解析一、背景知识：据传说，古罗马时代有一位名叫XXX的学者，他精通数学和物理。

有一天，一位罗马将军前来请教他一个难题：每天他从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题被称为“将军饮马”问题，据说XXX很快解决了它，从此这个问题流传至今。

二、将军饮马问题常见模型1.两定一动型：两个定点到一个动点的距离和最小例1：在一条定直线l上找一个动点P，使动点P到两个定点A和B的距离之和最小，即PA+PB最小。

作法：连接AB，与直线l的交点Q即为所求点，当动点P跑到点Q处时，PA+PB最小，且最小值等于AB。

原理：两点之间线段最短。

证明：连接AB，与直线l的交点Q，P为直线l上任意一点，在三角形PAB中，由三边关系可知：AP+PB≧AB（当且仅当PQ重合时取等）。

例2：在一条定直线l上找一个动点P，使动点P到两个定点A和B的距离之和最小，即PA+PB的和最小。

关键：找对称点。

作法：作定点B关于定直线l的对称点C，连接AC，与直线l的交点Q即为所求点，当动点P跑到点Q处时，PA+PB和最小，且最小值等于AC。

原理：两点之间，线段最短。

证明：连接AC，与直线l的交点Q，P为直线l上任意一点，在三角形PAC中，由三边关系可知：AP+PC≧AC（当且仅当PQ重合时取等）。

2.两动一定型例3：在∠XXX的内部有一点A，在OM上找一点B，在ON上找一点C，使得△BAC周长最短。

作法：作点A关于OM的对称点A’，作点A关于ON的对称点A’’，连接A’ A’’，与OM交于点B，与ON交于点C，连接AB，AC，△XXX即为所求。

原理：两点之间，线段最短。

例4：在∠XXX的内部有点A和点B，在OM上找一点C，在ON上找一点D，使得四边形ABCD周长最短。

作法：首先，我们作点A关于OM的对称点A'，作点B关于ON的对称点B'，然后连接A'B'，交OM于点C，交ON于点D，最后连接AC和BD，四边形ABCD即为所求。

将军饮马专题ppt课件

第8题图
返回
1 综合训练
1. 如图，在矩形ABCD中，AB＝2，AD＝1，点E为AB的中点，M、N是CD上的两动点，且MN＝1，则EM＋EN的最小值为____。
1 综合训练
2. 如图，在正方形ABCD中，E，F分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP＋EP最小值的是 ____。
之
间
，
线
段
最
短
2
用模型战试题
每一个试题都是模型，每一种模型都有方法
综合训练
针对训练1
2
1. 如图，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AB 边上一点，且AE＝2，则线段EF＋CF的最小值为( B ) A. 3 B. 2 3 C. 2 D. 2
第1题图
返回
2 针对训练2
两动一定型 2
例7
在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C，使得△BAC周长
最短．
在 OM上找一点C，在 ON上找一点D，使得四边形ABCD周长最短．
例9
在∠MON的内部有一点A，在OM上找一点B，在ON上找一点C，使得AB ＋BC最短．
【传说】
早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．
将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．
从此以后，这个被称为“将军饮马”的问题便流传至今．
A. 3 B. 2 3 C. 3 1 D. 3 2

将军饮马讲解

对“连”口诀最短路径问题
最短路径知识点三 ③双定双动：对“连”口诀:先对称后平移（先平移后对称），连接出最短方法一：先对称后平移
技巧：作对称（同侧变异侧）---对称点平移定长线段（“一定两动”化“两定一动”）---连接两定点--动点反向平移定长线段---连接所得点.
对“连”口诀最短路径问题
最短路径知识点三 ③双定双动：对“连”口诀:先对称后平移（先平移后对称），连接出最短方法二：先平移后对称
∴BC+AC = B’C+AC = B’A．
∴BC ’ +AC ’ = B’C ’ +AC ’
在△AB ’ C’中，AB ’ <C < BC ’ +AC ’ ，即AC+BC最小．
知识点
对“连”口诀横批：对勾模型
对
如图，在I上找一点P,使PA+PB最小
连
称
接
一
出
定
最
点
短
对“连”口诀最短路径问题
最短路径必考高频三大类型 ①双定单动：对“连”口诀:对称1动点，连接出最短 ②单定双动：对“连”口诀:双对称此定点，连接出最短 ③双定双动：对“连”口诀:先对称后平移（先平移后对称），连接出最短
对“连”口诀最短路径问题
最短路径必考知识点一 ①双定单动：对“连”口诀:对称1动点，连接出最短
定点双对称
连接出最短
关键点：动点所在的直线为对称轴
对“连”口诀最短路径问题
最短路径知识点三 ③双定双动：对“连”口诀:先对称后平移（先平移后对称），连接出最短
问题：本题拓展为在直线l上找两个动点P、Q（PQ两动点间距离为定值），使得AP+PQ+BQ 的距离之和最短，又该如何处理呢？（“两动一定型”）

初中数学-将军饮马问题-公开课课件课件全文

抽象：如图，在直线MN上找一点P, 使得PA+PB最小？
A
M
B
P
N
思考:在前面研究几何问题的过程中，你是否遇到过与此相类似求线段的距离最短或者线段和最小的问题？请举例说明.
垂线段最短 m
思考:在前面研究几何问题的过程中，你是否遇到过与此相类似求线段的距离最短或者线段和最小的问题的问题？请举例说明.
使AC+CD+BD+AB最短。
问题特征：两线两定两动
解决方法：依据两点之间，线段最短,通过两次轴对称, 将三条折线段化为一条直线段.
8/25/ቤተ መጻሕፍቲ ባይዱ024
联系中考
(2019中考) 如图，∠AOB=30°,角内有一点P，PO=10cm，两边上各有一点Q、R（均不同于点O），则 △PQR的周长的最小值是＿＿
Q A
P
O
B
R
如图所示，直线MN表示一条铁路，铁路两旁各有一点A和B，表示两个工厂．要在铁路上建一货站，使
´
它到两厂距离之和最短，这个货站应建在何处？
P´ P
方法:在解决选择位置、求最短距离等问题时，通常转化为“两点之间线段最短”
问题:如图,另一位将军也骑马从城堡A到城堡B，途中马也要到小溪边饮水一次.问这位将军怎样走路程最短？
M
P
连接AP, 则PA´=PA，
A´
则PA+ PB= PA ´+ PB= A´B
在直线MN上任意取一点P´ 连接AP´,BP´,A´P´,
则AP´=A´P´，则AP´+BP´= A´P´+ BP´
△BA´P´中，A ´B < BP´+A´P´，

将军饮马两定两动的思路和解法

将军饮马两定两动的思路和解法《将军饮马》这道题目，咱们首先得搞清楚其中的两定两动的思路和解法。

别急，我们一步一步来，理清楚这其中的奥妙。

1. 问题的背景1.1 题目介绍“将军饮马”这个名字一听就带着点古色古香的味道。

其实它讲的是一个关于将军、马匹和水源的问题。

题目一般是这样：将军带着一群马到河边饮水，河边有两条水源，一个快一个慢，河水的流速也各不相同。

任务是根据这些条件，找出马在不同的水源处饮水时所需要的时间。

1.2 关键概念在解题之前，我们先理清几个重要的概念。

所谓“两定两动”，就是指这道题目有两个定量（固定的量）和两个变量（可以变化的量）。

这其中包括水源流速、饮水量，以及马匹的饮水速度和时间。

2. 解题思路2.1 确定两个固定量首先，我们要搞明白题目中的两个固定量。

通常来说，一个是水源的流速，比如说水流得有多快；另一个是马匹的饮水速度，也就是每匹马每分钟能喝多少水。

这两个量就像是题目里的“固定资产”，用来帮助我们计算时间。

2.2 处理两个变量接下来，我们要关注两个变量：一个是马匹在不同水源处的饮水时间，另一个是水源的流量变化。

这就像是题目中的“活资产”，会因为不同的情况而有所不同。

我们需要根据水源的流量和饮水的时间来计算。

3. 解题步骤3.1 设定方程好啦，现在我们来动手解决问题。

首先要做的是设定方程。

假设马匹的饮水速度是(v)（每分钟多少水），水源流速是 (r)（每分钟多少水），那我们就能用这些数据来设定我们的方程式。

比如说，如果一个水源的流速是 (r_1)，另一个水源的流速是 (r_2)，马匹在第一个水源的饮水时间是 (t_1)，在第二个水源的饮水时间是 (t_2)，那么我们就可以列出类似这样的方程：[ v times t_1 + r_1 times t_1 = text{总水量} ]。

[ v times t_2 + r_2 times t_2 = text{总水量} ]。

3.2 求解方程接着，我们要解这些方程。

将军饮马问题讲义

将军饮马问题之阳早格格创做唐往诗人李颀的诗《古从军止》启头二句道:"黑日登山视烽火，薄暮饮马傍接河."诗中隐含着一个有趣的数教问题.如图所示，诗中将军正在瞅视烽火之后从山足下的A面出收，走到河边饮马后再到B面宿营.请问何如走才搞使总的路途最短?那个问题早正在古罗马时代便有了，传道亚历山大乡有一位粗通数教战物理的教者，名喊海伦.一天，一位罗马将军博程去考察他，背他请教一个百思不得其解的问题.将军每天从军营A出收，先到河边饮马，而后再去河岸共侧的B天启会，该当何如走才搞使路途最短?今后，那个被称为"将军饮马"的问题广大流传.将军饮马问题=轴对于称问题=最短距离问题（轴对于称是工具，最短距离是题眼）.所谓轴对于称是工具，即那类问题最时常使用的搞法便是做轴对于称.而最短距离是题眼，也便表示着归类那类的题手段缘由.比圆题目时常会出现线段a+b 那样的条件大概者问题.一往出现不妨赶快偶像到将军问题，而后利用轴对于称解题.一．六大模型1.如图，曲线l 战l 的同侧二面A、B，正在曲线l 上供做一面P，使PA+PB 最小.2.如图，曲线l 战l 的共侧二面A、B，正在曲线l 上供做一面P，使PA+PB 最小.3.如图，面P 是∠MON 内的一面，分别正在OM，ON 上做面A，B.使△PAB 的周少最小.4.如图，面P，Q 为∠MON 内的二面，分别正在OM，ON 上做面A，B.使四边形PAQB 的周少最小.5.如图，面A 是∠MON 中的一面，正在射线ON 上做面P，使PA 取面P 到射线OM 的距离之战最小6. .如图，面A 是∠MON 内的一面，正在射线ON 上做面P，使PA 取面P 到射线OM 的距离之战最小罕睹问题最先明黑几个观念，动面、定面、对于称面.动面普遍便是题目中的所供面，即那个大概的面.定面即为题目中牢固的面.对于称的面，做图所得的面，需要连线的面.1. 怎么对于称，做谁的对于称？.简朴道所有题目需要做对于称的面，皆是题手段定面.大概者道惟有定面才不妨去做对于称的.（不决定的面做对于称式不意思的）那么做谁的对于称面?最先要粗确闭于对于称的对于象肯定是一条线，而不是一个面.那么是哪一条线？普遍而止皆是动面天圆曲线.2. 对于称完以去战谁对接？一句话：战其余一个定面贯串.千万于不克不迭战一个动面贯串.粗确一个观念：定面的对于称面也是一个定面.比圆模型二战模型三.3. 所供面怎么决定？最先一定要明黑，所供面末尾反应正在图上一定是个接面.本量便是咱们所绘曲线战已知曲线的接面.底下咱们去瞅瞅将军饮马取二次函数分离的问题：1.如图，扔物线y=ax2+bx+c通过A（1，0）、B（4，0）、C（0，3）三面．（1）供扔物线的剖析式；（2）如图，正在扔物线的对于称轴上是可存留面P，使得四边形PAOC的周少最小？若存留，供出四边形PAOC周少的最小值；若不存留，请证明缘由．【分解】（1）设接面式为y=a（x﹣1）（x﹣4），而后把C面坐标代进供出a=，于是得到扔物线剖析式为y=x2﹣x+3；（2）先决定扔物线的对于称轴为曲线x=，连结BC接曲线x=于面P，如图，利用对于称性得到PA=PB，所以PA+PC=PC+PB=BC，根据二面之间线段最短得到PC+PA最短，于是可推断此时四边形PAOC的周少最小，而后估计出BC=5，再估计OC+OA+BC即可．【解问】解：（1）设扔物线剖析式为y=a（x﹣1）（x﹣4），把C（0，3）代进得a•（﹣1）•（﹣4）=3，解得a=，所以扔物线剖析式为y=（x﹣1）（x﹣4），即y=x2﹣x+3；（2）存留．果为A（1，0）、B（4，0），所以扔物线的对于称轴为曲线x=，连结BC接曲线x=于面P，如图，则PA=PB，PA+PC=PC+PB=BC，此时PC+PA最短，所以此时四边形PAOC的周少最小，果为BC==5，所以四边形PAOC周少的最小值为3+1+5=9．【面评】原题考查了待定系数法供二次函数的剖析式：正在利用待定系数法供二次函数闭系式时，要根据题目给定的条件，采用妥当的要领设出闭系式，进而代进数值供解．普遍天，当已知扔物线上三面时，常采用普遍式，用待定系数法列三元一次圆程组去供解；当已知扔物线的顶面大概对于称轴时，常设其剖析式为顶面式去供解；当已知扔物线取x轴有二个接面时，可采用设其剖析式为接面式去供解．也考查了最短路径问题．2．（2015•上乡区一模）设扔物线y=（x+1）（x﹣2）取x轴接于A、C二面（面A正在面C的左边），取y轴接于面B．（1）供A、B、C三面的坐标；（2）已知面D正在坐标仄里内，△ABD是顶角为120°的等腰三角形，供面D的坐标；（3）若面P、Q位于扔物线的对于称轴上，且PQ=，供四边形ABQP周少的最小值．【考面】二次函数概括题．【分解】（1）令x=0，供出取y轴的坐标；令y=0，供出取x 轴的坐标；（2）分三种情况计划：①当AB为底时，若面D正在AB上圆；若面D正在AB下圆；②当AB为腰时，A为顶面时，③当AB为腰时，A为顶面时；小心解问即可．（3）当AP+BQ最小时，四边形ABQP的周少最小，根据轴对于称最短路径问题解问．【解问】解：（1）当x=0时，y=﹣；当y=0时，x=﹣1大概x=2；则A（﹣1，0），B（0，﹣），C（2，0）；（2）如图，Rt△ABO中，OA=1，OB=，∴AB=2，∠ABO=30°，∠BAO=60°，∴△ABD是顶角为120°的等腰三角形．①当AB为底时，若面D正在AB上圆，由∠ABO=∠BAD=30°，AB=2，得D1（0，﹣），若面D正在AB下圆，由∠BAD=∠DBA=30°，AB=2，得D2（﹣1，﹣），②当AB为腰时，A为顶面时，∵∠DAB=120°，∠OAB=60°，AD=AB=2，∴面D正在y轴大概x轴上，若D正在y轴上，得D3（0，），若D正在x轴上，得D4（﹣3，0）；③当AB为腰时，A为顶面时，若面D正在第三象限，∵∠DBO=150°，BD=2，得D5（﹣1，﹣2）；若面D正在第四象限时，∵DB∥x轴，BD=2，得D6（2，﹣），∴切合央供的面D的坐标为（0，﹣），（﹣1，﹣），（0，），（﹣3，0），（﹣1，﹣2），（2，﹣）；（3）当AP+BQ最小时，四边形ABQP的周少最小，把面B进取仄移个单位后得到B1（0，﹣），∵BB1∥PQ，且BB1=PQ，∴四边形BB1PQ是仄止四边形，∴BQ=B1P，∴AP+BQ=AP+B1P，要正在曲线x=上找一面P，使得AP+B1P最小，做面B1闭于曲线x=的对于称面，得B2（1，﹣），则AB2便是AP+BQ的最小值，AB2==，AB=2，PQ=，∴四边形ABQP的周少最小值是+2．【面评】原题考查了二次函数概括题，波及二次函数取x轴的接面、取y轴的接面、等腰三角形的本量、勾股定理等真量，存留性问题的出现使得易度删大．。

[精选]将军饮马问题(讲)资料

类型一、基本模式类型二、轴对称变换的应用（将军饮马问题） 2、如图所示，如果将军从马棚M 出发，先赶到河 0A 上的某一位置 P ,再马上赶到河 0B 上的某一位置Q,然后立即返回校场 N.请为将军重新设计一条路线（即选择点P 和Q ）, 使得总路程M 卉PQ+ QN 最短.0B 上的某一位置 Q.请为将军设计一条路线（即选择点P 和Q ）,使得总路程 M 卉PQ 最短.3、将军要检阅一队士兵，要求（如图所示）：队伍长为a ,沿河0B 排开（从点P 到点Q ）;将军从马棚M 出发到达队头P ,从P 至Q 检阅队伍后再赶到校场 N.请问：在什么位置列队（即选择点P 和Q ）,可以使得将军走的总路程皿卉PQ^ QN 最短？将军饮马问题【变式】如图所示，将军希望从马棚4.如图，点边的距离之和最小，再马上赶到河P 至 U 0A5已知/ MON内有一点P, P关于OM ON的对称点分别是召和R, 隅分别交OM, ON于点A B,已知=15,则厶PAB的周长为（A. 15 B 7.5 C. 10 D. 246. 已知/ AOB试在/ AOB内确定一点P,如图，使P到OA OB的距离相等，并且到M N 两点的距离也相等•7、已知/ MON= 40 ° , P为/ MON内一定点，OM上有一点A, ON上有一点B,当△ PAB的周长取最小值时，求/ APB的度数.8. 如图，在四边形ABCD中，/ A= 90°, AD= 4,连接BD, BD丄CD / ADB=Z C.若P是BC边上一动点，贝U DP长的最小值为_______.练习1、已知点A在直线I夕卜，点P为直线I上的一个动点，探究是否存在一个定点B，当点P在直线I上运动时，点P与A、B两点的距离总相等，如果存在，请作出定点 B ;若不存在，请说明理由.A■2、如图，在公路a 的同旁有两个仓库 A 、B ，现需要建一货物中转站，要求到 A 、B 两仓库的距离和最短，这个中转站 M 应建在公路旁的哪个位置比较合理？A.■BA■----------------------------------------------------- a3、已知：A 、B 两点在直线I 的同侧，在I 上求作一点 M ，使得|AM -BM |最小.4、如图，正方形 ABCD 中，AB =8, M 是DC 上的一点，且 DM =2 , N 是AC 上的一动点，求DN MN 的最小值与最大值.A B,在坐标轴上找两点 C 、D,使得四边形ABCD 勺周长最小。

最短路径(将军饮马)问题(知识梳理与考点分类讲解)(人教版)(教师版) 24-25学年八年级数学上册

专题13.10最短路径（将军饮马）问题（知识梳理与考点分类讲解）第一部分【知识点归纳】【模型一：两定交点型】如图1，直线l和l的异侧两点A.B，在直线l上求作一点P，使PA+PB 最小；图1【模型二：两定一动型】如图2，直线l和l的同侧两点A.B，在直线l上求作一点P，使PA+PB 最小（同侧转化为异侧）；图2【模型三：一定两动型】如图3，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△PAB的周长最小。

图3【模型四：两定两动型】如图4，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。

使四边形PAQB的周长最小。

图4【模型五：一定两动（垂线段最短）型】如图5，点A是∠MON外的一点，在射线ON上作点P，使PA与点P到射线OM的距离之和最小。

图5【模型六：一定两动，找（作）对称点转化型】如图6，点A是∠MON内的一点，在射线ON 上作点P，使PA与点P到射线OM的距离之和最小。

图6【考点1】两定一动型；【考点2】一定两动（两点之间线段最短）型；【考点3】一定两动（垂线段最短）型；【考点4】两定两动型；【考点5】一定两动（等线段）转化型；.第二部分【题型展示与方法点拨】【考点1】两定一动型；【例1】（23-24八年级上·全国·课后作业）如图，在ABC ∆中，3,4AB AC ==，EF 垂直平分BC ，交AC 于点D ，则ABP 周长的最小值是（）A ．12B ．6C ．7D ．8【答案】C 【分析】本题主要考查了，轴对称﹣最短路线问题的应用，解此题的关键是找出P 的位置．凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，根据题意知点B 关于直线EF 的对称点为点C ，故当点P 与点D 重合时，AP BP +的值最小，即可得到ABP 周长最小．解：∵EF 垂直平分BC ，∴点B ，C 关于EF 对称．∴当点P 和点D 重合时，AP BP +的值最小．此时AP BP AC +=，∵3,4AB AC ==，ABP ∴ 周长的最小值是347AP BP AB AB AC ++=+=+=，故选：C ．【变式】（23-24八年级上·广东广州·期中）如图，在ABC V 中，1216AB AC ==，，20BC =．将ABC V 沿射线BM 折叠，使点A 与BC 边上的点D 重合，E 为射线BM 上的一个动点，则CDE 周长的最小值．【答案】24【详解】设BM 与AC 的交点为点F ，连接AE ，DF 先根据折叠的性质可得12BD AB ==，DF AF =，DE AE =，BDF BAF ∠=∠，再根据两点之间线段最短可得当点E 与点F 重合时，CDE 周长最小，进而求解即可．解：如图，设BM 与AC 的交点为点F ，连接AE ，DF ，由折叠的性质得：12BD AB ==，DF AF =，DE AE =，BDF BAF ∠=∠，20128CD BC BD ∴=-=-=，CDE ∴ 周长8CD DE CE AE CE =++=++，要使CDE 周长最小，只需AE CE +最小，由两点之间线段最短可知，当点E 与点F 重合时，最小值为AC ，∴CDE 周长为：681624AC +=+=．故答案为：24．【点拨】本题考查了折叠的性质等知识点，熟练掌握折叠的性质是解题关键．【考点2】一定两动（两点之间线段最短）型；【例2】（23-24八年级上·湖北省直辖县级单位·期末）如图，45MON ∠=︒，P 为MON ∠内一点，A 为OM 上一点，B 为ON 上一点，当PAB 的周长取最小值时，APB ∠的度数为（）A ．45︒B ．90︒C ．100︒D ．135︒【答案】B 【分析】本题主要考查了最短路线问题、四边形的内角和定理、轴对称的性质等知识点，掌握两点之间线段最短的知识画出图形是解题的关键．如图：作P 点关于OM ON 、的对称点A B ''、，连接A B ''，此时PAB 的周长最小为A B ''，求出A B ''即可．解：如图：作P 点关于OM ON 、的对称点A B ''、，然后连接A B ''，∵点A '与点P 关于直线OM 对称，点B '与点P 关于ON 对称，∴A P OM B P ON A A AP B B BP ''''⊥⊥==，，，，∴A APA B BPB ''''∠=∠∠=∠，，∵A P OM B P ON ''⊥⊥，，∴180MON A PB ''∠+∠=︒，∴18045135A PB ''∠=︒-︒=︒，在A B P ''△中，由三角形的内角和定理可知：18013545A B ''∠+∠=︒-︒=︒，∴45A PA BPB ''∠+∠=︒，∴1354590APB ∠=︒-︒=︒．故选：B ．【变式】（23-24八年级上·江苏无锡·期中）如图，45AOB ∠=︒，点M N 、分别在射线OA OB 、上，5MN =，15OMN S = ，点P 是直线MN 上的一个动点，点P 关于OA 的对称点为1P ，点P 关于OB 的对称点为2P ，连接1OP 、2OP 、12PP ，当点P 在直线MN 上运动时，则12OPP 面积的最小值是．【考点3】一定两动型（垂线段最短）；【例3】（22-23八年级上·湖北武汉·期末）如图，在ABC V 中，3AB =，4BC =，5AC =，AB BC ⊥，点P 、Q 分别是边BC 、AC 上的动点，则AP PQ +的最小值等于（）A ．4B ．245C ．5D ．275【答案】B 【分析】作A 过于BC 的对称点A '，过点A '作A Q AC '⊥，交AC 于点Q ，交BC 于点P ，根据对称可得：AP PQ A P PQ A Q ''+=+≥，得到当,,A P Q '三点共线时，AP PQ +最小，再根据垂线段最短，得到A Q AC '⊥时，A Q '最小，进行求解即可．解：作A 过于BC 的对称点A '，过点A '作A Q AC '⊥，交AC 于点Q ，交BC 于点P ，【变式】（23-24七年级下·陕西西安·阶段练习）如图，在Rt ABC △中，90ACB ∠=︒，3AC =，4BC =，5AB =，AD 是ABC V 的角平分线，若P Q 、分别是AD 和AC 边上的动点，则PC PQ +的最小值是．AD 是BAC ∠的平分线，1QAD Q AD∴∠=∠在AQD 与1AQ D 中【考点4】两定两动型；【例4】如图，已知24AOB ∠=︒，OP 平分AOB ∠，1OP =，C 在OA 上，D 在OB 上，E 在OP 上．当CP CD DE ++取最小值时，此时PCD ∠的度数为（）A ．36︒B ．48︒C ．60︒D ．72︒【答案】D 【分析】作点P 关于OA 的对称点P'，作点E 关于OB 的对称点'E ，连接'OP 、'PP 、'OE 、'EE 、''P E ，则由轴对称知识可知=''CP CD DE CP CD DE ++++，所以依据垂线段最短知：当''P C D E 、、、在一条直线上，且'''P E OE ⊥时，CP CD DE ++取最小值，根据直角三角形的两锐角互余及三角形外角的性质可以'P C PC =，'E D ED =，'1OP OP ==，=''CP CD DE CP CD DE ++++，'P OE ∠''P C D E 、、、在一条直线上，且''P E ''=9048=42OP E ∠︒-︒︒，'='''=7842CP P OP P OP E ∠∠-∠︒-︒=【答案】44βα-=︒【分析】本题考查轴对称—最短问题、三角形的内角和定理．三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题．OQM OQM NQP '∴∠=∠=∠，OPQ ∠∴1(180)2PQN AOB α∠=︒-=∠+∠44βα∴-=︒，故答案为：44βα-=︒．【考点5】一定两动（等线段）转化型；【例5】（20-21八年级上·湖北鄂州·期中）如图，AD 为等腰△ABC 的高，其中∠ACB =50°，AC =BC ，E ，F 分别为线段AD ，AC 上的动点，且AE =CF ，当BF ＋CE 取最小值时，∠AFB 的度数为（）A ．75°B ．90°C ．95°D ．105°【答案】C 【分析】先构造△CFH 全等于△AEC ，得到△BCH 是等腰直角三角形且FH=CE ，当FH+BF 最小时，即是BF+CE 最小时，此时求出∠AFB 的度数即可．解：如图，作CH ⊥BC ，且CH=BC ，连接HB ，交AC 于F ，此时△BCH 是等腰直角三角形且FH+BF 最小，∵AC=BC ，∴CH=AC ，∵∠HCB=90°，AD ⊥BC ，∴AD//CH ，∵∠ACB=50°，∴∠ACH=∠CAE=40°，∴△CFH ≌△AEC ，∴FH=CE ，∴FH+BF=CE+BF 最小，此时∠AFB=∠ACB+∠HBC=50°+45°=95°．故选：C ．【点拨】本题考查全等三角形的性质和判定、等腰三角形的性质、最短路径问题，关键是作出辅助线，有一定难度．【变式】（23-24七年级下·四川宜宾·期末）在ABC V 中，80CAB ∠=︒，2AB =，3AC =，点E 是边AB 的中点，CAB ∠的角平分线交BC 于点D ．作直线AD ，在直线AD 上有一点P ，连结PC 、PE ，则PC PE -的最大值是．∵CAB ∠的角平分线交∴FAP ∠∠=∵AP AP =，∴APF APE ≌∴PF PE =，第三部分【中考链接与拓展延伸】1、直通中考【例1】（2020·湖北·中考真题）如图，D 是等边三角形ABC 外一点．若8,6BD CD ==，连接AD ，则AD 的最大值与最小值的差为．【答案】12【分析】以CD 为边向外作等边三角形CDE ，连接BE ，可证得△ECB ≌△DCA 从而得到BE=AD ，再根据三角形的三边关系即可得出结论．解：如图1，以CD 为边向外作等边三角形CDE ，连接BE ，∵CE=CD ，CB=CA ，∠ECD=∠BCA=60°，∴∠ECB=∠DCA ，∴△ECB ≌△DCA （SAS ），∴BE=AD ，∵DE=CD=6，BD=8，∴8-6<BE<8+6，∴2<BE<14，∴2<AD<14．∴则AD 的最大值与最小值的差为12．故答案为：12【点拨】本题考查三角形全等与三角形的三边关系，解题关键在于添加辅助线构建全等三角形把AD 转化为BE 从而求解，是一道较好的中考题．【例2】（2020·新疆·中考真题）如图，在ABC V 中，90,60,4A B AB ∠=∠=︒=︒，若D 是BC 边上的动点，则2AD DC +的最小值为．在Rt DFC △中，30DCF ∠=︒，12DF DC ∴=，122()2AD DC AD DC +=+2()AD DF =+，∴当A ，D ，F 在同一直线上，即此时，60B ADB ∠=∠=︒，2、拓展延伸【例1】（23-24八年级上·江苏镇江·阶段练习）如图，AC 、BD 在AB 的同侧，点M 为线段AB 中点，2AC =，8BD =，8AB =，若120CMD ∠=︒，则CD 的最大值为（）A ．18B ．16C ．14D ．12【答案】C 【分析】本题考查等边三角形的判定和性质，两点之间线段最短，解题的关键是学会添加常用辅助线，学会利用两点之间线段最短解决最值问题．如图，作点A 关于CM 的对称点A '，点B 关于DM 的对称点B '，证明'' A MB 为等边三角形，即可解决问题．解：如图，作点A 关于CM 的对称点A '，点B 关于DM 的对称点B '，∵120CMD ∠=︒，∴60∠+∠=︒AMC DMB ，∴60''∠+∠=︒CMA DMB ，∴60''∠=︒A MB ，∵MA MB MA MB ''===，∴'' A MB 为等边三角形∵14CD CA A B B D CA AM BD ''''<++=++=，∴CD 的最大值为14，故选：C ．【例2】（22-23八年级上·湖北武汉·期末）如图，锐角ABC V 中，302A BC ∠=︒=，，ABC V 的面积是6，D 、E 、F 分别是三边上的动点，则DEF 周长的最小值是（）A ．3B ．4C ．6D ．7∴AM AE AN ==，MF =∵BAC BAD DAC ∠=∠+∠∴MAN MAB BAD ∠=∠+∠∴(2MAN BAE EAC ∠=∠+∠。

将军饮马问题(讲)电子教案

将军饮马问题(讲)将军饮马问题类型一、基本模式类型二、轴对称变换的应用（将军饮马问题）2、如图所示，如果将军从马棚M出发，先赶到河OA上的某一位置P，再马上赶到河OB上的某一位置Q，然后立即返回校场N．请为将军重新设计一条路线(即选择点P和Q)，使得总路程MP＋PQ＋QN最短．【变式】如图所示，将军希望从马棚M出发，先赶到河OA上的某一位置P，再马上赶到河OB上的某一位置Q．请为将军设计一条路线(即选择点P和Q)，使得总路程MP＋PQ最短．3、将军要检阅一队士兵，要求(如图所示)：队伍长为a，沿河OB排开(从点P到点Q)；将军从马棚M出发到达队头P，从P至Q检阅队伍后再赶到校场N．请问：在什么位置列队(即选择点P和Q)，可以使得将军走的总路程MP＋PQ＋QN最短?4. 如图，点M在锐角∠AOB内部，在OB边上求作一点P，使点P到点M的距离与点P到OA边的距离之和最小5已知∠MON内有一点P，P关于OM，ON的对称点分别是和，分别交OM, ON于点A、B，已知＝15，则△PAB 的周长为（）A. 15 B 7.5 C. 10 D. 246. 已知∠AOB，试在∠AOB内确定一点P，如图，使P到OA、OB的距离相等，并且到M、N 两点的距离也相等.7、已知∠MON＝40°，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，求∠APB的度数.8. 如图，在四边形ABCD中，∠A＝90°，AD＝4，连接BD，BD⊥CD，∠ADB＝∠C.若P是BC边上一动点，则DP长的最小值为______.练习1、已知点A在直线l外，点P为直线l上的一个动点，探究是否存在一个定点B，当点P 在直线l上运动时，点P与A、B两点的距离总相等，如果存在，请作出定点B；若不存在，请说明理由．2、如图，在公路a 的同旁有两个仓库A 、B ，现需要建一货物中转站，要求到A 、B 两仓库的距离和最短，这个中转站M 应建在公路旁的哪个位置比较合理？aBA3、已知：A 、B 两点在直线l 的同侧，在l 上求作一点M ，使得||AM BM -最小．4、如图，正方形ABCD 中，8AB =，M 是DC 上的一点，且2DM =，N 是AC 上的一动点，求DN MN +的最小值与最大值．NMD CB A5、如图，已知∠AOB 内有一点P ，试分别在边OA 和OB 上各找一点E 、F ，使得△PEF 的周长最小。

将军饮马问题(解析版)

将军饮马问题模型的概述：唐朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题：将军在观望烽火之后从山脚下的A点出发，走到河边让战马饮水后再到B 点宿营。

问如何行走才能使总的路程最短。

模型一(两点在河的异侧)：将军在观望烽火之后从山脚下的A点出发，走到河边让战马饮水后再到B 点宿营，将在何处渡河使行走距离最短并求最短距离。

方法：如右图，连接AB，与线段L交于点M,在M处渡河距离最短，最短距离为线段AB的长。

模型二(两点在河的同侧)：将军在观望烽火之后从山脚下的A点出发，需先走到河边让战马饮水后再到B点宿营，将在何处渡河使行走距离最短并求最短距离。

方法：如右图，作点B关于直线L的对称点B'，连接AB',与直线L的交点即为所求的渡河点，最短距离为线段AB'的长。

模型三：如图，将军同部队行驶至P处，准备在此驻扎，但有哨兵发现前方为两河AB、BC的交汇处，为防止敌军在对岸埋伏需派侦察兵到河边观察，再返回P处向将军汇报情况，问侦察兵在AB、BC何处侦查才能最快完成任务并求最短距离。

数学描述：如图在直线AB、BC上分别找点M、N，使得∆PMN周长最小。

方法：如右图，分别作点P关于直线AB、BC的对称点P'、P''，连接P'P''，与两直线的交点即为所求点M、N，最短距离为线段P'P''的长。

模型四如图，深夜为防止敌军在对岸埋伏，将军又派一队侦察兵到河边观察，并叮嘱观察之后先去存粮位置点Q处查看再返回P处向将军汇报情况，问侦察在AB、BC何处侦查才能最快完成任务并求最短距离。

数学描述：如图在直线AB、BC上分别找点M、N，使得四边形PQNM周长最小。

方法：如右图，分别作点P、点Q关于直线AB、BC的对称点P'、Q'，连接P'Q'，与两直线的交点即为所求点M、N，最短距离为线段(PQ+P'Q')的长。