电路课件 电路15 电路方程的矩阵形式
合集下载
电路课件 电路15 电路方程的矩阵形式

第十五章 电路方程的矩阵形式 25
用矩阵B表示的KCL矩阵形式-
1
l个独立回路电流可用一个l阶列向量 表示,即
il=[ il1 il2 … ill ]T
由于矩阵B的每一列,也就是矩阵BT 的每一行,表示每一对应支路与回路 的关联情况,所以按矩阵的乘法规则 可知支路电流i:
i=BTil
(15-6)
如所选独立回路组对应一个树的单连支回路组,
称基本回路矩阵,用Bf表示。
写Bf时,注意其行列次序如下:把l条连支依次 排列在对应于Bf的第1至第l列,然后再排列树支; 取每一单连支回路的序号为对应连支所在列的
序号,且以该连支的方向为对应的回路的绕行
方向,Bf中出现一个l阶的单位子矩阵,即
Bf=[1l|Bt]
并称降阶关联矩阵(今后主要用降阶关联矩阵, 往往略去“降阶”)。 例:把式(15-1)中第4行划去,得
矩阵A的某些列将只具有一个+1或一个-1,每 一个这样的列必对应于与划去结点相关联的一 条支路。被划去的行对应结点可当作参考结点。
2019/9/18
15-2 关联矩阵、回路矩阵、割集矩阵 -2
电路
第十五章 电路方程的矩阵形式
8 学时
§15-1 §15-2 §15-4 §15-5
第十五章 电路方程的矩阵形式
主要内容: 本章主要介绍电路方程的矩阵形式。 在图的基础上介绍几个重要矩阵:关联矩阵、
回路矩阵和割集矩阵,并导出用这些矩阵表 示的KCL、KVL方程。 导出回路电流(网孔电流)方程、结点电压方 程的矩阵形式。
压可用与该支路关联的两个结点的结
点电压(参考结点的结点电压为零)表
示,正是结点电压法的基本思想。
可认为该式是用矩阵A表示的KVL矩 阵形式。
用矩阵B表示的KCL矩阵形式-
1
l个独立回路电流可用一个l阶列向量 表示,即
il=[ il1 il2 … ill ]T
由于矩阵B的每一列,也就是矩阵BT 的每一行,表示每一对应支路与回路 的关联情况,所以按矩阵的乘法规则 可知支路电流i:
i=BTil
(15-6)
如所选独立回路组对应一个树的单连支回路组,
称基本回路矩阵,用Bf表示。
写Bf时,注意其行列次序如下:把l条连支依次 排列在对应于Bf的第1至第l列,然后再排列树支; 取每一单连支回路的序号为对应连支所在列的
序号,且以该连支的方向为对应的回路的绕行
方向,Bf中出现一个l阶的单位子矩阵,即
Bf=[1l|Bt]
并称降阶关联矩阵(今后主要用降阶关联矩阵, 往往略去“降阶”)。 例:把式(15-1)中第4行划去,得
矩阵A的某些列将只具有一个+1或一个-1,每 一个这样的列必对应于与划去结点相关联的一 条支路。被划去的行对应结点可当作参考结点。
2019/9/18
15-2 关联矩阵、回路矩阵、割集矩阵 -2
电路
第十五章 电路方程的矩阵形式
8 学时
§15-1 §15-2 §15-4 §15-5
第十五章 电路方程的矩阵形式
主要内容: 本章主要介绍电路方程的矩阵形式。 在图的基础上介绍几个重要矩阵:关联矩阵、
回路矩阵和割集矩阵,并导出用这些矩阵表 示的KCL、KVL方程。 导出回路电流(网孔电流)方程、结点电压方 程的矩阵形式。
压可用与该支路关联的两个结点的结
点电压(参考结点的结点电压为零)表
示,正是结点电压法的基本思想。
可认为该式是用矩阵A表示的KVL矩 阵形式。
电路课件-电路方程的矩阵形式

•
I
•
I
1 b
•
I
•
I
s1 sb
U• s1
•
U sb
bb階對角陣
•
•
•
•
U Z I Z Is Us
返回 上頁 下頁
②電路中電感之間有耦合
.
+. I1
返回 上頁 下頁
注意
③對應一組線性獨立的KCL方程的割集稱為獨 立割集 ,基本割集是獨立割集,但獨立割集 不一定是單樹支割集。
返回 上頁 下頁
15-2 關聯矩陣、回路矩陣、割集矩陣
1. 圖的矩陣表示
圖的矩陣表示是指用矩陣描述圖的拓撲性質,即 KCL和KVL的矩陣形式。有三種矩陣形式:
結點 回路 割集
.
I sk 0
Zk (Yk)=0
.
U sk 0 Zk (Yk)=0
返回 上頁 下頁
2.支路阻抗矩陣形式
①電路中電感之間無耦合
•
•
•
•
Uk
(I k
I sk )Zk
U sk
..
如有b條支路,則有
I k I ek Zk (Yk) -
.
U sk
+
•
•
•
•
.
U I I U 1 ( 1 s1)Z1 s1
ajk =0 支路 k 與結點 j 無關。
返回 上頁 下頁
例2-1 寫圖示電路的圖的關聯矩陣A 。 ②
支 解 結 123456
3
4
1 -1 -1 1 0 0 0 ①
6
Aa= 2 0 0 -1 -1 0 1
2
5
③
3 1 0 01 1 0 4 0 1 0 0 -1 -1
电路课件_15第十五章电路方程的矩阵形式

Bu
1 0 0
0 1 0
1 1 0
0 0 1
-1 0 -1
1 1 1
u1 u3 u5 u6 u2 u3 u6 u4 u5 u6 0 0 0
u1 u 2 u3 u4 u5 u6
4
8
Q3
5
树支
4
8
1
5
1
Q4
6
连支
6
7 7
2
3
3
2
Q3:1, 4,5
Q4:5,6,7,8
§ 15 - 2 关联矩阵、回路矩阵、割集矩阵
一:关联矩阵Aa
n个结点b条支路的有向图
一条支路连接于两个结点,称该支路与这两个结点相关联。
支路1 .... 支路b
Aa=
结点1 ....... 结点n
1 2 Aa= 3
-1 -1 +1 0 0 0 0 -1 -1 0 +1 0 0 +1 +1 4 0 +1 0 0 -1
0 -1 46
1 2
3
4 5 6
0 +1
1 Aa= 2 3
-1 -1 +1 0 0 0 0 -1 -1 0 +1 0 0 +1 +1 4 0 +1 0 0 -1
( n1 )b
2
i3
1
2
3
i4
6
Q1
3
i2
i6
4
5
3
2
i5
4
1
1
第15章电路方程的矩阵形式

(2)保留Q 中的一条支路,其于都移去, G还是连通的。
②
2
1
2
①5
③
1
5
①
43
4
④
6 6
Q1: { 2 , 5 , 4 , 6 }
②
③
3
④
②
②
1
2
①5
③
1
2
①5
③
43 ④6
43 ④6
Q2: { 2 , 3 , 6 }
Q3: { 1 , 5 , 4}
单树支割集(基本割集)
②
②
1
2
①5
③
43 ④6
Q1: { 2 , 3 , 6 }
设 I I1 I2 Ib T
IS IS1 IS 2 ISb T
15-3 结点电压方程的矩阵形式
Ik
Iek
U Sk
Yk ISk
U k
U U1 U 2 U b T
U S U S1 U S 2 U Sb T
②
基本回路
15.1 割集
基本割集
1
2
①5
③
43 ④6
{1,2,3,4} {1,4,5} {1,2,6}
{1,5,3,6} {2,3,6} {3,4,5}
2. 由某个连支bl确定的单连支回路应包含那些树支,每个
这种树支所构成的基本割集中含有bl 。
②
基本回路
基本割集
1
2
①5
③
43 ④6
{1,2,3,4} {1,4,5} {1,2,6}
u5
节点电压
un1
un
电路PPT课件第15章 电路方程的矩阵形式

ut
用树支电压表示连支电压
小结:
A
B
KCL Ai=0
KVL ATun=u
Ql
B
T t
BTil=i
it BTt il
Bu=0 ul = - Btut
Q
Qi=0 it Qlil
QTut=u ul QTl ut
§15-4 回路电流方程的矩阵形式
一. 复合支路
由RLC、电压源、电流源组成 参考方向如图所示 不存在无伴电流源
每一支路,连接在两个节 点上,必然要背离一个节 点,指向另一节点。
设④为参考节点
称A为降阶关联矩阵 (n-1)b , 表征独立节点与支路的关联性质
②
1
2
节支 1 2 3 4 5 6
①
5
③
1 1 0 0 -1 0 1
4
3
A= 2 -1 -1 0 0 1 0 3 0 1 1 0 0 -1
④
6
设:
支路电流
由于KCL适用于任何一个闭合面,对于每一个割集来说, 组成割集的所有支路的电流应满足KCL。
对于一个连通图,可有多个割集,可以列出与割集数相等 的KCL方程。这些方程彼此之间并不独立。
借助于“树”来确定独立割 集。
单树支割集(基本割集)
连支集合不能构成割集。即使所有连支都去掉,剩下 的树支仍然构成连通图,与割集的定义矛盾。
1 支路j在回路i中且与回路i关联,方向一致
bij= -1 支路j在回路i中且与回路i关联,方向相反 0 支路j 不在回路i中
4
5
2 33
选 4、5、6为树,连支顺序为1、2、3。
回支 4 5 6 1 2 3 1 1 -1 0 1 0 0
电路方程的矩阵形式简课件.ppt
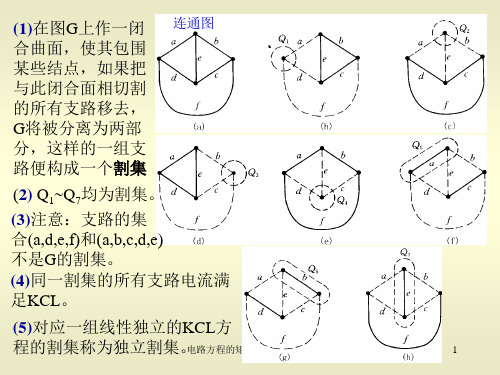
注意:被划去的行所 对应的结点可以作为 参考结点
电路方程的矩阵形式(简课件
5
用一个b阶列向量 ii1 i2 ibT表示b条支路电流
用矩阵A左乘电流列向量i, 得到一个(n-1) 阶列向量
显然, A i =0 —— (15-2)
是用A矩阵表示的KCL方程
电路方程的矩阵形式(简课件
6
例如,对于右图,有:
例如,对于右图,有: 的KVL的矩阵形式
u3
1 0 0
ut1
u5
ቤተ መጻሕፍቲ ባይዱ
0
u
uu16
QTf ut
0 1
u2
1
1 1 1 0
0011uuuttt132
ut2
ut1
ut3 ut2
ut3
ut1 ut3
u4
0 1 1
ut2 ut3
即:支路电压可以用树支电路电方压程(的割矩集阵形电式压(简)表课件示
i1 i2 i4 i6
0 0
0
i6
显然,Qi =0, 是用电Q路矩方程阵的表矩阵示形式的(K简课C件L方程
16
若(n-1)个树支电压用 (n-1)阶列向量表示
u t u t1 u t2 u t(n 1 )T
ut1
ut3
则每一条支路电压与树支电压的
关联情况为:
ut2
u QTf ut —(15-10) 即:为矩阵Qf表示
且它们的方向一致
1
bjk=-1表示支路k与回路j关联, 且它们的方向相反
bjk=0表示支路k与回路电j路无方程关的矩阵形式(简课件
9
如果所选独立回路对应一个“树”的单连支回路组(基本回路 组),则此回路矩阵就称为基本回路矩阵 Bf 。
电路第五版课件第十五章电路方程的矩阵形式

a
b
e
Q1 a
b e
Q2
a
b
e
d
c
d
c
d
c
f
f
f
a
b Q3 a
b
e
e
d
c
f
d
c
Q4
f
结论:汇集于 同一结点的支 路都是G的一个 割集。
特点:①全移,G一分为二 ②少移一条,G连通。
3
例:判断下图中各支路集合是否是图G的割集?
Q5
a
b
e
d
c
f
(b, d, e, f )是
Q6
a
b
e
d
c
f
(a, b, c, d ) 也是
Q7
a
b
e
d
c
f
(a, e, f ) 也是
特点:①全移,G一分为二 ②少移一条,G连通。
4
例:判断下图中各支路集合是否是图G的割集?
Q8 a d
b e
c
f
Q9 a d
b e
c
f
少移去e,G仍为两部分, 全移,G被分为三部分,
(a, d, e, f )不是G的割集。 (a, b, c, d ,e )不是G的割集
100
010
BT il=
0 1
0 1
1 0
1 0 1
il1
i1
il1 il2 il3
il2
il3 il1+il2
il1il3
i3 i4 i2 i5
i5 , i6 ]T ②
① i3 3 Ⅱ i2
2
4 i6Ⅲ
i4
电路第15章电路方程的矩阵形式

元件参数的识别
利用矩阵形式的电路方程,可以对电路中的元件参数进行 识别和估计,例如通过测量节点电压和支路电流来计算元 件的电阻、电容、电感等参数。
系统分析和控制
矩阵形式的电路方程可以用于系统分析和控制,例如稳定 性分析、频率响应分析、最优控制等。
02 电路元件的矩阵表示
电阻元件的矩阵表示
总结词
电阻元件在矩阵形式中表示为对角线矩阵,对角线上的元素为电阻值。
矩阵元素的选取
矩阵中的元素根据电路元件的类 型和连接方式进行选取,通常包 括电阻、电容、电感等元件的参 数。
矩阵形式的优点
矩阵形式能够简化电路的分析和 计算过程,提高计算效率和精度, 适用于大规模复杂电路的分析。
矩阵形式的电路方程
节点电压方程
在电路中选取节点电压作为未知 量,根据基尔霍夫定律建立节点 电压方程,并将其表示为矩阵形
线性
电路的输出信号与输入信号成正比,满足叠加定 理。
3
时不变
电路的参数不随时间变化。
线性时不变电路的矩阵形式
矩阵形式的电路方程
将电路中的元件参数和连接关系表示为矩阵形式,以便于分析和 计算。
状态变量
描述电路中电压和电流变化的变量,通常用向量表示。
状态方程
描述电路中状态变量之间关系的方程,通常表示为矩阵形式。
矩阵形式的电路方程广泛应用于电子工程、通信工程、控制工程等多个领域,尤其在处理大规模复杂电 路时表现出显著的优势。
电路方程的矩阵形式的展望
01
矩阵形式的进一步研究
随着电子技术和计算机技术的不断发展,对电路方程的矩 阵形式的研究将更加深入。未来研究将更加注重矩阵形式 的数学基础、算法优化和数值稳定性等方面。
02 03
利用矩阵形式的电路方程,可以对电路中的元件参数进行 识别和估计,例如通过测量节点电压和支路电流来计算元 件的电阻、电容、电感等参数。
系统分析和控制
矩阵形式的电路方程可以用于系统分析和控制,例如稳定 性分析、频率响应分析、最优控制等。
02 电路元件的矩阵表示
电阻元件的矩阵表示
总结词
电阻元件在矩阵形式中表示为对角线矩阵,对角线上的元素为电阻值。
矩阵元素的选取
矩阵中的元素根据电路元件的类 型和连接方式进行选取,通常包 括电阻、电容、电感等元件的参 数。
矩阵形式的优点
矩阵形式能够简化电路的分析和 计算过程,提高计算效率和精度, 适用于大规模复杂电路的分析。
矩阵形式的电路方程
节点电压方程
在电路中选取节点电压作为未知 量,根据基尔霍夫定律建立节点 电压方程,并将其表示为矩阵形
线性
电路的输出信号与输入信号成正比,满足叠加定 理。
3
时不变
电路的参数不随时间变化。
线性时不变电路的矩阵形式
矩阵形式的电路方程
将电路中的元件参数和连接关系表示为矩阵形式,以便于分析和 计算。
状态变量
描述电路中电压和电流变化的变量,通常用向量表示。
状态方程
描述电路中状态变量之间关系的方程,通常表示为矩阵形式。
矩阵形式的电路方程广泛应用于电子工程、通信工程、控制工程等多个领域,尤其在处理大规模复杂电 路时表现出显著的优势。
电路方程的矩阵形式的展望
01
矩阵形式的进一步研究
随着电子技术和计算机技术的不断发展,对电路方程的矩 阵形式的研究将更加深入。未来研究将更加注重矩阵形式 的数学基础、算法优化和数值稳定性等方面。
02 03
15电路方程的矩阵形式省名师优质课赛课获奖课件市赛课一等奖课件

3 0 1 -1 0 0 1
Bt
Bl
Ql BtT
矩阵形式旳KVL: [Q ]Tut=u
矩阵形式旳KVL: [Q ]Tut=u
4
5
1 0 0
u4
u4
3
2
6
1
0
0
1
1
1 0 1 1
0
1
0
1
u4 u5 u6
u4
u5 u6 u4 u5
u5
u6
u5
u6
4 ①
2
② 5
3
③
6 ④1
N个节点b条支路旳图用nb旳矩阵描述
节支 1 2 3 4 5 6 1 -1 -1 0 1 0 0 Aa= 2 0 0 1 -1 -1 0 3 1 0 0 0 11 4 0 1 -1 0 0 -1
ajk=1 ajk ajk= -1
ajk =0
支路k与节点j 关联,方向背离节点。 支路k与节点j 关联,方向指向节点 支路k与节点j无 关
QTut=u ul QlT ut
§ 15.3 节点法
一.节点方程旳矩阵式
设原则支路为:
电路分析根据: KCL [A][ i ]=0
.
IK
Zk
•
I ek
•
U SK
KVL [u]=[A]T[un] 元件特征
•
Ik 第k条支路电流
•
Uk 第k条支路电压
•
Usk 独立电压源
•
Isk 独立电流源
.
ISk
.
[Y]=[Z]-1
L2 M
0
M
Y
L1
Y3
j (L1L2 M 2 )
电路ch15电路方程矩阵形式

aij aij= -1
有向支路 j与节点 i关联且指向 i 节点
aij =0
j 支路与i节点无关
9
②
1
2
节支 1 2 3 4 5 6 1 1 0 0 -1 0 1
①
5
③
Aa=
2 3
-1 -1 0 0 1 0 0 1 1 0 0 -1
4
3
4 0 0 -1 1 -1 0
④
6
2.降阶关联矩阵A
Aa的每一列对应于一条支路。由于一条支路连接于两个节
Bl
Bt
16
2.回路矩阵形式的KVL
回支 4 5 6 1 2 3
1 1 -1 0 1 0 0
4
5
2 33
2
6
1
1
B = 2 1 -1 1 0 1 0 3 0 1 -1 0 0 1
Bt
Bl
设
uu41
支路电压
uu 52
ii 41
支路电流
ii 52
u
c
3. 平面图、非平面图
一个图画在平面上,各支路除了所连 接的节点外不再交叉,这样的图称为 平面图,反之称为非平面图。
f
4
4. 子图:若图G1的每一个节点和支路都是图G的节点与支路, 则称G1为G的子图。
5. 树、树支、连支:不包含回路但包含图的所有节点的连 通的子图称为树。组成树的支路称为树支,其余支路称为 连支。一个有n个节点、b条支路的连通图,将有(n-1)条树 支,(b-n+1)条连支。
A= 2 -1 -1
3 01
3456
0 -1 0 1 0010 1 0 0 -1
第十五章 电路方程的矩阵形式

割集与非割集示例
4 4 3 2 1 (a) 1 (b) (c) 6
①
4 3
5 6
(a)(b)为割集,(c)为非割集
1. 关联矩阵
一条支路连接两个结点,称该支路与这两个结点相关 联,结点和支路的关联性质可以用关联矩阵Aa描述。
N个结点b条支路的图用nb的矩阵描述 支路b
Aa=
结点n
n b
每一行对应一个结点,每一列对应一条支路, 矩阵Aa的每一个元素定义为:
1 0 0 0 1 0 0 0 1
1 -1 0 1 -1 1 0 1 -1
Bl
Bt
u u u u u u
1 2 3 4 5 6
u4 u5 u1 u4 u5 u6 u2 0 u5 u6 u3
矩阵形式的KVL: [ B ][ u ]= 0
Bl
= [ 1 Bt ]
Bt
②
引入回路矩阵[B]的作用: ① 用回路矩阵[B]表示矩阵形式的KVL方程 设
①
4 3
5 ③
[u ] [ u1 u 2 u3 u 4 u5 u6 ]T
u u
l
2
6
④1
t
[ B ][ u ]=
0 -1
关联矩阵Aa的特点: ① ② 每一列只有两个非零元素,一个是+1,一个是-1, Aa的每一列元素之和为零。 矩阵中任一行可以从其他n-1行中导出,即只有n-1 行是独立的。 支路b
引入降阶关联矩阵A A=
(n-1) b
结点(n-1)
② 4 ①
2 5
设④为参考节点,得降阶关联矩阵
③ 6
4 4 3 2 1 (a) 1 (b) (c) 6
①
4 3
5 6
(a)(b)为割集,(c)为非割集
1. 关联矩阵
一条支路连接两个结点,称该支路与这两个结点相关 联,结点和支路的关联性质可以用关联矩阵Aa描述。
N个结点b条支路的图用nb的矩阵描述 支路b
Aa=
结点n
n b
每一行对应一个结点,每一列对应一条支路, 矩阵Aa的每一个元素定义为:
1 0 0 0 1 0 0 0 1
1 -1 0 1 -1 1 0 1 -1
Bl
Bt
u u u u u u
1 2 3 4 5 6
u4 u5 u1 u4 u5 u6 u2 0 u5 u6 u3
矩阵形式的KVL: [ B ][ u ]= 0
Bl
= [ 1 Bt ]
Bt
②
引入回路矩阵[B]的作用: ① 用回路矩阵[B]表示矩阵形式的KVL方程 设
①
4 3
5 ③
[u ] [ u1 u 2 u3 u 4 u5 u6 ]T
u u
l
2
6
④1
t
[ B ][ u ]=
0 -1
关联矩阵Aa的特点: ① ② 每一列只有两个非零元素,一个是+1,一个是-1, Aa的每一列元素之和为零。 矩阵中任一行可以从其他n-1行中导出,即只有n-1 行是独立的。 支路b
引入降阶关联矩阵A A=
(n-1) b
结点(n-1)
② 4 ①
2 5
设④为参考节点,得降阶关联矩阵
③ 6
第十五章电路方程的矩阵形式
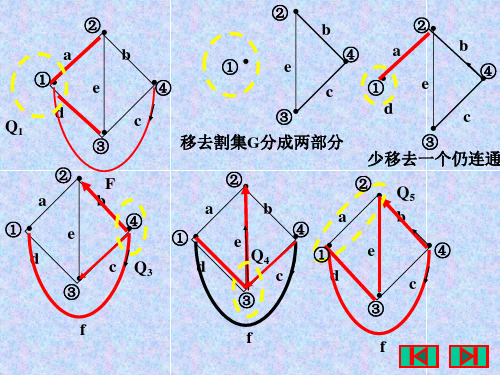
4
它的关联矩阵为:
0 0 -1 +1 0 0 0 +1 0
-1 0 +1 +1 +1 0 0 -1 -1
关联矩阵特点:1、每一列只有两个非零元素+1或-1
2、n个不是独立的
降阶关联矩阵:Aa的任一行划去而剩下的元素构成的矩阵
例:上面 划去An第4行
此时,A中某一此列只有+1
或-1,这列必与划去的结点
行对应割集 列对应支路
i 1
0 0 1
i 2
i 3
i 4
i 5
i 6
i i i
1
2
3
i i i
1
4
5
i i i
1
2
4
i 6
0 0 0
电路中(n-1)个树支电压,可用(n-1)阶列向量表示,即:
ut=(ut1 ut2。。。ut(n-1))T
因为选独立割 集一般是选单树支割集,所以树支电压又是独立 割集电压。
基本回路矩阵 回路组对应一个树的单连支回路组Bf 一个1 回i1路中只有
一个连支 其它为树支- - - 构成一个回路
4
3
65
1
1
6 3
2 2
63 5
例 上图选356为树支 则支路124即为连支
1 2 4 3 5 6
Bf 1
1
0
0
1
-1
1
2 0 1 0 1 0 1
3 0 0 1 0 - 1 1
例:上面的A 则
i1 i2 i3 0
Ai
i3
i4
i6
0即
i1
i2
i3
0
电路PPT课件第15章 电路方程的矩阵形式

ppt课件
11
§15- 3 关联矩阵、回路矩阵、割集矩阵
一. 关联矩阵A 一条支路连接于某两个结点,则称该支路与这两个结点 相关联。
用矩阵形式描述节点和支路的关联性质
关联矩阵
aij = 1 aij aij= -1
aij =0
Aa={aij}n b
节点数 支路数
有向支路 j 与节点 i 关联且背离节点 i
1. 回路的绕行方向取连支电流方向。 2. 支路排列顺序为先连(树)支后树(连)支。
1 支路j在回路i中且与回路i关联,方向一致
bij= -1 支路j在回路i中且与回路i关联,方向相反 0 支路j 不在回路i中
ppt课件
17
4
5
2 33
选 4、5、6为树,连支顺序为1、2、3。
②
1
2
①5
③
43 ④6
Q3: { 1 , 5 , 4}
②
1
2
①5
③
43 ④6
Q4: { 1 , 5 , 2 }
由于KCL适用于任何一个闭合面,对于每一个割集来说, 组成割集的所有支路的电流应满足KCL。
对于一个连通图,可有多个割集,可以列出与割集数相等 的KCL方程。这些方程彼此之间并不独立。
借助于“树”来确定独立割
R1
ppt课件抽象
i1 i2
i3
有 向 图2
连通图 图
不连通图
+
-
抽象 不连通图
+ -
二 . 名词和定义 1. 图 G={支路,节点}
抽象 连通图
① 1 ②ppt课件
允许孤立节点存在3
2.子图
路径:从图G的一个节点出发沿着一些支路连续移动到达 另一节点所经过的支路构成路经。
第15章电路方程的矩阵形式市公开课获奖课件省名师示范课获奖课件

A = 0 0 -1 -1 0 +1 +1 0 0 +1 +1 0
3 ① i3
i6 4 i4 ③ 结束
(3)用A表达KCL旳矩阵形式
b(=6)条支路电流能够用列向量表达
i = [i1, i2 , ···, i6 ]T
i1
2 i2
6 i5 5
④
1 i1
-1 -1 +1 0 0 0 Ai = 0 0 -1 -1 0 +1
15
356 1 2 4
Qf = [ 1t ┆Ql ] =
1 0 0 -1 -1 0 10 1 0
0 Q1 1 Q2
结束
0 0 1 -1 -1 -1 Q3
(1)用割集矩阵Q表达旳 KCL旳矩阵形式
因属同一割集旳全部支路 旳电流也满足KCL,所以
Q1 3 ①
2
③
Q3
4
6
④
5
Q2
Qi=0
②
-1 -1 1 0 0 0
在形式上相同。
所以对某些图G有 Qf = A
2. 对任一图G,当A、B、Q 旳列按相同旳支路
编号排列时:
ABT = 0 或 BAT = 0
QBT = 0 或 BQT = 0
3. 若A、Bf、Qf 相应同一种树,且支路编号按
先树支后连支旳相同顺序排列写出。
则有: BtT = -At-1Al
Ql = - BtT = At-1Al
d
c Q3
Q4
当割集旳全部支路连接 于同一结点时,割集旳 KCL变为结点旳KCL。
对较大规模旳电路,用 观察法选择一组独立割 集是困难旳。
借助于树,就比较以便。
2024/9/21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
序号,且以该连支的方向为对应的回路的绕行
方向,Bf中出现一个l阶的单位子矩阵,即
Bf=[1l|Bt]
(15-4)
式中下标l和t分别表示与连支和树支对应部分。
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -10
第十五章 电路方程的矩阵形式 22
例:图15-5a,选支路3、5、6为树支,则1、 2、4为连支,图15-5b示一组单连支回路,可 写成基本回路矩阵形式:
对应于一组线性独立的KCL方程的割集称独立 割集。
现在介绍借助于“树”确定一组独立割集方法。
2020/4/12
15-1 割 集 -4
第十五章 电路方程的矩阵形式 7
单树支割集或基本割集-1
一个连通图,任选一树,与树对应连支集合不能构成 一个割集,每一树支与一些相应连支可构成一个割集。
例:图15-2连通图G,选一树T,树支和连支分别用实 线和虚线表示,把全部连支移去,剩下树仍连通,即 连支集合不能构成一个割集。
2020/4/12
15-1 割 集 -7
第十五章 电路方程的矩阵形式 10
基本割集组
2020/4/12
15-1 割 集 -7
第十五章 电路方程的矩阵形式 11
15-2 关联矩阵、回路矩阵、割集矩阵
电路图中每一支路赋予参考方向,成为有向图。有向 图拓扑性质可用关联矩阵、回路矩阵和割集矩阵描述。
设一支路连接某两个结点,称该支路与这两个结点相 关联。支路与结点关联性质可用关联矩阵描述。
15-1 割 集 -3
第十五章 电路方程的矩阵形式 6
独立割集
KCL适用于任何一个闭合面,属同一割集所有 支路的电流应满足KCL。
当一个割集所有支路连接在同一结点,如图151点的上QK1、CLQ方2、程Q。3和Q4,则割集KCL方程变为结
对于连通图,总共可列出与割集数相等数目的 KCL方程,但这些方程并非都是线性独立的。
式15-6表明电路中各支路电流可
用与该支路关联的所有回路中的
回路电流表示,这正是回路电流
法的基本思想。
可认为该式是用矩阵B表示的KCL
矩阵形式。
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -16
第十五章 电路方程的矩阵形式 28
割集矩阵 -1
设一个割集由某些支路构成,称这些支路与该割集关 联。支路与割集关联性质可用割集矩阵描述。
2020/4/
回路矩阵-4
15-2 关联矩阵、回路矩阵、割集矩阵 -11
第十五章 电路方程的矩阵形式 23
用矩阵B表示的KVL的矩阵形式-
1
回路矩阵左乘支路电压列向量,乘积是一个l阶列向量。 矩阵B每一行表示每一对应回路与支路关联情况,乘 积列向量中每一元素将等于每一对应回路中各支路电 压代数和,即
KCL的矩阵形式(例)
例:图15-4有
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -4
第十五章 电路方程的矩阵形式 16
用矩阵A表示的KVL矩阵形式-
1
电路中b个支路电压可用b阶列向量表示, 即
u=[ u1 u2 … ub ]T
(n-1)个结点电压可用一(n-1)阶列向量表示, 即
第十五章 电路方程的矩阵形式 25
用矩阵B表示的KCL矩阵形式-
1
l个独立回路电流可用一个l阶列向量 表示,即
il=[ il1 il2 … ill ]T
由于矩阵B的每一列,也就是矩阵BT 的每一行,表示每一对应支路与回路 的关联情况,所以按矩阵的乘法规则 可知支路电流i:
i=BTil
(15-6)
矩阵A的某些列将只具有一个+1或一个-1,每 一个这样的列必对应于与划去结点相关联的一 条支路。被划去的行对应结点可当作参考结点。
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -2
第十五章 电路方程的矩阵形式 14
矩阵A表示的KCL的矩阵形
式
电路中b个支路电流可用一b阶列向量表示,即
2020/4/12
15-1 割 集 -5
第十五章 电路方程的矩阵形式 8
单树支割集或基本割集-2
另外,树是连接全部结点所需最少支路集合,移去任 一树支如bt,连接T1和T2的那些连支l1、l2、和l3与bt一 起必构成一个割集,因移去后,G将分离为两部分。
同理,每一树支都可与相应一些连支构成割集。 由树的一条树支与相应的一些连支构成的割集称为单
2020/4/12
15-1 割 集 -2
第十五章 电路方程的矩阵形式 5
一般在连通图G上作闭合面判断确定一个割集。
在G上作一闭合面,使其包围G某些结点,把闭合面相 切割所有支路全部移去,G被分离为两部分,这样一 组支路构成一个割集。
图15-1,示出闭合面(用蓝虚线)与割集支路相切割情况。
2020/4/12
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -14
第十五章 电路方程的矩阵形式 26
用矩阵B表示的KCL矩阵形式-
2
例:图15-5a有
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -15
第十五章 电路方程的矩阵形式 27
用矩阵B表示的KCL矩阵形式-3
i=BTil
(15-6)
本章介绍电路方程矩阵形式及其系统建立法, 是电路计算机辅助设计和分析所需基本知识。
2020/4/12
15-1 割 集 -0
第十五章 电路方程的矩阵形式 3
割 集 -1
第三章介绍图的定义及有关回路、树等 基本概念。
这里补充介绍割集概念,及与树有关的 基本割集组。
连通图G的一个割集:是G的一个支路集 合,把这些支路移去将使G分离为两个部 分,但如少移去一条支路,图仍连通。
故有
Bu=0
(15-5)
式15-5是用矩阵B表示的KVL的矩阵形式。
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -12
第十五章 电路方程的矩阵形式 24
用矩阵B表示的KVL的矩阵形式-
2
例:图15-5a,选15-5b所示一组独立回路,有
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -13
2020/4/12
回路矩阵-2
15-2 关联矩阵、回路矩阵、割集矩阵 -9
第十五章 电路方程的矩阵形式 21
回路矩阵 -3
如所选独立回路组对应一个树的单连支回路组,
称基本回路矩阵,用Bf表示。
写Bf时,注意其行列次序如下:把l条连支依次 排列在对应于Bf的第1至第l列,然后再排列树支; 取每一单连支回路的序号为对应连支所在列的
15-2 关联矩阵、回路矩阵、割集矩阵 -6
第十五章 电路方程的矩阵形式 18
用矩阵A表示的KVL矩阵形式-
3
u=ATun
(15-3)
可见式(15-3)表明:电路中各支路电
压可用与该支路关联的两个结点的结
点电压(参考结点的结点电压为零)表
示,正是结点电压法的基本思想。
可认为该式是用矩阵A表示的KVL矩 阵形式。
仅介绍独立割集矩阵,简称割集矩阵。
设有向图结点数为n,支路数为b,则独立割集数为(n1)。每个割集编号,指定一个割集方向(移去割集所有 支路,G分离为两部分后,从其中一部分指向另一部分 方向,即为割集方向,每一割集只有两个可能方向)。 割集矩阵为一个(n-1)×b矩阵,用Q表示。Q的行对应 割集,列对应支路,任一元素qjk定义如下:
这一特点,Aa中任一行必能从其他(n-1)行导出。
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -1
第十五章 电路方程的矩阵形式 13
降阶关联矩阵
如把Aa任一行划去,剩下(n-1)×b矩阵用A表示,
并称降阶关联矩阵(今后主要用降阶关联矩阵, 往往略去“降阶”)。 例:把式(15-1)中第4行划去,得
un=[ un1 un2 … un(n-1) ]T
由于矩阵A每一列,即矩阵AT每一行,表 示每一对应支路与结点的关联情况,有
u=ATun
2020/4/12
(15-3)
15-2 关联矩阵、回路矩阵、割集矩阵 -5
第十五章 电路方程的矩阵形式 17
用矩阵A表示的KVL矩阵形式-
2
例:图15-4有
2020/4/12
电路
第十五章 电路方程的矩阵形式
8 学时
§15-1 §15-2 §15-4 §15-5
第十五章 电路方程的矩阵形式
主要内容: 本章主要介绍电路方程的矩阵形式。 在图的基础上介绍几个重要矩阵:关联矩阵、
回路矩阵和割集矩阵,并导出用这些矩阵表 示的KCL、KVL方程。 导出回路电流(网孔电流)方程、结点电压方 程的矩阵形式。
设有向图结点数n,支路数b,结点与支路均编号。该 有向图的关联矩阵为一个(n×b)阶矩阵,用Aa表示。 行对应结点,列对应支路,任一元素ajk定义如下:
ajk=+1,表示支路k与结点j关联并且它的方向背离结点; ajk=-1,表示支路k与结点j关联并且它指向结点;
ajk=0,表示支路k与结点j无关联。
bjk=+1,表示支路k与回路j关联,且它们的方向一致; bjk=-1,表示支路k与回路j关联,且它们的方向相反; bjk=0,表示支路k与回路j无关联。
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -8
第十五章 电路方程的矩阵形式 20
例:图15-5a独立回路数等于3。选一组独立回 路图15-5b,对应回路矩阵为
2020/4/12
15-2 关联矩阵、回路矩阵、割集矩阵 -0
第十五章 电路方程的矩阵形式 12
