初一几何三角形练习题
(完整版)初一上册几何练习题50道

一.选择题1.如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()(A)锐角三角形(B)直角三角形(C)钝角三角形(D)等腰三角形2.下列给出的各组线段中,能构成三角形的是()(A)5,12,13(B)5,12,7(C)8,18,7(D)3,4,83.一个三角形的三边长分别是15,20和25,则它的最大边上的高为()(A)12(B)10(C)8(D)54.两条边长分别为2和8,第三边长是整数的三角形一共有()(A)3个(B)4个(C)5个(D)无数个5.下列图形中,不是轴对称图形的是()(A)线段MN(B)等边三角形(C)直角三角形(D)钝角∠AOB6.直角三角形两锐角的平分线相交所夹的钝角为()(A)125°(B)135°(C)145°(D)150°7.已知∠α,∠β是某两条平行线被第三条直线所截得的同旁内角,若∠α=50°,则∠β为()A.40°B.50°C.130°D.140°8.如图,下列推理中正确的是()A.若∠1=∠2,则AD∥BC B.若∠1=∠2,则AB∥DCC.若∠A=∠3,则AD∥BC D.若∠3=∠4,则AB∥DC9.下列图形中,可以折成长方体的是()10.一个几何体的三视图如图所示,那么这个几何体是()11.如图1,在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为() A.30°B.36°C.45°D.70°12.、如图2,AB∥CD,AC⊥BC于C,则图中与∠CAB互余的角有()A.1个B.2个C.3个D.4个图1 图2 图313. 如图3,直线AB、CD、EF相交于O,图中对顶角共有()A.3对B.4对C.5对D.6对14.下列说法错误的是()A.平面内的直线不相交就平行B.平面内三条直线的交点个数有1个或3个C.若a∥b,b∥c,则a∥cD.平面内过一点有且只有一条直线与已知直线垂直15. 2.设α是等腰三角形的一个底角,则α的取值范围是( )(A)0<α<90°(B)α<90°(C)0<α≤90°(D)0≤α<90°二.填空题1.有一个三角形的两边长为3和5,要使这个三角形是直角三角形,它的第三边等于2.如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是三角形。
(完整版)初中几何题练习

初中几何练习题一. 三角形1.三角形的有关概念 一、填空题:1、三角形的三边为1,a 1,9,则a 的取值范围是 。
2、已知三角形两边的长分别为1和2,如果第三边的长也是整数,那么第三边的长为 。
3、在△ABC 中,若∠C =2(∠A +∠B ),则∠C = 度。
4、如果△ABC 的一个外角等于1500,且∠B =∠C ,则∠A = 。
5、如果△ABC 中,∠ACB =900,CD 是AB 边上的高,则与∠A 相等的角是 。
6、如图,在△ABC 中,∠A =800,∠ABC 和∠ACB 的外角平分线相交于点D ,那么∠BDC = 。
7、如图,CE 平分∠ACB ,且CE ⊥DB ,∠DAB =∠DBA ,AC =18cm ,△CBD 的周长为28 cm ,则DB = 。
8、纸片△ABC 中,∠A =650,∠B =750,将纸片的一角折叠,使点C 落在△ABC 内(如图),若∠1=200,则∠2的度数为 。
9、在△ABC 中,∠A =500,高BE 、CF 交于点O ,则∠BOC = 。
第6题图FEDC BA第7题图EDC BA第8题图A二、选择题:1、若△ABC 的三边之长都是整数,周长小于10,则这样的三角形共有( )A 、6个B 、7个C 、8个D 、9个 2、在△ABC 中,AB =AC ,D 在AC 上,且BD =BC =AD ,则∠A 的度数为( )A 、300B 、360C 、450D 、720 3、等腰三角形一腰上的中线分周长为15和12两部分,则此三角形底边之长为( )A 、7B 、11C 、7或11D 、不能确定 4、在△ABC 中,∠B =500,AB >AC ,则∠A 的取值范围是( ) A 、00<∠A <1800 B 、00<∠A <800 C 、500<∠A <1300 D 、800<∠A <13005、如果三角形的一个外角等于它相邻内角的2倍,且等于它不相邻内角的4倍,那么这个三角形一定是( )A 、锐角三角形B 、直角三角形C 、钝角三角形D 、正三角形 三、解答题:1、有5根木条,其长度分别为4,8,8,10,12,用其中三根可以组成几种不同形状的三角形?2、长为2,3,5的线段,分别延伸相同长度的线段后,能否组成三角形?若能,它能构成直角三角形吗?为什么?3、如图,在△ABC 中,∠A =960,延长BC 到D ,∠ABC 与∠ACD 的平分线相交于1A ,∠1A BC 与∠1A CD 的平分线相交于2A ,依此类推,∠4A BC 与∠4A CD 的平分线相交于5A ,则∠5A 的大小是多少?2A 1A 第3题图DC B A4、如图,已知OA =a ,P 是射线ON 上一动点(即P 可在射线ON 上运动),∠AON =600,填空:(1)当OP = 时,△AOP 为等边三角形; (2)当OP = 时,△AOP 为直角三角形; (3)当OP 满足 时,△AOP 为锐角三角形; (4)当OP 满足 时,△AOP 为钝角三角形。
2024学年初中数学几何(三角形全等-倍长中线)模型专项练习(附答案)

2024学年初中数学几何(三角形全等-倍长中线)模型专项练习1.在等腰△ABC中,AB=AC,D为AB上一点,连接CD.E为CD中点.(1)如图1,连接AE,作EH⊥AC,若AD=2BD,S△BDC=6,EH=2,求AB的长;(2)如图2,点F为腰AC上一点,连接BF、BE.若∠A=∠ABE=∠CBF.求证:BD+CF=AB.2.如图1,在等腰Rt△ACB中,∠ACB=90°,AC=BC;在等腰Rt△DCE中,∠DCE=90°,CD=CE;点D、E分别在边BC、AC上,连接AD、BE,点N是线段BE的中点,连接CN与AD交于点G.(1)若CN=12.5,CE=7,求BD的值.(2)求证:CN⊥AD.(3)把等腰Rt△DCE绕点C转至如图2位置,点N是线段BE的中点,延长NC交AD于点H,请问(2)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.3.如图,在平行四边形ABCD中,点H为DC上一点,BD、AH交于点O,△ABO为等边三角形,点E在线段AO上,OD=OE,连接BE,点F为BE的中点,连接AF并延长交BC于点G,且∠GAD=60°.(1)若CH=2,AB=4,求BC的长;(2)求证:BD=AB+AE.4.已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF、CF.(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=,求此时线段CF的长(直接写出结果).5.在△ABC中,点D是BC的上一点,点E是△ABC外一点,且∠AEB=90°,过点C作CF⊥AF,垂足为F,连接DE,DF.(1)如图1,点D在AE上,D是BC中点,∠BAE=30°,∠CAE=45°,AB =2,求AC的长;(2)如图2,点D不在AE上,连接AD,延长CF至点G,连接GD且GD=AD.若BC平分∠ABE,∠G=∠DAB,求证:DE=DF.1参考答案1.在等腰△ABC 中,AB =AC ,D 为AB 上一点,连接CD .E 为CD 中点.(1)如图1,连接AE ,作EH ⊥AC ,若AD =2BD ,S △BDC =6,EH =2,求AB 的长;(2)如图2,点F 为腰AC 上一点,连接BF 、BE .若∠A =∠ABE =∠CBF .求证:BD +CF =AB .【过程解答】解:(1)∵AD =2BD ,S △BDC =6,∴S △ACD =2S △BCD =2×6=12,∵E 为CD 中点∴=6,∵EH ⊥AC ∴AC •EH =6∵EH =2∴AC =6∵AB =AC∴AB =6(2)如图2,延长BE 至G ,使EG =BE ,连接CG ,在△BED 和△GEC 中,∴△BED ≌△GEC (SAS )∴BD =CG ,∠ABE =∠G∵AB =AC∴∠ABC =∠ACB ,即:∠ABF +∠CBF =∠ACB∵∠A =∠CBF∴∠ABF +∠A =∠ACB∵∠BFC=∠ABF+∠A∴∠BFC=∠ACB∴BF=BC∵∠A=∠ABE=∠CBF∴∠A=∠G,∠ABF+∠EBF=∠CBG+∠EBF∴∠ABF=∠GBC在△ABF和△GBC中,∴AF=CG又∵BD=CG∴AF=BD∵AF+CF=AC,AB=AC∴BD+CF=AB2.如图1,在等腰Rt△ACB中,∠ACB=90°,AC=BC;在等腰Rt△DCE中,∠DCE=90°,CD=CE;点D、E分别在边BC、AC上,连接AD、BE,点N是线段BE的中点,连接CN与AD交于点G.23(1)若CN=12.5,CE=7,求BD的值.(2)求证:CN⊥AD.(3)把等腰Rt△DCE绕点C转至如图2位置,点N是线段BE的中点,延长NC交AD 于点H,请问(2)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由. 【过程解答】解:(1)∵∠ACB=90°,点N是线段BE的中点,∴BE=2CN=25,∵CE=7,∴BC ==24,∵CD=CE=5,∴BD=BC﹣CD=17;(2)在△ACD与△BCE中,,∴△ACD≌△BCE,∴∠CAD=∠CBE,∵∠ACB=90°,点N是线段BE的中点,∴CN=BN,∴∠CBE=∠NCD,∴∠NCD=∠CAD,∵∠NCD+∠NCA=90°,∴∠CAG+∠GCA=90°,∴∠CGA=90°,∴CN⊥AD;(3)(2)中的结论还成立,如图2,延长CN到F使FN=CN,连接BF,在△CEN与△BFN中,,∴△CEN≌△BNF,∴CE=BF,∠F=∠ECN,∵∠CBF=180°﹣∠F﹣∠BCF,∠DCA=360°﹣∠DCE﹣∠ACB﹣∠BCE=180°﹣∠ECF﹣∠BCF,∴∠CBF=∠DCA,∵CE=CD,∴BF=CD,在△ACD与△BCF中,,∴△ACD≌△BCF,∴∠DAC=∠BCF,∵∠BCF+∠ACH=90°,∴∠CAH+∠ACH=90°,∴∠AHC=90°,∴CN⊥AD.3.如图,在平行四边形ABCD中,点H为DC上一点,BD、AH交于点O,△ABO为等边三角形,点E在线段AO上,OD=OE,连接BE,点F为BE的中点,连接AF并延长交BC于点G,且∠GAD=60°.(1)若CH=2,AB=4,求BC的长;(2)求证:BD=AB+AE.45【过程解答】解:延长AH、BC相交于点M,∵▱ABCD∴CD=AB=4,CD∥AB∵CH=2∴DH=CD=2∵CD∥AB∴∠MHC=∠MAB,∠MCH=∠MBA∴△MCH∽△MBA∴∴=∴MH=AH,BM=2BC∵△ABO为等边三角形∴∠AOB=∠OAB=∠OBA=60°,OA=AB=4 ∴∠DOH=∠AOB=60°∴∠ODH=∠OBA=60°,∠OHD=∠OAB=60°∴∠DOH=∠ODH=∠OHD∴△DOH是等边三角形∴OH=OD=DH=2∴MH=AH=OA+OH=4+2=6,EM=OE+OH+MH=10∵OD=OE=2∴AE=OA﹣OE=4﹣2=2∴点E是OA的中点∵△ABO为等边三角形∴BE⊥OA,∠ABE=30°∴BE =AE=2在Rt△BEM中,∠BEM=90°∴BE2+EM2=BM2∴(2)2+102=BM2∴BM=4∴BC=2(2)作BM∥AH交AG的延长线于M.∵AE∥BM,∴∠EAF=∠M,∵EF=FB,∠AFE=∠MFB,∴△AEF≌△MBF(AAS),∴AE=BM,易证∠AOD=∠ABM=120°,∠DAO=∠MAB,∵AO=AB,∴△AOD≌△ABM(ASA),∴OD=BM=AE,6∴BD=BO+OD=AB+AE.4.已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF、CF.(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC =,求此时线段CF的长(直接写出结果).∴DF =BE,CF =BE,∴DF=CF.∵△ABC和△ADE是等腰直角三角形,∴∠ABC=45°∵BF=DF,∴∠DBF=∠BDF,∵∠DFE=∠ABE+∠BDF,∴∠DFE=2∠DBF,同理得:∠CFE=2∠CBF,∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°,∴DF=CF,且DF⊥CF.(2)(1)中的结论仍然成立.证明:如图,此时点D落在AC上,延长DF交BC于点G.∵∠ADE=∠ACB=90°,7∴DE∥BC.∴∠DEF=∠GBF,∠EDF=∠BGF.∵F为BE中点,∴EF=BF.∴△DEF≌△GBF.∴DE=GB,DF=GF.∵AD=DE,∴AD=GB,∵AC=BC,∴AC﹣AD=BC﹣GB,∴DC=GC.∵∠ACB=90°,∴△DCG是等腰直角三角形,∵DF=GF.∴DF=CF,DF⊥CF.(3)延长DF交BA于点H,∵△ABC和△ADE是等腰直角三角形,∴AC=BC,AD=DE.∴∠AED=∠ABC=45°,∵由旋转可以得出,∠CAE=∠BAD=90°,∵AE∥BC,∴∠AEB=∠CBE,∴∠DEF=∠HBF.∵F是BE的中点,∴EF=BF,∴△DEF≌△HBF,∴ED=HB,∵AC=,在Rt△ABC中,由勾股定理,得 AB=4,∵AD=1,∴ED=BH=1,∴AH=3,在Rt△HAD中由勾股定理,得DH=,∴DF=,∴CF=∴线段CF的长为.5.在△ABC中,点D是BC的上一点,点E是△ABC外一点,且∠AEB=90°,过点C作CF⊥AF,垂足为F,连接DE,DF.(1)如图1,点D在AE上,D是BC中点,∠BAE=30°,∠CAE=45°,AB=2,求AC的长;(2)如图2,点D不在AE上,连接AD,延长CF至点G,连接GD且GD=AD.若BC平分∠ABE,∠G=∠DAB,求证:DE=DF.【过程解答】(1)解:∵D是BC中点,∴BD=DC,∵CF⊥AE,∴∠CF A=∠CFD=90°,∵∠ABE=90°,∴∠ABE=∠CFD,在△BDE和△CDF中,,∴△BDE≌△CDF(AAS),∴BE=CF,∵∠ABE=90°,∠BAE=30°,AB=2,∴BE=CF=1,∵∠CF A=90°,∠CAE=45°,∴AC=CF=.(2)证明:∵BC平分∠ABE,∴∠1=∠2,∵∠CFE=∠BEF=90°,∴∠2=∠3,∴∠1=∠3,∴△ABD≌△GCD(ASA),∴BD=CD,。
三角形全等几何模型5一线三等角专项练习20202021学年七年级数学下册基础知识专项讲练北师大版
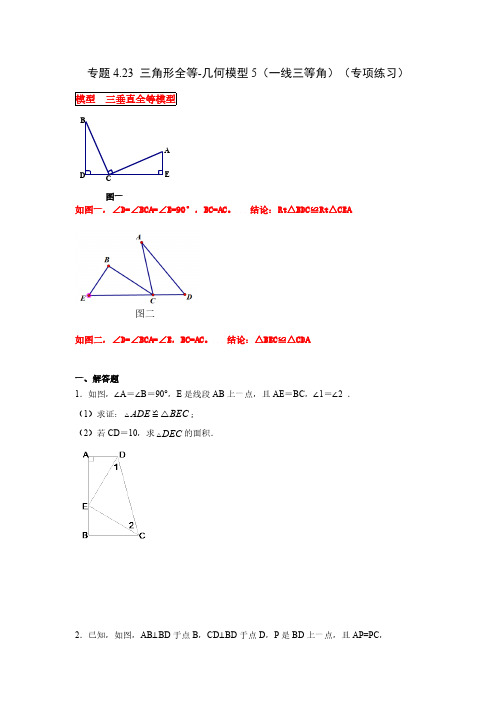
CD E BA专题4.23 三角形全等-几何模型5(一线三等角)(专项练习)模型 三垂直全等模型图一如图一,∠D=∠BCA=∠E=90°,BC=AC 。
结论:Rt △BDC ≌Rt △CEA图二如图二,∠D=∠BCA=∠E ,BC=AC 。
结论:△BEC ≌△CDA一、解答题1.如图,∠A =∠B =90°,E 是线段AB 上一点,且AE =BC ,∠1=∠2 .(1)求证:ADE V ≌BEC △;(2)若CD =10,求DEC V 的面积.2.已知,如图,AB ⊥BD 于点B ,CD ⊥BD 于点D,P 是BD 上一点,且AP=PC ,AP ⊥PC .(1)求证:△ABP ≌△PDC(2)若AB=3,CD=4,连接AC ,求AC 的长.3.如图,在ABC V 中,AB AC =,D 、A 、E 三点都在直线m 上,并且有BDA AEC BAC ÐÐÐ==,求证:DE BD CE =+.4.已知:如图,MS ⊥PS ,MN ⊥SN ,PQ ⊥SN ,垂足分别为S ,N ,Q ,MS =PS ,SN =4,MN =3.求NQ 的长.5.如图1,∠ACB =90°,AC =BC ,AD ⊥MN ,BE ⊥MN ,垂足分别为D 、E .(1)求证:△ADC ≌△CEB ;(2)猜想线段AD 、BE 、DE 之间具有怎样的数量关系,并说明理由;(3)题设条件不变,根据图2可得线段AD 、BE 、DE 之间的数量关系是 .6.如图,已知:ABC V 中,AB AC =,BAC 90Ð=°,分别过B ,C 向经过点A 的直线EF 作垂线,垂足为E ,F .(1)当EF 与斜边BC 不相交时,请证明EF BE CF(=+如图1);(2)如图2,当EF 与斜边BC 这样相交时,其他条件不变,证明:EF BE CF =-;7.如图,一条河流MN 旁边有两个村庄A ,B ,AD ⊥MN 于D .由于有山峰阻挡,村庄B 到河边MN 的距离不能直接测量,河边恰好有一个地点C 能到达A ,B 两个村庄,与A ,B 的连接夹角为90°,且与A ,B 的距离也相等,测量C ,D 的距离为150m ,请求出村庄B 到河边的距离.8.已知:AB BD ^,ED BD ^,AC CE =,BC DE =.(1)试猜想线段AC 与CE 的位置关系,并证明你的结论.(2)若将CD 沿CB 方向平移至图2情形,其余条件不变,结论12AC C E ^还成立吗?请说明理由.(3)若将CD 沿CB 方向平移至图3情形,其余条件不变,结论12AC C E ^还成立吗?请说明理由.9.如图,90ACB Ð=°,AC BC =,AD CE ^,BE CE ^,垂足分别为D ,E ,若9AD =,6DE =,求BE 的长.10.如图所示,A ,C ,E 三点在同一直线上,且ABC DAE △△≌.(1)求证:BC DE CE =+;(2)当ABC V 满足什么条件时,//BC DE ?11.已知:D ,A ,E 三点都在直线m 上,在直线m 的同一侧作ABC V ,使AB AC =,连接BD ,CE .(1)如图①,若90BAC Ð=°,BD m ^,CE m ^,求证ABD ACE @V V ;(2)如图②,若BDA AEC BAC Ð=Ð=Ð,请判断BD ,CE ,DE 三条线段之间的数量关系,并说明理由.12.如图,点C 在BE 上,AB ⊥BE ,DE ⊥BE ,且AB =CE ,AC =CD .判断AC 和CD 的关系并说明理由.13.直线CD 经过BCA Ð的顶点C ,CA=CB .E ,F 分别是直线CD 上两点,且BEC CFA a Ð=Ð=Ð.(1)(数学思考)若直线CD 经过BCA Ð的内部,且E ,F 在射线CD 上,请解决下面两个问题:①如图1,若90BCA Ð=°,90a Ð=°,求证:EF BE AF =-;②如图2,若090BCA °<Ð<°,当a Ð与BCA Ð之间满足________关系时,①中结论仍然成立,并给予证明.(2)(问题拓展)如图3,若直线CD 经过BCA Ð的外部,BCA a Ð=Ð,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.14.如图,已知在ABC V 中,AB AC =,90BAC Ð=°,别过B 、C 两点向过A 的直线作垂线,垂足分别为E 、F .求证:EF BE CF =+.15.在Rt ABC △中,90C Ð=°,8cm AC =,6cm BC =,点D 在AC 上,且6cm AD =,过点A 作射线AE AC ^(AE 与BC 在AC 同侧),若点P 从点A 出发,沿射线AE 匀速运动,运动速度为1cm/s ,设点P 运动时间为t 秒.连结PD 、BD .(1)如图①,当PD BD ^时,求证:PDA DBC △≌△;(2)如图②,当PD AB ^于点F 时,求此时t 的值.16.如图所示,△ABC 中,∠ACB=90°,AC=BC ,直线EF 经过点C ,BF ⊥EF 于点F ,AE ⊥EF于点E .(1)求证:△ACE ≌△CBF ;(2)如果AE 长12cm ,BF 长5cm ,求EF 的长.17.如图,90ACB Ð=°,AC BC =,AD CE ^,BE CE ^,垂足分别为D ,E ,2.5cm AD =,求1cm BE =,求DE 的长.18.已知AD ⊥AB 于A ,BE ⊥AB 于B ,点C 在线段AB 上,DC ⊥EC ,且DC=CE .(1)求证:AD+BE=AB ;(2)将△BEC 绕点C 逆时针旋转,使点B 落在AC 上,如图(2),试问:AD ,BE ,AB 又怎样的数量关系?说明理由.19.如图(1),已知ABC V 中,90BAC Ð=°,AB AC =;AE 是过A 的一条直线,且B ,C 在AE 的异侧,BD AE ^于D ,CE AE ^于E .(1)求证:BD DE CE =+;(2)若直线AE 绕A 点旋转到图(2)位置时(BD CE <),其余条件不变,问BD 与DE ,CE 的数量关系如何?请给予证明.(3)若直线AE 绕A 点旋转到图(3)位置时(BD CE >),其余条件不变,问BD 与DE ,CE 的数量关系如何?请直接写出结果,不需证明;(4)根据以上的讨论,请用简洁的语言表达直线AE 在不同位置时BD 与DE ,CE 的位置关系.20.如图,在ABC V 中,AB AC =,AB BC >,点D 在边BC 上,点E ,F 在线段AD 上,且2DF AF =,12BAC Ð=Ð=Ð.若BE 的长为5,求AD 的长.21.已知:如图,△ABC 中,∠BAC =90°,AB =AC ,l 是过点A 的一条直线,BD ⊥l ,CE ⊥l ,垂足分别为D 、E .(1) 如图(1),求证:DE =BD +CE ;(2) 若直线l 绕A 点旋转到图(2)位置时,其余条件不变,请把图形补充完整,写出BD 、CE 与DE 之间的数量关系,并证明你的结论.22.(1)如图1,已知OAB V 中,OA OB =,90AOB Ð=°,直线l 经过点O ,BC ⊥直线l ,AD ^ 直线l ,垂足分别为点C ,D .依题意补全图l ,并写出线段BC ,AD ,CD 之间的数量关系为______;(2)如图2,将(1)中的条件改为:在OAB V 中,OA OB =,C ,O ,D 三点都在直线l 上,并且有BCO ODA BOA Ð=Ð=Ð,请问(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,在ABC V 中,AB AC =,90CAB Ð=°,点A 的坐标为(0,1),点C 的坐标为()3,2,请直接写出点B 的坐标.23.在△ABC 中,AC=BC ,直线MN 经过点C ,AD ⊥MN 于点D ,BE ⊥MN 于点E ,且AD=CE ;(1)当直线MN 绕点C 旋转到如图1的位置时,求证:AC ⊥BC .(2)判断AD 、BE 、DE 这三条线段之间的数量关系,并说明理由.(3)当直线MN 绕点C 旋转到如图2的位置时,线段DE 、AD 、BE 之间又有什么样的数量关系?请你直接写出这个数量关系,不必证明.24.如图1所示,在△ABC 中,∠ACB=90°,AC= BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN 绕点C 旋转到图2(a)的位置,求证:①△ADC ≌△CEB;②DE=AD- BE .(2)当直线MN 绕点C 旋转到图2(b)的位置时,求证:DE= BE-AD .25.如图,90B C Ð=Ð=°,BAE CED Ð=Ð,且AB CE =.(1)试说明:ADE V 是等腰直角三角形;(2)若2CDE BAE Ð=Ð,求CDE Ð的度数.26.如图,已知在ABC V 中,AC BC AD ==,CDE B Ð=Ð,求证:ADE BCD △≌△.27.如图1,已知AB =AC ,AB ⊥AC .直线m 经过点A ,过点B 作BD ⊥m 于D , CE ⊥m 于E .我们把这种常见图形称为“K”字图.(1)悟空同学对图1进行一番探究后,得出结论:DE =BD +CE ,现请你替悟空同学完成证明过程.(2)悟空同学进一步对类似图形进行探究,在图2中,若AB =AC ,∠BAC =∠BDA =∠AEC ,则结论DE =BD +CE ,还成立吗?如果成立,请证明之.28.(1)如图①,已知:ABC V 中,90BAC Ð=°,AB AC =,直线m 经过点A ,BD m ^于D ,CE m ^于E ,请探索DE 、BD 、CE 三条线段之间的数量关系,直接写出结论;(2)拓展:如图2,将(1)中的条件改为:ABC V 中,AB AC =,D 、A 、E 三点都在直线m 上,并且BDA AEC BAC a Ð=Ð=Ð=,a 为任意锐角或钝角,请问(1)中结论是否还成立?如成立,请证明;若不成立,请说明理由;(3)应用:如图③,在ABC V 中,BAC Ð是钝角,AB AC =,BAD CAE ÐÐ>,BDA AEC BAC Ð=Ð=Ð,直线m 与BC 的延长线交于点F ,若2BC CF =,ABC V 的面积是16,求ABD △与CEF △的面积之和.29.如图(1)在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于点D ,BE ⊥MN 于点E .(1)求证:①△ADC ≌△CEB ;②DE =AD +BE .(2)当直线MN 绕点C 旋转到图(2)的位置时,DE 、AD 、BE 又怎样的关系?并加以证明.30.如图,在ABC V 中,90ACB Ð=°,AC BC =,直线MN 经过点C ,且AD MN ^于点D ,BE MN ^于点E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:①ADC CEB △≌△;②DE AD BE =+;(2)当直线MN 绕点C 旋转到如图2所示的位置时,求证:DE AD BE =-;(3)当直线MN 绕点C 旋转到如图3所示的位置时,试问DE ,AD ,BE 具有怎样的数量关系?请直接写出这个等量关系,不需要证明.31.已知:如图,在ABC D 中,90C Ð=°,点E 在AC 上,且AE BC =,ED AB ^于点D ,过A 点作AC 的垂线,交ED 的延长线于点F .求证:AB EF =.32.如图,两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置,PA 、PB 与直线MN 重合,且三角板PAC 、三角板PBD 均可绕点P 逆时针旋转(1)试说明∠DPC=90°;(2)如图②,若三角板PBD 保持不动,三角板PAC 绕点P 逆时针旋转旋转一定角度,PF 平分∠APD ,PE 平分∠CPD ,求∠EPF ;(3)如图③.在图①基础上,若三角板PAC 开始绕点P 逆时针旋转,转速为5°/秒,同时三角板PBD 绕点P 逆时针旋转,转速为1°/秒,(当PA 转到与PM 重合时,两三角板都停止转动),在旋转过程中,PC 、PB 、PD 三条射线中,当其中一条射线平分另两条射线的夹角时,请求出旋转的时间.33.(1)如图1,∠MAN =90°,射线AE 在这个角的内部,点B 、C 在∠MAN 的边AM ,AN 上,且AB =AC ,CF ⊥AE 于点F ,BD ⊥AE 于点D .求证:ABD CAF @V V .(2)如图2,点B 、C 在∠MAN 的边AM 、AN 上,点E 、F 在∠MAN 内部射线AD 上,∠1,∠2分别是ABE △,CAF V 的外角,已知AB =AC ,∠1=∠2=∠BAC ,求证:ABE CAF @V V ;(3)如图3,在ABC V 中,AB =AC ,AB >BC ,点D 在边BC 上,CD =2BD ,点E 、F 在线段AD 上,12BAC Ð=Ð=Ð,若ABC V 的面积是15,则ACF V 与BDE V 的面积之和是_________.34.如图(1)AB=9cm ,AC ⊥AB ,AC=BD=7cm ,点P 在线段AB 上以2cm/s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动,它们运动的时间为t (s ).(1)若点Q 的速度与点P 的速度相等,当t=1时.①求证:△ACP ≌△BPQ ;②判断此时PC 和PQ 的位置关系,并证明;(2)将图(1)中的“AC ⊥AB ,BD ⊥AB”,改为“∠CAB=∠DBA=70°”,得到图(2),其他条件不变.设点Q 的运动速度为x cm/s ,请问是否存在实数x ,使得△ACP 与△BPQ 全等?若存在,求出相应的x 和t 的值;若不存在,请说明理由.35.如图1,2OA =,4OB =,以A 点为顶点、AB 为腰在第三象限作等腰直角ABC D .(1)求点C 的坐标;(2)如图2,P 是y 轴负半轴上一个动点,当P 点向y 轴负半轴向下运动时,若以P 为直角顶点,PA 为腰作等腰直角APD D ,过点D 作DE x ^轴于点E ,求OP DE -的值;(3)如图3,已知点F 坐标为()3,3--,当G 在y 轴运动时,作等腰直角FGH D ,并始终保持90GFH Ð=°,FG 与y 轴交于点()0,G m ,FH 与x 轴交于点(),0H n ,求m 、n 满足的数量关系.36.已知:在ABC V 中,90BAC Ð=°,AB AC =,AE 是过点A 的一条直线,且BD AE ^于D ,CE AE ^于E .(1)当直线AE 处于如图①的位置时,有BD DE CE =+,请说明理由;(2)当直线AE 处于如图②的位置时,则BD 、DE 、CE 的关系如何?请说明理由.参考答案1.(1)证明见解析;(2)25【分析】(1)根据12Ð=Ð,∠A =∠B =90°,可得DE CE =,ADE V 和BEC △为直角三角形,利用“HL ”即可证明Rt ADE △≌Rt BEC △;(2)根据(1)中Rt ADE △≌Rt BEC △,则ADE BEC Ð=Ð,根据直角三角形的性质推出90AED BEC Ð+Ð=°,则可得DEC Ð为直角,又因为∠1=∠2,则可知DEC Ð为等腰直角三角形,进而通过等腰直角三角形的性质求出其面积.【详解】(1)∵12Ð=Ð,∴DE CE =,∵∠A =∠B =90°,在Rt ADE △和Rt BEC △中,DE EC AE BC =ìí=î,∴Rt ADE △≌Rt BEC △;(2)∵Rt ADE △≌Rt BEC △,∴ADE BEC Ð=Ð,∵90ADE AED Ð+Ð=°,∴90AED BEC Ð+Ð=°,∴90DEC Ð=°,∵12Ð=Ð,∴DE CE =,∴DEC V 为等腰直角三角形,∴其斜边CD 上的高为5,∴1105252DEC S =´´=△.【点拨】本题考查了直角三角形的判定和性质,全等三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题.2.(1)见解析;(2)【分析】(1)根据等角的余角相等证明BAP CPD Ð=Ð,继而证明()ABP PDC AAS @V V ;(2)根据全等三角形对应边相等性质及勾股定理解题.【详解】(1)证明:,AB BD CD BD^^Q 90B D \Ð=Ð=°90BAP APB \Ð+Ð=°AP PC^Q 90APB CPD \Ð+Ð=°BAP CPD\Ð=ÐAP PC=Q ()ABP PDC AAS \@V V ;(2)连接AC ,()ABP PDC AAS @QV V 3,4AB BP CD ===Q5AP \===在,5Rt APC AP PC ==VAC \==.【点拨】本题考查全等三角形的判定与性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.3.见解析【分析】首先根据等量代换得出CAE ABD Ð=Ð,从而可证ADB CEA △≌△,最后利用全等三角形的性质即可得出结论.【详解】证明:设BDA BAC a Ð=Ð=,∴180-DBA BAD BAD CAE a Ð+Ð=Ð+Ð=°,∴CAE ABD Ð=Ð,∵在ADB △和CEA V 中ABD CAE BDA CEA AB AC Ð=ÐìïÐ=Ðíï=î,∴()ADB CEA AAS ≌△△,∴AE BD =,AD CE =,∴DE AE AD BD CE =+=+.【点拨】本题主要考查全等三角形的判定及性质,掌握全等三角形判定方法和性质是解题的关键.4.NQ =1.【分析】首先求出∠M=∠PSQ ,进而利用AAS 证明△MNS ≌△SQP ,所以MN=SQ 问题可解.解:,MS ,PS MN SN PQ SN ^^^Q ,90MSP N SQP \Ð=Ð=Ð=°,M MSN MSN PSQ \Ð+Ð=Ð+Ð,M PSQ \Ð=Ð,在MNS △和SQP V 中,M PSQ MNS SQP MS PS Ð=ÐìïÐ=Ðíï=î,()MNS SQP AAS \△≌△,SQ MN \=,∵SN =4,MN =3,431NQ SN SQ SN MN \=-=-=-= .【点拨】本题考查了全等三角形的判定和性质,垂直定义,根据条件证MNS SQP △≌△是解此题的关键.5.(1)见解析;(2)AD =BE +DE ,见解析;(3)DE =AD +BE【分析】(1)由已知推出∠CDA=∠BEC=90°,因为∠ACD+∠BCE=90°,∠ACD +∠DAC =90°,推出∠DAC=∠ECB ,根据AAS 即可得到△ADC ≌△CEB ;(2)由(1)得到AD=CE ,CD=BE ,即可求出答案;(3)与(1)证法类似可证出∠ACD=∠CBE ,能推出△ADC ≌△CEB ,得到AD=CE ,CD=BE ,即可得到DE 、AD 、BE 之间的等量关系.(1)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠CDA =∠BEC =90°.∴∠ACD +∠DAC =90°.∵∠ACB =90°,∴∠ACD +∠BCE =90°.∴∠DAC =∠ECB .在△ADC 和△CEB 中,CDA BEC DAC ECB AC CB ÐÐìïÐÐíïî===,∴△ADC ≌△CEB .(2)AD =BE +DE .理由如下:由(1)知△ADC ≌△CEB .∴AD =CE ,CD =BE .∴AD =CE =CD +DE =BE +DE .(3)DE =AD +BE .理由:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC=90°,∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACD=90°,∴∠ACD=∠CBE ,又∵∠ADC=∠CEB ,AC=CB ,∴△ADC ≌△CEB ,∴AD=CE ,CD=BE ,∵CD+CE=DE ,∴DE=AD+BE .【点拨】本题主要考查了余角的性质,直角三角形的两锐角互余,全等三角形的判定和性质等知识点,能根据已知证明△ADC ≌△CEBE 是解此题的关键,题型较好,综合性比较强.6.(1)见解析;(2)见解析.【分析】(1)根据已知条件容易证明△BEA ≌△AFC ,然后利用对应边相等就可以证明题目的结论;(2)根据(1)知道△BEA ≌△AFC 仍然成立,则BE=AF ,AE=CF ,就可以求出EF=BE-CF .解:(1)BE EA ^Q ,CF AF ^,BAC BEA CFE 90ÐÐÐ\===°,EAB CAF 90ÐÐ\+=°,EBA EAB 90ÐÐ+=°,CAF EBA ÐÐ\=,在ABE V 和CAF V 中,BEA AFC EBA FACAB AC Ð=ÐìïÐ=Ðíï=îBEA \V ≌()AFC AAS V ,EA FC \=,BE AF =,EF EA AF BE CF \=+=+.(2)BE EA ^Q ,CF AF ^,BAC BEA CFE 90ÐÐÐ\===°,EAB CAF 90ÐÐ\+=°,ABE EAB 90ÐÐ+=°,CAF ABE ÐÐ\=,在ABE V 和ACF V 中,EBA FAC BEA CFAAB AC Ð=ÐìïÐ=Ðíï=îBEA \V ≌()AFC AAS V ,EA FC \=,BE AF =,∵EF AF AE =-,∴EF BE CF=-【点拨】本题主要考查了全等三角形的性质与判定,利用它们解决问题,经常用全等来证线段和的问题.7.150米【分析】根据题意,判断出△ADC ≌△CEB 即可求解.解:如图,过点B 作BE ⊥MN 于点E ,∵∠ADC =∠ACB =90°,∴∠A =∠BCE (同角的余角相等).在△ADC 与△CEB 中,90ADC CEB A BCEAC CB Ð=Ð=°ìïÐ=Ðíï=î∴△ADC ≌△CEB (AAS ).∴BE =CD =150m .即村庄B 到河边的距离是150米.【点拨】本题主要考查的是全等三角形的实际应用,熟练掌握全等三角形的判定及性质是解答本题的关键.8.(1)AC CE ^,见解析;(2)成立,理由见解析;(3)成立,理由见解析【分析】(1)先用HL 判断出Rt Rt ABC CDE ≌△△,得出A DCE Ð=Ð,进而判断出90DCE ACB Ð+Ð=°,即可得出结论;(2)同(1)的方法,即可得出结论;(3)同(1)的方法,即可得出结论.【详解】解:(1)AC CE ^理由如下:∵AB BD ^,ED BD ^,∴90B D Ð=Ð=°在Rt ABC △和Rt CDE △中AC CE BC DE=ìí=î∴()Rt Rt HL ABC CDE △△≌,∴A DCEÐ=Ð∵90B Ð=°,∴90A ACB Ð+Ð=°,∴()18090ACE DCE ACB Ð=°-Ð+Ð=°,∴AC CE ^;(2)成立,理由如下:∵AB BD ^,ED BD ^,∴90B D Ð=Ð=°,在1Rt ABC V 和2Rt C DE △中121AC C E BC DE=ìí=î,∴()12Rt Rt HL ABC C DE ≌△△,∴2A C E D Ð=Ð,∵90B Ð=°,∴190B A AC Ð+Ð=°,∴2190DC E AC B Ð+Ð=°,在12C FC V 中,()122118090C FC DC E AC B Ð=°-Ð+Ð=°,∴12AC C E ^;(3)成立,理由如下:∵AB BD ^,ED BD ^,∴190ABC D Ð=Ð=°在1Rt ABC V 和2Rt C DE △中121AC C E BC DE =ìí=î,∴()12Rt Rt HL ABC C DE ≌△△,∴2A C E D Ð=Ð,∵190ABC Ð=°,∴190B A AC Ð+Ð=°,在12C FC V 中,()2112180=90C FC DC E AC B Ð=°-Ð+а,∴12AC C E ^.【点拨】此题是几何变换综合题,主要考查了全等三角形的判定和性质,直角三角形的性质,判断出12Rt Rt ABC C DE ≌△△是解本题的关键.9.3【分析】根据同角的余角相等可得EBC DCA Ð=Ð,根据“AAS”可证CEB △≌ADC V ,可得9AD CE ==,即可求BE 的长.解:∵BE CE ^,AD CE ^,∴90E ADC Ð=Ð=°,∴90EBC BCE Ð+Ð=°.∵90BCE ACD Ð+Ð=°,∴EBC DCA Ð=Ð.在CEB △和ADC V 中,E ADC EBC ACD BC AC Ð=ÐìïÐ=Ðíï=î,∴CEB △≌ADC V (AAS ),∴BE CD =,9AD CE ==,∴963BE CD CE DE ==-=-=.【点拨】本题考查了全等三角形的判定和性质,直角三角形的性质,熟练运用全等三角形的判定是本题的关键.10.(1)证明见解析;(2)ACB Ð为直角时,//BC DE【分析】(1)根据全等三角形的性质求出BD=AE ,AD=CE ,代入求出即可;2)根据全等三角形的性质求出∠E=∠BDA= 90°,推出∠BDE=90° ,根据平行线的判定求出即可.【详解】(1)证明:∵ABC DAE △△≌,∴AE=BC ,AC=DE ,又∵AE AC CE =+,∴BC DE CE =+.(2)若//BC DE ,则BCE E Ð=Ð,又∵ABC DAE △△≌,∴ACB E Ð=Ð,∴ACB BCE Ð=Ð,又∵180ACB BCE Ð+Ð=°,∴90ACB Ð=°,即当ABC V 满足ACB Ð为直角时,//BC DE .【点拨】本题考查全等三角形的性质和平行线的判定的应用,关键是通过三角形全等得出正确的结论.11.(1)见详解;(2)DE =BD +CE .理由见详解【分析】(1)根据BD ⊥直线m ,CE ⊥直线m 得∠BDA =∠CEA =90°,而∠BAC =90°,根据等角的余角相等,得∠CAE =∠ABD ,然后根据“AAS”可判断△ABD ≌△CAE ;(2)由∠BDA =∠AEC =∠BAC ,就可以求出∠BAD =∠ACE ,进而由ASA 就可以得出△ABD ≌△CAE ,就可以得出BD =AE ,DA =CE ,即可得出结论.【详解】(1)证明:如图①,∵D ,A ,E 三点都在直线m 上,∠BAC =90°,∴∠BAD +∠CAE =90°,∵BD ⊥m ,CE ⊥m ,∴∠ADB =∠CEA =90°,∴∠BAD +∠ABD =90°,∴∠ABD =∠CAE ,在△ABD 和△CAE 中,ADB AEC ABD CAE AB AC ÐÐìïÐÐíïî===,∴△ABD ≌△CAE (AAS );(2)DE =BD +CE .理由如下:如图②,∵∠BDA =∠AEC =∠BAC ,∴由三角形内角和及平角性质,得:∠BAD +∠ABD =∠BAD +∠CAE =∠CAE +∠ACE ,∴∠ABD =∠CAE ,∠BAD =∠ACE ,在△ABD 和△CAE 中,ABD CAE AB ACBAD ACE ÐÐìïíïÐÐî===,∴△ABD ≌△CAE (ASA ),∴BD =AE ,AD =CE ,∴DE =AD +AE =BD +CE .【点拨】本题考查了全等三角形的判定与性质以及三角形内角和定理的综合应用,解题的关键是熟练掌握全等三角形的判定方法,灵活运用所学知识解决问题.12.AC ⊥CD ,理由见解析【分析】根据条件证明△ABC ≌△CED 就得出∠ACD=90°,则可以得出AC ⊥CD .【详解】解:AC ⊥CD .理由:∵AB ⊥BE ,DE ⊥BE ,∴∠B =∠E =90°.在Rt △ABC 和Rt △CED 中,AB CE AC CD =ìí=î,∴Rt △ABC ≌Rt △CED (HL ),∴∠A =∠DCE ,∠ACB =∠D .∵∠A+∠ACB =90°,∴∠DCE+∠ACB =90°.∵∠DCE+∠ACB+∠ACD =180°,∴∠ACD =90°,∴AC ⊥CD .【点拨】本题考查了全等三角形的判定及性质的运用,垂直的判定及性质的运用,解答时证明三角形全等是关键.13.(1)证明见解析;(2)180ACB a Ð+Ð=°,证明见解析;(3)EF BE AF =+,证明见解析.【分析】(1)①求出∠BEC =∠AFC =90°,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE =AF 即可;②当∠α+∠ACB =180°,证明∠BEC =∠AFC ,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE =AF 即可;(2)求出∠BEC =∠AFC ,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE=AF 即可.【详解】(1)①在图1中,90BEC AFC Ð=Ð=°Q ,90ACB Ð=°,90BCE ACF Ð+Ð=°,90EBC BCE Ð+Ð=°,EBC ACF \Ð=Ð,在BCE V 和CAF V 中,EBC ACF BEC AFC BC AC Ð=ÐìïÐ=Ðíï=î,()BCE CAF AAS \@V V ,BE CF \=,CE AF =,EF CF CE BE AF \=-=-;②当180ACB a Ð+Ð=°时,①中结论仍然成立;证明:在图2中,BEC CFA a Ð=Ð=ÐQ ,180ACB a Ð+Ð=°,BCE ACF EBC BCE \Ð+Ð=Ð+Ð,EBC ACF \Ð=Ð,在BCE V 和CAF V 中,EBC ACF BEC AFC BC AC Ð=ÐìïÐ=Ðíï=î,()BCE CAF AAS \@V V ,BE CF \=,CE AF =,EF CF CE BE AF \=-=-.故答案为180ACB a Ð+Ð=°;(2)不成立,结论:EF BE AF =+.理由:在图3中,BEC CFA a Ð=Ð=ÐQ ,a BCA Ð=Ð,又180EBC BCE BEC +Ð+Ð=°Q ,180BCE ACF ACB Ð+Ð+Ð=°,EBC BCE BCE ACF \Ð+Ð=Ð+Ð,EBC ACF \Ð=Ð,在BEC △和CFA △中,EBC FCA BEC CFA BC CA Ð=ÐìïÐ=Ðíï=î,()BEC CFA AAS \@V V ,AF CE \=,BE CF =,EF CE CF =+Q ,EF BE AF \=+.【点拨】本题综合考查三角形综合题、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,注意这类题目图形发生变化,结论基本不变,证明方法完全类似,属于中考常考题型.14.见解析【分析】证明△BEA ≌△AFC ,得到AE=CF ,BE=AF ,即可得到结论.证明:BE EA ^Q ,CF AF ^,90BAC BEA AFC \Ð=Ð=Ð=°,90EAB CAF \Ð+Ð=°,90EBA EAB Ð+Ð=°,CAF EBA \Ð=Ð,在ABE △和AFC △中,BEA AFC EBA CAF AB AC Ð=ÐìïÐ=Ðíï=î,(AAS)BEA AFC \△≌△.AE CF ∴=,BE AF =.EF AF AE BE CF \=+=+..【点拨】此题考查全等三角形的判定及性质,熟记三角形的判定定理是解题的关键.15.(1)见解析;(2)8秒【分析】(1)根据垂直及角之间的关系证明出PDA CBD Ð=Ð,又有90PAD C Ð=Ð=°,=6AD BC =,根据三角形全等的判定定理则可证明PDA DBC △≌△.(2)根据垂直及角之间的关系证明APF DAF Ð=Ð,又因为90PAD C Ð=Ð=°,AD BC =,则可证明PAD ACB △≌△,所以8cm AP AC ==,即t=8秒.(1)证明:PD BD ^Q,90PDB \Ð=°,即90BDC PDA Ð+Ð=°又90C Ð=°Q ,90BDC CBD Ð+Ð=°PDA CBD\Ð=Ð又AE AC ^Q ,90PAD \Ð=°90PAD C \Ð=Ð=°又6cm BC =Q ,6cmAD =AD BC\=在PAD △和DCB V 中PAD C AD CBPDA DBC Ð=Ðìï=íïÐ=Ðî()PDA DBC ASA \△≌△(2)PD AB ^Q ,90AFD AFP \Ð=Ð=°,即90PAF APF Ð+Ð=°又AE AC ^Q ,90PAF DAF \Ð+Ð=°APF DAF\Ð=Ð又90PAD C Ð=Ð=°Q ,AD BC=在APD △和CAB △中APD CAB PAD CAD BC Ð=ÐìïÐ=Ðíï=î()PAD ACB AAS \△≌△8cmAP AC \==即8t =秒.【点拨】本题主要考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理,灵活运用角之间的关系是解题关键.16.(1)证明见解析;(2)EF=17cm .【分析】(1)根据垂直的定义可得∠AEC=∠CFB=90°,然后求出∠EAC=∠FCB ,再利用“角角边”证明即可;(2)由全等三角形的性质可得:AE=CF ,CE=BF ,再根据线段的和差求解即可.【详解】(1)证明:在Rt △ACB 中,∵∠ACB=90°,∴∠ACE+∠BCF=90°∵AE ⊥EF ,BF ⊥EF∴∠ACE+∠EAC=90°∴∠CAE=∠BCF又∵ AC=CB∴△ACE ≌△CBF(ASA)(2)由△ACE ≌△CBF 可得:AE=CF=12cm , EC=BF=5cm ,∴EF=EC+CF=12+5=17cm .【点拨】本题考查了全等三角形的判定与性质,同角的余角相等的性质,熟练掌握三角形全等的判断方法并找出全等的条件是解题的关键.17. 1.5cm DE =.【分析】根据垂直定义求出∠BEC =∠ACB =∠ADC ,根据等式性质求出∠ACD =∠CBE ,根据AAS 证明△BCE ≌△CAD ;根据全等三角形的对应边相等得到AD =CE ,BE =CD ,利用DE =CE−CD ,即可解答.【详解】AD CE ^Q ,BE CE^90ADC CEB \Ð=Ð=°90BCE CBE \Ð+Ð=°又90ACB Ð=°Q 90BCE ACD \Ð+Ð=°CBE ACD\=Ð在ACD △和CBE △中ADC CEB ACD CBEAC BC Ð=ÐìïÐ=Ðíï=î()AAS ACD CBE \△≌△CD BE \=,AD CE=又 2.5cm AD =Q ,1cmBE =2.5cm CE \=,1cm=CD 2.51 1.5cm DE CE CD \=-=-=.【点拨】本题考查了全等三角形的性质和判定,垂线的定义等知识点的应用,解此题的关键是推出证明ACD CBE \V V ≌的三个条件.18.(1)见解析;(2)BE= AB+AD ,理由见解析.【分析】(1)利用余角的性质得到∠ACD=∠BEC ,从而证明△ACD ≌△BEC ,得到AD=BC ,AC=BE ,从而得到结论;(2)根据△ACD ≌△BEC ,得到AD=BC ,AC=BE ,从而得到BE=AC=AB+BC=AB+AD .【详解】解:(1)∵BE ⊥AB ,∴∠BCE+∠BEC=90°,∵DC ⊥EC ,∴∠ACD+∠BCE=90°,∴∠ACD=∠BEC ,在△ACD 和△BEC 中,A B ACD BECCD CE Ð=ÐìïÐ=Ðíï=î∴△ACD ≌△BEC (AAS ),∴AD=BC ,AC=BE ,∴AD+BE=AC+BC=AB ;(2)由(1)可得:△ACD ≌△BEC ,∴AD=BC ,AC=BE ,∴BE=AC=AB+BC=AB+AD .【点拨】本题考查了全等三角形的判定与性质,找出条件,证明全等,利用全等的性质得到线段的数量关系是本题考查的内容.19.(1)见解析;(2)BD DE CE =-,见解析;(3)BD DE CE =-;(4)当B ,C 在AE 的同测时,BD DE CE =-;当B ,C 在AE 的异侧时,若BD CE >,则BD DE CE =+,若BD CE <,则BD CE DE=-【分析】(1)在直角三角形中,由题中条件可得∠ABD=EAC ,又有AB=AC ,则有一个角及斜边相等,则可判定△BAD ≌△AEC ,由三角形全等可得三角形对应边相等,进而通过线段之间的转化,可得出结论;(2)由题中条件同样可得出△BAD ≌△AEC ,得出对应线段相等,进而可得线段之间的关系;(3)同(2)的方法即可得出结论.(4)利用(1)(2)(3)即可得出结论.【详解】解:(1)∵BD ⊥AE ,CE ⊥AE∴∠ADB=∠CEA=90°∴∠ABD+∠BAD=90°又∵∠BAC=90°∴∠EAC+∠BAD=90°∴∠ABD=∠CAE在△ABD 与△ACE 中ADB CEA ABD CAEAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△ACE∴BD=AE ,AD=EC ,∴BD=DE+CE(2)∵BD ⊥AE ,CE ⊥AE∴∠ADB=∠CEA=90°∴∠ABD+∠BAD=90°又∵∠BAC=90°∴∠EAC+∠BAD=90°∴∠ABD=∠CAE在△ABD 与△ACE 中ADB CEA ABD CAEAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△ACE∴BD=AE ,AD=EC∴BD=DE-CE ,(3)∵∠BAC=90°,∴∠BAD+∠EAC=90°,又∵BD ⊥AE ,CE ⊥AE ,∴∠BDA=∠AEC=90°,∠BAD+∠ABD=90°,∴∠ABD=∠EAC ,在△ABD 与△CAE 中,BDA AEC ABD EACAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△CAE ,∴BD=AE ,AD=CE ,∵DE=AD+AE=BD+CE ,∴BD=DE-CE .(4)归纳:由(1)(2)(3)可知:当B ,C 在AE 的同侧时,若BD> CE,则BD= DE +CE,若BD> CE,则BD= DE +CE,若BD< CE,则BD= CE- DE.【点拨】此题是几何变换综合题,主要考查了三角形全等的判定方法,余角的性质,线段的和差,熟练掌握全等三角形的判定和性质是解题的关键.20.15.【分析】解:由∠1=∠2=∠BAC ,得到∠BAE=∠ACF ,∠ABE=∠CAF 从而证明△ABE ≌△CAF(ASA).得到AF=BE ,再根据DF=2AF ,BE 的长为5,求得AD 的长.【详解】解:∵12BAC Ð=Ð=Ð,且1BAE ABE Ð=Ð+Ð,2CAF ACF Ð=Ð+Ð,∠BAC=∠BAE+∠CAF ,∴∠BAE=∠ACF ,∠ABE=∠CAF .在ABE △和CAF V 中,BAE ACF AB CAABE CAF Ð=Ðìï=íïÐ=Ðî∴()ABE CAF ASA ≌△△.∴AF BE=∵2DF AF =,BE 的长为5,∴10DF =,5AF BE ==,∴51015AD AF DF =+=+=.【点拨】本题考查了全等三角形的性质和判定,解题的关键是熟悉掌握全等三角形的性质和证明.21.(1)详见解析;(2)结论:DE =CE ﹣BD ,详见解析【分析】(1)利用已知得出∠CAE=∠ABD ,进而利用AAS 得出则△ABD ≌△CAE ,即可得出DE=BD+CE ;(2)利用已知得出∠CAE=∠ABD ,进而利用AAS 得出则△ABD ≌△CAE ,即可得出BD 、CE 与DE 之间的数量关系.【详解】解:(1)证明:∵BD ⊥l ,CE ⊥l ,∴∠BD A =∠AEC =90°又 ∵Rt ABC D ,∴∠BAD +∠CAE =90°,∠BAD +∠ABD =90°,∴∠CAE =∠ABD在△ABD 和△CAE 中=ABD CAE ADB CEAAB AC =ìïíï=î∠∠∠∠∴△ABD ≌ △CAE∴BD =AE ,AD =CE∵DE =AD +AE ,∴DE =CE +BD .(2) 如图②所示:结论:DE =CE ﹣BD证明:∵BD ⊥l ,CE ⊥l ,∴∠BD A =∠AEC = 90°∵∠BAD +∠CAE =90°,∠BAD +∠ABD =90°,∴∠CAE =∠ABD在△ABD 和△CAE 中==ABD CAE ADB CEAAB AC ìïíï=î∠∠∠∠∴△ABD ≌△CAE (AAS )∴BD =AE ,AD =CE∵DE =AD ﹣AE∴DE =CE ﹣BD【点拨】此题主要考查了全等三角形的判定与性质等知识,根据已知得出△ABD ≌△CAE 是解题关键.22.(1)补全如图所示见解析;CD BC AD =+;(2)成立,证明见解析;(3)点B 的坐标为()1,2-.【分析】(1)依题意补全图,易证△AOD ≌△OBC ,则有AD =CO ,OD =BC ,从而可得CD BC AD =+;(2)利用三角形内角和易证23ÐÐ=,再证明BCO ODA V V ≌,同(1)即可证明结论;(3)过B 、C 两点作y 轴垂线,构造如(1)图形,即可得三角形全等,再将线段关系即可求出点B 坐标.【详解】(1)补全图1如图所示,CD BC AD =+;证明:∵90AOB Ð=°,BC ⊥直线l ,AD ^ 直线l ,∴∠BCO =∠ODA =90°,∴∠BOC +∠OBC =90°,又∵90AOB Ð=°,∴∠BOC +∠AOD =90°,∴∠OBC =∠AOD ,在△AOD 和△OBC 中BCO ODA OBC AOD BO AO Ð=ÐìïÐ=Ðíï=î,∴△AOD ≌△OBC (AAS )∴AD =CO ,OD =BC ,∵CD OD CO =+,∴CD BC AD =+.(2)成立.证明:如图,∵12180BOA Ð+Ð=°-Ð,13180BOA Ð+Ð=°-Ð,BOA BCOÐ=Ð∴23ÐÐ=在BCO V 和ODA V中32BCO ODABO OA Ð=ÐìïÐ=Ðíï=î∴BCO ODA V V ≌(AAS )∴BC OD =,CO AD=∴CD CO OD AD BC=+=+(3)点B 的坐标为()1,2-.过程如下:过B 、C 两点作y 轴垂线,垂足分别为M 、N ,同理(1)可得,CN =AM ,AN =MB ,∵点A 的坐标为(0,1),点C 的坐标为()3,2,∴CN =AM =3,ON =2,OA =1,∴MB =AN =ON -OA =1,OM =AM -OA =2,∵点B 在第四象限,∴点B 坐标为:()1,2-.【点拨】主要考查了等腰直角三角形的性质,全等三角形的判定和性质、图形与坐标变换,构造出全等三角形是解本题的关键.23.(1)见解析;(2)DE =AD +BE ;见解析;(3)AD =DE +BE【分析】(1)利用垂直的定义得∠ADC =∠CEB =90°,再利用HL 证明Rt △ADC ≌Rt △CEB ,得到∠DAC =∠BCE ,再根据余角的定义得到∠ACD +∠BCE =∠ACB =90°,可得结论;(2)根据Rt △ADC ≌Rt △CEB 得到DC =BE ,从而利用等量代换得到DE =AD +BE ;(3)同理可证:Rt △ADC ≌Rt △CEB ,利用等量代换可得AD =DE +BE .【详解】解:(1)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠CEB =90°,在Rt △ADC 和Rt △CEB 中,AC BC AD CE =ìí=î,∴Rt △ADC ≌Rt △CEB (HL ),∴∠DAC =∠BCE ,∵∠ADC =90°,即∠DAC +∠ACD =90°,∴∠ACD +∠BCE =90°,即∠ACB =90°,∴AC ⊥BC ;(2)DE =AD +BE ,理由如下:∵Rt △ADC ≌Rt △CEB ,∴DC =BE ,∵AD =CE ,∴DE =DC +CE =AD +BE ;(3)AD =DE +BE ,同理可证:Rt △ADC ≌Rt △CEB (HL ),∴CD =BE ,∴AD =CE =DE +CD =DE +BE ,∴即AD =DE +BE .【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”、“HL ”;全等三角形的对应边、对应角相等.24.(1)①见解析;②见解析;(2)见解析.【分析】(1)①根据已知可利用AAS 证明△ADC ≌△CEB ;②由①证得△ADC ≌△CEB ,得出对应边相等,CE =AD ,CD =BE 由此可证DE =AD−BE ;(2)根据已知可利用AAS 证明△ADC ≌△CEB ,得出对应边相等,AD =CE ,CD =BE ,由此可证DE =BE−AD .【详解】证明:(1)①∵∠ADC =∠ACB =∠BEC =90°,∴∠CAD +∠ACD =90°,∠BCE +∠CBE =90°,∠ACD +∠BCE =90°.∴∠CAD =∠BCE .∵AC =BC ,∴△ADC ≌△CEB .②由①证得△ACD ≌△CBE .∴CE =AD ,CD =BE .∴DE =CE−CD =AD−BE .(2)∵∠ADC =∠CEB =∠ACB =90°,∴∠ACD =∠CBE ,又∵AC =BC ,∴△ACD ≌△CBE ,∴AD =CE ,CD =BE ,∴DE =CD−CE =BE−AD .【点拨】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,再根据全等三角形对应边相等得出结论.25.(1)见解析;(2)60°.【分析】(1)利用ASA 证明△BAE ≌△CED ,可证AE=DE ,后利用∠BAE+∠BEA=90°,证明∠BEA+∠CED=90°,问题得证;(2)利用直角三角形的两个锐角互余,求解即可.【详解】(1)∵90B C Ð=Ð=°,BAE CED Ð=Ð,且AB CE =,∴△BAE ≌△CED ,∴AE=DE ,∵∠BAE+∠BEA=90°,∴∠BEA+∠CED=90°,∴∠AED=90°,∴△AED 是等腰直角三角形;(2)∵2CDE BAE Ð=Ð,BAE CED Ð=Ð,∴2CDE CED Ð=Ð,∵∠CDE+∠CED=90°,∴∠CDE=60°.【点拨】本题考查了三角形的全等,等腰直角三角形的定义,直角三角形的锐角互余的性质,根据图形,结合条件选择对应判定方法,根据性质构造基本的计算等式是解题的关键.26.见解析.【分析】证明ADE BCD Ð=Ð,为三角形的全等提供条件即可.证明:ADE CDE B BCD Ð+Ð=Ð+ÐQ ,CDE B Ð=Ð,ADE BCD \Ð=Ð,AC BC =Q ,A B \Ð=Ð,在ADE V 和BCD △中A B AD BCADE BCD Ð=Ðìï=íïÐ=Ðî,ADE \V ≌BCD △(ASA) .【点拨】本题考查了ASA 证明三角形的全等,抓住题目的特点,补充全等需要的条件是解题的关键.27.(1)见解析;(2)成立,见解析【分析】(1)先证∠ABD=∠EAC ,再证△ABD ≌ △CAE (AAS )即可;(2)先证出∠ABD = ∠EAC ,再证△ABD ≌ △CAE (AAS )即可.证明:(1)∵AB ⊥AC,BD ⊥DE,CE ⊥DE,∴∠BDA=∠AEC=∠BAC=90°,∴∠DAB+∠ABD=∠EAC+∠DAB=90°,∴∠ABD=∠EAC,在△ABD 和 △CAE 中,ABD EAC BDA AEC AB AC Ð=ÐìïÐ=Ðíï=î,∴ △ABD ≌ △CAE (AAS ),∴ BD = AE ,AD = CE ,∴ DE = AE + DA ;(2)成立,理由如下:∵ ∠BAC + ∠BAD + ∠EAC = 180° ,∠ADB + ∠BAD + ∠ABD = 180°,∠BAC = ∠BDA ,∴∠ABD = ∠EAC ,在△ABD 和 △CAE 中,ABD EAC BDA AEC AB AC Ð=ÐìïÐ=Ðíï=î,∴ △ABD ≌ △CAE (AAS ),∴ BD = AE ,AD = CE ,∴ DE = AE + DA = BD + CE.【点拨】本题考查三角形全等的判定与性质,掌握三角形全等的判定与性质是解题关键.28.(1)DE BD CE =+;(2)成立,证明见详解;(3)8.【分析】(1)通过题中的直角和垂直条件,可得到CAE ABD Ð=Ð,然后证明△CAE ≌△ABD ,即得到BD AE =,AD CE =,然后通过等量代换即可得到结论;(2)同(1)中类似,先证明△CAE ≌△ABD 后得到对应边成比例即可;(3)证明△CAE ≌△ABD ,发现ABD △与CEF △的面积之和即为△ACF 的面积,然后根据2BC CF =即可得到答案.解:(1)DE BD CE =+,∵90BAC Ð=°,∴90BAD CAE Ð+Ð=°,∵BD m ^,CE m ^,∴90CEA BDA Ð=Ð=°,∴90BAD ABD Ð+Ð=°,∴CAE ABDÐ=Ð在△CAE 和△ABD 中,90CAE ABD AB ACCEA BDA Ð=Ð=Ð=Ð=°ìïíïî∴△CAE ≌△ABD ,∴BD AE =,AD CE =,∵DE AD AE =+,∴DE BD CE =+;(2)成立,∵BDA AEC BAC a Ð=Ð=Ð=,且180BAD BAC CAE Ð+Ð+Ð=°,∴180BAD CAE a Ð+Ð+=°,在△ABD 中,180BAD ABD BDA Ð+Ð+Ð=°,∴180BAD ABD a Ð+Ð+=°,∴CAE ABD Ð=Ð,在△CAE 和△ABD 中,。
初一数学几何大题

初⼀数学⼏何⼤题⼀、填空题:1. 在直⾓三⾓形中,已知⼀直⾓边为8 cm,另⼀直⾓边为6 cm,则斜边的⻓度是______ cm。
2. 在平⾏四边形中,对⾓线分别为10 cm和16 cm,这个平⾏四边形的⾯积是______ 平⽅厘⽶。
3. ⼀条直线穿过两个平⾏线,若与⼀个平⾏线的交点⾓为75°,则它与另⼀个平⾏线的交点⾓为______ 度。
⼆、选择题:1. 在梯形ABCD中,AB ∥ CD,AB = 6 cm,CD = 10 cm,AD = BC = 8 cm,则梯形的⾯积是下列哪个选项?A) 32 平⽅厘⽶B) 48 平⽅厘⽶C) 64 平⽅厘⽶D) 80 平⽅厘⽶2. 已知三⾓形的三个内⾓分别为30°、60°和90°,则这个三⾓形是下列哪个选项?A) 等边三⾓形B) 直⾓三⾓形C) 等腰三⾓形D) 钝⾓三⾓形三、解答题:1. 如图所⽰,在⻓⽅形ABCD中,对⾓线AC交BD于点E。
若AB = 12 cm,BC = 9 cm,求出三⾓形AEC的⾯积。
(题图:⻓⽅形ABCD,AC交BD于点E,AB = 12 cm,BC = 9 cm)2. 已知正⽅形的外边⻓为10 cm,⼀条边上有⼀个点P,连接点P与正⽅形的两个不相邻顶点,形成三⾓形。
求出三⾓形的周⻓。
四、综合应⽤题:1. ⼩明想要建造⼀个形状为梯形的花坛,已知上底⻓为6 m,下底⻓为10 m,⾼为4m。
若梯形花坛四周都铺上⽯⼦,每平⽅⽶需要5 kg的⽯⼦,⼩明需要准备多少公⽄的⽯⼦?2. 某校操场是⼀个⻓为80 m,宽为60 m的矩形,现在在操场的四个⾓上各建了⼀个相同的圆形花坛,且使得每个圆形花坛都刚好与其他两个圆形花坛的边界相切。
求这四个圆形花坛的直径⻓度。
根据任务要求,以上为初⼀数学⼏何⼤题的⽂档内容,排版整洁美观,符合语句通顺、⽆影响阅读体验的要求。
相似三角形几何题(含答案)

相似三角形几何题(WORD 版,有答案)1、如图,AD 是圆O 的直径,BC 切圆O 于点D ,AB 、AC 与圆O 相交于点E 、F 。
求证:AC AF AB AE ⋅=⋅;F O E DBA2为了加强视力保护意识,小明想在长为3.2米,宽为4.3米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、 丙位同学设计方案新颖,构思巧妙.(10分)(1)甲生的方案:如图1,将视力表挂在墙ABEF 和墙ADGF 的夹角处,被测试人站立 在对角线AC 上,问:甲生的设计方案是否可行?请说明理由.(2)乙生的方案:如图2,将视力表挂在墙CDGH 上,在墙ABEF 上挂一面足够大的平面镜,根据平面镜成像原理可计算得到:测试线应画在距离墙ABEF 米处.(3)丙生的方案:如图3,根据测试距离为5m 的大视力表制作一个测试距离为3m 的小视 力表.如果大视力表中“E ”的长是3.5cm ,那么小视力表中相应“E ”的长是多少cm ?3、如图,四边形ABCD 中,AD =CD ,∠DAB =∠ACB =90°,过点D 作DE ⊥AC ,垂足为F ,DE 与AB 相交于点E .(12分)(1)求证:AB ·AF =CB ·CD ;(2)已知AB =15 cm ,BC =9 cm ,P 是射线DE 上的动点.设DP =x cm (0x >),四边形BCDP 的面积为y cm 2.①求y 关于x 的函数关系式;②当x 为何值时,△PBC 的周长最小,并求出此时y 的值.HH(图1)(图2) (图3)3.5㎝ACF3mB5mDA B CD EF P ·4已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.(1)求证:△ABD∽△CBA;(2)作DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长.5.已知:如图,AB是半圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长.6.如图所示,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,试在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(A1,B1,C1三点都在格点上),并求出这个三角形的面积.7.如图所示,在5×5的方格纸上建立直角坐标系,A(1,0),B(0,2),试以5×5的格点为顶点作△ABC 与△OAB相似(相似比不为1),并写出C点的坐标.8.如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC 交AB 于E 点.(1)求∠D 的度数;(2)求证:AC 2=AD ·CE .9.已知:如图,△ABC 中,∠BAC =90°,AB =AC =1,点D 是BC 边上的一个动点(不与B ,C 点重合),∠ADE =45°.(1)求证:△ABD ∽△DCE ;(2)设BD =x ,AE =y ,求y 关于x 的函数关系式; (3)当△ADE 是等腰三角形时,求AE 的长.10.已知:如图,△ABC 中,AB =4,D 是AB 边上的一个动点,DE ∥BC ,连结DC ,设△ABC 的面积为S ,△DCE 的面积为S ′.(1)当D 为AB 边的中点时,求S ′∶S 的值; (2)若设,,y SS x AD ='=试求y 与x 之间的函数关系式及x 的取值范围.11.已知:如图,抛物线y =x 2-x -1与y 轴交于C 点,以原点O 为圆心,OC 长为半径作⊙O ,交x 轴于A ,B 两点,交y 轴于另一点D .设点P 为抛物线y =x 2-x -1上的一点,作PM ⊥x 轴于M 点,求使△PMB ∽△ADB 时的点P 的坐标.12.在平面直角坐标系xOy 中,已知关于x 的二次函数y =x 2+(k -1)x +2k -1的图象与x 轴交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C (0,-3). 求这个二次函数的解析式及A ,B 两点的坐标.13.如图所示,在平面直角坐标系xOy 内已知点A 和点B 的坐标分别为(0,6),(8,0),动点P 从点A开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P ,Q 移动的时间为t 秒.(1)求直线AB 的解析式;(2)当t 为何值时,△APQ 与△ABO 相似? (3)当t 为何值时,△APQ 的面积为524个平方单位?14.已知:如图,□ABCD 中,AB =4,BC =3,∠BAD =120°,E 为BC 上一动点(不与B 点重合),作EF ⊥AB 于F ,FE ,DC 的延长线交于点G ,设BE =x ,△DEF 的面积为S .(1)求证:△BEF ∽△CEG ;(2)求用x 表示S 的函数表达式,并写出x 的取值范围; (3)当E 点运动到何处时,S 有最大值,最大值为多少?15、已知:如图,在平面直角坐标系中,ABC△是直角三角形,90ACB∠=,点A C,的坐标分别为(30)A-,,(10)C,,43=ACBC.(13分)(1)求过点A B,的直线的函数表达式;(2)在x轴上找一点D,连接DB,使得ADB△与ABC△相似(不包括全等),并求点D的坐标;(3)在(2)的条件下,如P Q,分别是AB和AD上的动点,连接PQ,设AP DQ m==,问是否存在这样的m使得APQ△与ADB△相似,如存在,请求出m的值;如不存在,请说明理由.16.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙80cm,梯上点D距墙70cm,BD长55cm.求梯子的长.17.如图,已知AC⊥AB,BD⊥AB,AO=78cm,BO=42cm,CD=159cm,求CO和DO.18.如图,已知∠ACB=∠CBD=90°,AC=b,CB=a,当BD与a、b之间满足怎样的关系式时,△ACB∽△CBD?A COBxy19.(本题10分)正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点, 当M 点在BC 上运动时,保持AM 和MN 垂直,(1)证明:Rt Rt ABM MCN △∽△;(2)设BM x =,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 面积最大,并求出最大面积;(3)当M 点运动到什么位置时Rt Rt ABM AMN △∽△,求此时x 的值.20.(本题10分)如图1,在Rt ABC △中,90BAC ∠=°,AD BC ⊥于点D ,点O 是AC 边上一点,连接BO 交AD 于F ,OE OB ⊥交BC 边于点E .(1)求证:ABF COE △∽△;(2)当O 为AC 边中点,2ACAB=时,如图2,求OF OE 的值; (3)当O 为AC 边中点,ACn AB=时,请直接写出OF OE 的值.21(6分)一般的室外放映的电影胶片上每一个图片的规格为3.5cm ×3.5cm ,放映的银幕规格为2m ×2m ,若影机的光源距胶片20cm 时,问银幕应在离镜头多远的地方,放映的图像刚好布满整个银幕?DMA BCNBBA A C OE D DE C O F图1 图2 F22.(6分)如图13,四边形ABCD 、CDEF 、EFGH 都是正方形. (1)⊿ACF 与⊿ACG 相似吗?说说你的理由. (2)求∠1+∠2的度数.23.(6分)如图13,矩形ABCD 的对角线AC 、BD 相交于点O ,E 、F 分别是OA 、OB 的中点. (1)试问:△ADE 与△BCF 全等吗?请说明理由;(2)若AD = 4cm ,AB = 8cm ,求CF 的长.24(6分)已知:如图14,在△ABC 中,AB=AC=a ,M 为底边BC 上任意一点,过点M 分别作AB 、AC 的平行线交AC 于P ,交AB 于Q. (1)求四边形AQMP 的周长;(2)写出图中的两对相似三角形(不需证明);BACPQ MBCDOFF E O CBAAA A BBBCCCD DDOE FGPMN⑴⑵⑶25(6分)如图15,已知△ABC 、△DCE 、△FEG 是三个全等的等腰三角形,底边BC 、CE 、EG 在同一直线上,且AB=3,BC=1.连结BF ,分别交AC 、DC 、DE 于点P 、Q 、R.(1)求证:△BFG ∽△FEG ,并求出BF 的长; (2)观察图形,请你提出一个与点..P .相关..的问题,并进行解答(根据提出问题的层次和解答过程评分).26(6分)(1)如图16(1),在正方形ABCD 中,对角线AC 、BD 相交于点O ,易知AC ⊥BD ,AC CO =21; (2)如图16(2),若点E 是正方形ABCD 的边CD 的中点,即21=DC DE ,过D 作DG ⊥AE ,分别交AC 、BC 于点F 、G.求证:31=AC CF ; (3)如图16(3),若点P 是正方形ABCD 的边CD 上的点,且nDC DP 1=(n 为正整数),过点D 作DN ⊥AP ,分别交AC 、BC 于点M 、N ,请你先猜想CM 与AC 的比值是多少?然后再证明你猜想的结论.27(8分)如图17,已知矩形ABCD 的边长3cm 6cm AB BC ==,.某一时刻,动点M 从A 点出发沿AB 方向以1cm/s 的速度向B 点匀速运动;同时,动点N 从D 点出发沿DA 方向以2cm /s 的速度向A 点匀速运动,问:(1)经过多少时间,AMN △的面积等于矩形ABCD 面积的19? (2)是否存在时刻t ,使以A M N ,,为顶点的三角形与ACD △相似?若存在,求t 的值;若不存在,请说明理由.28.如图,已知⊙O 的弦CD 垂直于直径AB ,点E 在CD 上,且EC = EB .(1)求证:△CEB ∽△CBD ;(2)若CE = 3,CB=5 ,求DE 的长.29.如图,把菱形ABCD 沿着BD 的方向平移到菱形A /B /C /D /′的位置, (1)求证:重叠部分的四边形B /EDF /是菱形(2)若重叠部分的四边形B /EDF /面积是把菱形ABCD 面积的一半,且BD=2,求则此菱形移动的距离.30.如图,在Rt ABC △中,90C =∠,12BC AC ==,,把边长分别为123n x x x x ,,,,的n 个正方形依次放入ABC △中,请回答下列问题:(1n1 2 3 n x(2)第n 个正方形的边长n = ;(3)若m n p q ,,,是正整数,且m n p q x x x x =,试判断m n p ,,,的关系.AB C DMF E /CB/A/DB BC A2x3x1x答案1.方法1:连接ED,DF,证⊿ADE∽⊿ABD,得AB AE AD •=2同理可证⊿ADF∽⊿ACD,得AC AF AF •=2故,AE·AB=AF·AC方法2:连接EF,ED证⊿AEF∽⊿ACB2.⑴在Rt ⊿ABC中,AC=22CD AD +=223.42.3+>5故,可行;⑵ 1.8;⑶利用⊿AED∽⊿ACB可求得FD=2.1m3.(1)证⊿DA F∽⊿ABC(2) )0(273〉+=x x y(3)当点P 运动到点E 的位置,即x =12.5时,△PBC 的周长最小,此时y 的值为64.54.(1)4943+=x y(2)过点B作AB 的垂线交x 轴于点D , D 点的坐标为(3.25,0) (3)存在,m =925或36125 5.(1),BABDCB AB =CBA ABD ∠=∠,得△HBD ∽△CBA ; (2)△ABC ∽△CDE ,DE =1.5.6..cm 133提示:连结AC .7.提示:.52,10,25111111===C B B A C A △A 1B 1C 1的面积为5. 8.C (4,4)或C (5,2).9.提示:(1)连结OB .∠D =45°.(2)由∠BAC =∠D ,∠ACE =∠DAC 得△ACE ∽△DAC .A C OBxyD10.(1)提示:除∠B =∠C 外,证∠ADB =∠DEC .(2)提示:由已知及△ABD ∽△DCE 可得.22x x CE -=从而y =AC -CE =x 2- .12+x (其中20<<x ).(3)当∠ADE 为顶角时:.22-=AE 提示:当△ADE 是等腰三角形时,△ABD ≌△DCE .可得.12-=x当∠ADE 为底角时:⋅=21AE 11.(1)S '∶S =1∶4; (2)).40(41162<<+-=x x x y 12.提示:设P 点的横坐标x P =a ,则P 点的纵坐标y P =a 2-a -1.则PM =|a 2-a -1|,BM =|a -1|.因为△ADB 为等腰直角三角形,所以欲使△PMB ∽△ADB ,只要使PM =BM .即|a 2-a -1|=|a -1|.不难得a 1=0..2.2.2432-===a a a∴P 点坐标分别为P 1(0,-1).P 2(2,1).).21,2().21,2(43+--P P13.(1)y =x 2-2x -3,A (-1,0),B (3,0); (2))49,43(-D 或D (1,-2).14.(1);643+-=x y (2)1130=t 或;1350 (3)t =2或3.15.(1)略; (2));30(8311832≤<+-=x x x S 16.梯子长为cm 440 17.cm DO cm CO 65.55,35.103==(提示:设xcm DO =,则()cm x CO -=159,因为AB BD AB AC ⊥⊥,,︒=∠=∠90B A ,BOD AOC ∠=∠,所以△AOC ∽△BDO ,所以DO CO BO AO =即x x -=1594278,所以65.55=x ) 18.b a BD 2=(提示:由△ACB ∽△CBD ,得BC a a b BD CB CD AC ==,,所以b a BD 2=) (3)当x =3时,S 最大值33=.19.解:(1)在正方形ABCD 中,490AB BC CD B C ===∠=∠=,°,AM MN ⊥,90AMN ∴∠=°,90CMN AMB ∴∠+∠=°,在Rt ABM △中,90MAB AMB ∠+∠=°,CMN MAB ∴∠=∠,Rt Rt ABM MCN ∴△∽△,(2)Rt Rt ABM MCN △∽△,44AB BM x MC CN x CN∴=∴=-,,244x x CN -+∴=, ()222141144282102422ABCN x x y S x x x ⎛⎫-+∴==+=-++=--+ ⎪⎝⎭梯形·,当2x =时,y 取最大值,最大值为10.(3)90B AMN ∠=∠=°,∴要使ABM AMN △∽△,必须有AM AB MN BM=,由(1)知AM AB MN MC=,BM MC ∴=, ∴当点M 运动到BC 的中点时,ABM AMN △∽△,此时2x =.20.解:(1)AD BC ⊥,90DAC C ∴∠+∠=°.90BAC BAF C ∠=∴∠=∠°,.90OE OB BOA COE ∴∠+∠=⊥,°,90BOA ABF ∠+∠=°,ABF COE ∴∠=∠.ABF COE ∴△∽△;(2)解法一:作OG AC ⊥,交AD 的延长线于G .2AC AB =,O 是AC 边的中点,AB OC OA ∴==.由(1)有ABF COE △∽△,ABF COE ∴△≌△,BF OE ∴=.90BAD DAC ∠+∠=°,90DAB ABD DAC ABD ∠+∠=∴∠=∠°,,又90BAC AOG ∠=∠=°,AB OA =.ABC OAG ∴△≌△,2OG AC AB ∴==.OG OA ⊥,AB OG ∴∥,ABF GOF ∴△∽△,OF OG BF AB ∴=,2OF OF OG OE BF AB ===. 解法二:902BAC AC AB AD BC ∠==°,,⊥于D , Rt Rt BAD BCA ∴△∽△.2AD AC BD AB ∴==. 设1AB =,则2AC BC BO ===,12AD BD AD ∴=== 90BDF BOE BDF BOE ∠=∠=∴°,△∽△,BD BO DF OE∴=. 由(1)知BF OE =,设OE BF x ==, BA D E C O FGB ADE C O F5DF x=,x ∴=.在DFB △中2211510x x =+,3x ∴=.OF OB BF ∴=-==322OF OE ∴==. (3)OF n OE=. 21807cm 22.相似,450 23.(1)全等,略;(2)CF ==cm 24.(1) 2a ;(2)△ABC ∽△QBM ∽△PMC ; 25.(1)BF=BG=3;(2)略 26.(1)略;(2)猜想11+=n AC CM ,证明略 27.(1)经过1秒或2秒后;(2)经过32秒或125秒时 28.(1)证明:∵弦CD 垂直于直径AB ∴BC=BD ∴∠C =∠D 又∵EC = EB∴∠C =∠CBE ∴∠D =∠CBE 又∵∠C =∠C ∴△CEB ∽△CBD(2)解:∵△CEB ∽△CBD ∴CE CB CB CD= ∴CD=2252533CB CE == ∴DE = CD -CE =253-3 =163 29.(1)有平移的特征知A ´B ´∥AB,又CD ∥AB ∴A ´B ´∥CD,同理B ´C ´∥AD ∴四边形BEDF 为平行四边形∵四边形ABCD 是菱形 ∴AB=AD ∴∠ABD=∠ADB 又∠A ´B ´D=∠ABD ∴∠A ´B ´D=∠ADB ∴FB ´=FD∴四边形B ´EDF 为菱形.(2)∵菱形B ´EDF 与菱形ABCD 有一个公共角 ∴此两个菱形对应角相等 又对应边成比例 ∴此两个菱形相似∴B D BD '=,∴12B D '== ∴平移的距离BB ´=BD –B ´1 30.(1)2483927,, (2)23n ⎛⎫ ⎪⎝⎭.(3)m n p q x x x x = 22223333m n p q⎛⎫⎛⎫⎛⎫⎛⎫∴= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 2233m n p q ++⎛⎫⎛⎫∴= ⎪ ⎪⎝⎭⎝⎭.m n p q ∴+=+。
初一几何三角形练习题及答案

初一几何三角形练习题及答案1. 求下列三角形的内角和:a) 直角三角形b) 等边三角形c) 钝角三角形解答:a) 直角三角形的内角和为180度。
其中一个角为90度(直角),剩余两个角之和为90度。
b) 等边三角形的内角和为180度。
由于等边三角形的三条边长度相等,所以三个角也必定相等,每个角为60度,三个角之和为180度。
c) 钝角三角形的内角和为180度。
钝角三角形有一个角大于90度,其它两个角的和小于90度,但三个角之和仍然等于180度。
2. 给定一个三角形,如果已知两个角的度数,如何求出第三个角的度数?解答:三角形的内角和为180度。
已知两个角的度数后,可以用180度减去这两个角的度数,得到第三个角的度数。
例如,如果一个三角形的两个角分别为40度和60度,那么第三个角的度数为180度 - 40度 - 60度 = 80度。
3. 求下列三角形的周长:a) 边长分别为3 cm, 4 cm和 5 cm的三角形b) 边长分别为6 cm, 8 cm和 10 cm的三角形解答:a) 边长分别为3 cm, 4 cm和 5 cm的三角形的周长为3 cm + 4 cm + 5 cm = 12 cm。
b) 边长分别为6 cm, 8 cm和 10 cm的三角形的周长为6 cm + 8 cm +10 cm = 24 cm。
4. 求下列三角形的面积:a) 底边长为4 cm,高为3 cm的三角形b) 边长分别为5 cm, 7 cm和 8 cm的三角形解答:a) 底边长为4 cm,高为3 cm的三角形的面积为(4 cm * 3 cm) / 2 = 6 cm²。
b) 边长分别为5 cm, 7 cm和 8 cm的三角形的面积可以用海伦公式计算。
首先计算半周长:(5 cm + 7 cm + 8 cm) / 2 = 10 cm。
然后使用海伦公式:√(10 cm * (10 cm - 5 cm) * (10 cm - 7 cm) * (10 cm - 8 cm)) ≈ 17.32 cm²。
专题4.38+相似三角形几何模型-一线三等角(基础篇)(专项练习)
专题4.38 相似三角形几何模型-一线三等角(基础篇)(专项练习)一、单选题1. 如图,在正方形ABCD 中,P 是BC 上一点(点P 不与点B ,C 重合),连接AP .作PE ⊥AP ,PE 交CD 于点E .若AB =6,点P 为BC 的中点,则DE =( )A. 32 B. 92 C. 12 D. 532. 如图,在矩形ABCD 中,点E 、F 分别在边AD 、DC 上,ABE DEF △△∽,AB =6,DE =2,DF =3,则BE 的长是( )A. 12B. 15C.D. 3. 如图,在等边三角形ABC 中,AB =4,P 是边AB 上一点,BP =32,D 是边BC 上一点(点D 不与端点重合),作∠PDQ =60°,DQ 交边AC 于点Q .若CQ =a ,满足条件的点D 有且只有一个,则a 的值为( )A. 52 B. 83 C. 2 D. 34. 如图,在 ABC 中,AB =AC ,D 在AC 边上,E 是BC 边上一点,若AB =3,AE =2,∠AED =∠B ,则AD 的长为( )A. 35 B. 32 C. 43 D. 345. 如图,在ABC 中,AB AC =,点D 是边BC 上一点,且ADE B ∠=∠,下列说法错误的是( )A. AD CE BD DE⋅=⋅ B. ADE ACD C. ABD DCE △△ D. AD DE=6. 如图,在△ABC 中,AB =AC ,D 在AC 边上,E 是BC 边上一点,若AB =6,AE =,∠AED =∠B ,则AD 的长为( )A. 3B. 4C. 5D. 5.57. 如图,在等边三角形ABC 中,P 为边BC 上一点,D 为边AC 上一点,且∠APD =60°,BP =1,CD =23,则ΔABC 的边长为( )A. 3B. 4C. 5D. 68. 如图,D 是等边三角形ΔABC 边上的点,AD =3,BD =5,现将ΔABC 折叠,使点C 与点D 重合,折痕为EF ,且点E 点F 分别在边AC 和BC 上,则CE CF的值为( )A. 1113 B. 35 C. 45 D. 899. 如图,在矩形ABCD 中,E ,F ,G 分别在AB ,BC ,CD 上,DE ⊥EF ,EF ⊥FG ,BE =3,BF =2,FC =6,则DG 的长是( )A. 4B. 133 C. 143 D. 510. 如图,在测量旗杆高度的数学活动中,小达同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部.若眼睛距离地面 1.5AB =米,同时量得2BC =米,10CD =米,则旗杆高度DE 为( )A. 7.5米B. 403米C. 7米D. 9.5米二、填空题11. 如图,在矩形ABCD 中,E 是BC 上的点,点F 在CD 上,要使ABE ∆与CEF ∆相似,需添加的一个条件是_______(填一个即可).12. 如图,在边长为a 的正方形中,E 、F 分别为边BC 和CD 上的动点,当点E 和点F 运动时, AE 和EF 保持垂直.则①△ABE ∽△FCE ;②当12BE a =时、梯形ABCF 的面积最大;③当点E 运动到BC 中点时Rt ABE ∽Rt △AEF ;④当Rt ABE ∽Rt △AEF 时cos ∠AFE =12其中正确结论的序号是 .13. 如图,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点,且:1:4CF CD =,给出下列结论:①ABE ECF ∽;②ABE AEF ∽;③AE EF ⊥;④ADF ECF ∽.其中正确结论的序号为________.14. 如图,四边形ABCD 是正方形,6AB =,E 是BC 中点,连接DE ,DE 的垂直平分线分别交AB DE CD 、、于M 、O 、N ,连接EN ,过E 作EF EN ⊥交AB 于F ,则AF =______.15. 如图,在矩形ABCD 中,E ,F 分别是边BC ,CD 上的点,4AB =,8AD =,3CF =,若ABE △与以E ,C ,F 为顶点的三角形相似,则BE 的长为______.16. 如图,在等边三角形ABC 中,点D 、点E 分别在BC ,AC 上,且∠ADE =60°,(1)写出和∠CDE 相等的角:______;(2)若AB =3,BD =1,则CE 长为______.17. 如图,在矩形ABCD 中,点E 、F 分别在边AD 、DC 上,△ABE ∽△DEF ,AB =3,AE =4,DE =1.2,则EF =_____.18. 如图,D是等边三角形ABC的边AB上一点,且AD:1DB=:2,现将折叠,使点C与点D重合,折痕为EF,点E、F分别在AC和BC上,且ABCCE:CF的值为______.⊥交19. 如图,在矩形ABCD中,E是BC的中点,连接AE,过点E作EF AEDC于点F.若4BC=,则DF的长为______.AB=,620. 如图,将长方形纸片ABCD沿MN折叠,使点A落在BC边上点A′处,点D的对应点为D′,连接A'D′交边CD于点E,连接CD′,若AB=9,AD=6,A'点为BC 的中点,则线段ED'的长为_____.三、解答题21. 如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.22. 如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,连接AP、PD,∠APD=60°.(1)求证:△ABP∽△PCD;(2)若PC=2,求CD的长.23. 如图,在△ABC中,AD是角平分线,点E是边AC上一点,且满足ADE B∠=∠.(1)证明:ADB AED ∆∆ ;(2)若3AE =,5AD =,求AB 的长.24. 如图,在ABC 中,AB AC =,120BAC ∠=︒,D 为BC 边上一点,E 为AC 边上一点,且30ADE ∠=︒,求证:ABD DCE ∽△△.25. 在矩形ABCD 中,4AB =,6AD =,将矩形折叠,使点A 落在点P 处,折痕为DE .(1)如图①,若点P 恰好在边BC 上,连接AP ,求AP DE的值;(2)如图②,若E 是AB 的中点,EP 的延长线交BC 于点F ,求BF 的长.26. 通过对下面数学模型的研究学习,解决下列问题:(1)如图1,点A 在直线l 上,90,BAD AB AD ∠=︒=,过点B 作BC l ⊥于点C ,过点D 作DE l ⊥交于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90BCA AED ∠=∠=︒,可以推理得到()ABC DAE AAS ≌.进而得到结论:AC =_____,BC =_____.我们把这个数学模型称为“K 字”模型或“一线三直角”模型;(2)如图2,90,,,BAD MAN AB AD AM AN BM l ∠=∠=︒==⊥于点C ,NG l ⊥于点G ,由(1)易知NG =_______,ND 与直线l 交于点P ,求证:NP DP =.专题4.38相似三角形几何模型-一线三等角(基础篇)(专项练习)一、单选题【1题答案】【答案】B【解析】【分析】根据正方形的性质,余角,可证明出△ABP∽△PCE,再根据相似三角形的性质即可求出CE的值,最后根据线段的和差关系即可求解.【详解】解:在正方形ABCD中,AB=BC=CD=6,∠B=∠C=90°,∵P为BC中点,∴BP=PC=12AB=3,∵AP⊥PE,∴∠APE=90°=∠APB+∠EPC,∵∠B=90°,∴∠APB+∠BAP=90°,∴∠BAP=∠EPC,∵∠B=∠C=90°,∴△ABP∽△PCE,∴AB PCBP CE=,即633CE=,∴32 CE=,∴DE=CD-CE=39622 -=,故选:B.【点睛】本题主要考查了正方形的性质、相似三角形的判定与性质,证得△ABP∽△PCE是解答本题的关键.【2题答案】【答案】C【解析】【分析】利用相似三角形的性质求出AE的长,再利用勾股定理求解即可.【详解】解:∵ABE DEF ∽,∴AB AE DE DF=,∴623AE =,∴9AE =,∵矩形ABCD 中,∠A =90°,∴BE ===故选:C .【点睛】本题考查了矩形的性质、相似三角形的性质、勾股定理,解题关键是求出AE 的长后利用勾股定理求解.【3题答案】【答案】B【解析】【分析】先证明△BPD ∽△CDQ ,利用相似三角形的性质得出比例式,进而建立关于BD 的一元二次方程,再判别式为0,建立方程求解,即可得出结论.【详解】解:∵△ABC 是等边三角形,∴∠B =∠C =60°,∴∠BPD +∠BDP =180°-∠B =120°,∵∠PDQ =60°,∴∠BDP +∠CDQ =120°,∴∠BPD =∠CDQ ,∵∠B =∠C =60°,∴△BPD ∽△CDQ ,∴BP BD CD CQ=,∴324BD BD a=-,∴2BP 2-8BP +3a =0,∵满足条件的点P 有且只有一个,∴方程2BP 2-8BP +3a =0有两个相等的实数根,∴△=82-4×2×3a =0,∴a =83.故选:B .【点睛】此题是相似形综合题,主要考查了等式的性质,相似三角形的判定和性质,一元二次方程根的判别式,利用方程的思想解决问题是解本题的关键.【4题答案】【答案】C【解析】【分析】由等边对等角可得∠B =∠C ,即得出∠C =∠AED .再结合题意易证△EAD ∼△CAE ,即得出AD AE AE AC=,代入数据即可求出AD 的长.【详解】根据题意可知AB =AC =3,∴∠B =∠C ,∵∠B =∠AED ,∴∠C =∠AED ,又∵∠EAD =∠CAE ,∴△EAD ∼△CAE ,∴AD AE AE AC =,即223AD =,解得:43AD =,故选C .【点睛】本题考查等腰三角形的性质,相似三角形的判定和性质.掌握相似三角形的判定方法是解题关键.【5题答案】【答案】D【解析】【分析】根据AB AC =和ADE B ∠=∠,可证得△ABD ∽△DCE ,△ADE ∽△ACD ,再逐项判断即可求解.【详解】解:∵AB AC =,∴∠B =∠C ,∵∠ADC =∠B +∠BAD ,∠ADC =∠ADE +∠CDE ,ADE B ∠=∠,∴∠BAD =∠CDE ,∴△ABD ∽△DCE ,故C 正确,不符合题意;∴AD BD DE CE=,∴AD CE BD DE ⋅=⋅,故A 正确,不符合题意;∵AB AC =,∴∠B =∠C ,∵ADE B ∠=∠,∴∠ADE =∠C ,∵∠DAE =∠CAD ,∴△ADE ∽△ACD ,故B 正确,不符合题意;∴AD DE AC CD=,∠AED =∠ADC ,∵点D 是边BC 上一点,∴AC 不一定等于CD ,∴∠ADC 不一定等于∠DAC ,∴∠AED 不一定等于∠DAC ,∴AD 不一定等于DE ,故D 错误,符合题意;故选:D .【点睛】本题主要考查了相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的判定和性质定理.【6题答案】【答案】A【解析】【分析】由等边对等角可得B C ∠=∠,即得出C AED ∠=∠.再结合题意易证EAD CAE ,即得出AD AE AE AC=,代入数据即可求出AD 的长.【详解】根据题意可知6AB AC ==,∴B C ∠=∠.∵B AED ∠=∠,∴C AED ∠=∠.又∵EAD CAE∠=∠,∴EAD CAE,∴AD AEAE AC==解得:3AD=.故选A【点睛】本题考查等腰三角形的性质,三角形相似的判定和性质.掌握三角形相似的判定方法是解题关键.【7题答案】【答案】A【解析】【分析】根据等边三角形性质求出AB=BC=AC,∠B=∠C=60°,推出∠BAP=∠DPC,证△BAP∽△CPD,得出AB BPCP CD=,代入求出即可.【详解】解:∵△ABC是等边三角形,∴AB=BC=AC,∠B=∠C=60°,∴∠BAP+∠APB=180°-60°=120°,∵∠APD=60°,∴∠APB+∠DPC=180°-60°=120°,∴∠BAP=∠DPC,即∠B=∠C,∠BAP=∠DPC,∴△BAP∽△CPD,∴AB BP CP CD=∵23CD=,CP=BC-BP=x-1,BP=1,∴1213 xx= -解得:AB=3.故选A.【点睛】本题考查了相似三角形的性质和判定,等边三角形的性质,三角形的内角和定理的应用,关键是推出△BAP∽△CPD,主要考查了学生的推理能力和计算能力.【8题答案】【答案】A【解析】【分析】根据等边三角形的性质、相似三角形的性质得到∠AED=∠BDF,根据相似三角形的周长比等于相似比计算即可.【详解】解:∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,AB=AC=BC=3+5=8,由折叠的性质可知,∠EDF=∠C=60°,EC=ED,FC=FD,∴∠AED=∠BDF,∴△AED∽△BDF,∴1113 DE AE AD DEDF BD DF BF++==++,∴1113 CE DECF DF==,故选A.【点睛】本题考查的是翻转变换的性质、相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理、翻转变换的性质是解题的关键.【9题答案】【答案】B【解析】【分析】先运用勾股定理可求得EF, 过G作GH⊥DE垂足为H,则四边形EFGH 是矩形可得HG=EF,再说明△EBF∽△DAE、△DAE∽△GHD,进一步可得△EBF∽△GHD,最后运用相似三角形的性质解答即可.【详解】解:∵在Rt△BEF中,BF=2,BE=3∴EF==如图:过G作GH⊥DE垂足为H,∵DE⊥EF,EF⊥FG∴四边形EFGH是矩形∴HG=EF∵矩形ABCD∴∠A =∠B =90°∴∠AED +∠ADE =90°∵DE ⊥EF∴∠AED +∠BEF =90°∴∠BEF =∠ADE又∵∠A =∠B =90°∴△EBF ∽△DAE同理:△DAE ∽△GHD∴△EBF ∽△GHD∴DG HG EF BE =,=,解得DG =133. 故选B .【点睛】本题主要考查了矩形的判定与性质、运用勾股定理解直角三角形、相似三角形的判定与性质等知识点,灵活运用相似三角形的判定与性质是解答本题的关键.【10题答案】【答案】A【解析】【分析】由平面镜反射可得:,ACB DCE ∠=∠ 再证明,ABC EDC ∽再利用相似三角形的性质可得答案.【详解】解:由平面镜反射可得:,ACB DCE ∠=∠90,ABC EDC ∠=∠=︒,ABC EDC ∴ ∽,AB BC DE CD∴= 1.5AB =米,2BC =米,10CD =米,1.52,10DE ∴= 解得:7.5DE =,经检验:符合题意,∴ 旗杆高度DE 为7.5米.故选A【点睛】本题考查的是相似三角形的应用,掌握“利用相似三角形的性质列方程求解”是解本题的关键.二、填空题【11题答案】【答案】AE EF ⊥或∠BAE =∠CEF ,或∠AEB =∠EFC (任填一个即可)【解析】【分析】根据相似三角形的判定解答即可.【详解】∵矩形ABCD ,∴∠ABE =∠ECF =90︒,∴添加∠BAE =∠CEF ,或∠AEB =∠EFC ,或AE ⊥EF ,∴△ABE ∽△ECF ,故答案为:∠BAE =∠CEF ,或∠AEB =∠EFC ,或AE ⊥EF .【点睛】此题考查相似三角形的判定,关键是根据相似三角形的判定方法解答.【12题答案】【答案】①②③【解析】【分析】如图,证明∠B =∠C ,∠BAE =∠CEF ,得到①正确;证明S 梯形ABCF22111222,a a λλ=-++由12-<0,得到当λ=﹣1212()2a ⨯-=12a 时,梯形ABCF 的面积最大,得到②正确;证明AB AE BE EF=,由∠B =∠AEF =90°,得到Rt △ABE ∽Rt △AEF ,故③正确;证明cos ∠AFE =cos ∠AEB =12BE AE ≠,故④不正确.【详解】解:如图,∵四边形ABCD 为正方形,且AE ⊥EF ,∴∠B =∠AEF =∠C =90°,∴∠BAE +∠AEB =∠AEB +∠CEF ,∴∠BAE =∠CEF ,∴△ABE ∽△FCE ,故①正确;设BE =λ,则EC =a ﹣λ;∵△ABE ∽△ECF ,∴AB BE CE CF =,故2,CF aλλ=-+∴S 梯形ABCF =21()2a a aλλ-++22111222,a a λλ=-++∵12-<0,∴当λ=﹣1212()2a ⨯-=12a 时,梯形ABCF 的面积最大.故②正确.∵△ABE ∽△ECF ,∴AB AE CE EF=;若点E 为BC 的中点,则BE =CE ,∴AB AE BE EF =,而∠B =∠AEF =90°,∴Rt △ABE ∽Rt △AEF ,故③正确;∴∠AFE =∠AEB ,∴cos ∠AFE =cos ∠AEB =12BE AE ≠,故④不正确.故答案为①②③.【点睛】本题主要考查相似三角形的判定与性质,掌握相似三角形的判定定理,灵活运用勾股定理是解本题的关键【13题答案】【答案】①②③【解析】【分析】容易证明①△ABE ∽△ECF ;利用①可得90AEB FEC ∠+∠= ,,可得③AE ⊥EF ;且可得2AE AB EF EC ==,可证得②△ABE ∽△AEF ,而AD DF CE CF ≠,所以④不正确.【详解】∵E 为BC 中点,CF :CD =1:4,∴2AB BE CE CF==, 且∠B =∠C ,∴△ABE ∽△ECF ,∴①正确;∴∠BAE =∠FEC ,且90BAE AEB ∠+∠= ,∴90AEB FEC ∠+∠= ,∴90AEF ∠= ,∴AE ⊥EF ,∴③正确;由①可得2AE AB EF EC ==, ∴AB EC BE AE EF EF==,且90ABE AEF ∠=∠= , ∴△ABE ∽△AEF ,∴②正确;∵2,3DA DF CE CF==, ∴AD DF CE CF ≠, ∴△ADF 和△ECF 不相似,∴④不正确,综上可知正确的为:①②③,故答案为①②③.【点睛】考查相似三角形的判定与性质,掌握相似三角形的判定方法是解题的关键.【14题答案】【答案】2【解析】【分析】MN 垂直平分DE ,得出NE ND =,利用6DN NC +=,在ΔRt NCE 中利用勾股定理求得CN 的长,再证明FBE ECN ∆∆ ,利用相似比求得BF 的长度,进而求得AF 的长度.【详解】设CN x =,则6DN x=- MN 垂直平分DE∴6NE ND x==-在ΔRt NCE 中,222CN CE NE +=又∵E 是BC 中点∴3CE =2223(6)x x ∴+=-解得94x =又∵EF EN⊥90NEC FNB ∴∠+∠=,NEC EFB CNE FEB∴∠=∠∠=∠Δ~ΔFBE ECN∴FB CE BE CN∴=3934FB ∴=4FB ∴=642AF AB FB ∴=-=-=故答案为:2.【点睛】本题考查线段垂直平分线的应用,勾股定理及相似三角形的应用,解决本题的关键是各知识点的综合应用.【15题答案】【答案】26,或327【解析】【分析】设BE =x ,当ABE △∽△ECF 时,AB BE EC CF =即483x x =-,当ABE △∽△FCE 时,AB BE FC EC =即438x x=-,解方程即可.【详解】解:设BE =x ,当ABE △∽△ECF 时,AB BE EC CF =即483x x =-整理得28120x x -+=,解得1226x x ==,,经检验都符合题意,当ABE △∽△FCE 时,AB BE FC EC =即438x x =-,解得327x =.经检验符合题意,故答案为26,或327.【点睛】本题考查三角形相似性质,列分式方程,正确三角形相似性质,列分式方程是解题关键.【16题答案】【答案】 ①. ∠BAD ②. 23【解析】【分析】(1) 根据△ABC 是等边三角形,得到∠B =∠C = 60°, AB = BC ;又因为∠ADC =∠B +∠BAD ,∠EDC +∠ADE = ∠B +∠BAD 就得到∠EDC =∠BAD(2) 因为∠EDC =∠BAD ,∠C =∠B 得到△ABD ~△DCE ,得到AB BD CD EC= ,即可求出EC ;【详解】(1) 证明: ∵△ABC 是等边三角形,∠B =∠C = 60°, AB = BC ;又∵∠ADC =∠B +∠BAD∠EDC +∠ADE = ∠B +∠BAD又∵∠ADE =∠B =60°∴∠EDC =∠BAD所以和∠CDE 相等的角为:∠BAD故答案为:∠BAD(2) ∵∠EDC =∠BAD∴∠C =∠B△ABD ~△DCE ,AB BD CD EC ∴= 3,1BC AB BD ===又312CD BC BD =-=-=312EC∴= 解得:EC =23故答案为:23;【点睛】此题主要考查了等边三角形的性质和相似三角形的判定和性质,能够证得△ABD ~△DCE 是解答此题的关键.【17题答案】【答案】2【解析】【分析】由勾股定理,求出BE=5,由△ABE∽△DEF,得ABDE=BEEF,进而求出EF的长.【详解】解:在矩形ABCD中∠A=90°∵AB=3,AE=4∴BE=5∵△ABE∽△DEF∴ABDE=BEEF∴31.2=5EF解得EF=2故答案为:2.【点睛】本题主要考查相似三角形的性质,借助于矩形的性质和勾股定理求边长,熟练掌握以上性质是解题的关键.【18题答案】【答案】4 5【解析】【分析】设AD=k,则DB=2k,得到AB=AC=BC=3k,∠A=∠B=∠C=∠EDF =60°,进而证明△AED∽△BDF,得到△AED与△BDF的相似比为4:5,即可求出CE:CF=DE:DF=4:5,问题得解.【详解】解:设AD=k,则DB=2k,∵△ABC为等边三角形,△CEF折叠得到△DEF,∴AB=AC=BC=3k,∠A=∠B=∠C=∠EDF=60°,∴∠EDA+∠FDB=120°,∠EDA+∠AED=120°,∴∠FDB=∠AED,∴△AED∽△BDF,由△CEF折叠得到△DEF,得CE=DE,CF=DF,∴△AED的周长为4k,△BDF的周长为5k,∴△AED 与△BDF 的相似比为4:5,∴CE :CF =DE :DF =4:5.故答案为:45.【点睛】本题主要考查了相似的性质与判定、等边三角形的性质、翻折变换的性质及其应用等知识,熟知等边三角形、翻折变换的性质,借助相似三角形的判定与性质(用含有k 的代数式表示)将两条线段的比转化为相似比是解题的关键.【19题答案】【答案】74【解析】【分析】结合矩形的性质证明BAE CEF ∆∆ 可求得CF 的长,再利用DF CD DF =-可求解.【详解】解: 四边形ABCD 为矩形,90B C ∴∠=∠=︒,4CD AB ==,90BAE AEB ∴∠+∠=︒,EF AE ⊥ ,90AEF ∴∠=︒,90AEB CEF ∴∠+∠=︒,BAE CEF ∴∠=∠,BAE CEF ∴∆∆ ,::AB CE BE CF ∴=,E 是BC 的中点,6BC =,3BE CE ∴==,4AB = ,4:33:CF ∴=,解得94CF =,97444DF CD DF ∴=-=-=.故选:74.【点睛】本题主要考查矩形的性质,相似三角形的判定与性质,证明BAE CEF ∆∆ 是解题的关键.【20题答案】【答案】94【解析】【分析】根据折叠的性质可得'AM A M =,''90MA D A ∠=∠=︒,设'AM A M x ==,则9BM x =-,由线段中点可得''11322A B AC BC AD ====,在'Rt A BM 中,利用勾股定理可得'5A M =,4MB =,利用相似三角形的判定定理及性质可得''A BM ECA ,'''A E AC A M BM =,代入求解,同时根据线段间的数量关系即可得出结果.【详解】解:将长方形纸片ABCD 沿着MN 折叠,使点A 落在BC 边上点'A 处,∴'AM A M =,''90MA D A ∠=∠=︒,设'AM A M x ==,则9BM x =-,∵'A 是BC 的中点,∴''11322A B AC BC AD ====,在'Rt A BM 中,'22'2A B BM A M +=,即()22239+-=x x ,解得:5x =,∴'5A M =,4MB =,∵''90MA B EAC ∠+∠=︒,''90A EC EAC ∠+∠=︒,∴''MA B A EC ∠=∠,∵'90B ACE ∠=∠=︒,∴''A BM ECA ,∴'''A E ACA M BM=,即'354A E=,∴'15 4A E=,∴'''''159 644ED A D A E AD A E=-=-=-=,故答案为:9 4【点睛】题目主要考查长方形中的折叠问题,包括勾股定理,相似三角形的判定及性质等,结合图形,熟练掌握运用折叠的性质及相似三角形的性质是解题关键.三、解答题【21题答案】【答案】见解析【解析】【分析】根据正方形的性质得∠B=∠C=90°,再利用等角的余角相等得∠BEF=∠CFG,然后根据有两组角对应相等的两个三角形相似可得到△EBF∽△FCG.【详解】解:∵四边形ABCD为正方形,∴∠B=∠C=90°,∴∠BEF+∠BFE=90°,∵∠EFG=90°,∴∠BFE+∠CFG=90°,∴∠BEF=∠CFG,∴△EBF∽△FCG.【点睛】本题考查正方形的性质,相似三角形的判定,解的关键是掌握相似三角形的判定定理.【22题答案】【答案】(1)见解析(2)CD的长为2 3【解析】【分析】(1)由等边三角形和∠APD=60°得,∠B=∠C=∠APD=60°,∠APB+∠CPD=120°,在△APB中,∠APB+∠BAP=120°,由此可得∠BAP=∠CPD.因此△ABP∽△PCD;(2)由(1)的结论△ABP∽△PCD可得BP ABCD PC=,从而可以求出线段CD的长.【小问1详解】证明:∵等边三角形ABC,∴∠B=∠C=60°,∵∠APD=60°,∴∠APB+∠CPD=120°,在△APB中,∠APB+∠BAP=120°,∴∠BAP=∠CPD,∴△ABP∽△PCD;【小问2详解】解:等边三角形边长为3,PC=2,由(1)得△ABP∽△PCD,BP ABCD PC=,∴132 CD=,∴CD=23.答:CD的长为23.【点睛】本题考查了相似三角形的性质和判定,等边三角形的性质,三角形的内角和定理的应用,关键是推出△ABP∽△PCD.【23题答案】【答案】(1)见解析(2)25 3【解析】【分析】(1)证出∠BAD=∠EAD.根据相似三角形的判定可得出结论;(2)由相似三角形的性质可得出AD ABAE AD=,则可得出答案.【小问1详解】∵AD是∠BAC的角平分线,∴∠BAD=∠EAD.∵∠ADE=∠B,∴△ADB∽△AED.【小问2详解】∵△ADB∽△AED,∴AD AB AE AD=,∵AE=3,AD=5,∴535AB =,∴253 AB=.【点睛】本题考查了相似三角形的判定与性质以及三角形内角和定理,熟练掌握相似三角形的判定定理和性质定理是解题的关键.【24题答案】【答案】见解析【解析】【分析】利用三角形的外角性质证明∠EDC=∠DAB,即可证明△ABD∽△DCE.【详解】证明:∵AB=AC,且∠BAC=120°,∴∠ABD=∠ACB=30°,∵∠ADE=30°,∴∠ABD=∠ADE=30°,∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,∴∠EDC=∠DAB,∴△ABD∽△DCE.【点睛】本题考查了三角形相似的判定、等腰三角形的性质、三角形的外角性质,利用三角形的外角性质证明∠EDC=∠DAB是解题的关键.【25题答案】【答案】(1)2 3(2)3 2【解析】【分析】(1)根据矩形的性质可得∠BAD =∠ABC =90°,再由折叠的性质可得APB AED ∠=∠.可证得ABP △∽DAE △.即可求解;(2)过点E 作EH DP ∥交AD 于H ,由折叠的性质可得HED HDE ∠=∠,从而得到EH DH =.然后设EH DH x ==,则6AH x =-,由勾股定理可得103DH =,从而得到83AH =.再证得AEH △∽BFE △,即可求解.【小问1详解】解:在矩形ABCD 中,∠BAD =∠ABC =90°,∴90BAP APB ∠+∠=︒,由折叠性质得:AP DE ⊥,∴90BAP AED ∠+∠=︒,∴APB AED ∠=∠.∵90EAD ABP ∠=∠=︒,∴ABP △∽DAE △.∴4263AP AB DE AD ===.【小问2详解】解:过点E 作EH DP ∥交AD 于H ,∵EH DF ∥,∴HED EDP ∠=∠.∵由折叠性质得HDE EDP ∠=∠,∠DPE =∠A =90°,∴HED HDE ∠=∠,∴EH DH =.设EH DH x ==,则6AH x =-,∵E 是AB 的中点,∴2AE =,∵AE 2+AH 2=EH 2,∴()22226x x +-=,解得:103x =,即103DH =,∴83AH =.∵EH DF ∥,∴∠HEP =90°,∴∠AEH +∠BEF =90°,∵∠A =∠B =90°,∴∠AEH +∠AHE =90°,∴∠AHE =∠BEF ,∴AEH △∽BFE △,∴AE AH BF BE =,即8232BF =,解得32BF =,∴BF 的长为32.【点睛】本题主要考查了矩形与折叠问题,相似三角形的判定和性质,熟练掌握矩形与折叠的性质,相似三角形的判定和性质是解题的关键.【26题答案】【答案】(1)DE ,AE ;(2)AC .证明见详解.【解析】【分析】(1)根据(AAS)≌ABC DAE ,得出AC =DE ,BC =AE 即可;(2)过D 作DE ⊥直线l 于E ,先证△MCA ≌△AGN (AAS ),得出AC =NG ,由(1)知(AAS)≌ABC DAE ,得出AC =DE ,再证△NGP ≌△DEP (AAS )即可.【小问1详解】解:∵(AAS)≌ABC DAE ,∴AC =DE ,BC =AE ,故答案为DE ,AE ;【小问2详解】证明:过D 作DE ⊥直线l 于E ,∵90MAN ∠=︒,∴∠CAM +∠NAG =90°,∵BM ⊥l ,∴∠MCA =90°,∴∠M +∠CAM =90°,∴∠M =∠NAG ,∵NG l ⊥,∴∠AGN =90°,在△MCA 和△AGN 中,MCA AGN M GAN MA AN ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△MCA ≌△AGN (AAS ),∴AC =NG ,由(1)知(AAS)≌ABC DAE ,∴AC =DE ,∴NG =DE ,在△NGP 和△DEP 中,90NGP DEP GPN EPDNG DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△NGP ≌△DEP (AAS )∴NP =DP ,故答案为AC .【点睛】本题考查一线三直角全等问题,掌握余角性质,三角形全等判定与性质是解题关键.。
三角形练习题及答案

三角形练习题及答案三角形是数学中常见的几何形状,也是许多几何问题的基础。
通过解决三角形练习题,我们可以加深对三角形性质的理解,并且提高解决几何问题的能力。
本文将为大家提供一些三角形练习题及答案,希望能够帮助读者更好地掌握这一知识点。
题目一:已知三角形ABC,AB = 5cm,BC = 7cm,AC = 8cm。
求三角形ABC 的面积。
解答一:根据海伦公式,已知三角形的三边长度可以计算出其面积。
海伦公式的表达式为:面积= √(p × (p - a) × (p - b) × (p - c)),其中p为半周长,即p = (a + b + c)/2。
代入题目中的数据,我们可以得到p = (5 + 7 + 8)/2 = 10。
将p和三边的长度代入公式,计算得到面积= √(10 × (10 - 5) × (10 - 7) × (10 - 8)) = √(10 × 5 × 3 × 2) = √300 ≈ 17.32cm²。
因此,三角形ABC的面积约为17.32cm²。
题目二:已知三角形ABC,角A = 30°,角B = 60°,AB = 6cm。
求三角形ABC 的高。
解答二:在三角形ABC中,角A = 30°,角B = 60°,则角C = 180° - 30° - 60° = 90°。
由于角C为直角,可以利用三角形ABC的特殊性质求解。
在直角三角形ABC中,高等于底边乘以正弦值。
即高= AB × sin(A) = 6 ×sin(30°) = 6 × 0.5 = 3cm。
因此,三角形ABC的高为3cm。
题目三:已知三角形ABC,角A = 45°,角B = 45°,AB = 8cm。
七年级下几何练习题

七年级下几何练习题--------------------------------------------------------------------------作者: _____________--------------------------------------------------------------------------日期: _____________七年级下第九、第十章练习题1.如图(1),共有三角形的个数是 。
如图(2),共有三角形的个数是 。
2如图,在△ABC 中,AB=AC ,∠A=36°,∠ABC 和∠ACB 的平分线分别交AC 、AB 于D 、E ,则图中一共有 个等腰三角形。
3.如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE 等于 。
4.如果等腰三角形的两边长分别为3和5,那么这个三角形的周长是 。
5.三角形中,最大角α的取值范围是( ) A 、0°<α<90°B 、60°<α<180°C 、60°≤α<90 D 、60°≤α<180° 6.下列正多边形的组合中,能够铺满地面不留缝隙的是( ) A 、正八边形和正三角形 B 、正五边形和正八边形 C 、正六边形和正三角形; D 、正六边形和正五边形 7.下面的说法正确的个数是( )①三条线段首位顺次连结所组成的的图形叫三角形 ②直角三角形的高只有一条③三角形的高至少有一条在三角形内 ④三角形的高、内角平分线、中线不一定是线段⑤三角形具有稳定性⑥各内角相等的多边形是正多边形⑦等边三角形不是等腰三角形⑧同种的任意三角形和四边形都能铺满地面⑨只要围绕一点拼在一起的几种正多边形的内角之和为一个周角,就一定能拓展下去并铺满地面.正确的有( ) A 、3个 B 、4个 C 、5个 D 、6个 8.AD 是△ABC 的中线,△AB D 面积是5,则△ABC 面积为_______. 9.一个多边形最多有_____个内角是锐角.10. 若过m 边形的一个顶点有7条对角线,n 边形没有对角线,k 边形有k 条对角线,正h 边形的内角和与外角和相等,则代数式(m -k)(h-n)=_______。
初中数学数学全等三角形压轴几何题试题及解析

初中数学数学全等三角形压轴几何题试题及解析一、全等三角形旋转模型1.问题背景:如图1,在四边形ABCD 中,90BAD ∠=︒,90BCD ∠=︒,BA BC =,120ABC ∠=︒,60MBN ∠=︒,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .探究图中线段AE ,CF ,EF 之间的数量关系.小李同学探究此问题的方法是:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,再证明BFC BFE △≌△,可得出结论,他的结论就是_______________;探究延伸1:如图2,在四边形ABCD 中,90BAD ∠=︒,90BCD ∠=︒,BA BC =,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?请直接写出结论(直接写出“成立”或者“不成立”),不要说明理由. 探究延伸2:如图3,在四边形ABCD 中,BA BC =,180BAD BCD ∠+∠=︒,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?并说明理由.实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30的A 处舰艇乙在指挥中心南偏东70︒的B 处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50︒的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E 、F 处,且指挥中心观测两舰艇视线之间的夹角为70︒,试求此时两舰艇之间的距离.答案:E解析:EF=AE+CF .探究延伸1:结论EF=AE+CF 成立.探究延伸2:结论EF=AE+CF 仍然成立.实际应用:210海里.【分析】延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;探究延伸1:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;探究延伸2:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;实际应用:连接EF ,延长AE ,BF 相交于点C ,然后与探究延伸2同理可得EF=AE+CF ,将AE 和CF 的长代入即可.【详解】解:EF=AE+CF理由:延长FC 到G ,使CG AE =,连接BG ,在△BCG 和△BAE 中,90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=120°,∠MBN=60°,∴∠ABE+∠CBF=60°,∴∠CBG+∠CBF=60°,即∠GBF=60°,在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .探究延伸1:结论EF=AE+CF 成立.理由:延长FC 到G ,使CG AE =,连接BG ,在△BCG 和△BAE 中,90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=2∠MBN ,∴∠ABE+∠CBF=12∠ABC , ∴∠CBG+∠CBF=12∠ABC , 即∠GBF=12∠ABC , 在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .探究延伸2:结论EF=AE+CF 仍然成立.理由:延长FC 到G ,使CG AE =,连接BG ,∵180BAD BCD ∠+∠=︒,∠BCG+∠BCD=180°,∴∠BCG=∠BAD在△BCG 和△BAE 中,BC BA BCG BAE CG AE =⎧⎪∠=∠⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=2∠MBN ,∴∠ABE+∠CBF=12∠ABC , ∴∠CBG+∠CBF=12∠ABC , 即∠GBF=12∠ABC , 在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .实际应用:连接EF ,延长AE ,BF 相交于点C ,∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,∴∠EOF=12∠AOB ∵OA=OB ,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,∴符合探索延伸中的条件∴结论EF= AE+CF 仍然成立即EF=75×1.2+100×1.2=210(海里)答:此时两舰艇之间的距离为210海里.【点睛】本题考查了全等三角形的判定与性质.作辅助线构造全等三角形是解题的关键. 2.已知OP 平分∠AOB ,∠DCE 的顶点C 在射线OP 上,射线CD 交射线OA 于点F ,射线CE 交射线OB 于点G .(1)如图1,若CD ⊥OA ,CE ⊥OB ,请直接写出线段CF 与CG 的数量关系;(2)如图2,若∠AOB=120º,∠DCE=∠AOC ,试判断线段CF 与CG 的数量关系,并说明理由.答案:C解析:(1)CF=CG;(2)CF=CG,见解析【分析】(1)结论CF=CG,由角平分线性质定理即可判断.(2)结论:CF=CG,作CM⊥OA于M,CN⊥OB于N,证明△CMF≌△CNG,利用全等三角形的性质即可解决问题.【详解】解:(1)结论:CF=CG;证明:∵OP平分∠AOB,CF⊥OA,CG⊥OB,∴CF=CG(角平分线上的点到角两边的距离相等);(2)CF=CG.理由如下:如图,过点C作CM⊥OA,CN⊥OB,∵OP平分∠AOB,CM⊥OA,CN⊥OB,∠AOB=120º,∴CM=CN(角平分线上的点到角两边的距离相等),∴∠AOC=∠BOC=60º(角平分线的性质),∵∠DCE=∠AOC,∴∠AOC=∠BOC=∠DCE=60º,∴∠MCO=90º-60º =30º,∠NCO=90º-60º =30º,∴∠MCN=30º+30º=60º,∴∠MCN=∠DCE,∵∠MCF=∠MCN-∠DCN,∠NCG=∠DCE-∠DCN,∴∠MCF=∠NCG,在△MCF和△NCG中,CMF CNG CM CNMCF NCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MCF ≌△NCG (ASA ),∴CF=CG (全等三角形对应边相等);【点睛】本题考查三角形综合题、角平分线的性质、全等三角形的判定和性质,解题的关键是掌握角平分线的性质的应用,熟练证明三角形全等 .3.问题背景如图(1),在四边形ABCD 中,∠B+∠D =180°,AB =AD ,∠BAD =α,以点A 为顶点作一个角,角的两边分别交BC ,CD 于点E ,F ,且∠EAF 12=α,连接EF ,试探究:线段BE ,DF ,EF 之间的数量关系.(1)特殊情景在上述条件下,小明增加条件“当∠BAD =∠B =∠D =90°时”如图(2),小明很快写出了:BE ,DF ,EF 之间的数量关系为______.(2)类比猜想类比特殊情景,小明猜想:在如图(1)的条件下线段BE ,DF ,EF 之间的数量关系是否仍然成立?若成立,请你帮助小明完成证明;若不成立,请说明理由.(3)解决问题如图(3),在△ABC 中,∠BAC =90°,AB =AC =4,点D ,E 均在边BC 上,且∠DAE =45°,若BD 2=DE 的长.答案:B 解析:(1)BE +DF =EF ;(2)成立;(3)DE 52=【分析】(1)将△ABE 绕点A 逆时针旋转90°,得到△ADG ,由旋转的性质可得AE =AG ,BE =DG ,∠BAE =∠DAG ,根据∠EAF=12∠BAD 可得∠BAE+∠DAF =45°,即可得出∠∠EAF =∠FAG ,利用SAS 可证明△AFE ≌△AFG ,可得EF=FG ,进而可得EF=BE+FD ;(2)将△ABE 绕点A 逆时针旋转α得到△ADH ,由旋转的性质可得∠ABE =∠ADH ,∠BAE =∠DAH ,AE=AH,BE=DH,根据∠BAD=α,∠EAF12=α可得∠BAE+∠FAD12=α,进而可证明∠FAH=∠EAF,利用SAS可证明△AEF≌△AHF,可得EF=FH=BE+FD;(3)将△AEC绕点A顺时针旋转90°,得到△AE′B,连接DE′,由旋转的性质可得BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,BC=42,即可求出∠E′BD=90°,利用SAS可证明△AEF≌△AHF,可得DE=DE′,利用勾股定理求出DE的长即可的答案.【详解】(1)BE+DF=EF,如图1,将△ABE绕点A逆时针旋转90°,得到△ADG,∵∠ADC=∠B=∠ADG=90°,∴∠FDG=180°,即点F,D,G共线.由旋转可得AE=AG,BE=DG,∠BAE=∠DAG.∵∠BAE+∠DAF=∠BAD﹣∠EAF=90°﹣12∠BAD=90°-45°=45°,∴∠DAG+∠DAF=45°,即∠FAG=45°,∴∠EAF=∠FAG,∴△AFE≌△AFG(SAS),∴EF=FG.又∵FG=DG+DF=BE+DF,∴BE+DF=EF,故答案为BE+DF=EF.(2)成立.如图2,将△ABE绕点A逆时针旋转α得到△ADH,可得∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH.∵∠B+∠ADC=180°,∴∠ADH+∠ADC=180°,∴点C,D,H在同一直线上.∵∠BAD=α,∠EAF12=α,∴∠BAE+∠FAD12=α,∴∠DAH+∠FAD12=α,∴∠FAH=∠EAF,又∵AF=AF,∴△AEF≌△AHF(SAS),∴EF=FH=DF+DH=DF+BE;(3)DE523 =,如图3,将△AEC绕点A顺时针旋转90°,得到△AE′B,连接DE′.可得BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,在Rt△ABC中,∵AB=AC=4,∠BAC=90°,∴∠ABC=∠ACB=45°,BC=2,∴2,∴∠ABC+∠ABE′=90°,即∠E′BD=90°,∴E′B2+BD2=E′D2.易证△AE′D≌△AED,∴DE=DE′,∴DE2=BD2+EC2,即DE2222)(32)DE=+,解得23DE=.【点睛】本题考查旋转的性质、全等三角形的判定与性质、勾股定理,旋转后不改变图形的大小和形状,并且对应点到旋转中心的距离相等,对应点与旋转中心的连线的夹角等于旋转角,熟练掌握旋转的性质及全等三角形的判定定理是解题关键.4.探究问题:(1)方法感悟:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠BAF=45°,连接EF,求证DE+BF=EF.感悟解题方法,并完成下列填空:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.∵∠1=∠2,∠1+∠3=45°.即∠GAF=∠________.又AG=AE,AF=AE∴△GAF≌△________.∴ _________=EF,故DE+BF=EF.(2)方法迁移:如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF =∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.答案:E解析:(1)EAF、△EAF、GF;(2)DE+BF=EF.【解析】【分析】(1)利用角之间的等量代换得出∠GAF=∠FAE,再利用SAS得出△GAF≌△EAF,得出答案;(2)将△ADE顺时针旋转90°得到△ABG,再证明△AGF≌△AEF,即可得出答案;【详解】解:(1)如图①所示;根据等量代换得出∠GAF=∠FAE,利用SAS得出△GAF≌△EAF,∴GF=EF,故答案为:FAE;△EAF;GF;(2)DE+BF=EF,理由如下:假设∠BAD的度数为m,将△ADE绕点A顺时针旋转,m°得到△ABG,如图,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.∵,∴.∵∠1=∠2,∴∠1+∠3=.即∠GAF=∠EAF.∵在△AGF和△AEF中,,∴△GAF≌△EAF(SAS).∴GF=EF.又∵GF=BG+BF=DE+BF,∴DE+BF=EF.【点睛】此题主要考查了全等三角形的判定和性质、以及折叠的性质和旋转变换性质等知识,证得△GAF≌△EAF是解题的关键.5.(1)如图1,在OAB和OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.求:①ACBD的值;②∠AMB的度数.(2)如图2,在OAB和OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD 的延长线于点M .请判断AC BD的值及∠AMB 的度数,并说明理由; (3)在(2)的条件下,将OCD 点O 在平面内旋转,AC ,BD 所在直线交于点M ,若OD=2,OB=23,请直接写出当点C 与点M 重合时AC 的长.答案:A解析:(1)①1,②40°;(2)AC BD 3∠AMB=90°,见解析;(3)33【分析】(1)①根据已知条件证明△COA ≌△DOB ,即可证明AC=BD ;②根据△COA ≌△DOB 可得∠CAO=∠DBO ,根据已知条件可得∠OAB+∠ABO=140°,然后在△AMB 中,根据等角的转换即可得到答案; (2)根据已知条件证明△AOC ∽△BOD ,可得∠CAO=∠DBO ,进而可得∠MAB=∠OAB+∠DBO ,最后可得∠AMB=180°-(∠OAB+∠ABM+∠DBO )=90°;(3)分两种情况讨论,根据题(2),同理可得OAC OBD △△,90AMB ∠=︒,3AC BD=,设BD=x ,则3AC x = 用x 表示出AM 、BM 的长,在Rt AMB 中,根据勾股定理222AM BM AB +=列出方程,求解即可.【详解】 解:(1)①如图1,∵∠AOB=∠COD=40°,∴∠COA=∠DOB ,∵OC=OD ,OA=OB ,∴△COA ≌△DOB (SAS ),∴AC=BD , ∴AC BD =1, ②∵△COA ≌△DOB ,∴∠CAO=∠DBO ,∵∠AOB=40°,∴∠OAB+∠ABO=140°,在△AMB 中,∠AMB=180°﹣(∠CAO+∠OAB+∠ABD )=180°﹣(∠DBO+∠OAB+∠ABD )=180°﹣140°=40°,(2)如图2,AC BD=3,∠AMB=90°,理由是:在Rt △COD 中,∠DCO=30°,∠DOC=90°,∴3tan 303OD OC =︒=,同理得:3tan 303OB OA =︒=, ∴OD OB OC OA=, ∵∠AOB=∠COD=90°,∴∠AOC=∠BOD ,∴△AOC ∽△BOD ,∴AC OC BD OD==3,∠CAO=∠DBO , 在△AMB 中,∠AMB=180°﹣(∠MAB+∠ABM )=180°﹣(∠OAB+∠ABM+∠DBO )=90°;(3)AC 的长为23或43.①如图,点C 与点M 重合,同理可得:OAC OBD △△,90AMB ∴∠=︒,3AC BD =设BD=x ,则3AC x =,在Rt ODC 中,30OCD ∠=︒,OD=2,4CD ∴=,在Rt AOB 中,30OAB ∠=︒,33AB ∴=,在Rt AMB 中,222AM BM AB +=,即222(3)(4)(43)x x ++=,解得:x=2或-4(舍),323x =②如图,点C 与点M 重合,同理可得:90AMB ∠=︒,3AC BD =设BD=x ,则3x ,在Rt COD 中, 90OCD ∠=︒,OD=2,4CD ∴=,4BC x =-,在Rt AOB 中,30OAB ∠=︒,3OB =243AB OB ∴==,在Rt AMB 中,222AM BM AB +=, 即222(3)(4)(43)x x +-=,解得:x=4或-2(舍), 343x =综上所述,AC 的长为2343【点睛】本题主要考查三角形的综合运用,涉及全等三角形与相似三角形的性质和判定、勾股定理、解一元一次方程、图形旋转证明、特殊角的三角函数值等知识点,难度较大,第(1)题证明△COA ≌△DOB 是关键,第(2)题证明△AOC ∽△BOD 是关键,第(3)题要特别注意分情况讨论.6.发现规律:(1)如图①,ABC 与ADE 都是等边三角形,直线,BD CE 交于点F .直线BD ,AC 交于点H .求BFC ∠的度数(2)已知:ABC 与ADE 的位置如图②所示,直线,BD CE 交于点F .直线BD ,AC 交于点H .若ABC ADE α∠=∠=,ACB AED β∠=∠=,求BFC ∠的度数 应用结论:(3)如图③,在平面直角坐标系中,点O 的坐标为(0,0),点M 的坐标为(3,0),N 为y 轴上一动点,连接MN .将线段MN 绕点M 逆时针旋转60得到线段MK ,连接NK ,OK ,求线段OK 长度的最小值答案:A解析:(1)BFC ∠的度数为60︒;(2)BFC ∠的度数为180αβ︒--;(3)线段OK 长度的最小值为32 【分析】(1)通过证明BAD CAE ≅△△可得ABD ACE ∠=∠,再由三角形内角和定理进行求解即可;(2)通过证明ABC ADE 可得BAC DAE ∠=∠,AB AC AD AE=,可证ABD ACE ,可得ABD ACE ∠=∠,由外角性质可得BFC BAC ∠=∠,再有三角形内角和定理进行求解即可;(3)由旋转的性质可得MNK △是等边三角形,可得MK MN NK ==,60NMK NKM KNM ∠=∠=∠=︒,如图③将MOK 绕点M 顺时针旋转60︒,得到MQN △,连接OQ ,可得60OMQ ∠=︒,OK =NQ ,MO =MQ ,则当NQ 为最小值时,OK有最小值,由垂线段最短可得当QN y ⊥轴时,NQ 有最小值,由直角三角形的性质即可求解.【详解】(1)∵ABC 与ADE 是等边三角形∴AB=AC ,AD=AE ,60BAC DAE ABC ACB ∠=∠=∠=∠=︒∴BAD CAE ∠=∠∴()BAD CAE SAS ≅ ∴ABD ACE ∠=∠∵60ABD DBC ABC ∠+∠=∠=︒∴60ACE DBC ∠+∠=︒∴18060BFC DBC ACE ACB ∠=︒-∠-∠-∠=︒;(2)∵ABC ADE α∠=∠=,ACB AED β∠=∠=∴ABC ADE∴BAC DAE ∠=∠,AB AC AD AE= ∴BAD CAE ∠=∠,AB AD AC AE = ∴ABD ACE ∴ABD ACE ∠=∠ ∵BHC ABD BAC BFC ACE ∠=∠+∠=∠+∠ ∴BFC BAC ∠=∠ ∵180BAC ABC ACB ∠+∠+∠=︒ ∴180BFC αβ∠++=︒∴180BFC αβ∠=︒--;(3)∵将线段MN 绕点M 逆时针旋转60︒得到线段MK∴MN MK =,60NMK ∠=︒∴MNK △是等边三角形∴MK MN NK ==,60NMK NKM KNM ∠=∠=∠=︒如下图,将MOK 绕点M 顺时针旋转60︒,得到MQN △,连接OQ∴MOK MQN ≅,60OMQ ∠=︒∴OK =NQ ,MO =MQ∴MOQ △是等边三角形∴60QOM ∠=︒∴30NOQ ∠=︒∵OK =NQ∴当NQ 为最小值时,OK 有最小值,由垂线段最短可得当QN y ⊥轴时,NQ 有最小值 ∵点M 的坐标为(3,0)∴3OM OQ ==∵QN y ⊥轴,30NOQ ∠=︒ ∴1322NQ OQ == ∴线段OK 长度的最小值为32. 【点睛】本题属于几何变换综合题,考查了等边三角形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,旋转的性质,三角形内角和定理等知识,灵活运用这些性质进行推理是解决本题的关键.7.问题提出:(1)如图1,在ABC 中,AB AC BC =≠,点D 和点A 在直线BC 的同侧,BD BC =,90BAC ∠=︒,30DBC ∠=︒,连接AD ,将ABD △绕点A 逆时针旋转90︒得到ACD ',连接BD '(如图2),可求出ADB ∠的度数为______.问题探究:(2)如图3,在(1)的条件下,若BAC α∠=,DBC β∠=,且120αβ+=︒,DBC ABC ∠<∠ ,①求ADB ∠的度数.②过点A 作直线AE BD ⊥,交直线BD 于点E ,7,2BC AD ==.请求出线段BE 的长.答案:A解析:(1)30°;(2)①30︒;②73-【分析】(1)由旋转的性质,得△ABD ≌ACD '∆,则ADB AD C '∠=∠,然后证明BCD '∆是等边三角形,即可得到30ADB AD C '∠=∠=︒;(2)①将ABD △绕点A 逆时针旋转,使点B 与点C 重合,得到'ACD △,连接'BD .与(1)同理证明D BC '∆为等边三角形,然后利用全等三角形的判定和性质,即可得到答案;②由解直角三角形求出3DE =【详解】解:(1)根据题意,∵AB AC BC =≠,90BAC ∠=︒,∴ABC ∆是等腰直角三角形,∴45ABC ACB ∠=∠=︒,∵30DBC ∠=︒,∴15ABD ∠=︒,由旋转的性质,则△ABD ≌ACD '∆,∴ADB AD C '∠=∠,15ABD ACD '∠=∠=︒,BC CD '=,∴60BCD '∠=︒,∴BCD '∆是等边三角形,∴60BD C '∠=︒,BD CD ''=∵AB AC =,AD AD ''=,∴ABD '∆≌ACD '∆,∴30AD B AD C ''∠=∠=︒,∴30ADB AD C '∠=∠=︒;(2)①DBC ABC ∠<∠,60120α︒︒∴<<.如图1,将ABD △绕点A 逆时针旋转,使点B 与点C 重合,得到'ACD △,连接'BD .AB AC =,ABC ACB ∴∠=∠,BAC α∠=, ()111809022ABC αα︒︒∴∠=-=-, 1902ABD ABC DBC αβ︒∴∠=∠-∠=--, 119090180()22D CB ACD ACB αβααβ''︒︒︒∴∠=∠+∠=--+-=-+. 120,αβ︒+=60D CB '︒∴∠=.,BD BC BD CD '==,,BC CD '∴=D BC '∴为等边三角形,D B D C ''∴=,AD B AD C ''∴≌,AD B AD C ''∴∠=∠,1302AD B BD C ''︒∴∠=∠=, 30ADB ︒∴∠=.②如图2,由①知,30ADB ︒∠=,在Rt ADE △中,30,2ADB AD ︒∠==, 3DE ∴=.BCD '是等边三角形,7BD BC '∴==,7BD BD '∴==,73BE BD DE ∴=-=-.【点睛】本题考查了解直角三角形,旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质,等腰直角三角形的性质,以及三角形的内角和定理,解题的关键是熟练掌握所学的知识,正确利用旋转模型进行解题.8.定义:按螺旋式分别延长n边形的n条边至一点,若顺次连接这些点所得的图形与原多边形相似,则称它为原图形的螺旋相似图形.例如:如图1,分别延长多边形A1A2…A n 的边得A1′,A2′,…,A n′,若多边形A1′A2′…A n′与多边形A1A2…An相似,则多边形A1′A2′…A n′就是A1A2…A n的螺旋相似图形.(1)如图2,已知△ABC是等边三角形,作出△ABC的一个螺旋相似图形,简述作法,并给以证明.(2)如图3,已知矩形ABCD,请探索矩形ABCD是否存在螺旋相似图形,若存在,求出此时AB与BC的比值;若不存在,说明理由.(3)如图4,△ABC是等腰直角三角形,AC=BC=2,分别延长CA,AB,BC至A′,B′,C′,使△A′B′C′是△ABC的螺旋相似三角形.若AA′=kAC,请直接写出BB′,CC′的长(用含k的代数式表示)答案:A解析:(1)见解析;(2)AB:BC=1;(3)BB′2k,CC′=k.【分析】(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形,证明△DEF是等边三角形即可解决问题.(2)如图3中,假设存在.四边形EFGH是矩形ABCD的螺旋相似图形,设AB=CD=a,BC=AD=b,BE=DG=x,CF=AH=y.分两种情形,利用相似三角形的性质以及相似矩形的性质,构建关系式证明a=b即可解决问题.(3)如图4中,作B′T⊥CB交CB的延长线于T.设TB=TB′=m,证明△A′CC′≌△A′TB′(ASA),推出A′C=TC′,CC′=TB′=BT,构建关系式推出m=k即可解决问题.【详解】解:(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形.理由:∵△ABC是等边三角形,∴AB=BC=AC,∠CAB=∠ABC=∠ACB,∴∠DAE=∠FCD=∠EBF=120°,∵BE=CF=AD,∴CD=AE=BF,∴△FCD≌△DAE≌△EBF(SAS),∴DF=DE=EF,∴△DEF是等边三角形,∴△DEF∽△ABC,∴△DEF是△ABC的一个螺旋相似图形.(2)如图3中,假设存在.四边形EFGH是矩形ABCD的螺旋相似图形,设AB=CD=a,BC=AD=b,BE=DG=x,CF=AH=y.由题意:△BEF∽△AHE,∴EFEH =BEAH=BFAE,∴xy=b ya x++,当EFHE=BCAB=ba时,ba=xy=b ya x++,∴x=ba•y,ax+x2=by+y2,∴by +22b a •y 2=by +y 2, ∴a 2=b 2,∴a =b ,即AB :BC =1.当EF EH =AB BC =a b 时.a b =x y =b y a x++, ∴x =a b•y ,ax +x 2=by +y 2, ∴2a b •y +22a b•y 2=by +y 2, ∴22a b b -•y (1+y b)=0, ∵y ≠0,1+y b≠0, ∴a 2=b 2, ∴a =b ,即AB :BC =1,综上所述,AB :BC =1.(3)如图4中,作B ′T ⊥CB 交CB 的延长线于T .∵AC =BC =2,∠ACB =90°,∴∠ABC =∠CAB =45°,∴∠TBB ′=∠ABC =45°,∴∠TB ′B =∠TBB ′=45°,∴TB =TB ′,设TB =TB ′=m ,∵△A ′B ′C ′是△ABC 的螺旋相似三角形,∴A ′C ′=B ′C ′,∠A ′C ′B ′=90°,∵∠A ′C ′C +∠B ′C ′=90°,∠A ′CC +∠C ′A ′C =90°,∴∠C ′A ′C =∠B ′C ′T ,∵∠A ′CC ′=∠T =90°,∴△A ′CC ′≌△A ′TB ′(ASA ),∴A ′C =TC ′,CC ′=TB ′=BT ,∴2+2k =2+2m ,∴m =k ,∴BB′=2k,CC′=k.【点睛】本题属于相似形综合题,考查了等边三角形的性质,矩形的性质,等腰直角三角形的判定和性质等知识,解题的关键是理解题意,学会利用参数解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.9.已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时,请直接写出线段BD与CF的数量关系:;(2)如图2,当点D在线段BC的延长线上时,其它条件不变,若AC=2,CD=1,则CF= ;(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系:;②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.答案:B解析:(1)BD=CF;(2)221;(3)①CD=CF+BC,②等腰三角形,见解析【分析】(1)△ABC是等腰直角三角形,利用SAS即可证明△BAD≌△CAF;(2)同(1)相同,利用SAS即可证得△BAD≌△CAF,从而证得BD=CF,即可得到CF=CD+BC,然后求出答案;(3)中的①与(1)相同,可证明BD=CF,又点D、B、C共线,故:CD=BC+CF;②由(1)猜想并证明BD⊥CF,从而可知△FCD为直角三角形,再由正方形的对角线的性质判定△AOC三边的特点,再进一步判定其形状.【详解】解:(1)证明:∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°,∴∠BAD=∠CAF,在△BAD和△CAF中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAF (SAS ),∴BD=CF ,(2)与(1)同理,证△BAD ≌△CAF ;∴BD=CF ,∴CF=BC+CD ,∵AC=AB=2,CD=1,∴BC ==∴CF=1;(3)①BC 、CD 与CF 的关系:CD=BC+CF理由:与(1)同法可证△BAD ≌△CAF ,从而可得:BD=CF ,即:CD=BC+CF②△AOC 是等腰三角形理由:与(1)同法可证△BAD ≌△CAF ,可得:∠DBA=∠FCA ,又∵∠BAC=90°,AB=AC ,∴∠ABC=∠ACB=45°,则∠ABD=180°-45°=135°,∴∠ABD=∠FCA=135°∴∠DCF=135°-45°=90°∴△FCD 为直角三角形.又∵四边形ADEF 是正方形,对角线AE 与DF 相交于点O ,∴OC=12DF , ∴OC=OA ∴△AOC 是等腰三角形.【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点,一般情况下,要证明两条线段相等,就得证明这两条线段所在的两个三角形全等,关键是掌握图形特点挖掘题目所隐含的条件.10.如图,已知ABC 和ADE 均为等腰三角形,AC =BC ,DE =AE ,将这两个三角形放置在一起.(1)问题发现:如图①,当60ACB AED ∠∠︒==时,点B 、D 、E 在同一直线上,连接CE ,则CEB ∠= °,线段BD 、CE 之间的数量关系是 ;(2)拓展探究:如图②,当90ACB AED ∠∠︒==时,点B 、D 、E 在同一直线上,连接CE ,请判断CEB ∠的度数及线段BD 、CE 之间的数量关系,并说明理由;(3)解决问题:如图③,90ACB AED ∠∠︒==,25AC =,AE =2,连接CE 、BD ,在AED 绕点A 旋转的过程中,当DE BD ⊥时,请直接写出EC 的长.答案:C解析:(1)60BD CE ,=;(2)452CEB BD CE ∠︒=,=,理由见解析;(3)CE 的长为2或2【分析】(1)证明ACE ABD ≌,得出CE =BD ,AEC ADB ∠=∠,即可得出结论; (2)证明ACE ABD ∽,得出AEC ADB ∠=∠,2BD CE =,即可得出结论; (3)先判断出2BD CE =,再求出210AB =:①当点E 在点D 上方时,先判断出四边形APDE 是矩形,求出AP =DP =AE =2,再根据勾股定理求出,BP =6,得出BD =4;②当点E 在点D 下方时,同①的方法得,AP =DP =AE =1,BP =6,进而得出BD =BP +DP =8,即可得出结论.【详解】解:(1)ABC 为等腰三角形,60AC BC ACB ∠︒=,=,∴ABC 是等边三角形,同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAE AD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒=≌()故答案为:60CEB BD CE ∠=︒=;.(2)45CEB BD ∠︒=,,理由如下:在等腰三角形ABC 中,AC =BC ,90ACB ∠︒=,45AB CAB ∴∠︒,= ,同理,45AD ADE DAE ∠∠︒,==, ∴AE AC AD AB =,DAE CAB ∠∠=, EAC DAB ∴∠∠=,ACE ABD ∴∽ ,∴BD AD CE AE== ∴AEC ADB BD ∠∠=,,点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒==135AEC ∴∠︒=45CEB AEC AED ∴∠∠-∠︒==;(3)由(2)知,ACE ABD ∽,BD ∴,在Rt ABC 中,AC =AB ∴=,①当点E 在点D 上方时,如图③,过点A 作AP BD ⊥交BD 的延长线于P ,DE BD ⊥,PDE AED APD ∴∠∠∠==,∴四边形APDE 是矩形,AE DE = ,∴矩形APDE 是正方形,2AP DP AE ∴===,在Rt APB △中,根据勾股定理得,6BP ,4BD BP AP ∴-==,CE BD ∴= ②当点E 在点D 下方时,如图④同①的方法得,AP =DP =AE =2,BP =6,∴BD =BP +DP =8,CE ∴=综上CE 的长为或.【点睛】本题是几何变换的综合题,主要考查了旋转的性质,全等三角形的判定和定理,相似三角形的判定和性质,勾股定理,等边三角形的性质,判断出三角形ACE 和三角形ABD 相似是关键.11.如图.四边形ABCD 、BEFG 均为正方形.(1)如图1,连接AG 、CE ,请直接写出.....AG 和CE 的数量和位置关系(不必证明).(2)将正方形BEFG 绕点B 顺时针旋转β角(0180β︒︒<<),如图2,直线AG 、CE 相交于点M .①AG 和CE 是否仍然满足(1)中的结论?如果是,请说明理由:如果不是,请举出反例:②连结MB ,求证:MB 平分AME ∠.(3)在(2)的条件下,过点A 作AN MB ⊥交MB 的延长线于点N ,请直接写出.....线段CM 与BN 的数量关系.答案:A解析:(1)AG=EC ,AG ⊥EC ;(2)①满足,理由见解析;②见解析;(3)2.【分析】(1)由正方形BEFG 与正方形ABCD ,利用正方形的性质得到两对边相等,一对直角相等,利用SAS 得出三角形ABG 与三角形CBE 全等,利用全等三角形的对应边相等,对应角相等得到CE=AG ,∠BCE=∠BAG ,再利用同角的余角相等即可得证;(2)①利用SAS 得出△ABG ≌△CEB 即可解决问题;②过B 作BP ⊥EC ,BH ⊥AM ,由全等三角形的面积相等得到两三角形面积相等,而AG=EC ,可得出BP=BH ,利用到角两边距离相等的点在角的平分线上得到BM 为角平分线;(3)在AN 上截取NQ=NB ,可得出三角形BNQ 为等腰直角三角形,利用等腰直角三角形的性质得到BQ=2BN ,接下来证明BQ=CM ,即要证明三角形ABQ 与三角形BCM 全等,利用同角的余角相等得到一对角相等,再由三角形ANM 为等腰直角三角形得到NA=NM ,利用等式的性质得到AQ=BM ,利用SAS 可得出全等,根据全等三角形的对应边相等即可得证.【详解】解:(1)AG=EC ,AG ⊥EC ,理由为:∵正方形BEFG ,正方形ABCD ,∴GB=BE ,∠ABG=90°,AB=BC ,∠ABC=90°,在△ABG 和△BEC 中,BG BE ABC EBC BA BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△BEC (SAS ),∴CE=AG ,∠BCE=∠BAG ,延长CE 交AG 于点M ,∴∠BEC=∠AEM ,∴∠ABC=∠AME=90°,∴AG=EC ,AG ⊥EC ;(2)①满足,理由是:如图2中,设AM 交BC 于O .∵∠EBG=∠ABC=90°,∴∠ABG=∠EBC ,在△ABG 和△CEB 中,AB BC ABG CBE BG EB =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△CEB (SAS ),∴AG=EC ,∠BAG=∠BCE ,∵∠BAG+∠AOB=90°,∠AOB=∠COM ,∴∠BCE+∠COM=90°,∴∠OMC=90°,∴AG ⊥EC .②过B 作BP ⊥EC ,BH ⊥AM ,∵△ABG ≌△CEB ,∴S △ABG =S △EBC ,AG=EC , ∴12EC•BP=12AG•BH , ∴BP=BH ,∴MB 平分∠AME ;(3)2BN ,理由为:在NA 上截取NQ=NB ,连接BQ ,∴△BNQ 为等腰直角三角形,即2BN ,∵∠AMN=45°,∠N=90°,∴△AMN 为等腰直角三角形,即AN=MN ,∴MN-BN=AN-NQ ,即AQ=BM ,∵∠MBC+∠ABN=90°,∠BAN+∠ABN=90°,∴∠MBC=∠BAN ,在△ABQ 和△BCM 中,AQ BM BAN MBC AB BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABQ ≌△BCM (SAS ),∴CM=BQ ,则CM=2BN .【点睛】此题考查了正方形,全等三角形的判定与性质,等腰直角三角形的判定与性质,角平分线的判定,熟练掌握正方形的性质是解本题的关键.12.在平面直角坐标系中,点A 在y 轴正半轴上,点B 在x 轴负半轴上,BP 平分∠ABO . (1)如图1,点T 在BA 延长线上,若AP 平分∠TAO ,求∠P 的度数;(2)如图2,点C 为x 轴正半轴上一点,∠ABC =2∠ACB ,且P 在AC 的垂直平分线上. ①求证:AP //BC ;②D 是AB 上一点,E 是x 轴正半轴上一点,连接AE 交DP 于H .当∠DHE 与∠ABE 满足什么数量关系时,DP =AE .给出结论并说明理由.答案:D解析:(1)45°;(2)①见解析;②∠DHE +∠ABE =180°,理由见解析【分析】(1)由三角形的外角性质和角平分线的性质可得∠AOB =2∠P =90°,可求解;(2)①过点P 作PE ⊥AB 交BA 延长线于E ,过点P 作PF ⊥BC 于F ,连接PC ,由角平分线的性质可得PE =PF ,由垂直平分线的性质可得PA =PC ,由“HL ”可证Rt △APE ≌Rt △CPF ,可得∠EPA =∠CPF ,由四边形内角和定理可得∠EBF +∠EPF =180°,由角的数量关系可证∠ACB =∠PAC ,由平行线的判定可证AP ∥BC ;②如图3,在OE 上截取ON =OB ,连接AN ,通过证明△ADP ≌△NEA ,可得DP =AE .【详解】解:(1)∵BP 平分∠ABO ,AP 平分∠TAO ,∴∠PBT =12∠ABO ,∠TAP =12∠TAO , ∵∠TAO =∠ABO+∠AOB ,∠TAP =∠P+∠ABP ,∴∠AOB =2∠P =90°,∴∠P =45°;(2)①如图2,过点P 作PE ⊥AB 交BA 延长线于E ,过点P 作PF ⊥BC 于F ,连接PC ,又∵PB 平分∠ABC ,∴PE =PF ,∵P 在AC 的垂直平分线上,∴PA =PC ,∴∠PAC =∠PCA ,在Rt △APE 和Rt △CPF 中,AP PC PE PF =⎧⎨=⎩, ∴Rt △APE ≌Rt △CPF (HL ),∴∠EPA =∠CPF ,∴∠EPF =∠APC ,在四边形BEPF 中,∠EBF+∠BEP+∠EPF+∠PFB =180°,∴∠EBF+∠EPF =180°,∴∠ABC+∠APC =180°,∵∠APC+∠PAC+∠PCA =180°,∴∠ABC =∠PAC+∠PCA =2∠PAC ,∵∠ABC =2∠ACB ,∴∠ACB =∠PAC ,∴AP ∥BC ;②当∠DHE+∠ABE =180°时,DP =AE ,理由如下:如图3,在OE 上截取ON =OB ,连接AN ,∵OB =ON ,AO ⊥BE ,∴AB =AN ,∴∠ABN =∠ANB ,∵AP ∥BE ,BP 平分∠ABE ,∴∠APB =∠PBE =∠ABP ,∠ABN+∠BAP =180°,∴AP =AB ,∴AP =AN ,∵∠ANB+∠ANE =180°,∴∠BAP =∠ANE ,∵∠DHE+∠ABE =180°,∠DHE+∠ABE+∠BDH+∠BEH =360°,∴∠BDH+∠BEH =180°,∵∠ADP+∠BDP =180°,∴∠ADP =∠AEN ,在△ADP 和△NEA 中,DAP ANE ADP AEN AP AN ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADP ≌△NEA (AAS ),∴DP =AE .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,角平分线的性质,线段垂直平分线的性质,四边形内角和定理等知识,添加恰当辅助线构造全等三角形是本题的关键. 13.如图1,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC .(1)求证:△ABD ≌△ACE ;(2)如图2,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC ,∠ADB=90°,点E 在△ABC 内,延长DE 交BC 于点F ,求证:点F 是BC 中点;(3)△ABC 为等腰三角形,∠BAC=120°,AB=AC ,点P 为△ABC 所在平面内一点,∠APB=120°,AP=2,BP=4,请直接写出 CP 的长.答案:D解析:(1)证明见详解;(2)证明见详解;(3)2713【分析】(1)因为∠DAE=∠BAC ,可以得到∠DAB=∠EAC ,因为AD=AE ,AB=AC ,即可得到△ABD ≌△ACE ;(2)连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,由(1)可得△ABD ≌△ACE ,所以∠AEC=90°和CE=BD ,可以推出∠BDF=∠CEF ,再证明△DBF ≌△ECH ,所以BF=CH ,等量代换即可得到BF=FC ,即可解决;(3)点P 在△ABC 内部,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC ,可以得到△PP C '是直角三角形,利用勾股定理即可求出PC 的值;当点P 在△ABC 外部,将△APB 绕点A 逆时针旋转120︒得到PDC ∆,连接PP '和PC ,过点P 作PD ⊥'CP 于点D ,连接PD 可以得到△PP D ',△PP D '是直角三角形和,利用勾股定理即可求出'DP 及PC 的值.【详解】解:(1)证明:∵∠DAE=∠BAC∴∠DAB=∠EAC∵AD=AE ,AB=AC∴△ABD ≌△ACE(2)证明:连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,如图所示:∵△ADB≌△AEC∴BD=EC,∠ADB=∠AEC=90°∵AD=AE∴∠ADE=∠AED∵∠ADE+∠EDB=∠AED+∠CEH=90°∴∠EDB=∠CEH∵CF=CH∴∠CFH=∠CHF∴∠DFB=∠H∵CE=BD∴△DBF≌△ECH∴BF=CH∴BF=CF∴点F是BC的中点∆',连接(3)当点P在△ABC内部,如图所示,将△ABP逆时针旋转120°,得到ACPPP'和PC∆'∵将△ABP旋转120°得到ACP∴∠PAP'=120°,AP='AP=2,BP=CP'=4∴PP'3∵∠AP C'=120°,∠AP P'=30°,∴∠PP C'=90°,∴()2223427+=.当点P在△ABC外部,如图所示,将△APB 绕点A 逆时针旋转120︒到△'AP C ,过点P 作PD ⊥'CP 于点D ,连接PD , ∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4,∴PP '=23, ∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=150°,∴∠PP D '=30°,在Rt 'PDP 中,1'32PD PP ==, 22''3DP PP PD ∴=-=,''347DC DP P C ∴=+=+=,()222237213PC PD DC ∴=+=+= . 综上所述,27213PC =或【点睛】本题主要考查了全等三角形以及旋转,合理的作出辅助线以及熟练旋转的性质是解决本题的关键.14.矩形ABCD 中,6,8AB BC ==,点,M N 分别在边,BC AD 上,且3,2BM DN ==,连接MN 并延长,交CD 的延长线于点E ,点Q 为射线MN 上一动点,过点Q 作AQ 的垂线,交CD 于点P .(1)特例发现,如图,若点P 恰好与点D 重合,填空:①DE =________;②QA 与QP 的等量关系为_________.(2)拓展探究如图,若点Q 在MN 的延长线上,QA 与QP 能否相等?若能,求出DP 的长;若不能,请说明理由.(3)思维延伸如图,点G 是线段CD 上异于点D 一点,连接AG ,过点G 作直线GI AG ⊥,交直线MN 于点I ,是否存在点G ,使,AG GI 相等?若存在,请直接写出DG 的长;若不存在,请说明理由.答案:E解析:(1)①4; ②QA QP =;(2)QA 与QP 能够相等,理由详见解析;(3)(3),AG GI 能够相等,43DG =【分析】(1)①根据END EMC ,利用对应边成比例列式求出ED 长;②过点Q 作//HG BC ,交AB 于点H ,交DC 于点G ,设QG x =,利用AHQ QGD ,对应边成比例列式求出x ,得到这两个三角形其实是全等的,所以QA QP =;(2)过点Q 作QF AB ⊥,交BA 的延长线于点F ,延长FQ 交CE 于点G ,构造“k”字型全等三角形,设AF x =,再利用相似三角形的性质列式求解;(3)过点G 作GK AB ⊥于点K ,过点I 作IS KG ⊥,交KG 的延长线于点S ,延长AD 交IS 于点T ,同(2)构造“k”字型全等三角形,DG y =,再利用相似三角形的性质列式求解.【详解】(1)①∵//ND MC ,∴END EMC ,∴ED ND EC MC=, 835MC BC BM =-=-=,6DC =,265ED ED =+,解得4ED =, 故答案是:4;②如图,过点Q 作//HG BC ,交AB 于点H ,交DC 于点G ,可得HG AB ⊥,HG DC ⊥,∴90AHQ QGD ∠=∠=︒,∵AQ QD ⊥,∴90AQH DQG ∠+∠=︒,∵90QAH AQH ∠+∠=︒,∴QAH DQG ∠=∠,∴AHQ QGD ,∴AH HQ QG GD=, 设QG x =,8HQ x =-, ∵//QG MC ,∴EQG EMC ,。
初中数学四边形、三角形几何综合题目汇总(动点、旋转)大全
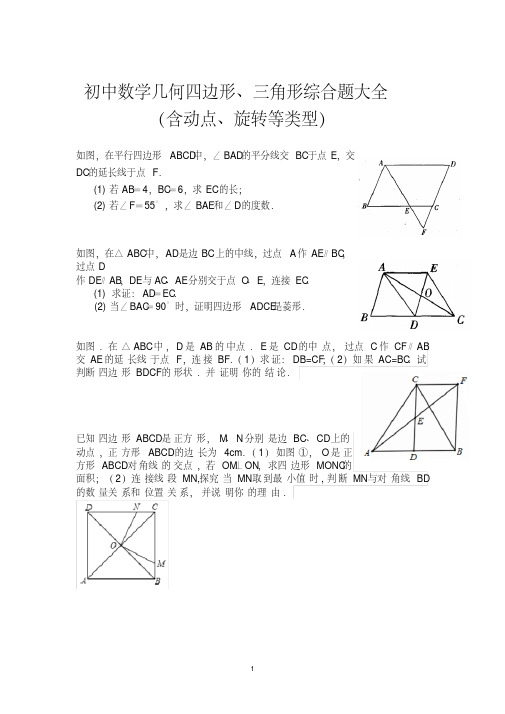
初中数学几何四边形、三角形综合题大全(含动点、旋转等类型)如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.(1)若AB=4,BC=6,求EC的长;(2)若∠F=55°,求∠BAE和∠D的度数.如图,在△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、E,连接EC.(1)求证:AD=EC.(2)当∠BAC=90°时,证明四边形ADCE是菱形.如图.在△ABC中,D是AB的中点.E是CD的中点,过点C作CF∥AB 交AE的延长线于点F,连接BF.(1)求证:DB=CF;(2)如果AC=BC.试判断四边形BDCF的形状.并证明你的结论.已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm.(1)如图①,O是正方形ABCD对角线的交点,若OM⊥ON,求四边形MONC的面积;(2)连接线段MN,探究当MN取到最小值时,判断MN与对角线BD 的数量关系和位置关系,并说明你的理由.已知四边形ABCD 是边长为2的菱形,∠BAD =60°,对角线AC 与BD 交于点O ,过点O 的直线EF 交AD 于点E ,交BC 于点F .(1)求证:△AOE ≌△COF ;(2)若∠EOD =30°,求CF 的长.已知,如图,在Rt △ABC 中,CD 是斜边上的中线,DE ⊥AB 交BC 于点F ,交AC 的延长线于点E .(1)△ADE ∽△FDB 吗?为什么?(2)你能推出结论CD 2=DE ·DF 吗?请试一试.如图,在四边形ABCD 中,AC 、BC 相交于点O ,∠ABD=∠ACD ,试找出图中的相似三角形,并加以证明.如图,E 、F 是□ABCD 的对角线AC 上的两点,且AE =CF .请你以点F 为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).(1)连结;(2)猜想:=;(3)证明:如图,将?ABCD 的边DC 延长到点E ,使CE=DC ,连接AE ,交BC 于点F .(1)求证:△ABF ≌△ECF ;(2)若∠AFC=2∠D ,连接AC 、BE ,求证:四边形ABEC 是矩形.ODCBABCDE FA在平行四边形ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2) ∠BAD=60°,AC平分∠BAD ,AC=2,求BN的长。
全等三角形综合练习初一几何压轴题

全等三角形综合练习 1姓名:____________一.解答题(共26小题)1.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.问题迁移:(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O 三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.2.已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD 之间的数量关系,不必写理由.3.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,第n次操作,分别作∠ABE n﹣1和∠DCE n﹣1的平分线,交点为E n.(1)如图①,求证:∠BEC=∠ABE+∠DCE;(2)如图②,求证:∠BE2C=∠BEC;(3)猜想:若∠E n=α度,那∠BEC等于多少度?(直接写出结论).4.阅读下面的材料,并完成后面提出的问题.(1)如图1中,AC∥DB,请你探究一下∠M,∠A与∠B的数量有何关系,并说明理由(2)如图2中,当点M向左移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?(3)如图3中,当点M向上移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?(4)如图4中,当点M向下移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?写出对应图形的数量关系,并选其中的一个图形加以证明5.已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;(2)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,利用(1)的结论,试求∠P的度数;(3)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B 之间存在着怎样的数量关系?并说明理由.6.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.7.(本题有3小题,第(1)小题为必答题,满分5分;第(2)、(3)小题为选答题,其中,第(2)小题满分3分,第(3)小题满分6分,请从中任选1小题作答,如两题都答,以第(2)小题评分.)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.注意:第(2)、(3)小题你选答的是第2小题.8.已知△ABC中,∠A=30°.(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC=°.(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C=°.(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n ﹣1个点),求∠BO n﹣1C(用n的代数式表示).(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1,若∠BO n﹣1C=60°,求n的值.9.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON 上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.(1)如图1,若AB∥ON,则①∠ABO的度数是;②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x=.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.10.如图,已△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明;②点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?(2)若点Q以②的运动速度从点C出发点P以原来运动速度从点B同时出发,都逆时针沿ABC的三边运动,求多长时间点P与点Q第一次在△ABC的哪条边上相遇?11.已知:如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.求证:AD⊥AE.12.如图,已知△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连结BE.(1)请判断线段AD、BE之间的数量关系,并说明理由;(2)求证:AM=CM+BE.13.如图①②,点E、F分别是线段AB、线段CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)线段AD和线段BC有怎样的数量关系?请说明理由;(2)当DG⊥GC时,试判断直线AD和直线BC的位置关系,并说明理由.14.如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).(1)用的代数式表示PC的长度;(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.15.如图①,AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s 的速度由A向B运动.同时点Q在线段BD上由点B向点D运动.它们运动的时间为t s.(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.(2)如图②,将“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,其他条件不变,设点Q运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应x,t的值;若不存在,说明理由.16.如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.求证:(1)△ABC≌△ADE;(2)BC⊥DE.17.如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.(1)求证:在运动过程中,不管t取何值,都有S△AED=2S△DGC.(2)当t取何值时,△DFE与△DMG全等.18.如图所示,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,CE与BD相交于点M,BD与AC交于点N,试猜想BD与CE有何关系?说明理由.19.如图,长方形ABCD中,AB=10cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E 运动,最终到达点E.若点P运动的时间为x秒,那么当x为何值时,△APE的面积等于32cm2?(提醒:同学们,要分类讨论哦!)20.如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.(1)用含t的式子表示线段AP、AQ的长;(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?(3)当t为何值时,PQ∥BC?21.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.22.如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D 不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.(1)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.(2)若DC=2,求证:△ABD≌△DCE.23.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF 对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.24.如图,△ABC中,AB=AC=18cm,BC=16cm,点D是AB的中点.有一点E在BC上从点B向点C运动,速度为2cm/s,同时有一点F在AC上从点C向点A运动,其中一点停止运动另一点也随之停止运动.问当点F的运动速度是多少时,△DBE和△EFC全等?25.已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s).(1)当动点P、Q同时运动2s时,则BP=cm,BQ=cm.(2)当动点P、Q同时运动t(s)时,分别用含有t的式子表示;BP=cm,BQ=cm.(3)当t为何值时,△PBQ是直角三角形?26.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.(1)点M、N运动几秒后,M、N两点重合?(2)点M、N运动几秒后,可得到等边三角形△AMN?(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.全等三角形综合练习1答案一.解答题(共26小题)1.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.问题迁移:(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O 三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.【解答】解:(1)∠CPD=∠α+∠β,理由如下:如图3,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;(2)当P在BA延长线时,∠CPD=∠β﹣∠α;理由:如图4,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;当P在AB延长线时,∠CPD=∠α﹣∠β.理由:如图5,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.2.已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD 之间的数量关系,不必写理由.【解答】解:(1)∠APB=∠PAC+∠PBD,如图1,过点P作PE∥l1,∴∠APE=∠PAC,∵l1∥l2,∴PE∥l2,∴∠BPE=∠PBD,∴∠APE+∠BPE=∠PAC+∠PBD,∴∠APB=∠PAC+∠PBD;(2)不成立,如图2:∠PAC=∠APB+∠PBD,理由:过点P作PE∥l1,∴∠APE=∠PAC,∵l1∥l2,∴PE∥l2,∴∠BPE=∠PBD,∵∠APB=∠APE﹣∠BPE=∠PAC﹣∠PBD,∴∠PAC=∠APB+∠PBD;如图3:∠PBD=∠PAC+∠APB,理由:过点P作PE∥l1,∴∠APE=∠PAC,∵l1∥l2,∴PE∥l2,∴∠BPE=∠PBD,∵APB=∠BPE﹣∠APE=∠PBD﹣∠PAC,∴∠PBD=∠PAC+∠APB.3.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,第n次操作,分别作∠ABE n﹣1和∠DCE n﹣1的平分线,交点为E n.(1)如图①,求证:∠BEC=∠ABE+∠DCE;(2)如图②,求证:∠BE2C=∠BEC;(3)猜想:若∠E n=α度,那∠BEC等于多少度?(直接写出结论).【解答】解:(1)如图①,过E作EF∥AB,∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2,∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE;(2)如图2,∵∠ABE和∠DCE的平分线交点为E1,∴由(1)可得,∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC;∵∠ABE1和∠DCE1的平分线交点为E2,∴由(1)可得,∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC;(3)如图2,∵∠ABE2和∠DCE2的平分线,交点为E3,∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;…以此类推,∠E n=∠BEC,∴当∠E n=α度时,∠BEC等于2nα度.4.阅读下面的材料,并完成后面提出的问题.(1)如图1中,AC∥DB,请你探究一下∠M,∠A与∠B的数量有何关系,并说明理由(2)如图2中,当点M向左移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?(3)如图3中,当点M向上移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?(4)如图4中,当点M向下移动到图2所示的位置时,∠M、∠A与∠B又有怎样的数量关系呢?写出对应图形的数量关系,并选其中的一个图形加以证明【解答】解:(1)∠AMB=∠A+∠B.理由:如图1,过点M作ME∥AC,∵AC∥DB,∴AC∥ME∥DB,∴∠A=∠AME,∠B=∠BME,∴∠A+∠B=∠AME+∠BME=∠AMB;(2)∠AMB+∠A+∠B=360°.理由:如图2,过点M作MF∥AC,∵AC∥DB,∴AC∥MF∥DB,∴∠A+∠AMF=180°,∠B+∠BMF=180°,∴∠AMB+∠A+∠B=∠A+∠AMF+∠B+∠BMF=360°;(3)∠A﹣∠B=∠AMB.理由:如图3,过点M作MG∥AC,∵AC∥DB,∴AC∥MG∥DB,∴∠A=∠AMG,∠B=∠BMG,∴∠A﹣∠B=∠AMG﹣∠BMG=∠AMB;(4)∠B﹣∠A=∠AMB.理由:如图4,过点M作MH∥AC,∵AC∥DB,∴AC∥MH∥DB,∴∠A=∠AMH,∠B=∠BMH,∴∠B﹣∠A=∠BMH﹣∠AMH=∠AMB.5.已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系∠A+∠D=∠C+∠B;;(2)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,利用(1)的结论,试求∠P的度数;(3)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B 之间存在着怎样的数量关系?并说明理由.【解答】解:(1)根据三角形内角和定理以及对顶角相等,可得结论:∠A+∠D=∠C+∠B;故答案为:∠A+∠D=∠C+∠B;(2)由(1)可知,∠1+∠D=∠P+∠3,①∠4+∠B=∠2+∠P,②∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠1=∠2,∠3=∠4,由①+②得:∠1+∠D+∠4+∠B=∠P+∠3+∠2+∠P,即2∠P=∠D+∠B,又∵∠D=40°,∠B=36°,∴2∠P=40°+36°=76°,∴∠P=38°;(3)∠P与∠D、∠B之间存在的关系为2∠P=∠D+∠B.∵∠1+∠D=∠P+∠3,①∠4+∠B=∠2+∠P,②∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠1=∠2,∠3=∠4,由①+②得:∠1+∠D+∠4+∠B=∠P+∠3+∠2+∠P,即2∠P=∠D+∠B.6.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.【解答】(1)证明:连接BF(如图①),∵△ABC≌△DBE(已知),∴BC=BE,AC=DE.∵∠ACB=∠DEB=90°,∴∠BCF=∠BEF=90°.在Rt△BFC和Rt△BFE中,∴Rt△BFC≌Rt△BFE(HL).∴CF=EF.又∵AF+CF=AC,∴AF+EF=DE.(2)解:画出正确图形如图②∴(1)中的结论AF+EF=DE仍然成立;(3)不成立.证明:连接BF,∵△ABC≌△DBE,∴BC=BE,∵∠ACB=∠DEB=90°,∴△BCF和△BEF是直角三角形,在Rt△BCF和Rt△BEF中,,∴△BCF≌△BEF(HL),∴CF=EF;∵△ABC≌△DBE,∴AC=DE,∴AF=AC+FC=DE+EF.7.(本题有3小题,第(1)小题为必答题,满分5分;第(2)、(3)小题为选答题,其中,第(2)小题满分3分,第(3)小题满分6分,请从中任选1小题作答,如两题都答,以第(2)小题评分.)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.注意:第(2)、(3)小题你选答的是第2小题.【解答】证明:(1)①∵∠ADC=∠ACB=∠BEC=90°,∴∠CAD+∠ACD=90°,∠BCE+∠CBE=90°,∠ACD+∠BCE=90°.∴∠CAD=∠BCE.∵AC=BC,∴△ADC≌△CEB.②∵△ADC≌△CEB,∴CE=AD,CD=BE.∴DE=CE+CD=AD+BE.解:(2)∵∠ADC=∠CEB=∠ACB=90°,∴∠ACD=∠CBE.又∵AC=BC,∴△ACD≌△CBE.∴CE=AD,CD=BE.∴DE=CE﹣CD=AD﹣BE.(3)当MN旋转到图3的位置时,AD、DE、BE所满足的等量关系是DE=BE﹣AD (或AD=BE﹣DE,BE=AD+DE等).∵∠ADC=∠CEB=∠ACB=90°,∴∠ACD=∠CBE,又∵AC=BC,∴△ACD≌△CBE,∴AD=CE,CD=BE,∴DE=CD﹣CE=BE﹣AD.8.已知△ABC中,∠A=30°.(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC=°.(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C=°.(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n ﹣1个点),求∠BO n﹣1C(用n的代数式表示).(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1,若∠BO n﹣1C=60°,求n的值.【解答】解:∵∠BAC=30°,∴∠ABC+∠ACB=150°,(1)∵点O是∠ABC与∠ACB的角平分线的交点,∴∠OBC+∠OCB=(∠ABC+∠ACB)=75°,∴∠BOC=105°;(2)∵点O2是∠ABC与∠ACB的三等分线的交点,∴∠O2BC+∠O2CB=(∠ABC+∠ACB)=100°,∴∠BO2C=80°;(3)∵点O n﹣1是∠ABC与∠ACB的n等分线的交点,∴∠O n﹣1BC+∠O n﹣1CB=(∠ABC+∠ACB)=×150°,∴∠BO n﹣1C=180°﹣×150°(4)由(3)得:180°﹣×150°=60°,解得:n=5.9.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.(1)如图1,若AB∥ON,则①∠ABO的度数是20°;②当∠BAD=∠ABD时,x=120°;当∠BAD=∠BDA时,x=60°.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.【解答】解:(1)①∵∠MON=40°,OE平分∠MON∴∠AOB=∠BON=20°∵AB∥ON∴∠ABO=20°②∵∠BAD=∠ABD∴∠BAD=20°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=120°∵∠BAD=∠BDA,∠ABO=20°∴∠BAD=80°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=60°故答案为:①20 ②120,60(2)①当点D在线段OB上时,若∠BAD=∠ABD,则x=20若∠BAD=∠BDA,则x=35若∠ADB=∠ABD,则x=50②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,所以只有∠BAD=∠BDA,此时x=125.综上可知,存在这样的x的值,使得△ADB中有两个相等的角,且x=20、35、50、125.10.如图,已△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明;②点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?(2)若点Q以②的运动速度从点C出发点P以原来运动速度从点B同时出发,都逆时针沿ABC的三边运动,求多长时间点P与点Q第一次在△ABC的哪条边上相遇?【解答】解:(1)①∵t=1(秒),∴BP=CQ=3(厘米)∵AB=12,D为AB中点,∴BD=6(厘米)又∵PC=BC﹣BP=9﹣3=6(厘米)∴PC=BD∵AB=AC,∴∠B=∠C,在△BPD与△CQP中,,∴△BPD≌△CQP(SAS),②∵V P≠V Q,∴BP≠CQ,又∵∠B=∠C,要使△BPD≌△CPQ,只能BP=CP=4.5,∵△BPD≌△CPQ,∴CQ=BD=6.∴点P的运动时间t===1.5(秒),此时V Q===4(厘米/秒).(2)因为V Q>V P,只能是点Q追上点P,即点Q比点P多走AB+AC的路程设经过x秒后P与Q第一次相遇,依题意得4x=3x+2×12,解得x=24(秒)此时P运动了24×3=72(厘米)又∵△ABC的周长为33厘米,72=33×2+6,∴点P、Q在BC边上相遇,即经过了24秒,点P与点Q第一次在BC边上相遇.11.已知:如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.求证:AD⊥AE.【解答】证明:在△ABD和△ACE中,,∴△ABD≌△ACE(SSS),∴∠EAC=∠DAB,∴∠DAE=∠BAC,∵AB⊥AC,∴∠BAC=90°,∴∠DAE=90°,即AD⊥AE.12.如图,已知△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连结BE.(1)请判断线段AD、BE之间的数量关系,并说明理由;(2)求证:AM=CM+BE.【解答】(1)解:结论:AD=BE,理由如下:∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,∴AC=BC,CD=CE,∠ACB﹣∠DCB=∠DCE﹣∠DCB,即∠ACD=∠BCE,在ACD和△BCE中,∴△ACD≌△BCE,∴AD=BE.(2)证明:∵△DCE为等腰直角三角形,∠DCE=90°,∴∠CDM=45°,∵CM⊥AE,∴∠DCM=45°,∴∠CDM=∠DCM=45°,∴CM=DM,∵AM=AD+DM,AD=BE,∴AM=CM+BE.13.如图①②,点E、F分别是线段AB、线段CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)线段AD和线段BC有怎样的数量关系?请说明理由;(2)当DG⊥GC时,试判断直线AD和直线BC的位置关系,并说明理由.【解答】解:(1)AD=BC.理由:∵GF垂直平分DC,∴GD=GC同理,GA=GB,在△ADG和△BCG中,,∴△ADG≌△BCG(SAS),∴AD=BC;(2)AD⊥BC.理由:延长AD,与CG相交于点O、与BC的延长线相交于点Q.∵△ADG≌△BCG,∴∠ADG=∠BCG,则∠GDO=∠QCO,∴∠QDC+∠QCD=∠DQC+∠DCG+∠QCG=∠QDC+∠GDQ+∠DCG=∠CDG+∠DCG,∵DG⊥GC,∴∠QDC+∠QCD=∠CDG+∠DCG=90°,∴∠Q=90°,∴AD⊥BC.14.如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).(1)用的代数式表示PC的长度;(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.【解答】解:(1)BP=2t,则PC=BC﹣BP=6﹣2t;(2)△BPD和△CQP全等理由:∵t=1秒,∴BP=CQ=2×1=2厘米,∴CP=BC﹣BP=6﹣2=4厘米,∵AB=8厘米,点D为AB的中点,∴BD=4厘米.∴PC=BD,在△BPD和△CQP中,,∴△BPD≌△CQP(SAS).15.如图①,AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s 的速度由A向B运动.同时点Q在线段BD上由点B向点D运动.它们运动的时间为t s.(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.(2)如图②,将“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,其他条件不变,设点Q运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应x,t的值;若不存在,说明理由.【解答】解:(1)当t=1时,AP=BQ=1,BP=AC=3,又∵∠A=∠B=90°,在△ACP和△BPQ中,,∴△ACP≌△BPQ(SAS).∴∠ACP=∠BPQ,∴∠APC+∠BPQ=∠APC+∠ACP=90°.∴∠CPQ=90°,即线段PC与线段PQ垂直.(2)①若△ACP≌△BPQ,则AC=BP,AP=BQ,,解得;②若△ACP≌△BQP,则AC=BQ,AP=BP,,解得;综上所述,存在或使得△ACP与△BPQ全等.16.如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.求证:(1)△ABC≌△ADE;(2)BC⊥DE.【解答】证明:(1)∵AB⊥AD,AC⊥AE,∴∠DAB=∠CAE=90°,∴∠DAB+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE,在△ABC和△ADE中,∴△ABC≌△ADE(SAS).(2)∵△ABC≌△ADE,∴∠E=∠C,∵∠E+∠AHE=90°,∠AHE=∠DHC,∴∠C+∠DHC=90°,∴BC⊥DE.17.如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.(1)求证:在运动过程中,不管t取何值,都有S△AED=2S△DGC.(2)当t取何值时,△DFE与△DMG全等.【解答】(1)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,∴DF=DM,∵S△AED=AE?DF,S△DGC=CG?DM,∴=,∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A 点运动,∴=2,即=2,∴在运动过程中,不管取何值,都有S△AED=2S△DGC.(2)解:设时间为t时,△DFE与△DMG全等,则EF=MG,①当M在线段CG的延长线上时,∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A 点运动,∴EF=AF﹣AE=10﹣2t,MG=AC﹣CG﹣AM=4﹣t,即10﹣2t=4﹣t,解得:t=6,当t=6时,MG=﹣2,所以舍去;②当M在线段CG上时,∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A 点运动,∴EF=AF﹣AE=10﹣2t,MG=AM﹣(AC﹣CG)=t﹣4,即10﹣2t=t﹣4,解得:t=,综上所述当t=时,△DFE与△DMG全等.18.如图所示,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,CE与BD相交于点M,BD与AC交于点N,试猜想BD与CE有何关系?说明理由.【解答】解:结论:BD=CE且BD⊥CE.理由:∵△ABC和△ADE是直角三角形,∴∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE,∠ABD=∠ACE,∵∠ABD+∠ANB+∠BAC=180°,∠ACE+∠CNM+∠NMC=180°,∠ANB=∠CNM,∴∠NMC=∠BAC=90°,∴BD⊥CE,即BD=CE且BD⊥CE.19.如图,长方形ABCD中,AB=10cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E 运动,最终到达点E.若点P运动的时间为x秒,那么当x为何值时,△APE的面积等于32cm2?(提醒:同学们,要分类讨论哦!)【解答】解:①如图1,当P在AB上时,∵△APE的面积等于32,∴×2x?8=32,解得:x=4;②当P在BC上时,∵△APE的面积等于32,∴S矩形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=32,∴10×8﹣(10+8﹣2x)×5﹣×8×5﹣×10×(2x﹣10)=32,解得:x=6.6;③当P在CE上时,∴(10+8+5﹣2x)×8=32,解得:x=7.5<(10+8+5),此时不符合;答:4或6.6.20.如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.(1)用含t的式子表示线段AP、AQ的长;(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?(3)当t为何值时,PQ∥BC?【解答】解:(1)∵Rt△ABC中,∠C=90°,∠A=60°,∴∠B=30°.又∵AB=12cm,∴AC=6cm,BP=2t,AP=AB﹣BP=12﹣2t,AQ=t;(2)∵△APQ是以PQ为底的等腰三角形,∴AP=AQ,即12﹣2t=t,∴当t=4时,△APQ是以PQ为底边的等腰三角形;(3)当PQ⊥AC时,PQ∥BC.∵∠C=90°,∠A=60°,∴∠B=30°∵PQ∥BC,∴∠QPA=30°∴AQ=AP,∴t=(12﹣2t),解得t=3,∴当t=3时,PQ∥BC.21.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠EDC=25°,∠DEC=115°;点D从B向C运动时,∠BDA逐渐变小(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.【解答】解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,小;(2)当DC=2时,△ABD≌△DCE,理由:∵∠C=40°,∴∠DEC+∠EDC=140°,又∵∠ADE=40°,∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,又∵AB=DC=2,∴△ABD≌△DCE(AAS),(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,理由:∵∠BDA=110°时,∴∠ADC=70°,∵∠C=40°,∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,∴∠DAC=∠AED,∴△ADE的形状是等腰三角形;∵当∠BDA的度数为80°时,∴∠ADC=100°,∵∠C=40°,∴∠DAC=40°,∴∠DAC=∠ADE,∴△ADE的形状是等腰三角形.22.如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.(1)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.(2)若DC=2,求证:△ABD≌△DCE.【解答】解:(1)∵∠B=∠C=50°,∠ADE=50°,∴∠BDA+∠EDC=∠CED+∠EDC=130°,∴∠BDA=∠CED,∵点D在线段BC上运动(点D不与B、C重合),∴AD≠AE,ⅰ)如图所示,当EA=ED时,∠EAD=∠ADE=50°,∴∠BDA=∠CED=50°+50°=100°;ⅱ)如图所示,当DA=DE时,∠EAD=∠AED=65°,∴∠BDA=∠CED=65°+50°=115°;(2)由(1)可得∠BDA=∠CED,又∵∠B=∠C=50°,AB=DC=2,∴在△ABD和△DCE中,,∴△ABD≌△DCE(AAS).23.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF 对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.,则∠BEC=55°,∠AEN=35°,∠BEC+∠AEN=90°.(1)若∠BEB′=110°(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.【解答】解:(1)由折叠的性质可得,∠BEC=∠B'EC,∠AEN=∠A'EN,,∵∠BEB′=110°∴∠AEA'=180°﹣110°=70°,,∠AEN=∠A'EN=∠AEA'=35°.∴∠BEC=∠B'EC=∠BEB′=55°∴∠BEC+∠AEN=55°+35°=90°;(2)不变.由折叠的性质可得:∠BEC=∠B'EC,∠AEN=∠A'EN,∵∠BEB′=m°,∴∠AEA'=180°﹣m°,可得∠BEC=∠B'EC=∠BEB′=m°,∠AEN=∠A'EN=∠AEA'=(180°﹣m°),∴∠BEC+∠AEN=m°+(180°﹣m°)=90°,故∠BEC+∠AEN的值不变;(3)由折叠的性质可得:∠B'CF=∠B'CE,∠B'CE=∠BCE,∴∠B'CF=∠B'CE=∠BCE=×90°=30°,在Rt△BCE中,∵∠BEC与∠BCE互余,∴∠BEC=90°﹣∠BCE=90°﹣30°=60°,∴∠B'EC=∠BEC=60°,∴∠AEA'=180°﹣∠BEC﹣∠B'EC=180°﹣60°﹣60°=60°,∴∠AEN=∠AEA'=30°,∴∠ANE=90°﹣∠AEN=90°﹣30°=60°,∴∠ANE=∠A'NE=60°,∴∠DNA'=180°﹣∠ANE﹣∠A'NE=180°﹣60°﹣60°=60°.故答案为:55,35,90.24.如图,△ABC中,AB=AC=18cm,BC=16cm,点D是AB的中点.有一点E在BC上从点B向点C运动,速度为2cm/s,同时有一点F在AC上从点C向点A运动,其中一点停止运动另一点也随之停止运动.问当点F的运动速度是多少时,△DBE和△EFC全等?【解答】解:设点F运动的时间为ts,点F运动的速度为xcm/s,则BE=2t,EC=16﹣2t,CF=tx,∵点D为AB的中点,∴BD=AB=9,∵∠B=∠C,∴当CE=BD,CF=BE时,可根据“SAS”判断△DBE≌△ECF,即16﹣2t=9,tx=2t,解得t=3.5,x=2;当CE=BE,CF=BD时,可根据“SAS”判断△DBE≌△EFC,即16﹣2t=2t,tx=9,解得t=4,x=2.25,综上所述,当点F的运动速度是2厘米/秒或2.25厘米/秒时,△DBE和△EFC全等.25.已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s).(1)当动点P、Q同时运动2s时,则BP=1cm,BQ=2cm.(2)当动点P、Q同时运动t(s)时,分别用含有t的式子表示;BP=(3﹣t)cm,BQ=t cm.(3)当t为何值时,△PBQ是直角三角形?【解答】解:(1)BQ=1×2=2(cm),BP=3﹣2=1(cm),故答案为1,2;(2)BP=(3﹣t)cm,BQ=tcm,故答案为(3﹣t),t;(3)根据题意,得AP=t cm,BQ=t cm.在△ABC中,AB=BC=3 cm,∠B=60°,∴BP=(3﹣t)cm.在△PBQ中,BP=(3﹣t)cm.,BQ=tcm,若△PBQ是直角三角形,则只有∠BQP=90°或∠BPQ=90°①当∠BQP=90°时,BQ=BP,即t=(3﹣t),解得t=1;②当∠BPQ=90°时,BP=BQ,即3﹣t=t.解得t=2.答:当t=1s或t=2s时,△PBQ是直角三角形.26.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.(1)点M、N运动几秒后,M、N两点重合?(2)点M、N运动几秒后,可得到等边三角形△AMN?(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.【解答】解:(1)设点M、N运动x秒后,M、N两点重合,x×1+12=2x,解得:x=12;(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①,AM=t×1=t,AN=AB﹣BN=12﹣2t,∵三角形△AMN是等边三角形,∴t=12﹣2t,解得t=4,∴点M、N运动4秒后,可得到等边三角形△AMN.(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,由(1)知12秒时M、N两点重合,恰好在C处,如图②,假设△AMN是等腰三角形,∴AN=AM,∴∠AMN=∠ANM,∴∠AMC=∠ANB,∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,在△ACM和△ABN中,∵,∴△ACM≌△ABN,∴CM=BN,设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,∴CM=y﹣12,NB=36﹣2y,CM=NB,y﹣12=36﹣2y,解得:y=16.故假设成立.∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.。
完整版)初一几何练习题及答案

完整版)初一几何练习题及答案初一几何:三角形一、选择题(本大题共24分)1.以下列各组数为三角形的三条边,其中能构成直角三角形的是()A。
17,15,8B。
1/3,1/4,1/5C。
4,5,6D。
3,7,112.如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()A。
锐角三角形B。
直角三角形C。
钝角三角形D。
等腰三角形3.下列给出的各组线段中,能构成三角形的是()A。
5,12,13B。
5,12,7C。
8,18,7D。
3,4,84.如图已知:Rt△ABC中,∠C=90°,AD平分∠BAC,AE=AC,连接DE,则下列结论中,不正确的是()A。
DC=DEB。
∠___∠ADEC。
∠DEB=90°D。
∠___∠DAE5.一个三角形的三边长分别是15,20和25,则它的最大边上的高为()A。
12B。
10C。
8D。
56.下列说法不正确的是()A。
全等三角形的对应角相等B。
全等三角形的对应角的平分线相等C。
角平分线相等的三角形一定全等D。
角平分线是到角的两边距离相等的所有点的集合7.两条边长分别为2和8,第三边长是整数的三角形一共有()A。
3个B。
4个C。
5个D。
无数个8.下列图形中,不是轴对称图形的是()A。
线段MNB。
等边三角形C。
直角三角形D。
钝角∠AOB9.如图已知:△ABC中,AB=AC,BE=CF,AD⊥BC于D,此图中全等的三角形共有()A。
2对B。
3对C。
4对D。
5对10.直角三角形两锐角的平分线相交所夹的钝角为()A。
125°B。
135°C。
145°D。
150°11.直角三角形两锐角的平分线相交所夹的钝角为()A。
125°B。
135°C。
145°D。
150°12.___已知:∠A=∠D,∠C=∠F,如果△ABC≌△DEF,那么还应给出的条件是()A。
AC=DEB。
AB=DFC。
初一数学_几何_三角形基础知识和基本练习题讲解
第七章三角形(一)——三角形的基本概念学习目标:1、明确三角形的相关概念;能正确对三角形进行分类;2、能利用三角形三边关系进行有关计算。
学习过程:三角形的有关概念——阅读课本第63至64页,回答以下问题:(1)三角形概念:由不在同一直线上的条线段连接所组成的图形。
(2)三角形的表示法(如图1)三角形ABC可表示为:;(3)ΔABC的顶点分别为A、、;(3)ΔABC的内角分别为∠ABC,,;(4)ΔABC的三条边分别为AB,,;或a,、;(5)顶点A的对边是,顶点B的对边分别是,顶点C的对边分别是。
三角形的分类:(1)下图中,每个三角形的内角各有什么特点?(2)下图中,每个三角形的三边各有什么特点?(3)结合以上图形你认为三角形可以如何分类?试一试①按角分类:②按边分类:第1题3、三角形的三边关系问题1:如图,现有三块地,问从A 地到B 地有几种走法,哪一种走法的距离最近?请将你的设计方案填写在下表中:(3)阅读课本第64页,填写:三角形两边的和 (4)用式子表示:BC + AC AB (填上“> ”或“ < ” ) ① BC + AB AC (填上“> ”或“ < ” ) ②AB + AC BC (填上“> ”或“ < ” ) ③4、三角形的稳定性问题2:盖房子时,在窗框未安装好前,木工师傅常先在窗框上斜钉一根木条,为什么?5、例题:用一条长为18cm 的细绳围成一个等腰三角形,如果腰长是底边的2倍,那么各边的长是多少? 解:设底边长为xcm ,则腰长是 cm 因为三角形的周长为 cm所以: 所以x= cm答:三角形的三边分别是 、 、课堂练习: A 组A 地(6)(5)(4)(3)(2)(1)1.①图中有 个三角形,分别为 ②△ABC 的三个顶点是 、 、 ; 三个内角是 、 、 ; 三条边是 、 、 ;2、如图中有 个三角形,用符号表示 3.判断下列线段能否组成三角形:①4,5,6 ( )②1,2,3 ( ) ③2,2,6 ( )④8,8,2 ( ) 4、下列的图形中具有稳定性的是 (写编号)5、等腰三角形一腰长为6,底边长为7,则另一腰为 ,周长为 。
初中数学相似三角形经典练习难题易错题(附详解)
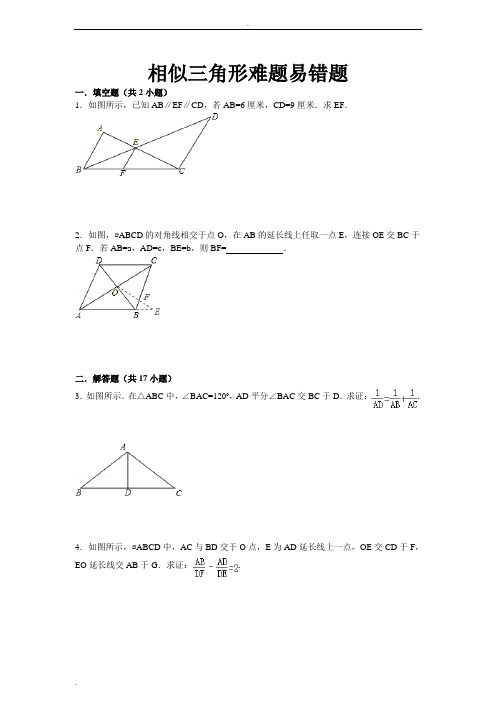
.相似三角形难题易错题一.填空题(共2小题)1.如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.2.如图,▱ABCD的对角线相交于点O,在AB的延长线上任取一点E,连接OE交BC于点F.若AB=a,AD=c,BE=b,则BF=_________.二.解答题(共17小题)3.如图所示.在△ABC中,∠BAC=120°,AD平分∠BAC交BC于D.求证:.4.如图所示,▱ABCD中,AC与BD交于O点,E为AD延长线上一点,OE交CD于F,EO延长线交AB于G.求证:.5.一条直线截△ABC的边BC、CA、AB(或它们的延长线)于点D、E、F.求证:.6.如图所示.P为△ABC内一点,过P点作线段DE,FG,HI分别平行于AB,BC和CA,且DE=FG=HI=d,AB=510,BC=450,CA=425.求d.7.如图所示.梯形ABCD中,AD∥BC,BD,AC交于O点,过O的直线分别交AB,CD 于E,F,且EF∥BC.AD=12厘米,BC=20厘米.求EF.8.已知:P为▱ABCD边BC上任意一点,DP交AB的延长线于Q点,求证:.9.如图所示,梯形ABCD中,AD∥BC,MN∥BC,且MN与对角线BD交于O.若AD=DO=a,BC=BO=b,求MN.10.P为△ABC内一点,过P点作DE,FG,IH分别平行于AB,BC,CA(如图所示).求证:.11.如图所示.在梯形ABCD中,AB∥CD,AB<CD.一条直线交BA延长线于E,交DC 延长线于J,交AD于F,交BD于G,交AC于H,交BC于I.已知EF=FG=GH=HI=IJ,求DC:AB.12.已知P为△ABC内任意一点,连AP,BP,CP并延长分别交对边于D,E,F.求证:(1)(2)三者中,至少有一个不大于2,也至少有一个不少于2.13.如图所示.在△ABC中,AM是BC边上的中线,AE平分∠BAC,BD⊥AE的延长线于D,且交AM延长线于F.求证:EF∥AB.14.如图所示.P,Q分别是正方形ABCD的边AB,BC上的点,且BP=BQ,BH⊥PC于H.求证:QH⊥DH.15.已知M是Rt△ABC中斜边BC的中点,P、Q分别在AB、AC上,且PM⊥QM.求证:PQ2=PB2+QC2.16.如图所示.在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB,CF平分∠BCD.求证:EF∥BC.17.如图所示.在△ABC内有一点P,满足∠APB=∠BPC=∠CPA.若2∠B=∠A+∠C,求证:PB2=PA•PC.(提示:设法证明△PAB∽△PBC.)18.已知:如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1.求证:CE⊥AD.19.如图所示,△ABC中,M、N是边BC的三等分点,BE是AC边上的中线,连接AM、AN,分别交BE于F、G,求BF:FG:GE的值.20.在△ABC中,∠A∶∠B∶∠C=1∶2∶4.求证提示:要证明如几何题的常用方法:①比例法:将原等式变为,故构造成以a+b、b为边且与a、c所在三角形相似的三角形。
三角形的内角和练习题

三角形的内角和练习题一、基础练习1、判断下列说法是否正确,并说明理由。
(1)一个三角形的内角和是180度。
(2)一个三角形的内角和等于3个直角。
(3)一个等边三角形的内角和等于一个等腰三角形的内角和。
2、一个三角形的三个内角分别为A、B、C,已知A=30度,B=80度,求C的度数。
二、提升练习1、一个三角形的三个内角分别为A、B、C,已知A=70度,B=90度,求C的度数。
2、一个等边三角形的三个内角分别为A、B、C,已知A=60度,求B 和C的度数。
3、一个等腰三角形的两个内角分别为A、B,已知A=80度,求B的度数(该三角形是等腰三角形,有两边长度相等)。
三、拓展练习1、一个四边形由两个等边三角形组成,它的四个内角分别为A、B、C、D,求A+B+C+D的度数。
2、一个五边形由三个等边三角形组成,它的五个内角分别为A、B、C、D、E,求A+B+C+D+E的度数。
3、一个n边形(n≥3)的所有内角之和是多少?在解答上述问题的过程中,我们可以使用三角形内角和定理以及多边形的内角和公式来进行计算。
我们还需要了解等边三角形和等腰三角形的性质,以便解决相关问题。
三角形的内角和教学设计一、教材分析三角形的内角和是义务教育课程标准实验教科书(人教版)四年级下册第8单元数学广角里的内容,本节课是在学生已经学习了三角形的概念及分类的基础上进一步研究三角形的有关知识,教材中安排了三部分内容:第一部分是例1通过测量计算三个内角的度数和,第二部分是例2通过撕拼、旋转、翻转等不同的方法验证三角形的内角和等于180度,第三部分是例3用已知的两个角度求出第三个角的度数。
通过这些活动,培养学生动手操作能力和数学思维能力。
同时,还体现了数学来源于生活,又应用于生活这一理念。
二、学情分析作为四年级的学生,他们已经具备了一定的观察、猜测、动手操作、积极思考的能力,因此他们可以根据自己的实际情况选择喜欢的方法来研究验证三角形的内角和。
初中数学几何练习(18)相似三角形的性质

初中数学几何练习十八:相似三角形的性质相似三角形的性质1、相似三角形的对应角相等,对应边成比例2、相似三角形对应高的比,对应中线的比和对应角平分线的比都等于相似比3、相似三角形的周长比等于相似比4、相似三角形的面积比等于相似比的平方一、选择题1、若ABC ∆∽'''C B A ∆,则相似比k 等于( )A 、''B A :AB B 、A ∠:'A ∠C 、ABC S ∆:'''C B A S ∆D 、ABC C ∆:'''C B A C ∆ 2、如果两个等腰直角三角形斜边比是1:2,那么它们的面积比是( )A 、1:1B 、1:2C 、1:2D 、1:43、如图,在ABC ∆中,D 为AC 边上一点,A DBC ∠=∠,BC=6,AC=3,则CD 的长为( )A 、1B 、23 C 、2 D 、25 4、如图,O 是ABC ∆内任意一点,CO CF BO BE AO AD 31,31,31===,则ABC ∆与DEF ∆的周长比是( )A 、1:3B 、3:2C 、3:1D 、2:35、如图,DE//FG//BC ,且DE 、FG 把ABC ∆的面积三等分,若BC=12,则FG 的长是( )A 、8B 、6C 、64D 、346、如图,正方形ABCD 的边BC 在等腰直角三角形PQR 的底边QR 上,其余两个顶点A 、D 在PQ 、PR 上,则PA :AQ 等于( )A 、1:2B 、1:2C 、1:3D 、2:37、如图,矩形ABCD ,AB=8厘米,AD=6厘米,EF 是对角线BD 的垂直平分线,则EF 的长为( )A 、415 厘米B 、315厘米C 、215厘米D 、8厘米 8、如图,ABC ∆中,DE//BC ,面积DBCE ABC S S 梯形=∆,则DE :BC 为( )A 、21B 、22 C 、41 D 、32 二、填空题9、两个相似三角形的面积之比为4:9,则这两个三角形的周长之比为________10、两个相似三角形的相似比为1:3,则它们对应高比为______11、已知ABC ∆∽'''C B A ∆,且BC : ''C B =3:2, ABC ∆的周长为24,则'''C B A ∆的周长为_________12、一个三角形周长为a,三边中点连线所组成的三角形的周长是__________13、已知ABC ∆的三边之比为3:4:6,且ABC ∆∽'''C B A ∆,若'''C B A ∆中最长边为10厘米,则它的最短边为_________厘米14、如果两个相似三角形的对应边的比是4:5,周长的和为18厘米,那么这两个三角形的周长分别是_______________15、ABC ∆中,BC=54厘米,CA=45厘米,AB=63厘米,另一个与它相似的三角形的最短边为15,则周长为____________16、已知,如图,D 是ABC ∆的边AB 上的一点,过D 作DE//BC 交AC 于E,AD:BD=3:2,则_______________:=∆BCED AD E S S 四边形三、简答题17、已知正方形ABCD,过C 的直线分别交AD 、AB 的延长线于E 、F ,且AE=15,AF=10 求(1)正方形ABCD 的边长;(2)若BE 交CD 于G ,则CG 的长为多少?18、已知矩形ABCD 中,AB=4,BC=12,点F 在AD 边上,AF :FD=1:3,BF CE ⊥于点E ,交AD 于点G ,求BCE ∆的周长19、如图,在ABC ∆中,,900=∠C D 是AC 上一点,AB DE ⊥于E ,若AB=10,BC=6,DE=2,求四边形DEBC 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一几何三角形练习题
一.选择题 (本大题共 24 分)
1.以下列各组数为三角形的三条边,其中能构成直角三角形的是()
(A)17,15,8 (B)1/3,1/4,1/5 (C) 4,5,6 (D) 3,7,11
2.如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()
(A)锐角三角形(B)直角三角形(C)钝角三角形(D)等腰三角形
3.下列给出的各组线段中,能构成三角形的是()
(A)5,12,13 (B)5,12,7 (C)8,18,7 (D)3,4,8
4.如图已知:Rt△ABC中,∠C=90°,AD平分∠BAC,AE=AC,连接DE,则下列结论中,不正确的是()
(A) DC=DE (B) ∠ADC=∠ADE (C) ∠DEB=90°(D) ∠BDE=∠DAE
5.一个三角形的三边长分别是15,20和25,则它的最大边上的高为()
(A)12 (B)10 (C) 8 (D) 5
6.下列说法不正确的是()
(A)全等三角形的对应角相等
(B)全等三角形的对应角的平分线相等
(C)角平分线相等的三角形一定全等
(D)角平分线是到角的两边距离相等的所有点的集合
7.两条边长分别为2和8,第三边长是整数的三角形一共有()
(A)3个(B)4个(C)5个(D)无数个
8.下列图形中,不是轴对称图形的是()
(A)线段MN (B)等边三角形(C) 直角三角形(D) 钝角∠AOB
9.如图已知:△ABC中,AB=AC,BE=CF,AD⊥BC于D,此图中全等的三角形共有()
(A)2对(B)3对(C)4对(D)5对
10.直角三角形两锐角的平分线相交所夹的钝角为()
(A)125°(B)135°(C)145°(D)150°
11.直角三角形两锐角的平分线相交所夹的钝角为()
(A)125°(B)135°(C)145°(D)150°
12.如图已知:∠A=∠D,∠C=∠F,如果△ABC≌△DEF,那么还应给出的条件是()
(A) AC=DE (B) AB=DF (C) BF=CE (D) ∠ABC=∠DEF
二.填空题 (本大题共 40 分)
1.在Rt△ABC中,∠C=90°,如果AB=13,BC=12,那么AC= ;如果AB=10,AC:BC=3:4,那么BC=
2.如果三角形的两边长分别为5和9,那么第三边x的取值范围是。
3.有一个三角形的两边长为3和5,要使这个三角形是直角三角形,它的第三边等于
4.如图已知:等腰△ABC中,AB=AC,∠A=50°,BO、CO分别是∠ABC和∠ACB的平分线,BO、CO 相交于O。
则:∠BOC=
5.设α是等腰三角形的一个底角,则α的取值范围是( )
(A)0<α<90°(B)α<90°(C) 0<α≤90°(D) 0≤α<90°
6.如图已知:△ABC≌△DBE,∠A=50°,∠E=30°
则∠ADB= 度,∠DBC= 度
7.在△ABC中,下列推理过程正确的是( )
(A)如果∠A=∠B,那么AB=AC
(B)如果∠A=∠B,那么AB=BC
(C) 如果CA=CB ,那么∠A=∠B
(D) 如果AB=BC ,那么∠B=∠A
8.如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是三角形。
9.等腰△ABC中,AB=2BC,其周长为45,则AB长为
10.命题“对应角相等的三角形是全等三角形”的逆命题是:
其中:原命题是命题,逆命题是命题。
11.如图已知:AB∥DC,AD∥BC,AC、BD,EF相交于O,且AE=CF,图中△AOE≌△,△ABC ≌△,全等的三角形一共有对。
12.如图已知:在Rt△ABC和Rt△DEF中
∵AB=DE(已知)
= (已知)
∴Rt△ABC≌Rt△DEF (________)
13.如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是三角形。
14.如图,BO、CO分别是∠ABC和∠ACB的平分线,∠BOC=136°,则= 度。
15.如果等腰三角形的一个外角为80°,那么它的底角为度
16.在等腰Rt△ABC中,CD是底边的中线,AD=1,则AC= 。
如果等边三角形的边长为2,那么它的高为。
17.等腰三角形的腰长为4,腰上的高为2,则此等腰三角形的顶角为( )
(A)30°(B)120°(C) 40°(D)30°或150°
18.如图已知:AD是△ABC的对称轴,如果∠DAC=30˚,DC=4cm,那么△ABC的周长为cm。
19.如图已知:△ABC中,AB=AC,AB的垂直平分线DE交AC于E,垂足为D,如果∠A=40˚,那么∠BEC= ;如果△BEC的周长为20cm,那么底边BC= 。
20.如图已知:Rt△ABC中,∠ACB=90˚˚,DE是BC的垂直平分线,交AB于E,垂足为D,如果AC=√3,BC=3,那么,∠A= 度。
△CDE的周长为。
三.判断题 (本大题共 5 分)
1.有一边对应相等的两个等边三角形全等。
()
2.关于轴对称的两个三角形面积相等()
3.有一角和两边对应相等的两个三角形全等。
()
4.以线段a、b、c为边组成的三角形的条件是a+b>c ()
5.两边和其中一边上的中线对应相等的两个三角形全等。
()
四.计算题 (本大题共 5 分)
1.如图已知,△ABC中,∠B=40°,∠C=62°,AD是BC边上的高,AE是∠BAC的平分线。
求:∠DAE的度数。
五.作图题 (本大题共 6 分)
1.如图已知△ABC,用刻度尺和量角器画出:∠A的平分线;AC边上的中线;AB边上的高。
2.如图已知:∠α和线段α。
求作:等腰△ABC,使得∠A=∠α, AB=AC,BC边上的高AD=α。
3.在铁路的同旁有A、B两个工厂,要在铁路旁边修建一个仓库,使与A、B两厂的距离相等,画出仓库的位置。
六.解答题 (本大题共 5 分)
1.如图已知:RtΔABC中,C=90°,DE⊥AB于D,BC=1,AC=AD=1。
求:DE、BE的长。
七.证明题 (本大题共 15 分)
1.若ΔABC的三边长分别为m2-n2,m2+n2,2mn。
(m>n>0)
求证:ΔABC是直角三角形
2.如图已知:△ABC中,BC=2AB,D、E分别是BC、BD的中点。
求证:AC=2AE
3.如图已知:△ABC中,∠ABC的平分线与∠ACB的外角平分线交于D,DE∥BC交AB于E,交AC 于F。
求证:BE=EF+CF。
