根的判别式的三种应用
运用根的判别式解题

运用根的判别式解题作者:曹经富来源:《数理化学习·初中版》2013年第08期根的判别式在求解一元二次方程的有关问题中占据重要的地位,现举例说明.一、不解一元二次方程,判断根的情况例1不解方程,判断下列方程的根的情况:(1) 2x2+3x=4 (2)ax2+bx=0(a≠0)分析:将方程化为一般形式,确定a、b、c的值,计算b2-4ac并与0进行比较.解:(1) 2x2+3x-4=0, a=2, b=3, c=-4,因为Δ=b2-4ac=32-4×2×(-4)=41>0.所以方程有两个不相等的实数根.(2)因为a≠0,所以方程是一元二次方程,此方程是缺少常数项的不完全的一元二次方程,将常数项视为零,因为Δ=(-b)2-4·a·0=b2,因为无论b取任何实数,b2均为非负数,所以Δ≥0,故方程有两个实数根.小结:解决这类问题的关键是需要我们牢记一元二次根的判别式的三种情况,尤其要注意系数是字母的一元二次方程,当b2-4ac>0,方程有两个不相等的实数根;当b2-4ac=0,方程有两个相等的实数根;当b2-4ac二、根据方程根的情况,确定待定字母系数的值或取值范围例2已知关于x的方程x2-2x-2n=0有两个不相等的实数根.(1)求n的取值范围;(2)若n分析:(1)关于x的方程x2-2x-2n=0有两个不相等的实数根,即判别式Δ=b2-4ac>0.即可得到关于n的不等式,从而求得n的范围.(2)利用配方法解方程,然后根据n的取值范围和限制条件“方程的两个实数根都是整数”来求n的值.解:(1)因为关于x的方程x2-2x-2n=0的二次项系数a=1、一次项系数b=-2、常数项c=-2n,所以Δ=b2-4ac=4+8n>0,解得,n>-12.(2)由原方程,得(x-1)2=2n+1,所以x=1±2n+1.因为方程的两个实数根都是整数,且n所以0所以2n+1=1,2n+1=4或2n+1=9,解得,n=0,n=1.5或n=4.小结:由于根的判别式是一元二次方程的系数联系的纽带,所以,涉及到一元二次方程(或二次三项式)中涉及到系数的问题时,可借助根的判别式来进行判定或者处理.方程有两个不相等的实数根,说明方程必为一元二次方程,关键是考虑b2-4ac>0,如果二次项的系数含有字母还要注意二次项系数不为零.三、判断当字母的值为何值时二次三项是完全平方式例3若关于a的二次三项式16a2+ka+25是一个完全平方式,则k= .解析:可以令二次三项等于0,若二次三项是完全平方式,则方程有两个相等的实数根.即Δ=0.令16a2+ka+25=0,因为方程有两个相等的实数根,所以Δ=k2-4×16×25=0,所以k=40或者-40.答案:40或者-40小结:当Δ=0时,二次三项式是一个完全平方式,把满足题目的所有条件列成一个方程求解.四、判断二次三项式能否分解因式例4已知 k为非正数,试判断二次三项式3x2-4x+2k在实数范围内能否分解因式.解析:假设二次三项式在实数范围内能分解因式,即3x2-4x+2k=3(x-x1)(x-x2),则方程3x2-4x+2k=0有两个实数根.有Δ=(-4)2-4×3×2k≥0,解得k≤23.因已知的k值在此范围内,所以已知式在实数范围内能分解因式.五、一元二次方程根的判别式在证明或几何求解中的应用例5已知关于x的方程x2-(k+1)x+(2k-2)=0.(1)求证:无论k取何值,此方程总有实数根;(2)若等腰△ABC的底边a=3,另两边b,c好是此方程的两根,求△ABC的周长.分析:(1)计算方程的根的判别式,若Δ=b2-4ac≥0,则证明方程总有实数根.(2)已知a=3,则a可能是底,也可能是腰,分两种情况求得b,c的值后,再求出△ABC的周长.注意两种情况都要用三角形三边关系定理进行检验.解:(1)证明:因为Δ=b2-4ac=(k+1)2-4·(2k-2)=k2-6k+9=(k-3)2≥0.所以无论k取何值,方程总有实数根.(2)①若a=3为底边,则c为底边,则b=c,则Δ=0.所以(k-3)2=0,解得:k=3.此时原方程化为x2-4x+4=0所以x1=x2=2,即b=c=2.此时△ABC三边为3,2,2.②若a=b为腰,则c为底边,不妨设b=a=3代入方程:32-3(k+1)+(2k-2)=0.所以k=4.则原方程化为x2-5x+6=0.(x-2)(x-3)=0,所以x1=2,x2=3.即b=3,c=2.此时△ABC三边为3,3,2能构成三角形.综上所述:△ABC三边为3,3,2.所以周长为8或7.小结:一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2-4ac,是每年中考的必考知识点.它是揭示根的性质与系数间联系的桥梁,是解决与一元二次方程相关问题的有力工具.当三角形的三边是某个方程的系数时,要想将这三边联系在一起,可以借用根的判别式来处理.六、应用根的判别式判断三角形的形状例6已知:a、b、c为ΔABC的三边,当m>0时,关于x的方程c(x2+m)+b(x2-m)-2max=0有两个相等的实数根.试判定ΔABC的形状.解析:整理原方程c(x2+m)+b(x2-m)-2max =0得:cx2+cm+bx2-bm-2max =0. 即(c+b)x2-2max +cm-bm=0.根据题意:因为方程有两个相等的实数根,所以Δ=(-2ma)2-4(c+b)(cm-bm)=0,即4ma2-4(c2m-bcm+bcm-b2m)=0.得ma2-c2m+b2m=0.所以Δ=m(a2+b2-c2)=0.又因为 m>0,所以a2+b2-c2=0,所以a2+b2=c2.又因为a,b,c为ΔABC的三边,所以ΔABC为RtΔ.小结:当三角形的三边是某个方程的系数时,要想将这三边联系在一起,可以借用根的判别式来处理.。
第09讲根的判别式及其应用(原卷版)2

第09讲 根的判别式及其应用【知识梳理】一:判别式的值与根的关系1.一元二次方程根的判别式:我们把24b ac -叫做一元二次方程20(0)ax bx c a ++=≠的根的判别式,通常用符号“∆”表示,记作2=4b ac ∆-.2.一元二次方程20(0)ax bx c a ++=≠,当2=40b ac ∆->时,方程有两个不相等的实数根;当2=40b ac ∆-=时,方程有两个相等的实数根;当2=40b ac ∆-<时,方程没有实数根.二:根的判别式的应用(1)不解方程判定方程根的情况;(2)根据参数系数的性质确定根的范围;(3)解与根有关的证明题.三:韦达定理韦达定理:如果12,x x 是一元二次方程20ax bx c ++= (0)a ≠的两个根,由解方程中的公式法得,1x ,2x . 那么可推得1212,b c x x x x a a+=-=. 这是一元二次方程根与系数的关系 【考点剖析】题型一:判别式的值与根的关系例1.不解方程,判别下列方程的根的情况:(1)24530x x --=;(2)22430x x ++=;(3)223x +=;(4)22340x x +-=.【变式1】已知关于x 的一元二次方程2(1)210m x mx -++=根的判别式的值为4,求m 的值.例2.当m 取何值时,关于x 的方程221(2)104x m x m +-+-=, (1)有两个不相等的实数根? (2)有两个相等的实数根?(3)没有实数根?【变式1】一元二次方程220x x --=的根的情况是( )A. 有两个相等的实数根;B. 有两个不相等的实数根;C. 没有实数根;D. 不确定.【变式2】关于x 的方程210x mx m -+-=根的情况,下列说法正确的是( )A. 没有实数根;B. 有两个不相等的实数根;C. 有两个不相等的实数根;D. 有两个实数根.【变式3】下列方程中,没有实数根的是( )A. 2250x x --=B. 2210x x -+=C. 220x x -=D. 225x x -=-【变式4】当a = 时,关于x 的方程2210x ax -+=有两个相等的实数根.【变式5】已知方程组18ax y x by -=⎧⎨+=⎩的解是23x y =⎧⎨=⎩,试判断关于x 的方程20x ax b ++=的根的情况. 【变式6】当k 为何值时,关于x 的方程224(21)0x kx k -+-=有实数根?并求出这时方程的根(用含k 的代数式表示).题型二:根的判别式的应用例3.证明:方程()()212x x k --=有两个不相等的实数根.【变式1】当k 为何值时,方程()()222210kx k x x k k --=--≠,(1)有两个不相等的实数根;(2)有两个相等的实数根;(3)没有实数根.【变式2】已知关于x 的一元二次方程()21230m x mx m +++-=有实数根,求m 的取值范围.【变式3】如果m 是实数,且不等式(1)1m x m +>+的解集是1x <,那么关于x 的一元二次方程21(1)04mx m x m -++=的根的情况如何?【变式4】已知关于x 的方程()21230m x mx m +++-=总有实数根,求m 的取值范围.题型三:韦达定理例4.写出下列一元二次方程(方程的根为12,x x )的两实数根的和与两实数根的积(1)2310x x -+=,12x x +=________;12x x =________;(2)23220x x --=,12x x += ________;12x x =________. 【变式1】已知方程2560x kx +-=的一个根是2,求另一根及k 值.【变式2】已知:关于x 的方程23190x x m -+=的一个根是1,求另一根及m 值.【变式3】如果5-是方程25100x bx +-=的一个根,求另一个根及b 值.【变式4】已知12,x x 是方程230x px q ++=的两个根,分别根据下列条件求出p q 、的值.(1)12x x ==; (2)1222x x =-+=--【变式5】设12,x x 是方程22430x x +-=的两个根,求()()1211x x ++的值.【变式6】已知方程22210x ax a +-+=的两个实根的平方和为174,求a 的值;【过关检测】一.选择题(共6小题)1.(2022秋•徐汇区期末)若方程x2﹣3x+m=0有一根是1,则另一根是()A.1B.2C.﹣1D.﹣22.(2022秋•青浦区校级期末)下列一元二次方程中,有两个相等的实数根的方程是()A.B.(x﹣2)2=5C.x2+2x=0D.3.(2022秋•虹口区校级期中)关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是()A.k>﹣1B.k<1C.k>﹣1且k≠0D.k<1且k≠04.(2022秋•黄浦区期中)下列方程中,无实数根的方程为()A.2x2+6x=3B.3x2+4x+6=0C.x2﹣2x=0D.3x2﹣4x﹣6=05.(2022秋•宝山区期中)已知关于x的一元二次方程ax2+bx﹣ab=0,其中a,b在数轴上的对应点如图所示,则这个方程的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.只有一个实数根6.(2022秋•闵行区期中)已知a、b、c是三角形三边的长,则关于x的一元二次方程ax2+2(b﹣c)x+a=0的实数根的情况是()A.有两个相等的实数根B.有两个不相等的实数根C.没有实数根D.无法确定二.填空题(共12小题)7.(2022秋•黄浦区校级月考)方程x2﹣3x+2=0两个根的和为,积为.8.(2022秋•普陀区校级期中)若关于x的方程x2+bx﹣c=0(c≠0)有两个相等的实数根,则代数式的值是.9.(2022秋•长宁区校级期中)已知关于x的方程(m+1)x2+2x=1,方程有两个不相等的实数根,那么m 的取值范围是.10.(2022秋•闵行区校级期中)若等腰三角形的一边长是2,另两边的长是关于x的方程x2﹣6x+m=0的两个根,则m的值为.11.(2022秋•浦东新区期中)已知关于x的方程mx2﹣2x+1=0有两个不相等的实数根,则m可取的最大整数是.12.(2022秋•徐汇区校级期中)如果关于x的一元二次方程x2+3x﹣2m=0没有实数根,那么m的取值范围是.13.(2022秋•浦东新区校级月考)等腰△ABC的一边长为3,另外两边的长是关于x的方程x2﹣10x+m=0的两个实数根,则m的值是.14.(2022秋•奉贤区校级期中)已知关于x的方程x2﹣2x﹣m2=0根的判别式的值36,则m=.15.(2022秋•奉贤区期中)当k时,关于x的方程有两个实数根.16.(2022秋•杨浦区期中)如果关于x的方程mx2﹣(2m+1)x+m﹣1=0有两个不相等的实数根,那么m 的取值范围是.17.(2022秋•虹口区校级期中)已知关于x的方程(m﹣3)x2﹣(m2﹣m+2)x+2m2+2m=0的根是正整数,则整数m的值为.18.(2022秋•黄浦区期中)写出一个一元二次方程,使它的一个根为1,另一个根为,这个方程的一般式是.三.解答题(共10小题)19.(2022秋•奉贤区期中)已知△ABC的两边是关于x的方程x2﹣10x+m=0的两根,第三边的长为4,当m为何值时,△ABC是等腰三角形?并求出这两边的长.20.(2022秋•静安区校级期中)已知关于x的一元二次方程(m+1)x2+2x=1(m为实数).(1)如果该方程有两个不相等的实数根,求m的取值范围.(2)如果该方程有两个相等的实数根,求m的取值范围.(3)如果该方程没有实数根,求m的取值范围.21.(2022秋•浦东新区期中)已知关于x的一元二次方程x2﹣mx+1=0有两个相等的实数根.求m的值并求出两个实数根.22.(2022秋•徐汇区校级期中)已知关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根.(1)求m的取值范围;(2)当m取最大非零整数时,求方程的两个根.23.(2022秋•杨浦区期末)关于x的一元二次方程mx2﹣(3m﹣1)x+2m﹣1=0,其根的判别式的值为1,求m的值及该方程的根.24.(2022秋•青浦区期中)若关于x的一元二次方程(m﹣1)x2﹣4mx+4m+6=0有实数根,求m能取的正整数值.25.(2022秋•奉贤区校级期中)已知关于x的方程(k﹣2)x2+6kx+4k﹣1=0.(1)只有一个根,求k的值,并求此时方程的根;(2)有两个相等的实数根,求k的值,并求此时方程的根.26.(2022秋•杨浦区期中)已知关于x的一元二次方程x2﹣2(m+1)x+m2+5=0.(1)如果方程有两个实数根,求m的取值范围;(2)如果等腰三角形ABC的一条边长为7,其余两边的边长恰好是该方程的两个根,求m的值.27.(2022秋•浦东新区校级月考)已知:设三角形ABC的三边a,b,c为方程4x2+4x+2b﹣c=0有两个相等的实数根,且a,b,c满足3a﹣2c=b.(1)求证:△ABC是等边三角形;(2)若a,b为方程x2﹣2kx+(﹣2k+3)=0的两根,求k的值.28.(2022秋•闵行区校级期中)已知关于x的一元二次方程(m﹣1)x2﹣(2m+5)x+(m+4)=0有两个实数根.(1)求m的取值范围;(2)请写出m的最小整数值,并求出此时方程的根.。
一元二次方程中根的判别式以及根与系数关系的应用

一元二次方程中根的判别式以及根与系数关系的应用【主体知识归纳】1.一元二次方程的根的判别式:b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式.通常用符号“Δ”来表示.2.对于一元二次方程ax2+bx+c=0(a≠0),当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程没有实数根.反过来也成立.3.如果关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根是x1,x2,b那么x1+x2=-ac,x1x2=a4. 如果关于x的一元二次方程x2+px+q=0(a≠0)的两个根是x1,x2,那么x1+x2=-p,x1x2=q【基础知识讲解】1.根的判别式以及根与系数的关系都体现了根与系数之间的联系22.根的判别式是指Δ=b2-4ac,而不是指Δ=.b4ac3.根的判别式与根与系数的关系都是在一元二次方程一般形式下得出的,因此,必须把所给的方程化为一般形式再判别根的情况.要注意方程中各项系数的符号.4.如果说一元二次方程有实根,那么应当包括有两个不相等的实数根和有两个相等的实数根两种情况,此时b2-4ac≥0,不要丢掉等号.5. 利用一元二次方程的根与系数的关系的前提是:(1)二次项系数a≠0,即保证是一元二次方程;(2)由于我们目前只研究实数根的问题,故还要考虑实数根存在的前提,即:b2-4ac≥06.判别式有以下应用:(1)不解方程,判定一元二次方程根的情况;(2)根据一元二次方程根的情况,确定方程中未知系数的取值范围;(3)应用判别式进行有关的证明.根与系数的关系有以下应用:(1)已知一根,求另一根及求知系数;(2)不解方程,求与方程两根有关的代数式的值;(3)已知两数,求以这两数为跟的方程;已知两数的和与积,求这两个数(4)确定方程中字母系数的取值范围(5)确定根的符号。
【例题罗列】根的判别式类型1:不解方程,判别下列方程的根的情况:(1)3x2-2x-1=0;(2)y2=2y-4;(3)(2k2+1)x2-2kx+1=0;(4)9x2-(p+7)x+p-3=0.(系数中有字母的情况)解:(1)∵Δ=(-2)2-4×3×(-1)=4+12>0,∴原方程有两个不相等的实数根.(2)原方程就是y2-2y+4=0.∵Δ=(-2)2-4×1×4=4-16<0,∴原方程无实数根.(3)∵2k2+1≠0,∴原方程为一元二次方程.又∵Δ=(-2k)2-4(2k2+1)×1=-4k2-4<0,∴原方程无实数根.(4)Δ=[-(p+7)]2-4×9×(p-3)=(p-11)2+36,∵不论p取何实数,(p-11)2均为非负数,∴(p-11)2+36>0,即Δ>0,∴原方程有两个不相等的实数根.升级:如果关于x的方程x2+2x=m+9没有实数根,试判断关于y的方程y2+my-2m+5=0的根的情况.这是一类需要自己找出隐含条件的题解:∵x2+2x-m-9=0没有实数根,∴Δ1=22-4(-m-9)=4m+40<0,即m<-10.又y 2+my -2m +5=0的判断式Δ2.Δ2=m 2-4(-2m +5)=m 2+8m -20当m <-10时,m 2+8m -20>0,即Δ2>0.∴方程y 2+my -2m +5=0有两个不相等的实数根.类型2:1.已知关于x 的一元二次方程(k -1)x 2+2kx +k +3=0.k 取什么值时,(1)方程有两个不相等的实数根? (2)方程有两个相等的实数根? (3)方程没有实数根?解:Δ=(2k )2-4(k -1)(k +3)=-8k +12.(1)当-8k +12>0,且k -1≠0,即k <且k ≠1时,方程有两个不相等23的实数根;(2)当-8k +12=0,且k -1≠0,即k =时,方程有两个相等的实数根;23(3)当-8k +12<0,且k -1≠0,即k >时,方程没有实数根.23说明:当已知方程为一元二次方程时,要特别注意隐含的条件:二次项系数不等于零.2.已知a 、b 、c 是△ABC 的三边,且方程a(1+x 2)+2bx-c(1-x 2)=0有两个相等的实数根,则此三角形为( )A 、等腰三角形 B 、等边三角形 C 、直角三角形 D 、斜三角形 看到有两个相同的实数根立即判断 应用根的判别式解:原方程可化为(a+c )x 2+2bx +a-c =0,Δ=(2b)2-4(a +c )(a -c )=0得到a 2=b 2+c 2,因此此三角形为直角三角形。
根的判别式及其应用-2023年新八年级数学核心知识点与常见题型(沪教版)(解析版)

根的判别式及其应用【知识梳理】一:判别式的值与根的关系1.一元二次方程根的判别式:我们把24b ac −叫做一元二次方程20(0)ax bx c a ++=≠的根的判别式,通常用符号“∆”表示,记作2=4b ac ∆−.2.一元二次方程20(0)ax bx c a ++=≠,当2=40b ac ∆−>时,方程有两个不相等的实数根; 当2=40b ac ∆−=时,方程有两个相等的实数根; 当2=40b ac ∆−<时,方程没有实数根. 二:根的判别式的应用(1)不解方程判定方程根的情况; (2)根据参数系数的性质确定根的范围; (3)解与根有关的证明题. 三:韦达定理韦达定理:如果12,x x 是一元二次方程20ax bx c ++= (0)a ≠的两个根,由解方程中的公式法得,1x 2x = 那么可推得1212,b cx x x x a a+=−=. 这是一元二次方程根与系数的关系【考点剖析】 题型一:判别式的值与根的关系例1.不解方程,判别下列方程的根的情况:(1)24530x x −−=; (2)22430x x ++=;(3)223x +=;(4)22340x x +−=.【答案】(1)方程有两不等实根;(2)方程无实数根;(3)方程有两相等实根; (4)方程有两不等实根.【答案】【答案】【解析】(1)4a =,5b =−,3c =−,24730b ac ∆=−=>,方程有两不等实根;2a =,4b =,3c =,2480b ac ∆=−=−<,方程无实数根;2a =,b =−3c =,240b ac ∆=−=,方程有两相等实根;(4)2a =,3b =,4c =−,24410b ac ∆=−=>,方程有两不等实根.【总结】考查一元二次方程根的判别式判定方程根的情况,先将方程整理成一般形式,列出方程中的a 、b 、c ,再代值计算∆,根据∆与0的大小关系确定方程根的情况,注意a 、c 异号时则必有两不等实根.【变式1】已知关于x 的一元二次方程2(1)210m x mx −++=根的判别式的值为4,求m 的值. 【答案】0.【答案】【答案】【解析】∵1a m =−,2b m =,1c =, ∴()()()2224241414b ac m m m m ∆=−=−⨯−=−+=,整理即得20m m −=,解得:11m =,20m =,同时方程是一元二次方程,知10a m =−≠,故1m ≠,由此得0m =.【总结】考查一元二次方程根的判别式判定方程根的情况,对于含有字母系数的一元二次方程,尤其是二次项系数中含有字母的情况,一定要注意字母所隐含的取值范围,即二次项系数不能为0. 例2.当m 取何值时,关于x 221(2)104x m x m +−+−=,(1)有两个不相等的实数根? (2)有两个相等的实数根?(3)没有实数根? 【答案】(1)2m <;(2)2m =;(3)2m >.【解析】对此方程,1a =,2b m =−,2114c m =−,则()22214241484b ac m m m ⎛⎫∆=−=−−−=−+ ⎪⎝⎭,由此可知,(1)当480m ∆=−+>,即2m <时,方程有两个不相等的实数根; (2)当480m ∆=−+=,即2m =时,方程有两两个相等的实数根; (3)当480m ∆=−+<,即2m >时,方程无实数根.【总结】考查一元二次方程根的判别式判定方程根的情况,对于系数含有字母的情况,先确定其∆值,方程可由∆值判定其根的情况,同样地,可由方程根的情况确定其∆值与0的大小关系,可在此基础上进行分类讨论.【变式1】一元二次方程220x x −−=的根的情况是( )A. 有两个相等的实数根;B. 有两个不相等的实数根;C. 没有实数根;D. 不确定. 【答案】B【解析】因为2(1)41(2)1890∆=−−⨯⨯−=+=>,所以方程有两个不相等的实数根. 【变式2】关于x 的方程210x mx m −+−=根的情况,下列说法正确的是( )A. 没有实数根;B. 有两个不相等的实数根;C. 有两个不相等的实数根;D. 有两个实数根. 【答案】D【解析】 因为判别式2224(1)44(2)0m m m m m ∆=−−=−+=−≥,故原方程有两个实数根,故选D. 【变式3】下列方程中,没有实数根的是( )A. 2250x x −−=B. 2210x x −+=C. 220x x −= D. 225x x −=−【答案】D.【解析】A 、420240∆=+=>,有两不等实数根;B 、440∆=−=,有两个相等实数根;C 、40∆=>,有两个不相等的实根;D 、420160∆=−=−<,无实数根. 故正确答案选D.【变式4】当a = 时,关于x 的方程2210x ax −+=有两个相等的实数根.【答案】1±【解析】由2440a ∆=−=得,1a =±.【变式5】已知方程组18ax y x by −=⎧⎨+=⎩的解是23x y =⎧⎨=⎩,试判断关于x 的方程20x ax b ++=的根的情况.【答案】方程无实数根.【答案】【答案】【解析】方程组18ax y x by −=⎧⎨+=⎩的解是23x y =⎧⎨=⎩,代入即得:231238a b −=⎧⎨+=⎩,可解得:22a b =⎧⎨=⎩, 此时方程即为2220x x ++=,其中1a =,2b =,2c =,2480b ac ∆=−=−<,可知方程无实数根. 【总结】考查一元二次方程根的判别式判定方程根的情况,对于系数含有字母的情况,根据题目条件确定字母取值,再确定其∆值,判定方程解的情况.【变式6】当k 为何值时,关于x 的方程224(21)0x kx k −+−=有实数根?并求出这时方程的根(用含k 的代数式表示).【答案】14k ≥时,方程有实数根;方程的根为2x k =± 【答案】【答案】【解析】对此方程,1a =,4b k =−,()221c k =−,则()()22244421164b ac k k k ∆=−=−−−=−,因为方程有实数根,则有1640k ∆=−≥,即14k ≥时,方程有实数根;根据一元二次方程求根公式,可知方程解为()4222k b x k a −−−===【总结】考查一元二次方程根的判别式判定方程根的情况,对于系数含有字母的情况,先确定其∆值,方程可由∆值判定其根的情况,同样地,可由方程根的情况确定其∆值与0的大 题型二:根的判别式的应用例3.证明:方程()()212x x k −−=有两个不相等的实数根.【解析】证明:对原方程进行整理,即为:22320x x k −+−= 其中1a =,3b =−,22c k =−则()()22224342410b ac k k ∆=−=−−−=+>恒成立,由此可证得方程有两个不相等的实数根.【总结】将方程整理成一元二次方程的一般形式,方程的根的情况,只需要根据方程的∆值即可以确定下来.【变式1】当k 为何值时,方程()()222210kx k x x k k −−=−−≠,(1)有两个不相等的实数根;(2)有两个相等的实数根;(3)没有实数根.【答案】(1)54k <且1k ≠;(2)54k =;(3)54k >.【答案】【答案】【解析】将方程整理成关于x 的一元二次方程的一般形式,即得:()()()212210k x k x k −−−++=,此时,1a k =−,()22b k =−−,1c k =+,由方程为一元二次方程,可知10a k =−≠,故1k ≠;()()()224424111620b ac k k k k ∆=−=−−−+=−+,由此可知,(1)当16200k ∆=−+>,即54k <且1k ≠时,方程有两不等实根; (2)当16200k ∆=−+=,即54k =时,方程有两相等实根; (3)当16200k ∆=−+<,即54k >时,方程无实根.【总结】考查一元二次方程根的判别式判定方程根的情况,首先将方程整理成一元二次方程的一般形式,然后确定二次项系数不能为0的情况,然后确定其∆值,可由方程根的情况确定其∆值与0的大小关系,可在此基础上进行分类讨论.【答案】【答案】【变式2】已知关于x 的一元二次方程()21230m x mx m +++−=有实数根,求m 的取值范围.【答案】32m ≥−且1m ≠−.【答案】【答案】【解析】由原方程是一元二次方程,可知10m +≠,即1m ≠−;对此方程, 其中1a m =+,2b m =,c m =−,方程有实根,则必有:()()()22424138120b ac m m m m ∆=−=−+−=+≥,可解得32m ≥−;即m 的取值范围为32m ≥−且1m ≠−.【总结】对于形如20ax bx c ++=的方程,首先要根据题意确定相关隐含条件,既要保证一元二次方程的二次项系数不能为0,然后在此基础上进行解题和计算.【变式3】如果m 是实数,且不等式(1)1m x m +>+的解集是1x <,那么关于x 的一元二次方程21(1)04mx m x m −++=的根的情况如何?【答案】方程无实根.【答案】【答案】【解析】由(1)1m x m +>+的解集是1x <,可知10m +<,即1m <−,对一元二次方程21(1)04mx m x m −++=而言,其中a m =,()1b m =−+,14c m =, 则()221414214b ac m m m m ∆=−=+−⋅=+,1m <−时,0∆<恒成立,由此可知方程无实数根.【总结】探求含有字母的一元二次方程根的情况,需要根据题目条件确定相关字母取值范围,再根据其∆值确定相关方程根的情况.【变式4】已知关于x 的方程()21230m x mx m +++−=总有实数根,求m 的取值范围.【答案】32m ≥−.【答案】【答案】【解析】(1)当10m +=,即1m =−时,方程为一元一次方程240x −−=,方程有实根; 当10m +≠,即1m ≠−时,方程为一元二次方程,其中1a m =+,2b m =,3c m =−,方程有实根,则必有:()()()22424138120b ac m m m m ∆=−=−+−=+≥,可解得32m ≥−且1m ≠−;综上所述,m 的取值范围为32m ≥−.【总结】对于形如20ax bx c ++=的方程,首先要根据题意确定二次项系数能否为0,在此基础上进行相关分类讨论和计算. 题型三:韦达定理例4.写出下列一元二次方程(方程的根为12,x x )的两实数根的和与两实数根的积 (1)2310x x −+=,12x x +=________;12x x =________;(2)23220x x −−=,12x x += ________;12x x =________.【答案】(1)3,1;(2)23,【答案】【答案】23−.【解析】(1)1a =,3b =−,1c =,根据一元二次方程根与系数的关系,可得123b x x a +=−=,121c x x a ==;(2)3a =,2b =−,2c =−,根据一元二次方程根与系数的关系,可得1223b x x a +=−=,1223c x x a ==−;【总结】考查一元二次方程根与系数的关系,在方程有实数根的前提下,由一般式确定相应的a 、b 、c 值即可快速得到结果.【变式1】已知方程2560x kx +−=的一个根是2,求另一根及k 值.【答案】方程另一根为35x =−,【答案】【答案】7k =−.【解析】根据韦达定理,可知方程两根满足条件,125kx x +=−,1265x x =−, 令12x =,则可求得235x =−,代入可得12755k x x +=−=,可得7k =−. 【总结】考查韦达定理的应用,本题可根据一元二次方式根的定义代入求值计算,但是更简单的,可以通过韦达定理直接快速得到题目结果.【变式2】已知:关于x 的方程23190x x m −+=的一个根是1,求另一根及m 值.【答案】方程另一根为163x =,【答案】【答案】16m =.【解析】根据韦达定理,可知方程两根满足条件,12193x x +=,123mx x =,令11x =,则可求得2163x =,代入可得121633m x x ==,可得16m =.【总结】考查韦达定理的应用,本题可根据一元二次方式根的定义代入求值计算,但是更简单的,可以通过韦达定理直接快速得到题目结果.【变式3】如果5−是方程25100x bx +−=的一个根,求另一个根及b 值.【答案】方程另一根为25x =,【答案】【答案】23b =.【解析】根据韦达定理,可知方程两根满足条件,125b x x +=−,121025x x −==−,令15x =−,则可求得225x =,代入可得122355b x x +=−=−,可得23b =.【总结】考查韦达定理的应用,本题可根据一元二次方式根的定义代入求值计算,但是更简单的,可以通过韦达定理直接快速得到题目结果.【变式4】已知12,x x 是方程230x px q ++=的两个根,分别根据下列条件求出p q 、的值. (1)12x x == (2)1222x x =−+=− 【答案】(1)0p =,21q =−;(2)12p =,3q =.【答案】【答案】【解析】(1)根据韦达定理,可得1203px x +=−=,1273q x x ==−,可得0p =,21q =−; (2)根据韦达定理,可得1243px x +=−=−,1213q x x ==,可得12p =,3q =. 【总结】考查韦达定理的应用,可快速由方程的根得到方程中的相关字母量.【变式5】设12,x x 是方程22430x x +−=的两个根,求()()1211x x ++的值.【答案】【答案】【答案】52−.【解析】根据韦达定理,可得方程两根满足12422x x +=−=−,1232x x =−, 由此()()()()121212*********x x x x x x ⎛⎫++=+++=−+−+=− ⎪⎝⎭. 【总结】考查韦达定理的应用,只需将所求式子转化为只含有两根之和和两根之积的式子即可进行求解计算.【变式6】已知方程22210x ax a +−+=的两个实根的平方和为174,求a 的值;【答案】【答案】【答案】3a =.【解析】根据韦达定理,可得方程两根满足122ax x +=−,12122a x x −=,依题意有 2212174x x +=,即()221212121227224a a x x x x −⎛⎫+−=−−⨯= ⎪⎝⎭,整理即得28330a a +−=,解得:111a =−,23a =;同时,韦达定理的前提是方程有实数根,由此需满足()2242211680a a a a ∆=−⨯−+=+−≥,仅在3a =时0∆≥成立,综上所述,可得3a =.【总结】考查韦达定理的应用,只需将所求式子转化为只含有两根之和和两根之积的式子即可进行求解计算,但一定要注意现阶段韦达定理的前提是方程有实数根,即还需满足0∆≥.【过关检测】一.选择题(共6小题)1.(2022秋•徐汇区期末)若方程﹣3x +m =0有一根是1,则另一根是( ) A .1B .2C .﹣1D .﹣2【分析】根据根与系数的关系列出关于另一根n 的方程,解方程即可得到答案. 【解答】解:设方程的另一根为n , ∵方程x2﹣3x+m =0有一根是1, ∴1+n =3,解得:n =2, 故选:B .【点评】本题考查了一元二次方程的解,根于系数的关系,解题的关键是弄清楚一元二次方程的两根之和与系数a 、b 的关系.2.(2022秋•青浦区校级期末)下列一元二次方程中,有两个相等的实数根的方程是( )A .B .(x ﹣2)2=5C .x 2+2x =0D .【分析】先把四个方程化为一般式,再计算各方程的根的判别式的值,然后根据根的判别式的意义进行判断.【解答】解:A.x2﹣x+=0,∵Δ=(﹣1)2﹣4×1×=0,∴方程有两个相等的实数根;B.x2﹣4x﹣1=0,∵Δ=(﹣4)2﹣4×(﹣1)=20>0,∴方程有两个不相等的实数根;C.x2+2x=0,∵Δ=22﹣4×1×0=4,∴方程有两个不相等的实数根;D.2x2﹣x+1=0,∵Δ=(﹣)2﹣4×2×1=﹣6<0,∴方程没有实数根.故选:A.ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系,当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.上面的结论反过来也成立.3.(2022秋•虹口区校级期中)关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是()A.k>﹣1B.k<1C.k>﹣1且k≠0D.k<1且k≠0【分析】根据一元二次方程的定义和△的意义得到k≠0且Δ>0,即(﹣2)2﹣4×k×(﹣1)>0,然后解不等式即可得到k的取值范围.【解答】解:∵关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,∴k≠0且Δ>0,即(﹣2)2﹣4×k×(﹣1)>0,解得k>﹣1且k≠0.故选:C.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2﹣4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.也考查了一元二次方程的定义.4.(2022秋•黄浦区期中)下列方程中,无实数根的方程为()A.2x2+6x=3B.3x2+4x+6=0C.x2﹣2x=0D.3x2﹣4x﹣6=0【分析】先分别计算各方程的根的判别式的值,然后根据根的判别式的意义判断四个方程的根的情况即可.【解答】解:A.方程化为一般式为2x2+6x﹣3=0,Δ=62﹣4×2×(﹣3)=60>0,则方程有两个不相等的实数根,所以A选项不符合题意;B.Δ=42﹣4×3×6=﹣56<0,则方程没有实数根,所以B选项符合题意;C.Δ=(﹣2)2﹣4×0=4>0,则方程有两个不相等的实数根,所以C选项不符合题意;D.Δ=(﹣4)2﹣4×3×(﹣6)=88>0,则方程有两个不相等的实数根,所以D选项不符合题意.故选:B.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.5.(2022秋•宝山区期中)已知关于x的一元二次方程ax2+bx﹣ab=0,其中a,b在数轴上的对应点如图所示,则这个方程的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.只有一个实数根【分析】根据一元二次方程根的判别式得Δ=b2+4a2b,根据根据a,b在数轴上的对应点,可得a<0,b>0,即可确定判别式得符号,进一步确定根的情况.【解答】解:在一元二次方程ax2+bx﹣ab=0中,Δ=b2+4a2b,根据a,b在数轴上的对应点,可得a<0,b>0,∴Δ>0,∴方程有两个不相等的实数根,故选:A.【点评】本题考查了一元二次方程根的情况,熟练掌握根的判别式与根的情况的关系是解题的关键.6.(2022秋•闵行区期中)已知a、b、c是三角形三边的长,则关于x的一元二次方程ax2+2(b﹣c)x+a=0的实数根的情况是()A.有两个相等的实数根B.有两个不相等的实数根C.没有实数根D.无法确定【分析】Δ=[2(b﹣c)]2﹣4a2=4(b﹣c+a)(b﹣c﹣a),根据三角形的三边关系可知Δ<0,可知一元二次方程根的情况.【解答】解:Δ=[2(b﹣c)]2﹣4a2=4(b﹣c+a)(b﹣c﹣a),∵a、b、c是三角形三边的长,∴b﹣c+a>0,b﹣c﹣a<0,∴Δ=4(b﹣c+a)(b﹣c﹣a)<0,∴原方程没有实数根,故选:C.【点评】本题考查了一元二次方程根的判别式,三角形的三边关系,熟练掌握根的判别式与根的情况的关系是解题的关键.二.填空题(共12小题)7.(2022秋•黄浦区校级月考)方程x2﹣3x+2=0两个根的和为,积为.【分析】直接利用根与系数的关系求解.【解答】解:根据根与系数的关系x2﹣3x+2=0两个根的和为3,积为2.故答案为:3,2.【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,则x1+x2=﹣,x1x2=.8.(2022秋•普陀区校级期中)若关于x的方程x2+bx﹣c=0(c≠0)有两个相等的实数根,则代数式的值是.【分析】根据方程的系数,结合根的判别式Δ=0,即可得出b2=﹣4c,将其代入中,即可求出结论.【解答】解:∵关于x的方程x2+bx﹣c=0(c≠0)有两个相等的实数根,∴Δ=b2﹣4×1×(﹣c)=0,∴b2=﹣4c,又∵c≠0,∴==﹣2.故答案为:﹣2.【点评】本题考查了根的判别式,牢记“当Δ=0时,方程有两个相等的实数根”是解题的关键.9.(2022秋•长宁区校级期中)已知关于x的方程(m+1)x2+2x=1,方程有两个不相等的实数根,那么m 的取值范围是.【分析】利用二次项系数非零及根的判别式Δ>0,即可得出关于m的一元一次不等式组,解之即可得出m 的取值范围.【解答】解:将原方程转化为一般形式得(m+1)x2+2x﹣1=0,∵方程有两个不相等的实数根,∴,解得:m>﹣2且m≠﹣1,∴m的取值范围是m>﹣2且m≠﹣1.故答案为:m>﹣2且m≠﹣1.【点评】本题考查了根的判别式以及一元二次方程的定义,利用二次项系数非零及根的判别式Δ>0,找出关于m的一元一次不等式组是解题的关键.10.(20222,另两边的长是关于x的方程x2﹣6x+m=0的两个根,则m的值为.【分析】讨论:当底边长为2时,则腰长为方程x2﹣6x+m=0的两个根,利用判别式的意义得到∴△=(﹣6)2﹣4m=0,解方程得到m的值;当腰长为2,则x=2为方程x2﹣6x+m=0的一个根,求出m=8,方程化为x2﹣6x+8=0,解得x1=2,x2=4,然后根据三角形三边的关系可判断这种情况不符合题意.【解答】解:当底边长为2时,则腰长为方程x2﹣6x+m=0的两个根,∴△=(﹣6)2﹣4m=0,解得m=9;当腰长为2,则x=2为方程x2﹣6x+m=0的一个根,∴4﹣12+m=0,解得m=8,方程化为x2﹣6x+8=0,解得x1=2,x2=4,∵2+2=4,∴2、2、4不符合三角形三边的关系,舍去,综上所述,m的值为9.故答案为9.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.也考查了三角形三边的关系.11.(2022秋•浦东新区期中)已知关于x的方程mx2﹣2x+1=0有两个不相等的实数根,则m可取的最大整数是.【分析】由二次项系数非零及根的判别式Δ>0,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围.【解答】解:∵关于x的方程mx2﹣2x+1=0有两个不相等的实数根,∴Δ=(﹣2)2﹣4m×1>0且m≠0,解得:m<1且m≠0.故答案为:﹣1.【点评】本题考查了根的判别式以及一元二次方程的定义,根据二次项系数非零及根的判别式Δ>0,找出关于m的一元一次不等式组是解题的关键.12.(2022秋•徐汇区校级期中)如果关于x的一元二次方程x2+3x﹣2m=0没有实数根,那么m的取值范围是.【分析】根据关于x的一元二次方程x2+3x﹣2m=0没有实数根,得出Δ=9﹣4×(﹣2m)<0,从而求出m的取值范围.【解答】解:∵一元二次方程x2+3x﹣2m=0没有实数根,∴Δ=9﹣4×(﹣2m)<0,∴m<﹣,故答案为:m<﹣.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式,关键是掌握Δ=b2﹣4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.13.(2022秋•浦东新区校级月考)等腰△ABC的一边长为3,另外两边的长是关于x的方程x2﹣10x+m=0的两个实数根,则m的值是.【分析】结合根与系数的关系,分已知边长3是底边和腰两种情况讨论.【解答】解:设关于x的方程x2﹣10x+m=0的两个实数根分别为a、b.∵方程x2﹣10x+m=0有两个实数根,∴Δ=100﹣4m≥0,得m≤25.①当底边长为3时,另两边相等时,a+b=10,∴另两边的长都是为5,则m=ab=25;②当腰长为3时,另两边中至少有一个是3,则3一定是方程x2﹣10x+m=0的根,而a+b=10,∴另一根为:7.∵3+3<7,不能构成三角形.∴m的值为25.故答案为:25.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2﹣4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.也考查了三角形三边的关系以及等腰三角形的性质.14.(2022秋•奉贤区校级期中)已知关于x的方程x2﹣2x﹣m2=0根的判别式的值36,则m=.【分析】根据根的判别式得出方程(﹣2)2﹣4×1×(﹣m2)=36,求出方程的解即可.【解答】解:∵关于x的方程x2﹣2x﹣m2=0根的判别式的值36,∴Δ=(﹣2)2﹣4×1×(﹣m2)=36,解得:m=±2,故答案为:±2.【点评】本题考查了根的判别式,能熟记根的判别式的内容是解此题的关键.15.(2022秋•奉贤区期中)当k时,关于x的方程有两个实数根.【分析】根据一元二次方程的定义和根的判别式的意义得到k≠0且Δ=(﹣1)2﹣4k×≥0,然后求出两不等式的公共部分即可.【解答】解:根据题意得k≠0且Δ=(﹣1)2﹣4k×≥0,解得k≤且k≠0,即k的取值范围为k≤且k≠0.故答案为:≤且k≠0.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.16.(2022秋•杨浦区期中)如果关于x的方程mx2﹣(2m+1)x+m﹣1=0有两个不相等的实数根,那么m 的取值范围是.【分析】根据一元二次方程的定义和根的判别式的意义得到m≠0且Δ=[﹣(2m+1)]2﹣4m(m﹣1)>0,然后求出两不等式的公共部分即可.【解答】解:根据题意得m≠0且Δ=[﹣(2m+1)]2﹣4m(m﹣1)>0,解得m>﹣且m≠0,即m的取值范围为m>﹣且m≠0,故答案为:m>﹣且m≠0,【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.上面的结论反过来也成立.也考查了一元二次方程的定义.17.(2022秋•虹口区校级期中)已知关于x的方程(m﹣3)x2﹣(m2﹣m+2)x+2m2+2m=0的根是正整数,则整数m的值为.【分析】利用因式分解法求出方程的两个根,再根据方程的两个实数根都为正整数,即可求出m的值.【解答】解:当m﹣3=0,即m=3时,方程为8x+24=0,解得x=﹣3,不合题意舍去;当m﹣3≠0,即m≠3时,(m﹣3)x2﹣(m2﹣m+2)x+2m2+2m=0[(m﹣3)x﹣(2m+2)](x﹣m)=0,∴x1==,x2=m,∵方程的两个实数根都为正整数,∴是正整数,∴m=4或5或7或11,故答案为:3或4或5或7或11.【点评】本题考查了因式分解法解一元二次方程,解题的关键是结合方程的解为正整数,找出关于m的分式方程.18.(2022秋•黄浦区期中)写出一个一元二次方程,使它的一个根为1,另一个根为,这个方程的一般式是.【分析】根据根与系数的关系:x1+x2=﹣,x1•x2=,首先写出两根之和,再写出两根之积,可直接得到方程.【解答】解:∵1+(﹣)=1﹣,1×(﹣)=﹣,∴这个方程的一般式是x2+(﹣1)x﹣=0.故答案为:x2+(﹣1)x﹣=0.【点评】此题主要考查了根与系数的关系,将根与方程的系数相结合解题是一种经常使用的解题方法.三.解答题(共10小题)19.(2022秋•奉贤区期中)已知△ABC的两边是关于x的方程x2﹣10x+m=0的两根,第三边的长为4,当m为何值时,△ABC是等腰三角形?并求出这两边的长.【分析】设△ABC的两边a、b是关于x的方程x2﹣10x+m=0的两根,利用根与系数的关系得到a+b=10,ab=m,讨论:当a=b=5时,易得m=25,△ABC为等腰三角形;当a=4或b=4时,a=6,则m=24,△ABC为等腰三角形.【解答】解:设△ABC的两边a、b是关于x的方程x2﹣10x+m=0的两根,则a+b=10,ab=m,当a=b=5时,m=5×5=25,△ABC为等腰三角形;当a=4时,b=6,则m=24,△ABC为等腰三角形;当b=4时,a=6,则m=24,△ABC为等腰三角形;综上所述,当m=25时,△ABC为等腰三角形,这两边的长分别为5,5;当m=24时,△ABC为等腰三角形,这两边的长分别为4,6.【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=﹣,x1x2=.也考查了等腰三角形的判断.20.(2022秋•静安区校级期中)已知关于x的一元二次方程(m+1)x2+2x=1(m为实数).(1)如果该方程有两个不相等的实数根,求m的取值范围.(2)如果该方程有两个相等的实数根,求m的取值范围.(3)如果该方程没有实数根,求m的取值范围.【分析】先求出Δ=4+4(m+1)=4m+8,(1)根据该方程有两个不相等的实数根,可得Δ=4m+8>0,m+1≠0,进一步求解即可;(2)根据该方程有两个相等的实数根,可得Δ=4m+8=0,进一步求解即可;(3)根据该方程没有实数根,可得Δ=4m+8<0,进一步求解即可.【解答】解:关于x的一元二次方程(m+1)x2+2x=1(m为实数),a=m+1,b=2,c=﹣1,∴Δ=4+4(m+1)=4m+8,(1)根据题意,得Δ=4m+8>0,m+1≠0,解得m>﹣2且m≠﹣1;(2)根据题意,得Δ=4m+8=0,解得m=﹣2;(3)根据题意,得Δ=4m+8<0,解得m<﹣2.【点评】本题考查了一元二次方程根的判别式,熟练掌握一元二次方程根的情况与根的判别式的关系是解题的关键.21.(2022x的一元二次方程x2﹣mx+1=0有两个相等的实数根.求m的值并求出两个实数根.【分析】由一元二次方程x2﹣mx+1=0有两个相等的实数根,得Δ=0,即Δ=m2﹣4=0,可解得m=±2,然后把m=±2代入方程,解此方程即可.【解答】解:∵关于x的一元二次方程x2﹣mx+1=0有两个相等的实数根,∴Δ=0,即Δ=m2﹣4=0,解得m=±2,当m=2时,原方程变为:x2﹣2x+1=0,∴(x﹣1)2=0,解得x1=x2=1,当m=﹣2时,原方程变为:x2+2x+1=0,∴(x+1)2=0,解得x1=x2=﹣1.【点评】此题主要考查了一元二次方程的解法和根的判别式,熟记一元二次方程ax2+bx+c=0(a≠0)的解与b2﹣4ac的关系:当b2﹣4ac>0时,方程有两个不相等的实数根;当b2﹣4ac=0时,方程有两个相等的实数根;当b2﹣4ac<0时,方程无解是解决问题的关键.22.(2022秋•徐汇区校级期中)已知关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根.(1)求m的取值范围;(2)当m取最大非零整数时,求方程的两个根.【分析】(1)根据方程的系数结合根的判别式Δ≥0,即可得出关于m的一元一次不等式,解之即可得出m 的取值范围;(2)由(1)的结论可得出m可取的最大非零整数为﹣1,将其代入原方程中,再利用公式法解一元二次方程,即可求出此时方程的两个根.【解答】解:(1)∵关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根,∴Δ=b2﹣4ac=[﹣(2m﹣2)]2﹣4×1×m2=4﹣8m≥0,解得:m≤,∴m的取值范围为m≤.(2)∵m≤,∴当m取最大非零整数时,m=﹣1.当m=﹣1时,原方程为x2+4x+1=0,解得:x1==﹣2﹣,x2==﹣2+.∴当m取最大非零整数时,方程的两个根分别为x1=﹣2﹣,x2=﹣2+.【点评】本题考查了根的判别式以及公式法解一元二次方程,解题的关键是:(1)牢记“当Δ≥0时,方程有两个实数根”;(2)代入m的值,利用公式法求出一元二次方程的解.23.(2022秋•杨浦区期末)关于x的一元二次方程mx2﹣(3m﹣1)x+2m﹣1=0,其根的判别式的值为1,求m的值及该方程的根.【分析】由一元二次方程的Δ=b2﹣4ac=1,建立m的方程,求出m的解后再化简原方程并求解.【解答】解:由题意知,m≠0,Δ=b2﹣4ac=[﹣(3m﹣1)]2﹣4m(2m﹣1)=1,∴m1=0(舍去),m2=2,∴原方程化为:2x2﹣5x+3=0,解得,x1=1,x2=.【点评】本题考查了一元二次方程根的判别式的应用.切记不要忽略一元二次方程二次项系数不为零这一隐含条件.24.(2022秋•青浦区期中)若关于x的一元二次方程(m﹣1)x2﹣4mx+4m+6=0有实数根,求m能取的正整数值.【分析】根据一元二次方程的定义和根的判别式的意义得到m﹣1≠0且Δ=(﹣4m)2﹣4(m﹣1)(4m+6)≥0,然后求出m的取值范围,进而求出结果.【解答】解:根据题意得m﹣1≠0且Δ=(﹣4m)2﹣4(m﹣1)(4m+6)≥0,解得m≤3且m≠1.故m能取的正整数值为2,3.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2﹣4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.也考查了一元二次方程的定义.25.(2022秋•奉贤区校级期中)已知关于x的方程(k﹣2)x2+6kx+4k﹣1=0.(1)只有一个根,求k的值,并求此时方程的根;(2)有两个相等的实数根,求k的值,并求此时方程的根.【分析】(1)由题意得k﹣2=0≠0,即k=2,列出方程求解可得;(2)根据题意得:k﹣2≠0且Δ=0,解方程可得k的值,再代入列出关于x的方程,求解可得.【解答】解:(1)因为只有一个根所以k﹣2=0且6k≠0,解得k=2,∴方程为12x+7=0,解得x=,所以方程的根为x=;(2)根据题意,得:k﹣2≠0,即k≠2,Δ=0,即(6k)2﹣4(k﹣2)×(4k﹣1)=0,解得k1=,k2=﹣2,当k=时,方程为9x2﹣6x+1=0,即(3x﹣1)2=0,解得:x1=x2=,当k=﹣2时,方程为4x2+12x+9=0,即(2x+3)2=0,解得:x1=x2=﹣.【点评】本题主要考查根的判别式与一元二次方程的定义,一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:①当Δ>0时,方程有两个不相等的两个实数根;②当Δ=0时,方程有两个相等的两个实数根;③当Δ<0时,方程无实数根.26.(2022秋•杨浦区期中)已知关于x的一元二次方程x2﹣2(m+1)x+m2+5=0.(1)如果方程有两个实数根,求m的取值范围;(2)如果等腰三角形ABC的一条边长为7,其余两边的边长恰好是该方程的两个根,求m的值.【分析】(1)根据方程的系数结合根的判别式Δ≥0,即可得出关于m的一元一次不等式,解之即可得出实数m的取值范围;(2)分7为等腰三角形的底或腰两种情形,讨论求解即可.【解答】解:(1)∵关于x的一元二次方程x2﹣2(m+1)x+m2+5=0有实数根,∴Δ=[﹣2(m+1)]2﹣4(m2+5)=8m﹣16≥0,解得:m≥2,∴当方程有两个实数根,m的取值范围为m≥2.(2)当7为底时,由题意得,Δ=,则8m﹣16=0,解得m=2,此时一元二次方程x2﹣6x+9=0解得x=3,因为3+3<7,舍去;当7为腰时,将x=7代入得49﹣14(m+1)+m2+5=0,解得m=4或m=10,当m=10时,得三边长为7、7、15,因为7+7<15(舍去),当m=4时,算得三边长为3、7、7,可以构成三角形,故m的值为4.【点评】本题考查了等腰三角形的性质,一元二次方程的根与系数的关系,根的判别式,解题的关键是学会利用一元二次方程的根与系数的关系,把问题转化为方程解决.27.(2022秋•浦东新区校级月考)已知:设三角形ABC的三边a,b,c为方程4x2+4x+2b﹣c=0有两个。
第二讲 根的判别式及其应用

例4.已知关于x的方程x2-(k+2)x+2k=0.
(2)若等腰∆ABC的一边a=1,另两边长b、c恰是这个方程的两个根,求
△ABC的周长.
(2)②若b≠c,则b=a=1或c=a=1,即方程有一根为1,
【解析】
把x=1代入方程x2-(k+2)x+2k=0,得1-(k+2)+2k=0,解得k=1,
∴∆=b2-4ac =[-2(k+1)]2-4×1×(-k2+2k-1) =8+8k2 >0,
∴此方程有两个不相等的实数根,故选C.
k2≥
例2.当m为什么值时,关于x的方程 m2 −4 x2 +2 m+1 x+1=0有实根.
【点拨】讨论:分 m2 −4=0和m2 −4≠0 两种情况.
【解析】当m2−4=0,
一元二次方程ax2+bx+c=0 的根的判别式
△=b2-4ac
一元二次方程的根的情况取决于
2
Δ=b -4ac>0
方程有两个不相等的实数根.
Δ=b2-4ac的符号.
Δ=b2-4ac=0
方程有两个相等的实数根.
Δ=b2-4ac<0
方程没有实数根.
反之也成立
注意
(1)使用判别式之前,一定要先把方程变化为一般形式,正确找出a、
∴方程总有两个实数根;
m 2 ( m 2)
x
(2)由求根公式得 x1=1,x2= 2 ,∵x1=1为整数,
2m
m
2
∴必须x2= 为整数即可,∵ m取正整数 ∴m =1或2.
m
例6.已知关于x的方程mx 2-(m+2)x+2=0(m≠0).
一元二次方程根的判别式知识点

一元二次方程根的判别式知识点及应用1、一元二次方程ax2+bx+c=0(a≠0)的根的判别式定理:在一元二次方程ax2+bx+c=0(a≠0)中,Δ=b24ac若△>0则方程有两个不相等的实数根若△=0则方程有两个相等的实数根若△<0则方程没有实数根2、这个定理的逆命题也成立,即有如下的逆定理:在一元二次方程ax2+bx+c=0(a≠0)中,Δ=b24ac若方程有两个不相等的实数根,则△>0若方程有两个相等的实数根,则△=0若方程没有实数根,则△<0特别提示:(1)注意根的判别式定理与逆定理的使用区别:一般当已知△值的符号时,使用定理;当已知方程根的情况时,使用逆定理。
(2)一元二次方程ax2+bx+c=0(a≠0)(Δ=b24ac)3、一元二次方程根的判别式的多种应用:一、不解方程,判断一元二次方程根的情况。
二、例1、判断下列方程根的情况三、2x2+x━1=0;x2—2x—3=0;x2—6x+9=0;2x2+x+1=0二、?已知一元二次方程根的情况,求方程中字母系数所满足的条件。
例2、当m为何值时关于x的方程(m—4)x2—(2m—1)x+m=0 有两个实数根?三、?证明方程根的性质。
例3、求证:无论m为任何实数,关于x的方程x2+(m2+3)x+0.5(m2+2)=0恒有两个不相等的实数根。
四、?判断二次三项式能否在实数范围内因式分解。
例4、当m为何值时,关于x的二次三项式mx2-2(m+2)x+(m+5)能在实数范围内因式分解。
五、?判定二次三项式为完全平方式。
例5、若x2-2(k+1)x+k2+5是完全平方式,求k的值。
例6、当m为何值时,代数式(5m-1)x2-(5m+2)x+3m—2是完全平方式。
六、?利用判别式构造一元二次方程。
例7、已知:(z-x)2-4(x-y)(y-z)=0(x≠y)求证:2y=x+z七、?限制一元二次方程的根与系数关系的应用。
例8、已知关于x的方程x2-(k-1)x-3k-2=0的两个实数根的平方和为17,求k的值。
2024九年级数学下册提练第3招根的判别式的八种常见应用课件新版新人教版

(2)若一次函数 y=kx+b(k≠0)的图象与反比例函数 y=mx
(m≠0)b(k≠0)的图象与反比例函
数 y=mx (m≠0)的图象只有一个交点,
y=2x+12,
∴y=mx
只有一组解,
即2x2+12x-m=0有两个相等的实数根, ∴Δ=122-4×2×(-m)=0,∴m=-18. 把m=-18代入2x2+12x-m=0,求得该方程的解为 x1=x2=-3, 把x=-3代入y=2x+12,得y=6, ∴所求的交点坐标为(-3,6).
【解】△ABC是直角三角形.理由: ∵方程有两个相等的实数根, ∴(2b)2-4(a+c)(a-c)=0, ∴4b2-4a2+4c2=0,∴a2=b2+c2, ∴△ABC是直角三角形.
(3)如果△ABC是等边三角形,试求这个一元二次方程 的根. 【解】如果△ABC是等边三角形,那么a=b=c. 当a=b=c时,原方程可整理为2ax2+2ax=0. ∴x2+x=0.解得x1=0,x2=-1.
如图,过B作HF⊥x轴,过A作AH⊥HF于H,过E作 EF⊥HF于F,
则 AH=1,BH=2,EF=4,BF=4,HF=6,
∴S△ABE=S 梯形 AEFH-S△BEF-S△ABH= (AH+E2F)×HF-EF×2BF-AH×2BH= (1+24)×6-4×24-1×22=6,∴A,B 两点的坐标分别为 (1,4),(2,2),△ABE 的面积为 6.
(3)直线y=mx-3m绕点C旋转,直接写出当直线与反比例 函数的图象无交点时m的取值范围. 【解】由题意知 C(3,0), 令 mx-3m=4x,整理得 mx2-3mx-4=0, 令 Δ=9m2+16m<0,解得-196<m<0, ∴当直线与反比例函数的图象无交点时 m 的取值范围 为-196<m<0.
根的判别式及根与系数的关系

例 1 如果关于 x 的一元二次方程 kx2- 2k+1x+1=0 有 两个不相等的实数根,那么 k 的取值范围是( D )
A.k<12 B.k<12且 k≠0 C.-12≤k<12 D.-12≤k<12且 k≠0
k≠0, 解:由题意,得2(k+ -1≥2k0+,1)2-4k>0,解得-12≤k<12且 k ≠0,故选 D.点拨:本题考察了Δ>0 的同时,还考察了隐含 条件 k≠0 和 2k+1≥0
解:(1)将原方程整理为 x2+2(m-1)x+m2=0.∵原方程有两
个实根,∴Δ=[2(m-1)]2-4m2=-8m+4≥0,解得 m≤12 (2)∵x1,x2 为 x2+2(m-1)x+m2=0 的两个实数根,∴y=
x1+x2=-2m+2,且 m≤12,∵y 随 m 的增大而减小,∴当 m=12时,y 取得最小值 1
专题课堂(三) 根的判别式及根与系数的关系
根的判别式的应用 类型:(1)通过求b2-4ac的值,判断一元二次方程的根的情 况; (2)根据方程根的情况求出字母系数的取值范围. 注意:(1)应用根的判别式时要准确确定a,b,c的值; (2)此判别式只适用于一元二次方程,当无法判定方程是不 是一元二次方程时,应对方程进行分类讨论.
1.(2015·珠海)一元二次方程 x2+x+14=0 的根的情况是 ( B) A.有两个不相等的实数根 B.有两个相等的实数根 C.无实数根 D.无法确定根的情况 2.(2015·成都)关于 x 的一元二次方程 kx2+2x-1=0 有两 个不相等的实数根,则 k 的取值范围是( D ) A.k>-1 B.k≥-1 C.k≠0 D.k>-1 且 k≠0 3.(2015·黄冈)若方程 x2-2x-1=0 的两根分别为 x1,x2, 则 x1+x2-x1x2 的合应用 类型:(1)不解方程,求与方程的根有关的代数式的值; (2)已知方程一根,求方程的另一根; (3)与根的判别式进行综合应用. 例2 已知关于x的一元二次方程x2=2(1-m)x-m2的两个实 数根为x1,x2. (1)求m的取值范围; (2)设y=x1+x2,当y取得最小值时,求相应m的值,并求出 最小值.
根的判别式的应用

根的判别式的应用根的判别式内容:一元二次方程在一般形式下,即形如:ax2+bx+c=0(a、b、c为常数,a≠0),当Δ=b2﹣4ac>0时,方程有两个不相等的实数根;当Δ=b2﹣4ac=0时,方程有两个相等的实数根;当Δ=b2﹣4ac<0时,方程没有实数根.根的判别式的应用:一、判断方程根的情况例1:一元二次方程y2+2(y﹣1)=3y的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根解:y2+2(y﹣1)=3y,y2+2y﹣2=3y,y2﹣y﹣2=0,∵a=1,b=﹣1,c=﹣2,∴Δ=b2﹣4ac=(﹣1)2﹣4×1×(﹣2)=9>0,∴有两个不相等的实数根.故选:A.练习1:1.关于x的一元二次方程x2+mx﹣m﹣2=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.实数根的个数由m的值确定2.下列一元二次方程中,无实数根的是()A.x2﹣2x﹣3=0B.x2+3x+2=0C.x2﹣2x+1=0D.x2+2x+3=03.已知关于x的一元二次方程x2+bx﹣2=0,则下列关于该方程根的判断,正确的是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.实数根的个数与实数b的取值有关二、根据方程根的情况求字母的取值范围例2:如果关于x的一元二次方程ax2+2x﹣1=0有两个不相等的实数根,则a的取值范围是()A.a>﹣1B.a≥﹣1C.a≥﹣1且a≠0D.a>﹣1且a≠0解:∵关于x的一元二次方程ax2+2x﹣1=0有两个不相等的实数根,∴a≠0,Δ=22﹣4a×(﹣1)=4+4a>0,解得:a>﹣1且a≠0,故选:D.练习2:1.关于x的一元二次方程﹣kx2﹣6x+3=0有两个不相等的实数根,则k的取值范围是()A.k>﹣3B.k<3C.k<3且k≠0D.k>﹣3且k≠02.已知关于x的一元二次方程(m+1)x2﹣2x﹣1=0有实数根,则m的取值范围是()A.m≥﹣2 B.m≤﹣2 C.m≥﹣2且m≠﹣1 D.m≤﹣2且m≠﹣13.若实数a使关于x的一元二次方程(a+1)x2﹣3x+1=0有两个不相等的实数根,则实数a的取值范围是()A.a<B.a<且a≠﹣1C.a>D.a>且a≠﹣14.若一元二次方程kx2﹣4x﹣5=0有两个实数根,求k的取值范围.5.若关于x的一元二次方程(a﹣1)x2+2(a+1)x+a+5=0有实根,则实数a的取值范围是.6.已知关于x的方程mx2+(2m-1)x+m=0.(1)若方程有两个不相等的实数根,则m.(2)若方程有两个相等的实数根,则m.(3)若方程有两个实数根,则m.(4)若方程有实数根,则m.三、与新运算(定义)的综合例3:定义:如果一元二次方程ax2+bx+c=0(a≠0)“满足a+b+c=0”,那我们称这个方程为“蜻蜓”方程,已知关于x的方程ax2+bx+c=0(a≠0)是“蜻蜓”方程,且有两个相等的实数根,下列结论正确的是()A.a=c≠b B.a=b≠c C.b=c≠a D.a=b=c解:把x=1代入方程ax2+bx+c=0得出a+b+c=0,∴b=﹣a﹣c,∵方程有两个相等的实数根,∴Δ=b2﹣4ac=(﹣a﹣c)2﹣4ac=(a﹣c)2=0,∴a=c,∴a=c≠b,故选:A.练习3:1.定义比如,4⊗2=2,1⊗5=1.若实数k满足k[x2⊗(x+1)]﹣1=0,并且这个关于x的方程有两个不相等的实数解,则k的取值范围是.2.如果a2+b2=c2,那么把形如ax2+cx+b=0(a≠0)的方程称为“勾系方程”.(1)当a=3,b=4时,写出相应的“勾系方程”:;(2)求证:关于x的“勾系方程”ax2+cx+b=0(a≠0)必有实数根.3.定义新运算,对干任意实数m,n.都有m☆n=m2n+n.例如:﹣3☆2=(﹣3)2×2+2=20.若2☆a的值小于0.请判断方程:2x2﹣bx+a=0的根的情况.四、利用根的判别式判断三角形的形状例4:已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a,b,c分别为△ABC三边的长.(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;(3)如果△ABC是等边三角形,试求这个一元二次方程的根.解:(1)△ABC是等腰三角形;理由:把x=﹣1代入方程得a+c﹣2b+a﹣c=0,则a=b,所以△ABC为等腰三角形;(2)△ABC为直角三角形;理由:根据题意得Δ=(2b)2﹣4(a+c)(a﹣c)=0,即b2+c2=a2,所以△ABC为直角三角形;(3)∵△ABC为等边三角形,∴a=b=c,∴方程化为x2+x=0,解得x1=0,x2=﹣1.练习4:1.已知关于x的一元二次方程x2﹣(2k+4)x+k2+4k+3=0.(1)求证:不论k取何值,此一元二次方程总有两个不相等的实数根;(2)若此一元二次方程的两根是Rt△ABC两直角边AB、AC的长,斜边BC的长为10,求k的值.2.边长为整数的直角三角形若其两直角边长是方程x2﹣(k+2)x+4k=0的两根,求k的值并确定直角三角形三边之长.五、证明一元二次方程有(无)实数根例5:关于x的一元二次方程x2﹣mx+2m﹣4=0.(1)求证:方程总有两个实数根;(2)若方程有一个根为1,求m的值.(1)证明:x2﹣mx+2m﹣4=0,Δ=(﹣m)2﹣4×1×(2m﹣4)=m2﹣8m+16=(m﹣4)2,∵不论m为何值,(m﹣4)2≥0,∴Δ≥0,∴方程总有两个实数根;(2)解:把x=1代入关于x的一元二次方程x2﹣mx+2m﹣4=0,得1﹣m+2m﹣4=0.解得m=3.练习5:1.已知关于x的一元二次方程2mx2﹣(5m﹣1)x+3m﹣1=0.(1)求证:无论m为任意实数,方程总有实数根;(2)如果这个方程的根的判别式的值等于2,求m的值.2.已知关于x的方程x2﹣4mx+4m2﹣9=0.(1)求证:该方程有两个不相等的实数根;(2)若该方程有一个根﹣1,求m的值.3.已知关于x的方程x2+(a﹣2)x﹣a=0.(1)求证:不论a取何实数,该方程都有两个不相等的实数根;(2)若此方程两个实数根都是正实数,求a取值范围.4.已知一元二次方程﹣x2+(2a﹣2)x﹣a2+2a=0.(1)求证:方程有两个不等的实数根;(2)若方程只有一个实数根小于1,求a的取值范围.六、与韦达定理的结合运用例6:已知:x1,x2是关于x的方程x2+mx﹣m=0的两个实数根,x1,x2满足(x1﹣x2)2=5,且x1•x2<0.(1)求m的值.(2)不解方程,求3x1﹣x24.解:∵x1,x2是关于x的方程x2+mx﹣m=0的两个实数根,∴x1+x2=﹣m,x1x2=﹣m,∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=m2+4m,∴m2+4m=5,解得m1=1,m2=﹣5,如果m2=﹣5,那么x1x2=5>0,不合题意舍去,当m1=1时,满足Δ>0,且x1•x2<0,∴m=1;(2)当m=1时,原方程即为x2+x﹣1=0,∴x1+x2=﹣1,x1x2=﹣1,x12=1﹣x1,x22=1﹣x2,∴x12+x22=2﹣(x1+x2)=3,∴3x1﹣x24=3x1﹣(1﹣x2)2=3x1﹣1+2x2﹣x22=2x1+2x2﹣(1﹣x1+x22)=2(x1+x2)﹣(x12+x22)=﹣2﹣3=﹣5.练习6:1.已知关于x的方程x2+(2k﹣1)x+k2﹣1=0的两根为x1,x2,满足:x12+x22=16+x1x2,求实数k的值.2.已知关于x的一元二次方程(x﹣m)2+6x=4m﹣3有实数根.(1)求m的取值范围;(2)设方程的两实根分别为x1与x2若x1x2﹣x12﹣x22=﹣7,求m的值.3.已知x1,x2是关于x的一元二次方程x2﹣4x+m=0的两个实数根.(1)求m的取值范围;(2)若x1+x2﹣x1x2=1,计算m的值.4.已知关于x的一元二次方程(m﹣2)x2+(2m+1)x+m=0有两个实数根x1,x2.(1)求m的取值范围.(2)若|x1|=|x2|,求m的值及方程的根.。
根的判别式的六种常见应用 (共15张PPT)

1. 已知方程x2-2x-m=0没有实数根,其中m 是实数,试判断方程x2+2mx+m(m+1)=0 有无实数根. ∵x2-2x-m=0没有实数根, 解: ∴Δ1=(-2)2-4· (-m)=4+4m<0,即m<-1. 对于方程x2+2mx+m(m+1)=0, Δ2=(2m)2-4· m(m+1)=-4m>4, ∴方程x2+2mx+m(m+1)=0有两个不相等的
故当m为1时,▱ABCD是菱形. 1 2 此时原方程为x -x+ =0, 4 1 解得x1=x2= . 2 1 即菱形ABCD的边长为 . 2
(2)由题意知2是关于x的方程x2-mx+
的一个根,
1 m - =0 4 2
1 m ∴将x=2代入原方程得4-2m+ - =0, 4 2 5 5 2 解得m= ,故原方程为x - x+1=0, 2 2 1 1 解得x1=2,x2= . ∴AD= . 2 2 骣 1÷ 2+ ÷ 故▱ABCD的周长为2× ç =5. ç ÷ ç 桫 2
应用
6
利用根的判别式探求菱形条件
7.已知▱ABCD的两边AB,AD的长是关于x的方程 1 m 2 x -mx+ - =0的两个根. 4 2 (1)m为何值时,▱ABCD是菱形?并求出菱形的
边长. (2)若AB的长为2,求▱ABCD的周长是多少?
(1)由题意,得Δ=0, 解: 骣 m 1÷ 2 2-2m+1=0. ç - ÷ 即m -4 ç = m ç 桫 2 4÷ ∴m=1.
应用
4 利用根的判别式解与函数综合问题
5.y= k-1 x+1是关于x的一次函数,则关于x 的一元二次方程kx2+2x+1=0的根的情况为 ( A )
A.没有实数根
B.有一个实数根 C.有两个不相等的实数根 D.有两个相等的实数根
根的判别式的应用

情境导入鲁迅先生在《古小说钩沉》辑本中有一则《执竿入城》的寓言:“鲁有执长竿入城门者,初竖执之,不可入,横执之,亦不可入,计无所出,俄有老父至,曰:吾非圣人,但见事多矣,何不以锯中截而入?遂依而截入.”我国当代数学家许淳舫教授将寓言《执竿入城》编成了一道趣味数学题,收入《古算趣味》中:笨人持竿要进屋,无奈门框拦住竹;横多四尺竖多二,没法急得放声哭;有个自作聪明者,教他斜竹对两角;笨伯依言试一试,不多不少刚抵足;借问竿长多少数,谁人算得我佩服.同学们,你能根据诗中的内容列出方程吗?这个方程和我们之前学过的方程又有什么不同?重点难点根的判别式的应用河南刘振超自主学习课堂探究1.用根的判别式判定方程根的情况例A.有两个不相等的实数根B. 有两个相等的实数根B.没有实数根 D. 无法判断解题思路:先找出a,b,c的值,再计算根的判别式b2-4ac的值,由 与0的关系来判断方程根的情况.解:2.确定方程中字母的取值范围例2(2017•淄博)若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则实数k的取值范围是()A.k>-1 B.k>-1且k≠0 C.k<-1 D.k<-1或k=0解题思路:根据方程根的情况,得∆>0,从而建立关于k的不等式,解这个不等式,求得k的取值范围,然后再根据一元二次方程的定义可知k≠0,进而可知k的取值范围.解:3.判别三角形的形状例3关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.解题思路:根据方程根的情况,可得∆=0,从而建立关于a,b,c的等式,然后将等式进行变形,即可判断△ABC的形状.交流探索例4已知关于x的方程x2-(m+2)x+(2m-1)=0,试判断方程根的情况.解题思路:欲判断方程根的情况,需要准确找出a,b,c的值,然后计算b2-4ac,得出含m 的代数式,再将这个代数式用配方法化成(x-h)2+k的形式,即可判断出方程根的情况. 解:参考答案课堂探究:例1 B例2 B例3 解:∵方程有两个相等的实数根,∴∆=(2b)2-4(a+c)(a-c)=0,∴4b2-4a2+4c2=0,∴a2=b2+c2.∴△ABC是直角三角形.交流探索:解:例4 在方程x2-(m+2)x+(2m-1)=0中,∆=[-(m+2)]2-4(2m-1)=m2-4m+8=(m-2)2+4,∵(m-2)2≥0,∴(m-2)2+4>0.∴方程x2-(m+2)x+(2m-1)=0总有两个不相等的实数根.。
根的判别式的六种常见应用

根的判别式的六种常见应用方法指导:对于一元二次方程ax2+bx+c=0(a≠0),式子b2-4ac的值决定了一元二次方程的根的情况,利用根的判别式可以不解方程直接判断方程根的情况,反过来,利用方程根的情况可以确定方程中待定系数的值或取值范围.应用1:利用根的判别式判断一元二次方程根的情况1.已知方程x2-2x-m=0没有实数根,其中m是实数,试判断方程x2+2mx+m(m+1)=0有无实数根.2.已知关于x的方程x2+2mx+m2-1=0.(1)不解方程,判别方程根的情况;(2)若方程有一个根为3,求m的值.应用2:利用根的判别式求字母的值或取值范围3.已知关于x的一元二次方程mx2-(m+2)x+2=0,(1)证明:不论m为何值,方程总有实数根;(2)m为何整数时,方程有两个不相等的正整数根.应用3:利用根的判别式求代数式的值4.已知关于x的方程x2+(2m-1)x+4=0有两个相等的实数根,求m-1(2m-1)2+2m的值.应用4:利用根的判别式解与函数综合问题5.y =k -1x +1是关于x 的一次函数,则一元二次方程kx 2+2x +1=0的根的情况为( )A .没有实数根B .有一个实数根C .有两个不相等的实数根D .有两个相等的实数根应用5: 利用根的判别式确定三角形的形状6.已知a ,b ,c 是三角形的三边长,且关于x 的一元二次方程(a +c)x 2+bx +a -c 4=0有两个相等的实数根,试判断此三角形的形状.应用6: 利用根的判别式探求菱形条件7.已知▱ABCD 的两边AB ,AD 的长是关于x 的方程x 2-mx +m 2-14=0的两个根. (1)m 为何值时,▱ABCD 是菱形?并求出菱形的边长.(2)若AB 的长为2,求▱ABCD 的周长是多少?参考答案1.解:∵x 2-2x -m =0没有实数根,∴Δ1=(-2)2-4·(-m)=4+4m<0,即m<-1.对于方程x 2+2mx +m(m +1)=0,Δ2=(2m)2-4·m(m +1)=-4m>4,∴方程x 2+2mx +m(m +1)=0有两个不相等的实数根.2.解:(1)Δ=b 2-4ac =(2m)2-4×1×(m 2-1)=4m 2-4m 2+4=4>0, ∴方程有两个不相等的实数根.(2)将x =3代入方程中,得9+2m ×3+m 2-1=0,即m 2+6m +9=1,∴(m +3)2=1.∴m +3=±1. ∴m 1=-2,m 2=-4.3.(1)证明:Δ=[-(m +2)]2-8m =m 2-4m +4=(m -2)2.∵不论m 为何值,(m -2)2≥0,即Δ≥0.∴不论m 为何值,方程总有实数根.(2)解:解关于x 的一元二次方程mx 2-(m +2)x +2=0,得x =m +2±Δ2m =m +2±(m -2)2m. ∴x 1=2m,x 2=1. ∵方程的两个根都是正整数,∴2m是正整数,∴m =1或m =2. 又∵方程的两个根不相等,∴m ≠2,∴m =1.4.解:∵关于x 的方程x 2+(2m -1)x +4=0有两个相等的实数根, ∴Δ=(2m -1)2-4×1×4=0,即2m -1=±4.∴m =52或m =-32. 当m =52时,m -1(2m -1)2+2m =52-116+5=114; 当m =-32时,m -1(2m -1)2+2m =-32-116-3=-526.5.A 解析:∵y =k -1x +1是关于x 的一次函数, ∴k -1≠0.∴k -1>0,解得k>1.又一元二次方程kx 2+2x +1=0的判别式Δ=4-4k , ∴Δ<0.∴一元二次方程kx 2+2x +1=0无实数根,故选A .6.解:∵方程(a +c)x 2+bx +a -c 4=0有两个相等的实数根, ∴Δ=b 2-4(a +c)·a -c 4=b 2-(a 2-c 2)=0. 即b 2+c 2=a 2,∴此三角形是直角三角形.7.解:(1)∵▱ABCD 是菱形,∴AB =AD.∴Δ=0,即m 2-4⎝⎛⎭⎫m 2-14=m 2-2m +1=0,∴m =1.此时原方程为x 2-x +14=0, ∴x 1=x 2=12, ∴当m =1时,▱ABCD 是菱形,菱形ABCD 的边长为12. (2)∵AB =2,∴将x =2代入原方程得4-2m +m 2-14=0, 解得m =52, 故原方程为x 2-52x +1=0, 解得x 1=2,x 2=12,∴AD =12. 故▱ABCD 的周长为2×⎝⎛⎭⎫2+12=5.。
根的判别式的应用课件

判别式的未来发展
随着数学和其他学科的发展,判别式的研究和应用将更 加深入和广泛,未来可能会发现更多判别式的应用场景 。
THANKS
感谢观看
1. 当 $\Delta > 0$ 时,函数图像与 x 轴有两个交点;
案例三:利用判别式绘制二次函数的图像
2. 当 $\Delta = 0$ 时,函 口方向,我们可以绘 制出函数的图像。
3. 当 $\Delta < 0$ 时,函数图像与 x 轴 没有交点。
详细描述
如果一个二次方程的两个根相等,那么这两 个根就具有对称性。此外,如果一个二次方 程的两个根互为相反数,那么这两个根也具 有对称性。这种对称性可以用于解决一些数 学问题,例如找到函数图像的对称轴等。
根与函数的零点
总结词
函数的零点与二次方程的根具有密切关系, 通过观察函数的零点可以获得二次方程的信 息。
详细描述:对于一元 二次方程 $ax^2 + bx + c = 0$,判别式 $\Delta = b^2 4ac$。根据 $\Delta$ 的值,我们可以判断 方程实数根的个数
1. 当 $\Delta > 0$ 时,方程有两个不同 的实数根;
2. 当 $\Delta = 0$ 时,方程有两个相同 的实数根;
一元二次不等式的解法
总结词
利用判别式可以快速求解一元二次不等式,进而求出其整数解。
详细描述
对于一元二次不等式ax^2 + bx + c > 0(a≠0),可以利用判别式将其转化为几个一次不等式组,从而求解其 整数解。
二次函数图像的绘制
总结词
通过判别式可以判断二次函数的图像是开口向上还是向下,以及与x轴有无交点。
(完整版)一元二次方程根的判别式知识点
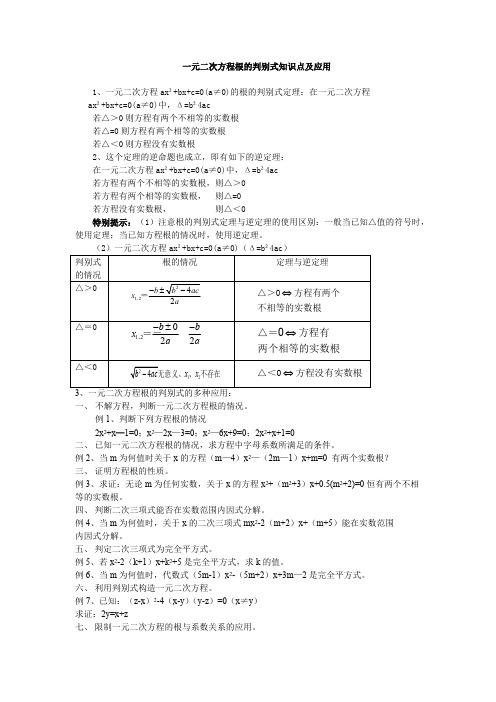
一元二次方程根的判别式知识点及应用1、一元二次方程ax²+bx+c=0(a≠0)的根的判别式定理:在一元二次方程ax²+bx+c=0(a≠0)中,Δ=b²4ac若△>0则方程有两个不相等的实数根若△=0则方程有两个相等的实数根若△<0则方程没有实数根2、这个定理的逆命题也成立,即有如下的逆定理:在一元二次方程ax²+bx+c=0(a≠0)中,Δ=b²4ac若方程有两个不相等的实数根,则△>0若方程有两个相等的实数根,则△=0若方程没有实数根,则△<0特别提示:(1)注意根的判别式定理与逆定理的使用区别:一般当已知△值的符号时,使用定理;当已知方程根的情况时,使用逆定理。
(2)一元二次方程ax²+bx+c=0(a≠0)(Δ=b²4ac)一、不解方程,判断一元二次方程根的情况。
例1、判断下列方程根的情况2x2+x━1=0;x2—2x—3=0;x2—6x+9=0;2x2+x+1=0二、已知一元二次方程根的情况,求方程中字母系数所满足的条件。
例2、当m为何值时关于x的方程(m—4)x2—(2m—1)x+m=0 有两个实数根?三、证明方程根的性质。
例3、求证:无论m为任何实数,关于x的方程x2+(m2+3)x+0.5(m2+2)=0恒有两个不相等的实数根。
四、判断二次三项式能否在实数范围内因式分解。
例4、当m为何值时,关于x的二次三项式mx2-2(m+2)x+(m+5)能在实数范围内因式分解。
五、判定二次三项式为完全平方式。
例5、若x2-2(k+1)x+k2+5是完全平方式,求k的值。
例6、当m为何值时,代数式(5m-1)x2-(5m+2)x+3m—2是完全平方式。
六、利用判别式构造一元二次方程。
例7、已知:(z-x)2-4(x-y)(y-z)=0(x≠y)求证:2y=x+z七、限制一元二次方程的根与系数关系的应用。
例8、已知关于x的方程x2-(k-1)x-3k-2=0的两个实数根的平方和为17,求k的值。
第5课 一元二次方程根的判别式

第5课 一元二次方程根的判别式【预习参考】《校本教材》七年级(下)P28——P34【学习目标】1.灵活应用△的值判断一元二次方程根的情况;2.能根据一元二次程根的情况反解字母系数的取值。
【学习重点】一元二次方程根的判别式及其应用.【知识储备】1. 一元二次方程ax 2+bx+c=0的求根公式为:x =,其中△= 。
2. 对于字母m ,当m >0时,它有 个平方根,它们互为 ,用符号表示为: ; 当m =0时,它的平方根为 ; 当m <0时,它 平方根.【学习过程】第一环节 自主做学——见龙在田一.基础训练1. 一元二次方程:230x x +-=中,a 为 ,b 为 ,c 为 ,△= 。
2. 一元二次方程250y -=中,a 为 ,b 为 ,c 为 ,△= 。
3. 一元二次方程2315x x x -=-中,a 为 ,b 为 ,c 为 ,△= 。
二.解读教材问题1:ax 2+bx+c=0的判别式与根的情况 222404040b ac b ac b ac ⎧∆=-〉⇔⎪∆=-=⇔⎨⎪∆=-〈⇔⎩时方程有两个不相等的实数根时方程有两个相等的实数根时方程没有实数根即时训练:不解方程,利用判别式判断下列一元二次方程根的情况:(1)22340x x +-= (2)216924y y +=(3)25(1)70x x +-= (4)25x +=归纳总结:对于一元二次方程20ax bx c ++=(0a ≠)①利用判别式判断一元二次方程根的情况首先应将一元二次方程化为一般式;再利用法则判断; ②技巧:观察:当a 、c 异号时,△一定大于零,即方程一定有两个不相等实数根. 第二环节 合作探究——腾龙在天三.挖掘教材问题1: 求证:不论m 取何值时,关于x 的方程2(3)1x m x --=一定有两个不相等的实数根归纳总结:此类证明题的一般步骤:(1)计算24b ac -;(2)利用配方将24b ac -变形成非负数的和的形式;(3)说理,即说明△的符号;(4)得出所要求证的结论.问题2:已知一元二次方程2410kx x -+=(1)k 为何值时,方程有两个实数根?(2)k 为何值时,方程有实数根?(3)k 为何值时,该方程没有实数根?归纳小结:此类方程中,二次项的系数含有字母,因而要注意在求解过程中需同时满足⎧⎨∆⎩二次项系数不等于零的取值范围即时训练:当k 取什么值时,关于x 的一元二次方程2(21)10kx k x k +++-=有实数根第三环节 总结反思——亢龙有悟四.反思小结1.一元二次方程的根的判别式有三种情况:① ② ③2.对于含字母系数的一元二次方程,应用判别式解决有关问题时,应注意:①常用数学方法:配方法,转化成非负数的数学模型;②问题的完整性:即 .【达标练习】1.一般地,对于一元二次方程ax 2+bx +c =0(a ≠0)(1)当b 2-4ac ≥0时,它的根的情况是 ;(2)当b 2-4ac <0时,它的根的情况是 .2.关于x 方程ax 2+bx +c =0(a ≠0)有两个相等的实数根,则____ _ ___,•若有两个不相等的实数根,则______ ___,若方程无实数解,则__ __ ________.3.若方程3x 2+bx +1=0无实数解,则b 应满足的条件是__ ______.4.不解方程,判定2x 2-3=4x 的根的情况是 .5.不解方程,判断所给方程:①x 2+3x +7=0;②x 2+4=0;③x 2+x -1=0中,有实数根的方程有( )A .0个B .1个C .2个D .3个6.已知k ≠1,一元二次方程(k -1)x 2+kx +1=0有根,求k 的取值范围。
根的判别式的十种常见应用(专题)

第3讲:根的判别式的十种常见应用--专题二 类型一:不解一元二次方程,判别根的情况(1)04322=+-x x (2))0(02≠=-a bx ax练1. 不解方程,判断下列一元二次方程的根的情况.(1)0)1(422=-+-k kx x (2))0(02≠=+a bx ax (3))0(02≠=+a c ax类型二:根据方程根的情况,确定字母的值或取值范围k 为何值时,关于x 的方程0542=-+-k x x(1)有两个不相等的实数根(2)有两个相等的实数根(3)没有实数根练2. 证明:不论m 取何值时,关于x 的方程2)2)(1(m x x =--总有两个不相等的实数根类型三:证明系数为字母的一元二次方程没有实数根求证:关于x 的方程0)4(2)1(222=++-+m mx x m 没有实数根。
练3. 若关于x 的一元二次方程022=-+k x x 没有实数根,则k 的取值范围是?类型四:应用根的判别式判断三角形的形状已知三角形的两边AB ,AC 的长是关于x 的一元二次方023)32(22=++++-k k x k x 的两个实数根,第三边长为5.(1)当k 为何值时,三角形ABC 是以BC 为斜边的直角三角形?(2)当k 为何值时,三角形ABC 是等腰三角形?并求三角形ABC 的周长。
练4. 已知c b a ,,,是三角形的三条边长,且关于x 的方程0)()(2)(2=-+-+-b a x a b x b c ,有两个相等的实数根,试判断三角形的形状?类型五:判断当字母为何值时,二次三项式为完全平方式(1)若关于a 的二次三项式25162++ka a 是一个完全平方式,求k 的值;(2)若关于a 的二次三项式142++a ka 是一个完全平方式,求k 的值。
练5. 若关于x 的二次三项式322-+-a ax x 是一个完全平方式,则a 的值为多少?类型六:判断抛物线与直线的交点情况当m 取何值时,抛物线122-++=m x x y 与直线m x y 2+=只有一个交点?练6. 已知抛物线22x y =,直线b kx y +=经过点(2,6)。
一元二次方程根的判别式的六种常见应用

一元二次方程根的判别式的六种常见应用应用1:利用根的判别式判断一元二次方程根的情况已知方程x 2-2x -m =0没有实数根,其中m 是实数,试判断方程x 2+2mx +m (m +1)=0有无实数根.解:∵x 2-2x -m =0没有实数根,∴Δ1=(-2)2-4·(-m )=4+4m <0,即m <-1.对于方程x 2+2mx +m (m +1)=0,Δ2=(2m )2-4·m (m +1)=-4m >4,∴方程x 2+2mx +m (m +1)=0有两个不相等的实数根.同类变式2.已知关于x 的方程x 2+2mx +m 2-1=0.(1)不解方程,判别方程根的情况;(2)若方程有一个根为3,求m 的值.应用2:利用根的判别式求字母的值或取值范围3.已知关于x 的一元二次方程mx 2-(m +2)x +2=0,(1)证明:不论m 为何值,方程总有实数根;(2)m 为何整数时,方程有两个不相等的正整数根.证明:(1)Δ=[-(m +2)]2-8m=m 2-4m +4=(m -2)2.∵(m -2)2≥0,即Δ≥0.∴不论m 为何值,方程总有实数根.(2)解关于x 的一元二次方程mx 2-(m +2)x +2=0, 得 ∴x 1=2/m ,x 2= 1. ∵方程的两个根都是正整数, ∴ 是正整数,∴m =1或m =2. 又∵方程的两个根不相等, ∴m≠2,∴m =1.应用3:利用根的判别式求代数式的值4.已知关于x 的方程x 2+(2m -1)x +4=0有两个相等的实数根,求 的值. 解:∵关于x 的方程x 2+(2m -1)x +4=0有两个相等的实数根,∴Δ=(2m -1)2-4×1×4=0,即2m -1=±4. ∴m =5/2 或m =-3/2. 当m =5/2时, 当m =--3/2时, 应用4:利用根的判别式解与函数综合问题5.y x +1是关于x 的一次函数,则关于x 的一元二次方程kx 2+2x +1=0的根的情况为222.22m m m x m m 21(21)2m x m 251112;(21)216514m m m 231152.(21)216326m m m()A.没有实数根B.有一个实数根C.有两个不相等的实数根D.有两个相等的实数根∵y=x+1是关于x的一次函数,∴,∴k-1>0,解得k>1,又关于x的一元二次方程kx2+2x+1=0的判别式Δ=4-4k ,∴Δ<0,∴关于x的一元二次方程kx2+2x+1=0无实数根,故选A.应用5:利用根的判别式确定三角形的形状6.已知a,b,c是三角形的三边长,且关于x的一元二次方程(a+c)x2+bx+=0有两个相等的实数根,试判断此三角形的形状.解:∵方程(a+c)x2+bx+=0有两个相等的实数根,∴Δ=b2-4(a+c)·=b2-(a2-c2)=0.∴b2+c2=a2.∴此三角形是直角三角形.应用6:利用根的判别式探求菱形条件7.已知▱ABCD的两边AB,AD的长是关于x的方程x2-mx+-=0的两个根.(1)m为何值时,▱ABCD是菱形?并求出菱形的边长.(2)若AB的长为2,求▱ABCD的周长是多少?(1)由题意,得Δ=0,解:即m2-4 =m2-2m+1=0.∴m=1.故当m为1时,▱ABCD是菱形.此时原方程为x2-x+=0,解得x1=x2=.即菱形ABCD的边长为.4a c-4a c-4a c-2m14124m141212(2)由题意知2是关于x 的方程x 2-mx + - =0的一个根, ∴将x =2代入原方程得4-2m + - =0, 解得m = ,故原方程为x 2- x +1=0, 解得x 1=2,x 2= . ∴AD = . 故▱ABCD 的周长为2× = 5. 2m 142m 1452521212122。
考点03 配方法、根的判别式以及根与系数关系的9考点归类-解析版 2023-2024学年九年级数学考

考点03 配方法、根的判别式以及根与系数关系的9考点归类1,配方法的应用的方法技巧(1)比较大小:配方法不但可以解一元二次方程,而且能求代数式的最值,还能用于比较代数式的大小.用配方法比较代数式的大小,主要是用作差法将代数式作差后得到的新代数式配方,根据新代数式与0的关系确定代数式的大小(2)求最值:用配方法求代数式的最值是将代数式配方为完全平方式与常数的和的形式,根据完全平方式的非负性确定代数式的最值;(3)未知系数的取值:配方法在求值中的应用,将原等式右边变为0,左边配成完全平方式后,再运用非负数的性质求出待定字母的取值.(4)用配方法构造“非负数之和”解决问题:通过配完全平方式,利用“非负性”解决问题。
2,根的判别式的应用的方法【技巧】根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:①当△>0时,方程有两个不相等的实数根;②当△=0时,方程有两个相等的实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.(1)判断根的情况:式子b2-4ac叫做方程ax2+bx+c=0(a≠0)根的判别式,通常用希腊字母△表示它,即△=b2-4ac.(2)求字母的值或取值范围:根据判别式,确定与0的关系,直接代入解不等式即可。
(3)与三角形结合:一般会把根与三角形的边进行结合考察,考虑到三角形的三边关系能否构成三角形即可,有时候还会与等腰三角形结合。
(4)与一次函数结合:通过一次函数与方程和不等式的关系,观察图像即可。
3,根与系数的关系方法根与系数的关系:若x1,x2是一元二次方程ax²+bx+c=0(a≠0)的两根时,x1+x2=-ba ,x1x2=ca.考点1比较大小考点2求最值考点3未知系数的取值考点4用配方法构造“非负数之和”解决问题考点5判断根的情况考点6求字母的值或取值范围考点7与三角形结合考点8与一次函数结合考点9 根与系数的关系求变形式子考点1 利用配方法比较大小【详解】(1)224622x x x -+=-+(),所以当2x =时,代数式246x x -+有最小值,这个最值为2,故答案为:2-;2;2;小;2;(2)2123x x ---()222x x =-+2110x =-+()>则2123x x -->.【点睛】本题考查的是配方法的应用,掌握配方法的一般步骤是解题的关键,注意偶次方的非负性的应用.2.(2022秋·七年级单元测试)我们知道20a ≥,所以代数式2a 的最小值为0.学习了多项式乘法中的完全平方公式,可以逆用公式,即用()2222a ab b a b ±+=±来求一些多项式的最小值.例如,求263x x ++的最小值问题.解:∵()2226369636x x x x x ++=++-=+-,又∵()230x +≥,∴()2366x +-≥-,∴263x x ++的最小值为6-.请应用上述思想方法,解决下列问题:(1)探究:()2245____________x x x -+=+;(2)求224x x +的最小值.(3)比较代数式:21x -与23x -的大小.【答案】(1)2-,1(2)2-(3)21>23x x --【分析】(1)根据完全平方式的特征求解.(2)先配方,再求最值.(3)作差后配方比较大小即可.【详解】(1)解:22245441(2)1x x x x x -+=-++=-+.(2)222242(211)2(1)2x x x x x +=++-=+-,故答案为:2,2-(2)解:221612611x x x x --+=-+2692x x =-++()232x =-+()30,x -³Q()23220,x \-+³>21612.x x \->-(3)解:()222323x x x x -++=--+()22113x x =--+-+()214x =--+ ()210,x --£Q ()2144,x \--+£ ∴223x x -++的最大值为4.【点睛】本题考查的是配方法的应用,掌握“配方法的步骤与非负数的性质”是解本题的关键.考点2利用配方法求最值【分析】(1)根据完全平方式的特征求解;(2)先配方,再求最值;(3)作差后配方比较大小.【详解】(1)解:()2224644222x x x x x +=-++=-+-故当20x -=,即2x =时,代数式246x x -+最小值为2;(2)∵224250x x y y -+++=,则2244210x x y y -++++=,∴()()22210x y -++=,即20x -=,10y +=,∴2x =,1y =-,∴211x y +=-=;(3)()()2221232211x x x x x ---=-+=-+,∵()210x -≥,∴()2110x -+>,∴2123x x ->-.【点睛】本题考查配方法的应用,正确配方,充分利用平方的非负性是求解本题的关键.7.(2023春·陕西咸阳·八年级统考期末)把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.如:①用配方法分解因式: ²43a a ++.解:原式:²441(2)²1(21)(21)(3)(1)a a a a a a a =++-=+-=+++-=++②2246M a a =-+, 利用配方法求M 的最小值.解:2²462(²21)622(1)²4M a a a a a =-+=-++-=-+222(1)02(1)44a a -≥∴-+≥,,∴当1a =时,M 有最小值4.请根据上述材料解决下列问题:(1)用配方法因式分解²412x x --;(2)若 2441M x x =+-, 求M 的最小值.【答案】(1)(6)(2)x x -+考点3 利用配方法未知系数的取值∴2a =,1b =,∴1a b -=,故选A .【点睛】本题考查了解一元二次方程的方法—配方法,熟练一元二次方程的解法是解题的关键.10.(2023春·山东威海·八年级统考期末)用配方法解方程2610x x --=,若配方后结果为2()x m n -=,则n 的值为( )A .10-B .10C .3-D .9【答案】B【分析】利用配方法将方程2610x x --=配成2()x m n -=,然后求出n 的值即可.【详解】∵2610x x --=,∴261x x -=,∴26919x x -+=+,即2(3)10x -=, 10n ∴=.故选:B .【点睛】本题主要考查了利用配方法解一元二次方程,熟练掌握配方法的步骤是解题的关键.11.(2023秋·全国·九年级专题练习)用配方法解一元二次方程2630x x ++=时,将它化为2()x m n +=的形式,则m n -的值为( )A .6-B .3-C .0D .2【答案】B【分析】由2630x x ++=,配方可得()236x +=,进而可得m n ,的值,然后代入m n -,计算求解即可.【详解】解:∵2630x x ++=,∴2696x x ++=,∴()236x +=,∴3m =,6n =,∴3m n -=-,故选:B .【点睛】本题考查了配方法解一元二次方程,代数式求值.解题的关键在于正确的配方求出m n ,的值.考点4 用配方法构造“非负数之和”解决问题∵三角形的三条边为a,b,c,∴b-a<c<b+a,∴3<c<13.又∵这个三角形的最大边为c,∴8<c<13.故选:C.【点睛】本题考查了配方法在三角形的三边关系中的应用,熟练掌握配方法、偶次方的非负性及三角形的三边关系是解题的关键.14.(2023春·浙江·七年级专题练习)已知2248200++-+=,那么y x=()x y x yA.-16B.16C.-8D.8【答案】B【分析】利用配方法把已知条件变形为(x+2)2+(y-4)2=0,再根据非负数的性质得x+2=0,y-4=0,即可求出x与y的值,进一步代入求得答案即可.【详解】∵x2+4x+y2-8y+20=0,∴x2+4x+4+y2-8y+16=0,∴(x+2)2+(y-4)2=0,∴x+2=0,y-4=0,∴x=-2,y=4,∴x y=16.故选B.【点睛】此题考查配方法的应用,非负数的性质,掌握完全平方公式是解决问题的关键.15.(2023春·山东淄博·八年级统考期中)不论x、y为什么实数,代数式x2+y2+2x-4y+9的值()A.总不小于4B.总不小于9C.可为任何实数D.可能为负数【答案】A【分析】要把代数式x2+y2+2x-4y+9进行拆分重组凑完全平方式,来判断其值的范围即可.【详解】x2+y2+2x-4y+9=(x2+2x+1)+(y2-4y+4)+4=(x+1)2+(y-2)2+4,∵(x+1)2≥0,(y-2)2≥0,∴(x+1)2+(y-2)2+4≥4,考点5 利用根的判别式判断根的情况根.20.(2023·全国·九年级假期作业)若1x =是一元二次方程220(0)ax bx a -+=≠的一个根,那么方程220ax bx ++=的根的情况是( )A .有两个不相等的实数根B .有一个根是=1x -C .没有实数根D .有两个相等的实数根【答案】B【分析】先将1x =代入220(0)ax bx a -+=≠中得到20a b -+=,再根据一元二次方程根的判别式进行求解即可得出结论.【详解】解:∵1x =是一元二次方程220(0)ax bx a -+=≠的一个根,∴20a b -+=,即2b a =+,对于方程220ax bx ++=,∵242b a ∆=-⨯()228a a =+-()220a =-≥,∴方程220ax bx ++=有两个实数根,故选项A 、C 、D 错误,不符合题意;当=1x -时,2220ax bx a b ++=-+= ,即=1x -是方程220ax bx ++=的一个根,故选项B 正确,符合题意,故选:B .【点睛】本题考查了一元二次方程的解和根的判别式,解答的关键是理解一元二次方程的解的意义,掌握一元二次方程20ax bx c ++=根的情况与根的判别式24b ac ∆=-的关系:当0∆>时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程没有实数根.考点6 利用根的判别式求字母的值或取值范围故选:A .【点睛】本题考查了根的判别式:一元二次方程200ax bx c a ++=≠()的根与24b ac ∆=-有如下关系:当0∆>时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当0∆<时,方程无实数根.24.(2023春·吉林长春·八年级长春外国语学校校考期末)已知关于x 的一元二次方程()21210k x x --+=有两个实数根,则k 的取值范围是( )A .21k k ≤-≠且B .21k k ≤≠且C .21k k ≥-≠且D .2k ≥【答案】B【分析】根据方程有两个实数根,得出0∆≥且10k -≠,求出k 的取值范围,即可得出答案.【详解】解:由题意知,24441840b ac k k ∆=-=--=-≥(),且10k -≠,解得:2k ≤,且1k ≠,则k 的取值范围是2k ≤,且1k ≠,故选:B .【点睛】此题考查了根的判别式,(1)一元二次方程根的情况与判别式∆的关系:①0∆>⇔方程有两个不相等的实数根;②0∆=⇔方程有两个相等的实数根;③0∆⇔<方程没有实数根.(2)一元二次方程的二次项系数不为0.考点7 利用根的判别式与三角形结合【详解】(1)证明:2(2)42k k∆=+-⨯2448k k k=++-2(2)0k =-≥所以此方程总有实根.(2)解:①若b c =,则此方程有两个相等实根此时20k -=,则2k =,原方程为:2440x x -+=,122x x ==,∴另外两边长为2和2,②若a c =,则1a =是方程2(2)20x k x k -++=的根,∴21(2)20k k -++=,∴1k =,原方程为2320x x -+=,解得:11x =,22x =,而1、1、2为边不能构成三角形.所以,三角形另外两边长为2,2.【点睛】本题考查了一元二次方程根的判别式、解一元二次方程、等腰三角形存在性、三角形三边关系等知识点,熟练掌握相关知识点是解决本题的关键.26.(2023春·广东河源·九年级校考开学考试)若方程(c 2+a 2)x +2(b 2-c 2)x +c 2-b 2=0有两个相等的实数根,且a ,b ,c 是三角形ABC 的三边,证明此三角形是等腰三角形.【答案】见解析【分析】先根据方程有两个相等的实数根得出△=0,再得出b 、c 的关系即可.【详解】解:Δ=[2(b 2-c 2)]2-4(c 2+a 2)(c 2-b 2)=4(b 2-c 2)(b 2-c 2+a 2+c 2)=4(b+c )(b-c )(b 2+a 2).∵方程有两个相等实根.∴Δ= 0,即4(b+c )(b-c )(b 2+a 2)=0.∵a ,b ,c 是三角形的三边,∴b+c≠0,a 2+b 2≠0,只有b-c=0,解得b=c .出判别式的值的情况,从而得到关于a、b、c及k的等式是解题的关键.28.(2011秋·江苏无锡·九年级统考期中)已知关于x的方程22a x bx c x-+++=有两个相等的实数(1)2(1)0根,试证明以a、b、c为三边的三角形是直角三角形.【答案】【详解】考点:根的判别式;勾股定理的逆定理.分析:先把方程变为一般式:(c-a)x2+2bx+a+c=0,由方程有两个相等的实数根,得到△=0,即△=(2b)2-4(c-a)(a+c)=4(b2+c2-a2)=0,则有b2+c2-a2=0,即b2+c2=a2,根据勾股定理的逆定理可以证明以a、b、c 为三边的三角形是直角三角形.解答:证明:a(1-x2)+2bx+c(1+x2)=0去括号,整理为一般形式为:(c-a)x2+2bx+a+c=0,∵关于x的一元二次方程a(1-x2)+2bx+c(1+x2)=0有两个相等的实数根.∴△=0,即△=△=(2b)2-4(c-a)(a+c)=4(b2+c2-a2)=0,∴b2+c2-a2=0,即b2+c2=a2.∴以a、b、c为三边的三角形是直角三角形.点评:本题考查了一元二次方程的根的判别式和勾股定理的逆定理等知识.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.考点8 利用根的判别式与一次函数结合【分析】根据一元二次方程2210mx x --=无实数根得0m ≠且2(2)4(1)0m ∆=--⨯-<,即可得1m <-,又∵20b =>,可得一次函数2y mx =+的图象经过一、二、四象限,即可得.【详解】解:∵一元二次方程2210mx x --=无实数根,∴0m ≠且2(2)4(1)0m ∆=--⨯-<,440m +<,44m <-,1m <-,又∵20b =>,∴一次函数2y mx =+的图象经过一、二、四象限,∴一次函数2y mx =+的图象不经过第三象限,故选:C .【点睛】本题考查了一元二次方程的根的判别式,一次函数的图像性质,解题的关键是理解题意,掌握这些知识点.30.(2023·广东汕头·广东省汕头市聿怀初级中学校考三模)一元二次方程2240x x --=有两个实数根a ,b ,那么一次函数(1)y ab x a b =-++的图象一定不经过的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】D【分析】根据根与系数的关系即可求出ab 与a b +的值,然后根据一次函数的图象与性质即可求出答案.【详解】解:由根与系数的关系可知:2a b +=,4ab =-,∴15ab -=∴一次函数解析式为:52y x =+,故一次函数的图象一定不经过第四象限.故选:D .【点睛】本题考查了一元二次方程,解题的关键是熟练运用根与系数的关系以及一次函数的图象与性质.31.(2020秋·贵州贵阳·九年级校考阶段练习)若关于x 的一元二次方程2210x x kb ++=-没有实数根,则一次函数y kx b =+的大致图象可能是( )A .B .C .D .【答案】A【分析】首先根据一元二次方程没有实数根确定k ,b 的取值范围,然后根据一次函数的性质确定其图象的位置.【详解】解:∵方程2210x x kb ++=-没有实数根,∴()4410kb ∆=-+<,解得:0kb >,即k b 、同号,当00k b >>,时,一次函数y kx b =+的图象过一,二,三象限,当00k b <<,时,一次函数y kx b =+的图象过二,三,四象限,故选:A .【点睛】本题考查了根的判别式及一次函数的图象的问题,解题的关键是根据一元二次方程的根的判别式确定k ,b 的取值范围,难度不大.32.(2023·安徽合肥·统考二模)关于x 的一元二次方程2210mx x --=无实数根,则一次函数y mx m =-的图像不经过( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】C【分析】根据一元二次方程根与判别式的关系,求得m 的取值范围,再根据一次函数的图象与系数的关系求解即可.【详解】解:∵一元二次方程2210mx x --=无实数根∴224(2)4(1)0b ac m ∆=-=--⨯⨯-<,解得1m <-,由一次函数y mx m =-可得0k m =<,0b m =->,∴一次函数y mx m =-过一、二、四象限,不过第三象限,故选:C【点睛】此题考查了一元二次方程根与判别式的关系,以及一次函数图象与系数的关系,解题的关键是熟练掌握相关基础知识.考点9 利用根与系数的关系求变形式子。
专题训练(二) 根的判别式的三种应用

专题训练(二)根的判别式的三种应用►应用一应用一元二次方程的根的判别式判断方程根的情况1.2017·锦州关于x的一元二次方程x2+4kx-1=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法判断2.已知a,b,c分别是三角形的三边长,则方程(a+b)x2+2cx+(a+b)=0的根的情况是()A.没有实数根B.可能有且只有一个实数根C.有两个相等的实数根D.有两个不相等的实数根3.2018·福建已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是()A.1一定不是关于x的方程x2+bx+a=0的根B.0一定不是关于x的方程x2+bx+a=0的根C.1和-1都是关于x的方程x2+bx+a=0的根D.1和-1不都是关于x的方程x2+bx+a=0的根►应用二根据一元二次方程根的情况求字母系数的取值范围4.2017·齐齐哈尔 若关于x 的方程kx 2-3x -94=0有实数根,则实数k 的取值范围是( )A .k =0B .k ≥-1且k ≠0C .k ≥-1D .k >-15.如果关于x 的一元二次方程kx 2-2k +1x +1=0有两个不相等的实数根,那么k 的取值范围是( )A .k <12B .k <12且k ≠0C .-12≤k <12D .-12≤k <12且k ≠0 6.2017·营口 若关于x 的一元二次方程(k -1)x 2+2x -2=0有两个不相等的实数根,则k 的取值范围是__________.7.2017·岳阳 在△ABC 中,BC =2,AB =2 3,AC =b ,且关于x 的方程x 2-4x +b =0有两个相等的实数根,则AC 边上的中线长为________.8.关于x 的一元二次方程x 2-x +p -1=0有两个实数根x 1,x 2.(1)求p 的取值范围;(2)若[2+x 1(1-x 1)][2+x 2(1-x 2)]=9,求p 的值.► 应用三 证明一元二次方程根的情况9.已知关于x 的一元二次方程(x -1)(x -4)=p 2,p 为实数.(1)求证:方程有两个不相等的实数根;(2)p为何值时,方程有整数解?(直接写出三个,不需要说明理由)10.已知关于x的一元二次方程x2-(k+3)x+3k=0.(1)求证:不论k取何实数,该方程总有实数根;(2)若等腰三角形ABC的一边长为2,另两边长恰好是方程的两个根,求△ABC的周长.详解详析1.A [解析] 在方程x 2+4kx -1=0中,Δ=b 2-4ac =(4k )2-4×1×(-1)=16k 2+4. ∵16k 2+4>0,∴方程x 2+4kx -1=0有两个不相等的实数根.故选A.2.A [解析] Δ=(2c )2-4(a +b )2=4(c -a -b )(c +a +b ).∵a ,b ,c 分别是三角形的三边长,∴c -a -b <0,c +a +b >0,∴Δ<0,∴原方程没有实数根.故选A.3.D [解析] 依题意,得4b 2-4(a +1)2=0.由此得b =±(a +1).于是方程x 2+bx +a =0化为x 2±(a +1)x +a =0.(1)1是方程x 2-(a +1)x +a =0的根,可见选项A 错误;(2)a =0,b =1时是选项B 的一个特例,此时0是方程x 2+bx +a =0的根,可知选项B 错误;(3)1是方程x 2-(a +1)x +a =0的根,但-1不是;-1是方程x 2+(a +1)x +a =0的根,但1不是.因此±1不可能同时是方程x 2+bx +a =0的根,可见选项C 错误;(4)由(3)的理由可知选项D 正确.故选D.4.C [解析] 关于x 的方程kx 2-3x -94=0有实数根,分两种情况求解: (1)若k ≠0,则Δ=b 2-4ac =(-3)2-4k ·(-94)=9+9k ≥0,∴k ≥-1且k ≠0. (2)若k =0,则原方程可化为-3x -94=0,此时方程有解,∴k =0符合要求. 综上所述,k ≥-1.5.D [解析] k 需满足⎩⎪⎨⎪⎧k ≠0,2k +1≥0,Δ>0.由此求得-12≤k <12且k ≠0.故选D.6.[答案] k >12且k ≠1 [解析] 根据题意得k -1≠0且Δ=22-4(k -1)×(-2)>0.解得k >12且k ≠1. 7.[答案] 2[解析] 因为关于x 的方程x 2-4x +b =0有两个相等的实数根,所以Δ=b 2-4ac =(-4)2-4b =16-4b =0,得AC =b =4.因为BC =2,AB =2 3,所以BC 2+AB 2=AC 2,所以△ABC 为直角三角形,AC 为斜边,则AC 边上的中线长为斜边的一半,为2.8.解:(1)由题意,得Δ=(-1)2-4(p -1)≥0.解得p ≤54. (2)由[2+x 1(1-x 1)][2+x 2(1-x 2)]=9,得(2+x 1-x 12)(2+x 2-x 22)=9.∵x 1,x 2是方程x 2-x +p -1=0的两个实数根,∴x 12-x 1+p -1=0,x 22-x 2+p -1=0.∴x 1-x 12=p -1,x 2-x 22=p -1.∴(2+p -1)(2+p -1)=9,即(p +1)2=9.解得p 1=2,p 2=-4.∵p ≤54,∴舍去p 1=2.∴p =-4. 9.解:(1)证明:原方程可化为x 2-5x +4-p 2=0.∵Δ=b 2-4ac =(-5)2-4(4-p 2)=4p 2+9>0,∴不论p 为何实数,方程总有两个不相等的实数根.(2)原方程可化为x 2-5x +4-p 2=0.由求根公式得方程的根为x =5±4p 2+92. ∵方程有整数解,∴找到p 的值,使5±4p 2+92为整数即可, ∴p 可取0,2,-2,10,-10等,此时方程有整数解.10.解:(1)证明:∵Δ=b 2-4ac =[-(k +3)]2-4·3k =(k -3)2≥0,∴不论k 取何实数,该方程总有实数根.(2)当△ABC 的底边长为2时,方程有两个相等的实数根,则(k -3)2=0,解得k =3,方程为x 2-6x +9=0,解得x 1=x 2=3,此时三角形的三边长分别为2,3,3,故△ABC 的周长为2+3+3=8;当△ABC 的一腰长为2时,方程有一根为2,把x =2代入方程,得22-2(k +3)+3k =0,解得k =2,方程为x 2-5x +6=0,解得x 1=2,x 2=3,此时三角形的三边长分别为2,2,3,故△ABC 的周长为2+2+3=7.综上,△ABC 的周长为8或7.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根的判别式的三种应用
类型一:判断方程的解的情况
类型二、求字母系数的取值范围
类型三、证明一元二次方程根的情况
根、有两个不相等的实数、有两个相等的实数根
、只有一个实数根
、没有实数根
的根的情况是()
的一元二次方程、关于D C B A ax x x 0112=-+时,求方程的根
)当(况
时,判断方程的根的情)当(的一元二次方程、已知关于3231.
0222-===++m m m x x x 1
22
2
2
-012)1(12≠〈〉〈〈=+--k k D k C k B k A k x x k x 且、、、、的取值范围()
,则有两个不相等的实数根的方程、已知关于()()这两个实数根。
相等的实数根,并求出数,使原方程有两个不选取一个合适的非零整对有实数根?取什么值时,原方程没当的方程、已知关于m m m x m x x 2)1(.
012222=++-()的值。
出该方程的根;求取当最大整数值时:求)当(的最大整数值
)求(有实数根。
的一元二次方程
、已知关于11873222109863222+---
=+--x x x x a a x x a x 的值。
,求满足条件的整数大于根都是整数,且有一根)如果方程的两个实数(实数根:
)求证:方程总有两个(的方程、已知关于m m x m mx x 121).
0(03)3(12≠=++-()的值。
是等腰三角形时,求,当的长为实数根,第三边的长是这个方程的两个的两边若相等的实数根;
求证:该方程有两个不、已知一元二次方程k ABC BC AC AB ABC k k x k x ∆∆=+++-5,2)1(.
0)12(222
一元二次方程的解法归类
类型一、缺少一次项选直接开平方的策略
解下列方程:
类型二、缺少常数项选因式分解法的策略
解下列方程:
类型三、遇到大系数选配方法的策略
解下列方程:
类型四、遇到字母系数讨论的策略
()049312=--x )(()()251622
=-x x x =21)(()()()()22212+=+-x x x ()98562412=-x x ()012622=--x x ()09991632=--x x ()()()是常数的方程、解关于c m x c c x mx x ,.01=-+-()()()()的值成立?若存在,请求出使得是否存在实数是方程的两个实数根,,设的值。
,求若方程的一个根为的取值范围
求有实数根。
的方程、已知关于m m m m m x m x x 6-312101222222=+=+-+αββαβα。
若不存在,请说明理由。
