一次函数的图像与性质拔高讲义
第2讲 一次函数的图像及性质(讲义)解析版

2
(1)当 x 取何值时, y = 2 ? (2)当 x 取何值时, y > 2 ? (3)当 x 取何值时, y < 2 ? (4)当 x 取何值时, 0 < y < 2 ?
2 (4)令 0 < 1 x - 3 < 2 ,解得: 6 < x < 10 .
2 【总结】本题考察了一次函数与不等式的关系,本题也可以通过函数图像求解. 例 10.已知函数 f (x) = -3x + 1 .
(1)当 x 取何值时, f (x) = -2 ? (2)当 x 取何值时, 4 > f (x) > -2 ? (3)在平面直角坐标系中,在直线 f (x) = -3x + 1 上且位于 x 轴下方所有点,它们的横 坐标的取值范围是什么?
A. x < 0
B. x > 0
C. x < 2
D. x > 2 .
【答案】A
【分析】根据题意在函数图像中寻找 y > 3 时函数图像所在的位置,发现此时函数图像对
应的 x 范围是小于零,从而得出答案
【详解】解:∵由函数图象可知,当 x<0 时函数图象在 3 的上方,
∴当 y>3 时,x<0.
故选:A.
【总结】本题考察了一次函数与一元一次不等式的关系. 例 8.已知 y = kx + b(k ¹ 0) 的函数图像如图所示:
(1)求在这个函数图像上且位于 x 轴上方所有点的横坐标的取值范围; (2)求不等式 kx + b £ 0 的解集.
一次函数图像与性质ppt课件

图
象时,只要描出函数图象中的两个点就可画出此
函 数的图象.
b ,0 k
(2)一般地,一次函数y=kx+b(k,b是常数,k≠0)
都过(0,b) (与y轴交点坐标)和(
)(与x轴交点
总结
一次函数的图象是一条直线,我们称它为直线 y=kx+b;它必过(0,b)和( b , 0 )两点.
k
例1 画出函数y=-6x与y=-6x+5的图象.
从 k、b的值看一次函数的图像 (1)当k>0,b>0时,图象过一、二、三象限; (2)当k>0,b<0时,图象过一、三、四象限; (3)当k<0,b>0时,图象过一、二、四象限; (4)当k<0,b<0时,图象过二、三、四象限.
例2 已知直线y=(1-3k)x+2k-1. (1)k为何值时,直线与y轴交点的纵坐标是-2?
一次函数的图象是一条直线,这条直线与坐标轴 有交点,正比例函数只有一个交点,一般的一次函数 有两个交点. 注意:一次函数图象的画法与我们前边学过的函数图 象的画法一样,其步骤为列表、描点、连线.通过实际 操作,我们可得出:
(1)一次函数 y=kx+b(k,b是常数,k≠0)的图象是
一
条直线.由两点确定一条直线可知,在画一次函数
要点精析: (1)在实际问题中,当自变量x的取值受限制时,一次函 数 y=kx+b的图象就不一定是一条直线了,有时是线段、 射线或直线上的部分点. (2)k决定直线的倾斜角度: k>0⇔直线y=kx+b在x轴上方的部分与x轴正方向的夹 角为锐角; k<0⇔直线y=kx+b在x轴上方的部分与x轴正方向的夹 角为钝角; k1=k2⇔直线y1=k1x+b1∥直线y2=k2x+b2(b1≠b2). (3)k>0⇔y随x的增大而增大;k<0⇔y随x的增大而减小 .
第3讲(学生)一次函数的图象和性质讲义

第3讲(学生)一次函数的图象和性质讲义编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(第3讲(学生)一次函数的图象和性质讲义)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为第3讲(学生)一次函数的图象和性质讲义的全部内容。
第3讲一次函数的图象和性质(1)学习目标:学会用图表描述变量的变化规律,会准确地画出函数图象,结合函数图象,能体会出函数的变化情况学习重点:函数的图象学习难点:函数图象的画法学习过程引入:信息1:下图是一张心电图,信息2:下图是自动测温仪记录的图象,他反映了北京的春季某天气温T如何随时间的变化二变化,你从图象中得到了什么信息?问题:正方形的边长x与面积S的函数关系为S=x2,你能想到更直观地表示S与x 的关系的方法吗?一般地,对于一个函数,如果把自变量与函数的每对对应诃子分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象(graph).•已经知道了形如y=•kx•(k•是常数, k ≠0 )的函数,•叫做正比例函数,其中k 叫做比例系数.那么正比例函数的图象有什么特征呢?范例:例1.画出下列正比例函数的图象,并进行比较,寻找两个函数图象的相同点与不同点,考虑两个函数的变化规律.1.y=2x 2.y=—2x2.y=列表表示几组对应值:y3.两个图象的共同点:都是经过原点的直线.不同点:函数y=2x 的图象从左向右呈上升状态,即随着x 的增大y 也增大;经过第一、三象限.函数y=—2x 的图象从左向右呈下降状态,即随x 增大y 反而减小;•经过第二、四象限. 1比较可以看出:两个图象都是经过原点的直线.函数y=x•的图象从左向右上升,经过一、三象限,即随x增大y也增大;函数y=—x•的图象从左向右下降,经过二、四象限,即随x增大y反而减小.归纳:正比例函数图象的规律:正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线.•当x〉0时,图象经过一、三象限,从左向右上升,即随x的增大y也增大;当k〈0时,•图象经过二、四象限,从左向右下降,即随x增大y反而减小.正是由于正比例函数y=kx(k是常数,k≠0)的图象是一条直线,•我们可以称它为直线y=kx.思考:经过原点与点(1,k)的直线是哪个函数的图象?画正比例函数的图象时,•怎样画最简单?为什么?经过原点与点(1,k)的直线是函数y=kx的图象.画正比例函数图象时,只需在原点外再确定一个点,即找出一组满足函数关系式的对应数值即可,如(1,k).因为两点可以确定一条直线.Ⅲ.练习用你认为最简单的方法画出下列函数图象:1.y=x 2.y=-3x练习1、某函数具有下面的性质:(1).它的图象是经过原点的一条直线.(2).y随x增大反而减小.121232请你举出一个满足上述条件的函数,写出解析式,画出图象.2。
辅导讲义3(一次函数的图像及性质)

面积相等的两部分,那么b的值为
16.(2011湖北黄石)已知梯形ABCD的四个顶点的坐标分别为A(-1,0),B(5,0),C(2,2),D(0,2),直线y=kx+2将梯形分成面积相等的两部分,则k的值为
考点4用待定系数法求一次函数的解析式
[例4](2011广东株洲)直线L过A、B两点,A( , ),B( , ),
则直线L的解析式为.
22.(桂林)如图,是一个正比例函数的图像,把该图像向左平移
一个单位长度,得到的函数图像的解析式为.
23.(天津)已知一次函数的图象过点 与 ,则该函数的图象与 轴交点的坐标为__________.
A.y=x+1B.y=x-1C.y=xD.y=x-2
19.把直线一次函数y=6x+1向下平移2个单位,再向右移动3个单位得到的图像解析式为________
20.(湖北黄石)将函数y=-6x的图象 向上平移5个单位得直线 ,则直线 与坐标轴围成的三角形面积为.
21.直线L1经过点A(-3,1)、B(0,2),该直线向右平移3个单位得到直线L2,则直线L2的解析式为.
2.已知直线y=2x+8与x轴和y轴的交点的坐标分别是_______、_______;
与两条坐标轴围成的三角形的面积是__________.
3.一次函数 与x轴和y轴的交点的坐标分别是_______、_______;
与两条坐标轴围成的三角形的面积是__________.
考点2一次函数y=kx+b(k 0)图像与性质
学员编号:年级:课时数:3课时
学员姓名:辅导科目:学科教师:
人教版初二下册数学第19章《一次函数》讲义第19讲一次函数的图象及性质(1)(有答案)

人教版初二下册数学第19章《一次函数》讲义第19讲一次函数的图象及性质(1)(有答案)〔1〕形如y=kx +b (k,b 是常数,k≠0),那么y 叫做x 的一次函数.由于当b=0时,y=kx ,那么y 叫做x 的正比例函数,所以〝正比例函数是特殊的一次函数〞。
〔2〕正比例函数与一次函数图象之间的关系一次函数y=kx +b 的图象是一条直线,它可以看作是由直线y=kx 平移|b|个单位长度而失掉〔当b>0时,向上平移;当b<0时,向下平移,〕普通地,形如y=kx (k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数. 注:正比例函数普通方式 y=kx 〔k 不为零〕① k 不为零; ② x 指数为1; ③ b 取零当k>0时,直线y=kx 经过三、一象限,从左向右上升,即随x 的增大y 也增大;当k<0时,•直线y=kx 经过二、四象限,从左向右下降,即随x 增大y 反而减小.(1) 解析式:y=kx 〔k 是常数,k≠0〕(2) 必过点:〔0,0〕、〔1,k 〕(3) 走向:k>0时,图像经过一、三象限; k<0时,•图像经过二、四象限(4) 增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小(5) 倾斜度:|k|越大,越接近y 轴;|k|越小,越接近x 轴普通地,形如y=kx +b(k,b 是常数,k≠0),那么y 叫做x 的一次函数.注:一次函数普通方式 y=kx+b (k 不为零)① k 不为零; ②x 指数为1; ③ b 取恣意实数一次函数y=kx+b 的图象是经过〔0,b 〕和〔-kb ,0〕两点的一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx 平移|b|个单位长度失掉.〔当b>0时,向上平移;当b<0时,向下平移〕〔1〕解析式:y=kx+b (k 、b 是常数,k ≠0)〔2〕必过点:〔0,b 〕和〔-kb ,0〕 〔3〕走向: k>0,图象经过第一、三象限;k<0,图象经过第二、四象限b>0,图象经过第一、二象限;b<0,图象经过第三、四象限⇔⎩⎨⎧>>00b k 直线经过第一、二、三象限 ⇔⎩⎨⎧<>00b k 直线经过第一、三、四象限 ⇔⎩⎨⎧><00b k 直线经过第一、二、四象限 ⇔⎩⎨⎧<<00b k 直线经过第二、三、四象限 〔4〕增减性: k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小.〔5〕倾斜度:|k|越大,图象越接近于y 轴;|k|越小,图象越接近于x 轴.〔6〕图像的平移: 当b>0时,将直线y=kx 的图象向上平移b 个单位;当b<0时,将直线y=kx 的图象向下平移b 个单位.考点1、一次函数〔正比例〕的定义例1、在糖水中继续放入糖x 〔g 〕、水y 〔g 〕,并使糖完全溶解,假设甜度坚持不变,那么y 与x 的函的函数关系一定是〔 〕A 、正比例函数B 、正比例函数C 、图象不经过原点的一次函数D 、二次函数例2、直角三角形两个锐角∠A 与∠B 的函数关系是〔 〕A 、正比例函数B 、一次函数C 、正比例函数D 、二次函数 例3、假定y=〔m -3〕x+1是一次函数,那么〔 〕A 、m=3B 、m=-3C 、m≠3D 、m≠-3例4、以下效果中,是正比例函数的是〔 〕A 、矩形面积固定,长和宽的关系B 、正方形面积和边长之间的关系C 、三角形的面积一定,底边和底边上的高之间的关系D 、匀速运动中,速度固定时,路程和时间的关系例5、假定函数y=-2x m+2+n -2是正比例函数,那么m 的值是_____,n 的值为_____. 例6、我们知道,海拔高度每上升1km ,温度下降6℃.某时辰测量我市空中温度为20℃.设高出空中xkm 处的温度为y ℃,那么y 与x 的函数关系式为 ,y_____x 的一次函数〔填〝是〞或〝不是〞〕.例7、y=〔k -1〕x IkI +〔k 2-4〕是一次函数.〔1〕求k 的值; 〔2〕求x=3时,y 的值; 〔3〕当y=0时,x 的值.例8、红星机械厂有煤80吨,每天需烧煤5吨,求工厂余煤量y 〔吨〕与烧煤天数x 〔天〕之间的函数表达式,指出y 是不是x 的一次函数,并求自变量x 的取值范围. 例9、举一反三:1、以下函数中,是一次函数的有〔 〕A 、xy 2 B 、X -1=0 C 、y=2〔x -1〕 D 、y=x 2+1 2、y=〔m -1〕x |m|+3m 表示一次函数,那么m 等于〔 〕A 、1B 、-1C 、0或-1D 、1或-13、假定函数y=〔k -1〕x+k 2-1是正比例函数,那么k 的值是〔 〕A 、-1B 、1C 、-1或1D 、恣意实数4、当自变量x= 时,正比例函数y=〔n+2〕x n 的函数值为3.5、函数y=3x+1,当自变量添加3时,相应的函数值添加______。
一次函数的性质和图像(一)课件

经济问题中的应用
在经济学中,许多经济指标之间的关系可以用一次函数来描述,如价格与需求的 关系、成本与产量的关系等。通过这些实例,可以了解一次函数在经济分析中的 应用。
像会向右平移。
03
一次函数的应用
一次函数在实际生活中的应用
一次函数在经济学中的应用
一次函数可以用来描述经济现象之间的关系,例如成本与产量的 关系、价格与需求量的关系等。
一次函数在物理学中的应用
在物理学中,一次函数可以用来描述线性关系,例如速度与时间的 关系、力与位移的关系等。
一次函数在工程领域的应用
02
一次函数的图像
一次函数图像的绘制
步骤二
在坐标系上选择一个点,例如 原点$(0,0)$。
步骤四
在坐标系上标出该点,即 $(0,1)$。
步骤一
确定函数表达式。例如,$y = 2x + 1$。
步骤三
使用一次函数的表达式,计算 出该点沿x轴和y轴的坐标值。 例如,$y = 2(0) + 1 = 1$。
一次函数的图像是一条直线,其斜率 为$a$,截距为$b$。
一次函数的图像可以通过平移得到, 向上平移$k$个单位得到$y = ax + b + k$,向下平移$k$个单位得到$y = ax + b - k$。
一次函数的单调性由斜率$a$决定, 当$a > 0$时,函数为增函数;当$a < 0$时,函数为减函数。
一次函数在概率统计问题中的应用
03
在概率统计问题中,一次函数可以用来描述概率分布、平均数
一次函数图像和性质说课课件

提倡学生互相交流
鼓励学生之间互相交流学习心得和解题方法,促进共同进步。
激发学生探究兴趣
通过一些趣味性的问题或实验,激发学生的探究兴趣,培养学生 的自主学习能力。
THANKS FOR WATCHING
感谢您的观看
解题思路
将已知的两点坐标代入一次函数的一般式,得到关于$k$ 和$b$的二元一次方程组,解方程组即可求出$k$和$b$ 的值,从而得到一次函数的表达式。
解题思路
将已知的点坐标代入直线方程,求出$b$的值,即可得到 直线的表达式。
判断一次函数图像位置关系
例题1
解题思路
例题2
解题思路
判断直线$y=x+1$与 $y=-2x+4$的图像位置 关系,并求出它们的交 点坐标。
连线绘制
将描出的点用直线连接起来,即可得 到一次函数的图像。注意要保持直线 的平滑和连续性。
检查图像
在绘制完成后,要检查图像是否符合 一次函数的特征,如直线是否过原点、 斜率是否正确等。
直线方程在坐标系中表示形式
一般式
直线方程的一般式为Ax+By+C=0(A、B不同时为 零),它可以表示任何一条直线。
教学方法与手段
01
02
03
04
讲授法
通过教师的系统讲解,引导学 生理解一次函数图像和性质的
基本概念和方法。
演示法
利用多媒体课件进行动态演示 ,帮助学生直观地理解一次函 数图像和性质的变化规律。
探究法
通过问题设置和情境创设,引 导学生自主探究一次函数图像 和性质在实际问题中的应用。
练习法
通过课堂练习和课后作业,巩 固学生对一次函数图像和性质
一次函数的图像和性质讲义-综合提高版

一次函数的图像和性质讲义-综合提高版内容指引:知识点+例题+达纲测试训练+答案 一、一次函数的图像1.正比例函数y=kx(k ≠0,k 是常数)的图像是经过O (0,0)和M (1,k )两点的一条直线(如图13-17).(1)当k >0时,图像经过原点和第一、三像限;(2)k <0时,图像经过原点和第二、四像限.2.一次函数y=kx+b(k 是常数,k ≠0)的图像是经过A (0,b )和B (-kb,0)两点的一条直线,当kb ≠0时,图像(即直线)的位置分4种不同情况:(1)k >0,b >0时,直线经过第一、二、三像限,如图13-18A (2)k >0,b <0时,直线经过第一、三、四像限,如图13-18B (3)k <0,b >0时,直线经过第一、二、四像限,如图13-18C (4)k <0,b <0时,直线经过第二、三、四像限,如图13-18D3.一次函数的图像的两个特征(1)对于直线y=kx+b(k ≠0),当x=0时,y=b 即直线与y 轴的交点为A (0,b ),因此b 叫直线在y 轴上的截距.(2)直线y=kx+b(k ≠0)与两直角标系中两坐标轴的交点分别为A (0,b )和B (-kb ,0).设直线与x 的夹角为α,则tg α=|kb b|=|k|,由于角α:0<α<90°,tg α>,因此|k|=tg α.4.一次函数的图像与直线方程(1)一次函数y=kx+b(k ≠0)的图像是一条直线,因此y=kx+b(k ≠0)也叫直线方程.但直线方程不一定都是一次函数.(2)与坐标轴平行的直线的方程.①与x轴平行的直线方程形如:y=a(a是常数).a>0时,直线在x轴上方;a=0时,直线与x轴重合;a<0时,直线在x轴下方.(如图13-19)②与y轴平行的直线方程形如x=b(b是常数),b>0时,直线在y轴右方,b=0时,直线与y轴重合;b<0时,直线在y轴左方,(如图13-20).二、两条直线的关系1.与坐标轴不平行的两条直线l1:y1=k1x+b1,l2:y2=k2x+b,若l1若l2相交,则k1≠k2;若k1≠k2,则l1与l2不平行,其交点是联立这两条直线的方程,求得的公共解.三、一次函数的增减性1.增减性如果函数当自变量在某一取范围内具有函数值随自变量的增加(或减少)而增加(或减少)的性质,称为该函数当自变量在这一取值范围内具有增减性,或称具有单调性.2.一次函数的增减性一次函数y=kx+b在x取全体实数时都具有如下性质:(1)k>0时,y随x的增加而增加;(2)k<0时,y随x的增加而减小.3.待定系数法求一次函数的解析式:若已知一次函数的图像(即直线)经过两个已在点A(x1,y1)和B(x2,y2)求这个一次函数的解析式,其方法和步骤是:(1)设一次函数的解析式:y=kx+b(k≠0)(2)将A、B两点的坐标代入所设函数的解析式,得两个方程:y1=k1x1+b①y2=k2x2+b2②(3)联立①②解方程组,从而求出k、b值.这一先设系数k、b,从而通过解方程求系数的方法以称为待定系数法.【重点难点解析】例1已知一次函数y=(m+3)x+(4-n),(1)m为何值时,y随x的增大而减小;(2)n为何值时,函数的图像与y轴的交点x轴下方;(3)m、n为何值时,函数图像与y=x+2的图像平行.解:(1)当m+3<0,即m<-3时,y随x的增大而减小;(2)当4-n<0,即n>4时,函数的图像与y轴的交点在x下方;(3)当m+3=1且4-n ≠2时,即m=-2, n ≠2时,函数的图像是一条与y=x+2平行的直线.例2 当a 、b >0,ac <0,直线ax+by+c=0不通过哪个像限. 解:∵b ≠0 ∴由原函数式变形得: y=-b a x-bc ∴ab >0 ∴-b a<0 又∵ac <0,∴-bc>0直线ax+by+c=0不通过第三像限. 例3 直线l 1:y 1=k 1x+b 1 与y=2x 平行且通过A (3,4),直线l 2:y 2=k 2x+b 2通过B (1,3),C (-1,5),求l 1和l 2的解析式.解:∵y 1=k 1x+b 1与y=2x 平行且通过A (3,4)∴⎩⎨⎧=+=4b 3k 2k 111解这个方程组得:⎩⎨⎧==-2b 2k 11∴l 1的解析式为:y=2x-2∵y 2=k 2x+b 2通过B (1,3)和C (-1,5)两点,将两点的坐标代入解析式得:∴l 2的解析式为:y=-x+4例4 已知一个正比例函数和一个一次函数,它们的图像都经过P (-2,1),且一次函数在y 轴上的截距为3.(1)求这两个函数的解析式;(2)在同一坐标系中,分别画出两个函数的图像;(3)求这两个函数的图像与y 轴围成的三角形的面积.解:(1)设正比例函数和一次函数的解析式分别为y=k 1x 和 y=k 2x+b.由y=k 1x 过点(-2,1)得1=-2k 1 ∴k 1=-21由y=k 2x+b 过点(-2,1),截距为3 得:b=3 -2k 2+b=1 解得:k 2=1 b=3(2)过点O (0,0)、P (-2,1)两点画一条直线,即得函数y=-21x 的图像.经过A (0,3)和P (-2,1)画一条直线即得y=x+3的直线,如图13-21(3)直线y=x+3与y 轴交于点A (0,3)过P 作PH ⊥y 轴,则OA=3,PH=|-2|=2,而函数与y 轴所围成的三角形面积即是△APO 的面积.S △APO=21·AO ·PH =21×3×2=3例5 已知y-(m-3)与x (m 是常数)成正比例,且 x=6时,y=1;x=-4时, y=-4.(1)求y 与x 之间的函数关系式;(2)在直角坐标系中,画出这个函数的图像;(3)求出这个函数的图像与坐标轴的两个交点之间的距离.解:∵y-(m-3)与x 成正比例∴可设y-(m-3)=kx,即y=kx+m-3①⎩⎨⎧-=+-=+1m k 44m k 6故所求函数关系式为:y=21x-2 (2)经过A (6,1)和B (-4,-4)画直线即是函数y=21x-2的图像.如图13-22(3)当x=0时:y=21×0-2=-2 当y=0时,0=21x-2 x=4 ∴C (4,0),D (0,-2)|CD|=52242222=+=+OD OC综上所述5例可见,本节重点为:①根据直线所通过的点的条件求直线方程;②根据直线方程求作直线的图像;③根据增减性、截距求直线方程;④根据两直线的位置关系求直线方程;本节的难点是求直线围成的图形的面积.解决重难点的方法是运用待定系数法和数形结合的方法.【难题巧解点拨】例6 已知函数y=|x-a|+|x+19|+|x-a-96|,其中a 为常数,且满足19<a <96,当自变量x 的取值范围为a ≤x ≤96时,求y 的最大值.解:∵19<a <96,a ≤x ≤96∴x-a ≥0,x+19>10,x-a-96<0则y=x-a+x+19+a+96-x=115+x 函数y=15+x 是一次函数,其增减性表明y 随x 的增大而增大. ∴在a ≤x ≤96的x 取值范围内,当x=96时,y 取最大值,即: y max =96+115=211说明:含绝对值的函数首先要讨论绝对值的式子的正负性质,再根据绝对值定义化简,从而得到一次函数;讨论在某一自变量的取值范围内最大值或最小值要根据一次函数的性质和自变量x 范围的两端点取值来求.例7 如图13-23在平面直角坐标系中,点O ′的坐标为(0,3),⊙O ′与y 轴交于原点O 和点A ,又B 、C 、E 三点的坐标分别为(0,-2)、(4,0)、(x ,0),且0<x <4.(1)求点A 的坐标;(2)当点E 在线段OC 上移动时,直线BE 与⊙O ′有哪几种位置关系?(3)求出直线BE 与⊙O ′每种位置关系时,x 的取值范围.分析:直线与圆有三种位置关系,从直线与圆相切这种特殊情形,用运动变化的观点寻求结论成立的条件是解本题的关键.解:(1)∵O ′(0,3) ∴⊙′的半径为: OO ′=3,∴OA=2·OO ′=2×3=6,∴A (0,6)(2)∵点B 在⊙O ′外,BE 与⊙O ′有三种位置关系:相离、相切、相交; (3)当直线BE 与⊙O ′相切于D 点时,连结O ′D ,则△O ′BD 是Rt △. O ′D=3, O ′B=5,BD=4,OB=2,OE=x∵△O ′BD ∽△EBO∴BD OB D O OE =' 即423=x ,解得:x=23故当23<x <4时,直线BE 与⊙O ′相离;当x=23时,直线BE 与⊙O ′相切.当0<x <23时,直线BE 与⊙O ′相交.例8 如图13-24,某航空公司托运行李的费用与托运行李重量的关系为一直线,由图中可知行李的重量不超过多少公斤,就可以免费托运?解:设直线方程为:y=kx+b (k 、b 是常数,k ≠0)由图可知:x=20时,y=330;x=40时,y=630;把x,y 的对应取值代入直线方程,得:解这个方程组,得:k=30,b=-570 ∴直线方程为:y=30x-570若y=0时,30x-570=0, ∴x=19答:只要行李重量不超过19公斤时,就可免费托运.【命题趋势分析】由于一次函数是最基本的函数内容,是初中重点之一,在实际中应用十分广泛,因此是中考热点考题.有关一次函数考试主要是概念、图像、性质三个基本内容和待定系数法、数形结合法两种数学方法.【典型热点考题】例9 填空题:已知直线l:y=-3x+2,现在4个命题:①点P (1,-1)在直线l 上;②若直线l 与x 轴、y 轴分别交于A 、B 两点,则AB=1032;③若点M (31,1),N (a 、b )都在直线l 上,且a >31,则b >1;④若点Q 到两坐标轴的距离相等,且点Q 在l 上,则点Q 在第一或第四像限.其中正确的命题是 .(注意:在横线上填上你认为正确的命题序号)(2000年厦门市中考题)分析:检验①:只需将x=1,y=-1代入函数式看是否适合,当x=1时,y=-3+2=-1,即P(1,-1)在直线y=-3x+2上,①命题正确;检验②;当y=0时,求得x=32,即A (32,0),当x=0时,y=2,即B (0,2),∴AB=10322)32(22=+,命题②正确;检验③,若M (31,1),N(a,b)都在y=-3x+2上,根据直线的性质,k=-3<0,y 随x 的增加而减小,∴a >31时,应该有b <0,因此b >1错误,即命题③错误;检验④,∵Q 到两坐标轴的距离相等,设Q (m 、n ),则|m|=|n|,且n=-3m+2,由此解得:⎩⎨⎧-==11n m 或⎪⎪⎩⎪⎪⎨⎧==2121n m 因此Q 点在第一或第四像限,命题④正确.因此,选①、②、④填空.例10 某居民小区按照分期付款的形式福利售房,政府给予一定的贴息,小明家购得一套现价为120000元的房子,购房时首期(第一年)付款30000元,从第二年起,以后每年应付房款5000元与上一年剩余欠款利息的和,设剩余欠款年利率为0.4%.(1)若第x (x ≥2)年小明家交付房款y 元,求年付款y (元)与x (年)的函数关系式;(2)将第三年,第十年应付房款填入下列表格中:(2000年大连市中考题)年份 第一年 第二年 第三年 …… 第十年 交房款(元)300005360……分析:首期付款后共余120000-30000=90000元房款,以后每年付款应为5000,与上一年所欠余款×0.4%,即余款的利息之和.解:(1)y=5000+[90000-5000(x-2)] ×0.4% =5400-20x (x ≥2)(2)当x=3时,y=5340,当 x=10 时,y=5200, 因此第三年应付款5340元,第十年应付款5200元. 例11 已知直线x-2y=-k+6和x+3y=4y+1,若它们的交点在第四像限内,(1)求k 的取值范围,(2)若k 为非负整数,点A 的坐标为(2,0),点P 在直线x-2y=-k+6上,求使△PAO 为等腰三角形的点P 的坐标.(2000年西安市中考题)解:(1)依题意:解这个方程组,得:x=k+4,y=k-1 ∵两直线的交点在第四像限 ∴k+4>0,且k-1<0解不等式组得:-4<k <1 (2)∵k 为非负整数,∴k=0 ∴直线x-2y=-k+6即为:y=x 21-3设P (a ,b )为直线y=x 21-3上一点,作PE ⊥x 轴,垂足为E ,若使PO=PA ,则应有OE=AE ,即E (1,0)∵a=1,∴b=-25∴P 1(1,- 25) 若使PO=OA=2,则a 2+b 2=4,a 2+(21a-3)2=4,45a 2-3a+5=0, △=9-25<0此方程无解.若使PA=OA=2,则(2-a )2+b 2=4,(2-a)2+(21a-3)2=4, ∴45a 2-7a+9=0,a 1=2,a 2=518,当a 1=2时,b 1=-2,当a 2=518时 ,b 2=-56. ∴P 2(2,-2)或P 3(518,56)综合上所述,点P 的坐标为(1,-25),(2,-2),(518,-56)如图13-25.【同步达纲练习】(时间:45分钟,满分:100分)一、选择题(10分×6=60分)(1)一次函数y=kx+b 的图像经过点(m,-1)和点(1,m),其中,m <-1,则k 和b 满足的条件是( )A.k <0,b <0B.k >0,b >0C.k <0,b >0D.k >0,b <0(2)若一次函数y=(1-2k)x-k (x 为自变量)的函数值y 随x 的增大而增大,且此函数的图像不经过第二像限,则k 的取值范围是( )A.k <21 B.k >0 C.0<k <21 D.k <0或k >21 (3)当mn <0 mp >0时,一次函数y=mnx p m 的图像不经过的像限是( ) A.第一像限 B.第二像限 C.第三像限 D.第四像限(4)一次函数y=kx+b 的图像如图13-26,那么k 、b 应满足的条件是( ) A.k >0,b >0 B.k >0,b <0 C.k <0,b >0 D.k <0,b <0 (5)已知函数y=xk的图像经过点(-1,1),则函数y=kx+3的图像是( )(6)直线y=kx+b 与直线 y=-x 垂直,并且经过点(-1,1),那么直线y=kx+b 的解析式为( )A.y=-x-2B.y=x+2C.y=x-2D.y=-x+2 三、解答题(10分×3=30分)(7)已知一次函数y=(3-k)x+2k+1.①如果它的图像经过(-1,2)点,求k 的值;②如果它的图像经过第一、二、四像限,求k 的取值范围.(8)已知y+b 与x-1(其中b 是常数)成正比例.①证明:y 是x 的一次函数;②若这个一次函数的图像经过点(25,0),且与坐标轴在第一像限内围成的三角形的面积为425,求这个一次函数,并画出它的图像.(9)已知一次函数y=(p+3)x+(2-q).①p 为什么实数时y 随x 的增大而增大?②q 为什么实数时,函数图像与y 轴的交点在x 轴的上方;③p 、q 为什么实数时,函数的图像过原点?(10)如图13-27,在直角坐标系中,点A (x 1,-3)在第三像限,点B (x 2,-1)在第四像限,线段AB 与y 轴交于点D ,∠AOB=90°,①当x 2=1时,求图像经过A 、B 的一次函数的解析式;②当△OAB 的面积等于9时,设∠AOD=α,求sin α·cos α的值.【素质优化训练】一个水池的容积是100m 3,现存水20m 3,今要灌满水池,已知进水管的流量是每小时8m 3,写出水池的水量υ与进水时间t 之间的函数关系式,并画出图像.【生活实际应用】某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出货,可获利15%,并可用本和利再投资其它商品,到月末又可获利10%;如果月末出售可获利30%,但要付出仓储费用200元,请问根据商场的资金状况,如何购销获利最多?【知识探究学习】求直线方程的几种方法:1.如图1,若l 与x 轴的夹角为α(0<α<90),直线与y 轴交于点(0,b ),则直线l 方程即为:y=tg α·x+b2.若l 与x 的夹角为α(0<α<90),且经过点M (x 1,y 1),如图2,则直线l 的方程即可写为:αtg x x y y =--113.若l 经过A (x 1,y 1),B (x 2,y 2),则直线l 的方程即可写为:122122x x xx y y y y --=--11参考答案:【同步达纲练习】一、A C D D C B二、(7)k=34,k >3,(8)①y=kx-(k+b)(k ≠0);②y=-2x+5;(9)①P >-3,②q <2,③p ≠3且 q=2;(10)①y=21x-32;②sin α·cos α=61 【素质优化训练】1. v=20+8t(0≤t ≤10)【生活实际应用】设商场投资x 元,在月初出售,到月末可获得y 1元,在月末出售可获利y 2元. y 1=0.265x ,y 2=0.3x-700(1) 当y 1=y 2时,x=20000(2) y 1<y 2时,x >20000(3) y 1>y 2时,x <2000。
一次函数的图像与性质拔高讲义

一次函数的图像与性质拔高讲义一、【知识点拨】1、一次函数:形如y=kx+b (k ≠0, k, b 为常数)的函数。
注意:(1)k ≠0,否则自变量x 的最高次项的系数不为1;(2)当b=0时,y=kx ,y 叫x 的正比例函数。
2、图象:一次函数的图象是一条直线,(1)两个常用的特殊点:与y 轴交于(0,b );与x 轴交于(-,0) (2)由图象可以知道,直线y=k x+b 与直线y=k x 平行,例如直线:y=2x+3与直线y=2x-5都与直线y=2x 平行。
3、性质:(1)增减性 k>0时,y 随x 增大而增大 k<0时,y 随x 增大而减小 (2)图象的位置二、【典型例题剖析】例1(1)已知直线y=kx+b 经过点(3,-1)和点(-6,5),则k=_______,b=______.教师寄语:沟潭之水,凝滞沉闷,飞瀑之流,奋迅高亢——同是为水,性却异,前者满足安逸,后者进取不已。
奋斗者的幸福是从痛苦起步的,享乐者的痛苦是从“幸福”开始的。
(2)已知一次函数y=kx+5过点P(-1,2),则k=________. 例2(1)一次函数1-=x y 的图象不经过( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限(2)如图,表示一次函数y =mx+n 与正比例函数y=mnx(m ,n 是常数,且 mn ≠0)图像的是( ).例3.直线y=kx+b 与直线y=5-4x 平行,且与直线y=-3(x-6)相交,交点在y 轴上,求此直线解析式。
例4. 已知函数221(43)3a a y a a x --=-++是一次函数,则a 的值为 ( )例5如图,一次函数y =kx +b (k <0)的图象经过点A .当y <3时,x 的取值范围是 .例6(2011山东省潍坊, 14,3分)一个y 关于x 的函数同时满足两个条件:①图象过(2,1)点;②当0x >时.y 随x 的增大而减小,这个函数解析式为_______________ (写出一个即可)三【知识点分类专练】知识点1:一次函数的定义xy:一次函数通常可以表示 的形式,其中k 、b 是 ,k 0.特别地,当 时,一次函数y =kx (常数k ≠0)也叫 .正比例函数也是一次函数,它是一次函数的特例. 【课堂练习】:1、下列函数:①y=-8x;②y=8x;③y=8x 2;④y=8x+1;⑤y=53++z x .其中是一次函数的有( )A.1个B.2个C.3个D.4个 2、(1)若函数y=(m —2)x+5是一次函数,则m 满足的条件是 。
一次函数的图像和性质PPT演示课件

1.下列函数中,是正比例函数的是
A.y=-8x
B.y=-x8
C.y=5x2+6
D.y=-0.5x-1
2.一次函数 y=x-2 的图象不经过 ( B )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
( A)
•32
3.已知正比例函数 y=kx(k≠0)的图象经过点(1,-2),则正比例
函数的解析式为
考点聚焦
考点1 一次函数与正比例函数的概念
•1
考点2 一次函数的图象和性质 (2)正比例函数与一次函数的性质
第一、三 象限
第二、四 象限
•2
第一、二、 三象限
第一、三、 四象限
第一、二、 四象限
第二、三、 四象限
•3
考点3 两条直线的位置关系
k1≠k2 k1=k2,b1≠b2
•4
考点4 两直线的交点坐标及一次函数的图象与坐标 轴围成的三角形的面积
•21
变式题
5.已知直线 y=kx+b 经过点(k,3)和(1,k),则 k
的值为( B )
A. 3
B.± 3
C. 2
D.± 2
•22
变式题
▪ 6、在平面直角坐标系中,点O为原点,直线y
=kx+b交x轴于点A(-2,0),交y轴于点
B.若△AOB的面积为8,则k的值为( D ) ▪ A.1 B.2 C.-2或4 D.4或-4
图10-2 •26
变式题
▪ 1(1)根据图象信息可求得关于x的不等式 ▪ kx+b>0的解集为____________ ▪ (2)根据图象信息可求得关于x的不等式 ▪ kx+b≥0的解集为____________ ▪ (3)根据图象信息可求得关于x的不等式 ▪ kx+b≤0的解集为____________
一次函数图象与性质课件

一次函数在距离与时间问题中的应用
总结词:匀速运动
详细描述:在距离、时间和速度的问题中,如果速度保持不变,则距离和时间之间存在一次函数关系 。例如,匀速行驶的汽车,其行驶的距离是时间的线性函数。
和b是常数,k≠0。
它表示的是一种线性关系,即因 变量y与自变量x之间的变化关系
。
当k>0时,函数为增函数,随着 x的增加,y也增加;当k<0时, 函数为减函数,随着x的增加,y
减少。
一次函数的表示方法
一次函数可以用解析 式表示为y=kx+b, 其中k和b是常数且 k≠0。
还可以通过表格的形 式表示,列出一些自 变量x的值和对应的 因变量y的值。
一次函数在交通运输中的应用
总结词
运输量与运输成本的关系
详细描述
在交通运输中,一次函数可以用来表示运输量与运输成本之 间的关系。随着运输量的增加,运输成本也会相应增加,这 种关系可以用一次函数来表示。通过分析这种关系,可以更 好地制定运输计划和控制运输成本。
2023
PART 05
总结与展望
REPORTING
2023
REPORTING
THANKS
感谢观看
数。通过求解这个方程,可以预测不同投资额下的预期回报率。
一次函数在生产计划中的应用
总结词
生产量与生产要素的关系
详细描述
在生产计划中,一次函数可以用来表示生产量与生产要素之间的关系。例如, 生产量与劳动力、原材料、设备等生产要素之间存在线性关系,可以用一次函 数来表示这种关系,从而更好地安排生产计划。
一次函数图像与性质课件

03 一次函数的性质
单调性
一次函数在其定义域内要么是增函数,要么是减函数。
当一次函数的比例系数大于0时,函数是增函数;当比例系数小于0时,函数是减函 数。
通过观察一次函数的图像,可以直观地判断函数的单调性。
奇偶性
一次函数既不是奇函数也不是偶函数,因为它不满足奇函数或偶函数的 定义。
奇函数和偶函数的定义是基于原点对称的,而一次函数的图像是一条直 线,不一定关于原点对称。
04 一次函数的应用
实际问题中的一次函数模型
匀速运动模型
01
当物体以恒定速度移动时,其位移和时间之间呈一次函数关系。
线性增长或减少模型
02
例如,人口自然增长、产品均匀生产等问题中,数量随时间呈
线性增ቤተ መጻሕፍቲ ባይዱ或减少。
比例关系模型
03
在实际问题中,两个变量之间往往存在比例关系,这种关系可
以用一次函数来描述。
利用一次函数解决实际问题
求解最值问题
通过一次函数的单调性, 可以方便地求解实际问题 中的最大值或最小值。
预测和决策
利用一次函数模型对实际 数据进行拟合,可以预测 未来趋势,为决策提供科 学依据。
优化资源配置
在生产、销售等领域,通 过一次函数模型可以优化 资源配置,降低成本,提 高效率。
一次函数在其他领域的应用
一次函数图像与性质课件
目录
• 引言 • 一次函数的图像 • 一次函数的性质 • 一次函数的应用 • 一次函数的综合题型 • 一次函数与其他知识点的联系
01 引言
函数的定义与分类
函数的定义
函数是一种特殊的对应关系,它 表达了自变量与因变量之间的依 赖关系。
函数的分类
第12章一次函数期末复习一次函数的图象及其性质课件

复习要点 3.正比例函数y =kx的图象及其性质
当k>0时,y随着x的增大而增大;图象经过第三、一象限.
当k<0时,y随着x的增大而减小;图象经过第二、四象限.
y
y
y=kx
O
x
y=kx
O
x
复习要点
4.一次函数y=kx+b与正比例函数y=kx图象的关系
A.y=-2x+3
B.y=-2+3x
C.y=-3x-2
D.y=3-2x
4.一次函数y=mx+|m-1|的图象过点(0,2),且y
随x的增大而增大,则m=( B ).
A.-1 B.3 C.1 D.-1或3
练习巩固
5.点A(4,m) ,B(4.7,n)都在直线y=2.3x-5上,则
m与n之间的关系是( B ).
Ox
∴ m+1=-1<0
A.
B.
y
即k<0
y
∵ m<-2 ∴-m>2
O x∴ 1-m>1 +2>0
C.
即b>0
Ox
D.
10.直线y=kx+2与y=2x+k在同一坐标系内的
大致图象是( D ).
y
k>0
k<0
O
x
y k>0
k<0
O
x
A. y k<0 k>0
O
x
B.
y k<0 k<0
b>0
O
x
C.
D.
y
y=kx+b y=kx
O
x
y=kx+b
复习要点 8.用待定系数法求一次函数解析式一般步骤: (1)先设出一次函数解析式为y=kx+b; (2)将已知两点的坐标代入所设的解析式,建立
一次函数的图像和性质(拔高)3.6

课题 一次函数的图像与性质1、一次函数的图像的画法(1)画函数图像的三步:列表-描点-连线. (2)一次函数的图象是一条直线。
一次函数y=kx+b (k 、b 是常数,且k ≠0)的图象是一条直线。
一次函数y=kx+b 也称为直线y=kx+b ,这时,我们把一次函数的解析式y=kx+b 称为这一直线的表达式。
(3)因为一次函数y=kx+b (k 、b 是常数,且k ≠0)的图象是一条直线,根据“两点确定一条直线”的基本性质,画一次函数的图象时只需描出图象上的两个点,再作过这两点的直线即可。
2、一次函数的图像的性质(1)一次函数与x 轴交点的纵坐标为0,与y 轴交点的横坐标为0.(2)一次函数111(y k x b k =+、110b k ≠为常数,)与222(y k x b k =+、220b k ≠为常数,)的图像平行时,则12k k =。
反之,当12k k =时,两直线平行,且当12k k =,12b b =时,两直线重合。
(3)当一次函数111(y k x b k =+、110b k ≠为常数,)与222(y k x b k =+、220b k ≠为常数,)的图像的截距相同且不平行时,则12b b =,12k k ≠。
(4)一次函数y=kx+b (k 、b 是常数,且k ≠0)当k>0时函数值随着x 的增大而增大、减小而减小,即该函数为增函数;当k<0时函数值随着x 的增大而减小、减小而增大。
即该函数为减函数。
3、一次函数图像的平移一次函数y=kx+b (k 、b 是常数,且k ≠0)的图象向上平移h 个单位后的函数解析式为y=kx+b+h;向下平移h 个单位后的函数解析式为y=kx+b-h 。
4、一次函数图像经过的象限示意图k 、b 的符号直线y=kx+b 经过的象限增减性一.基础练习:1. 一次函数y=3x-6的图像是 ,它与x 轴的交点坐标是 ,它与y 轴的交点坐标是2. 将直线y=x 向下平移4个单位,得到直线3. 将直线y=-3x-5向上平移4个单位,得到直线4. 若直线y=3x-5与直线y=kx-4相互平行,则k=5. 若直线y=-2x-5与直线y=6x+b 相交于y 轴上同一点,则b=6. 请你在不同的平面直角坐标系中画出下列函数的图像 (1)1105y x =+ (2)1722y x =+(3)4833y x =-- (4)1344y x =--7、已知一次函数2(4)20y m x m =-+-=和22(1)4y m x m =-+-的图像与y 轴的较交点到原点的距离相等,求m 的值。
《一次函数的图像和性质》一次函数PPT课件

②y=-3x+4, ④y=x-6;
①3 ④ ; 函数y随x的增大而增大的是__________
② 函数y随x的增大而减小的是___________ ; ① 图象在第一、二、三象限的是________ 。
小试牛刀 2、已知函数 y = kx的图象在二、四象限,那 么函数y = kx-k的图象可能是( B )
y
y
y
y
o
x
o
x
o
x
o
x
A
B
C
D
已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件 的m的值:
1 (1)函数值y 随x的增大而增大; m 2 1 (2)函数图象与y 轴的负半轴相交; m 1且m 2 (3)函数的图象过第二、三、四象限; 1 m 1 2 (4)函数的图象过原点。 m 1
一次函数y=kx+b (k‡0)的性质:
当k>0时,y随x的增大而增大;
y
x
一次函数y=kx+b (k‡0)的性质: 当k<0时,y随x的增大而减小. y
x
一次函数图象与性质
y
一 次 函 数 y=kx+b
图象
b
o
x
y o
y x
y x o
b
b
k>0 b<0
o
b
k<0 b<0
x
k,b的符号
k>0 b>0 一、二、三 y随x的增 大而增大
(1)直线y=3x-2可由直线y=3x向 下 平 移 2 单位得到。
(2)直线y=x+2可由直线y=x-1向 上 平 移 3 单位得到。
一次函数的图像与性质课件PPT
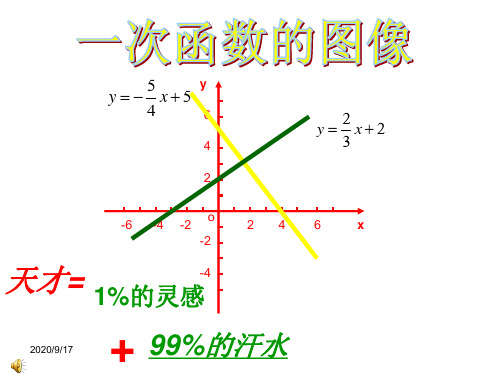
K不同 b相同 直线(图象)相交
y 1x2 2
y1x 2
y 1x2 2
y1x 2
K相同 b不同 直线(图象)平行
y 3x 2
y 3x
请比较下列函数y=x, y=x+2,y=x-2的图 象有什么异同点?
这几个函数的图象形状都 是 直线,并且倾斜程度_相_ 同_ 函数y=x的图象经过原点,函 数y=x+2的图象与y轴交于点 (__0_,_2),即它可以看作由直 线y=x向_上_平移 2 个单位长度 而得到.函数y=x-2的图象与 y轴交于点_(0,-_2)_,即它可 以看作由直线y=x向下 平移 __2__ 个单位长度而得到.
(当b>0时,向上平移;当b<0 时,向下平移)
直线y=kx+b与y轴相交于点(0, b), b叫做直线
y=kx+b在y轴上的截距,简称截距.
注意: 截距b不是距离,它可以是正数,也可以是负数或零.
b就是与y轴交点的纵坐标 正在原点上方,负在原点下方
k叫直线y=kx+b的斜率.
如何画出一次函数y=kx+b的图象?
在同一平面直角坐标系中画出下列函数的图象
1 y 1 x
2
y 1x2 2
2 y 1 x 2
2
y1x 2
3 y 3x
4 y 3x 2
y 3x 2 y 3x
一次函数y=kx+b (k≠0)的图象是一条直线,这条
直线通常又称为直线y=kx+b(k≠0)
正比例函数y=kx(k≠0)是经过原点(0,0)的一条
-4
x
平行
(3)直线y=2x+6与y=-x+6的位置关系如何?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数专项练习例1 (1)已知直线y=kx+b 经过点(3,-1)和点(-6,5),则k=_______,b=______.(2)已知一次函数y=kx+5过点P(-1,2),则k=________. 例2(1)一次函数1-=x y 的图象不经过( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限(2)如图,表示一次函数y =mx+n 与正比例函数y=mnx(m ,n 是常数,且 mn ≠0)图像的是( ).例3.直线y=kx+b 与直线y=5-4x 平行,且与直线y=-3(x-6)相交,交点在y 轴上,求此直线解析式。
例4. 已知函数221(43)3a a y a a x --=-++是一次函数,则a 的值为 ( )例5如图,一次函数y =kx +b (k <0)的图象经过点A .当y <3时,x 的取值范围是 .例6一个y 关于x 的函数同时满足两个条件:①图象过(2,1)点;②当0x >时.y 随x 的增大而减小,这个函数解析式为_______________ (写出一个即可)【知识点分类专练】知识点1:一次函数的定义:一次函数通常可以表示 的形式,其中k 、b 是 ,k 0.特别地,当 时,一次函数y =kx (常数k ≠0)也叫 .正比例函数也是一次函数,它是一次函数的特例. 1、下列函数:①y=-8x;②y=8x;③y=8x 2;④y=8x+1;⑤y=53++z x .其中是一次函数的有( )A.1个B.2个C.3个D.4个 2、(1)若函数y=(m —2)x+5是一次函数,则m 满足的条件是 。
(2)当m= 时,函数y=3x2m+1+3是一次函数。
(3)已知函数y=(k-1)x+k 2-1,当k________时,它是一次函数,当k=_______•时,它是正比例函数. (4) (1)2my m x=++,当m = ,y 是x 的一次函数.3、下列说法不正确的是( )A 一次函数不一定是正比例函数。
B 不是一次函数就一定不是正比例函数。
C 正比例函数是特殊的一次函数D 不是正比例函数就一定不是一次函数。
4、下列函数中一次函数的个数为( )①y=2x ;②y=3+4x ;③y=1/2;④y=ax (a≠0的常数);⑤xy=3;⑥2x+3y-1=0 A .3个 B.4个 C.5个 D.6个5、若一次函数1)1(2-+-=m x m y 的图象经过原点,则m 的值为( )A.-1B.1±C.1D.任意实数知识点2:一次函数图像1、已知一次函数y=kx+1()0k ≠的函数解析式中k<0,则一次函数y=x+k 的图象大致是图中的( )2、如图,函数y=kx+b ,其中k>0, kb<0,它的大致图象是( )A B3、若ab>0,bc<0,则直线y=a bx b c-- 经过( )A.第一、二、三象限B.第一、三、四象限C.第二、三、四象限D.第一、二、四象限4、如果一次函数y=kx+b 的图象经过第一、三、四象限,则 ( )A.k>0,b>0B.k>0,b <0C.k<0,b>0D.k<0,b<06、如图所示,若kb<0,且b-k>0,则函数y=kx+b 的大致图象是( )O Axy O Bxy O Cxy O Dxy7、已知函数y=x+b ,当b<0时,函数图象不经过( )A.第一象限B.第二象限B.第三象限C.第四象限8、已知直线y=kx+b(k≠0)与x 轴的交点在x 轴的正半轴上,下列结论: ①k>0,b> 0;②k<0,b>0;③k>0,b<0;④k<0,b<0,其中正确的有( ) A.1个 B.2个 C.3个 D.4个知识点3:一次函数的性质⑴正比例函数y=kx (k ≠0)是特殊的一次函数,当k>0时,图象过______象限,y 随x 的增大而__ __; 当k<0时,图象过______象限;y 随x 的增大而 ___.⑵一次函数y=kx+b(k ≠ 0)的图象平行于直线y = kx ,可由它平移而得, 当k>0时,y 随x 的增大而_______ __; 当k<0时,y 随x 的增大而____ _____.1.已知一次函数21y x =+,则y 随x 的增大而_______________(填“增大”或“减D小”).2.有下列函数:①y=2x, ②y=-2x+1,③y=x+5, ④ y=2x-3 。
其中过原点的直线是_____;函数y 随x 的增大而增大的是___________;函数y 随x 的增大而减小的是______;图象过第一、二、三象限的是_____;互相平行的直线是____ _______。
3.一次函数(26)5y m x =-+中,y 随x 的增大而减小,则m 的取值范围是________. 4、一次函数y=-6+x 中,y 随x 的增大而_________. 5、一次函数y=12-x+5中,y 随x 的增大而________. 6、若函数y=kx 的图象经过第二、四象限,则函数y=-kx-2的图象不经过第_______象限. 7、如果一次函数y=(m-1)x+(n- 2) 的图象不经过第一象限, 则m 的取值范围是_______,n 的取值范围是_________.8、点p 1(x 1,y 1)和点p 2(x 2,y 2)是一次函数y= - 4x+3图象上的两个点,且x 1<x 2,则y 1与y 2的大小关系是( )A. y 1>y 2B. y 1>y 2>0C. y 1<y 2D. y 1=y 2四【中考题中图像与性质的题型】1.已知一次函数y =mx +n -2的图象如图所示,则m .n 的取值范围是( ) A .m >0,n <2 B .m >0,n >2 C .m <0,n <2 D .m <0,n >22.关于一次函数y=-x+1的图像,下列所画正确的是( ).3.直线y =x ﹣1的图象经过的象限是( )A 、第一、二、三象限B 、第一、二、四象限C 、第二、三、四象限D 、第一、三、四象限4.已知一次函数y =kx +b 的图象经过第一、二、三象限,则b 的值可以是( ) A.﹣2 B.﹣1 C.0 D.25.如图的坐标平面上有四直线L 1、L 2、L 3、L 4.若这四直线中,有一直线为方程式3x ﹣5y+15=0的图形,则此直线为何?( )A 、L 1B 、L 2C 、L 3D 、L 46.在平面直角坐标系xOy 中,点P (2,a )在正比例函 数x y 21=的图象上,则点Q (a ,3a -5)位于第 象限. 7.(2011四川雅安,10,3分)已知一次函数y=kx+b ,k 从2,﹣3中随机取一个 值,b 从1,﹣1,﹣2中随机取一个值,则该一次函数的图象经过二、三、四象 限的概率为( )A.13B.23 C.16D.12五【当堂小测验】一、选择题:1. 两个一次函数①1y ax b =+与②2y bx a =+在同一坐标系中的大致图象是( )2. 点1(5,)A y -和2(2,)B y -都在直线32y x =-+上,则1y 与2y 的关系式是( ) A.12y y ≤B.12y y =C.12y y <D.12y y >3. 如图,,OA BA 分别表示甲、乙两名学生运动的一次函数图象,图中s 和t 分别表示运动的路程和时间,根据图象判断快者的速度比慢者的速度每秒快( ) A. 2.5m B. 2m C. 1.5m D. 1mxyOA.xyOD.xy O C.xyO4. 已知一次函数(2)(1)y m x m =++-,若y 随x 的增大而减小,且该函数图象与x 轴的交点在原点右侧,则m 的取值范围是( )A.2m >-B.1m <C.21m -<<D.2m <-5. 无论m 为何实数,直线2y x m =+与直线4y x =-+的交点都不可能在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限二、填空题:6. 一条直线过点(2,3)A -和点(3,2)B -,则该直线的解析式为____________________;7. 直线y kx b =+与直线0.5y x =平行,且与直线32y x =+交于点(0,2),则该直线的函数关系式是_____________8. 直线4y x =+和直线4y x =-+与x 轴所围成的三角形的面积为____________; 9. 若点(1,3)A 、(2,0)B -、(2,)C a 在一条直线上,则a =_____________; 10. 已知直线:32L y x =-+,现有4个命题:①点3(,0)2P -在直线L 上;②直线L 可以由直线31y x =-+向上平行移动1个单位长度得到;③若点1(,1)3M 、(,)N a b 都在直线L 上,且13a >,则1b <;④若点Q 到两坐标轴的距离相等,且点Q 在直线L 上,则点Q 在第一或第四象限。
其中正确的命题是__________________。
三、解答题:如图,直线6y kx =+与x 轴、y 轴分别交于点,E F ,点E 的坐标为(8,0)-,点A 的坐标为(6,0)-。
(1)求k 的值; (2)若点(,)P x y 是第二象限内直线上的一个动点,在点P 运动过程中,试写出OPA ∆的面积S 与x 的函数关系式,并写出自变量x 的取值范围;(3)当点P 运动到什么位置时,OPA ∆的面积为278,并说明理由。
xyOFE A。
