初二数学经典几何题型及答案
初二几何考试题及答案

初二几何考试题及答案一、选择题(每题3分,共15分)1. 在一个直角三角形中,一个锐角是30°,另一个锐角的度数是多少?A. 60°B. 45°C. 30°D. 90°答案:A2. 一个等腰三角形的底边长为6厘米,腰长为8厘米,那么这个三角形的周长是多少?A. 22厘米B. 26厘米C. 30厘米D. 34厘米答案:B3. 下列哪个图形是轴对称图形?A. 平行四边形B. 等腰梯形C. 任意三角形D. 不规则五边形答案:B4. 一个圆的半径为5厘米,那么这个圆的面积是多少?A. 78.5平方厘米B. 25π平方厘米C. 50π平方厘米D. 100π平方厘米答案:C5. 一个等边三角形的边长为10厘米,那么这个三角形的高是多少?A. 5厘米B. 10厘米C. 15厘米D. 20厘米答案:C二、填空题(每题3分,共15分)6. 一个等腰三角形的两个底角相等,如果一个底角为40°,那么顶角的度数是________。
答案:100°7. 一个圆的周长为31.4厘米,那么这个圆的半径是________厘米。
答案:58. 在一个平行四边形中,如果一组对边的长度分别为8厘米和6厘米,那么这个平行四边形的周长是________厘米。
答案:289. 一个直角三角形的两条直角边长分别为3厘米和4厘米,那么这个三角形的斜边长是________厘米。
答案:510. 一个扇形的圆心角为60°,半径为4厘米,那么这个扇形的面积是________平方厘米。
答案:6.28三、解答题(每题10分,共20分)11. 已知一个等腰三角形的底边长为10厘米,腰长为12厘米,求这个三角形的面积。
解答:首先,我们需要找到等腰三角形的高。
由于等腰三角形的两个底角相等,我们可以将底边平分,得到两个直角三角形。
每个直角三角形的底边为5厘米(10厘米的一半),斜边为12厘米。
初二数学空间几何练习题及答案

初二数学空间几何练习题及答案1. 问题描述:一辆汽车从A地出发,以每小时60千米的速度向东行驶3小时后,在B地停留一小时,然后以每小时80千米的速度向南行驶4小时。
求汽车最后所在的位置离出发点的距离和方向角。
解答:首先,根据题目可知,汽车向东行驶的距离为60千米/小时× 3小时 = 180千米。
然后,在B地停留一小时后,汽车向南行驶的距离为80千米/小时 × 4小时 = 320千米。
由此可得出汽车最后所在位置的坐标为(180, -320)。
根据坐标计算公式,最后所在位置离出发点的距离可以使用勾股定理计算:√[(180)^2 + (-320)^2] ≈ 363.66千米。
根据反正切函数,最后所在位置相对于东方向的方向角可以计算为:tan^(-1)(-320/180) ≈ -59.04°。
因此,汽车最后所在的位置离出发点的距离约为363.66千米,方向角为-59.04°。
2. 问题描述:一个长方体的长、宽、高分别为5厘米、3厘米和2厘米。
求该长方体的表面积和体积。
解答:首先,根据长方体的定义,它有6个面,包括上下底面、前后面和左右侧面。
上下底面的面积为5厘米 × 3厘米 = 15平方厘米。
前后面的面积为5厘米 × 2厘米 = 10平方厘米。
左右侧面的面积为3厘米 × 2厘米 = 6平方厘米。
因此,长方体的表面积为15平方厘米 + 15平方厘米 + 10平方厘米 + 10平方厘米 + 6平方厘米 + 6平方厘米 = 62平方厘米。
其次,长方体的体积可以通过计算长、宽、高的乘积得到:5厘米 × 3厘米 × 2厘米 = 30立方厘米。
因此,该长方体的表面积为62平方厘米,体积为30立方厘米。
3. 问题描述:一根铁丝长12米,将它围绕一个底面为直径2米的圆柱体卷了一圈,并围成一个长方体。
求该长方体的体积。
解答:首先,根据题目可知,铁丝的长度等于长方体的周长,也就是2πr,其中r为圆柱体的半径。
初二几何经典难题集锦(含答案)

初二几何经典训练题1、如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.⑴求证:四边形ABFE是等腰梯形;⑵求AE的长.2、如图,矩形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OB的中点.(1)求证:△ADE≌△BCF;(2)若AD=4cm,AB=8cm,求CF和OF的长。
3、如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=12cm,BC=8cm,DC=13cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为ycm2.(1)求A D的长及t的取值范围;(2)当1.5≤t≤t0(t0为(1)中t的最大值)时,求y关于t的函数关系式;(3)请具体描述:在动点P、Q的运动过程中,△PQB的面积随着t的变化而变化的规律。
4、如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,GF与AB相交于点G,若CF=15cm,求GF 之长。
5、如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE =∠C。
(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,求AE的长;(3)在(1)、(2)的条件下,若AD=3,求BF的长(计算结果可含根号)。
6、如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA =15mm,DO=24mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离。
7、如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,(1)若AB=6,求线段BP的长;(2)观察图形,是否有三角形与△ACQ全等?并证明你的结论.8、如图已知点E、F在△ABC的边AB所在的直线上,且AE=BF,FH∥FG∥AC,FH、EG分别交边BC所在的直线于点H、G。
几何初二试题及答案

几何初二试题及答案一、选择题1. 已知一个三角形的两边长分别为3和4,第三边的长x满足的不等式是:A. 1 < x < 7B. 4 < x < 7C. 1 < x < 4D. 3 < x < 7答案:D2. 一个圆的半径为5cm,那么这个圆的周长是多少?A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案:D3. 已知一个矩形的长为6cm,宽为4cm,那么这个矩形的面积是多少?A. 20cm²B. 24cm²C. 18cm²D. 16cm²答案:B二、填空题1. 平行四边形的对角线互相______。
答案:平分2. 如果一个角的度数是30°,那么它的余角是______。
答案:60°3. 一个直角三角形的两条直角边分别为3和4,那么它的斜边长是______。
答案:5三、简答题1. 描述如何使用勾股定理来计算直角三角形的斜边长。
答案:首先确定直角三角形的两条直角边的长度,设为a和b。
根据勾股定理,斜边c的长度可以通过公式c = √(a² + b²) 来计算。
2. 解释什么是相似三角形,并给出一个例子。
答案:相似三角形是指两个三角形的对应角相等,对应边的比例相等的三角形。
例如,如果三角形ABC与三角形DEF的角A等于角D,角B等于角E,角C等于角F,并且边AB与边DE、边BC与边EF、边AC与边DF的长度比例相等,那么这两个三角形就是相似的。
四、解答题1. 已知一个等腰三角形的底边长为10cm,两腰的长度为13cm,求这个三角形的面积。
答案:首先,我们可以将等腰三角形分成两个直角三角形,通过底边的中点。
这样,每个直角三角形的底边长度为5cm,斜边为13cm。
根据勾股定理,我们可以计算出高h:h = √(13² - 5²) = √(169 - 25) = √144 = 12cm。
(完整版)八年级数学几何经典题【含答案】
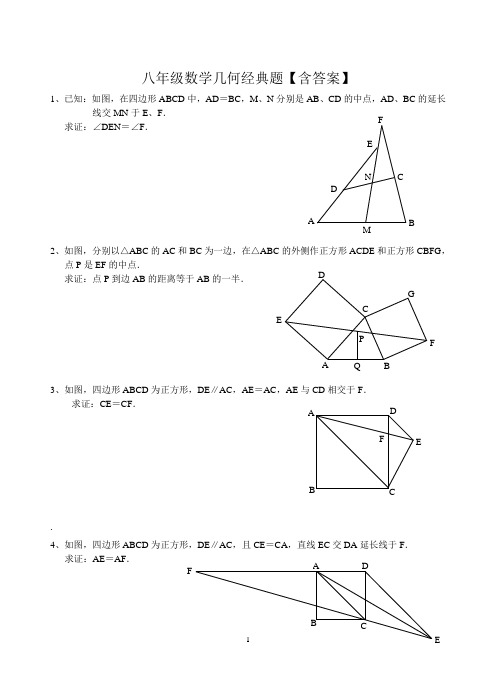
F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
初二几何试题及答案

初二几何试题及答案1. 已知三角形ABC中,AB=AC,D是BC边上的中点。
求证:AD垂直于BC。
答案:因为AB=AC,所以三角形ABC是等腰三角形。
根据等腰三角形的性质,底边的中线、高线和角平分线重合。
因此,AD既是BC边上的中线,也是高线,所以AD垂直于BC。
2. 一个矩形的长是宽的两倍,且对角线长为10cm。
求矩形的长和宽。
答案:设矩形的宽为x cm,则长为2x cm。
根据勾股定理,对角线的长度满足方程x^2 + (2x)^2 = 10^2。
解得x^2 + 4x^2 = 100,即5x^2 = 100,所以x^2 = 20,x = √20。
因此,矩形的宽为√20 cm,长为2√20 cm。
3. 一个圆的直径是10cm,求这个圆的面积。
答案:圆的面积公式为A = πr^2,其中r是圆的半径。
因为直径是10cm,所以半径r = 10/2 = 5cm。
代入公式得A = π * 5^2 = 25π cm^2。
4. 一个梯形的上底是8cm,下底是12cm,高是5cm。
求梯形的面积。
答案:梯形的面积公式为A = (a + b) * h / 2,其中a和b分别是上底和下底的长度,h是高。
代入数据得A = (8 + 12) * 5 / 2 = 20 * 5 / 2 = 50 cm^2。
5. 已知一个直角三角形的两条直角边分别是6cm和8cm,求斜边的长度。
答案:根据勾股定理,斜边的长度c满足方程c^2 = a^2 + b^2,其中a和b分别是两条直角边的长度。
代入数据得c^2 = 6^2 + 8^2 = 36+ 64 = 100,所以c = √100 = 10cm。
6. 一个正六边形的边长是4cm,求它的面积。
答案:正六边形可以被分成6个等边三角形,每个等边三角形的边长都是4cm。
等边三角形的面积公式为A = (√3 / 4) * a^2,其中a是边长。
因此,正六边形的面积为6 * (√3 / 4) * 4^2 = 6 * √3 * 4 = 24√3 cm^2。
[初二数学几何试题](含答案)
](https://img.taocdn.com/s3/m/03755b4f6fdb6f1aff00bed5b9f3f90f76c64df5.png)
初二数学几何试题一、选择题(每题2分,共20分)1. 在下列图形中,哪一个不是平面图形?A. 三角形B. 四边形C. 球体D. 圆形2. 下列哪个图形的周长等于其直径的两倍?A. 正方形B. 长方形C. 圆形D. 等边三角形3. 下列哪个角度不是锐角?A. 45度B. 60度C. 90度D. 120度4. 下列哪个图形不是轴对称图形?A. 矩形B. 梯形C. 正方形D. 圆形5. 下列哪个图形不是中心对称图形?A. 正方形B. 长方形C. 等边三角形D. 矩形6. 下列哪个图形不是旋转对称图形?A. 正方形B. 矩形C. 等边三角形D. 圆形7. 下列哪个图形的面积不是边长的平方?A. 正方形B. 长方形C. 矩形D. 圆形8. 下列哪个图形的周长不是边长的两倍?A. 正方形B. 长方形C. 矩形D. 圆形9. 下列哪个图形的内角和不是360度?A. 四边形B. 五边形C. 六边形D. 七边形10. 下列哪个图形的对角线长度不等于边长的平方根的两倍?A. 正方形B. 长方形C. 矩形D. 圆形二、填空题(每题2分,共20分)1. 一个正方形的边长是5厘米,那么它的周长是______厘米,面积是______平方厘米。
2. 一个长方形的长是8厘米,宽是4厘米,那么它的周长是______厘米,面积是______平方厘米。
3. 一个圆的半径是3厘米,那么它的周长是______厘米,面积是______平方厘米。
4. 一个等边三角形的边长是6厘米,那么它的周长是______厘米,面积是______平方厘米。
5. 一个直角三角形的两个直角边分别是3厘米和4厘米,那么它的斜边长度是______厘米,面积是______平方厘米。
6. 一个梯形的上底是5厘米,下底是10厘米,高是4厘米,那么它的面积是______平方厘米。
7. 一个平行四边形的底是6厘米,高是8厘米,那么它的面积是______平方厘米。
8. 一个正六边形的边长是4厘米,那么它的周长是______厘米,面积是______平方厘米。
初二几何经典试题及答案

初二几何经典试题及答案一、选择题1. 下列关于线段的说法,正确的是()A. 线段是直线的一部分B. 线段有两个端点C. 线段可以无限延长D. 线段是有限长的答案:B2. 一个三角形的内角和为()A. 90°B. 180°C. 360°D. 720°答案:B3. 一个圆的半径是3,那么它的直径是()A. 6B. 9C. 12D. 15答案:A二、填空题4. 已知一个直角三角形的两直角边长分别为3和4,那么斜边的长度是____。
答案:55. 一个圆的周长是6.28,那么它的半径是____。
答案:16. 一个等腰三角形的底角为45°,那么它的顶角是____。
答案:90°三、解答题7. 已知一个等腰三角形的底边长为6,两腰长为5,求三角形的面积。
答案:首先,我们可以利用勾股定理求出高,即高=√(5² - (6/2)²) = √(25 - 9) = √16 = 4。
然后,三角形的面积=(底边长×高)/2= (6×4)/2 = 12。
8. 已知一个圆的半径为7,求圆的面积。
答案:圆的面积=πr² = 3.14×7² = 3.14×49 = 153.86。
9. 已知一个正方形的对角线长为10,求正方形的面积。
答案:首先,我们可以利用勾股定理求出正方形的边长,即边长=√(10²/2) = √50。
然后,正方形的面积=边长² = 50。
四、证明题10. 证明:等腰三角形的两个底角相等。
答案:设等腰三角形的顶角为A,底角分别为B和C。
因为AB=AC,所以三角形ABC是等腰三角形。
根据等腰三角形的性质,底角B和C相等,即B=C。
11. 证明:圆的直径是圆内最长的弦。
答案:设圆的直径为AB,圆心为O,弦CD。
因为OA=OB,所以∠AOB=∠BOC。
又因为∠AOB=2∠COD,所以∠COD<∠AOB。
(完整版)八年级数学几何经典题【含答案】

F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
初二数学几何试题及答案

初二数学几何试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是直角三角形的判定条件?A. 两角之和为90°B. 两边之和大于第三边C. 斜边的平方等于两直角边的平方和D. 任意两边之和大于第三边2. 一个圆的半径是5厘米,那么它的直径是:A. 10厘米B. 15厘米C. 20厘米D. 25厘米3. 如果一个三角形的三个内角分别为40°、60°和80°,那么这个三角形是:A. 直角三角形B. 钝角三角形C. 锐角三角形D. 不能确定4. 一个矩形的长是10厘米,宽是6厘米,那么它的面积是:A. 60平方厘米B. 100平方厘米C. 120平方厘米D. 150平方厘米5. 一个等腰三角形的底边长为8厘米,腰长为5厘米,那么它的高是:A. 3厘米B. 4厘米C. 6厘米D. 8厘米6. 一个正方形的对角线长度为10厘米,那么它的边长是:A. 5厘米B. 7.07厘米C. 8厘米D. 10厘米7. 一个梯形的上底是4厘米,下底是8厘米,高是6厘米,那么它的面积是:A. 12平方厘米B. 24平方厘米C. 30平方厘米D. 40平方厘米8. 一个平行四边形的对角线互相垂直,那么这个平行四边形是:A. 矩形B. 菱形C. 正方形D. 梯形9. 一个正五边形的内角和是:A. 540°B. 720°C. 900°D. 1080°10. 一个圆的周长是62.8厘米,那么它的半径是:A. 10厘米B. 11厘米C. 12厘米D. 13厘米二、填空题(每题4分,共20分)1. 如果一个三角形的两个内角分别为30°和60°,那么第三个内角是______°。
2. 一个圆的周长是31.4厘米,那么它的直径是______厘米。
3. 一个直角三角形的两条直角边长分别为3厘米和4厘米,那么它的斜边长是______厘米。
初二数学试题及答案几何

初二数学试题及答案几何初二数学试题及答案(几何)一、选择题(每题2分,共10分)1. 在直角三角形中,如果一个锐角是30°,那么另一个锐角的度数是多少?A. 30°B. 45°C. 60°D. 90°答案:C2. 一个圆的半径是5厘米,那么这个圆的周长是多少?A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案:C3. 如果一个平行四边形的对角线互相平分,那么这个平行四边形是:A. 矩形B. 菱形C. 正方形D. 梯形答案:A4. 一个正多边形的内角和是900°,那么这个多边形的边数是多少?A. 6B. 8C. 10D. 12答案:B5. 在一个三角形中,如果两个内角的度数之和是90°,那么第三个内角的度数是多少?A. 45°B. 90°C. 180°D. 不能确定答案:B二、填空题(每题2分,共10分)1. 一个圆的直径是10厘米,那么这个圆的半径是________厘米。
答案:52. 如果一个三角形的三边长分别为3厘米、4厘米、5厘米,那么这个三角形是________三角形。
答案:直角3. 一个正六边形的内角是________度。
答案:1204. 一个长方形的长是8厘米,宽是4厘米,那么这个长方形的面积是________平方厘米。
答案:325. 如果一个圆的周长是31.4厘米,那么这个圆的直径大约是________厘米。
答案:10三、简答题(每题5分,共15分)1. 请解释什么是相似三角形,并给出一个例子。
答案:相似三角形是指两个三角形的对应角相等,对应边成比例的三角形。
例如,如果有两个三角形,它们的三个内角都是45°、45°和90°,那么这两个三角形就是相似的。
2. 圆的面积公式是什么?请用一个圆的半径为r来表示。
答案:圆的面积公式是A = πr²,其中A表示面积,r表示半径。
(完整word版)初二数学经典几何题型及答案

初二数学经典几何题型1.已知:如图, P 是正方形ABCD内点,∠ PAD=∠ PDA= 150.求证:△ PBC是正三角形.证明以下。
第一, PA=PD,∠ PAD=∠ PDA=(180° - 150°)÷2=15°,∠PAB=90° - 15°=75°。
A D 在正方形ABCD以外以 AD为底边作正三角形ADQ,连结PQ,则P∠P DQ=60°+15°=75°,相同∠ PAQ=75°,又 AQ=DQ,,PA=PD,因此△PAQ≌△ PDQ,那么∠ PQA=∠PQD=60°÷ 2=30°,在△ PQA中,∠A PQ=180° - 30° - 75°=75°=∠ PAQ=∠ PAB,于是 PQ=AQ=AB,明显△ PAQ≌△ PAB,得∠ PBA=∠PQA=30°,PB=PQ=AB=BC,∠ PBC=90° - 30°=60°,因此△PBC是正三角形。
BC2.已知:如图,在四边形 ABCD中, AD=BC,M、N 分别是 AB、CD的中点, AD、BC的延伸线交 MN于 E、F.求证:∠ DEN=∠ F.F证明 : 连结 AC,并取 AC的中点 G,连结 GF,GM.又点 N为 CD的中点 , 则 GN=AD/2;GN∥ AD,∠GNM=∠ DEM;(1)同理 :GM=BC/2;GM∥ BC,∠ GMN=∠ CFN;(2)又 AD=BC,则 :GN=GM,∠ GNM=∠ GMN故. : ∠ DEM=∠ CFN.3、如图,分别以△ABC的 AC和 BC为一边,在△ ABC的外侧作正方形的中点.求证:点 P 到边 AB的距离等于 AB的一半.EN CDA BMACDE和正方形CBFG,点 P 是 EF证明:分别过 E、 C、 F 作直线 AB 的垂线,垂足分别为 M、 O、 N,在梯形 MEFN中, WE平行 NF由于 P为 EF 中点, PQ平行于两底因此 PQ为梯形 MEFN中位线,因此 PQ=( ME+ NF) /2又由于,角 0CB+角 OBC=90°=角 NBF+角 CBO因此角 OCB=角 NBF而角 C0B=角 Rt=角 BNFCB=BF因此△ OCB全等于△ NBF△MEA全等于△OAC(同理)因此 EM= AO, 0B= NF因此 PQ=AB/2.4、设 P 是平行四边形ABCD内部的一点,且∠PBA=∠ PDA.求证:∠DGCEP FA Q BPAB=∠ PCB.过点 P作 DA的平行线,过点 A 作 DP的平行线,二者订交于点E;连结 BE由于 DP//AE, AD//PE因此,四边形 AEPD为平行四边形A D 因此,∠ PDA=∠AEP已知,∠ PDA=∠PBAP因此,∠ PBA=∠AEP因此, A、 E、 B、 P 四点共圆B C因此,∠ PAB=∠PEB由于四边形 AEPD为平行四边形,因此:PE//AD,且 PE=AD而,四边形 ABCD为平行四边形,因此:AD//BC,且 AD=BC因此, PE//BC ,且 PE=BC即,四边形 EBCP也是平行四边形因此,∠ PEB=∠PCB因此,∠ PAB=∠PCB5.P 为正方形ABCD内的一点,而且PA= a, PB= 2a, PC=3a正方形的边长.解:将△ BAP绕 B 点旋转 90°使 BA 与 BC重合, P 点旋转后到 Q点,连结 PQ 由于△ BAP≌△ BCQ因此 AP= CQ, BP= BQ,∠ ABP=∠ CBQ,∠ BPA=∠BQC 由于四边形 DCBA是正方形因此∠ CBA=90°,因此∠ ABP+∠ CBP=90°,因此∠ CBQ+∠ CBP=90°即∠ PBQ=90°,因此△ BPQ是等腰直角三角形因此 PQ=√ 2*BP,∠ BQP= 45由于 PA=a, PB=2a, PC=3a因此 PQ=2√2a, CQ= a,因此 CP^2= 9a^2, PQ^2+CQ^2= 8a^2+ a^2=9a^2因此 CP^2= PQ^2+ CQ^2,因此△ CPQ是直角三角形且∠ CQA=90°因此∠ BQC=90°+ 45°= 135°,因此∠BPA=∠ BQC=135°作 BM⊥ PQ则△ BPM是等腰直角三角形因此 PM= BM=PB/√2=2a/ √2=√ 2a因此依据勾股定理得:AB^2=AM^2+ BM^2=(√2a+ a)^2 +( √2a)^2=[5 +2√2]a^2A DPBC因此 AB=[ √(5 +2√2)]a6.一个圆柱形容器的容积为 V 立方米,开始用一根小水管向容器内灌水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管灌水。
八年级数学几何经典题【含答案】
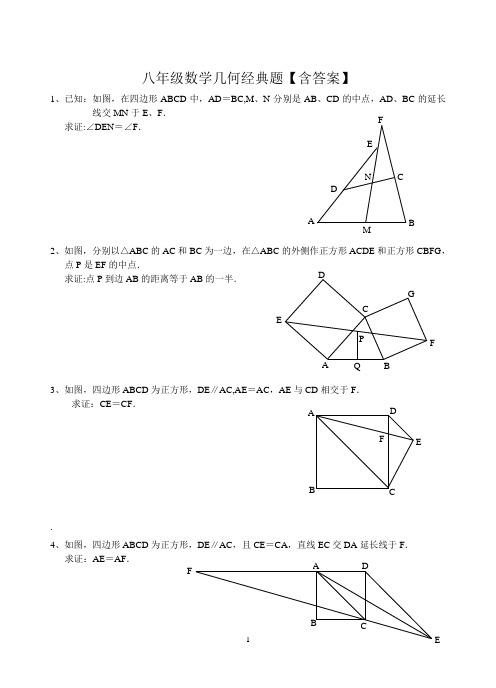
F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC ,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1。
如下图连接AC 并取其中点Q ,连接QN 和QM,所以可得∠QMF=∠F,∠QNM=∠DEN 和∠QMN=∠QNM,从而得出∠DEN =∠F 。
2。
过E,C ,F 点分别作AB 所在直线的高EG,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI,由△BFH ≌△CBI ,可得FH=BI.从而可得PQ=2AI BI=2AB,从而得证。
初二数学几何试题及答案解析

初二数学几何试题及答案解析一、选择题(每题3分,共15分)1. 下列哪个选项是矩形的性质?A. 对角线相等B. 对边平行C. 对角线互相垂直D. 四个角都是直角答案:D解析:矩形的定义是四个角都是直角的平行四边形,因此选项D是正确的。
2. 一个三角形的两边长分别为3和4,第三边的长度可能是多少?A. 1B. 7C. 5D. 6答案:C解析:根据三角形的三边关系,任意两边之和大于第三边,任意两边之差小于第三边。
因此,第三边的长度应该在1和7之间,即1 < 第三边 < 7。
选项C的5满足这个条件。
3. 一个等腰三角形的底角为45°,那么顶角的度数是多少?A. 45°B. 90°C. 60°D. 135°答案:B解析:等腰三角形的两个底角相等,所以另一个底角也是45°。
三角形内角和为180°,所以顶角的度数为180° - 45° - 45° = 90°。
4. 一个圆的半径为5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π答案:B解析:圆的面积公式为A = πr²,其中r是半径。
将半径5代入公式,得到面积为π × 5² = 25π。
因此,正确答案是B。
5. 下列哪个选项是菱形的性质?A. 对角线相等B. 对角线互相垂直C. 对边平行D. 四个角都是直角答案:B解析:菱形的定义是四边相等且对角线互相垂直的平行四边形,因此选项B是正确的。
二、填空题(每题3分,共15分)6. 一个等边三角形的内角和为______。
答案:180°解析:任何三角形的内角和都是180°,等边三角形也不例外。
7. 如果一个直角三角形的两条直角边长分别为6和8,那么斜边的长度为______。
答案:10解析:根据勾股定理,直角三角形的斜边长度等于两直角边长度的平方和的平方根。
初二几何经典试题及答案

初二几何经典试题及答案一、选择题1. 在一个直角三角形中,如果一个锐角是30°,那么另一个锐角的度数是()。
A. 30°B. 60°C. 90°D. 120°答案:B解析:直角三角形中两个锐角互为余角,所以另一个锐角为90°-30°=60°。
2. 一个等腰三角形的两边长分别为3cm和6cm,那么这个三角形的周长是()。
A. 9cmB. 12cmC. 15cmD. 18cm答案:D解析:等腰三角形的两边相等,所以底边为3cm,腰长为6cm,周长为3cm+6cm+6cm=15cm。
3. 一个平行四边形的对角线互相平分,那么这个平行四边形是()。
A. 矩形B. 菱形C. 正方形D. 任意平行四边形答案:D解析:平行四边形的对角线互相平分是平行四边形的基本性质,所以这个平行四边形可以是任意平行四边形。
二、填空题4. 如果一个三角形的三边长分别为a、b、c,且满足a²+b²=c²,那么这个三角形是______三角形。
答案:直角解析:根据勾股定理,如果一个三角形的三边长满足a²+b²=c²,那么这个三角形是直角三角形。
5. 在一个矩形中,如果长为6cm,宽为4cm,那么这个矩形的对角线长为_______cm。
答案:5解析:根据勾股定理,矩形的对角线长为√(6²+4²)=√(36+16)=√52=5cm。
三、计算题6. 已知一个等腰三角形的底边长为8cm,腰长为10cm,求这个等腰三角形的面积。
答案:24cm²解析:等腰三角形的高可以通过勾股定理求得,高h=√(10²-(8/2)²)=√(100-16)=√84=2√21cm。
等腰三角形的面积S=1/2×底×高=1/2×8cm×2√21cm=24cm²。
初二几何测试题及答案大全

初二几何测试题及答案大全一、选择题(每题2分,共10分)1. 下列哪个选项表示的是线段?A. 直线的一部分B. 射线的一部分C. 线段的一部分D. 曲线的一部分答案:A2. 一个角的度数是30°,这个角是:A. 锐角B. 直角C. 钝角D. 平角答案:A3. 一个三角形的两边长分别是3厘米和4厘米,第三边的长度可能为:A. 1厘米B. 5厘米C. 7厘米D. 9厘米答案:B4. 一个圆的半径是5厘米,那么这个圆的直径是:A. 10厘米B. 15厘米C. 20厘米D. 25厘米答案:A5. 下列哪个选项是平行四边形的性质?A. 对边相等B. 对角相等C. 对边平行D. 所有选项都是答案:D二、填空题(每题1分,共10分)6. 平行四边形的对角线______。
答案:互相平分7. 如果一个三角形的三边长分别为a、b、c,那么这个三角形的周长是______。
答案:a+b+c8. 一个圆的周长公式是______。
答案:2πr9. 直角三角形的两条直角边的平方和等于______。
答案:斜边的平方10. 如果一个角是直角的一半,那么这个角是______。
答案:45°三、计算题(每题5分,共15分)11. 已知一个三角形的两边长分别为6厘米和8厘米,如果这个三角形是直角三角形,求第三边的长度。
答案:根据勾股定理,第三边的长度为√(8² - 6²) = √(64 - 36) = √28 ≈ 5.29厘米。
12. 已知一个圆的直径为10厘米,求这个圆的面积。
答案:圆的面积公式为πr²,其中r为半径,即直径的一半,所以面积为π×(10/2)² = 25π ≈ 78.54平方厘米。
13. 已知一个平行四边形的对边分别为5厘米和7厘米,求这个平行四边形的面积,如果高为4厘米。
答案:平行四边形的面积公式为底×高,所以面积为5×4 = 20平方厘米。
(完整版)初中数学几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)E经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)D经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。
初二几何经典试题及答案

初二几何经典试题及答案一、选择题1. 若一个三角形的两边长分别为3和5,第三边的长为整数,则第三边的长可能是()。
A. 2B. 4C. 6D. 7答案:B解析:根据三角形的三边关系,任意两边之和大于第三边,任意两边之差小于第三边。
所以第三边的长应该在2和8之间(不包括2和8),即2<第三边<8。
因此,第三边的长可能是4。
2. 已知一个等腰三角形的两边长分别为4和6,那么这个三角形的周长可能是()。
A. 14B. 16C. 18D. 20答案:C解析:等腰三角形的两边相等,所以有两种情况:①4是腰长,6是底边长,周长=4+4+6=14;②6是腰长,4是底边长,周长=6+6+4=16。
因此,这个三角形的周长可能是14或16。
3. 一个多边形的内角和是外角和的3倍,那么这个多边形的边数是()。
A. 5B. 6C. 7D. 8答案:B解析:多边形的外角和是360°,内角和是外角和的3倍,即内角和为1080°。
根据多边形内角和公式(n-2)×180°,可得(n-2)×180°=1080°,解得n=8。
因此,这个多边形的边数是8。
二、填空题4. 一个三角形的三个内角的度数之比为2:3:4,那么这个三角形的三个内角分别是______。
答案:36°,54°,90°解析:设三个内角分别为2x,3x,4x,根据三角形内角和为180°,可得2x+3x+4x=180°,解得x=20°。
因此,三个内角分别为36°,54°,90°。
5. 一个等腰三角形的底角为40°,那么这个三角形的顶角为______。
答案:100°解析:等腰三角形的两个底角相等,所以另一个底角也是40°。
根据三角形内角和为180°,可得顶角=180°-40°-40°=100°。
初二数学试题及答案几何

初二数学试题及答案几何初二数学试题及答案(几何)一、选择题(每题3分,共30分)1. 下列哪个图形是轴对称图形?A. 平行四边形B. 等腰三角形C. 矩形D. 任意四边形答案:B2. 一个角的补角是它的余角的三倍,这个角的度数是多少?A. 30°B. 45°C. 60°D. 90°答案:C3. 已知一个直角三角形的两条直角边长分别为3和4,那么斜边的长度是多少?A. 5B. 6C. 7D. 8答案:A4. 一个等腰三角形的底角是70°,那么顶角的度数是多少?A. 40°B. 70°C. 80°D. 90°答案:A5. 如果一个三角形的两边长分别为5和7,且第三边长为整数,那么第三边的可能长度是多少?A. 1, 2, 3, 4, 5, 6, 7, 8B. 2, 3, 4, 5, 6, 7, 8C. 3, 4, 5, 6, 7, 8D. 4, 5, 6, 7, 8答案:C6. 一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 20π厘米C. 25π厘米D. 30π厘米答案:C7. 一个扇形的圆心角是60°,半径是10厘米,那么这个扇形的面积是多少?A. 50π平方厘米B. 100π平方厘米C. 150π平方厘米D. 200π平方厘米答案:A8. 如果一个多边形的内角和是900°,那么这个多边形有多少条边?A. 5B. 6C. 7D. 8答案:C9. 一个正五边形的每个内角的度数是多少?A. 108°B. 120°C. 144°D. 150°答案:A10. 一个正方形的对角线长度是10厘米,那么它的边长是多少?A. 5厘米B. 7.07厘米C. 10厘米D. 14.14厘米答案:B二、填空题(每题3分,共30分)11. 一个等腰三角形的顶角是120°,那么它的底角是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A PC DBF 初二数学经典几何题型1.已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.证明如下。
首先,PA=PD ,∠PAD=∠PDA=(180°-150°)÷2=15°,∠PAB=90°-15°=75°。
在正方形ABCD 之外以AD 为底边作正三角形ADQ , 连接PQ , 则∠PDQ=60°+15°=75°,同样∠PAQ=75°,又AQ=DQ,,PA=PD ,所以△PAQ ≌△PDQ , 那么∠PQA=∠PQD=60°÷2=30°,在△PQA 中,∠APQ=180°-30°-75°=75°=∠PAQ=∠PAB ,于是PQ=AQ=AB , 显然△PAQ ≌△PAB ,得∠PBA=∠PQA=30°,PB=PQ=AB=BC ,∠PBC=90°-30°=60°,所以△PBC 是正三角形。
2.已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .证明:连接AC,并取AC 的中点G,连接GF,GM. 又点N 为CD 的中点,则GN=AD/2;GN ∥AD,∠GNM=∠DEM;(1) 同理:GM=BC/2;GM ∥BC,∠GMN=∠CFN;(2) 又AD=BC,则:GN=GM,∠GNM=∠GMN.故:∠DEM=∠CFN.3、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.证明:分别过E 、C 、F 作直线AB 的垂线,垂足分别为M 、O 、N , 在梯形MEFN 中,WE 平行NF因为P 为EF 中点,PQ 平行于两底 所以PQ 为梯形MEFN 中位线,所以PQ =(ME +NF )/2又因为,角0CB +角OBC =90°=角NBF +角CBO所以角OCB=角NBF 而角C0B =角Rt =角BNFCB=BF所以△OCB 全等于△NBF △MEA 全等于△OAC (同理) 所以EM =AO ,0B =NF 所以PQ=AB/2.4、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .过点P 作DA 的平行线,过点A 作DP 的平行线,两者相交于点E ;连接BE因为DP//AE ,AD//PE所以,四边形AEPD 为平行四边形 所以,∠PDA=∠AEP 已知,∠PDA=∠PBA 所以,∠PBA=∠AEP所以,A 、E 、B 、P 四点共圆 所以,∠PAB=∠PEB因为四边形AEPD 为平行四边形,所以:PE//AD ,且PE=AD 而,四边形ABCD 为平行四边形,所以:AD//BC ,且AD=BC 所以,PE//BC ,且PE=BC即,四边形EBCP 也是平行四边形 所以,∠PEB=∠PCB 所以,∠PAB=∠PCB5.P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC=3a 正方形的边长.解:将△BAP 绕B 点旋转90°使BA 与BC 重合,P 点旋转后到Q 点,连接PQ 因为△BAP ≌△BCQ所以AP =CQ ,BP =BQ ,∠ABP =∠CBQ ,∠BPA =∠BQC 因为四边形DCBA 是正方形 所以∠CBA =90°,所以∠ABP +∠CBP =90°,所以∠CBQ +∠CBP =90°即∠PBQ =90°,所以△BPQ 是等腰直角三角形所以PQ =√2*BP,∠BQP =45 因为PA=a ,PB=2a ,PC=3a所以PQ =2√2a,CQ =a ,所以CP^2=9a^2,PQ^2+CQ^2=8a^2+a^2=9a^2 所以CP^2=PQ^2+CQ^2,所以△CPQ 是直角三角形且∠CQA =90° 所以∠BQC =90°+45°=135°,所以∠BPA =∠BQC =135° 作BM ⊥PQ则△BPM 是等腰直角三角形所以PM =BM =PB/√2=2a/√2=√2a 所以根据勾股定理得: AB^2=AM^2+BM^2=(√2a+a)^2+(√2a)^2 =[5+2√2]a^2所以AB =[√(5+2√2)]a6.一个圆柱形容器的容积为V 立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水。
向容器中注满水的全过程共用时间t 分。
求两根水管各自注水的速度。
解:设小水管进水速度为x ,则大水管进水速度为4x 。
由题意得:t x v x v =+82 解之得:tv x 85=经检验得:tvx 85=是原方程解。
∴小口径水管速度为t v 85,大口径水管速度为tv 25。
7.如图11,已知正比例函数和反比例函数的图像都经过点M (-2,1),且P (1,-2)为双曲线上的一点,Q 为坐标平面上一动点,PA 垂直于x 轴,QB 垂直于y 轴,垂足分别是A 、B . (1)写出正比例函数和反比例函数的关系式;(2)当点Q 在直线MO 上运动时,直线MO 上是否存在这样的点Q ,使得△OBQ 与△OAP 面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图12,当点Q 在第一象限中的双曲线上运动时,作以OP 、OQ 为邻边的平行四边形OPCQ ,求平行四边形OPCQ 周长的最小值.解:(1)设正比例函数解析式为y kx =,将点M (2-,1-)坐标代入得12k,所以正比例函数解析式为12yx 同样可得,反比例函数解析式为2y x(2)当点Q 在直线DO 上运动时, 设点Q 的坐标为1()2Q m m ,,图于是211112224OBQS OB BQ m m m △, 而1(1)(2)12OAPS △,所以有,2114m ,解得2m =±所以点Q 的坐标为1(21)Q ,和2(21)Q , (3)因为四边形OPCQ 是平行四边形,所以OP =CQ ,OQ =PC ,而点P (1-,2-)是定点,所以OP 的长也是定长,所以要求平行四边形OPCQ 周长的最小值就只需求OQ 的最小值.因为点Q 在第一象限中双曲线上,所以可设点Q 的坐标为2()Q n n,,由勾股定理可得222242()4OQn nn n,所以当22()0nn即20n n时,2OQ 有最小值4,又因为OQ 为正值,所以OQ 与2OQ 同时取得最小值, 所以OQ 有最小值2.由勾股定理得OP OPCQ 周长的最小值是8.如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C 不重合),点E 在射线BC 上,且PE=PB .(1)求证:① PE=PD ; ② PE ⊥PD ; (2)设AP =x , △PBE 的面积为y .① 求出y 关于x 的函数关系式,并写出x 的取值范围; ② 当x 取何值时,y 取得最大值,并求出这个最大值. 解:(1)证法一:① ∵ 四边形ABCD 是正方形,AC 为对角线, ∴ BC=DC , ∠BCP =∠DCP=45°. ∵ PC =PC ,∴ △PBC ≌△PDC (SAS ).∴ PB = PD , ∠PBC =∠PDC .又∵ PB = PE ,A D P1∴ PE =PD .② (i )当点E 在线段BC 上(E 与B 、C 不重合)时, ∵ PB =PE ,∴ ∠PBE =∠PEB , ∴ ∠PEB =∠PDC ,∴ ∠PEB +∠PEC =∠PDC +∠PEC =180°,∴ ∠DPE =360°-(∠BCD +∠PDC +∠PEC )=90°, ∴ PE ⊥PD . )(ii )当点E 与点C 重合时,点P 恰好在AC 中点处,此时,PE ⊥PD . (iii )当点E 在BC 的延长线上时,如图. ∵ ∠PEC =∠PDC ,∠1=∠2, ∴ ∠DPE =∠DCE =90°, ∴ PE ⊥PD . 综合(i )(ii )(iii ), PE ⊥PD .(2)① 过点P 作PF ⊥BC ,垂足为F ,则BF =FE . ∵ AP =x ,AC =2, ∴ PC =2- x ,PF =FC =x x 221)2(22-=-. BF =FE =1-FC =1-(x 221-)=x 22.∴ S △PBE =BF ·PF =x 22(x 221-)x x 22212+-=. 即 x x y 22212+-= (0<x <2).② 41)22(21222122+--=+-=x x x y .∵ 21-=a <0, ∴ 当22=x 时,y 最大值41=.(1)证法二:① 过点P 作GF ∥AB ,分别交AD 、BC 于G 、F . 如图所示. ∵ 四边形ABCD 是正方形,∴ 四边形ABFG 和四边形GFCD 都是矩形,△AGP 和△PFC 都是等腰直角三角形. ∴ GD=FC =FP ,GP=AG =BF ,∠PGD =∠PFE =90°.又∵ PB =PE ,∴ BF =FE , ∴ GP =FE ,∴ △EFP ≌△PGD (SAS ). ∴ PE =PD .② ∴ ∠1=∠2.∴ ∠1+∠3=∠2+∠3=90°.ABCPDE F A B CPDE F G 123∴ ∠DPE =90°.∴ PE ⊥PD . (2)①∵ AP =x , ∴ BF =PG =x 22,PF =1-x 22.∴ S △PBE =BF ·PF =x 22(x 221-)x x 22212+-=. 即 x x y 22212+-= (0<x <2).② 41)22(21222122+--=+-=x x x y .∵ 21-=a <0, ∴ 当22=x 时,y 最大值41=.9、如图,直线y=k 1x+b 与反比例函数 y=k2x 的图象交于A (1,6),B (a ,3)两点. (1)求k 1、k 2的值.(2)直接写出 k1x+b-k2x >0时x 的取值范围;(3)如图,等腰梯形OBCD 中,BC ∥OD ,OB=CD ,OD 边在x 轴上,过点C 作CE ⊥OD 于点E ,CE 和反比例函数的图象交于点P ,当梯形OBCD 的面积为12时,请判断PC 和PE 的大小关系,并说明理由.10、如图12,已知直线12y x =与双曲线(0)ky k x=>交于A B ,两点,且点A 的横坐标为4.(1)求k 的值; (2)若双曲线(0)ky k x=>上一点C 的纵坐标为8,求AOC △的面积; (3)过原点O 的另一条直线l 交双曲线(0)ky k x=>于P Q ,两点(P 点在第一象限),若由点A B P Q ,,,为顶点组成的四边形面积为24,求点P 的坐标.图12。
