反比例函数函数K的几何意义.ppt

合集下载

反比例函数中K的几何意义课件

总结词
k值决定了反比例函数图像的形状和位置。
详细描述
在反比例函数y=k/x中，k值决定了图像的形状和位置。当k>0时，图像出现在第一象限和第三象限；当k<0时，图像出现在第二象限和第四象限。
k的正负与图像的位置
总结词
k的正负决定了图像所在的象限。
详细描述
当k>0时，图像分布在第一象限和第三象限；当k<0时，图像分布在第二象限和第四象限。
拓展反比例函数的应用领域
随着科学技术的发展，反比例函数的应用领域也在不断扩大。未来我们可以尝试将反比例函数应用于其他领域，如经济学、生物学等，以解决实际问题。
探索与其他数学知识的联系
反比例函数作为数学中的一个重要概念，与其他数学知识有着密切的联系。未来我们可以进一步探索反比例函数与其他数学知识之间的联系，以促进数学学科的发展。
k值对反比例函数图像的影响
随着k值的增大或减小，反比例函数的图像会向内或
反比例函数在实际生活中有着广泛的应用，如电流与电阻、电容与电压
等物理量之间的关系可以用反比例函数来描述。
对反比例函数的研究展望
深入探究反比例函数的性质
尽管我们已经对反比例函数的性质有了一定的了解，但仍有许多未知的性质等待我们去发现和研究。例如，反比例函数的极限行为、奇偶性等性质。
反比例函数的性质
反比例函数具有以下性质：当 x 增大时，y 值会减小；当 x 减小时，y 值会增大。这是因为 xy =
k 的关系。
在图像上，反比例函数的两个分支在 x 轴和 y 轴上分别趋于无穷
大和无穷小。
反比例函数在坐标系中的图像是不闭合的，且无限接近于坐标轴
。
Part
02

反比例函数k几何意义3课件

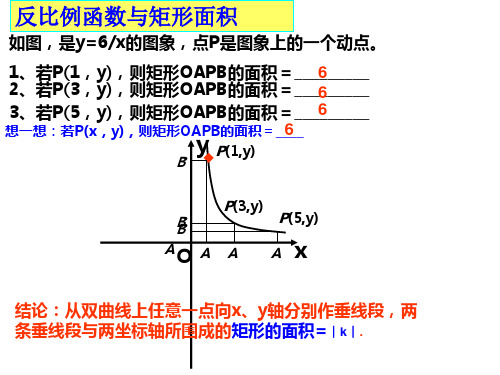
如3x图上，，点且AA在B双∥曲x轴线，Cy、 1x
D在x轴上，若四边形ABCD为矩形，则它的
面积为 .
E
趁热打铁，大显身手（提高篇）
4.（2011年陕西）如图，过y轴正半轴上的任意一点P，作x
轴的平行线，分别与反比例函数y＝－ 4 和y＝ 2 图象交于点
x
x
A和点B．若点C 是x轴上任意一点，连接AC、BC，则△ABC的面
是____B___ A、10 B、5 C、2 D、1
y
BA
P O P’
x
曲直结合
y y 4 x
⑴直线OA与双曲线的另一交点B的坐标．
A(2, 2)
B（-2,-2）
O
C
B
D
x
⑵△BDA的面积是多少？
8
一千里之行始于足下
1.如图,点P是反比例函数 y 图2象上的一
x
点,PD⊥x轴于D.则△POD的面积为 1 .
时，求p的值。
.
拓
如图，已知正方形OABC的面积为9，点
展 O为坐标原点，点A在x轴上，点C在y轴上，
提点B在函数y=k/x的图象上，点P(m,n) 是图
高象上任意一点，过点 P分别作x轴，y轴的垂
线，垂足分别为E, F，
若设矩形OEPF和正方形OABC不重合部分的面积为S，写出S关于m的函数关系式．
AE C
B
o
D
x
直击中考 ☞
如图，直线AB过点A（m, 0）、B（0, n）（其中
m＞0, n＞0）．反比例函数
（p>0）
的图象与直线AB交于C、D两点，连结OC、OD．
（1）已知m＋n＝10，△AOB的面积为S，

反比例函数中k的几何意义-优质课公开课课件一等奖

坐标轴围成的矩形的面积，发现，无论图像
上的点如何移动，矩形的面积却始终不变，
且刚好为。接着，我们发现双曲线上的点
||
与坐标轴围成的三角形的面积始终为，可
2
见值常常与图形的面积相联系。
PPT模板：/moban/
PPT素材：/sucai/
PPT背景：/beijing/
3
相交于、两

点，过作 ⊥ 轴，过作 ⊥ 轴，则
图中阴影部分的面积为（）
A、2
B、3
C、4
D、6
3

点和点都在反比例函数 = 的图像上
⊥ 轴， ⊥ 轴
△ = △
3
=
2
阴影部分的面积就是两个三角形面积之和，为3
正确答案是选项B。
我们通过探究反比例函数图像上的点与
历史课件：/kejian/lishi/
PPT背景：/beijing/
PPT图表：/tubiao/
PPT下载：/xiazai/
PPT教程： /powerpoint/
资料下载：/ziliao/
数学课件：/kejian/shuxue/
英语课件：/kejian/yingyu/
美术课件：/kejian/meishu/
科学课件：/kejian/kexue/
物理课件：/kejian/wuli/
PPT图表：/tubiao/
PPT下载：/xiazai/
PPT教程： /powerpoint/
A、2
B、4
C、6
D、8
两个矩形的面积相等，且都为比例系数4。
1 = 矩形 − 阴影矩形 = 4 − 1 = 3
2 = 矩形 − 阴影矩形 = 4 − 1 = 3

反比例函数中K的几何意义上课ppt课件

别向x轴、y轴作垂线
⑴若P的坐标是（-1,3）则PM=__3__,PN=_1___
⑵若F的坐标是（0.5，-6），则FB=_6___,FA=_0_.5__
⑶若P的坐标是（x，y），则PM=__y__,PN=__x__ y
P
N
B
x
M0
平面直角坐标系内任意一点P(x,y)
.
AF
P到x轴的距离是这点纵坐标的绝对值即是 y
1
1.理解并掌握反比例函数中 ∣K∣的几何意义； 2.能灵活运用∣K∣的几何意义求图形面积； 3.能根据图形面积求出K值
2
概念回顾
定义
形如__y_＝__kx___(k≠0，k为常数)的函数叫做反比例函数
关系式
防错提醒
y k 或y＝kx－1或xy＝k(k≠0) x
(1)k≠0；(2)自变量x≠0；(3)函数值y≠0
5 2
B
D
x
14
变式练习

y 6
已知：如图,反比例函数
与x一次函数
y=kx+1的图像交于A、B两点,点A的纵坐标是3.
（1）求这个一次函数的解析式（2）求△AOB的面积.
解
:
(2)
y

6 x
,
y x 1.
解得xy

3,2或xy

2, 3.
A(2,3),B(3,2).
为什么？数缺形时少直觉，形少数时难入微．
21
反比例函数 y kx上一点P（x0，y0），过点P 分别作PA⊥y轴，PB⊥X轴，垂足分别为A、
B，则矩形AOBP的面积为 k ；
且S△AOP= S△BOP = k

第26章反比例函数——反比例函数中k的几何意义课件

6

拓展3 : A（x1，y1）在反比例函数y= （＞）图像上
2

(3) 如图，点B（x2，y2 ）为反比例函数y=- （x <0）图像上一点.求△OAB的面积.
补
E
S△AOB= S梯形ABEF-S△AOF-S△BOE
=S梯形ABEF-3-1
=S梯形ABEF-4
| −
|(| |+| | )
2
(1) 如图，点B（x2，y2 ）为反比例函数y= （x＞0）图像上一点.

若A，B为两函数同一象限的点，求 △ OAB的面积.
S△AOE≠S△BOF
S△AOB= S梯形AEFB+S△AOE-S△BOF
=S梯形AEFB+3-1
=S梯aAEFB+2
E
F
| − |(| |+| | )
=
等底等高，
面积不变
N
x
利用平行转化解决面积问题
变形
等底等高，
面积不变
变形
利用平行转化解决面积问题
1、如图6, P是反比例函数y=(x>0)图象上的一点,PM⊥y,点Q,N在x轴
4
上,QN∥PM，且QN=PM,四边形PMQN的面积为4,则k=____________.
6
D
2、如图，已知点A在反比例函数y=
6

1、如图，反比例函数y= 的图像经过A（1，6），B（3，2）两点，求△AOB 的面积
.
F
方法2: S△AOB= S△AOE-S△BOE
或S△AOB= S△OBF-S△OAF
补
E
F
G
E
方法3: S△AOB= S矩形OEGF-S△BOE-S△ABG- S△OAF

人教版初三数学9年级下册第26章(反比例函数)反比例函数k的几何意义课件(17张ppt)

(3)若点(a,y)在该函数图象上,且a＞－2,求y的取值范围.
7.【例 4】如图,在平面直角坐标系中,反比例函数 y＝k(k＞0)的
x
图象经过点 A(2,m),过点 A 作 AB⊥x 轴于点 B,且△AOB 的面积
为 5. (1)求k和m的值; (2)当x≥8时,求函数值y的取值范围.
解:(1)∵A(2,m),
第二十六章反比例函数与反比例函数有关的面积问题
k 的几何意义及应用
函数
图象形状图象位置增减性延伸性对称性
y
函数图象的在每一支
双曲线既
k＞0
两支分支分曲线上,y 双曲线向是轴对称
O x 别位于第一、都随x的增四边无限图形(对称
三象限
大而减小延伸,与轴:y=±x),
y 函数图象的在每一支坐标轴没又是中心
自主归纳
y
P(m,n) B
oA
x
K与图形面积
S矩形OAPB OA• AP
m•n
k
反比例函数图像上任意一点向x轴和y轴作垂线，
得到矩形的面积为 S矩形OAPB k
如图:连接OP，则
SOAP
1 • OA • AP 2
y
1 m•n
2
P(m,n) B
oA
x
1 k 2
反比例函数图像上任意一点向x轴或y轴作垂线，
5.若D、E、F是此反比例函数在第三象限图像上的三个点，
过D、E、F分别作x轴的垂线，垂足分别为M，N、K，连接
OD、OE、OF，设△ ODM、△OEN、 △OFK 的面积分别
为S1、S2、S3，则下列结论成立的是( D )
y A（1，4）A S1﹤S2 Nhomakorabea﹤ S3

《反比例函数图像性质-k的几何意义》课件

随着x的增大或减小，曲线会逐渐靠近坐标轴，但永远不会与坐标轴相交。
曲线形状
图像是由两支分别位于第一和第三象限的曲线组成，这两支曲线关于原点对称。
k<0时图像特征
1 2
图像位于第二、四象限
当k<0时，反比例函数的图像会出现在第二和第四象限。
曲线形状
图像同样是由两支分别位于第二和第四象限的曲线组成，这两支曲线也关于原点对称。
图像的性质。
总结
反比例函数的图像性质与 $k$ 的正负有关。当 $k > 0$ 时，图像位于第一、三象限；当 $k < 0$
时，图像位于第二、四象限。
涉及综合应用问题
01
例题5
已知反比例函数 $y = frac{k}{x}$ 的图像与一次函数 $y = ax + b$ 的
图像交于点 $M(2,1)$ 和 $N(-1,-2)$，求这两个函数的解析式。
反比例函数的极限与连续性问题
讨论反比例函数在特定点的极限行为，以及在定义域内的连续性。
反比例函数与其他函数的复合问题
研究反比例函数与其他基本函数（如幂函数、三角函数等）的复合性质及图像特征。
THANK YOU
06
总结回顾与拓展延伸
重点知识点总结回顾
反比例函数图像的基本性质
反比例函数图像为双曲线，当k>0时，图像位于第一、三象限；当k<0时，图像位于第二、四象限。
k的几何意义
k的绝对值表示双曲线与坐标轴所围成的矩形的面积。当k>0时，矩形在第一象限；当 k<0时，矩形在第二象限。
反比例函数图像的对称性
通过中心对称性，我们可以更好地理解反比例函数的性质和行为，以及它在解决实际问题中的应

九年级数学反比例函数解析式中k的几何意义课件

(1)判断该函数图象的另一支所在的象限，并求m的取值范围； (2)如图，O 为坐标原点，点A 在该反比例函数位于第一象限的图象上，点B 与点A关于x轴对称，若△OAB的面积为6，求m的值．
解：(1)根据反比例函数的图象关于原点对称，知该函数图象的另一支在第三象限，且 m －7＞0，故 m＞7.
(2)∵点 B 与点 A 关于 x 轴对称，且△OAB 的面积为 6， ∴△OAC 的面积为 3.
o
B
A
x
C
课堂小结
性质：反比例函数图象上的点向坐标轴作
垂线，围成的矩形或三角形的面积不变性
y S矩形AOBP=|k|
k
S△PAO=S△PBO= 2
思想：分类讨论和数形结合
B
o
P(m,n) Ax
课堂演练
1.如图，A,B是双曲线 y 3上的点，分别经过A,B两点向X轴、y轴作
x
4 垂线段，若S阴影 1，则S1 S2
向
x 轴、y 轴作垂线，围成面积分别为S1，S2的矩形，
填写下页表格：
探究
y
5 4
y 4 x
3 2 1 S1
－5－4－3－2－－11 O 1
•P
S2 23
•Q
4 5x
－2
－3
－4
－5
S1的值 S2的值
S1与S2的
关系
P (2，2) Q (4，1)
4 4
S1=S2
猜想 S1， S2 与 k的关系
S1=S2=k
x
4
y x
S1的值
S2的值 S1与S2的关系猜想与k的关系
P（-1,4）
Q（-2,2）
4
4
S1=S2

1.2反比例函数k的几何意义PPT优秀课件

S OA 1 2 POA A P 1 2|m |•|n|1 2|k|
y
y
P(m,n)
P(m,n)
2021/6/3
oA
x
oA
x
18
2.如图,点P是反比例函数图象上的一点,过点P分别向x
轴、y轴作垂线,若阴影部分面积为1,则这个反比例函
数的关系式是
.y 2 x
y
y
P
P
C o O D xx
y k (k 0) 的面积不变性
3.如图，S矩形
OAPB= __y__,S△OAP= .
y 4
BP P
x
OA
x
4.观察图中各个三角形的面积，你有什么发现？
y
o
A
y 4 x
x
2021/6/3
10
反比例函数 y
k x
上一点P（x0，y0），过点
P分别作PA⊥y轴，PB⊥X轴，垂足分别为A、
B，则矩形AOBP的面积为 k ；
且S△AOP= S△BOP = k
。
2
2021/6/3
11
1.通过本节课的学习，你有什么收获？还有什么困惑吗？
2.你对自己本节课的表现满意吗？为
什么？数缺形时少直觉，
形少数时难入微．
2021/6/3
12
如图 ,在y1(x0)的图像上有A三 ,B,C点, x
经过三点分x轴别引向垂,交线x轴于 A1,B1,C1三点 , 边结 OA,OB,OC,记OA1A,OB1B,OCC 1的面积分别 S1,为 S2,S3,则有__. y
则 S矩O 形APBOAAP |m|•|n||k|(如图)所
y
y

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

反比函数k的几何意义主要体现在其图像与坐标轴所围成的面积上。在反比函数的图像中，k值决定了曲线与坐标轴所围成的矩形面积的大小。具体来说，当k值确定时，反比函数图像上任意一点与坐标原点所构成的矩形面积都等于k的绝对值。பைடு நூலகம்一性质在解题中具有重要意义，可以通过给定的几何条件，如矩形的面积、三角形的面积等，来求解k值。文档通过多个例题，详细展示了如何利用这一性质求解k值，包括通过矩形面积公式、三角形面积公式等几何方法。此外，文档还强调了数形结合、转化思想等数学思想方法在解题中的应用，帮助读者更好地理解和掌握反比函数k的几何意义。