格林公式
格林公式
= ∫L Pdx + Qdy + ∫L Pdx + Qdy + ∫L Pdx + Qdy
1 2 3
= ∫L Pdx + Qdy
L3
D3
D2
L2
( L1, L2 , L3对D来说为正方向 )
D1
L1
L
证明(3)
若区域不止由一条闭曲 线所围成.添加直线段 AB,CE. 则 D 的边界曲线由 AB, L2 ,BA, AFC,CE, L3 , EC 及 CGA 构成. D 由(2)知
o
L
B
x
解 引入辅助曲线 L , L = OA + AB + BO
应用格林公式 ,
(
P = 0, Q = x 有
y
− ∫∫ dxdy = ∫ xdy
L D
A
D
= ∫OA xdy + ∫AB xdy + ∫BO xdy , 由于 ∫OA xdy = 0,
o
L
B
x
∫BO xdy = 0,
1 2 ∴ ∫ xdy = − ∫∫ dxdy = − πr . AB 4 D
∂P ∂ 2u ⇒ = ∂y ∂x∂y
=
∂ u ∂Q = ∂y∂x ∂x
2
(4) ⇒ (1) :
(1)对 D内任意一条闭路径 L, ∫ Pdx + Qdy = 0;
L
∂Q ∂P (4) = , ∀( x , y ) ∈ D . ∂x ∂y
D′
L D
设 L 是 D 内一条闭路径, L 所围有界闭区域 D ′ ⊂ D , 则在 D ′内 ∂ Q = ∂ P , ∂x ∂y
格林公式

L D
8
64 3
o
A x
例 3计算
2xydx x2dy 其中 L 为抛物线 yx2 L
上从O(0 0)到B(1 1)的一段弧
解 这里P2xy Qx2
P Q 2x 所 以 积 分 因为 y x
L
2 xydx x 2 dy 与 路 径 无 关
M
计算抛物线 ( x y ) ax ( a 0 )
曲线 AMO 表示为
解:ONA为直线 y=0
y ax x , x [ 0 , a ]
1
N
A ( a ,0 )
A
L xdy 2
1
ydx
2 ONA
xdy ydx
1
2 AMO
xdy ydx
1
2 AMO
L
x 2
解
P y Q x
y x
(x
2
2 xy ) 2 x
4
P y
Q x
,
(x y ) 2x
2
原积分与路径无关
故原式
1 0
x dx
2
1 0
( 1 y ) dy
4
23 15
.
例2. 计算 圆周
其中L 为上半 从 O (0, 0) 到 A (4, 0)
(2) 对D 中任一分段光滑曲线 L, 曲线积分 与路径无关, 只与起止点有关. (3) 在 D 内每一点都有
P y Q x .
L Pd x Qd y
例1 计算 ( x 2 xy ) dx ( x y ) dy 其中L为由点
§11.3 格林(Green)公式

下面证明 如图,
A(x0 , y0 )
B(x,y) M(x+Dx,y)
O
G
x
2. 平面上曲线积分与路径无关的等价条件
类似可证
y
A(x0 , y0 )
B(x,y) M(x+Dx,y)
O
G
x
( ξ 介于 x 与 x +Dx 之间 )
2. 平面上曲线积分与路径无关的等价条件
如果存在某一函数 u (x, y) 使 du = Pdx + Qdy,则
(Ⅰ) 沿任一闭曲线L的积分
(Ⅱ) 曲线积分
与路径无关;
(Ⅲ)存在某一函数 u (x, y) 使 du = Pdx + Qdy;
(Ⅳ)在G内
证明略.
2. 平面上曲线积分与路径无关的等价条件
如果存在某一函数 u (x, y) 使 du = Pdx + Qdy,如何求 u (x, y)?
此时,积分与路径无关,只与起点和终点有关,如图,记
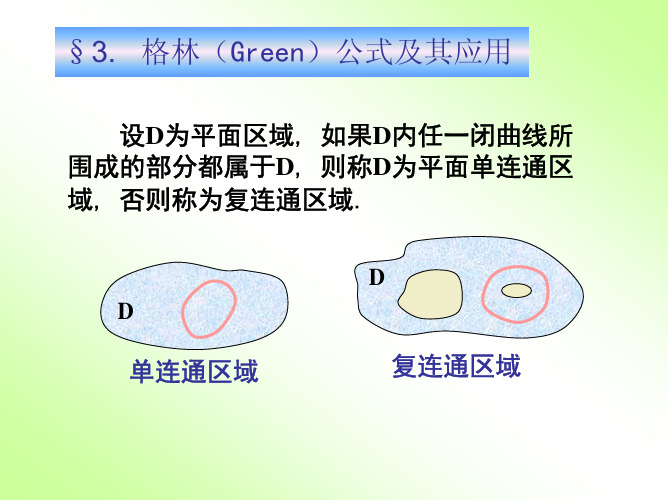
1. 区域的连通性
设 D 为平面区域,如果 D 内任一闭曲线所围成的部分 都属于 D,则称 D 为平面单连通区域,否则称为复连通区域.
例 D1,D2为图中浅色区域.
D2 D1
单连通区域
复连通区域
1. 格林(Green)公式
L
D
L
Dl
边界曲线 L 的正向: 当观察者沿边界行走时,区域 D 总在他的左边。
§11.3 格林(Green)公式
1. 格林(Green)公式 2. 平面上曲线积分与路径无关的
等价条件 3. 曲线积分的基本定理
§11.3 格林(Green)公式
1. 格林(Green)公式 2. 平面上曲线积分与路径无关的
格林公式

L1 : y 1 ( x : 1 2) L L1 L2 , 其中, 取积分路径: L2 : x 2 ( y : 1 3)
y
2 2 3 2
则
(2, 3) .
(2,1)
4 1 ( x 1)d x 1 (2 y )d y 3
(1,1)
.
o
x
例6
y
L
o
D A(2,0) x l
5d xd y
D
0
2
8 5 x d x . 3 2
2
例4
计算
其中L为一无重点且不过原点
的分段光滑逆时针向闭曲线. 解 令 则
y
L
D
o
x
记 L 所围成的闭区域为 D .
(1) 当( 0, 0) D 时, 由格林公式知
(2) 当(0,0) D 时, 作位于 D 内圆周 l : x 2 y 2 r 2 ,
D
yx
o
x
1 0 d x x (1 x )d y . 3
1 1
例3
计0,0)到点A(2,0)的上半圆周 x y 2 x .
解
令 P x 2 2 y , Q 3 x ye y , 则
设 l : y 0 ( x : 2 0), 则 利用格林公式 , 得
1 故 . 0d x y d y xy d x y ( x )d y 0 0 (0,0) 2
(1,1) 2
计算
解
令
则
y
(1,1) .
o
故原曲线积分在全平面内与路径无关.
(1,0)
x
L1 : y 0 ( x : 0 1) 取积分路径:L L1 L2 , 其中, L2 : x 1 ( y : 0 1) 2 2 4 ( x 2 xy )d x ( x y )d y 故 L
微积分 格林公式

A.
证明 : 例2、
2 xydx
D
x dy 0 , D 分段光滑 .
2
求 例3、 e
D
y
2
dxdy , D 是以 O ( 0 , 0 ), A ( 1 ,1 ), B ( 0 ,1 ) 为顶点 .
xdy ydx
的三角形闭区域
设 例4、 D 是包含原点的有界闭区
y
Q ( x , y ) dy
y0
y0
Q ( x 0 , y ) dy
例7、 已知 du
xdy ydx x
2
y
2
( x 0 ), 求 u ( x , y ).
P 全微分方程: ( x , y ) dx Q ( x , y ) dy 0
(
Q x
P y
)
例8、 解全微分方程 作业
(4)
Q x
P y
在 G 内处处成立 .
关键:
Q x
P y
P ( x , y ) dx
L
Q ( x , y ) dy 与路径无关
.
例5、计算
L
(x
2
2 xy ) dx ( x
2
y ) dy , 其中 L 为
4
由点 O ( 0 , 0 )到点 B ( 1 ,1 )的曲线弧 y sin
( x, y)
( x0 , y)
( x, y)
( x0 , y0 )
(1 )
u 按(1): ( x , y ) u 按(2): ( x , y )
( x, y0 ) ( x0 , y0 )
格林公式及其应用

Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
格林公式几何意义

格林公式几何意义一、格林公式。
设闭区域D由分段光滑的曲线L围成,函数P(x,y)及Q(x,y)在D上具有一阶连续偏导数,则有underset{D}{∬ }((∂ Q)/(∂ x)-(∂ P)/(∂ y))dxdy = ∮_LPdx + Qdy,其中L是D的取正向的边界曲线。
二、格林公式的几何意义。
1. 平面向量场的环量与旋度。
- 从向量场的角度来看,设→F(x,y)=P(x,y)→i+Q(x,y)→j是平面向量场。
- 曲线积分∮_LPdx + Qdy表示向量场→F沿闭曲线L的环量,它反映了向量场绕闭曲线L旋转的趋势。
- 而(∂ Q)/(∂ x)-(∂ P)/(∂ y)可以看作是向量场→F的某种“旋度”(在二维情况下的一种类似概念)。
- 格林公式表明,向量场在闭曲线L上的环量等于向量场的“旋度”在闭曲线L所围成的区域D上的积分。
这就像在流体力学中,如果把向量场看作是流体的速度场,环量表示流体绕闭曲线的旋转程度,而旋度表示流体在区域内每一点的旋转趋势,格林公式建立了这两者之间的联系。
2. 区域的面积计算。
- 当P=-y,Q = x时,根据格林公式underset{D}{∬ }((∂ Q)/(∂ x)-(∂ P)/(∂ y))dxdy=underset{D}{∬ }(1 + 1)dxdy = 2underset{D}{∬ }dxdy,而∮_LPdx+Qdy=∮_L-ydx + xdy。
- 此时underset{D}{∬ }dxdy=(1)/(2)∮_L-ydx + xdy,这就给出了用曲线积分计算平面区域D面积的一种方法。
从几何意义上讲,区域D的面积与沿其边界曲线L的特定曲线积分建立了联系。
通过对边界曲线L的积分(这里是-ydx + xdy的积分),可以得到区域D的面积信息。
09 第四节 格林公式

3) 利用第二类曲线积分可求闭曲线所围区域的面积 利用第二类曲线积分可求闭曲线所围区域的面积.
∂Q ∂ P − )dxdy = ∫ Pdx + Qdy 格林公式: 格林公式 ∫∫ ( ∂y D ∂x ∂D +
的面积A 闭区域 D 的面积 = ∫∫ dxdy .
D
取 P = 0, Q = x , 得 A =
解 记原积分 = ∫ P ( x , y )dx + QP ( x , y )dy ,
x 则 Q x = e cos y , Py = e cos y − m ,
y
D
O
L
x
Ax
作定向线段 OA : y = 0, x : 0 → a , 它与 所围闭区域记为 D, 它与L所围闭区域记为
则原积分 =
L+ OA
o
A(a,0)
曲线弧 AO : y = ax − x , x : a → 0,
∴A= −
∂D +
0
∫ ydx = −( ∫
OA
+
∫ ) ydx
AO a
1 2
1 2 = 0 − ∫a ( ax − x )dx = ∫ ( a x − x )dx = a . 0 6 1 1 或 : A = ∫ xdy − ydx = ( ∫ + ∫ ) xdy − ydx 2 ∂D + 2 OA AO a a 1 2 1 0 a = ∫a [ x( − 1) − ( ax − x )]dx = ∫ 0 xdx = 6 a . 4 2 2 ax
xdy − ydx ∫ x 2 + y 2 = ∫∫ 0 dxdy = 0 . L D
o
L
D
§11.2(2)格林公式

Q P ∫∫D( x y )dxdy = ∫L Pdx + Qdy
4
2) 若D不满足以上条件, 则可通过加辅助线将其分割 为有限个上述形式的区域 , 如图 Q P ∫∫D( x y ) dxdy
y
1 D2 D
L
= ∑∫∫
k =1 n
n
Dk
(
Q P ) dxdy x y
Dn
o
x
= ∑∫
k =1
du = xy2 dx + x2 ydy. (0,0)( Nhomakorabea, y) .
= ∫ x 0 dx + ∫
0
x
y 2 x y dy 0
(x,0)
=∫
y 2 x y dy 0
18
xd y y d x 在右半平面 ( x > 0 ) 内存在原函 例6. 验证 2 2 x +y y 数 , 并求出它. (x, y) y x , Q= 2 证: 令 P = 2 2 x +y x + y2 2 2 o (1,0) ( x,0) x P y x Q 则 = 2 = ( x > 0) 2 2 x (x + y ) y 由定理 2 可知存在原函数 定理
Q P ∫∫ x y dxdy = ∫ Pdx + Qdy ( 格林公式 ) D L
或
∫∫ P
D
x
y
Q
dxdy = ∫ Pdx + Qdy
L
2
证明: 证明 1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 且 1(x) ≤ y ≤ 2 (x) y E D: d a ≤ x ≤b
y0 x0 x0 y y0 x
格林公式
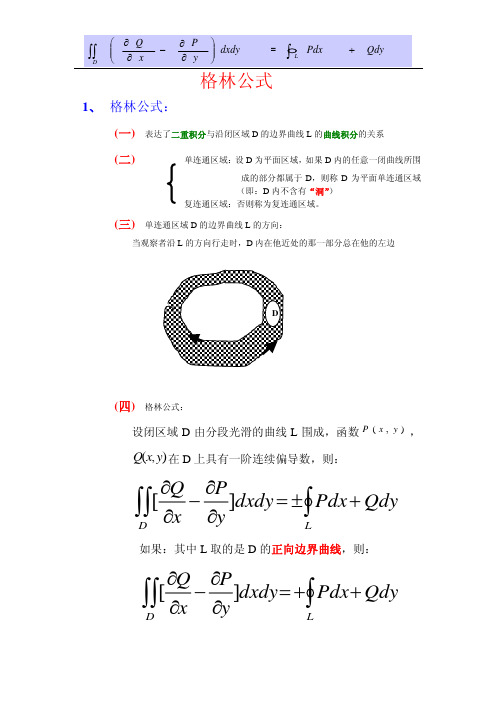
−
∂ P ∂ y
⎞ ⎟ ⎟ dxdy ⎠
=
∫
L
Pdx
+
Qdy
3、 附加知识
(1) 椭圆的参数方程:
x2 y2 + =1 a2 b2
x = acos θ
y = bcos θ
椭圆的面积公式: π ab
(2) 当 f(x)为奇函数,即 f(-x)=-f(x)
−a
∫ f ( x)dx = 0
a
a
(3) 当 f(x)为偶函数,即 f(-x)=f(x)
P(x, y) , Q(x, y) 在区域 D 内具有
一阶连续偏导数,如果对于 G 内的任意 A B 两点, 以及 G 内从 A 点到 B 点的任意两条曲线 L 1 , L 2 ,等式:
L1
∫
Pdx
+ Qdy
=
L2
∫
Pdx
+ Qdy
恒
成立,就说曲线积分
L
∫
Pdx
+ Qdy
在 G 内与路径
无关,否则便说与路径有关。
(三)
单连通区域 D 的边界曲线 L 的方向:
当观察者沿 L 的方向行走时,D 内在他近处的那一部分总在他的左边
D
(四)
格林公式:
设闭区域 D 由分段光滑的曲线 L 围成,函数 P ( x , y ) ,
Q(x, y) 在 D 上具有一阶连续偏导数,则:
∂Q ∂P Pdx + Qdy ∫D∫[ ∂x − ∂y ]dxdy = ±∫ L
∫∫
D
⎛ ∂ Q ⎜ ⎜ ∂ x ⎝
−
∂ P ∂ y
⎞ ⎟ ⎟ dxdy ⎠
=
§2 格林公式及其应用

1
力场势函数) 。 力场势函数)
1 F ( M ) 可理解为电荷体密度或质量密度。 称为体位势: 可理解为电荷体密度或质量密度。 − ∆ V ( M 0 ) 称为体位势: 4π
(2.11)
证 明: 将调和函数基本积分公式应用到Γa 上有:
1 ∂ 1 1 ∂u u( M 0 ) = − ∫∫ u r − r dS = 0 4π Γa ∂n r r ∂n
上页 下页 返回
1 1 1 ∂ 1 在Γa 上 = , r = − 2 ,所以 r a ∂n r a 1 ∂u 1 ∂u r r ∫∫ r ∂n dS = a ∫∫ ∂n dS = 0 Γa Γa
1 1 1 ∂u ∂ 1 1 ∂u − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 2 ∫∫ udS − ∫∫ r dS r ∂n r r ∂ n ε Γε ∂n ε Γε Ω\ Kε Γ
ε ε ε
上页 下页 返回
1 ∂u 1 ∂u dS , 即 u∗ 和 udS , r = 记u = 2 ∫∫ r 2 ∫∫ 4πε Γε ∂n 4πε Γε ∂n
当 u 是Ω 内的调和函数, M 0 ≠ Ω ,则由格林第二公式 有:
∂ 1 u( M ) r ∫∫ ∂n rM 0 M Γ
1 ∂u( M ) − r dS = 0 r ∂n M0M
当 u 是 Ω 内的调和函数,M 0 ∈ ∂Ω = Γ ,类似基本积分公 内的调和函数, 式的推导, 式的推导,记 Γε′ = Γε I Ω , Γ ′ = Γ \ K ε ,则有
微积分格林公式

已知du P( x, y)dx Q( x, y)dy,如何求u( x, y)?
(x, y) (x0 , y)
全微分方程:P( x, y)dx Q( x, y)dy 0 ( Q P ) x y
例8、 解全微分方程 : ( x 2 y)dx ( x sin2 y)dy 0. 作业 习题8-4:3、4(1)(3)
B
L2
A
L3
定理:设G是平面单连通区域, P( x, y),Q( x, y) C (1) (G), 则以下四个条件等价: (1)对G内任一分段光滑闭曲线C ,
P( x, y)dx Q( x, y)dy 0;
C
(2) P( x, y)dx Q( x, y)dy在G内与路径无关; L
例4、设D是包含原点的有界闭区域,求 xdy ydx. D x 2 y 2
二、曲线积分与路径无关的条件
P( x, y)dx Q( x, y)dy只与L的两个端点有关而与
L
积 分 路 径 无 关, 则 称 之 为 积 分 与 路 径 无关, 否 则 称
与 路 径 有 关.
L1
D1
L
(2)
B
A (3)
面积公式:A dxdy 1 xdy ydx (P y,Q x)
D
2 D
例1、求椭圆x a cos , y bsin 所围成图形的面积A.
例2、证明 : 2xydx x 2dy 0, D 分段光滑. D
例3、求 e y2 dxdy, D是以O(0,0), A(1,1), B(0,1)为顶点 D 的三角形闭区域.
高数格林公式

2
通过格林公式,可以将二重积分转化为曲线积分 来计算,这在某些情况下可以大大简化计算过程。
3
此外,格林公式还揭示了平面区域内向量场与标 量场之间的关系,为多元函数微积分中的场论问 题提供了有力工具。
与场论初步知识联系
01
场论是研究向量场和标量场的数学分支,而格林公式正是场论 中的一个基本定理。
02
04
培养抽象思维能力和逻辑推理能力,为进一步学习高等数学打下坚实 的基础。
02 格林公式基本概念
曲线积分与路径无关条件
曲线积分与路径无关的定义
若在所有以A、B为端点的光滑曲线族上,曲线积分∫L P(x,y)dx+Q(x,y)dy 的值都是相同的,则称此曲线积分与 路径无关。
曲线积分与路径无关的条件
径为平面区域D的边界曲线。
格林公式的证明需要运用到微积分基本定理和斯托克 斯定理等相关知识。
学习目标与要求
ቤተ መጻሕፍቲ ባይዱ
01
掌握格林公式的基本形式和证明方法,理解其几何意义和物理应用。
02
能够熟练运用格林公式解决平面区域上的二重积分和曲线积分问题。
03
了解格林公式在电磁学、流体力学、热力学等领域的应用实例,提高 解决实际问题的能力。
高数格林公式
目 录
• 引言 • 格林公式基本概念 • 格林公式证明方法 • 格林公式应用举例 • 格林公式与相关知识点联系 • 拓展与延伸
01 引言
背景与意义
格林公式是高等数学中的一个 重要概念,它揭示了平面区域 上二元函数与其偏导数之间的
关系。
在实际应用中,格林公式被 广泛应用于电磁学、流体力 学、热力学等领域,是解决 复杂物理问题的有力工具。
格林公式讲解

格林公式讲解格林公式是微积分中的重要公式,它是一个用于计算曲面积分和线积分的公式。
本文将详细讲解格林公式的含义、推导过程、应用和意义。
一、格林公式的含义格林公式是矢量微积分中的重要公式,其含义是将一个曲面积分转化为一个线积分,从而方便我们进行计算。
换句话说,该公式描述了曲线与其所包围的面积之间的关系。
二、格林公式的推导过程假设有一个平面曲线Γ,它是由两个点 A 和 B 组成的。
我们还可以将该曲线细分成许多小线段,每个小线段长为Δl。
现在想要计算曲线Γ 所包围的面积 A。
为了计算这个面积,我们需要将曲线Γ 分成无数个小曲线段。
假设有一小段曲线γ,它被如下两个点所包围:1、x1、y1、z1;2、x2、y2、z2;该小段曲线的长度为Δl,宽度为Δh。
现在我们要计算该小段曲线所围成的面积。
根据微积分的定义,该小段曲线所包围的面积为:ΔA = Δl*Δh现在我们将其中一个点移动一个微小的距离Δx 和Δy。
现在,我们来计算ΔA1 和ΔA2。
同时,我们将由两个新的曲线γ1 和γ2 所包围的面积也进行计算。
因此,我们可以得出以下结果:ΔA1 = (2z1Δx + ∂z/∂x Δx2 + ∂z/∂y ΔxΔy)ΔlΔA2 = (2z2Δx + ∂z/∂x Δx2 + ∂z/∂y ΔxΔy)ΔlΔAy = (∂z/∂y Δy2 + ∂z/∂x ΔxΔy)ΔlΔAx = (∂z/∂x Δx2 + ∂z/∂y ΔxΔy)Δl现在,我们可以将所有的ΔA 相加,得出曲线Γ 所包围的总面积:A = ∫(∂z/∂x dx + ∂z/∂y dy)三、格林公式的应用格林公式可以用来计算面积、体积、弧线长度等,在求解不定积分、偏微分方程、几何学等领域中都有广泛的应用。
四、格林公式的意义格林公式不仅仅是一种计算曲线所包围区域的面积的方法,它也是微积分中非常重要的一种工具。
它可以将微积分中的概念从平面向高维空间进行扩展,为我们探索更广泛和更复杂的数学领域提供了强有力的支持。
格林(Green)公式及其应用

• 格林公式简介 • 格林公式的基本性质 • 格林公式的应用 • 格林公式的扩展 • 格林公式的实际例子 • 总结与展望
01
格林公式简介
格林公式的定义
格林公式是一个数学定理,用于描述二维平面上的向量场和路径之间的关系。它 指出,在一个封闭的区域内,沿任意路径的积分等于该区域内散度的体积分。
在实变函数中的应用
证明定理
格林公式在证明实变函数中的一些定 理中发挥了重要作用,如黎曼定理和 克雷洛夫定理等。
求解积分方程
利用格林公式,可以将积分方程转化 为边界积分方程,从而简化求解过程。
04
格林公式的扩展
高维格林公式
总结词
高维格林公式是格林公式在高维空间中 的推广,它描述了高维空间中向量场和 标量场之间的关系。
THANKS
感谢观看
格林公式的变种
总结词
格林公式的变种是原始格林公式的不同形式 或应用,它们在特定情况下可能更加方便或 有效。
详细描述
随着数学和物理学的发展,人们发现了许多 格林公式的变种。这些变种可能在某些特定 情况下更加适用,例如在处理非线性问题或 复杂边界条件时。了解这些变种有助于我们
更好地理解和应用格林公式。
03
格林公式在数学分析中占有重要的地位,是微积分学中的基本定理之一。它为 解决许多复杂的积分问题提供了一种有效的方法,使得许多难以计算的问题变 得简单明了。
对未来研究的展望
随着数学和其他学科的发展,格 林公式在各个领域的应用越来越 广泛。未来,我们可以进一步探 索格林公式的各种应用,如数值 计算、物理模拟、图像处理等。
解决偏微分方程的实例
总结词
格林公式还可以用于解决偏微分方程的问题,通过将 偏微分方程转化为等价的积分方程,可以简化求解过 程。
高数下之---7,格林公式

y
d x ( xy
2 2
3
xe
2 y )d y ,
其中L为圆周 x y 2 x 的正向. 解 P e y , Q xy 3 xe y 2 y
P y
Q x
y
e ,
y
Q x
y
3
y e
3
y
O
. 1
2
x
P y
由格林公式有 I y d x d y 0
5
( x
Q
P y
)d x d y
L P d x Q d y
E
Q x
dxdy
c
d
dy
2( y)
Q x
D
c c
D d
1( y)
dx
y
x 1( y)
d
Q ( x , y )
2( y)
1
dy ( y)
D
B
d
Q ( 2 ( y ), y ) d y
2
P y
19
Q x
P y
D
(
Q x
P y
)d x d y
L P d x Q d y
L
( 1 ) 当 ( 0 , 0 ) D 时,即L为不包围原点
y
的任一闭曲线.
由格林公式
L
xd y yd x x y
2 2
D
0
O
y
x
( 2 ) 当 ( 0 , 0 ) D 时, 即L为包围原点在内的任一
L1
L D
D1
第3节格林公式

第3节格林公式
格林公式又叫做牛顿-格林公式,它是著名物理学家威廉·牛顿和美国数学家和天文学家兼历史学家乔治·格林发现的定律,它对太阳系中的行星运动以及影响行星运动的力有关。
牛顿在1687年发表《自然哲学的数学原理》一书中给出了牛顿定律,这是关于行星运动的公式;而格林在1748年发现了牛顿定律中的影响因子,也就是格林定律,是一个换算关系:
$$ \frac{d^2x}{dt^2} = − \frac{GM}{r^2}x $$
其中,x表示行星位置的矢量,r表示行星距离太阳的距离,G表示万有引力常数,M表示太阳的质量。
格林公式为牛顿定律的简化形式,表达的是牛顿三大定律中动力学原理:行星运行轨道的变化(受太阳的引力影响)与行星距离太阳的距离成反比。
也就是说,行星离太阳越远,受到引力的作用就越弱,运行轨道的变化就越小。
格林公式是用来描述星体运动的数学公式,在天文学研究和航天工程中都有广泛的应用。
格林公式可以用来研究各种行星运行轨道的变化,可以为航天器如卫星的轨道分析等提供技术支持。
格林公式也可以用来研究行星的控制台轨道,以及探测其他行星的引力影响,以改善天文学的研究内容等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L
1 ∴ ∫ − y d x + x d y 是 L 所围区域 D 的面积 . 2 L 例1 求椭圆 x = a cos θ , y = b sin θ 所围成图形的面积 A . 1 解 A = ∫ − ydx + xdy 2L 1 2π = ∫ − b sin θ ⋅ d ( a cos θ ) + a cos θ ⋅ d ( b sin θ ) 2 0 2π 1 = ab ∫ dθ = πab. 7 2 0
∂Q ∂P ∵ = ∂x ∂y
y yd x − x d y , 其中 L 为圆 课堂练习 求 ∫ 2 2 L 2( x + y ) P214.3 周 ( x − 1 ) 2 + y 2 = 2 , L 的方向逆时针 . O l D 所围区域为 解 设 L所围区域为 D . y −x P( x, y) = , Q( x, y) = . 2 2 2 2 2( x + y ) 2( x + y ) x2 − y2 ∂P ∂Q ∵ = = 在 D 内不连续 , ( 0,0 )是奇点 . 2 2 2 ∂ y 2( x + y ) ∂x ∴ D 上不能用格林公式 (见 P 202 定理 1条件 ).
在 D 内作小圆周 l : x 2 + y 2 = r 2方向逆时针 (如图 ).
ydx − xdy 用P 205 第 8 −10 ∫ 2( x 2 + y 2 ) ======== 行的方法得 L
L
x
∫
( 小圆 )
l
y d x − x d y 曲线L上的积分可以化成同 上的积分可以化成同 上的积分. 2 ( x 2 + y 2 ) 方向的小圆周 l 上的积分.
∂Q dxdy. 类似可证 ∫ Qdy = ∫∫ L ∂x D
5
a
b x
书中未证,P205例4用到 用到) 书中未证 例 用到 ( 2) D是复连通区域时 (如图) (书中未证
将 D沿辅助线 AB 割开 , 得到以 L1 + BA + L2 + AB 为 正向边界的单连通区域 .由(1)知 x ∫LP+(AB , y )dx + Q( x, y )dy L1 L2 A B L1 + BA + 2 D ∂Q ∂P ) d x d y成立 . = ∫∫ ( − ∂x ∂y D
13
上的积分可以化成同方向的小圆周 上的积分. 曲线L上的积分可以化成同方向的小圆周 l 上的积分.
xdy − ydx xdy − ydx =∫ 2 ⇒∫ 2 2 x + y2 x +y l L
x = r cos t, l : 2 y = r sint, t从0变到 π .
y
L
D
O
2
=∫
2π
( 3,0)
x
10
课堂练习 求 ∫ ( xy 2 − sin x )dx + x 2 ydy其中 L 为抛
物线 x = y 2 上由点 A(1,1)到 O ( 0,0 )的一段弧 .
, . 直的直线 解 为计算上简便加辅助线常选水平和垂 y 加水平直线 OB 和垂直直线 BA L A(1,1)
L
使之封闭 , 所围区域为 D ( 如图 ). 原式 = ∫ ⋯
L
从 A(1,0)到 B ( −1,0)的一段 .
如图 解 加水平直线 BA 使之封闭 (如图 ).
y
I=
∫ =∫
L
xdx + xy dy
xdx + xydy − ∫
BA
B(−1,0) −
L + BA
xdx + xydy
D O
x
A (1 ,0 )
= ∫∫ ( y − 0)dxdy −
D
π
1 0 0
∫
=∫
2π
0
− r 2 sin2 t − r 2 cos2 t = r cos t 2 d t = − π. l : x = r sint,,t从0变到 π . y 2 2r 15
= ∫ P[ x , ϕ 1 ( x )]dx + ∫ P[ x , ϕ 2 ( x )]dx
a b
b
y
∂P ∂P d xdy = 又 , ∫∫ ∂y D
a
= ∫ {P[ x,ϕ1( x)] − P[ x,ϕ2 ( x)]}dx;
∂P ∂P ∫a dx ∫ϕ1 ( x ) ∂y dy
b
L 2: y = ϕ 2( x )
D
L
L2
D
L1
3
注意, 可以是单连通域也可以是复连通域 可以是单连通域也可以是复连通域. 注意,D可以是单连通域也可以是复连通域.
2.格林公式 2.格林公式
定理 1 设闭区域 D 由分段光滑的曲线 L 所围成 , 函数 P ( x , y ), Q ( x , y )在 D 上具有一阶连续偏导数 , ∂Q ∂P 则有 ∫ P d x + Q d y = ∫∫ ∂ x − ∂ y dxdy , L D 其中 L 是 D 的正向边界曲线 . P 若D上有 、Q的偏导数不连 上述等式称为格林公式. 上述等式称为格林公式. 续的点则不能用格林公式 ,则不能用格林公式 .
0
= ∫ d t = 2 π.
0
2π
r 2 cos 2 t + r 2 sin 2 t dt 2 r
D1
l : x + y = r2
2
x
( P 当奇点0,0) ∈ D时, 若不注意是否满足 202定理1 公式 的条件而直接使用格林 , 则
xdy − y dx ∂Q ∂P . ∫ x2 + y2 = ∫∫ ( ∂x − ∂y )dxdy ===0 为错误结果 L D 14
4
∂Q ∂P 格林公式 ∫ P d x + Q d y = ∫∫ ∂ x − ∂ y dxdy L D (1 证 ) D 是单连通区域时 ( 如图 ) x = x, ∵ ∫ Pdx = ∫ Pdx + ∫ Pdx L2 : x从b变到 . x从a变到a. b 1 L L1 L2 2 x), y = ϕ1( x), b a
格林公式及其应用
一、格林公式 二、平面曲线积分与路径无关的条件 三、二元函数的全微分求积
1
一、格林公式
1.单(复)连通区域及其边界曲线的正向 1.单 连通区域及其边界曲线的正向
设 设 D 为平面区域 , 如果 D 内任意一条闭曲线 所围的部分都属于 D , 则称 D 是平面 单连通区域 , 否则称为 复连通区域 .
l ( ). 在D内作小圆周 : x + y = r 方向逆时针如图 l 设L与 共同围成的复连通区域 D . 为 1 ∂Q ∂P ∵ , 在复连通域 D1上连续 , ∴ D1上能用格林公式 . ∂x ∂y y
2 2 2
∂Q ∂P − )dxdy = 0, ⇒ ∫ Pdx + Qdy = ∫∫ ( ∂x ∂y D1 L +l −
D D
ϕ2 ( x)
∴ ∫ Pdx = − ∫∫
L D
∫ [ P ( x , y )] d x = ∫ {P[ x,ϕ ( x)] − P[ x,ϕ ( x)]}dx; O ∂P
=
a b
a 2 1
b
ϕ2( x) ϕ1 ( x )
L 1: y = ϕ 1( x )
∂y . 故格林公式成立
d xdy .
L l−
L D
O
⇒ ∫ Pdx + Qdy + ∫ Pdx + Qdy = 0,
D1
⇒ ∫ Pdx + Qdy = − ∫ Pdx + Qdy = ∫ Pdx + Qdy
L l− l
l
x
⇒ ∫ Pdx + Qdy = ∫ Pdx + Qdy.
L l
上的积分可以化成同 曲线L上的积分可以化成同 上的积分. 方向的小圆周 l 上的积分.
又
∂Q ∂P ⇒ ∫ P( x y)dx + Q( x y)dy = ( 要证 ∫ P( x,,y)dx + Q( x,,y)dy = ∫∫∫⋯+ ∫⋯ xdy. )d − ∂x BA+y ∂AB D + L2 L11 +L2 L+L2 L1 ∂Q ∂P D为复连通区域 ⋯ = ∫∫ ( = )dxdy. 证毕 − 证毕. ∫L +AB ∂x ∂y L1 +BA+ 2 D
D为复连通区域
6
BA+ AB
∫ P( x, y)dx + Q( x, y)dy = ∫
BA
⋯+ ∫ ⋯ = ∫ ⋯− ∫ ⋯ = 0.
AB
BA BA
∂Q ∂P ∫L P ( x , y )d x + Q ( x , y )d y = ∫∫ ∂ x − ∂ y dxdy D 3.格林公式的简单应用 顺便说一下格林公式的记忆方法 格林公式的简单应用 (1)计算平面区域的面积 (1)计算平面区域的面积
∫
1
0
ydy
= 0 − [cos x ]
1 0
1 1 2 − y = − cos 1 . 2 2 0
1
11
(3)计算曲线 (3)计算曲线 L 所围区域 D 内有奇点的曲线积分 x d y − yd x , 其中 L为一条无重点 , 分段光 例4 计算 ∫ 2 2 x +y L 滑且不经过原点的连续 闭曲线 , 方向逆时针 . −y x , Q( x , y ) = 2 . 解 P( x, y) = 2 2 2 x +y x +y y2 − x2 ∂P ∂Q = 2 = 在( 0,0)处不连续 , 称( 0,0)是奇点 . 2 2 ∂y ( x + y ) ∂x 设 L所围成的平面区域为 D . y 所围成的平面区域为 ∂Q ∂P L (1)当( 0,0 ) ∉ D时 , , 在 D上连续 , D ∂x ∂y
