5.偏摩尔量与化学势解读
物理化学简明教程(印永嘉)-化学势ppt课件
第三章 化学势
返回目录 退出
14
dG(CCl4) = 碘(CCl4)( –dn碘) dG(H2O) = 碘(H2O)dn碘
H2O
dn
CCl4
总的吉布斯函数变化为
dG= [ 碘 (H2O) – 碘(CCl4)] dn碘
平衡时dG=0,
碘(CCl4)=碘(H2O)
第三章 化学势
返回目录 退出
15
推广到任意两相:
时,过程即达平衡。 (本质未变,只是由单组份演变为多组分)
因此化学势的物理意义是:物质的化学势是决 定物质传递方向和限度的强度因素。
第三章 化学势
返回目录 退出
13
2.化学势在多相平衡中的应用
化学势判据: 条件: 密闭系统,( )T, p , W’=0时
(dG)T,p=BdnB =0 可逆或平衡
现在有一系统: I2分别溶解在水和四氯化碳中成两相(如图)。
-----B物质的偏摩尔量(与 组成有关)
第三章 化学势
返回目录 退出
4
则在定温定压的条件下(dT, dp为0),上式可 表示为:
dX X BdnB
B
X是系统中任意一个容量性质。 如为体积,则此式的物理意义为:增加dn摩尔
物质所引起的V的变化,等于该组成下的摩尔体 积乘以该摩尔数。(不是与摩尔量的偏差)
dH = TdS + Vdp + Wr’
(2)
(dH)S,P= Wr’
第三章 化学势
返回目录 退出
11
②多组分系统基本公式:
G=f(T, p, nB , nC , nD , )
dG
G T
p,nB
dT
G p
T ,nB
物化试题综合卷

试题A一、填空(7小题,共27分)[8分]1. 已知∆fH ((NH2)2CO , s , 298 K) =-333.1 kJ·mol-1;∆fH (NH3 , g , 298 K) =-46.19 kJ·mol-1;∆fH (CO2 , g , 298 K) =-393.5 kJ·mol-1;∆fH (H2O , l , 298 K) =-285.84 kJ·mol-1;则利用酶催化连续合成尿素的如下反应2NH3(g) + CO2(g) == (NH2)2CO(s) + H2O(l) 的∆rH (298 K) = ,∆rU (298 K)= 。
[2分]2. 写出化学势的两个定义式:μB =⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽=⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽。
[4分]3. 25 ℃反应N2O4(g) ==2NO2(g)的标准平衡常数K =0.1132,同温度下系统中N2O4(g) 的分压力为1013.25 kPa,NO2(g) 的分压力为 101.325 kPa,则反应将向⎽⎽⎽⎽⎽⎽进行。
(选填左、右)。
[2分]4. 在多相催化反应中,通常把吸附控制、表面反应控制及解吸控制统称为控制。
[4分]5. 电池 Pt ⎢ H2(g, p1) ⎢ HCl(aq) ⎢ Cl2(g, p2) ⎢Pt的反应可以写成:H2(g, p1)+ Cl2(g, p2) 2HCl(aq), E1,∆rGm, 1或H2(g, p1)+ Cl2(g, p2) HCl(aq),E2,∆rGm, 2试表示出 E1与E2的关系⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽;∆rGm,1与∆rGm,2 的关系⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽。
[4分]6.胶体分散系统的粒子尺寸为⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽之间,属于胶体分散系统的有(1)⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽;(2)⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽;(3)⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽。
化学势和偏摩尔量

化学势得广义定义就是:保持某热力学函数得两个特征变量与除B以外得其他组分不变时,该热力学函数对B物质得量求偏微分。
通常所说得化学势就是指它得狭意定义,即偏摩尔Gibbs自由能,即在等温、等乐下,保持除B以外得其它物质组成不变时,Gibbs自中能B物质得量得改变得变化率称为化学势。
偏摩尔量是指在温度、乐九及除了组分B以外其余组分的物质的量均不变的条件下,广度量X随组分B的物质的量nB变化率XB称为组分B的偏摩尔量。
简单地说,化学势其实就是偏摩尔吉布斯自由能,是偏摩尔量的一种。
但偏摩尔量不全是化学势。
一个体系里可以有好几种偏摩尔量。
如U,F,H,G,S 等的偏摩尔量。
事实上所有体系容量性质都可以有偏摩尔量。
化学势只是其中一种,就是G的偏摩尔量。
化学势是偏摩尔量中最重要的一种。
除了考推导能力以外其他的偏摩尔量很少用到。
从实用的角度看,引入偏摩尔量概念的最主要的目的就是为了说明化学势。
但是二者不能混为一谈。
偏摩尔量与化学势的区别

偏摩尔量与化学势的区别偏摩尔量和化学势是描述化学系统中物质变化和平衡的重要概念,它们在理论和实际应用中有着不同的含义和用途。
下面我将从多个角度对它们进行全面的解释。
1. 定义和概念:偏摩尔量,偏摩尔量是指在混合物中某种组分的摩尔量的变化。
它描述了混合物中某种组分的浓度对混合物性质的影响。
化学势,化学势是指单位物质在化学系统中的自由能变化。
它描述了物质在化学反应中的倾向性和平衡状态。
2. 表达方式:偏摩尔量,偏摩尔量通常用Δ表示,表示在反应或混合过程中某种组分的摩尔量的变化。
化学势,化学势通常用μ表示,表示单位物质在化学系统中的自由能变化。
3. 物理意义:偏摩尔量,偏摩尔量描述了混合物中某种组分的浓度变化对混合物性质的影响。
它可以用于计算反应的平衡常数、溶液的浓度、物质的扩散速率等。
化学势,化学势描述了物质在化学反应中的倾向性和平衡状态。
它可以用于判断反应的进行方向、计算反应的平衡常数、预测溶解度、推导化学平衡的条件等。
4. 应用领域:偏摩尔量,偏摩尔量在化学工程、热力学、溶液化学等领域具有广泛的应用。
例如,在化学反应工程中,通过研究反应物和产物的偏摩尔量变化,可以确定反应的最佳条件和反应的平衡状态。
化学势,化学势在化学热力学、电化学、物理化学等领域有着重要的应用。
例如,在电化学反应中,通过比较不同物质的化学势变化,可以预测电池的电动势和电流方向。
综上所述,偏摩尔量和化学势在描述化学系统中物质变化和平衡方面具有不同的含义和用途。
偏摩尔量描述了混合物中某种组分的浓度变化对混合物性质的影响,而化学势描述了物质在化学反应中的倾向性和平衡状态。
它们在不同的领域和问题中起着重要的作用。
第三章化学势效果

K
å 恒温恒压时:dG = midni
i= 1
2019/9/17
长江大学化工学院
7
三. 化学势
结论:以偏摩尔吉布斯函数(自由能)定义
的化学势(mi)表示定温定压下,在无限大量的 体系中加入1moli物质时,所引起的体系的布斯函数 (自由能)的增加值
化学势(mi)的其它定义
K
å dG = - SdT + VdP+ midni
i= 1
U = f (S ,V , n1, n2 ,...nK )
å 抖U
U
K ?U
\ dU = ( 抖S )V ,nK dS + ( V )S ,nK dV + i= 1 ( ? ni )S ,V ,n j¹ i dni ......(4)
对比(3)和(4)得
¶U mi = ( ¶ ni )S ,V ,n j¹ i
又
对纯组份理想气体来说:Gm =
m; V m =
RT P
蝌 \
m
dm=
P RT dP ? m
mq (T ) + R T ln P
mq
P P q
Pq
讨 论 : 规 定 理 想 气 体 的 压 力 为 P q (1 0 5 P a )时 的 状 态
为它的标准态,此状态下物质的化学势称为
标 准 态 的 化 学 势 mq (T )
åK ¶ G
dG
=
-
SdT
+
VdP +
i= 1
( ¶ ni )T ,P ,n j¹ i dni
2019/9/17
长江大学化工学院
6
三. 化学势
将偏摩尔吉布斯函数(自由能)定义为第i种物质
2.13偏摩尔量和化学势讲解
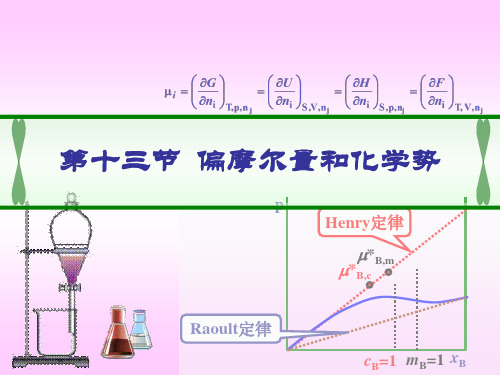
X X dX dT dp X B ,m dnB T p ,ni B p T ,ni
一、偏摩尔量
2. 多组分系统的偏摩尔量
VB ,m V n B T , p , n j B U B ,m U H H B ,m n n B T , p , n j B B T , p , n j B GB , m G n B T , p , n j B
二、化学势
(2) 化学势广义定义
U H 广义定义: B nB S ,V ,n j B nB S , p ,n j B F G nB T ,V ,n j B nB T , p ,n j B
G f(T , p, n1 , n2 ,..........)
-SdT
Vdp
B
B
dnB
dG SdT Vdp ( B dnB )
B
二、化学势
(2) 化学势广义定义 dU = TdS - pdV
U f( S ,V , n1 , n2 ,....)
U U U dU dS dV dnB S V ,ni V S ,ni B nB S ,V , n jB
一、偏摩尔量
3. 偏摩尔量的集合公式 因为偏摩尔量是强度性质,所以只要多组分系统中各物质的 比例(组成)不变,则某个物质的偏摩尔量也不变。
dX
T,p
X B ,m dnB
B
在保持偏摩尔量不变的情况下对上式积分
X X 1,m dn1 X 2,m dn2 X i ,m dni
物理化学主要公式及使用条件(第四、五章)

第四章 多组分系统热力学 主要公式及其适用条件1. 偏摩尔量:定义: C n p,T,n X X ⎪⎪⎭⎫⎝⎛∂∂=B B (1)其中X 为广延量,如V ﹑U ﹑S ......全微分式:d ⎛⎫∂∂⎛⎫=++ ⎪ ⎪∂∂⎝⎭⎝⎭∑B B B B Bd d d p,n T,n X X X T p X n T p (2)总和: ∑=BB B X n X (3)2. 吉布斯-杜亥姆方程在T ﹑p 一定条件下,0d BB B =∑X n , 或0d BBB =∑Xx 。
此处,x B 指B 的摩尔分数,X B 指B 的偏摩尔量。
3. 偏摩尔量间的关系广延热力学量间原有的关系,在它们取了偏摩尔量后,依然存在。
例:H = U + PV ⇒ H B = U B + PV B ; A = U - TS ⇒ A B = U B - TS B ; G = H – TS ⇒ G B = H B - TS B ;…...S T G ;S T G ;V p G V p Gn p,p n T,TB B B B BB -=⎪⎭⎫ ⎝⎛∂∂⇒-=⎪⎭⎫⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂⇒=⎪⎪⎭⎫ ⎝⎛∂∂4. 化学势定义 Cn p,T,n G G μB B ⎪⎪⎭⎫⎝⎛∂∂==B5. 单相多组分系统的热力学公式∑+-=BBB d d d d n μV p S T U∑++=BBB d d d d n μp V S T H ∑+-=BBB d d d d n μV p T S -A∑++=BBB d d d d n μp V T S -GCCCCB B B B B n p,T,n V,T,n p,S,n V,S,n G n A n H n U μ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂====但按定义,只有 CB n p,T,n G ⎪⎪⎭⎫ ⎝⎛∂∂才是偏摩尔量,其余3个均不是偏摩尔量。
6. 化学势判据在d T = 0 , d p = 0 δW ’= 0 的条件下,⎪⎭⎫⎝⎛≤α=<∑∑平衡自发,,00α0 )()d (αBB B n μ 其中,∑α指有多相共存,)(αB μ指 α相内的B 物质。
偏摩尔量和化学势

一、偏摩尔量
2. 多组分系统的偏摩尔量 等温等压下
X dX dnB B nB T , P , n j B
X B ,m X nB T , P ,n j B
定义:偏摩尔量
指的是多组分系统中B物质的某种广度性质的偏摩尔量(换 句话说,就是某种组分的物质的量对某个系统性质的贡献 的大小) 那么对于多组分系统的某个广度性质则存在
B
dH TdS Vdp BdnB
B
dA sdT pdV BdnB
X f(T , p, n1 , n2 ,...........ni )
当系统状态发生微小变化时,用全微分表示
X X X dX dT dn1 T P ,ni p T ,ni n1 T , P ,n j1 X dn2 ......... n2 T , P ,n j2
X X dX dT dp X B ,m dnB T p ,ni B p T ,ni
一、偏摩尔量
2. 多组分系统的偏摩尔量
VB ,m V n B T , p , n j B U B ,m U H H B ,m n n B T , p , n j B B T , p , n j B GB , m G n B T , p , n j B
G dG SdT VdP dnB n B T , P , n j B
U dU TdS pdV dnB nB V , S ,n j B
F dF SdT pdV dnB n B T ,V ,n jB
化学势和偏mol量

化学势和偏mol量
化学势和偏mol量是热力学中的重要概念,被广泛应用于许多化学过程的研究和计算。
化学势是一种能量测量,代表单位物质所拥有的自由能量。
在化学反应中,化学势的变化可以帮助我们理解反应的方向和速率,并且可以用来计算气体、液体和固体的热力学性质。
化学势可以通过以下公式计算得出:
μ=(∂G/∂n)T,P
其中,μ代表化学势,G代表体系的吉布斯自由能,n代表物质的摩尔数,T和P分别代表温度和压力。
偏mol量也是一个重要的物理量,指的是单位物质所含的某种物质的量。
偏mol量在反应热力学和化学平衡中也起到非常重要的作用,可以用来计算溶液中物质的浓度和活度系数。
偏mol量可以通过以下公式计算得出:
xi=ni/∑i ni
其中,xi代表物质i的偏mol量,ni代表物质i的摩尔数,∑i ni代表体系中各种物质的总摩尔数。
通过化学势和偏mol量的计算,我们可以更深入地了解热力学中的各种化学和物理过程,为实际应用提供了更多的指导意义。
化学势

习题5
P93
类型:证明化学势的广义定义式
dA=dG-pdV-Vdp
从定义A=G-PV
将dG = - SdT + VdP + ∑μidni代入上式:
dA = - SdT -pdV + ∑μidni (1)
令 A = ƒ( T、V、n1、n2、n3 … ni ) dA= (∂A/∂T)V,nk dT + (∂A/∂V)T,nk dV + ∑(∂A/∂ni)T,V,njdni = - SdT -pdV + ∑(∂A/∂ni)T,V,njdni (2) (1)=(2) 得:μi=(∂A/∂ni)T,V,nj
纯态,标准态化学势μθ(pg, T)] 作为基准。 (pg —理想气体)
1mol,pg,T, Pθ, μθ(pg,T)→1mol,pg,T, P, μ(pg,T,P) 应用 dG = - SdT + VdP ∵ ∴ 积分得 μ(pg, T,P)-μθ(pg, T)= RT∫PθP dlnP = RTln(P / Pθ) dT = 0 dμ = dGm =VmdP = RT / P dP = RTdlnP 于 1 mol pg
3、实际气体的化学势——逸度的概念
(1)逸度的概念:
对于实际气体,不能用上述关系表示吉布斯自由能或化
学势。为此路易斯(Lewis)提出简单硬凑法,将实际气 体压力P乘上一个校正因子γ ,再代入理想气体化学势表 示式。即
μ = μθ + RT ln (γ P / Pθ) 此式即可表示实际气体。其中γ P称为“逸度”, 用符号ƒ表示。即 ƒ = γ P
( ) T,P,δW′=0
i(α)
μiα 根据化学势判据
i( β)
化学式与偏摩尔量的有关题目

化学式与偏摩尔量的有关题目
1.溶液的化学势等于溶液中各组分化学势之和。
解:错,对溶液整体没有化学势的概念。
2.系统达到平衡时,偏摩尔量为一个确定的值。
解:错,不同相中的偏摩量一般不相同。
3.对于纯组分,化学势等于其吉布斯函数。
解:错,纯组分物质的化学势应等于摩尔吉布斯函数。
4.在同一稀溶液中组分B的浓度可用xB、mB、CB表示,因而标准态的选择是不相同的,所以相应的化学势也不同。
解:错,化学势与标准态、浓标的选择无关。
5.水溶液的蒸气压一定小于同温度下纯水的饱和蒸气压。
解:错,当溶质不挥发时才一定成立。
6.将少量挥发性液体加入溶剂中形成稀溶液,则溶液的沸点一定高于相同压力下纯溶剂剂的沸点。
溶液的凝固点也一定低于相同压力下纯溶剂的凝固点。
解:错,因加人挥发性溶质,沸点不一定升高。
凝固点是否降低要看溶质是否析出。
7.纯物质的熔点一定随压力升高而增加,蒸气压一定随温度的增加而增加,沸点一定随压力的升高而升高。
解:第一个结论错,如水的熔点随压力增大而降低。
后两个结论都正确。
8.理想稀溶液中溶剂分子与溶质分子之间只有非常小的作用力,以至可以忽略不计。
解:错,两种分子之间的作用力和同种分子之间的作用力都较大,不可忽略。
9.当温度一定时,纯浴剂的饱和蒸气压越大,溶剂的液相组成也越大。
解:错,液相组成与纯溶剂的蒸(压无关。
10.在一定的温度和同一溶剂中,某气体的亨利系数越大,则此气体在该溶剂中的溶解度也越大。
解:错,当压力一定时,溶解度与亨利系数成反比。
溶液概述偏摩尔量和化学势

多组分系统热力学及其在溶液中的应用(10学时)物理化学教研室2011 年3 月第一讲 :溶液概述、偏摩尔量和化学势【本讲重点】1、 多组分系统组成的表示及其相互关系;2、 偏摩尔量和化学势的定义,二者的区别和在多相组分系统中引入两种概念的意义。
【本讲难点】偏摩尔量与化学势的概念 【授课方法】讲授【教学手段】多媒体教学与黑板讲述相结合 【计划课时】24.1 引言一、溶液的定义 广义定义:广义地说,两种或两种以上物质彼此以分子或离子状态均匀混合所形成的体系称为溶液。
二、溶液的分类1、按溶液以物态:可分为气态溶液、固态溶液和液态溶液。
2、根据溶液中溶质的导电性:可分为电解质溶液和非电解质溶液。
本章主要讨论液态的非电解质溶液。
三、溶剂和溶质液态溶液:如果都是液态,则把含量多的一种称为溶剂,含量少的称为溶质。
非液态溶液:如果组成溶液的物质有不同的状态,通常将液态物质称为溶剂,气态或固态物质称为溶质。
四、混合物混合物(理想溶液):多组分均匀体系中,溶剂和溶质不加区分,各组分均可选用相同的标准态,使用相同的经验定律,这种体系称为混合物,也可分为气态混合物、液态混合物和固态混合物。
4.2溶液组成的表示法在液态的非电解质溶液中,溶质B 的浓度表示法主要有如下四种: 1.物质B 的质量浓度BB def/m V ρ溶质B 的质量与混合物总体积之比称为溶质B 的物质的量分数,单位为: 3kgm - 。
2.物质的量浓度cBBdefBn c V溶质B 的物质的量与溶液体积V 的比值称为溶质B 的物质的量浓度,或称为溶质B 的浓度,单位是mol/m 3,但常用单位是mol/L 。
3.物质的量分数B BAdefAn x n ∑溶质B 的物质的量与溶液中总的物质的量之比称为溶质B 的物质的量分数,又称为摩尔分数,单位为1。
4.质量摩尔浓度BBAdef n m m溶质B 的物质的量与溶剂A 的质量之比称为溶质B 的质量摩尔浓度,单位是mol/kg 。
物理化学简明教程(印永嘉)_化学势582111435

第三章 化学势
返回目录 退出
24
以1mol该气体为系统,在一定温度下,
T, p*
T, p
(Gm )T ( p) ( p ) RT ln f / f
( p)
(T ) RT
ln
f p
第三章 化学势
返回目录 退出
25
从定义式出发
Vm=RT/p +α
dGm = Vmdp=(RT/p +α)dp
T , p,nCB
V
浓度 V水/cm3 V乙醇/cm3 V总/cm3
20.8% 150 50 195
44.1% 100 100 192
70.3% 50 150 193
单组份系统是 过原点的直线
nB
第三章 化学势
返回目录 退出
7
2. 偏摩尔量的集合公式(积分式)
若是二组分系统,则 dX=XAdnA+XBdnB 如:A和B的偏摩尔体积分别为VA ,VB, 则 ( )T,p dV=VAdnA+VBdnB 但VA,VB均为变量,不能直接积分。
第三章 化学势
返回目录 退出
29
2. 理想液态混合物的定义
(1)一定温度和压力下,液态混合物中任一组分在 任意浓度范围内都服从拉乌尔定律——称为理想 液态混合物。
(2)微观解释:同纯物质处境
理想液态混合物就是混合物中各种分子之间的相互作用 力完全相同。以物质B和物质C形成理想混合物为例,混合 物中任何一种物质的分子B不论它全部为B分子所包围,或 全部为C分子所包围,或一部分为B分子另一部分为C分子 所包围,其处境与它在纯物质时的情况完全相同。
体单独占有混合气体总体积时的行为相同。所以理想气体
5.偏摩尔量与化学势解读

?
2 偏摩尔量及其物理意义 多组分系统的任一广度量X 是任意两个独立变量(T, p, V)和组 成的函数
X X T , p, nB , nC , nD ,...
系统微变时, X相应的变化
X X X dX dT dp dnB T p ,nB p T ,nB nB T , p ,nC X dnC .... nC T , p ,nC
—— nB表示总组成nB, nC, nD…均不发生变化; —— nC表示,除 B 以外,其它组分的物质的量 均不变
令 XB
X n B T , p ,n
C
X X dX dT dp X BdnB T p ,nB p T ,nB
式中XB即为广度量X的偏摩尔量
X XB n B T , p ,nC
——偏摩尔量
偏摩尔量的物理意义:在一定温度、压力下,将1 mol组 分 B加到无限大量的均相多组分系统中所引起的广度量X 的改变。 对偏摩尔量的强调: • X 必须是系统的广度量, 强度量不存在偏摩尔量 • 恒温,恒压下 是对某组分的物质的量求偏导(的变化率) • 偏摩尔量是强度量
得到多组分系统的热力学基本方程
dU TdS pdV BdnB
B
dH TdS Vdp BdnB
B
dA SdT pdV BdnB
B
dG SdT Vdp BdnB
B
式中
U H A G B n n n n B S ,V , nC B S , p , nC B T , S , nC B T , p ,nC G 以 B 最为常用 n B T , p ,nC
偏摩尔量与化学势

化学势在相变中应用
如果上述相转移过程是自发从α相到β相进行的
则(dG)T,p<0,可得
B
B
dnB
0
又因为已假设B物质是由α相转移到β相,即 dnB 0
故
B
B
由此可见,物质的相变总是自发从μB较大的相流向μB 较小的相;直到物质B在两相中的μB相等达到平衡。
化学势在化学变化中的应用
因为恒温恒压下的化学变化总是自发朝向吉布斯自由能变小于零的 方向进行,直至吉布斯自由能变为零达到平衡,即
理想气体混合物中,由于各组分分子模型都相似,分
子间作用力相似,所以相当于一种理想气体的混合,
对于混合物中任一组分B来说,其化学势
(B T ,
p)
B
(T
,
p
)
RT
ln
pB p
根据道尔顿分压定律
得混合物中任意组分B的化学势
(B T ,
p)
B
(T
,
p)
RT
ln
p p
RT
ln
xB
* B
(T
,
p)
RT
dn2
......
当系统在恒温恒压下发生变化时,定义偏摩尔量
ZB
Z nB
T , p,nC(C B)
表示:在恒温恒压下,向组成一定的系统中加入l mol任意 组分B而引起系统中某一广延性质Z的改变量。
多组分体系的偏摩尔热力学函数值
使用偏摩尔量时应注意: 1.偏摩尔量的含义是:在恒温、恒压、保持B物质以外的所有组分的物质的量不 变的条件下,改变物质的量所引起广延性质Z的变化值,或在恒温、恒压条件下, 在大量的组成恒定的系统中加入单位物质的量的B物质所引起广延性质Z的变化 值。
《偏摩尔量》PPT课件

y
1 x z
y
z z w x y w y x y
x
z y
x
y
y
z x
y
x
2021/4/25
13
1.22 混合物及溶液
1. 概念
含一个以上组分的系统称多组分系统 多组分均相系统又可以区分为混合物或溶液
溶液中的各组分区分为溶剂及溶质,并选用不 同的标准态加以研究
H2O,18.07cm3 + C2H5OH,5.74cm3
定温、定压混合
混合物, 23.30cm3
298K,101.325kPa
23.30cm3≠23.81cm3
2021/4/25
17
说明什么?
18.07cm3 (T,p) 水单独存在或在大量水中体积贡献都是
18.07 cm3; 但同样量的水对乙醇水混合物的体积贡献不是 18.07cm3
滴加2
• 定温、定压、n1不变条件下,滴加2
• 测定n2和V
n2
……
V
……
组分 1,2
• 利用实验数据绘制 V—n2 曲线
2021/4/25
20
• 利用实验数据绘制 V—n2 曲线
如何从V—n2图得到浓度是
V V'
x2'=n2 ' /(n1+n2 ' )的V2=?
.. ..
n2 ' n2
V n2
T,p,n1
公式
2021/4/25
33
2. 再谈热力学基本方程
已学过组成一定,量一定的均相系统的热力学基本方程
利用化学势,热力学基本方程可扩展到 多组分组成可变的均相系统 多组分组成可变的多相系统
化学平衡基础知识讲义

(二)恒温恒压均相化学反应体系 0 = ΣBB,
化学反应体系:封闭的单相体系,不作非膨胀功, 发生了一个化学反应,设为:
aA + bB → gG + hH
根据反应进度的定义,可以得到:
d dnB B
dnB Bd
( d G ) T ,p B d n B BB d
B
B
rGmG T,p BB
常见的偏摩尔量
Vi
V ni
T , p,n ji
Hi
H ni
T, p,nji
Fi
F ni
T , p,n ji
Gi
G ni
T
,
p,n
ji
2 化学势
(1) 化学势的定义
混合物(或溶液)中组分B的偏摩尔吉布斯函数GB又称
为B的化学势,用B表示,其定义为:
def
B GB
nGBT,p,nC
若将混合物的吉布斯函数G表示成T,P及构成此混合物 各组分nB,nC,nD….的函数,即
混合物的组成不随时间而改变 — 化学反应的限度
化学平衡是动态平衡,即,正向反应进行和逆相进行的 速率相等
(1) 化学反应的方向和限度
一气象反应为例:在将A 和B放在一起,首先有一 混合过程,此过程在等温 等压下是自发的,混合过 程ΔG;然后ΔG随反 应进度而变化,见右图, 随着增大,ΔG由负值逐 渐向正值转变。实际反应 只能达到ΔG的最小值零, 再增大, ΔG,反应 只会向反方向进行。
化学平衡基础知识讲义
路漫漫其悠远
少壮不努力,老大徒悲伤
化学势
1. 偏摩尔量
偏摩尔量的定义
体系的状态函数中V,U,H,S,A,G 等是广度性质
,与物质的量有关。以 X 代表任一广度性质,即:
4-2多组分系统热力学-偏摩尔量与化学势

物理化学(上册)
绪论
第一章气体
第二章热力学第一定律
第三章热力学第二定律
第四章多组分系统热力学
第五章化学平衡
第六章相平衡
单组分化学势就是摩尔量吉布斯函数,用
多组分系统热力学基本关系式(适用条件封闭系统多组分)
由热力学基本关系式可以得到化学势广义定义
多相多组分化学势判据:
3. 多相多组分平衡时:
1.标准态:T温度、
2m3m
3.真实气体的化学势表示为:
1.逸度和逸度系数
2.逸度和逸度系数计算
1.以气体的标准态为标准态
m2m3m
2.以液体的标准态为标准态
以液体的标准态为标准态时:
物理化学。
第三章偏摩尔量与化学势

第三章偏摩尔量与化学势1.有一水和乙醇形成的均相混合物,水的物质的量分数0.4,乙醇的偏摩尔体积57.5cm3·mol-1,混合物的密度为0.8494g·cm-3。
试计算混合物中水的偏摩尔体积。
解:设n A+n B=1mol,则n A=0.4mol,n B=0.6mol。
V=n A V A+n B V B(0.4×18+0.6×46)/0.8494=0.4V A+0.6×57.5V A=16.18ml·mol-12.有一水和乙醇形成的均相混合物,水的物质的量分数0.4,乙醇的偏摩尔体积57.5cm3·mol-1,水的偏摩尔体积16.18cm3·mol-1。
试计算该液体混合物的密度。
解:设n A+n B=1mol,则n A=0.4mol,n B=0.6mol。
V=n A V A+n B V B(0.4×18+0.6×46)/ρ=0.4×16.18+0.6×57.5ρ=0.84943.计算(a)1mol水溶于大量的1mol·kg-1的甘氨酸溶液中,体系的体积改变多少?(b) 1mol甘氨酸固体溶于水配制成1mol·kg-1的水溶液时,体系的体积改变多少?解:(a)ΔV=V(水)-V m(水)=18.05-18.07cm3=-0.02cm3(b) 混合前V(始)=n(水)V m(水)+n(甘,s)V m(甘,s)混合前V(终)= n(水)V(水)+n(甘,s)V(甘,s)ΔV= V(终)- V(始)= n(水)[V(水)-V m(水)]+n(甘,s)[V(甘,s)-V m(甘,s)]=[1000/18.015][18.05-18.07]+1×(44.88-46.71)cm3=-2.94cm34. 已知纯水的密度为0.9991g·cm-3,c B=1mol·dm-3时,浓度为1mol·dm-3的乙醇水溶液的密度为0.8498 g·cm-3,水和乙醇的偏摩尔体积分别为14.58 cm3·mol-1、58.04cm3·mol-1。
偏摩尔量与化学势解读

引言
• 上节我们讨论了恒定组成体系的各热力学 关系式,在几个热力学关系式中都只涉及 两个变量,这只有对组成不变的体系才是 正确的。
• 当体系由于和环境交换物质而引起组成的 变化、或由于不可逆的化学变化、或体系 内部不可逆的物质传输而引起组成变化时 体系的Gibbs方程就不适用了。
• 其物理意义是在等温等压下,在大量体系 中,除了组分B以外,保持其它组分的量不 变(nC不变),加入1mol物质B所引起的 体系容量性质Z的改变;
• 或是在等温等压下,向有限体系中加入dnB 以后,体系容量性质改变dZ,则
Z B,m
dZ dnB
注意
• 等温、等压条件 • 加入B后,体系浓度没有改变 • Z是体系的某种容量性质 • 若体系只有一种组分(即纯物质),则其
G nB
T ,P,nC (C B)
• 此式定义的化学势是偏摩尔量,即偏摩尔 吉布斯自由能就是化学势。
2.化学势的应用
• 我们已知吉布斯自由能变化可用于计算、 判断过程自发的方向
k
dG SdT VdP B dnB B 1
• 等温等压无非膨胀功的条件下
k
dG B dnB B 1
• 对于组成可变的体系,在热力学函数的表 示中都应包含有各物质的量作为变量。
• 对于多组分体系,有两个概念很重要:一 个是偏摩尔量,一个是化学势。
第一节 多组分体系中的偏摩尔量和化学势 • 一、偏摩尔量 1.定义
设有一个均相体系是由组分1,2,3…,k 组成的,体系的任一种容量性质Z(如 V,S,H,U,G等)除了与温度压力有关以外, 还与体系中各组分的数量—物质的量(n1, n2,n3……nk)有关,则Z 的函数可以写作
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
