固体磁性第3章
固体物理学_2版(陈长乐编著)PPT模板

05 4 . 5 能 带理 论的其
他近似方法
02 4 . 2 周 期场 中单电
子状态的一般属性
04 4 . 4 紧 束缚 近似
06 4 . 6 晶 体中 电子的
准经典运动
第一部分
第4章能带理论
4.7固体导电性能的能 带论解释
本章要点
习题
4.8能态密度 思考题
第一部分
第5章金属电子论
01 5 . 1 金 属电 子的统
实验测定
06 3 . 6 晶 格振 动的热
力学函数模式密度
第一部分
第3章晶格振动与晶体的 热学性质
1 3.7晶格热 容
3.8晶体的
2 状态方程 和热膨胀
3 3.9晶格热 传导
4 本章要点
5 思考题
6 习题
第一部分
第4章能带理论
01 4 . 1 能 带理 论的基
本假定
03 4 . 3 近 自由 电子近
2.3晶体结合类型与原 子的负电性
思考题
2.2晶体结合的基本类 型及特性
本章要点
习题
第一部分
第3章晶格振动与晶体的热学性质
01 3 . 1 一 维晶 格振动
02 3 . 2 三 维晶 格振动
03 3 . 3 正 则坐 标与声
子
05 3 . 5 离 子晶 体中的
长光学波
04 3 . 4 晶 格振 动谱的
计分布费米能
03 5 . 3 金 属费 米面的
试验测定
05 5 . 5 功 函数 接触电
势
02 5 . 2 金 属的 费米面
04 5 . 4 金 属的 电导与
热导
06 5 . 6 金 属的 光学性
固体材料的磁性研究

固体材料的磁性研究近年来,固体材料的磁性研究在科学界引起了极大的关注。
磁性材料不仅在磁存储、磁传感器和电磁设备等领域有着广泛的应用,而且对于深入了解物质的性质和相互作用也起着关键的作用。
本文将就固体材料的磁性研究进行探讨。
首先,固体材料的磁性是由其中所含的磁性原子或离子所决定的。
磁性原子或离子具有自旋磁矩,其自旋在外加磁场的作用下产生磁矩的定向,从而呈现出磁性行为。
根据材料的磁性表现,可将固体材料分为顺磁性、抗磁性和铁磁性。
顺磁性材料中的磁矩与外加磁场平行或反平行,导致磁性的增强或削减。
顺磁性物质在外加磁场的作用下会产生磁化强度增加的现象,这种材料常见的例子有铁、铝和锶等元素。
抗磁性材料中的磁矩与外加磁场方向始终垂直,使材料在外加磁场作用下呈现出磁矩的减小。
抗磁性材料的一个例子是铜。
最重要的是铁磁性材料,铁磁性材料中的磁矩与外加磁场平行或反平行,可以自发地在无外加磁场时形成磁畴结构。
铁磁性材料的晶体结构中,磁矩呈现出有序排列的状态,即形成各向同性的磁畴。
在铁磁性材料中,磁畴之间存在磁畴壁,通过改变外加磁场的方向,可以通过壁移动或磁畴翻转的方式实现磁化翻转。
铁磁性材料常见的例子有铁、镍和钴等元素。
在固体材料的磁性研究中,单晶材料和多晶材料的磁性行为往往有所差异。
单晶材料中,由于晶体的各向异性,磁性行为往往更加复杂。
而多晶材料中,不同晶粒间的晶界会对磁性行为产生影响。
此外,对于一些非晶态或纳米晶材料,其磁性行为也具有独特的特点。
除了材料本身的特性外,外部条件对于固体材料的磁性研究也具有重要作用。
温度是一个重要的因素,温度的变化会导致材料的磁性行为发生改变。
低温下,材料往往呈现出强磁性,而高温下,材料可能失去磁性或呈现出顺磁性。
此外,压力和磁场等外部条件也会对材料的磁性行为产生明显的影响。
通过改变外部条件,可以实现对固体材料磁性的控制和调控。
固体材料的磁性研究不仅涉及到实验和观测,还需要理论模型的构建和计算模拟的开展。
固体物理(黄昆)第一章总结

固体物理(黄昆)第一章总结.doc固体物理(黄昆)第一章总结固体物理学是一门研究固体物质微观结构和宏观性质的学科。
黄昆教授的《固体物理》一书为我们提供了深入理解固体物理的基础。
本总结旨在概述第一章的核心内容,包括固体的分类、晶体结构、晶格振动和固体的电子理论。
一、固体的分类固体可以根据其结构特征分为晶体和非晶体两大类。
晶体具有规则的几何外形和有序的内部结构,而非晶体则没有长程有序性。
晶体又可以根据其内部原子排列的周期性分为单晶体和多晶体。
二、晶体结构晶体结构是固体物理学的基础。
黄昆教授详细讨论了晶格、晶胞、晶向和晶面等概念。
晶格是描述晶体内部原子排列的数学模型,而晶胞是晶格的最小重复单元。
晶向和晶面则分别描述了晶体中原子排列的方向和平面。
三、晶格振动晶格振动是固体物理中的一个重要概念,它涉及到晶体中原子的振动行为。
黄昆教授介绍了晶格振动的量子化描述,包括声子的概念。
声子是晶格振动的量子,它们与晶体的热传导和电导等性质密切相关。
四、固体的电子理论固体的电子理论是固体物理学的核心内容之一。
黄昆教授从自由电子气模型出发,介绍了固体中电子的行为和性质。
自由电子气模型假设电子在固体中自由移动,不受原子核的束缚。
这一模型可以解释金属的导电性和热传导性。
五、能带理论能带理论是固体电子理论的一个重要组成部分。
黄昆教授详细讨论了能带的形成、能隙的概念以及电子在能带中的分布。
能带理论可以解释不同固体材料的导电性差异,是现代半导体技术和电子器件设计的基础。
六、固体的磁性固体的磁性是固体物理中的另一个重要主题。
黄昆教授讨论了磁性的来源,包括原子磁矩和电子自旋。
磁性固体可以分为顺磁性、抗磁性和铁磁性等类型,它们的磁性行为与电子结构密切相关。
七、固体的光学性质固体的光学性质涉及到固体对光的吸收、反射和透射等行为。
黄昆教授介绍了固体的光学性质与电子结构之间的关系,包括光的吸收和发射过程。
八、固体的热性质固体的热性质包括热容、热传导和热膨胀等。
固体磁性1-绝缘体顺磁性和抗磁性

e e e ee F
gB Bz ( J 1/ 2) gB Bz / 2
gB Bz ( J 1/ 2) gB Bz / 2
低温极限 kBT gB JBz
取Bz 104 gauss 则 T 1K
此时,磁矩倾向于平行排列。
高温极限 kBT gB JBz
磁化率
0
N V
(gB )2 3
J (J 1) kBT
n0
E0 En
8m
(xi2 yi2 ) 0
i
磁化强度 M N E0
V Bz
磁化率
0
M Bz
0
N V
q2
4m
0
i
(xi2 yi2 ) 0
2B2 |
n0
0 (Lz gsSz ) n En E0
|2
练习:
(1)证明 [L g0S,n J ] i n(L g0S)
(2)已知: Jx 0 Jy 0 Jz 0 0 证明: 0 (L gsS) 0 0
外层电子的哈密顿量
H
i
H (0) i
i j
e2
40
| ri
1 rj
|
i
H soc i
第一项是常见的单电子哈密顿量
i 标记第i个电子
H (0) i
pi2 2m
V பைடு நூலகம்ri )
V 是电子感受到的离 子实的势能
第二项是电子电子相互作用能。
第三项是自旋轨道耦合。
H soc i
(r)li
si
最低阶近似 (舍弃哈量后两项)
d 电子在正八面体晶体场(阴离子)中的劈裂 高能态 低能态
自由离子d轨道
球形场
正八面体场 (Oh群)
固体物理基础第3章-晶格振动与晶体的热学性质

3-2 一维单原子链模型
格波的色散关系 4 2 2 aq sin ( )
m 2 • ω取正值,则有 (3)
(q)
aq 2 sin( ) m 2 • 频率是波数的偶函数
• 色散关系曲线具有周期性, 仅取简约布里渊区的结果即可 • 由正弦函数的性质可知,只有满足 0 2 / m 的格波 才能在一维单原子链晶体中传播,其它频率的格波将被强
原子n和原子n+1间的距离
非平衡位置
原子n和原子n+1间相对位移
a n1 n
n1 n
3-2 一维单原子链模型
• 忽略高阶项,简谐近似考虑原子 振动,相邻原子间相互作用势能 1 d 2v v(a ) ( 2 ) a 2 2 dr • 相邻原子间作用力 dv d 2v f , ( 2 )a d dr • 只考虑相邻原子的作用,第n个原 子受到的作用力
• 连续介质中的波(如声波)可表示为 Ae ,则可看出 • 格波和连续介质波具有完全类似的形式 • 一个格波表示的是所有原子同时做频率为ω的振动 • 格波与连续介质波的主要区别在于(2)式中,aq取值任意加减 2π的整数倍对所有原子的振动没有影响,所以可将波数q取值 限制为 q a a
V
O
a
r
• 第n个原子的运动方程
(n1 n ) (n n1 ) (n1 n1 2n )
(1)
平衡位置
d 2 n m 2 ( n1 n 1 2n ) dt
非平衡位置
——牛顿第二定律F=ma
3-2 一维单原子链模型
• 上述(1)式的解(原子振动位移)具有平面波的形式
a
)
固体物理-第七章 固体的磁性

7.1.1. 原子磁矩
这里所讨论的是孤立原子的磁矩。
1.电子轨道磁矩
核外电子绕原子核运动具有角动量p, 同时还形成环电流. 此环流产生磁矩,即轨道磁矩, 根据量子力学的结果, 电子的轨 道磁矩ml与其角动量pl成正比,
7.1.1.11
7.1. 原子的磁性
J 为总角量子数, 有效原子磁矩的大小为 mJ =|-gePJ/2m|=g[J(J +1)]1/2mB 7.1.1.12 为了求出g , 把7.1.1.11式两边点乘PJ得 , g=mJ PJ/(-ePJ2/2m) 把mJ =-e(PJ +PS )/2m代入,得 g =(PJ+PS )PJ/PJ2=1+PSPJ/PJ2 7.1.1.13 把PL=PJ – PS两边平方 PSPJ=(PJ2-PL2+PS2)/2 因此, g=1+(PJ2-PL2+PS2)/(2PJ2) 7.1.1.14
对于L-S耦合有, PL =i pli PS =i psi PJ=PL+PS 7.1.1.9 则原子磁矩 m = mL +mS = -e (PJ +PS )/2m 7.1.1.10
7.1.1.10式表明, 原子磁矩m与总角动量PJ不在同一方向,如果引入有效原子磁矩mJ, 即,
m在PJ方向的分量则有 mJ =-gePJ /2m
A为电子进动轨道面积,
如果固体中单位体积内含有N个原子,每个原子 有Z个电子,则 磁化强度为 DM=N1zDmj=-Ne2B1z (X j2¯+y j2¯)/4m
单位体积中总的感应磁矩,即
固体物理课程教学大纲

固体物理课程教学大纲一、引言固体物理是物理学的重要分支之一,研究物质的结构、性质和相互作用。
本课程的教学旨在帮助学生建立对固体物理的基础理论和实践技能的深入理解。
通过学习本课程,学生将能够掌握固体物理的核心概念、实验技术和解决实际问题的能力。
二、课程目标1. 掌握固体物理的基础知识和理论框架;2. 熟悉固体的晶体结构和缺陷状况;3. 理解固体的电学、磁学和光学性质;4. 学习固体材料的力学行为和热传导特性;5. 培养工程实践中解决固体物理问题的能力。
三、教学内容与安排1. 第一章:晶体结构- 1.1 原子与晶体结构基本概念- 1.2 晶体的晶格结构- 1.3 晶体缺陷与点阵缺陷- 1.4 晶体的形貌与表面结构2. 第二章:固体的电学性质- 2.1 电导现象与欧姆定律- 2.2 半导体与导体- 2.3 极化与介电材料- 2.4 超导电性3. 第三章:固体的磁学性质- 3.1 磁介质与磁性材料- 3.2 磁场与磁化强度- 3.3 磁性材料的磁性行为- 3.4 磁性材料的应用与技术4. 第四章:固体的光学性质- 4.1 光的传播与折射- 4.2 光与固体材料的相互作用 - 4.3 固体的吸收与发射- 4.4 材料的光学性质与应用5. 第五章:固体的力学行为- 5.1 弹性与塑性行为- 5.2 多晶体的力学行为- 5.3 固体的蠕变现象- 5.4 特殊力学性质与应用6. 第六章:固体的热传导特性- 6.1 热传导基本原理- 6.2 热电材料与热电效应- 6.3 热导率的测量与表征- 6.4 热传导的现象与应用四、教学方法与手段1. 授课方式:采用讲授与互动相结合的方式进行课堂教学;2. 实验教学:通过实验教学,让学生更好地理解课程的概念与原理;3. 论文阅读:引导学生阅读相关领域的研究论文,拓宽知识面;4. 课程设计项目:组织学生进行课程设计项目,提高实际问题解决能力;5. 网络资源利用:推荐学生利用网络资源深入学习与研究。
第三章 第三节 Weiss分子场理论

参见姜寿亭《铁磁性理论》 1.14 p59-63
“简洁是智慧的灵魂” —— 莎士比亚
外斯的分子场理论可以说是宏观理论的典范。他只用了 一个参数:Hmf,就解释了复杂的铁磁现象。
外斯(Weiss, Pierre)
法国物理学家。1865年3月25日生于莱茵省的米卢兹;1940年10月24日卒于 里昂。外斯出生在阿尔萨斯,父亲是个缝纫用品商。当时,阿尔萨因普法战 争割让给了德国,不过,外斯一家仍留在当地。他在德国和瑞士读书,但二 十一岁决定还是当个法国人。1887年,他以班上第一名的成绩从苏黎世工业 学院毕业,随后便去巴黎深造。他对磁学特别有兴趣。1907年,他对铁磁性 做出了解释。他认为,一个个原子磁体可以形成非同寻常的强耦合,从而使 它们都按一个方向排列,这便形成了强度累加起来的“磁畴”。铁中便存在 这种磁畴,但各个磁畴的取向可能是任意的;一旦外磁场的作用使它们沿一 个方向排列起来,整块铁就成了一个大磁体。 1919年,阿尔萨斯又回归法国, 外斯便在斯特拉斯堡创建了一个物理研究所。后来,该所成了磁学研究的中 心。外斯于1936年退休。后来又看到德国军队在第二次世界大战中再度占领 阿尔萨斯。他逃难到里昂,于法国屈辱地宣布投降不久以后去世。
第三节 Weiss分子场理论
“分子场”理论的两点假设: 1907年,外斯在顺磁性朗之万理论基础上提出了“分子场”
理论。构成这个理论的基础是两个重要的假设。 (1) 分子场假设:
物质具有铁磁性的基本条件:(1)物质中的原子有磁矩;(2) 原子磁矩之间有相互作用。实验事实:铁磁性物质在居里温度 以上是顺磁性;居里温度以下原子磁矩间的相互作用能大于热 振动能,显现铁磁性。
BT
固体的磁性 基础知识

固体的磁性 基础知识1. 磁性的一种分类方式根据磁化率χ的大小符号以及与温度、磁场的关系,可以把物质的磁性分成五类:(1)抗磁性,磁化强度与磁场方向相反,χ < 0,其值约为10-7~10-6;(2)顺磁性,磁化强度与磁场方向相同,χ > 0,其值约为10-6~10-5;(3)反铁磁性,χ > 0,其值约为10-4;(4)亚铁磁性,χ > 0,其值约为10-1~104;(5)铁磁性,χ > 0,其值约为10-1~106抗磁性的χ几乎与温度无关,其余均与温度有关;亚铁磁性和铁磁性为强磁性,其余为弱磁性。
2. 原子磁矩构成固体物质的原子中,电子磁矩比原子核的磁矩大三个数量级,所以电子磁矩对固体的磁性起主要作用。
2.1 独立原子的磁矩原子中电子的磁矩由轨道磁矩和自旋磁矩两部分组成。
电子的轨道磁矩为L 是电子的轨道角动量,µL 的绝对值为其中l 是电子轨道角动量量子数,µB 是波尔磁子,其大小为电子的自旋磁矩为 = -2L e mμL =(1)L Bl l 2B e m S e mμSS 是电子的自旋角动量,µS 的绝对值及其在z 方向的投影分别为如果原子中只有一个电子,则原子磁矩为J 是电子的总角动量。
如果原子中有多个电子,原子的总角动量有LS 耦合和JJ 耦合两种耦合方式,分别适用于原子序数比较小和原子序数比较大(Z > 80)的耦合方式。
常见的3d 族和4f 族元素,电子之间的轨道-轨道与自旋-自旋偶合较强,适合使用LS 耦合。
2.2 晶场效应原子结合成晶体后,原子的电子状态发生变化,价电子参与各种类型的键合,而处在格点位置的离子也不同于孤立离子,其电子状态因受周围离子所产生的静电场的作用而发生变化,这种静电场称为晶体电场,它所造成的影响称为晶场效应。
晶场效应有两种:一是离子中简并的电子态发生劈裂,二是电子的轨道角动量的贡献部分或者全部被冻结。
固体物理第三章 晶格振动与晶体热学性质

固体物理第三章晶格振动与晶体热学性质第三章晶格振动与晶体的热学性质晶格振动是描述原子在平衡位置附近的振动,由于晶体内原子间存在着相互作用力,各个原子的振动也不是孤立的,而是相互联系的,因此在晶体内形成各种模式的波。
只有当振动微弱时,原子间非谐的相互作用可以忽略,即在简谐近似下,这些模式才是独立的。
由于晶格的周期性条件,模式所取的能量值不是连续的而是分立的。
对于这些独立而又分立的振动模式,可以用一系列独立的简谐振子来描述。
和光子的情形相似,这些谐振子的能量量子称为声子。
这样晶格振动的总体就可以看成声子系综。
若原子间的非谐相互作用可以看作微扰项,则声子间发生能量交换,并且在相互作用过程中,某些频率的声子产生,某些频率的声子湮灭。
当晶格振动破坏了晶格的周期性,使电子在晶格中的运动受到散射而电阻增加,可以看作电子受到声子的碰撞,晶体中的光学性质也与晶格振动有密切关系,在很大程度上可以看作光子与声子的相互作用乃至强烈耦合。
晶格振动最早是用于研究晶体的热学性质,其对晶体的电学性质、光学性质、超导电性、磁性、结构相变等一系列物理问题都有相当重要的作用,是研究固体宏观性质和微观过程的重要基础。
ωη§3-1 简谐近似和简正坐标由原子受力和原子间距之间的关系可以看出,若离开平衡位置的距离在一定限度,原子受力和该距离成正比。
这时该振动可以看成谐振动.用n μϖ表示原子偏离平衡位置(格点)位移矢量,对于三维空间,描述N 个原子的位移矢量需要3N 个分量,表为)3,,2,1(N i i Λ=μ将体系的势函数在平衡位置附近作泰勒展开:高阶项+∑⎪⎪⎭⎫ ⎝⎛∂∂∂+∑∂∂+===j i N j i j i i N i i V V V V μμμμμμ031,2031021)(第一项为平衡位置的势能,可取为零,第二项为平衡位置的力,等于零。
若忽略高阶项,因为势能仅和位移的平方成正比,即为简谐近似。
23121i N i i m T μ&∑==引入合适的正交变换,将动能和势能用所谓的简正坐标表示成仅含平方∑==N j j ij i i Q a m 31μ项而没有交叉项,即:由分析力学,基本形式的拉格朗日方程为:)32,1(,N i q Q T Q T dt d i i i Λ&==∂∂-⎪⎪⎭⎫ ⎝⎛∂∂其中)32,1(,1N i q f q i j N j j i Λϖϖ=∂∂⋅∑==μ朗日方程:)32,1(,0N i Q L Q L dt d i i Λ&==∂∂-⎪⎪⎭⎫ ⎝⎛∂∂则正则方程为:)3,2,1(,02N i Q Q i i i Λ&&==+ω其解为:)sin(δω+=t A Q i i 当考察某一个j Q 时,则:)sin(δωμ+=t A m a j i iji 晶体参与的振动,且它们的振动频率相同。
磁化学

基本概念
磁化和电极化现象类似,只不过是将原子或分 子内的电流线圈重新排列,或在物质内部诱导产生 磁偶极。 M :单位体积磁偶极矩 M = 0–1mB
(1.15)
m:磁化率 0:真空透过率 mol = K Mr/103 = m Mr/103 (m3 mol–1)
(K:质量磁化率)
固体表面物理化学国家重点实验室
基本概念
电极化 P :单位体积诱导偶极矩
P = 0eE
(1.11)
e:电极化率
0:真空介电常数
(8.854210–12 J–1C2m–1) (b) 极化度: 非极性物质(大部分是绝缘体),极化主要是较弱
的变形效应,施加电场造成原子核和电子轨道的相
对移动,诱导产生电偶极矩
固体表面物理化学国家重点实验室
基本概念
5. Ørsted:(1819) 电流产生磁场 6. Ampé re:(1820-25) 电流线圈在某处产生的
磁作用相当于一个磁棒。
7. Faraday:(1831) 发现电磁感应 (1845) 创造名词 magnetic field 8. 经典电磁理论 9. 量子力学
第十二章
参 考 资 料
1) 姜寿亭、李卫 编著的第一版《凝聚态磁性物理》2005年版 2) Richard L. Carlin著《Magnetochemistry》1986年版 Springer-Verlag (注:南京大学翻译过该书) 3) A. F. Orchard著《Magnetochemistry》2003年版 Oxford Higher Education出版 4) Olivier Kahn著《Molecular Magnetism》,Wiley-VCH出版 5) Stephen Blundell著《Magnetism in Condensed Matter》, Oxford Higher Education出版 6) J. S. Miller和M. Drillon编著《Magnetism: Molecules to Materials》(I-V),Wiley-VCH出版 7) K. H. J. Buschow和F. R. de Boer著《Physics of Magnetism and Magnetic Materials》 Kluwer Academic/Plenum Publishers出版
固体SO3的分子结构
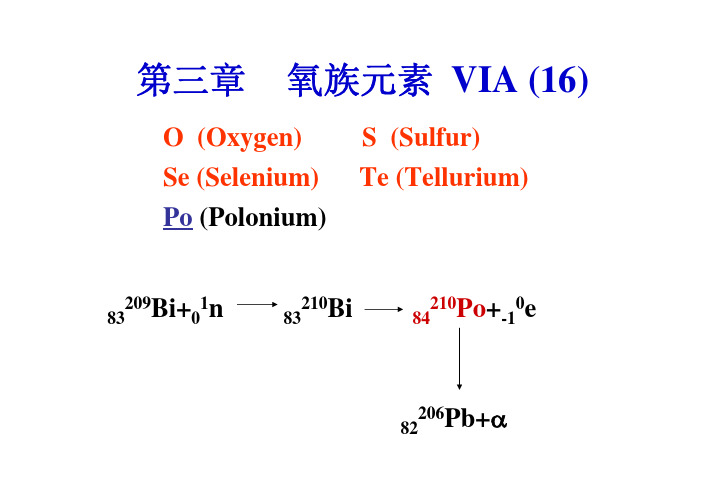
第三章氧族元素VIA (16)83209Bi+1n83210Bi84210Po+-10e82206Pb+ O (Oxygen) S (Sulfur)Se (Selenium) Te (Tellurium) Po(Polonium)本章要点:1.掌握氧的成键特征;2.掌握氧、臭氧、过氧化氢的结构、性质和用途;3.掌握硫的成键特征;4.掌握硫的各种氧化态的重要化合物的结构、性质、制备和用途, 以及相互转化关系。
§3-1 氧族元素在自然界的存在形式O: 单质(O 2 、O 3)和化合态S: 单质和化合态Se, Te:分布于金属硫化物矿中自然硫黄碲矿(墨西哥)自然碲§3-2 氧族元素的通性一、氧族元素的物理性质•元素O S Se Te •电子构型:[2e][8e] [18e] [18e]2s22p4 3s23p4 4s24p4 5s25p4•常见氧化态-2,-1,0 -2,0,+2 -2,0,+2-2,0,+2+4,+6 +4,+6+4,+6•电负性 3.44 2.58 2.55 2.10•共价半径/pm 66 104 117 137•M2-离子半径/pm 140 184 198 221§3-3 氧及其化合物空气的组成CO 2O 2ArN 2沸点/K 194.7 90.1 87.2 77.2一、氧气的制备1.实验室制法2 KClO 32 KCl +3 O 22. 工业制法---液态空气的分馏MnO 2空气的分离:•气态空气加压力,冷却液化空气+CO(s)2•77K,精馏液化空气+ N(g)2•87.2K, 精馏液化空气+ Ar(g)•90.1K, 精馏O(g)2•O2+ Pt + 3 F2= O2+[PtF6]-O2+ PtF6= O2PtF6•O2的第一电离势:1175.7kJ/mol •Xe的第一电离势:1171.5 kJ /mol •第一个稀有气体化合物•Xe+PtF6= Xe+[PtF6]-基态O2,O2+, O2-, O22-的电子结构分子/离子能级键级磁性例O2KK(σ2s)2(σ2s*)2(σ2p)2(π2p)4 (π2p*)2 2 顺O2O2+KK(σ2s)2(σ2s*)2(σ2p)2(π2p)4 (π2p*)1 2.5 顺O2[PtF6]O2-KK(σ2s)2(σ2s*)2(σ2p)2(π2p)4 (π2p*)3 1.5 顺KO2O22-KK(σ2s)2(σ2s*)2(σ2p)2(π2p)4 (π2p*)4 1 逆Na2O2三、氧气的化学性质1.强氧化性2.生成氧化物,过氧化物,超氧化物O+,含氧酸中的配位键,3.配位性: H3与血红素的二价铁络合•激发单线态氧分子在水溶液中的寿命:寿命:10-6~10-5s ,能量差:+ 92.0kJ/mol :寿命:10-9 s, 能量差:+154.8 kJ/mol )O (Δ21g 1∑+g 211)O (•单线态氧生成:光敏化法, 微波放电, 化学方法五、臭氧(Ozone )1. O2的同素异形体----O 32. 大气臭氧层的光化学平衡(高度20~40 km)形成: O 2+ h νO + OO + O 2 O 3消除: O 3+ h νO + O 2λ<185 nm λ= 220~320 nm 平衡:3. 大气层中臭氧空洞的形成•CF2Cl2+ hνCF2Cl ∙+ Cl∙Cl∙+ O3ClO∙+ O2ClO∙+ O Cl∙+ O2•NO2+ hνNO + ONO + O3NO2+ O2NO2+ O NO + O2λ<221 nmλ<426 nm4. 臭氧的化学性质-----氧化性比氧气更强2PbS + 3 O2= 2 PbO+ 2 SO2PbS+ 2 O3= Pb SO4+ O2CN-+O3 = OCN-+O2O2和O3的混合气体中O3浓度的测定:pH=9O3 + 2I-+ H2O = O2 + I2+ 2OH-路易斯结构式:O 3的化学键结构•2σ+ 1 ∏43•2σ:O (2) sp 2+ O (1) p yO (2) sp 2+ O (3) p y•1 ∏43:O (1) p z + O (2) p z + O (3) p z •∏34的键级=1平均每一个O-O 键的键级=1.56.离域∏p-p 键定义:含有三个或三个以上原子的π键叫离域π键,用表示,n代表原子数,m代表电子数.离域∏p-p 键生成的条件:a . 成键原子必须在同一个平面上, 或在同一条直线上.b. 具有π对称性的原子轨道,线形组合成具有π对称性的分子轨道。
(凝聚态物理专业论文)Ising模型磁性质的理论研究

摘要
磁性是物质的基本属性之一,对物质磁性质及其机理的研究一直是凝聚态物 理中重要的研究课题之一。近年来,层状高温超导材料、磁性多层膜、人造磁性 超品格、有机聚合物磁性材料的制备技术和实验研究发展迅速,这些新材料表现 出了许多奇特的磁性质,具有广阔的应用前景,这极大地促进了新型磁性材料的 理论研究。作为描述固体磁性的Ising模型也受到了许多理论工作者的关注。
上世纪20年代,量子力学迅速发展起来,人们开始用量子力学来解释物质 磁性的起源。1928年,W.Heisenberg把铁磁物质的自发磁化归结为原子磁矩之 间的直接交换作用,建立了局域性电子自发磁化的Heisenberg交换作用理论模 型,从而正确地揭示了自发磁化的量子本质。这一理论不但成功地解释了物质存 在铁磁性、反铁磁性和亚铁磁性等实验事实,而且为进一步导出低温自旋波理论、 铁磁相变理论及铁磁共振理论奠定了基础。
H=忑∑氓1%,slisU+JlH秣㈨islis㈨+“.蠢tt乳IsliSⅧ、)
I(,.』)Leabharlann 我们用相关有效场理论对系统的磁性质进行了研究,推导出了系统磁矩和 相变温度的表达式。研究了温度、交换相互作用常数和稀磁浓度对各层原子磁矩 和相变温度的影响,还给出了磁矩随原子层数的变化规律。研究结果表明,对自 旋值较小的原子层来说,层间交换相互作用比层内交换相互作用对该层磁矩的影 响大得多,这直接导致低自旋材料在界面处出现磁矩最大值,而高自旋材料在界 面处出现磁矩最小值。我们还发现,稀磁情况下磁矩随温度的变化趋势与未稀磁 时类似,不同的是磁矩大小相应减小。
expressed as
H=一∑∑(‘。,S,,甄+以tf+。S,,S…,,+‘,『_。S,,S,..,,) , (,,』)
The effective field theory、析t11 correlations based on Ising model is discussed in detail.We investigate the magnetization,critical temperature and compensation
CH1-2-抗磁
的电荷和质量,μ为导磁率,v为电子的速度。该频率被称为拉莫尔频率。
具有自旋与磁矩特性的磁性核处于磁感应强度为B的均匀磁场中时,若此原子 核的磁矩μ与B的方向不同时,在磁场作用下,原子核将受到一个垂直于μ与B 形成平面的力矩T,在力矩T的作用下自旋角动量P的方向会连续发生变化,但 大小保持不变,自旋核将发生像陀螺受重力作用是一样的进动。原子核既自旋, 又围绕外磁场方向发生的进动也成为拉莫尔进动。
抗磁磁化率的实验值
四. 金属传导电子的抗磁性 — Landau 量子理论
传导电子的运动路径受外磁场影响,产生Landau抗磁性
1.定性解释
传导电子的运动速度可分解为平行和 垂直于磁场的两个分量
v v// v
e
z
B0
沿平行于磁场方向运动的电子其运动 不受影响
磁化率
0 M / B0 0 Ne Zr 2 / 3 ~ 105 Z
(2.8)
0 ,为抗磁性
实际: 所有任何物质均有此抗磁性, 仅是当还有其它磁性时, 此类磁性太小可忽略
磁性的 量子性?
很小,且与温度无关。可见此经典理论就可成功描述抗磁性
等价范佛莱克量子理论: 胡安 章维益
第一章内容
序现象 • • • • • • • • 文起源
知其所以然!
§1-1 磁性的微观起源 §1-2 抗磁性 §1-3 顺磁性 §1-4 铁磁性 §1-5 *反铁磁 fluctuation §1-6 自旋波 §1-7 *磁阻错(自旋玻璃.自旋液体.自旋冰) §1-8 磁电阻(磁电耦合一) -自旋电子学-07Noble Prize §1-9 Hall effects (磁电耦合二) - 量子、分数量子、拓扑绝缘体
材料化学导论第6章-固体的磁性和磁性材料
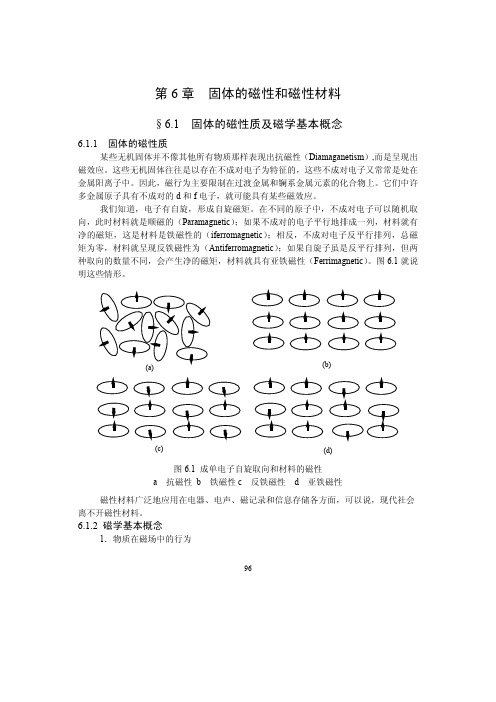
96第6章 固体的磁性和磁性材料§6.1 固体的磁性质及磁学基本概念6.1.1 固体的磁性质某些无机固体并不像其他所有物质那样表现出抗磁性(Diamaganetism ),而是呈现出磁效应。
这些无机固体往往是以存在不成对电子为特征的,这些不成对电子又常常是处在金属阳离子中。
因此,磁行为主要限制在过渡金属和镧系金属元素的化合物上。
它们中许多金属原子具有不成对的d 和f 电子,就可能具有某些磁效应。
我们知道,电子有自旋,形成自旋磁矩。
在不同的原子中,不成对电子可以随机取向,此时材料就是顺磁的(Paramagnetic );如果不成对的电子平行地排成一列,材料就有净的磁矩,这是材料是铁磁性的(iferromagnetic );相反,不成对电子反平行排列,总磁矩为零,材料就呈现反铁磁性为(Antiferromagnetic );如果自旋子虽是反平行排列,但两种取向的数量不同,会产生净的磁矩,材料就具有亚铁磁性(Ferrimagnetic )。
图6.1就说明这些情形。
(b)(d)(c)图6.1 成单电子自旋取向和材料的磁性a 抗磁性b 铁磁性c 反铁磁性d 亚铁磁性磁性材料广泛地应用在电器、电声、磁记录和信息存储各方面,可以说,现代社会离不开磁性材料。
6.1.2 磁学基本概念1.物质在磁场中的行为97首先,我们讨论不同材料在磁场中的行为。
如果磁场强度为H ,样品单位体积的磁矩为I ,那么样品的磁力线密度,即所谓磁通量 (Magnetic induction )B 为:B = H + 4πI 6.1.1导磁率(Permeability )P 和磁化率(Susceptinity )K 定义为: P = HB = 1 + 4πK 6.1.2 K = HI 6.1.3 摩尔磁化率χ为χ= dM κ 6.1.4 式中M 是分子量,d 式样品密度。
根据、K 、χ及其与温度和磁场的依赖关系可以区分不同种类的磁行为,这总结在表6.1中。
固体物理第一章第三节泡利顺磁性

以表示B=0时电子的能量,则当B0时其能
量为:
BB
为简单起见,我们首先看T=0K时的情形,此
时费米分布函数为1。在没有外磁场时, 自旋磁
矩在空间没有择优取向。按照泡利原理,自旋
磁矩沿空间某方向的电子数与沿相反方向的电
子数应该相等。 (c)高能态的电子转向低能态,导致两种自旋取向的电子数目不等,出现净磁矩,产生顺磁效应。
具有平行于B的自旋磁矩的电子数目增大。 自旋顺磁性理论是泡利研究出来的,他证明了金属中的导电电子的行为与费米-狄拉克所支配的自由电子气一样。 一、 泡利顺磁性的起因
施加磁场后,在磁场的作用下,自旋取向 在T≠0K时,费米分布函数在整个积分区间不再等于1,要遇到上一节所讲的费米积分.
二、金属泡利顺磁性的物理机制示意图
由于B=1Tቤተ መጻሕፍቲ ባይዱ, µBB约为10-5eV,而费米能级约 为2-10eV.说明发生反转的只能是能量较高的那
部分电子,而且数目极少,位于费米面附近。
图中为了好表示,故意夸大了µBB的范围。 所以,发生反转的电子数约为:
Z
1 2
g(F0 )
1 2
g(F0
)
BB
每反转一个电子,沿磁场方向磁矩的改变为2µB
1 g ( ) 2
1 g ( ) 2
(c)B0,达到平衡
(a) B=0
g()g()12g()
(b) B 0,未平衡,自旋取向与磁场相反的电子具有较高
的能量,与磁场相同的电子具有较低的能量.从而高能
态的电子要转向低能态。 (c)高能态的电子转向低能态,导致两种自旋取向的电
子数目不等,出现净磁矩,产生顺磁效应。
所以,反转Z个电子后的沿磁场方向的总磁
矩为: 2B Z 2B 1 2 g (F 0)B B B 2 B g (F 0 )
固体物理学基础晶体的磁性与磁场效应

固体物理学基础晶体的磁性与磁场效应在固体物理学中,晶体的磁性及其在磁场中的行为是一个广泛研究的课题。
磁性材料的研究不仅具有科学意义,也具有重要的应用价值。
本文将从晶体的磁性起源、基本磁性效应以及磁场对晶体的影响等方面进行探讨。
一、晶体的磁性起源晶体的磁性起源于其中的原子、离子或分子的磁性,这种磁性来源称为局域磁性。
例如,某些过渡金属离子由于其未成对电子的存在,表现出明显的磁性。
此外,晶体中的局域磁性也可以来自于自旋轨道耦合、晶体场效应等因素。
二、基本磁性效应1. 磁化强度与磁化率晶体的磁性可以通过磁化强度和磁化率来描述。
磁化强度是单位体积内的磁矢量总和。
而磁化率则是磁化强度和外加磁场之间的比例关系。
通过测量磁化强度和磁场的关系,可以更加深入地研究晶体的磁性行为。
2. 磁畴和磁畴壁晶体中的磁化强度通常会出现一定的排列顺序,形成磁畴。
磁畴是具有相同磁导数的磁区域。
而磁畴之间的过渡区域称为磁畴壁。
磁畴和磁畴壁的形成与晶体中的磁性相互作用密切相关。
三、磁场对晶体的影响1. 各向异性磁性晶体的结构对其磁性行为有着重要的影响。
晶体中的各向异性磁性意味着晶体在不同方向上具有不同的磁性。
各向异性磁性的形成源于晶体结构中的非球形电子云对磁场的不同响应。
2. 磁滞效应当外加磁场改变时,晶体中的磁化强度并不会立即跟随磁场的变化而变化,而是存在一定的滞后现象,这种现象称为磁滞效应。
磁滞效应与晶体中的磁畴和磁畴壁有着密切的联系。
3. 磁各向异性晶体在磁场中的响应也受到磁各向异性的影响。
磁各向异性是指晶体在不同磁场方向上表现出不同的磁性响应。
晶体中的磁各向异性可以通过测量磁化强度随磁场方向变化的关系来确定。
四、磁场效应的应用晶体的磁场效应在各个领域都有广泛的应用。
在磁记录领域,磁场对晶体的影响被用于磁存储器的设计和制造。
在磁共振成像领域,晶体的磁性行为可以被用于图像的获取和分析。
此外,磁场效应还可以应用于磁传感器、磁随机存取存储器等领域。
第三章 第九节 铁磁性的能带理论模型

4s
3 d
原子间距
电子数相等;而对于3d能带, 由于交换分裂导致其正负副 能带高度不等(3d负副能带 高),充满电子的程度也不 一样。
由3d正负副能带中电子 浓度差数即可得到原子磁矩 (如教材P148表3-10),(非μB 的整数倍)。
图3-29 3d和4s正、负能级及电子 分布
3d电子有部分 成为4s自由电 子,对磁性没 有贡献。
1945年12月,珀塞尔和他的小组在石蜡样品中观察到质子的核磁共振吸收 信号,1946年1月,布洛赫和他的小组在水样品中也观察到质子的核感应信号。 他们两人用的方法稍有不同,几乎同时在凝聚态物质中发现了核磁共振。他 们发现了斯特恩开创的分子束方法和拉比的分子束磁共振方法,精确的测量 了核磁矩。以后许多物理学家进入了这个领域,形成了一门新兴实验技术, 几年内便取得了丰硕的成果。
能带模型的简单介绍:
根据集体电子论,过渡金属的4s电子在晶格中游动,其
总能量即为动能:
E
1 2
2k 2 m*
m*:电子的有效质量 由能带论知,具有能量为E的电子数目按能态密度D(E)分布:
D(E)
D
1 K E
dA
D:状态分布密度;dA:等能面的面积元; K E 沿等能面
法线方向能量的改变率。
因此,电子分布于若干密集能态组成的能带中。
1952年诺贝尔物理学奖 ——核磁共振
珀塞尔
布洛赫
1952年诺贝尔物理学奖授予美国加利福尼亚州斯坦福大学的布洛赫(Felix Bloch,1905—1983)和美国马萨诸塞州坎伯利基哈佛大学的珀塞尔 (Edward Purcell,1912—1997),以表彰他们发展了核磁精密测量的新方法 及由此所作的发现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A atomic Weight, N A Avogadro no.
2 (3) peff (3kC / N B ), C is obtained by T above TC .
peff g J J ( J 1) .
(4) pc / ps
2 2 peff gJ J ( J 1), For 3d elements ,
Sm2 Fe17 N X (CX ), etc.
(3)磁及磁光记录材料 : CoCr 膜,Tb (Gd) -Fe-Co, 等非晶膜 , 2 3 4 H :10 Oe 颗粒膜 ( ) C HC ~ 10 10 Oe
(4) 微波材料 (5) 传感器、换能器等. Magnetoelastic, magnetostrictive, MR, GMR, magneto-caloric, etc. (6) 自旋电子学(Spintronics).
第三章 固体材料中的 磁有序
3-1 铁磁性Ferromagnetism
3-1-1 特性 0 5 ~ 10 10 1、T<TC , FM态: ,“易”饱和, *非线性 M-H 曲线及磁滞回线
MS M
HC : M HC and B HC
M
Hc Hc
M R , BR 4M R (or BR= 0 M R)
当T<TC时,外场H0时,M>MS(内禀磁化)
当T>TC时,无自发磁化,MS=0,材料为顺磁性
3J M S / M 0 1 J 1 T / Tc
J 1 BJ ( ) 3J
g J J B 0 ( H M ) / kT
J 1 g J J B 0 ( H M ) M M 0 BJ ( ) Ng J J B 3J kT 2 2 Ng J J ( J 1) B 0 C ( H M ) ( H M ) 3kT T C C C M H T C T C T p
2 g J 2, peff 2s(2s 2) pc ( pc 2), pc is 2s obtained from peff .
局域化模型, 非局域化模型,
pc / ps 1.
pc/ps >1.
(5) TC :由TC附近的Ms-T曲线外推 (也可由其他曲线得到) T , C T , T T , T , T , etc)
2、 T > TC PM mostly.
c ~ T
图36-2
3-1-2 FM 材料
1、Materials: (1) 元素:9 ,(3 3d metals, Fe, Co, Ni; 6 4f metals) , (2) 合金及化合物 : FM-FM, FM-NFM ( ( Fe Si, Fe Al etc))
M 0 Ng J JB
H 应该足够大以致和热运动能相当. T≠0K 时,磁能和热运动能相竞争
仿照对顺磁性的处理 0 BJ ( ) 其中M 0 Ng J J B
g J J B 0 ( H M ) / kT M NkT H 2 M0 0M 0 M 0
Fe
3.06 -2
Co (fcc) 2.01 -1.5
Ni
4.06 -0.9
Pd
2.31 5
0.48 2.25
1 1
Actually FM TM: <0 Exchange energy of CE of Li etc. is larger than Fe, Co, Ni ! But N( EF ) is small !
2、应用
(1) 软磁材料 ~ 高 () ~102 105 , low HC (101 103 Oe ) , 较好的 f. Fe-Si, Fe–Ni, Fe-Co-Ni, 等非晶合金, 立方铁氧体. (2)硬磁材料. ( HC 100Oe ), 六角铁氧体, TMNx (Cx ) Alnico , MnAlC, SmCos , Sm2Co17, Nd2 Fe14B, SmFe 11
Co
Ni
2.39
p (4s)
-0.21
-0.28
ps
2.18
g
2.091
pL
0.0918
pspin
2.214
ps
2.216
1.99
1.715
2.187
0.1472
1.568
1.715
0.62
-0.105
0.515
2.183
0.0507
0.563
0.606
4. results
(1) 可依据Fermi-Dirac统计计算出Ms-T, χ -T, Tc.
AFM-NFM(Cu2 MnAl, MnAlC etc ), TM(PM) –NFM( ZrZn2 ,
Sc3 ln, Au4V ,Weak FM); compounds (CrO2 , EuO, S , ferrites)
(3) 特殊 FM 有机FM; Low-d, MML(磁性多层膜) and UTF(超薄膜), UFP(超细颗粒), FM半导体.
MnO, MnS, MnF2, MnTe, FeF2, Fe Cl2, FeO, CoCl2, CoO, NiO.
2 n E Eex Ek U n 2 Ni ( E ) n2 (1 U Ni ( E )) Ni ( E )
出现铁磁性的条件 E 0
即: U Ni (E) 1
如果UNi (E) 1, 无自发磁化。加外磁场 时
U m2 Eex 2 4 B m2 Ek 2 4 B Ni ( E )
(2) 问题 .
计算出的Tc偏高。 计算结果Tc: Fe :4400-6200K, Co: 3300-4800K, Ni:2900K. Tc 以上χ-T不同于居里-外斯定律.
3-2 反铁磁性Antiferromagnetism (AFM) 亚铁磁性Ferrimagnetism (FIM)
3-2-1 AFM 1、 特性. (1) T< TN , AFM态,
当T<TC时,材料呈铁磁性
3J M S / M 0 H 0时, g J J B 0 M / kT J 1 T / Tc MS 3J M S / M 0 BJ ( ) M0 J 1 T / Tc
M S M 0 BJ ( )
MS / M0 T 3J 1 Tc J 1 BJ (M S / M 0 ) MS T fJ ( ) M0 Tc
M NkT 当H 0时, 2 M0 0M 0
从布里渊函数求解自发磁化强度的图解法:
随温度上升,减小,自发磁化强度MS减小,当 达到某一临界温度TC时,MS =0,铁磁性消失。
NkTc J 1 2 3J 0 M 0
2 2 Ng J J ( J 1) 0 B Tc 3k
3-1-3 Weiss分子场理论(MF), 局域模型 1、基本假设: 分子场导致自发磁化. MF : H M , Heff H M , EJ gJ mJ B Heff . For T= 0K, M = M 0 Ng J J B Nps , ps g J J B . 完全饱和
(1) 判据:
U Ni ( E ) 1
(2) 传导电子系统铁磁性条件 ① U 0 , large; ② N(EF ) large. (3) 增强的顺磁性
1
pe
pe ( Pauli) 1
Some theoretical values
Li
N(E )
F
V
1.64 2.24
C Ng J J ( J 1) B / 3k
2 2
2 2
N eff 3k
2
C, eff g J J ( J 1) B ,
peff 有效Bohr磁子数= gJ J ( J 1)
(If H 0 C-W Law becomes Curie law
1 >1, 1
3. 电子分布及饱和磁矩
(1) 实验 3d Fe Co 4.8 5.0
3d
4s 0.6 0.7
ps
2.2 1.7
2.6 3.3
Ni
5.0
4.4
0.6
0.6
(2) Experimental values of ps ’s (neutron diffraction) p (3d) Fe
dB J ( ) dB J ( ) d dM M0 M0 dH dH d dH g J J 0 B dM ( ) M 0 BJ (1 ) kT dH ( ) g J J0 B / kT M 0 BJ ( ) g J J0 B / kT 1 M 0 BJ 3J ( )C BJ J 1 3J ( ) T TC BJ J 1 2 2 Ng J J ( J 1) 0 B 其中C 3k
M s =0
--
104 ~ 106
When T
(2) T>TN ,PM态,
C T P
T
化合物 ,局域磁矩,
P < 0 K,
0
(3)T = TN, = max.
金属中, 巡游电子, (T ) 较复杂.
2、AFM材料.
(1) (TM)和Ⅴ,Ⅵ,Ⅶ元素形成的化合物, 如
EH 0 mH
能量的总变化 m2 E (1 U Ni ( E )) m0 H 2 4 B N i ( E )
E 由能量极小条件 0, 得 m 2 2 2 B N i ( E ) 2 0 B Ni ( E ) m 0 H 1 U Ni ( E ) 1 U Ni ( E ) 交换增强顺磁性
