平行线与角平分线模型,九年级上册数学平行线与角平分线类相似经典例题讲解及答案解析
2022年中考数学几何模型之角平分线的五种模型(讲+练)(解析版)

专题01 角平分线的五种模型模型一、角平分线垂两边例1.如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为()A.3:2B.6:4C.2:3D.不能确定【答案】A【详解】过点D作DE⊥AB于E,DF⊥AC于F.∵AD为∠BAC的平分线,∴DE=DF,又AB:AC=3:2,∴S△ABD:S△ACD=(12AB•DE):(12AC•DF)=AB:AC=3:2.故选A.例2.如图,∠AOP=∠BOP=15°,PC//OA,PD⊥OA,若PC=4,则PD的长为___.【答案】2【详解】解:过P作PE⊥OB,交OB与点E,∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,∴PD=PE,∵PC//OA,∴∠CPO=∠POD,又∠AOP=∠BOP=15°,∴∠CPO=∠BOP=15°,又∠ECP为△OCP的外角,∴∠ECP=∠COP+∠CPO =30°,在直角三角形CEP 中,∠ECP =30°,PC =4,∴PE =12PC =2,则PD =PE =2.故答案为:2. 【变式训练1】如图所示,在四边形ABCD 中,DC //AB ,∠DAB =90°,AC ⊥BC ,AC =BC ,∠ABC 的平分线交A D ,AC 于点E 、F ,则BFEF的值是___________.11221BCBC BC ==--【详解】解:如图,作FG ⊥AB 于点G ,∠DAB -90°,∴FG /AD ,∴BF EF =BGAGAC ⊥BC ,∴∠ACB =90° 又BF 平分∠ABC ,∴FG =FC 在Rt △BGF 和Rt △BCF 中BF BFCF GF=⎧⎨=⎩ ∴△BGF ≌△BCF (HL ),∴BC =BGAC =BC ,∴∠CBA =45°,∴AB =2BC1BF BG BC EF AG AB BG ∴====- 【变式训练2】如图,BD 平分ABC 的外角∠ABP ,DA =DC ,DE ⊥BP 于点E ,若AB =5,BC =3,求BE 的长.【答案】1【详解】解:过点D 作BA 的垂线交AB 于点H ,∵BD平分△ABC的外角∠ABP,DH⊥AB,∴DE=DH,在Rt△DEB和Rt△DHB中,DE DHDB DB=⎧⎨=⎩,∴Rt△DEB≌Rt△DHB(HL),∴BE=BH,在Rt△DEC和Rt△DHA中,DE DHDC DA=⎧⎨=⎩,∴Rt△DEC≌Rt△DHA(HL),∴AH=CE,由图易知:AH=AB−BH,CE=BE+BC,∴AB−BH=BE+BC,∴BE+BH=AB−BC=5−3=2,而BE=BH,∴2BE=2,故BE=1.【变式训练3,的平分线相交于点E,过点E作交AC于点F,则EF的长为.【答案】【解析】延长FE交AB于点D G H,如图所示:四边形BDEG是矩形,平分CE平分,四边形BDEG是正,,设,则,,,解得,,即,解得,.模型二、角平分线垂中间例.如图,已知,90,,BAC AB AC BD ∠=︒=是ABC ∠的平分线,且CE BD ⊥交BD 的延长线于点E .求证:2BD CE =. 【答案】见解析【详解】证明:如图,延长CE 与BA 的延长线相交于点F ,∵90,90EBF F ACF F ∠+∠=︒∠+∠=︒,∴EBF ACF ∠=∠,在ABD △和ACF 中,EBF ACF AB AC BAC CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ABD ACF ASA △≌△,∴BD CF =,∵BD 是ABC ∠的平分线,∴EBC EBF ∠=∠.在BCE ∆和BFE ∆中,EBC EBF BE BE CEB FEB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BCE BFE ASA ≌△△, ∴CE EF =,∴2CF CE =, ∴2BD CF CE ==.【变式训练1】如图,已知△ABC ,∠BAC =45°,在△ABC 的高BD 上取点E ,使AE =BC . (1)求证:CD =DE ;(2)试判断AE 与BC 的位置关系?请说明理由;【答案】(1)见解析;(2)AE BC ⊥,理由见解析;(3)【详解】(1)证明:∵BD AC ⊥,45BAC ∠=︒,∴90,45EDA BDC ABD BAD ∠=∠=︒∠=∠=︒,∴AD BD =,在Rt ADE △和Rt BDC 中,∵AD BDAE BC =⎧⎨=⎩ ∴()Rt ADE Rt BDC HL ≅,∴CD =DE ; (2)AE BC ⊥,理由如下:如图,延长AE ,交BC 于点F , 由(1)得,90EAD EBF EAD AED ∠=∠∠+∠=︒,∵AED AEF ∠=∠,∴90BEF EBF ∠+∠=︒,∴90EFB =︒,即AE BC ⊥;【变式训练2】如图,D 是△ABC 的BC 边的中点,AE 平分∠BAC ,AE ⊥CE 于点E ,且AB =10,AC =16,则DE 的长度为________【答案】3【解答】解:如图,延长CE ,AB 交于点F .AE 平分∠BAC ,AE ⊥EC ,∴∠F AE =∠CAE ,∠AEF =∠AEC =90°在△AFE 和△ACE 中,EAF EAC AE AE AEF AEC =⎧⎪=⎨⎪=⎩∠∠∠∠,∴△AFE ≌ACE (ASA ),∴AF =AC =16,EF =EC ,∴B F =6又D 是BC 的中点,∴BD =CD ,∴DE 是△CBF 的中位线,∴DE =12BF =3,故答案为:3. 【变式训练3】如图,在ABC ∆中,CD 是ACB ∠的平分线,AD CD ⊥于点D ,DE //BC 交AB 于点E ,求证:EA EB =.【答案】见解析【解答】证明:延长AD 交BC 于点F .CD 平分ACF ∠, ACD FCD ∴∠=∠.又,,AD CD CD CD ⊥=ADC ∴∆≌FDC ∆,AD FD ∴=. 又DE ∥BC ,EA EB ∴=.模型三、角平分线+平行线构造等腰三角形例.如图所示,在△ABC 中,BC =6,E 、F 分别是AB 、AC 的中点,动点P 在射线EF 上,BP 交CE 于D,∠CBP 的平分线交CE 于Q ,当CQ =13CE 时,EP +BP =________.【答案】12【解答】解:如图,延长BQ 交射线EF 于点M .E 、F 分别是AB 、AC 的中点,∴EF //BC ,∴∠CBM =∠EMBBM 平分∠ABC ,∴∠ABM =∠CBM ,∴∠EMB =∠EBM ,∴EB =EM ,∴EP +BP =EP +PM =EM CQ =13CE ,∴EQ =2CQ由EF //BC 得,△EMQ ∽△CBQ∴2 212 12EM EQEM BC EP BP BC CQ==∴==∴+=【变式训练1】如图,平分于点C ,,求OC 的长?【解析】如图所示:过点D 作交OA 于点E ,则,平分,,中,,.【变式训练2C=90°,AD平分∠CAB,BE平分∠ABC,AD、BE相交于点F,且,则AC=.【解析】过点E于G,连接CF,如图所示:分别是,CF是的平分线,,,由勾股定理可得.模型四、利用角平分线作对称例.平分.【答案】见解析【解析】证明:在AB上截取,连接DE,如图所示:.【变式训练】AD是△ABC的角平分线,过点D作DE⊥AB于点E,且DE=3,S△ABC=20.(1)如图1,若AB=AC,求AC的长;(2)如图2,若AB=5,请直接写出AC的长.【答案】(1)203;(2)253【详解】解:(1)如图1,作DF⊥AC于F,∵AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,∴DF =DE =3, 由题意得,12×AB ×3+12×AC ×3=20,解得,AC =AB =203; (2)如图2,作DF ⊥AC 于F ,∵AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,∴DF =DE =3, 由题意得,12×5×3+12×AC ×3=20,解得,AC =253. 模型五、内外模型例.如图,在△ABC 中,AB=AC ,∠A=30°,E 为BC 延长线上一点,∠ABC 与∠AC E 的平分线相交于点D ,则∠D 的度数为( )A .15°B .17.5°C .20°D .22.5°【答案】A4321DA【解析】∵∠ABC与∠AC E的平分线相交于点D,∴∠DCE=∠DCA,∠CBD=∠ABD,即.的外角的平分线CP与内角BP交于点P,若,则.【解析】平分平分又,过点P的延长线,垂足分别为点E、F、G,如图所示:由角平分线的性质可得,AP是.课后训练1.如图,BD是ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE 的长为()A .2B .1.5C .1D .0【答案】C【详解】解:如图,过点D 作DF AB ⊥于F ,BD 是ABP ∠的角平分线,DF AB ⊥,DE ⊥BP ,DE DF ∴=,在Rt BDE 和Rt BDF 中,BD BDDE DF =⎧⎨=⎩,()Rt BDE Rt BDF HL ∴△≌△,BE BF ∴=,在Rt ADF 和Rt CDE △中,DA DCDE DF=⎧⎨=⎩,()Rt ADF Rt CDE HL ∴△≌△,AF CE ∴=,AF AB BF =-,CE BC BE =+,AB BF BC BE ∴-=+,2BE AB BC ∴=-,5AB =,3BC =,2532BE ∴=-=,解得:1BE =.故选:C .2.如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F ,若7ABC S =△,32=DE ,5AB =,则AC 的长为( )A .133B .4C .5D .6【答案】A【详解】∵AD 是ABC ∆中BAC ∠的平分线,DE AB ⊥于点E ,DF AC ⊥交AC 于点F ,∴32DF DE ==. 又∵ABCABD ACDSSS=+,5AB =,∴1313752222AC =⨯⨯+⨯⨯,∴133AC =.故选:A . 3.如图,在Rt △ABC 中,∠C =90°,∠BAC 的平分线交BC 于点D ,CD =2,BD =3,Q 为AB 上一动点,则DQ 的最小值为( )A.1B.2C.2.5D【答案】B【详解】解:作DH⊥AB于H,如图,∵AD平分∠BAC,DH⊥AB,DC⊥AC,∴DH=DC=2,∵Q为AB上一动点,∴DQ的最小值为DH的长,即DQ的最小值为2.故选:B.4.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD 的面积是______.【答案】30【详解】过D作DE⊥AB,交BA的延长线于E,则∠E=∠C=90°,∵∠BCD=90°,BD平分∠ABC,∴DE=DC=4,∴四边形ABCD的面积S=S△BCD+S△BAD=12×BC×CD+12×AB×DE=12×9×4+12×6×4=30,故答案为:30.5.如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为______.【答案】8【详解】解:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF=2,∴△ABC的面积=12×5×2+12×3×2=8,故答案侍:8.6.在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角∠ACD和∠ABC的平分线交于点E,则∠AEB=_____︒【答案】25【详解】解:如图示:过点E ,分别作EF BD ⊥交BD 于点E ,EG AC ⊥交AC 于点G ,EH AB ⊥,交AB 延长线于点H , ∵BE 平分ABC ∠,CE 平分ACD ∠,∴EH EF =,EG EF =,∴EH EG =,∴AE 平分HAC ∠, ∵62ABC ∠=︒,50∠=°ACB ,∴6250112HAC ABC ACB ∠=∠+∠=︒+︒=︒,∴111125622EAO HAC ∠=∠=⨯︒=︒, ∵BE 平分ABC ∠,62ABC ∠=︒∴11623122EBC ABC ∠=∠=⨯︒=︒ 在AOE △和BOC 中,OBC OCB OAE AEB ∠+∠=∠+∠∴31505625AEB OBC OCB OAE ∠=∠+∠-∠=︒+︒-︒=︒,故答案是:25. 7.如图,DE ⊥AB 于E ,DF ⊥AC 于F ,若BD =CD ,BE =CF .(1)求证:AD 平分∠BAC :(2)已知AC =18,BE =4,求AB 的长. 【答案】(1)见解析;(2)10AB =.【详解】(1)证明:DE AB ∵⊥,DF AC ⊥,90E DFC ∴∠=∠=︒,在Rt BED 和Rt CFD △中,BD CD BE CF =⎧⎨=⎩,∴Rt BED Rt CFD ≅()HL ,DE DF ∴=,DE AB ∵⊥,DF AC ⊥,AD ∴平分BAC ∠;(2)解:DE DF =,AD AD =,Rt ADE Rt ADF ∴≅()HL ,AE AF ∴=,AB AE BE AF BE AC CF BE =-=-=--,184410AB ∴=--=.8.如图1,在平面直角坐标系中,△ABC 的顶点A (-4,0),B (0,4),AD ⊥BC 交BC 于D 点,交y 轴正半轴于点E (0,t )(1)当t=1时,点C 的坐标为 ; (2)如图2,求∠ADO 的度数;(3)如图3,已知点P (0,3),若PQ ⊥PC ,PQ=PC ,求Q 的坐标(用含t 的式子表示). 【答案】(1)点C 坐标(1,0);(2)∠ADO =45°;(3)Q (-3,3-t ). 【详解】(1)如图1,当t =1时,点E (0,1), ∵AD ⊥BC , ∴∠EAO +∠BCO =90°, ∵∠CBO +∠BCO =90°,∴∠EAO =∠CBO ,在△AOE 和△BOC 中,∵90EAO CBOAO BO AOE BOC ∠=∠⎧⎪=⎨⎪∠=∠︒⎩=,∴△AOE ≌△BOC (ASA ),∴OE =OC =1,∴点C 坐标(1,0). 故答案为:(1,0);(2)如图2,过点O 作OM ⊥AD 于点M ,作ON ⊥BC 于点N ,∵△AOE ≌△BOC ,∴S △AOE =S △BOC ,且AE =BC , ∵OM ⊥AE ,ON ⊥BC ,∴OM =ON ,∴OD 平分∠ADC ;AD ⊥BC ,90ADC ∴∠=︒∴∠ADO =1452ADC ∠=︒;(3)如图3,过P 作GH ∥x 轴,过C 作CG ⊥GH 于G ,过Q 作QH ⊥GH 于H ,交x 轴于F ,∵P (0,3),C (t ,0),∴CG =FH =3,PG =OC =t , ∵∠QPC =90°,∴∠CPG +∠QPH =90°, ∵∠QPH +∠HQP =90°,∴∠CPG =∠HQP ,∵∠QHP=∠G=90°,PQ=PC,∴△PCG≌△QPH,∴CG=PH=3,PG=QH=t,∴Q(-3,3-t).。
模型平行线角平分线等腰三角形三者知二推一

模型“平行线”、“角平分线”、“等腰三角形”三者知二推一【几何模型】“角平分线”、“平行线”、“等腰三角形”三者知其二必推出其一。
初中数学学习难在几何题没有思路当然了,有了思路就感觉简单了,那么为什么没有思路?关键是没有掌握几何证明题的本质,他是一个推理过程,就是具备什么条件,一定会具有一个结论。
往往对推理过程不熟练,思考不到条件下结论存在性,挖空心思也写不出步骤。
这就需要训练做题,思考总结出具备什么条件会有什么结论,做题时直奔主题,不用再思考了,日积月累,书到渠成,再解决几何问题就不难了。
在△ABC中,∠BAC=α[定值],BC=a[定值],可得“定弦定角”模型,找隐圆;【例题】:挖掘定角与定线背景内涵,思考最值问题第25题初审可知第三问考查定角定中线模型(附尺规作图)及解法;联想到定角定高模型(参考题:2020年沈河一模第25题);最后小编原创题考查定角定角平分线。
【思维教练3】—“知识储备”前文已更新:倍长中线,构造“定弦定角”模型,找到隐圆求解。
亦可构造等边三角形转化线段,得:“共顶点的两个等边三角形”;其中,方法二:根据“垂线段最短”得:CK≤CG,则CK的最大值为2√(3),CM+CN=EF+EN=FN;【你看出思路了吗】小编原创试题“考查定角定角平分线”,1.如图,点A、B、C、D在⊙O上,AD平分∠BAC.若∠B O C=120°,则∠C AD的度数为.2.如图,AD是△ABC的外接圆⊙O的直径.若∠BCA=50°,则∠AD B的度数为.3.已知圆锥的底面半径为1cm,高为cm,则它的侧面展开图的面积为cm².4.如图,AB是半圆O的直径.弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离为.5.如图,在⊙O中,点A在弧BC上.若∠B O C=100°,则∠BA C的度数为.▱ABCD的6.如图,若用半径为8,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面圆半径是.7.如图,已知锐角△ABC内外接于半径为2的⊙O.若OD⊥BC于点D,∠BAC=60°,则OD=.8.如图,AD是△ABC的外接圆⊙O的直径.若∠BAD=40°,则∠AC B的度数为.9.已知圆锥的母线长为3,底面圆半径为1,则该圆锥的侧面展开图的面积为.10.已知圆锥的底面圆半径为3,侧面面积为12,则该圆锥的母线长为.11.在⊙O中,若弦BC垂直平分半径O A,则弦BC所对的圆周角等于.12.如图,已知AB是⊙O的直径.P A切⊙O于点A,线段P O交⊙O于点C,连接BC.若∠P=36°,则∠B=.13.用一个圆心角为90°,半径为20 cm的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面圆半径是.14.已知圆锥的底面圆半径为2.5,母线长为9,则该圆锥的侧面展开图的圆心角度数为.15.如图,在边长为2的正方形ABCD中,对角线AC的中点为点O,分别以点A、C为圆心,以AO的长为半径画弧,分别与正方形ABCD的边相交,则图中阴影部分的面积为.(结果保留)16.如图,在△A BC中,∠C=90°,AC=4,BC=3.若以A C所在直线为轴,把△A BC旋转一周,得到一个圆锥,则这个圆锥的侧面面积是.17.如图,在△A BC中,若∠A CB=45°,A B=6.则△A BC的面面积的最大值是.18.如图,在扇形△AO B中,OA=O B=2,∠AO B=90°,点C为弧A B上一点.∠AO C=30°,连接BC,过点C作OA的垂线交OA于点D,则图中阴影部分的面积为.19.如图,点A、B、C、D为一个正多边形的顶点,点O为正多边形的中心,若∠AD B=18°,则这个正多边形的边数为.20.如图,在半径为6的⊙O中.若∠AO B=60°,则图中阴影部分的面积为.21.用一个圆心角为120°,半径为4的扇形制作一个圆锥的侧面(接缝忽略不计),则此圆锥的底面圆半径是.3一.圆典型基本模型图模型1图形:⑴如图,A B是⊙O的直径,点C、E是⊙O上的两点.基本结论有:①A C平分∠B AE是;②A D⊥CD;③CD是⊙O的切线;三个论断,知二推一.⑵⑶⑷⑸⑹④⑤⑥如图,A B是⊙O的直径,点C、E是⊙O上的两点.20.如图,在半径为6的⊙O中.若∠AO B=60°,则图中阴影部分的面积为.接圆的直径.若∠BCA=50°,则∠AD B的度数为.∠A BACDB O=90°,2.如图,在每个小正方形边长为1的网格中,△ABC的顶点A、B、C均在格点上,AB与网格交于点D.AD的长为;OP.AB2A2B,A′B′OP.AB2A2B,A′B′OP.AB2A2B,A′B′(2)点P是边AC上一点,当△APD∽△ABC时,仅用无刻度的直尺确定点P的位置,简单说明作图方法(不要求证明).≌≌≌1.如图,在每个小正方形的边长为1的网格中,点O、点A在格点上,⊙O的半径为3,点B、点C在⊙O上.½∥⅓⅔¼°²³ⁿ∵∴⑥⑦½∥⅓⅔¼°²³ⁿ∵∴⑥⑦½∥⅓⅔¼°²³ⁿ∵∴⑥⑦´'´'´'(1)若∠⊥CAO=90°,ADAC的长为;①②③B.②④①②③B.②④(2)若∠BAO=60°,仅用无刻度的直尺确定点B的位置,简单说明作图方法.⊙O上.2.如图,在每个小正方形边长为1的网格中,△ABC的顶点A、B、C均在格点上,AB与格交于点D.(2)点P是边AC上一点,当△APD∽△ABC时,仅用无刻度的直尺确定点P的位置,简单说明作图方法(不要求证明).过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.AB2A2B,BD=n•BF,沿A→B→C→D→A方向运动到点A 处停止.过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB∏于点C,交QO的延长线于点E,连接PQ,cm BD=n•BF,沿A→B→C→①②⑤①②⑤①②⑤精选试题解析(1)。
角平分线四大模型总结+习题+解析(最全版)
⾓平分线四⼤模型总结+习题+解析(最全版)⾓平分线四⼤辅助线模型⾓平分线的性质为证明线段或⾓相等开辟了新的途径,同时也是全等三⾓形知识的延续,⼜为后⾯⾓平分线的判定定理的学习奠定了基础.涉及到⾓平分线的考点主要是性质、判定以及四⼤辅助线模型,在初⼆上期中、期末考试中都是经常考察的⽅向。
⾓平分线性质:⾓平分线上的点到⾓两边的距离相等.⾓平分线判定:到⾓的两边距离相等的点在⾓的⾓平分线上.四⼤模型1、⾓平分线+平⾏线,等腰三⾓形必出现已知:OC平分∠AOB,CD∥OB交OA于D.则△ODC为等腰三⾓形,OD=CD.2、⾓平分线+两垂线,线等全等必出现已知:OC平分∠AOB.辅助线:过点C作CD⊥OA,CE⊥OB.则CD=CE,△ODC ≌△OEC.3、⾓平分线+⼀垂线,中点全等必出现已知:OC平分∠AOB,DC垂直OC于点C.辅助线:延长DC交OB于点E.则C是DE的中点,△ODC ≌△OEC.4、⾓平分线+截长补短线,对称全等必出现已知:OC平分∠AOB,截取OE=OD,连接CD、CE.则△ODC和△OCE关于OC对称,即△ODC ≌△OEC.【核⼼考点⼀】⾓平分线的性质与判定1.(2016?张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上⼀个动点,若3PA =,则PQ 的最⼩值为( )A B .2C .3D .2.(2016秋?抚宁县期末)如图,在ABC ?中,AD 是它的⾓平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ??= )A .3:4B .4:3C .16:9D .9:163.(2017春?崇仁县校级⽉考)如图,在ABC ?中,90ACB ∠=?,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )A .2cmB .3cmC .4cmD .5cm4.(2018春?⼤东区期中)如图,在Rt ABC ?中,90C ∠=?,BD 是⾓平分线,若CD m =,2AB n =,则ABD ?的⾯积是( )A .mnB .5mnC .7mnD .6mn5.(2019秋?樊城区期末)⼩明同学在学习了全等三⾓形的相关知识后发现,只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线.如图:⼀把直尺压住射线OB ,另⼀把直尺压住射线OA 并且与第⼀把直尺交于点P ,⼩明说:“射线OP 就是BOA ∠的⾓平分线.”他这样做的依据是( )A .⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B .⾓平分线上的点到这个⾓两边的距离相等C .三⾓形三条⾓平分线的交点到三条边的距离相等D .以上均不正确6.(2019秋?梁平区期末)如图,若BD AE ⊥于B ,DC AF ⊥于C ,且DB DC =,40BAC ∠=?,130ADG ∠=?,则DGF ∠=.7.(2018春?开江县期末)如图,在Rt ABC ?中,90C ∠=?,以顶点A 为圆⼼,适当长为半径画弧,分别交AB 、AC 于点M 、N ,再分别以点M 、N 为圆⼼,⼤于12MN 的长为半径画弧,两弧交于点P ,射线AP 交边BC 于点D .下列说法错误的是( ) A .CAD BAD ∠=∠B .若2CD =,则点D 到AB 的距离为2C .若30B ∠=?,则CDA CAB ∠=∠D .2ABD ACD S S ??=8.(2014秋?西城区校级期中)如图,点E 是AOB ∠的平分线上⼀点,EC OA ⊥,ED OB ⊥,垂⾜分别是C ,D .下列结论中正确的有( )(1)ED EC =;(2)OD OC =;(3)ECD EDC ∠=∠;(4)EO 平分DEC ∠;(5)OE CD ⊥;(6)直线OE 是线段CD 的垂直平分线.A .3个B .4个C .5个D .6个9.(2019春?杜尔伯特县期末)如图:在ABC ?中,90C ∠=?,AD 是BAC ∠的平分线,DE AB ⊥于E ,F 在AC 上,BD DF =,证明:(1)CF EB =.(2)2AB AF EB =+.10.(2019秋?垦利区期中)如图,ABC⊥⊥且平分BC,DE AB中,AD平分BAC∠,DG BC于E,DF AC⊥于F.(1)判断BE与CF的数量关系,并说明理由;(2)如果8AB=,6AC=,求AE、BE的长.11.(2017秋?遂宁期末)某地区要在区域S内(即COD∠内部)建⼀个超市M,如图所⽰,按照要求,超市M到两个新建的居民⼩区A,B的距离相等,到两条公路OC,OD的距离也相等.这个超市应该建在何处?(要求:尺规作图,不写作法,保留作图痕迹)【核⼼考点⼆】⾓平分线+⾓两边垂线12.(2019秋?肥城市期末)如图,//AB CD ,BP 和CP 分别平分ABC ∠和DCB ∠,AD 过点P ,且与AB 垂直,垂⾜为A ,交CD 于D ,若8AD =,则点P 到BC 的距离是.13.(2015?湖州)如图,已知在ABC ?中,CD 是AB 边上的⾼线,BE 平分ABC ∠,交CD 于点E ,5BC =,2DE =,则BCE ?的⾯积等于( )A .10B .7C .5D .414.(2010秋?涵江区期末)如图所⽰,在Rt ABC ?中,90C ∠=?,BC AC =,AD 平分BAC ∠交BC 于D ,求证:AB AC CD =+.15.(2012秋?蓬江区校级期末)如图,已知90∠=∠=?,M是BC的中点,DM平分B C∠.求证:ADC(1)AM平分DAB∠;(2)DM AM⊥.16.(2016秋?西城区校级期中)已知:如图,12∠=∠,P为BN上的⼀点,PF BC⊥于F,=,PA PC(1)求证:180∠+∠=?;PCB BAP(2)线段BF、线段BC、线段AB之间有何数量关系?写出你的猜想及证明思路.【核⼼考点三】⾓平分线+垂线17.(2017秋?和平区校级⽉考)如图.在ABC ?中,BE 是⾓平分线,AD BE ⊥,垂⾜为D ,求证:21C ∠=∠+∠.18.(2013秋?昌平区期末)已知:如图,在ABC ?中,AD 平分BAC ∠,CD AD ⊥于点D ,DCB B ∠=∠,若10AC =,6AD=,求AB 的长.19.如图所⽰,ABC ?中,ACB ABC ∠>∠,AE 平分BAC ∠,CD AE ⊥于D ,求证:ACD B ∠>∠.20.已知:如图,在ABC ?中,3ABC C ∠=∠,12∠=∠,BE AE ⊥.求证:2AC AB BE -=.21.(2019秋?下陆区期中)如图,BD 是ABC ∠的⾓平分线,AD BD ⊥,垂⾜为D ,20DAC ∠=?,38C ∠=?,则BAD ∠=.22.(2019秋?曲⾩市校级⽉考)如图,在ABC ?中,AB AC =,90BAC ∠=?,BD 平分ABC ∠交AC 于D ,过C 作CE BD ⊥交BD 延长线于E .求证:12CE BD =.23.(2019?沂源县⼀模)(1)如图(a)所⽰,BD、CE分别是ABC的外⾓平分线,过点A作AD BD⊥,AE CE⊥,垂⾜分别为D、E,连接DE,求证:1() 2DE AB BC AC=++;(2)如图(b)所⽰,BD、CE分别是ABC的内⾓平分线,其他条件不变,DE与ABC三边有怎样的数量关系?并证明这个数量关系;(3)如图(c)所⽰,BD为ABC的内⾓平分线,CE为ABC的外⾓平分线,其他条件不变,DE与ABC三边⼜有怎样的数量关系?并证明这个数量关系.24.(2017秋?夏⾢县期中)如图,在ABC ?中,ABC ∠、ACB ∠的平分线相交于F ,过F 作//DE BC ,交AB 于D ,交AC 于E ,那么下列结论:①BDF ?、CEF ?都是等腰三⾓形;②DE DB CE =+;③AD DE AE AB AC ++=+;④BF CF =.正确的有.25.(2019秋?垦利区期末)如图,平⾏四边形ABCD 中,3AB cm =,5BC cm =;,BE 平分ABC ∠,交AD 于点E ,交CD 延长线于点F ,则DE DF +的长度为.26.(2010秋?海淀区期末)如图,BD 是ABC ?的⾓平分线,//DE BC ,DE 交AB 于E ,若AB BC =,则下列结论中错误的是( )A .BD AC ⊥B .A EDA ∠=∠C .2AD BC =D .BE ED =27.如图,若BD 、CD 分别平分ABC ∠和ACB ∠,过D 作//DE AB 交BC 于E ,作//DF AC 交BC 于F ,求证:BC 的长等于DEF ?的周长.28.(2018秋?邳州市期中)如图,在四边形ABCD中,对⾓线AC平分BAD >,∠,AB AD 下列结论正确的是()A.AB AD CB CD->-B.AB AD CB CD-=-C.AB AD CB CD-<-D.AB AD-与CB CD-的⼤⼩关系不确定29.(2012?⿇城市校级模拟)在ABC∠的外⾓平分线,P是AD上的任意中,AD是BAC⼀点,试⽐较PB PC+与AB AC+的⼤⼩,并说明理由.30.(2018秋?万州区期中)已知:如图,在四边形ABCD中,AC平分BAD ∠,CE AB⊥于=+.E,且180B D∠+∠=?,求证:AE AD BE31.(2017秋?海淀区期中)如图,已知AD是BAC∠=?,C=+,31的⾓平分线,AC AB BD 求B∠的度数.32.(2019秋?平⼭县期中)如图,90∠=?,OM平分AOB∠,将直⾓三⾓板的顶点PAOB在射线OM上移动,两直⾓边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.33.(2016秋?丰宁县期中)如图,在ABC ?中,100A ∠=?,40ABC ∠=?,BD 是ABC ∠的平分线,延长BD ⾄E ,使DE AD =.求证:BC AB CE =+.34.(2018秋?丰城市期中)在ABC ?中,2ACB B ∠=∠,(1)如图1,当90C ∠=?,AD 为BAC ∠的⾓平分线时,在AB 上截取AE AC =,连接DE ,求证:AB AC CD =+;(2)如图2,当90C ∠≠?,AD 为BAC ∠的⾓平分线时,线段AB 、AC 、CD ⼜有怎样的数量关系?请直接写出你的结论,不需要证明;(3)如图3,当AD 为ABC ?的外⾓平分线时,线段AB 、AC 、CD ⼜有怎样的数量关系?请写出你的猜想,并说明理由.35.(2019春?利津县期末)如图,在ABC∠平分线,AD的垂直平分线分中,AD是BAC别交AB、BC延长线于F、E.求证:(1)EAD EDA∠=∠;(2)//DF AC;(3)EAC B∠=∠.36.(2014?西城区⼆模)在ABC>,AD平分BAC∠交BC于点∠为锐⾓,AB AC,BACD.(1)如图1,若ABC是等腰直⾓三⾓形,直接写出线段AC,CD,AB之间的数量关系;(2)BC的垂直平分线交AD延长线于点E,交BC于点F.①如图2,若60∠=?,判断AC,CE,AB之间有怎样的数量关系并加以证明;ABE②如图3,若AC AB+,求BAC∠的度数.⾓平分线四⼤辅助线模型--解析⼀.⾓平分线的性质与判定(共11⼩题)1.(2016?张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上⼀个动点,若3PA =,则PQ 的最⼩值为( )A B .2C .3D .【分析】⾸先过点P 作PB OM ⊥于B ,由OP 平分MON ∠,PA ON ⊥,3PA =,根据⾓平分线的性质,即可求得PB 的值,⼜由垂线段最短,可求得PQ 的最⼩值.【解答】解:过点P 作PB OM ⊥于B , OP 平分MON ∠,PA ON ⊥,3PA =,3PB PA ∴==,PQ ∴的最⼩值为3.故选:C .2.(2016秋?抚宁县期末)如图,在ABC ?中,AD 是它的⾓平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ??= )A .3:4B .4:3C .16:9D .9:16【分析】利⽤⾓平分线的性质,可得出ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼相等,估计三⾓形的⾯积公式,即可得出ABD ?与ACD ?的⾯积之⽐等于对应边之⽐.【解答】解:AD 是ABC ?的⾓平分线,∴设ABD ?的边AB 上的⾼与ACD ?的AC 上的⾼分别为1h ,2h ,12h h ∴=,ABD ∴?与ACD ?的⾯积之⽐:8:64:3AB AC ===,故选:B .3.(2017春?崇仁县校级⽉考)如图,在ABC ?中,90ACB ∠=?,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )A .2cmB .3cmC .4cmD .5cm【分析】根据⾓平分线的性质得到ED EC =,计算即可.【解答】解:BE 平分ABC ∠,DE AB ⊥,90ACB ∠=?, ED EC ∴=,3AE DE AE EC AC cm ∴+=+==,故选:B .4.(2018春?⼤东区期中)如图,在Rt ABC ?中,90C ∠=?,BD 是⾓平分线,若CD m =,2AB n =,则ABD ?的⾯积是( )A .mnB .5mnC .7mnD .6mn【分析】过点D 作DE AB ⊥于E ,根据⾓平分线上的点到⾓的两边距离相等可得DE CD =,然后根据三⾓形的⾯积公式即可得到结论.【解答】解:如图,过点D 作DE AB ⊥于E ,BD 是ABC ∠的平分线,90C ∠=?,DE CD m ∴==,ABD ∴?的⾯积122n m mn =??=,故选:A.5.(2019秋?樊城区期末)⼩明同学在学习了全等三⾓形的相关知识后发现,只⽤两把完全相同的长⽅形直尺就可以作出⼀个⾓的平分线.如图:⼀把直尺压住射线OB,另⼀把直尺压住射线OA并且与第⼀把直尺交于点P,⼩明说:“射线OP就是BOA∠的⾓平分线.”他这样做的依据是()A.⾓的内部到⾓的两边的距离相等的点在⾓的平分线上B.⾓平分线上的点到这个⾓两边的距离相等C.三⾓形三条⾓平分线的交点到三条边的距离相等D.以上均不正确【分析】过两把直尺的交点C作CE AO=,再根据⾓⊥,CF BO⊥,根据题意可得CE CF的内部到⾓的两边的距离相等的点在这个⾓的平分线上可得OP平分AOB∠;【解答】解:(1)如图所⽰:过两把直尺的交点P作PE AO⊥,⊥,PF BO两把完全相同的长⽅形直尺,PE PF∴=,∠(⾓的内部到⾓的两边的距离相等的点在这个⾓的平分线上),OP∴平分AOB故选:A.。
北师大版初三数学上册《平行线分线段成比例及相似多边形》知识讲解及例题演练-word文档资料

平行线分线段成比例及相似多边形【学习目标】1. 平行线分线段成比例及其推论.2. 平行线分线段成比例及其推论的应用.3. 相似多边形的有关概念.【要点梳理】要点一、平行线分线段成比例及其推论平行线分线段成比例,一般地,有如下基本事实:两条直线被一组平行线所截,所得的对应线段成比例.推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.要点诠释:(1).对应线段成比例可用下面的语言形象表示:右全左全右上左上全上全上下上下上===,,等等. (2)有推论可以得出以下结论:要点二、行线分线段成比例及其推论的应用行线分线段成比例及其推论的应用主要是来求线段的长度.要点三、相似多边形的有关概念相似多边形:各角分别相等、各边成比例的两个多边形叫做相似多边形.它的符号是“∽”,读作“相似于”.相似比:相似多边形的对应边的比叫做相似比.要点诠释: (1)相似图形就是指形状相同,但大小不一定相同的图形;(2)“全等”是“相似”的一种特殊情况,即当“形状相同”且“大小相同”时,两个图形是全等.(3)相似多边形的定义既是判定方法,又是它的性质.【典型例题】类型一、平行线分线段成比例及其推论1、如图,直线AD ∥BE ∥CF ,BC=13AC ,DE=4,那么EF 的值是__________.AB BC =【答案】2.2、如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.【思路点拨】【答案与解析】【总结升华】此题考查了平行线段成比例,关键是根据平行线等分线段定理进行解答.举一反三【变式】如图,直线a∥b∥c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,已知AC=4,CE=6,BD=3,则BF等于______________.【答案】7.5.类型二、平行线分线段成比例及其推论的应用3、如图,已知梯形ABCD中,AB∥DC,△AOB的面积等于9,△AOD的面积等于6,AB=7,求CD的长.【思路点拨】根据△AOB的面积等于9,△AOD的面积等于6,可知OB:OD的值,再根据平行线分线段成比例即可求解.【答案与解析】解:∵AB∥DC,==4举一反三【变式】如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,ADAB=A.4.5 B.8 C.10.5 D.144A 23B32C 6 D16【答案】B.举一反三【变式】如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于()A.5:8 B.3:8 C.3:5 D.2:5【答案】解:∵AD:DB=3:5,∴BD:AB=5:8,∵DE∥BC,∴CE:AC=BD:AB=5:8,∵EF∥AB,∴CF:CB=CE:AC=5:8.故选A.类型三、相似多边形的有关概念5、如图是一个由12个相似(形状相同,大小不同)的直角三角形所组成的图案,它是否有点像一个商标图案?你能否也用相似图形设计出几个美丽的图案?最好再给你设计的图案取一个名字.【思路点拨】相似图形是指形状相同的图形.根据相似图形进行变换可以形成一些美丽的图案.【答案与解析】解:由12个相似的直角三角形形成的图案很有创意,给人以美的享受,可以作为一个商标的图案.以下几个图案分别是用相似形设计的美丽图案.【总结升华】考查的是相似图形,相似图形是指形状相同的图形.把一组相似图形进行变换可以得到美丽的图案.。
初中数学复习几何模型专题讲解29--- 平行线中和角平分线有关的图形

初中数学复习几何模型专题讲解专题29 平行线中和角平分线有关的图形一、单选题1.在钝角△ABC中,延长BA到D,AE是∠DAC的平分线,AE//BC,则与∠B相等的角有()A.1个B.2个C.3个D.4个【答案】C【分析】依据角平分线的性质和平行线的性质即可求解.【详解】解析:依据角平分线的性质和平行线的性质,可知∠B =∠DAE=∠CAE=∠C故选C.【点睛】此题主要考查角平分线的性质与平行线的性质,解题的关键是熟知角平分线的性质.2.如图,点A、C为∠FBE边上的两点,AD∥BE,AC平分∠BAD,若∠F AD=45°,则∠ACE=()A.45°B.67.5°C.112.5°D.135°【答案】C【分析】先根据平角的定义求出∠BAD,根据角平分线的性质求出∠DAC,再利用平行线的性质,得到∠ACB的度数.最后通过平角求出∠ACE.【详解】解:∵∠F AD=45°,∴∠BAD=180°-45°=135°.∵AC平分∠BAD,∴∠DAC=12BAD∠=67.5°.∵AD∥BE,∴∠ACB=∠DAC=67.5°.∴∠ACE=180°-67.5°=112.5°.故选:C.【点睛】本题考查平行的性质和角平分线的性质,解题关键是运用题目中的条件去求解角的度数,能够从角平分线和平行这两个条件想到图中存在等腰三角形.3.如图,已知BM平分∠ABC,且BM//AD,若∠ABC=70°,则∠A的度数是()A.30°B.35°C.40°D.70°【答案】B【分析】先根据角平分线的性质,求出∠ABC的度数,再由平行线的性质得到∠A的度数.【详解】解:∵BM平分∠ABC,∴∠MBA=12∠ABC=35°.∵BM∥AD,∴∠A=∠MBA=35°.故选:B.【点睛】本题考查的是角平分线的性质,平行线的性质,掌握以上知识是解题的关键.二、解答题4.如图所示,直线AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF、∠DFE 的平分线相交于点K.(1)求∠EKF的度数;(2)如图(2)所示,作∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.(3)在图(2)中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,……,请直接写出∠K4的度数.【答案】(1)∠EKF=90°;(2)∠K=2∠K1,证明见解析;(3)∠K4=5.625°.【分析】(1)过K作KG∥AB,交EF于G,根据平行于同一条直线的两直线平行可得AB∥KG∥CD,从而得出∠BEK=∠EKG,∠GKF=∠KFD,∠BEK+∠FEK+∠EFK+∠DFK=180°,然后根据角平分线的定义即可求出∠BEK+∠DFK=90°,从而得出结论;(2)根据角平分线的定义可得∠BEK1=∠KEK1,∠KFK1=∠DFK1,结合(1)的结论可得∠BEK1+∠DFK1=45°,从而求出∠K1,即可得出结论;(3)根据(2)中的规律即可得出结论.【详解】(1)如图(1),过K作KG∥AB,交EF于G,∵AB∥CD,∴AB∥KG∥CD,∴∠BEK=∠EKG,∠GKF=∠KFD,∠BEK+∠FEK+∠EFK+∠DFK=180°,∵EK、FK分别为∠BEF与∠EFD的平分线,∴∠BEK=∠FEK,∠EFK=∠DFK,∴2(∠BEK+∠DFK)=180°,∴∠BEK+∠DFK=90°,则∠EKF=∠EKG+∠GKF=90°;(2)∠K=2∠K1,理由为:∵∠BEK、∠DFK的平分线相交于点K1,∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,∴∠BEK+∠KFD=90°,即∠BEK1+∠DFK1=45°,同(1)得∠K1=∠BEK1+∠DFK1=45°,则∠K=2∠K1;(3)如图(3),根据(2)中的规律和推导方法可得:∠K2=12∠K1=22.5°,∠K3=12∠K2=11.25°,∠K4=12∠K3=5.625°.【点睛】此题考查的是平行线的性质及判定,掌握平行线的各个性质定理是解题关键.5.如图,已知AM∥BN,∠A=64°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)①∠ABN的度数是;②∵AM∥BN,∴∠ACB=∠;(2)求∠CBD的度数;(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由:若变化,请写出变化规律;(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是.【答案】(1)①116,︒②CBN;(2)58︒;(3)不变,:2:1APB ADB∠∠=,理由见解析;(4)29.︒【分析】(1)①由平行线的性质,两直线平行,同旁内角互补可直接求出;②由平行线的性质,两直线平行,内错角相等可直接写出;(2)由角平分线的定义可以证明∠CBD=12∠ABN,即可求出结果;(3)不变,∠APB:∠ADB=2:1,证∠APB=∠PBN,∠PBN=2∠DBN,即可推出结论;(4)可先证明∠ABC=∠DBN,由(1)∠ABN=116°,可推出∠CBD=58°,所以∠ABC+∠DBN=58°,则可求出∠ABC的度数.【详解】解:(1)①∵AM//BN,∠A=64°,∴∠ABN=180°﹣∠A=116°,故答案为:116°;②∵AM//BN,∴∠ACB=∠CBN,故答案为:CBN;(2)∵AM//BN,∴∠ABN+∠A=180°,∴∠ABN=180°﹣64°=116°,∴∠ABP+∠PBN=116°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=116°,∴∠CBD=∠CBP+∠DBP=58°;(3)不变,∠APB:∠ADB=2:1,∵AM//BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1;(4)∵AM//BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD =∠CBD+∠DBN∴∠ABC =∠DBN ,由(1)∠ABN =116°,∴∠CBD =58°,∴∠ABC+∠DBN =58°,∴∠ABC =29°,故答案为:29°.【点睛】本题考查了角平分线的定义,平行线的性质等,解题关键是能熟练运用平行线的性质并能灵活运用角平分线的定义等.6.如图1,在平面直角坐标系中,(,0),(,2)A a C b ,且满足2(2)20a b ++-=,过C 作CB x ⊥轴于B .(1)求ABC ∆的面积.(2)若过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,求AED ∠的度数.(3)在y 轴上存在点P 使得ABC ∆和ACP ∆的面积相等,请直接写出P 点坐标.【答案】(1)4;(2)45︒;(2)(0,3)P 或(0,1)-.【分析】(1)根据非负数的性质易得2a =-,2b =,然后根据三角形面积公式计算; (2)过E 作//EF AC ,根据平行线性质得////BD AC EF ,且1312CAB ∠=∠=∠,1422ODB ∠=∠=∠,所以112()2AED CAB ODB ∠=∠+∠=∠+∠;然后把90CAB ODB ∠+∠=︒ 代入计算即可;(3)分类讨论:设(0,)P t ,当P 在y 轴正半轴上时,过P 作//MN x 轴,//AN y 轴,//BM y 轴,利用4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形可得到关于t 的方程,再解方程求出t ; 当P 在y 轴负半轴上时,运用同样方法可计算出t .【详解】解:(1)2(2)20a b ++-=,20a ∴+=,20b -=,2a ∴=-,2b =,CB AB ⊥(2,0)A ∴-,(2,0)B ,(2,2)C ,ABC ∆∴的面积12442=⨯⨯=; (2)解://CB y 轴,//BD AC ,5CAB ∴∠=∠,又∵590ODB ∠+∠=︒,∴90CAB ODB ∠+∠=︒,过E 作//EF AC ,如图①,//BD AC , ////BD AC EF ∴, 31∴∠=∠,42∠=∠ AE ∵,DE 分别平分CAB ∠,ODB ∠,即:132CAB ∠=∠,142ODB ∠=∠, 112()452AED CAB ODB ∴∠=∠+∠=∠+∠=︒;(3)(0,1)P -或(0,3). 解:①当P 在y 轴正半轴上时,如图②,设(0,)P t , 过P 作//MN x 轴,//AN y 轴,//BM y 轴,4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形, ∴4(2)(2)42t t t t -+---=,解得3t =, ②当P 在y 轴负半轴上时,如图③4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形 ∴4(2)(2)42t t t t -+-+--=,解得1t =-,综上所述:(0,3)P 或(0,1)-.【点睛】本题考查了平行线的判定与性质:两直线平行,内错角相等.也考查了非负数的性质、坐标与图形性质以及三角形面积公式.构造矩形求三角形面积是解题关键.7.阅读下面材料:彤彤遇到这样一个问题:已知:如图甲,AB //CD ,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED . 求证:∠BED =∠B +∠D .彤彤是这样做的:过点E 作EF //AB ,则有∠BEF =∠B .∵AB //CD ,∴EF//CD.∴∠FED=∠D.∴∠BEF+∠FED=∠B+∠D.即∠BED=∠B+∠D.请你参考彤彤思考问题的方法,解决问题:如图乙.已知:直线a//b,点A,B在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.(1)如图1,当点B在点A的左侧时,若∠ABC=60°,∠ADC=70°,求∠BED的度数;(2)如图2,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,直接写出∠BED的度数(用含有α,β的式子表示).【答案】(1)65°;(2)11 18022αβ︒-+【分析】(1)如图1,过点E作EF∥AB,当点B在点A的左侧时,根据∠ABC=60°,∠ADC=70°,参考彤彤思考问题的方法即可求∠BED的度数;(2)如图2,过点E作EF∥AB,当点B在点A的右侧时,∠ABC=α,∠ADC=β,参考彤彤思考问题的方法即可求出∠BED的度数.【详解】(1)如图1,过点E作EF∥AB,有∠BEF=∠EBA.∵AB∥CD,∴EF∥CD.∴∠FED=∠EDC.∴∠BEF+∠FED=∠EBA+∠EDC.即∠BED=∠EBA+∠EDC,∵BE平分∠ABC,DE平分∠ADC,∴∠EBA=12∠ABC=30°,∠EDC=12∠ADC=35°,∴∠BED=∠EBA+∠EDC=65°.答:∠BED的度数为65°;(2)如图2,过点E作EF∥AB,有∠BEF+∠EBA=180°.∴∠BEF=180°﹣∠EBA,∵AB∥CD,∴EF∥CD,∴∠FED=∠EDC.∴∠BEF+∠FED=180°﹣∠EBA+∠EDC.即∠BED=180°﹣∠EBA+∠EDC,∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠EBA =12∠ABC =12α,∠EDC =12∠ADC =12β, ∴∠BED =180°﹣∠EBA +∠EDC =180°﹣12α +12β. 答:∠BED 的度数为180°﹣12α +12β. 【点睛】本题考查了平行线的判定与性质以及角平分线的定义,解决本题的关键是熟练掌握平行线的判定与性质.8.如图,已知//AM BN ,60A ∠=︒,点P 是射线AM 上一动点(与点A 不重合),BC ,BD 分别平分ABP ∠和PBN ∠,分别交射线AM 于点C ,D .(1)求CBD ∠的度数(2)当点P 运动时,:APB ADB ∠∠的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;(3)当点P 运动到某处时,ACB ABD =∠∠,求此时ABC ∠的度数.【答案】(1)60°;(2)不变,∠APB :∠ADB=2:1;(3)30°【分析】(1)根据角平分线的定义只要证明∠CBD=12∠ABN 即可; (2)不变.可以证明∠APB=∠PBN ,∠ADB=∠DBN=12∠PBN . (3)想办法证明∠ABC=∠CBP=∠DBP=∠DBN 即可解决问题;【详解】解:(1)∵AM∥BN,∴∠ABN=180°-∠A=120°,又∵BC,BD分别平分∠ABP和∠PBN,∴∠CBD=∠CBP+∠DBP=12(∠ABP+∠PBN)=12∠ABN=60°,(2)不变.理由如下:∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,又∵BD平分∠PBN,∴∠ADB=∠DBN=12∠PBN=12∠APB,∴∠APB:∠ADB=2:1.(3)∵AM∥BN,∴∠ACB=∠CBN,又∵∠ACB=∠ABD,∴∠CBN=∠ABD,∴∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,∴∠ABC=∠CBP=∠DBP=∠DBN,∴∠ABC=14∠ABN=30°,【点睛】本题考查平行线的性质、角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.9.如图,已知AB∥CD,BE平分∠ABC,交CD于点D,∠CDE=160°,求∠C的度数【答案】140°【分析】先根据邻补角的定义求出∠CDB的度数,再根据平行线的性质及角平分线的定义得出∠ADB及∠ABC的度数,由平行线的性质可得出∠C的度数.【详解】解:∵∠CDE=160°,∴∠CDB=180°-∠CDE=180°-160°=20°,∵AB∥CD,∴∠ABD=∠CDB=20°,∵BE平分∠ABC,∴∠ABC=2∠ABD=2×20°=40°,∴∠C=180°-∠ABC=180°-40°=140°.【点睛】本题考查的是平行线的性质、角平分线的定义及邻补角的性质,熟知平行线的性质是解答此题的关键.10.如图,已知:AD⊥BC于D,EG⊥BC于G,AD平分∠BAC,求证:∠1=∠E.下面是部分推理过程,请你填空或填写理由证明:∵AD⊥BC,EG⊥BC (已知),∴∠ADC=∠EGC=90∘(),∴AD∥EG(),∴∠2=______,( )∠3=______(两直线平行,同位角相等) .又∵AD平分∠BAC(),∴∠2=∠3(),∴∠1=∠E()【答案】垂直的定义;同位角相等,两直线平行;∠1;两直线平行,内错角相等;∠E;已知;角平分线的定义;等量代换【分析】根据平行线的性质和判定以及角平分线的定义证明即可.【详解】证明:∵AD⊥BC,EG⊥BC (已知),∴∠ADC=∠EGC=90°(垂直的定义),∴AD//EG(同位角相等,两直线平行),∴∠2=1,(两直线平行,内错角相等)∠3=∠E(两直线平行,同位角相等) .又∵AD平分∠BAC(已知),∴∠2=∠3(角平分线的定义),∴∠1=∠E(等量代换).【点睛】本题主要考查平行线的性质及判定,角平分线的定义,掌握平行线的性质及判定是解题的关键.AB CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,11.已知直线//CM交AB于点H,过点A作AG⊥AC交CM于点G.(1)如图1,点G在CH的延长线上时,若∠GAB =36°,求∠MCD的度数;(2)如图2,点G在CH上时,试说明:2∠MCD+∠GAB=90°.【答案】(1)63°;(2)见解析【分析】(1)依据AG⊥AC,∠GAB=36°,可得∠CAH的度数,依据角平分线的定义以及平行线的性质,即可得到∠MCD的度数;(2)结合(1)得ACD+∠CAH=180°,再依据角平分线的定义,即可得2∠MCD+∠GAB=90°.【详解】(1)∵AG⊥AC,∠GAB=36°,∴∠CAH=90°-36°=54°,∵AB∥CD,∴∠ACD+∠CAH=180°,∴∠ACD=126°,∵CM是∠ACD的平分线,∴∠ACH=∠DCM=63°;(2)∵∠ACH=∠DCM,∴∠ACD=2∠MCD,由(1)得ACD+∠CAH=180°,∵AG⊥AC,∴∠CAG=90°,∴2∠MCD+90°+∠GAB=180°,∴2∠MCD+∠GAB=90°.【点睛】本题主要考查了平行线的性质,垂直的定义,角平分线的定义,利用两直线平行,同旁内角互补是解决问题的关键.12.阅读理解:我们知道“三角形三个内角的和为180°”,在学习平行线的性质之后,可以对这一结论进行推理论证.请阅读下面的推理过程:如图①,过点A作DE//BC∴∠B=∠EAB,∠C=∠DAC又∵∠EAB+∠BAC+∠DAC=180°∴∠B+∠BAC+∠C=180°即:三角形三个内角的和为180°.阅读反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC、∠B、∠C“凑”在一起,得出角之间的关系.方法运用:如图②,已知AB//DE,求∠B+∠BCD+∠D的度数.(提示:过点C作CF//AB)深化拓展:如图③,已知AB//CD,点C在点D的右侧,∠ADC=70°,点B在点A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,且点E在AB与CD两条平行线之间,求∠BED的度数.【答案】方法运用:360°;深度拓展:65°【分析】方法运用:过C作CF∥AB,根据平行线的性质得到∠D=∠FCD,∠B=∠BCF,然后根据已知条件即可得到结论;深化拓展:过点E作EF∥AB,然后根据两直线平行内错角相等,再利用角平分线的定义和等量代换即可求∠BED的度数.【详解】方法运用:解:过点C作CF∥AB∴∠B=∠BCF∵CF∥AB且AB∥DE∴CF∥DE∴∠D=∠DCF∵∠BCD+∠BCF+∠DCF=360°∴∠B+∠BCD+∠D=360°深化拓展:过点E作EF∥AB∴∠BEF=∠ABE又∵BE平分∠ABC,∠ABC=60°∴∠BEF=∠ABE=12∠ABC=30°∵EF∥AB,AB∥CD∴EF∥CD∴∠DEF=∠EDC又∵DE平分∠ADC,∠ADC=70°∴∠DEF=∠EDC=12∠ADC=35°∴∠BED=∠BEF+∠DEF=30°+35°=65°【点睛】本题主要考查平行线的性质和角平分线的定义,能够作出平行线是解题的关键.13.在综合与实践课上,老师让同学们以“三条平行线m,n,l(即始终满足m∥n∥l)和一副直角三角尺ABC,DEF(∠BAC=∠EDF=90°,∠FED=60°,∠DFE=30°,∠ABC=∠ACB=45°)”为主题开展数学活动.操作发现(1)如图1,展翅组把三角尺ABC的边BC放在l上,三角尺DEF的顶点F与顶点B 重合,边EF经过AB,顶点E恰好落在m上,顶点D恰好落在n上,边ED与n相交所成的一个角记为∠1,求∠1的度数;(2)如图2,受到展翅组的启发,高远组把直线m向下平移后使得两个三角尺的两个直角顶点A、D分别落在m和l上,顶点C恰好落在n上,边AC与l相交所成的一个角记为∠2,边DF与m相交所成的一个角记为∠3,请你说明∠2﹣∠3=15°;结论应用(3)老师在点评高远组的探究操作时提出,在(2)的条件下,若点N是直线n上一点,CN恰好平分∠ACB时,∠2与∠3之间存在一个特殊的倍数关系,请你直接写出它们之间的倍数关系,不需要说明理由.【答案】(1)75°;(2)见解析;(3)∠2=3∠3【分析】(1)利用三角板的度数,求出∠DBC的度数,再利用平行线的性质得到∠BDN的度数,由此得到∠1的度数;(2)过B点作BG∥直线m,利用平行线的性质可得到∠3=DBG和∠LAB=∠ABG,再利用等量代换得到∠3+∠LAB=75°,利用余角性质得到∠LAB=90°-∠2,由此证明结论;(3)结论:∠2=3∠3.利用(2)中结论,结合平行线的性质得到∠2和∠3的度数由此证明结论.【详解】(1)∵直线n∥直线l,∴∠DBC=∠BDN,又∵∠DBC=∠ABC﹣∠ABD=45°﹣30°=15°,∴∠BDN=15°,∴∠1=90°﹣15°=75°.(2)如图所示,过B点作BG∥直线m,∵BG∥m,l∥m,∴BG∥l(平行于同一直线的两直线互相平行),∵BG∥m,∴∠3=DBG,又∵BG∥l,∴∠LAB=∠ABG,∴∠3+∠LAB=∠DBA=30°+45°=75°,又∵∠2和∠LAB互为余角,∴∠LAB =90°﹣∠2,∴∠3+90°﹣∠2=75°,∴∠2﹣∠3=15°.(3)结论:∠2=3∠3.理由:在(2)的条件下,∠2﹣∠3=15°,又∵CN 平分∠BCA ,∴∠BCN =∠CAN =22.5°,又∵直线n ∥直线l ,∴∠2=22.5°,∴∠3=7.5°,∴∠2=3∠3.【点睛】考查平行线的性质并结合了三角板中的特殊角度,学生需要作辅助线利用平行线的传递性将特殊的角的关系联系起来,熟悉掌握平行线之间角的关系是解题的关键. 14.如图,AB CD ∥,点E 、F 分别在直线AB 、CD 上,点O 在直线AB 、CD 之间,100EOF ∠=︒.(1)求BEO DFO ∠+∠的值;(2)如图2,直线MN 交BEO ∠、CFO ∠的角平分线分别于点M 、N ,求EMN FNM∠-∠的值;(3)如图3,EG 在AEO ∠内,AEG n OEG ∠=∠,FK 在DFO ∠内,DFK n OFK ∠=∠.直线MN 交FK 、EG 分别于点M 、N ,若50FMN ENM ∠-∠=︒,则n 的值是__________.【答案】(1)260° ;(2)40°;(3)53【分析】(1)如下图,过点O 作OG AB ,可得出AB OG CD ,然后利用平行的性质进行角度转换可得出答案;(2)如图,过点M 作MK AB ,过点N 作NH CD ∥,然后设BEM OEM x ∠=∠=,CFN OFN y ∠=∠=,利用方程思想进行角度推导,可得出答案;(3)如下图,过点O 作AB 的平行线OQ ,同样利用方程思想进行推导转化,可得出n 的值.【详解】(1)证明:过点O 作OG AB∵AB CD ∥∴AB OG CD∴180BEO EOG ∠+∠=︒,180DFO FOG ∠+∠=︒∴360BEO EOG DFO FOG ︒∠+∠+∠+∠=即360BEO EOF DFO ∠+∠+∠=︒∵100EOF ∠=︒∴260BEO DFO ︒∠+∠=(2)解:过点M 作MK AB ,过点N 作NH CD ∥,∵EM 平分BEO ∠,FN 平分CFO ∠设BEM OEM x ∠=∠=,CFN OFN y ∠=∠=∵260BEO DFO ︒∠+∠=∴21802260BEO DFO x y ︒︒∠+∠=+-=∴40x y -=︒∵MK AB ,NH CD ∥,AB CD ∥ ∴AB MK NH CD∴EMK BEM x ∠=∠=,HNF CFN y ∠=∠=,KMN HNM ∠=∠∴()EMN FNM EMK KMN HNM HNF ∠∠=∠+∠-∠+∠-x KMN HNM y =+∠-∠-40x y ︒=-=(3)如下图,过点O 作AB 的平行线OQ设∠NEO=x ,则∠AEN=nx设∠OFM=y,则∠MFD=ny∵AB∥CD,AB∥OQ∴AB∥OQ∥CD∴∠EOQ=∠AEO=(n+1)x,∠QOF=180°-(n+1)y∵∠EOF=100°∴∠EOQ+∠QOF=100°,化简得:(n+1)(y-x)=80°在△NPE中,∠ENP=180°-x-∠NPE在四边形POFM中,∠PMF=360°-y-100°-∠OPM∵∠PMF-∠ENP=50°∴∠PMF-∠ENP=50=360°-y-100°-∠OPM-(180°-x-∠NPE) ∵∠NPE=∠OPM∴∠PMF-∠ENP化简后得:150°+(y-x)=180°∴y-x=30°∵(n+1)(y-x)=80°∴解得:n=53.【点睛】本题考查平行线的综合应用,解题关键是构造平行线,然后利用方程思想进行角度转化求解.15.如图,已知∠AOB,作∠AOB的平分线OC,将直角尺DEMN如图所示摆放,使EM边与OB边重合,顶点D落在OA边上,DN边与OC交于点P.(1)猜想DOP是三角形;(2)补全下面证明过程:∵OC平分∠AOB∴=∵DN∥EM∴=∴=∴=【答案】等腰,∠DOP,∠BOP,∠DPO,∠BOP,∠DOP,∠DPO,OD,PD,见解析【分析】(1)三角形的种类有多种,从边和角的关系上看常见的有:等腰三角形、等边三角形、直角三角形、观察此三角形即可大体猜想出三角形的类型;(2)根据角平分线的性质和平行线的性质,求得∠DOP=∠DPO,即可判断三角形的形状.【详解】解:(1)我们猜想△DOP是等腰三角形;(2)补全下面证明过程:∵OC平分∠AOB,∴∠DOP =∠BOP ,∵DN ∥EM ,∴∠DPO =∠BOP ,∴∠DOP =∠DPO ,∴OD =PD .故答案为:等腰,∠DOP ,∠BOP ,∠DPO ,∠BOP ,∠DOP ,∠DPO ,OD ,PD .【点睛】本题考查了角平分线的性质和平行线的性质及等腰三角形,解决本题的关键是掌握平行线的性质定理,找到相等的角.16.在小学认识三角形的基础上我们来继续学习三角形.三角形可用符号“”表示. 例:如图1中的三角形可记作“ABC ”;在一个三角形中,如果有两个角相等,我们新定义这个三角形为等角三角形.(1)如图1,ABC ∠的角平分线交AC 于D ,//DE BC 交AB 于E ,①请在图1中依题意补全图形;②判断EBD △是不是等角三角形;(直接写出结论即可).(2)如图2,AF 是GAC ∠的角平分线,//BC AF .判断ABC 是不是等角三角形,并说明理由.(3)如图3,BM ,CM 分别是ABC ∠和ACB ∠的角平分线,请过图中某一点,作一条图中已有线段的平行线,使图中出现一个或两个等角三角形,标出字母,并就出现的一个三角形是等角三角形说明理由.【答案】(1)①见解析;②△EBD 是等角三角形;(2)△ABC 是等角三角形,理由见解析;(3)见解析【分析】(1)①根据题意画出图形即可;②根据角平分线定义可得∠ABD =∠DBC ,根据平行线的性质可得∠EDB =∠DBC ,进而可得∠EBD =∠EDB ,从而可得△EBD 是等角三角形;(2)根据平行线的性质可得∠1=∠B ,∠2=∠C ,再根据角平分线的性质可得∠1=∠2,进而可得结论;(3)过点M 作GH ∥BC ,交AB 于点G ,交AC 于点H ,利用平行线的性质和角平分线定义解答即可.【详解】解:(1)①补全图形如图4所示.②△EBD是等角三角形.理由:∵BD平分∠ABC,∴∠ABD=∠DBC,∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴△EBD是等角三角形;(2)△ABC是等角三角形.理由如下:如图5,∵AF∥BC,∴∠1=∠B,∠2=∠C,∵AF是∠GAC的角平分线,∴∠1=∠2,∴∠B=∠C,∴△ABC是等角三角形.(3)过点M作GH∥BC,交AB于点G,交AC于点H,如图6,出现两个等角三角形分别是:△GBM和△HMC.下面说明△GBM是等角三角形.理由:∵GH∥BC,∴∠1=∠2,∵BM是∠ABC角平分线,∴∠GBM=∠2,∴∠1=∠GBM,所以△GBM是等角三角形.【点睛】此题主要考查了平行线的性质以及角平分线的定义,正确理解题意、熟练掌握平行线的性质是解题的关键.17.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E 2,第三次操作,分别作∠ABE 2和∠DCE 2的平分线,交点为E 3,…,第n 次操作,分别作∠ABE n ﹣1和∠DCE n ﹣1的平分线,交点为E n .(1)如图①,已知∠ABE=50°,∠DCE=25°,则∠BEC = °;(2)如图②,若∠BEC=140°,求∠BE 1C 的度数;(3)猜想:若∠BEC =α度,则∠BE n C = °.【答案】(1)75;(2)70°;(3)2n α⎛⎫ ⎪⎝⎭【分析】(1)先过E 作EF ∥AB ,根据AB ∥CD ,得出AB ∥EF ∥CD ,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE=75°;(2)先根据∠ABE 和∠DCE 的平分线交点为E 1,运用(1)中的结论,得出∠BE 1C=∠ABE 1+∠DCE 1=12∠ABE+12∠DCE=12∠BEC ; (3)根据∠ABE 1和∠DCE 1的平分线,交点为E 2,得出∠BE 2C=14∠BEC ;根据∠ABE 2和∠DCE 2的平分线,交点为E 3,得出∠BE 3C=18∠BEC ;…据此得到规律∠E n =12n ∠BEC ,最后求得∠BE n C 的度数.【详解】解:(1)如图①,过E 作EF ∥AB ,∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2,∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE=75°;故答案为:75;(2)如图2,∵∠ABE和∠DCE的平分线交点为E1,∴由(1)可得,∠BE1C=∠ABE1+∠DCE1=12∠ABE+12∠DCE=12∠BEC;∵∠BEC=140°,∴∠BE1C=70°;(3)如图2,∵∠ABE1和∠DCE1的平分线交点为E2,∴由(1)可得,∠BE 2C=∠ABE 2+∠DCE 2=12∠ABE 1+12∠DCE 1=12∠CE 1B=14∠BEC ; ∵∠ABE 2和∠DCE 2的平分线,交点为E 3,∴∠BE 3C=∠ABE 3+∠DCE 3=12∠ABE 2+12∠DCE 2=12∠CE 2B=18∠BEC ; …以此类推,∠E n =12n ∠BEC , ∴当∠BEC=α度时,∠BE n C 等于2n α⎛⎫ ⎪⎝⎭°. 故答案为:2n α⎛⎫ ⎪⎝⎭. 【点睛】本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.18.完成下面的证明.如图:BAP ∠与APD ∠互补,BAE CPF ∠=∠,求证:E F ∠=∠.对于本题小明是这样证明的,请你将他的证明过程补充完整.证明:BAP ∠与APD ∠互补,(已知)//AB CD ∴.( )BAP ∴∠= .(两直线平行,内错角相等)BAE CPF ∠=∠,(已知)BAP BAE APC CPF ∴∠-∠=∠-∠,(等量代换)即EAP ∠= .∴ .(内错角相等,两直线平行)E F ∴∠=∠.( )19.如图,//AB CD ,点C 在点D 的右侧,ABC ∠,ADC ∠的平分线交于点E (不与B ,D 点重合),70ADC ∠=︒.设BED n ∠=︒.(1)若点B 在点A 的左侧,求ABC ∠的度数(用含n 的代数式表示)(2)将(1)中的线段BC 沿DC 方向平移,当点B 移动到点A 右侧时,请画出图形并判断ABC ∠的度数是否改变.若改变,请求出ABC ∠的度数(用含n 的代数式表示);若不变,请说明理由.【答案】同旁内角互补,两直线平行;APC ∠;APF ∠;//AE FP ;两直线平行,内错角相等.【分析】已知∠BAP 与∠APD 互补,根据同旁内角互补两直线平行,可得AB ∥CD ,再根据平行线的判定与性质及等式相等的性质即可得出答案.【详解】证明:BAP ∠与APD ∠互补,(已知)//AB CD ∴(同旁内角互补,两直线平行).BAP ∴∠=APC ∠(两直线平行,内错角相等), BAE CPF ∠=∠,(已知)BAP BAE APC CPF ∴∠-∠=∠-∠,即EAP ∠=APF ∠,//AE FP ∴(内错角相等,两直线平行),E F ∴∠=∠(两直线平行,内错角相等). 故答案为:同旁内角互补,两直线平行;APC ∠;APF ∠;//AE FP ;两直线平行,内错角相等.【点睛】本题考查了平行线的判定与性质和等式的性质,关键是正确理解与运用平行线的判定与性质.20.如图,AC ∥DE ,BD 平分∠ABC 交AC 于F ,∠ABC=70°,∠E=50°,求∠D ,∠A 的度数.【答案】95,60D A ∠=︒∠=︒【分析】根据BD 平分∠ABC ,∠ABC=70°得出1352ABF DBC ABC ∠=∠=∠=︒,再根据//,50AC CE E ∠=︒得出50∠=°ACB ,从而计算,D A ∠∠.【详解】∵根据BD 平分∠ABC 交AC 于F ,∠ABC=70° ∴1352ABF DBC ABC ∠=∠=∠=︒ 又∵//,50AC CE E ∠=︒∴50∠=°ACB∴180705060A ∠=︒-︒-︒=︒180355095BFC ∠=︒-︒-︒=︒∴95D BFC ∠=∠=︒综上所述:95,60D A ∠=︒∠=︒【点睛】本题考查了三角形的内角和定理以及平行线的性质,转化相关的角度是解题关键. 21.直线AB ∥CD ,直线EF 分别交AB 、CD 于点A 、C ,CM 是ACD ∠的平分线,CM 交AB 于点N .(1)如图①,过点A 作AC 的垂线交CM 于点M ,若55MCD ∠=,求MAN ∠的度数; (2)如图②,点G 是CD 上的一点,连接MA 、MG ,180MGD EAB ∠+∠=,MC 平分AMG ∠.①AMG ∠和EAB ∠满足怎么样的数量关系时EC AM ⊥?②若36AMG ∠=,求ACD ∠的度数.【答案】(1)20°;(2)①当AMG ∠+EAB ∠=180°时,EC AM ⊥;②108°【分析】(1)根据角平分线的定义求出∠ACD ,然后根据平行线的性质可得∠EAB=∠ACD=110°,然后根据垂直的定义求出∠MAE=90°,即可求出结论;(2)①当AMG ∠+EAB ∠=180°时,根据平行线的性质可推出∠AMG +∠ACD=180°,然后根据角平分线的定义可得出∠ACM +∠AMC=90°,利用三角形的内角和即可求出∠MAC=90°,从而得出EC AM ⊥;②设∠ACD=x ,根据角平分线的定义可得∠GCM=12ACD ∠=12x ,∠GMC=12∠AMG =18°,根据平行线的性质可得∠EAB=∠ACD=x ,从而得出∠MGD=180°-x ,然后根据三角形外角的性质列出方程即可求出结论.【详解】解:(1)∵CM 是ACD ∠的平分线,55∠=︒MCD∴∠ACD=2∠MCD=110°∵AB ∥CD ,∴∠EAB=∠ACD=110°∵MA ⊥AC∴∠MAE=90°∴∠MAN=∠EAB -∠MAE=20°(2)①当AMG ∠+EAB ∠=180°时,EC AM ⊥ ∵AB ∥CD ,∴∠EAB=∠ACD∴∠AMG +∠ACD=180°∵CM 是ACD ∠的平分线,MC 平分AMG ∠∴∠ACM=12ACD ∠,∠AMC=12∠AMG ∴∠ACM +∠AMC=12ACD ∠+12∠AMG =()12∠∠+ACD AMG =90° ∴∠MAC=180°-(∠ACM +∠AMC )=90° ∴EC AM ⊥;②设∠ACD=x∵CM 是ACD ∠的平分线,MC 平分AMG ∠,36∠=︒AMG∴∠GCM=12ACD ∠=12x ,∠GMC=12∠AMG =18° ∵AB ∥CD ,∴∠EAB=∠ACD=x∵180MGD EAB ∠+∠=∴∠MGD=180°-x∵∠MGD=∠GCM +∠GMC即180-x=12x +18 解得:x=108即∠ACD=108°【点睛】此题考查的是平行线的性质、垂直的定义、三角形内角和定理和三角形外角的性质,掌握平行线的性质、垂直的定义、三角形内角和定理和三角形外角的性质是解决此题的关键.22.已知AB//CD,点E是平行线之间一点.(测量发现)连结EA,EC,分别做∠EAB与ECD的角平分线交于点F,通过测量我们发现∠AEC=2∠AFC.(探索新知)如图,若∠EAF=14∠EAB,∠ECF=14∠ECD,试探索∠AFC与∠AEC之间的关系,请说明理由.(合理猜想)若∠EAF=1n∠EAB,∠ECF=1n∠ECD,请猜想∠AFC与∠AEC之间的关系,不必说明理由.【答案】∠AFC=34∠AEC,理由见解析;∠AFC=1nn∠AEC【分析】探索新知:过点F作FH//AB,先证∠BAE+∠DCE=∠AEC,再根据∠EAF=14∠EAB,∠ECF=14∠ECD即可证明;合理猜想:过点F作FH//AB,先证∠BAE+∠DCE=∠AEC,再根据∠EAF=1n∠EAB,∠ECF=1n∠ECD,即可证明.【详解】探索新知:过点F作FH//AB,∵AB//CD,∴FH//CD,∴∠AFH=∠FAB,∠CFH=∠FCD,∴∠BAC+∠DCA=180°,∵∠EAC+∠ECA+∠AEC=180°,∴∠BAE+∠DCE=∠AEC,∵∠EAF=14∠EAB,∠ECF=14∠ECD,∴∠FAB+∠FCD=34∠AEC,∴∠AFC=34∠AEC;合理猜想:过点F作FH//AB,∵AB//CD,∴FH//CD,∴∠AFH=∠FAB,∠CFH=∠FCD,∴∠BAC+∠DCA=180°,∵∠EAC+∠ECA+∠AEC=180°,∴∠BAE+∠DCE=∠AEC,∵∠EAF=1n∠EAB,∠ECF=1n∠ECD,∴∠FAB+∠FCD=1nn-∠AEC,∴∠AFC=1nn-∠AEC.【点睛】本题是对平行线性质的考查,熟练掌握平行线的性质定理是解决本题的关键.23.AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E.∠ADC=70°.(1)求∠EDC 的度数;(2)若∠ABC=30°,求∠BED 的度数;(3)将线段BC沿DC方向移动,使得点B在点A的右侧,其他条件不变,若∠ABC =n°,请直接写出∠BED 的度数(用含n的代数式表示).【答案】(1)35︒(2)50︒(3)12152n ︒-︒ 【分析】(1)根据角平分线定义即可得到答案;(2)过点E 作//EF AB ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解;(3)过点E 作//EF AB ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解.【详解】解:(1)∵DE 平分ADC ∠,70ADC ∠=︒ ∴1352EDC ADC ∠=∠=︒; (2)过点E 作//EF AB ,如图:∵DE 平分ADC ∠,70ADC ∠=︒;BE 平分ABC ∠,30ABC ∠=︒ ∴1352EDC ADC ∠=∠=︒,1152ABE ABC ∠=∠=︒ ∵//AB CD ,//EF AB∴////AB EF CD∴35FED CDE ∠=∠=︒,15FEB ABE ∠=∠=︒∴50BED FED FEB ∠=∠+∠=︒;(3)过点E 作//EF AB ,如图:∵DE 平分ADC ∠,70ADC ∠=︒;BE 平分ABC ∠,ABC n ∠=︒ ∴1352EDC ADC ∠=∠=︒,1122ABE ABC n ∠=∠=︒ ∵//AB CD ,//EF AB∴////AB EF CD∴35FED CDE ∠=∠=︒,11801802FEB ABE n ∠=︒-∠=︒-︒ ∴113518021522BED FED FEB n n ∠=∠+∠=︒+︒-︒=︒-︒. 故答案是:(1)35︒(2)50︒(3)12152n ︒-︒ 【点睛】本题考查了角平分线的定义、平行线的判定和性质以及角的和差,解答本题的关键是作出辅助线,要求同学们掌握平行线的性质,难度中等.24.如图①,BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠,设BAD ∠=α,BCD β∠=.(1)若110αβ+=︒,则MBC NDC ∠+∠= ︒;(2)若BE 与DF 相交于点G ,且25BGD ∠=︒,求α、β所满足的等量关系式,并说明理由;(3)如图②,若αβ=,试判断BE 、DF 的位置关系,并说明理由.【答案】(1)110;(2)50βα-=︒,理由见解析;(3)BE DF ∥,理由见解析【分析】(1)根据四边形的内角和与邻补角的性质即可求解;(2)连接BD ,先得到1()2CBG CDG αβ∠+∠=+,再根据三角形的内角和得到角度的关系即可求解;(3)由(1)有,∠MBC +∠NDC =αβ+,BE 、DF 分别平分四边形的外角∠MBC 和∠NDC ,则∠CBE +∠CDH =12(αβ+),∠CBE +β−∠DHB =12(αβ+),根据α=β,则有∠CBE +β−∠DHB =12(β+β)=β,得到∠CBE =∠DHB ,故可得到BE ∥DF .【详解】解:(1)∵∠ABC +∠ADC =360°−(αβ+)=250°,∴∠MBC +∠NDC =180°−∠ABC +180°−∠ADC =360°-(∠ABC +∠ADC )=αβ+=110°.故答案为:110;(2)50βα-=︒.理由如下:如解图①,连接BD ,由(1)知,MBC NDC αβ∠+∠=+, BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠, ∴12CBG MBC ∠=∠,12CDG NDC ∠= ()1111()2222CBG CDG MBC NDC MBC NDC αβ∴∠+∠=∠+=∠+=+. 在△BCD 中,∠BDC +∠CBD =180°−∠BCD =180°−β, 在△BDG 中,∠GBD +∠GDB +∠BGD =180°,∴∠CBG +∠CBD +∠CDG +∠BDC +∠BGD =180°,∴(∠CBG +∠CDG )+(∠BDC +∠CBD )+∠BGD =180°, ∴12(αβ+)+180°−β+25°=180°, 整理得50βα-=︒;(3)BE DF ∥.理由如下,如解图②所示,延长BC 交DF 于点H ,由(1)、(2)可知,MBC NDC αβ∠+∠=+,1()2CBE CDH αβ∠+∠=+.BCD CDH DHC ∠=∠+∠,CDH BCD DHC DHC β∴∠=∠-∠=-∠,1()2CBE DHC βαβ∴∠+-∠=+. αβ=,1()2CBE DHB ββββ∴∠+-∠=+=, CBE DHB ∴∠=∠,BE DF ∴∥.【点睛】此题考查了平行线的性质及其判定,多边形的内角和公式,利用多边形的内角和公式倒角为解题关键.25.已知AM ∥CN ,点B 为平面内一点,AB ⊥BC 于B(1)如图1,直接写出∠A 和∠C 之间的数量关系;(2)如图2,过点B 作BD ⊥AM 于点D ,求证:∠ABD=∠C ;(3)如图3,在(2)问的条件下,点E.F 在DM 上,连接BE.BF.CF ,BF 平分∠DBC ,BE 平分∠ABD ,若∠FCB+∠NCF=180°,∠ABF=2∠ABE ,求∠EBC 的度数.【答案】(1)90°;(2)详见解析;(3)105°【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.【详解】解:(1)如图1,AM与BC的交点记作点O,∵AM∥CN,∴∠C=∠AOB,∵AB⊥BC,∴∠A+∠AOB=90°,∴∠A+∠C=90°;(2)如图2,过点B作BG∥DM,∵BD⊥AM,∴DB⊥BG,即∠ABD+∠ABG=90°,又∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,BG∥AM,∴CN∥BG,∴∠C=∠CBG,∴∠ABD=∠C;(3)如图3,过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)可得∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,∴∠AFC=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,①由AB⊥BC,可得β+β+2α=90°,②由①②联立方程组,解得α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.。
2023中考数学常见几何模型《角平分线的基本模型(二)非全等类》含答案解析
专题08 角平分线的重要模型(二)非全等类角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
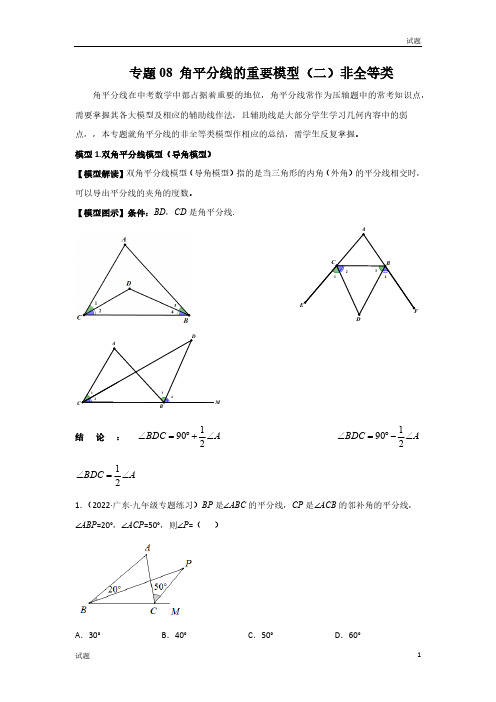
模型1.双角平分线模型(导角模型)【模型解读】双角平分线模型(导角模型)指的是当三角形的内角(外角)的平分线相交时,可以导出平分线的夹角的度数。
【模型图示】条件:BD ,CD 是角平分线.结论:1902BDC A ∠=︒+∠ 1902BDC A ∠=︒-∠ 12BDC A ∠=∠1.(2022·广东·九年级专题练习)BP 是∠ABC 的平分线,CP 是∠ACB 的邻补角的平分线,∠ABP =20°,∠ACP =50°,则∠P =( )A .30°B .40°C .50°D .60°2.(2022·山东·济南中考模拟)如图1,在△ABC中,∠BAC的平分线AD与∠BCA的平分线CE交于点O.(1)求证:∠AOC=90°+1∠ABC;2(2)当∠ABC=90°时,且AO=3OD(如图2),判断线段AE,CD,AC之间的数量关系,并加以证明.3.(2022•蓬溪县九年级月考)某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC= ;(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC 与∠A的数量关系,并说明理由.(4)如图4,△ABC外角∠CBM、∠BCN的平分线交于点Q,∠A=64°,∠CBQ,∠BCQ的平分线交于点P,则∠BPC= °,延长BC至点E,∠ECQ的平分线与BP的延长线相交于点R,则∠R= °.4.(2022·辽宁沈阳·九年级期中)阅读下面的材料,并解决问题(1)已知在△ABC中,∠A=60°,图1-3的△ABC的内角平分线或外角平分线交于点O,请直接写出下列角度的度数,如图1,∠O= ;如图2,∠O= ;如图3,∠O= ;(2)如图4,点O是△ABC的两条内角平分线的交点,求证:∠O=90°+1∠A(3)如图5,在△ABC2中,∠ABC的三等分线分别与∠ACB的平分线交于点O1O2,若∠1=115°,∠2=135°,求∠A 的度数.模型2.角平分线加平行线等腰现(角平分线+平行线)【模型解读】1)过角平分线上一点作角的一边的平行线,构造等腰三角形;2)有角平分线时,过角一边上的点作角平分线的平行线,交角的另一边的直线于一点,也可构造等腰三角形。
专题16 角平分线四大模型(解析版)

中考常考几何模型专题16 角平分线四大模型1、角平分线上的点向两边作垂线如图,P 是∠MON 的平分线上一点,过点 P 作 PA⊥OM 于点 A,PB⊥ON 于点 B。
结论:PB=PA。
2、截取构造对称全等如图,P 是∠MON 的平分线上一点,点 A 是射线 OM 上任意一点,在 ON上截取 OB=OA,连接 PB。
结论:△OPB≌△OPA。
3、角平分线+垂线构造等腰三角形如图,P 是∠MO 的平分线上一点,AP⊥OP 于 P 点,延长 AP 于点 B。
结论:△AOB 是等腰三角形。
4、角平分线+平行线如图,P 是∠MO 的平分线上一点,过点 P 作 PQ∥ON,交 OM 于点 Q。
结论:△POQ 是等腰三角形。
模型精练:1.(2019•东平县二模)如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=()A.40°B.45°C.50°D.60°2.(2019•桂平市期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=12cm,BD=8cm,那么点D到直线AB的距离是()A.2cm B.4cm C.6cm D.10cm3.(2020•浙江自主招生)如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是()A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定4.(2019•兰山区一模)如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB 于M,交AC于N,若BM+CN=11,则线段MN的长为.5.如图,已知等腰直角三角形ABC中,AB=AC,∠BAC=90°,BF平分∠ABC,CD⊥BD交BF的延长线于点D,试说明:BF=2CD.6.如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E (1)若∠C=30°,求证:AB=2BE.(2)若∠C≠30°,求证:BE=12(AC﹣AB).7.(2019•沂源县期末)如图,在△ABC中,AB=AC,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD,求证:∠ECA=40°.8.(2019•临洮县期末)已知△ABC中,AB=AC,∠A=108°,BD平分∠ABC,求证:BC=AC+CD.9.(2019•自贡期中)如图,在四边形ABCD中,BC>BA,AD=DC,(1)若BD⊥CD,∠C=60°,BC=10,求AD的长;(2)若BD平分∠ABC,求证:∠A+∠C=180°.10.(2019•宜昌期中)(1)已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的外角平分线,交CB边的延长线于点D.求证:BD=AB+AC;(2)对于任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图2,请你写出线段AC、AB、BD之间的数量关系并加以证明.11.(2019•潮南区期中)在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.(1)求证:∠2=∠1+∠C;(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.12.(2019•蔡甸区校级月考)如图,在△ABC,AD平分∠BAC,E、F分别在BD、AD上,且DE=CD,EF=AC,求证:EF∥AB.13.(2019•崇安区校级月考)如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB﹣BC的理由.14.(2019•江夏区校级月考)如图1,AB∥CD,P为AB、CD之间一点(1)若AP平分∠CAB,CP平分∠ACD.求证:AP⊥CP;(2)如图(2),若∠BAP=25∠BAC,∠DCP=25∠ACD,且AE平分∠BAP,CF平分∠DCP,猜想∠E+∠F的结果并且证明你的结论;(3)在(1)的条件下,当∠BAQ=13∠BAP,∠DCQ=13∠DCP,H为AB上一动点,连HQ并延长至K,使∠QKA=∠QAK,再过点Q作∠CQH的平分线交直线AK于M,问当点H在射线AB上移动时,∠QMK的大小是否变化?若不变,求其值;若变化,求其取值范围.15.(2019•东湖区校级月考)(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有个等腰三角形;EF与BE、CF之间的数量关系是,△AEF的周长是(2)如图2,若将(1)中“△ABC中,AB=AC=10”改为“若△ABC为不等边三角形,AB=8,AC =10”其余条件不变,则图中共有个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.中考常考几何模型专题16 角平分线四大模型1、角平分线上的点向两边作垂线如图,P 是∠MON 的平分线上一点,过点 P 作 PA⊥OM 于点 A,PB⊥ON 于点 B。
中考数学复习《角、相交线与平行线》经典题型及测试题(含答案)

中考数学复习《角、相交线与平行线》经典题型及测试题(含答案)命题点分类集训命题点1 线段【命题规律】主要考查:①两点之间线段最短;②两点确定一条直线这两个基本事实.【命题预测】与图形的变换中立体图形的侧面展开结合,求两点之间的最短距离,另外也会与对称性结合,考查两线段和的最小值.1. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )A. 垂线段最短B. 经过一点有无数条直线C. 经过两点,有且仅有一条直线D. 两点之间,线段最短1. D第1题图第2题图2. 如图,AB⊥AC,AD⊥BC,垂足分别为A,D.则图中能表示点到直线距离的线段共有( )A. 2条B. 3条C. 4条D. 5条2. D【解析】AD是点A到直线BC的距离;BA是点B到直线AC的距离;BD是点B到直线AD的距离;CA是点C到直线AB的距离;CD是点C到直线AD的距离,共5条,故答案为D.命题点2 角、余角、补角及角平分线【命题规律】主要考查:①角度的计算(度分秒之间的互化);②余角、补角的计算;③角平分线的性质.【命题预测】角、余角、补角及角平分线等基本概念是图形认识的基础,应给予重视.3. 下列各图中,∠1与∠2互为余角的是( )3. B4. 如图,OP为∠AOB的平分线,PC⊥OB于点C,且PC=3,点P到OA的距离为________.4. 3【解析】如解图,过点P作PD⊥OA于点D,∵OP为∠AOB的平分线,PC⊥OB于点C,∴PD=PC,∵PC=3,∴PD=3,即点P到点OA的距离为3.5. 1.45°=________′.5. 87【解析】∵1°=60′,∴0.45°=27′,∴1.45°=87′.6. 已知∠A=100°,那么∠A的补角为________度.6. 80【解析】用180度减去已知角,就得这个角的补角.即∠A的补角为:180°-100°=80°.命题点3 相交线与平行线【命题规律】考查形式:①三线八角中同位角、内错角、同旁内角的识别或计算,有时综合对顶角、邻补角求角度;②综合角平分线、垂线求角度;③综合三角形的相关知识求角度;④根据角的关系判断两直线的关系.【命题预测】平行线性质是认识图形的基础知识,也是全国命题的潮流和方向.7. 如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )A. 同位角B. 内错角C. 同旁内角D. 对顶角7. B【解析】根据相交线的性质及角的定义可知∠1与∠2的位置关系为内错角,故选B.第7题图第8题图第9题图8. 如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=110°,则∠2等于( )A. 50°B. 70°C. 90°D. 110°8. B【解析】如解图,∵a∥b,∴∠3+∠4=180°,∵c∥d,∴∠2=∠4,∵∠1=∠3,∴∠2=180°-∠1=70°,故本题选B.9. 如图,在下列条件中,不能..判定直线a与b平行的是( )A. ∠1=∠2B. ∠2=∠3C. ∠3=∠5D. ∠3+∠4=180°9. C【解析】逐项分析如下:选项逐项分析正误A∵∠1=∠2,即同位角相等,两直线平行,∴a∥b √B∵∠2=∠3,即内错角相等,两直线平行,∴a∥b √∵∠3、∠5既不是a与b被第三直线所截的同位角,也不是内错角,×C∴∠3=∠5,不能够判定a与b平行D∵∠3+∠4=180°,即同旁内角互补,两直线平行,∴a∥b √10. 如图,将一块直角三角板的直角顶点放在直尺的一边上,如果∠1=50°,那么∠2的度数是( )A. 30°B. 40°C. 50°D. 60°10. B 【解析】如解图,∠1+∠3=90°,∴∠3=90°-∠1=90°-50°=40°,由平行线性质得∠2=∠3=40°.11. 如图所示,AB ∥CD ,EF ⊥BD ,垂足为E ,∠1=50°,则∠2的度数为( )A . 50°B . 40°C . 45°D . 25°11. B 【解析】∵EF ⊥BD ,∠1=50°,∴∠D =90°-50°=40°,∵AB ∥CD ,∴∠2=∠D =40°.第10题图 第11题图 第12题图 第13题图12. 如图,AB ∥CD ,直线EF 与AB ,CD 分别交于点M ,N ,过点N 的直线GH 与AB 交于点P ,则下列结论错误的是( )A . ∠EMB =∠END B . ∠BMN =∠MNC C . ∠CNH =∠BPGD . ∠DNG =∠AME12. D 【解析】A.两直线平行,同位角相等,∴∠EMB =∠END ;B.两直线平行,内错角相等,∴∠BMN =∠MNC ;C.两直线平行,同位角相等,∴∠CNH =∠APH ,又∠BPG =∠APH ,∴∠CNH =∠BPG ;D.∠DNG 和∠AME 无法推导数量关系,故不一定相等,答案为D.13. 如图,直线a∥b,∠1=45°,∠2=30°,则∠P=________°.13. 75 【解析】如解图,过点P 作PH ∥a ∥b ,∴∠FPH =∠1,∠EPH =∠2,又∵∠1=45°,∠2=30°,∴∠EPF =∠EPH +∠HPF =30°+45°=75°.命题点4 命 题【命题概况】命题考查的知识点比较多,一般几个知识点结合考查,考查形式有:①下面说法错误(正确)的是;②写出命题…的逆命题;③能说明…是假命题的反例.【命题趋势】命题为新课标新增内容,考查知识比较综合,是全国命题点之一.14. (2016宁波)能说明命题“对于任何实数a ,|a|>-a”是假命题的一个反例可以是( )A . a =-2B . a =13C . a =1D . a = 214. A 【解析】由于一个正数的绝对值是它本身,它的相反数是一个负数,所以当a =13,1,2时,|a |>-a 总是成立,当a =-2时,|-2|=2=-(-2),此时|a |=-a ,故本题选A.15. 写出命题“如果a =b ,那么3a =3b”的逆命题...:________________________. 15. 如果3a =3b ,那么a =b 【解析】命题由条件和结论构成,则其逆命题只需将原来命题的条件和结论互换即可,即将结论作为条件,将条件作为结论. ∵命题“如果a =b ,那么3a =3b ,”中条件为“如果a =b ”,结论为“那么3a =3b ”,∴其逆命题为“如果3a =3b ,那么a =b ”.中考冲刺集训一、选择题1. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )A. 65°B. 55°C. 45°D. 35°第1题图第2题图第3题图2. 如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠AED=( )A. 65°B. 115°C. 125°D. 130°3. 如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )A.75°36′B.75°12′C.74°36′D.74°12′二、填空题4. 如图,平行线AB,CD被直线AE所截,∠1=50°,则∠A=________.第4题图第5题图第6题图5. 如图,直线CD∥EF,直线AB与CD、EF分别相交于点M、N,若∠1=30°,则∠2=________.6. 如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放.若∠EMB=75°,则∠PNM等于________度.7. 如图,直线AB∥CD,BC平分∠ABD.若∠1=54°,则∠2=________°.第7题图第8题图第9题图8. 如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=________.9.如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD=________.答案与解析:1. B【解析】∵DA⊥AC,∠ADC=35°,∴∠ACD=90°-∠ADC=90°-35°=55°,∵AB∥CD,∴∠1=∠ACD=55°,故选B.2. B【解析】∵AB∥CD,∴∠C+∠CAB=180°,∵∠C=50°,∴∠CAB=130°,∵AE平分∠CAB,∴∠EAB=12∠CAB=65°.又∵AB∥CD,∴∠AED+∠EAB=180°,∴∠AED=180°-∠EAB=180°-65°=115°.3. B【解析】根据平面镜反射原理可知,∠ADC=∠ODE,∵DC∥OB,∴∠ADC=∠AOE,∴∠ODE=∠AOE=37°36′,∴∠DEB=∠ODE+∠AOE=37°36′+37°36′=75°12′,故选B.4. 50°5. 30°6. 307. 72【解析】∵CD∥AB,∴∠CBA=∠1=54°,∠ABD+∠CDB=180°,∵CB平分∠ABD,∴∠DBC=∠CBA=54°,∴∠CDB=180°-54°-54°=72°,∴∠2=∠CDB=72°.8. 15°【解析】由两直线平行,内错角相等,可得∠A=∠AFE=30°,∠C=∠CFE,由∠AFC=15°,可得∠CFE=∠C=∠AFE-∠AFC=15°.第9题解图9. 2【解析】如解图,过点P作PE⊥OB于点E,∵OP平分∠AOB,∴PD=PE,∠AOB=2∠AOP=30°,∵PC∥OA,∴∠ECP=∠AOB=30°,∴PE=12PC=2,∴PD=PE=2.。
【数学中考一轮复习】角平分线常考模型(含答案)

专项训练角平分线常考模型模型一角平分线+垂直一边方法点拨:若PA⊥OM于点A,如图所示,可以过P点作PB⊥ON于点B,则PB=PA.可记为“图中有角平分线,可向两边作垂线,垂线段相等”,显然这个基本图形中可以利用角平分线的性质定理,也可以得到一组全等三角形;注意:题目一般只有一条垂线,需要自行补出另一条垂线,甚至只给一条角平分线,自行添加两条垂线.1.如图所示,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是()A.3B.4C.5D.62.如图所示,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,若AC=3,BC=4,则S△ABD :S△ACD为()A.5:4B.5:3C.4:3D.3:43.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB,∠AFD=90°,AB=10,DF=2,则S△ABD=_________.模型二角平分线+斜线方法点拨:若点A是射线OM上任意一点,如图,可以在ON上截取OB=OA,连接PB,构变式模型:采用截长补短法构造全等三角形如图所示,在△ABC中,BC>BA,BO是∠ABC的平分线.(截长法)在BC上截取线段BE=BA,连接OE,则△BEO≌△BAO;(补短法)延长BA至点D,使BD=BC,连接OD,则△BDO≌△BCO.解题通法:遇到角平分线时,通常过角平分线上的一点向两边作垂线或在角平分线的两端取相等的线段(截长或补短)构造全等三角形.4.如图所示,在△ABC中,∠ACB=2∠B,∠1=∠2,求证:AB=AC+CD.5.如图所示,在四边形ABCD中,BC>BA,AD=CD,∠ABD=∠DBC.(1)点D到∠ABC的两边BA,BC的距离是否相等?(2)求∠A+∠C的度数.模型三角平分线+垂线方法点拨:若AP⊥OP于点P如图所示,可延长AP交ON于点B构造△AOB是等腰三角形,P是底边AB的中点,可记为“角平分线加垂线,三线合一试试看”,实际上这是“两线合一”的一种情形,这个图形中隐含着全等和等腰三角形.6.如图所示,在△ABC中,∠ABC=60°、D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF=3,则线段BE的长为()A.3B.2C.3D.237.如图所示,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则CD的长是___________.8.如图所示,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.(1)若AD=1,求DC;(2)求证:BD=2CE.模型四角平分线+平行线方法点拨:若过点P作PQ∥ON交OM于点Q,如图所示,可以构造△POQ是等腰三角形,可记为“角平分线+平行线,等腰三角形必呈现”,这个基本图形很常见,其变式有以下四种:解题通法:遇到角平分线及平行线,除了可以得到角度的关系,还可以得到等腰三角形.9.如图所示,在△ABC中,BD平分∠ABC,DE∥BC,交AB于点E,若AB=7cm,AE=4cm.则DE的长为_________cm.10.如图所示,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若BE=6,DC=8,DE=20,则FG=___________.11.如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB,AC于点D,E.(1)△BDO是等腰三角形吗?请说明理由.(2)若AB=10,AC=6,求△ADE的周长.模型五角平分线+对角互补方法点拨:若∠A+∠C=180°,BD是∠ABC的平分线,则AD=CD.12.已知:如图所示,AD平分∠BAC,∠B+∠C=180°,∠B<90°,求证:DB=DC.13.感知:如图1所示,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图2所示,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.14.如图所示,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:(1)△CBE≌△CDF;(2)AB+DF=AF.模型六 夹角模型方法点拨:BP ,CP 分别是∠ABC ,∠ACB 的角平分线,则:∠P =90°+21∠A. BP ,CP 分别是∠ABC ,∠ACE 的角平分线,则:∠P =21∠A. BP ,CP 分别是∠CBD ,∠BCE 的角平分线,则:∠P =90°-21∠A.15.如图所示,点O 在△ABC 内,且到三边的距离相等.若∠A =40°,则∠BOC 等于( )A.110°B.115°C.125°D.130°16.如图所示,BE ⊥AC 于点D ,且AB =CB ,BD =ED ,若∠ABC =54°,则∠E =_________.17.如图所示,点O 是△ABC 边AC 上的一个动点,过O 点作直线MN ∥BC.设MN 交∠ACB 的平分线于点E ,交∠ACB 的外角平分线于点F. (1)求证:OE =OF ;(2)若CE =8,CF =6,求OC 的长.跟踪训练1.如图所示,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,若CD=4,AB=14,则=()S△ABDA.56B.28C.14D.122.如图所示,在△ABC中,∠B=45°,∠C=75°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为E,若DE=2,则AB的长为()A.6B.2+4C.2+23D.2+233.如图所示,已知△ABC的周长是10,点O为∠ABC与∠ACB的平分线的交点,且OD⊥BC于D.若OD=2,则△ABC的面积是()A.20B.12C.10D.84.如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D.若BD=5,DC=3,则AC的长为A.6B.43C.53-2D.85.已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=__________.6.如图所示,四边形ABCD中,∠A=∠B=90°,AB边上有一点E,CE,DE分别是∠BCD 和∠ADC的角平分线,如果△CDE的面积是12,CD=8,那么AB的长度为__________.7.如图所示,在△ABC中,BI,CI分别平分∠ABC,∠ACF,DE过点I,且DE∥BC.BD=8cm,CE=5cm,则DE等于__________.8.如图所示,点E是∠AOB平分线上的一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD交OE于点F,∠AOB=60°.(1)求证:△OCD是等边三角形;(2)若S=83,EF=2,求DF的长.△ODE9.如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E. (1)求证:∠AEC=∠ACE;(2)若∠AEC=2∠B,AD=1,求BD的长.10.(1)如图①所示,△ABC中,∠ABC,∠ACB的平分线交于O点,过O点作EF∥BC交AB,AC于点E,F,试猜想EF,BE,CF之间有怎样的关系,并说明理由;(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其他条件不变,请直接写出EF,BE,CF之间的关系____________.11.如图所示,在平行四边形ABCD中,CM平分∠BCD交AD于点M.(1)若CD=2,求DM的长;(2)若M是AD的中点,连接BM,求证:BM平分∠ABC.参考答案1.D2.B3.104.证明:延长AC 至点E ,使AE =AB ,连接 DE ,∵AB =AE ,∠1=∠2,AD =AD ,∴△ABD ≌△AED (SAS ).∴∠B =∠E ,∵∠ACD =∠E +∠CDE ,∠ACD =2∠B ,∴∠ACD =2∠E. ∴∠E =∠CDE.∴CD =CE.∴AB =AE =AC +CE =AC +CD. 5.解:(1)过D 作出DE ⊥BA 于E ,DF ⊥BC 于F.如图所示.结论:DE =DF.理由:∵∠ABD =∠DBC ,DE ⊥BA 于E ,DF ⊥BC 于F ,∴DE =DF.(2)在Rt △DEA 和Rt △DFC 中,⎩⎨⎧,DF =DE ,DC =AD ∴Rt △DEA ≌Rt △DFC (HL )∴∠C =∠EAD.∵∠BAD +∠EAD =180°,∴∠BAD +∠C =180°. 6.C 7.228.解:(1)如图1所示,过点D 作DH ⊥BC 于H ,∵AB =AC ,∠BAC =90°,∴∠BCA =45°.∴DH =CH.(2)证明:如图2所示,延长CE ,BA 相交于点F ,∵∠EBF +∠F =90°,∠ACF +∠=90°,∴∠EBF =∠AC.在△ABD 和△ACF 中⎪⎩⎪⎨⎧,CAF =∠BAC ∠AC =AB ,ACF =∠EBF ∠∴ABD ≌ACF (ASA )∴BD =CF.在△BCE 和△BF 中,⎪⎩⎪⎨⎧,FEB =∠CEB ∠,BE =BE ,CBF =∠EBF ∠∴△BCE ≌△BFE (ASA ).∴CE =EF.∴BD =2CE.9.3 10.611.解:(1)△BDO 是等腰三角形∵BO 平分∠ABC ,∴∠DBO =∠CBO∵DE ∥BC ,∴∠CBO =∠DOB.∴∠DBO =∠DOB.∴BD =DO.∴△BDO 是等腰三角形;(2)同理△CEO 是等腰三角形,∵BD =OD ,CE =OE ,∴△ADE 的周长=AD +AE +DE =AB +AC =10+6=16.12.证明:作DE ⊥AB 于E ,DF ⊥AC 于F ,∵AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,∴DE =DF.∵∠B +∠ACD =180°,∠ACD +∠FCD =180°,∴∠B =∠FCD.在△DFC 和△DEB 中,⎪⎩⎪⎨⎧,DE =DF ,B =∠FCD ∠,DEB =∠F ∠∴△DFC ≌△DEB (AAS ).∴DC =DB.13.证明:过点D 作DE ⊥AB 于点E ,DF ⊥AC 于点F.∵AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,∴DE =DF ,∠F =∠DEB =90°.∵∠EBD +∠ACD =180°,∠ACD +∠FCD =180°,∴∠EBD =∠FCD.在△DFC 和△DEB 中,⎪⎩⎪⎨⎧,DE =DF ,EBD =∠FCD ∠,DEB =∠F ∠∴△DFC ≌△DEB (AAS ).∴DC =DB.14.解:(1)∵AC 平分∠BAD ,CE ⊥AB ,CF ⊥AD ,∴CE =CF.∵∠ABC +∠D =180°,∠ABC +∠EBC =180°,∴∠EBC =∠D.在△CBE 与△CDF 中,⎪⎩⎪⎨⎧︒∠∠,CF =CE 90=CFD =CEB ∠,D =EBC ∠,∴△CBE ≌△CDF (AAS );(2)在Rt △ACE 与Rt △ACF 中,⎩⎨⎧,AC =AC CF =CE ∴△CE ≌△ACF (HL ).∴AE =AF.∴AB +DF =AB +BE =AE =AF.15.A 16.27°17.解:(1)证明:∵MN 交∠ACB 的平分线于点E ,交∠ACB 的外角平分线于点F ,∴∠2=∠5,∠4=∠6.∵MN ∥BC ,∴∠1=∠5,∠3=∠6.∴∠1=∠2,∠3=∠4.∴EO =CO ,FO =CO.∴OE =OF ;(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°.∵CE =8,CF =6,∴EF =2268+=10.∴OC =21EF =5. 跟踪训练1.B2.D3.C4.A5.46.67.3cm8.解:(1)证明:∵点E 是∠AOB 平分线上的一点, EC ⊥OB , ED ⊥OA ,∴ED =CE.在Rt △ODE 与Rt △OCE 中,⎩⎨⎧,OE =OE ,CE =ED ∴Rt △ODE ≌Rt △OCE (HL ).∴OD =OC. ∴∠AOB =60°,∴△OCD 是等边三角形;(2)∵△OCD 是等边三角形,OF 是∠COD 的平分线,∴OE ⊥DC ,∴∠AOB =60°,∴∠AOE =∠BOE =30°.∵∠ODF =60°,ED ⊥OA ,∴∠EDF =30°.∴DE =2EF =4.∵∠AOE =30°, DE ⊥AO ,∴OE =2DE =8.∵S △ODE =83=21×OE ×DF ,∴DF =23. 9.解:(1)证明:∵∠ACB =90°,CD ⊥AB ,∴∠ACD +∠A =∠B +∠A =90°. ∴∠ACD =∠B.∵CE 平分∠BCD ,∴∠BCE =∠DCE.∴∠B +∴BCE =∠ACD +∠DCE.即∠AEC =∠ACE ;(2)∵∠AEC =∠B +∠BCE ,∠AEC =2∠B ,∴∠B =∠BCE.又∵∠ACD =∠B ,∠BCE =∠DCE ,∴∠ACD =∠BCE =∠DCE.又∵∠ACB =90°,∴∠ACD =30°,∠B =30°.∴Rt △ACD 中,AC =2AD =2.∴Rt △ABC 中,AB =2AC =4.∴BD =AB-AD =4-1=3.10.解: (1)EF =BE +CF ,理由: ∵BO 平分∠ABC , CO 平分∠ACB ,∴∠EBO =∠OBC ,∠FCO =∠OCB.∵EF//BC ,∴∠EOB =∠OBC ,∠FOC =∠OCB.∴∠EBO =∠EOB ,∠FOC =∠FCO. ∴BE =OE ,CF =OF.∴EF =OE +OF =BE +CF ;(2)EF =BE-CF ,理由:∵BO 平分∠ABC , CO 平分∠ACD ,∴∠EBO =∠OBC ,∠FCO =∠OCD. ∵EF// BC ,∴∠EOB =∠OBC ,∠FOC =∠OCD.∴∠EBO =∠EOB ,∠FOC =∠FCO.∴BE =OE ,CF =OF.∴EF =OE-OF =BE-CF.故答案为:EF =BE-CF.11.解:(1)∵四边形ABCD 是平行四边形,∴AD// BC.∴∠BCM =∠DMC.∵CM 平分∠BCD ,∴∠BCM =∠DCM.∴∠DMC =∠DCM.∴DM =DC =2;(2)如图,延长BA , CM ,交于点E ,则∠AME =∠DMC ,∵BE// CD ,∴∠D =∠EAM ,∠E =∠DCM.∵M 是AD 的中点,∴DM =AM.∴△CDM ≌△EAM (ASA ).∴E М=CM.∵CM平分∠BCD,∴∠BCM=∠DCM.∴∠E=∠BCM.∴BE=BC. ∴BM平分∠ABC.。
2023年中考数学常见几何模型全归纳之模型 角平分线的基本模型(一)全等类(解析版)

专题07 角平分线的重要模型(一)全等类角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,本专题就角平分线的全等类模型作相应的总结,需学生反复掌握。
模型1.角平分线构造轴对称模型(角平分线+截线段等)【模型解读与图示】已知如图1,OP为AOB∠的角平分线、PM不具备特殊位置时,辅助线的作法大都为在OB上截取ON OM=,连结PN即可.即有OMP∆≌ONP∆,利用相关结论解决问题.图1 图21.(2022·湖北十堰·九年级期末)在△ABC中,△ACB=2△B,如图①,当△C=90°,AD为△BAC的角平分线时,在AB上截取AE=AC,连结DE,易证AB=AC+CD.(1)如图②,当△C≠90°,AD为△BAC的角平分线时,线段AB,AC,CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;(2)如图③,当AD为△ABC的外角平分线时,线段AB,AC,CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.【答案】(1)AB AC CD=+;证明见解析;(2)AB AC CD+=;证明见解析.【分析】(1)首先在AB上截取AE=AC,连接DE,易证△ADE△△ADC(SAS),则可得△AED=△C,ED=CD,又由△AED=△ACB,△ACB=2△B,所以△AED=2△B,即△B=△BDE,易证DE=CD,则可求得AB=AC+CD;(2)首先在BA的延长线上截取AE=AC,连接ED,易证△EAD△△CAD,可得ED=CD,△AED=△ACD,又由△ACBAB∥CD⇒AB+CD=BCFDEBAC=2△B ,易证DE =EB ,则可求得AC +AB =CD .【详解】(1)猜想:AB AC CD =+. 证明:如图②,在AB 上截取AE AC =,连结DE ,△AD 为ABC 的角平分线时,△BAD CAD ∠=∠,△AD AD =,△()SAS ADE ADC ≌△△, △AED C ∠=∠,ED CD =,△2ACB B ∠=∠,△2AED B ∠=∠.△B EDB ∠=∠,△EB ED =,△EB CD =,△AB AE DE AC CD =+=+.(2)猜想:AB AC CD +=.证明:在BA 的延长线上截取AE AC =,连结ED .△AD 平分FAC ∠,△EAD CAD ∠=∠.在EAD 与CAD 中,AE AC =,EAD CAD ∠=∠,AD AD =,△EAD CAD ≌△△. △ED CD =,AED ACD ∠=∠.△FED ACB ∠=∠.又2ACB B ∠=∠,FED B EDB ∠=∠+∠,EDB B ∠=∠.△EB ED =.△EA AB EB ED CD +===.△AC AB CD +=.【点睛】此题考查三角形综合题、全等三角形的判定与性质、等腰三角形的判定、角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.2.(2022·山东烟台·九年级期末)已知在ABC 中,满足2ACB B ∠=∠,(1)【问题解决】如图1,当90C ∠=︒,AD 为BAC ∠的角平分线时,在AB 上取一点E 使得AE AC =,连接DE ,求证:AB AC CD =+.(2)【问题拓展】如图2,当90C ∠≠︒,AD 为BAC ∠的角平分线时,在AB 上取一点E 使得AE AC =,连接DE ,(1)中的结论还成立吗?若成立,请你证明:若不成立,请说明理由.(3)【猜想证明】如图3,当AD 为ABC 的外角平分线时,在BA 的延长线上取一点E 使得AE AC =,连接DE ,线段AB 、AC 、CD 又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明. 【答案】(1)证明见解析(2)成立,证明见解析(3)猜想AB AC CD +=,证明见解析【分析】(1)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED ACD ∠=∠,再根据三角形的外角性质可得45B BDE ∠=∠=︒,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证;(2)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED C ∠=∠,再根据三角形的外角性质可得B BDE ∠=∠,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证;(3)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED ACD ∠=∠,从而可得FED ACB ∠=∠,再根据三角形的外角性质可得B BDE ∠=∠,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证.证明:△AD 为BAC ∠的角平分线,△EAD CAD ∠=∠,在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS ≅,△ED CD =,AED ACD ∠=∠,又△90ACB ∠=︒,2ACB B ∠=∠,△45B ∠=︒,90AED ∠=︒,△45AED BDE B ∠=∠=∠-︒,△B BDE ∠=∠,△EB ED =,△EB CD =,△AB AE EB AC CD =+=+.(2)解:(1)中的结论还成立,证明如下:△AD 为BAC ∠的角平分线时,△EAD CAD ∠=∠,在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS ≅,△AED C ∠=∠,ED CD =,△2ACB B ∠=∠,△2AED B ∠=∠,又△AED B EDB ∠=∠+∠,△B EDB ∠=∠,△EB ED =,△EB CD =,△AB AE EB AC CD =+=+.解:猜想AB AC CD+=,证明如下:△AD平分EAC∠,△EAD CAD∠=∠,在AED与ACD△中,AE ACEAD CAD AD AD=⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS≅,△ED CD=,AED ACD∠=∠,如图,△180180AED ACD︒-∠=︒-∠,即FED ACB∠=∠,△2ACB B∠=∠,△2FED B∠=∠,又△FED B EDB∠=∠+∠,△EDB B∠=∠,△EB ED=,△AB AE EB ED CD+===,△AB AC CD+=.【点睛】本题主要考查了三角形全等的判定与性质、等腰三角形的判定,熟练掌握三角形全等的判定方法是解题关键.3.(2022·浙江·九年级期中)(1)如图1,在△ABC中,△ACB=2△B,△C=90°,AD为△BAC的平分线交BC 于D,求证:AB=AC+CD.(提示:在AB上截取AE=AC,连接DE)(2)如图2,当△C≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,直接写出结果,不需要证明.(3)如图3,当△ACB≠90°,△ACB=2△B ,AD为△ABC的外角△CAF的平分线,交BC的延长线于点D,则线段AB、AC、CD又有怎样的数量关系?写出你的猜想,并加以证明.【答案】(1)见解析;(2)AB=AC+CD;(3)AB=CD﹣AC【分析】(1)在AB上截取AE=AC,连接DE,根据角平分线的定义得到△1=△2.推出△ACD△△AED(SAS).根据全等三角形的性质得到△AED=△C=90,CD=ED,根据已知条件得到△B=45°.求得△EDB=△B=45°.得到DE=BE,等量代换得到CD=BE.即可得到结论;(2)在AC取一点E使AB=AE,连接DE,易证△ABD△△AED,所以△B=△AED,BD=DE,又因为△B=2△C,所以△AED=2△C,因为△AED是△EDC的外角,所以△EDC=△C,所以ED=EC,BD=EC,进而可证明AB+BD=AE+EC=AC;(3)在AB的延长线AF上取一点E,使得AE=AC,连接DE.证明△ACD△△AED,根据全等三角形的性质得到DE=BE,BE=CD,即可得出结论.【详解】(1)证明:在AB上取一点E,使AE=AC△AD为△BAC的平分线△△BAD=△CAD.在△ACD和△AED中,AE AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩△△ACD △△AED (SAS ).△△AED =△C =90°,CD =ED ,又△△ACB =2△B ,△C =90°,△△B =45°. △△EDB =△B =45°.△DE =BE , △CD =BE .△AB =AE +BE , △AB =AC +CD .(2)证明:在AB 取一点E 使AC=AE ,在△ACD 和△AED 中,AC AE BAD EAD AD AD ===⎧⎪∠∠⎨⎪⎩, △△ACD△△AED ,△△C=△AED ,CD=DE ,又△△C=2△B ,△△AED=2△B ,△△AED 是△EDC 的外角,△△EDB=△B ,△ED=EB ,△CD=EB ,△AB=AC+CD ;(3)猜想:AB =CD ﹣AC证明:在BA 的延长线上取一点E ,使得AE =AC ,连接DE ,在△ACD和△AED中,AC AECAD EADAD AD=⎧⎪∠=∠⎨⎪=⎩,△△ACD△△AED(SAS),△△ACD=△AED,CD=DE,△△ACB=△FED,又△△ACB=2△B△△FED=2△B,又△△FED=△B+△EDB,△△EDB=△B,△DE=BE,△BE=CD,△AB=BE-AE△AB=CD﹣AC.【点睛】本题考查全等三角形的判定和性质,关于线段和差关系的证明,通常采用截长补短法. 4.(2022·北京九年级专题练习)在四边形ABDE中,C是BD边的中点.(1)如图(1),若AC平分BAE∠,90ACE∠=︒,则线段AE、AB、DE的长度满足的数量关系为______;(直接写出答案)(2)如图(2),AC平分BAE∠,EC平分AED∠,若120ACE∠=︒,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明.【答案】(1)AE=AB+DE;(2)AE=AB+DE+12BD,证明见解析.【分析】(1)在AE上取一点F,使AF=AB,由三角形全等的判定可证得△ACB≌△ACF,根据全等三角形的性质可得BC=FC,∠ACB=∠ACF,根据三角形全等的判定证得△CEF≌△CED,得到EF=ED,再由线段的和差可以得出结论;(2)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG,根据全等三角形的判定证得△ACB≌△ACF和△ECD≌△ECG,由全等三角形的性质证得CF=CG,进而证得△CFG是等边三角形,就有FG=CG=12BD,从而可证得结论.【详解】解:(1)如图(1),在AE上取一点F,使AF=AB.∵AC平分∠BAE,∴∠BAC=∠FAC.在△ACB和△ACF中,AB AFBAC FACAC AC⎧⎪∠∠⎨⎪⎩===∴△ACB≌△ACF(SAS).∴BC=FC,∠ACB=∠ACF.∵C是BD边的中点,∴BC=CD.∴CF=CD.∵∠ACE=90°,∴∠ACB+∠DCE=90°,∠ACF+∠ECF=90°.∴∠ECF=∠ECD.在△CEF和△CED中,CF CDECF ECDCE CE⎧⎪∠∠⎨⎪⎩===∴△CEF≌△CED(SAS).∴EF=ED.∵AE=AF+EF,∴AE=AB+DE.故答案为:AE=AB+DE;(2)AE=AB+DE+12BD.证明:如图(2),在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.∵C 是BD 边的中点,∴CB =CD =12BD .∵AC 平分∠BAE ,∴∠BAC =∠FAC . 在△ACB 和△ACF 中,AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩===∴△ACB ≌△ACF (SAS ).∴CF =CB ,∠BCA =∠FCA .同理可证:△ECD ≌△ECG ∴CD =CG ,∠DCE =∠GCE .∵CB =CD ,∴CG =CF .∵∠ACE =120°,∴∠BCA +∠DCE =180°−120°=60°.∴∠FCA +∠GCE =60°.∴∠FCG =60°.∴△FGC 是等边三角形.∴FG =FC =12BD .∵AE =AF +EG +FG ,∴AE =AB +DE +12BD .【点睛】本题主要考查了全等三角形的判定与性质的运用,能熟练应用三角形全等的判定和性质是解决问题的关键.模型2.角平分线垂两边(角平分线+外垂直)【模型解读与图示】已知如图1,OP 为OAB ∠的角平分线、PM OA ⊥于点M 时,辅助线的作法大都为过点P 作PN OB ⊥即可.即有PM PN =、OMP ∆≌ONP ∆等,利用相关结论解决问题.图1 图2 图3邻等对补模型:已知如图2,AP 是∠CAB 的角平分线,EP =DP辅助线:过点P 作PG ⊥AC 、PF ⊥AB结论:①︒=∠+∠180EPD BAC (D P E A 、、、四点共圆);②EG DF =;③DF AE AD 2+= 1.(2022·北京·中考真题)如图,在ABC ∆中,AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____. D B【答案】1【分析】作DF AC ⊥于点F ,由角平分线的性质推出1DF DE ==,再利用三角形面积公式求解即可.【详解】解:如图,作DF AC ⊥于点F ,△AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,△1DF DE ==, △1121122ACD S AC DF ∆=⋅=⨯⨯=.故答案为:1. 【点睛】本题考查角平分线的性质,通过作辅助线求出三角形ACD 中AC 边的高是解题的关键. 2.(2022·山东泰安·中考真题)如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =( )A .40°B .45°C .50°D .60°【答案】C 【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠FAP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC =∠ACD ﹣∠ABC =2x °﹣(x °﹣40°)﹣(x °﹣40°)=80°,∴∠CAF =100°,在Rt △PFA 和Rt △PMA 中,{PA PAPM PF ==,∴Rt △PFA ≌Rt △PMA (HL ),∴∠FAP =∠PAC =50°.故选C .【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM =PN =PF 是解题的关键.3.(2022·江苏扬州·中考真题)如图,在ABCD 中,BE 、DG 分别平分ABC ADC ∠∠、,交AC 于点E G 、.(1)求证:,BE DG BE DG =∥;(2)过点E 作EF AB ⊥,垂足为F .若ABCD 的周长为56,6EF =,求ABC ∆的面积. 【答案】(1)见详解(2)84【分析】(1)由平行四边形的性质证()ABE CDG ASA ∆≅∆即可求证;(2)作EQ BC ⊥,由ΔΔΔABC ABE EBC S S S =+即可求解;(1)证明:在ABCD 中,△//AB CD ,△BAE DCG ∠=∠,△BE 、DG 分别平分ABC ADC ∠∠、,ABC ADC ∠=∠,△ABE CDG ∠=∠,在ABE ∆和CDG ∆中,△ABCD的周长为AB BC+=BE平分∠EQ EF=ABCS S∆∆=4.(2022·河北·九年级专题练习)已知OP平分△AOB,△DCE的顶点C在射线OP上,射线CD交射线OA 于点F,射线CE交射线OB于点G.(1)如图1,若CD△OA,CE△OB,请直接写出线段CF与CG的数量关系;(2)如图2,若△AOB=120°,△DCE=△AOC,试判断线段CF与CG的数量关系,并说明理由.【答案】(1)CF =CG ;(2)CF =CG ,见解析【分析】(1)结论CF =CG ,由角平分线性质定理即可判断.(2)结论:CF =CG ,作CM △OA 于M ,CN △OB 于N ,证明△CMF △△CNG ,利用全等三角形的性质即可解决问题.【详解】解:(1)结论:CF =CG ;证明:△OP 平分△AOB ,CF △OA ,CG △OB ,△CF =CG (角平分线上的点到角两边的距离相等);(2)CF =CG .理由如下:如图,过点C 作CM △OA ,CN △OB ,△OP 平分△AOB ,CM △OA ,CN △OB ,△AOB =120°,△CM =CN (角平分线上的点到角两边的距离相等),△△AOC =△BOC =60°(角平分线的性质),△△DCE =△AOC ,△△AOC =△BOC =△DCE =60°,△△MCO =90°-60° =30°,△NCO =90°-60° =30°,△△MCN =30°+30°=60°,△△MCN =△DCE ,△△MCF =△MCN -△DCN ,△NCG =△DCE -△DCN ,△△MCF =△NCG ,在△MCF 和△NCG 中,CMF CNG CM CNMCF NCG ∠=∠⎧⎪=⎨⎪∠=∠⎩△△MCF △△NCG (ASA ),△CF =CG (全等三角形对应边相等).【点睛】本题考查三角形综合题、角平分线的性质、全等三角形的判定和性质,解题的关键是掌握角平分线的性质的应用,熟练证明三角形全等.模型3.角平分线垂中间(角平分线+内垂直)【模型解读与图示】已知如图1,OP 为AOB ∠的角平分线,PM OP ⊥于点P 时,辅助线的作法大都为延长MP 交OB 于点N 即可。
平行线中的四大经典模型(浙教版)(解析版)
平行线中的四大经典模型【浙教版】【模型1 “猪蹄”型(含锯齿型)】1.(2020下·湖北武汉·七年级统考期末)如图,AB∥CD,EF平分∠BED,∠DEF+∠D=66°,∠B−∠D=28°,则∠BED=.【答案】80°【分析】过E点作EM∥AB,根据平行线的性质可得∠BED=∠B+∠D,利用角平分线的定义可求得∠B+3∠D=132°,结合∠B-∠D=28°即可求解.【详解】解:过E点作EM∥AB,∴∠B=∠BEM,∵AB∥CD,∴EM∥CD,∴∠MED=∠D,∴∠BED=∠B+∠D,∵EF平分∠BED,∴∠DEF=1∠BED,2∵∠DEF+∠D=66°,∠BED+∠D=66°,∴12∴∠BED+2∠D=132°,即∠B+3∠D=132°,∵∠B-∠D=28°,∴∠B=54°,∠D=26°,∴∠BED=80°.故答案为:80°.【点睛】本题主要考查平行线的性质,角平分线的定义,作出辅助线证出∠BED=∠B+∠D是解题的关键.2.(2023上·辽宁鞍山·七年级统考期中)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,∠BCD=n°,则∠BED的度数为.(用含n的式子表示)n°【答案】40°+12【分析】首先过点E作EF∥AB,由平行线的传递性得AB∥CD∥EF,再根据两直线平行,内错角相等,得n°,∠EDC=40°,再由出∠BCD=∠ABC=n°,∠BAD=∠ADC=80°,由角平分线的定义得出∠ABE=12两直线平行,内错角相等得出∠BEF=∠ABE=1n°∠FED=∠EDC=40°,由∠BED=∠BEF+∠FED即可2得出答案.【详解】解:如图,过点E作EF∥AB,则AB∥CD∥EF,∵AB∥CD,∴∠BCD=∠ABC=n°,∠BAD=∠ADC=80°,又∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=12∠ABC=12n°,∠EDC=12∠ADC=12×80°=40°,∵AB∥EF∥CD,∴∠BEF=∠ABE=12n°,∠FED=∠EDC=40°,∴∠BED=∠FED+∠BEF=40°+12n°,故答案为:40°+12n°.【点睛】本题考查平行线的性质,角平分线的定义,解题关键是作出正确的辅助线,掌握平行线的性质和角平分线的定义.3.(2023下·广东河源·七年级河源市第二中学校考期中)已知直线l1∥l2,A是l1上的一点,B是l2上的一点,直线l3和直线l1,l2交于C和D,直线CD上有一点P.(1)如果P点在C,D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.(2)若点P在C,D两点的外侧运动时(P点与C,D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)【答案】(1)∠PAC+∠PBD=∠APB(2)当点P在直线l1上方时,∠PBD−∠PAC=∠APB;当点P在直线l2下方时,∠PAC−∠PBD=∠APB.【分析】(1)过点P作PE∥l1,由“平行于同一条直线的两直线平行”可得出PE∥l1∥l2,再由“两直线平行,内错角相等”得出∠PAC=∠APE、∠PBD=∠BPE,再根据角与角的关系即可得出结论;(2)按点P的两种情况分类讨论:①当点P在直线l1上方时;②当点P在直线l2下方时,同理(1)可得∠PAC=∠APE、∠PBD=∠BPE,再根据角与角的关系即可得出结论.【详解】(1)解:∠PAC+∠PBD=∠APB.过点P作PE∥l1,如图1所示.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠APE+∠BPE,∴∠PAC+∠PBD=∠APB.(2)解:结论:当点P在直线l1上方时,∠PBD−∠PAC=∠APB;当点P在直线l2下方时,∠PAC−∠PBD=∠APB.①当点P在直线l1上方时,如图2所示.过点P作PE∥l1.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠BPE−∠APE,∴∠PBD−∠PAC=∠APB.②当点P在直线l2下方时,如图3所示.过点P作PE∥l1.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠APE−∠BPE,∴∠PAC−∠PBD=∠APB.【点睛】本题考查了平行线的性质以及角的计算,解题的关键是根据“两直线平行,内错角相等”找到相等的角.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质得出相等(或互补)的角是关键.4.(2023下·山东聊城·七年级统考阶段练习)已知直线AB//CD,EF是截线,点M在直线AB、CD之间.(1)如图1,连接GM,HM.求证:∠M=∠AGM+∠CHM;(2)如图2,在∠GHC的角平分线上取两点M、Q,使得∠AGM=∠HGQ.试判断∠M与∠GQH之间的数量关系,并说明理由.【答案】(1)证明见详解(2)∠GQH=180°−∠M;理由见详解【分析】(1)过点M作MN∥AB,由AB∥CD,可知MN∥AB∥CD.由此可知:∠AGM=∠GMN,∠CHM=∠HMN,故∠AGM+∠CHM=∠GMN+∠HMN=∠M;(2)由(1)可知∠AGM+∠CHM=∠M.再由∠CHM=∠GHM,∠AGM=∠HGQ,可知:∠M=∠HGQ+∠GHM,利用三角形内角和是180°,可得∠GQH=180°−∠M.【详解】(1)解:如图:过点M作MN∥AB,∴MN∥AB∥CD,∴∠AGM=∠GMN,∠CHM=∠HMN,∵∠M=∠GMN+∠HMN,∴∠M=∠AGM+∠CHM.(2)解:∠GQH=180°−∠M,理由如下:如图:过点M作MN∥AB,由(1)知∠M=∠AGM+∠CHM,∵HM平分∠GHC,∴∠CHM=∠GHM,∵∠AGM=∠HGQ,∴∠M=∠HGQ+∠GHM,∵∠HGQ+∠GHM+∠GQH=180°,∴∠GQH=180°−∠M.【点睛】本题考查了利用平行线的性质求角之间的数量关系,正确的作出辅助线是解决本题的关键,同时这也是比较常见的几何模型“猪蹄模型”的应用.5.(2023下·福建莆田·七年级莆田第二十五中学校考阶段练习)如图,AB//CD,点E在直线AB,CD内部,且AE⊥CE.(1)如图1,连接AC,若AE平分∠BAC,求证:CE平分∠ACD;(2)如图2,点M在线段AE上,①若∠MCE=∠ECD,当直角顶点E移动时,∠BAE与∠MCD是否存在确定的数量关系?并说明理由;∠ECD(n为正整数),当直角顶点E移动时,∠BAE与∠MCD是否存在确定的数量关系?并②若∠MCE=1n说明理由.【答案】(1)见解析;(2)①∠BAE +12∠MCD =90°,理由见解析;②∠BAE +n n+1∠MCD =90°,理由见解析.【分析】(1)根据平行的性质可得∠BAC +∠DCA =180°,再根据AE ⊥CE 可得∠EAC +∠ECA =90°,根据AE 平分∠BAC 可得∠BAE =∠EAC ,等量代换可得∠ECD +∠EAC =90°,继而求得∠DCE =∠ECA ;(2)①过E 作EF ∥AB ,先利用平行线的传递性得出EF ∥AB ∥CD ,再利用平行线的性质及已知条件可推得答案;②过E 作EF ∥AB ,先利用平行线的传递性得出EF ∥AB ∥CD ,再利用平行线的性质及已知条件可推得答案.【详解】(1)解:因为AB//CD ,所以∠BAC +∠DCA =180°,因为AE ⊥CE ,所以∠EAC +∠ECA =90°,因为AE 平分∠BAC ,所以∠BAE =∠EAC ,所以∠BAE +∠DCE =90°,所以∠EAC +∠DCE =90°,所以∠DCE =∠ECA ,所以CE 平分∠ACD ;(2)①∠BAE 与∠MCD 存在确定的数量关系:∠BAE +12∠MCD =90°, 理由如下: 过E 作EF ∥AB ,∵AB∥CD,∴EF∥AB∥CD,∴∠BAE=∠AEF,∠FEC=∠DCE,∵∠E=90°,∴∠BAE+∠ECD=90°,∵∠MCE=∠ECD,∴∠BAE+12∠MCD=90°;②∠BAE与∠MCD存在确定的数量关系:∠BAE+nn+1∠MCD=90°,理由如下:过E作EF∥AB,∵AB∥CD,∴EF∥AB∥CD,∴∠BAE=∠AEF,∠FEC=∠DCE,∵∠E=90°,∴∠BAE+∠ECD=90°,∵∠MCE=1n∠ECD,∴∠BAE+nn+1∠MCD=90°.【点睛】本题主要考查平行线的性质和角平分线的定义,解决本题的关键是要添加辅助线利用平行性质. 6.(2023·全国·七年级专题练习)(1)如图1,已知AB//CD,∠ABF=∠DCE,求证:∠BFE=∠FEC(2)如图2,已知AB//CD,∠EAF=14∠EAB,∠ECF=14∠ECD,求证:∠AFC=34∠AEC【答案】(1)见解析;(2)见解析【分析】(1)如图:延长BF、DC相较于E,由AB//CD可得∠ABF=∠E,再结合∠ABF=∠DCE可得∠DCE=∠E,即可得当BE//DE,最后运用两直线平行、内错角相等即可证明结论;(2)如图2:连接AC,设∠EAF=x,∠ECF=y,∠EAB=4x,∠ECD=4y,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=180°-(4x+4y),再求出∠AEC和∠AFC,最后比较即可得到结论.【详解】(1)证明:如图:延长BF、DC相较于G∵AB//CD∴∠ABF=∠G∵∠ABF=∠DCE∴∠DCE=∠G∴BG//CE∴∠BFE=∠FEC;(2)如图2:连接AC,设∠EAF=x,∠ECF=y,∠EAB=4x,∠ECD=4y,∵AB//CD,∴∠BAC+∠ACD=180°∴∠CAE+4x+∠ACE+4y=180°∴∠CAE+∠ACE=180°-(4x+4y),∠F AC+∠FCA=180°-(3x+3y),∴∠AEC=180°-(∠CAE+∠ACE)=180°-[80°-(4x+4y)]=4x+4y=4(x+y)∠AFC=180°-(∠F AC+∠FCA)=180°-[180°-(3x+3y))]=3x+3y=3(x+y),∴∠AFC=34∠AEC.【点睛】本题主要考查了平行线的判定与性质、三角形内角和定理的应用等知识点,灵活应用平行线的判定与性质以及三角形内角和定理正确的表示角成为解答本题的关键.7.(2017下·湖北武汉·七年级统考期中)如图1,已知AB∥CD,∠B=30°,∠D=120°;(1)若∠E=60°,则∠F=;(2)请探索∠E与∠F之间满足的数量关系?说明理由;(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.【答案】(1)90°(2)∠F=∠E+30°,理由见解析(3)15°【分析】(1)如图1,分别过点E,F作EM//AB,FN//AB,根据平行线的性质得到∠B=∠BEM=30°,∠MEF=∠EFN,∠D+∠DFN=180°,代入数据即可得到结论;(2)如图1,根据平行线的性质得到∠B=∠BEM=30°,∠MEF=∠EFN,由AB//CD,AB//FN,得到CD//FN,根据平行线的性质得到∠D+∠DFN=180°,于是得到结论;(3)如图2,过点F作FH//EP,设∠BEF=2x°,则∠EFD=(2x+30)°,根据角平分线的定义得到∠PEF=1 2∠BEF=x°,∠EFG=12∠EFD=(x+15)°,根据平行线的性质得到∠PEF=∠EFH=x°,∠P=∠HFG,于是得到结论.【详解】(1)解:如图1,分别过点E,F作EM//AB,FN//AB,∴EM//AB//FN,∴∠B=∠BEM=30°,∠MEF=∠EFN,又∵AB//CD,AB//FN,∴CD//FN,∴∠D+∠DFN=180°,又∵∠D=120°,∴∠DFN=60°,∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,∴∠EFD=∠MEF+60°∴∠EFD=∠BEF+30°=90°;故答案为:90°;(2)解:如图1,分别过点E,F作EM//AB,FN//AB,∴EM//AB//FN,∴∠B=∠BEM=30°,∠MEF=∠EFN,又∵AB//CD,AB//FN,∴CD//FN,∴∠D+∠DFN=180°,又∵∠D=120°,∴∠DFN=60°,∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,∴∠EFD=∠MEF+60°,∴∠EFD=∠BEF+30°;(3)解:如图2,过点F作FH//EP,由(2)知,∠EFD=∠BEF+30°,设∠BEF=2x°,则∠EFD=(2x+30)°,∵EP平分∠BEF,GF平分∠EFD,∴∠PEF=12∠BEF=x°,∠EFG=12∠EFD=(x+15)°,∵FH//EP,∴∠PEF=∠EFH=x°,∠P=∠HFG,∵∠HFG=∠EFG−∠EFH=15°,∴∠P=15°.【点睛】本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质定理是解题的关键.8.(2020下·浙江绍兴·七年级统考期末)问题情境:如图1,已知AB∥CD,∠APC=108°.求∠PAB+∠PCD 的度数.经过思考,小敏的思路是:如图2,过P作PE∥AB,根据平行线有关性质,可得∠PAB+∠PCD=360°−∠APC=252°.问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.(1)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.(3)问题拓展:如图4,MA1∥NA n,A1−B1−A2−⋯−B n−1−A n是一条折线段,依据此图所含信息,把你所发现的结论,用简洁的数学式子表达为.【答案】(1)∠CPD=∠α+∠β,理由见解析(2)∠CPD=∠β-∠α或∠CPD=∠α-∠β(3)∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1【分析】(1)过P作PE∥AD,根据平行线的判定可得PE∥AD∥BC,再根据平行线的性质即可求解;(2)过P作PE∥AD,根据平行线的判定可得PE∥AD∥BC,再根据平行线的性质即可求解;(3)问题拓展:分别过A2,A3…,An-1作直线∥A1M,过B1,B2,…,Bn-1作直线∥A1M,根据平行线的判定和性质即可求解.【详解】(1)∠CPD=∠α+∠β,理由如下:如图,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;(2)当P在BA延长线时,∠CPD=∠β-∠α;理由:如图,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE-∠DPE=∠β-∠α;当P在BO之间时,∠CPD=∠α-∠β.理由:如图,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE-∠CPE=∠α-∠β.(3)问题拓展:分别过A2,A3…,An-1作直线∥A1M,过B1,B2,…,Bn-1作直线∥A1M,由平行线的性质和角的和差关系得∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1.故答案为:∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1.【点睛】本题主要考查了平行线的判定和性质的应用,主要考查学生的推理能力,第(2)问在解题时注意分类思想的运用.9.(2020下·重庆九龙坡·七年级统考期末)已知,AB∥CD.点M在AB上,点N在CD上.(1)如图1中,∠BME、∠E、∠END的数量关系为:;(不需要证明)如图2中,∠BMF、∠F、∠FND的数量关系为:;(不需要证明)(2)如图3中,NE平分∠FND,MB平分∠FME,且2∠E+∠F=180°,求∠FME的度数;(3)如图4中,∠BME=60°,EF平分∠MEN,NP平分∠END,且EQ∥NP,则∠FEQ的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ的度数.【答案】(1)∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND;(2)120°;(3)不变,30°【分析】(1)过E作EH∥AB,易得EH∥AB∥CD,根据平行线的性质可求解;过F作FH∥AB,易得FH∥AB∥CD,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∠BME+∠END)+∠BMF-∠FND=180°,可求解∠BMF=60°,进而可求解;(3)根据平行线的性质及角平分线的定义可推知∠FEQ=1∠BME,进而可求解.2【详解】解:(1)过E作EH∥AB,如图1,∴∠BME=∠MEH,∵AB∥CD,∴HE∥CD,∴∠END=∠HEN,∴∠MEN=∠MEH+∠HEN=∠BME+∠END,即∠BME=∠MEN﹣∠END.如图2,过F作FH∥AB,∴∠BMF=∠MFK,∵AB∥CD,∴FH∥CD,∴∠FND=∠KFN,∴∠MFN=∠MFK﹣∠KFN=∠BMF﹣∠FND,即:∠BMF=∠MFN+∠FND.故答案为∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.(2)由(1)得∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.∵NE平分∠FND,MB平分∠FME,∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,∵2∠MEN +∠MFN =180°,∴2(∠BME +∠END )+∠BMF ﹣∠FND =180°,∴2∠BME +2∠END +∠BMF ﹣∠FND =180°,即2∠BMF +∠FND +∠BMF ﹣∠FND =180°,解得∠BMF =60°,∴∠FME =2∠BMF =120°;(3)∠FEQ 的大小没发生变化,∠FEQ =30°.由(1)知:∠MEN =∠BME +∠END ,∵EF 平分∠MEN ,NP 平分∠END ,∴∠FEN =12∠MEN =12(∠BME +∠END ),∠ENP =12∠END ,∵EQ ∥NP ,∴∠NEQ =∠ENP ,∴∠FEQ =∠FEN ﹣∠NEQ =12(∠BME +∠END )﹣12∠END =12∠BME ,∵∠BME =60°,∴∠FEQ =12×60°=30°.【点睛】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键.10.(2023下·辽宁大连·如图,AB//CD ,点O 在直线CD 上,点P 在直线AB 和CD 之间,∠ABP =∠PDQ =α,PD 平分∠BPQ .(1)求∠BPD 的度数(用含α的式子表示);(2)过点D 作DE//PQ 交PB 的延长线于点E ,作∠DEP 的平分线EF 交PD 于点F ,请在备用图中补全图形,猜想EF 与PD 的位置关系,并证明;(3)将(2)中的“作∠DEP的平分线EF交PD于点F”改为“作射线EF将∠DEP分为1:3两个部分,交PD于点F”,其余条件不变,连接EQ,若EQ恰好平分∠PQD,请直接写出∠FEQ=__________(用含α的式子表示).【答案】(1)∠BPD=2α;(2)画图见解析,EF⊥PD,证明见解析;(3)45°−α2或45°−32α【分析】(1)根据平行线的传递性推出PG//AB//CD,再利用平行线的性质进行求解;(2)猜测EF⊥PD,根据PD平分∠BPQ,∠BPD=2α,推导出∠BPD=∠DPQ=2α,再根据DE//PQ、EF平分∠DEP,通过等量代换求解;(3)分两种情况进行讨论,即当∠PEF:∠DEF=1:3与∠DEF:∠PEF=1:3,充分利用平行线的性质、角平分线的性质、等量代换的思想进行求解.【详解】(1)过点P作PG//AB,∵AB//CD,PG//AB,∴PG//AB//CD,∴∠BPG=∠ABP=α,∠DPG=∠PDQ=α,∴∠BPD=∠BPG+∠DPG=2α.(2)根据题意,补全图形如下:猜测EF⊥PD,由(1)可知:∠BPD=2α,∵PD平分∠BPQ,∠BPD=2α,∴∠BPD=∠DPQ=2α,∵DE//PQ,∴∠EDP=∠DPQ=2α,∴∠DEP=180°−∠BPD−∠EDP=180°−4α,又EF平分∠DEP,∠PEF=12∠DEP=90°−2α,∴∠EFD=180°−∠PEF−∠BPD=90°,∴EF⊥PD.(3)①如图1,∠PEF:∠DEF=1:3,由(2)可知:∠EPD=∠DPQ=∠EDP=2α,∠DEP=180°−4α,∵∠PEF:∠DEF=1:3,∴∠PEF=14∠DEP=45°−α,∠DEF=34∠DEP=135°−3α,∵DE//PQ,∴∠DEQ=∠PQE,∠EDQ+∠PQD=180°,∵∠EDP=2α,∠PDQ=α,∴∠EDQ=∠EDP+∠PDQ=3α,∠PQD=180°−∠EDQ=180°−3α,又EQ平分∠PQD,∴∠PQE=∠DQE=∠DEQ=12∠PQD=90°−32α,∴∠FEQ=∠DEF−∠DEQ=135°−3α−(90°−32α)=45°−32α;②如图2,∠DEP=180°−4α,∠PQD=180°−3α(同①);若∠DEF:∠PEF=1:3,则有∠DEF=14∠DEP=14×(180°−4α)=45°−α,又∠PQE=∠DQE=12∠PQD=12×(180°−3α)=90°−32α,∵DE//PQ,∴∠DEQ=∠PQE=90°−32α,∴∠FEQ=∠DEQ−∠DEF=45°−12α,综上所述:∠FEQ=45°−32α或45°α2,故答案是:45°−α2或45°−32α.【点睛】本题考查了平行线的性质、角平分线、三角形内角和定理、垂直等相关知识点,解题的关键是掌握相关知识点,作出适当的辅助线,通过分类讨论及等量代换进行求解.【模型2 “铅笔”型】1.(2012下·广东茂名·七年级统考期中)如图,AB∥ED,∠B+∠C+∠D=()A.180°B.360°C.540°D.270°【答案】B【分析】过C点作直线CF∥AB,根据平行线的性质可得∠B+∠BCF=180°,∠FCD+∠D=180°,然后再计算∠B+∠C+∠D即可.【详解】如图,过C点作直线CF∥AB,∵AB∥ED,∴CF∥ED,∴∠B+∠BCF=180°,∠FCD+∠D=180°,∴∠B+∠BCF+∠FCD+∠D=360°,即∠B+∠BCD+∠D=360°.故选:B【点睛】本题主要考查了平行线的性质,熟练掌握平行线的性质是解题的关键.2.(2012·江苏常州·七年级统考期中)一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=.【答案】270°【分析】过B作BF∥AE,则CD∥BF∥AE.根据平行线的性质即可求解.【详解】过B作BF∥AE,∵CD∥AE,则CD∥BF∥AE,∴∠BCD+∠1=180°,又∵AB⊥AE,∴AB⊥BF,∴∠ABF=90°,∴∠ABC+∠BCD=90°+180°=270°.故答案为:270.【点睛】本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.3.(2023下·陕西西安·七年级西安市第八十三中学校联考期中)如图1所示的是一个由齿轮、轴承、托架2所示的是手动变速箱托架工作时某一时刻的示意图,已知AB∥CD,CG∥EF,∠BAG=150°,∠DEF=130°,则∠AGC的度数是.【答案】80°【分析】过点F作FM∥CD,因为AB∥CD,所以AB∥CD∥FM,再根据平行线的性质可以求出∠MFA,∠EFM,进而可求出∠EFA,再根据平行线的性质即可求得∠AGC.【详解】解:如图,过点F作FM∥CD,∵AB∥CD,∴AB∥CD∥FM,∴∠DEF+∠EFM=180°,∠MFA+∠BAG=180°,∵∠BAG=150°,∠DEF=130°,∴∠MFA=30°,∠EFM=50°,∴∠EFA=∠EFM+∠AFM=80°,∵CG∥EF,∴∠AGC=∠EFA=80°.故答案为80°.【点睛】本题考查平行线的性质,解题关键是结合图形利用平行线的性质进行角的转化和计算.4.(2023下·广东东莞·七年级东莞市长安实验中学校考期中)如图,已知AB∥CD.(1)如图1所示,∠1+∠2=;(2)如图2所示,∠1+∠2+∠3=;并写出求解过程.(3)如图3所示,∠1+∠2+∠3+∠4=;(4)如图4所示,试探究∠1+∠2+∠3+∠4+⋯+∠n=.【答案】(1)180°;(2)360°;(3)540°;(4)(n-1)×180°【分析】(1)由两直线平行,同旁内角互补,可得答案;(2)过点E作AB的平行线,转化成两个图1,同理可得答案;(3)过点E,点F分别作AB的平行线,转化成3个图1,可得答案;(4)由(2)(3)类比可得答案.【详解】解:(1)如图1,∵AB∥CD,∴∠1+∠2=180°(两直线平行,同旁内角互补).故答案为:180°;(2)如图2,过点E作AB的平行线EF,∵AB∥CD,∴AB∥EF,CD∥EF,∴∠1+∠AEF=180°,∠FEC+∠3=180°,∴∠1+∠2+∠3=360°;(3)如图3,过点E,点F分别作AB的平行线,类比(2)可知∠1+∠2+∠3+∠4=180°×3=540°,故答案为:540°;(4)如图4由(2)和(3)的解法可知∠1+∠2+∠3+∠4+…+∠n=(n-1)×180°,故答案为:(n-1)×180°.【点睛】此题考查了平行线的性质.注意掌握辅助线的作法是解此题的关键.5.(2020下·江苏淮安·七年级统考期末)问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC 的度数.思路点拨:小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可分别求出∠APE、∠CPE的度数,从而可求出∠APC的度数;小丽的思路是:如图3,连接AC,通过平行线性质以及三角形内角和的知识可求出∠APC的度数;小芳的思路是:如图4,延长AP交DC的延长线于E,通过平行线性质以及三角形外角的相关知识可求出∠APC 的度数.问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算,你求得的∠APC的度数为°;问题迁移:(1)如图5,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.【答案】110;(1)∠CPD=∠α+∠β,理由见解析;(2)∠CPD=∠β−∠α或∠CPD=∠a−∠β,理由见解析【分析】小明的思路是:过P作PE∥AB,构造同旁内角,利用平行线性质,可得∠APC=110°.(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠a=∠DPE,∠β=∠CPE,即可得出答案;(2)画出图形(分两种情况:①点P在BA的延长线上,②点P在AB的延长线上),根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【详解】解:小明的思路:如图2,过P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠APE=180°−∠A=50°,∠CPE=180°−∠C=60°,∴∠APC=50°+60°=110°,故答案为:110;(1)∠CPD=∠α+∠β,理由如下:如图5,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠a=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠a+∠β;(2)当P在BA延长线时,∠CPD=∠β−∠α;理由:如图6,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE−∠DPE=∠β−∠α;当P在BO之间时,∠CPD=∠a−∠β.理由:如图7,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE−∠CPE=∠α−∠β.【点睛】本题考查了三角形的内角和定理,平行线的判定和性质,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.6.(2020下·内蒙古·七年级校考期中)综合与探究:(1)问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.小明想到一种方法,但是没有解答完:如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.∴∠APE=180°−∠PAB=180°−130°=50°.∵AB∥CD.∴PE∥CD.…………请你帮助小明完成剩余的解答.(2)问题探究:请你依据小明的思路,解答下面的问题:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.当点P在A,B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.【答案】(1)110°;(2)∠CPD=∠α+∠β,理由见解析【分析】(1)过P作PE//AB,构造同旁内角,通过平行线性质,可得∠APC=50°+60°=110°.(2)过P作PE//AD交CD于E,推出AD//PE//BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【详解】解:(1)过P作PE∥AB,∴∠APE+∠PAB=180°,∴∠APE=180°−∠PAB=180°−130°=50°.∵AB∥CD,∴PE∥CD.∴∠CPE+∠PCD=180°,∴∠CPE=180°−120°=60°,∴∠APC=50°+60°=110°.(2)∠CPD=∠α+∠β,如图3,过P作PE//AD交CD于E,∵AD//BC,∴AD//PE//BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;【点睛】本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.7.(2020下·天津滨海新·七年级统考期末)如图1,四边形MNBD为一张长方形纸片.(1)如图2,将长方形纸片剪两刀,剪出三个角(∠BAE、∠AEC、∠ECD),则∠BAE+∠AEC+∠ECD=__________°.(2)如图3,将长方形纸片剪三刀,剪出四个角(∠BAE、∠AEF、∠EFC、∠FCD),则∠BAE+∠AEF+∠EFC+∠FCD=__________°.(3)如图4,将长方形纸片剪四刀,剪出五个角(∠BAE、∠AEF、∠EFG、∠FGC、∠GCD),则∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=___________°.(4)根据前面探索出的规律,将本题按照上述剪法剪n刀,剪出(n+1)个角,那么这(n+1)个角的和是____________°.【答案】(1)360;(2)540;(3)720;(4)180n.【分析】(1)过点E作EH∥AB,再根据两直线平行,同旁内角互补即可得到三个角的和等于180°的2倍;(2)分别过E、F分别作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;(3)分别过E、F、G分别作AB180°的三倍;(4)根据前三问个的剪法,剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.【详解】(1)过E作EH∥AB(如图②).∵原四边形是长方形,∴AB∥CD,又∵EH∥AB,∴CD∥EH(平行于同一条直线的两条直线互相平行).∵EH∥AB,∴∠A+∠1=180°(两直线平行,同旁内角互补).∵CD∥EH,∴∠2+∠C=180°(两直线平行,同旁内角互补).∴∠A+∠1+∠2+∠C=360°,又∵∠1+∠2=∠AEC,∴∠BAE+∠AEC+∠ECD=360°;(2)分别过E、F分别作AB的平行线,如图③所示,用上面的方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°;(3)分别过E、F、G分别作AB的平行线,如图④所示,用上面的方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°;(4)由此可得一般规律:剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.故答案为:(1)360;(2)540;(3)720;(4)180n.【点睛】本题主要考查了多边形的内角和,作平行线并利用两直线平行,同旁内角互补是解本题的关键,总结规律求解是本题的难点.8.(2023下·浙江·七年级期末)已知AB//CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P.(1)如图1所示时,试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?并说明理由.(2)除了(1)的结论外,试问∠AEP,∠EPF,∠PFC还可能满足怎样的数量关系?请画图并证明(3)当∠EPF满足0°<∠EPF<180°,且QE,QF分别平分∠PEB和∠PFD,①若∠EPF=60°,则∠EQF=__________°.②猜想∠EPF与∠EQF的数量关系.(直接写出结论)【答案】(1)∠AEP+∠PFC=∠EPF)∠AEP+∠EPF+∠PFC=360°;(3)①150°或30;②∠EPF+2∠EQF=360°或∠EPF=2∠EQF【分析】(1)由于点P是平行线AB,CD之间有一动点,因此需要对点P的位置进行分类讨论:如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为:∠EPF=∠AEP+∠PFC;(2)当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为:∠AEP+∠EPF+∠PFC=360°;(3)①若当P点在EF的左侧时,∠EQF=∠BEQ+∠QFD=150°;当P点在EF的右侧时,可求得∠BEQ+∠QFD=30°;②结合①可得∠EPF=180°−2∠BEQ+180°−2∠DFQ=360°−2(∠BEQ+∠PFD),由∠EQF=∠BEQ+∠DFQ,得出∠EPF+2∠EQF=360°;可得EPF=∠BEP+∠PFD,由∠BEQ+∠DFQ=∠EQF,得出∠EPF= 2∠EQF.【详解】解:(1)如图1,过点P作PG//AB,∵PG//AB,∴∠EPG=∠AEP,∵AB//CD,∴PG//CD,∴∠FPG=∠PFC,∴∠AEP+∠PFC=∠EPF;(2)如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为:∠AEP+∠EPF+∠PFC=360°;过点P作PG//AB,∵PG//AB,∴∠EPG+∠AEP=180°,∵AB//CD,∴PG//CD,∴∠FPG+∠PFC=180°,∴∠AEP+∠EPF+∠PFC=360°;(3)①如图3,若当P点在EF的左侧时,∵∠EPF=60°,∴∠PEB+∠PFD=360°−60°=300°,∵EQ,FQ分别平分∠PEB和∠PFD,∴∠BEQ=12∠PEB,∠QFD=12∠PFD,∴∠EQF=∠BEQ+∠QFD=12(∠PEB+∠PFD)=12×300°=150°;如图4,当P点在EF的右侧时,∵∠EPF=60°,∴∠PEB+∠PFD=60°,∴∠BEQ+∠QFD=12(∠PEB+∠PFD)=12×60°=30°;故答案为:150°或30;②由①可知:∠EQF=∠BEQ+∠QFD=12(∠PEB+∠PFD)=12(360°−∠EPF),∴∠EPF+2∠EQF=360°;∠EQF=∠BEQ+∠QFD=12(∠PEB∠PFD)=12∠EPF,∴∠EPF=2∠EQF.综合以上可得∠EPF与∠EQF的数量关系为:∠EPF+2∠EQF=360°或∠EPF=2∠EQF.【点睛】本题主要考查了平行线的性质,平行公理和及推论等知识点,作辅助线后能求出各个角的度数,是解此题的关键.9.(2023下·浙江宁波·七年级统考期中)如图,AB//CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一个动点P,满足0°<∠EPF<180°.(1)试问:∠AEP,∠EPF,∠PFC满足怎样的数量关系?解:由于点P是平行线AB,CD之间一动点,因此需对点P的位置进行分类讨论.如图1,当点P在EF的左侧时,易得∠AEP,∠EPF,∠PFC满足的数量关系为∠AEP+∠PFC=∠EPF;如图2,当点P在EF的右侧时,写出∠AEP,∠EPF,∠PFC满足的数量关系_________.(2)如图3,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.①若∠EPF=100°,则∠EQF的度数为______;②猜想∠EPF与∠EQF的数量关系,并说明理由;③如图4,若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3,以此类推,则∠EPF与∠EQ2020F满足怎样的数量关系?(直接写出结果)【答案】(1)∠AEP+∠EPF+∠PFC=360°;(2)①130°;②∠EPF+2∠EQF=360°,见解析;③∠EPF+22021∠EQ2020F=360°【分析】(1)过点P作PH//AB,利用平行线的性质即可求解;(2)根据(1)的结论结合角平分线的定义,平角的定义,运用整体思想即可求解.【详解】解:(1)如图2,当点P在EF的右侧时,过点P作PM//AB,则PM//CD,∴∠AEP+∠EPM=180°,∠PFC+∠MPF=180°,∴∠AEP+∠EPM+∠PFC+∠MPF=360°,即:∠AEP+∠EPF+∠PFC=360°;故答案为:∠AEP+∠EPF+∠PFC=360°;(2)①由(1)得:∠DFQ+∠BEQ=∠EQF,∠PEA+∠PFC=∠EPF,∵∠EPF=100°,∴∠PEA+∠PFC=100°,∵QE,QF分别平分∠PEB和∠PFD,∴∠DFP=2∠DFQ,∠BEP=2∠BEQ,∵∠PFC+∠DFP=180°,∠PEA+∠BEP=180°,∴∠PFC+2∠DFQ=180°,∠PEA+2∠BEQ=180°,∴∠PFC+2∠DFQ+∠PEA+2∠BEQ=360°,∴100°+2∠DFQ+2∠BEQ=360°,∴∠DFQ+∠BEQ=130°,∴∠EQF=∠DFQ+∠BEQ=130°,故答案为:130°;②∠EPF+2∠EQF=360°,理由如下:∵QE,QF分别平分∠PEB和∠PFD,∴∠DFP=2∠DFQ,∠BEP=2∠BEQ,∵∠PFC+∠DFP=180°,∠PEA+∠BEP=180°,∴∠PFC+2∠DFQ=180°,∠PEA+2∠BEQ=180°,∴∠PFC+2∠DFQ+∠PEA+2∠BEQ=360°,∴∠PFC+∠PEA +2(∠DFQ +∠BEQ)=360°,∵由(1)得:∠DFQ+∠BEQ=∠EQF,∠PEA+∠PFC=∠EPF,∴∠EPF +2∠EQF=360°;③∵Q1E,Q1F分别平分∠QEB和∠QFD,∴∠DFP=2∠DFQ=22∠DFQ1,∠BEP=2∠BEQ=22∠BEQ1,∵∠PFC+∠DFP=180°,∠PEA+∠BEP=180°,∴∠PFC+22∠DFQ1=180°,∠PEA+22∠BEQ1=180°,∴∠PFC+22∠DFQ1+∠PEA+22∠BEQ1=360°,∴∠PFC+∠PEA +22(∠DFQ1 +∠BEQ1)=360°,∵由(1)得:∠DFQ1+∠BEQ1=∠EQ1F,∠PEA+∠PFC=∠EPF,∴∠EPF +22∠EQ1F=360°;同理可得:∠EPF +23∠EQ2F=360°,∠EPF +24∠EQ3F=360°,……∴∠EPF+22021∠EQ2020F=360°.【点睛】本题主要考查了平行线的性质,平行公理及推论,角平分线的定义等知识点,作辅助线后能求出各个角的度数,利用整体思想解决第(2)问是解此题的关键.10.(2020下·辽宁大连·七年级统考期末)阅读下面材料,完成(1)~(3)题.数学课上,老师出示了这样—道题:如图1,已知AB//CD,点E,F分别在AB,CD上,EP⊥FP,∠1=60°.求∠2的度数.同学们经过思考后,小明、小伟、小华三位同学用不同的方法添加辅助线,交流了自己的想法:小明:“如图2,通过作平行线,发现∠1=∠3,∠2=∠4,由已知EP⊥FP,可以求出∠2的度数.”小伟:“如图3这样作平行线,经过推理,得∠2=∠3=∠4,也能求出∠2的度数.”小华:∵如图4,也能求出∠2的度数.”(1)请你根据小明同学所画的图形(图2),描述小明同学辅助线的做法,辅助线:______;(2)请你根据以上同学所画的图形,直接写出∠2的度数为_________°;老师:“这三位同学解法的共同点,都是过一点作平行线来解决问题,这个方法可以推广.”请大家参考这三位同学的方法,使用与他们类似的方法,解决下面的问题:(3)如图,AB//CD,点E,F分别在AB,CD上,FP平分∠EFD,∠PEF=∠PDF,若∠EPD=a,请探究∠CFE与∠PEF 的数量关系((用含α的式子表示),并验证你的结论.【答案】(1)过点Р作PQ//AC;(2)30;(3)∠CFE−2∠PEF=180∘−a.【分析】(1)根据图中所画虚线的位置解答即可;(2)过点Р作PQ//AC,根据平行线的性质可得∠1=∠3,∠2=∠4,由EP⊥FP可得∠3+∠4=90°,即可得出∠1+∠2=90°,进而可得答案;(3)设∠CFE=x,∠PEF=∠PDF=y,过点P作PQ//AB,根据平行线的性质可得∠BEP+∠EPQ= 180°,∠CFE=∠FEB=x,∠PDF=∠DPQ,进而根据角的和差关系即可得答案.【详解】(1)由图中虚线可知PQ//AC,∴小明同学辅助线的做法为过点Р作PQ//AC,故答案为:过点Р作PQ//AC(2)如图2,过点Р作PQ//AC,∵AB//CD,∴PQ//AB//CD,∴∠1=∠3,∠2=∠4,∵EP⊥FP,∴∠EPF=∠3+∠4=90°,∴∠1+∠2=90°,∵∠1=60°,∴∠2=30°,故答案为:30(3)如图,设∠CFE=x,∠PEF=∠PDF=y,过点P作PQ//AB,∴∠BEP+∠EPQ=180°,∠CFE=∠FEB=x∵AB//CD,∴PQ//CD,∴∠PDF=∠DPQ∴∠DPQ=∠EHF=∠PDF=y∵∠CFE=∠FEB=x=∠FEP+∠BEP∴x=y+(180−a+y)∴x−2y=180−α,即∠CFE−2∠PEF=180∘−a.【点睛】本题考查平行线的性质,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;正确作出辅助线,熟练掌握平行线的性质是解题关键.【模型3 “鸡翅”型】1.(2023下·湖南株洲·七年级统考期末)①如图1,AB∥CD,则∠A+∠E+∠C=360°;②如图2,AB ∥CD,则∠P=∠A−∠C;③如图3,AB∥CD,则∠E=∠A+∠1;④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α−∠β+∠γ=180°.以上结论正确的个数是()A.1个B.2个C.3个D.4个【答案】C【分析】①过点E作直线EF∥AB,由平行线的性质:两直线平行,同旁内角互补,即可得出结论;②如图2,先根据三角形外角的性质得出∠1=∠C+∠P,再根据两直线平行,内错角相等即可作出判断;③如图3,过点E作直线EF∥AB,由平行线的性质可得出∠A+∠AEC﹣∠1=180°,即得∠AEC=180°+∠1﹣∠A;④如图4,根据平行线的性质得出∠α=∠BOF,∠γ+∠COF=180°,再利用角的关系解答即可.【详解】解:①如图1,过点E作直线EF∥AB,∵AB∥CD,∴AB∥CD∥EF,∴∠A+∠1=180°,∠2+∠C=180°,∴∠A+∠1+∠2+∠C=360°,∴∠A+∠AEC+∠C=360°,故①正确;②如图2,∵∠1是△CEP的外角,∴∠1=∠C+∠P,∵AB∥CD,∴∠A=∠1,即∠P=∠A﹣∠C,故②正确;③如图3,过点E作直线EF∥AB,∵AB∥CD,∴AB∥CD∥EF,∴∠A+∠3=180°,∠1=∠2,∴∠A+∠AEC﹣∠1=180°,即∠AEC=180°+∠1﹣∠A,故③错误;④如图4,∵AB∥EF,∴∠α=∠BOF,∵CD∥EF,∴∠γ+∠COF=180°,∵∠BOF=∠COF+∠β,∴∠COF=∠α﹣∠β,∴∠γ+∠α﹣∠β=180°,故④正确;综上结论正确的个数为3,故选:C.【点睛】本题考查的是平行线的性质及三角形外角的性质,熟练掌握平行线的性质,根据题意作出辅助线是解答此题的关键.2.(2023上·七年级课时练习)(1)已知:如图(a),直线DE∥AB.求证:∠ABC+∠CDE=∠BCD;(2)如图(b),如果点C在AB与ED之外,其他条件不变,那么会有什么结果?你还能就本题作出什么新的猜想?【答案】(1)见解析;(2)当点C在AB与ED之外时,∠ABC−∠CDE=∠BCD,见解析【分析】(1)由题意首先过点C作CF∥AB,由直线AB∥ED,可得AB∥CF∥DE,然后由两直线平行,内错角相等,即可证得∠ABC+∠CDE=∠BCD;(2)根据题意首先由两直线平行,内错角相等,可得∠ABC=∠BFD,然后根据三角形外角的性质即可证得∠ABC-∠CDE=∠BCD.【详解】解:(1)证明:过点C作CF∥AB,∵AB∥ED,∴AB∥ED∥CF,∴∠BCF=∠ABC,∠DCF=∠EDC,∴∠ABC+∠CDE=∠BCD;(2)结论:∠ABC-∠CDE=∠BCD,证明:如图:∵AB∥ED,∴∠ABC=∠BFD,在△DFC中,∠BFD=∠BCD+∠CDE,∴∠ABC=∠BCD+∠CDE,∴∠ABC-∠CDE=∠BCD.若点C在直线AB与DE之间,猜想∠ABC+∠BCD+∠CDE=360°,。
2023年中考数学专题《平行线四大模型》含答案解析

专题03 平行线四大模型(知识解读)【专题说明】历年中考考试中,有不少题目都考查了平行线的性质及应用,现汲取四大模型,供同学们赏析,希望能到达指导学习之目的。
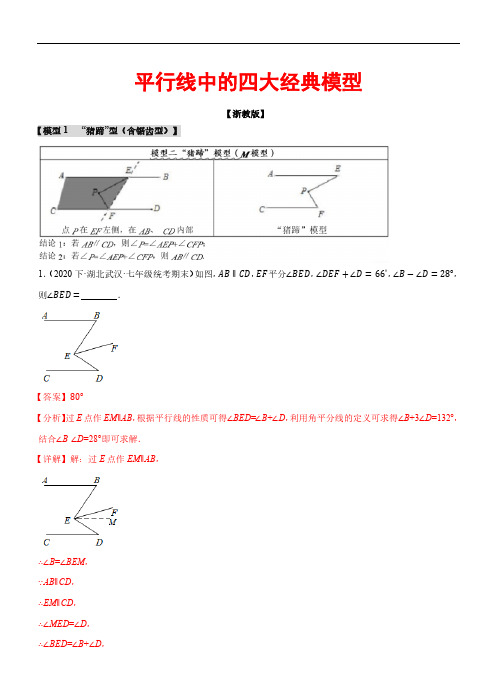
【方法技巧】模型一“铅笔”模型点P在EF右侧,在AB、CD内部“铅笔”模型结论1:若AB∥CD,则∠P+∠AEP+∠PFC=3 60°结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.模型二“猪蹄”模型(M模型)点P在EF左侧,在AB、CD内部“猪蹄”模型结论1:若AB∥CD,则∠P=∠AEP+∠CFP;结论2:若∠P=∠AEP+∠CFP,则AB∥CD.模型三“臭脚”模型点P在EF右侧,在AB、CD外部“臭脚”模型结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD模型四“骨折”模型点P在EF左侧,在AB、CD外部·“骨折”模型结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.【典例分析】【模型1 “铅笔”模型】【典例1】如图,直线a∥b,点M、N分别在直线a、b上,P为两平行线间一点,那么∠1+∠2+∠3等于( )A.360°B.300°C.270°D.180°【答案】A【解答】解:如图,过点P作PA∥a,则a∥b∥PA,∴∠3+∠NPA=180°,∠1+∠MPA=180°,∴∠1+∠2+∠3=180°+180°=360°.故选:A.【变式1-1】把一块等腰直角三角尺和直尺按如图所示的方式放置,若∠1=32°,则∠2的度数为( )A.20°B.18°C.15°D.13°【答案】D【解答】解:如图,过点O作OP∥AB,则OP∥AB∥CD,∴∠1=∠3,∠2=∠4,∵∠3+∠4=45°,∴∠1+∠2=45°,∴∠2=45°﹣∠1=45°﹣32°=13°.故选:D.【典例2】问题情境:(1)如图1,AB∥CD,∠BAP=120°,∠PCD=130°,求∠APC的度数.(提示:如图2,过P作PE∥AB)问题迁移:(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP =α,∠PCB=β,α、β、∠DPC之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出α、β、∠DPC之间的数量关系.(提示:三角形内角和为180°)【解答】解:(1)∵AB∥CD,∠PAB=120°,∠PCD=130°,∴∠PAB+∠APE=180°,∠EPC+∠C=180°,∴∠APE=180°﹣120°=60°,∠EPC=180°﹣130°=50°,∴∠APC=∠APE+∠EPC=60°+50°=110°;(2)∠CPD=∠α+∠β,理由如下:如图3,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;(3)①当P在OA延长线时,∠CPD=∠β﹣∠α;②当P在AB延长线时,∠CPD=∠α﹣∠β,①当P在OA延长线时,∠CPD=∠β﹣∠α;理由:如图4,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;②当P在AB延长线时,∠CPD=∠α﹣∠β,理由:如图5,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.【变式2-1】已知,AB∥CD,试解决下列问题:(1)如图1,∠1+∠2= ;(2)如图2,∠1+∠2+∠3= ;(3)如图3,∠1+∠2+∠3+∠4= ;(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n= .【解答】解:(1)∵AB∥CD,∴∠1+∠2=180°(两直线平行,同旁内角互补);(2)过点E作一条直线EF∥AB,∵AB∥CD,∴CD∥EF,∴∠1+∠AEF=180°,∠FEC+∠3=180°,∴∠1+∠2+∠3=360°;(3)过点E、F作EG、FH平行于AB,∵AB∥CD,∴AB∥EG∥FH∥CD,∴∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°;∴∠1+∠2+∠3+∠4=540°;(4)根据上述规律,显然作(n﹣2)条辅助线,运用(n﹣1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n﹣1).【变式2-2】如图,已知BQ∥GE,AF∥DE,∠1=50°.(1)求∠AFG的度数;(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.【解答】解:(1)∵BQ∥GE,∠1=50°,∴∠E=∠1=50°,∵AF∥DE,∴∠AFG=∠E=50°;(2)过点A作AM∥BQ,由(1)得∠AFG=∠E=50°,∵BQ∥GE,∴AM∥BQ∥GE,∴∠FAM=∠AFG=50°,∠MAQ=∠Q=15°,∴∠FAQ=∠FAM+∠MAQ=65°,∵AQ平分∠FAC,∴∠QAC=∠FAQ=65°,∴∠MAC=∠QAC+∠MAQ=80°,∵AM∥BQ,∴∠ACB=∠MAC=80°.【模型2 “猪蹄”模型(M模型)】【典例3】【问题背景】同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.【问题解决】(1)如图1,AB∥CD,E为AB、CD之间一点,连接AE、CE.若∠A=42°,∠C=28°.则∠AEC= .【问题探究】(2)如图2,AB∥CD,线段AD与线段BC交于点E,∠A=36°,∠C=54°,EF平分∠BED,求∠BEF的度数.【问题拓展】(3)如图3.AB∥CD,线段AD与线段BC相交于点G,∠BCD=56°,∠GDE=20°,过点D作DF∥CB交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数.【解答】解:(1)延长CE交AB于点F,∵AB∥CD,∴∠AFC=∠C=28°,∵∠AEC是△AEF的一个外角,∴∠AEC=∠A+∠AFC=∠A+∠C=70°,故答案为:70°;(2)利用(1)的结论可得:∠AEC=∠A+∠C=36°+54°=90°,∴∠AEC=∠BED=90°,∵EF平分∠BED,∴∠BEF=∠BED=45°,∴∠BEF的度数为45°;(3)∵BC∥DF,∴∠CDF=180°﹣∠BCD=124°,∵DG平分∠CDF,∴∠CDG=∠CDF=62°,∵AB∥CD,∴∠BAG=∠CDG=62°,∵AE平分∠BAD,∴∠BAE=∠BAD=31°,∵∠GDE=20°,∴∠EDH=180°﹣∠CDG﹣∠GDE=98°,利用(1)的结论可得:∠AED=∠BAE+∠EDH=31°+98°=129°,∴∠AED的度数为129°.。
角平分线的四大模型-【压轴必刷】中考数学压轴大题之经典模型(解析版)

角平分线的四大模型解题策略模型1角平分线的点向两边作垂线如图,P 是∠MON 的平分线上一点,过点P 作PA ⏊OM 于点A ,PB ⏊ON 于点B ,则PB =PA模型分析利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口模型2截取构造对称全等如图,P 是∠MON 的平分线上一点,点A 是射线OM 上任意一点,在ON 上截取OB =OA ,连接PB ,则△OPB ≌△OPA 模型分析利用角平分线图形的对称性,在铁的两边构造对称全等三角形,可以得到对应边,对应角相等,利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧模型3角平分线+垂线构造等腰三角形如图,P 是∠MON 的平分线上一点,AP ⏊OP 于P 点,延长AP 交ON 于点B ,则△AOB 是等腰三角形.模型4角平分线+平行线模型分析有角平分线时,常过角平分线上一点作角的一边的平行线.构造等腰三角形,为证明结论提供更多的条件,体现了用平分线与等腰三角形之间的密切关系.A B MNO PAB MNO P A B MNO PO P QMN经典例题【例1】(2022·黑龙江·哈尔滨市第六十九中学校八年级阶段练习)四边形ABCD 中,DA =DC ,连接BD .(1)如图1,若BD 平分∠ABC ,求证:∠A +∠C =180°.(2)如图2,若BD =BC ,∠BAD =150°,求证:∠DBC =2∠ABD .(3)如图3,在(2)的条件下,作AE ⊥BC 于点E ,连接DE ,若DA ⊥DC ,BC =2,求DE 的长度.【答案】(1)见解析;(2)见解析;(3)2【分析】(1)过点D 分别作DF ⊥BC 于点F ,DE ⊥BA 交BA 的延长线于点E ,根据角平分线的性质可得ED =FD ,结合已知条件HL 证明Rt △DAE ≌Rt △DCF ,继而可得∠C =∠EAD ,根据平角的定义以及等量代换即可证明∠BAD +∠BCD =180°;(2)过点D 分别作DF ⊥BC 于点F ,DE ⊥BA 交BA 的延长线于点E ,过点B 作BG ⊥DC ,根据含30度角的直角三角形的性质可得ED =12AD ,根据三线合一,可得DG =12DC ,进而可得DE =DG ,根据角平分线的判定定理可推出∠ABD =∠DBG =12∠DBC ,进而即可证明∠DBC =2∠ABD ;(3)先证明四边形DMEF 是矩形,证明△MAD ≌△FCD ,进而证明四边形DMEF 是正方形,设∠ABD =α,根据(2)的结论以及三角形内角和定理,求得α=15°,进而求得∠DBC =30°,根据含30度角的直角三角形的性质,即可求得EF ,进而在Rt △DEF 中,勾股定理即可求得DE 的长.【详解】(1)如图,过点D 分别作DF ⊥BC 于点F ,DE ⊥BA 交BA 的延长线于点E ,∵BD 平分∠ABC ,∴ED =FD∵DA =DC ,在Rt △DAE 与Rt △DCF 中AD =DC ED =FD∴Rt △DAE ≌Rt △DCF (HL )∴∠C =∠EAD∴∠DAB +∠EAD =∠DAB +∠C =180°即∠BAD +∠BCD =180°(2)如图,过点D 作DE ⊥BA 交BA 的延长线于点E ,过点B 作BG ⊥DC ,∵BD =BC∴DG =GC =12DC ,∠DBG =∠CBG =12∠DBC∵∠BAD =150°,∴∠EAD =180°-150°=30°∴ED =12AD ∵DA =DC∴ED =DG∵ED ⊥BE ,DG ⊥BG∴∠EBD =∠GBD∴∠ABD =12∠DBC 即∠DBC =2∠ABD(3)如图,过点D 分别作DF ⊥BC 于点F ,DM ⊥EA 交EA 的延长线于点M ,∵AE ⊥BC ,DM ⊥ME ,DF ⊥FE∴四边形DMEF 是矩形∴∠MDF =90°∴∠MDA +∠ADF =90°∵DA ⊥DC∴∠ADC =90°∴∠ADF +∠FDC =90°∴∠FDC =∠MDA在△MAD 与△FCD 中∠MDA =∠FDC ∠DMA =∠DFC DA =DC∴△MAD ≌△FCD∴DM =DF ,∠MDA =∠FDC∴四边形DMEF 是正方形∴DF =EF设∠ABD =α∴∠DBC =2∠ABD =2α∵BD =BC∴∠BDC =∠BCD =12(180°-2α)=90-α∴∠MDA =∠FDC =90°-∠BCD =α∴∠DAE =∠M +∠MDA =90°+α∵∠BAD =150°∴∠BAE =60-α在△BAE 中∠ABE =90°-∠BAE =30°+α∵∠ABE =∠ABD +∠DBC =α+2α=3α∴α=15°∴∠DBC =2α=30°∵BD=2∴DF=12BD=12×2=1在Rt△DEF中,EF=DF=1∴DE=EF2+DF2=2【点睛】本题考查了三角形全等的性质与判定,角平分线的性质与判定,三角形内角和定理,三角形的外角性质,勾股定理,正方形的性质与判定,正确的添加辅助线是解题的关键.【例2】(2022·山西·交城县教学研究办公室八年级期中)综合与实践:问题情境:已知OM是∠AOB的平分线,P是射线OM上的一点,点C,D分别在射线OA,OB上,连接PC,PD.(1)初步探究:如图1,当PC⊥OA,PD⊥OB时,PC与PD的数量关系是;(2)深入探究:如图2,点C,D分别在射线OA,OB上运动,且∠AOB=90°,当∠CPD=90°时,PC与PD在(1)中的数量关系还成立吗?请说明理由;(3)拓展应用:如图3,如果点C在射线OA上运动,且∠AOB=90°,当∠CPD=90°时,点D落在了射线OB的反向延长线上,若点P到OB的距离为3,OD=1,求OC的长(直接写出答案).【答案】(1)PC=PD(2)PC与PD在(1)中的数量关系还成立,理由见解析(3)OC的长为7【分析】(1)根据角平分线的性质进行解答即可;(2)过点P作PE⊥OA,PF⊥OB,垂足分别为E,F,根据“ASA”证明△CPE≌△DPF即可得出结论;(3)过点P作PE⊥OA,PF⊥OB,垂足分别为E,F,先证明四边形OEPF为正方形,然后证明△CPE≌△DPF(ASA),根据正方形的性质以及全等三角形的性质可得结论.【详解】(1)解:∵OM是∠AOB的平分线,PC⊥OA,PD⊥OB,∴PC=PD,故答案为:PC=PD;(2)还成立,理由如下:过点P作PE⊥OA,PF⊥OB,垂足分别为E,F,∵OM平分∠AOB,∴PE=PF,∠PEC=∠PFD=90°,∵∠AOB=90°,∴∠EPF =360°-∠DEO -∠AOB -∠DFO =90°,∵∠CPD =90°∴∠CPD -∠EPD =∠EPF -∠EPD ,即∠CPE =∠DPF ,在△CPE 和△DPF 中,∠CPE =∠DPFPE =PF ∠PEC =∠PFD,∴△CPE ≌△DPF ASA ,∴PC =PD ;(3)过点P 作PE ⊥OA ,PF ⊥OB ,垂足分别为E ,F ,∴四边形OEPF 为矩形,∵OM 是∠AOB 的平分线,∴PE =PF =3,四边形OEPF 为正方形,∵∠AOB =90°,∠OEP =90°,∠OFP =90°,∴∠EPF =90°,∵∠CPD =90°,∴∠CPE +∠EPD =∠EPD +∠DPF =90°,∴∠CPE =∠DPF ,在△CPE 和△DPF 中,∠CPE =∠DPFPE =PF ∠CEP =∠DFP,∴△CPE ≌△DPF (ASA ),∴CE =DF ,∵OD =1,∴DF =OD +OF =1+3=4,∴OC =OE +CE =3+4=7.【点睛】本题考查了全等三角形的判定与性质,正方形的判定与性质,角平分线的性质,熟练掌握相关图形的判定定理以及性质定理是解本题的关键.【例3】(2021·全国·八年级专题练习)如图,已知B (-1,0),C (1,0),A 为y 轴正半轴上一点,点D 为第二象限一动点,E 在BD 的延长线上,CD 交AB 于F ,且∠BDC =∠BAC .(1)求证:∠ABD =∠ACD ;(2)求证:AD 平分∠CDE ;(3)若在点D 运动的过程中,始终有DC =DA +DB ,在此过程中,∠BAC 的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数.【答案】(1)见解析;(2)见解析;(3)不变,60°【分析】(1)根据∠BDC=∠BAC,∠DFB=∠AFC,再结合∠ABD+∠BDC+∠DFB=∠BAC+∠ACD+∠AFC=180°,即可得出结论;(2)过点A作AM⊥CD于点M,作AN⊥BE于点N.运用“AAS”证明△ACM≌△ABN得AM=AN.根据“到角的两边距离相等的点在角的平分线上”得证;(3)运用截长法在CD上截取CP=BD,连接AP.证明△ACP≌ABD得△ADP为等边三角形,从而求∠BAC的度数.【详解】(1)证明:∵∠BDC=∠BAC,∠DFB=∠AFC,又∵∠ABD+∠BDC+∠DFB=∠BAC+∠ACD+∠AFC=180°,∴∠ABD=∠ACD;(2)过点A作AM⊥CD于点M,作AN⊥BE于点N.则∠AMC=∠ANB=90°,∵OB=OC,OA⊥BC,∴AB=AC,∵∠ABD=∠ACD,∴△ACM≌△ABN(AAS),∴AM=AN,∴AD平分∠CDE(到角的两边距离相等的点在角的平分线上);(3)∠BAC的度数不变化.在CD上截取CP=BD,连接AP.∵CD=AD+BD,∴AD=PD,∵AB=AC,∠ABD=∠ACD,BD=CP,∴△ABD≌△ACP,∴AD=AP,∠BAD=∠CAP,∴AD=AP=PD,即△ADP是等边三角形,∴∠DAP=60°,∴∠BAC=∠BAP+∠CAP=∠BAP+∠BAD=60°.【点睛】此题考查全等三角形的判定与性质,运用了角平分线的判定定理和“截长补短”的数学思想方法,综合性较强.【例4】(2021·贵州·九年级专题练习)【特例感知】(1)如图(1),∠ABC是⊙O的圆周角,BC为直径,BD平分∠ABC交⊙O于点D,CD=3,BD=4,求点D到直线AB的距离.【类比迁移】(2)如图(2),∠ABC是⊙O的圆周角,BC为⊙O的弦,BD平分∠ABC交⊙O于点D,过点D作DE⊥BC,垂足为点E,探索线段AB,BE,BC之间的数量关系,并说明理由.【问题解决】(3)如图(3),四边形ABCD为⊙O的内接四边形,∠ABC=90°,BD平分∠ABC,BD=72,AB=6,求△ABC的内心与外心之间的距离.【答案】(1)125;(2)AB+BC=2BE,理由见解析;(3)5.【分析】(1)如图①中,作DF⊥AB于F,DE⊥BC于E.理由面积法求出DE,再利用角平分线的性质定理可得DF=DE解决问题;(2)如图②中,结论:AB+BC=2BE.只要证明ΔDFA≅ΔDEC(ASA),推出AF=CE,RtΔBDF ≅RtΔBDE(HL),推出AF=BE即可解决问题;(3)如图③,过点D作DF⊥BA,交BA的延长线于点F,DE⊥BC,交BC于点E,连接AC,作△ABC△ABC的内切圆,圆心为M,N为切点,连接MN,OM.由(1)(2)可知,四边形BEDF是正方形,BD是对角线.由切线长定理可知:AN=6+10-82=4,推出ON=5-4=1,由面积法可知内切圆半径为2,在RtΔOMN中,理由勾股定理即可解决问题;【详解】解:(1)如图①中,作DF⊥AB于F,DE⊥BC于E.图①∵BD平分∠ABC,DF⊥AB,DE⊥BC,∴DF=DE,∵BC是直径,∴∠BDC=90°,∴BC=BD2+CD2=42+32=5,∵12·BC·DE=12·BD·DC,∴DE=125,∴DF =DE =125.故答案为125(2)如图②中,结论:AB +BC =2BE .图②理由:作DF ⊥BA 于F ,连接AD ,DC .∵BD 平分∠ABC ,DE ⊥BC ,DF ⊥BA ,∴DF =DE ,∠DFB =∠DEB =90°,∵∠ABC +∠ADC =180°,∠ABC +∠EDF =180°,∴∠ADC =∠EDF ,∴∠FDA =∠CDE ,∵∠DFA =∠DEC =90°,∴ΔDFA ≅ΔDEC (ASA ),∴AF =CE ,∵BD =BD ,DF =DE ,∴Rt ΔBDF ≅Rt ΔBDE (HL ),∴BF =BE ,∴AB +BC =BF -AF +BE +CE =2BE .(3)如图③,过点D 作DF ⊥BA ,交BA 的延长线于点F ,DE ⊥BC ,交BC 于点E ,连接AC ,作△ABC △ABC 的内切圆,圆心为M ,N 为切点,连接MN ,OM .由(1)(2)可知,四边形BEDF 是正方形,BD 是对角线.图③∵BD =72,∴正方形BEDF 的边长为7,由(2)可知:BC =2BE -AB =8,∴AC =62+82=10,由切线长定理可知:AN =6+10-82=4,∴ON=5-4=1,设内切圆的半径为r,则12×r×10+12×r×6+12×r×8=12×6×8解得r=2,即MN=2,在RtΔOMN中,OM=MN2+ON2=22+12=5.故答案为5.【点睛】本题属于圆综合题,考查了角平分线的性质定理,全等三角形的判定和性质,勾股定理,解直角三角形,正方形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.培优训练一、解答题1.(2022·全国·八年级课时练习)已知:如图,在四边形ABCD中,BD平分∠ABC,∠A+∠C=180°,BC>BA.求证:点D在线段AC的垂直平分线上.【答案】见解析【分析】在BC上截取BE=BA,连接DE,证明△ABD≌△BED,可得出∠C=∠DEC,则DE=DC,从而得出AD=CD即可证明.【详解】证:如图,在BC上截取BE=BA,连接DE,∵BD=BD,∠ABD=∠CBD,∴△BAD≌△BED,∴∠A=∠DEB,AD=DE,∵∠A+∠C=180°,∠BED+∠DEC=180°,∴∠C=∠DEC,∴DE=DC,∴AD=CD,∴点D在线段AC的垂直平分线上.【点睛】本题考查全等三角形的判定与性质,以及垂直平分线的判定等,学会做辅助线找出全等三角形是解题的关键.2.(2022·全国·八年级课时练习)如图,△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC交BC于点D,过点B作BE⊥AD,交AD延长线于点E,F为AB的中点,连接CF,交AD于点G,连接BG.(1)线段BE与线段AD有何数量关系?并说明理由;(2)判断△BEG的形状,并说明理由.【答案】(1)BE=12AD,见解析;(2)△BEG是等腰直角三角形,见解析【分析】(1)延长BE、AC交于点H,先证明△BAE≌△HAE,得BE=HE=12BH,再证明△BCH≌△ACD,得BH=AD,则BE=12AD;(2)先证明CF垂直平分AB,则AG=BG,再证明∠CAB=∠CBA=45°,则∠GAB=∠GBA= 22.5°,于是∠EGB=∠GAB+∠GBA=45°,可证明△BEG是等腰直角三角形.【详解】证:(1)BE=12AD,理由如下:如图,延长BE、AC交于点H,∵BE⊥AD,∴∠AEB=∠AEH=90°,∵AD平分∠BAC,∴∠BAE=∠HAE,在△BAE和△HAE中,∠AEB=∠AEHAE=AE∠BAE=∠HAE,∴△BAE≌△HAE(ASA),∴BE=HE=12BH,∵∠ACB=90°,∴∠BCH=180°-∠ACB=90°=∠ACD,∴∠CBH=90°-∠H=∠CAD,在△BCH和△ACD中,∠BCH=∠ACDBC=AC∠CBH=∠CAD,∴△BCH≌△ACD(ASA),∴BH=AD,∴BE=12AD.(2)△BEG是等腰直角三角形,理由如下:∵AC=BC,AF=BF,∴CF⊥AB,∴AG=BG,∴∠GAB=∠GBA,∵AC=BC,∠ACB=90°,∴∠CAB=∠CBA=45°,∴∠GAB=1∠CAB=22.5°,2∴∠GAB=∠GBA=22.5°,∴∠EGB=∠GAB+∠GBA=45°,∵∠BEG=90°,∴∠EBG=∠EGB=45°,∴EG=EB,∴△BEG是等腰直角三角形.【点睛】本题考查等腰直角三角形的判定与性质,全等三角形的判定与性质等,理解等腰直角三角形的基本性质,并且掌握全等三角形中常见辅助线的作法是解题关键.3.(2022·江苏·八年级专题练习)在△ABC中,AD为△ABC的角平分线,点E是直线BC上的动点.(1)如图1,当点E在CB的延长线上时,连接AE,若∠E=48°,AE=AD=DC,则∠ABC的度数为 .(2)如图2,AC>AB,点P在线段AD延长线上,比较AC+BP与AB+CP之间的大小关系,并证明.(3)连接AE,若∠DAE=90°,∠BAC=24°,且满足AB+AC=EC,请求出∠ACB的度数(要求:画图,写思路,求出度数).【答案】(1)108°;(2)AC+BP>AB+PC,见解析;(3)44°或104°;详见解析.【分析】(1)根据等边对等角,可得∠E=∠ADE,∠DAC=∠C,再根据三角形外角的性质求出∠ADE=2∠DAC=48°,由此即可解题;(2)在AC边上取一点M使AM=AB,构造△ABP≅△AMP,根据MP+MC>PC即可得出答案;(3)画出图形,根据点E的位置分四种情况,当点E在射线CB延长线上,延长CA到G,使AG=AB,可得GC=EC,可得∠G=∠GEC,设∠ACB=2x,则∠G=∠GEC=90°-x;根据∠BAC= 24°,AD为△ABC的角平分线,可得∠BAD=∠DAC=12°,可证△AGE≅△ABE(SAS),得出∠ABE=∠G=90°-x,利用还有∠ABE=24°+2x,列方程90°-x=24°+2x;当点E在BD上时,∠EAD<90°,不成立;当点E在CD上时,∠EAD<90°,不成立;当点E在BC延长线上,延长CA 到G,使AG=AB,可得GC=EC,得出∠G=∠GEC,设∠ACB=2x,则∠G=∠GEC=x;∠BAC=24°,根据AD为△ABC的角平分线,得出∠BAD=∠DAC=12°,证明△AGE≅△ABE (SAS),得出∠ABE=∠G=x,利用三角形内角和列方程x+24°+2x=180°,解方程即可.【详解】解:(1)∵AE=AD=DC,∴∠E=∠ADE,∠DAC=∠C,∵∠E=48°,∠ADE=∠DAC+∠C,∴∠ADE=2∠DAC=48°,∵AD为△ABC的角平分线,即∠BAC=2∠DAC,∴∠BAC=48°;∴∠ABC=180°-48°-24°=108°(2)如图2,在AC边上取一点M使AM=AB,连接MP,在△ABP和△AMP中,AB=AM∠BAP=∠MAPAP=AP,∴△ABP≅△AMP(SAS),∴BP=MP,∵MP+MC>PC,MC=AC-AM,∴AC-AB+BP>PC,∴AC+BP>AB+PC;(3)如图,点E在射线CB延长线上,延长CA到G,使AG= AB,∵AB+AC=EC,∴AG+AC=EC,即GC=EC,∴∠G=∠GEC,设∠ACB=2x,则∠G=∠GEC=90°-x;又∠BAC=24°,AD为△ABC的角平分线,∴∠BAD=∠DAC=12°,又∵∠DAE=90°,∴∠BAE=90°-∠BAD=78°,∠GAE=90°-∠DAC=78°,∴∠BAE=∠GAE,在△AGE和△ABE中,AE=AE∠GAE=∠BAEAG=AB,∴△AGE≅△ABE(SAS),∴∠ABE=∠G=90°-x,又∵∠ABE=∠BAC+∠ACB=24°+2x,∴90°-x=24°+2x,解得:x=22°,∴∠ACB=2x=44°;当点E在BD上时,∠EAD<90°,不成立;不成立;当点E在CD上时,∠EAD<90°,如图,点E在BC延长线上,延长CA到G,使AG=AB,∵AB+AC=EC,∴AG+AC=EC,即GC=EC,∴∠G=∠GEC,设∠ACB=2x,则∠G=∠GEC=x;又∵∠BAC=24°,AD为△ABC的角平分线,∴∠BAD=∠DAC=12°,又∵∠DAE=90°,在△AGE和△ABE中,AE=AE,∠GAE=∠BAEAG=AB∴△AGE ≅△ABE (SAS ),∴∠ABE =∠G =x ,∴x +24°+2x =180°,解得:x =52°,∴∠ACB =2x =104°.∴∠ACB 的度数为44°或104°.【点睛】本题主要考查了等腰三角形性质、全等三角形判定和性质,角平分线,三角形外角性质,三角形内角和,解一元一次方程,根据角平分线模型构造全等三角形转换线段和角的关系是解题关键.4.(2022·全国·八年级课时练习)如图,在△ABC 中,∠C =90°,AD 是∠BAC 的角平分线,交BC 于点D ,过D 作DE ⊥BA 于点E ,点F 在AC 上,且BD =DF .(1)求证:AC =AE ;(2)若AB =7.4,AF =1.4,求线段BE 的长.【答案】(1)见解析;(2)3【分析】(1)证明△ACD ≌△AED (AAS ),即可得出结论;(2)在AB 上截取AM =AF ,连接MD ,证△FAD ≌△MAD (SAS ),得FD =MD ,∠ADF =∠ADM ,再证Rt △MDE ≌Rt △BDE (HL ),得ME =BE ,求出MB =AB -AM =6,即可求解.【详解】解:(1)证明:∵AD 平分∠BAC ,∴∠DAC =∠DAE ,∵DE ⊥BA ,∴∠DEA =∠DEB =90°,∵∠C =90°,∴∠C =∠DEA =90°,在△ACD 和△AED 中,∠C =∠DEA∠DAC =∠DAE AD =AD,∴△ACD ≌△AED (AAS ),∴AC =AE ;(2)在AB 上截取AM =AF ,连接MD ,在△FAD 和△MAD中,AF=AM∠DAF=∠DAMAD=AD,∴△FAD≌△MAD(SAS),∴FD=MD,∠ADF=∠ADM,∵BD=DF,∴BD=MD,在Rt△MDE和Rt△BDE中,MD=BDDE=DE,∴Rt△MDE≌Rt△BDE(HL),∴ME=BE,∵AF=AM,且AF=1.4,∴AM=1.4,∵AB=7.4,∴MB=AB-AM=7.4-1.4=6,∴BE=12BM=3,即BE的长为3.【点睛】本题考查了全等三角形的判定与性质、角平分线定义、直角三角形的性质、三角形的外角性质等知识;证明△FAD≌△MAD和Rt△MDE≌Rt△BDE是解题的关键.5.(2022·江苏·八年级专题练习)如图1,在△ABC中,CM是AB边的中线,∠BCN=∠BCM交AB延长线于点N,2CM=CN.(1)求证AC=BN;(2)如图2,NP平分∠ANC交CM于点P,交BC于点O,若∠AMC=120°,CP=kAC,求CPCM的值.【答案】(1)见解析;(2)2k k+1【分析】(1)延长CM至点D,使CM=DM,可证ΔACM≅ΔBDM,由全等三角形的性质从而得出AC=BD,根据题目已知,可证ΔDCB≅ΔNCB,由全等三角形的性质从而得出BN=BD,等量代换即可得出答案;(2)如图所示,作CQ=CP,可证ΔCPO≅ΔCQO,由全等三角形的性质相等角从而得出∠1=∠2=∠3,进而得出∠4=∠5,故可证ΔNOB≅ΔNOQ等量转化即可求出CPCM的值.【详解】(1)如图1所示,延长CM至点D,使CM=DM,在△ACM与△BDM中,CM=DM∠AMC=∠BMDAM=BM,∴ΔACM≅ΔBDM,∴AC=BD,∵2CM=CN,∴CD=CN,在△DCB与△NCB中,CD=CN∠DCB=∠NCBCB=CB,∴ΔDCB≅ΔNCB,∴BN=BD,∴AC=BN;(2)如图所示,∵∠AMC=120°,∴∠CMN=60°,∵NP平分∠MNC,∠BCN=∠BCM,∠PNC+∠BCN=12∠AMC=60°,∴∠CON=120°,∠COP=60°,∴∠CMN+∠BOP=180°,作CQ=CP,在△CPO与△CQO中,CQ=CP∠QCO=∠PCOCO=CO,∴ΔCPO≅ΔCQO,∴∠1=∠2=∠3,∴∠4=∠5,在△NOB与△NOQ中,∠4=∠5∠BNO=∠QNONO=NO,∴ΔNOB≅ΔNOQ,∴BN=NQ,∴CN=CP+NB,∴2CM=CP+AC,设AC=a,∴CP=ka,CM=a(k+1)2,∴CP CM =2kk+1.【点睛】本题考查全等三角形的综合应用,掌握全等三角形的判定与性质是解题的关键.6.(2022·全国·八年级课时练习)(1)如图1,射线OP平分∠MON,在射线OM,ON上分别截取线段OA,OB,使OA=OB,在射线OP上任取一点D,连接AD,BD.求证:AD=BD.(2)如图2,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,求证:BC=AC+AD.(3)如图3,在四边形ABDE中,AB=9,DE=1,BD=6,C为BD边中点,若AC平分∠BAE,EC平分∠AED,∠ACE=120°,求AE的值.【答案】(1)见详解;(2)见详解;(3)AE=13【分析】(1)由题意易得∠AOD=∠BOD,然后易证△AOD≌△BOD,进而问题可求证;(2)在BC上截取CE=CA,连接DE,由题意易得∠ACD=∠ECD,∠B=30°,则有△ACD≌△ECD,然后可得∠A=∠CED=60°,则根据三角形外角的性质可得∠EDB=∠B=30°,然后可得DE=BE,进而问题可求证;(3)在AE上分别截取AF=AB,EG=ED,连接CF、CG,同理(2)可证△ABC≌△AFC,△CDE≌△CGE,则有∠ACB=∠ACF,∠DCE=∠GCE,然后可得∠ACF+∠GCE=60°,进而可得△CFG 是等边三角形,最后问题可求解.【详解】证明:(1)∵射线OP平分∠MON,∴∠AOD=∠BOD,∵OD=OD,OA=OB,∴△AOD≌△BOD(SAS),∴AD=BD.(2)在BC上截取CE=CA,连接DE,如图所示:∵∠ACB=90°,∠A=60°,CD平分∠ACB,∴∠ACD=∠ECD,∠B=30°,∵CD=CD,∴△ACD≌△ECD(SAS),∴∠A=∠CED=60°,AD=DE,∵∠B+∠EDB=∠CED,∴∠EDB=∠B=30°,∴DE=BE,∴AD=BE,∵BC=CE+BE,∴BC=AC+AD.(3)在AE上分别截取AF=AB=9,EG=ED=1,连接CF、CG,如图所示:同理(1)(2)可得:△ABC≌△AFC,△CDE≌△CGE,∴∠ACB=∠ACF,∠DCE=∠GCE,BC=CF,CD=CG,DE=GE=1,∵C为BD边中点,∴BC=CD=CF=CG=3,∵∠ACE=120°,∴∠ACB+∠DCE=60°,∴∠ACF+∠GCE=60°,∴∠FCG=60°,∴△CFG是等边三角形,∴FG=CF=CG=3,∴AE=AF+FG+GE=9+3+1=13.【点睛】本题主要考查三角形全等的性质与判定、角平分线的定义、等腰三角形的性质与判定及等边三角形的性质与判定,解题的关键是构造辅助线证明三角形全等.7.(2022·全国·八年级课时练习)已知:AD是△ABC的角平分线,且AD⊥BC.(1)如图1,求证:AB=AC;(2)如图2,∠ABC=30°,点E在AD上,连接CE并延长交AB于点F,BG交CA的延长线于点G,且∠ABG=∠ACF,连接FG.①求证:∠AFG=∠AFC;②若S△ABG:S△ACF=2:3,且AG=2,求AC的长.【答案】(1)见解析;(2)①见解析;②6.【分析】(1)用ASA证明△ABD≌△ACD,即得AB=AC;(2)①证明△BAG≌△CAE可得AG=AE,再用SAS证明△FAG≌△FAE,即得∠AFG=∠AFC;②过F作FK⊥AG于K,由S△ABG:S△ACF=2:3,可得S△CAE:S△ACF=2:3,S△FAE:S△ACF=1:3,而△FAG≌△FAE,故S△FAG:S△ACF=1:3,即得AG:AC=1:3,根据AG=2,可求AC=6.【详解】解:(1)证明:∵AD 是△ABC 的角平分线,∴∠BAD =∠CAD ,∵AD ⊥BC ,∴∠ADB =∠ADC ,在△ABD 和△ACD 中,∠BAD =∠CADAD =AD ∠ADB =∠ADC,∴△ABD ≌△ACD ASA ,∴AB =AC ;(2)①∵AB =AC ,∠ABC =30°,AD ⊥BC ,∴∠BAD =∠CAD =60°,∴∠BAG =60°=∠CAD ,在△BAG 和△CAE 中,∠BAG =∠CAEAB =AC ∠ABG =∠ACE,∴△BAG ≌△CAE ASA ,∴AG =AE ,在△FAG 和△FAE 中,AG =AE∠GAF =∠EAF AF =AF,∴△FAG ≌△FAE SAS ,∴∠AFG =∠AFC ;②过F 作FK ⊥AG 于K ,如图:由①知:△BAG ≌△CAE ,∵S △ABG :S △ACF =2:3,∴S △CAE :S △ACF =2:3,∴S △FAE :S △ACF =1:3,由①知:△FAG ≌△FAE ,∴S △FAG :S △ACF =1:3,∴12AG ⋅FK :12AC ⋅FK =1:3,∴AG :AC =1:3,∵AG =2,∴AC =6.【点睛】本题主要考查了全等三角形的性质与判定,解题的关键在于能够熟练掌握全等三角形的相关知识.8.(2022·全国·八年级)如图1,在△ABC 中,AF ,BE 分别是∠BAC 和∠ABC 的角平分线,AF 和BE 相交于D 点.(1)求证:CD 平分∠ACB ;(2)如图2,过F 作FP ⊥AC 于点P ,连接PD ,若∠ACB =45°,∠PDF =67.5°,求证:PD =CP ;(3)如图3,若2∠BAF +3∠ABE =180°,求证:BE -BF =AB -AE.【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.【分析】(1)过D 点分别作三边的垂线,垂足分别为G 、H 、K ,根据角平分线的定义可证得DG =DH =DK ,从而根据角平分线的判定定理可证得结论;(2)作DS ⊥AC ,DT ⊥BC ,在AC 上取一点Q ,使∠QDP =∠FDP ,通过证明△SQD ≌△TFD 和△QDP ≌△FDP 得到∠PDC =∠PCD =22.5°,从而根据等角对等边判断即可;(3)延长AB 至M ,使BM =BF ,连接FM ,通过证明△AFC ≌△AFM 得到AC =AM ,再结合CE =EB 即可得出结论.【详解】(1)证明:如图所示,过D 点分别作三边的垂线,垂足分别为G 、H 、K ,∵AF ,BE 分别是∠BAC 和∠ABC 的角平分线,∴DG =DH =DK ,∴CD 平分∠ACB ;(2)证明:如图,作DS ⊥AC ,DT ⊥BC ,在AC 上取一点Q ,使∠QDP =∠FDP .∵CD 平分∠ACB ,∴DS =DT ,∵∠QDP =∠FDP =67.5°,∠ACB =45°,∴∠QDF +∠ACB =135°+45°=180°,在四边形QDFC 中,∠CQD +∠DFC =180°,又∵∠DFT +∠DFC =180°,∴∠CQD =∠DFT ,在△SQD 和△TFD 中,∠CQD =∠DFTDS =DT∠DSQ =∠DTF =90°∴△SQD ≌△TFD ,∴QD =FD ,在△QDP 和△FDP 中QD =FD∠QDP =∠FDPDP =DP∴△QDP ≌△FDP,∴∠QPD =∠FPD =45°又∵∠QPD =∠PCD +∠PDC ,∠PCD =22.5°,∴∠PDC =∠PCD =22.5°,∴CP =PD ;(3)证明:延长AB 至M ,使BM =BF ,连接FM .∵AF ,BE 分别是∠BAC 和∠ABC 的角平分线,∴2∠BAF +2∠ABE +∠C =180°,又∵2∠BAF +3∠ABE =180°,∴∠C =∠ABE =∠CBE ,∴CE =EB ,∵BM =BF ,∴∠BFM =∠BMF =∠ABE =∠CBE =∠C ,在△AFC 和△AFM 中,∠C =∠BMF∠CAF =∠BAF AF =AF,∴△AFC ≌△AFM ,∴AC =AM ,∴AE +CE =AB +BM ,∴AE +BE =AB +BF ,∴BE -BF =AB -AE .【点睛】本题考查角平分线的性质与判断,以及全等三角形的判定与性质,灵活结合角平分线的性质构造辅助线是解题关键.9.(2022·湖南·宁远县至善学校八年级阶段练习)在平面直角坐标系中,点A 的坐标是(0,a ),点B 的坐标(b ,0)且a ,b 满足a 2-12a +36+a -b =0.(1)求A 、B 两点的坐标;(2)如图(1),点C 为x 轴负半轴一动点,OC <OB ,BD ⊥AC 于D ,交y 轴于点E ,求证:OD 平分∠CDB .(3)如图(2),点F 为AB 的中点,点G 为x 正半轴点B 右侧的一动点,过点F 作FG 的垂线FH ,交y 轴的负半轴于点H ,那么当点G 的位置不断变化时,S △AFH -S △FBG 的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.【答案】(1)A(0,6),B(6,0);(2)证明见解析;(3)不变化,S△AFH-S△FBG=9.【分析】(1)由非负性可求a,b的值,即可求A、B两点的坐标;(2)过点O作OM⊥BD于M,ON⊥AC于N,根据全等三角形的判定和性质解答即可;(3)由于点F是等腰直角三角形AOB的斜边的中点,所以连接OF,得出OF=BF.∠BFO=∠GFH,进而得出∠OFH=∠BFG,利用等腰直角三角形和全等三角形的判定和性质以及三角形面积公式解答即可.【详解】解:(1)∵a2-12a+36+a-b=0∴(a-6)2+a-b=0,∴a-6=0a-b=0,即a=b=6.∴A(0,6),B(6,0).(2)如图,过点O作OM⊥BD于M,ON⊥AC于N,根据题意可知∠ACO+∠CAO=90°.∵BD⊥AC,∴∠BCD+∠CBE=90°,∴∠CAO=∠CBE.∵A(0,6),B(6,0),∴OA=OB=6.在△AOC和△BOE中,∠CAO=∠EBOOA=OB∠AOC=∠BOE=90°,∴△AOC≅△BOE(ASA).∴OE=OC,AC=BE,S△AOC=S△BOE.∴1 2AC·ON=12BE·OM,∴OM=ON,∴点O一定在∠CDB的角平分线上,即OD平分∠CDB.(3)如图,连接OF,∵△AOB是等腰直角三角形且点F为AB的中点,∴OF⊥AB,OF=FB,OF平分∠AOB.∴∠OFB=∠OFH+∠HFB=90°.又∵FG⊥FH,∴∠HFG=∠BFG+∠HFB=90°,∴∠OFH=∠BFG.∵∠FOB=12∠AOB=45°,∴∠FOH=∠FOB+∠HOB=45°+90°=135°.又∵∠FBG=180°-∠ABO=180°-45°=135°,∴∠FOH=∠FBG.在△FOH和△FBG中∠OFH=∠BFG OF=BF∠FOH=∠FBG ,∴△FOH≅△FBG(ASA).∴S△FOH=S△FBG,∴S△AFH-S△FBG=S△AFH-S△FOH=S△FOA=12S△AOB=12×12OA·OB=14×6×6=9.故不发生变化,且S△AFH-S△FBG=9.【点睛】本题为三角形综合题,考查非负数的性质,角平分线的判定,等腰直角三角形的性质和判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,正确添加辅助线,构造全等三角形解决问题,属于中考压轴题.10.(2022·全国·八年级课时练习)已知:如图,AC∥BD,AE、BE分别平分∠CAB和∠ABD,点E在CD上.用等式表示线段AB、AC、BD三者之间的数量关系,并证明.【答案】AC+BD=AB,理由见见解析【分析】在BA上截取BF=BD,连接EF,先证得△BEF≌△BED,可得到∠BFE=∠D,再由AC∥BD,可得∠AFE=∠C,从而证得△AEF≌△AEC,可得AF=AC,即可求解.【详解】解:AC+BD=AB,证明如下:在BA上截取BF=BD,连接EF,如图所示:∵AE、BE分别平分∠CAB和∠ABD,∴∠EAF=∠EAC,∠EBF=∠EBD,在△BEF和△BED中,BF=BD∠EBF=∠EBDBE=BE,∴△BEF≌△BED(SAS),∴∠BFE=∠D,∵AC∥BD,∴∠C+∠D=180°,∵∠AFE+∠BFE=180°,∴∠AFE+∠D=180°,∴∠AFE=∠C,在△AEF和△AEC中,∠EAF=∠EAC∠AFE=∠CAE=AE,∴△AEF≌△AEC(AAS),∴AF=AC,∵AF+BF=AB,∴AC+BD=AB.【点睛】本题主要考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质定理是解题的关键.11.(2022·全国·八年级课时练习)已知点C是∠MAN平分线上一点,∠BCD的两边CB、CD分别与射线AM、AN相交于B,D两点,且∠ABC+∠ADC=180°.过点C作CE⊥AB,垂足为E.(1)如图1,当点E在线段AB上时,求证:BC=DC;(2)如图2,当点E在线段AB的延长线上时,探究线段AB、AD与BE之间的等量关系;(3)如图3,在(2)的条件下,若∠MAN=60°,连接BD,作∠ABD的平分线BF交AD于点F,交AC于点O,连接DO并延长交AB于点G.若BG=1,DF=2,求线段DB的长.【答案】(1)见解析;(2)AD-AB=2BE,理由见解析;(3)3.【分析】(1)过点C作CF⊥AD,根据角平分线的性质得到CE=CF,证明△BCE≌△DCF,根据全等三角形的性质证明结论;(2)过点C作CF⊥AD,根据角平分线的性质得到CE=CF,AE=AF,证明△BCE≌△DCF,得到DF=BE,结合图形解答即可;(3)在BD上截取BH=BG,连接OH,证明△OBH≌△OBG,根据全等三角形的性质得到∠OHB=∠OGB,根据角平分线的判定定理得到∠ODH=∠ODF,证明△ODH≌△ODF,得到DH=DF,计算即可.【详解】(1)证明:如图1,过点C作CF⊥AD,垂足为F,∵AC平分∠MAN,CE⊥AB,CF⊥AD,∴CE=CF,∵∠CBE+∠ADC=180°,∠CDF+∠ADC=180°,∴∠CBE=∠CDF,在△BCE和△DCF中,∠CBE=∠CDF∠CEB=∠CFD=90°CE=CF,∴△BCE≌△DCF(AAS)∴BC=DC;(2)解:AD-AB=2BE,理由如下:如图2,过点C作CF⊥AD,垂足为F,∵AC平分∠MAN,CE⊥AB,CF⊥AD,∴CE=CF,AE=AF,∵∠ABC +∠ADC =180°,∠ABC +∠CBE =180°,∴∠CDF =∠CBE ,在△BCE 和△DCF 中,∠CBE =∠CDF∠CEB =∠CFD =90°CE =CF,∴△BCE ≌△DCF (AAS ),∴DF =BE ,∴AD =AF +DF =AE +DF =AB +BE +DF =AB +2BE ,∴AD -AB =2BE ;(3)解:如图3,在BD 上截取BH =BG ,连接OH ,∵BH =BG ,∠OBH =∠OBG ,OB =OB在△OBH 和△OBG 中,BH =BG∠OBH =∠OBG OB =OB,∴△OBH ≌△OBG (SAS )∴∠OHB =∠OGB ,∵AO 是∠MAN 的平分线,BO 是∠ABD 的平分线,∴点O 到AD ,AB ,BD 的距离相等,∴∠ODH =∠ODF ,∵∠OHB =∠ODH +∠DOH ,∠OGB =∠ODF +∠DAB ,∴∠DOH =∠DAB =60°,∴∠GOH =120°,∴∠BOG =∠BOH =60°,∴∠DOF =∠BOG =60°,∴∠DOH =∠DOF ,在△ODH 和△ODF 中,∠DOH =∠DOFOD =OD ∠ODH =∠ODF,∴△ODH ≌△ODF (ASA ),∴DH =DF ,∴DB =DH +BH =DF +BG =2+1=3.【点睛】本题考查了角平分线的性质,三角形全等的判定和性质,关键是依照基础示例引出正确辅助线.12.(2022·全国·八年级)在平面直角坐标系中,点A -5,0 ,B 0,5 ,点C 为x 轴正半轴上一动点,过点A 作AD ⊥BC 交y 轴于点E .(1)如图①,若点C 的坐标为(3,0),试求点E 的坐标;(2)如图②,若点C 在x 轴正半轴上运动,且OC <5,其它条件不变,连接DO ,求证:OD 平分∠ADC(3)若点C 在x 轴正半轴上运动,当∠OCB =2∠DAO 时,试探索线段AD 、OC 、DC 的数量关系,并证明.【答案】(1)(0,3);(2)详见解析;(3)AD =OC +CD【分析】(1)先根据AAS 判定△AOE ≌△BOC ,得出OE =OC ,再根据点C 的坐标为(3,0),得到OC =2=OE ,进而得到点E 的坐标;(2)先过点O 作OM ⊥AD 于点M ,作ON ⊥BC 于点N ,根据△AOE ≌△BOC ,得到S △AOE =S △BOC ,且AE =BC ,再根据OM ⊥AE ,ON ⊥BC ,得出OM =ON ,进而得到OD 平分∠ADC ;(3)在DA 上截取DP =DC ,连接OP ,根据三角形内角和定理,求得∠PAO =30°,进而得到∠OCB =60°,根据SAS 判定△OPD ≌△OCD ,得OC =OP ,∠OPD =∠OCD =60°,再根据三角形外角性质得PA =PO =OC ,故AD =PA +PD =OC +CD .【详解】(1)如图①,∵AD ⊥BC ,BO ⊥AO ,∴∠AOE =∠BDE ,又∵∠AEO =∠BED ,∴∠OAE =∠OBC ,∵A (-5,0),B (0,5),∴OA =OB =5,∴△AOE ≌△BOC ,∴OE =OC ,又∵点C 的坐标为(3,0),∴OC =3=OE ,∴点E 的坐标为(0,3);(2)如图②,过点O 作OM ⊥AD 于点M ,作ON ⊥BC 于点N ,∵△AOE ≌△BOC ,∴S △AOE =S △BOC ,且AE =BC ,∵OM ⊥AE ,ON ⊥BC ,∴OM =ON ,∴OD 平分∠ADC ;(3)如所示,在DA 上截取DP =DC ,连接OP ,∵∠OCB =2∠DAO ,∠ADC =90°∴∠PAO +∠OCD =90°,∴∠DAC =90°3=30°,∠DCA =2×90°3=60°∵∠PDO =∠CDO ,OD =OD ,∴△OPD ≌△OCD ,∴OC =OP ,∠OPD =∠OCD =60°,∴∠POA=∠PAO=30°∴PA=PO=OC∴AD=PA+PD=OC+CD即:AD=OC+CD.【点睛】本题属于三角形综合题,主要考查了全等三角形的判定与性质,角平分线的判定定理以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,运用全等三角形的性质进行求解.13.(2022·全国·八年级)如图1,点A是直线MN上一点,点B是直线PQ上一点,且MN⎳PQ.∠NAB和∠ABQ的平分线交于点C.(1)求证:BC⊥AC;(2)过点C作直线交MN于点D(不与点A重合),交PQ于点E,①若点D在点A的右侧,如图2,求证:AD+BE=AB;②若点D在点A的左侧,则线段AD、BE、AB有何数量关系?直接写出结论,不说理由.【答案】(1)见解析;(2)见解析;(3)BE=AD+AB【分析】(1)由平行线性质可得∠NAB+∠ABQ=180°,再由角平分线定义可得∠BAC=12∠NAB,∠CBA=12∠ABQ,再利用三角形内角和定理即可得∠C=90°,即可证明BC⊥AC;(2)①延长AC交PQ点F,先证明AC=FC,再证明△ACD≌△FCE,即可得AD+BE=AB;②方法与①相同.【详解】解:(1)∵MN∥PQ∴∠NAB+∠ABQ=180°∵AC平分∠NAB,BC平分∠ABQ∴∠BAC=12∠NAB,∠CBA=12∠ABQ∴∠BAC+∠ABC=12×180°=90°在△ABC中,∵∠BAC+∠ABC+∠C=180°∴∠C=180°-(∠BAC+∠ABC)=180°-90°=90°∴BC⊥AC;(2)①延长AC交PQ于点F∵BC⊥AC∴∠ACB=∠FCB=90°∵BC平分∠ABF∴∠ABC=∠FBC∴BC=BC∴△ABC≌△FBC∴AC =CF ,AB =BF∵MN ∥BQ∴∠DAC =∠EFC∵∠ACD =∠FCE∴△ACD ≌△FCE∴AD =EF∴AB =BF =BE +EF =BE +AD即:AB =AD +BE②线段AD ,BE ,AB 数量关系是:AD +AB =BE如图3,延长AC 交PQ 点F ,∵MN ⎳PQ .∴∠AFB =∠FAN ,∠DAC =∠EFC∵AC 平分∠NAB∴∠BAF =∠FAN∴∠BAF =∠AFB∴AB =FB∵BC ⊥AC∴C 是AF 的中点∴AC =FC在△ACD 与△FCE 中∠DAC =∠EFC AC =FC ∠ACD =∠FCE∴△ACD ≅△FCE (ASA )∴AD =EF∵AB =FB =BE -EF∴AD +AB =BE【点睛】本题考查了平行线性质,全等三角形性质判定,等腰三角形性质等,解题关键正确添加辅助线构造全等三角形.14.(2018·湖北武汉·八年级期中)在平面直角坐标中,等腰Rt △ABC 中,AB =AC ,∠CAB =90°,A (0,a ),B (b ,0).(1)如图1,若2a-b+(a-2)2=0,求△ABO的面积;(2)如图2,AC与x轴交于D点,BC与y轴交于E点,连接DE,AD=CD,求证:∠ADB=∠CDE;(3)如图3,在(1)的条件下,若以P(0,-6)为直角顶点,PC为腰作等腰Rt△PQC,连接BQ,求证:AP∥BQ.【答案】(1)△ABO的面积=4;(2)证明见解析;(3)证明见解析.【分析】(1)根据绝对值和偶次方的非负性求出a,b,根据三角形的面积公式计算;(2)作AF平分∠BAC交BD于F点,分别证明△ACE≌△BAF,△CED≌△AFD,根据全等三角形的性质证明;(3)过C点作CM⊥y轴于M点,过D点作DN⊥y轴于N点,证明△ACM≌△BAO,根据全等三角形的性质得到CM=AO=2,AM=BO=4,证明四边形ONQB为平行四边形,得到答案.【详解】解:(1)∵2a-b+(a-2)2=0,∴2a-b=0,a-2=0,解得,a=2,b=4,∴A(0,2),B(4,0),∴OA=2,OB=4,∴△ABO的面积=12×2×4=4;(2)作AF平分∠BAC交BD于F点,∵AB=AC,∠CAB=90°,∴∠C=∠ABC=∠DAF=∠BAF=45°,∵∠CAE+∠BAO=∠ABF+∠BAO=90°,∴∠CAE=∠ABF,在△ACE和△BAF中,∠CAE=∠ABFAC=AB∠ACE=∠BAF,∴△ACE≌△BAF(ASA),∴CE=AF,在△CED和△AFD中,CD=AD∠C=∠DAFCE=AF,∴△CED≌△AFD(SAS)∴∠CDE=∠ADB;(3)过C点作CM⊥y轴于M点,过D点作DN⊥y轴于N点,则∠AMC=∠BOA=90°,∵∠CAM+∠BAO=∠ABO+∠BAO=90°,∴∠CAM=∠ABO,在△ACM和△BAO中,。
2024年中考数学复习 三角形中的特殊模型-平分平行(射影)构等腰、角平分线第二定理模型(原卷+答案

三角形中的特殊模型-平分平行(射影)构等腰、角平分线第二定理模型角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
平分平行(射影)构等腰模型、角平行线第二定理模型(内角平分线定理和外角平分线定理模型)平分平行(射影)构等腰1)角平分线加平行线必出等腰三角形.模型分析:由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.平行线、角平分线及等腰,任意由其中两个条件都可以得出第三个。
(简称:“知二求一”,在以后还会遇到很多类似总结)。
平行四边形中的翻折问题就常出现该类模型。
图1图2图3条件:如图1,OO'平分∠MON,过OO'的一点P作PQ⎳ON. 结论:△OPQ是等腰三角形。
条件:如图2,△ABC中,BD是∠ABC的角平分线,DE∥BC。
结论:△BDE是等腰三角形。
条件:如图3,在△ABC中,BO平分∠ABC,CO平分∠ACB,过点O作BC的平行线与AB,AC分别相交于点M,N.结论:△BOM、△CON都是等腰三角形。
2)角平分线加射影模型必出等腰三角形.→图4条件:如图4,BE平分∠CBA,∠ACB=∠CDA=90°. 结论:三角形CEF是等腰三角形。
1(2023·浙江·八年级假期作业)如图,已知∠AOB,以点O为圆心,以任意长为半径画弧,与OA、OB分别于点C、D,再分别以点C、D为圆心,以大于12CD为半径画弧,两弧相交于点E,过OE上一点M作MN∥OA,与OB相交于点N,∠MOB=50°,则∠AOM=.2(2023·浙江·八年级期中)如图,已知△ABC的两边AB=5,AC=8,BO、CO分别平分∠ABC、∠ACB,过点O作DE∥BC,则△ADE的周长等于.3(2023·广东·八年级期末)如图,▱ABCD中,AB=3cm,BC=5cm,BE平分∠ABC交AD于E点,CF 平分∠BCD交AD于F点,则EF的长为cm.4(2023.江苏八年级期中)如图,已知:在△ABC中,∠BAC=90°,AD⊥BC于D,∠BCA的角平分线交AD与F,交AB于E,FG⎳BC交AB于G.AE=4cm,AB=12cm,则BG=,GE=.角平行线第二定理(内角平分线定理和外角平分线定理)模型1)内角平分线定理图1图2图3条件:如图1,在△ABC中,若AD是∠BAC的平分线。
平行线及角平分线类相似

平行线及角平分线类相似中考要求重难点1.相似定义,性质,判定,应用和位似2.相似的判定和证明3.相似比的转化课前预习上一节课我们知道了相似三角形的由来,那你是否知道其他跟金子塔有关的不可思议的事实呢?不仅建造金字搭的技术中,表现了古埃及人的非凡的数学天才;而且,它本身的许多数据,也说明了古埃及人的数学才华,巧夺天工,比如,胡夫金字塔底面周长365米,恰好是一年的天娄;周长乘以2,正是赤道的时分度;搭高乘以10九次方,正是地球到太阳的距离;周长除以塔塔高的2倍,正是圆周率3.1415926……;塔的自重乘以10的15次方,正好是地球的重量;塔里放置的棺材內部尺寸,正好是几千年后希腊数学家华连哥拉斯发现华连哥拉斯数——345::.数学的趣味是无法言语的,同学们可以从身边的点滴去发现其中的奥秘.例题精讲模块一 平行线类相似平行线类相似的基本模型有【例1】 如图,在ABCD 中,点E 在线段DC 上,若12DE EC =∶∶,则BF BE =∶ .EAD BCF【难度】1星【解析】过E 点作AD 的平行线交AC 于H ,可求出结果.HFCBD AE【答案】35∶【巩固】如图,在ABC △中,,,DE BC DG AC CF AB ∥∥∥,则图中与ABC △相似的三角形(ABC △除外)有哪些?GFA BCDE【难度】1星【解析】根据三角形相似的判定定理,可知道ABC ADE DBG FCG △∽△∽△∽△ 【答案】ABC ADE DBG FCG △∽△∽△∽△【拓展】如图,点1234,,,A A A A 在射线OA 上,点123,,B B B 射线OB 上,且112233A B A B A B ∥∥,21A B ∥32A B43A B ∥.若212323,A B B A B B △△的面积分别为1,4,则图中三个阴影三角形面积之和为 .4321【难度】3星【解析】由平行得到相似的三角形.已知212A B B △△A 2B 1B 2,323A B B △的面积分别为1,4,且两三角形相似,因此可得出223312A B A B =,由于223A B A △与233B A B △是等高不等底的三角形,所以面积之比即为底之边比,因此这两个三角形的面积比为1:2,根据323A B B △的面积为4,可求出223A B A △的面积,同理可求出334A B A △和112A B A △的面积.即可求出阴影部分的面积.【答案】10.5∵212A B B △,323A B B △的面积分别为1,4 又∵22332132,A B A B A B A B ∥∥∴2233212323,OB A OB A A B B A B B ∠=∠∠=∠ ∴122233B B A B B A △∽△ ∴1222233312B B A B B B A B == ∴233412A A A A = ∵22323322323331,4A B A B A B S A B A B B S A B ==△△△的面积是4 ∴223323122A B A A B B S S ==△△(等高的三角形的面积的比等于底边的比)同理可得:3343232248A B A A B B S S ==⨯=△△,1122121110.522A B A A B B S S ==⨯=△△∴三个阴影面积之和为0.52810.5++=.【例2】 如图,已知DE AB ∥,2OA OC OE =⋅,求证:AD BC ∥.DOECB A【难度】2星【解析】由一个平行得到比例线段OE ODOA OB=,再根据已知条件2OA OC OE =⋅,以及线段间的等量代换得到OD OAOB OC=,得到证明AOD COB ∆∆∽,得到相等的角DAO BCO ∠=∠,最后得到证明AD BC ∥. 【答案】∵DE AB ∥∴AOB EOD ∆∆∽,OE ODOA OB=, 又∵2OA OC OE =⋅, ∴OE OAOA OC =, ∴OD OAOB OC=, ∵AOD COB ∠=∠, ∴AOD COB ∆∆∽, ∴DAO BCO ∠=∠, ∴AD BC ∥【巩固】在平行四边形ABCD 中,点E 为AD 的中点,连接BE ,交AC 于点F ,则AF CF ∶=( )FED CBA【难度】2星【解析】根据四边形ABCD 是平行四边形,求证AFE BCF △∽△,然后利用其对应边成比例即可求得答案.【答案】12∶∵四边形ABCD 是平行四边形, ∴AFE BCF △∽△, ∴AE AFBC CF=,∵点E 为AD 的中点, ∴12AE AF BC CF ==,【巩固】如图,在ABC ∆的边AB 上取一点D ,在AC 取一点E ,使AD AE =,直线DE 和BC 的延长线相交于P ,求证:BP BDCP CE=. PEDCBA【难度】2星【解析】根据所要证明的结论,由三点定形法可初步判定需要证明PCE PDB △∽△,但根据所给的已知条件无法找到有利的条件得到证明,于是回到题中看看怎么样能利用到已知条件AD AE =,于是尝试着过C 作平行线得到证明.4321MPE D CBA【答案】过C 作CM AB ∥交DP 于M ,∵CM AB ∥, ∴PCM PBD ∆∆∽, ∴BP BDCP CM=, ∵CM AB ∥, ∴14∠=∠, 又∵AD AE =,∴12∠=∠,∴24∠=∠, ∵23∠=∠, ∴34∠=∠, ∴CM CE = ∴BP BDCP CE=【拓展】如图,在ABC △中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=____ ___. MECBA【难度】3星【解析】先介绍常规的解法:BCFE DMA BCFED M A如图,过点C 作DE 或AB 的平行线均可,不妨以左图为例来说明. 过点C 作//CF DE ,交AB 于点F . ∵AM MC =,//CF DE ∴AE EF = ∵14AE AB =∴2BF EF= ∵//CF DE ∴2BC BFCD EF== 当然,过点M 、点E 作适当的平行线,均可作出此题,这里不再给出. 以上这些解法均属于常规解法,下面介绍特殊的解法: 看ABC ∆为直线EM D 所截,由梅涅劳斯定理可知,1AE BD CM EB DC MA⋅⋅= 又14AE AB =,AM CM =,故32BD BC DC CD=⇒= 上述图形是一个经典的梅氏定理的基本图形,解类似的题时,梅氏定理的运用能够带来立竿见影的效果,很快得出答案,梅氏定理的证明见变式1,先讲变式1再介绍本解法.【答案】2【拓展】如图,AD 是ABC △的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.AB CDEF【难度】3星【解析】1()过点D 、E 、F 作平行线均可构造出平行线的基本图形,然后利用 这些基本图形的性质来解题.以下给出6种辅助线(还有几种没给 出),解题过程不再给出.HAB C DEF ABCD EF HHAB CDEFHAB CD EFHAB CDEFHABCD EF当然,本题也可由梅氏定理直接得出结果. 看ADC ∆被直线BEF 所截,由梅氏定理可得1AF CB DEFC BD EA⋅⋅= 又AE DE =,BD CD =,故12AF FC =. 2()结论依然成立,解法同上(包括用梅氏来解题),不再给出. 【答案】1()见解析;2()结论依然成立模块二 角平分线类相似问题角平分线类的相似模型如下:方法点播:角平分线类得相似问题基本就这样的两种模型,辅助线的做法也如图中虚线所示,学生在学这部分知识时,不管是平时测验和期中、期末考试,只要涉及到角平分线和证明相似问题就可以试着做这样的辅助线,基本都可以解决.【例1】 如图,AD 是ABC △的角平分线,求证:AB BDAC CD=D CB A【难度】3星【解析】由角平分线类的相似模型可作出辅助线:过点C 作CE AD ∥交直线AB 于E ,再根据平行得到相似的比例线段,最后题目得证.321EDCBA【答案】过C 作CE AD ∥交直线AB 于E .∵CE AD ∥, ∴1E ∠=∠,23∠=∠ 又∵AD 平分BAC ∠, ∴12∠=∠, ∴3E ∠=∠, ∴AE AC =,由CE AD ∥可得:AB BDAE CD=, ∴AB BDAC CD=【巩固】 已知ABC △中,BAC ∠的外角平分线交对边BC 的延长线于D ,求证:AB BDAC CD=DCBA【难度】4星【解析】由外角平分线证明相似的模型可作辅助线:过C 作CE AD ∥交直线AB 于E ,根据平行得到成比例线段AB BD AE CD =,再根据角与角相等的等量代换证明AE AC =,结论得证AB BDAC CD=. F 4321E DCBA【答案】过C 作CE AD ∥交直线AB 于E∵CE AD ∥, ∴13∠=∠,24∠=∠ 又∵AD 平分CAF ∠, ∴12∠=∠, ∴34∠=∠, ∴AE AC =, 由CE AD ∥可得:AB BDAE CD=, ∴AB BDAC CD=【巩固】在Rt ABC △中,线段CE 平分ACB ∠交AB 于点E ,交斜边上的高AD 于点O ,过O 引BC 的平行线交于F .求证:AE BF =.321OF E DCBA【难度】3星【解析】在相似问题中遇到证明线段相等的问题时一定要能想到:这个证明可能是由两组成比例线段进行等量代换得到.本题由角平分线得到角相等再由都是直角三角形,可证明一组相似三角形得到一组成比例线段CD AC OD AE =,再根据平行线分三角形两边成比例得到比例线段ADABOD BF =,最后再根据一组相似三角形得到成比例线段AD AB CD AC =,等量代换得到ODBFOD AE =,题目得证AE BF =.【答案】∵CE 平分ACB ∠∴23∠=∠∴Rt CAE Rt CDO △∽△ ∴CDACOD AE =又∵OF BC ∥ ∴ADABOD BF =又∵Rt ABD Rt CAD △∽△ ∴AD AB CD AC =,即ODBFOD AE =∴AE BF =注意:应用比例线段证明两直线平行或两线段相等时,(1)要注意如果相关的比例式较多,一时难以作出选择,应将所有相关的比例式都写出来,然后再仔细对比、分析选出有用的。
专题06 全等模型-角平分线模型(解析版)

专题06全等模型-角平分线模型角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各类模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,本专题就角平分线的几类全等模型作相应的总结,需学生反复掌握。
模型1.角平分线垂两边(角平分线+外垂直)【模型解读与图示】条件:如图1,OC 为AOB ∠的角平分线、CA OA ⊥于点A 时,过点C 作CA OB ⊥.结论:CA CB =、OAC ∆≌OBC ∆.图1图2常见模型1(直角三角形型)条件:如图2,在ABC ∆中,90C ∠=︒,AD 为CAB ∠的角平分线,过点D 作DE AB ⊥.结论:DC DE =、DAC ∆≌DAE ∆.(当ABC ∆是等腰直角三角形时,还有AB AC CD =+.)图3常见模型2(邻等对补型)条件:如图3,OC 是∠COB 的角平分线,AC =BC ,过点C 作CD ⊥O A 、CE ⊥OB 。
结论:①180BOA ACB ∠+∠=︒;②AD BE =;③2OA OB AD =+.例1.(2022·北京·中考真题)如图,在ABC ∆中,AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____.【答案】1【分析】作DF AC ⊥于点F ,由角平分线的性质推出1DF DE ==,再利用三角形面积公式求解即可.【详解】解:如图,作DF AC ⊥于点F ,∵AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,∴1DF DE ==,∴1121122ACD S AC DF ∆=⋅=⨯⨯=.故答案为:1.【点睛】本题考查角平分线的性质,通过作辅助线求出三角形ACD 中AC 边的高是解题的关键.例2.(2022·山东泰安·中考真题)如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =()A .40°B .45°C .50°D .60°【答案】C 【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠FAP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°,∴∠CAF=100°,在Rt△PFA和Rt△PMA中,{PA PA PM PF==,∴Rt△PFA≌Rt△PMA(HL),∴∠FAP=∠PAC=50°.故选C.【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM=PN=PF是解题的关键.例3.(2023·山东·七年级专题练习)如图,∠D=∠C=90°,点E是DC的中点,AE平分∠DAB,∠DEA =28°,求∠ABE的大小.【答案】28°【分析】过点E作EF⊥AB于F,根据角平分线上的点到角的两边距离相等可得DE=EF,根据线段中点的定义可得DE=CE,然后求出CE=EF,再根据到角的两边距离相等的点在角的平分线上证明即可得出BE平分∠ABC,即可求得∠ABE的度数.【详解】如图,过点E作EF⊥AB于F,∵∠D=∠C=90°,AE平分∠DAB,∴DE=EF,∵E是DC的中点,∴DE=CE,∴CE=EF,又∵∠C=90°,∴点E在∠ABC的平分线上,∴BE平分∠ABC,又∵AD∥BC,∴∠ABC+∠BAD=180°,∴∠AEB=90°,(1)填空:角平分线的性质定理:角平分线上的点到.符号语言:∵如图1,OP 为COD ∠上的平分线,且,∴.(2)解答:已知:如图2,60AOB ∠=︒,OP 为AOB ∠的平分线,以点P 为顶点的CPD ∠与角的两边相交于点C 、D ,且120CPD ∠=︒.求证:PC PD =.(3)作图:根据以上种情况,再次寻找其它情况,点P P 为AOB ∠的平分线上的点,请你用尺规作图作PE OA ⊥于E ,作PF OB ⊥于F ,90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒,OP 平分AOB ∠,PE PF ∴=,在四边形EOFP 中,60AOB ∠=︒,90PEO PFO ∠=∠=︒,36060290120EPF ∴∠=︒-︒-⨯︒=︒,120CPD ∠=︒ ,CPD EPF ∴∠=∠,CPD EPD EPF EPD ∴∠-∠=∠-∠,CPE DPF ∴∠=∠,PEC PFD ∴≅ (ASA )PC PD ∴=;(3)证明:如图2,作射线PC ,交OA 于C ,作PCN AOB ∠=∠,反向延长NP ,交OB 于D ,则PC PD =;,(4)解:如图3,当ODP ∠和OCP ∠互补时,PC PD =,理由如下:作PE OA ⊥于E ,作PF OB ⊥于F ,90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒,OP 平分AOB ∠,PE PF ∴=,在四边形EOFP 中,90PEO PFO ∠=∠=︒,360290180EPF AOB ∴∠+∠=︒-⨯︒=︒,180CPD AOB ∠+∠=︒ ,CPD EPF ∴∠=∠,CPD EPD EPF EPD ∴∠-∠=∠-∠,CPE DPF ∴∠=∠,PEC PFD ∴≅ (ASA)PC PD ∴=.【点睛】本题考查全等三角形的判定,角平分线的性质等知识,解决问题的关键是熟练掌握有关基础知识.模型2.角平分线垂中间(角平分线+内垂直)【模型解读与图示】条件:如图1,OC 为AOB ∠的角平分线,AB OC ⊥,结论:△AOC ≌△BOC ,OAB ∆是等腰三角形、OC 是三线合一等。
初中数学经典几何模型04-角平分线模型在三角形中的应用(含答案)

初中数学经典几何模型专题04 角平分线模型在三角形中的应用在初中几何证明中,常会遇到与角平分线有关的问题。
不少同学遇到这类问题时,不清楚应该怎样去作辅助线。
实际上这类问题是有章可循的,其策略是:明确辅助线作用,记清相应模型辅助线作法,理解作辅助线以后的目的。
能做到这三点,就能在解题时得心应手。
【知识总结】【模型】一、角平分线垂两边 角平分线+外垂直当已知条件中出现OP 为OAB ∠的角平分线、PM OA ⊥于点M 时,辅助线的作法大都为过点P 作PN OB ⊥即可.即有PM PN =、OMP ∆≌ONP ∆等,利用相关结论解决问题.【模型】二、角平分线垂中间 角平分线+内垂直当已知条件中出现OP 为AOB ∠的角平分线,PM OP ⊥于点P 时,辅助线的作法大都为延长MP 交OB 于点N 即可.即有OMN ∆是等腰三角形、OP 是三线等,利用相关结论解决问题.【模型】三、角平分线构造轴对称 角平分线+截线段等当已知条件中出现OP 为AOB ∠的角平分线、PM 不具备特殊位置时,辅助线的作法大都为在OB 上截取ON OM =,连结PN 即可.即有OMP ∆≌ONP ∆,利用相关结论解决问题.【模型】四、角平分线加平行线等腰现 角平分线+平行线当已知条件中出现OP 为AOB ∠的角平分线,点P 角平分线上任一点时,辅助线的作法大都为过点P 作PM //OB 或PM //OA 即可.即有OMP ∆是等腰三角形,利用相关结论解决问题.1、如图, ABN CBN ∠=∠, P 为BN 上的一点,并且PD BC ⊥于点D ,2AB BC BD +=,求证:180BAP BCP ∠+∠=︒.2、如图,在ABC ∆中,CD 是ACB ∠的平分线,AD CD ⊥于点D ,DE //BC 交AB 于点E ,求证:EA EB =.3、已知:如图7,2,,AB AC BAD CAD DA DB =∠=∠=,求证:DC AC ⊥.4、如图,AB //CD ,AE 、DE 分别平分BAD ∠和ADC ∠.探究:在线段AD 上是否存在点M ,使得2AD EM =.【基础训练】1、如图所示,在四边形ABCD中,DC//AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线交AD,AC于点E、F,则BFEF的值是___________.2、如图,D是△ABC的BC边的中点,AE平分∠BAC,AE⊥CE于点E,且AB =10,AC =16,则DE的长度为______3、如图所示,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当CQ =13CE时,EP+BP =________.【巩固提升】1、如图,F,G是OA上两点,M,N是OB上两点,且FG =MN,S△PFG=S△PMN,试问点P是否在∠AOB 的平分线上?2、已知:在△ABC中,∠B的平分线和外角∠ACE的平分线相交于D,DG//BC,交AC于F,交AB于G,求证:GF =BG CF.3、在四边形ABCD中,∠ABC是钝角,∠ABC+∠ADC =180°,对角线AC平分∠BAD.(1)求证:BC =CD;(2)若AB +AD =AC,求∠BCD的度数;4、如图,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC =a、AC =b、AB =c.(1)求线段BG的长(2)求证:DG平分∠EDF.5、如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),∠B PC=∠BP A,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x.CD的长度是否随着x的变化而变化?若变化,请用含x的代数式表示CD的长度;若不变化,请求出线段CD的长度.6、已知:平面直角坐标系中,四边形OABC的顶点分别为0(0,0)、A(5,0)、B(m,2)、C(m-5,2).(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OP A=90°?若存在,求出m的取值范围;若不存在,请说明理由.(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.7、我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”。
2021-2022学年通用版九年级数学专题讲练《角平分线、平行线与等腰三角形模型》(含答案)

专题六、“角分线、平行线与等腰三角形”模型常见模型1、已知:BD 平分∠ABC ,ED ∥BC结论:①BE =ED. ②△BDE 是等腰三角形2、已知:△ABC ,AB =AC ,AE 是外角∠BAD 的平分线结论:AE ∥BC3、已知:∠EAC 为△ABC 的外角,AB =AC ,AD ∥BC结论:①AD 平分∠EAC ;②∠1=∠2模型应用:1. (2010·深圳)如图所示,在□ABCD 中,AB =5,AD =8,DE 平分∠ADC ,则BE =________答案:32. (2016·深圳改编)如图,在 ABCD 中,AB =6,BC =10,以点B 的圆心,以任意长为半径作弧,分别交BA ,BC 于点P ,Q ,再分别以P ,Q 为圆心,以大于21PQ 的长为半径作弧,两弧在∠ABC 内交于点M ,连接BM 并延长交AD 于点E ,则DE 的长为________.答案:43.已知:如图,在△ABC 中,∠ABC ,∠ACB 的平分线交于点F ,过点F 作DE ∥BC ,分别交AB ,AC 于点D ,E.求证:DE =BD +CE.证明:∵∠ABC和∠ACB的平分线交于F点,∴∠ABF=∠FBC,∠ACF=∠FCB.∵DE∥BC,∴∠FBC=∠BFD,∠FCB=∠EFC,∴∠DBF=∠DFB,∠ECF=∠EFC,∴DB=DF,EC=EF.∵DE=DF+EF,∴DE=BD+CE.4. 已知:AD平分∠BAC,CE∥AD. 求证:AC=AE.证明:∵CE∥AD,∴∠BAD=∠E,∠DAC=∠ACE.∵∠BAD=∠DAC,∴∠E=∠ACE,∴AC=AE.5. (2009·深圳)如图,AB是⊙O的直径,AB=10,DC切⊙O于点C,AD⊥DC,垂足为D,AD交⊙O于点E.求证:AC平分∠BAD.证明:连接OC,由DC是切线得OC⊥DC.又AD⊥DC,∴AD∥OC,∴∠DAC=∠ACO.又由OA=OC,得∠BAC=∠ACO,∴∠DAC=∠BAC.即AC平分∠BAD.6、如图,在□ABCD 中,∠ABC ,∠BCD 的平分线BE ,CF 分别与AD 相交于点E ,F ,BE 与CF 相交于点G.(1)求证:BE∠CF ;(2)若AB =3,BC =5,CF =2,求BE 的长.(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠ABC+∠BCD=180°∵∠ABC ,∠BCD 的平分线BE ,CF 分别与AD 相交于点E 、F ,∴∠EBC+∠FCB=︒=∠+∠902121DCB ABC ,∴EB ⊥FC. (2)解:过A 作AM∠FC ,∠AM∠FC ,∠∠AOB =∠FGB ,∠EB∠FC ,∠∠FGB =90°,∠∠AOB =90°,∠BE 平分∠ABC ,∠∠ABE =∠EBC ,∠AD∠BC ,∠∠AEB =∠CBE ,∠∠ABE =∠AEB ,∠AB =AE =3,∠AO∠BE ,∠BO =EO ,在⎪⎩⎪⎨⎧∠=∠=∠=∠∆∆BOM AOE EO BO MBO AEO MOB AOE 中,和 ,),(MO AO ASA MOB AOE =∴∆≅∆∴,,FC AM CM AF ∥∥∴四边形AMCF 是平行四边形,∴AM=FC=2,∴AO=1,∴EO=,2222=-AO AE .24=∴BE7、(2012·深圳改编)如图,将矩形ABCD 沿直线EF 折叠,使点C 与点A 重合,折痕交AD 于点E ,交BC 于点F ,连接AF ,CE ,求证:四边形AFCE 为菱形.证明:∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠AEF =∠EFC ,由折叠的性质,可得∠AEF =∠CEF ,AE =CE ,AF =CF ,∴∠EFC =∠CEF ,∴CF =CE ,∴AF =CF =CE =AE ,∴四边形AFCE 为菱形8、已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△CFE 中,以点C 为圆心,以任意长为半径作AD ,再分别以点A 和点D 为圆心,大于21AD 长为半径作弧,交EF 于点B ,AB ∥CD. 求证:四边形ACDB 为△CFE 的亲密菱形.证明:∵由已知得,AC =CD ,AB =DB ,由已知尺规作图痕迹得:BC 是∠FCE 的角平分线,∴∠ACB =∠DCB ,又∵AB ∥CD ,∴∠ABC =∠DCB ,∴∠ACB =∠ABC ,∴AC =AB ,又∵AC =CD ,AB =DB ,∴AC =CD =DB =BA ,∴四边形ACDB 为△CFE 的亲密菱形.。
