全国2010年4月自学考试离散数学试题
离散数学自学考试复习题

A.{{a},{b,c},{d}} B.{{a,b},{c},{d}} C.{{a},{b},{c},{d}} D.{{a,b},{c,d}} 44.设A={Ø},B=P(P(A)),以下正确的式子是( ) A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈B C.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B 45.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是( ) A.(X-Y)-Z=X-(Y∩Z) B.(X-Y)-Z=(X-Z)-Y C.(X-Y)-Z=(X-Z)-(Y-Z) D.(X-Y)-Z=X-(Y∪Z) 46.设*是集合A上的二元运算,称Z是A上关于运算*的零元,若( ) A.有x*Z=Z*x=Z B.ZA,且有x*Z=Z*x=Z C.ZA,且有x*Z=Z*x=x D.ZA,且有x*Z=Z*x=Z 47.在自然数集N上,下列定义的运算中不可结合的只有( ) A.a*b=min(a,b) B.a*b=a+b C.a*b=GCD(a,b)(a,b的最大公约数) D.a*b=a(mod b) 48.设R为实数集,R+={x|x∈R∧x>0},*是数的乘法运算,<R+,*>是一 个群,则下列集合关于数的乘法运算构成该群的子群的是( ) A.{R+中的有理数} B.{R+中的无理数} C.{R+中的自然数} D.{1,2,3} 49.设<A,*,>是环,则下列正确的是( ) A.<A,>是交换群 B.<A,*>是加法群 C.对*是可分配的 D.*对是可分配的 50.下列各图不是欧拉图的是( )
37.下列是两个命题变元p,q的小项是( ) A.p∧┐p∧q B.┐p∨q C.┐p∧q D.┐p∨p∨q 38.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不 滑”可符号化为( ) A.p→┐q B.p∨┐q C.p∧q D.p∧┐q 39.下列语句中是命题的只有( ) A.1+1=10 B.x+y=10 C.sinx+siny<0 D.x mod 3=2 40.下列等值式不正确的是( ) A.┐(x)A(x)┐A B.(x)(B→A(x))B→(x)A(x) C.(x)(A(x)∧B(x))(x)A(x)∧(x)B(x) D.(x)(y)(A(x)→B(y))(x)A(x)→(y)B(y) 41.谓词公式(x)P(x,y)∧(x)(Q(x,z)→(x)(y)R(x,y,z)中量词x的辖域是( ) A.(x)Q(x,z)→(x)(y)R(x,y,z)) B.Q(x,z)→(y)R(x,y,z) C.Q(x,z)→(x)(y)R(x,y,z) D.Q(x,z) 42.设R为实数集,函数f:R→R,f(x)=2x,则f是( ) A.满射函数 B.入射函数 C.双射函数 D.非入射非满射 43.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪IA,则 对应于R的A的划分是( )
全国2010年4月高等教育自学考试离散数学试题

全国2010年4月高等教育自学考试离散数学试题 课程代码:02324一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均不得分。
1.下列句子为命题的是( ) A.全体起立! B.x =0C.我在说谎D.张三生于1886年的春天2.下列式子不是..谓词合式公式的是( ) A.),()()),(),()((z x R z z x Q y x P x ∃∨→∀ B. ),()(),(),())((y x P x z x Q y x P y x ∃∧∨∀∀ C. ))()()(())()()(x Q x P x x Q x P x ∨⌝∀⇔→∀ D. ),()()(z y Q x P x ∧∃3.下列式子为矛盾式的是( ) A.P P ⌝∧ B.)(Q P P ∧∨C.P P ⌝∨D.)(Q P ∨⌝ Q P ⌝∧⌝4.设给定赋值N 如下:个体域为自然数集;特定元素a =0;特定函数f (x ,y )=x+y,g (x ,y )=xy ;特定谓词F (x ,y )为x =y 。
在赋值N 下,下列公式为真的是( ) A. )),,(()(x a x g F x ∀B. ))),,(()),,(()()((x a y f F y a x f F y x →∀∀C. )),,(())()((z y x f F z y x ∀∀∀D. )),(),,(())((y x g y x f F y x ∀∀5.对于公式),()()),(),()((z x R z z x Q y x P x ∃∨→∀,下列说法正确的是( ) A.y 是自由变元 B.x 是约束变元C. )(x ∀的辖域是),()()),(),((z x R z z x Q y x P ∃∨→D. )(x ∀的辖域是P (x ,y )6.设论域为{l ,2},与公式)()(x A x ∃等价的是( ) A.A (1)∨A (2) B. A (1)→A (2) C.A (1)D. A (2)→A (1)7.设Z +是正整数集合,f :Z +→Z +,f (n )=2n -2,则f ( )A.仅是入射B.仅是满射C.是双射D.不是函数8.下列关系矩阵所对应的关系具有反自反性的是( ) A.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001110101 B. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101110001 C. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001100100 D. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001010101 9.设R 1和R 2是集合A 上的相容关系,下列关于21R R ⊕的说法正确的是( ) A.一定是相容关系B.一定不是相容关系C.可能是也可能不是相容关系D.一定是等价关系10.设A 是奇数集合,下列构成独异点的是( ) A.<A ,+> B.<A ,-> C.<A ,×>D.<A ,÷>11.设A 是整数集,下列说法正确的是( ) A.<A ,+>有零元 B.<A ,÷>有零元 C.<A ,+>有幺元D.<A ,÷>有幺元12.下列说法不正确...的是( ) A.在实数集上,乘法对加法是可分配的 B.在实数集上,加法对乘法是可分配的 C.在某集合的幂集上,∪对∩是可分配的 D.在某集合的幂集上,∩对∪是可分配的 13.右图的最大入度是( ) A.0 B.1 C.2 D.314.下列可一笔画成的图形是( )15.一棵树有5个3度结点,2个2度结点,其它的都是l 度结点,那么这棵树的结点数是( ) A.13 B.14 C.16 D.17二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
离散数学试题与参考答案

离散数学试题与参考答案(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《离散数学》试题及答案一、选择题:本题共5小题,每小题3分,共15分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 命题公式Q Q P →∨)(为 ( )(A) 矛盾式 (B) 可满足式 (C) 重言式 (D) 合取范式2.设P 表示“天下大雨”, Q 表示“他在室内运动”,则命题“除非天下大雨,否则他不在室内运动”符号化为( )。
(A). P Q →; (B).P Q ∧; (C).P Q ⌝→⌝; (D).P Q ⌝∨.3.设集合A ={{1,2,3}, {4,5}, {6,7,8}},则下式为真的是( ) (A) 1A (B) {1,2, 3}A (C) {{4,5}}A (D) A4. 设A ={1,2},B ={a ,b ,c },C ={c ,d }, 则A ×(B C )= ( )(A) {<1,c >,<2,c >} (B) {<c ,1>,<2,c >} (C) {<c ,1><c ,2>,} (D) {<1,c >,<c ,2>} 5. 设G 如右图:那么G 不是( ). (A)哈密顿图; (B)完全图;(C)欧拉图; (D) 平面图.二、填空题:本大题共5小题,每小题4分,共20分。
把答案填在对应题号后的横线上。
6. 设集合A ={,{a }},则A 的幂集P (A )=7. 设集合A ={1,2,3,4 }, B ={6,8,12}, A 到B 的关系R =},,2,{B y A x x y y x ∈∈=><, 那么R -1=8. 在“同学,老乡,亲戚,朋友”四个关系中_______是等价关系. 9. 写出一个不含“→”的逻辑联结词的完备集 . 10.设X ={a ,b ,c },R 是X 上的二元关系,其关系矩阵为M R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001001101,那么R 的关系图为三、证明题(共30分)11. (10分)已知A 、B 、C 是三个集合,证明A ∩(B ∪C)=(A ∩B)∪(A ∩C) 12. (10分)构造证明:(P (Q S))∧(R ∨P)∧Q R S13.(10分)证明(0,1)与[0,1),[0,1)与[0,1]等势。
自考离散数学考试题库及答案

自考离散数学考试题库及答案一、选择题1. 在离散数学中,命题逻辑的主要研究对象是什么?A. 命题的真假B. 命题的类型C. 命题的表达D. 命题的证明答案:A2. 有限集合M的基数是指什么?A. M中元素的数量B. M的子集数量C. M的幂集D. M的幂集的基数答案:A3. 以下哪个不是图论中的基本概念?A. 顶点B. 边C. 集合D. 子图答案:C二、填空题4. 在命题逻辑中,德摩根定律表示了________和________之间的逻辑关系。
答案:¬(P ∧ Q);¬P ∨ ¬Q5. 一个集合的幂集是指该集合所有________的集合。
答案:子集6. 在图论中,无向图中的路径是顶点和边的________。
答案:交替序列三、解答题7. 证明:若命题P是真命题,则其否定¬P是假命题。
证明:根据命题逻辑的定义,一个命题要么是真要么是假。
如果P 是真命题,那么根据否定的定义,¬P表示P不是真的,这与P是真命题的事实相矛盾。
因此,¬P必须是假命题。
8. 给定集合A={1, 2, 3},求其幂集及其基数。
解答:集合A的幂集包括A的所有子集,即∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}。
共有2^3=8个子集,所以A的幂集的基数是8。
四、应用题9. 在一个无向图中,定义了两个顶点之间的距离为它们之间的最短路径上的边数。
如果图G中有两个顶点u和v,且它们之间的距离是3,证明存在一个顶点w,使得u和w之间的距离是1,v和w之间的距离是2。
证明:由于u和v之间的距离是3,根据距离的定义,存在一条最短路径连接u和v,这条路径至少包含3条边。
设这条路径为u=w1, w2, w3, w4=v,其中每对相邻的顶点之间存在一条边。
根据题设,我们可以取w2作为w,这样u和w之间的距离是1(因为它们之间有一条边w1w2),而v和w之间的距离是2(因为它们之间有两条边w2w3和w3w4)。
【全国自考历年真题10套】02324离散数学2013年4月至2019年10月试题

注意事项:
1.答题前,考生务必将自己的考试课程名称、姓名、准考证号用黑色字迹的签字笔或 钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用 2B 铅笔把答题纸上对应题目的答案标号涂黑。如需改动, 用橡皮擦干净后,再选涂其他答案标号。不能答在试题卷上。
一、单项选择题(本大题共 15 小题,每小题 1 分,共 15 分)
A. (∃x)( A(x) ∧ B(x)) ⇔ (∃x) A(x) ∧ (∃x)B(x)
B. A →(∃x)B(x) ⇔ (∃x)( A → B(x))
C.(∃x)A(x) → B ⇔ (∀x)( A(x) → B)
D. ¬(∃x)A(x) ⇔ (∀x)¬A(x)
4.设 A(x): x 是鸟, B(x): x 会飞,命题“没有不会飞的鸟”符号化为
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出并将“答题纸”
的相应代码涂黑。错涂、多涂或未涂均不得分。
1.设 p:天下雨;q:我走路上学。命题“只要不下雨,我就走路上学”可符号化为
A.p → q
B.q →p
C.┐p → q D.q → ┐p
2.设简单无向图 G 有 16 条边,有 3 个 4 度结点,有 4 个 3 度结点,其余结点的度数均小 3,则 G 中的结点个数至.少.为
02324# 离散数学试题 第 3 页 (共 4 页)
02324# 离散数学试题 第 4 页 (共 4 页)
绝密★考试结束前
全国 2014 年 4 月高等教育自学考试
离散数学试题
课程代码:02324
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分
注意事项: 1.答题前,考生务必将自己的考试课程名称、姓名、准考证号用黑色字迹的签字笔或
离散考试试题及答案

离散考试试题及答案一、选择题(每题5分,共20分)1. 在离散数学中,下列哪个概念不是布尔代数的基本运算?A. 与B. 或C. 非D. 模答案:D2. 集合论中,下列哪个符号表示“属于”关系?A. ∈B. ∉C. ⊆D. ⊂答案:A3. 命题逻辑中,下列哪个符号表示“蕴含”关系?A. ∧B. ∨C. →D. ↔答案:C4. 关系R在集合A上是自反的,意味着什么?A. 对于所有a∈A,(a, a)∈RB. 对于所有a∈A,(a, a)∉RC. 对于所有a∈A,(a, b)∈RD. 对于所有a∈A,(a, b)∉R答案:A二、填空题(每题5分,共20分)1. 一个集合的基数是集合中元素的________。
答案:数量2. 在有向图中,如果存在一条从顶点u到顶点v的路径,则称顶点v 是顶点u的________。
答案:可达的3. 一个图是连通的,当且仅当图中任意两个顶点都是________。
答案:连通的4. 在命题逻辑中,一个命题的否定是________。
答案:它的对立命题三、简答题(每题10分,共30分)1. 请解释什么是图的哈密顿回路。
答案:哈密顿回路是一个图中的闭合回路,它恰好访问图中的每个顶点一次。
2. 描述一下什么是二元关系,并给出一个例子。
答案:二元关系是定义在两个集合上的一个关系,它关联了第一个集合中的元素和第二个集合中的元素。
例如,小于关系是数字集合上的一个二元关系。
3. 什么是图的生成树?答案:图的生成树是图的一个子图,它包含图中的所有顶点,并且是一棵树,即它是连通的且没有环。
四、计算题(每题15分,共30分)1. 给定一个集合A={1,2,3,4,5},计算它的幂集。
答案:幂集P(A)={∅, {1}, {2}, {3}, {4}, {5}, {1,2}, {1,3}, {1,4}, {1,5}, {2,3}, {2,4}, {2,5}, {3,4}, {3,5}, {4,5},{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}, {1,2,3,4}, {1,2,3,5}, {1,2,4,5}, {1,3,4,5}, {2,3,4,5}, {1,2,3,4,5}, A}。
离散数学自考试题及答案

离散数学自考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,下列哪个符号表示“属于”关系?A. ∈B. ∉C. ⊆D. ⊂答案:A2. 命题逻辑中,下列哪个命题是永真命题?A. (p ∧ ¬p) → qB. p ∨ (q ∧ ¬q)C. (p → q) ∧ (q → p)D. ¬(p → ¬p)答案:B3. 函数f: A → B中,如果A中的每个元素都映射到B中的不同元素,则称f为:A. 注入函数B. 满射C. 双射D. 单射答案:C4. 在图论中,下列哪项不是无向图的基本术语?A. 顶点B. 边C. 路径D. 子图答案:D5. 以下哪个算法用于判断一个图是否包含汉密尔顿回路?A. 深度优先搜索B. 广度优先搜索C. 弗洛伊德算法D.Dijkstra算法答案:A6. 命题逻辑中,德摩根定律描述了哪些命题的等价关系?A. ¬(p ∧ q) ≡ ¬p ∨ ¬qB. ¬(p ∨ q) ≡ ¬p ∧ ¬qC. ¬(p → q) ≡ p ∧ ¬qD. 所有以上答案:D7. 在关系数据库中,下列哪个操作用于删除表中的行?A. SELECTB. INSERTC. DELETED. UPDATE答案:C8. 以下哪个是有限自动机的组成部分?A. 状态B. 转移C. 输入D. 所有以上答案:D9. 在布尔代数中,下列哪个操作不是基本操作?A. ANDB. ORC. NOTD. XOR答案:D10. 以下哪个是命题逻辑中的有效论证形式?A. 假言三段论B. 假言推理C. 析取三段论D. 所有以上答案:D二、填空题(每题2分,共20分)11. 在集合{1, 2, 3}的幂集中,含有2个元素的子集有_________。
答案:{{1, 2}, {1, 3}, {2, 3}}12. 如果命题P表示“今天是晴天”,命题Q表示“我去公园”,那么(P ∧ Q)表示_________。
离散数学期末考试题及详细答案

离散数学期末考试题及详细答案一、选择题(每题5分,共20分)1. 下列哪一项是图论中的基本概念?A. 集合B. 函数C. 映射D. 顶点答案:D2. 在逻辑中,下列哪一项表示合取?A. ∨B. ∧C. →D. ¬答案:B3. 以下哪个命题是真命题?A. p ∧ ¬pB. p ∨ ¬pC. p → ¬pD. ¬p → p答案:B4. 在集合论中,下列哪个符号表示集合的交集?A. ∪B. ∩C. ⊆D. ⊂答案:B二、填空题(每题5分,共20分)1. 如果一个图是无环的,则称该图为________。
答案:树2. 在布尔代数中,逻辑或运算的符号是________。
答案:∨3. 如果一个函数f: A → B,则称A为函数f的________。
答案:定义域4. 一个集合的子集个数是2的该集合元素个数次方,这个结论被称为________。
答案:幂集定理三、简答题(每题10分,共30分)1. 请简述图的邻接矩阵和邻接表的定义。
答案:邻接矩阵是一个二维数组,其元素表示图中两个顶点之间是否存在边。
邻接表是图的一种表示方法,其中每个顶点对应一个链表,链表中存储的是与该顶点相邻的顶点。
2. 什么是哥德尔不完备性定理?答案:哥德尔不完备性定理表明,在任何包含基本算术的一致形式系统内,都存在这样的命题:这个命题既不能被证明为真,也不能被证明为假。
3. 请解释什么是二元关系,并给出一个例子。
答案:二元关系是定义在两个集合上的一个子集,它包含所有满足特定条件的有序对。
例如,整数集合上的大于关系就是一个二元关系。
四、计算题(每题15分,共30分)1. 给定一个集合A={1,2,3,4},请计算集合A的幂集。
答案:集合A的幂集是{∅, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,2,4}, {1,3,4},{2,3,4}, {1,2,3,4}}。
自考离散数学考试题及答案

自考离散数学考试题及答案一、选择题(每题2分,共10分)1. 在集合论中,下列哪个符号表示“属于”关系?A. ∈B. ∉C. ⊆D. ∩答案:A2. 有限自动机中的一个状态不包括以下哪个元素?A. 初始状态B. 终止状态C. 转移函数D. 输入符号答案:C3. 在命题逻辑中,德摩根定律描述了哪些命题的等价性?A. (¬P ∧ ¬Q) ↔¬(P ∨ Q)B. (P ∨ Q) ↔¬(¬P ∧ ¬Q)C. (P ∧ Q) ↔¬(P ∨ Q)D. (¬P ∨ ¬Q) ↔¬(P ∧ Q)答案:A4. 以下哪个算法是用于解决图的最短路径问题?A. 欧几里得算法B. 迪杰斯特拉算法C. 快速排序算法D. 弗洛伊德算法答案:B5. 布尔代数中,一个表达式可以有的最大项数是多少?A. nB. 2^nC. n^2D. 2n答案:B二、填空题(每题3分,共15分)6. 在关系数据库中,确保实体完整性的约束称为________。
答案:主键7. 一个有向图中,如果存在从顶点A到顶点B的路径,则称顶点A可以________顶点B。
答案:到达8. 在命题逻辑中,如果命题P和命题Q都为真,则命题P → Q的真值是________。
答案:真9. 一个命题函数的真值表中,如果某一行的P和Q都为假,那么这一行的结果是________。
答案:真10. 在图论中,一个完全图是指图中任意两个顶点都________。
答案:相连三、解答题(共75分)11. (15分)证明:在任何非空集合中,至少存在一个元素不包含于该集合的任何子集中。
答案:略12. (20分)给定一个有向图,描述如何使用拓扑排序算法来对图中的顶点进行排序。
答案:略13. (20分)解释什么是正规表达式,并给出一个例子来说明如何使用它来匹配字符串。
答案:略14. (20分)证明:在任何无向图中,边数最多的生成子图最多有3n/2条边,其中n是顶点的数量。
自考离散数学试题及答案

自考离散数学试题及答案一、选择题(每题2分,共20分)1. 在集合论中,下列哪个符号表示“属于”关系?A. ∈B. ∉C. ⊆D. ⊂答案:A2. 命题逻辑中,下列哪个表达式表示“非”操作?A. ∧B. ∨C. ¬D. →答案:C3. 在下列哪个图论的术语中,表示图中任意两个顶点都相连?A. 无向图B. 有向图C. 完全图D. 二分图答案:C4. 布尔代数中,下列哪个操作是“或”?A. ∧C. ¬D. →答案:B5. 以下哪个是等价关系的属性?A. 自反性B. 对称性C. 反对称性D. 传递性答案:A6. 有限自动机中,状态可以被分为哪两种类型?A. 初始状态和终止状态B. 接受状态和拒绝状态C. 确定状态和非确定状态D. 静态状态和动态状态答案:B7. 在关系数据库中,下列哪个操作用于删除表中的行?A. INSERTB. DELETEC. UPDATED. SELECT答案:B8. 以下哪个是谓词逻辑中的量词?B. ∃C. ∧D. ∨答案:A9. 在命题逻辑中,德摩根定律描述了哪些逻辑运算的对偶性?A. ∧ 和∨B. ¬和→C. ¬和↔D. → 和↔答案:A10. 树的深度优先搜索(DFS)算法通常使用哪种数据结构来实现?A. 队列B. 栈C. 链表D. 哈希表答案:B二、填空题(每题3分,共30分)11. 在集合{1, 2, 3, 4, 5}中,子集的总数是_________。
答案:3212. 如果命题P为真,则命题P → Q的真值表中,Q的值必须为_________。
答案:真13. 在有向图中,一个顶点的入度是指_________。
答案:指向该顶点的边的数量14. 一个关系R(A, B, C)中,如果对于任意两个元组,当它们在属性A上的值相等时,它们在属性B和C上的值也相等,则称R具有_________。
答案:候选键15. 在布尔代数中,表达式(A ∧ B) ∨ (A ∧ ¬B)的结果是_________。
《离散数学》试题含答案

《离散数学》试题含答案⼀、填空题1设集合A,B,其中A={1,2,3}, B= {1,2}, 则A - B=____________________; ρ(A) - ρ(B)=__________________________ .2. 设有限集合A, |A| = n, 则|ρ(A×A)| = __________________________.3.设集合A = {a, b}, B = {1, 2}, 则从A到B的所有映射是__________________________ _____________, 其中双射的是__________________________.4. 已知命题公式G=?(P→Q)∧R,则G的主析取范式是_________________________________________________________________________________________.5.设G是完全⼆叉树,G有7个点,其中4个叶点,则G的总度数为__________,分枝点数为________________.6设A、B为两个集合, A= {1,2,4}, B = {3,4}, 则从A?B=_________________________; A?B=_________________________;A-B=_____________________ .7. 设R是集合A上的等价关系,则R所具有的关系的三个特性是______________________,________________________, _______________________________.8. 设命题公式G=?(P→(Q∧R)),则使公式G为真的解释有__________________________,_____________________________, __________________________.9. 设集合A={1,2,3,4}, A上的关系R1 = {(1,4),(2,3),(3,2)}, R1 = {(2,1),(3,2),(4,3)}, 则R1?R2 =________________________,R2?R1 =____________________________, R12=________________________.10. 设有限集A, B,|A| = m, |B| = n, 则| |ρ(A?B)| = _____________________________.11设A,B,R是三个集合,其中R是实数集,A = {x | -1≤x≤1, x∈R}, B = {x | 0≤x < 2, x∈R},则A-B =__________________________ , B-A = __________________________ ,A∩B = __________________________ , .13.设集合A={2, 3, 4, 5, 6},R是A上的整除,则R以集合形式(列举法)记为__________________________________________________________________.14. 设⼀阶逻辑公式G = ?xP(x)→?xQ(x),则G的前束范式是__________________________ _____.15.设G是具有8个顶点的树,则G中增加_________条边才能把G变成完全图。
离散数学考试试题(A卷及答案)

离散数学考试试题(A 卷及答案)一、 (10 分)判断下列公式的类型(永真式、永假式、可满足式)?1)((P Q)∧Q)一 ((Q∨R)∧Q) 2)((Q P)∨P)∧ (P∨R)3)((P∨Q)R)((P∧Q)∨R)解: 1)永真式; 2) 永假式; 3)可满足式。
二、 (8 分) 个体域为{1, 2},求x3y (x+y=4)的真值。
解:x3y (x+y=4) 一 x ((x+1=4)∨(x+2=4))一((1+1=4)∨(1+2=4))∧((2+1=4)∨(2+1=4))一(0∨0)∧(0∨1)一1∧1一0三、 (8 分) 已知集合 A 和 B 且|A|=n, |B|=m,求 A 到 B 的二元关系数是多少? A 到 B 的函数数是多少?解:因为|P(A×B) |=2|A×B|=2|A| |B|=2mn,所以 A 到 B 的二元关系有 2mn 个。
因为|BA|= |B| |A|=mn,所以 A 到 B 的函数 mn 个。
四、 (10 分) 已知 A={1,2,3,4,5}和 R={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>},求 r(R) 、s(R)和 t(R)。
解: r(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<1,1>,<2,2>,<3,3>,<4,4>,<5,5>} s(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<3,2>,<4,3>,<4,5>}t(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<1,1>,<1,3>,<2,2>,<2,4>,<1,4>}五、 (10 分) 75 个儿童到公园游乐场,他们在那里可以骑旋转木马,坐滑行铁道,乘宇宙飞船,已知其中20 人这三种东西都乘过,其中 55 人至少乘坐过其中的两种。
2010~2011学年度第一学期离散数学试题A卷及答案

2010~2011学年度第 一 学期《离散数学》试卷(A 卷)适用专业年级:2009信息与计算科学 网络工程 软件工程及计算机科学与技术专业(本)考 试 形 式:( )开卷、(√)闭卷二级学院: 行政班级: 学 号: 教 学 班: 任课教师: 姓 名: 注:学生在答题前,请将以上内容完整、准确填写,填写不清者,成绩不计。
一、选择题(每小题 3分,共 15 分。
请将答案填在下面的表格内)1.设命题公式G :()p q r ⌝↔∧,则使公式G 取值为1的,,p q r 赋值分别为( )(A )0,0,0 (B )0,0,1 (C )0,1,1 (D )1,1,1 2.以下的联结词不是联结词完备集的是( ) (A )1{}S =⌝∧, (B )1{}S =⌝∨, (C )1{}S =∧∨→↔,,,(D )1{}S =↓3.下述等价式不正确的是( ) (A )()()xAx x A x ⌝∀⇔∃⌝ (B )()()xA x x A x ⌝∃⇔∀⌝(C )()()x A x B xA x B∀→⇔∃→() (D )()()x A x B xA x B∃→⇔∃→()4.设集合A={a,b },A 上的关系R={<a,a >,<b,b > },则R 是( ) (A )是等价关系但不是偏序关系 (B )是偏序关系但不是等价关系 (C ) 既是等价关系又是偏序关系 (D )既不是等价关系又不是偏序关系 5.无向图G 是欧拉图当且仅当G 是连通的且( )………………………………………线………………………………………订………………………………………装…………………………………………………(A )G 中各顶点的度数均相等 (B )G 中各顶点的度数之和为偶数(D )G 中各顶点的度数均为奇数二、填空题(每题 3分,共15分)1.“有的运动员不是大学生”符号化为 . (设P(x):x 是运动员;Q(x):x 是大学生)2. 设S ={<1,2>,<2,4>,<3,3>},R ={<1,3>,<2,4>,<4,2>}, 则S R = .3.下图所具有的关系性质有: .4.设有一棵树,它有2个2度结点,1个3度结点,3个4度结点,其余为叶 则它的树叶数为 个. 共有6个结点11条边,则它的面数为 . 三、计算题: 求公式()p q r →⌝↔的主析取范式和主合取范式(10 分)四、演绎证明: 前提:p ,,,q pr q s r p q∨→→→⌝∧⌝ 结论:s (10分)五、设A={1,2,3,4},R 是A 上的一个关系,R={<a,b>|a ,b ∈A ,(a-b)/2=k ,k ∈Z},证明R 是A 上的等价关系,并按关系R 给出A 上的划分。
离散数学考试试题(A、B卷及答案)

离散数学考试试题(A卷及答案)一、证明题(10分)1) (P∧Q∧A→C)∧(A→P∨Q∨C)⇔ (A∧(P↔Q))→C。
P<->Q=(p->Q)合取(Q->p)证明: (P∧Q∧A→C)∧(A→P∨Q∨C)⇔(⌝P∨⌝Q∨⌝A∨C)∧(⌝A∨P∨Q∨C)⇔((⌝P∨⌝Q∨⌝A)∧(⌝A∨P∨Q))∨C反用分配律⇔⌝((P∧Q∧A)∨(A∧⌝P∧⌝Q))∨C⇔⌝( A∧((P∧Q)∨(⌝P∧⌝Q)))∨C再反用分配律⇔⌝( A∧(P↔Q))∨C⇔(A∧(P↔Q))→C2) ⌝(P↑Q)⇔⌝P↓⌝Q。
证明:⌝(P↑Q)⇔⌝(⌝(P∧Q))⇔⌝(⌝P∨⌝Q))⇔⌝P↓⌝Q。
二、分别用真值表法和公式法求(P→(Q∨R))∧(⌝P∨(Q↔R))的主析取范式与主合取范式,并写出其相应的成真赋值和成假赋值(15分)。
主析取范式与析取范式的区别:主析取范式里每个括号里都必须有全部的变元。
主析取范式可由析取范式经等值演算法算得。
证明:公式法:因为(P→(Q∨R))∧(⌝P∨(Q↔R))⇔(⌝P∨Q∨R)∧(⌝P∨(Q∧R)∨(⌝Q∧⌝R))⇔(⌝P∨Q∨R)∧(((⌝P∨Q)∧(⌝P∨R))∨(⌝Q∧⌝R))分配律⇔(⌝P∨Q∨R)∧(⌝P∨Q∨⌝Q)∧(⌝P∨Q∨⌝R)∧(⌝P∨R∨⌝Q)∧(⌝P ∨R∨⌝R)⇔(⌝P∨Q∨R)∧(⌝P∨Q∨⌝R)∧(⌝P∨⌝Q∨R)⇔4M∧5M使(非P析取Q析取R)为0所赋真值,即100,二进制M∧6为4⇔0m∨1m∨2m∨3m∨7m所以,公式(P→(Q∨R))∧(⌝P∨(Q↔R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
真值表法:P Q R Q↔R P→(Q∨R)⌝P∨(Q↔R) (P→(Q∨R))∧(⌝P∨(Q↔R))0 0 0 0 0 1 0 1 00 1 11 0 0 1 0 1 1 1 0 1 1 1 1111111111111111111111由真值表可知,公式(P→(Q∨R))∧(⌝P∨(Q↔R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
离散数学考试试题及答案

离散数学考试试题及答案离散数学考试试题及答案离散数学是计算机科学和数学中的一门重要学科,它研究的是离散的结构和对象。
离散数学的理论和方法在计算机科学、信息科学、通信工程等领域具有广泛的应用。
下面将为大家提供一些离散数学考试试题及答案,希望对大家的学习和复习有所帮助。
1. 集合论题目(1) 设A={1,2,3,4,5},B={3,4,5,6,7},求A∪B的结果。
答案:A∪B={1,2,3,4,5,6,7}(2) 设A={1,2,3,4,5},B={3,4,5,6,7},求A∩B的结果。
答案:A∩B={3,4,5}(3) 设A={1,2,3,4,5},B={3,4,5,6,7},求A-B的结果。
答案:A-B={1,2}2. 图论题目(1) 给定一个无向图G,顶点集为V={A,B,C,D,E},边集为E={(A,B),(A,C),(B,D),(C,D),(D,E)},求该图的邻接矩阵。
答案:邻接矩阵为:A B C D EA 0 1 1 0 0B 1 0 0 1 0C 1 0 0 1 0D 0 1 1 0 1E 0 0 0 1 0(2) 给定一个有向图G,顶点集为V={A,B,C,D,E},边集为E={(A,B),(B,C),(C,D),(D,E),(E,A)},求该图的邻接表。
答案:邻接表为:A ->B ->C ->D ->E -> AB -> CC -> DD -> EE -> A3. 命题逻辑题目(1) 判断以下命题是否为永真式:(p∨q)∧(¬p∨r)∧(¬q∨¬r)。
答案:是永真式。
(2) 给定命题p:如果天晴,那么我去游泳;命题q:我没有去游泳。
请判断以下命题的真假:(¬p∨q)∧(p∨¬q)。
答案:是真命题。
4. 关系代数题目(1) 给定关系R(A,B,C)和S(B,C,D),求R⋈S的结果。
离散数学考试试题及答案

离散数学考试试题及答案一、单项选择题(每题5分,共20分)1. 在离散数学中,以下哪个概念不是布尔代数的基本元素?A. 逻辑与B. 逻辑或C. 逻辑非D. 逻辑异或答案:D2. 下列哪个命题不是命题逻辑中的命题?A. 所有学生都是勤奋的B. 有些学生是勤奋的C. 学生是勤奋的D. 勤奋的学生答案:D3. 在集合论中,以下哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 以下哪个图不是无向图?A. 简单图B. 完全图C. 有向图D. 多重图答案:C二、填空题(每题5分,共20分)1. 如果一个命题的逆否命题为真,则原命题的________为真。
答案:逆命题2. 在图论中,如果一个图的任意两个顶点都由一条边连接,则称这个图为________图。
答案:完全3. 一个集合的幂集是指包含该集合的所有________的集合。
答案:子集4. 如果一个函数的定义域和值域都是有限集合,那么这个函数被称为________函数。
答案:有限三、简答题(每题10分,共30分)1. 请简述什么是图的欧拉路径。
答案:欧拉路径是一条通过图中每条边恰好一次的路径。
2. 解释什么是二元关系,并给出一个例子。
答案:二元关系是指定义在两个集合之间的关系,它将第一个集合中的元素与第二个集合中的元素联系起来。
例如,小于关系就是一个二元关系。
3. 请说明什么是递归函数,并给出一个简单的例子。
答案:递归函数是一种通过自身定义来计算函数值的函数。
例如,阶乘函数就是一个递归函数,定义为:n! = n * (n-1)!,其中n! = 1当n=0时。
四、计算题(每题10分,共30分)1. 计算以下逻辑表达式:(P ∧ Q) ∨ ¬R答案:首先计算P ∧ Q,然后计算¬R,最后计算两者的逻辑或。
2. 给定集合A = {1, 2, 3},B = {2, 3, 4},求A ∪ B。
答案:A ∪ B = {1, 2, 3, 4}3. 已知函数f(x) = 2x + 3,求f(5)。
4月全国自考离散数学试题及答案解析试卷及答案解析真题
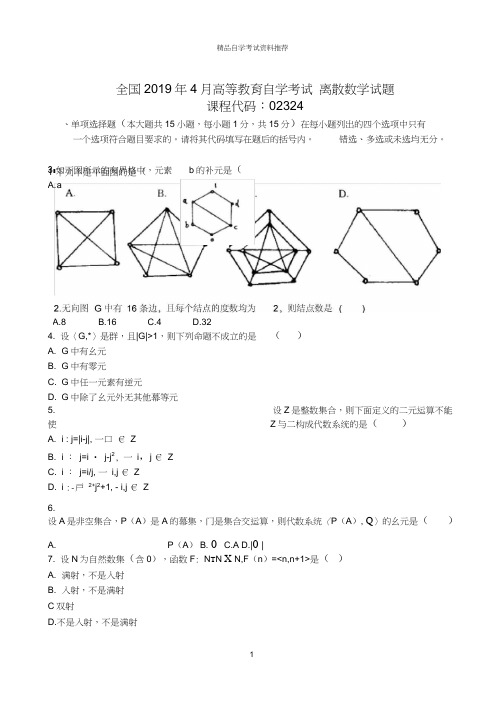
4. 设〈G,*〉是群,且|G|>1,则下列命题不成立的是 ( )A. G 中有幺元B. G 中有零元C. G 中任一元素有逆元D. G 中除了幺元外无其他幕等元 5. 设Z 是整数集合,则下面定义的二元运算不能使Z 与二构成代数系统的是()A. i : j=|i-j|, 一口 € ZB. i : j=i • j-j 2, 一 i ,j € ZC. i : j=i/j, 一 i,j € ZD. i :-戸 2+j 2+1, - i,j € Z6.设A 是非空集合,P (A )是A 的幕集,门是集合交运算,则代数系统〈P (A ), Q 〉的幺元是( )A.P (A ) B. 0 C.A D.|0 |7. 设N 为自然数集(含0),函数F : N T N X N,F (n )=<n,n+1>是( )A. 满射,不是入射B. 入射,不是满射 C 双射D.不是入射,不是满射全国2019年4月高等教育自学考试 离散数学试题课程代码:02324、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个选项中只有 一个选项符合题目要求的。
请将其代码填写在题后的括号内。
错选、多选或未选均无分。
C.4 A.8B.16 D.321•下列不是平面图的是( 3•如下图所示的有界格中,元素 A. a B.b 的补元是(8•设A={a,b,c},则下列是集合A的划分的是()A. {{b,c},{c}}B.{{a,b},{a,c}}C.{{a,b},c}D.{{a},{b,c}}9•设集合X={0,1,2,3} ,R 是X 上的二元关系,R={<0,0>,<0,2>,<1,2>,<1,3>,<2,0>,<2,1>,<3,3,>},则R的关系矩阵M R是()-10101[10101000们[111011100B.001110100011A.00011100C.0101D.0001-001 1_10001_11110_11010一10. 下列命题中,不正确的是()A. { 0 } € { 0 ,{ 0}}B. { 0 } € { 0 ,{{ 0 }}}C. { 0 }』{ 0,{ 0 }}D. 0 三{ 0 ,{ 0 }}11. 设个体域是正整数集,则下列公式中真值为真的公式是()A. ( - x)( y)(x • y=0)B. ( —x)( y)(x • y=1)C. ( x)( y)(x • y=2)D. (一x)( - y)( z)(x-y=z)12. 令F(x):x是金属,G(y):y是液体,H(x,y):x可以溶解在y中,则命题“任何金属可以溶解在某种液体中”可符号化为()A. (- x)(F(x) A ( y)(G(y) A H(x,y)))B. (-x)( (x)F(x) T (G(y) H(x,y)))C. (—x)(F(x) T( y)(G(y) A H(x,y)))x)(F(x) T( y)(G(y) T H(x,y))13. 在个体域D={a,b}中,与公式(x)A(x)等价又不含量词的公式是()A.A(a) A A(b)B.A(a) T A(b)C.A(a) V A(b)D.A(b) T A(a)14. 下列句子是命题的是()A. 水开了吗?B. x>1.5C. 再过5000年,地球上就没水了。
离散数学考试题及详细参考答案

离散数学考试题(后附详细答案)一、命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.二、简答题(共6道题,共32分)1.求命题公式(P→(Q→R))↔(R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)∀x∃y(x+y=4)b)∃y∀x (x+y=4)3.求∀x(F(x)→G(x))→(∃xF(x)→∃xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A⋃B)-C=(A-B) ⋃(A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)三、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→⌝F)→⌝C, B→(A∧⌝S)⇒B→Eb)∀x(P(x)→⌝Q(x)), ∀x(Q(x)∨R(x)),∃x⌝R(x) ⇒∃x⌝P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠∅且B≠∅,关系R满足:<<x1,y1>,<x2,y2>>∈R,当且仅当< x1, x2>∈R1且<y1,y2>∈R2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全国2010年4月自学考试离散数学试题
课程代码:02324
一、单项选择题(本大题共15小题,每小题1分,共15分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均不得分。
1.下列句子为命题的是( )
A.全体起立!
B.x =0
C.我在说谎
D.张三生于1886年的春天
2.下列式子不是..
谓词合式公式的是( ) A.),()()),(),()((z x R z z x Q y x P x ∃∨→∀
B. ),()(),(),())((y x P x z x Q y x P y x ∃∧∨∀∀
C. ))()()(())()()(x Q x P x x Q x P x ∨⌝∀⇔→∀
D. ),()()(z y Q x P x ∧∃
3.下列式子为矛盾式的是( )
A.P P ⌝∧
B.)(Q P P ∧∨
C.P P ⌝∨
D.)(Q P ∨⌝ Q P ⌝∧⌝
4.设给定赋值N 如下:个体域为自然数集;特定元素a =0;特定函数f (x ,y )=x+y,g (x ,y )=xy ;特定谓词F (x ,y )为x =y 。
在赋值N 下,下列公式为真的是( )
A. )),,(()(x a x g F x ∀
B. ))),,(()),,(()()((x a y f F y a x f F y x →∀∀
C. )),,(())()((z y x f F z y x ∀∀∀
D. )),(),,(())((y x g y x f F y x ∀∀
5.对于公式),()()),(),()((z x R z z x Q y x P x ∃∨→∀,下列说法正确的是( )
A.y 是自由变元
B.x 是约束变元
C. )(x ∀的辖域是),()()),(),((z x R z z x Q y x P ∃∨→
D. )(x ∀的辖域是P (x ,y )
6.设论域为{l ,2},与公式)()(x A x ∃等价的是( )
A.A (1)∨A (2)
B. A (1)→A (2)
C.A (1)
D. A (2)→A (1)
7.设Z +是正整数集合,f :Z +→Z +,f (n )=2n -2,则f ( )
A.仅是入射
B.仅是满射
C.是双射
D.不是函数
8.下列关系矩阵所对应的关系具有反自反性的是( )
A.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001110101
B. ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡101110001
C. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001100100
D. ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡001010101 9.设R 1和R 2是集合A 上的相容关系,下列关于21R R ⊕的说法正确的是( )
A.一定是相容关系
B.一定不是相容关系
C.可能是也可能不是相容关系
D.一定是等价关系
10.设A 是奇数集合,下列构成独异点的是( )
A.<A ,+>
B.<A ,->
C.<A ,×>
D.<A ,÷>
11.设A 是整数集,下列说法正确的是( )
A.<A ,+>有零元
B.<A ,÷>有零元
C.<A ,+>有幺元
D.<A ,÷>有幺元
12.下列说法不正确...
的是( ) A.在实数集上,乘法对加法是可分配的
B.在实数集上,加法对乘法是可分配的
C.在某集合的幂集上,∪对∩是可分配的
D.在某集合的幂集上,∩对∪是可分配的
13.右图的最大入度是( )
A.0
B.1
C.2
D.3
14.下列可一笔画成的图形是(
)
15.一棵树有5个3度结点,2个2度结点,其它的都是l 度结点,那么这棵树的结点数是
( )
A.13
B.14
C.16
D.17
二、填空题(本大题共10小题,每小题2分,共20分)
请在每小题的空格中填上正确答案。
错填、不填均不得分。
16.请写出表示分配律的两个命题公式等价定理________,________。
17.n 个命题变元的________称为大项,其中每个变元与它的否定不能同时出现,但两者必须________。
18.在谓词推理过程中,由)()(x P x ∀得到P (a ),其中a 为论域的某个个体,用的是________规则,记为________规则。
19.请用联结词⌝,∨表示联结词∧和联结词→:________,________。
20.设A ={1,2,3,4},B ={2,4,6},则A -B =________,A ⊕B =________。
21.给出A ={l ,2}上的一个等价关系________,并给出其对应的划分________。
22.设A ={l ,2,3,4},A 上的二元关系R ={<1,2>,<2,3>,<3,2>},S ={<l ,3>,<2,3>,<4,3>},则R ∩S =________,(R —S )-1=________。
23.代数系统<A ,+,。
>是域,则________和________都是交换群。
24.若图中存在________,它经过图中所有的________,则称该图为汉密尔顿图。
25.n 点完全图记为K n ,那么当________时,K n 是平面图,当_____时,K n 是非平面图。
三、计算题(本大题共6小题,每小题5分,共30分)
26.列出)(P Q → ))((Q R P →∨的真值表。
27.用等值演算求→P (Q R )的主析取范式。
28.设A ={1,2,3,4},给定A 上的二元关系R ={<1,2>,<2,1>,<2,3>,<3,4>},求R 的传递闭包。
29.求右图所示格的所有5元和6元子格。
30.求<Z 7一{0},⊗>的所有生成元及所有2阶、3阶子群,其中⊗为模7乘法。
31.用矩阵的方法求右图中结点v 1,v 3之间长度为2的路径的数目。
四、证明题(本大题共3小题,第32小题8分,第33、34小题各6分,共20分)
32.用推理方法证明:
)(
,,,S P R R Q Q P ∧⌝⌝⌝∨⌝→ S ⌝。
33.设H 是G 的非空子集,则<H ,·>是群<G ,·>的子群当且仅当对任意a ,b ∈H 有a ·b -1∈H 。
34.证明整数集Z 上的大于等于关系“≥”是一个偏序关系。
五、综合应用题(本大题共2小题,第35小题6分,第36小题9分,共15分)
35.将下面命题符号化,并构造推理证明:
所有有理数是实数,有些有理数是整数,所以有些实数是整数。
36.某城市拟在六个区之间架设有线电话网,其网点间的距离如下列有权矩阵给出,请绘出有权图,给出架设线路的最优方案,并计算线路的总长度。
⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0061050007089670302
1003040580401092010。
