GPS七参数的计算
GPS入门+四,七参数设置

入门疑难解答:1.用gps测图本地中央子午线是118度而我把它设置成117度了,怎么扭转成118度的平面坐标?扭转后误差大吗?答: 是高精度测量还是手持机测量.如果是手持机它一般只手机经纬度,对你输入的中央子午线没任何关系,直接改为118就可以了,在说怎么会有118的中央子午线呢,北京54本来就是117或123114°<X<=120°都属于在6度带上的20带,所以无影响.2.某地的经度为116度23分,计算它所在的6度带和3度带号,相应6度带和3度带的中央子午线的经度是多少答:若按6°带,该区属于20带,则转换的坐标为:x=2769558.792,y=20457640.788(Y 坐标即东坐标,20457640.788中前面20两位数是带数,为了区分不影响坐标值,通常是以中央子午线为X坐标,赤道为Y坐标建立坐标系; 又因中国版图东西跨度大也就造成了带数较多,有可能20带的坐标在21带(以21带建立坐标系)上的坐标值为负,所以坐标一般向东+500000便于计算,若按3°带,该区为39带,坐标为:x=2769558.792,y=39457640.788为20345,其所处的六度带的中央经线经度为:6°×20-3°=117°(适用于1∶2.5万和1∶5万地形图)。
三度带中央经线经度的计算:中央经线经度=3°×当地带号116.23度23分=116.383度6度带计算:116.383/6=19.397 即20带中央经线经度=20*6-3=117度3度带计算:116.383/6=38.794 即39带中央经线经度=39*3=117度GPS数设置。
南方RTK使用中参数的求取及分类一、控制点坐标库的应用GPS 接收机输出的数据是WGS-84 经纬度坐标,需要转化到施工测量坐标,这就需要软件进行坐标转换参数的计算和设置,控制点坐标库就是完成这一工作的主要工具。
七参数 四参数 高程拟合 适用范围

七参数四参数高程拟合适用范围在地理测量学领域,七参数和四参数的概念是常见且重要的。
这两种参数与高程拟合相关,主要用于地球表面的测量和建模。
本文将介绍七参数和四参数的定义、计算方法以及各自的适用范围。
一、七参数七参数是指用于地球表面精确测量的参数集合。
它由三个旋转参数(即绕X、Y和Z轴的旋转角度)、三个平移参数(即沿X、Y和Z 轴的平移距离)以及一个尺度因子参数组成。
这些参数可以用来将地球表面上的点从一个坐标系统转换到另一个坐标系统。
七参数的计算通常需要通过相关算法和数学模型来完成。
其中旋转参数和平移参数可以通过大地测量技术和测角仪等设备进行测量,而尺度因子参数可以通过大地水准测量和高程基准面来确定。
通过这些参数,可以对地球表面上的点进行准确的坐标转换和测量。
七参数适用范围广泛,主要用于大尺度地形测量、航空摄影测量、遥感影像处理等领域。
它能够解决地球表面局部变形、形变监测和地壳运动等问题,具有重要的实际应用价值。
二、四参数四参数是指用于地球表面近似测量的参数集合。
它由两个旋转参数(即绕Z轴的旋转角度和绕X轴的斜率角度)和两个平移参数(即沿X和Y轴的平移距离)组成。
四参数可以用来进行粗略的坐标转换和测量,尤其适用于地球表面小范围的测量和建模。
四参数的计算相对简单,通常可以通过简化的数学模型和算法来完成。
这些参数可以通过全球导航卫星系统(GNSS)和全球定位系统(GPS)等技术进行测量,也可以通过辅助设备和软件进行计算和调整。
四参数适用范围相对狭窄,主要用于地图制图、城市规划、地理信息系统(GIS)等领域。
它能够满足一般性的坐标转换和测量需求,具有简便、快速和经济的特点。
三、高程拟合高程拟合是指根据一定的模型和算法,对地球表面上的高程数据进行拟合和估算的过程。
在地理测量学中,高程拟合通常与坐标转换和大地水准测量紧密相关。
高程拟合的常用模型包括二次曲线拟合、三次样条插值和贝塞尔曲线拟合等。
这些模型基于地球表面的几何性质和地域特征,通过最小二乘法和拟合优度等统计指标,对高程数据进行曲线拟合和插值处理,从而得到地形表面的高程模型。
(TGO)关于七参数求法

输入中央子午线
再输入长半轴与扁率
Hale Waihona Puke 基准转换选七参数分别将TGO求出的七个参数输入即可
点接受
水平平差和垂直平差选无平差,然后接受即可
再接受,参数设置完毕
方法
七参数
绕X轴旋转
-0°00'01.047243"
绕Y轴旋转
0°00'00.018181"
绕Z轴旋转
0°00'00.387181"
沿x轴转换
90.623m
沿Y轴转换
73.722m
沿Z轴转换
-14.381m
比例因子(ppm)
281.953
回到顶部
将七参数输入到手簿里面就可以了
新任务,点坐标系统
点键入参数
点改变选择当地坐标系
确认
插入点
将三个点的WGS84和当地坐标分别输入,注意点名不能一样
输入后点插入
点“测量”-“GPS点校正”
选7参数,水平平差,垂直平差空着,然后点“点列表”
分别选取两套坐标
点确认
点计算
会出来残差,如果残差过大,可能是点输入错误或者精度不够造成的
再点报告就可以看到七参数了
数据传送参数
GPS七参数的计算

通过三个或三个以上已知点求解七参数模型中的参数:不同空间直角坐标系之间的变换,其参数有(ΔX0,ΔY0,ΔZ0,ωX,ωY,ωZ,m)七个,其中(ΔX0,ΔY0,ΔZ0)为坐标平移量,(ωX,ωY,ωZ)为坐标轴间的三个旋转角度(又称为欧拉角),m为尺度因子。
七参数模型如图。
以WGS84坐标系转换为北京54坐标系为例:为计算模型中的七个参数,至少需要三个已知点的北京54空间坐标(X,Y,Z)BJ54和WGS-84空间坐标(X,Y,Z)WGS84,利用最小二乘法求出七参数。
然而,我们已知的三个公共控制点的坐标成果,一种是GPS 观测中可直接获得的WGS84椭球下的大地坐标经纬度(B,L,H),另一种是工程测量中使用的是高斯投影后的平面直角坐标(x,y,h)。
即已知的三个公共控制点的坐标成果就是这两种形式的坐标表来表示的。
首先,我们要把这两种形式的坐标都转换为七参数模型中的空间直角坐标。
步骤如下:1.将WGS84椭球下的大地坐标经纬度(B,L,H),采用WGS84椭球参数,转换为WGS84的空间直角坐标(X,Y,Z)2.将北京54投影平面直角坐标(x,y,h),采用克拉索夫斯基椭球参数,转换为大地坐标((B,L,H)后,再转换为北京54的空间直角坐标(X,Y,Z)。
3.将转换得到的三个公共点的北京54空间坐标(X,Y,Z)BJ54和WGS-84空间坐标(X,Y,Z)WGS84代入七参数模型中,求解七个参数。
以上转换过程十分复杂,即涉及到大地坐标经纬度与空间直角坐标的换算,还涉及到空间直角坐标与平面直角坐标的投影。
通常,我也使用已有的计算程序来求解七参数的,在很多这些求解七参数的程序中,直接采用的是WGS84的大地坐标和北京54大地坐标来计算,就是你只需输入三个已知点的一套WGS84的大地坐标和一套北京54大地坐标,即可为你求解出七参数。
在很多GPS基线解算与平差软件中,都提供了求解七参数/四参数的工具,你可以自己试试。
利用七参数进行坐标转换公式

利用七参数进行坐标转换公式
坐标转换是指将一种坐标系中的坐标转换为另一种坐标系中的
坐标。
在测量、地图制图和地理信息系统等领域中,常常需要进行坐标转换。
常用的坐标转换方法有七参数法、四参数法和三参数法等。
七参数法是较为精确的坐标转换方法,适用于大范围、大量数据的坐标转换。
七参数法基于地球的旋转和形状变化,通过旋转角、旋转轴、比例因子和三个方向的平移量来描述坐标系之间的差异。
假设已知两种坐标系的某一点的坐标(X,Y,Z),且已知它们之间的七参数,可以通过以下公式进行坐标转换:
X1 = s*(X - Z*y + Y*z) + Tx
Y1 = s*(Y + Z*x - X*z) + Ty
Z1 = s*(Z - Y*x + X*y) + Tz
其中,s为比例因子,Tx、Ty、Tz分别为三个方向的平移量,x、y、z为旋转轴的方向余弦值。
需要注意的是,七参数法所描述的坐标系之间的差异是三维的,因此在进行坐标转换时,需要考虑高程的变化。
如果只需要进行水平坐标的转换,可以采用四参数法或三参数法。
总之,选择合适的坐标转换方法和参数,可以提高坐标转换的精度和效率,为地理空间信息的采集、存储和处理提供基础支撑。
- 1 -。
七参数转换法推导公式

七参数转换法推导公式七参数转换法是一种地理坐标系转换的方法,用于将一个坐标系中的坐标转换到另一个坐标系中。
它通过七个参数来描述两个坐标系之间的差异,从而实现坐标的转换。
下面将对七参数转换法的原理进行推导,并给出相应的公式。
我们假设有两个坐标系,分别为坐标系A和坐标系B。
其中,坐标系A的原点为(Xa, Ya, Za),坐标系B的原点为(Xb, Yb, Zb)。
我们需要将坐标系A中的点(Pa, Qa, Ra)转换到坐标系B中,得到坐标(Pb, Qb, Rb)。
根据七参数转换法的原理,我们知道坐标系A和坐标系B之间的差异主要包括平移、旋转和尺度变换。
下面对这三个差异分别进行推导。
1. 平移差异假设坐标系A和坐标系B之间的平移差异为(dx, dy, dz),则坐标系A中的点(Pa, Qa, Ra)经过平移变换后得到坐标系B中的点(Pb', Qb', Rb'),其中:Pb' = Pa + dxQb' = Qa + dyRb' = Ra + dz2. 旋转差异假设坐标系A和坐标系B之间的旋转差异为(ωx, ωy, ωz),其中ωx表示绕x轴旋转的角度,ωy表示绕y轴旋转的角度,ωz表示绕z轴旋转的角度。
我们可以通过旋转矩阵来描述旋转变换。
假设旋转矩阵为R,则坐标系A中的点(Pa, Qa, Ra)经过旋转变换后得到坐标系B中的点(Pb'', Qb'', Rb''),其中:Pb'' = R11 * Pa + R12 * Qa + R13 * RaQb'' = R21 * Pa + R22 * Qa + R23 * RaRb'' = R31 * Pa + R32 * Qa + R33 * Ra3. 尺度变换差异假设坐标系A和坐标系B之间的尺度变换差异为(m, n, p),其中m 表示x轴的尺度变换比例,n表示y轴的尺度变换比例,p表示z轴的尺度变换比例。
七参数四参数转化

七参数四参数转化七参数和四参数转化是在大地测量中常用的两种经纬度转换方法,用于将不同坐标参考系下的坐标相互转换。
下面将详细介绍七参数和四参数转化的原理和应用。
1.七参数转化七参数转化是一种常用的大地测量中的坐标转换方法,其基本原理是通过七个参数来描述两个坐标参考系的空间相对关系。
这七个参数包括三个平移参数(dx, dy, dz),三个旋转参数(rx, ry, rz),以及一个尺度因子(s)。
假设我们有一个已知坐标参考系A,以及一个需要转换到的目标坐标参考系B,我们可以通过测量的方式获得A到B之间的七个参数,并利用这些参数将A坐标系下的点转换到B坐标系下的点。
七参数转化的公式如下:Xb = s(Rx * Xa - Ry * Za + Rz * Ya) + dxYb = s(Ry * Xa + Rx * Za - Rz * Xa) + dyZb = s(Rz * Xa + Rx * Ya + Ry * Xa) + dz其中(Xa,Ya,Za)是坐标参考系A中的点的坐标,(Xb,Yb,Zb)是坐标参考系B中的点的坐标。
七参数转化广泛应用于地理信息系统(GIS)、大地测量、导航等领域。
通过七参数转化,可以将不同坐标系统下的点转换到同一坐标系统下,实现数据融合和统一管理。
四参数转化是七参数转化的一种特殊情况,即在七参数转化中忽略了旋转和尺度因子的影响。
四参数转化只考虑了平移因子,即通过三个平移参数(dx, dy, dz)来描述两个坐标参考系的空间相对关系。
四参数转化的公式如下:Xb = Xa + dxYb = Ya + dyZb = Za + dz其中(Xa,Ya,Za)是坐标参考系A中的点的坐标,(Xb,Yb,Zb)是坐标参考系B中的点的坐标。
四参数转化通常应用于简单的坐标系转换,适用于小区域的坐标变换问题。
总结:七参数和四参数转化是大地测量中常用的坐标转换方法,用于将不同坐标参考系下的点的空间位置相互转换。
两种七参数坐标转换方法

两种七参数坐标转换方法七参数坐标转换方法是一种将不同坐标系之间的坐标进行转换的方法。
常用于地理信息系统(GIS)、大地测量学和空间测量学等领域。
以下介绍两种常见的七参数坐标转换方法:1.七参数最小二乘法:七参数最小二乘法是通过最小化两个坐标系之间的残差平方和来求解七个参数的方法。
假设有两个坐标系A和B,七个参数分别为平移量(ΔX,ΔY,ΔZ)、旋转角度(θX,θY,θZ)和尺度比例(k)。
通过找到最佳的七个参数值,使得在坐标系A和B之间的转换中,两个坐标系之间的差异最小。
2.矩阵变换法:矩阵变换法是将坐标系A和坐标系B之间的转换表示为一个矩阵的乘法运算。
这种方法将七个参数分别表示为一个3×3的旋转矩阵R和一个3×1的平移矩阵T。
具体的转换公式为:```BX=RX*AX+T```其中,BX和AX分别为坐标系B和坐标系A中的坐标值,RX为旋转矩阵,T为平移矩阵。
通过确定旋转矩阵和平移矩阵的数值,可以将坐标系A中的坐标转换为坐标系B中的坐标。
这两种七参数坐标转换方法在实际应用中都有其优缺点。
七参数最小二乘法在计算过程中需要通过迭代方法来找到最优的参数值,计算量较大;而矩阵变换法相对来说计算较为简单。
然而,七参数最小二乘法在处理大数据集时可能会得到更精确的结果。
对于具体的应用场景,可以根据实际需求选择合适的方法。
此外,在实际应用中,还有一些常见的改进七参数坐标转换方法,例如七参数地面控制点法和七参数线性组合法等。
这些方法通过引入更多的控制点或采用线性组合的方式,可以提高坐标转换的精度和稳定性。
总的来说,七参数坐标转换方法是地理信息系统、大地测量学和空间测量学等领域中常用的一种坐标转换方法,通过确定平移量、旋转角度和尺度比例等参数,可以将不同坐标系之间的坐标进行转换。
在实际应用中,可以根据具体需求选择合适的转换方法,并根据实际情况进行适当的改进。
七参数计算公式

七参数计算公式七参数计算公式什么是七参数计算公式?七参数计算公式,也称作七参数转换公式,是地理信息系统(GIS)中一种用于处理地图投影和坐标转换的数学公式。
通过该公式,可以将某个地理坐标系统下的坐标转换为另一个地理坐标系统下的坐标。
七参数公式的计算原理七参数的计算原理基于相似性变换和坐标运算。
具体来说,这其中涉及到尺度因子、平移、旋转和投影四个方面的参数。
七参数公式的组成七参数计算公式主要由以下几个部分组成:1.尺度因子(Scale Factor)–表示不同地图投影之间比例误差的参数。
–一般为一个实数,用于缩放或放大坐标。
–通常用S表示。
2.X轴旋转角(ΔX Rotation)–表示绕X轴旋转的角度。
–一般为一个实数,用于调整X轴方向的坐标。
–通常用RX表示。
3.Y轴旋转角(ΔY Rotation)–表示绕Y轴旋转的角度。
–一般为一个实数,用于调整Y轴方向的坐标。
–通常用RY表示。
4.Z轴旋转角(ΔZ Rotation)–表示绕Z轴旋转的角度。
–一般为一个实数,用于调整Z轴方向的坐标。
–通常用RZ表示。
5.X轴平移参数(ΔX Translation)–表示在X轴方向上的平移量。
–一般为一个实数,用于调整X轴方向的坐标。
–通常用DX表示。
6.Y轴平移参数(ΔY Translation)–表示在Y轴方向上的平移量。
–一般为一个实数,用于调整Y轴方向的坐标。
–通常用DY表示。
7.Z轴平移参数(ΔZ Translation)–表示在Z轴方向上的平移量。
–一般为一个实数,用于调整Z轴方向的坐标。
–通常用DZ表示。
七参数公式的示例下面是一个七参数计算公式的示例:X' = S*(X - RZ*Y + RY*Z) + DXY' = S*(RZ*X + Y - RX*Z) + DYZ' = S*(-RY*X + RX*Y + Z) + DZ其中,(X, Y, Z)是原始坐标系统下的坐标,(X’, Y’, Z’)是转换后的坐标。
icoord 转换坐标 七参数计算

icoord 转换坐标七参数计算一、引言在地理信息系统(GIS)中,坐标转换是一个常见的操作。
为了实现不同坐标系之间的转换,我们通常使用七参数法。
这是一种基于地图投影和坐标变换的算法,常用于高精度定位和地理数据采集等领域。
本文将详细介绍七参数计算的基本原理和具体应用。
二、七参数概述坐标转换的七参数包括三个旋转角(x,y,z)和四个平移参数(dx,dy,dz,dx0)。
这些参数描述了坐标系之间的差异,通过一系列复杂的数学运算,可以将一种坐标系下的坐标转换为另一种坐标系下的坐标。
在实际应用中,我们需要根据实际情况选择合适的参数值,以保证转换结果的准确性。
三、转换步骤1.收集数据:需要转换的原始坐标数据是必须的。
通常需要至少三个不同的点在两个坐标系之间进行测量,以获取七参数值。
2.计算旋转角和平移参数:根据测量结果,使用适当的算法计算旋转角和平移参数。
通常使用最小二乘法或其他优化算法进行求解。
3.转换坐标:根据计算得到的旋转角和平移参数,将原始坐标转换为目标坐标系下的坐标。
四、应用场景七参数计算在许多领域都有应用,如航空摄影测量、卫星定位、GIS数据转换等。
特别是在高精度定位和地图制作等领域,七参数计算具有重要意义。
通过使用七参数法,我们可以将不同来源、不同精度、不同坐标系下的地理数据统一到一个标准化的框架下,方便数据的共享和应用。
五、注意事项1.参数选择:在实际应用中,需要根据测量数据的特点和精度要求选择合适的参数值。
如果参数选择不当,可能会导致转换结果的不准确。
2.数据质量:测量数据的质量对七参数计算结果的影响很大。
因此,在应用七参数计算前,需要对数据进行仔细检查和校准。
3.误差处理:由于测量误差和计算误差的存在,七参数计算结果可能存在一定的误差。
在实际应用中,需要根据具体情况对误差进行适当的处理。
总之,七参数计算是一种高精度的坐标转换方法,适用于各种地理信息系统中的坐标转换需求。
通过正确的参数选择、数据校准和误差处理,我们可以获得准确可靠的坐标转换结果。
七参数计算步骤

七参数计算步骤;
用于计算两个坐标系统之间的转换关系,包括“四参数+高程拟合”、“七参数”、“一步法”、“三参数”。
这里以计算七参数为例子:
1、先将移动台设置好并达到固定解,然后设置好坐标系统及中央子午线,在不带任何参
数的情况下对参与解算的控制点进行采集。
2、将控制点(已知点)导入控制点库,避免在添加点的时候要一个个输入进去。
3、控制点采集完毕后点击“参数”——“坐标系统(左上角)”——选择“参数计算”—
—计算类型选择“七参数”——点击“添加”——在点库中调取出相应的点,源点表示实测的原始点,目标点表示已知点,将所有的点都对应起来保存——点击“解算”。
——点击“运用”
注:源点表示实测的原始点,目标点表示已知点(两个点是在不同坐标系下的同一个点)。
所有点都添加完毕。
所有点添加完毕后点击“解算”点名前方打钩表示参与解算。
解算完后会出现“七参数结果”——点击“运用”。
拖动滚动条查看平面和高程中误差是否满
足要求(一般在3公分以下)。
如果有个别点不满足要求,将其点名前方钩取消掉不参与解算。
参数运用完后可在“椭球转换”中查看。
然
后将移动台在已知点上检查,看手簿显示坐标是否与控制点坐标吻合。
4、如果移动台接收的差分源发生改变(接收其他基站的信号)移动台需要做点平移进行校正。
测得当前点(控制点)坐标,调取已知点坐标或输入然后点“计算”
dx/dy/dh是当前点与控制点计算出来的差值,点击应用后当前坐标会显示准确坐标。
七参数求解过程
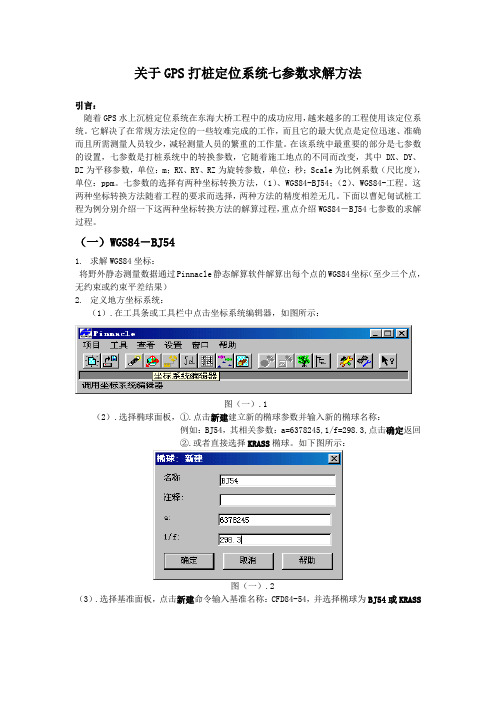
关于GPS打桩定位系统七参数求解方法引言:随着GPS水上沉桩定位系统在东海大桥工程中的成功应用,越来越多的工程使用该定位系统。
它解决了在常规方法定位的一些较难完成的工作,而且它的最大优点是定位迅速、准确而且所需测量人员较少,减轻测量人员的繁重的工作量。
在该系统中最重要的部分是七参数的设置,七参数是打桩系统中的转换参数,它随着施工地点的不同而改变,其中DX、DY、DZ为平移参数,单位:m;RX、RY、RZ为旋转参数,单位:秒;Scale为比例系数(尺比度),单位:ppm。
七参数的选择有两种坐标转换方法,(1)、WGS84-BJ54;(2)、WGS84-工程。
这两种坐标转换方法随着工程的要求而选择,两种方法的精度相差无几。
下面以曹妃甸试桩工程为例分别介绍一下这两种坐标转换方法的解算过程,重点介绍WGS84-BJ54七参数的求解过程。
(一)WGS84-BJ541.求解WGS84坐标:将野外静态测量数据通过Pinnacle静态解算软件解算出每个点的WGS84坐标(至少三个点,无约束或约束平差结果)2.定义地方坐标系统:(1).在工具条或工具栏中点击坐标系统编辑器,如图所示:图(一).1(2).选择椭球面板,①.点击新建建立新的椭球参数并输入新的椭球名称:例如:BJ54,其相关参数:a=6378245,1/f=298.3,点击确定返回②.或者直接选择KRASS椭球。
如下图所示:图(一).2(3).选择基准面板,点击新建命令输入基准名称:CFD84-54,并选择椭球为BJ54或KRASS图(一).3(4).选择平面坐标系统面板,点击新建命令建立平面坐标系统名称:CFD84-54点击新建命令输入如下内容:①.基准面名称:CFD84-54;②.影方式:TMERC TM投影(一个投影带):③.单位名称:Meters;④.点击编辑投影进入下一栏:⑤.输入:中央子午线:118°30′;尺比度:1;E偏移量:500000。
万能地图下载器中的七参数是什么
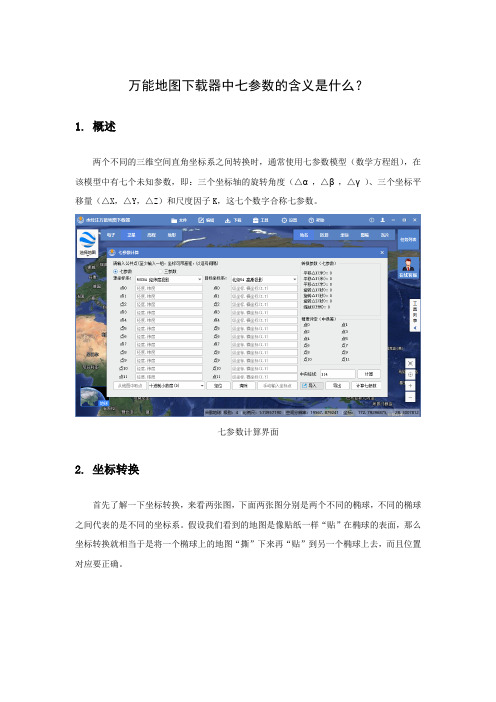
万能地图下载器中七参数的含义是什么?1.概述两个不同的三维空间直角坐标系之间转换时,通常使用七参数模型(数学方程组),在该模型中有七个未知参数,即:三个坐标轴的旋转角度(△α,△β,△γ)、三个坐标平移量(△X,△Y,△Z)和尺度因子K,这七个数字合称七参数。
七参数计算界面2.坐标转换首先了解一下坐标转换,来看两张图,下面两张图分别是两个不同的椭球,不同的椭球之间代表的是不同的坐标系。
假设我们看到的地图是像贴纸一样“贴”在椭球的表面,那么坐标转换就相当于是将一个椭球上的地图“撕”下来再“贴”到另一个椭球上去,而且位置对应要正确。
WGS84参考椭球某个坐标系下的参考椭球由于两个椭球的表面不完全一样,为了保证重新“贴”到另一个椭球后位置对应准确,在“贴”之前需要对之前的地图进行相关的处理,处理需要按照相关的参数来,这个参数就是我们常说的“七参数”。
3.七参数各参数含义接下来分别说一说七个参数的各个参数,首先是三个方向的旋转角度(△α,△β,△γ),通过按顺序旋转三个坐标轴指定角度,可以使两个空间直角坐标系的XYZ轴重合在一起。
从下图中可以看到,有两个空间坐标系X1Y1Z1和X2Y2Z2,假设要将X1Y1Z1坐标系和X2Y2Z2坐标系完全重合,首先需要将XYZ轴旋转一定的角度,这个旋转的角度就是七参数中的三个旋转角度:△α,△β和△γ。
变换方式然后是三个方向的平移量(△X,△Y,△Z),即两个空间坐标系的坐标原点之间坐标差值。
如上图所示,旋转虽然三个方向的坐标轴是重合,但是长度却不一致,所以需要对三个方向坐标轴进行移动,向坐标点移动,这个移动的多少就是七参数中的三个移动量:△X,△Y和△Z。
最后是尺度因子K,即两个空间坐标系内的同一段直线的长度比值,实现尺度的比例转换。
通常K值几乎等于1。
K也可以叫变形系数,就是坐标系由原来的比如斜坐标系变成直角坐标系,变形系数K反映了变化程度或者说是如何变化的。
4.七参数计算七参数计算包括布尔莎模型,一步法模型,海尔曼特等,常见的为布尔莎模型。
GPS七参数计算

GPS七参数计算工具坐标转换问题得详细了解对于测量很重要,那么请与我一起来讨论这个问题。
ﻩ首先,我们要弄清楚几种坐标表示方法。
大致有三种坐标表示方法:经纬度与高程,空间直角坐标,平面坐标与高程。
我们通常说得WGS-84坐标就是经纬度与高程这一种,北京54坐标就是平面坐标与高程着一种。
现在,再搞清楚转换得严密性问题,在同一个椭球里得转换都就是严密得,而在不同得椭球之间得转换这时不严密得.举个例子,在WGS-84坐标与北京54坐标之间就是不存在一套转换参数可以全国通用得,在每个地方会不一样,因为它们就是两个不同得椭球基准。
那么,两个椭球间得坐标转换应该就是怎样得呢?一般而言比较严密得就是用七参数法,即X平移,Y平移,Z平移,X旋转,Y旋转,Z旋转,尺度变化K。
要求得七参数就需要在一个地区需要3个以上得已知点,如果区域范围不大,最远点间得距离不大于30Km(经验值),这可以用三参数,即X平移,Y平移,Z平移,而将X旋转,Y旋转,Z旋转,尺度变化K视为0,所以三参数只就是七参数得一种特例。
在本软件中提供了计算三参数、七参数得功能。
在一个椭球得不同坐标系中转换需要用到四参数转换,举个例子,在深圳既有北京54坐标又有深圳坐标,在这两种坐标之间转换就用到四参数,计算四参数需要两个已知点.本软件提供计算四参数得功能。
现在举个例子说明:在珠江有一个测区,需要完成WGS-84坐标到珠江坐标系(54椭球)得坐标转换,整个转换过程就是这样得:ﻩﻩﻩ本软件使用说明:ﻩ本软件采用文件化管理,用户可以将一种转换作为一个文件保存下来,下次使用时从文件菜单中选择打开这个文件来调用所有已有得转换参数。
实例一:转换要求:用户在一个佛山测区内使用RTKGPS接收机接受了一些点得WGS—84得坐标,现在希望将其转换为北京54与佛山坐标系下得坐标。
用户有佛山测区得一些控制点,这些控制点有WGS-84坐标,也有北京—54坐标也有佛山坐标.分析:WGS-84坐标与北京54坐标就是不同两个椭球得坐标转换,所以要求得三参数或七参数,而北京54与佛山坐标都就是同一个椭球,所以她们之间得转换就是地方坐标转换,需要求得地方转化四参数,因为要求得到得北京54就是平面坐标所以需要设置投影参数。
七参数计算公式范文

七参数计算公式范文七参数计算公式是用于描述平面、大地坐标系与空间坐标系之间的转换关系的一种数学模型。
它由七个参数组成,分别表示三个平移参数、三个旋转参数和一个尺度参数。
这些参数可以用于将一个空间坐标点的三维坐标转换为大地坐标系下的经纬度和高程,或者将大地坐标系下的经纬度和高程转换为空间坐标系的三维坐标。
七参数计算公式可以分为两个部分:平面坐标转换和高程转换。
平面坐标转换部分用于计算平面坐标系下的坐标与大地坐标系下经纬度之间的转换关系,包括平移和旋转;高程转换部分用于计算平面高程与大地高程之间的转换关系,包括尺度。
平面坐标转换部分的计算公式如下:X' = X0 + (1 + m) * (x*cosθ - y*sinθ) + dxY' = Y0 + (1 + m) * (x*sinθ + y*cosθ) + dy其中,X'和Y'是平面坐标系下的坐标,X0和Y0是坐标系的原点坐标,(x, y)是空间坐标系下的坐标,m是尺度参数,θ是旋转角度,dx和dy是平移参数。
高程转换部分的计算公式如下:Z' = Z0 + hz + m * (z*cosθ' - x*sinθ' + y*(sinα*cosθ' + cosα*sinθ')) + dz其中,Z'是大地高程,Z0是坐标系原点的大地高程,hz是平面高程,z是空间坐标系下的高程,θ'是旋转角度的负值,α是倾角,dz是高程平移参数。
这些参数的确定可以通过观测平面和空间坐标点之间的对应关系进行。
一般来说,会选择一部分具有已知坐标的点进行观测和计算,通过最小二乘法求解出七个参数的估计值。
然后,再通过反复观测和计算,逐步调整参数的估计值,使得计算结果与实际观测值最接近。
最终确定的七个参数就是平面与大地坐标系转换关系的准确描述。
在实际应用中,七参数计算公式广泛应用于地理信息系统、测量与地图制图等领域。
GPS入门+四-七参数设置

入门疑难解答:1.用gps测图本地中央子午线是118度而我把它设置成117度了,怎么扭转成118度的平面坐标?扭转后误差大吗?答: 是高精度测量还是手持机测量.如果是手持机它一般只手机经纬度,对你输入的中央子午线没任何关系,直接改为118就可以了,在说怎么会有118的中央子午线呢,北京54本来就是117或123114°〈X<=120°都属于在6度带上的20带,所以无影响。
2.某地的经度为116度23分,计算它所在的6度带和3度带号,相应6度带和3度带的中央子午线的经度是多少答:若按6°带,该区属于20带,则转换的坐标为:x=2769558.792,y=20457640.788(Y 坐标即东坐标,20457640。
788中前面20两位数是带数,为了区分不影响坐标值,通常是以中央子午线为X坐标,赤道为Y坐标建立坐标系; 又因中国版图东西跨度大也就造成了带数较多,有可能20带的坐标在21带(以21带建立坐标系)上的坐标值为负,所以坐标一般向东+500000便于计算,若按3°带,该区为39带,坐标为:x=2769558.792,y=39457640.788为20345,其所处的六度带的中央经线经度为:6°×20-3°=117°(适用于1∶2。
5万和1∶5万地形图)。
三度带中央经线经度的计算:中央经线经度=3°×当地带号116.23度23分=116.383度6度带计算:116.383/6=19。
397 即20带中央经线经度=20*6-3=117度3度带计算:116.383/6=38.794 即39带中央经线经度=39*3=117度GPS数设置。
南方RTK使用中参数的求取及分类一、控制点坐标库的应用GPS 接收机输出的数据是WGS—84 经纬度坐标,需要转化到施工测量坐标,这就需要软件进行坐标转换参数的计算和设置,控制点坐标库就是完成这一工作的主要工具。
七参数计算公式范文

七参数计算公式范文
地理坐标系转换是将一个地理坐标系的坐标点转换到另一个地理坐标系下的坐标点。
常见的地理坐标系包括WGS84、北京54等。
下面是七参数计算公式的详细介绍:
1.平移参数:
平移参数表示两个坐标系之间的平移关系,即在x、y、z轴方向上的平移量。
可以用一个三维向量表示,分别为∆X、∆Y、∆Z。
2.旋转参数:
旋转参数表示两个坐标系之间的旋转关系,即绕x、y、z轴旋转的角度。
可以用欧拉角表示,分别为ω、φ、κ。
其中,ω表示绕z轴旋转的角度,φ表示绕x轴旋转的角度,κ表示绕y轴旋转的角度。
3.缩放参数:
缩放参数表示两个坐标系之间的尺度关系,即坐标点的缩放比例。
可以用一个实数表示,即缩放因子s。
X2=X1+∆X+(1+s)*Y1*κ-s*Z1*φ
Y2=Y1+∆Y-(1+s)*X1*κ+s*Z1*ω
Z2=Z1+∆Z+(1+s)*X1*φ-s*Y1*ω
其中,X1、Y1、Z1表示原始地理坐标系下的坐标点,X2、Y2、Z2表示目标地理坐标系下的坐标点。
需要注意的是,七参数计算公式只是理论上的模型,实际应用时可能还需要考虑其他因素,如椭球体参数的影响等。
在实际计算中,可能还需要考虑更复杂的转换模型和精度控制方法。
总之,七参数计算公式是进行地理坐标系转换的一种方法,通过平移参数、旋转参数和缩放参数实现。
它在大地测量、航空航天等领域有着广泛的应用。
GPS七参数计算

GPS七参数计算工具坐标转换问题得详细了解对于测量很重要,那么请与我一起来讨论这个问题。
ﻩ首先,我们要弄清楚几种坐标表示方法。
大致有三种坐标表示方法:经纬度与高程,空间直角坐标,平面坐标与高程。
我们通常说得WGS-84坐标就是经纬度与高程这一种,北京54坐标就是平面坐标与高程着一种。
现在,再搞清楚转换得严密性问题,在同一个椭球里得转换都就是严密得,而在不同得椭球之间得转换这时不严密得.举个例子,在WGS-84坐标与北京54坐标之间就是不存在一套转换参数可以全国通用得,在每个地方会不一样,因为它们就是两个不同得椭球基准。
那么,两个椭球间得坐标转换应该就是怎样得呢?一般而言比较严密得就是用七参数法,即X平移,Y平移,Z平移,X旋转,Y旋转,Z旋转,尺度变化K。
要求得七参数就需要在一个地区需要3个以上得已知点,如果区域范围不大,最远点间得距离不大于30Km(经验值),这可以用三参数,即X平移,Y平移,Z平移,而将X旋转,Y旋转,Z旋转,尺度变化K视为0,所以三参数只就是七参数得一种特例。
在本软件中提供了计算三参数、七参数得功能。
在一个椭球得不同坐标系中转换需要用到四参数转换,举个例子,在深圳既有北京54坐标又有深圳坐标,在这两种坐标之间转换就用到四参数,计算四参数需要两个已知点.本软件提供计算四参数得功能。
现在举个例子说明:在珠江有一个测区,需要完成WGS-84坐标到珠江坐标系(54椭球)得坐标转换,整个转换过程就是这样得:ﻩﻩﻩ本软件使用说明:ﻩ本软件采用文件化管理,用户可以将一种转换作为一个文件保存下来,下次使用时从文件菜单中选择打开这个文件来调用所有已有得转换参数。
实例一:转换要求:用户在一个佛山测区内使用RTKGPS接收机接受了一些点得WGS—84得坐标,现在希望将其转换为北京54与佛山坐标系下得坐标。
用户有佛山测区得一些控制点,这些控制点有WGS-84坐标,也有北京—54坐标也有佛山坐标.分析:WGS-84坐标与北京54坐标就是不同两个椭球得坐标转换,所以要求得三参数或七参数,而北京54与佛山坐标都就是同一个椭球,所以她们之间得转换就是地方坐标转换,需要求得地方转化四参数,因为要求得到得北京54就是平面坐标所以需要设置投影参数。
七参数转换法推导公式

七参数转换法推导公式七参数转换法是大地测量中常用的一种方法,用于将不同大地坐标系之间的坐标转换为相互对应的坐标。
这种方法基于七个参数的数学模型,通过对观测数据进行处理和计算,得到坐标转换的公式。
七参数转换法的基本思想是,在两个大地坐标系之间建立一个七参数的转换模型,通过对大地测量数据进行观测和处理,计算出这七个参数的具体数值,从而实现坐标的转换。
这七个参数分别是三个平移参数(dx, dy, dz),三个旋转参数(rx, ry, rz),以及一个尺度参数(s)。
平移参数表示两个坐标系之间的平移差别,旋转参数表示两个坐标系之间的旋转差别,尺度参数表示两个坐标系之间的尺度差别。
具体的转换公式如下:X' = X + dx - Y*rz + Z*ry + sY' = Y + X*rz + Z*rx + sZ' = Z - X*ry + Y*rx + s其中,(X, Y, Z)是原始坐标系的坐标,(X', Y', Z')是目标坐标系的坐标。
通过这个公式,可以将原始坐标系的坐标转换为目标坐标系的坐标。
七参数转换法的推导过程比较复杂,需要依据大地测量的理论和观测数据进行数学推导。
这里不再详细介绍推导的具体步骤和过程,只简要说明一下。
需要建立两个大地坐标系之间的联系,确定两个坐标系的原点和坐标轴方向。
然后,在这两个坐标系中选择若干个控制点,测量这些控制点在两个坐标系中的坐标。
接下来,根据测量数据,建立坐标转换的数学模型。
通过对测量数据进行处理和计算,得到七个参数的数值。
将这七个参数代入转换公式,即可实现坐标的转换。
七参数转换法在实际应用中具有广泛的用途。
例如,当需要将GPS 测量得到的坐标转换为地理坐标时,就可以使用七参数转换法。
又或者,在不同的大地坐标系中进行坐标转换时,也可以使用这种方法。
七参数转换法是一种重要的大地测量方法,通过对大地测量数据进行处理和计算,可以实现不同大地坐标系之间的坐标转换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通过三个或三个以上已知点求解七参数模型中的参数:
不同空间直角坐标系之间的变换,其参数有(ΔX0,ΔY0,ΔZ0,ωX,ωY,ωZ,m)七个,其中(ΔX0,ΔY0,ΔZ0)为坐标平移量,(ωX,ωY,ωZ)为坐标轴间的三个旋转角度(又称为欧拉角),m为尺度因子。
七参数模型如图。
以WGS84坐标系转换为北京54坐标系为例:
为计算模型中的七个参数,至少需要三个已知点的北京54空间坐标
(X,Y,Z)BJ54和WGS-84空间坐标(X,Y,Z)WGS84,利用最小二乘法求出七参数。
然而,我们已知的三个公共控制点的坐标成果,一种是GPS观测中可直接获得的WGS84椭球下的大地坐标经纬度(B,L,H),另一种是工程测量中使用的是高斯投影后的平面直角坐标(x,y,h)。
即已知的三个公共控制点的坐标成果就是这两种形式的坐标表来表示的。
首先,我们要把这两种形式的坐标都转换为七参数模型中的空间直角坐标。
步骤如下:
1.将WGS84椭球下的大地坐标经纬度(B,L,H),采用WGS84椭球参数,转换为WGS84的空间直角坐标(X,Y,Z)
2.将北京54投影平面直角坐标(x,y,h),采用克拉索夫斯基椭球参数,转换为大地坐标((B,L,H)后,再转换为北京54的空间直角坐标(X,Y,Z)。
3.将转换得到的三个公共点的北京54空间坐标(X,Y,Z)BJ54和WGS-84空间坐标(X,Y,Z)WGS84代入七参数模型中,求解七个参数。
以上转换过程十分复杂,即涉及到大地坐标经纬度与空间直角坐标的换算,还涉及到空间直角坐标与平面直角坐标的投影。
通常,我也使用已有的计算程序来求解七参数的,在很多这些求解七参数的程序中,直接采用的是WGS84的大地坐标和北京54大地坐标来计算,就是你只需输入三个已知点的一套WGS84的大地坐标和一套北京54大地坐标,即可为你求解出七参数。
在很多GPS基线解算与平差软件中,都提供了求解七参数/四参数的工具,你可以自己试试。
需要注意的是,在求解七参数前必须设置高斯投影参数:
中央子午线,x坐标常数和y坐标常数,以及比例因子。
