等比数列的概念完整PPT课件
合集下载
《等比数列的概念》课件

03
等比数列的应用
等比数列在数学中的应用
解题技巧
等比数列是数学中常见的数列类型, 它在解决数学问题时具有广泛的应用 。例如,在求解一些复杂数学问题时 ,可以利用等比数列的性质简化计算 过程。
公式推导
等比数列的通项公式和求和公式在数 学中经常被用来推导其他公式或解决 一些复杂的数学问题。这些公式是等 比数列应用的基石,能够提供解决问 题的有效途径。
等比数列的公比
总结词
表示等比数列中任意两项的比值
详细描述
等比数列的公比是任意两项的比值,通常用字母 q 表示。公比是等比数列中相 隔一项的两个数的比值,即 a_n/a_(n-1)。公比反映了等比数列中每一项与前一 项的比值。
等比数列的项数与项的关系
总结词
表示等比数列中项数与项的关系
详细描述
在等比数列中,任意一项的值可以用首项、公比和项数来表 示。例如,第 n 项的值可以用 a_n=a_1×q^(n-1) 来表示, 其中 a_1 是首项,q 是公比,n 是项数。这个公式揭示了等 比数列中项数与项的关系。
《等比数列的概念》ppt课件
目录 Contents
• 等比数列的定义 • 等比数列的性质 • 等比数列的应用 • 练习题与答案
01
等比数列的定义
等比数列的文字定义
总结词:简洁明了
详细描述:等比数列是一种特殊的数列,其中任意两个相邻项之间的比值都相等 。
等比数列的数学符号定义
总结词:专业严谨
详细描述:等比数列通常表示为 a_n,其中 a 是首项,r 是公比,n 是项数。其数学定义是 a_n = a * r^(n-1),其中 r ≠ 0。
等比数列与等差数列的区别
总结词:对比分析
等比数列课件ppt

02
等比数列的通项公式
等比数列的通项公式推导
01
02
03
定义等比数列
等比数列是一个序列,其 中任意两个相邻项的比值 都相等。
推导通项公式
假设等比数列的首项为 $a_1$,公比为$r$,则第 $n$项$a_n$的通项公式 为$a_n = a_1 times r^{(n-1)}$。
证明通项公式
通过数学归纳法或迭代法 证明通项公式的正确性。
等比数列课件
• 等比数列的定义与性质 • 等比数列的通项公式 • 等比数列的求和公式 • 等比数列的应用 • 习题与解答
01
等比数列的定义与性质
等比数列的定义
总结词
等比数列是一种特殊的数列,其 中任意两个相邻项之间的比值都 相等。
详细描述
等比数列中,任意两个相邻项的 商是常数,这个常数被称为公比 。在等比数列中,每一项都是前 一项与公比的乘积。
举例说明
通过具体的例子来解释等比数列求和公式的推导过程。
等比数列求和公式的应用
解决实际问题
等比数列求和公式在解决实际问题中有着广泛的应用,如金融、工程、物理等 领域。
举例说明
通过具体的例子来展示等比数列求和公式的应用。
等比数列求和公式的变体
等差数列与等比数列的关系
01
等差数列和等比数列是两种不同的数列,但它们之间存在一定
01
第三组数列是等比数列,因为相 邻两项的比值都是1/2。
02
第四组数列也是等比数列,因为 相邻两项的比值都是1/2。
习题二:等比数列的通项公式
01
题目:已知等比数列的首项为 a,公比为q,求第n项的通项
公式。
02
答案与解析
等比数列的概念PPT优秀课件

(3) (4) (5) (6)
公比 q=2 递增数列 公比 q=3 递增数列
1 , x , x , x , x , ( x 0 )
234
公比 d= x
1 公比 q= 递减数列 2
1 1 1 1 , , , , 2 4 8 16
5,5,5,5,5,5,… 1,-1,1,-1,1,…
公比 q=1 非零常数列 公 比q= -1 摆动数列
为0.
等比数列、等差数列定义比较
等比数列:如果一个数列从第2项起,每一项与它 的前一项的比等于同一个常数(指与n无关的数), 这个数列就叫做等比数列,这个常数叫做等比数 列的公比,公比通常用字母q表示。 等差数列:如果一个数列从第2项起,每一项与它的 前一项的差等于同一个常数,那么这个数列就叫 做等差数列.这个常数叫做等差数列的公差,公差通 常用字母d来表示.
讨论
已知等比数列 (1) 首项
a n
a1
: 能不能是零?
Why? 不能!!!
(2)公比q能不能是零?
Why? 不能!!!
等比中项
观察如下的两个数之间,插入一个什么数后者三个数就会成 为一个等比数列: (1)1,±3 , 9 (3)-12, ±6 ,-3 (2)-1, ±2 ,-4 (4)1,±1 ,1
如果在a与b中间插入一个数G,使a,G,b成等比数列, 那么G叫做a与b的等比中项。
G ab G ab
2
等比中项与等差中项比较
G ab G ab
2
ab A 2
现给出等差中项的性质 1、在等差数列中,从第二项起,每 一项是相邻两项的等差中项。 2、在等差数列中,数列中的某一项 是与它“等距离”的两项的等差中 项。 你能类比中项的性质吗?可以用数学 式子表示吗?
公比 q=2 递增数列 公比 q=3 递增数列
1 , x , x , x , x , ( x 0 )
234
公比 d= x
1 公比 q= 递减数列 2
1 1 1 1 , , , , 2 4 8 16
5,5,5,5,5,5,… 1,-1,1,-1,1,…
公比 q=1 非零常数列 公 比q= -1 摆动数列
为0.
等比数列、等差数列定义比较
等比数列:如果一个数列从第2项起,每一项与它 的前一项的比等于同一个常数(指与n无关的数), 这个数列就叫做等比数列,这个常数叫做等比数 列的公比,公比通常用字母q表示。 等差数列:如果一个数列从第2项起,每一项与它的 前一项的差等于同一个常数,那么这个数列就叫 做等差数列.这个常数叫做等差数列的公差,公差通 常用字母d来表示.
讨论
已知等比数列 (1) 首项
a n
a1
: 能不能是零?
Why? 不能!!!
(2)公比q能不能是零?
Why? 不能!!!
等比中项
观察如下的两个数之间,插入一个什么数后者三个数就会成 为一个等比数列: (1)1,±3 , 9 (3)-12, ±6 ,-3 (2)-1, ±2 ,-4 (4)1,±1 ,1
如果在a与b中间插入一个数G,使a,G,b成等比数列, 那么G叫做a与b的等比中项。
G ab G ab
2
等比中项与等差中项比较
G ab G ab
2
ab A 2
现给出等差中项的性质 1、在等差数列中,从第二项起,每 一项是相邻两项的等差中项。 2、在等差数列中,数列中的某一项 是与它“等距离”的两项的等差中 项。 你能类比中项的性质吗?可以用数学 式子表示吗?
等比数列的概念(课件)高二数学(人教A版2019选择性必修第二册)

4 = 3 = 1 2 = 1 3 ,
由此可得
……
= 1 −1 ≥ 2 .
又1 = 1 0 = 1 1−1 ,这就是说,当n=1时上式也成立.
首项为1 ,公比为q 的等比数列{ }的通项公式为
= 1 −1
过关测试
1.判断正误
1 1 1
B.a,a2,a3,…
C.s-1,(s-1)2,(s-1)3,…
D.0,0,0,…
2,
2
)
解析:A、C、D 不是等比数列,A 中不满足定义,C、D 中项可为 0,不符
合定义.
答案:B
3.2+ 3和 2- 3的等比中项是
A.1 B.-1
(
C.±1 D.2
答案:C
4.若数列x,x2,x3,x4,…为等比数列,则x应满足的条件是________.
(2)当 1 > 0, 0 < < 1或 1 < 0, > 1 时,等比数列{ }为递减数列;
(3)当q=1时,数列{ }为常数列;
(4)当q<0时,数列{ }为摆动数列.
典型例题
【典例1】 若等比数列{ }的第4项和第6项分别为48和12,求{ }的第5项.
分析:
(1)根据已知条件,建立关于a1,q的方程组,求出a1,q后再求an,这是常规方
法.
(2)充分利用各项之间的关系,直接求出q后,再求a1,最后求an,这种方法带有
一定的技巧性,能简化运算.
已知数列{an}是等比数列,公比q<1,且a2=2,a1+a2+a3=7.
(1)求{an}的通项公式.
(2)设bn=log2an,求数列{bn}的前n项和.
数列①~⑥的公比依次是
由此可得
……
= 1 −1 ≥ 2 .
又1 = 1 0 = 1 1−1 ,这就是说,当n=1时上式也成立.
首项为1 ,公比为q 的等比数列{ }的通项公式为
= 1 −1
过关测试
1.判断正误
1 1 1
B.a,a2,a3,…
C.s-1,(s-1)2,(s-1)3,…
D.0,0,0,…
2,
2
)
解析:A、C、D 不是等比数列,A 中不满足定义,C、D 中项可为 0,不符
合定义.
答案:B
3.2+ 3和 2- 3的等比中项是
A.1 B.-1
(
C.±1 D.2
答案:C
4.若数列x,x2,x3,x4,…为等比数列,则x应满足的条件是________.
(2)当 1 > 0, 0 < < 1或 1 < 0, > 1 时,等比数列{ }为递减数列;
(3)当q=1时,数列{ }为常数列;
(4)当q<0时,数列{ }为摆动数列.
典型例题
【典例1】 若等比数列{ }的第4项和第6项分别为48和12,求{ }的第5项.
分析:
(1)根据已知条件,建立关于a1,q的方程组,求出a1,q后再求an,这是常规方
法.
(2)充分利用各项之间的关系,直接求出q后,再求a1,最后求an,这种方法带有
一定的技巧性,能简化运算.
已知数列{an}是等比数列,公比q<1,且a2=2,a1+a2+a3=7.
(1)求{an}的通项公式.
(2)设bn=log2an,求数列{bn}的前n项和.
数列①~⑥的公比依次是
等比数列的概念及基本运算ppt课件

篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
点评:(1)解决等比数列问题,关键是抓住首项 a1 和 公比 q,求解时,要注意方程思想的运用.
(2)运用等比数列求和公式时,要注意公比 q 是否为 1.当 n 较小时,直接利用前 n 项和的意义展开,不仅可避 开公比 q 的讨论,还可使求解过程简捷.
q3=-2, 所以a1=1,
或q3=-12, a1=-8.
所以 a1+a10=a1(1+q9)=-7.
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
a111--qq10=10, (2)(方法一)设公比为 q,则a111--qq20=30, 得 1+q10=3,所以 q10=2. 所以 S30=a111--qq30=a111--qq10(1+q10+q20) =10(1+2+22)=70. (方法二)因为 S10,S20-S10,S30-S20 仍成等比数列, 又 S10=10,S20=30, 所以 S30-30=30-10102=40,所以 S30=70. 答案:(1)D (2)70
A.8
B.9
C.10
D.11
解:因为 a5a7=a62,a7a9=a82, 所以 a5a7+2a6a8+a7a9=a62+2a6a8+a28=(a6+a8)2=100.又 an> 0,所以 a6+a8=10.
答案:C
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
2.(2015·新课标卷Ⅱ)已知等比数列{an}满足 a1=3,a1+a3
高一数学《等比数列的定义》PPT课件

等比数列
观察下面几个数列,看其有何 共同特点?
q=2 1 , 2 , 4 , 8 , 1 6 , 2 2;
5 6 3
5,25,125,625,…; q=5 1 1 1 1 , ,, ,; q=-1/2 2 4 8
共同特点:从第二项起,每一项与 前一项的比都等于同一个常数。
an1 1 等比数列的定义: q an
2 x 5 x 4 0 x 1 , 或 x 4 x 4 (舍) x 1
例 2 :已知等比数列 { a , { b 的项数相 n} n}
求证: { a b } 是等比数列。 n n
证明:设 a , b 首项分别为 a , q ; b , q n n 1 1 1 2
(与 n无关的数或式子)
问题1:等比数列中的项及公比能否为零 为什么?
a 0 ( n N ) , q 0 n
பைடு நூலகம்
判断下列数列是否是等比数列,如果是,请写出 它的公比。
2 , 2 , 2 , 2 , 3 , 3 , 3 , 3 0 , 2 , 0 , 2 0 , 0 , 0 , 0 a , a
a a q (a , q 0)
写出这几个等比数列的通项公式,首项,公 比 1,2,4,8,…263;
a 2 ( n 6 4 ) n
n 1
n 1
5,25,125,625,…;a 5 5 n
5
n
1 1 1 1 an ( ) 1 , ,, ,; 2 2 4 8
(2)等比数列的通项公式: (3)等比中项目:
a a q ( aq , 0 ) n 1 1
2 a a a n n 1 n 1
观察下面几个数列,看其有何 共同特点?
q=2 1 , 2 , 4 , 8 , 1 6 , 2 2;
5 6 3
5,25,125,625,…; q=5 1 1 1 1 , ,, ,; q=-1/2 2 4 8
共同特点:从第二项起,每一项与 前一项的比都等于同一个常数。
an1 1 等比数列的定义: q an
2 x 5 x 4 0 x 1 , 或 x 4 x 4 (舍) x 1
例 2 :已知等比数列 { a , { b 的项数相 n} n}
求证: { a b } 是等比数列。 n n
证明:设 a , b 首项分别为 a , q ; b , q n n 1 1 1 2
(与 n无关的数或式子)
问题1:等比数列中的项及公比能否为零 为什么?
a 0 ( n N ) , q 0 n
பைடு நூலகம்
判断下列数列是否是等比数列,如果是,请写出 它的公比。
2 , 2 , 2 , 2 , 3 , 3 , 3 , 3 0 , 2 , 0 , 2 0 , 0 , 0 , 0 a , a
a a q (a , q 0)
写出这几个等比数列的通项公式,首项,公 比 1,2,4,8,…263;
a 2 ( n 6 4 ) n
n 1
n 1
5,25,125,625,…;a 5 5 n
5
n
1 1 1 1 an ( ) 1 , ,, ,; 2 2 4 8
(2)等比数列的通项公式: (3)等比中项目:
a a q ( aq , 0 ) n 1 1
2 a a a n n 1 n 1
等比数列课件.ppt经典实用
(5)a,a,a,a,a 不一定
非零常数列才是等比数列 是否存在既是等比数列又是等差数列的数列?
非零常数列
•等比数列课件.ppt
想一想 已知等比数列a1,a2,a3…an…, 公比为q,能否用a1,q和n表示an?
•等比数列课件.ppt
方法一 不完全归纳法
a2=a1q, a3=a2q=(a1q)q=a1q2,
•等比数列课件.ppt
对折报纸若干次所得 报纸的层数得到的数 列 2,4,8,16…
•等比数列课件.ppt
方法二 aa21=q aa32=q
累乘法
a4=a3q=(a1q2)q=a1q3, ……
…… a4
a3
=q
由此得到
×) aann-1=q
an=a1qn-1. a1与q均不为0.n=1时,仍 然成立。
an a1
=qn-1
an=a1qn-1
•等比数列课件.ppt
(1)an=a1qn-1 (2) an=amqn-m(n,m ∈N*)
•等比数列课件.ppt
由例1,例2
归纳:在等比数列中,知道其中任意两 项,则可以求任意指定的项。
•等比数列课件.ppt
数列 定义 公差(比)
等差数列 an - an-1 =d d 叫公差
等比数列
an q(n2)且nN* an1
q叫公比
定义变形
an=an-1+d
an=an-1 q
通项公式 一般形式
1,
1, 2
1 4
,
...,
1 2
n 1
, ...
1,2,22,23,…,263
这三个数列分别有什么特点? 这三个数列有什么共同特点?
•等比数列课件.ppt
非零常数列才是等比数列 是否存在既是等比数列又是等差数列的数列?
非零常数列
•等比数列课件.ppt
想一想 已知等比数列a1,a2,a3…an…, 公比为q,能否用a1,q和n表示an?
•等比数列课件.ppt
方法一 不完全归纳法
a2=a1q, a3=a2q=(a1q)q=a1q2,
•等比数列课件.ppt
对折报纸若干次所得 报纸的层数得到的数 列 2,4,8,16…
•等比数列课件.ppt
方法二 aa21=q aa32=q
累乘法
a4=a3q=(a1q2)q=a1q3, ……
…… a4
a3
=q
由此得到
×) aann-1=q
an=a1qn-1. a1与q均不为0.n=1时,仍 然成立。
an a1
=qn-1
an=a1qn-1
•等比数列课件.ppt
(1)an=a1qn-1 (2) an=amqn-m(n,m ∈N*)
•等比数列课件.ppt
由例1,例2
归纳:在等比数列中,知道其中任意两 项,则可以求任意指定的项。
•等比数列课件.ppt
数列 定义 公差(比)
等差数列 an - an-1 =d d 叫公差
等比数列
an q(n2)且nN* an1
q叫公比
定义变形
an=an-1+d
an=an-1 q
通项公式 一般形式
1,
1, 2
1 4
,
...,
1 2
n 1
, ...
1,2,22,23,…,263
这三个数列分别有什么特点? 这三个数列有什么共同特点?
•等比数列课件.ppt
等比数列(53张PPT)

⇐把an+1=2an+1变形为an+1+1=2(an+1)
人教A版· 数学· 必修5
进入导航
第二章 2.4 第1课时
系列丛书
[解]
(1)∵an+1=2an+1,
∴an+1+1=2(an+1). an+1+1 ∴ =2. an+1 ∴{an+1}是首项为a1+1=2,公比为2的等比数列. (2)由(1)知an+1=(a1+1)qn-1=2· 2n-1=2n, ∴an=2n-1.
Байду номын сангаас
人教A版· 数学· 必修5
进入导航
第二章 2.4 第1课时
系列丛书
[点评]
证明一个数列是等比数列的常用方法.
an+1 an (1)定义法: a =q(常数)或 =q(常数)(n≥2)⇔{an} a n n -1 为等比数列. (2)等比中项法:a 等比数列. (3)通项法:an=a1qn-1(其中a1,q为非零常数,n∈N+) ⇔{an}为等比数列.
n-1 a q 通项公式是an= 1 .
3.等比中项 (1)如果三个数x,G,y组成 等比数列 ,则G叫做x和y的 等比中项.
2 G (2)如果G是x和y的等比中项,那么 =xy,即G=± xy .
人教A版· 数学· 必修5
进入导航
第二章 2.4 第1课时
系列丛书
思考感悟
1.如何理解等比数列的定义?
∴数列{an}是等比数列.
人教A版· 数学· 必修5
进入导航
第二章 2.4 第1课时
系列丛书
[错因分析] 忽略了由Sn求an需n≥2,除此之外,还要 保证从第二项起每一项与它的前一项的比都等于同一非零 常数.
人教A版· 数学· 必修5
进入导航
等比数列定义及性质PPT课件

a1 首项为 a 1,公比为 q 的等比数 列的通项公式:
a n= a 1 q n-1 (a 1 ≠0 且 q ≠0
n ∈N +)
练习:写出下列等比数列通项公式
(1) 2,4,8,16,… a n =2n
(2) 2,2
2 , 4, 4
2…
n 1
a n= 2 2
(3)
1,
1 2
,Байду номын сангаас
1 4
,
1 8
,
…
.
1
一、温故知新:
1、等差数列定义: an-an-1=d(d为常数) 2、等差数列单调性:d>0单调递增
d<0单调递减 d=0常数列
3、 等 差 数 列 的: 通an项 a1公 (n式 1)d
用什么方法推出的呢?
.
2
观察以上数列各有什么特点:
1, 2, 4, 8, … (1) 1.对于数列(1),从第2项起,每一项 与前一项的比都等于___2_
an q(n 2) a n 1
或 a n 1 q ( n 1) an
(2)既是等比数列又是等差数列的数列存在吗? 如果存在,你能举出例子吗?
非零的常数数列既是等差数列又是等比数列
.
5
探究: (1)等比数列的各项能等于0吗?为什么?
(2)公比q能等于0吗?
等差数列
由于等差数列是 作差 故a n , d 没 有要求
的前一项的差等于同 的前一项的 _比等于 _
一个常数,那么这个数 同一个常数,那么这个
列就叫做等差数列. 数列就叫做 等比数列
这个常数叫做等差数 这个常数叫做等 比 数
列的公差
列的 _公__比__
a n= a 1 q n-1 (a 1 ≠0 且 q ≠0
n ∈N +)
练习:写出下列等比数列通项公式
(1) 2,4,8,16,… a n =2n
(2) 2,2
2 , 4, 4
2…
n 1
a n= 2 2
(3)
1,
1 2
,Байду номын сангаас
1 4
,
1 8
,
…
.
1
一、温故知新:
1、等差数列定义: an-an-1=d(d为常数) 2、等差数列单调性:d>0单调递增
d<0单调递减 d=0常数列
3、 等 差 数 列 的: 通an项 a1公 (n式 1)d
用什么方法推出的呢?
.
2
观察以上数列各有什么特点:
1, 2, 4, 8, … (1) 1.对于数列(1),从第2项起,每一项 与前一项的比都等于___2_
an q(n 2) a n 1
或 a n 1 q ( n 1) an
(2)既是等比数列又是等差数列的数列存在吗? 如果存在,你能举出例子吗?
非零的常数数列既是等差数列又是等比数列
.
5
探究: (1)等比数列的各项能等于0吗?为什么?
(2)公比q能等于0吗?
等差数列
由于等差数列是 作差 故a n , d 没 有要求
的前一项的差等于同 的前一项的 _比等于 _
一个常数,那么这个数 同一个常数,那么这个
列就叫做等差数列. 数列就叫做 等比数列
这个常数叫做等差数 这个常数叫做等 比 数
列的公差
列的 _公__比__
等比数列课件.ppt

③
-2, 2, -2, 2, ….
④
共同特点:从第二项起,每一项与前一项 的比都等于同一个常数.
讲授新课
1. 等比数列的定义: 一般地,若一个数列从第二项起,每一
项与它的前一项的比等于同一个常数,这个 数列就叫做等比数列.这个常数叫等比数列的 公比,用字母q (q≠0) 表示.
2.等比数列定义的符号语言:
等比数列的通项公式:叠乘法
a2 a3 a4 a5 ...... an an qn1
a1 a2 a3 a4
an1 a1
an a1q n1
等比数列注: (1)等比数列的首项不为0; (2)等比数列的每一项都不为0,即an 0 (3) q=1时,{an}为常数列;
湖南省长沙市一中卫星远程学校
不是 不是 是 a1=x0, q=x 不是
小结:判断一个数列是不是等比数列, 主要是由定义进行判断:
看 an1 是不是同一个常数? an
注意:
(1) 等比数列{an}中, an≠0; (2)公比q一定是由后项比前项所得,而不
能用前项比后项来求,且q≠0; (3)若q=1,则该数列为常数列.
(4)常数列 a, a , a , a , …
等比数列
问题情境:
情境一:折纸
如果能将一张厚度为0.05mm的报纸对折,
再对折,再对折‥‥‥依次对折50次,你相
信这时报纸的厚度可以在地球和月球之间 建一座桥?
对折 纸的
n
次数
对 折 一 次
对 折 二 次
对 折 三 次
对
对
折 四 次
…...
折
n
次
…...
纸的
2
层数
48
等比数列的概念优秀课件

n a S 3 c, (1)、设数列 n 的前项和为 n 若a n 是等比数列,求 c 。
(2)、已知 a n 是无穷等比数列,公比 a a , a a , a a , 1 2 3 4 5 6 为q ,在数列 a n 中, , 组成一个新数列,这个数列是等比数列 吗?如果是,它的公比是多少?结论可 以推广吗?
a n
复习数列的有关概念2 如果数列 a n 的第n项 a n 与n之间的
关系可以用一个公式来表示,这个公式就叫 做这个数列的通项公式。
S a a a a a n 1 2 3 n 1 n 叫做数列 a n 的前n项和。
n1 ) S 1( a n S n2 ) n S n 1(
为0.
等比数列、等差数列定义比较
等比数列:如果一个数列从第2项起,每一项与它 的前一项的比等于同一个常数(指与n无关的数), 这个数列就叫做等比数列,这个常数叫做等比数 列的公比,公比通常用字母q表示。 等差数列:如果一个数列从第2项起,每一项与它的 前一项的差等于同一个常数,那么这个数列就叫 做等差数列.这个常数叫做等差数列的公差,公差通 常用字母d来表示.
等比数列(一) --等比数列概念
等比数列的概念
复习数列的有关概念1
按一定的次序排列的一列数叫做数列。 数列中的每一个数叫做这个数列的项。 数列中的各项依次叫做这个数列的 第1项(或首项)用 a 1 表示,
第2项用 a 2表示 …,第n项用 a n 表示, …, 数列的一般形式可以成: a 1 , a 2 , a 3 , …, a n , … , 简记:
a a ( 是与 n 无关的数或式子 n 1 n d
a n 的前n项和
A
(2)、已知 a n 是无穷等比数列,公比 a a , a a , a a , 1 2 3 4 5 6 为q ,在数列 a n 中, , 组成一个新数列,这个数列是等比数列 吗?如果是,它的公比是多少?结论可 以推广吗?
a n
复习数列的有关概念2 如果数列 a n 的第n项 a n 与n之间的
关系可以用一个公式来表示,这个公式就叫 做这个数列的通项公式。
S a a a a a n 1 2 3 n 1 n 叫做数列 a n 的前n项和。
n1 ) S 1( a n S n2 ) n S n 1(
为0.
等比数列、等差数列定义比较
等比数列:如果一个数列从第2项起,每一项与它 的前一项的比等于同一个常数(指与n无关的数), 这个数列就叫做等比数列,这个常数叫做等比数 列的公比,公比通常用字母q表示。 等差数列:如果一个数列从第2项起,每一项与它的 前一项的差等于同一个常数,那么这个数列就叫 做等差数列.这个常数叫做等差数列的公差,公差通 常用字母d来表示.
等比数列(一) --等比数列概念
等比数列的概念
复习数列的有关概念1
按一定的次序排列的一列数叫做数列。 数列中的每一个数叫做这个数列的项。 数列中的各项依次叫做这个数列的 第1项(或首项)用 a 1 表示,
第2项用 a 2表示 …,第n项用 a n 表示, …, 数列的一般形式可以成: a 1 , a 2 , a 3 , …, a n , … , 简记:
a a ( 是与 n 无关的数或式子 n 1 n d
a n 的前n项和
A
等比数列概念及性质.ppt

1 n ( ) 6
已知
an ,bn 是项数相同的等比数列, 求证 an bn 是等比数列.
证明:设数列 an 首项为a1,公比为q1 ;bn 首项为b1,公比为q 2 那么数列 an bn 的第n项与第n+1项 分别为:
an1 bn1 a1b1 (q1q2 ) n q1q2 .它是一个与n无关的常数, n 1 an bn a1b1 (q1q2 )
① 1,-1,1,…,(-1)n+1 ;√
②1,2,4,6…;× ③a,a,a,…,a; ×
④已知a1=2,an=3an+1 ; √
⑤
m, 2m, 4m ,8m ,...
2
3
×
⑥2a,2a,2a,…,2a. √
2、求出下列等比数列中的未知项: 1 (1)2,a,8;(2)-4,b,c, . 2
思考2:公比q<0时,等比数列呈现怎样的特 点? 正负交替
思考4:等比数列的通项公式与函数有怎样的关系?
例如:数列{an}的首项是a1=1,公比q=2,则通项公式是:
an 2n -1 ______
上式还可以写成
an 8
·
1 n an 2 2
7
6
5 4
可见,这个等比数列
1 的图象都在函数 2 的图象上,如右图所示。
y 2
x
3
2 1
0
· ·
例题3:一个等比数列的第3项和第4 项分别是12和18,求它的第1项和第2 项。
1.在等比数列{an}中,已知
a 3 20, a 6 160
求an.
四. 应用示例
例2.根据右图的框图,写出所打印 数列的前5项,并建立数列的递 推公式.这个数列是等比数列吗?
等比数列的概念ppt课件

P:表示本金;r:表示年利率; n:表示本金存储年限;F:表示最终取款. 假设银行存款期利率不变,那么可以把存款模型表示为 单利模型:F=P(1+nr); 复利模型:F=P(1十r)n 一般情况下,存款利率是一个正数.因此,在上述两个模型中的基本系 数1十nr和1+r都是大于1的,这说明最终取款F都是年限n的增函数.虽然指 数形式的增函数比线性形式的增函数增加的快,但这个性质针对的是同样 的利率.事实上,银行在设计利率时充分考虑到这个性质.必须注意到,上 述两个模型中的年利率是不一样的,存款年限越长的年利率越高.通过例1 可以看到,这个差异还是比较大的.
例1 李先生有3万元闲置资金,打算在某银行定期存款三年.该银行参考央行 公布 的利率,确定利率一年期为2.07%,三年期为3.75%.现在李先生有两种 存款方式可供 选择,一种方式是整存整取三年定期;另一种方式是一年后取 出本金和利息,转存两次.假设存款期内年利率不发生变化,李先生应该选用 哪种存款方式呢?
股票 基金
债券 房地产
1.含义:
一、储蓄存款
谁在存?
居民个人
存什么?
人民币或外币 (合法拥有)
到哪里存?有什么凭证?
储蓄机构 存折、存单等
有何好处?
支取本金+获得 (存款)利息
唯一收益
储蓄存款的分类
活期储蓄 •储户可以随时存入和提取、不规定存期、存 款金额和次数不受限制的储蓄方式。 •事先约定期限、存入后不到期一般不得提前
分析:两种方式主要区别在于计息方式,通常称第一种方式为单 利计息,第二种方 式为复利计息.
例1 李先生有3万元闲置资金,打算在某银行定期存款三年.该银行参考央行 公布 的利率,确定利率一年期为2.07%,三年期为3.75%.现在李先生有两种 存款方式可供 选择,一种方式是整存整取三年定期;另一种方式是一年后取 出本金和利息,转存两次.假设存款期内年利率不发生变化,李先生应该选用 哪种存款方式呢?
例1 李先生有3万元闲置资金,打算在某银行定期存款三年.该银行参考央行 公布 的利率,确定利率一年期为2.07%,三年期为3.75%.现在李先生有两种 存款方式可供 选择,一种方式是整存整取三年定期;另一种方式是一年后取 出本金和利息,转存两次.假设存款期内年利率不发生变化,李先生应该选用 哪种存款方式呢?
股票 基金
债券 房地产
1.含义:
一、储蓄存款
谁在存?
居民个人
存什么?
人民币或外币 (合法拥有)
到哪里存?有什么凭证?
储蓄机构 存折、存单等
有何好处?
支取本金+获得 (存款)利息
唯一收益
储蓄存款的分类
活期储蓄 •储户可以随时存入和提取、不规定存期、存 款金额和次数不受限制的储蓄方式。 •事先约定期限、存入后不到期一般不得提前
分析:两种方式主要区别在于计息方式,通常称第一种方式为单 利计息,第二种方 式为复利计息.
例1 李先生有3万元闲置资金,打算在某银行定期存款三年.该银行参考央行 公布 的利率,确定利率一年期为2.07%,三年期为3.75%.现在李先生有两种 存款方式可供 选择,一种方式是整存整取三年定期;另一种方式是一年后取 出本金和利息,转存两次.假设存款期内年利率不发生变化,李先生应该选用 哪种存款方式呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) 1,3,9,27,…
1. 各项不能为零,即 a n 0
2. 公比不能为零,即 q 0
(2) 1, 1, 1, 1 , 3. 当q>0,各项与首项同号
2 4 8 16
(3) 5, 5, 5, 5,…
当q<0,各项符号正负相间
4. 数列 a, a , a , …
(4) 1,-1,1,-1,…
a 0 时,既是等差数列
(5) 1,0,1,0,…
又是等比数列;
(6) 0,0,0,0,…
a 0 时,只是等差数列
.
而不是等比数列.
等差数列通项公式的推导: an an1 d
方法一:(叠加法)
a2a1d
a3 a2 d a4…a3…d
(n-1)个 式子
an1an2 d
an an1 d
ana1(n1)d .
3
因此 a aq1638
2
1
32
16
答:这个数列的第1项与第2项分别是 与 8.
.
3
课堂互动
(1)一个等比数列的第5项是 4 ,公比是 1 ,求它的第1项;
9
3
解:设它的第一项是 a ,则由题意得 1
a1
( 1)51 3
4 9
解得, a1 3 6
答:它的第一项是36 .
(2)一个等比数列的第2项是10,第3项是20,求它的第1项与第4项.
解:设它的第一项是 a ,公比是 q ,则由题意得 1 a1q10 , a1q2 20
解得, a1 5 , q 2 因此 a4 a1q340 答:它的第一项是5.,第4项是40.
等比数列的例题
例2 已知 an,bn是项数相同的等比数列, 求证 an bn是等比数列.
证明:设数列an 首项为a 1,公比为q 1;b n 首项为b 1 ,公比为q 2 那么数列 an bn的第n项与第n+1项 分别为:
anam(nm)d
(n, m N* )
试问:在等比数列 a n 中,如果知道 a m 和公
比q,能否求 a n ?如果能,请写出表达式。
an amqnm (n,mN*)
.
等比中项的定义
如果在a与b中间插入一个数G,使a,G,b成 等比数列,那么G就叫做a与b的等比中项 在这个定义下,由等比数列的定义可得
以上两个实例所包含的数学问题:
(1) 1 ,1
,1
,1
1
, ,…
2 4 8 16
(2) 1 ,2 ,4 ,8 ,16 ,32 ,… .
等比数列概念
等比数列
❖ 一般地,如果一个数列从第2项起,每一
项与它的前一项的 比 等于同一个常数, 那么这个数列就叫做等比数列 ,这个常数叫 做等比数列的公比(q)。
a 1 q 1 n 1 b 1 q 2 n 1 与 a 1 q 1 n b 1 q 2 n
即为 a 1 b 1(q 1q 2)n 1与 a 1 b 1(q 1q 2)n
an an 1b bn n1aa11 bb11((qq11 qq22))nn 1q1q2.它是一个与n无关的常数,
所以 an bn是一个以 q.1q2 为公比的等比数列
Gb 即 aG G 2 ab
G ab
.
等比数列的通项公式练习
课后练习P53 A1 , 7
.
典型例题
例1 一个等比数列的第3项与第4项分别 是12与18,求它的第1项与第2项.
a 解:设这个等比数列的第1项是 ,公比是q ,那么 1 aq2 12 1
aq3 18 1
解得,
q3 2
16
,
a 1
aa38142或 8aa831428∵ 公比 q 为整数
aa83
4 128
q5 12832 q2 4
∴ a 10 = a 3×q 10 -3= -4×(. -2) 7= 512
回顾小结
等比数列
名称
等差数列
从第2项起,每一项与它前 概念 从第2项起,每一项与它前
一项的比等同一个常数
一项的差等同一个常数
公比(q)
常数
公差(d)
q可正可负,但不可为零 性质 d可正可负,且可以为零
an a1•qn1 通项 ana1(n1)d
(3) 5,5,5,5,5,5,…
是,公比 q= 1
2
是,公比 q=1
(4) 1,-1,1,-1,1,…
是,公 比q= -1
(5) 1,0,1,0,1,…
不是等比数列
(6) 0,0,0,0,0,…
不是等比数列
(7) 1,x,x2,x3,x4,L(x0)是,公比 q= x
.
对概念的更深理解
an1 q(是与 n无关的数,或 且q式 0) 子 an
合作交流
例3、等比数列 { a n } 中, a 4 ·a 7 = -512,a 3 + a 8 = 124, 公比 q 为整数,求 a 10. 法一:直接列方程组求 a 1、q。
法二:在法一中消去了 a 1,可令 t = q 5
法三:由 a 4 ·a 7 = a 3 ·a 8 = -512 a3 212 a34 512 0 a 312 或 a 8 3 4
方法二:(归纳法)
a2 a1d
a3 a2 d
(a1 d ) d
a12d
a4 a3d
(a1 2d ) d
…a1
3d
…
ana1(n1)d
an 等比数列通项公式的推导:an 1
q n2
方法一:叠乘法
方法二:归纳法
a2 q
a1
a3 q a2 a4 q
…a 3 …
(n-1)个 式子
an q
a n 1
a2 a1q
a3
aa12qq2(a1q)q
a4 a3q(a1q2)q
a1q3
……
an a1
qn1
.
an a1qn1
等比数列的通项公式
a 等比数列 a n ,首项为 1 ,公比为q,则通项公式为
an a1•qn1
当q=1时,这是 一个常函数。
an 0
.
变形结论:
在等差数列 a n 中
等差列
❖ 一般地,如果一个数列从第2项起,每一
项与它的前一项的 差 等于同一个常数, 那么这个数列就叫做等差数列 ,这个常数叫 做等差数列的公差(. d)。
课堂互动
观察并判断下列数列是否是等比数列:
(1) 1,3,9,27,81,…
是,公比 q=3
(2) 1, 1, 1, 1 ,
2 4 8 16
临沂一中高二数学组
.
旧知回顾
名称 概念
等差数列
从第2项起,每一项与它前
一项的差等同一个常数
常数
公差(d)
性质
d可正可负,且可以为零
通项
ana1(n1)d
通项 变形
anak(n(n,kk)Nd*)
.
创设情景,引入新课
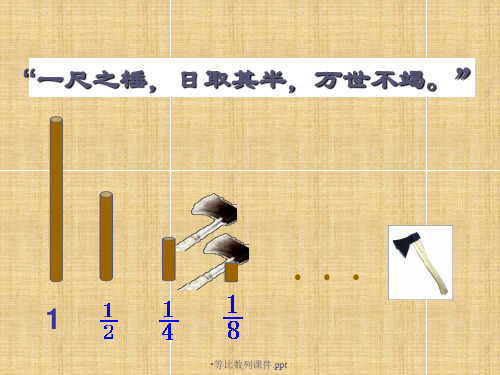
(1)“一尺之棰,日取其半,万世不竭.”
(2) 一位数学家说过:你如果能将一张 纸对折38次,我就能顺着它在今天晚上爬 上月球。
