mathematica实验报告3(图形绘制)
mathematica数学实验报告

mathematica数学实验报告本次实验使用Mathematica进行数学建模实验,主要包括以下内容:三角函数、极限和导数、积分和微分方程。
一、三角函数1. 三角函数的绘制使用Mathematica的Plot函数绘制正弦函数和余弦函数的图像。
代码:Plot[{Sin[x], Cos[x]}, {x, -2 Pi, 2 Pi},PlotStyle -> {Blue, Red}, PlotTheme -> "Web"]结果:在x趋近于4时的极限。
代码:Limit[x^2/(4 - x), x -> 4]结果:82. 求函数的导数使用Mathematica的D函数计算函数x^3 - 3x的导数。
代码:D[x^3 - 3x, x]结果:3 x^2 - 3三、积分和微分方程1. 求定积分使用Mathematica的Integrate函数计算函数e^x * cos(x)在0到π/2之间的定积分。
代码:Integrate[E^x * Cos[x], {x, 0, Pi/2}]结果:1/2 (1 + E^(π/2))2. 解微分方程使用Mathematica的DSolve函数求解微分方程y''(x) + 4y(x) = 0。
代码:DSolve[y''[x] + 4 y[x] == 0, y[x], x]结果:y[x] -> C[1] Cos[2 x] + C[2] Sin[2 x]本次实验使用Mathematica进行数学建模实验,主要包括三角函数的绘制、求三角函数的值,函数的极限、导数,积分和微分方程等内容。
Mathematica第3章 图形

Show[GraphicsArray[{{…},{ 绘制图形矩阵 …},…{…}}]] Show[Graphics[]] 显示图形
演示3.3.nb
补1二维图形元素
用图形元素绘图适合于绘制结构复杂的 图形。Mathematica中提供了各种如绘制 点、线段、圆弧等函数。我们可用 Graphics作出平面图形的表达式,再用 Show显示完成的图形。下表给出常用的 二维图形元素:
可选项名称 1、PlotRange
2、AspectRatio 3、Axes
系统默认值
Automatic(自定)
含义(格式)
PlotRange->All(函数值全部 图形) PlotRange->{y1,y2} 图形的高宽比 AspectRatio->m/n Axes -> True draws all axes. Axes -> False draws no axes. Axes -> {False, True} draws y axis but no x axis PlotLabel->”…”:图形上方居 中增加标记 AxesLabel->”…”:坐标轴上 增加标记
演示3.4.nb
3.6 等高线与密度图
等高线指曲面上具有相同高度的点连线, 方程表示为两个曲面的交 z=f(x,y),z=zj,(j=1,2,…) 则会得到投影曲线族。 密度图是反映投影曲线族的曲线密度分 布,用明暗度来表示曲线投影前的高度,oz轴 为正向,越高越亮。
等值线与密度图
函数 意义 ContourPlot[f,{x,xmin,xmax},{y, 绘出x和y的函数f的 ymin,ymax},可选项] 等值线图 DensityPlot[f,{x,xmin,xmax},{y,y 绘出f的密度图 min,ymax},可选项]
Mathematica实验报告

Mathematica 实验报告【实验名称】利用MA THEMA TICA 作图、运算及编程.【实验目的】1。
掌握用MA THEMATICA 作二维图形,熟练作图函数Plot 、ParametricPlot 等应用,对图形中曲线能做简单的修饰.2。
掌握用MATHEMA TICA 做三维图形,对于一些二元函数能做出其等高线图等,熟练函数Plot3D ,ParametricPlot 的用法。
3、掌握用MA THEMATICA 进行微积分基本运算:求极限、导数、积分等。
【实验原理】1.二维绘图命令:二维曲线作图:Plot[fx,{x ,xmin,xmax}],二维参数方程作图:ParametricPlot[{fx ,fy},{t ,tmin ,tmax}]2.三维绘图命令:三维作图plot3D [f,{x ,xmin ,xmax},{y,ymin ,ymax}],三维参数方程作图:ParameticaPlot3D[{fx,fy ,fz },{t ,tmin,tmax }]【实验内容】(含基本步骤、主要程序清单及异常情况记录等)1。
作出函数)sin(22y x z +=π的图形. 步骤: z=Sin [Pi Sqrt[x^2+y^2]];Plot3D [z ,{x,-1,1},{y,—1,1},PlotPoints →30,Lighting →True]2。
椭球面()⎪⎪⎩⎪⎪⎨⎧=∈⎪⎭⎫ ⎝⎛-∈==u z v u v u y v u x R R R R R R sin ,,,2,0,2,2,sin cos cos cos 332121πππ自行给定,作图. 步骤:ParametricPlot3D [{4Cos[u ]Cos[v],3Cos [u]Sin[v],2Sin[u]},{u ,—Pi/2,Pi/2},{v,0,2Pi}]3.做出极坐标描绘的图形:)cos 1(4θ+=r步骤:r [t_]:=4(1+Cos[t ]);ParametricPlot [{r [t ]Cos[t],r [t ]Sin [t]},{t,0,2Pi}]【实验结果】结果1:结果2:结果3:【总结与思考】MATHEMATICA作图的常见错误:General::spell1: Possible spelling error,因为在MATHEMATICA中作图函数大小写有区别.由于拼写间要有空格,易导致错误。
mathematica实验报告

mathematica实验报告Mathematica 实验报告一、实验目的本实验旨在深入了解和掌握 Mathematica 软件的基本功能和操作方法,通过实际的案例和问题解决,提升运用 Mathematica 进行数学计算、数据分析、图形绘制以及编程的能力。
二、实验环境操作系统:Windows 10Mathematica 版本:121三、实验内容与步骤(一)数学计算1、基本运算在 Mathematica 中,直接输入数学表达式进行计算,例如:计算 2+ 3 4 的结果,输入`2 + 3 4` ,得到结果 14。
2、函数计算使用内置函数进行复杂的数学运算,如计算正弦函数`SinPi / 6`的值,结果为 05。
(二)数据分析1、数据导入通过`Import` 函数导入外部数据文件,如 CSV 格式的数据文件。
假设我们有一个名为`datacsv` 的文件,包含两列数据`x` 和`y` ,使用`data = Import"datacsv"`即可将数据导入。
2、数据处理对导入的数据进行处理,如计算平均值、方差等统计量。
可以使用`Meandata` 计算平均值,`Variancedata` 计算方差。
(三)图形绘制1、二维图形绘制简单的函数图形,如`PlotSinx, {x, 0, 2 Pi}`绘制正弦函数在`0` 到`2 Pi` 区间的图形。
2、三维图形绘制三维图形,如`Plot3Dx^2 + y^2, {x, -2, 2},{y, -2, 2}`绘制一个抛物面。
(四)编程实践1、定义函数使用`Function` 关键字定义自己的函数,例如定义一个计算阶乘的函数`factorialn_ := Ifn == 0, 1, n factorialn 1` 。
2、循环结构使用`For` 循环和`While` 循环实现重复操作,例如使用`For`循环计算 1 到 10 的和,`sum = 0; Fori = 1, i <= 10, i++, sum += i; sum` 。
Mathematica实验报告
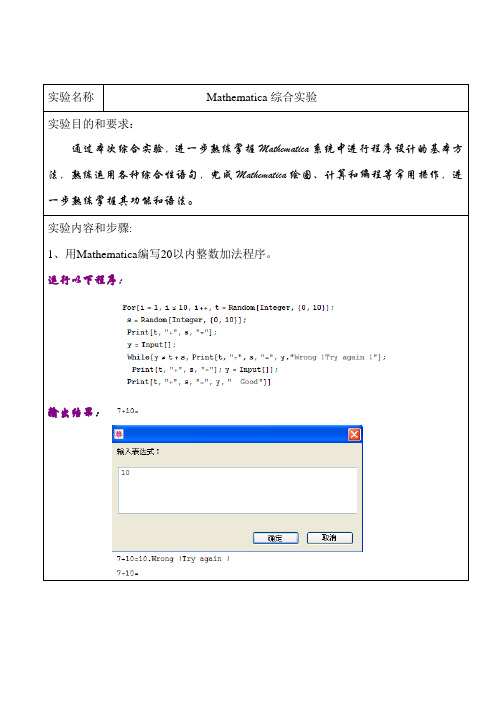
实验名称Mathematica综合实验实验目的和要求:通过本次综合实验,进一步熟练掌握Mathematica系统中进行程序设计的基本方法,熟练运用各种综合性语句,完成Mathematica绘图、计算和编程等常用操作,进一步熟练掌握其功能和语法。
实验内容和步骤:1、用Mathematica编写20以内整数加法程序。
运行以下程序:输出结果:2、编写程序,列出9*9的乘法表来。
输入程序:9*9乘法表3、编写程序,输入两个正整数,用“辗转相除法”求它们的最大公约数。
辗转相除法:(1) 以大数m作被除数,小数n做除数,相除后余数为r。
(2) 若r ≠ 0,则m ← n,n ← r,继续相除得到新的r。
若仍有r ≠ 0,则重复此过程,直到r = 0为止。
(3) 最后的n就是最大公约数。
Mathematica代码如下:运行结果4、统计一个班级某次考试个分数段的人数。
输入程序:运行结果:5、编写程序用切线法求方程的解。
Mathematica语句和运行结果如下:6、编写Mathematica程序显示二维码图像。
输入程序:二维码图像7、用0~8这九个数字,组成一个二位数和一个三位数相乘使他们的积恰好是四位数.数字不能重复。
即□□×□□□=□□□□输入以下Mathematica程序:输出结果:8、用Mathematica编写程序绘制一个围棋棋盘.输入以下程序:围棋棋牌9、假设新开辟的国家公园里没有兔子和狐狸,现引进兔子和狐狸个50只,n 个月后兔子和狐狸的数量分别记为n R 和n F ,假定有⎩⎨⎧+=-=++nn n n n n F R F F R R 6.02.02.01.111Mathematica 程序如下:运行结果如下:注释:在一段时间内,兔子和狐狸的数量均会减少,但最终均会趋于一个稳定值。
10、有一个木工、一个电工和一个油漆工,三人协商合作装修他们的房子,并达成如下协议:a.每人总共工作10天(包括给自己家干活);b.每人日工资根据市场价确定在60 80 元之间;c.每人的总支出与每人的总收入相等。
数学实验mathmaticas

t3=ParametricPlot3D[{u,v,0},{u,-0.5, 1}, {v,-0.5,1},AxesLabel->{“x”,“y”,“z”},PlotPoints->50,
DisplayFunction->Identity];
Show[t1, t2, t3, DisplayFunction -> $DisplayFunction];
三、程序设计
1.实验对象:
输入命令:
t1 = ParametricPlot3D[{Sin[u]*Cos[v], Sin[u]*Sin[v], Cos[u]}, {u,
0, \[Pi]/2}, {v, 0, 2*\[Pi]}, PlotPoints -> 30,
DisplayFunction -> Identity];
t2 = ParametricPlot3D[{(0.5 + 0.5*Cos[u]), 0.5*Sin[u], v}, {u, 0,
2*\[Pi]},{v,-1,1}, PlotPoints->30,
DisplayFunction -> Identity];
t3 = ParametricPlot3D[{u, v, 0}, {u, -1, 1}, {v, -1, 1}, PlotPoints -> 30,
Show[g1,g2,DisplayFunction -> $DisplayFunction]]
五、程序运行结果
六、结果的讨论和分析
有图像可以看出,逼近函数f(x)的效果随n的增大而越来越好。通过实验,更直观的感受到傅里叶级数在函数模拟上的广泛用途。
Mathematica画图

绘制由方程F(x,y)=0所确定的隐函数的图像
常用选择项有:
PlotRange->{c,d} 指定因变量的范围为[c,d]
AspectRatio->Automatic 图形高宽比为1:1(系
统默认值为0.618:1)
AxesLabel->{x,f(x)} 指定坐标轴的名称
的图形
(3)
绘制椭球面
x2 a2
y2 b2
z2 c2
1 的图形
四、利用Mathematica图形绘制功能理解极限 概念,验证方程根的情况
学生实验: 一、基础部分
1.作函数 f (x) x3 3x2 1 在(-2,4)内的图形
2.作函数 f (x) sin 1 x, g(x) cos1 x 在[-4π,4π]上的图形
-4
-2
2
4
f[x_]:=1-x/;x≥0
-1
-2
Plot[f[x],{x,-5,5}]
-3
-4
(2)在同一坐标系内作出多个函数图形 Clear[x] Plot[{sin[x],cos[x]},{x,0,2*Pi}] 作 y sin x ,y cosx 在区间[0,2π]上的图像。 对比:Plot[{sin[x],cos[x]},{x,0,2Pi}, AspectRatio->Automatic] Plot[{sin[x],cos[x]},{x,0,2Pi}, AspectRatio->Automatic,PlotStyle>{{RGBColor[1,0,0],Thickness[0.001], Dashing[{0.02,0.01}]}}]
高数mathematica上机实验报告

15-16-2《高等数学》数学实验报告学号:姓名:得分: . ..实验:已知函数f(x)=(5≤x≤4),作出并比较当c分别取1,0,1,2,3时的图形,并从图上观察极值点、驻点、单调区间、凹凸区间以及渐进线。
当c=时In[1]= f[x]:=1/(-1+2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[3]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[5]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[7]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[7]=Out[8]=极大值点为x=,驻点为x=,单调递增区间为,单调递减区间为,下凸区间为,上凸区间为,渐进线为x=,x=当c=0时In[9]= f[x]:=1/(2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[11]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[13]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[15]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[15]=Out[16]=极大值点为x=,驻点为,单调递增区间为,单调递减区间为,下凸区间为,上凸区间为,渐进线为x=,x=0当c=1时In[17]= f[x]:=1/(1+2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[19]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[21]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[23]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[23]=Out[24]=无极值点,无驻点,单调递增区间为,单调递减区间为,下凸区间为,无上凸区间,渐进线为x=当c=2时In[25]= f[x]:=1/(2+2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[27]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[29]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[31]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[31]=Out[32]=极大值点为x=,驻点为,单调递增区间为单调递减区间,下凸区间为,上凸区间为,无渐进线当c=3时In[33]= f[x]:=1/(3+2*x+x^2)Plot[f[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]In[35]= f'[x]:=Dt[f[x],x]Plot[f'[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f'[x]"]In[37]= f''[x]:=Dt[f[x],{x,2}]Plot[f''[x]//Evaluate,{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0],PlotLabel→"A Graph of f''[x]"]In[39]=Solve[f'[x]==0,x]Solve[f''[x]==0,x]Out[39]=Out[40]=极大值点为x=,驻点为,单调递增区间为单调递减区间,下凸区间为,上凸区间为,无渐进线。
mathematica实验报告3(图形绘制)

2.运行结果()A准确,表现效果好;B正确;C部分结果不准确;D有较严重错误.
3.其它问题______________________________________________________________________.
4.综合评定()A优秀;B良好;C合格;D不合格;E有明显抄袭或雷同现象.
三、实验内容
1.绘制下列显式平面曲线(可选项取默认值)。
(1) ;
(2) 。
2.绘制下列隐函数平面曲线(可选项取默认值)。
(1) ;
(2) 。
3.绘制下列极坐标式平面曲线(可选项取默认值)。
(1) ;
(2) 。
4.绘制下列Байду номын сангаас间曲线。
(1) ;
(2) 。
5.绘制下列曲面。
(1) ,在矩形域 上;
(2) ,在矩形域 上。
新疆财经大学《数学软件》实验报告
实验3图形绘制
班级专业:数学-08-01姓名:崔仁霞李海燕学号:*******************日期:成绩:
一、实验目的
1.熟悉Mathematica绘图命令;
2.掌握平面图形及空间图形的绘制方法及图形的控制方法。
二、实验准备
命令:Plot、ParametricPlot、ImplicitPlot、PolarPlot、ListPlot、Show、PlotStyle、ParametricPlot3D、Plot3D、ListPlot3D等命令。
6.已知 个 值的数据为:
试绘制此数据曲面的图形。
四、程序、命令与结果
一,(1)命令:
结果:
(2)命令:
结果:
二,(1)命令:
Mathematica 图形绘制

第2章图形绘制平面图形空间图形:曲线与曲面2.1 曲线与曲面表示法2.1.1 平面曲线表示法(1)直角坐标显式(简称显式):y=f(x)(2)直角坐标隐式(简称隐式):F(x,y)=0(3)参数式:x=x(t),y=y(t)(4)极坐标式:ρ=ρ(θ)(5)列表式(又称数据形式,或称离散点形式)(6)图形式(画出曲线的图形)2.1.2 空间曲线表示法(1)参数形式x=x(t),y=y(t),z=z(t)(2)交截形式f(x,y,z)=0∩φ(x,y,z)=0这是用两张曲面的交线来表示空间曲线。
在理论研究与实际应用中,常常是通过引入参数t将交截式转化为参数式来讨论问题的。
2.1.3 曲面表示法(1)直角坐标显式(简称显式):z=f(x,y)(2)直角坐标隐式(简称隐式):F(x,y,z)=0(3)参数形式:x=x(u,v),y=y(u,v),z=z(u,v)(4)数据形式:即是将曲面上的点表示为x={xi},y={yj},z={zij} (i=1,2,…,m;j=1,2,…,n)的形式,其中xi与yj为向量x与y中的元素,zij为矩阵z中的元素。(5)图形形式(画出曲面的图形)曲面表示的上述5种形式在一定条件下也是可以互相转化的,在实际问题中用得最多的是(1),(3),(5)三种形式。2.2 平面曲线的绘制法2.2.1 显式Plot[f(x),{x,x1,x2},可选项]Plot[{f1(x),f2(x),…},{x,x1,x2},可选项]Note:原式用InputForm查看;不连续图形可能有失真。
2.2.2 参数式ParametricPlot[{x(t),y(t)},{t,t1,t2},可选项]ParametricPlot[{{x1(t),y1(t)},{x2(t),y2(t)},…},{t,t1,t2},可选项]2.2.3隐式ImplicitPlot[F[x,y]==0,{x,x1,x2},可选项]Note:先调入程序包<<Graphics`ImplicitPlot`<<Graphics`2.2.4极坐标式PolarPlot[ρ(θ),{ θ, θ1, θ2}]Note:先调入程序包<<Graphics`Graphics`<<Graphics`2.2.5数据形式ListPlot[{{x1,y1},{ x2,y2},。
mathematica 实验报告

mathematica 实验报告Mathematica 实验报告引言:Mathematica 是一款强大的数学软件,它能够帮助用户进行各种数学计算、数据分析和可视化等工作。
本实验报告将介绍我在使用 Mathematica 进行实验时的一些经验和心得。
一、实验目的本次实验的目的是通过使用 Mathematica,掌握其基本操作和功能,了解其在数学计算和数据处理方面的应用。
二、实验步骤1. 安装和启动 Mathematica首先,我在官方网站下载了 Mathematica 的安装包,并按照提示完成了安装。
然后,我启动了 Mathematica 软件,进入了主界面。
2. 基本操作在主界面中,我发现 Mathematica 提供了一个强大的交互式界面,用户可以通过键入命令和运行代码来实现各种功能。
我尝试了一些基本操作,比如进行简单的数学计算、定义变量和函数等。
3. 数据处理和分析Mathematica 提供了丰富的数据处理和分析功能,使得用户可以轻松处理和分析各种数据。
我使用了一些内置的函数和工具,对一些实验数据进行了处理和分析。
例如,我使用了 ListPlot 函数绘制了一些实验数据的散点图,并使用了Fit 函数进行了数据拟合。
4. 可视化Mathematica 还提供了强大的可视化功能,用户可以通过绘制图表和图形来展示数据和结果。
我使用了 Plot 函数绘制了一些函数的图像,并使用了 Graphics 函数绘制了一些几何图形。
5. 编程和自动化Mathematica 具有强大的编程功能,用户可以编写自己的函数和程序来实现复杂的计算和操作。
我尝试了一些简单的编程,比如编写了一个计算斐波那契数列的函数。
此外,我还了解到 Mathematica 支持自动化操作,可以通过编写脚本和批处理文件来实现自动化的计算和分析。
三、实验结果与分析通过使用 Mathematica,我成功完成了实验的各项任务,并取得了一些令人满意的结果。
微积分基础实验报告mathematica

微积分基础实验报告mathematica微积分基础实验报告【实验目的】1.验证Sinx 的泰勒级数;2.了解函数的升降情况以及求零点和极值;3.了解正弦函数的叠加图像;4.了解无极限的函数例;5.了解无穷积分;6.通过无穷大数列求自然对数 e 【实验要求】1.观察多项式函数、、的图像逼进正弦曲线的情况。
2.观察函数及其导函数的图像,了解图像的升降情况以及凹凸情况,求出零点与极值。
3.观察函数与的图像,了解随着k的增大,图像的变化。
4.(1)绘制函数在区间x [-1,1]上的图像,观察图像当x0时的变化情况。
(2)在函数中取3000 个点,绘制散点图。
观察这些点的分布。
5.绘制函数与的图像,观察当n 增加时p(x)向sinx 逼近的现象。
63xx y 120 65 3x xx y ! 7 ! 5 ! 37 5 3x x xx y63xx y 21 "2xy x kkymk) 1 2 sin(1 211mkkkxy1sinxy1sin x y sin nkkxx x p12 22) 1 ( ) (6.(1)通过计算与的值,观察这些值的变化趋势。
(2)绘制, 与y=e 的图像,观察当x 增大时图像的走向。
(3)计算的近似值,观察这些近似值对e 的逼近情况。
】【实验内容】(主要包含问题分析、计算过程、实验结果等,按课程要求完成)问题的分析(1)分别用不同颜色的曲线绘制出区间上正弦曲线以及多项式函数、、的图像。
(2)根据理论知识可知,多项式项数越多越接近正弦曲线的图像。
(1)分别用不同颜色的曲线绘制出区间上函数及其导函数的图像。
(2)当y’0 时,函数下降,当y’0 时函数上升,当y’=0 时,函数图像存在极值。
当y’上升时,函数图像为凸函数,当y’下降时,函数图像为凹图像。
当y’取极值时,函数图像出现拐点。
(3)通过图像得出零点近似值,以及函数极小值的近似值,通过编程nnna)11 ( 1)11 (nnnAxxy10)1011 ( 1 10)1011 (xxy1!11kke] , [ x63xx y 120 65 3x xx y ! 7 ! 5 ! 37 5 3x x xx y ] 4 , 4 [ x63xx y21 "2xy得出精确的零点与极值。
函数的图像绘制(mathematica数学实验报告)

分析:从此图像中可以大致看出导函数的正负,则可以确定原函数的增减性,当y 0'≥,即大致 2.60x -≤≤时导函数小于零,则原函数在此区间内是减函数;y 0'≤ ,即大致 2.6x ≤-或0x ≥时导函数大于零,则在原函数此区间内是增函数。
另一方面,从原函数与y 轴的大致交点,结合Mathematica 软件,可以求得原函数的根,如下:分析:此程序编写错误,从原图像中大致可以看出其与y 轴的交点在 4.1-附近,故应如下编写:从而得到原函数的根为: 4.13638x =-。
求根的原理是:将函数323127y x x =++在4.1x =-附近看作一次函数()()()4.1 4.1 4.1y f f x '≈-+--,其中()2924f m m m '=+是y 在 4.1x =-处的倒数值。
认为一次方程()()()4.1 4.1 4.10f f x '-+--=的解是比 4.1-更好的近似值,用它代替 4.1-再求出根的更好的近似值。
可以由以下语句产生:分析:程序运行错误的原因是将递归求根函数[, 4.1,4]Nestlist h -错写成[, 4.1,6]Nextlist h -。
正确运行如下:得到6次求根结果。
还可以利用Mathematica 编程求出原函数的极小值,如下:得到了极小值,很容易会想到如何求其极大值?Mathematica 没有提供求极大值的函数,所以不能直接求解,但可以求()0f x -=的极小值,即为原函数的极大值,具体运行如下:(2)正弦函数的叠加在数学的学习当中,我们经常会遇到这种题:画出区间[2,2]x ππ∈-上的函数1sin sin 3,,3y x x =+()11sin 21,,21m k y k x k ==∑--当n 很大时,不可能用Plot 语句中直接输入函数来画出函数图像,而要使用如下语句:[_,_]:[[*]/,{,1,,2}];[[,4],{,2,2}]f x n Sum Sin k x k k n Plot f x x Pi Pi =-当n=4时,运行如下:给n再取更大的值,例如,当n=611与n=1000时,运行如下:从图像中可以看出此种函数是周期函数。
Mathematica绘图总结

Mathematica绘图总结第一篇:Mathematica绘图总结Mathematica绘图总结Mathematica是一个强大的数学工具,它可以广泛应用到数学的各个领域中。
而Mathematica的绘图以其丰富的形式,多样的变化,鲜明的色彩给人以直观的视觉感受,并加深我们对抽象的数学的直观理解。
·二维作图基本绘图命令Plot[f,{x,xmin,xmax},选项]:f[x]在区间[xmin,xmax]上的函数曲线Plot[{fl, f2..},{x,xmin,xmax},选项]:在同一图形上画几条曲线ListPlot[{y1,y2,..}]:绘出由离散点对(n,yn)组成的图ListPlot[{{x1,y1},{x2,y2},}}:绘出由离散点对(xi,yi)组成的图ParametricPlot[{fx,fy},{t,tmin,tmax}]:由参数方程在参数变化范围内产生的曲线2常用选项Plot 函数的选项,告诉系统如何显示图形,以及对坐标轴、刻度等细节的处理等。
PlotRange:作图显示的值域范围AspectRatio:图形的纵横比PlotLabel->label:标题文字 Axes:分别制定是否画x,y轴AxesLabel->{xlabel,ylabel}:x,y轴上的说明文字AxesOrigin->{x,y}:坐标轴原点位置 Frame:是否画边框FrameLabel->{xmlabel,ymlabel,xplabel,yplabel}:边框四边上的文字 Ticks:设置坐标轴上刻度的位置lotsytle->{{style1},{style2},..}:曲线的线性颜色等属性PlotPoints:曲线取样点,越大越细致·三维作图基本绘图命令 Plot3D[f,{x,xmin,xmax},{y,ymin,ymax},选项]:二维函数flx,y]的空间曲面ListPlot3D[array]:二维数据阵array的立体高度图ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}]:三维参数图形ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]:二维函数f在指定区间上的等高线图2常用选项Axes:是否包括轴PlotLabel:在轴上加标志PlotLabel:设置x,y,z 轴的标志AspectRatio:图形的高度与宽度之比ViewPoint:观察曲面所在的点,可以设定任何观察点Boxed True:是否在曲面周围加立体框 BoxRatios:三维立体边长比率·等值线图和密度图ContourPlot [f[x,y],{x,xmin,xmax},{y,ymin,ymax},选项]:等值线图 Densityplot [f[x,y],{x,xmin,xmax},{y,ymin,ymax},选项]:密度图·用图形元素绘图Point [{x, y}]:点的位置在{x,y},x 和y 为坐标值 Line [{{x1,y1}, {x2,y2},…}]:依次连接相邻两点的线段Rectangle [{xmin,ymin}, {xmax,ymax}]:以{xmin,ymin}和{xmax,ymax}为对角线坐标的填实矩形Polygon [{x1,y1}, {x2,y2},…]:以{x1,y1},{x2,y2},…为顶点的封闭多边形Raster [{{a11,a12,…}, {a21,a22,…},…}]:灰度颜色的矩阵Circle [{x,y}, r]:圆心在{x,y},半径为r 的圆Circle [{x,y}, {rx,ry}]]:圆心在{x,y}, 长短半轴为rx和ry的椭圆Circle [{x,y}, r, {t1,t2}]:从弧度t1 到弧度t2 的圆弧Circle [{x,y}, {rx,rt}, {t1,t2}]:从弧度t1 到弧度t2 的椭圆弧 Disk [{x,y}, r]:圆心在{x,y},半径为r 的填实圆Point[{x,y,z}]:点{x,y,z} Line[{{x1,y1,z1},{x2,y2,z2},…}]:通过点{x1,y1,z1},{x2,y2,z2},…的线Polygon[{{x1,y1,z1},{x2,y2,z2},…}]:具有指定角的填实多边形Cuboid[{x0,y0,z0},{x1,y1,z1}]:以{x0,y0,z0}和{x1,y1,z1}为对角线的立方体 Text [expr,{x,y,z}]:在{x,y,z}处的文本·图形显示Show[graphics,options]:显示一组图形对象,options为选项设置 Show[g1,g2…]:在一个图上叠加显示一组图形对象GraphicsArray[{g1,g2,...}]:在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]:把选中的notebook中的图画循环放映·着色及其他GrayLevel[level]:灰度level为0~1间的实数RGBColor[red,green,blue]:RGB颜色,均为0~I间的实数Hue[h,s,b]:亮度,饱和度等,均为0~1间的实数CMYKColor[cyan,magenta,yellow,block]:CMYK颜色Thickness[r]:设置线宽为r PointSize[d]:设置绘点的大小Dashing[{r1, r2...}]画一个单元的间隔长度的虚线 ImageSize->{x,y}:显示图形大小(单位为像素)总结:Mathematica中作图的命令繁多复杂,我们要将这些命令熟练掌握,灵活运用,才能做出精美的图案。
Mathematica图形绘制.

教 据一些数据,画出空间曲面图形
案
上页 下页 退出
为了更好地理解ListPlot3D命令,下面以一个实际例子
哈 来说明它. 假设你要绘制某个地区的某个矩形区域的
工 程
三维地形图,你将此矩形区域放到平面直角坐标系中,
大 设X为南北方向,Y为东西方向,Z为地面高度,将X,Y轴
学 分成若干网格,在每一网格点上,你都可以得到一个高
的
值
1.01, 0.82, 0.65, 0.5, 0.37, 0.26, 0.17, 0.1, 0.05, 0.02, 0.01, 0.02, 0.05, 0.1, 0.17,
具
计
0.26, 0.37, 0.5, 0.65, 0.82, 1.01 , 1., 0.81, 0.64, 0.49, 0.36, 0.25, 0.16, 0.09, 0.04, 0.01, 6.16298 10 33, 0.01, 0.04, 0.09, 0.16, 0.25, 0.36, 0.49, 0.64, 0.81, 1. ,
上页 下页 退出
因此,x2+ y2+ z2=1在球坐标下的方程是r=1,方程x2-
哈 y2= z是马鞍面,以下命令画出二者相交后的图形.
工 r 1;
程 a1 : ParametricPlot3D r Sin Cos , r Sin Sin , r Cos ,
大
学
, 0, , , 0, 2 ;
a2 : Plot3D x^2 y^ 2, x, 1, 1 , y, 1, 1 ;
教 案
上页 下页 退出
@8@D@D<8 <D
Plot Sin x , Cos x , x, 0, 4 Pi
综合数学实验报告(mathematica)

综合数学实验报告(mathematica)数学综合实验报告学院:数学与统计学院专业:数学与应用数学姓名:##########学号:##########班级:##########综合实验实验一:观察数列极限一、实验目的利用数形结合的方法观察数列的极限,可以从点图上看出数列的收敛性,以及近似地观察出数列的收敛值;通过编程可以输出数列的任意多项值,以此来得到数列的收敛性。
通过此实验对数列极限概念的理解形象化、具体化。
二.实验环境学校机房,Mathematica 4.0软件三、实验的基本理论和方法1、Mathematica中常用的函数及函数调用的方法;2、对Fabonacci数列、调和级数以及3n+1问题规律的掌握。
四、实验内容及步骤设为实数列,为定数.若对任给的正数,总存在正整数,使得当时有,则称数列收敛于定数称为数列的极限,并记作或。
下面,我们以求为例进行实验,程序编写及运行如下:程序运行结果如下:五、实验结果和结果分析由运行结果和图像可知,发现在时,函数值无限靠近2.7左右。
实验二:函数图像绘制一、实验目的通过函数图形来认识函数,运用函数的图形来观察和分析函数的有关性态,建立数形结合的思想。
二.实验环境学校机房,Mathematica 4.0软件三、实验的基本理论和方法1、Mathematica中常用绘图函数Plot在绘制一元函数时的方法;2、函数迭代法的基本理论以及在Mathematica中的使用。
四、实验内容及步骤1、求的所有根(先画图再求解)。
2、求方程与的根。
3、求下列各题的解。
(1);(2),求;(3)(精确到17位有效数字);(4);(5)将在处展开(最高次幂为8);(6),求。
4、作sinx的n阶Taylor展开(n=10,30,60)并比较图像5、已知函数,作出并比较当分别取-1,0,1,2,3时的图形,并从图形上观察极值点、驻点、单调区间、凹凸区间以及渐近线。
在mathematica中输入下面语句:Do[Plot[1/(x^2+2x+c),{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]],{c,-1,3}]程序运行结果如下:实验结果和结果分析观察图可得:第一幅图:极大值点为,驻点为,单调区间为增、,减、,凸区间为、,凹区间为,渐近线为水平,垂直, .第二幅图:极大值点为,驻点为,单调区间为增、,减、,凸区间为、,凹区间.第三幅图:没有极值点,没有驻点,单调增区间为,单调减区间为,凸区间为、.第四、五幅图:极大值点为,驻点为,单调区间为增,减,凸区间为、.实验三:泰勒公式与函数逼近一、实验目的利用Mathematica计算函数的各阶泰勒多项式,并通过绘制曲线图形,根据图形观察泰勒展开的误差,进一步掌握泰勒展开与函数逼近的思想,并对泰勒公式与原函数作出比较。
Mathematica数学实验——一元函数图象的绘制

教师指导实验4实验名称:一元函数图象的绘制一、问题:绘制常见的一元初等函数的图象。
二、实验目的:学会使用Mathematica 进行函数图象的绘制,并对图形作简单的修饰。
三、预备知识:本实验所用的Mathematica 命令提示。
1、Plot[f(x),{x,a,b}] 绘制函数()f x 在区间[,]a b 上的图象2、Plot[{f 1(x),f 2(x)},{x,a,b}] 绘制函数12(),()f x f x 在区间[,]a b 上的图象3、图形修饰选项的介绍:AspectRatio (图形的高宽比设置)RGBColor (颜色设置) AxesLabel (坐标轴标记设置)GridLines (网格线设置)PlotStyle (图形的属性设置) PlotLabel (图形的标注设置)Thickness (图形的相对线宽设置)四、实验的内容和要求:1、在同一坐标系绘制函数sin y x =和cos y x =在[2,2]ππ-的图象,并作一定的修饰;2、分别绘制函数22()x f x e -=和()ln sin()f x x x x =+的图象并作一定的修饰。
五、操作提示1、在同一坐标系绘制函数sin y x =和cos y x =在[2,2]ππ-的图象,并作一定的修饰; Plot[{Sin[x],Cos[x]},{x,-2π,2π}]在同一坐标系绘制函数sin y x =和cos y x =在[2,2]ππ-的图象 Plot[{Sin[x],Cos[x]},{x,-2π,2π},AxesLabel->(“x ”,”y ”)]对坐标轴进行标记Plot[{Sin[x],Cos[x]},{x,-2π,2π},AxesLabel->(“x ”,”y ”),AspectRatio->1/(2π)]设定图形的高宽比为1:2πPlot[{Sin[x],Cos[x]},{x,-2π,2π},AxesLabel->(“x ”,”y ”),AspectRatio->1/(2π)PlotStyle->{{RGBColor[1,0,0],Thickness[0.01]},{RGBColor[0,0,1], Thickness[0.01]}}]设定正弦线和余弦线的颜色分别为红色和蓝色,相对线宽均为0.01Plot[{Sin[x],Cos[x]},{x,-2π,2π},AxesLabel->(“x ”,”y ”),AspectRatio->1/(2π)PlotStyle->{{RGBColor[1,0,0], Thickness[0.01]},{RGBColor[0,0,1], Thickness[0.01]}},PlotPoints->50]规定绘图时取的最少点数50,增加图形的光滑度最终图形显示为2、分别绘制函数22()x f x e-=和()ln sin()f x x x x =+的图象并作一定的修饰。
数学实验用Mathematica画函数图形

实验2
空间图形的画法
y2 y2
x x
( 4 ) 画球面 f ( x, y ) 1 x2 y2 的图形。
x2 y2
( 5 ) 画函数 f ( x, y ) e 2 的图形。
( 6 ) 画双曲抛物面 f ( x, y ) x2 y2 的图形。
2
实验2 空间图形的画法
实验内容
✓ 空间曲线的绘制,并给出你的结论。
✓ PlotPoints:用于说明采样点的基本点数 如: Plot [{Sin[x], Sin[2*x]/2,Sin[3*x]/3},{x, -2Pi, 2Pi},
PlotStyle->{RGBColor[1,0,0], RGBColor[0,1,0], RGBColor[0,0,1]}] 如: Plot [Exp[x], {x, -5, 2}, PlotStyle->{RGBColor[1,0,0], Dashing[{0.02,0.02}],Thickness[0.01]},PlotPoints->1000] 如: Plot [Sin[1/x], {x, -0.01, 0.01}, PlotPoints->100]
a(t a(1
si nt ) cos t )
(a
2)的图形
(2)、画星形线
x
y
acos3t asi n3 t
的图形
✓ 极坐标方程画图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3图形绘制
班级专业:数学-08-01姓名:崔仁霞李海燕学号:*******************日期:成绩:
一、实验目的
1.熟悉Mathematica绘图命令;
2.掌握平面图形及空间图形的绘制方法及图形的控制方法。
二、实验准备
命令:Plot、ParametricPlot、ImplicitPlot、PolarPlot、ListPlot、Show、PlotStyle、ParametricPlot3D、Plot3D、ListPlot3D等命令。
D许多命令都有问题或错误.
2.运行结果()A准确,表现效果好;B正确;C部分结果不准确;D有较严重错误.
3.其它问题______________________________________________________________________.
4.综合评定()A优秀;B良好;C合格;D不合格;E有明显抄袭或雷同现象.
三、实验内容
1.绘制下列显式平面曲线(可选项取默认值)。
(1) ;
(2) 。
2.绘制下列隐函数平面曲线(可选项取默认值)。
(1) ;
(2) 。
3.绘制下列极坐标式平面曲线(可选项取默认值)。
(1) ;
(2) 。
4.绘制下列空间曲线。
(1) ;
(2) 。
5.绘制下列曲面。(1) ,在矩形域 来自;(2) ,在矩形域 上。
6.已知 个 值的数据为:
试绘制此数据曲面的图形。
四、程序、命令与结果
一,(1)命令:
结果:
(2)命令:
结果:
二,(1)命令:
结果:
(2)命令:
结果:
三,(1)命令:
结果:
(2)命令:
结果:
四,(1)命令:
结果:
(2)命令:
结果:
五,(1)命令:
结果:
(2)命令:
结果:
六,命令:
结果:
成绩评定:1.程序、命令()A准确、简洁、效率高;B命令基本准确,但有少量问题;C部分命令有问题;
