湍流边界层结构 Turbulent Boundary Layer Structure
流体力学中的流体中的湍流边界层

流体力学中的流体中的湍流边界层流体力学是研究流体的运动规律和性质的学科,湍流边界层则是流体力学中一个重要概念。
本文将对流体力学中的湍流边界层进行详细的介绍和论述。
一、湍流边界层的定义湍流边界层是指在流体中,当流动达到一定速度时,边界层内会出现湍流现象。
边界层是指流体靠近固体边界时速度逐渐减小,同时摩擦力逐渐增大的区域。
湍流边界层的形成使得流体流动变得非常复杂,是流体力学中的一个重要研究对象。
二、湍流边界层的特征1. 非线性:湍流边界层的速度和摩擦力分布呈现出非线性分布,即速度和摩擦力随着距离的增加而发生剧烈变化。
2. 随机性:湍流边界层的湍流运动是随机的,速度和摩擦力的变化具有不可预见性。
3. 涡旋结构:湍流边界层中存在大量的涡旋结构,这些涡旋会不停地生成、移动和消失,对流体的运动产生明显的影响。
三、湍流边界层的数学模型为了研究湍流边界层的运动规律,研究者提出了一系列的数学模型。
其中最著名的是雷诺平均纳维-斯托克斯(RANS)方程。
RANS方程是一组描述湍流边界层中平均速度和摩擦力变化的偏微分方程,通过求解这组方程可以得到湍流边界层的平均流动特性。
四、湍流边界层的应用湍流边界层在工程领域有着广泛的应用。
在飞机设计中,研究湍流边界层可以帮助减小气动阻力,提高飞行效率。
在水利工程中,研究湍流边界层可以帮助提高水泵效率和减少流体阻力。
在能源领域,湍流边界层的研究可以改善风力发电机的叶片设计,提高电能转化效率。
五、湍流边界层的挑战和前景湍流边界层的研究仍然面临着一些挑战。
湍流边界层的数学模型仍然不够精确,目前还没有能够完全描述湍流边界层的理论。
此外,湍流边界层的计算复杂度较高,需要大量的计算资源支持。
然而,随着计算机技术的不断进步,湍流边界层的研究将会取得更大的突破,为各个领域的工程应用提供更多的可能性。
六、结论湍流边界层是流体力学中的一个重要概念,具有非线性、随机性和涡旋结构等特征。
通过数学模型的建立和求解,可以揭示湍流边界层的运动规律。
第一章 流体流动2..

)
盐城师范学院
---化工原理---
1.4.2 流体在圆管内的速度分布 速度分布:流体在圆管内流动时,管截面上 质点的速度随半径的变化关系。 无论是滞流或湍流,在管道任意截面上,流体质点的速度 沿管径而变化,管壁处速度为零,离开管壁以后速度渐增, 到管中心处速度最大。速度在管道截面上的分布规律因流 型而异。
层流边界层 湍流边界层
u∞
u∞
u∞
δ
A x0
层流内层
平板上的流动边界层
盐城师范学院
转折点:
Re x
u x
---化工原理---
5 105 ~ 2 106
边界层厚度δ随x增加而增加
层流: 4.64 x (Rex )0.5
层流边界层
湍流边界层
x
x
0.5
u∞
u∞
u∞
湍流: 0.376 0.2
(a)
过渡流
(b)
湍流 (Turbulent flow)
(c)
两种稳定的流动状态:层流、湍流。
盐城师范学院
---化工原理---
层流:
* 流体质点做直线运动;
* 流体分层流动,层间不相混合、不碰撞; * 流动阻力来源于层间粘性摩擦力。 湍流: 主体做轴向运动,同时有径向脉动;
特征:流体质点的脉动 。
r2 u umax 1 R 2
盐城师范学院
---化工原理---
r2 dVs umax 2r 1 R 2 dr
积分此式可得
2 r r R Vs 2umax r 0 r 1 R 2 dr R 2 4 r r 2umax 2 R 2u / 2 max 2 4R 0
第10章 湍流边界层

第10章 湍流边界层10.1 壁面湍流特性和速度分布规律当边界层内流体及管内流体处于层流流动状态时,流体受到壁面的限制仅仅表现在粘性切应力作用下,进行粘性旋涡的扩散;而当处于湍流流动状态时,流体受到壁面的限制则是在粘性切应力和湍流附加切应力的同时作用下,进行旋涡的扩散。
由于湍动旋涡的扩散速度远大于粘性旋涡扩散的速度,因此,在相同条件下,湍流速度边界层的厚度要比层流速度边界层厚。
但在高雷诺数的条件下,湍流速度边界层仍是贴近壁面的薄层,因此,建立湍流边界层方程的前提条件与层流时相同。
但是,由于两种切应力的作用,湍流速度边界层的结构要比层流速度边界层复杂得多。
因此,一定要先了解壁面湍流的分层结构和时均速度分布规律。
10.1.1 壁面湍流分层结构及其特性在壁面湍流中,随着壁面距离的变化,粘性切应力和湍流附加切应力各自对流动的影响也发生变化。
以y 表示离开壁面的垂直距离,随着y 的增加,粘性切应力的影响逐渐减小,而湍流附加切应力的影响开始不断增大,而后逐渐减小。
这就形成了具有不同流动特征的区域。
壁面湍流速度边界层可以分为内层(壁面区),包括粘性底层、过度层(重叠层)和对数律层(完全湍流层);外层,包括尾迹律层和粘性顶层(间歇湍流层)。
定义()ρτwx v v ==** (10.1.1) 因为*v 具有速度的量纲,故称为壁面切应力速度,它在湍流中是一个重要的特征速度。
以下对各层的划分做详细说明。
粘性底层:所在厚度约为*50v y ν≤≤,其内粘性切应力起主要作用,湍流附加切应力可以忽略,流动接近于层流状态,因此在早期研究中称之为层流底层。
由于近期的实验研究,观察到该层内有微小旋涡及湍流猝发起源的现象,因此称为粘性底层。
过渡层:所在厚度约为**305vy vνν≤≤,其内粘性切应力和湍流附加切应力为同一数量级,流动状态极为复杂。
由于其厚度不大,在工程计算中,有时将其并入对数律层的区域中。
对数律层:所在厚度约为()δνν2.01030*3*≈≤≤v y v ,其内流体受到的湍流附加切应力大于粘性切应力,因而流动处于完全湍流状态。
大气边界层

湍流的产生
机械湍流( mechanical Turbulence) 热力湍流( thermal Turbulence )或对流湍 流(convective turbulence) 惯性湍流(inertial Turbulence)
机械湍流( mechanical Turbulence)
由风切变产生 风切变产生的原因:地面摩擦力,地形建筑 等障碍物的阻挡等。
9.4.4 The Marine Boundary Layer
9.4.4 The Marine Boundary Layer
9.4.4 The Marine Boundary Layer
9.4.5 Stormy Weather
9.4.5 Stormy Weather
9.4.5 Stormy Weather
惯性湍流(inertial Turbulence)
由大湍涡产生,湍流串级(turbulent cascade) Small eddies can also be generated along the edges of larger eddies, a process called the turbulent cascade, where some of the inertial energy of the larger eddies is lost to the smaller eddies
湿度通量
Байду номын сангаас
9.2.4 The Global Surface Energy Balance
9.2.4 The Global Surface Energy Balance
9.3 Vertical Structure 垂直结构
9.3.1 Temperature
层流和湍流

E( ) Ce 2/3 5/3 f L fh
log E()
Energy containing
range
Inertial subrange
log
Dissipation range
British scientist Osborne Reynolds (1842–1912) discovered that the flow regime depends mainly on the ratio of inertial forces to viscous forces in the fluid.
Re=2300 Re=11000
length scale : h (n 3 / e )1/4 velocity scale : uh (en )1/4 time scale : th (n / e )1/2
(uh /h) 1/th Reh huh /n 1
Andrey Kolmogorov and Kolmogorov microscopic scale
turbulent湍流
湍流: 能量和运动尺度Scales of motion
Length scale L
长度尺度:L 脉动速度:uo 特征时间(turn over time): L/ uo 脉动能量uo2 能量耗散率e= uo2/(L/ uo )= uo3 /L 最小旋涡尺度h=(n3/e)1/4; L/h=(uoL/n) 3/4=Reo3/4 最小速度尺度v=(ne)1/4; Reh~1 最小时间尺度:t=(n/e)1/2;
Turbulence 2014
孔板
网
湍流
管内流动 Internal flow 外流 External flow
液体流动的边界层结构与湍流行为研究

液体流动的边界层结构与湍流行为研究液体的流动是一种普遍存在的现象,在许多工程和科学领域都有重要的应用。
而流体的边界层结构和湍流行为对于流动的理解和控制至关重要。
本文将探讨液体流动的边界层结构以及湍流的起源和特征。
一、液体流动的边界层结构边界层是指在液体流动中靠近固体表面的一层液体,其速度和剪切应力都受到固体表面的影响。
边界层的结构对于流体的传热、传质和力学特性有重要影响。
1. 边界层厚度边界层的厚度决定了流体的传热和传质速率。
通常来说,边界层厚度在固体表面附近很薄,但随着距离的增加逐渐增大。
边界层厚度的大小取决于液体的粘度以及流动的速度等因素。
2. 边界层速度剖面边界层中,流体的速度与距离表面的距离之间存在关系。
通常情况下,靠近固体表面时流体速度较低,呈现一种逐渐增加的趋势。
而随着距离的增加,流速逐渐接近主流速度。
3. 边界层的剪切应力边界层中的流体存在剪切应力,即流体层与固体表面之间的相互作用力。
剪切应力的分布对于边界层结构和流动特性起到重要的调控作用。
二、湍流的起源和特征湍流是一种流动状态,液体在其中呈现出无规则的脉动和旋转。
湍流的起源和特征对于流体力学的研究和应用具有重要意义。
1. 湍流的起源湍流的形成和持续主要受到两个因素的影响:流体的惯性和流动的不稳定性。
当流体的惯性作用足够大以克服粘性阻力时,流动就会变得不稳定,并进入湍流状态。
2. 湍流的特征湍流的特征主要包括湍流的流速分布、湍流的旋转和湍流的能量耗散。
湍流中的涡旋结构对于物体的传热和物质的传输起到重要的作用,湍流的能量耗散则决定了湍流流场的稳定性和演化规律。
三、研究方法和应用为了更好地理解和掌握液体流动的边界层结构和湍流行为,科学家们采用了各种研究方法和工具。
例如,实验室内的流动实验、数值模拟和理论分析等方法都可以用于研究流体的边界层结构和湍流行为。
对于这些研究成果的应用,也广泛地涉及到了许多领域。
在工程上,研究湍流行为可以帮助我们提高流体传热效率、减小阻力损失,以及改善能源利用效果。
CFD分析基础-边界、网格、湍流模型

Realizable k–ε (RKE) 模型
术语 realizable 意味着这个模型满足在雷诺压力上的特定数学约束,
与物理紊流流动一致. uiuj 0
法向应力为正: 关于 Reynolds 剪切压力的Schwarz’不等式 :
uiuj
2
ui2u
2 j
标准 k–ε 模型和 RNG k–ε 模型都不是可实现的
LES(大涡模拟)基本原理
动量、质量、能量及其他被动标量大多由大尺度涡输 送
大涡结构(又称拟序结构)受流场影响较大,是由所 涉及流动的几何形状和边界条件决定的。
小尺度涡则认为是各向同性的受几何形状与边界条件 影响较小。
大涡模拟通过滤波处理,将小于某个尺度的旋涡从流 场中过滤掉,只计算大涡,然后通过求解附加方程得 到小涡的解。
标准 k–ε 模型的变形. “realizability” 来自允许确定的数学约束的改变的最终根据改善这种模型的性能.
Standard k–ω
SST k–ω Reynolds Stress
两个输运方程模型解出 k 和 ω, 指定的耗散率 (ε / k) 基于 Wilcox (1998). 这是默认的 k–ω模型. 在有界 壁面和低雷诺数流动中显示了较高性能. 显示了对过渡的较好预测. 用来解决过渡, 自由剪切, 和可压 流动.
DES(分离涡模拟模式) LES/ 4 fps
Example: Flow Around a Cylinder
wall
2 ft
1 ft
2 ft
wall
5 ft
14.5 ft
Compute drag coefficient of the cylinder
Turbulence Modeling Approach
(完整版)流体力学常用名词中英文对照

(完整版)流体力学常用名词中英文对照流体力学常用名词流体动力学fluid dynamics 连续介质力学mechanics of continuous 介质medium 流体质点fluid particle 无粘性流体nonviscous fluid, inviscid 连续介质假设continuous medium hypothesis 流体运动学fluid kinematics 水静力学hydrostatics 液体静力学hydrostatics 支配方程governing equation 伯努利方程Bernoulli equation 伯努利定理Bernonlli theorem 毕奥- 萨伐尔定律Biot-Savart law 欧拉方程Euler equation 亥姆霍兹定理Helmholtz theorem 开尔文定理Kelvin theorem 涡片vortex sheet 库塔- 茹可夫斯基条件Kutta-Zhoukowski condition 布拉休斯解Blasius solution 达朗贝尔佯廖d'Alembert paradox 雷诺数Reynolds number 施特鲁哈尔数Strouhal number 随体导数material derivative 不可压缩流体incompressible fluid 质量守恒conservation of mass 动量守恒conservation of momentum 能量守恒conservation of energy 动量方程momentum equation 能量方程energy equation 控制体积control volume 液体静压hydrostatic pressure 涡量拟能enstrophy 压差differential pressure 流[动]flow 流线stream line 流面stream surface 流管stream tube 迹线path, path line 流场flow field 流态flow regime 流动参量flow parameter 流量flow rate, flow discharge 涡旋vortex 涡量vorticity 涡丝vortex filament 涡线vortex line 涡面vortex surface 涡层vortex layer 涡环vortex ring 涡对vortex pair 涡管vortex tube 涡街vortex street 卡门涡街Karman vortex street 马蹄涡horseshoe vortex 对流涡胞convective cell 卷筒涡胞roll cell 涡eddy 涡粘性eddy viscosity 环流circulation 环量circulation 速度环量velocity circulation 偶极子doublet, dipole 驻点stagnation point 总压[ 力] total pressure 总压头total head 静压头static head 总焓total enthalpy 能量输运energy transport 速度剖面velocity profile 库埃特流Couette flow 单相流single phase flow 单组份流single-component flow 均匀流uniform flow 非均匀流nonuniform flow 二维流two-dimensional flow 三维流three-dimensional flow 准定常流quasi-steady flow 非定常流unsteady flow, non-steady flow 暂态流transient flow 周期流periodic flow 振荡流oscillatory flow 分层流stratified flow 无旋流irrotational flow 有旋流rotational flow 轴对称流axisymmetric flow 不可压缩性incompressibility 不可压缩流[动] incompressible flow 浮体floating body 定倾中心metacenter 阻力drag, resistance 减阻drag reduction 表面力surface force 表面张力surface tension 毛细[ 管]作用capillarity 来流incoming flow 自由流free stream 自由流线free stream line 外流external flow 进口entrance, inlet 出口exit, outlet 扰动disturbance, perturbation 分布distribution 传播propagation 色散dispersion 弥散dispersion 附加质量added mass ,associated mass 收缩contraction 镜象法image method 无量纲参数dimensionless parameter 几何相似geometric similarity 运动相似kinematic similarity 动力相似[ 性] dynamic similarity 平面流plane flow 势potential 势流potential flow 速度势velocity potential 复势complex potential 复速度complex velocity 流函数stream function 源source 汇sink 速度[ 水] 头velocity head 拐角流corner flow 空泡流cavity flow 超空泡supercavity 超空泡流supercavity flow 空气动力学aerodynamics 低速空气动力学low-speed aerodynamics 高速空气动力学high-speed aerodynamics 气动热力学aerothermodynamics 亚声速流[ 动] subsonic flow 跨声速流[ 动] transonic flow 超声速流[ 动] supersonic flow 锥形流conical flow 楔流wedge flow 叶栅流cascade flow 非平衡流[ 动] non-equilibrium flow 细长体slender body 细长度slenderness 钝头体bluff body 钝体blunt body 翼型airfoil 翼弦chord 薄翼理论thin-airfoil theory 构型configuration 后缘trailing edge 迎角angle of attack 失速stall 脱体激波detached shock wave 波阻wave drag 诱导阻力induced drag 诱导速度induced velocity 临界雷诺数critical Reynolds number 前缘涡leading edge vortex 附着涡bound vortex 约束涡confined vortex 气动中心aerodynamic center 气动力aerodynamic force 气动噪声aerodynamic noise 气动加热aerodynamic heating 离解dissociation 地面效应ground effect 气体动力学gas dynamics 稀疏波rarefaction wave 热状态方程thermal equation of state 喷管Nozzle 普朗特- 迈耶流Prandtl-Meyer flow 瑞利流Rayleigh flow 可压缩流[ 动] compressible flow 可压缩流体compressible fluid 绝热流adiabatic flow 非绝热流diabatic flow 未扰动流undisturbed flow 等熵流isentropic flow 匀熵流homoentropic flow 兰金- 于戈尼奥条件Rankine-Hugoniot condition 状态方程equation of state 量热状态方程caloric equation of state 完全气体perfect gas 拉瓦尔喷管Laval nozzle 马赫角Mach angle 马赫锥Mach cone 马赫线Mach line 马赫数Mach number 马赫波Mach wave 当地马赫数local Mach number 冲击波shock wave 激波shock wave 正激波normal shock wave 斜激波oblique shock wave 头波bow wave 附体激波attached shock wave 激波阵面shock front 激波层shock layer 压缩波compression wave 反射reflection 折射refraction 散射scattering 衍射diffraction 绕射diffraction 出口压力exit pressure 超压[ 强] over pressure 反压back pressure 爆炸explosion 爆轰detonation 缓燃deflagration 水动力学hydrodynamics 液体动力学hydrodynamics 泰勒不稳定性Taylor instability盖斯特纳波Gerstner wave 斯托克斯波Stokes wave 瑞利数Rayleigh number 自由面free surface 波速wave speed, wave velocity 波高wave height 波列wave train 波群wave group 波能wave energy 表面波surface wave表面张力波capillary wave 规则波regular wave 不规则波irregular wave 浅水波shallow water wave 深水波deep water wave 重力波gravity wave 椭圆余弦波cnoidal wave 潮波tidal wave 涌波surge wave 破碎波breaking wave 船波ship wave 非线性波nonlinear wave 孤立子soliton 水动[力]噪声hydrodynamic noise 水击water hammer 空化cavitation 空化数cavitation number 空蚀cavitation damage 超空化流supercavitating flow 水翼hydrofoil 水力学hydraulics 洪水波flood wave 涟漪ripple 消能energy dissipation 海洋水动力学marine hydrodynamics 谢齐公式Chezy formula 欧拉数Euler number 弗劳德数Froude number 水力半径hydraulic radius 水力坡度hvdraulic slope 高度水头elevating head 水头损失head loss 水位water level 水跃hydraulic jump 含水层aquifer 排水drainage 排放量discharge 壅水曲线back water curve 压[强水]头pressure head 过水断面flow cross-section 明槽流open channel flow 孔流orifice flow 无压流free surface flow 有压流pressure flow 缓流subcritical flow急流supercritical flow 渐变流gradually varied flow 急变流rapidly varied flow 临界流critical flow 异重流density current, gravity flow 堰流weir flow 掺气流aerated flow 含沙流sediment-laden stream 降水曲线dropdown curve 沉积物sediment, deposit 沉[降堆]积sedimentation, deposition 沉降速度settling velocity 流动稳定性flow stability 不稳定性instability 奥尔- 索末菲方程Orr-Sommerfeld equation 涡量方程vorticity equation 泊肃叶流Poiseuille flow 奥辛流Oseen flow 剪切流shear flow 粘性流[动]viscous flow 层流laminar flow 分离流separated flow 二次流secondary flow 近场流near field flow 远场流far field flow 滞止流stagnation flow 尾流wake [flow]回流back flow 反流reverse flow 射流jet 自由射流free jet 管流pipe flow, tube flow 内流internal flow 拟序结构coherent structure 猝发过程bursting process 表观粘度apparent viscosity 运动粘性kinematic viscosity 动力粘性dynamic viscosity 泊poise 厘泊centipoise 厘沱centistoke 剪切层shear layer 次层sublayer流动分离flow separation 层流分离laminar separation 湍流分离turbulent separation 分离点separation point 附着点attachment point 再附reattachment 再层流化relaminarization 起动涡starting vortex 驻涡standing vortex 涡旋破碎vortex breakdown 涡旋脱落vortex shedding 压[力]降pressure drop 压差阻力pressure drag 压力能pressureenergy 型阻profile drag 滑移速度slip velocity 无滑移条件non-slip condition 壁剪应力skin friction, frictional drag 壁剪切速度friction velocity 磨擦损失friction loss 磨擦因子friction factor 耗散dissipation 滞后lag 相似性解similar solution 局域相似local similarity 气体润滑gas lubrication 液体动力润滑hydrodynamic lubrication 浆体slurry 泰勒数Taylor number 纳维- 斯托克斯方程Navier-Stokes equation 牛顿流体Newtonian fluid 边界层理论boundary later theory 边界层方程boundary layer equation 边界层boundary layer 附面层boundary layer 层流边界层laminar boundary layer 湍流边界层turbulent boundary layer 温度边界层thermal boundary layer 边界层转捩boundary layer transition 边界层分离boundary layer separation 边界层厚度boundary layer thickness 位移厚度displacement thickness 动量厚度momentum thickness 能量厚度energy thickness 焓厚度enthalpy thickness 注入injection 吸出suction 泰勒涡Taylor vortex 速度亏损律velocity defect law 形状因子shape factor 测速法anemometry 粘度测定法visco[si] metry 流动显示flow visualization 油烟显示oil smoke visualization 孔板流量计orifice meter 频率响应frequency response 油膜显示oil film visualization 阴影法shadow method 纹影法schlieren method 烟丝法smoke wire method 丝线法tuft method 说明氢泡法nydrogen bubble method 相似理论similarity theory 相似律similarity law 部分相似partial similarity 定理pitheorem, Buckingham theorem 静[态]校准static calibration 动态校准dynamic calibration 风洞wind tunnel 激波管shock tube 激波管风洞shock tube wind tunnel 水洞water tunnel 拖曳水池towing tank 旋臂水池rotating arm basin 扩散段diffuser 测压孔pressure tap 皮托管pitot tube 普雷斯顿管preston tube 斯坦顿管Stanton tube 文丘里管Venturi tube U 形管U-tube 压强计manometer 微压计micromanometer 多管压强计multiple manometer 静压管static [pressure]tube 流速计anemometer 风速管Pitot- static tube 激光多普勒测速计laser Doppler anemometer ,laser Doppler velocimeter 热线流速计hot-wire anemometer 热膜流速计hot- film anemometer 流量计flow meter 粘度计visco[si] meter 涡量计vorticity meter 传感器transducer , sensor 压强传感器pressure transducer 热敏电阻thermistor 示踪物tracer 时间线time line 脉线streak line 尺度效应scale effect 壁效应wall effect 堵塞blockage 堵寒效应blockage effect 动态响应dynamic response 响应频率response frequency 底压base pressure 菲克定律Fick law 巴塞特力Basset force 埃克特数Eckert number 格拉斯霍夫数Grashof number 努塞特数Nusselt number 普朗特数prandtl number 雷诺比拟Reynolds analogy 施密特数schmidt number 斯坦顿数Stanton number 对流convection 自由对流naturalconvection, free convec-tion 强迫对流forced convection 热对流heat convection 质量传递mass transfer 传质系数mass transfer coefficient 热量传递heat transfer 传热系数heat transfer coefficient 对流传热convective heat transfer 辐射传热radiative heat transfer 动量交换momentum transfer 能量传递energy transfer 传导conduction 热传导conductive heat transfer 热交换heat exchange 临界热通量critical heat flux 浓度concentration扩散diffusion 扩散性diffusivity 扩散率diffusivity 扩散速度diffusionvelocity 分子扩散molecular diffusion 沸腾boiling 蒸发evaporation 气化gasification 凝结condensation 成核nucleation 计算流体力学computational fluid mechanics 多重尺度问题multiple scale problem 伯格斯方程Burgers equation 对流扩散方程convection diffusion equationKDU 方程KDV equation 修正微分方程modified differential equation 拉克斯等价定理Lax equivalence theorem 数值模拟numerical simulation 大涡模拟large eddy simulation 数值粘性numerical viscosity 非线性不稳定性nonlinear instability 希尔特稳定性分析Hirt stability analysis 相容条件consistency condition CFL 条件Courant- Friedrichs- Lewy condition ,CFL condition 狄里克雷边界条件Dirichlet boundary condition 熵条件entropy condition 远场边界条件far field boundary condition 流入边界条件inflow boundary condition 无反射边界条件nonreflecting boundary condition 数值边界条件numerical boundary condition 流出边界条件outflow boundary condition 冯. 诺伊曼条件von Neumann condition 近似因子分解法approximate factorization method 人工压缩artificial compression 人工粘性artificial viscosity 边界元法boundary element method 配置方法collocation method 能量法energy method 有限体积法finite volume method 流体网格法fluid in cell method,FLIC method 通量校正传输法flux-corrected transport method 通量矢量分解法flux vector splitting method 伽辽金法Galerkin method 积分方法integral method标记网格法marker and cell method, MAC method 特征线法method ofcharacteristics 直线法method of lines 矩量法moment method 多重网格法multi- grid method 板块法panel method 质点网格法particle incell method, PIC method 质点法particle method 预估校正法predictor-corrector method 投影法projection method 准谱法pseudo-spectral method 随机选取法random choice method 激波捕捉法shock-capturing method 激波拟合法shock-fitting method 谱方法spectral method 稀疏矩阵分解法split coefficient matrix method 不定常法time-dependent method 时间分步法time splitting method 变分法variational method 涡方法vortex method 隐格式implicit scheme 显格式explicit scheme 交替方向隐格式alternating direction implicit scheme, ADI scheme 反扩散差分格式anti-diffusion difference scheme 紧差分格式compact difference scheme 守恒差分格式conservation difference scheme 克兰克- 尼科尔森格式Crank-Nicolson scheme 杜福特- 弗兰克尔格式Dufort-Frankel scheme 指数格式exponential scheme 戈本诺夫格式Godunov scheme 高分辨率格式high resolution scheme 拉克斯- 温德罗夫格式Lax-Wendroff scheme 蛙跳格式leap-frogscheme 单调差分格式monotone difference scheme 保单调差分格式monotonicity preserving diffe-rence scheme 穆曼- 科尔格式Murman-Cole scheme 半隐格式semi-implicit scheme 斜迎风格式skew-upstream scheme 全变差下降格式total variation decreasing scheme TVD scheme 迎风格式upstream scheme , upwind scheme 计算区域computational domain 物理区域physical domain 影响域domain of influence 依赖域domain of dependence区域分解domain decomposition 维数分解dimensional split 物理解physical solution 弱解weak solution 黎曼解算子Riemann solver 守恒型conservation form 弱守恒型weak conservation form强守恒型strong conservation form 散度型divergence form 贴体曲线坐标body-fitted curvilinear coordi-nates [ 自] 适应网格[self-] adaptive mesh 适应网格生成adaptive grid generation 自动网格生成automatic gridgeneration 数值网格生成numerical grid generation 交错网格staggered mesh 网格雷诺数cell Reynolds number 数植扩散numericaldiffusion 数值耗散numerical dissipation 数值色散numerical dispersion 数值通量numerical flux 放大因子amplification factor 放大矩阵amplification matrix 阻尼误差damping error 离散涡discrete vortex 熵通量entropy flux 熵函数entropy function 分步法fractional step method。
边界层壁面摩擦速度

壁面摩擦速度的确定对于湍流边界层问题,准确计算摩擦速度(friction velocity )u τ是一个非常关键的问题。
直接测量壁面的速度梯度对于实验来说是很难获得的,尤其是对于粗糙壁面,另外采用积分动量方法又很不准确。
这就是为什么到目前为止,绝大多数计算摩擦速度的方法是间接的,并且依赖于壁面法则(Walker 2014)。
壁面相似方法(Wall Similarity Method )被认为是计算摩擦速度的一种有效方法,根据对数区方程中常数B 可以将其分为:通过方法本身推倒获得或预先固定的两种方式。
典型的方法有:Clauser Chart Method (CCM )(Clauser 1954),Standard (SBM ) and Modified (MBM ) Bradshaw Methods ,Standard Slope Method (SSM )等。
1. The Clauser chart method首先,假设湍流边界层重叠区域的速度分布遵循对数形式: ()1ln()yu U y B u vττκ=+ 其中,κ和B 是与雷诺数无关的常数 。
我们将上式两边同时乘以/u U τ∞ 得到:()11ln()ln()u u u u yU U y B U U v U U U ττττκκ∞∞∞∞∞∞⎡⎤⎛⎫⎛⎫=++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦ 因为摩擦系数()22/f C u U τ∞= ,Clauser chart 方程可以写成:()ln()yU U y U v ∞∞⎡⎢=++⎢⎣ 因为()U y 和U ∞ 可以直接通过实验测量,方程中唯一待定的参数就是摩擦系数C f 。
通过选取在区域50,0.2y η+><内最接近数据的直线,对应的C f 即为所求。
()2/2(ln(/))f d u U C d yU v κ⎛⎫= ⎪⎝⎭通常在文献中可以找到不同的参数0.380.45,3.5 6.1B κ<<<<,从而造成实验获得C f 的不确定性。
平板湍流边界层

湍流平板边界层的流速分布与分区结构
紊流边界层的流速分布在其不同的分区中具有不同的规律,与 圆管紊流相似。图11-1为紊流边界层中流速分布分区结构的 典型示意图。在紊流边界层中除粘性底层、过渡区及紊流区 (对数区)以外,还存在一个尾流区或称为外区(outer layer)。而粘性底层、过渡区和对数区则统称为内区(inner layer)。在紊流边界层中,对于分区界限各家试验略有出入。 一般用y 表示x2 ,认为: 粘性底层: 0 y 5 10 过渡区:5 10 y 30 70 对数区: 30 70 y , y 0.2
湍流平板边界层的流速分布与分区结构
图 11 3(a)流动显示图 ,
y 8
图 11 3(a)流动显示图 ,
y 82
图 11 3(c)流动显示图 ,
y 407
图 11 3(d)流动显示图 ,
y 531
湍流平板边界层的流速分布与分区结构
8 图11-3(a)表示 y 处平面上流动显示,此处位于粘 性底层上部或过渡区下部。由照片可见此处流速具有 大小相间的流速带,湍动剧烈,但湍动的三维性不明 显。
以上三个区域统称内区。 尾流区(外区): 0.2 y 1.0
湍流平板边界层的流速分布与分区结构
湍流平板边界层的流速分布与分区结构
平板紊流边界层各个分区中的流速分布为: 粘性底层: 对数区: 尾流区:
u yu 或写为 u
u y (11-7)
( 11-8 u 5.85 lg y 5.) 56
湍流平板边界层
§湍流平板边界层的流速分布与分区结构 §湍流平板边界层的紊动特性 §湍流平板边界层的能量平衡 §湍流平板边界层厚度和阻力 §粗糙平板紊流边界层
流体力学中的流体中的湍流边界层控制

流体力学中的流体中的湍流边界层控制流体力学中的湍流边界层控制流体力学是研究流体运动及其相互作用的学科,湍流边界层控制则是流体力学中的一个重要分支。
湍流边界层控制是指通过改变边界层流动的性质和结构,从而实现对湍流的控制和抑制。
本文将从湍流边界层的概念入手,探讨湍流边界层控制的方法和应用。
一、湍流边界层的概念及特性湍流边界层是指由于领域内流体速度分布的不均匀性而形成的一种流动状态。
它具有以下特性:1. 流体速度的剧烈变化:湍流边界层中的速度变化非常剧烈,存在许多涡旋结构,流场变得不规则且混乱。
2. 粘性的作用:由于边界效应,流体黏附于流动物体表面,这种黏附作用会在流动中起到重要作用。
3. 边界层的扩张:湍流边界层随着流动的延伸,会逐渐向流场的远处扩张,形成较宽的区域。
二、湍流边界层控制的方法为了实现对湍流边界层的控制,科学家们提出了多种方法和技术。
以下将介绍几种主要的湍流边界层控制方法:1. 波动发生器法:通过在边界层表面安装特殊的波动发生器,产生控制边界层流动的波动信号,从而实现湍流边界层的控制和抑制。
2. 增加表面粗糙度:通过增加流体与固体边界的接触面积,增加摩擦力,从而减小湍流边界层的厚度和湍流强度。
3. 热源控制法:通过在流体表面施加瞬态热源,改变湍流边界层的温度分布,以影响流体的速度场,从而控制湍流的发生和传播。
4. 基于流动控制器的方法:通过在流体中添加控制器,如旋转体、流动栅格等,来改变湍流边界层的结构和性质。
三、湍流边界层控制的应用湍流边界层的控制对于许多领域都具有重要意义,以下列举几个典型的应用案例:1. 飞行器气动外形优化:湍流边界层的控制可减小阻力,提高飞行器的气动性能,使其在空气中的运动更加稳定和高效。
2. 汽车减阻与增稳:通过控制湍流边界层,可以有效减小汽车外表面的阻力,提高汽车行驶的稳定性和燃油经济性。
3. 管道流体输送:在管道中控制湍流边界层可以减小流体的能量损失和泄漏,提高输送效率和安全性。
边界层理论

边界层(Boundary Layer)是高雷诺数绕流中紧贴物面的粘性力不可忽略的流动薄层,又称流动边界层、附面层。
这个概念由近代流体力学的奠基人,德国人Ludwig Prandtl(普朗特)于1904年首先提出。
从那时起,边界层研究就成为流体力学中的一个重要课题和领域。
在边界层内,紧贴物面的流体由于分子引力的作用,完全粘附于物面上,与物体的相对速度为零。
边界层又称附面层,它是指流体流经固体表面时,靠近表面总会形成那么一个薄层,在此薄层中紧贴表面的流体流速为零,但在垂直固体表面的方向(法向)上速度增加的很快,即具有很大的速度梯度,甚至对粘性很小的流体,也不能忽略它表现出来的粘性力。
而在此边界层外,流体的速度梯度很小,甚至对粘度很大的流体而言,其粘性力的影响也可以忽略,流体的流速与绕流固体表面前的流速V0一样。
这样就可把边界层外流动的流体运动视为理想流体运动,不考虑粘性力的影响。
边界层内、外区域间没有明显的分界面,而把边界层边缘上的流体流速V x视为V x=0.99 V0,因此从固体表面至V x=0.99 V0处的垂直距离视为边界层的厚度δ。
这样大雷诺数下绕过固体的流动便简化为研究边界层中的流动问题。
边界层内的流动可以是层流,也可以是带有层流底层的紊流,还可以是层流、紊流混合的过渡流。
图1 边界层结构综上所述,边界层的特征可归结为:(1)与固体长度相比,边界层厚度很小;(2)边界层内沿边界层厚度方向上的速度梯度很大;(3)边界层沿流动方向逐渐增厚;(4)由于边界层很薄,故可近似地认为,边界层截面上的压力等于同一截面上边界层外边界上的压力;(5)边界层内粘性力和惯性力士同一数量级的;(6)如在整个长度上边界层内都是层流,称层流边界层;仅在起始长度上的是层流,而在其他部分为紊流的称混合边界层。
以上定义的边界层为速度边界层,另外在其他学科领域中对于边界层的应用还是十分广泛的,主要有温度边界层和浓度边界层。
层流与湍流

' ' x y 2
江苏大学
Jiangsu University
式中: ,亦称为混合长度,但已无物理意 义。在湍流固体边壁或近壁处,普朗特假设混合长度正比于质点 到管壁的径向距离,即:
2 l 2 C1C2 L1
l ky
k ——由实验决定的无量纲常数。例如圆管层流时为0.4; y ——至壁面的距离。
2
τ
2 p1 v12 p2 v2 z1 z2 hf g 2g g 2g p hf g
p2 p1 r l 2
在壁面处取得最大切应力:
l v2 hf d 2g
p d o l 4
0
8
v2
5
4.2 圆管层流
二、速度分布
对照达西公式:
l v2 hf d 2g 所以,层流沿程阻力系数为
64 64 v d Re
8
4.2 圆管层流
三、圆管的起始段 起始段长度l:从进口速度 接近均匀到管中心流速 到达最大值的距离。
江苏大学
Jiangsu University
式中α,b为系数,随入口后的 距离而改变。
dvx vx vx ( y L1 ) vx ( y) L1 dy
第二章可压缩平板湍流边界层结构系综研究思路

北京大学博士学位论文第二章可压缩平板湍流边界层结构系综研究思路在绪论部分,我们提出湍流研究的突破需要创新思想,并引出了“结构系综动力学”这一有望解决真实湍流问题的理论。
本章我们将首先对这一理论的思想和概念、研究方法和步骤,以及其在IWTF研究中取得的成果作概要介绍。
然后探讨从IWTF到CWTF需要解决的新问题,并简单介绍和讨论SED理论在可压缩槽道流研究中的实践,接着正式引入CTBL的概念并对其研究历史作全面综述。
在综述的基础上,指出CTBL具有马赫数、壁面温度、雷诺数三个维度。
在对这三个维度中的热点和难题进行讨论后,本章将提出“孤维研究、逐维突破”的CWTF总体研究思路,进而具体给出CTBL结构系综研究思路。
2.1结构系综理论的提出2.1.1结构系综理论的思想和概念SED是一个定量刻画远离平衡态的湍流系统统计运动规律的理论,其通过在不封闭的系综平均N-S方程外引进新的物理原理来封闭湍流,给出湍流宏观运动的统计平均解,包含一套完整的概念、研究思想和方法[24–26]。
SED理论的雏形形成于2009年[27],在2012年取得关键性进步[12],正逐步发展为比较成熟的理论。
下面我们根据佘振苏教授在各个场合的阐述和陈曦的博士论文[12],对该理论的一些思想、概念、方法等进行简要概述。
在对湍流进行长期思考后,佘振苏教授认识到:真实湍流系统既是一个同时包含物理空间动量能量输运和尺度空间能量级串的远离平衡态系统,又是一个包含两类复杂性的复杂系统1。
因此,对湍流这样一个机械物理系统中复杂度最大、内容最丰富、结构最多样的系统建立理论,必须在非平衡态系统和复杂系统两个点上同时突破。
然而,自上个世纪以来,湍流研究一直由传统自然科学研究所采用的还原论主导。
人们从单一维度、单一层次来认识湍流,寄希望于发现湍流的一个基本结构。
显然,对于湍流这样一个非平衡态系统,如果仅存在一个基本结构,那么统计系综层面上一定是近平衡态系统(包含较强的均匀性)。
流体力学中的湍流边界层

流体力学中的湍流边界层湍流边界层是流体力学中一个重要的概念,它在流体流动中起着至关重要的作用。
湍流边界层是指流体在固体边界附近出现湍动现象的一层区域。
在此,将介绍湍流边界层的基本概念、特点以及其在流体力学中的应用。
一、湍流边界层的基本概念湍流边界层是指流体在与固体表面接触的区域内,由于流体的湍动而形成的一层动量和能量传输较强的流动层。
湍流边界层的出现与流体黏性有关,主要包括两个区域:靠近固体表面的黏性子层和较远离固体表面的湍动子层。
1. 黏性子层黏性子层位于流体与固体表面直接接触的区域,特点是流速变化缓慢、剪切应力主导、湍动强度较弱。
黏性子层的厚度与黏性流体性质相关,黏性较小的流体黏性子层厚度较大。
2. 湍动子层湍动子层位于黏性子层之上,主要特点是流速变化剧烈、湍动强度较大。
湍动子层中的湍流涡旋互相交错、不断破裂与重组,形成了湍流边界层内的流动。
二、湍流边界层的特点湍流边界层在流体力学中有以下几个显著的特点:1. 局部流速变化剧烈湍流边界层中的流速变化剧烈,流速的横向分布呈现出复杂的涡旋结构。
这种流速变化的不规则性使得湍流边界层内的流动难以预测和描述。
2. 高湍动强度湍流边界层内湍动强度较大,湍流涡旋的大小和速度均较黏性子层中的流动要大得多。
湍动的存在导致湍流边界层内的流体混合和动量传输增强。
3. 二次流现象与涡旋结构湍流边界层中的流动往往伴随着二次流现象和复杂的涡旋结构。
二次流现象是指流体在边界层中沿壁面方向发生的流动,而涡旋结构则表现为湍流涡旋的大小、密度和分布等特性。
三、湍流边界层在流体力学中的应用湍流边界层在许多工程和科学应用中起着重要作用,下面介绍其中几个常见的应用。
1. 阻力与摩擦系数计算湍流边界层的存在会导致流体流动阻力的增加,因此在设计和计算中需要考虑湍流边界层对阻力的影响。
摩擦系数是评估湍流边界层影响的一个重要参数,它描述了湍流边界层相对黏性子层的流动速度与剪切应力之间的关系。
中科大FLUENT讲稿第四章,湍流流动的近壁处理
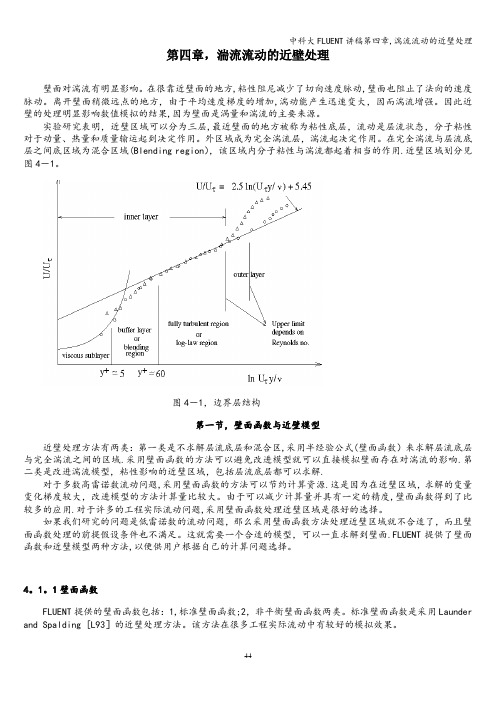
第四章,湍流流动的近壁处理壁面对湍流有明显影响。
在很靠近壁面的地方,粘性阻尼减少了切向速度脉动,壁面也阻止了法向的速度脉动。
离开壁面稍微远点的地方,由于平均速度梯度的增加,湍动能产生迅速变大,因而湍流增强。
因此近壁的处理明显影响数值模拟的结果,因为壁面是涡量和湍流的主要来源。
实验研究表明,近壁区域可以分为三层,最近壁面的地方被称为粘性底层,流动是层流状态,分子粘性对于动量、热量和质量输运起到决定作用。
外区域成为完全湍流层,湍流起决定作用。
在完全湍流与层流底层之间底区域为混合区域(Blending region),该区域内分子粘性与湍流都起着相当的作用.近壁区域划分见图4-1。
图4-1,边界层结构第一节,壁面函数与近壁模型近壁处理方法有两类:第一类是不求解层流底层和混合区,采用半经验公式(壁面函数)来求解层流底层与完全湍流之间的区域.采用壁面函数的方法可以避免改进模型就可以直接模拟壁面存在对湍流的影响.第二类是改进湍流模型,粘性影响的近壁区域,包括层流底层都可以求解.对于多数高雷诺数流动问题,采用壁面函数的方法可以节约计算资源.这是因为在近壁区域,求解的变量变化梯度较大,改进模型的方法计算量比较大。
由于可以减少计算量并具有一定的精度,壁面函数得到了比较多的应用.对于许多的工程实际流动问题,采用壁面函数处理近壁区域是很好的选择。
如果我们研究的问题是低雷诺数的流动问题,那么采用壁面函数方法处理近壁区域就不合适了,而且壁面函数处理的前提假设条件也不满足。
这就需要一个合适的模型,可以一直求解到壁面.FLUENT提供了壁面函数和近壁模型两种方法,以便供用户根据自己的计算问题选择。
4。
1。
1壁面函数FLUENT提供的壁面函数包括:1,标准壁面函数;2,非平衡壁面函数两类。
标准壁面函数是采用Launder and Spalding [L93]的近壁处理方法。
该方法在很多工程实际流动中有较好的模拟效果。
4。
1。
1.1 标准壁面函数根据平均速度壁面法则,有:**1ln()U Ey k=4-1 其中,1/41/2*/p pw U C k U μτρ≡,1/41/2*p p C k y y μρμ≡,并且k =0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Streak breakdown
Flow visualisation (1)
Streak breakdown
Flow visualisation (2)
Streak breakdown
Flow visualisation (3)
Streak breakdown
Flow visualisation (4)
Streak breakdown
Flow visualisation (5)
Streak breakdown
Flow visualisation (6)
Streak breakdown
DNS results
Jimenez and Pinelli (1999)
Near-wall structure
Introduction
Near-wall structure
There are many different turbulence events in turbulent boundary layers, such as Ejection Sweep Burst Inrush…
Introduction
Introduction
Turbulent boundary layers
Kline et al. (1967)
Introduction
Turbulent boundary layers
Kline et al. (1967)
Introduction
Near-wall structure
Robinson et al. (1989)
Hairpin structure (5)
Hutchins (2003)
Near-wall structure
Conceptual model
Stage 1: Deformation of spanwise vortices Stage 2: Development of hairpins Stage 3: Production of counter-rotating longitudinal vortices
Ejection event
Choi et al. (2003)
Large-scale turbulence
Hairpin structure (1)
Head and Bandyopadhyay (1981)
Large-scale turbulence
Hairpin structure (2)
Zhou et al. (1999)
Conclusions
Near-wall structures are vitally important for energy production in the turbulent boundary layers. There is also a growing evidence to suggest that the hairpin structures contribute much to the self-sustaining mechanisms of turbulence.
Near-wall structure
Characterisation of sweeps
Near-wall structure
Ejection event
The streak breakdown is preceded by sweep events on both flanks of lowspeed streaks, suggesting that the sweep events act as main agents for local disturbance. This leads to an ejection of low-speed fluids.
Introduction
Coherent structure
Brown & Roshko (1974)
Introduction
Coherent structure
Bradshaw et al. (1964)
Introduction
Near-wall structure
Recent results revealed the existence of coherent structure in turbulent boundary layers, where the sequence of events is quasi-periodic. It is believed that there is a self-sustaining mechanism for the turbulence structure. Energy production during the turbulence events accounts for 80% of the total energy production.
Turbulent Boundary Layer Structures
Kwing-So Choi University of Nottingham
Introduction
Coherent Structure
Turbulent shear flows look random and chaotic, but there are identifiable structures within. The coherent structure in turbulent shear flows is dynamically significant, contributing much to the turbulent energy production. It is, therefore, important to understand the coherent structure for flow control purpose.
Introduction
Near-wall structure
Soldati (2001)
Near-wall structure
Sweep events
Take place in the near-wall region (y+ < 15) Induced by the quasi-longitudinal vortices Splash high-momentum fluid onto the wall Increase local skin-friction Contribute to the Reynolds stress production Q4 events (+u and -v)
Large-scale turbulence
Hairpin structure (3)
Adrian et al. (2000)
Large-scale turbulence
Hairpin structure (4)
Robinson et al. (1988)
Large-scale turbuNear-wall structure
There are many different types of structure in turbulent boundary layer, including Low speed streaks Quasi-streamwise vortices Hairpin vortices Banana eddies…
Turbulent boundary layers
Kasagi and Hirata (1980)
Introduction
Turbulent boundary layers
Kline et al. (1967)
Introduction
Turbulent boundary layers
Kline et al. (1967)
