矩阵论PPT讲解
合集下载
矩阵论第一章第二节PPT课件
分析： 设 dimV n, 1, 2, , n 是V的一组基，
线性变换 在这组基下的矩阵为A.
设 0是 的特征值，它的一个特征向量 在基
1,2,
, n 下的坐标记为
x01 ,
x0n
则 ( )在基 1, 2 ,
, n下的坐标为
x01 A ,
x0n
x01
而0
的坐标是
0
x0n
21 11
k 1 k
k k 1
.
例. 在线性空间 P3 中，线性变换 定义如下：
(1 ) (2 )
( 5, 0, (0, 1,
3) 6)
,
(3 ) (5, 1,9)
其中, 12((01,,10,,12)) 3 (3, 1,0)
（1）求 在标准基 1, 2 , 3 下的矩阵. （2）求 在 1,2 ,3 下的矩阵.
② 若 是 的属于特征值 0的特征向量，则 k (k P,k 0) 也是 的属于0 的特征向量.
(k ) k ( ) k(0 ) 0(k )
由此知，特征向量不是被特征值所唯一确定的， 但是特征值却是被特征向量所唯一确定的，即
若 ( ) 且 ( ) ，则 .
2、特征值与特征向量的求法
5 0 5
因而，
AX
0 3
1 6
1 9
,
5 0 5
5 0 5 1 0 3 1
A
0 3
1 6
1 9
X
1
0 3
1 6
1 9
0 2
1 1
1 0
1 7
5 4 27
20 5 18
20
2 24
（2）设 在1,2 ,3下的矩阵为B，则A与B相似，且
《矩阵论》课件 共39页PPT资料
n
x 1
xi ;
i1
1
x
2
n i1
xi
2 2
;
x
max
1 i n
xi
;
1
x
n p i 1
xi
p p ,
p1
x , x , x , x ( p 1)都是 C n上的向量范数。
1
2
p
引6理 .1.1 如 果p实 1,q数 1且111,则 对 pq
向 量 范,数1,,n为V的 一 组,V基中 任 一 向量
n
可唯一地表示为xii, x(x1,, xn)T Pn. i1
则 是x1,, xn的连续函. 数
定义6.1.2 设 , 是n维线性V空 上间 定义的 ab
种 向 量,范 如数 果 存 在 两 无个关与的 正 常
其中p 实 1,q 数 1且 111. pq
定理6.1.2（Minkowski不等式）
设 x ( x 1 , ,x n ) T ,y ( y 1 , ,y n ) T C n ,则
1
1
1
i n1xiyi p p i n1xi p p i n1yi p p
定理6.1.5 设V是 数 域 P上 的n维 线 性 空,间 1,,n 为V的 一 组,基 则V中 任 一 向可 量唯 一 地 表 示
n
xii , x (x1,, xn)T Pn.又 设 是Pn上 的
i1
向 量 范,数 令 v
x,
则 是V上的向量范. 数 v
定理6.1.6 设 是数域 P上n维线性空V上 间的任一
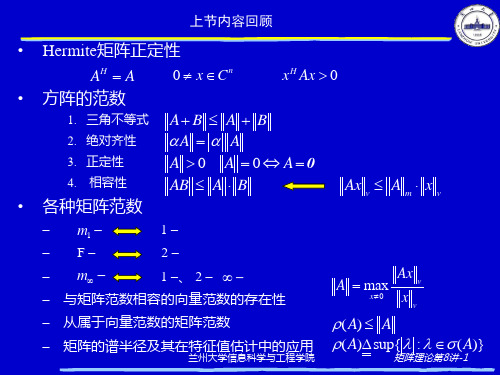
矩阵理论-第八讲.ppt
k
逆命题不成立
A(k )
(1)k
1
1
k
1 2
: Cmn R
k A(k) ?
lim A(k) lim
k
F k
6
(k
1 1)2
6
{a1(1k )} 不收敛
兰州大学信息科学与工程学院
矩阵理论第8讲-13
矩阵序列
推论：
设 {A(k) : A(k) C mn , k 0,1, lim A(k) A 0
A)
A
A
兰州大学信息科学与工程学院
矩阵理论第8讲-8
矩阵的条件数
– 当A与b二者均有扰动时，由于Ax = b的线性特性，其扰动结果为二者 扰动之和
x A1 b A1 b A A1 b
x
x
b
b
A
x
A1 A
A1 A
A
x
(1 A1 A )
(1 A1
A
A)
A
A
注意到当 A1 A 1 时
为A的奇异值
兰州大学信息科学与工程学院
矩阵理论第8讲-4
矩阵的条件数
用MATLAB验证
的条件数
2 1
A
2
1.0001
与下面的方程组进行比较：
1
2
2 1
x1 x2
7 1
用
1
2
2 0.999
x1 x2
7 1.001
来验证其对误差的鲁棒性（Robustness）
兰州大学信息科学与工程学院
A A1
A A1
A A1
1 A1 A 1 A A1 A
A
兰州大学信息科学与工程学院
矩阵理论第8讲-9
逆命题不成立
A(k )
(1)k
1
1
k
1 2
: Cmn R
k A(k) ?
lim A(k) lim
k
F k
6
(k
1 1)2
6
{a1(1k )} 不收敛
兰州大学信息科学与工程学院
矩阵理论第8讲-13
矩阵序列
推论：
设 {A(k) : A(k) C mn , k 0,1, lim A(k) A 0
A)
A
A
兰州大学信息科学与工程学院
矩阵理论第8讲-8
矩阵的条件数
– 当A与b二者均有扰动时，由于Ax = b的线性特性，其扰动结果为二者 扰动之和
x A1 b A1 b A A1 b
x
x
b
b
A
x
A1 A
A1 A
A
x
(1 A1 A )
(1 A1
A
A)
A
A
注意到当 A1 A 1 时
为A的奇异值
兰州大学信息科学与工程学院
矩阵理论第8讲-4
矩阵的条件数
用MATLAB验证
的条件数
2 1
A
2
1.0001
与下面的方程组进行比较：
1
2
2 1
x1 x2
7 1
用
1
2
2 0.999
x1 x2
7 1.001
来验证其对误差的鲁棒性（Robustness）
兰州大学信息科学与工程学院
A A1
A A1
A A1
1 A1 A 1 A A1 A
A
兰州大学信息科学与工程学院
矩阵理论第8讲-9
西北工业大学矩阵论课件PPT第一章例题矩阵的相似变换
2
例 已知一个12阶矩阵的不变因子是
1,1,, 1，( 1)2，( 1)2( 2)，
9
( 1)2( 2)(2 3)2
求A的Jordan标准形。 解 A的初等因子为
( 1)2，( 1)2，( 2)，( 1)2，( 2) ( 3i)2，( 3i)2
故A的Jordan标准形为：
1 1
从而A的不变因子为
d1() D1() 1，
d2
()
D2 ( ) D1( )
1
11
1
2
J
11 1
2
3i 1
3i
3i
1 3i
例 求下列矩阵的Jordan标准形：
1)
3 A 1
1 1
0 0
；
1 1 2
解
3 1 0 I A 1 1 0
1
1 2
一阶子式共有9个， 显然 D1() 1；
二阶子式共有 C32 C32 9 个：
3 1 ( 2)2， 3 0 0，
01，
p2
11，
p3
1 1
1
1
0
故相似变换阵
P
1 0
1 1
11，使得
1 1 0
P 1AP
1
2
3
2)
3 A 1
1
解 可求得
1 1
0 0
；
1 2
det(I A) ( 2)3
所以A的特征值为 1 2 3 2
对应三重特征值2有两个线性无关的特征向量
(1, 1, 0)T， (0, 0, 1)T
1 2 1
1 1 2
则微分方程组可写成矩阵形式
d x Ax dt
(课件)矩阵论
=
aB 11 1
+
(a12
−
a 11
)
B 2
+
( a 21
−
a 12
)
B 3
+
( a 22
−
a
21
)
B 4
坐标为
β
=
(a11
,
a 12
−
a 11
,
a
21
−
a 12
,
a 22
− a21 )Τ
[注] 一个元素在两个不同的基下的坐标可能相同，也可能不同．
例如：
A
=
E 22
在上述两个基下的坐标都是 (0,
0,
(Ⅱ) 定义的数乘运算封闭, 即
∀ x ∈V , ∀ k ∈ K , 对应唯一 元素(kx)∈V , 且满足 (5) 数对元素分配律： k( x + y) = kx + ky (∀y ∈V ) (6) 元素对数分配律： (k + l )x = kx + lx (∀l ∈ K ) (7) 数因子结合律： k(lx) = (kl )x (∀l ∈ K ) (8) 有单位数：单位数1∈ K , 使得 1x = x . 则称V 为 K 上的线性空间．
mn
∑ ∑ (2) A = (ai j )m×n =
ai j Ei j ．
i=1 j=1
故 Ei j (i = 1,2,L, m ; j = 1,2,L, n) 是 R m×n 的一个基, dimR m×n = mn .
第一章 线性空间与线性变换（第 1 节）
5
2．坐标：给定线性空间V
n
的基
x 1
解 采用中介法求过渡矩阵.
矩阵论复习概要课件.ppt
单位矩阵(m<n)，则
Hn
Hm O
O 是n阶
Inm
Householder矩阵.
2.设Tm是m阶Givens矩阵, In-m是n-m阶单位矩
阵(m<n)，则
Tn
Tm O
I
O
nm
是n阶Givens矩阵.
3.用Householder变换求
1 4 1 1
A
1 1
0 1
1 1
1 1
1 3 1 1
是可逆矩阵，则
1
0
etAdt
(
).
10. 已知
8 A 2
2 5
2 4
,
b(t
)
0 e9t
2 4 5
e9t
(1) 求etA; (2)用矩阵函数的方法求微 分方程 d x(t) Ax(t) b(t) 满足初始条件
dt
x(0)=(0,1,1)T的解.
11. 设X=(xij)nnRnn, 则
1. 判断 1，sinx, cosx 的线性相关性. 2. 若1, 2, …, r线性无关，则向量组1= 1+k1r , 2= 2+k2r , , r= r (kiK)也线性无关.
3. 求向量组
12
((1,21,,11,,10,1))12
(2,1,0,1) (1,1,3,7)
分别生成的子空间的交的基和维数.
4. 设 V1, V2 分别是
V1 (x1, x2 , xn ) x1 x2 xn 0, xi K V2 (x1, x2 , xn ) xi xi1 0, xi K
证明 Kn=V1V2 5. 设 S,A,T分别为Knn中对称，反对称，上三角方
矩阵论矩阵的分解 ppt课件
结论：如果矩阵A能用两行互换以外的 初等行变换 化为阶梯形，则A有LU分解。
三角分解的存在性和惟一性
定理3.1 （P.62） ：
• 矩阵的k 阶主子式：取矩阵的前k行、前k列得到 的行列式，k=1，2， … ，n。
• 定理: AFnn有惟一LDV分解的充要条件是A的顺 序主子式Ak非零，k =1，2，…，n-1。
LU分解：AFnn， 有下三角形矩阵L ，上 三角形矩阵U ，使得A=LU。
LDV分解：AFnn， L、V分别是主对角线 元素为1的下三角形和上三角形矩阵，D为 对角矩阵，使得A=LDV。
已知的方法：Gauss-消元法
例题1 （P.61eg1）设
2 2 3
A
4
7
7
求A的LU和LDV分解。 2 4 5
2 、Schur 分解
定理3.7（P.74 ）对矩阵ACnn，存在酉矩
阵U和上三角矩阵T，使得 UHAU=T=
1
2
证明要点：
n
➢A=PJ AP–1 ，
➢P=UR
➢A= PJ AP–1 =U（RJR–1 ）UH =UTUH。
二、正规矩阵（Normal Matrices）
1、 定义3.3（P.77 ）A是正规矩阵 AHA=AAH。 常见的正规矩阵：
对角矩阵 对称和反对称矩阵：AT=A，AT=–A。 Hermite矩阵和反Hermite矩阵：AH=A，AH=–A 正交矩阵和酉矩阵：ATA=AAT=I，AHA=AAH=I。
例题1 （P.78，eg 10）设A为正规矩阵，B酉相似于A，
证明B也是正规矩阵。
正规是酉相似的不变性质
例题2、AFmn，矩阵AHA 和矩阵AAH是正规矩阵。
在内积空间中讨论问题，涉及：
矩阵论课件
P 是数域， 若 n是正整数， 则系数属于 P 而未知元为 x 的
所有次数不超过 n 的多项式的集合，此集合连同零多 项式在内按通常多项式的加法及数与多项式的乘法， 构成数域 P 上的一个线性空间全体记作： Pn [ x ].
4 December 2014 河北科技大学
机动 目录 上页 下页 返回 结束
, t 可以由1 , 2 ,
, s 线性表
, t 线性相关.
推论1 若 1 , 2 ,
, t 可 以 由 1 , 2 ,
, s 线 性 表 示 ， 且
1 , 2 , , t 线性无关，则 t s .
推论2 若 1 , 2 ,
, t 与 1 , 2 , , s 等 价 ，且 均 线性 无
实数域 R 上的线性空间简称为实线性空间； 复数域 C 上的线性空间简称为复线性空间.
下面看几个线性空间的例子.
4 December 2014
河北科技大学
机动 目录 上页 下页 返回 结束
矩阵论
例1 若 P= 是数域，V 是分量属于 P= 的 n元有序数组的集合
V a1 , a2 ,
, an | ai P，i 1, 2,
矩阵论
例4 所有定义在区间 a , b a t b 上的实值连续
函数全体构成的集合， 按照函数的加法及数与函数 的数量乘法，构成实数域 R 上的一个线性空间，记 作： R a , b .
例5 实（复）系数齐次线性方程组 Ax 0（ A R mn
或 C mn ； x R n 或 C n ；行向量和列向量不做区别） 的解空间 S 构成 R 或C 上的一个线性空间.
才成立，称 x1 , x2 ,
矩阵论简明教程整理全PPT课件
k
ei
e
H j
E ei , ej , k
第45页/共188页
Remark
det E u,v, det In uvH det 1 vHu
1 vHu (由n Im AB m In BA 得到）
第46页/共188页
四、其他特殊矩阵
1幂零矩阵：Ak 0, k : 某正整数; 2幂等矩阵：A2 A; 3 实对称正定矩阵：
a a jn 1 j1 2 j2
anjn
j1 j2 jn
第13页/共188页
二、块矩阵的行列式
1、设A Cmm , B Cmn , C Cnm , D Cnn , 则
1 A
0A
BA
0 AD
0D 0D CD
2 A B 1mn C D 1mn B A
CD
AB
DC
3 A B m A B
minrank A, rank B
第30页/共188页
推论1
设ACmn , B Cnk ,且AB 0,则
rank A rank B n
第31页/共188页
§1.4 特殊矩阵
一、 几类基本的特殊矩阵
1、零矩阵，单位矩阵 2、对角矩阵
a11
D
a22
diag
a11
,
a22
,
ann
第50页/共188页
§2.1 矩阵的特征值与特征向量
一、特征值与特征向量 1、定义 定义1
设ACnn ,若存在数 C和x Cn , x 0使得 Ax x
则称是A的特征值，x称为A属于的特征向量。
第51页/共188页
2、特征多项式 定义2
设ACnn , 称In A为A的特征矩阵，称detIn A 为A的特征多项式,称detIn A 0为A的特征方程。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(5) x, yy, x x, xy, y (Cauchy-Schwarz不等式)
利用内积可以定义向量的长度和正交:
定义: 设 x 1,2,,n T Cn, 令
n
x x, x 2
k 2
k 1
称 x 为向量 x的长度或2范数. 2
A 有 n 个线性无关的特征向量. 推论1: 若 A C nn 的特征值两两相异,则 A可对角化.
推论2: 设 1, 2 ,, s是 n 阶方阵 A 的所有互不相
同的特征值, 其重数分别为 r1, r2 ,, rs . 若每个 i 都
有 ri 个线性无关的特征向量 i 1, 2, , s , 则 A 可
(3) AT 的特征值为1, 2 ,, n , 而 AH a ji nn 的特
征值为 1, 2 ,, n.
§1. 2 相似对角化
• 矩阵(方阵)相似的定义. • 矩阵相似的性质(6条). • 矩阵可对角化的条件.
定理1.8: 设 A C nn , 则 A 可对角化的充要条件是
Jordan矩阵 J 相似. 且这个Jordan矩阵 J 除Jordan
块的排列顺序外由 A 唯一决定.
将方阵 A C nn 相似变换为Jordan标准形的方法:
1) 特征向量法
设 A C nn , 如果i 是 A 的单特征值, 则对应一
阶Jordan块 Ji i ; 如果i 是 A 的 ri ri 1重特征
称 x, y为向量 x 与 y 的内积.
• 内积的性质
定理 1.18: 设 x, y, z C n , C, 则
(1) x, y y, x
(2) x, y x, y, x, y x, y
(3) x y, z x, z y, z, x, y z x, y x, z (4) x, x 0, 且仅当 x 0时才有 x, x 0.
推论: f A 0 f 0
定理1.3: 矩阵的属于不同特征值的特征向量线性无 关.
定理1.4: 设 A aij nn 的特征值为 1, 2 ,, n , 则:
(1) trA 1 2 n
(2) det A 12 n
(研究生课程)
高等工程数学
教师: 李晓东
• 课程主要内容：
矩阵论：矩阵的相似变换；向量范数与矩阵范数 的理论及应用；矩阵分析及应用；矩阵的各种分 解方法等。 泛函分析：距离空间；赋范空间与Banach空间； 内积空间与Hilbert空间等。
• 主要参考书目：
1．徐仲等著，《矩阵论简明教程》，科学出 版 社，2007。 2．姚泽清等著，《应用泛函分析》，科学出版 社，2008。
§1. 5 向量的内积
<<线性代数>>课程中对 n 维向量的内积是在实 数域中定义的, <<矩阵论>>对 n 维向量的内积将在
复数域中定义.
定义: 设 x 1,2,,n T Cn, y 1,2,,n T Cn.
令
n
x, y y H x kk
k 1
定理 1.13 (Cayley-Hamilton): 设 A C nn ,
detI A, 则 A 0.
定理1.13说明: 设 A C nn , 则 A 的任意次幂都
可转化为 A 的 n 1 次多项式计算.
定义: 设 A C nn , f 是多项式. 如果有 f A O, 则
多项式和相同的最小多项式.
定理1.17: 设 A C nn , 1, 2 ,, t 是 A的所有互不
相同的特征值, 则
mA 1m1 2 m2 t mt
其中 mi 是 A的Jordan标准形 J 中含i的Jordan块的
最高阶数.
数重数.
定理1.2: 设 A C nn , A 的 n 个特征值为1, 2,, n ,
对应的特征向量为 x1, x2 ,, xn ,又设 f 为一多项式,
则 f A 的特征值为 f 1, f 2 ,, f n , 对应的特征
向量仍为 x1, x2 ,, xn.
第一章：矩阵的相似变换
§1. 1 特征值与特征向量
• 有关定义回顾: 特征值; 特征向量; 特征矩阵; 特征多项式.
• 矩阵的特征值与特征向量的性质. 定理1.1: 设 i 是 A C nn 的 ri 重特征值, 对应 i
有 si 个线性无关的特征向量, 则: 1 si r i 简言之: 矩阵特征值的几何重数小于或等于其代
值, 则对应 i 有几个线性无关的特征向量, 就有几个 以 i 为对角元素的Jordan块, 这些Jordan块的阶数
之和等于 ri . 由 A 的所有特征值对应的Jordan块构成 的Jordan矩阵即为 A 的Jordan标准形.
2) 初等变换法 3) 行列式因子法
§1. 4 Caylay-Hamilton定理
称 f 为 A 的零化多项式. 在 A的所有零化多项式
中, 次数最低的首一多项式称为 A 的最小多项式. 记 为 mA.
定理 1.14: 设 A C nn , 则 A的最小多项式 mA 整除
A的任一零化多项式, 且最小多项式是唯一的.
定理 1.16: 相似矩阵具有相同的特征值,相同的特征
对角化.
§1. 3 Jordan标准形介绍
定义: 形如
i 1
Ji
i
1
i ri ri
的矩阵称为 ri 阶Jordan块. 由若干个Jordan块构成
的分块对角阵 J diagJ1, J 2 ,, J s 称为Jordan矩阵.
定理1.9(Jordan): 设 A C nn, 则 A 一定与一个
利用内积可以定义向量的长度和正交:
定义: 设 x 1,2,,n T Cn, 令
n
x x, x 2
k 2
k 1
称 x 为向量 x的长度或2范数. 2
A 有 n 个线性无关的特征向量. 推论1: 若 A C nn 的特征值两两相异,则 A可对角化.
推论2: 设 1, 2 ,, s是 n 阶方阵 A 的所有互不相
同的特征值, 其重数分别为 r1, r2 ,, rs . 若每个 i 都
有 ri 个线性无关的特征向量 i 1, 2, , s , 则 A 可
(3) AT 的特征值为1, 2 ,, n , 而 AH a ji nn 的特
征值为 1, 2 ,, n.
§1. 2 相似对角化
• 矩阵(方阵)相似的定义. • 矩阵相似的性质(6条). • 矩阵可对角化的条件.
定理1.8: 设 A C nn , 则 A 可对角化的充要条件是
Jordan矩阵 J 相似. 且这个Jordan矩阵 J 除Jordan
块的排列顺序外由 A 唯一决定.
将方阵 A C nn 相似变换为Jordan标准形的方法:
1) 特征向量法
设 A C nn , 如果i 是 A 的单特征值, 则对应一
阶Jordan块 Ji i ; 如果i 是 A 的 ri ri 1重特征
称 x, y为向量 x 与 y 的内积.
• 内积的性质
定理 1.18: 设 x, y, z C n , C, 则
(1) x, y y, x
(2) x, y x, y, x, y x, y
(3) x y, z x, z y, z, x, y z x, y x, z (4) x, x 0, 且仅当 x 0时才有 x, x 0.
推论: f A 0 f 0
定理1.3: 矩阵的属于不同特征值的特征向量线性无 关.
定理1.4: 设 A aij nn 的特征值为 1, 2 ,, n , 则:
(1) trA 1 2 n
(2) det A 12 n
(研究生课程)
高等工程数学
教师: 李晓东
• 课程主要内容：
矩阵论：矩阵的相似变换；向量范数与矩阵范数 的理论及应用；矩阵分析及应用；矩阵的各种分 解方法等。 泛函分析：距离空间；赋范空间与Banach空间； 内积空间与Hilbert空间等。
• 主要参考书目：
1．徐仲等著，《矩阵论简明教程》，科学出 版 社，2007。 2．姚泽清等著，《应用泛函分析》，科学出版 社，2008。
§1. 5 向量的内积
<<线性代数>>课程中对 n 维向量的内积是在实 数域中定义的, <<矩阵论>>对 n 维向量的内积将在
复数域中定义.
定义: 设 x 1,2,,n T Cn, y 1,2,,n T Cn.
令
n
x, y y H x kk
k 1
定理 1.13 (Cayley-Hamilton): 设 A C nn ,
detI A, 则 A 0.
定理1.13说明: 设 A C nn , 则 A 的任意次幂都
可转化为 A 的 n 1 次多项式计算.
定义: 设 A C nn , f 是多项式. 如果有 f A O, 则
多项式和相同的最小多项式.
定理1.17: 设 A C nn , 1, 2 ,, t 是 A的所有互不
相同的特征值, 则
mA 1m1 2 m2 t mt
其中 mi 是 A的Jordan标准形 J 中含i的Jordan块的
最高阶数.
数重数.
定理1.2: 设 A C nn , A 的 n 个特征值为1, 2,, n ,
对应的特征向量为 x1, x2 ,, xn ,又设 f 为一多项式,
则 f A 的特征值为 f 1, f 2 ,, f n , 对应的特征
向量仍为 x1, x2 ,, xn.
第一章：矩阵的相似变换
§1. 1 特征值与特征向量
• 有关定义回顾: 特征值; 特征向量; 特征矩阵; 特征多项式.
• 矩阵的特征值与特征向量的性质. 定理1.1: 设 i 是 A C nn 的 ri 重特征值, 对应 i
有 si 个线性无关的特征向量, 则: 1 si r i 简言之: 矩阵特征值的几何重数小于或等于其代
值, 则对应 i 有几个线性无关的特征向量, 就有几个 以 i 为对角元素的Jordan块, 这些Jordan块的阶数
之和等于 ri . 由 A 的所有特征值对应的Jordan块构成 的Jordan矩阵即为 A 的Jordan标准形.
2) 初等变换法 3) 行列式因子法
§1. 4 Caylay-Hamilton定理
称 f 为 A 的零化多项式. 在 A的所有零化多项式
中, 次数最低的首一多项式称为 A 的最小多项式. 记 为 mA.
定理 1.14: 设 A C nn , 则 A的最小多项式 mA 整除
A的任一零化多项式, 且最小多项式是唯一的.
定理 1.16: 相似矩阵具有相同的特征值,相同的特征
对角化.
§1. 3 Jordan标准形介绍
定义: 形如
i 1
Ji
i
1
i ri ri
的矩阵称为 ri 阶Jordan块. 由若干个Jordan块构成
的分块对角阵 J diagJ1, J 2 ,, J s 称为Jordan矩阵.
定理1.9(Jordan): 设 A C nn, 则 A 一定与一个