立体图形
生活中常见的立体图形
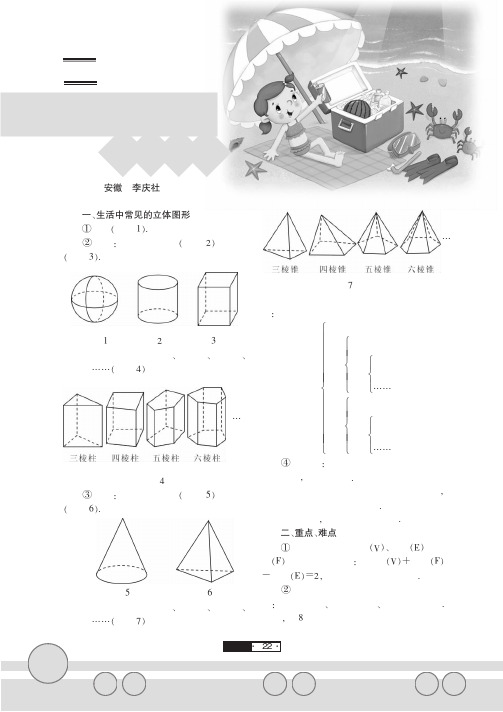
线平行一、生活中常见的立体图形①球体（如图1）．②柱体：柱体分为圆柱（如图2）和棱柱（如图3）．图1图2图3而棱柱又分为三棱柱、四棱柱、五棱柱、六棱柱……（如图4）图4③锥体：锥体分为圆锥（如图5）和棱锥（如图6）．图5图6而棱锥又分为三棱锥、四棱锥、五棱锥、六棱锥……（如图7）图7它们之间的关系可以用下面的示意图来表示：立体图形球体柱体圆柱棱柱三棱柱四棱柱五棱柱……………………………………锥体圆锥棱锥三棱锥四棱锥五棱锥………………………………………………………………………④多面体：由若干个平面多边形所围成的几何体，叫做多面体．多面体是从另外的角度观察几何体的，它与前面的分类有重叠部分.如长方体既可以叫做四棱柱，又可以叫做六面体．二、重点、难点①凸多面体的顶点数（V ）、棱数（E ）和面数（F ）之间满足关系式：顶点数（V ）＋面数（F ）－棱数（E ）＝2，这就是著名的欧拉公式．②我们可以用运动的观点观察几何图形：点运动成线、线运动成面、面运动形成体．例如，图8中的圆锥可以看作是由直角三角数学篇生活中常见的安徽李庆社立体图形……２２··数学篇线平行形绕着它的一条直角边所在的直线旋转一周得到的立体图形．图8三、典型例题分析例１写出下列立体图形的名称．图9分析：识别立体图形，关键是要搞清楚它们的特征.锥体只有一个底面，柱体有两个底面;圆柱、圆锥先找圆形底面，再由侧面确定是圆锥还是圆柱；棱锥的侧面是三角形，棱柱的侧面是长方形．解：这4个立体图形的名称依次是，三棱柱、四棱锥、圆柱、圆锥．例２下列立体图形中属于四棱柱的是（）．图10分析：四棱柱属于棱柱，它有两个互相平行且形状大小一样的四边形底面，有四个侧面而且都是长方形．图形A 称为圆台．图形B 是四棱锥.图形D 是四棱锥被截去一个角，它叫作六面体，也叫作棱台．解：选C.例３圆柱可以看作是由一个（）经过旋转得到的．A ．矩形B ．直角梯形C ．直角三角形D ．半圆分析：用运动的观点容易得出，矩形绕它的一边所在的直线旋转一周得到圆柱体；半圆绕它的直径所在的直线旋转一周得到球体；直角三角形绕它的一条直角边所在的直线旋转一周得到圆锥；直角梯形绕着垂直于底边的腰所在的直线旋转一周得到圆台．解：选A ．例４图11-1是正方体木块，把它切去一块，可得到如图11-2、11-3、11-4、11-5所示的木块．我们知道，正方体木块有8个顶点、12条棱、6个面，请你将图11-2、11-3、11-4、11-5中的木块的顶点数、棱数、面数填入下表.观察上表，请你归纳上述各种木块的顶点数、棱数、面数之间的数量关系，并表示出来．分析：首先由图形确定各自的顶点数、棱数、面数，再观察每个图形中三个数据之间的关系，然后根据数据间的关系推断出一般的规律．解：表格中应填入的四行数据分别为7，12，7；8，12，6；6，9，5；10，15，7.可得出数量关系：顶点数＋面数－棱数＝2．图顶点数棱数面数11-1812611-211-311-411-5图11-1图11-2图11-3图11-4图11-5２３··。
《立体图形的认识》课件
立体图形的分类
立体图形根据形状和面的数量可以进行分类。 常见的立体图形有棱柱体、棱锥体、球体和圆柱体。 每种图形都图形由边、面和顶点组成。 边连接不同的面，面包围了立体图形的空间。 顶点是边和面相交的点。
立体图形的投影
立体图形的投影是将三维物体映射到二维平面上。 正视图、俯视图和侧视图可以用来表示不同的投影。 投影可以帮助我们更好地理解立体图形的形状和尺寸。
《立体图形的认识》PPT课件
# 立体图形的认识 ## 什么是立体图形 - 立体图形是具有长度、宽度和高度的物体 - 分为棱柱体、棱锥体、球体、圆柱体等不同类型 - 立体图形是三维空间中的形状 ## 立体图形的要素 - 立体图形由三个要素组成：边、面和顶点 - 正视图和俯视图展示了立体图形的不同面向 - 立体图形可以用示意图来展示 ## 立体图形的投影 - 投影是将三维物体在二维平面上的表示 - 正视图、俯视图和侧视图都可以用于投影 - 通过投影实例和解析来理解立体图形 ## 立体图形的空间关系 - 研究立体图形之间的距离、交点和交线 - 研究立体图形的相交和不相交的关系
立体图形的空间关系
研究立体图形之间的距离、交点和交线的关系。 了解立体图形的相交关系和不相交关系。 利用特定方法可以构建复杂的立体图形。
立体图形的特点
立体图形具有三个要素和投影方法。 通过研究立体图形的空间关系和构建方法，我们可以更好地理解它们。 在实例讲解和练习中，我们将加深对立体图形的认识。
认识立体图形
认识立体图形立体图形是我们生活中常见的一种形态，它与平面图形有所不同，拥有立体感和空间感。
我们可以在建筑物、家具、车辆等各个领域中看到立体图形的存在。
本文将介绍一些常见的立体图形，并探讨它们的各个方面。
一、正方体正方体是一种具有六个面的立体图形，每个面都是一个正方形。
正方体的六个面相互平行，并且相邻的两个面之间的边长相等。
正方体具有六个顶点和12条边。
我们可以通过观察正方体的各个面和边来感受它的立体感。
正方体在建筑、设计、游戏等领域中得到广泛应用。
二、长方体长方体是一种具有六个面的立体图形，每个面都是一个长方形。
长方体的六个面相互平行，并且相邻的两个面之间的边长相等。
长方体具有八个顶点和12条边。
它在日常生活中常见于建筑物、电视机、书桌等物体的形状。
三、球体球体是一种具有无限个面的立体图形，它的每个面都称为球面。
球体具有无数个顶点和边。
球体是一种特殊的立体图形，因为它的表面在任何点上都是相等的。
我们可以通过触摸、旋转球体来感受它的特殊性。
四、圆柱体圆柱体是一种具有三个面的立体图形，它由两个平行的圆面和一个侧面组成。
圆柱体的侧面是一个矩形，其长和高分别等于两个圆的周长和两个平行圆的距离。
圆柱体具有两个顶点和三个边。
圆柱体在容器、管道、柱子等物体的形状中得到广泛应用。
五、圆锥体圆锥体是一种具有二个面的立体图形，它由一个圆面和一个侧面组成。
圆锥体的侧面是一个三角形，其底边是一个圆，顶点位于圆的中心。
圆锥体具有一个顶点和两个边。
圆锥体在一些建筑物、灯罩、冰淇淋锥等形状中常见。
六、棱柱棱柱是一种具有多个面的立体图形，它的底面和顶面是相似且平行的多边形。
棱柱的侧面是由底面和顶面的对应边连接而成的一系列矩形或平行四边形。
棱柱具有多个顶点和边，其个数取决于底面的边数。
棱柱在柱子、柜子、建筑物等方面有广泛应用。
通过了解和认识这些常见的立体图形，我们能够更好地理解和感受它们在我们生活中的存在和应用。
立体图形让我们的环境更加多样化和有趣，也给我们带来了更多的创造和发现的机会。
总结立体图形的知识点
总结立体图形的知识点一、立体图形的定义立体图形是指有三个维度的图形，它具有长度、宽度和高度。
在数学中，我们所说的立体图形通常是指三维几何图形，它们存在于空间中，具有一定的体积和表面积。
而与之相对应的是平面图形，它只具有长度和宽度，无法展现出立体图形那种立体感。
二、常见的立体图形1. 正方体：正方体是一种每个面都是正方形的立体图形。
它具有六个面、十二条边和八个顶点。
2. 长方体：长方体是一种每个面都是矩形的立体图形。
它也具有六个面、十二条边和八个顶点。
3. 圆柱体：圆柱体由两个平行的并且相等的圆面以及一个侧面围成。
它的侧面是一个矩形，其长度等于两个圆面的周长，宽度等于两个圆面之间的距离。
4. 圆锥体：圆锥体由一个圆锥面和一个圆锥侧面构成。
它的侧面是一个扇形，其面积等于圆锥底面积与母线的乘积除以2。
5. 球体：球体是由无数个半径相等的点构成的图形。
它的表面是完全封闭的，不像其他立体图形有明显的边界。
球体的表面积和体积的计算比较特殊，需要使用一些特殊的公式来得到。
三、计算立体图形的表面积和体积1. 表面积：对于常见的立体图形，我们可以通过公式来计算其表面积。
例如，正方体的表面积就等于六个面积之和，而长方体的表面积也可以用公式2lw + 2lh + 2wh进行计算。
其他立体图形的表面积计算也可以通过相应的公式来完成。
2. 体积：立体图形的体积是指其所围成的空间的大小。
计算立体图形的体积也需要使用相应的公式。
例如，正方体的体积就等于边长的立方，而长方体的体积可以用公式lwh来计算。
其他立体图形的体积计算同样也可以通过相应的公式来完成。
四、立体图形的性质1. 对称性：许多立体图形具有一定的对称性。
例如，正方体在某些对角线上是对称的，长方体也在某些对角线上是对称的。
这种对称性在几何学中是一个重要的性质。
2. 体积与形状的关系：在相同的表面积条件下，立体图形的体积越大，其形状就越扁。
这是由于形状的扁平程度与立体图形的体积具有一定的关系。
几何中的立体图形基本概念
几何中的立体图形基本概念一、立体图形的定义与分类1.定义：立体图形是三维空间中的图形，具有长度、宽度和高度。
a)立体几何图形的分类：锥体、柱体、球体、平面立体图形等。
b)根据表面特征分类：直纹立体图形、曲面立体图形等。
二、常见立体图形的基本性质与特征a)定义：底面为平面，顶点在底面上的图形。
i)圆锥：底面为圆，侧面为曲面。
ii)棱锥：底面为多边形，侧面为三角形。
iii)所有锥体的侧面积相等。
iv)锥体的体积与底面半径和高度有关。
b)定义：底面为平行四边形的立体图形。
c)分类：棱柱、圆柱等。
i)柱体的底面积相等。
ii)柱体的体积与底面积和高度有关。
d)定义：所有点与中心点距离相等的立体图形。
πR³。
i)球体的表面积和体积公式为：S=4πR²，V=43ii)球体的直径等于两倍的半径。
4.平面立体图形：a)定义：由平面图形旋转而成的立体图形。
b)分类：圆柱、圆锥、棱柱等。
c)性质：平面立体图形的表面积和体积与平面图形的性质有关。
三、立体图形的计算方法a)圆锥体积公式：V=1πR²h。
3b)棱锥体积公式：V=13Bh ，其中B 为底面积。
c)棱柱体积公式：V=Bh ，其中B 为底面积。
d)圆柱体积公式：V=πR²h 。
e)体积公式：V=43πR³。
f) 表面积公式：S=4πR²。
四、立体图形的实际应用a)应用：漏斗、沙堆等。
b)应用：柱子、烟囱等。
c)应用：球体、地球等。
4. 平面立体图形：a) 应用：各种容器、家具等。
通过以上知识点的学习，学生可以对几何中的立体图形有更深入的了解，并能够运用所学知识解决实际问题。
习题及方法：1.习题：计算一个底面半径为3cm ，高为4cm 的圆锥体的体积。
答案：V=13πR²h=13π×3²×4=12πcm³解题思路：根据圆锥体的体积公式V=13πR²h ，将给定的数值代入公式计算。
立体图形的知识点整理
立体图形的知识点整理一、长方体、正方体都有6个面，12条棱，8个顶点。
正方体是特殊的长方体。
二、圆柱的特征：一个侧面、两个底面、无数条高。
三、圆锥的特征：一个侧面、一个底面、一个顶点、一条高。
四、表面积：立体图形所有面的面积的和，叫做这个立体图形的表面积。
五、体积：物体所占空间的大小叫做物体的体积。
容器所能容纳其它物体的体积叫做容器的容积。
六、圆柱和圆锥三种关系：①等底等高：体积1︰3②等底等体积：高1︰3③等高等体积：底面积1︰3七、等底等高的圆柱和圆锥：①圆锥体积是圆柱的1/3，②圆柱体积是圆锥的3倍，③圆锥体积比圆柱少2/3，④圆柱体积比圆锥多2倍。
八、等底等高的圆柱和圆锥：锥1、差2、柱3、和4。
九、立体图形公式推导：【1】圆柱的侧面展开后得到一个什么图形?这个图形的各部分与圆柱有何关系?(圆柱侧面积公式的推导过程)①圆柱的侧面展开后一般得到一个长方形。
②长方形的长相当于圆柱的底面周长，长方形的宽相当于圆柱的高。
③因为：长方形面积=长×宽，所以：圆柱侧面积=底面周长×高。
④圆柱的侧面展开后还可能得到一个正方形。
正方形的边长=圆柱的底面周长=圆柱的高。
【2】我们在学习圆柱体积的计算公式时，是把圆柱转化成以前学过的一种立体图形(近似的)进行推导的，请你说出这种立体图形的名称以及它与圆柱体有关部分之间的关系?①把圆柱分成若干等份，切开后拼成了一个近似的长方体。
②长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高。
③因为：长方体体积=底面积×高，所以：圆柱体积=底面积×高。
即：V=Sh。
【3】请画图说明圆锥体积公式的推导过程?①找来等底等高的空圆锥和空圆柱各一只。
②将圆锥装满沙子，倒入圆柱中，发现三次正好装满，将圆柱里的沙子倒入圆锥中，发现三次正好倒完。
③通过实验发现：圆锥的体积等于和它等底等高的圆柱体积的三分之一;圆柱的体积等于和它等底等高的圆锥体积的三倍。
《生活中的立体图形》课件
球体
球体是由所有点到中心都相等的点组成的立体 图形，常见于球形物体、球体体育用品。
立体图形的应用
生活中的立体图形 应用
立体图形应用于建筑设计、 艺术装饰、雕塑和商品设计 等各个方面。
工业生产中的立体 图形应用
立体图形在工业生产中用于 设计产品原型、模具制作和 机械加工等工艺过程中。
计算机图形学中的 立体图形应用
《生活中的立体图形》 PPT课件
欢迎来到《生活中的立体图形》PPT课件！本课程将带您深入探索立体图形 的概念、特点以及应用。让我们一起开始这个有趣而令人惊叹的旅程吧！
立体图形的概念及特点
立体图形概念
立体图形是指具有三个尺 寸的物体，具有长度、宽 度和高度，给人以立体感。
立体图形的特点
立体图形具有真实感、立 体感，能够在三维空间中 存在和移动。
立体图形在计算机图形学中 被广泛应用于建模、动画、 虚拟现实和游戏开发等领域。
立体图形的绘制与制作
1 立体图形的绘制方法
绘制立体图形可以使用手工绘画、制作模型或借助计算机辅助绘图软件进行创作。
2 立体图形的制作方法
制作立体图形可以通过剪纸、折纸、雕刻和三维打印等技术进行实现。
立体图形的知形与平面图形 的区别
立体图形拥有第三个尺寸， 而平面图形只有两个尺寸。
常见的立体图形
正方体
正方体具有六个面，每个面都是相等的正方形。 它常被用于建筑、家具和玩具制作。
圆柱体
圆柱体具有两个平行的圆形底面和一个侧面， 常见于筒形物体、管道和柱子。
圆锥体
圆锥体具有一个圆形底面和一个顶点，常见于 锥形物体、冰淇淋和交通路标。
2 立体图形的拓展应用
解答关于立体图形的常见问题，例如如何 计算体积、表面积以及图形变换。
认识立体图形
教案认识立体图形一、引言1.1了解立体图形的概念1.1.1立体图形是有长度、宽度和高度三个维度的图形。
1.1.2立体图形与平面图形的区别在于其具有厚度和体积。
1.1.3立体图形在我们的生活中无处不在，如建筑物、家具、玩具等。
1.2立体图形的分类1.2.1根据形状和特征，立体图形可分为几何体和非几何体。
1.2.2几何体包括球体、圆柱体、圆锥体等，具有明确的数学定义和公式。
1.2.3非几何体如建筑物、动物等，形状多样，没有固定的数学公式。
1.3学习立体图形的意义1.3.1学习立体图形有助于培养学生的空间想象力和抽象思维能力。
1.3.2立体图形是数学、物理、工程等领域的基础知识，对学生的未来发展具有重要意义。
1.3.3通过学习立体图形，学生可以更好地理解和欣赏我们生活中的三维世界。
二、知识点讲解2.1立体图形的构成要素2.1.1立体图形由顶点、边和面组成。
2.1.2顶点是立体图形的角点，边是连接顶点的线段，面是由边围成的平面。
2.1.3立体图形的顶点、边和面的数量和形状决定了其独特的性质和特征。
2.1.4例如，正方体有8个顶点、12条边和6个面，球体没有顶点和边，只有一个曲面。
2.2立体图形的测量2.2.1立体图形的测量包括计算其表面积、体积和质心等参数。
2.2.2表面积是指立体图形所有面的总面积，体积是指立体图形所占空间的大小。
2.2.3质心是立体图形的平衡点，也是立体图形的几何中心。
2.2.4通过测量，我们可以了解立体图形的大小、形状和结构特点。
2.3立体图形的投影2.3.1立体图形的投影是将三维图形映射到二维平面上的一种方法。
2.3.2投影分为正投影和斜投影，不同方向的投影可以展示立体图形的不同视角。
2.3.3通过观察投影，我们可以推断出立体图形的形状、大小和相对位置。
2.3.4投影在工程设计、制图和艺术创作等领域有着广泛的应用。
三、教学内容3.1认识立体图形的种类3.1.1教学内容应涵盖各种常见的立体图形，如球体、圆柱体、圆锥体、正方体等。
观察立体图形
立体图形在建筑设计中可以 增强结构的稳定性，如埃菲
尔铁塔的钢架结构
立体图形在建筑设计中可以 优化空间利用，如北京国家
体育场的鸟巢形设计
产品设计中的应用
立体图形在产品 设计中的应用： 如家具、建筑、 交通工具等
立体图形在包装 设计中的应用： 如包装盒、包装 袋等
立体图形在广告 设计中的应用： 如广告牌、海报 等
立体图形在室内 设计中的应用： 如室内布局、装 饰等
艺术创作中的应用
雕塑：立体图形在雕塑创作中的应用，如立体主义雕塑等 建筑：立体图形在建筑设计中的应用，如立体主义建筑等 绘画：立体图形在绘画创作中的应用，如立体主义绘画等 设计：立体图形在设计领域的应用，如立体主义设计等
05
立体图形在科学领域的应用
立体化学：研究分子立体结 构的学科
立体异构体：具有相同分子 式但立体结构不同的化合物
立体专一性：某些化学反应 或生物过程对立体结构的选
择性
生物学中的应用
蛋白质结构：通过立体图形展 示蛋白质的三维结构
细胞生物学：立体图形用于展 示细胞的结构和功能
遗传学：立体图形用于展示DN、 RN等遗传物质的结构
药物设计：立体图形用于设计 药物分子，提高药物疗效
学习几何知识，理解立体图形 的结构和性质
练习绘画和雕塑，增强对立体 图形的感知和表现能力
观察角度的选择
正视图：观察立体图形的正面， 了解其形状和结构
俯视图：观察立体图形的顶部， 了解其深度和厚度
添加标题
添加标题
添加标题
添加标题
侧视图：观察立体图形的侧面， 了解其高度和宽度
透视图：观察立体图形的透视效 果，了解其空间感和立体感
ቤተ መጻሕፍቲ ባይዱ2
《立体图形》空间与图形课件
② 用铁丝做一个长10厘米，宽5厘米，高4 厘米的长方体框架，至少需要多长的铁丝？ 在这个长方体框架外面糊一层纸，至少需要 多少平方厘米的纸？
4
5 10
（ 10 + 5 + 4）×4=76 （厘米）
(10×5+10×4+5×4)×2=220(平方厘米)
练习四
1、一个近似于圆锥的沙堆，测得底面直径是４米，高 是1.5米。每立方米沙约重1.7吨，这堆沙约重多少吨？ （得数保留整吨数） 2、一个无盖的圆柱形水桶，侧面积是188.4平方 分米，底面周长是62.8分米。做这个水桶至少要多 少平方分米？这个水桶的容积是多少立方分米？
3.14×6=18.84(平方分米)
将一个圆柱体沿着底面直径切成两个半圆柱,表面积增
2、将一个圆柱加 体体积了是4沿0多平着少方立底厘方米面厘,圆米直柱?的径底切面直成径两为4个厘米,这个圆柱的 半圆柱,表面积增加了40平方厘米,圆柱的 底面直径为4厘米,这个圆柱的体积是多少 立方厘米?
(1) 要在一个长和宽都是30厘米，高是5分米长方
18.84 × 4
练习三
①把两个棱长是4厘米的正方体木块粘合成一个 长方体，这个长方体的表面积是多少平方厘米？
方法一、（8×4+8×4+4×4）×2=160（平方厘米） 方法二、8×4×4 + 4×4×2=160（平方厘米） 方法三、4×4×10=160（平方厘米）
方法四、4×4×12- 4×4×2=160（平方厘米）
六年级数学下册
我们学过哪些立体图形
高 h
长a
宽b
长方体
棱长a
正方体
高 h
底面半径 r
圆柱
高 h
底面半径 r
生活中的立体图形
生活中的立体图形引言立体图形是指在三维空间中具有长度、宽度和高度的图形。
在我们的日常生活中，我们经常会遇到各种各样的立体图形，例如盒子、球体和圆柱体等等。
这些立体图形不仅仅是一种几何形状，它们在我们的生活中扮演着重要的角色，就像我们周围的建筑物、容器和各种物体一样。
本文将介绍生活中常见的几种立体图形以及它们的应用。
一、盒子盒子是一种常见的立体图形，它具有六个面，包括四个侧面、一个底面和一个顶面。
盒子通常用来储存物品或包装物品。
在我们的日常生活中，我们经常会使用盒子来存放食物、书籍、衣物等等。
此外，盒子还经常用于运输物品，在物流行业中扮演着重要的角色。
二、球体球体是另一个常见的立体图形，它是由一个平面围绕着一个点旋转形成的图形。
球体在体育运动、音乐乐器和家居装饰中都有重要的应用。
在体育运动中，例如足球、篮球和网球，都是使用球体形状的球进行比赛。
此外，许多乐器，如打击乐器中的铜钹和木琴，也具有球体形状。
在家居装饰中，人们经常使用球体形状的装饰物来增添居家的美感。
三、圆柱体圆柱体是一个由圆形底面和一个平行于底面的圆形顶面连接而成的立体图形。
它不仅仅在我们的日常生活中发挥着储存和运输物品的作用，还在建筑、工程和设计领域中被广泛应用。
在建筑中，圆柱体形状常用于柱子和柱头的设计，为建筑物增添了美观和稳定性。
在工程领域中，圆柱体常用于管道和容器的设计和制造。
在设计领域中，圆柱体形状的物体常用于产品设计，例如圆柱形的笔筒和香薰瓶等。
四、棱柱体棱柱体是一个由多个相等的侧面连接而成的立体图形，它有两个平行且相等的底面。
棱柱体在建筑、工程和数学等领域有广泛的应用。
在建筑中，棱柱体常用于建筑物的设计，例如建筑立面的设计。
在工程领域中，棱柱体形状的物体常用于制造容器和管道。
在数学中，棱柱体经常被用作教学工具，帮助学生理解几何概念。
结论生活中的立体图形在我们的日常生活中无处不在。
从盒子到球体，再到圆柱体和棱柱体等等，这些立体图形不仅仅是一种几何形状，它们还扮演着各种重要的角色。
《认识立体图形》PPT课件大班数学
常见的立体图形：长方体、 正方体、球体、圆柱体等
定义：三维图形，是相对于 二维图形而言的
立体图形的应用：在建筑、机 械制造、艺术等领域都有广泛
的应用
立体图形的特点
色彩丰富，可以表现出多种 颜色和质感。
细节表现力强，能够展现出 物体的细节和特征。
立体感பைடு நூலகம்，能够呈现三维空 间的视觉效果。
层次感强，可以表现出物体 之间的前后关系和空间感。
圆柱体
定义：以矩形的一边所在直线为旋转轴旋转形成的面所围成的旋转体叫做圆柱体 公式：底面积×高 侧面展开图：长方形 体积：底面积×高
球体
特点：表面积相同，体积相 同，形状相同
与其他图形的比较：球体与长 方体、正方体、圆柱体等三维
图形不同
定义：球体是一个三维图形， 是包围球心的空间
常见应用：篮球、足球等球 类运动中的球
理解拆解的步骤和方法
学会还原的基本技巧
实践操作，还原被拆解的 立体图形
立体图形的属性与特点
正方体的属性与特点
属性：有6个面，每个面都 是正方形
特点：长、宽、高都相等， 体积为边长的立方
长方体的属性与特点
定义：长方体是一种具有六个面的几何体，每个面都是矩形或正方形 属性：长方体具有六个面、十二条棱和八个顶点 特点：长方体的相对面平行且相等，相邻面互相垂直 体积：长方体的体积可以通过其长度、宽度和高度的乘积得出
5-6岁：能正确 命名立体图形并 找出相应的实物
6-7岁：能对立 体图形进行分类、 测量并比较大小
7-8岁：能理解立 体图形的组合与分 解，发展空间观念
了解立体图形的特点
培养幼儿的空间观念
培养观察和想象能力
添加标题
《认识立体图形》
认识图形
1、长方体（不容易滚动）
长方体是长长的，有6个平平的面，有些面是一样的，有些面是不一样，长方体相对面相等，用它可以画出长方形。
平时见到的火柴盒、文具盒都是长方体。
2、正方体（不容易滚动）
正方体四四方方的，它也有6个平平的面，它的边也是直直的。
而且它的棱都是一样长，每个面都一样大，无论怎么平放在桌子上，它的高矮都是一样的，用它可以画出正方形。
魔方就是正方体。
3、圆柱体（能滚动又能立起来）
圆柱就像一根柱子。
它有上下两个圆圆的面，而且大小一样，用它可以画出圆形；另一个面是弯曲的，我们把弯曲的面放在桌子上就可以滚动它。
4、球（能任意滚动）
圆圆的，可以滚来滚去的就是球。
平时玩的皮球、篮球、踢的足球都是球。
立体图形的拼组
（1）用长方体或正方体可以拼组成不同的立体图形。
（2）用小的圆柱可以拼组成更大的圆柱。
5、要拼出一个大的正方体，至少需要4个同样的小正方体。
6、2个正方体可以拼成一个长方体。
7、用4个相同的长方体，可以拼出3种不同的长方体。
立体图形的知识点
立体图形的知识点在日常生活中，我们经常会接触到各种立体图形，比如球体、立方体、圆柱体等等。
这些立体图形在建筑、工程、艺术等领域有着广泛的应用。
为了更好地理解和应用这些图形，我们需要了解立体图形的基本概念、性质和公式。
一、基本概念1.立体图形立体图形是具有一定体积的图形，包括球体、立方体、圆柱体、圆锥体、棱锥体、棱柱体等。
2. 体积体积是立体图形所占的空间大小，用“立方米”等单位来表示。
立体图形的体积公式有很多，下面将分别介绍不同立体图形的体积公式。
3. 表面积表面积是立体图形外部的总面积，用“平方米”等单位表示。
同样，在下面将分别介绍不同立体图形的表面积公式。
二、性质和公式1. 球体球体的体积公式为V=4/3πr³，其表面积公式为S=4πr²。
这里，V表示体积，S表示表面积，r表示球的半径，π表示圆周率，约为3.1415。
2. 立方体立方体的体积公式为V=a³，其表面积公式为S=6a²。
这里，a 表示立方体的边长。
3. 圆柱体圆柱体的体积公式为V=πr²h，其表面积公式为S=2πrh+2πr²。
这里，r表示底面圆的半径，h表示圆柱的高。
4. 圆锥体圆锥体的体积公式为V=1/3πr²h，其表面积公式为S=πr(r+√(r²+h²))。
这里，r表示底面圆的半径，h表示圆锥的高。
5. 棱锥体棱锥体的体积公式为V=1/3Sh，其中S表示底面的面积，h表示棱锥的高。
其表面积公式为S=B+L，其中B表示底面的面积，L表示侧面的面积。
6. 棱柱体棱柱体的体积公式为V=Bh，其中B表示底面的面积，h表示棱柱的高。
其表面积公式为S=2B+Ph，其中P表示侧面的周长。
总结通过了解不同立体图形的基本概念、性质和公式，我们可以更好地理解和应用在不同领域中。
在实际应用过程中，应根据具体情况选择合适的公式，进行计算和应用。
因此，了解这部分知识点对我们的学习和工作都有一定的帮助。
立体图形的概念(如圆柱、圆锥、球体等)
平面设计：立体图形在平面设计中的应用，如海报设计、广告设计等
立体图形的制作方法
准备材料：纸板、剪刀、胶水等
设计立体图形：根据立体图形的概念，设计出立体图形的平面图
剪裁纸板：根据平面图，剪裁出立体图形的各个部分
组装立体图形：将剪裁好的纸板按照立体图形的构造进行组装，形成立体图形
编辑模型：对模型进行编辑，如修改尺寸、添加细节等
切片处理：将模型进行切片处理，生成3D打印所需的文件
汇报人：XXX
感谢您的观看
立体图形的角：构成立体图形的角，可以是锐角、直角或钝角
立体图形的边和角的关系：边和角是立体图形的基本构成要素，它们共同决定了立体图形的形状和性质
立体图形的边和角的应用：在几何学、工程学、建筑学等领域，立体图形的边和角有着广泛的应用
面积：立体图形表面的大小，通常用平方米或平方厘米等单位表示
体积：立体图形所占空间的大小，通常用立方米或立方厘米等单位表示
立体图形的构成要素
面：由线围成的封闭区域，表示一个平面或一个曲面。
点：立体图形中最基本的构成要素，表示一个位置或一个方向。
线：由点连接而成的直线或曲线，表示一个方向或一个轨迹。
立体图形：由点、线、面构成的三维空间图形，表示一个实体或一个空间。
立体图形的边：构成立体图形的直线部分，可以是直线、曲线或折线
计算方法：根据立体图形的形状和性质，选择合适的公式进行计算
应用：在工程、建筑、设计等领域，需要计算立体图形的面积和体积，以便进行设计和施工
立体图形的性质
立体图形的形状：由多个平面图形组成，如立方体、圆柱体等
立体图形的大小：由长度、宽度、高度三个维度决定，如立方体的体积、圆柱体的体积等
立体图形的表面积：由各个平面图形的面积之和决定，如立方体的表面积、圆柱体的表面积等
小学数学课件立体图形的认识
教学反思与改进的方法
回顾教学过程：分析立体图形教学实践中的亮点和不足 收集学生反馈：了解学生对立体图形的掌握程度和学习需求 对比教学目标：评估实际教学效果与预期目标的差距 改进教学方法：根据反思结果调整教学策略，提高教学质量
教学实践经验的总结与分享
立体图形教学实践：注重实际操作 与感知
学生反馈：及时了解学生掌握情况， 调整教学策略
立体图形在生活中的应用
建筑学：建筑设计利用立体图形的空间特性，创造出各种风格的建筑 艺术：立体图形在雕塑、绘画等领域中广泛应用，丰富了艺术的表现形式 工业设计：立体图形的运用使得产品外观更加美观，功能更加完善 包装设计：立体图形的包装设计能够吸引消费者的注意力，提高商品的销售量
立体图形的面
伤
利用软件制作立体图形的方法
选择合适的软件：如SketchUp、AutoCAD等 创建基本形状：使用软件的基本绘图工具创建立体图形的基本形状 调整细节：使用软件的编辑工具调整立体图形的细节，如线条、角度等
渲染效果：使用软件的渲染工具为立体图形添加材质和光照效果，使其更加逼真
制作立体图形的注意事项
确定制作材料：根据立体图形的 特点和需求选择合适的材料，如 纸、塑料、木材等。
确定尺寸和比例：根据实际需求 和用途，确定立体图形的尺寸和 比例，确保其真实性和美观度。
设计结构：根据立体图形的特点 和制作要求，设计合理的结构， 确保其稳定性和可操作性。
确定制作方法：根据立体图形的 特点和材料，选择合适的制作方 法，如折叠、拼装、雕刻等。
注意安全：在制作立体图形的 过程中，要注意安全，避免使 用危险的工具和材料，同时也 要注意防止意外伤害的发生。
教学方法的选择
实物教学：通过观察实物模型，帮助学生建立立体感 多媒体教学：利用三维动画和立体图像，展示立体图形的结构和特点 互动教学：组织学生动手制作立体图形，培养实践能力和创新思维 游戏化教学：设计有趣的数学游戏，让学生在游戏中学习立体图形的知识
立体图形知识点梳理总结
立体图形知识点梳理总结立体图形是指在三维空间中存在的图形。
它具有体积和表面积的概念。
立体图形是立体几何的研究对象，包括了各种各样的形态，如立方体、长方体、圆柱体、球体、锥体等等。
掌握立体图形的知识对于学生学习数学和物理都是非常重要的。
本文将系统地总结立体图形的相关知识点，包括定义、性质、计算公式等内容，帮助读者更好地理解和掌握立体图形的概念。
一、基本概念1. 立体图形的定义立体图形是在三维空间中存在的图形。
它具有长度、宽度和高度三个方向。
立体图形由许多平面图形组成，例如长方体由6个矩形组成，圆柱体由两个平行的圆面和一个侧面组成。
2. 常见立体图形的名称和特点（1）长方体- 定义：长方体是六个面都是矩形的立体图形。
- 性质：长方体的体积为长×宽×高，表面积为2×(长×宽+长×高+宽×高)。
（2）正方体- 定义：正方体是六个面都是正方形的立体图形。
- 性质：正方体的体积为边长的立方，表面积为6×(边长的平方)。
（3）圆柱体- 定义：圆柱体是由两个相同的平行圆面和一个侧面组成的立体图形。
- 性质：圆柱体的体积为底面积×高，表面积为2×底面积+侧面积。
（4）球体- 定义：球体由无数个与球心距离相等的点组成的立体图形。
- 性质：球体的体积为4/3×π×半径的立方，表面积为4×π×半径的平方。
（5）圆锥体- 定义：圆锥体是由一个圆锥面和一个底面组成的立体图形。
- 性质：圆锥体的体积为1/3×底面积×高，表面积为π×底面半径×斜高+底面积。
二、计算公式1. 计算立体图形的体积和表面积（1）长方体的体积和表面积计算公式- 体积：V=长×宽×高- 表面积：S=2×(长×宽+长×高+宽×高)（2）正方体的体积和表面积计算公式- 体积：V=边长的立方- 表面积：S=6×(边长的平方)（3）圆柱体的体积和表面积计算公式- 体积：V=底面积×高- 表面积：S=2×底面积+侧面积（4）球体的体积和表面积计算公式- 体积：V=4/3×π×半径的立方- 表面积：S=4×π×半径的平方（5）圆锥体的体积和表面积计算公式- 体积：V=1/3×底面积×高- 表面积：S=π×底面半径×斜高+底面积2. 其他常见立体图形的计算公式（1）平面图形组成的立体图形的计算- 若一个立体图形由多个平面图形组成，可以通过计算每个平面图形的面积和相加来得到立体图形的体积和表面积。
关于立体图形的知识点
关于立体图形的知识点立体图形是和平面图形齐名的一类图形，它们共同构成了我们周围丰富多彩的空间世界。
通过对立体图形的学习，我们可以更好地理解空间结构、提高数学思维能力以及应用数学知识解决实际生活问题。
本文将从以下几个方面对立体图形的知识点进行介绍。
一、立体图形的基本概念立体图形是由面、棱、角组成的三维空间图形。
常见的立体图形有正方体、长方体、棱锥、棱台、球、圆锥、圆柱等。
正方体是一种所有面均为正方形且相邻面之间互相垂直的立体图形。
长方体是一种所有面均为矩形且相邻面之间互相垂直的立体图形。
棱锥是一种底面为多边形，顶部连接一个顶点与底面上所有顶点的直线的立体图形。
棱台是一种顶部与底部均为多边形，侧面由连接底面和顶面相对顶点的直线所组成的立体图形。
球是一种表面上所有点距离球心相等的立体图形。
圆锥是以底面圆上所有点到固定点的直线为母线，绕母线旋转一周所得的立体图形。
圆柱是以底面圆上所有点与固定点的距离为高，绕高速旋转一周所得的立体图形。
二、立体图形的面积和体积计算对于各种不同形状的立体图形，其面积和体积的计算公式也不尽相同。
正方体的表面积为6a²，其中a为正方体的边长，体积为a³。
长方体的表面积为2(ab+ac+bc)，其中a、b、c为长方体的三条边的长度，体积为abc。
棱锥的表面积为L+πr²，其中L为底面周长与顶点连线的长度之和，r为底面半径，体积为1/3Bh，其中B为底面积，h为棱锥高。
棱台的表面积为L+（上底面积+下底面积+底面积）*h，其中L为底面周长与顶点连线的长度之和，上底面积和下底面积分别为顶面和底面的面积，体积为1/3h（上底面积+下底面积+底面积），其中h为棱台高。
球的表面积为4πr²，其中r为球半径，体积为4/3πr³。
圆锥的表面积为πr²+πrL，其中r为底面半径，L为直截线长度，体积为1/3πr²h，其中h为圆锥高。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
立体图形1．如下图，不是正方体展开图的是（）A、 B、 C、 D、2．如下图所示，用一个平面去截一个圆柱，则截得的形状应为( ).A B C D3．用平面去截下列几何体，截面的形状不可能是圆的几何体是A. 球B. 正方体C. 圆锥D. 圆柱4．直四棱柱，长方体和正方体之间的包含关系是5．下列图形中是正方体表面展开图的是（）6．下列几何体中，截面不可能是三角形的是（）（A）长方体（B）正方体（C）圆柱（D）圆锥7．一个正方体的表面展开如图所示，则正方体中的A所在面的对面所标的字是（）A、深B、圳C、大D、会8．右图可以折叠成的几何体是（）A．三棱柱B．四棱柱C．圆柱D．圆锥9．下列图形中，不可能围成正方体的有（）个A、1B、2C、3D、410．将一个直角三角板绕直角边旋转一周，则旋转后所得几何体是（）A．圆柱B．圆C．圆锥D．三角形11．如图是一个几何体的三视图，根据图中提供的数据（单位：cm）可求得这个几何体的体积为A．2cm3 B．3cm3 C．6cm3 D．8cm312．一些完全相同的小正方形搭成一个几何体，这个几何体从正面和左面看所得的平面图形均如图所示，小正方体的块数可能有（）（A）7种（B）8种（C）9种（D）10种13．在如图所示的长方体中，和棱AB平行的梭有（）A.3条B.4条C.5条D.6条14．下列平面图形中不能围成正方体的是（）．A、B、第30题图C 、D 、15．如图是由若干个同样大小的正方体搭成几何体从上往下看到的图形，小正方形中的数字表示该位置立方体的个数，则这个几何体从正面看应该是（ ）16．如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“共”字一面的相对面上的字是A ．美B ．丽C ．家D ．园17．棱长是1cm 的小立方体组成如图所示的几何体，那么这个几何体的表面积A. 36cm 2B. 33cm 2C.30cm 2D.27cm 218．下列立体图形中，有五个面的是 ( )A ．四棱锥B ．五棱锥C ．四棱柱D ．五棱柱19．在矩形ABCD 中，AB ＝3cm ，AD ＝2cm ，则以AB 所在直线为轴旋转一周所得的圆柱的表面积为（ ）A cmB cm ..172022ππC cmD cm ..213022ππ20．小丽制作了一个对面图案均相同的正方体礼品盒（如图所示），则这个正方体礼品盒的平面展开图可能是（ ）A ．B ．C ．D ．）21．现有一个只有三个面上印有图案的不透明的正方形纸盒，如图所示，在下面的四个图形中，往下．．折叠能围成图甲的是（▲）22．在Rt△ABC中，∠C=90°，AB=5，BC=3，以AC所在的直线为轴旋转一周，所得圆锥的表面积为（）A．12π B．15π C．24π D．30π23．如图（1），是由五个边长为1的小正方形拼成，现将图（1）通过分割重新拼成一个大正方形（如图（2）），则拼成的大正方形的边长是（）A．整数 B．有理数 C．正有理数 D．24．下列图形中，不是三棱柱的表面展开图的是（）25．将正方形纸片两次对折，并剪出一个菱形小洞后铺平，得到的图形是（）26．下列立体图形中，侧面展开图是扇形的是(▲)27．下列图形，经过折叠不能折成立方体的是（）A．B．C．D．28．圣诞节时小华制作了一个如下左图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是：（）29．一个正方体的水晶砖，体积为l00cm3，它的棱长大约在A．4～5cm B．5～6cmC．8～9cm D．9～10cm30．如图，从正上方看下列各几何体，得到图形(1)的几何体是( )31．如图所示为一个无盖长方体盒子的展开图（重叠部分不计），根据图中数据，可知该无盖长方体的容积为（）A．4 B．6 C．8 D．1232．如图（1）所示，将三角形绕直线l旋转一周，可以得到图（2）所示的立方图的是（）33．下面哪个平面图形不能围成正方体( )34．一个直棱柱有12个顶点，那么它的面的个数是（）A 、10个B 、9个C 、8个D 、7个35．如图，上边水平放置的圆柱形物体的三视图是下边的（ ）．36．如图是无盖长方体盒子的表面展开图(重叠部分不计)，则盒子的容积为( ) (A)4． (B)6． (C)12． (D)1537．如图，上下底面为全等的正六边形礼盒，其正视图与侧视图均由矩形构成，正视图中大矩形边长如图所示，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为（ ）A ．320cmB ．395.24 cmC ．431.76 cmD ．480 cm38．如图是一个圆锥的主视图，则这个圆锥的全面积是A . π12B . π15 C. π21 D. π2439．如图，用高为6cm ，底面直径为4cm 的圆柱A的侧面积展开图，再围成不同于A 的另一个圆柱B ，则圆柱B 的体积为第7题40．一个圆锥的底面半径为6㎝，圆锥侧面展开图扇形的圆心角为240°，则圆锥的母线长为A ．9㎝B ．12㎝C ．15㎝D ．18㎝41．若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面的正方体棱长为1，如果塔形露在外面的面积超过7，则正方体的个数至少是A 、2B 、3C 、4D 、5 42．从上向下看图(1),应是如图(2)中所示的( )43．将如图1所示的直角三角形绕直线l 旋转一周，得到的立体图形是（ ）44．一个长8厘米，宽7厘米，高6厘米的长方体容器平放在桌面，里面盛有高2厘米的水（如图一）; 将这个长方体沿着一条宽旋转90°，平放在桌面（如图二）. 在旋转的过程中，水面的高度最高可以达到 ( )(A) 38厘米 (B) 4厘米 (C) 3厘米 (D) 417厘米45．如图①是一个正三棱柱毛坯，将其截去一部分，得到一个工件如图②．则这个工件的俯视图、主视图依次是 ( )A ．c 、aB ．c 、dC ．b 、dD ．b 、a 46．下面的几何体的左视图是47．已知圆锥的底面半径为2cm ，母线长为5cm ，则圆锥的侧面积是 （ ） A ．220cmB ．220cm πC ．210cm πD ．25cm π48．以下几何图形中，表示立体图形的是（ ）49．在棱柱中（ ） A.只有两个面平行 B.所有的棱都平行C.所有的面都是平行四边形D.两底面平行，且各侧棱也互相平行50．如图是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体的“着”相对的面上的汉字是冷 B ．静 C ．应 D ．考51．如图1所示的立方体，如果把它展开，可以是下列图形中的（ ）52．如图，是一个正方体纸盒的展开图，若在其中三个正方形A 、B 、C 中分别填入适当的数，使得它们折成正方体后相对的面上两个数互为相反数，则填入正方形A 、B 、C 中的三个数依次是 （ ）图1A ．1、－3、0B ．0、－3、1C ．－3、0、1D ．－3、1、0 53．如图，是某种几何体表面展开图的图形．这个几何体是A ．圆锥B ．球C ．圆柱D ．棱柱 54．用一个平面去截一个圆柱，得到的图形不可能是55．一个正方体盒子的每个面上都写有一个字，分别是：我、喜、欢、数、学、课，其平面展开图如图所示．那么在该正方体盒子中，与“我”相对的面上所写的字是（ ）A ．欢B ．数C ．学D ．课 56．如图中的立方体展开后，应是图中的（ ）．57．下列图形中不能折成立方体的是（ ）A.B.C.D.58．如图是一个几何体表面展开图(字在外表面上．．．．．．)，面“江”的对面所写的字是（ ） 我春都花江爱A ．我B ．爱C ．春D ．都 59．一个几何体的展开图如图所示，则该几何体的顶点有（ ）Ａ．10个Ｂ．8个Ｃ．6个 Ｄ．4个60．如图是可以沿线折叠成一个带数字的正方体的展开图，每三个带数字的面交于正方体的一个顶点，则相交于同一个顶点的三个面上的三数字之和的最小值是 （ ）A ．6B ．7C ．9D ．1161．下列几何体中，正视图、左视图、俯视图完全相同的是 A. 圆柱 B. 圆锥 C. 棱锥 D. 球 62．将一个正方体沿着某些棱剪开，展成一个平面图形，至少需要剪的棱的条数是（ ） A.5 B.6 C.7 D.863．一个正方体的表面展开图如图所示，每一个面上都写有一个整数，并且相对两个面上所写的两个整数之和都相等，那么（ ）A ．a =1，b =5B ．a =5，b =1C ．a =11，b =5D ．a =5，b =1164．如图是一个正方体的表面展开图，则原正方体中与“建”字所在的面相对的面上标的是( )A ．美B ．丽C ．广D ．安65．如图，有一圆心角为120 o 、半径长为6cm 的扇形，若将OA 、OB 重合后围成一圆锥侧面，那么圆锥的高是（ ）A ．32 cmB ．35cmC ．62cmD ．24cm66．如图所示，小红要制作一个母线长为8cm ，底面圆周长是12πcm 的圆锥形小漏斗，若不计损耗，则她所需纸板的面积是（ ）A ．60πcm 2B ．96πcm 2C ．120πcm 2D ．48πcm 267．下列图形能围成一个无盖正方体的是 （填序号）68．如图所示，几何体的左视图是69．如图是纸盒的外表面，下面能由它折叠而成的是（ ）70．下列图形中，不是正方体展开图形的是( )71．如图，有一圆心角为120 o、半径长为6cm 的扇形，若将OA 、OB重合后围成一圆锥侧面，那么圆锥的高是（ ）A ．24cmB ．35cmC ．62cmD ．32cm72．小红将考试时自勉的话“细心、规范、勤思”写在一个正方体的六个①②④③⑤⑥A ．B ．C ．D ．面上，其平面展开图如图所示，那么在该正方体中，和“细”相对的字是规 B 、范 C 、勤 D 、思 73．下列平面图形中，不是．．正方体的展开图是（ ）A. B. C. D.74．如图，把左边的图形折起来，它会变成右边的正方体（ ）.75．如图，圆锥的底面半径6cm OB =，高8cm OC =．则这个圆锥的侧面积是（ ）A ．230cm B ．230cm π C ．260cm π D ．2120cm76．有一个正方体的六个面上分别标有数字1、2、3、4、5、6，从三个不同的角度观察这个正方体所得到的结果如图所示，如果标有数字6的面所对面上的数字记为a ，2的面所对面上数字记为b ，那么a+b 的值为 A ．6 B ．7 C ．8 D ．977．下列说法错误．．的是 （ ）． A ．长方体、正方体都是棱柱 B ．球体的三种视图均为同样大小的图形C ．三棱柱的侧面是三角形D ．六棱柱有六条棱、六个侧面、侧面为长方形 78．如图所示的几何体的俯视图是（ ）．第2题图A ．B ．C ． D79．某同学把图1所示的几何体从不同方向看得到的平面图形画出如图2所示其中正确的是（ ）A ．①②B ．①③ B ．②③ B ．②80．已知圆锥的底面半径为6cm ，高为8cm ，则圆锥的侧面积为（ ） A. 236cm π B. 248cm π C. 602cm D. 280cm π 81．如图所示的正方体的展开图是（ ）82．从不同方向看到的一立体图形如图所示，那么这个立体图形应是（ ）A 、长方体B 、圆柱体C 、圆锥体D 、球体 83．如图，圆柱的底面直径和高均为4，动点P 从A 点出发，沿着圆柱的侧面移动到BC 的中点S 的最短距离是84．如图所示，有一个长、宽各2米，高为3米且封闭的长方体纸盒，一只昆虫从顶点A 要爬到顶点B ，那么这只昆虫爬行的最短路程为A 、3米B 、4米C 、5米D 、6米85．如图是某一立方体的侧面展开图，则该立方体是（ ）图2图1A B C D86．如图摆放的正六棱柱的俯视图是（）87．将图2①围成图2②的正方体，则图②中的红心“”标志所在的正方形是正方体中的A．面CDHEB．面BCEFC．面ABFGD．面ADHG88．将如图形状的纸片折成一个立方体，数字在与数字2所在平面相对的平面上.89．用一个平面截一个正方体，截面最多是边形90．直五棱柱共有个顶点。