中线的用法(倍长中线法)
5.倍长中线法

DC BA全等三角形问题中常见的辅助线——倍长中线法△ABC 中,AD 是BC 边中线方式1:直接倍长,(图1): 延长AD 到E ,使DE =AD ,连接BE 方式2:间接倍长1) (图2)作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E , 连接BE 2) (图3)延长MD 到N ,使DN =MD ,连接CD【经典例题】例1已知,如图△ABC 中,AB =5,AC =3, 则中线AD 的取值范围是_________.(提示:画出图形,倍长中线AD ,利用三角形两边之和大于第三边)例2:已知在△ABC 中,AB =AC ,D 在AB 上,E 在AC 的延长线上, DE 交BC 于F ,且DF =EF . 求证:BD =CE .(提示:方法1:过D 作DG ∥AE 交BC 于G ,证明ΔDGF ≌ΔCEFEDFC BA方法2:过E 作EG ∥AB 交BC 的延长线于G ,证明ΔEFG ≌ΔDFB方法3:过D 作DG ⊥BC 于G ,过E 作EH ⊥BC 的延长线于H ,证明ΔBDG ≌ΔECH )例3、如图,△ABC 中,E 、F 分别在AB 、AC 上,DE ⊥DF ,D 是中点,试比较BE +CF 与EF 的大小.变式:如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F . 求证:EF CF BE >+(提示:方法1:在DA 上截取DG =BD ,连结EG 、FG , 证明ΔBDE ≌ΔGDE ΔDCF ≌ΔDGF 所以BE =EG 、CF =FG 利用三角形两边之和大于第三边 方法2:倍长ED 至H ,连结CH 、FH ,证明FH =EF 、CH =BE ,利用三角形两边之和大于第三边)例4:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE =AC ,延长BE 交AC 于F ,求证:AF =EF(提示:方法1:倍长AD 至G ,连接BG ,证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形。
倍长中线法

倍长中线法
倍长中线的意思是:延长底边的中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,则对应角对应边都对应相等。
此法常用于构造全等三角形,进而证明边之间的关系。
倍长中线法
中文名倍长中线
思想方法构造全等三角形领域平面几何外文名nethod of times the length of line 目的证明边之间的关系
1定义
所谓“倍长中线”,就是加倍延长中线,使所延长部分与中线相等,
然后往往需要连接相应的顶点,则对应角对应边都对应相等。
常用于构造全等三角形。
中线倍长法多用于构造全等三角形和证明边之间的关系(一般都是原题已经有中线时用,不太会有自己画中线的时候)。
说简单一点,倍长中线就是指:延长中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,构造全等三角形。
高手过招必备技能——“倍长中线法”

高手过招必备技能——“倍长中线法”三大辅助线技巧——倍长中线【方法说明】遇到一个中点的时候,通常会延长过该中点的线段.倍长中线指延长一边的中线至一点,使所延长部分与该中线相等,并连接该点与这一条边的一个顶点,得到两个三角形全等.如图所示,点D为△ABC 边BC的中点.延长AD至点E,使得DE=AD,并连接BE,则△ADC≌△EDB(SAS).【方法归纳】1.如图,AD为△ABC边BC的中线.延长AD至点E,使得AD =DE.若连接BE,则△ADC≌△EDB(SAS);若连接CE,则△ADB≌△EDC(SAS).2.如图,点D为△ABC边BC的中点.延长ED至点F,使得DE =DF,并连接BF,则△EDC≌△FDB(SAS).3.如图,AB∥CD,点E为线段AD的中点.延长CE交AB于点F,则△EDC≌△EAF(ASA).【典型例题】1.(09莱芜)已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)求证:EG=CG;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF 中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).【思路点拨】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG =EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF 的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.还知道EG⊥CG.【解题过程】解:(1)∵四边形ABCD是正方形,∴∠DCF=90°,在Rt△FCD中,∵G为DF的中点,∴CG=1/2FD,同理,在Rt△DEF中,EG=1/2FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.【方法一】连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG;∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM 是矩形,在矩形AENM中,AM=EN,在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.【方法二】延长CG至M,使MG=CG,连接MF,ME,EC,在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG.∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC,EF=BE,∴△MFE≌△CBE,∴∠MEF=∠CEB.∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=1/2MC,∴EG=CG.(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F 作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC,∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形,∵G为CM中点,∴EG=CG,EG⊥CG.。
倍长中线最全总结。例题+练习(附答案)

倍长中线最全总结。
例题+练习(附答案)中线是三角形中的重要线段之一。
在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线。
倍长中线指的是延长三角形中线,使得延长后的线段是原中线的2倍。
其目的是为了构造一对8字型全等三角形(SAS),从而实现边角的转移。
以三角形ABC为例,延长中线AD至点E,使得DE=AD,连接BE。
根据三角形的SAS全等条件,可以得出结论:△ACD≌△BED,AC=BE,∠CAD=∠BED,AC∥BE。
同样地,延长中线CD至点F,使得DE=DF,连接CF。
根据三角形的SAS全等条件,可以得出结论:△BED≌△CFD,CF=BE,∠CFD=∠BED,CF∥BE。
在利用倍长中线法时,需要注意延长哪一条线段或者类中线。
倍长之后,需要考虑连接哪一条线段从而构造全等,实现所需的线段进行转移。
举例来说,如图所示,在三角形ABC中,需要证明AB+AC>2AD。
延长中线AD至点E,使得DE=AD,构造△ADC和△EDB,根据三角形的三边关系可得AB+AC>2AD。
另外,还有一道题目是需要求解AD的取值范围。
在三角形ABC中,D为BC的中点。
根据三角形的三边关系可得5-3<2AD<5+3,即AD的取值范围为1<AD<4.证明:延长AD到F,使DF=AD,连接BF(如图)。
因为AD是中线,所以BD=DC=AC,又因为DF=AD,所以BD=BF,所以AB>BF。
由三角形的三边关系,在三角形ABF中,有AB+BF>AF,即2AD<AB+AC,证毕。
2)因为AD是中线,所以BD=DC=AC,又因为DF=AD,所以BD=BF,所以AB>BF。
由相似三角形ADC和FDB,得到∠CAD=∠F,由边的大小关系可得到∠BAD>∠DAC,证毕。
3)同(2),由相似三角形ADC和FDB,得到AE/AD=BF/BD<1,即AE<AD,证毕。
初中数学倍长中线法

初中数学倍长中线法
在初中数学中,倍长中线法是一种求解三角形面积的方法。
它基于中线的性质:连接三角形两边中点的线段叫做中线,且中线的长度等于这两边之和的一半。
因此,对于任意三角形ABC,可以先求出它的三条中线长度,分别记为m<sub>a</sub>、m<sub>b</sub>、m<sub>c</sub>。
然后,用海龙公式:
s = √[s(s-a)(s-b)(s-c)]
其中,s 是三角形的半周长,a、b、c是三边长度。
而半周长 s 可以用三条中线的长度求出:
s = 1/2(m<sub>a</sub> + m<sub>b</sub> + m<sub>c</sub>) 这样,就可以用倍长中线法求出任意三角形的面积了。
需要注意的是,倍长中线法只适用于求解面积,不能用来求解三角形的其他属性。
但在一些实际问题中,求解面积就足够了。
- 1 -。
第二讲中线倍长法

第二讲:全等三角形之倍长中线法图1:△ABC 中,AD 是BC 边中线 图2:方式1:延长AD 到E ,使DE=AD ,连接BE图3:方式2:间接倍长,在AB 上取点M ,延长MD 到N , 使DN=MD ,连接CD 图4:方式3:间接倍长,作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E ,连接BE 典型例题例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围。
例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:(2004•郑州)已知:如图,△ABC (AB ≠AC )中,D 、E 在BC 上,且DE=EC ,过D 作DF∥BA 交AE 于点F ,DF=AC .求证:AE 平分∠BAC .FEC AB DFEDABC例5:如图,D 是△ABC 的BC 边上一点且CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线. 求证:∠C=∠BAE .例6:如图,在四边形ABCD 中,AB ∥CD ,点E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F .例7:如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+例8:已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图DF CBEADABCMTE。
倍长中线法

倍长中线法
知识网络详解:
中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.
所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.
倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)
倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线
经典例题讲解:
例1:△ABC中,AB=5,AC=3,求中线AD的取值范围
例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
例3:已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC 于F,求证:AF=EF
例4:已知:如图,在ABC 中,ACAB ,D、E在BC上,且DE=EC,过D作BADF//交AE 于点F,DF=AC.
求证:AE平分∠BAC
例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE
、如图,△ABC中,BD=DC=AC,E是DC的中点,求证,AD平分∠BAE
在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论
.。
倍长中线法(经典例题)
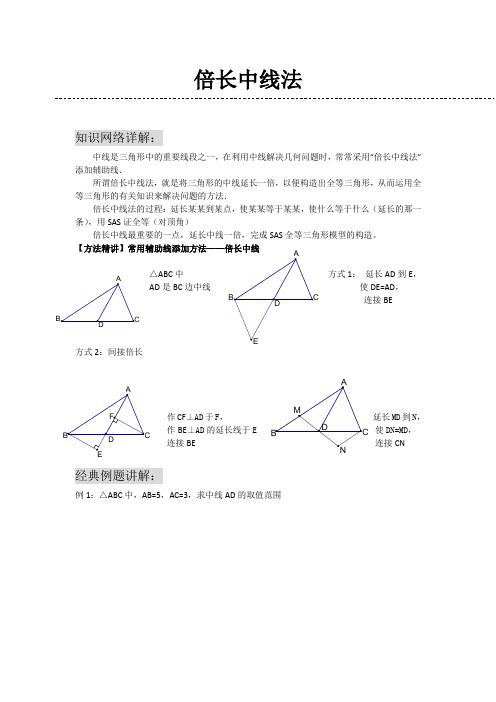
倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC 中 方式1: 延长AD 到E ,AD 是BC 边中线 使DE=AD ,连接BE方式2:间接倍长作CF ⊥AD 于F , 延长MD 到N ,作BE ⊥AD 的延长线于E 使DN=MD , 连接BE 连接CN经典例题讲解:例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围D ABCEDAB C F EDC B AN D C B AM例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠FE DA B CFEC ABD AB F D E C例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.E D ABCF EAB C D3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图DF CBEADABCMTE。
倍长中线法加倍法

求证:
例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD 旳中线,
求证:∠C=∠BAE
1、如图,△ABC中,BD=DC=AC,E是DC旳中点, 求证,AD平分∠BAE。
• 倍长中线最主要旳一点,延长中线一倍,完毕 SAS全等三角形模型旳构造。
例1:△ABC中,AB=5,AC=3, 求中线AD旳取值范围。
例2:已知在△ABC中,AB=AC,D在AB上,E 在AC旳延长线上,DE交BC于F,且DF=EF,
求证:BD=CE
例3:已知在△ABC中,AD是BC边上旳中线,E 是AD上一点,且BE=AC,延长BE交AC于F,
倍长中线法(加倍法)
• 知识网络详解: • 中线是三角形中旳主要线段之一,在利用中线
处理几何问题时,经常采用“倍长中线法”添加辅 助线.
• 所谓倍长中线法,就是将三角形旳中线延长一 倍,以便构造出全等三角形,从而利用全等三角 形旳有关知识来处理问题旳措施.
• 倍长中线法旳过程:延长某某到某点,使某某 等于某某,使什么等于什么(延长旳那一条), 用SAS证全等(对顶角)
完整版)倍长中线法(经典例题)

完整版)倍长中线法(经典例题)
倍长中线法是解决几何问题中常用的方法之一。
在利用中线解决问题时,我们可以通过添加辅助线,采用倍长中线法来构造全等三角形,从而运用全等三角形的知识来解决问题。
具体来说,倍长中线法的过程是:延长某一中线一倍,使其构造出全等三角形,然后利用全等三角形的有关知识来解决问题。
在构造全等三角形时,我们可以采用两种常用的方法:一是将中线延长到某一点,使其等于另一条中线,然后利用对顶角的SAS证明全等;二是通过间接倍长的方法,利用垂线和平行线构造出全等三角形。
倍长中线法最重要的一点是延长中线一倍,完成SAS全等三角形模型的构造。
我们可以通过经典例题来练这种方法,例如求中线的取值范围、证明BD等于CE、证明AF等于EF 等问题。
自检自测题也是巩固这种方法的好办法。
例如证明AD平分∠BAE、探究线段AB与AF、CF之间的数量关系、证明BE+CF>EF等问题都可以通过倍长中线法来解决。
专题05 倍长中线问题(解析版)

专题05 倍长中线问题【要点提炼】一、【倍长中线法】中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)+倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
二、【倍长中线法拓展;两次全等】通常,在倍长中线后的第一组全等只是一个基础,往往还需证明第二组全等,但是难点就在于如何去倍长中线,倍长中线后去连接什么线,这是问题的关键。
这时一般需要去试错,尤其是当有两个中点时,一般是倍长中线后大概率会有另一组的全等。
三、【倍长中线的常见类型】1.基本型如图1,在中,为边上的中线.延长至点E,使得.若连结,则;若连结,则;若连结则四边形是平行四边形.2.中点型如图2, C为AB的中点.若延长EC 至点F ,使得CF EC =,连结AF ,则BCE ACF ∆≅∆;若延长DC 至点G ,使得CG DC =,连结BG ,则ACD BCG ∆≅∆.总结:在线段AB 外,与中点C 连结的点有E 和D .事实上,EC 和DC 分别是ABE ∆和ABD ∆的中线,只不过是三角形不完整罢了,本质就是隐蔽的“基本型”3.中点+平行线型如图3, //AB CD ,点E 为线段AD 的中点.延长CE 交AB 于点F (或交BA 延长线于点F ),则EDC EAF ∆≅∆.小结 若按“中点型”来倍长,则需证明点F 在AB 上,为了避免证明三点共线,点F 就直接通过延长相交得到.因为有平行线,内错角相等,故根据“AAS ”或“ASA ”证明全等.这里“中点+平行线型”可以看做是“中点型”的改良版.【专题训练】一、解答题(共14小题)1.小明遇到这样一个问题,如图1,△ABC 中,AB =7,AC =5,点D 为BC 的中点,求AD 的取值范围.小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.请回答:(1)小明证明△BED≌△CAD用到的判定定理是:(用字母表示)(2)AD的取值范围是小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.参考小明思考问题的方法,解决问题:如图3,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=2,BF=4,∠GEF=90°,求GF的长.【答案】【第1空】SAS【第2空】1<AD<6【解答】解:(1)如图2中,延长AD到E,使DE=AD,连接BE.在△BED和△CAD中,,∴△BED≌△CAD(SAS).(2)∵△BED≌△CAD,∴BE=AC=5,∵AB=7,∴2<AE<12,∴2<2AD<12,∴1<AD<6.故答案分别为SAS,1<AD<6.解决问题:如图3中,解:延长GE交CB的延长线于M.∵四边形ABCD是正方形,∴AD∥CM,∴∠AGE=∠M,在△AEG和△BEM中,,∴△AEG≌△BEM,∴GE=EM,AG=BM=2,∵EF⊥MG,∴FG=FM,∵BF=4,∴MF=BF+BM=2+4=6,∴GF=FM=6.【知识点】四边形综合题2.自主学习,学以致用先阅读,再回答问题:如图1,已知△ABC中,AD为中线.延长AD至E,使DE=AD.在△ABD 和△ECD中,AD=DE,∠ADB=∠EDC,BD=CD,所以,△ABD≌△ECD(SAS),进一步可得到AB=CE,AB∥CE等结论.在已知三角形的中线时,我们经常用“倍长中线”的辅助线来构造全等三角形,并进一步解决一些相关的计算或证明题.解决问题:如图2,在△ABC中,AD是三角形的中线,F为AD上一点,且BF=AC,连结并延长BF交AC于点E,求证:AE=EF.【解答】证明:延长AD到G,使DF=DG,连接CG,∵AD是中线,∴BD=DC,在△BDF和△CDG中∴△BDF≌△CDG,∴BF=CG,∠BFD=∠G,∵∠AFE=∠BFD,∴∠AFE=∠G,∵BF=CG,BF=AC,∴CG=AC,∴∠G=∠CAF,∴∠AFE=∠CAF,∴AE=EF.【知识点】全等三角形的判定与性质3.阅读并解答问题.如图,已知:AD为△ABC的中线,求证:AB+AC>2AD.证明:延长AD至E使得DE=AD,连接EC,则AE=2AD ∵AD为△ABC的中线∴BD=CD在△ABD和△CED中,∴△ABD≌△CED∴AB=EC在△ACE中,根据三角形的三边关系有AC+EC AE而AB=EC,AE=2AD∴AB+AC>2AD这种辅助线方法,我们称为“倍长中线法”,请利用这种方法解决以下问题:(1)如图,已知:CD为Rt△ABC的中线,∠ACB=90°,求证:CD=;(2)把(1)中的结论用简洁的语言描述出来.【答案】>【解答】解:(1)证明:延长CD至E使DE=CD,连接EB,AE.∵CD为Rt△ABC的中线,∴AD=CD,∵CD=DE,∠ADC=∠EDB,∴△ADC≌△EDB,∴∠ACD=∠DEB,AC=BE,∴AC∥BE,∴四边形ACBE是平行四边形,又∵∠ACB=90°,∴平行四边形ACBE是矩形,∴AB=CE,CD=DE=AD=BD,∴CD=AB;(2)直角三角形斜边上的中线等于斜边的一半.【知识点】直角三角形斜边上的中线、全等三角形的判定与性质4.我们定义:如图1,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△AB'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.特例感知:(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=BC;②如图3,当∠BAC=90°,BC=8时,则AD长为.猜想论证:(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.拓展应用(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2,AB=2.在四边形内部是否存在点P,使△PDC是△P AB的“旋补三角形”?若存在,给予证明,并求△P AB的“旋补中线”长;若不存在,说明理由.【解答】解:(1)①如图2中,∵△ABC是等边三角形,∴AB=BC=AC=AB′=AC′,∵DB′=DC′,∴AD⊥B′C′,∵∠BAC=60°,∠BAC+∠B′AC′=180°,∴∠B′AC′=120°,∴∠B′=∠C′=30°,∴AD=AB′=BC,故答案为.②如图3中,∵∠BAC=90°,∠BAC+∠B′AC′=180°,∴∠B′AC′=∠BAC=90°,∵AB=AB′,AC=AC′,∴△BAC≌△B′AC′,∴BC=B′C′,∵B′D=DC′,∴AD=B′C′=BC=4,故答案为4.(2)结论:AD=BC.理由:如图1中,延长AD到M,使得AD=DM,连接B′M,C′M∵B′D=DC′,AD=DM,∴四边形AC′MB′是平行四边形,∴AC′=B′M=AC,∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,∴∠BAC=∠MB′A,∵AB=AB′,∴△BAC≌△AB′M,∴BC=AM,∴AD=BC.(3)存在.理由:如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接P A、PD、PC,作△PCD的中线PN.连接DF交PC于O.∵∠ADC=150°,∴∠MDC=30°,在Rt△DCM中,∵CD=2,∠DCM=90°,∠MDC=30°,∴CM=2,DM=4,∠M=60°,在Rt△BEM中,∵∠BEM=90°,BM=14,∠MBE=30°,∴EM=BM=7,∴DE=EM﹣DM=3,∵AD=6,∴AE=DE,∵BE⊥AD,∴P A=PD,PB=PC,在Rt△CDF中,∵CD=2,CF=6,∴tan∠CDF=,∴∠CDF=60°∴∠ADF=90°=∠AEB,∴∠CBE=∠CFD,∵∠CBE=∠PCF,∴∠CFD=∠PCF,∵∠CFD+∠CDF=90°,∠PCF+∠CPF=90°,∴∠CPF=∠CDF=60°=∠CDF易证△FCP≌△CFD,∴CD=PF,∵CD∥PF,∴四边形CDPF是矩形,∴∠CDP=90°,∴∠ADP=∠ADC﹣∠CDP=60°,∴△ADP是等边三角形,∴∠ADP=60°,∵∠BPF=∠CPF=60°,∴∠BPC=120°,∴∠APD+∠BPC=180°,∴△PDC是△P AB的“旋补三角形”,∵AB=2.∴△P AB的“旋补中线”长=AB=.【知识点】四边形综合题5.我们定义:如果两个三角形的两组对应边相等,且它们的夹角互补,我们就把其中一个三角形叫做另一个三角形的“夹补三角形”,同时把第三边的中线叫做“夹补中线.例如:图1中,△ABC 与△ADE的对应边AB=AD,AC=AE,∠BAC+∠DAE=180°,AF是DE边的中线,则△ADE 就是△ABC的“夹补三角形”,AF叫做△ABC的“夹补中线”.特例感知:(1)如图2、图3中,△ABC与△ADE是一对“夹补三角形”,AF是△ABC的“夹补中线”;①当△ABC是一个等边三角形时,AF与BC的数量关系是:;②如图3当△ABC是直角三角形时,∠BAC=90°,BC=a时,则AF的长是;猜想论证:(2)在图1中,当△ABC为任意三角形时,猜想AF与BC的关系,并给予证明.拓展应用:(3)如图4,在四边形ABCD中,∠DCB=90°,∠ADC=150°,BC=2AD=6,CD=,若△P AD是等边三角形,求证:△PCD是△PBA的“夹补三角形”,并求出它们的“夹补中线”的长.【解答】解:(1)∵△ABC与△ADE是一对“夹补三角形”,∴AB=AD,AC=AE,∠BAC+∠DAE=180°,①∵△ABC是等边三角形,∴AB=AC=BC,∠BAC=60°∴AD=AE=AB=AC,∠DAE=120°,∴∠ADE=30°,∵AF是“夹补中线”,∴DF=EF,∴AF⊥DE,在Rt△ADF中,AF=AD=AB=BC,故答案为:AF=BC;②当△ABC是直角三角形时,∠BAC=90°,∵∠DAE=90°=∠BAC,易证,△ABC≌△ADE,∴DE=BC,∵AF是“夹补中线”,∴DF=EF,∴AF=DE=BC=a,故答案为a;(2)解:猜想:AF=BC,理由:如图1,延长DA到G,使AG=AD,连EG∵△ABC与△ADE是一对“夹补三角形”,∴AB=AD,AC=AE,∠BAC+∠DAE=180°,∴AG=AB,∠EAG=∠BAC,AE=AC,∴△AEG≌△ACB,∴EG=BC,∵AF是“夹补中线”,∴DF=EF,∴AF=EG,∴AF=BC;(3)证明:如图4,∵△P AD是等边三角形,∴DP=AD=3,∠ADP=∠APD=60°,∵∠ADC=150°,∴∠PDC=90°,作PH⊥BC于H,∵∠BCD=90°∴四边形PHCD是矩形,∴CH=PD=3,∴BH=6﹣3=3=CH,∴PC=PB,在Rt△PCD中,tan∠DPC==,∴∠DPC=30°∴∠CPH=∠BPH=60°,∠APB=360°﹣∠APD﹣∠DPC﹣∠BPC=150°,∴∠APB+∠CPD=180°,∵DP=AP,PC=PB,∴△PCD是△PBA的“夹补三角形”,由(2)知,CD=,∴△P AB的“夹补中线”==.【知识点】四边形综合题6.如图1,在△ABC中,点D是BC的中点,延长AD到点G,使DG=AD,连接CG,可以得到△ABD≌△GCD,这种作辅助线的方法我们通常叫做“倍长中线法”.如图2,在△ABC中,点D是BC的中点,点E是AB上一点,连接ED,小明由图1中作辅助线的方法想到:延长ED到点G,使DG=ED,连接CG.(1)请直接写出线段BE和CG的关系:;(2)如图3,若∠A=90°,过点D作DF⊥DE交AC于点F,连接EF,已知BE=3,CF=2,其它条件不变,求EF的长.【答案】BE=CG【解答】解:(1)∵点D是BC的中点,∴BD=CD,在△EBD和△GCD中,∵,∴△EBD≌△GCD(SAS),∴BE=CG,故答案为:BE=CG;(2)如图,连接GF,由(1)知△EBD≌△GCD,∴∠B=∠GCD,BE=CG=3,又∵∠A=90°,∴∠B+∠BCA=90°,∴∠GCD+∠BCA=90°,即∠GCF=90°,∵CG=3,CF=2,∴FG==,∵DF⊥DE,且DE=DG,∴EF=FG=.【知识点】全等三角形的判定与性质7.[方法呈现](1)如图①,△ABC中,AD为中线,已知AB=3,AC=5,求中线AD长的取值范围.解决此问题可以用如下方法:延长AD至点E,使DE=AD,连结CE,则易证△DEC≌△DAB,得到EC=AB=3,则可得AC﹣CE<AE<AC+CE,从而可得中线AD长的取值范围是.[探究应用](2)如图②,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系,并写出完整的证明过程.(3)如图③,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.【答案】2<AD<8【解答】解:(1)由题意知AC﹣CE<AE<AC+CE,即5﹣4<AD<5+3,∴2<AD<8,故答案为:2<AD<8;(2)如图②,延长AE,DC交于点F,∵AB∥CD,∴∠BAF=∠F,在△ABE和△FCE中CE=BE,∠BAF=∠F,∠AEB=∠FEC,∴△ABE≌△FEC(AAS),∴CF=AB,∵AE是∠BAD的平分线,∴∠BAF=∠F AD,∴∠F AD=∠F,∴AD=DF,∵DC+CF=DF,∴DC+AB=AD.(3)如图③,延长AE,DF交于点G,同(2)可得:AF=FG,△ABE≌△GEC,∴AB=CG,∴AF+CF=AB.【知识点】四边形综合题8.数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在△ABC中,AB=8,AC=6,D是BC的中点,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,请补充完整证明“△ADC≌△EDB”的推理过程.(1)求证:△ADC≌△EDB证明:∵延长AD到点E,使DE=AD在△ADC和△EDB中AD=ED(已作)∠ADC=∠EDB()CD=BD(中点定义)∴△ADC≌△EDB()(2)探究得出AD的取值范围是;【感悟】解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】(3)如图2,△ABC中,∠B=90°,AB=2,AD是△ABC的中线,CE⊥BC,CE=4,且∠ADE =90°,求AE的长.【答案】【第1空】对顶角相等【第2空】SAS【第3空】1<AD<7【解答】解:(1)证明:延长AD到点E,使DE=AD,在△ADC和△EDB中,AD=ED(已作),∠ADC=∠EDB(对顶角相等),CD=BD(中点定义),∴△ADC≌△EDB(SAS),故答案为:对顶角相等,SAS;(2)∵△ADC≌△EDB,∴BE=AC=6,8﹣6<AE<8+6,∴1<AD<7,故答案为:1<AD<7;(3)延长AD交EC的延长线于F,∵AB⊥BC,EF⊥BC,∴∠ABD=∠FCD,在△ABD和△FCD中,,∴△ABD≌△FCD,∴CF=AB=2,AD=DF,∵∠ADE=90°,∴AE=EF,∵EF=CE+CF=CE+AB=4+2=6,∴AE=6.【知识点】三角形综合题9.我们定义:在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△AB'C'叫△ABC的“旋补三角形”,△AB'C'的边B'C'上的中线AD叫做△ABC的“旋补中线”.下面各图中,△AB'C'均是△ABC的“旋补三角形”,AD均是△ABC的“旋补中线”.(1)如图1,若△ABC为等边三角形,BC=8,则AD的长等于;(2)如图2,若∠BAC=90°,求证:AD=BC;(3)如图3,若△ABC为任意三角形,(2)中结论还成立吗?如果成立,给予证明;如果不成立,说明理由.【解答】解:(1)如图1中,∵△ABC是等边三角形,∴AB=BC=AC=AB′=AC′,∵DB′=DC′,∴AD⊥B′C′,∵∠BAC=60°,∠BAC+∠B′AC′=180°,∴∠B′AC′=120°,∴∠B′=∠C′=30°,∴AD=AB′=BC=4,(2)证明:如图2中,∵AB绕点A旋转得到AB',AC绕点A旋转得到AC',∴AB′=AB,AC'=AC,∵∠BAC=90°,α+β=180°,∠B′AC′=360°﹣(α+β)﹣∠BAC,∴∠B′AC′=360°﹣180°﹣90°=90°,∴∠BAC=∠B′AC′,∴△BAC≌△B′AC′(SAS)∴BC=B′C′,∵AD是△AB'C'边B'C'上的中线,∠B′AC′=90°.∴AD=B′C′.∴AD=BC.(3)结论AD=BC成立.理由:如图3中,延长AD到A′,使得AD=DA′,连接B′A′,C′A′.∴AD=AA′,∵B′D=DC′,AD=DA′,∴四边形AB′A′C′是平行四边形,∴AC′=B′A′=AC,∵∠BAC+∠B′AC′=360°﹣180°=180°,∠B′AC′+∠AB′M=180°,∴∠BAC=∠AB′A′,∵AB=AB′,∴△BAC≌△AB′A′(SAS)∴BC=AA′,∴AD=BC.【知识点】几何变换综合题10.阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理﹣﹣“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:AB2+AC2=2AD2+2BD2.小明尝试对它进行证明,部分过程如下:解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,同理可得:AC2=AE2+CE2,AD2=AE2+DE2,为证明的方便,不妨设BD=CD=x,DE=y,∴AB2+AC2=AE2+BE2+AE2+CE2=…(1)请你完成小明剩余的证明过程;理解运用:(2)①在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=;②如图3,⊙O的半径为6,点A在圆内,且OA=2,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为;拓展延伸:(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5,以A (﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.【解答】解:(1)过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,同理可得:AC2=AE2+CE2,AD2=AE2+DE2,为证明的方便,不妨设BD=CD=x,DE=y,∴AB2+AC2=2AE2+(x+y)2+(x﹣y)=2AE2+2x2+2y2、=2AE2+2BD2+2DE2=2AD2+2BD2.(2)①∵AB2+AC2=2AD2+2BD2,∴62+42=2AD2+2×42,∴AD=②如图3中,∵AF是△ABC的中线,EF是△AEO的中线,OF是△BOC的中线,∵2EF2+2AE2=AF2+OF2,2AF2+2BF2=AB2+AC2,OF2=OB2﹣BF2,∴4EF2=2OB2﹣4AE2=2OB2﹣OA2,∴EF2=OB2﹣OA2=16,∴EF=4(负根以及舍弃),故答案为.4.(3)如图4中,连接OA,取OA的中点E,连接DE.由(2)的②可知:DE═OB2﹣OA2=,在△ADE中,AE=,DE=,∵AD≤AE+DE,∴AD长的最大值为+=10.【知识点】圆的综合题11.[问题提出]如图①,在△ABC中,若AB=6,AC=4,求BC边上的中线AD的取值范围.[问题解决]解决此问题可以用如下方法,延长AD到点E使DE=AD,再连结BE(或将△ACD绕着点D逆时针装转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断,由此得出中线AD的取值范围是[应用]如图②,如图,在△ABC中,D为边BC的中点,已知AB=5,AC=3,AD=2.求BC的长[拓展]如图③,在△ABC中,∠A=90°,点D是边BC的中点,点E在边AB上,过点D作DF⊥DE交边AC于点F,连结EF,已知BE=4,CF=5,则EF的长为【解答】解:(1)在△DAC和△DEB中,,∴△DAC≌△DEB(SAS),∴AC=EB=4,∵AB﹣BE<AE<AB+BE,AB=6,∴2<AE<10,∴1<AD<5,故答案为:1<AD<5;(2)延长AD到E,使得AD=DE,连接BE,如图②,在△DAC和△DEB中,,∴△DAC≌△DEB(SAS),∴AC=EB=3,∵AE=2AD=4,AB=5,∴BE2+AE2=AB2,∴∠AEB=90°,∴BD=,∴BC=2BD=2;(3)延长FD到G,使得DG=FD,连接BG,EG,如图③,在△BDG和△CDF中,,∴△BDG≌△CDF(SAS),∴BG=CF=5,DG=DF,∠DBG=∠DCF,∵DE⊥DF,∴EG=EF,∵∠A=90°,∴∠ABC+∠ACB=90°,∴∠ABC+∠DBG=90°,∴EG=,∴EF=,故答案为:.【知识点】全等三角形的判定与性质、直角三角形斜边上的中线、垂线段最短、三角形三边关系、解直角三角形12.我们定义:如图1,在△ABC看,把AB绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.特例感知:(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=BC;②如图3,当∠BAC=90°,BC=8时,则AD长为.猜想论证:(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.【解答】解:(1)①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=BC;理由:∵△ABC是等边三角形,∴AB=BC=AC=AB′=AC′,∵DB′=DC′,∴AD⊥B′C′,∵∠BAC=60°,∠BAC+∠B′AC′=180°,∴∠B′AC′=120°,∴∠B′=∠C′=30°,∴AD=AB′=BC,故答案为.②如图3,当∠BAC=90°,BC=8时,则AD长为4.理由:∵∠BAC=90°,∠BAC+∠B′AC′=180°,∴∠B′AC′=∠BAC=90°,∵AB=AB′,AC=AC′,∴△BAC≌△B′AC′,∴BC=B′C′,∵B′D=DC′,∴AD=B′C′=BC=4,故答案为4.(2)猜想.证明:如图,延长AD至点Q,则△DQB'≌△DAC',∴QB'=AC',QB'∥AC',∴∠QB'A+∠B'AC'=180°,∵∠BAC+∠B'AC'=180°,∴∠QB'A=∠BAC,又由题意得到QB'=AC'=AC,AB'=AB,∴△AQB'≌△BCA,∴AQ=BC=2AD,即.【知识点】几何变换综合题13.如图1,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM(点D与点A重合除外)上时,以CD为一边且在CD的下方作等边△CDE,连接BE.(1)判断AD与BE是否相等,请说明理由;(2)如图2,若AB=8,点P、Q两点在直线BE上且CP=CQ=5,试求PQ的长;(3)在第(2)小题的条件下,当点D在线段AM的延长线(或反向延长线)上时.判断PQ的长是否为定值,若是请直接写出PQ的长;若不是请简单说明理由.【解答】解:(1)AD=BE.理由如下:∵△ABC,△CDE都是等边三角形,∴AC=BC,CD=CE,∵∠ACD+∠BCD=∠ACB=60°,∠BCE+∠BCD=∠DCE=60°,∴∠ACD=∠BCE,在△ACD和△BCE中,∵,∴△ACD≌△BCE(SAS),∴AD=BE;(2)如图,过点C作CN⊥BQ于点N,∵CP=CQ,∴PQ=2PN,∵△ABC是等边三角形,AM是中线,∴CM⊥AD,CM=BC=×8=4,∴CN=CM=4(全等三角形对应边上的高相等),∵CP=CQ=5,∴PN===3,∴PQ=2PN=2×3=6;(3)PQ的长为定值6.∵点D在线段AM的延长线(或反向延长线)上时,△ACD和△BCE全等,∴对应边AD、BE上的高线对应相等,∴CN=CM=4是定值,∴PQ的长是定值.【知识点】全等三角形的判定与性质、等边三角形的性质14.我们定义:如图1,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)并缩短一半得到AB',把AC绕点A逆时针旋转β并缩短一半得到AC',连接B'C'.当α+β=180°时,我们称△AB'C'是△ABC的“旋半三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋半中线”,点A 叫做“旋半中心”.特例感知:(1)在图2,图3中,△AB'C'是△ABC的“旋半三角形”,AD是△ABC的“旋半中线”.①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=BC;②如图3,当∠BAC=90°,BC=4时,则AD长为.猜想论证:(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.拓展应用:(3)如图4,在平面直角坐标系中,△ABC的坐标分别是A(4,3),B(1,0),C(5,0),△AB′C′是△ABC的“旋半三角形”,AD是△ABC的“旋半中线”,连结OD,求OD的最大值是多少?并请直接写出当OD最大时点D的坐标.【解答】解:(1)①如图2中,∵△ABC是等边三角形,∴AB=BC=AC=2AB′=2AC′,∵DB′=DC′,∴AD⊥B′C′,∵∠BAC=60°,∠BAC+∠B′AC′=180°,∴∠B′AC′=120°,∴∠B′=∠C′=30°,∴AD=AB′=BC,故答案为:.②如图3中,∵∠BAC=90°,∠BAC+∠B′AC′=180°,∴∠B′AC′=∠BAC=90°,∵AB=AB′,AC=AC′,∴△BAC∽△B′AC′,∴BC=2B′C′,∵B′D=DC′,∴AD=B′C′=BC==1,故答案为:1;(2)结论:AD=BC.理由:如图1中,延长AD到M,使得AD=DM,连接B′M,C′M∵B′D=DC′,AD=DM,∴四边形AC′MB′是平行四边形,∴AC′=B′M=AC,∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,∴∠BAC=∠MB′A,∵AB=AB′,∴△BAC∽△AB′M,∴BC=2AM,∴AD=BC.(3)如图4,∵AD=BC,BC=4,∴AD=1,∴D在以A为圆心,以1为半径的圆上,∴当D运动到直线OA与半圆相交时OD最大,∵A(4,3),∴OA=5,∵AD=1,∴OD的最大值是6.过A作AE⊥x轴于E,过D作DF⊥x轴于F,∴AE∥DF,∴△AOE∽△DOF,∴==,∵OE=4,AE=3,∴OF=,DF=,∴D(,).【知识点】几何变换综合题。
倍长中线法

几何模型02——倍长中线法当线段出现一个中点时,特别是三角形中,常常采用“倍长中线法”添加辅助线.倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法. 倍长中线法:△ABC 中AD 是BC 边中线方式1: 延长AD 到E , 使DE=AD ,连接BE例1.已知:如图,AD 是△ABC 的中线,求证:AB +AC >2AD .证明:延长AD 到M ,使DM =AD ,连接BM ,CM ,∵AD 是△ABC 的中线,∴BD =DC ,∵AD =DM ,∴四边形ABMC 是平行四边形,∴BM =AC ,在△ABM 中,AB +BM >AM ,即AB +AC >2AD .例2.已知,如图△ABC 中,AB =5,AC =3,则中线AD 的取值范围是 . 解:延长AD 到点E ,使AD =ED ,连接CE ,∵AD 是△ABC 的中线,∴BD =CD ,在△ABD 和△ECD 中∴△ABD ≌△ECD (SAS ),∴AB =EC ,在△AEC 中,AC +EC >AE , 且EC ﹣AC <AE ,即AB +AC >2AD ,AB ﹣AC <2AD ,∴2<2AD <8,∴1<AD <4,故答案为:1<AD <4.E D A B C练习1.如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是.例3.如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.解:延长FD至点G,使得DG=DF,连接BG,EG,∵在△CDF和△BDG中,,∴△CDF≌△BDG(SAS),∴BG=CF=4,∠C=∠DBG,∵∠C+∠ABC=90°,∴∠DBG+∠ABC=90°,即∠ABG=90°,∵DE⊥FG,DF=DG,∴EF=EG==5.练习2.如图,已知AD为△ABC的中线,DE平分∠ADB交AB于点E,DF平分∠ADC交AC于点F.求证:BE+CF>EF.练习3.如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,求GF的长.练习4.如图,在梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD 的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6.求CE的长.例4.如图,在△ABC中,AB=AC,E是AB中点,延长AB到D,使BD=BA,延长CE至F,使得EF=CE.求证:CD=2CE.证明:方法一:如右图1,取AC的中点H,连接BH,∵BD=BA,∴BH是△ACD的中位线,∴CD=2BH,又∵E是AB的中点,AB=AC,∴AE=AH=AB,在△ABH和△ACE中,,∴△ABH≌△ACE(SAS),∴CE=BH,∴CD=2CE.方法二:∵点E为AB的中点,∴BE=AE,在△BEF和△AEC中,,∴△BEF≌△AEC(SAS),∴BF=AC,∠EBF=∠A,∵AB=AC=BD,∴∠ACB=∠ABC,BF=BD,∵∠CBD=∠A+∠ACB,∠CBF=∠ABC+∠EBF,∴∠CBD=∠CBF,在△CBD和△CBF中,,∴△CBD≌△CBF(SAS),∴CD=CF,∵CF=CE+EF,CE=EF,∴CF=2CE,∴CD=2CE.练习5.已知:如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点.求证:CD=2CE练习6.已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE.练习7.如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.求证:AD是∠EAC的平分线.例5.如图,在△ABC中,AD平分∠BAC,E为BC的中点,过点E作EF∥AD 交AB于点G,交CA的延长线于点F.求证:BG=CF.证明:作CM∥AB交FE的延长线于M.∵BG∥CM,∴∠B=∠MCE,∵E是BC中点,∴BE=EC,在△BEG和△CEM中,,∴△BEG≌△CEM,∴BG=CM,∵AD∥EF,∴∠1=∠FGA,∠2=∠F,∵∠1=∠2,∴∠F=∠FGA,∵AB∥CM,∴∠FGA=∠M,∴∠F=∠M,∴CF=CM,∴BG=CF.练习8.已知:如图,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,过D 作DF∥BA交AE于点F,DF=AC.求证:AE平分∠BAC.例6.已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.证明:延长AD至点G,使得AD=DG,连接BG,CG,∵AD=DG,BD=CD,∴四边形ABGC是平行四边形,∴AC=AF=BG,AB=AE=CG,∠BAC+∠ABG=180°,∵∠EAF+∠BAC=180°,∴∠EAF=∠ABG,在△EAF和△BAG中,,∴△EAF≌△BAG(SAS),∴EF=AG,∵AG=2AD,∴EF=2AD.练习9.如图,两个正方形ABDE和ACGF,点P为BC中点,连接P A交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.方式2:间接倍长作CF ⊥AD 于F , 延长MD 到N ,作BE ⊥AD 的延长线于E 使DN=MD , 连接BE 连接CN例7.如图,△ABC 中,AB =AC ,点D 在AB 上,点E 在AC 的延长线上,DE 交BC 于F ,且DF =EF ,求证:BD =CE .证明:如图,过点D 作DG ∥AE ,交BC 于点G ;则△DGF ≌△ECF ,∴DG =CE ;∵AB =AC ,∴∠B =∠ACB ;∵DG ∥AE ,∴∠DGB =∠ACB ,∴∠DBG =∠DGB ,∴DG =BD ,∴BD =CE .练习9.如图,△ABC 中,点D 在AB 上,E 是AC 延长线上一点,BD =CE ,DE 交BC 于点F ,DF =EF ,DP ∥AE 交BC 于点P ,求证:AB =AC .F E D C B A N D C B A M课后练习1、如图1已知:AD为△ABC的中线,易证AB+AC>2AD.(1)如图2,在△ABC中,AC=5,AB=13,D为BC的中点,DA⊥AC.求△ABC的面积.(2)问题2:如图3,在△ABC中,AD是三角形的中线.点F在中线AD上,且BF=AC,连接并延长BF交AC于点E.求证AE=EF.2.已知:如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F,试探究线段AB与AF,CF之间的数量关系,并说明理由.3.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,求证:(1)AE平分∠DAB;(2)AB+CD=AD.4.在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证EG=CG且EG⊥CG.(1)将△BEF绕点B逆时针旋转90°,如图(2),证明:EG=CG且EG⊥CG.(2)如图(3)将△BEF绕点B逆时针旋转180°,证明:EG=CG且EG⊥CG.5.如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作FM∥AD交AC于F,求FC的长.6.如图所示,∠BAC=∠DAE=90°,M是BE的中点,AB=AC,AD=AE,求证:AM⊥CD.7.已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.。
和三角形中线有关的题型的证法—倍长中线法
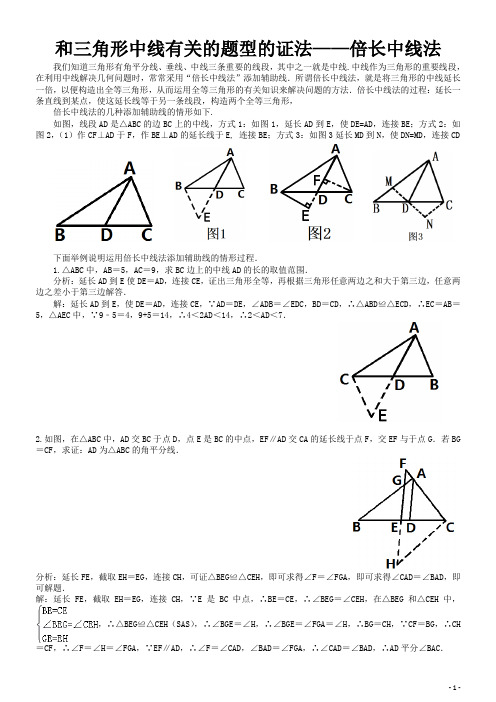
和三角形中线有关的题型的证法——倍长中线法我们知道三角形有角平分线、垂线、中线三条重要的线段,其中之一就是中线.中线作为三角形的重要线段,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长一条直线到某点,使这延长线等于另一条线段,构造两个全等三角形,倍长中线法的几种添加辅助线的情形如下.如图,线段AD是△ABC的边BC上的中线,方式1:如图1,延长AD到E,使DE=AD,连接BE;方式2:如图2,(1)作CF⊥AD于F,作BE⊥AD的延长线于E, 连接BE;方式3:如图3延长MD到N,使DN=MD,连接CD下面举例说明运用倍长中线法添加辅助线的情形过程.1.△ABC中,AB=5,AC=9,求BC边上的中线AD的长的取值范围.分析:延长AD到E使DE=AD,连接CE,证出三角形全等,再根据三角形任意两边之和大于第三边,任意两边之差小于第三边解答.解:延长AD到E,使DE=AD,连接CE,∵AD=DE,∠ADB=∠EDC,BD=CD,∴△ABD≌△ECD,∴EC=AB=5,△AEC中,∵9﹣5=4,9+5=14,∴4<2AD<14,∴2<AD<7.2.如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交EF与于点G.若BG =CF,求证:AD为△ABC的角平分线.分析:延长FE,截取EH=EG,连接CH,可证△BEG≌△CEH,即可求得∠F=∠FGA,即可求得∠CAD=∠BAD,即可解题.解:延长FE,截取EH=EG,连接CH,∵E是BC中点,∴BE=CE,∴∠BEG=∠CEH,在△BEG和△CEH中,,∴△BEG≌△CEH(SAS),∴∠BGE=∠H,∴∠BGE=∠FGA=∠H,∴BG=CH,∵CF=BG,∴CH =CF,∴∠F=∠H=∠FGA,∵EF∥AD,∴∠F=∠CAD,∠BAD=∠FGA,∴∠CAD=∠BAD,∴AD平分∠BAC.3.如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=900,连接DE,DF,EF.(1)求∠ECF的度数;(2)求证:△DEF为等腰直角三角形.分析:(1)先依据等腰直角三角形的性质求得∠ECA、∠FCB的度数,然后依据∠ECA+∠ECF+∠FCB=180°求解即可;(2)延长ED到点G,使得DG=DE,连接BG,FG,然后依据SAS证明△EDA≌△GDB,接下来依据SAS证明△ECF≌△GBF,最后再证明△EFD≌△GFD,从而可证明△DEF为等腰直角三角形.解:(1)∵△ACE和△CBF均为等腰直角三角形,∴∠ECA=450,∠FCB=450.∵∠ECA+∠ECF+∠FCB=1800,∴∠ECF=900.(2)证明:延长ED到点G,使得DG=DE,连接BG,FG.∵D为线段AB的中点,∴AD=BD.∵在△EDA和△GDB中,,∴△EDA≌△GDB(SAS).∴EA=GB,∠A=∠GBD=450.∵△ACE与△BCF是等腰直角三角形∴CF=FB,AE=EC,∠A=∠ECA=∠FCB=∠FBC=450.∴CF=FB,EC=BG,∠ECF=900.∵在△ECF和△GBF中,,∴△ECF≌△GBF(SAS).∴EF=GF,∠EFC=∠GFB.∵∠CFB=∠CFG+∠GFB=900,∴∠EFG=∠EFC+∠CFG=900.∵在△EFD和△GFD中,,∴△EFD≌△GFD.∴∠EDF=∠GDF=900,∠EFD=∠GFD=450.∴ED=DF,∴△DEF为等腰直角三角形.4.如图,由△ABC的顶点A引一条射线AD,与边BC交于D点,作BE⊥AD于点E,CF⊥AD于点F,为了使BE=CF,射线AD应该具有什么性质?分析:当射线AD是BC的中线时,BE=CF,可通过证明△BED≌△CFD证明.解:当射线AD是BC的中线时,BE=CF.理由如下:∵BE⊥AD,CF⊥AD,垂足分别为E,F,∴∠BED=∠CFD=900,∵D是BC中点,∴BD=CD,∵∠BDE=∠CFD,在△BED和△CFD中,,∴△BED≌△CFD(AAS),∴BE=CF.5.如图,在△ABC中,D是BC边上的一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.(1)求证:AD是△ABC的中线;(2)如果AB=4,AC=6,S△ABC=10,AD长为偶数,求BE的长.分析:(1)欲证明AD 是△ABC 的中线,只要证明BD =CD ,即证明△BED ≌△CFD 即可;(2)S △ABC =10,S △ABD =AD ·BE ÷2=5,求出AD 可取的数,BE 长的结果就求出来了.解:(1)证明:∵BE ⊥AD ,CF ⊥AD ,∴∠BED =∠F =90°,在△BED 和△CFD 中,,∴△BED ≌△CFD ,∴BD =CD ,∴AD 是△ABC 的中线;(2)延长AF 至G ,使DG=AD ,连接CG ,易证△CGD ≌△BAD ,∴CG=AB=4,∵AC=6,∴AG 的取值范围是2<AG <10,∴1<AG <5,∵AG 为偶数,∴AG 可取2或4,∵S △ABC =10,BD=CD ,∴S △ABD =AD ·BE ÷2=5,∴BE=5或2.56.如图,△ABC 中,AB =AC ,点D 在AB 上,点E 在AC 的延长线上,DE 交BC 于F ,且DF =EF ,求证:BD =CE .分析:如图,作辅助线;证明△DGF ∽△ECF ,得到DG =CE ,此为解决该问题的关键性结论;证明BD =GD ,即可解决问题.证明:如图,过点D 作DG ∥AE ,交BC 于点G ;则△DGF ∽△ECF ,∴DG :CE =DF :EF ,而DF =EF ,∴DG =CE ;∵AB =AC ,∴∠B =∠ACB ;∵DG ∥AE ,∴∠DGB =∠ACB ,∴∠DBG =∠DGB ,∴DG =BD ,∴BD =CE .7.已知:在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE =AC ,延长BE 交AC 于F ,求证:AF =EF .分析:根据点D 是BC 的中点,延长AD 到点G ,得到△ADC ≌△GDB ,利用全等三角形的对应角相等,对应边相等进行等量代换,得到△AEF 中的两个角相等,然后用等角对等边证明AE 等于EF .证明:如图,延长AD 到点G ,使得AD =DG ,连接BG .∵AD 是BC 边上的中线(已知),∴DC =DB ,在△ADC 和△GDB 中,⎪⎩⎪⎨⎧=∠=∠=DB DC GDB ADC DGAD ,∴△ADC ≌△GDB (SAS ),∴∠CAD =∠G ,BG =AC ,又∵BE =AC ,∴BE =BG ,∴∠BED =∠G ,∵∠BED =∠AEF ,∴∠AEF =∠CAD ,即:∠AEF =∠FAE ,∴AF =EF .8.如图,CE 、CB 分别是△ABC 与△ADC 的中线,且∠ACB =∠ABC .求证:CD =2CE分析:过B 作BF ∥AC 交CE 的延长线于F ,由E 为AB 中点,得到AE =EB ,再由BF 与AC 平行,得到两对内错角相等,利用AAS 得到三角形ACE 与三角形BFE 全等,利用全等三角形的对应边相等得到CE =EF ,AC =BF ,即CF =2CE ,再由已知角相等,利用等角对等边得到AC =AB ,根据B 为AD 中点,得到AC =AB =BD =BF ,利用外角性质及等量代换得到夹角相等,利用SAS 得到三角形CBD 与三角形CBF 全等,利用全等三角形对应边相等得到CD =CF ,等量代换即可得证.证明:过B作BF∥AC交CE的延长线于F,∵CE是中线,BF∥AC,∴AE=BE,∠A=∠ABF,∠ACE=∠F,在△ACE 和△BFE中,,∴△ACE≌△BFE(AAS),∴CE=EF,AC=BF,∴CF=2CE,又∵∠ACB=∠ABC,CB 是△ADC的中线,∴AC=AB=BD=BF,∵∠DBC=∠A+∠ACB=∠ABF+∠ABC,∴∠DBC=∠FBC,在△DBC和△FBC 中,,∴△DBC≌△FBC(SAS),∴DC=CF=2CE.9.如图,△ABC中,点D是BC的中点,点E、F分别在AB、AC上,且DE⊥DF,求证:BE+CF>EF.分析:如图,延长ED使得DM=DE,连接FM,CM.由△BDE≌△CDM(SAS),推出BE=CM,由DE=DM,DF⊥EM,推出FE=FM,在△FCM中利用三边关系定理即可解决问题;证明:如图,延长ED使得DM=DE,连接FM,CM.∵BD=DC,∠BDE=∠CDM,DE=DM,∴△BDE≌△CDM(SAS),∴BE=CM,∵DE=DM,DF⊥EM,∴FE=FM,∵CM+CF>FM,∴BE+CF>EF.10.如图,AB=AE,AB⊥AE,AD=AC.AD⊥AC,点M为BC的中点,求证:DE=2AM.分析:延长AM至N,使MN=AM,证△AMC≌△NMB,推出AC=BN=AD,求出∠EAD=∠ABN,证△EAD≌△ABN即可.证明:延长AM至N,使MN=AM,连接BN,∵点M为BC的中点,∴CM=BM,在△AMC和△NMB中∴△AMC≌△NMB(SAS),∴AC=BN,∠C=∠NBM,∵AB⊥AE,AD⊥AC,∴∠EAB=∠DAC=900,∴∠EAD+∠BAC=1800,∴∠ABN=∠ABC+∠C=1800﹣∠BAC=∠EAD,在△EAD和△ABN中,∵,∴△ABN≌△EAD (SAS),∴DE=AN=2MN.跟踪练习:1.如图,AD为△ABC中BC边上的中线(AB>AC)(1)求证:AB﹣AC<2AD<AB+AC;(2)若AB=8cm,AC=5cm,求AD的取值范围.2.如图,∠ACB=900,D是AB中点,连接CD,求证:CD=AB/23.△ABC中,D为BC的中点,AB=5,AD=6,AC=13,试判断AD与AB的位置关系4.如图,在△ABC中,AD为BC上的中线,E为AC的一点,BE与AD交于点F,若AE=EF,求证:AC=BF5.如图,△ABC中,∠A=900,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长6.如图,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,过D作DF∥BA交AE于点F,DF=AC.求证:AE平分∠BAC.7.如图,AD是△ABC的中线,(1)求证:AB+AC>2AD;(2)过点D作DE∥AB交AC于E,过点D作DF∥AC交AB于F,求证:DE=AB.8.已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.9.阅读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.求证:AB=CD.分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.10.如图,在△ABC中,∠B=60°,CE、AF是△ABC的角平分线,交于点O,求证:AC=AE+CF.11.如图,AB⊥AC,AB=AC,AD⊥AE,AE=AD,F为CD的中点,探究BE与AF的关系,并给出你的证明.跟踪练习答案1.(1)证明:如图延长AD至E,使AD=DE,连接BE.在△ACD和△EBD中,,∴△ACD≌△EBD(SAS),∴AC=BE(全等三角形的对应边相等),在△ABE中,由三角形的三边关系可得AB﹣AC<AE<AB+BE,即AB﹣AC <2AD<AB+AC;(2)解:∵AB=8cm,AC=5cm,∴8﹣5<2AD<8+5,∴<AD<.2.证明:延长CD至P,使D为CP中点,连接AP.∵DP=DC,DA=DB,∠ADP=∠CDB,∴△ADP≌△BDC,∴AP=BC,∠P=∠PCB∵∠PCB+∠ACP=900,∴∠P+∠ACP=900,∴∠CAP=900,∴∠CAP=∠ACB.在△ACP与△ABC中,AP=BC,AC=AC,∠CAP=∠ACB,∴△ACP≌△CAB,∴CP=AB,∵CD=CP/2,∴CD=AB/23.解:延长AD至E,使得AD=DE,连接BE,∵D为BC的中点,∴BD=CD,在△ADC和△EDB中,,∴△ADC≌△EDB(SAS),∴EB=AC=13,∵AD=6,∴AE=12,∵52+122=132,∴AB2+AE2=EB2,∴∠BAE=90°,∴AD⊥AB.4.分析:延长AD至G,使DG=AD,连接BG,可证明△BDG≌△CDA(SAS),则BG=AC,∠CAD=∠G,根据AE=EF,得∠CAD=∠AFE,可证出∠G=∠BFG,即得出AC=BF.∴△BDG≌△CDA(SAS),证明:延长AD至G,使DG=AD,连接BG,在△BDG和△CDA中,∵,∴BG=AC,∠CAD=∠G.又∵AE=EF,∴∠CAD=∠AFE .又∠BFG=∠AFE,∴∠CAD=∠BFG,∴∠G=∠BFG,∴BG=BF,∴AC=BF.5.分析:延长FD至点G,使得DG=DF,连接BG,EG,易证△CDF≌△BDG,可得BG=CF=4,∠C=∠DBG,可证明∠ABG=900,再根据等腰三角形底边三线合一性质可得EF=EG,即可求得EF的长,即可解题.解:延长FD至点G,使得DG=DF,连接BG,EG,∵在△CDF和△BDG中,,∴△CDF≌△BDG(SAS),∴BG=CF=4,∠C=∠DBG,∵∠C+∠ABC=900,∴∠DBG+∠ABC=900,即∠ABG=900,∵DE⊥FG,DF=DG,∴EF=EG ==5.6.分析:延长FE 到G ,使EG =EF .连接CG ,由于已知条件通过SAS 证得△DEF ≌△CEG 得到DF =GC ,∠DFE =∠G ,由平行线的性质和已知条件得到∠G =∠CAE ,故有∠BAE =∠CAE ,结论可得.证明:如图,延长FE 到G ,使EG =EF ,连接CG .在△DEF 和△CEG 中,∵,∴△DEF ≌△CEG .∴DF =GC ,∠DFE =∠G .∵DF ∥AB ,∴∠DFE =∠BAE .∵DF =AC ,∴GC =AC .∴∠G =∠CAE .∴∠BAE =∠CAE .即AE 平分∠BAC .7.分析:(1)延长AD 到E 使AD =DM ,连接BM ,利用已知条件可证明△BDM ≌△ADC ,所以AM =2AD ,BM =AC ,由三角形的三边关系定理即可证明AB+AC >2AD ;(2)根据三角形中位线定理即可证明DE =AB .证明:(1)延长AD 到M 使AD =DM ,连接BM ,∵AD 是△ABC 的中线,∴BD =CD ,在△BDM 和△ADC 中,,∴△BDM ≌△ADC ,∴AC =BM ,AM =2AD ,∵AB+BM >AM ,∴AB+AC >2AD ;(2)∵DE ∥AB 交AC 于E ,DF ∥AC 交AB 于F ,∴四边形ABCD 是平行四边形,∴DE =AF ,∵BD =CD ,∴BF =AF ,∴DE =AB .8.分析:延长AD 至点G ,使得AD =DG ,连接BG ,CG ,易证四边形ABGC 是平行四边形,即可求得∠EAF =∠ABG ,即可求证△EAF ≌△BAG ,即可解题.证明:延长AD 至点G ,使得AD =DG ,连接BG ,CG ,∵AD =DG ,BD =CD ,∴四边形ABGC 是平行四边形,∴AC =AF =BG ,AB =AE =CG ,∠BAC+∠ABG =1800,∵∠EAF+∠BAC =1800,∴∠EAF =∠ABG ,在△EAF 和△BAG 中,⎪⎩⎪⎨⎧=∠=∠=BG AF ABG EAF AB AE ,∴△EAF ≌△BAG (SAS ),∴EF =AG ,∵AG =2AD ,∴EF =2AD .9.分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB =CD ,必须添加适当的辅助线,构造全等三角形或等腰三角形.解:证明:方法一:作BF ⊥DE 于点F ,CG ⊥DE 于点G .∴∠F =∠CGE =90°.又∵∠BEF =∠CEG ,BE =CE ,∴△BFE≌△CGE.∴BF=CG.在△ABF和△DCG中,∵∠F=∠DGC=90°,∠BAE=∠CDE,BF=CG,∴△ABF≌△DCG.∴AB=CD.方法二:作CF∥AB,交DE的延长线于点F.∴∠F=∠BAE.又∵∠ABE=∠D,∴∠F=∠D.∴CF=CD.∵∠F =∠BAE,∠AEB=∠FEC,BE=CE,∴△ABE≌△FCE.∴AB=CF.∴AB=CD.方法三:延长DE至点F,使EF=DE.又∵BE=CE,∠BEF=∠CED,∴△BEF≌△CED.∴BF=CD,∠D=∠F.又∵∠BAE=∠D,∴∠BAE=∠F.∴AB=BF.∴AB=CD.10.分析:在AC上取一点H,使AH=AE,根据角平分线的定义可得∠EAO=∠HAO,然后利用“边角边”证明△AEO 和△AHO全等,根据全等三角形对应角相等可得∠AE0=∠AHO,根据角平分线的定义可得∠1=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠3=60°,再根据角平分线的定义和三角形的内角和定理求出∠4=60°,从而得到∠3=∠4,然后利用“边角边”证明△CFO和△CHO全等,根据全等三角形对应边相等可得CF=CH,再根据AC=AH+CH代换即可得证.证明:如图,在AC上取一点H,使AH=AE,∵AF是△ABC的角平分线,∴∠EAO=∠HAO,在△AEO和△AHO中,,∴△AEO≌△AHO(SAS),∴∠AE0=∠AHO,∵CE是△ABC的角平分线,∴∠1=∠2,∵∠1+∠3=∠AHO,∠2+∠B=∠AEO,∴∠3=∠B=60°,又∵∠B=60°,CE、AF是△ABC的角平分线,∴∠4=∠1+∠CAF=(180°﹣∠B)=(180°﹣60°)=60°,∴∠3=∠4,在△CFO和△CHO中,,∴△CFO≌△CHO(ASA),∴CF=CH,由图可知,AC=AH+CH,∴AC=AE+CF.11.分析:延长FA交BE于H,延长AF到G使FG=AF,连接CG,根据全等三角形的性质得到CG=AD,∠G=∠FAD,根据三角形的内角和和平角的定义得到∠ACG=∠BAE,根据全等三角形的性质得到∠CAG=∠B,等量代换即可得到结论.解:BE⊥AF,理由:延长FA交BE于H,延长AF到G使FG=AF,连接CG,∵F为CD的中点,∴CF=DF,在△CFG 与△DFA中,,∴△CFG≌△DFA,∴CG=AD,∠G=∠FAD,∵AB⊥AC,AD⊥AE,AE=AD,∴∠BAC =∠DAE=90°,AE=CG,∴∠BAE=360°﹣90°﹣90°﹣∠CAD=180°﹣∠CAD,∵∠ACG=180°﹣∠CAF﹣∠G =180°﹣∠CAE﹣∠DAF=180°﹣∠CAD,∴∠ACG=∠BAE,在△ACG与△BAE中,,∴△ACG≌△BAE,∴∠CAG=∠B,∵∠BAH+∠CAG=90°,∴∠BAH+∠B=90°,∴∠AHB=90°,∴AF⊥BE.。
倍长中线法(经典例题)

倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC 中 方式1: 延长AD 到E ,AD 是BC 边中线 使DE=AD ,连接BE方式2:间接倍长DABCED ABCFA DAM作CF⊥AD于F,延长MD到N,作BE⊥AD的延长线于E 使DN=MD,连接BE 连接CN经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CEAD例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EFFEDABC例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAEABFDECE DABC自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.FEABCD3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图DF CBEADABCMTEWelcome To Download !!!欢迎您的下载,资料仅供参考!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
针对对象:初二学生 期末分值:8~10分
(2013·台州市中考)在△ABC中,AD为BC边上的中线, 且AD平分∠BAC,则△ABC为___________三角形。
A
B
D
C
造全等——倍长中线法
A
A
2
B
1D
C
2
B
D1
C
E
E
倍长中线造法:延长AD到点E,使得AD=DE,连结BE(或者EC)。
AD=DE ∴△ADC ≌ △BDE (SAS) ∴AC=BE,∠E=∠1,∠EBD=∠C
∵三角形两边之和大于第三边 ∴AB+BE>AE ∴AB+AC>2AD
题型识别: 出现中线
口诀: 倍长中线
步骤: 延长一倍 构造全等 边角关系
【例2】如图在△ABC,AB=5,AC=3,则中线AD
的取值范围是? A
的取值范围是? A 75
接例1,BE=AC=5, AE=2AD=14
B
D
C ∵在△ABE中,
AE-BE<AB<AE+BE
∴9<AB<19
E
题型识别: 出现中线
口诀: 倍长中线
步骤: 延长一倍 构造全等 边角关系
【例4】如图在△ABC,AB=AC,延长AB到D,使得BD=
AB,取AB的中点E,连结CD和CE,求证CD=2CE。
∴ ∠CBF=∠CBD
∵CB=CB
∵△CBF≌△BCD SAS
∴CD=CF
∴CD=2CE
(2013·台州市中考)在△ABC中,AD为BC边上的中线, 且AD平分∠BAC,则△ABC为___________三角形。
A
B
D
C
THANK YOU
全等原因:SAS
注意:往左往右都可以,只连一条。
题型识别: 出现中线
口诀: 倍长中线
步骤: 延长一倍 构造全等 边角关系
【例1】如图AD是△ABC的中线,求证AB+AC>2AD
A
证明:延长AD到点E,使得AD=DE,
1
连结BE。
B
D
E
∵AD是△ABC的中线 ∴BD=DC
C ∵BD=DC, ∠BDE= ∠ADC,
C
2 3
A E 1B
F
证明:延长AE到点F,使得CE=EF,连结BF。
∵E是AB的中点 ∴AE=EB
∵CE=EF,∠AEC=∠BEF
∴△AEC≌△BEF(SAS)
∴∠A=∠1,∠F=∠ACE,FB=AC
D
∵ AC=AB=BD ∴∠2=∠3, FB=BD=AC=AB
∵∠CBF=∠1+∠3,∠CBD=∠A+∠2
接上题,BE=AC=3,AB+形两边之差小于第三边
∴AB-BE<AE
B
D
C ∴AB-BE<2AD
∴AB-BE<2AD<AB+BE
∴2<2AD<8
E
∴1<AD<4
题型识别: 出现中线
口诀: 倍长中线
步骤: 延长一倍 构造全等 边角关系
【例3】如图在△ABC,AC=5,中线AD=7,则AB边
