电子科技大学离散数学第8章-函数ppt课件
合集下载
离散数学(函数)PPT课件

证 先证明FG是函数.
因为F, G是关系, 所以FG也是关系. 若对某个x∈dom(FG)有 xF Gy1和 xFGy2, 则
<x, y1>∈FG∧<x, y2>∈FG
t1(<x,t1>∈F∧<t1,y1>∈G)∧t2(<x,t2>∈F∧<t2,y2>∈G)
t1t2(t1=t2∧<t1,y1>∈G∧<t2,y2>∈G) (F为函数)
.
函数的定义
设A, B为集合, 如果 f 为函数, domf=A, ranfB,
则称 f 为从A到B的函数, 记作 f:A→B.
.
函数的定义
在<x,y> f 中,
定义域
domf A
例:d设omXf ={张A 三、李四、王五}, Y ={值法域国、(函美数国像、的俄集罗合斯)、英国} f ={<r张an三f ,美B国, ><李四,俄罗斯>
.
函数的复合
定理 设f:A→B, g:B→C (1) 如果 f:A→B, g:B→C满射, 则 fg:A→C也满射 (2) 如果 f:A→B, g:B→C单射, 则 fg:A→C也单射 (3) 如果 f:A→B, g:B→C双射, 则 fg:A→C也双射 定理 设 f:AB, 则 f = f IB = IAf
4.2 逆函数和复合函数
❖复合函数 ❖反函数
关系与逆关系: < y,x >R-1 <x,y>R 函数与反函数。 可能出现的问题: 定义域 (dom(f -1) A) 函数值 (一对多)
.
函数的复合
设F, G是函数, 则FG也是函数, 且满足 (1) dom(FG)={x|x∈domF∧F(x)∈domG} (2) x∈dom(FG)有FG(x)=G(F(x))
离散数学PPT教学课件 数理逻辑ppt8

或者 ( x)( R(x, 或者 ( y)(P(x)∧Q(y)∧┐ y)(P(x)∧P(y)→ ┐ T(x,y)) y)) ( 1)兔子比乌龟跑得快;
( ( x)(P(x)∧( x) (y)(P(x)∧Q(y)→R(x, y)(Q(y)→R(x, y))) y)) ( 4 )不存在跑得同样快的两只兔子。
2018/7/1 84-1
电子科技大学离散数学课程组——国家级精品课程
例4.2.4 将下列命题符号化 ┐( ( x)( x) ( y)(P(x)∧Q(y)→R(x, y)) ┐ y)(P(x)∧P(y)∧T(x, y)) (2)有的兔子比所有乌龟跑得快; (3)并不是所有的兔子都比乌龟跑得快;
2018/7/1 84-8
电子科技大学离散数学课程组——国家级精品课程
4.3.2
自由变元和约束变元
定义4.3.4 给定一个合适公式G,若变元x出现在使 用变元的量词的辖域之内,则称变元x的出现为约束 出现(Bound Occurrence),此时的变元x称为约束 变元(Bound Variable)。若x的出现不是约束出现, 则称它为自由出现 (Free Occurrence) ,此时的变 量词辖域的确定方法: 元x 称为自由变元(Free Variable)。 (1)若量词后有括号,则括号内的子公式就是 该量词的辖域; (2)若量词后无括号,则与量词邻接的子公式 为该量词的辖域。
2018/7/1 84-7
电子科技大学离散数学课程组——国家级精品课程
例子
(x)(y)(P(x, y)→(Q(x, y)∨R(x, a, f(z)))),
(x)(P(x)∨(y)R(x, y)),
(x)(P(x) →R(x))。
等都是公式。 而 (x)P(x)→R(x)(y), (y)(x)(∨P(x,y))。 等则不是公式。
离散数学-----函数_图文

(4) f : R→R, f(x)=2x+1
是满射、单射、双射的, 因为它是单调函数并且ranf=R.
*
12
8.3 一些常用函数
• 定义8.7
(1) 设f:A→B, 如果存在 c∈B 使得对所有的
x∈A 都有 f(x)=c, 则称 f : A→B是常函数.
(2) 称 A 上的恒等关系 IA为 A 上的恒等函数, 对所
不同的等价关系确定不同的自然映射,
恒等关系所确定的自然映射是双射, 而其他的自然映射一般来说只是满射.
*
18
8.4 函数的复合和反函数
• 例:
gοf
g
A
f
a b
B
1 2
C
c
3
D
gοf={<a,2>,<b,2>,<c,1>}
*
19
8.4 函数的复合和反函数
• 定理8.1
设f, g是函数, 则f∘g也是函数, 且满足
8.5 集合的势
• 一个结论:
从上例可以看出:
• 这说明: 无限集合能与它的真子集等势,这在有限集合中是不可能
的。
这是无限集合与有限集合的本质区别之一。
*
34
8.5 集合的势
• 例3: N×N≈N
解:分析
*
35
8.5 集合的势
• 定理8.7(Cantor定理)
N与R不等势,且|N|<|R|
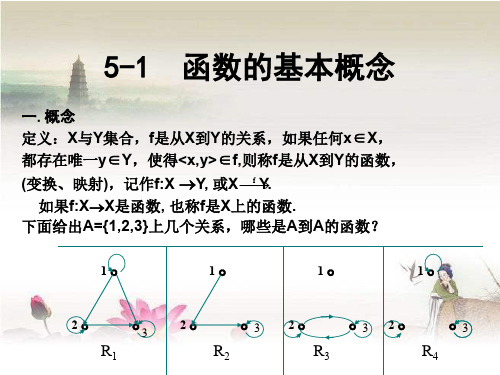
B的二元关系中,哪些是A到B的函数?
f1={<1,a>,<1,b>,<2,b>,<3,c>,<4,c>} f2={<1,a>,<2,b>,<3,b>,<4,c>} f3={<1,a>,<2,a>, <3,c>} f4={<1,a>,<2,a>, <3,a>,<4,a>}
是满射、单射、双射的, 因为它是单调函数并且ranf=R.
*
12
8.3 一些常用函数
• 定义8.7
(1) 设f:A→B, 如果存在 c∈B 使得对所有的
x∈A 都有 f(x)=c, 则称 f : A→B是常函数.
(2) 称 A 上的恒等关系 IA为 A 上的恒等函数, 对所
不同的等价关系确定不同的自然映射,
恒等关系所确定的自然映射是双射, 而其他的自然映射一般来说只是满射.
*
18
8.4 函数的复合和反函数
• 例:
gοf
g
A
f
a b
B
1 2
C
c
3
D
gοf={<a,2>,<b,2>,<c,1>}
*
19
8.4 函数的复合和反函数
• 定理8.1
设f, g是函数, 则f∘g也是函数, 且满足
8.5 集合的势
• 一个结论:
从上例可以看出:
• 这说明: 无限集合能与它的真子集等势,这在有限集合中是不可能
的。
这是无限集合与有限集合的本质区别之一。
*
34
8.5 集合的势
• 例3: N×N≈N
解:分析
*
35
8.5 集合的势
• 定理8.7(Cantor定理)
N与R不等势,且|N|<|R|
B的二元关系中,哪些是A到B的函数?
f1={<1,a>,<1,b>,<2,b>,<3,c>,<4,c>} f2={<1,a>,<2,b>,<3,b>,<4,c>} f3={<1,a>,<2,a>, <3,c>} f4={<1,a>,<2,a>, <3,a>,<4,a>}
离散数学ch8[2]函数的复合与反函数PPT课件
![离散数学ch8[2]函数的复合与反函数PPT课件](https://img.taocdn.com/s3/m/c97764ac866fb84ae45c8dbb.png)
14.11.2020
24
单侧逆函数:存在的充要条件
集合X 集合X
14.11.2020
集合Y 集合Y
满射f(x)
g(y)
25
单侧逆函数:存在的充要条件
函数f存在逆函数的充要条件是函数f是双射
证明: 设f: X→Y, 必要性: 若f是双射,由逆函数引理知,逆函数存在。 充分性: 若函数f存在逆函数f-1,则由逆函数性质知,
f-1ºf=Ix,fºf-1=Iy。 ∴f有左,右逆元,由2知,f是既满又单,
∴f是双射函数。
14.11.2020
26
置换:定义
置换
设 X={x1,x2,...,xn}是一个有穷集合。 从集合 X 到 X 的双射函数, 称为集合 X 中的置换或排列, 并记作 p:XX。 集合 X 的基数|X|=n 称为置换的阶。
∴gºf是函数。
14.11.2020
4
复合函数:复合函数性质
性质:
a)若g,f是满射,则gºf是满射。
b)若g,f是单射,则gºf是单射。
c) 若g,f是双射,则gºf是双射。
14.11.2020
5
复合函数:复合函数性质
性质:
a)若g,f是满射,则gºf是满射证明:
设f: X→Y, g:Y→Z, 则gºf:X→Z,
单侧逆函数
单侧逆函数
设f: X→Y,g:Y→X, 如果gºf=Ix,则称 g是f的左逆元(左逆函数),
f是g的右逆元(右逆函数)。
14.11.2020
20
单侧逆函数:存在的充要条件
左逆函数,右逆函数存在的充要条件
a) f有左逆元当且仅当f是单射。
b) f有右逆元当且仅当f是满射。
《离散数学函数》课件

映射和函数
研究集合之间的映射关系和函数 的定义与分类。
初等函数
1 常函数
2 线性函数
3 正比例函数
了解常数函数及其在数学中 的特点。
研究线性函数的性质和特点。
学习正比例函数的图像和应 用。
4 幂函数
5 指数函数
6 对数函数
探索幂函数的定义及其多种 表现。
了解指数函数及其在数学和 科学中的应用。
研究对数函数的定义和性质。
小结
本章内容回顾
对第一章至第七章内容进行简 要回顾和概括。
知识点总结
总结重点知识点和核心概念。
拓展阅读建议
提供额外阅读资源以深入学习 离散数学函数。
函数极限的定义
学习函数极限的定义和基本计算 方法。
极限运算法则
掌握计算函数极限时的常用运算 法则。
函数连续性的定义
了解连续函数的定义及其特性。
离散数学函数的应用
1 离散数学函数在算机科学中的应用
探索离散数学函数在算法设计、数据结构等方面的应用。
2 例如:哈希函数、调度算法、图像处理等
研究哈希函数、调度算法、图像处理等实际应用情景。
《离散数Байду номын сангаас函数》PPT课 件
欢迎来到《离散数学函数》PPT课件!在本课程中,您将学习离散数学的基本 概念及函数的重要性。准备好迈向数学的精彩世界吧!
离散数学基础
命题和命题公式
学习如何构建和解读命题及命题的逻辑关系。
命题逻辑
探索命题逻辑的运算和规则,理解命题的真值表。
命题的复合和否定
学会将命题组合成复合命题以及应用否定运算。
函数基础
函数定义
了解函数的定义及其在数学中的重要性。
第8章-函数PPT课件

例8.6
例8.6 对于给定的集合A和B构造双射函数 f:A→B。 1)A=P({1,2,3}), B={0,1}{1,2,3}
(2)A=[0,1], B=[1/4,1/2] (3)A=Z, B=N (4)A=[/2,3/2], B=[1,1]
例8.6的解答
(1)A=P({1,2,3}), B={0,1}{1,2,3}
能构成f:A→B, f 不是单射的,因为f(3)=f(5)=9, f 不是满射的,因为7ran f。 (1)A={1,2,3,4,5},B={6,7,8,9,10},
f={<1,7>,<2,6>,<4,5>,<1,9>,<5,10>} 不能构成f:A→B,因为<1,7>∈f 且<1,9>∈f 。
例8.5
对于函数F,如果有 xFy,则记作y=F(x),并称y为F在x的 值。
举例 判断下列关系是否为函数 F1={<x1,y1>,<x2,y2>,<x3,y2>} F2={<x1,y1>,<x1,y2>}
是函数 不是函数
函数是特殊的二元关系。
说明
函数的定义域为dom F,而不是它的真子集。 一个x只能对应唯一的y。
换句话说,如果对于x1、x2A有f(x1)=f(x2),则一定有
x1=x2。
不同类型的对应关系的示例
1 a
2 b
3 c
4
单射
a
1
b
2
c
3
d
4
双射
1 a
2 b
3 c
4
不是函数
a
1
b
离散数学PPT教学课件 数理逻辑ppt8

2018/7/1
84-16
电子科技大学离散数学课程组——国家级精品课程
例4.3.3(续)
(2)构造解释I2为
P(a) = 0,P(b) = 1,Q(a) = 0,Q(b) = 1,
则(P(a)→Q(a))∧(P(b)→Q(b))在此解释I2 下真值为1,(P(a)∨P(b))→(Q(a)∧Q(b))在此解 释I2下真值为0,即I2使得等价联结词前面的 (x)(P(x)→Q(x))为真,而使得等价联结词后面的 ((x)P(x)→(x)Q(x))为假,因此,这样的解释使 得公式(x)(P(x)→Q(x))((x)P(x)→(x)Q(x)) 的真值为假。
2018/7/1 84-8
电子科技大学离散数学课程组——国家级精品课定义4.3.4 给定一个合适公式G,若变元x出现在使 用变元的量词的辖域之内,则称变元x的出现为约束 出现(Bound Occurrence),此时的变元x称为约束 变元(Bound Variable)。若x的出现不是约束出现, 则称它为自由出现 (Free Occurrence) ,此时的变 量词辖域的确定方法: 元x 称为自由变元(Free Variable)。 (1)若量词后有括号,则括号内的子公式就是 该量词的辖域; (2)若量词后无括号,则与量词邻接的子公式 为该量词的辖域。
规则2(自由变元的代入规则):
(1)将公式中出现该自由变元的每一处都用新的个 体变元替换; (2)新变元不允许在原公式中以任何约束形式出现
2018/7/1 84-12
电子科技大学离散数学课程组——国家级精品课程
例4.3.2
(1)将公式(x)(P(x)→Q(x, y))∧R(x, y)中的 约束变元x进行改名; (2)将公式(x)(P(x)→Q(x, y))∧R(x, y)中的 自由变元y进行代入。
电子科技大学离散数学第8章-函数

R11={<a,1>,<a,2>,<b,1>};
R12={<a,1>,<a,2>,<b,2>};
R13={<a,1>,<b,1>,<b,2>};
R14={<a,2>,<b,1>,<b,2>};
R15={<a,1>,<a,2>,<b,1>,<b,2>}。
2019/6/2
67-12
A到B不同的函数
从A到B的不同的函数仅有22=4个。分别如下: f1={<a,1>,<b,1>}, f2={<a,1>,<b,2>}, f3={<a,2>,<b,1>}, f4={<a,2>,<b,2>}。
67-11
A到B不同的关系
R0=Φ;R1={<a,1>};R2={<a,2>};R3={<b,1>};
R4={<b,2>};R5={<a,1>,<b,1>};R6={<a,1>,<b,2>};
R7={<a,2>,<b,1>};R8={<a,2>,<b,2>};
R9={<a,1>,<a,2>};R10={<b,1>,<b,2>};
2019/6/2
67-6
例8.2.1
设 A={1,2,3,4} , B={a,b,c,d} , 试 判 断 下 列 关 系 哪 些是函数。如果是函数,请写出它的值域。 ( 1 ) f1 = {<1,a>,<1,b>,<2,c>,<3,b>}, 其 中 A = {1,2,3},B={a,b, c}; ( 2 ) f2 = {<a,b>,<b,b>,<c,c>}, 其 中 A = {a,b,c},B ={b,c}; (3)f3={<x,y>|y−x=1,x,y∈R},其中A=B=R (4)f4={<x,y>|y−x=1,x,y∈Z+},其中A=B=Z+
离散数学第八章(第1讲)

(2)无向图,有向图
a
d
每一条边都是无向边的图称无向图。
b
c
每一条边都是有向边的图称有向图。 a
d
b
c
例:将右图用二元组表示为: G=〈V,E〉 其中V={a,b,c,d} E={<a,b>,<b,a>,<b,d>,<d,a>,<d,d>,<c,c>} 则:G=〈V,E〉= 〈 {a,b,c,d} , {<a,b>,<b,a>,<b,d>,<d,a>,<d,d>,<c,c>} 〉
A
最大度,记为:△(G)=max{d(v)| vV} B
E
最小度,记为:δ(G)=min{d(v)| vV}
D
C
定理1 (握手定理) :每个图中,结点度数的总和等于边 数的两倍。即
deg(v) 2 E
vV
证:∵每条边必关联两个结点,而一条边给于关联的每 个结点的度数为1。 故上述定理成立。
例:在一次10周年同学聚会上,想统计所有人握手的 次数之和,应该如何建立该问题的图论模
a
h
b
c
g
d h
b
c
g
d
a
h
f (a)
f e
e
(b)
f (c)
(13)生成子图:如果G的子图包含G的所有结点,则称 该子图为G的生成子图。
如下图,(b)、(c)都是(a)的生成子图。
v1
v4
v1
v4
v1
v4
v2
v3
(a)
v2
v3
v2
(b)
离散数学(函数)课件

02
函数的运算
函数的加法
总结词
函数的加法是一种对应关系,表示将函数$f$和$g$的每一个输出值都加上一定的量。
详细描述
函数的加法是一种二元运算,表示将函数$f$和$g$的每一个输出值都加上一定的量。具体来说,如果函数$f$和 $g$的定义域分别为$D_f$和$D_g$,那么函数$f+g$的定义域为$D_{f+g} = D_f cap D_g$,对于任意$x in D_{f+g}$,有$(f+g)(x) = f(x) + g(x)$。
详细描述
幂函数的形式为 y=x^n,其中 n 是实数。当 n>0 时,幂函数是增函数;当 n<0 时,幂函数是减函数;当 n=0 时,幂函数值为 1。幂函数在离散数学中可 用于表示一些复杂的关系。
指数函数
总结词
指数函数是指数等于输入值的函数。
详细描述
指数函数的形式为 y=a^x,其中 a 是实数且 a>0,a≠1。当 a>1 时,指数函 数是增函数;当 0<a<1 时,指数函数是减函数。指数函数在离散数学中可用于 表示概率和统计中的分布情况。
函数的三要素包括定义域、值域和对应法则。
函数的表示方法
01
02
03
解析法
通过公式来表示函数,例 如y=f(x)。
表格法
通过表格的形式列出函数 的输入和输出值。
图象法
通过绘制函数图像来表示 函数。
函数的性质
单调性
函数在某个区间内单调增 加或单调减少。
有界性
函数在某个区间内有上界 和下界。
奇偶性
函数是否关于原点对称或 关于y轴对称。
函数的复合
电子科技大学离散数学第8章 函数

R11={<a,1>,<a,2>,<b,1>}; R12={<a,1>,<a,2>,<b,2>}; R13={<a,1>,<b,1>,<b,2>}; R14={<a,2>,<b,1>,<b,2>};
R15={<a,1>,<a,2>,<b,1>,<b,2>}。
2019/1/31 67-12
A到B不同的函数
显然f2是满射函数。但是,X中元素0和1有相同的象 1,所以f2不是单射函数;
2019/1/31 67-23
例8.2.5 解
3. 由已知得,
1 f(n)= , n = 0,1,2, n+1
显然,f是双射函数。
2019/1/31
67-24
例8.2.6
设A=B=R(实数集)。试判断下列函数的类型。 (1)f1={<x,x2>|x∈R}; (2)f2={<x,x+1>|x∈R}; (3)f3={<x,ex>|x∈R}; 解(1)f1仅是一般函数; (2)f2是双射函数; (3)f3是单射函数。
离散数学
电子科技大学
2019年1月31日星期四
第8章 函数
1 2
函数的概念 特殊函数
内 容 提 要
3
函数的复合运算
函数的逆运算
4
5
2019/1/31
函数的运算定理
67-2
8.1 本章学习要求
重点掌握 1 1 函数的概念 2 单射、满射 和双射函数的 概念 3 函数的复合 运算和逆运算 2019/1/31 一般掌握
R15={<a,1>,<a,2>,<b,1>,<b,2>}。
2019/1/31 67-12
A到B不同的函数
显然f2是满射函数。但是,X中元素0和1有相同的象 1,所以f2不是单射函数;
2019/1/31 67-23
例8.2.5 解
3. 由已知得,
1 f(n)= , n = 0,1,2, n+1
显然,f是双射函数。
2019/1/31
67-24
例8.2.6
设A=B=R(实数集)。试判断下列函数的类型。 (1)f1={<x,x2>|x∈R}; (2)f2={<x,x+1>|x∈R}; (3)f3={<x,ex>|x∈R}; 解(1)f1仅是一般函数; (2)f2是双射函数; (3)f3是单射函数。
离散数学
电子科技大学
2019年1月31日星期四
第8章 函数
1 2
函数的概念 特殊函数
内 容 提 要
3
函数的复合运算
函数的逆运算
4
5
2019/1/31
函数的运算定理
67-2
8.1 本章学习要求
重点掌握 1 1 函数的概念 2 单射、满射 和双射函数的 概念 3 函数的复合 运算和逆运算 2019/1/31 一般掌握
离散数学 函数 PPT
1 X。f 。Y g 。X 1
1。X IX 。X 1
。 。a
2
b。
。2
2。
。2
c
4.定理4,令 f:XY, g:YX是两个双射函数,则
(g f) -1 =f -1 g-1
1。
1。
1。
1。
2。
。 3
2。
。3
2。
。3 2。
。3
R1
R2
R3
R4
下面哪些是R到R的函数?
f={<x,y>|x,y∈R∧y= _1x_} g={<x,y>|x,y∈R∧x2+y2=4 } h={<x,y>|x,y∈R∧y= x2 } r ={<x,y>|x,y∈R∧y=lgx } v ={<x,y>|x,y∈R∧y= √ x }
五 .两个函数相等
设有两个函数f:AB g:AB, f=g 当且仅当 对任何x∈A,有f(x)=g(x)。
六. 函数的类型
例子:
1234X。。。。f
。Ya 。b 。c
Rf=Y
1234X。。。。g
。Ya 。b 。c
RgY
X12。。1 h 3。
Y。1 a 。b 。c
。d
RhY1 一对一
1 X。1 s 。Y a
由关系复合性质3得, f是入射的和g是 满射的。 同理由 f g = IY,得g是入射的和f 是 满射的。所 以f和g都可逆。
⑵显然f-1和g具有相同的定义域和陪域。
⑶证明它们的对应规律相同。
任取yY, f-1(y)= f-1 IY (y) = f-1 (f g) (y) = (f-1 f) g (y) =( IX g) (y) =g(y) 所以f-1 =g 注: f-1 =g 的两个条件必须同时满足,缺一不可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
67-11
A到B不同的关系
R0=Φ;R1={<a,1>};R2={<a,2>};R3={<b,1>};
R4={<b,2>};R5={<a,1>,<b,1>};R6={<a,1>,<b,2>};
R7={<a,2>,<b,1>};R8={<a,2>,<b,2>};
R9={<a,1>,<a,2>};R10={<b,1>,<b,2>};
时,称f为一个变换。
2020/4/23
67-15
将定义8.2.2的描述数学化为
1. f:A→B 是 单 射 当 且 仅 当 对 任 意 x1,x2∈A , 若 x1≠x2,则f(x1)≠f(x2);
f(A)为函数f的值域,记为ranf。
当<x,y>∈f时,通常记为y=f(x),这时称x为
函数f的自变量,y为x在f下的函数值(或象), 也
称x为y在f下的原象 。
2020/4/23
67-5
结论
如果关系f是函数,那么 1. <x,y>∈f y=f(x); 2. <x,y>∈f ∧ <x,z>∈f y=z; 3. |f|=|A|; 4. f(x)表示一个变值,f代表一个集合,因此f≠f(x)。 如果关系f具备下列两种情况之一,那么f就不是函数: 1. 存在元素a∈A,在B中没有象; 2. 存在元素a∈A,有两个及两个以上的象。
3. 每一个函数的基数都为|A|个(|f|=|A|),但关 系的基数却为从零一直到|A|×|B|。
2020/4/23
(集合基数的差别)
67-14
8.2.2函数的类型
定义8.2.2 设f是从A到B的函数, 对任意x1,x2∈A,如果x1≠x2,有f(x1)≠f(x2), 则称f为从A到B的单射(不同的x对应不同的y); 如果ranf=B,则称f为从A到B的满射; 若f是满射且是单射,则称f为从A到B的双射。 若A=B,则称f为A上的函数;当A上的函数f是双射
2020/4/23
67-4
8.2.1函数的定义
定义8.2.1 设f是集合A到B的关系,如果对每个 x∈A,都存在惟一的y∈B,使得<x,y>∈f,则称关 系f为A到B的函数(Function)(或映射(Mapping)、 变换(Transform)),记为f:A→B。
A为函数f的定义域,记为domf=A;
2020/4/23
67-7
例8.2.1 解
(1)在f1中,因为元素1有两个元素a,b与它对应,所 以f1不是A到B函数; (2)在f2中,每个元素都有惟一的象和它对应,所以 f2是A到B函数。Ranf2={b,c}; (3)在f3中,因为每个元素都有惟一的象和它对应, 所以f3是A到B函数,且ranf3=R; (4)在f4中,因为每个元素都有惟一的象和它对应, 所以f4是A到B函数,且ranf4={2,3,4,…}。
2020/4/23
67-13
函数与关系的差别
函数是一种特殊的关系,它与一般关系比较具备如 下差别:
1. 从A到B的不同的关系有2|A||B|个;但从A到B的 不同的函数却仅有|B||A|个。 (个数差别)
2. 关系的第一个元素可以相同;函数的第一元素 一定是互不相同的。
(集合元素的第一个元素存在差别)
R11={<a,1>,<a,2>,<b,1>};
R12={<a,1>,<a,2>,<b,2>};
R13={<;
R14={<a,2>,<b,1>,<b,2>};
R15={<a,1>,<a,2>,<b,1>,<b,2>}。
2020/4/23
67-12
A到B不同的函数
从A到B的不同的函数仅有22=4个。分别如下: f1={<a,1>,<b,1>}, f2={<a,1>,<b,2>}, f3={<a,2>,<b,1>}, f4={<a,2>,<b,2>}。
2020/4/23
67-10
例8.2.3
设A={a,b},B={1,2},请分别写出A到B的不同关系 和不同函数。 解 因为|A|=2,|B|=2,所以|A×B|=|A|×|B|=4, 即A×B={<a,1>,<a,2>,<b,1>,<b,2>},此时从A到 B的不同的关系有24=16个。
2020/4/23
2 1 单射、满射 和双射函数的 证明 2 置换的定义
了解 3
1 置换的计算
67-3
8.2 函数
函数也叫映射、变换或对应。 函数是数学的一个基本概念。这里将高等数学 中连续函数的概念推广到对离散量的讨论,即将函 数看作是一种特殊的二元关系。 函数的概念在日常生活和计算机科学中非常重 要。如各种高级程序语言中使用了大量的函数。实 际上,计算机的任何输出都可看成是某些输入的函 数。
2020/4/23
67-8
例8.2.2
设P是接受一个整数作为输入并产生一个整数作为 输出的计算机程序。令A=B=Z,则由P确定的关系fp 定义如下: 如果<m,n>∈fp当且仅当输入m时,由程序P所产生的 输出是n。 请判断fp是否为函数。
2020/4/23
67-9
例8.2.2 解
显然,fp是一个函数。因为,任意一个特殊的输入 对应唯一的输出。 可用任意一个可能的输入集合A对应输出集合B而推 广到一般情形的程序。所以,通常把函数看做输入 -输出的关系。
2020/4/23
67-6
例8.2.1
设 A={1,2,3,4} , B={a,b,c,d} , 试 判 断 下 列 关 系 哪 些是函数。如果是函数,请写出它的值域。 ( 1 ) f1 = {<1,a>,<1,b>,<2,c>,<3,b>}, 其 中 A = {1,2,3},B={a,b, c}; ( 2 ) f2 = {<a,b>,<b,b>,<c,c>}, 其 中 A = {a,b,c},B ={b,c}; (3)f3={<x,y>|y−x=1,x,y∈R},其中A=B=R (4)f4={<x,y>|y−x=1,x,y∈Z+},其中A=B=Z+
离散数学
电子科技大学
2020年4月23日星期四
第8章 函数
1
函数的概念
内
2
特殊函数
容 提
3 函数的复合运算
要
4
函数的逆运算
5 函数的运算定理
2020/4/23
67-2
8.1 本章学习要求
重点掌握
1
1 函数的概念 2 单射、满射 和双射函数的 概念 3 函数的复合 运算和逆运算
2020/4/23
一般掌握
