循环结构复习学案
《第14课 循环结构(二)》学历案-小学信息技术浙教版23五年级下册

《循环结构(二)》学历案(第一课时)一、学习主题本节课的学习主题为“循环结构(二)”,是小学信息技术课程中关于编程思维培养的重要一环。
通过本课的学习,学生将进一步理解循环结构的概念,掌握循环语句的编写,为后续的编程学习打下坚实的基础。
二、学习目标1. 知识与技能:(1)理解循环结构的概念及作用。
(2)掌握循环语句的编写方法。
(3)能够运用循环语句解决实际问题。
2. 过程与方法:(1)通过观察、分析,理解循环结构的运行过程。
(2)通过实践操作,掌握循环语句的编写技巧。
3. 情感态度与价值观:(1)培养学生的编程兴趣和逻辑思维。
(2)提高学生的自主学习和合作学习能力。
三、评价任务1. 课堂表现评价:观察学生在课堂上的学习状态、参与度及对知识的理解程度。
2. 作业评价:通过学生完成的作业,评价学生对循环结构知识的掌握情况及运用能力。
3. 小组互评:小组内成员互相评价,促进相互学习,共同进步。
四、学习过程1. 导入新课:通过回顾上节课的内容,引出本节课的学习主题——循环结构。
2. 新课讲解:通过图文并茂的方式,讲解循环结构的概念及作用,使学生明确学习目标。
3. 实践操作:教师演示循环语句的编写方法,学生跟随练习,巩固知识。
4. 小组合作:学生分组进行实践操作,编写简单的循环程序,解决实际问题。
5. 交流分享:小组代表展示作品,其他小组进行评价和交流。
五、检测与作业1. 检测:通过课堂小测验,检测学生对循环结构知识的掌握情况。
2. 作业:布置相关练习题,要求学生运用所学知识编写循环程序,并记录编写过程中遇到的问题及解决方法。
3. 拓展延伸:鼓励学生回家后与家长共同探讨循环结构的实际应用,拓宽学生的视野。
六、学后反思1. 学生反思:学生应总结本节课的学习内容,思考自己在哪些方面做得好,哪些方面需要改进。
2. 教师反思:教师应对本节课的教学过程进行反思,总结教学经验,为今后的教学提供借鉴。
3. 改进措施:针对学生在学习过程中遇到的问题,教师可调整教学方法和策略,提高教学效果。
北师大版必修三 循环结构 学案

2.3 循环结构知识点循环结构[填一填]1.循环结构(1)定义:按照一定条件,反复执行某一步骤的算法结构称为循环结构,反复执行的部分称为循环体.(2)循环变量:控制着循环的开始和结束的变量,称为循环变量.(3)循环的终止条件:决定是否继续执行循环体的判断条件,称为循环的终止条件.2.在画出算法流程图之前,需要确定三件事(1)确定循环变量和初始条件;(2)确定算法中反复执行的部分,即循环体;(3)确定循环的终止条件.3.循环结构的算法流程图的基本模式[答一答]如何理解循环结构中的计数变量和累计变量?提示:在大部分循环结构中会有一个计数变量和一个累计变量.计数变量用于记录循环次数,累计变量用于输出结果,它们一般是同步执行,累计一次,计数一次,例如i=i+1,sum=sum+t.i=i+1的含义是:将变量i的值加1,然后把计算结果再存储到变量i中,即i在原值的基础上又增加了1.变量sum作为累加变量,用来表示所求数据的和.如sum的初值为0,当第一个数据送到变量t中时,累加的动作为sum=sum+t,即把sum的值与变量t的值相加,将所得结果再送到变量sum中,如此循环,则可实现数的累加求和.类似于这个原理,我们也可以实现累乘求积的问题.在具体画算法框图时,要注意:流程线上要有标志执行顺序的箭头;判断框后边的流程线应根据情况标注“是”或“否”;在循环结构中,要注意根据条件设计合理的计数变量、累加变量等,特别是条件的表述要恰当、精确.画循环结构算法框图的要领:①确定循环变量和初始条件;②确定算法中反复执行的部分,即循环体;③确定循环的转向位置;④确定循环的终止条件.类型一循环结构的基本概念例1在使用循环结构描述一个具体问题的算法时,循环变量的初始值()A.是唯一的B.是固定不变的C.根据结构特点有时可以变化D.以上答案都不对解析循环结构中,若循环体不同,所给的循环变量的初值可以不同,故选C.答案 C规律方法对循环结构的有关概念的正确理解是解循环结构题目的关键,应认真掌握.下面的算法流程图中是循环结构的是(C)A.①②B.②③C.③④D.②④解析:①为顺序结构,②为条件结构,③④为循环结构.类型二含循环结构的程序的运行例2如果执行如图所示的算法框图,输入x=-2,h=0.5,那么输出的各个数的和等于()A.3B.3.5C.4D.4.5思路探究本题主要考查循环结构内嵌套多个选择结构的算法框图,需要反复进行判断和运算直到满足条件.题中涉及三个变量,注意每个变量的运行结果和执行情况.解析按照算法框图依次执行为:初始值x=-2,h=0.5.(1)x=-2,h=0.5,y=0;(2)x=-1.5,h=0.5,y=0;(3)x=-1,h=0.5,y=0;(4)x=-0.5,h=0.5,y=0;(5)x=0,h=0.5,y=0;(6)x=0.5,h=0.5,y=0.5;(7)x=1,h=0.5,y=1;(8)x=1.5,h=0.5,y=1;(9)x=2,h=0.5,y=1.所以输出的各个数的和等于3.5.答案 B规律方法对于循环结构的算法框图的读图问题,要读懂框图的执行方向和其中的判断条件,明确循环次数,弄清每次的赋值.如图所示,算法框图的输出结果是( D )A.16B.2524C.34D.1112解析:第一次循环,s =12,n =4;第二次循环,s =34,n =6;第三次循环,s =1112,n =8.此时跳出循环,输出s =1112.类型三 含循环结构算法框图的设计例3 写出一个求满足1×3×5×7×…×n >60 000的最小正整数n 的算法,并画出相应的算法框图.思路探究 本题需要重复执行乘法,故引入循环结构,算法的结束需要引入一个累乘变量来控制.解 算法如下: 1.令s =1; 2.令n =1;3.如果s ≤60 000,那么n =n +2,s =s ×n ,重复执行第3步,否则,执行第4步; 4.输出n .算法框图如图所示.规律方法 设计循环结构的算法框图的注意点解决具体的循环结构的算法问题,要尽可能少地引入循环变量,否则较多的变量会使得设计程序比较麻烦,同时应尽可能使得循环嵌套的层数少.另外,要注意:(1)在循环结构中,循环变量要赋初始值,循环变量的自加不要忘记,自加多少不能弄错. (2)循环结构中循环的次数要严格把握,区分“<”与“≤”等.另外,同一问题利用两种不同的结构解决时,其判断条件不同.设计一个算法计算11×2+12×3+13×4+14×5+15×6的值,并画出相应的算法框图.解:具体算法步骤如下: 1.k =1,S =0;2.S =S +1k (k +1),k =k +1;3.若k <6,则反复执行第2步,否则,执行第4步; 4.输出S .相应的算法框图如图.类型四 循环结构的实际应用例4 用分期付款的方式购买价格为2 150元的冰箱,如果购买时先付1 150元,以后每月付50元,并加付欠款的利息,若一个月后付第一个月的分期付款,月利率为1%,那么购冰箱钱全部付清后,实际共付出款额多少元?画出算法框图.思路探究 用循环结构设计算法解决应用问题.解 购买时付款1 150元,余款1 000元分20次分期付款,每次的付款数为: a 1=50+(2 150-1 150)×1%=60(元), a 2=50+(2 150-1 150-50)×1%=59.5(元), ……a n =50+[2 150-1 150-(n -1)×50]×1%=60-12(n -1).∴a 20=60-12×19=50.5(元),总和S =1 150+60+59.5+…+50.5=2 255(元). 算法框图如图:规律方法用循环结构设计算法解决应用问题的步骤:1.审题;2.建立数学模型;3.用自然语言表述算法步骤;4.确定每一个算法步骤所包含的逻辑结构,对于要重复执行的步骤,通常用循环结构来设计,并用相应的算法框图表示,得到表示该步骤的算法框图;5.将所有步骤的算法框图用流程线连接起来,并加上终端框,得到表示整个算法的算法框图.以下是某次考试中某班15名同学的数学成绩:72,91,58,63,84,88,90,55,61,73,64,77,82,94,60,画出求80分以上的同学的平均分的算法框图.解:程序框图如下:——易错警示——循环结束的条件判断不准致误例5如图所示,若此程序运行结果为S=720,则在判断框中应填入关于k的判断条件是()A.k≥6B.k=7 C.k≥8D.k≥9错解本题可以按照开始的输入值、程序执行的规律和输出结果进行综合解决.容易出错的地方是不清楚这个判断条件是什么,本题是当不满足判断框中的条件时结束循环,当判断框中的条件满足时执行循环,故应该从k=10开始按照递减的方式逐步进行,直到S的输出结果为720.错解分析考生应注意题中“否”对应着输出框,所以只有不满足判断框内的条件时,循环才能结束.另外,计数变量k在题中不仅体现了循环的次数,而且还参与了累乘变量的变化过程,如果计数变量k的变化与累乘变量的变化的先后顺序改变,则k的初始值和判断框中的条件也要发生变化.正解第一次运行结果为S=10,k=9;第二次运行结果为S=10×9=90,k=8;第三次运行结果为S=720,k=7.这个程序满足判断框的条件时执行循环,故判断条件是k≥8.故选C.答案 C执行如图所示的算法框图,如果输出的a值大于2 015,那么判断框内应填(C)A.k≤6 B.k<5C.k≤5 D.k>6解析:第一次循环,a=4×1+3=7,k=1+1=2;第二次循环,a=7<2 015,故继续循环,所以a=4×7+3=31,k=2+1=3;第三次循环,a=31<2 015,故继续循环,所以a=4×31+3=127,k=3+1=4;第四次循环,a=127<2 015,故继续循环,所以a=4×127+3=511,k=4+1=5;第五次循环,a=511<2 015,故继续循环,所以a=4×511+3=2 047,k=5+1=6;第六次循环,a=2 047>2 015,故不符合条件,终止循环,输出a值.所以判断框内应填的条件是k≤5.一、选择题1.以下说法不正确的是(C)A.顺序结构是由若干个依次执行的处理步骤组成的,每一个算法都离不开顺序结构B.循环结构是在一些算法中从某处开始按照一定条件,反复执行某一处理步骤,故循环结构中一定包含选择结构C.循环结构中不一定包含选择结构D.用算法流程图表示算法,使之更加直观形象,容易理解解析:任何算法都是由若干个顺序结构组成,循环结构中要对是否循环进行判断,所以一定包含选择结构,故选C.2.执行两次下图所示的算法框图,若第一次输入的a的值为-1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a的值分别为(C)A.0.2,0.2 B.0.2,0.8C.0.8,0.2 D.0.8,0.8解析:本题考查了循环结构.第一次输入a=-1.2<0→a=-1.2+1=-0.2<0→a=-0.2+1=0.8>0且a<1→输出a=0.8;第二次输入a=1.2≥1→a=1.2-1=0.2→输出a=0.2.3.如图所示,算法框图的输出结果是(B)A.3 B.4C.5 D.8解析:本题考查了算法循环结构的直到型的流程图及赋值语句问题.x 1248y 123 4二、填空题4.阅读如图所示的算法框图,运行相应的程序,若输入m的值为2,则输出的结果i =4.解析:本题考查算法框图的循环结构.i=1,A=2,B=1;i=2,A=4,B=2;i=3,A=8,B=6;i=4,A=16,B=24;此时A<B,则输出i=4.5.执行如图所示的算法框图,若输入n的值为8,则输出s的值为8.解析:本题考查算法框图的循环结构.第1次,i =2,s =2,第2次i =4,s =12(2×4)=4;第3次,i =6,s =13(4×6)=8,第4次,i =8,输出s =8.注意变量赋值的顺序.三、解答题6.已知有一列数12,23,…,n n +1,设计算法求这列数前100项的和. 解:S 1 赋值i =1,S =0S 2 S =S +i i +1S 3 i =i +1S 4 判断i >100S 5 i >100,则输出S否则,返回S 2S 6 结束程序框图:。
VB循环结构复习学案

主题:循环结构一、考点点击:1、学会使用循环结构设计程序的基本方法。
二、学习目标:1、掌握for循环语句、do……loop循环语句的格式及执行流程2、学会用循环控制结构来解决实际问题三、活动形式在教师引导下的自主学习四、考点注解:学会使用循环结构设计程序的基本方法。
按条件重复执行一种操作的结构称为循环结构。
循环结构有两种形式,即当型循环结构和直到型循环结构。
(1)当型循环结构:先进行判断,然后根据判断结果(真或假)再决定是否执行循环体的循环结构称为当型循环结构,如左图所示。
(2)直到型循环结构:先执行一次循环体,然后再根据判断结果(真或假)决定是否继续执行循环体的循环结构称为直到型循环结构,如下图所示。
从上述两种循环结构的流程图可以看出,对于当型循环结构,程序有可能一次也不执行循环体;对于直到型循环结构,程序至少要执行一次循环体。
循环语句实现循环结构。
VB中循环语句有两种:Do…Loop语句和For…Next语句。
Do…Loop语句是条件型循环,当循环的执行是由条件控制,在循环的次数不确定时通常选用该语句;For语句是计数循环,在循环次数已知时选用该语句。
(一)、do……loop循环(二)For…Next 语句在循环次数已知的情况下,采用 For…Next 语句实现循环结构是比较合适的选择。
For…Next 语句的格式如下:(三)、循环结构例题对比求1+2+3+……+100的值1、当for语句中省略step时默认值是12、在do……loop 循环中要注意变量初值的设置和循环变量的增值问题五、习题训练:1 .[ 单选题1 分]在VB中,某同学要计算1+3+5+……+9的值,他应用循环结构语句如下:s=0 FOR i=1 TO 9 STEP? s=s+i请问语句中的“?”代表的值是()A、-1B、-2C、2D、12.[ 多选题2 分]如下VisualBasic程序段,用到了哪些控制结构()。
Private Sub command1_click() S=0 i=16 Do S=S+I i=i+1 Until S>=100 Print"i的值为:";I EndSubA、顺序结构B、循环结构C、层次结构D、选择结构3. [ 单选题1 分].以下是一段VisualBasic程序,它的基本结构属于()…Do S=S+I i=i+1 Loop Until S>=100…A、顺序结构B、选择结构C、循环结构D、树型结构4. [ 单选题1 分]执行下列VB程序段后,变量j的值为()S=0 For j=1 to 10 Step 2 S=S+j Next jA、1B、10C、11D、125. [ 单选题1 分]有如下VB程序段,对该程序段执行过程描述正确的是()Do S=S+1 Loop Until S>100A、如果S>100,则退出循环B、如果S<=100,则重复执行S=S+1C、如果S>100,则重复执行S=S+1D、不论S初值为多少,至少执行一次S=S+16. [ 单选题1 分]在结构化程序设计中通常包含三种不同的控制结构,即:顺序结构、选择结构、循环结构。
1、1循环结构学案

1、1、2循环结构一、学习目标1、熟练掌握两种循环结构的特点及功能.2、能用两种循环结构画出求和等实际问题的程序框图,进一步理解学习算法的意义.二、基础知识<1>什么是循环结构、循环体?<2>试用程序框图表示循环结构.<3>请你简要解释直到型循环结构和当型循环结构.三、练习例1:教材例6、设计一个计算1+2+…+100的值的算法,并画出程序框图. 例2:画出求21+22+23+…2100的值的程序框图.结论:<1>在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.反复执行的步骤称为循环体.<2>见教材第13页图1.1—12,1.1—13.<3>①直到型循环结构:这个循环结构有如下特征:在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.因此,这种循环结构称为直到型循环结构.②当型循环结构:这种循环结构有如下特征:在每次执行循环提前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.这种循环称为当型循环结构.从以上两种不同形式的循环结构可以看出,循环结构中一定包含条件结构,用于确定何时终止执行循环体.2. 算法分析:通常,我们按照下列过程计算1+2+…+100的值.第一步,0+1=1第二步,1+2=3第三步,3+3=6第四步,6+4=10……第100步,4950+100=5050显然,这个过程中包含重复操作的步骤,可以用循环结构表示.分析上述计算过程,可以发现每一步都可以表示为:第(i-1)步的结果+i=第i步的结果.为了方便、有效的表示上述过程,我们用一个累加变量S来表示每一步的计算结果,即把S+i的结果仍记为S,从而把第i步表示为S=S+i.其中S的初始值为0,i依次取为1,2,…,100.由于i同时记录了循环的次数,所以也称为计数变量.解决这一问题的算法是:第一步,令i=1,S=0.第二步,若i≤100成立,则执行第三步;否则,输出S,结束算法.第三步,S=S+i.第四步,i=i+1.返回第二步.程序框图如图所示(当型循环结构)。
2013必修3循环结构学案

高一数学必修3学案 04
1.1.3《循环结构》
一、复习引入:
1
二、概念形成:
1、赋值语句:
1、定义:在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构。
循环结构的一般形式:
班级 姓名
三、概念应用;
例1、画出计算10099321+++++ 的算法的程序框图。
练习:1、画出计算1+
3121++…+10
1
值得程序框图。
2. 画出求+++531…1917++的算法的程序框图。
四、归纳总结
1、知识:
2、题型与方法:
3、注意问题:
五、体验高考(选做)
1.(2008山东卷)执行程序框图,若输入p =0.8,则输出的n = .
2.(2009山东卷理)执行下边的程序框图,输出的T = .
3.(2010山东文数)(13)执行右上图所示的程序框图,若输入4x =,则输出y 的值为 .
(2010山东理数)(13)执行右上图所示的程序框图(同文图),若输入10x =,则输出y 的值为 .
4.(2011·山东高考理科)执行下图所示的程序框图,输入2=l ,3=m ,5=n ,则输出的y 的值是______
09山东理
10山东卷
5.(。
高中数学 第二章 算法初步 2.3 循环结构学案 北师大版必修3(1)

2.3 循环结构[学习目标] 1.掌握循环结构的有关概念.2.理解循环结构的基本模式,会用循环结构描述算法.3.体会循环结构在重复计算中的重要作用.知识点一常量与变量的概念1.循环结构的定义在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.反复执行的步骤称为循环体.2.循环结构的特点(1)重复性:在一个循环结构中,总有一个过程要重复一系列的步骤若干次,而且每次的操作完全相同.(2)判断性:每个循环结构都包含一个判断条件,它决定这个循环的执行与终止.(3)函数性:循环变量在构造循环结构中起了关键作用,蕴含着函数的思想.3.设计一个算法的算法框图的步骤(1)用自然语言表述算法步骤;(2)确定每一个算法步骤所包含的逻辑结构,并用相应的算法框图表示,得到该步骤的算法框图;(3)将所有步骤的算法框图用流程线连接起来,并加上终端框,得到表示整个算法的算法框图.思考(1)循环结构的算法框图中一定含有判断框吗?(2)任何一个算法的算法框图中都必须含有三种基本逻辑结构吗?答(1)循环结构的算法框图中一定含有判断框.(2)不一定.但必须会有顺序结构.知识点二循环结构的设计过程循环结构的算法框图的基本模式,如图所示.题型一循环结构的识别与解读例1 (1)当m=7,n=3时,执行如图所示的算法框图,输出S的值为( )A.7 B.42C.210 D.840(2)如图所示,算法框图(算法框图)的输出结果是( )A.34 B.55 C.78 D.89答案(1)C (2)B解析(1)算法框图的执行过程如下:m=7,n=3时,m-n+1=5,k=m=7,S=1,S=1×7=7;k=k-1=6>5,S=6×7=42;k=k-1=5=5,S=5×42=210;k=k-1=4<5,输出S=210.故选C.(2)当输入x=1,y=1,执行z=x+y及z≤50,x=y,y=z后,x,y,z的值依次对应如下:x=1,y=1,z=2;x=1,y=2,z=3;x=2,y=3,z=5;x=3,y=5,z=8;x=5,y=8,z=13;x=8,y=13,z=21;x=13,y=21,z=34;x=21,y=34,z=55.由于55≤50不成立,故输出55.故选B.反思与感悟高考中对算法框图的考查类型之一就是读图,解决此类问题的关键是根据算法框图理解算法的功能.考查的重点是算法框图的输出功能、算法框图的补充,以及算法思想和基本的运算能力、逻辑思维能力,试题难度不大,大多可以按照算法框图的流程逐步运算而得到.跟踪训练1 阅读如图所示的算法框图,运行相应的程序,若输入m的值为2,则输出的结果i=________.答案 4解析m=2,A=1,B=1,i=0.第一次:i=0+1=1,A=1×2=2,B=1×1=1,A>B;第二次:i=1+1=2,A=2×2=4,B=1×2=2,A>B;第三次:i=2+1=3,A=4×2=8,B=2×3=6,A>B;第四次:i=3+1=4,A=8×2=16,B=6×4=24,A<B;终止循环,输出i=4.题型二用循环结构解决累加、累乘问题例2 设计一个计算1+2+…+100的值的算法,并画出算法框图.解方法一第一步,令i=1,S=0.第二步,若i≤100成立,则执行第三步;否则,输出S,结束算法.第三步,S=S+i.第四步,i=i+1,返回第二步.算法框图:方法二第一步,令i=1,S=0.第二步,S=S+i.第三步,i=i+1.第四步,若i>100不成立,则返回第二步;否则,输出S,结束算法.算法框图:反思与感悟循环结构分为两种:一种循环结构是先执行一次循环体,然后再判断是否继续执行循环体,是在条件不满足时执行循环体,另一种循环结构是先判断是否执行循环体,是在条件满足时执行循环体.跟踪训练2 设计一个算法,求13+23+33+…+1003的值,并画出算法框图.解算法如下:第一步,使S=0.第二步,使I=1.第三步,使S=S+I3.第四步,使I=I+1.第五步,若I>100,则输出S,算法结束;否则,返回第三步.算法框图如图所示:题型三确定循环变量最值的框图例3 写出一个求满足1×3×5×7×…×i>50 000的最小正整数i的算法,并画出相应的算法框图.解算法如下:1.S=1.2.i=3.3.如果S≤50 000,那么S=S×i,i=i+2,重复第3步;否则,执行第4步.4.i=i-2;5.输出i.算法框图如图所示:反思与感悟 1.在使用循环结构时,需恰当地设置累加(乘)变量和计数变量,在循环体中要设置循环体终止的条件.2.在最后输出结果时,要避免出现多循环一次或少循环一次的情况出现.跟踪训练3 求使1+2+3+4+5+…+n>100成立的最小自然数n的值,只画出算法框图.解算法框图如下:题型四循环结构的实际应用例4 某工厂2013年生产小轿车200万辆,技术革新后预计每年的生产能力比上一年增加5%,问最早哪一年该厂生产的小轿车数量超过300万辆?写出解决该问题的一个算法,并画出相应的算法框图.解算法如下:1.令n=0,a=200,r=0.05.2.T=ar(计算年增量).3.a=a+T(计算年产量).4.如果a≤300,那么n=n+1,返回第2步;否则执行第5步.5.N=2 014+n.6.输出N.算法框图如图所示.反思与感悟这是一道算法的实际应用题,解决此类问题的关键是读懂题目,建立合适的模型,找到解决问题的计算公式.跟踪训练4 电脑游戏中,“主角”的生命机会往往被预先设定,如某枪战游戏中,“主角”被设定生命机会5次,每次生命承受射击8枪(被击中8枪则失去一次生命机会).假设射击过程均为单发发射,试将“主角”耗用生命机会的过程设计成一个算法框图.解方法一“主角”所有生命机会共能承受8×5=40(枪)(第40枪被击中则生命结束).设“主角”被击中枪数为i(i=0,1,2,…,39),算法框图可设计为如图1.方法二与方法一相对,电脑中预先共承受枪数40,“主角”生命机会以“减法”计数,算法框图可设计为如图2.累加变量和计数变量的应用例5 画出求满足12+22+32+…+n2>2 0152的最小正整数n的算法框图.错解如图(1).错解分析累加变量的初始值为1,第一次运算为S=1+12导致错误.一般把计数变量的初始值设为1,累加变量的初始值设为0,本例中S=0,i=1.自我矫正算法框图如图(2)所示:图(1) 图(2)1.下列关于循环结构的说法正确的是( )A.循环结构中,判断框内的条件是唯一的B.判断框中的条件成立时,要结束循环向下执行C.循环体中要对判断框中的条件变量有所改变才会使循环结构不会出现“死循环”D.循环结构就是无限循环的结构,执行程序时会永无止境地运行下去答案 C解析由于判断框内的条件不唯一,故A错;由于循环结构中,判断框中的条件成立时可能和执行循环体,故B错;由于循环结构不是无限循环的,故C正确,D错.2.阅读如图所示的算法框图,则输出的S等于( )A.14 B.30C.20 D.55答案 B解析第一次循环,S=1,i=2;第二次循环,S=1+22=5,i=3;第三次循环,S=5+32=14,i=4;第四次循环,S=14+42=30,i=5,满足条件,输出S=30.第2题图第3题图3.如图所示的算法框图输出的S是126,则①应为( )A.n≤5 B.n≤6 C.n≤7 D.n≤8答案 B解析2+22+23+24+25+26=126,所以应填“n≤6”.4.执行如图的程序框图,如果输入的a=4,b=6,那么输出的n=( )A.3 B.4C.5 D.6答案 C解析第一次循环a=6-4=2,b=6-2=4,a=4+2=6,i=6,n=1;第二次循环a=-6+4=-2,b=4-(-2)=6,a=6-2=4,i=10,n=2;第三次循环a=6-4=2,b=6-2=4,a=4+2=6,i=16,n=3;第四次循环a=4-6=-2,b=4-(-2)=6,a=6-2=4,i=20,n=4,满足题意,结束循环.第4题图第5题图5.如图所示的算法框图,当输入x的值为5时,则其输出的结果是________.答案 2解析∵x=5>0,∴x=5-3=2,∵x=2>0,∴x=2-3=-1.∴y=0.5-1=2.1.(1)循环结构是指在算法中需要重复执行一条或多条指令的控制结构;(2)在循环结构中,通常都有一个起循环计数作用的变量;(3)循环变量、循环体、循环终止条件称为循环结构的三要素.2.画算法框图要注意:(1)使用标准的框图符号;(2)框图一般按从上到下、从左到右的方向画;(3)除判断框外,大多数框图符号只有一个进入点和一个退出点,判断框是具有超过一个退出点的唯一符号;(4)一种判断是“是”与“否”两分支的判断,而且有且仅有两个结果,另一种是多分支判断,有几种不同的结果;(5)在图形符号内描述的语言要非常简练、清楚.。
循环结构学案

1.1.2程序框图与算法的基本逻辑结构—循环结构【学习目标】
1、理解循环结构,能识别和理解简单的框图的功能。
2、运用循环结构设计程序框图解决简单的问题
【学习重点】理解循环结构,能识别和画简单的循环结构框图。
【学习难点】循环结构中的循环条件和循环体的确定。
【学习过程】
(一)创设情境
引例:写出1+2+3+4+…+100算法步骤,并画出程序框图。
(二)授新设疑
①讲解新知
1、循环结构定义:
2、循环结构的框图表示
②探究新知
写出1+2+3+4+…+100算法步骤,并画出程序框图。
③循序渐进,理解新知
上述程序框图用的是直到型循环结构,如果用当型循环结构如何表示呢
④合作探究,掌握新知
观察刚刚得到的程序框图,完成以下四个问题:
(1)什么情况下可以考虑使用循环结构?
(2)循环结构的三要素是什么?
(3)在循环结构中是否一定含有条件结构?
(4)结合当型循环结构与直到型循环结构的特征,完成以下判断
①当型循环至少执行一次循环体()
②直到型循环可以不执行循环体()
(三)实例剖析
例7:某工厂2005年的年生产总值是200万元,技术革新后预计以后每年的年生产总值都比上一年增长5%,设计一个程序框图,输出预计年生产值超过300万元的最早年份。
(四)知能训练
练习1: 图A为计算1+2+3+4+5+…+100的程序框图.
在①处填--------.
练习2:图B为计算1×2×3×4×5的程序框图.在②处填--------,在③处填-----------.
(五)总结归纳:
(六)课后作业:。
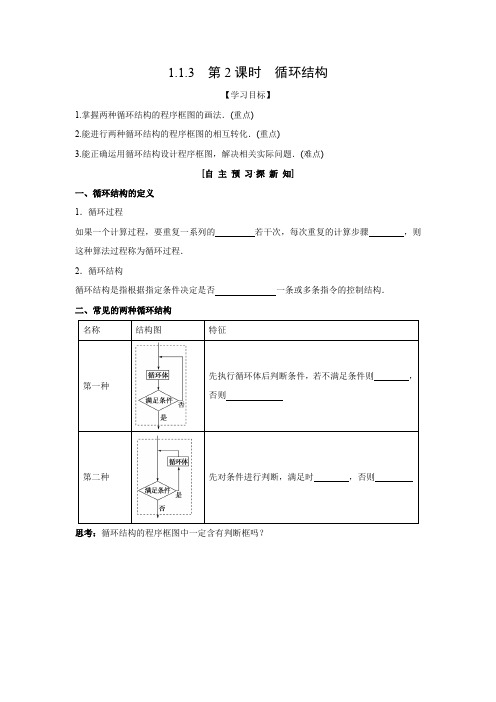
学案4:1.1.3 第2课时 循环结构
1.1.3 第2课时循环结构【学习目标】1.掌握两种循环结构的程序框图的画法.(重点)2.能进行两种循环结构的程序框图的相互转化.(重点)3.能正确运用循环结构设计程序框图,解决相关实际问题.(难点)[自主预习·探新知]一、循环结构的定义1.循环过程如果一个计算过程,要重复一系列的若干次,每次重复的计算步骤,则这种算法过程称为循环过程.2.循环结构循环结构是指根据指定条件决定是否一条或多条指令的控制结构.二、常见的两种循环结构名称结构图特征先执行循环体后判断条件,若不满足条件则,第一种否则第二种先对条件进行判断,满足时,否则思考:循环结构的程序框图中一定含有判断框吗?【基础自测】1.思考辨析(1)循环结构是在一些算法中从某处开始,按照一定条件反复执行处理某一步骤,因此循环结构一定包含条件分支结构.()(2)循环结构中不一定包含条件分支结构.()(3)循环结构中反复执行的步骤叫做循环体.()2.下列框图是循环结构的是()A.①②B.②③C.③④D.②④3.下列程序框图中,循环体是________.4.阅读如图所示的框图,运行相应的程序,输出S的值为________.[合作探究·攻重难]类型一含循环结构的程序的运行【例1】执行如图所示的程序框图,输出的S值为()A.1B.3C.7D.15[思路探究]根据程序框图进行判断,要注意程序终止的条件.[规律方法]1.如果算法问题里涉及的运算进行多次重复的操作,且先后参与运算的各数之间有相同的变化规律,就可以引入循环变量参与运算,构成循环结构.2.在循环结构中,要注意根据条件设置合理的计数变量,累加(乘)变量,同时条件的表述要恰当,精确.3.累加变量的初值一般为0,而累乘变量的初值一般为1,累加(乘)和计数一般是同步进行的,累加(乘)一次,计数一次.[跟踪训练]1.阅读如图所示的程序框图,运行相应的程序,输出的n的值为()A.1B.2C.3 D.4类型二含循环结构程序框图的设计[探究问题]1.什么样的算法问题要用循环结构?它与顺序结构、条件分支结构有什么联系?2.在循环结构中,计数变量和累加(乘)变量有什么作用?3.循环结构的判断框中的条件是唯一的吗?【例2】设计一个算法,求1×2×3×…×100的值,并画出程序框图.[思路探究]式中各项相乘,且各项有规律递增,所以引入累乘变量S和计数变量i,利用S =S×i,i=i+1这两个式子反复执行,因此需要利用循环结构设计程序框图.母题探究:1.(变条件)设计一个计算1+2+3+…+100的算法,并画出程序框图.2.(变结论)根据例2选择另外一种循环结构,画出它的程序框图.[规律方法]利用循环结构设计算法框图需要注意的问题.要注意循环条件、变量初值、循环体各语句之间的影响.(1)注意各个语句顺序不同对结果的影响;(2)注意各个变量初始值不同对结果的影响;(3)要对循环开始和结束的变量及结束时变量的值认真检验,以免出现多循环或者漏循环.类型三循环结构的实际应用【例3】用分期付款的方式购买价格为2 150元的冰箱,如果购买时先付1 150元,以后每月付50元,并加付欠款的利息,若一个月后付第一个月的分期付款,月利率为1%,那么购冰箱钱全部付清后,实际共付出款额多少元?画出程序框图.[思路探究]根据题中条件解决该问题需选择循环结构画流程图.[规律方法]用循环结构设计算法解决应用问题的步骤:(1)审题,恰当设未知数;(2)建立数学模型;(3)用自然语言表述算法步骤;(4)确定每一个算法步骤所包含的逻辑结构,对于要重复执行的步骤,通常用循环结构来设计,并用相应的程序框图表示,得到表示该步骤的程序框图;(5)将所有步骤的程序框图用流程线连接起来,并加上起、止框,得到表示整个算法的程序框图.[跟踪训练]2.某班共有学生50人,在一次数学测试中,要搜索出测试中及格(60分及以上)学生的成绩,试设计一个算法,并画出程序框图.[当堂达标·固双基]1.下列关于循环结构的说法正确的是()A.循环结构中,判断框内的条件是唯一的B.判断框中的条件成立时,要结束循环向下执行C.循环体中要对判断框中的条件变量有所改变才会使循环结构不会出现“死循环”D.循环结构就是无限循环的结构,执行程序时会永无止境地运行下去2.执行如图所示的程序框图,若输出的b的值为16,则图中判断框内①处应填()A.3B.4C.5D.123.如图所示的程序框图中,语句“S=S×n”将被执行的次数是()A.4 B.5 C.6 D.74.运行如图1141程序框图,输出的结果为________.1 3+15+…+1999的值的一个程序框图.5.画出计算1+【参考答案】[自主预习·探新知]一、循环结构的定义1.计算步骤完全相同2.重复执行二、常见的两种循环结构执行循环体终止循环执行循环体终止循环思考:[提示]在循环结构中需要判断是否执行循环体,故循环结构的程序框图中一定含有判断框.【基础自测】1.[答案](1)√(2)×(3)√2.C[①是顺序结构,②是条件分支结构,③④是循环结构.]3.②[在循环结构中,反复执行的处理步骤是循环体.]4.-4[S=0,n=3,S=0+(-2)3=-8,n=3-1=2≤1不成立;故S=-8+(-2)2=-4,n=2-1=1≤1成立.故输出S的值为-4.][合作探究·攻重难]类型一含循环结构的程序的运行【例1】C[程序框图运行如下:k=0<3,S=0+20=1,k=1<3;S=1+21=3,k=2<3;S=3+22=7,k=3.输出S=7.][跟踪训练]1.B[当n=1时,21>12满足条件,继续循环得n=2,22>22不成立,不满足条件,所以输出n=2.]类型二含循环结构程序框图的设计[探究问题]1.[提示]如果算法问题涉及的运算有许多重复的步骤,且变量间有相同规律,可用循环结构.循环结构中有顺序结构与条件分支结构.2.[提示]一般地,循环结构中都有一个计数变量和累加(乘)变量:计数变量用于记录循环次数,同时它的取值还可能用于判断循环是否终止;累加(乘)变量用于表示每一步的计算结果.计数变量和累加(乘)变量一般是同步执行的,累加(乘)一次,计数一次.3.[提示]不是.在设计具体的程序框图时,循环结构的判断框中的条件可能根据选择模型的不同而不同,也可能由于具体算法的特点而不同,但不同的条件应该有相同的确定的结果.【例2】[解]算法如下:S1令S=1.S2令i=2.S3S=S×i.S4i=i+1.S5若i>100,则输出S;否则,返回S3.该算法的程序框图如图所示.母题探究:1. [解]算法是:S1令i=1,S=0.S2若i≤100成立,则执行S3;否则,输出S,结束算法.S3 S =S +i .S4 i =i +1,返回S2. 程序框图:2.[解] 程序框图:类型三 循环结构的实际应用 【例3】[解] 购买时付款1 150元,余款1 000元分20次分期付款,每次的付款数为: a 1=50+(2 150-1 150)×1%=60(元), a 2=50+(2 150-1 150-50)×1%=59.5(元), ……a n =50+[2 150-1 150-(n -1)×50]×1%=60-12(n -1),∴a 20=60-12×19=50.5(元),总和S =1 150+60+59.5+…+50.5=2 255(元).程序框图如图:[跟踪训练]2.[解]算法步骤如下:S1把计数变量n的初始值设为1.S2输入一个成绩r,比较r与60的大小.若r≥60,则输出r,然后执行下一步;若r<60,则执行下一步.S3使计数变量n的值增加1.S4判断计数变量n与学生个数50的大小,若n≤50,返回S2;若n>50,则结束.程序框图如图:[当堂达标·固双基]1.C[由循环结构的特点知,A、B、D错误,C正确.]2.A[按照程序框图依次执行:初始a=1,b=1;第一次循环后,b=21=2,a=1+1=2;第二次循环后,b=22=4,a=2+1=3;第三次循环后,b=24=16,a=3+1=4,而此时应输出b的值,故判断框中的条件应为“a≤3”.]3.B[由程序框图知:S=1×2×3×…×n.又1×2×3×4×5=120<200,1×2×3×4×5×6=720>200.故语句“S=S×n”被执行了5次.]4.28[n=1,S=1;n=2,S=3;n=3,S=6;n=4,S=10;n=5,S=15;n=6,S=21;n=7,S=28.]5.[解]程序框图如图所示:。
循环结构学案

§1.2.3循环结构一、教学目标:1.通过模仿,操作,探索,经历通过设计流程图表表达问题的过程在具体问题的解决过程中,理解循环结构流程图;2.经过分析具体问题,抽象出算法的过程中培养抽象概括能力,语言表达能力和逻辑思维能力;3.理解循环结构的要素:循环体,循环终止条件二、教学过程:(一)复习:顺序结构特征图选择结构特征图(二)情景问题问题:你知道在申办奥运会的最后阶段。
国际奥委会是如何通过投票决定主办权归属的吗?你能用算法结构表述上面的操作过程吗?试用流程图表示上述算法:归纳:1.循环结构2.直到型循环结构特征图3.(1)循环体:(2)循环终止的条件:(三)例题1.写出求12345⨯⨯⨯⨯值的一个算法.分析:(1)思路1:优点:缺点:(2)思路2.优点:(3)用流程图表示写出求135799⨯⨯⨯⨯⨯的值的算法.并用流程图表示.(四)例题2:根据给出的算法,分析该算法所解决的是什么问题, 并画出相应的流程图?S1 0S ←;S2 1I ←;S3 输入G ;S4 S S G ←+;S5 1I I ←+;S6 若I 不大于100,转S3;否则,转S7S7 /100A S ←;S8 输出A .思考:(1)S4与S5能否调换顺序?(2)能否将S5调至S3之前?(3)①阅读P15《探究—拓展》,区别两种循环结构②当型循环结构特征图③用当型循环结构表示例题2(五)练习1:先分步写出计算246100++++的一个算法,再画出流程图.练习2:下面表示了一个什么样的算法? i N 代表第i 个学生的学号, i G 代表第i 个学生的成绩. (1,2,,50i =) (六)小结:(七)作业。
循环结构 学案 导学案 课件

2.预习
(1)请大家举出一些常见的需要反复计算的例子.
(2)什么是循环结构、循环体?
(3)试用程序框图表示循环结构.
(4)指出两种循环结构的相同点和不同点.
二、合作探究
例1 设计一个计算1+2+……+100的值的算法,并画出程序框图.
1)从1加到100你知道结果是多少吗?
课题:
循环结构
学习目标:
1、知道程序框图的含义,会读程序框图,知道各种程序框及流程线的功能和作用;
2、通过模仿、操作、探索,经历通过设计程序框图表达解决问题的算法的过程,学习程序框图的画法;
3、在具体问题解决过程中,知道程序框图的循环结构。
学 习 活 动 内 容
一、自主学习
1.复习回顾
1、什么叫做顺序结构,它有什么特点?
【课堂训练】
1.由相应的程序框图如右图,补充完整一个计算1+2+3+…+100的值的算法.(用循环结构)
第一步,设i的值为_____________.
第二步,设S的值为_____________.
第三步,如果i≤100执行第_____________步,否则,转去执行第_____________步.
第四步,计算S+i并将结果代替_____________.
第五步,计算_____________并将结果代替i.
第六步,转去执行第三步.
第七步,输出S的值并结束算法.
2、设计1 ×3 ×5 ×7 ×9 ×11的算法,并画出程序框图.
2)怎么计算的结果?
3)能写出它的算法和程序框图吗?
4)i有什么作用?S呢?
5)如何使程序结束?6)来自当型结构和直到型结构表示循环体?
人教A版高中数学必修三循环结构学案新

一、学习目标:了解程序流程图循环结构的概念,会用通用的图形符号表示算法。
通过模仿、操作、探索,学会灵活、正确地画程序流程图,经历通过设计程序流程图表达解决问题的过程。
二、学习重点:循环结构的基本概念、基本图形符号三、学习过程:问题1:学校春运会比赛在400米环形跑场上进行,请你构造一个能判断一个选手跑完全程10000米算法?第一步:第二步:第三步:第四步:请你就上面的算法用流程图来表示:方法一(当型循环结构): 方法二(直到型循环结构):剖析一下:当型循环与直到循环的区别:_______________________________________________________________________________________________________________________选择结构与循环结构的区别与联系: _________________________________________总结: 循环结构:在一些算法中,也经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这种结构称为循环结构.当型循环结构 直到型循环结构注:用“满足条件?循环体”填空.否 是 是 否问题2:根据求1×2×3×4×5的值的算法,并画出流程图.算法1: 算法2:S1 先算T←1×2 S1 T←1S2 T←T×3 S2 I←2S3 T←_______ S3 T←_________S4 T←T×5 S4 I←I+1S5 输出T S5 如果I不大于5,返回S3,否则输出T画出流程图:例题2 设计一个计算10个数的平均数的算法.S1 S←0 {把0赋值给变量S}S2 I←1 {____________________} S3 输入G {输入一个数据}S4 S←S+ G {把_____值赋给变量____} S5 _____________{I+1赋值给变量I}S6 如果I不大于10,转S3 {___________________} S7 ____________ {把S/10存放到A}S8 输出A {输出平均值}画出流程图:巩固练习:1.算法:S1 输入nS2 判断n是否是2,若n=2,则n满足条件,若n>2,则执行S3 S3 依次从2到n一1检验能不能整除n,若不能整除n,满足条件.则这个算法是检验n是_______.(A)质数(B)奇数(C)偶数(D)约数2.右图给出的是计算111124620+++⋅⋅⋅+的值的一个程序流程图,其中判断框内应填入的条件是_______.A.i>10B. i<10C.i>20D.i<203.有如下程序流程图(如右图所示),则该程序流程图表示的算法的功能是_________________________.4.求1+2+3+┅+100用如下的算法,请用流程图表示,并指明对应的逻辑结构:_______________________循环结构.第一步:S←0,I←0;第二步:检验I≤100;第三步:若I≤100,则S←_________,I←__________,转第二步;第四步:输出S;5.设计一个流程图,求满足10<x2<1 000的所有正整数x的值.6.用N i代表第i学生的学号, G i代表第i个学生的成绩(i=1,2,...,50),大于或等于60分的输出合格,否则输出不合格。
2.3循环结构(导学案)

高一年级数学学科导学案课题:2.3循环结构学习目标:1.了解循环结构的有关概念。
2.理解循环结构的三要素。
3.掌握循环结构的应用。
重点:理解循环结构难点:循环结构框图的表示。
预习案一、教材助读1.循环结构的有关概念(1)定义:如果一个计算结构,需要反复进行相同的操作,每次操作步骤完全相同,则这种算法结构叫做循环结构。
(2)在循环结构中,反复执行的部分,称为,控制循环的开始和结束的量称为,判断是否循环体的部分称为循环的条件。
2.用循环结构来描述算法时,在画出算法框图之前,需要确定三件事:(1)确定和条件;(2)确定算法中的部分,即;(3)确定循环的。
这样,循环结构的算法框图的基本模式如图:名称特征作用顺序结构完成一个步骤,再进行另一个步骤,即按顺序完成一组工作选择结构根据对条件的判断决定下一步工作体现了数学中分类讨论思想循环结构重复完成一部分工作的算法设计简化算法二、预习自测1.下列各题设计算法时,必须要用到循环结构的有。
①求二元一次方程组的解②求分段函数的函数值③求1+2+3+…+100④求满足1+2+3+4+5+…+n>100的最小的正整数n2.如图所示的算法框图中,第一次输出的数是,第二次输出的数是,第三次输出的数是。
我的疑惑:时间:2014年月日编号:主编人:曹廷玉编制成员:曹廷玉、邵艳彬、李瑞华、牛贝莉、席曦、郭涛、姚祁教师评价:_____________探究案探究一利用循环结构解决累加、累乘问题例1 如图所示的是求12+22+32+…+1002的值的算法框图,则正整数n=变式练习:(1)画出1+2+3+4+5+…+1000的程序框图。
(2)画出1×2×3×4×…×2014的程序框图。
探究二利用循环结构求满足条件的最值问题例2如图是求满足12+22+32+…+n2>100的最小正整数n的算法框图,则“”应填变式练习:已知1×2×3×4×…×n>2014,如何寻找满足满足条件的n的最小正整数,画出算法框图。
12.2程序框图(第4课时循环结构)学案

和桥中专高二《数学》目标教学导学学案班级________________ 姓名_________________课题:§12.2程序框图(第四课时 循环结构)一、学习要求:1、理解基本算法结构——循环结构。
2、会设计简单的循环结构程序框图。
3、能够读懂循环结构程序框图。
二、预复习要求:1、按照一定的 反复 某些步骤的情况,就是循环结构。
成为循环体。
(在循环结构中必须包含执行或终止循环体的条件,否则该循环为_________)2、循环结构三要素: 、 、 。
3、循环结构中的几个常用变量:(1)计数变量:(用来记录某个事件发生的_____) (2)累加变量:(用来计算数据_______) (3)累乘变量:(用来计算数据_______) 三、典型例题分析:例1、某班有40名学生,依次输入这40名学生的数学考试成绩,输出全班学生的数学总分和平均分.请画出解决这个问题的算法的程序框图.例2、设计一个算法,计算100321++++ 的值,并画出程序框图。
例3、设计一个算法,从输入的5个数中找出最大的数,并画出程序框图。
四、课堂练习1、设计一个算法,计算100321⨯⨯⨯⨯ 的值,并画出程序框图。
2、李大爷现在手上有1万元人民币,他按照定期一年,到期自动转存的方式存入银行。
如果当前定期一年的利率为3.5%,那么5年后他连本带利可以得到多少钱?请你设计一个算法,帮李大爷算一算(假设5年内利率不变,并且不计利息税)。
3、设计一个算法,从输入的5个数中找出最小的数,并画出程序框图。
4、如下图所示的程序框图,运行程序, 则输出S 值为________________。
高一数学循环结构复习教案

高一数学循环结构复习教案教学目标:把握程序框图循环结构的概念,会用通用的图形符号表示算法,通过仿照、操作、探究,学会灵活、正确地画程序框图,经历通过设il•程序框图表达解决咨询题的过程。
教学重点:循环结构的差不多概念、差不多图形符号教学难点:能综合运用这些知识正确地画出程序框图.课型:新授课教学手段:多媒体教学过程:一、创设情境咨询题1:写岀1+2+3+4+5的一个算法。
第一步:sum—0:第二步:sum—sum+1:第三步:sum—sum+2:第四步:sum—sum+3:第五步:sum—sum+4:第六步:sum—sum+5 第七步:输出sum.二.活动尝试按照通常的加法运算法那么,能够从前往后依次运算下去,过程如下: 1+2+3+4+5 在1的基础上加2二3*3+4+5 先运算1+2,得运算结果3二6 #+5 在运算结果3的基础上再加3,得运算结果6二10丄+5 再在上述运算结果6上加4,得运算结果10 分析上述运算过程,事实上,是一个运算过程的重复,立即上一步的运算结果加下一个数,直至加到5,每次得到的和"都在向最后结果靠拢,直到加到5时候,那个 ''和"确实是所要求的结果,如此的称为累加变量,那个程序要写出来要6、7步。
依照那个思想,我们先设左一个 ''和"(sum),通过一种手续不断地让那个 '、和"增加,直到最后结果是所求结果。
三、师生探究我们引进一个计数变量,通过循环结构实现程序简单化:51sum—052i-1Sum=SmD ■ i53 sum —sum+i54 i-i+1S5假如i 不大于5,那么返回执行S3, S4, S5:假如大于5,那么算法终止。
S6输出sum与上例比较会发觉,对操纵循环体的条件进行判左,当条件不满足时,执行循环,而当满足 时终止循环,进行下一步。
这种结构叫循环结构。
四、数学理论循环结构:在一些算法中,也经常会显现从某处开始,按照一定条件,反复执行某一处理 循环体:反复执行的处理步骤称为循环体.计数变量:在循环结构中,通常都有一个起到循环计数作用的变量,那个变量的取值一 样都含在执行或终止循环体的条件中.当型循环:在每次执行循环体前对操纵循环条件进行判定,当条件满足时执行循环体, 不满足那么停止.宜到型循环:在执行了一次循环体之后,对操纵循环体进行判左,当条件不满足时执行 循环体,满足那么停止.当型循环与宜到循环的区不:①当型循环能够不执行循环体,直到循环至少执行一次循 环体.②当型循环先判泄后执行,直到型循环先执行后判左.③对同一算法来讲,当型循环和直 到循环的条件互为反条件.S-1 ssa 五、 巩固运用 例题1写出求 1X2X3X4X5的值的一个算法 算法1: 算法2: S1 先算T-1X2 S1 T-1 S2 T —TX3S2 1-2 S3 T-TX4S3 T-TXI S4T-TX5 S4 I-I+1 S5 输出T S5假如I 不大于5,返回S3,否那么输岀T 延伸:设计一个运算 1, 2, 3, 10的平均数的算法.选择结构与循环结构的区不与联系区不:选择结构通过判左分支,只是执行一次;循环结构通过条件判 圧能够反复执行. T-TXI I_I+1 步骤的情形,这种结构称为循环结构.当型循环结构 直^型循环结构分析:先设计一个循环依次输入1-10,再用一个变量存放这些数的累加和,最后除以10。
《程序的循环结构》教案

《程序的循环结构》教案教学目标:1.了解程序中循环结构的基本概念和作用;2.掌握使用循环结构实现程序重复执行的方法;3.能够灵活运用循环结构解决实际问题。
教学重点和难点:1.理解循环结构的概念和使用方法;2.熟练运用循环结构编写程序。
教学内容:一、复习回顾在之前的学习中,我们学习了程序的顺序结构和分支结构,它们分别表示程序的从上到下的执行顺序和根据条件选择执行的不同路径。
而在实际的程序开发中,我们通常还需要处理一些需要重复执行的任务,这时就需要用到程序的循环结构。
二、引入1.什么是循环结构?循环结构是程序设计语言中的一种基本结构,可以使一段代码重复执行多次,直到满足一些条件才结束。
通过循环结构,我们可以简化程序的编写,减少代码的重复性。
2.循环结构的种类常见的循环结构有以下几种:- while循环:在指定条件为真时循环执行代码块;- for循环:指定循环次数来执行代码块;- do...while循环:先执行一次代码块,然后在指定条件为真时继续执行。
三、实践练习接下来,让我们通过几个实例来练习使用循环结构编写程序。
1. 使用while循环打印1到10的数字:```pythonnum = 1while num <= 10:print(num)num += 1```2. 使用for循环计算1到100的和:```pythontotal = 0for i in range(1, 101):total += iprint("1到100的和为:%d" % total)```3. 使用do...while循环实现一个猜数字游戏:```pythonimport randomcorrect_num = random.randint(1, 100)guess = 0while guess != correct_num:guess = int(input("请输入一个数字:"))if guess < correct_num:print("猜小了!")elif guess > correct_num:print("猜大了!")else:print("恭喜你,猜对了!")```四、拓展应用现在让我们尝试一些更复杂的问题,使用循环结构解决实际场景中的问题。
11.2.3 循环结构 导学案(含答案)

11.2.3 循环结构导学案(含答案)11.2.3循环结构循环结构学习目标1.掌握两种循环结构的程序框图的画法.2.能进行两种循环结构的程序框图的转化.3.能正确设计程序框图,解决有关实际问题知识链接1算法的基本逻辑结构有顺序结构.条件结构.循环结构;2在程序框图中,“i1”表示“把数值1赋值给变量i,使得i的值变成了1”;3在对数的运算中,log25log583.预习导引1循环结构的定义在算法中,从某处开始按照一定的条件重复执行某些步骤的结构称为循环结构,其中反复执行的步骤形成循环体2常见的两种循环结构名称结构图特征直到型循环结构先执行循环体后判断条件p,若不满足条件p则执行循环体,否则终止循环当型循环结构先对条件p进行判断,满足时执行循环体,否则终止循环题型一当型循环结构与直到型循环结构的应用例1设计一个计算12100的值的算法,并画出程序框图解算法是S1令i1,S0.S2若i100成立,则执行S3;否则,输出S,结束算法S3SSi.S4ii1,返回S2.程序框图规律方法当型循环结构与直到型循环结构的联系和区别1联系当型循环结构与直到型循环结构可以相互转化;循环结构中必然包含条件结构,以保证在适当的时候终止循环;循环结构只有一个入口和一个出口;循环结构内不存在死循环,即不存在无终止的循环2区别直到型循环结构是先执行一次循环体,然后再判断是否继续执行循环体,当型循环结构是先判断是否执行循环体;直到型循环结构是在条件不满足时执行循环体,当型循环结构是在条件满足时执行循环体要掌握这两种循环结构,必须抓住它们的区别跟踪演练1对于例1,请选择另外一种循环结构,画出它的程序框图解程序框图如图所示题型二求满足条件的最小大整数问题例2写出一个求满足1357n50000的最小正整数n的算法,并画出相应的程序框图解算法如下S1S1.S2i3.S3如果S50000,执行S4;否则,执行S5.S4SSi,ii2,返回S3.S5ii2.S6输出i.程序框图如图所示规律方法1.在使用循环结构时,需恰当地设置累加乘变量和计数变量,在循环体中要设置循环终止的条件2在最后输出结果时,要避免出现多循环一次或少循环一次的情况出现跟踪演练2求使12345n100成立的最小自然数n的值,只画出程序框图解程序框图如下题型三循环结构程序框图的识别与解读例31如图所示,程序框图的输出结果是A.16B.2524C.34D.11122执行如图所示的程序框图,输出的s值为A.12B.56C.76D.712答案1D2B解析1s0,n2,28,s01212;n224,48,s121434;n426,68,s3*******;n628,88不成立,输出s的值为1112.2执行程序框图,s12,k2;s121356,k3,此时退出循环故输出的s的值为56,故选B.规律方法高考中对程序框图的考查类型之一就是读图,解决此类问题的关键是根据程序框图理解算法的功能考查的重点是程序框图的输出功能.程序框图的补充,以及算法思想和基本的运算能力.逻辑思维能力,试题难度不大,大多可以按照程序框图的流程逐步运算而得到跟踪演练3阅读如图所示的程序框图,运行相应的程序,若输入m的值为2,则输出的结果i________.答案4解析m2,A1,B1,i0.第一次i011,A122,B111,AB;第二次i112,A224,B122,AB;第三次i213,A428,B236,AB;第四次i314,A8216,B6424,AB;终止循环,输出i4.题型四循环结构的实际应用例4某工厂xx年生产小轿车200万辆,技术革新后预计每年的生产能力比上一年增加5,问最早哪一年该厂生产的小轿车数量超过300万辆写出解决该问题的一个算法,并画出相应的程序框图解算法如下S1令n0,a200,r0.05.S2Tar 计算年增量S3aaT计算年产量S4如果a300,那么nn1,返回S2;否则执行S5.S5Nxxn.S6输出N.程序框图如图所示规律方法这是一道算法的实际应用题,解决此类问题的关键是读懂题目,建立合适的模型,找到解决问题的计算公式跟踪演练4某班共有学生50人在一次数学测试中,要搜索出测试中及格60分以上的成绩,试设计一个算法,并画出程序框图解算法步骤如下S1把计数变量n的初始值设为1.S2输入一个成绩r,比较r与60的大小若r60,则输出r,然后执行下一步;若r50,则结束程序框图如图课堂达标1下列关于循环结构的说法正确的是A循环结构中,判断框内的条件是唯一的B判断框中的条件成立时,要结束循环向下执行C循环体中要对判断框中的条件变量有所改变才会使循环结构不会出现“死循环”D循环结构就是无限循环的结构,执行程序时会永无止境地运行下去答案C解析由于判断框内的条件不唯一,故A错;由于当型循环结构中,判断框中的条件成立时执行循环体,故B 错;由于循环结构不是无限循环的,故C正确,D错2如图所示是一个循环结构的算法,下列说法不正确的是A是循环变量初始化,循环就要开始B为循环体C是判断是否继续循环的终止条件D 可以省略不写答案D3直到型循环结构对应的框图为答案B4执行如图所示的程序框图,若输入n的值为3,则输出s的值是A1B2C4D7答案C解析当i1时,s1111;当i2时,s1212;当i3时,s2314;当i4时,退出循环,输出s4;故选C.4如下程序框图,当输入x的值为5时,则其输出的结果是________答案2解析x5,x0,x532,x0.x2310.y0.512.课堂小结1循环结构需要重复执行同一操作的结构称为循环结构,即从某处开始,按照一定条件反复执行某一处理步骤反复执行的处理步骤称为循环体1循环结构中一定包含条件结构;2在循环结构中,通常都有一个起循环计数作用的变量,这个变量的取值一般都含在执行或中止循环体的条件中2程序框图中的任何结构内的每一部分都有机会被执行到,也就是说对每一个框来说都应当有一条从入口到出口的路径。
第4结构循环结构学案

第三课时循环结构【知识结构】【学习目标】1.通过模仿,操作,探索,经历通过设计流程图表表达问题的过程在具体问题的解决过程中,理解循环结构流程图;2.经过分析具体问题,抽象出算法的过程中培养抽象概括能力,语言表达能力和逻辑思维能力;3.理解循环结构的要素:循环体,循环终止条件【预习评价】1.在算法中,的结构称为循环结构. 2.先判断所给条件p是否成立,若p成立,则执行A,再判断条件p是否成立;若p仍成立,则又执行A,如此反复,直到某一次条件p不成立时为止.这样的循环结构称为. 3.先执行A,再判断所给条件p是否成立,若p不成立,则再执行A,如此反复,直到p 成立,该循环过程结束. 这样的循环结构称为.【经典范例】⨯⨯⨯⨯的一个算法,并画出流程图.例1:写出求12345【解】例2:设计一个计算10个数的平均数的算法,并画出流程图.【解】【随堂练习一】⨯⨯⨯⨯⨯的值的算法,并用流程图表示.1.写出求13571002.先分步写出计算2+4+6+…+100的一个算法,再画出流程图.++(共6个5)的值的不同结构的算法流程图.若有60例35个5呢?例4:画出求111113243599101++++⨯⨯⨯⨯的值的算法流程图.例5:写出求112212+++(共n 个2)的值的一个算法,并画出流程图.【随堂练习二】1. 画出求111113243599101++++⨯⨯⨯⨯的值的算法流程图.2. 已知函数2()f x x =,把区间[]3,3-十等分,画出依次求各等分点函数值的算法流程图.【分层训练】1.下列叙述正确的是①.顺序结构中一定有选择结构②.顺序结构中一定有循环结构③.循环结构中一定包含选择结构④.选择结构中一定包含循环结构2.下列叙述不正确的是①.任何一个算法都离不开顺序结构②.在选择结构中,条件是否成立有不同的流向③.循环结构形式不唯一④.循环结构中的循环体至少被执行一次3.用循环结构设计算法,需要完成三部分内容:(1)确定;(2)确定;(3)确定.4.图(Ⅰ)中的箭头a指向①处时,输出,指向②处时,输出;图(Ⅱ)中的箭头b指向③处时,输出,指向④处时,输出.(Ⅰ)(Ⅱ)5.下图表示的算法解决的问题是,其结果为,把该流程图改为当型循环结构.6.给出下面的算法:S1 屏幕上显示两个两位正整数;S2 提示用户输入这两数之和;S3 判断计算结果是否正确,如果是,则显示“正确”;否则显示“错误!再示一次”,然后继续输入计算结果,直到结果正确为止.S4 询问用户是否继续练习,如果回答“Y”,则重复上述过程;如果回答“N”,则结束程序.根据以上叙述,完成表示该算法的流程图.7.画出求1×4×7×10×13×16的值的不同结构的算法流程图.822(共n个2)的值的算法步骤,并画出流程图.9.画出求2+22+23+…+210的算法流程图.+++++++++++的算法流程图.10.画出求1(12)(123)(123100)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主题:循环结构
一、考点点击:
1、学会使用循环结构设计程序的基本方法。
二、学习目标:
1、掌握for循环语句、do……loop循环语句的格式及执行流程
2、学会用循环控制结构来解决实际问题
三、活动形式
在教师引导下的自主学习
四、考点注解:
学会使用循环结构设计程序的基本方法。
按条件重复执行一种操作的结构称为循环结构。
循环结构有两种形式,即当型循环结构和直到型循环结构。
( 1)当型循环结构:先进行判断,然后根据判断结果(真或假)再决定是否执行循环体的循环结构称为当型循环结构,如左图所示。
( 2)直到型循环结构:先执行一次循环体,然后再根据判断结果(真或假)决定是否继续执行循环体的循环结构称为直到型循环结构,如下图所示。
从上述两种循环结构的流程图可以看出,对于当型循环结构,程序有可能一次也不执行循环体;对于直到型循环结构,程序至少要执行一次循环体。
循环语句实现循环结构。
VB中循环语句有两种:Do…Loop语句和For…Next语句。
……loop循环
(二)For…Next 语句
在循环次数已知的情况下,采用For…Next语句实现循环结构是比较合适的选择。
For…Next语句的格式如下:
(三)、循环结构例题对比
求1+2+3+……+100的值
1、当for语句中省略step时默认值是1
2、在do……loop 循环中要注意变量初值的设置和循环变量的增值问题
五、习题训练:
1 .[ 单选题 1 分 ]在VB中,某同学要计算1+3+5+……+9的值,他应用循环结构语句如下:s=0 FOR i=1 TO 9 STEP s=s+i请问语句中的“”代表的值是()
A、-1
B、-2
C、2
D、1
2.[ 多选题 2 分]如下VisualBasic程序段,用到了哪些控制结构()。
Private Sub command1_click() S=0 i=16 Do S=S+I i=i+1 Until S>=100 Print"i的值为:";I EndSub
A、顺序结构
B、循环结构
C、层次结构
D、选择结构
3. [ 单选题 1 分 ].以下是一段VisualBasic程序,它的基本结构属于()…Do S=S+I i=i+1 Loop Until S>=100…
A、顺序结构
B、选择结构
C、循环结构
D、树型结构
4. [ 单选题 1 分 ]执行下列VB程序段后,变量j的值为()
S=0 For j=1 to 10 Step 2 S=S+j Next j
A、1
B、10
C、11
D、12
5. [ 单选题 1 分 ]有如下VB程序段,对该程序段执行过程描述正确的是()
Do S=S+1 Loop Until S>100
A、如果S>100,则退出循环
B、如果S<=100,则重复执行S=S+1
C、如果S>100,则重复执行S=S+1
D、不论S初值为多少,至少执行一次S=S+1
6. [ 单选题 1 分 ]在结构化程序设计中通常包含三种不同的控制结构,即:顺序结构、选择结构、循环结构。
下列说法正确的是()
A、一个程序只能包含一种结构
B、一个程序最多可以包含两种结构
C、一个程序可以包含以上三种结构
D、一个程序必须包含以上三种结构
7. [ 单选题 1 分 ]求解S=2+4+6+8+10的VB程序如下,试问程序中的“step”表示()。
S=0 For i=2 to 10 step 2S=s+I Next i
A、函数
B、步长
C、表达式
D、变量
8.阅读下列程序段,程序运行后在文本框中显示的结果是
Private Sub Form_Click()
Dim s As Integer
Dim i As Integer
s = 0
For i = 1 To 100
s = s + i
Next i
= s
End Sub
A 、5051
B 、5050
C 、10101
D 、10100
9.执行以下语句后,a的值是
Dim a As Integer
a = 1
Do While a <> 100
a = a + 2
Loop
A 、101
B 、溢出
C 、99
D 、100
10.补充完善下列程序段
①求s=2+4+6+……+100之和。
Dim i As Integer
Dim s As Integer
s=0
For i=2 To 100 Step 2
s=_________
Next i
Print s
②输出100以内(包含100)能被3整除的数。
Dim I As Integer
I=1
Do
If I Mod 3=0 Then
Print I
End If
I=I+1
Loop Until _________
③
Function func()
Dim i As Integer
Dim s As Integer
s = 0
For i = 10 To 100 Step 10
s = ___________
Next i
func = "s=" & s
End Function
④算法描述
'某学校组织一次读书活动,计划购买各种各样书写笔作为奖品。
'用100元买100支笔,其中钢笔每支5元,圆珠笔每支1元,铅笔1元买6支,'求可行的方案数有多少种
'注:请不要更改原程序结构,删除(1)、(2)、(3),并在对应位置填写正确的代码Function func()
Dim i, j, k As Integer 'i,j,k变量分别存储购买三种笔所用的总金额
func = (1)
For i = 0 To 100
For j = 0 To 100
For k = 0 To 100
If (i + j + k) = 100 (2) (i / 5 + j + 6 * k) = 100 Then func = func + 1
End If
Next k
Next (3)
Next i
End Function
⑤
Private Sub Command1_Click()
Dim sum
sum = (1)
For i = 1 To 6
k = 2 ^ i
sum = (2) + k
Next
= sum
out (sum)
End Sub
⑥
Private Sub Command1_Click()
s = 1
For i = 1 To 10
s = s * (1)
Next
func = s
= func
out (func)
End Sub
⑦
Private Sub Command1_Click() s = 0
For i = 1 To (1)
k = i / (1 + (2))
s = s + k
Next
func = s
= func
out (func)
End Sub。
