地图中的数学基础理论
地图之数学基础

X' Y' 2 1 2 m n
该方程证明:地球面上的微小圆, 投影后通常会变为椭圆,即︰
2
2
微小圆→变形椭圆
以O'为原点,以相交成θ角的两共 轭直径为坐标轴的椭圆方程式。
特别方向︰变形椭圆上相互垂直的两个方向(a,b)及 经向和纬向(m,n)
长轴方向(极大值)a
短轴方向(极小值)b
经线方向m;纬线方向n 据阿波隆尼定理,有 m2 + n2 = a2 + b2
地图投影
1地图投影的意义 地球椭球体表面是不可展曲面,要将曲面 上的客观事物表示在有限的平面图纸上,必 须经过由曲面到平面的转换。 地图投影︰在地球椭球面和平面之间建立 点与点之间函数关系的数学方法,称为地图 投影。 x =f (φ, λ)
y =f2(φ,λ)
1
地图投影的实质︰是将地球椭球面上的经 纬线网按照一定的数学法则转移到平面上。
面积比和面积变形︰投影平面上微小面积(变 形椭圆面积)dF′与球面上相应的微小面积(微小圆 面积)dF之比。
P表示面积比 Vp表示面积变形
dF ' πab P 2 a b dF πl
P = a‧b = m ‧ n
Vp p 1
(θ = 90)
= 0不变 > 0变大 < 0变小
P = m ‧ n ‧ sinθ
M为比例尺分母) • 当制图区域相当大,制图时对景物的缩小比率也相当大,在这种情况
下采用的地图投影比较复杂,地图上的长度也因地点和方向不同而有
所变化。在这种情况下所注明的比例尺含义,其实质是在进行地图投 影时,对地球半径缩小的比率,称为地图主比例尺,地图经过投影后, 地图上只有个别的点或线没有长度变形。其它大于或小于主比例尺的 比例尺称为局部比例尺。 • 地图比例尺的精确定义︰地图上沿某方向的微分线段和地面上相应微 分线段水平长度之比。
《地图数学基础》课件

表达的内容和尺度来决定。
03
地图比例尺
比例尺定义与表示
比例尺定义
地图上的长度与实际地面相应长度之 间的比例关系。
比例尺表示
通常以分数形式表示,如1:10000, 表示地图上1单位长度代表实际地面 10000单位长度。
比例尺与地图精度
比例尺越大,地图精 度越高,表示的地物 地貌越详细。
地图精度还受到地图 投影、制图方法等因 素的影响。
城市规划与管理
地图数学基础在城市规划与管理 中发挥着重要作用,如城市空间 布局规划、城市交通规划、城市 环境监测等。
自然资源管理
地图数学基础在自然资源管理中 应用广泛,如土地资源调查、森 林资源监测、水资源管理等。
灾害监测与应急响
应
地图数学基础能够为灾害监测和 应急响应提供精确的地理信息支 持,如地震、洪涝、火灾等灾害 的监测和预警。
展和地理信息系统的普及,地图数学基础逐渐成为地理信息科学领域的
研究热点。
02
当前研究热点
目前,地图数学基础的研究热点包括地图自动综合、空间数据挖掘、时
空数据分析等方向,这些方向的研究成果将不断推动地图数学基础的进
步和发展。
03
未来展望
随着人工智能、大数据等技术的不断发展,地图数学基础将在智慧城市
、环境保护、公共安全等领域发挥更加重要的作用,其理论和方法也将
THANKS
感谢观看
不断创新和完善。
02
地图投影
投影分类
等面积投影
等方位投影
保持面积不变,但形状和方向可能会 改变。
保持方向不变,但面积和距离可能会 改变。
等距离投影
保持距离不变,但面积和方向可能会 改变。
高等数学知识地图
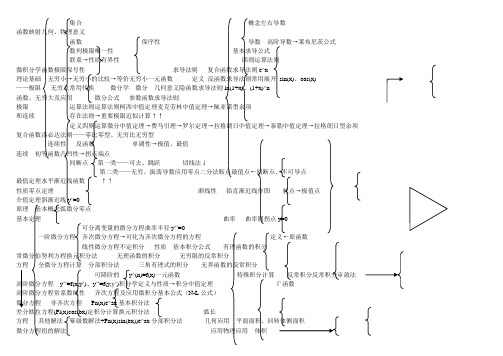
集合概念左右导数函数映射几何、物理意义函数保序性导数高阶导数→莱布尼茨公式数列极限唯一性基本求导公式联系→性质有界性四则运算法则微积分学函数极限保号性求导法则复合函数求导法则e^x理论基础无穷小→无穷小的比较→等价无穷小一元函数定义反函数求导法则常用展开sin(x)、cos(x)——极限无穷及常用代换微分学微分几何意义隐函数求导法则ln(1+x)、(1+x)^n函数、无穷大及应用微分公式参数函数求导法则极限运算法则运算法则柯西中值定理麦克劳林中值定理→佩亚诺型余项和连续存在法则→重要极限近似计算↑↑定义四则运算微分中值定理→费马引理→罗尔定理→拉格朗日中值定理→泰勒中值定理→拉格朗日型余项复合函数洛必达法则——零比零型、无穷比无穷型连续性反函数单调性→极值、最值连续初等函数凸凹性→拐点端点间断点第一类——可去、跳跃切线法↓第二类——无穷、振荡导数应用零点二分法鞍点最值点←间断点、不可导点最值定理水平渐近线函数↑↑性质零点定理渐线性铅直渐近线作图驻点→极值点介值定理斜渐近线y’=0原理基本概念弧微分零点基本定理曲率曲率圆拐点y=0可分离变量的微分方程曲率半径y’’=0一阶微分方程齐次微分方程→可化为齐次微分方程的方程定义←原函数线性微分方程不定积分性质基本积分公式有理函数的积分常微分伯努利方程换元积分法无理函数的积分无穷限的反常积分方程全微分方程计算分部积分法三角有理式的积分无界函数的反常积分可降阶的y^(n)=f(x)一元函数特殊积分计算反常积分反常积分审敛法高阶微分方程y’’=f(x,y’)、y’’=f(y,y’)积分学定义与性质→积分中值定理Γ函数高阶微分方程常系数线性齐次方程及应用微积分基本公式(N-L公式)微分方程非齐次方程Pn(x)e^ax基本积分法差分欧拉方程(Pl(x)cos(bx)定积分计算换元积分法弧长方程其他解法幂级数解法+Pn(x)sin(bx))e^ax分部积分法几何应用平面面积、回转体侧面积微分方程组的解法应用物理应用体积概念、性质条件收敛比较平面点集定义几何级数绝对收敛比值理论基础极限最值定理p级数审敛法根值多元函数连续介值定理常数项级数正项级数极限偏导数定义、计算交错级数多元函数高阶偏导数无穷级数线性性质收敛区间微分学微分法全微分微分积分性收敛域及应用求导法则——复合函数、隐函数敛散性收敛半径→求法应用grad 函数项级数近似计算解微分方程三角级数→正交性↓定义傅立叶级数敛散性→狄利克雷收敛定理X、Y型函数展开R、θ型定义、坐标表示重积分概念模方向角截面法方向方向余弦多元函数三重积分柱坐标面积投影法向量运算加减法方向数积分学球坐标乘法→数乘、数量积、向量积、混合积及应用应用相互关系平行、垂直夹角、投影第一类曲线积分——定义、性质、计算空间方程——一般式、点法式、截距式、三点式↓联系↑解析几何面平面关系——平行、垂直、相交、夹角曲线积分第二类曲线积分——定义、性质、计算与距离——点面、线面、面面线面积分格林公式→平面曲线积分与路径无关的条件向量代数二次曲面——九种常见曲面及方程斯托克斯公式→空间曲线积分与路径无关的条件曲面法线与切平面第一类曲面积分——定义、性质、计算方程——一般式、点向式、参数式、两点式曲面积分↓联系↑直线关系——平行、垂直、相交、异面、夹角——平面束第二类曲面积分——定义、性质、计算线距离——点线、线线概念→数量场、矢量场高斯公式→延任意闭曲面的曲面积分为零的条件方程方向导数→梯度grad曲线投射——投影柱面、投影曲线场论通量→散度div 哈密顿算子▽→拉普拉斯算子△切线与法平面环量→旋度rot。
地图的数学基础

研究全球区域投影时,可将地球视为圆球体。 主要有圆柱投影、伪圆柱投影、多圆锥投影等。 世界各国编制世界航海图、时区图时,经常 采用正轴圆柱投影; 编制世界行政区划图时,欧美一些国家常采 用摩尔维特投影、桑逊投影等, 中国主要采用等差分纬线多圆锥投影和正切差 分纬线多圆锥投影。
伪方位投影
多圆锥投影
1.纬线为同轴圆弧 其圆心均位于中 央经线上; 2.中央经线为直线, 3.其余经线均为对 称于中央经线的 曲线。
多圆锥投影示意图
等差分纬线多圆锥投影
1.经线对称于中央直经线,离中央 经线愈远,经线间隔成等差比例递减; 2.纬线投影为对称于赤道的同轴圆 弧,其圆心位于中经上; 3.极点表示为圆。圆长度为赤道投 影长度的二分之一。 它是任意投影。我国的世界地图 多采用该投影。 我国位于地图中接近中央的位置, 形状比较正确。
等积
投影特性: 1.等积(P=1); 2.所有纬线无长度变形(n=1); 3.中央经线保持等长(m=1)。 4.该投影离中经愈远、纬度愈高变形愈大。 适于:沿赤道或中央经线伸展的地区。
伪圆柱投影(桑逊投影)
经线为对称于中经(直线)的正弦曲线; 纬线为等距平行线,
⑵ 摩尔威特(Mollweide)投影
40°44 ′11.8 ″
S90 = Searth / 2
常用于编制世界地图
及东、西半球地图
伪圆柱投影
等积
基于正弦与摩尔维特投影的分瓣投影
40° 正弦 投影 40°
⑶ 古德(Goode)投影
美地理学家古德(J.Paul Goode)于1923年提出在整 个制图区域主要部分中央都设置一条中央经线,分别进 行投影,则全图就分成几瓣,各瓣沿赤道连接在一起。
第三章 地图的数学基础

第三章地图的数学基础第一节地图投影的概念地图投影是地图学重要组成部分之一,是构成地图的数学基础,在地图学中的地位是相当重要的。
地图投影研究的对象就是如何将地球体表面描写到平面上,也就是研究建立地图投影的理论和方法,地图投影的产生、发展、直到现在,已有一千多年的历史,研究的领域也相当广泛,实际上它已经形成了一门独立的学科。
我们学习投影的目的主要是了解和掌握最常用、最基本的投影性质和特点以及他们的变形分布规律,从而能够正确的辨认使用各种常用的投影。
一、地球的形状和大小地球的形状近似于一个球体,但并不是一个正球体,而是一个极半径略短、赤道半径略长,北极略突出、南极略扁平,近似于梨形的椭球体。
这个不规则的地球体满足不了测绘工作的需要,于是人们选择了一个最接近地球形状的旋转椭圆体表示地球,称为地球椭球体。
地球椭球体的大小,由于推算所用资料、年代和方法不同,许多科学家所测定地球椭球体的大小也不尽相同,我国1953年以前采用海福特椭球体,从1953年起采用克拉索夫斯基椭球体,它的长半径a=6378245m,短半径b=6356863m ,偏率d=a-b/a=1:298.3 这是原苏联科学家克拉索夫斯基1940年测定的。
由于地球椭球体长短半径差值很小,约21km,在制作小比例尺地图时,因为缩小的程度很大,如制作1:1000万地图,地球椭球体缩小1000万倍,这时长短半径之差只是2.1mm,所以在制作小比例尺地图时,可忽略地球扁率,将地球视为圆球体,地球半径为6371km。
制作大比例尺地图时必须将地球视为椭球体。
二、地图表面和地球球面的矛盾地图通常是绘在平面介质上的,而地球体表面是曲面,因此制图时首先需要把曲面展成平面,然而,球面是个不可展的曲面,要把球面直接展成平面,必然要发生断裂或褶皱。
无论是将球面沿经线切开,或是沿纬线切开,或是在极点结合,或是在赤道结合,他们都是有裂隙的。
三、地图投影的概念球面上任一点的位置是用地理坐标(φ、λ)表示的,而平面上点的位置是用直角坐标(纵坐标是x,横坐标是y)表示的,所以要将地球球面上的点转移到平面上,必须采用一定的数学方法来确定地理坐标与平面坐标之间的关系。
地图的数学基础

我国所采用的参照椭球体 1954年北京坐标系采用1940年克拉索夫斯基椭球体
参数; 1980年西安坐标系采用1975年IUGG(国际大地测量
与地球物理联合会)椭球体参数; 2000年国家大地坐标系 全球定位系数则采用WGS-84世界大地坐标系统,
G873)椭球体。
地球体
自然表面
大地水准面
天文纬度:在地球上定义为铅垂线与赤道平面间的 夹角。
② 大地经纬度:表示地面点在参考椭球面上的位置,
用大地经度λ 、大地纬度 和大地高 h表示。
大地经度λ :指参考椭球
面上某点的大地子午面与 本初子午面间的两面角。 东经为正,西经为负。
大地纬度 :指参考椭球面
上某点的垂直线(法线)与 赤道平面的夹角。北纬为正, 南纬为负。
(二)地球的物理表面
当海洋静止时,自由水面与该面上各点的重力方 向(铅垂线)成正交,这个面叫水准面。
大地水准面:假定海水静止不动,将海水面无限延 伸,穿出大陆包围地球的球体。它实际是一个起伏不 平的重力等位面——地球物理表面。
大地体:大地水准面包围的形体。
研究大地水准面的意义 1. 地球形体的一级逼近__大地体:
物理表面
测量实施的 基础面
参考椭球面
数学表面
测量计算的 基础面
自然面、物理面、数学面关系图
自然表面
大地水准面
参考椭球面
二、地理坐标
用经线、纬线、经度、纬度表示地面点位的球面 坐标。
天文经纬度 大地经纬度 地心经纬度
① 天文经纬度:表示地面点在大地水准面上的位 置,用天文经度和天文纬度表示。
天文经度:观测点天顶子午面与格林尼治天顶子午 面间的两面角。在地球上定义为本初子午面与观测 点之间的两面角。
第二讲 地图数学基础
• 地图是地理学和地质学等区域性学科的“第二 语言”。
• 地球科学既是地图学的应用对象又是地图学的 研究对象,地图作为科学研究的有效工具,促 进了地球科学的发展。
• 地理学和地质学等区域性学科又是地图学,特 别是专题地图学的科学内容基础和主要资料来 源。
• 地图学与地学等区域性学科相结合,形成地球 学20科20/8/1各2 部门或区域的专题地图学,如地质制图
2020/8/12
2020/8/12
国家大地原点(陕西泾阳)
主要的地球椭球体元素
名称 地心 地轴 地极 子午面 子午圈 首子午面 首子午线 法线 平行面 平行圈 赤道面 赤道圈 地理坐标系
现代地图学与测绘学的关系
• 没有精密的测量就没有精确的地图;测制地形图 的过程中,各种成图要素的表示方法,地图概括 及其编辑工作,都需要地图学方面的知识。
• 在我国,行政部门与学会组织,都把地图学与测 量学结合在一起统一管理,把地图学作为测绘学 的一个分支;同样地理学的相关单位也把地图学 作为地理学的组成学科之一。在国家科学分类系 统中,地图学作为理科,在地球科学大类中,同 自然地理学、地质学、海洋学等并列为二级学科
• 美国的地质调查局(USGS)甚至把地质学、地理学、测 绘学组合在一起,除编制生产地形图、地质图、还编制生 产其他专题地图。
2020/8/12
二.地球的形状与大小
2.1地球的自然表面(自然球体) 2.2地球的物理表面(大地体) 2.3地球的数学表面(旋转椭球体)
2020/8/12
2020/8/12
2020/8/12
2.3.2我国与测量制图相关的几个椭球体参数
• 参考椭球体定位:地球的长半径、短半径和扁 率测定后,还必须确定大地水准面与椭球体面 的相对关系,即确定与局部地区大地水准面符 合最好的一个地球椭球体-参考椭球体,这项 工作就是参考椭球体定位。
地图的数学基础(najin)

墨卡托投影属于正轴等角圆柱投影。该投 影设想与地轴方向一致的圆柱与地球相切或 相割,将球面上的经纬线网按等角的条件投 影到圆柱面上,然后把圆柱面沿一条母线剪 开并展成平面。经线和纬线是两组相互垂直 的平行直线,经线间隔相等,纬线间隔由赤 道向两极逐渐扩大(如图)。图上无角度变 形,但面积变形较大。
(2)空间斜轴墨卡托投影 (Space Oblique Mercator Projection)
假想一个扁率极小的椭 圆,绕大地球体短轴旋转所 形成的规则椭球体称之为地 球椭球体
地球椭球体三要素: 长半径 a 短半径 b 扁率f
图2-2 地球自然 表面、大 地水准面 和地球椭 球体的关 系
由于推算的年代、使用的方法以及测定地区
的不同,地球椭球体的数据并不一致,近一个世 纪来,世界上推出了几十种地球椭球体数据。
(3)长度比和长度变形
长度比 µ 是投影面上一微小线段ds’和椭
球面上相应微小线段ds之比。用公式表达为:
µ=ds’/d s
长度比用于表示投影过程中,某一方向上 长度变化的情况。µ>1,说明投影后长度拉长, µ<1,说明投影后长度缩短了;µ=1,则说明 特定方向上投影后长度没有变形。
注意长度比与比例尺区别:
1:295.0
埃及,加拿大,美国,墨西哥,法国
1:293.47
越南,罗马尼亚,法国,南非
地图学的数学基础

不同的比例尺适用于不同的制图需求和目的,应根据实际情况进行选择。
04 地图符号与注记
地图符号的分类与特点
分类
按性质可分为几何符号、艺术符号和 透视符号;按形状可分为点状符号、 线状符号和面状符号。
特点
具有形象性、约定性、定位性和可量 测性。
地图注记的要素与原则
动态可视化
运用动画技术实现地图数据的动态可视化表达,展示要素的空间变 化过程和趋势。
交互式可视化
提供用户与地图的交互功能,如缩放、平移、旋转等,以及要素选择、 属性查询等交互操作,增强用户体验和数据分析效果。
06 地图制图的数学方法
制图综合的数学方法
地图综合算法
包括基于规则的算法、基于知识的算法和基于机器学习的算法等, 用于从大量地理数据中提取关键信息并进行综合。
地图比例尺是表示地图上某一长 度与相应地面长度之间的比例关
系。
比例尺反映了地图对地面的缩小 程度,是地图的基本要素之一。
比例尺通常表示为分数或比值的 形式,如1:10000,表示地图上 1单位长度对应地面上10000单
位长度。
地图比例尺的表示方法
数字式
用数字直接表示比例尺, 如1:50000,简洁明了。
利用数学方法确定注记的位置、方向和排列方式,确保注记在地图上的正确配置 和显示。同时,还可以通过数学运算对注记进行缩放、旋转和平移等操作,以适 应不同比例尺和投影方式下的地图显示需求。
05 地图数据的处理与分析
地图数据的获取与处理
数据来源
地图数据可以通过多种途径获取, 包括卫星遥感、航空摄影、地面 测量等。
网络分析方法
如最短路径分析、可达性分析、中心性分析等,用于研究地理网 络的结构和功能。
地图中的数学基础理论

高斯投影的基本条件: (1) 中央经线和赤道的投影为 直线,且为投影的对称轴; (2) 投影后无角度变形,即同 一地点的各方向上长度比不变 ; (3) 中央经线投影后保持长度 不变,即m0=1。
高斯投影经纬网形状:
中央经线和赤道投影为互相垂直 的直线
其余经线的投影为对称凹向中央 经线的曲线,纬线的投影为对称 凸向赤道的曲线
实际远洋航行时,一般把大圆航线展绘到墨卡托投影的海 图上,然后把大圆航线分成几段,每一段连成直线,就是 等角航线。船只航行时,总的情况来说,大致是沿大圆航 线航行。因而走的是一条较近路线,就每一段来说,走的 又是等角航线,不用随时改变航向,从而领航十分方便。
三、等距正轴切圆柱投影
投影条件:圆柱面切于赤道,故赤道的投影为正长,经线 投影后的长度为正长。
二、墨卡托投影
赤道投影为正长,纬线投影成和赤道等 长的平行线段,即离赤道越远,纬线投 影的长度也越大,为了保持等角条件, 必须把地图上的每一点的经线方向上的 长度比和纬线方向上的长度比相等。所 以随着纬线长度比的增加,相应经线方 向上的长度比也得增加,并且增加的程 度相等。所以在墨卡托投影中,从赤道 向两极,纬线间隔越来越大。
六、方位投影变形性质的图形判别
方位投影经纬线形式具有共同的特征,判别时先看构成形 式(经纬线网),判别是正轴、横轴、斜轴方位投影。
正轴投影,纬线为以投影中心为圆心的同心圆,经线为放 射状直线,夹角相等。横轴投影,赤道与中央经线为垂直 的直线,其他经纬线为曲线。斜轴投影,除中央经线为直 线外,其余的经纬线均为曲线。
长半径和纬线方向一致,短半径与经线方 向一致,且等于微圆半径r,又因自投影中 心,纬线扩大程度越来越大,所以变形 椭圆的长半径也越来越长,椭圆越来越扁。 常用来做两极的投影。
第2章 地图的数学基础

面积比与面积变形
• 面积比P就是投影面上的微分面积与球面上相应的微分 面积之比,即投影面上的变形椭圆的面积与球面上微分 圆的面积之比。 • P=a·b P=a·b=m·n P=m·n·sinθ • 面积比也是一个变量,在地图上会因点的位置不同而不 同。 • 面积变形(Vp)指面积比与1的差值,Vp = P-1 • 面积比同长度比一样,也是一个只有大于1或小于1(个 别地方等于1)而没有负值的相对数量,而面积变形则 有正有负。 • 面积比大于1,面积变形为正,表示投影后面积增大; 面积比小于1,面积变形为负,表示投影后面积缩小; 面积比等于1,面积变形为零,表示投影后面积不变。
2.2我国的大地坐标系统
大 地 控 制 网 平面控制网(由三角测量或导线测量完成 )
大地原点 大地坐标系 三角点△、导线点□ 地理坐标 1980中国国家大地坐标系 平面位置
高程控制网(由水准测量或三角高程测量完成)
高 绝对高程 水准原点 水准点 程 相对高程 高程系 1985年国家高程基准 值
高程位置 地面点位
• 地理坐标,就是用经纬度表示地面 点位置的球面坐标。 1.天文经纬度
2.大地经纬度 3.地心经纬度
大地体
地球椭球体 地球椭球体
天文经纬度:
天文经度
天文测量法
天文纬度(铅垂线与赤道面 的夹角)
大地体
测有天文经纬度坐标的地面点, 称为天文点,它是一种地面控制 点。如大地坐标原点。符号为☆
大地水准面 铅 垂 线
§4 地图投影的应用
制图区 域范围
地图比例尺 教学内容 投影方法
1:100万
中 小
等角圆锥投影
4.1 地形图投影
大中比例尺
高斯—克吕格投影
地图学第三章 地图的数学基础(全)_OK

1
• 坐标网
• 球面坐标系(大地坐标系)
地 图 投 • 平面直角影坐标系(高斯平面直角坐标系)
• 比例尺
2
第二节 地图投影
为什么学习地图投影 ?
建立平面坐标系的需要
制图的需要 简化计算的需要
3
4
一、地图投影的概念
地图投影 依据一定的数学法则,将不可展的地球曲
面运用特定的数学方法展示到平面上,最终在地表面 点与地图平面点之间建立一一对应的关系
6
7
8
• 1. 变形的概念
• 长度变形 • 面积变形 • 角度变形
9
2.变形椭圆
取地面上一个微分圆(小到可忽略地球曲面的 影响,把它当作平面看待),它投影到平面上通常 会变为椭圆,通过对这个椭圆的研究,分析地图投 影的变形状况。这种图解方法就叫变形椭圆。
X ' m X
为经线长度比;
Y'n Y
34
• 切圆锥投影:相切的纬线是没有变形的线,称为标准纬线
• 从标准纬线向南、北方向变形逐渐增大
• 割圆锥投影:有两条相切的纬线是标准纬线
• 之间,纬线长度比 < 1;
• 之外:
〉1;
• 离标准纬线越远,变形越大。
35
• 3、适用地区 • 适于制作中纬度沿东西方向延伸地区的地图。 • 世界上广大陆地位于中纬度地区,圆锥投影的经纬线网形状简单,所以被广泛应 用
/ 2) / 2)
sin esin
21
四、投影的分类
• 1、按变形性质分类
影等 角 投
ω=0 θ = 900 a = b或m=n
22
影等 面 积 投
Vp = 0 P = ab = 1 a = 1/b 或 b=1/a
地图的数学基础2

§3 常见地图投影一.方位投影以平面为投影面,使平面与椭球体相切或相割,将球面上的经纬线网投影到平面上形成方位投影。
1、变形分布规律其等变形线是以投影中心为圆心的同心圆。
投影中心是没有变形的点,从投影中心向四周变形逐渐增大。
在投影平面上,由投影中心向各方向的方位角保持不变。
2、正轴方位投影切点在北极或南极,又叫极地投影。
经纬线形状:纬线为同心圆,经线为自圆心辐射的直线,其夹角等于经差。
在正轴投影中,因为经线和纬线正交,所以经纬线方向和主方向一致。
一般用于绘制南、北半球地图或北极、南极区域地图。
按变形性质又可以分为等积、等角、等距投影等。
1)正轴等角方位投影经纬线形状:纬线为同心圆,经线为自圆心辐射的直线,其夹角等于经差。
经线和纬线正交,所以经纬线方向和主方向一致。
在中央经线上纬线间隔自投影中心向外逐渐增大;经线夹角等于相应的经差。
投影变形情况:①无角度变形,任一点长度比相同,极值长度比相等(a=b),经纬线长度比相等(m=n)。
②微分圆投影后保持正圆性质。
③极点为投影中心,是无变形点,距投影中心愈远长度变形和面积变形愈大, 在投影边缘面积变形是中心的四倍。
2)正轴等距方位投影经纬线形状:纬线为同心圆,经线为自圆心辐射的直线,其夹角等于经差。
经线和纬线正交,所以经纬线方向和主方向一致。
经线投影后保持正长,所以投影后的纬线间距相等。
投影变形情况:①经线方向没有长度变形(m=1),各纬圈间的距离与实地相等。
②极点为投影中心,为无变形点。
③等变形线是以极点为中心的同心圆,距投影中心愈远角度变形和面积变形愈大。
等距切方位投影亦称波斯托等距方位投影。
3)正轴等积方位投影经纬线形状:纬线为同心圆,经线为自圆心辐射的直线,其夹角等于经差。
经线和纬线正交,所以经纬线方向和主方向一致。
在中央经线上纬线间隔自投影中心向外逐渐减小。
投影变形情况:①没有面积变形,面积比等于1,但角度变形较大②沿经线长度比大于1,沿纬线长度比小于1,两者互为倒数,面积比等于1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、横轴方位投影
平面与球面相切,其切点位于赤道上的任意点。特点:通 过投影中心的中央经线和赤道投影为直线,其他经纬线都 是对称于中央经线和赤道的曲线。
等距方位投影属于任意投影,它既不等积也不等角。投影后经 线保持正长,经线上纬距保持相等。
纬线投影后为同心圆,经线投影为交于纬线圆心的直线束,经 线投影后保持正长,所以投影后的纬线间距相等。经纬线投影 后正交,经纬线方向为主方向。
角度、面积等变形线为以投影中心为圆线的同心圆。 球面上的微圆投影为椭圆,且误差椭圆的
五、 横轴、斜轴方位投影变形分布规律
投影面在p点与地球面相切,过新极点p可做许多大图, 命名为垂直圈,再作垂直于垂直圈的各圈,命名为等高圈 。这样垂直圈相当于地理坐标系的经线圈,等高圈相当于 纬线圈,等高圈和垂直圈投影后的形式和变形分布规律和 正轴方位投影时,情况完全一致。
正轴、横轴、斜轴方位投影的误差分布规律是一致的。等 变形线都是以投影中心为圆心的同心圆,不同的是在横轴 和斜轴方位投影中,主方向和等高圈垂直圈一致,而经纬 线方向不是主方向。
的经差,沿经线方向上的长度比大于1,赤道上各点沿经线方 向上的长度变形比原来扩大1倍。 投影的误差分布规律:由投影中心向外逐渐增大。 经纬线投影后,仍保持正交,所以经纬线方向就是主方向,又 因为m = n,即主方向长度比相等, 无角度变形,但面积变形较大,边缘面积变形是中心的四倍。
2.正轴等距方位投影
四、斜轴方位投影
斜轴等距方位投影:中央经线上 的纬线间隔相等。
斜轴等积方位投影:中央经线上 自投影中心向上、向下纬线间隔 是逐渐缩小的。
斜轴等角方位投影:中央经线上 投影中心向上、向下纬线间隔逐 渐增大。
五、 横轴、斜轴方位投影变形分布规律
横轴和斜轴方位投影的变形大小和分布规律与正轴投影完 全一致,横轴、斜轴投影由于投影面中心不在地理坐标极 点上,如果仍用地理坐标决定地面点的位置,而将这一点 投影到平面上,就变得复杂了。但是如果我们在地球表面 上重新建立一种新的坐标系,使新坐标系的极点在投影面 的中心点上,这样对于横轴和斜轴投影来说,投影面与新 极点的关系,也就和正轴投影的投影面与地理极的关系一 样了,这样问题就简单多了,正轴的公式就可以应用到横 轴和斜轴投影中去,而只是地面上点的位置用不同的坐标 系表示而以。
三、横轴方位投影
横轴等距方位投影:中央经线上 从中心向南北,纬线间隔相等; 赤道上,自投影中心向东西, 经线间隔逐渐扩大。
横轴等积方位投影:中央经线上 从中心向南北,纬线间隔逐渐 缩小;赤道上,自投影中心向 东西,经线间隔也是逐渐缩小 的。
四、斜轴方位投影
投影面切于两极和赤道间的任意一点上。中央经线投影为 直线,其他经线投影为对称于中央经线的曲线,纬线投影 为曲线。
正轴圆柱投影
经线投影为平行直线,间距 和经差成正比。
纬线投影成为一组与经线正 交的平行直线,间距视投影 条件而异。
和圆柱面相切的赤道弧长或 相割的两条纬线的弧长为正 长无变形。
圆柱投影按变形性质可分为 等角圆柱投影、等积圆柱投 影和任意圆柱投影。
二、墨卡托投影
等角正轴切圆柱投影是荷兰地图学家墨卡托于1569年所 创,所以又称墨卡托投影。
六、方位投影变形性质的图形判别
方位投影经纬线形式具有共同的特征,判别时先看构成形 式(经纬线网),判别是正轴、横轴、斜轴方位投影。
正轴投影,纬线为以投影中心为圆心的同心圆,经线为放 射状直线,夹角相等。横轴投影,赤道与中央经线为垂直 的直线,其他经纬线为曲线。斜轴投影,除中央经线为直 线外,其余的经纬线均为曲线。
等变形线都是以投影中心为圆 心的同心圆。 包括等角、等积、 等距三种变形性质,主要用于 制作两极地区图。
1.正轴等角方位投影
投影条件:视点位于球面上,投影面切于极点。 纬线投影为以极点为圆心的同心圆,纬线方向上的长度比大于
1。赤道上的长度变形比原来扩大1倍。 经线投影为以极点为圆心的放射性直线束,经线夹角等于相应
地图中的数学基础理论
1. 方位投影分类
根据投影面和地球球相切位置不同 当投影面切于地球极点时,为。 当投影面切于赤道时,为横轴方位投影。 当投影面切于既不在极点也不在赤道时,斜轴方位投影。
二、正轴方位投影
投影中心为极点,纬线为同心 圆,经线为同心圆的半径,两 条经线间的夹角与实地相等。
根据中央经线上经纬线图的间隔变化,判别变形性质。等 角投影,中央经线上,纬线间隔从投影中心向外逐渐增大; 等积投影,逐渐缩小;等距投影,间隔相等。
方位投影总结
特点:投影平面上,由投影中心(平面与球面的切点)向 各方向的方位角与实地相等,其等变形线是以投影中心为 圆心的同心圆。
绘制地图时,总是希望地图上的变形尽可能小,且分布较 均匀。一般要求等变形线最好与制图区域轮廓一致。因此, 方位投影适合绘制区域轮廓大致为圆形的地图。
圆柱面和地球体相切时,称为切圆柱投影,和地球体相 割时称为割圆柱投影。
由于圆柱和地球体相切相割的位置不同,圆柱投影又分 为正轴、横轴和斜轴圆柱投影三种。
正轴、横轴和斜轴圆柱投影
正轴圆柱投影:圆柱轴和地球地轴一致; 横轴圆柱投影:圆柱轴和地轴垂直并通过地心; 斜轴圆柱投影:圆柱轴通过地心,和地轴不垂直不重合。
从区域所在的地理位置来说,两极地区和南、北半球图采 用正轴方位投影;赤道附近地区和东、西半球图采用横轴 方位投影;其他地区和水、陆半球图采用斜轴方位投影。
第五节 圆柱投影
一、圆柱投影的概念和种类
假定以圆柱面作为投影面,把地球体上的经纬线网投影 到圆柱面上,然后沿圆柱面的母线把圆柱切开展成平面, 就得到圆柱投影。
二Hale Waihona Puke 墨卡托投影赤道投影为正长,纬线投影成和赤道等 长的平行线段,即离赤道越远,纬线投 影的长度也越大,为了保持等角条件, 必须把地图上的每一点的经线方向上的 长度比和纬线方向上的长度比相等。所 以随着纬线长度比的增加,相应经线方 向上的长度比也得增加,并且增加的程 度相等。所以在墨卡托投影中,从赤道 向两极,纬线间隔越来越大。
