等式约束极值问题-外点罚函数法
第二节 罚函数法

β ∈ (0,1) ,允许误差 ε > 0 ,置 k = 1 ;
k −1 x 为初点,求解无约束优化问题 Step2: 以
min G ( x, r ) = f ( x) + rB( x) s.t. x ∈ int S
设其极小点为 x ;
G ( x, r ) = f ( x) − r ∑ ln g i ( x)
m
-----对数障碍函数
由 G( x, r ) 的定义, r 取值越小,问题
min G ( x, r ) = f ( x) + rB( x) s.t. x ∈ int S
的最优解越接近约束优化问题的最优解。 2. 内点罚函数法的计算步骤
k min H ( x) x Step4: 以 为初始点求解无约束问题 x∈Sk k +1 的最优解
x k +1 ,其中
H k +1 ( x) = −∑ gi ( x) + rk +1 ∑ gi ( x)
i∈I k i∈J k
, Sk = {x | gi ( x) > 0, i ∈ J k }
令 rk + 2 = βrk +1 , k = k + 1, 返回 Step2. 注:该算法中,对于 k = 0,1,2,L ,有 I k +1 ⊂ I k , J k +1 ⊃ J k ,且 最后某个 I k = ∅ 。 三. 广义乘子法 1. 对于等式约束优化问题
φ ( x, y , ω , σ ) = f ( x ) − ∑ ω j ( g j ( x ) − y j ) +
2 j =1 l
1 外罚函数法

算法步骤 Step 1
外罚函数法
Step 2
Step 3
举例
外罚函数法
解
举例
外罚函数法
举例
外罚函数法
外罚函数法
收敛性分析
≤
外罚函数法
收敛性分析
min F ( x , σ k ). n
x∈R
这种通过求解一系列无约束问题来获得约束问题最优解的方法 统称为序列无约束极小化方法(sequential unconstrained 统称为序列无约束极小化方法 minimization technique),简称 ,简称SUMT法. 法
外罚函数法
外罚函数法实施中的问题和说明
罚函数
罚因子
罚项
min F ( x , σ ) n
x∈R ∈
通过求解无约束问题(10.1.6) 通过求解无约束问题 能够得到一般约束问题(10.1.1) 能够得到一般约束问题 的近似解. 的近似解
性质
外罚函数法
min F ( x , σ 1 ) n
x∈R ∈
随着罚因子的不断增大,无约束问题 随着罚因子的不断增大,无约束问题(10.1.6)的最优解快 的最优解快 速向约束问题(10.1.1)的可行域边界靠拢;并且罚因子越 的可行域边界靠拢; 速向约束问题 的可行域边界靠拢 大,该最优解越靠近约束问题的最优解. 该最优解越靠近约束问题的最优解
第十章 罚函数法与广义乘子法
可行方向法:在可行域内寻找使目标函数下降的点列. 可行方向法:在可行域内寻找使目标函数下降的点列. 但是, 但是,这类方法对于带非线性约束的最优化问题求解 效果一般都不太理想. 效果一般都不太理想. 罚函数法: 利用原问题的目标函数和约束条件构造 罚函数法 新的目标函数--罚函数 罚函数, 新的目标函数 罚函数 把约束最优化问题转化为 相应的罚函数的无约束最优化问题来求解. 相应的罚函数的无约束最优化问题来求解
一、惩罚函数法(SUMT)

(4)应注意的问题
(a) 在step2中,可用无约束优化问题的算法求解
min
x R n
k
(
x
)
f ( x ) k p( x )
(b) 在实际计算中,判断x* (k ) D 用 g j ( x* (k )) ( j 1,2,, m)或 k p( x) .
(c)
k 1 k
x
)
算法步骤相同
(8) 算法收敛性:
f(x ) f(x )
k 1
k
p(x ) p(x )
k 1
k
k(1 x ) (k x )
k 1
k
结论 1. 若点列{ x } 是由外点法产生的,则有 k
列 { x }的任何极限点一定是所求问题的极小点。 k
都是 R 上的连续函数,则由外点法产生的点 n
解:构造增广函数k ( x)如下: k ( x) (x 1)2 k min2{ x 2,0}
( x 1)2
(x 1)2 k ( x 2)2
if x 2 if x 2
dk (
dx
x)
(2 x 1)
(2 x 1)
2k
(
x
因子的缩小系数), k : k 1,转 step 2。
(4) 例子:试用内点法(内部惩罚函数法)求解如下优化问题 min f ( x) 1 x3 3 s.t. x 1 0
解:构造增广函数 k ( x)如下:
k(x)
x3
k
1 x1
由
d k ( x)
dx
x2
k
(2)q( x) if x D
matlab用外点罚函数法求解等式约束最优化问题

一、引言我们需要明确什么是等式约束最优化问题。
在实际应用中,经常会遇到这样的问题:在满足一定的条件约束下,寻找一个使得某个目标函数达到最优值的解。
而等式约束最优化问题就是在满足一系列等式约束条件的前提下,求解出目标函数的最优值和对应的解向量。
在数学领域,等式约束最优化问题有着重要的理论和实际意义,对于工程、经济、管理等领域都有着广泛的应用。
二、问题描述一个典型的等式约束最优化问题可以用如下的数学形式来描述:minimize f(x)subject to:g(x) = 0其中,f(x)是目标函数,x是自变量向量,g(x)是等式约束条件函数。
三、外点罚函数法外点罚函数法是一种常用的方法,用于求解等式约束最优化问题。
它的基本思想是通过对目标函数和约束条件进行适当的变换,将等式约束问题转化为无约束问题。
具体地,外点罚函数法通过引入罚函数,将约束条件融入到目标函数中,构造出一个新的优化问题。
然后将这个新问题求解为原问题的近似解。
在优化的过程中,罚函数的惩罚项会惩罚那些违反约束条件的解,从而使得优化过程能够逼近满足约束条件的最优解。
四、matlab中的外点罚函数法求解在matlab中,可以利用现成的优化工具箱来求解等式约束最优化问题。
其中,fmincon函数是用来求解带有等式约束的最优化问题的。
它允许用户自定义目标函数和约束条件函数,并指定优化的初始点和其他参数。
通过在fmincon函数中调用外点罚函数法求解等式约束最优化问题,可以得到目标函数的最优值和对应的解向量。
五、实例分析为了更加直观地理解matlab中外点罚函数法的应用,我们来举一个简单的实例。
假设我们要求解如下的等式约束最优化问题:minimize f(x) = x1^2 + x2^2subject to:g(x) = x1 + x2 - 1 = 0我们需要将目标函数和约束条件转化成matlab可以识别的形式。
我们可以利用fmincon函数来求解这个最优化问题。
罚函数法

外罚函数法算法
Step1: 给出 x0 ∈ Rn (可是不可行点), > 0(ε =10−4 ) ε 罚因子 σ1(σ1 =1) , 放大系数 C(C =10) , k =1. Step2: 以 xk−1 为初始点求无约束问题: ~ m P( x,σk ) = f ( x) +σk P( x) 得 xk = x(σk ). in ~ Step3: 若 σk P(xk ) < ε , 则 x* = xk ,停; 否则转step4 Step4: 令 σk+1 = Cσk , k = k +1, 转step2.
Q f (xk ) ≤ P(xk ,σk ) ≤ f x
设其极限为 f . ∴ { f (xk )} 亦为单调有界序列, ~ ∴ lim σk P(xk ) = lim [P(xk ,σk ) − f (xk )] = p0 − f 0 k→+∞ k→+∞ ~ Q σk →+∞ ∴ lim P(xk ) = 0 k→+∞ ~ ~ ~ 且 P(x) 连续; P(~) = 0 即 ~ 为可行解 x ∴ x Q x →x
0
( )
*
Q x 为最优解;∴ f x* ≤ f (~) x ~, f (x) 连续; f (~) = lim f (x ) ≤ f (x* ) ∴ x Q xk → x k k→+∞ * ~) 即 ~ 为(3)的整体最优解. ∴ f x = f (x x
k *
( )
( )
外罚函数法评价
(1) 如果有了求解无约束问题的好算法,利用 外罚函数法求解约束问题很方便. (2) 每个近似解 x(σk ) 往往不是可行解,这是某 些实际问题所无法接受的. 内罚函数法可以解决. (3) 由收敛性定理 σk 取越大越好, σk 越大将 而 造成增广目标函数 P( x,σ ) 的Hesse阵条件数越 大,趋于病态,给无约束问题求解增加很大困 难,甚至无法求解.乘子法可解决这个问题.
第一章 第五节 有约束条件的极值问题

一般地,有约束问题模型为 (1)Min f(x) i=1,2,...,m hi(x)=0 可用如下形式惩罚函数
F( X , µ) = f (x) + µ∑(hi (x)) 2
i=1
m
(2)Min f(x) 2 gj(x)≥0 j=1,2,...,l 其惩罚函数可为 F(X,μ)=f(x)+μψ(x)
∂F = (x1 +1)2 + 2µ(x1 −1) = 0 ∂x1
∂F = 1+ 2µx2 = 0 ∂x ∂x2
r 解得 x = (x , x )T = (−1− µ + µ2 + 4µ ,− 1 µ)T 1 2 2 取μ1=0.001,β=10为初始值,然后μ2…μ8μ9,分 别取0.01,0.1,1,10,100,1000,10000,100000得 X*=(0.9999,-0.000005)T 本 题 最 优 解 为 X*=(1,0)T, 最 优 目 标 函 数 值 f(X*)=8/3。
第五节 有约束条件的极值问题 Min f(x) hi(x)=0 gj(x)≥0 i=1,2,...,m j=1,2,...,l
对于有约束条件问题采取制约函数法: 可将有约束条件的问题转化为一系列无约束极值问题。 常用的制约函数有两类; 一为惩罚函数,二为障碍函数。 对应于两种函数有外点法和内点法。
一 外点法 以例来说明外点法基本思路: Min f(x)=x12+x22 x1+x2-2=0 该问题的可行域是直线 x1 + x2 − 2 = 0 构造出这样的函数,对可行点不加“惩罚”,对非可 行点给以正无穷大的“惩罚”,即 当x1+x2=2时 当x1+x2≠2时 F(X)=x12+x22 F(X)=+∞
1 2 m f (x) = (x1 +1) + x2 in 3 x1 −1≥ 0 x2 ≥ 0
分享:惩罚函数法(内点法、外点法)求解约束优化问题最优值

分享:惩罚函数法(内点法、外点法)求解约束优化问题最优值1 用外点法求下列问题的最优解方法一:外点牛顿法:clcm=zeros(1,50);a=zeros(1,50);b=zeros(1,50);f0=zeros(1,50);% a b为最优点坐标,f0为最优点函数值,f1 f2最优点梯度。
syms x1 x2 e; %e为罚因子。
m(1)=1;c=10;a(1)=0;b(1)=0; %c为递增系数。
赋初值。
f=x1^2+x2^2+e*(1-x1)^2;f0(1)=1;fx1=diff(f,'x1');fx2=diff(f,'x2');fx1x1=diff(fx1,'x1');fx1x2=diff(fx1,'x2');fx2x1=diff(fx2,'x1');fx2x2=diff(fx2,'x2');%求偏导、海森元素。
for k=1:100 %外点法e迭代循环.x1=a(k);x2=b(k);e=m(k);for n=1:100 %梯度法求最优值。
f1=subs(fx1); %求解梯度值和海森矩阵f2=subs(fx2);f11=subs(fx1x1);f12=subs(fx1x2);f21=subs(fx2x1);f22=subs(fx2x2);if(double(sqrt(f1^2+f2^2))<=0.001) %最优值收敛条件a(k+1)=double(x1);b(k+1)=double(x2);f0(k+1)=double(subs (f));break;elseX=[x1 x2]'-inv([f11 f12;f21 f22])*[f1 f2]';x1=X(1,1);x2=X(2,1);endendif(double(sqrt((a(k+1)-a(k))^2+(b(k+1)-b(k))^2))<=0.001)&&(double(abs((f0(k+1)-f0(k))/f0(k)))<=0.001) %罚因子迭代收敛条件a(k+1) %输出最优点坐标,罚因子迭代次数,最优值b(k+1)kf0(k+1)break;elsem(k+1)=c*m(k);endend方法二:外点梯度法:clcm=zeros(1,50);a=zeros(1,50);b=zeros(1,50);f0=zeros(1,50);syms d x1 x2 e;m(1)=1;c=10;a(1)=0;b(1)=0;f=x1^2+x2^2+e*(1-x1)^2; f0(1)=1;fx1=diff(f,'x1');fx2=diff(f,'x2');for k=1:100x1=a(k);x2=b(k);e=m(k);for n=1:100f1=subs(fx1);f2=subs(fx2);if(double(sqrt(f1^2+f2^2))<=0.002)a(k+1)=double(x1);b(k+1)=double(x2);f0(k+1)=double(subs (f));break;elseD=(x1-d*f1)^2+(x2-d*f2)^2+e*(1-(x1-d*f1))^2;Dd=diff(D,'d'); dd=solve(Dd); x1=x1-dd*f1; x2=x2-dd*f2;endendif(double(sqrt((a(k+1)-a(k))^2+(b(k+1)-b(k))^2))<=0.001)&&(double(abs((f0(k+1)-f0(k))/f0(k)))<=0.001) a(k+1)b(k+1)kf0(k+1)break;elsem(k+1)=c*m(k);endend2,点法求下列问题的最优解内点牛顿法clcm=zeros(1,50);a=zeros(1,50);b=zeros(1,50);f0=zeros(1,50);syms x1 x2 e;m(1)=1;c=0.2;a(1)=2;b(1)=-3;f=x1^2+x2^2-e*(1/(2*x1+x2-2)+1/(1-x1)); f0(1)=15;fx1=diff(f,'x1');fx2=diff(f,'x2');fx1x1=diff(fx1,'x1');fx1x2=diff(f x1,'x2');fx2x1=diff(fx2,'x1');fx2x2=diff(fx2,'x2');for k=1:100x1=a(k);x2=b(k);e=m(k);for n=1:100f1=subs(fx1);f2=subs(fx2);f11=subs(fx1x1);f12=subs(fx1x2);f21=subs(fx2x1);f22=subs(fx2x2);if(double(sqrt(f1^2+f2^2))<=0.002)a(k+1)=double(x1);b(k+1)=double(x2);f0(k+1)=double(subs (f));break;elseX=[x1 x2]'-inv([f11 f12;f21 f22])*[f1 f2]';x1=X(1,1);x2=X(2,1);endendif(double(sqrt((a(k+1)-a(k))^2+(b(k+1)-b(k))^2))<=0.001)&&(double(abs((f0(k+1)-f0(k))/f0(k)))<=0.001) a(k+1)b(k+1)kf0(k+1)break;elsem(k+1)=c*m(k);endend。
惩罚函数法

解出x1,x2
5M 4 M 5 x1 x2 2.5 2M 1 2
此时x1,x2则满足约束条件,是原问题的解。
§2惩罚函数法
§2惩罚函数法
§2惩罚函数法
§2惩罚函数法
§2惩罚函数法
§2惩罚函数法 例:内点法求解约束问题 min f (u ) au(a 0) s.t.g (u ) b u 0(b 0)
§2惩罚函数法
§2惩罚函数法
§2罚函数法
§2惩罚函数法
§2惩罚函数法
§2惩罚函数法
s.t. h (xi)=x1+ x2-5=0
该问题只有等式约束 解:首先建立罚函数:
F ( x, M ) f ( x) Mp( x)
P( x)
(max( 0, g
i 1
l
i
( x )))
2
( h j ( x ))
j 1
m
2
( x1 x 2 5) 2
F ( x, M ) ( x1 4) 2 ( x2 4) 2 M ( x1 x2 5) 2
此时的x1,x2不满足约束条件,不是原问题的解。
当x 不属于 S 时
F§2惩罚函数法 ( x2 4) 2 M ( x1 x2 5) 2 ( x, M ) ( x1 4) 2
F 2( x1 4) 2M ( x1 x 2 5) 0 x1 F 2( x 2 4) 2M ( x1 x 2 5) 0 x 2
*
rk a 2 (b u )
rk a
F (u , rk ) f (u ) rk a (b rk 0
1 1 au rk g (u ) bu
第11讲 外点惩罚函数法

k
p m
∑
u =1
1 gu (X )
ห้องสมุดไป่ตู้
式中,惩罚因子 r 是一个递增的正数序列 k 且 lim r = ∞
k→∞
2.外点惩罚函数法的一般形式 考虑不等式约束优化设计时:对
minf (X),
k
x ∈R
n
st.
m k
gu (X) ≥ 0, (u =1,2⋯m)
0 , g u ( X )}
2
构造一般形式的外点惩罚函数为:
P(X ,r ) = f (X ) + r
∑ {min[
u =1
其中: (1)当满足所有约束条件时惩罚项为0,即
k
v =1
gu ( X ) = gu ( X ) − δu ≥ 0
(u = 1,2⋯m)
这样用重新定义的约束函数来构造惩罚函数, 得到最优设计方案。 外点惩罚函数法的迭代步骤: 1.给定初始点 X ,初始惩罚因子 迭代精度
0
ε
r
1
,维数n ;
和递增系数 C > 1
2 构造外点惩罚函数 P( X k , r k ) ; 3 选用无约束优化方法来求解惩罚函数极小点
外点惩罚函数法
1.外点法和内点法的区别 内点法将惩罚函数定义于可行域内且求解无 约束优化问题的搜索点总是保持在可行域内,一 般只用于不等式约束情况;外点法即可用于求解 不等式约束优化问题,又可用于求解等式约束优 化问题,主要特点是惩罚函数定义在可行域的外 部,从而在求解系列无约束优化问题的过程中, 从可行域外部逐渐逼近原约束优化问题最优解。
等式约束极值问题-外点罚函数法

0
1.0000
FE = 0;
for i=1:length(h)
FE = FE + (h(i))^2;
end
x1 = transpose(x0);
x2 = inf;
while 1
M = c1*p;
FF = M*FE;
SumF = f + FF;
[x2,minf] = minNT(SumF,transpose(x1),var);
三、主要仪器设备
操作系统为Windows 2000及以上的电脑,并装有matlab软件
四、实验操作方法和步骤
根据外点罚函数法的步骤,读懂下列的程序,并用该程序求解所给多维函数极值。
五、实验记录与处理(数据、图表、计算等)
>> syms x y;
>> minGeneralPF(x^2+y^2,[1,1],y^2-1,1000,2,[x,y],0.0001)
if norm(x2 - x1)<=eps
x = x2;
break;
else
c1 = M;
x1 = x2;
end
end
minf = subs(f,var,x);
format short;
%牛顿法求解无约束最优化问题
function [x,minf] = minNT(f,x0,var,eps)
format long;
pv = subs(jacf,var,x0);
p = -inv(pv)*transpose(v);
p = double(p);
x1 = x0 + p;
x0 = x1;
end
x = x1;
外点惩罚函数法

对于任意给定的惩罚因子r(k)>0,函数Ф (x,r(k))是 凸的。令函数Ф (x,r(k))的一阶导数为零,可得其无 约束极值点x*(r(k))=1-1/(4r(k))和惩罚函数值为
下表列出了当惩罚因子赋予不同值时的条件最优解。由此 可见,当惩罚因子递增时,其极值点x*(r(k))离约束最优 点x*越来越近。当r(k)→∞时, x*(r(k))→x*=1,趋于 真正的约束最优点。因此,无约束极值点x*(r(k))将沿直 线Ф (x*,r(k))=1/2+x*/2从约束区域外向最优点x*收 敛。
条件,就认为已经达到约束边界。这样只能取得一个接近
于可行域的非可行设计方案。当要求严格满足不等式的约 束条件时,为了最终取得一个可行的最优化设计方案,必
须对那些要求严格满足的约束条件,增加约束欲量—— δ
,定义新的约束条件 g'u(x)=gu(x)+δ ≤0 u=1,2,……m
用外点罚函数法解等式约束优化问题
使用中的问题
外点惩罚函数法的初始点x(0),可以任意选择,因
为不论初始点选在可行域内或外,只要f(x)的无约束极
值点不在可行域内,其函数Ф (x,r(k))的极值点均在 约束可行域外。这样,当惩罚因子的增大倍数不太大时, 用前一次求得的无约束极值点x*r(k-1),作为下次求 minФ (x,r(k))的初始点x(0),对于加快搜索速度是
r(k)与r(0)的选择
r(k)
在外点法中,惩罚因子r(k)通常是按下面递推公式增加的, 即 r(k)=α r(k-1);其中α 为递增系数一般取5~10。
r(0)的选择:
r(0)过大,惩罚函数比原目标函数大得多,使函数性态遭到破 坏,从而惩罚函数的等值线变形或偏心,求极值困难; r(0)过小,会使迭代次数增加。
最优性条件和罚函数法.ppt

d d
0 0
i I( x*) 。
分析:
(1) 如果 I (x*)中只有一个指标,不妨设 g1(x)为积极约束。 则不存在向量d 使得
成立。
g1 f
( (
x*)T x*)T
d d
0 0
则不存在向量d 使得 fg1((xx**))TTdd00 成立。
g1( x*) x*
g1( x) 0
f ( x*)
f
x
(
x*
,
y*
)
*
x
(
x*
,
y*
)
0
f
y
(
x*
,
y*
)
*
y
(
x*
,
y*
)
0
( x* , y* ) 0
推广到多元情况,可得到对于等式约束的情况:
分量形式:
min s.t.
f (x) hj ( x)
0,
j 1,2,, l
若x*是其最优解 , 则存在υ*∈ Rl 使
l
f ( x* ) *jh j ( x* ) 0
证明: 令 x' x t d , t 0。则对任意的i I( x) ,有 gi ( x') gi ( x) t gi ( x)T d o(|| td ||2 ) t gi ( x)T d o(|| td ||2 ) 0
x' Q ,即d 为可行方向。 可行下降方向: 设点 x Q,给定向量d ,如果d 既是点 x 处的可行方向, 又是该点的下降方向,则称 d 为点 x 处的可行下降方向。
g3(x)
2 0。 2
x2 g2( x) 0
I( x) {1, 2 }。
8-1 外点法

非线性规划
第八章 惩罚函数法
这一章将讨论非线性规划
min f(x)
g i (x) 0 ,i 1,2 , m s .t h j (x) 0 ,j 1,2 , l
习惯上取
[ max { 0 , g i (x)}]
[ h j (x)]
或
2
2
[ max { 0 , g i (x)}]
h j (x)
其中, 1 , 1 是给定的常数。
2 计算步骤
n 1°给定初点 x R ,初始惩罚因子 1 放大系数c>1, 允许误差 0 ,置 k 1 (0)
这时,
F(x,σ ) f(x)
惩罚函数只含目标函数。 当 x 不是不等式约束问题(b)的可行解时, g i (x) 0 成立,此时, g i (x) 0 ,
因此,
max { 0 , g i (x)} g i (x)
与(1)的讨论类似,当 x 不是不等式约束 问题(b)的可行解时,并且 是很大的正数, 求解等式约束问题(b)的最优解,可以转化成 求解一系列的无约束最优化问题
x x
(k) (k 1)
设 0 k k 1
是罚因子取 k 时无约束问题的极小点; 是罚因子取 k 1 时无约束问题的极小点,
F x k , k F x k 1 , k 1
则下列结论成立: 1)
2) 3)
F x F x
最优化理论第五章-惩罚函数法

课堂练习:
外点法求解
称为SUMT方法 基本步骤:
序列无约束极小化方法
收敛于
1.3. 外点法收敛性
定理2: 定理3:
的最优解。
2. 内点罚函数法
2.1 思想:从内点出发,保持在可行域内部进行搜索。
只适用于不等式约束问题
两种形式:
原始问题的解
2.2 r如何取值?
r太大,问题的解不精确
计算步骤: ∆例题: 解得:
2.3. 收敛性
例:乘子法求解:
3.3. 不等式约束的乘子法
转化为
等式
定义增广Lagrange函数。 求得原问题的解
用配方法整理则有: 增广Lagrange函数变为
一般问题
例题:
则
作业:
1. 阅读MATLAB中optimization toolbox 中的Quasi-Newton Method 和 Least-Squares Method 算法,用Lsqnonlin()函数 求解
有约束最优化:
可行域
定义:局部极小点,局部严格极小点
一阶条件(必要条件) 二阶条件(必要条件)
惩罚函数法 可行方向法,二次规划
1. 外点罚函数法
1.1 罚函数概念
a 对于等式约束:
对于线性约束可 消元处理
第2项很大
很大的正数
b. 不等式约束
转化为 c.一般情况:
罚回来
过大,计算困难 太小,远离约束问题的最优解
定理:问题
∆ 外点法 内点法
应用序列无约束极小化方法,简单
成为病态矩阵 无法求解
增大
3. 乘子法(Hestenes, Powell)提出
惩罚函数法

显然 p( x) 满恰足前面的条件(1)和(2)。
连续, 也连续。 结论 1 : 如果 g j ( x ) j = 1,2, L , m ) ( 连续,那么 p( x ) 也连续。
事实上,只须注意: 事实上,只须注意: f1 ( x ) + f 2 ( x ) − f1 ( x ) − f 2 ( x ) min { f 1 ( x ), f 2 ( x )} = 2
m
n
得到其最优解 x * (λ k ),记为 x k + 1。 step 3 . 如果 µ k q( x k + 1 ) ≤ ε , 则 x k + 1 就是问题 min f ( x ) 的最优解, stop;否则转 step 4。 的最优解, (A):
x∈ D
step 4 . 给定 µ k + 1 < µ k(可取 µ k + 1 = βµ k 这里 β < 1 为惩罚 因子的缩小系数) , 因子的缩小系数) k := k + 1, 转 step 2。
x∈ D
: 证明 : 因为 x * (λ k ) 是(B) min ϕ k ( x ) 的最优解 。
x∈ R n
所以 ϕ k ( x * (λ k )) ≤ ϕ k ( x ) , ∀ x ∈ R n 。
, 又 x * (λ k ) ∈ D, 即g j ( x * (λ k )) ≥ 0 j = 1,2,L, m ) ( 所以 p( x * (λ k ) ) = 0 。
1 ∑ 例如: 例如: q( x ) = 或 q( x ) = j =1 g ( x ) j
m m
1 等; 2 j =1 g ( x )
罚函数法(SUMT法)

线性规划3-6
一.外点法迭代原理
(NP) min f (X )
( X , M ) f ( X ) M [min(0, gi ( X ))]2
设min( X , M )的最优解为 X (M ) XRn
s.t. gi ( X ) 0
i 1,2, , m
20 若 X (M ) D, 当M很大时, X *(M)也会相当靠近
设min( X , M )的最优解为 X (M ) XRn
s.t. gi ( X ) 0
i 1,2, , m
20 若 X (M ) D, 当M很大时, X *(M)也会相当靠近
(NP) 可行域D的边界,是(NP)的最优解X *的近似解
证明: X ( M ) D, 至少存在 i0 使 gi0 (X(M)) 0
D
g2(X ) 0
g1( X ) 0
X (k)(Mk )
X
x1
线性规划3-6
一.外点法迭代原理
(NP) min f (X )
s.t. gi ( X ) 0
i 1,2, , m
( NP) min f (X )
s.t
.
gi hj
( (
X X
) )
0, 0,
i j
1, 2,L 1, 2,L
m
构造罚函数: ( X , M ) f ( X ) M [min( 0, gi ( X ))]2
罚函数的特点:
罚因子 i1 惩罚项
f (X ),
XD
(X , M) f (X) + 很大的正数, X D
( NP) 求解 min( X , M ) 设其最优解为 X*(M), XRn
研究 X*(M) 与(NP)的最优解 X* 之间的关系
外罚函数法求解约束问题

外罚函数法是一种求解约束优化问题的方法,它的基本思想是在目标函数中引入一个罚因子,将约束条件转化为无约束条件,通过迭代求解无约束优化问题,从而逐渐逼近约束条件下的最优解。
在外罚函数法中,首先定义一个辅助函数F(x,μ),其中x是决策变量,μ是罚因子。
在可行域内部,F(x,μ)与原问题的取值相同;在可行域外部,F(x,μ)的取值远远大于目标函数的取值。
对于约束问题s.t. minf(x)hj(x)=0,j=1,⋯,lminf(x)s.t.hj(x)=0,j=1,⋯,l,可定义辅助函数F(x,μ)=f(x)+μ∑j=1lh2j(x)F(x,μ)=f(x)+μ∑j=1lhj2(x)。
对于约束问题s.t. minf(x)gi(x)≥0,i=1,⋯,mminf(x)s.t. gi(x)≥0,i=1,⋯,m,可定义辅助函数F(x,μ)=f(x)+μ∑i=1m(max{0,gj(x)})2F(x,μ)=f(x)+μ∑i=1m(max{0,gj(x)})2。
在外罚函数法中,通常采用迭代的方法求解无约束优化问题。
给定初始点x 0 x^{0}x0,设ϵ > 0 , c > 1 \epsilon >0, c>1ϵ>0,c>1为给定实数,选择序列{ σ k } {\sigma_{k}}{σk},使得σ k → + ∞\sigma_{k}\to+\inftyσk→+∞,令k = 1 k=1k=1;以x k − 1 x^{k-1}xk−1为初始点,求解无约束优化问题min { P ( x , σ k ) = f ( x ) + σ k P ~ ( x ) } \min{P(x,\sigma_{k})=f(x)+\sigma_{k}\tilde{P}(x) }min{P(x,σk)=f(x)+σkP~(x)}得到最优解x k x^{k}xk。
需要注意的是,外罚函数法的效果与罚因子的选择、罚因子的迭代策略以及初始点的选择等因素有关。
外部罚函数法讨论区间

外部罚函数法讨论区间外部罚函数法(Exterior Penalty Function Method)是一种常用于求解约束优化问题的数学方法。
该方法通过将约束条件转化为一系列罚函数,将约束优化问题转化为非约束优化问题来求解。
在本文中,我们将对外部罚函数法进行详细的讨论,包括其基本原理、数学模型、求解步骤以及优缺点等。
一、基本原理外部罚函数法的基本原理是通过引入罚函数将约束条件转化为目标函数的一部分。
通过调整罚函数的形式和参数,可以使得在优化过程中逐步接近约束条件,最终得到一个满足约束条件的最佳解。
外部罚函数法可以分为两类:等式约束问题和不等式约束问题。
对于等式约束问题,外部罚函数法可以通过将约束条件表示为罚函数的形式,将原优化问题转化为一个非约束优化问题。
一般而言,等式约束问题的罚函数形式为:f(x)+λh(x),其中f(x)是目标函数,h(x)是约束条件,λ是一个罚参数。
通过调整罚参数λ的大小,可以逐步消除等式约束条件,使得目标函数逼近约束条件。
对于不等式约束问题,外部罚函数法可以通过将约束条件表示为罚函数的形式,将原优化问题转化为一个约束优化问题。
一般而言,不等式约束问题的罚函数形式为:f(x)+λg(x),其中f(x)是目标函数,g(x)是约束条件,λ是一个罚参数。
通过调整罚参数λ的大小,可以使得罚函数f(x)+λg(x)逼近0,从而满足不等式约束条件。
二、数学模型min f(x)s.t.h(x)=0g(x)≤0其中,h(x)=0表示等式约束条件,g(x)≤0表示不等式约束条件。
三、求解步骤1.选择一个初始解x0,设置罚参数λ的初值。
2. 将原优化问题转化为无约束优化问题:min f(x) + λh(x) 或min f(x) + λg(x)。
3.利用常用的无约束优化算法来求解上述无约束优化问题,得到一个新的解x14.判断新的解x1是否满足约束条件,如果满足则停止求解,否则继续迭代。
5.更新罚参数λ的值,即λ=αλ,其中α是一个常数。
约束条件极值 2
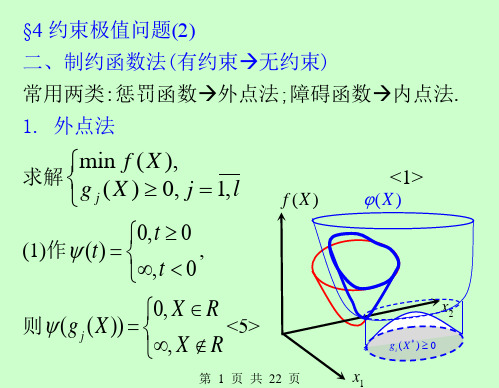
§4约束极值问题(2)二、制约函数法(有约束→无约束)常用两类:惩罚函数→外点法;障碍函数→内点法.1. 外点法求解min(),()0,1,jf Xg X j l⎧⎨≥=⎩<1>(1)作0,0 (),0tttψ≥⎧=⎨∞<⎩,则0, (()),jX R g XX Rψ∈⎧=⎨∞∉⎩<5> 2x()f X()0ig X*≥*()Xϕ再作1()()(())ljj X f X g X ϕψ==+∑ <6>设min ()X ϕ极小值有限,极小值点X *, 即1()()(())min lj j X f X g X ϕψ***==+=∑则必X R *∈,(否则()X ϕ*=∞)→()()min X f X ϕ**==,X R *∈→X *→是<1>之解.缺点: 是边界处不连续且无导数,难于操作.(2) 改进令20,0(),0t t t t ψ≥⎧=⎨<⎩(在0t =, ψ,ψ'连续), 且10,(())(0,),lj j X Rg X X R ψ=∈⎧=⎨∞∉⎩∑.注1: 若原极小点在R 内部,则仍在内部取到;注2: 若原极小点在R 的边界上,则新目标函数的无约束极小值可能不是原问题的解.1x 2x ()f X ()0g X *≥*()X ϕ再改进取M 为充分大正数, 作1(,)()(())lj j P X M f X M g X ψ==+∑,(对不在R 的点作惩罚放大) 或等价21(,)()[min(0,())]ljj P X M f X Mg X ==+∑从而使min (,)P X M 的解()X M 是原问题的极小解,或近似解. 基本分析惩罚因子 惩罚项若()X M R *∈, 则必是原问题的解.这是因为: 对X R ∀∈, 有1()()(())(,)lj j f X f X M g X P X M ψ==+=∑((),)(())P X M M f X M **≥≥(3) 惩罚分析1(,)()(())lj j P X M f X M g X ψ==+∑当120......k M M M <<<<<时(惩罚越来越大){()}k X M 从R 的外部→R 的边界→X * 如min ()/2,0.(0)f x x a x a a =-⎧⎨-≥>⎩其解为x a *=(见右图)a[O()f x x而2min (,)(/2)[min(,0)]P x M x a M x a =-+- 当x a ≥时,d 1d P P x=⇒ ,min (,)2aP a M =最小;当x a <,则由d 12()0d PM x a x =+-=, 得 1()2x M a M =-及1min (,)24a P a M M=-,1M =()M t ψ10M =100M =a1,10,100,...(),min ((),)2M x M x a a P x M M *=⎧→=⎪−−−−−→⎨→⎪⎩经济解释 ()()0j f X g X ⎧⎨≥⎩价格规定,正规,最宜; 违规惩罚; 大违大罚.总代价:1(,)()(())lj j P X M f X M g X ψ==+∑对于等式约束问题{min (),()0,1,i f X h X i m==()M t ψ1M =10M =100M =a()()k g X采用21(,)()[()]mii P X M f X Mh X ==+∑对于有等式和不等式约束, 用21(,)()[()]mi i P X M f X M h X ==+∑21[min((),0)]lj j M g X =+∑(4) 外点步骤<1>令1k =, 取10(1),0.010k M M ε>==>如.<2> 求 ()min (,)(,)nk k k X EP X M P X M ∈=<3> 若某()()k j g X ε->(其意: ()k X在R 外),或某()()k i h X ε>(其意义: ()k X 离边界较远).则再取1k k M M +>(如15k k M M +=),1k k =+,转<2>;否则停.例11求 ()2min ()1/2,0.f x x x ⎧=-⎪⎨≤⎪⎩ (0x *=)解 作 22(,)(1/2)[min(0,)]P x M x M x =-+-令d 2(1/2)2[min(0,)]0d Px M x x=---= 当0x ≥时,有1/20x Mx -+=1()2(1)x M M =⇒+ 0,0,1,10,100,...x M *==0M =(,)P x M 10M =0.50.25x补充例11’ 12211211min (),()0,()0,f X x xg X x x g X x =+⎧⎪=-+≥⎨⎪=≥⎩解 设221212(,){[min(0,)]P X M x x M x x =++-+21[min(0,)]}x +令1211212{[min(0,2()]x P M x x x =+--+ 1[min(0,)]}0x +=,221212min(0,)0x P M x x =+-+=,对使0g ≤的点,即21210,0x x x -+<<推得3112121212221,2x x x x Mx x M ⎧-+=-⎪⎪⎨⎪-+=-⎪⎩1221,2(1)11,4(1)2x M x M M ⎧=-⎪+⎪⇒⎨⎪=-⎪+⎩1(1/4,7/16)2(1/6,2/9),3(1/8,29/192)4(1/10,23/200)TT T T M X⎧-⎧⎪⎪-⎪⎪=⇒=⎨⎨-⎪⎪⎪⎪-⎩⎩O2()0g X =1x ()X M R1()0g X =2x O 12x x +=常数2. 内点法原理: 要求始终在R 内部.为此在边界上设一屏障,一旦太靠近边界, 有越界趋势时, 新目标函数值迅速增大, 从而可行点始终在内部而不越界, 因此问题变为无约束极值. 具体为 (1) 原min (),{|()0,1,}j f X R X g X j l ⎧⎨=≥=⎩(2) 化作0min (,)k X R P X r ∈, 其中障碍函数(,)k P X r 为11(,)(),(0)()lk k k j j P X r f X r r g X ==+>∑,0{|()0,1,}j R X g X j l =>=,或1(,)()log(()),(0)lk kjkj P X r f X r g X r==->∑,上式中第二项为障碍项, 正数0k r >称为障碍因子. 一旦X →R 的边界,必有某()0j g X →→(,)k P X r →∞→可行点()k XR ∈内部(始终)若原X R *∈内部, 则只需某个k r ,就()k X X *→,若原X R *∈边界上, 则通过12.......0k r r r >>>>>使()k XX *→的边界附近, 某一精度为止.(3) 步骤<1> 取(0)0X R ∈,1(1)0,0r ε=>>,并令1k = <2> 构造(,)k P X r (障碍项: 用倒数或对数) <3> 以(1)0k X R -∈为初始点,求得极小值()min (,)(,)k k k X R P X r P X r ∈=,()0k X R ∈(一维搜索,注意步长,不可越界)<4> 检验11()lk j jr g X ε=≤∑或1log(())lk j j r g X ε=≤∑满足, 则停, ()k X X *≈;否则再取1k k r r +<(如1/5k k r r +=), 并令1k k =+.准则也可()(1)k k X X ε--<或()(1)()()k k f X f X ε--<例12用内点法求解min ()2,0f X x x =-≥.解 构造(,)2kk r P x r x x=-+, 由 2d (,)10d k k P x r rx x=-= 得()k k x r r =, 令0k r →,得0x *=. min 2f =-(4) 初始内点的确定(也是一个迭代过程)(,)k P x r x0.01k r =0.1k r =1k r =0.3160.1任取(0)X(不一定恰为内点), 令(0)0{|()0,1}j T j g X j l =>≤≤和(0)0{|()0,1}j T j g X j l =≤≤≤若0T 空,则(0)X 即为初始内点;若0T 非空, 则以0T 中约束函数的负为假拟目标函数,以0T 中约束函数为障碍项, 构成无约束极值问题, 此时的惩罚函数如右图所示,求得(1)X , 再检验, 若不符, 继续并减小,...r1()0g X =(0)X ← 2()0g X =(0)1()0g X >(0)2()0g X ≤ 21(,)()()k k r P X r g X g X =-+一般步骤:<1> 任取(0)00,0(1),n X E r r ∈>=令0;k = <2> 定出指标集(){|()0,1}k k j T j g X j l =>≤≤ (){|()0,1}k k j T j g X j l =≤≤≤,<3> 若k T =∅, 则()k X在R 内部, 初始点找到;若k T ≠∅, 则转 <4> <4> 构造函数1(,)(),0()k k k j k k j T j T j P X r g X r r g X ∈∈=-+>∑∑, 以()k X 为初始点, 在 {|()0,}k j kR X g X j T =>∈内极小化min (,),,k k P X r X R ∈ 得 (1),k k X R+∈令 10k k r r +<<(如115k k r r +=), 1k k =+, 转<2>.作业4.3试用罚函数法(SUMT 外点法)求解22122min ()2f X x x x =+=并写出当罚因子1M =和10M =时的近似解.4.4试用障碍函数法(SUMT 内点法)求解3121min ()(1)3f X x x =++ 1122()10()0g X x g X x =-≥⎧⎨=≥⎩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
for i=1:length(h)
FE = FE + (h(i))^2;
end
x1 = transpose(x0);
x2 = inf;
while 1
M = c1*p;
FF = M*FE;
SumF = f + FF;
[x2,minf] = minNT(SumF,transpose(x1),var);
pv = subs(jacf,var,x0);
p = -inv(pv)*transpose(v);
p = double(p);
x1 = x0 + p;
x0 = x1;
end
x = x1;
minf = subs(f,var,x);
format short;
>> syms x y;
>> minGeneralPF(x^2+y^2,[1,1],y^2-1,1000,10,[x,y],0.0001)
if nargin == 3
eps = 1.0e-6nspose(x0);
gradf = jacobian(f,var);
jacf = jacobian(gradf,var);
while tol>eps
v = subs(gradf,var,x0);
tol = norm(v);
if norm(x2 - x1)<=eps
x = x2;
break;
else
c1 = M;
x1 = x2;
end
end
minf = subs(f,var,x);
format short;
%牛顿法求解无约束最优化问题
function [x,minf] = minNT(f,x0,var,eps)
format long;
ans =
0
1.0000
三、主要仪器设备
操作系统为Windows 2000及以上的电脑,并装有matlab软件
四、实验操作方法和步骤
根据外点罚函数法的步骤,读懂下列的程序,并用该程序求解所给多维函数极值。
五、实验记录与处理(数据、图表、计算等)
>> syms x y;
>> minGeneralPF(x^2+y^2,[1,1],y^2-1,1000,2,[x,y],0.0001)
重庆科技学院学生实验报告
课程名称
最优化方法与应用
实验项目名称
等式约束极值问题-外点罚函数法
开课学院及实验室
实验日期
学生姓名
学号
专业班级
指导教师
实验成绩
一、实验目的和要求
1.熟悉外点罚函数法的思想和步骤;
2.掌握外点罚函数法求解等式约束的多维极值问题。
二、实验内容和原理
1.对所给等式约束的多维极值问题用matlab编程进行求解;
ans =
0
0
Minf=0
>>六、实验结果及分析
运用所给程序能够求出最优解X=(0,0)最优值0,
附录function [x,minf] = minGeneralPF(f,x0,h,c1,p,var,eps)
format long;
if nargin == 6
eps = 1.0e-4;
end
k = 0;
