抛物线经典习题练习题
高三抛物线练习题答案

高三抛物线练习题答案1. 练习题一题目:求解抛物线y = ax^2 + bx + c的顶点坐标。
解答:首先,我们知道抛物线的顶点坐标为(-b/2a, c - b^2/4a)。
在题目中给定了抛物线的表达式为y = ax^2 + bx + c,因此我们可以直接利用该表达式计算顶点坐标。
答案:顶点坐标为(-b/2a, c - b^2/4a)。
2. 练习题二题目:已知抛物线的焦点为F,直线l是该抛物线的准线,证明直线l过焦点F的垂线。
解答:首先,根据焦准定义可知,抛物线上的每一点到焦点的距离与该点到准线的距离相等。
设P为抛物线上的任意一点,d1为焦点F到点P的距离,d2为点P到准线l的距离。
根据问题所求证,我们需要证明直线l过点P的垂线。
假设直线l不过点P的垂线,即直线l与过点P的垂线的交点为Q。
由于点P到焦点F的距离等于点P到准线l的距离,可知点Q也同时满足该条件。
然而,这与焦准定义相矛盾,因为焦准定义要求点P到焦点F的距离与点P到准线l的距离相等,但我们假设的交点Q违反了这个条件。
因此,通过反证法可证明直线l过焦点F的垂线。
答案:直线l过焦点F的垂线。
3. 练习题三题目:已知抛物线y = x^2的焦点为F,点P为抛物线上的一点,且点P到焦点F的距离为2。
求点P的坐标。
解答:根据已知条件,我们知道焦点F的坐标为(0, 1)。
要求点P的坐标,我们首先需要知道点P在抛物线上的纵坐标,即抛物线的函数表达式为y = x^2,代入点P的横坐标为x,得到点P的纵坐标为x^2。
由于点P到焦点F的距离为2,可以利用距离公式得到方程:√((x-0)^2 + (x^2-1)^2) = 2化简上述方程,得到:x^4 - x^2 - 3 = 0解这个方程,可以得到x的两个解,再带入y = x^2即可求得点P的坐标。
答案:点P的坐标为(-√3, 3)和(√3, 3)。
通过以上三个练习题的解答,我们可以发现在高三抛物线练习题中,需要灵活运用抛物线的性质和公式,进行问题求解。
高考数学专题《抛物线》习题含答案解析

专题9.5 抛物线1.(2020·全国高考真题(理))已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =( ) A .2 B .3 C .6 D .9【答案】C 【解析】设抛物线的焦点为F ,由抛物线的定义知||122A p AF x =+=,即1292p=+,解得6p.故选:C.2.(2020·北京高三二模)焦点在x 轴的正半轴上,且焦点到准线的距离为4的抛物线的标准方程是( ) A .x 2=4y B .y 2=4x C .x 2=8y D .y 2=8x【答案】D 【解析】根据题意,要求抛物线的焦点在x 轴的正半轴上, 设其标准方程为22(0)y px p =>, 又由焦点到准线的距离为4,即p =4, 故要求抛物线的标准方程为y 2=8x , 故选:D.3.(全国高考真题)设F 为抛物线2:4C y x =的焦点,曲线()0ky k x=>与C 交于点P ,PF x ⊥轴,则k =( )A .12B .1C .32D .2【答案】D 【解析】由抛物线的性质可得(1,2)221kP y k ⇒==⇒=,故选D. 4.(2020·全国高考真题(文))设O 为坐标原点,直线2x =与抛物线C :22(0)y px p =>交于D ,E 两点,若OD OE ⊥,则C 的焦点坐标为( ) A .1,04⎛⎫⎪⎝⎭B .1,02⎛⎫ ⎪⎝⎭C .(1,0)D .(2,0)练基础【答案】B 【解析】因为直线2x =与抛物线22(0)y px p =>交于,E D 两点,且OD OE ⊥, 根据抛物线的对称性可以确定4DOx EOx π∠=∠=,所以()2,2D ,代入抛物线方程44p =,求得1p =,所以其焦点坐标为1(,0)2, 故选:B.5.(2019·四川高三月考(文))若抛物线22y px =的准线为圆2240x y x ++=的一条切线,则抛物线的方程为( ) A.216y x =- B.28y x =-C.216y x =D.24y x =【答案】C 【解析】∵抛物线22y px =的准线方程为x=2p-,垂直于x 轴. 而圆2240x y x ++=垂直于x 轴的一条切线为4x =-, 则42p=,即8p =. 故抛物线的方程为216y x =. 故选:C .6.(2019·北京高考真题(文))设抛物线y 2=4x 的焦点为F ,准线为l .则以F 为圆心,且与l 相切的圆的方程为__________. 【答案】(x -1)2+y 2=4. 【解析】抛物线y 2=4x 中,2p =4,p =2, 焦点F (1,0),准线l 的方程为x =-1, 以F 为圆心,且与l 相切的圆的方程为 (x -1)2+y 2=22,即为(x -1)2+y 2=4.7.(2019·山东高三月考(文))直线l 与抛物线22x y =相交于A ,B 两点,当AB 4=时,则弦AB 中点M 到x 轴距离的最小值为______. 【答案】32【解析】由题意,抛物线22x y =的焦点坐标为(0,12),根据抛物线的定义如图,所求d=111A B AF BF 113M 2222A B AB M ++--==≥= 故答案为:32. 8.(2021·沙湾县第一中学(文))设过抛物线y 2=4x 的焦点F 的直线交抛物线于A ,B 两点,且直线AB 的倾斜角为4π,则线段AB 的长是____,焦点F 到A ,B 两点的距离之积为_________.【答案】8 8 【分析】由题意可得直线AB 的方程为1y x =-,然后将直线方程与抛物线方程联立方程组,消去y 后,利用根与系数的关系,结合抛物线的定义可求得答案 【详解】解:由题意得(1,0)F ,则直线AB 的方程为1y x =-,设1122(,),(,)A x y B x y ,由241y x y x ⎧=⎨=-⎩,得2610x x -+=, 所以12126,1x x x x +==, 所以12628AB x x p =++=+=,因为11221,122=+=+=+=+p pAF x x BF x x , 所以()()1212121116118AF BF x x x x x x ⋅=+⋅+=+++=++=, 故答案为:8,89.(2021·全国高三专题练习)已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点(),3A m -到焦点F 的距离为5,则m 的值为__________;抛物线方程为__________. 【答案】答案见解析 答案见解析 【分析】由于抛物线的开口方向未定,根据点(),3A m -在抛物线上这一条件,抛物线开口向下,向左、向右均有可能,以此分类讨论,利用焦半径公式列方程可得p 的值,根据点(),3A m -在抛物线上可得m 的值. 【详解】根据点(),3A m -在抛物线上,可知抛物线开口向下,向左、向右均有可能, 当抛物线开口向下时,设抛物线方程为22x py =-(0p >), 此时准线方程为2py =,由抛物线定义知(3)52p --=,解得4p =.所以抛物线方程为28x y ,这时将(),3A m -代入方程得m =±当抛物线开口向左或向右时,可设抛物线方程为22y ax (0a ≠),从p a =知准线方程为2ax =-,由题意知()25232am am⎧+=⎪⎨⎪-=⎩,解此方程组得11192a m =⎧⎪⎨=⎪⎩,22192a m =-⎧⎪⎨=-⎪⎩,33912a m =⎧⎪⎨=⎪⎩,44912a m =-⎧⎪⎨=-⎪⎩,综合(1)、(2)得92m =,22y x =; 92m =-,22y x =-;12m =,218y x =; 12m =-,218y x =-;m =±28xy .故答案为:92,92-,12,12-,±22y x =,22y x =-,218y x =,218y x =-,28x y .10.(2019·广东高三月考(理))已知F 为抛物线2:4T x y =的焦点,直线:2l y kx =+与T 相交于,A B 两点.()1若1k =,求FA FB +的值;()2点(3,2)C --,若CFA CFB ∠=∠,求直线l 的方程.【答案】(1)10(2)3240x y +-= 【解析】(1)由题意,可得()0,1F ,设221212,,,44x x A x B x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,联立方程组224y kx x y=+⎧⎨=⎩,整理得2480x kx --=,则124x x k +=,128x x =-,又由22121144x x FA FB +++=+()2121222104x x x x +-=+=.(2)由题意,知211,14x FA x ⎛⎫=- ⎪⎝⎭,222,14x FB x ⎛⎫=- ⎪⎝⎭,()3.3FC =--, 由CFA CFB ∠=∠,可得cos ,cos ,FA FC FB FC =又2114x FA =+,2214x FB =+,则FA FC FB FC FA FC FB FC =, 整理得()1212420x x x x ++-=,解得32k =-, 所以直线l 的方程为3240x y +-=.1.(2021·吉林长春市·高三(理))已知M 是抛物线24y x =上的一点,F 是抛物线的焦点,若以Fx 为始边,FM 为终边的角60xFM ∠=,则FM 等于( ) A .2 B C .D .4【答案】D 【分析】设点200,4y M y ⎛⎫ ⎪⎝⎭,取()1,0a =,可得1cos ,2FM a <>=,求出20y 的值,利用抛物线的定义可求练提升得FM 的值. 【详解】设点()00,M x y ,其中2004y x =,则()1,0F ,2001,4y FM y ⎛⎫=- ⎪⎝⎭,取()1,0a =,则211cos ,2y FM a FM a FM a-⋅<>===⋅⎛,可得4200340480y y -+=,因为20104y ->,可得204y >,解得2012y =,则20034y x ==,因此,014MF x=+=. 故选:D.2.(2017·全国高考真题(文))过抛物线2:4C y x =的焦点F 的直线交C 于点M (在x 轴上方),l 为C 的准线,点N 在l 上且MNl ⊥,则点M 到直线NF 的距离为()A. B. D.【答案】A 【解析】设直线l 与x 轴相交于点P ,与直线MN 相交于点Q ,(1,0)F ,设||||MN MF m ==,因为||2,30PF NQM =∠=,所以||4,||2QF QM m ==, 所以42m m +=,解得:4m =,设00(,)M x y ,由焦半径公式得:014x +=, 所以03x=,0y =,所以sin sin 42NP MNF NFP NF ∠=∠===,所以点M 到直线NF 的距离为||sin 4NM MNF ⋅∠=⋅=3.(2020·广西南宁三中其他(理))已知抛物线28C y x =:的焦点为F ,P 是抛物线C 的准线上的一点,且P 的纵坐标为正数,Q 是直线PF 与抛物线C 的一个交点,若PQ =,则直线PF 的方程为( )A .20x y --=B .20x y +-=C .20x y -+=D .20x y ++=【答案】B 【解析】过Q 点作QH PM ⊥于H ,因为PQ =,由抛物线的定义得PQ =,所以在Rt PQH ∆中,4PQH π∠=,所以4PFM π∠=,所以直线PF 的斜率为1k =-,所以直线PF 的方程为()()012y x -=--, 即20x y +-=, 故选B.4.(2020·浙江高三月考)如图,已知抛物线21:4C y x =和圆222:(1)1C x y -+=,直线l 经过1C 的焦点F ,自上而下依次交1C 和2C 于A ,B ,C ,D 四点,则AB CD ⋅的值为( )A .14B .12C .1D .2【答案】C 【解析】因为抛物线21:4C y x =的焦点为(1,0)F ,又直线l 经过1C 的焦点F ,设直线:(1)l y k x =-,由24(1)y x y k x ⎧=⎨=-⎩得2222(24)0k x k x k -++=, 设1122(,),(,)A x y B x y ,则121=x x由题意可得:1111=-=+-=AB AF BF x x , 同理2=CD x ,所以12cos01︒⋅=⋅⋅==AB CD AB CD x x . 故选C5.【多选题】(2022·全国高三专题练习)已知抛物线21:C y mx =与双曲线222:13y C x -=有相同的焦点,点()02,P y 在抛物线1C 上,则下列结论正确的有( )A .双曲线2C 的离心率为2B .双曲线2C 的渐近线为y x = C .8m =D .点P 到抛物线1C 的焦点的距离为4【答案】ACD 【分析】由双曲线方程写出离心率、渐近线及焦点,即可知A 、B 、C 的正误,根据所得抛物线方程求0y ,即知D 的正误. 【详解】双曲线2C 的离心率为2e ==,故A 正确;双曲线2C 的渐近线为y =,故B 错误; 由12,C C 有相同焦点,即24m=,即8m =,故C 正确; 抛物线28y x =焦点为()2,0,点()02,P y 在1C 上,则04y =±,故()2,4P 或()2,4P -,所以P 到1C 的焦点的距离为4,故D 正确. 故选:ACD .6.【多选题】(2021·海南鑫源高级中学)在下列四个命题中,真命题为( )A .当a 为任意实数时,直线(a -1)x -y +2a +1=0恒过定点P ,则过点P 且焦点在y 轴上的抛物线的标准方程是243x y =B .已知双曲线的右焦点为(5,0),一条渐近线方程为2x -y =0,则双曲线的标准方程为221205x y -= C .抛物线y =ax 2(a ≠0)的准线方程14y a=-D .已知双曲线2214x y m +=,其离心率()1,2e ∈,则m 的取值范围(-12,0)【答案】ACD 【分析】求出直线定点设出抛物方程即可判断A ;根据渐近线方程与焦点坐标求出,a b 即可判断B ;根据抛物线方程的准线方程公式即可判断C ;利用双曲线离心率公式即可判断D . 【详解】对A 选项,直线(a -1)x -y +2a +1=0恒过定点为()2,3P -,则过点P 且焦点在y 轴上的抛物线的标准方程设为22x py =,将点()2,3P -代入可得23p =,所以243x y =,故A 正确;对B 选项,知5,2bc a==,又22225a b c +==,解得225,20a b ==,所以双曲线的标准方程为221520x y -=,故B 错; 对C 选项,得21x y a =,所以准线方程14y a=-,正确;对D 选项,化双曲线方程为2214x y m-=-,所以()1,2e =,解得()12,0m ∈-,故正确.故选:ACD7.(2021·全国高二课时练习)已知点M 为抛物线2:2(0)C y px p =>上一点,若点M 到两定点(,)A p p ,,02p F ⎛⎫⎪⎝⎭的距离之和最小,则点M 的坐标为______.【答案】,2p p ⎛⎫⎪⎝⎭【分析】过点M 作抛物线准线的垂线,垂足为B ,根据抛物线的定义可得||||MF MB =, 易知当A ,B ,M 三点共线时||MB MA +取得最小值且为||AB ,进而可得结果. 【详解】过点M 作抛物线准线的垂线,垂足为B ,由抛物线的定义,知点M 到焦点,02p F ⎛⎫⎪⎝⎭的距离与点M 到准线的距离相等,即||||MF MB =,所以||||||||MF MA MB MA +=+, 易知当A ,B ,M 三点共线时,||MB MA +取得最小值, 所以min 3(||||)||2p MF MA AB +==,此时点M 的坐标为,2p p ⎛⎫⎪⎝⎭. 故答案为:2p p ⎛⎫⎪⎝⎭,8.(2021·全国高二课时练习)抛物线()220y px p =>的焦点为F ,已知点A ,B 为抛物线上的两个动点,且满足120AFB ∠=︒,过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N ,则MN AB的最大值为______.【分析】设=AF a ,=BF b ,根据中位线定理以及抛物线定义可得()12MN a b =+,在AFB △中,由余弦定理以及基本不等式可得)AB a b ≥+,即可求得MN AB 的最大值.【详解】设=AF a ,=BF b ,作AQ 垂直抛物线的准线于点Q ,BP 垂直抛物线的准线于点P .由抛物线的定义,知AF AQ =,BF BP =.由余弦定理得()2222222cos120AB a b ab a b ab a b ab =+=︒=++=+-.又22a b ab +⎛⎫≤ ⎪⎝⎭,∴()()()()22221344a b ab a b a b a b +-≥+-+=+,当且仅当a b =时,等号成立,∴)AB a b ≥+,∴()1a b MN AB +≤=MN AB9.(2020·山东济南外国语学校高三月考)抛物线C :22y x =的焦点坐标是________;经过点()4,1P 的直线l 与抛物线C 相交于A ,B 两点,且点P 恰为AB 的中点,F 为抛物线的焦点,则AF BF +=________.【答案】1,02⎛⎫⎪⎝⎭9【解析】抛物线C :22y x =的焦点1,02F ⎛⎫⎪⎝⎭. 过A 作AM ⊥准线交准线于M ,过B 作BN ⊥准线交准线于N ,过P 作PK ⊥准线交准线 于K ,则由抛物线的定义可得AM BN AF BF +=+. 再根据P 为线段AB 的中点,119(||||)||4222AM BN PK +==+=, ∴9AF BF +=,故答案为:焦点坐标是1,02⎛⎫ ⎪⎝⎭,9AF BF +=.10.(2019·四川高考模拟(文))抛物线C :()220x py p =>的焦点为F ,抛物线过点(),1P p .(Ⅰ)求抛物线C 的标准方程与其准线l 的方程;(Ⅱ)过F 点作直线与抛物线C 交于A ,B 两点,过A ,B 分别作抛物线的切线,证明两条切线的交点在抛物线C 的准线l 上.【答案】(Ⅰ)抛物线的标准方程为24x y =,准线l 的方程为1y =-;(Ⅱ)详见解析. 【解析】(Ⅰ)由221p p =⨯,得2p =,所以抛物线的标准方程为24x y =,准线l 的方程为1y =-.(Ⅱ)根据题意直线AB 的斜率一定存在,又焦点()0,1F ,设过F 点的直线方程为1y kx =+,联立241x yy kx ⎧=⎨=+⎩,得,2440x kx --=. 设()11,A x y ,()22,B x y ,则124x x k +=,124x x =-.∴()22221212122168x x x x x x k +=+-=+.由214y x =得,1'2y x =,过A ,B 的抛物线的切线方程分别为 ()()1112221212y y x x x y y x x x ⎧-=-⎪⎪⎨⎪-=-⎪⎩, 即21122211241124y x x x y x x x ⎧=-⎪⎪⎨⎪=-⎪⎩,两式相加,得()()2212121148y x x x x x =+-+,化简,得()221y kx k =-+,即()21y k x k =--, 所以,两条切线交于点()2,1k -,该点显然在抛物线C 的准线l :1y =-上.1.(2021·全国高考真题)抛物线22(0)y px p =>的焦点到直线1y x =+,则p =( ) A .1 B .2 C .D .4【答案】B 【分析】首先确定抛物线的焦点坐标,然后结合点到直线距离公式可得p 的值. 【详解】抛物线的焦点坐标为,02p ⎛⎫ ⎪⎝⎭,其到直线10x y -+=的距离:d == 解得:2p =(6p =-舍去). 故选:B.2.(2021·天津高考真题)已知双曲线22221(0,0)x y a b a b-=>>的右焦点与抛物线22(0)y px p =>的焦点重合,抛物线的准线交双曲线于A ,B 两点,交双曲线的渐近线于C 、D 两点,若|CD AB .则双曲线的离心率为( ) A B C .2D .3练真题【答案】A 【分析】设公共焦点为(),0c ,进而可得准线为x c =-,代入双曲线及渐近线方程,结合线段长度比值可得2212a c =,再由双曲线离心率公式即可得解. 【详解】设双曲线22221(0,0)x y a b a b-=>>与抛物线22(0)y px p =>的公共焦点为(),0c ,则抛物线22(0)y px p =>的准线为x c =-,令x c =-,则22221c ya b-=,解得2b y a =±,所以22b AB a =, 又因为双曲线的渐近线方程为b y x a =±,所以2bcCD a=,所以2bc a c ,所以222212a cbc =-=,所以双曲线的离心率ce a== 故选:A.3.(2020·北京高考真题)设抛物线的顶点为O ,焦点为F ,准线为l .P 是抛物线上异于O 的一点,过P 作PQ l ⊥于Q ,则线段FQ 的垂直平分线( ). A .经过点O B .经过点P C .平行于直线OP D .垂直于直线OP【答案】B 【解析】如图所示:.因为线段FQ 的垂直平分线上的点到,F Q 的距离相等,又点P 在抛物线上,根据定义可知,PQ PF =,所以线段FQ 的垂直平分线经过点P .故选:B.4.(2021·全国高考真题)已知O 为坐标原点,抛物线C :22y px =(0p >)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ OP ⊥,若6FQ =,则C 的准线方程为______. 【答案】32x =-【分析】先用坐标表示P Q ,,再根据向量垂直坐标表示列方程,解得p ,即得结果. 【详解】抛物线C :22y px = (0p >)的焦点,02p F ⎛⎫⎪⎝⎭,∵P 为C 上一点,PF 与x 轴垂直, 所以P 的横坐标为2p,代入抛物线方程求得P 的纵坐标为p ±, 不妨设(,)2pP p ,因为Q 为x 轴上一点,且PQ OP ⊥,所以Q 在F 的右侧, 又||6FQ =, (6,0),(6,)2pQ PQ p ∴+∴=- 因为PQ OP ⊥,所以PQ OP ⋅=2602pp ⨯-=, 0,3p p >∴=,所以C 的准线方程为32x =-故答案为:32x =-.5.的直线过抛物线C :y 2=4x 的焦点,且与C 交于A ,B 两点,则AB =________.【答案】163【解析】∵抛物线的方程为24y x =,∴抛物线的焦点F 坐标为(1,0)F ,又∵直线AB 过焦点F AB 的方程为:1)y x =- 代入抛物线方程消去y 并化简得231030x x -+=, 解法一:解得121,33x x ==所以12116||||3|33AB x x =-=-= 解法二:10036640∆=-=> 设1122(,),(,)A x y B x y ,则12103x x +=, 过,A B 分别作准线1x =-的垂线,设垂足分别为,C D 如图所示.12||||||||||11AB AF BF AC BD x x =+=+=+++1216+2=3x x =+故答案为:1636.(2020·浙江省高考真题)如图,已知椭圆221:12x C y +=,抛物线22:2(0)C y px p =>,点A 是椭圆1C 与抛物线2C 的交点,过点A 的直线l 交椭圆1C 于点B ,交抛物线2C 于M (B ,M 不同于A ).(Ⅰ)若116=p ,求抛物线2C 的焦点坐标; (Ⅱ)若存在不过原点的直线l 使M 为线段AB 的中点,求p 的最大值.【答案】(Ⅰ)1(,0)32;【解析】 (Ⅰ)当116=p 时,2C 的方程为218y x =,故抛物线2C 的焦点坐标为1(,0)32;(Ⅱ)设()()()112200,,,,,,:A x y B x y M x y I x y m λ=+,由()22222222220x y y my m x y mλλλ⎧+=⇒+++-=⎨=+⎩, 1200022222,,222m m my y y x y m λλλλλλ--∴+===+=+++, 由M 在抛物线上,所以()222222244222m pm mp λλλλλ=⇒=+++, 又22222()220y pxy p y m y p y pm x y mλλλ⎧=⇒=+⇒--=⎨=+⎩, 012y y p λ∴+=,2101022x x y m y m p m λλλ∴+=+++=+,2122222mx p m λλ∴=+-+.由2222142,?22x y x px y px ⎧+=⎪⇒+=⎨⎪=⎩即2420x px +-=12x p ⇒==-222221822228162p p p m p p p λλλλλ+⇒-=+⋅=++≥+,18p ≥,21160p ≤,p ≤ 所以,p,此时A . 法2:设直线:(0,0)l x my t m t =+≠≠,()00,A x y .将直线l 的方程代入椭圆221:12x C y +=得:()2222220m y mty t +++-=,所以点M 的纵坐标为22M mty m =-+.将直线l 的方程代入抛物线22:2C y px =得:2220y pmy pt --=,所以02M y y pt =-,解得()2022p m y m+=,因此()220222p m xm+=,由220012x y +=解得22212242160m m p m m ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,所以当m t ==p .。
初三抛物线练习题和答案

初三抛物线练习题和答案一、选择题1. 下列哪个点不在抛物线y = 2x² - 4x + 1上?A. (-1, 7)B. (0, 1)C. (1, -1)D. (2, 1)答案:C2. 抛物线y = -3x² + 6x - 9的开口方向是:A. 向上B. 向下答案:B3. 抛物线y = x² + 2x - 3的顶点坐标是:A. (-1, 0)B. (-1, -4)C. (-1, -2)D. (1, 4)答案:C二、填空题1. 抛物线y = 2x² - 4x + 1的对称轴方程是______。
答案:x = 12. 抛物线y = -x² + 4x + 5的焦点坐标为(2, 4),则抛物线的方程为______。
答案:y = -(x - 2)² + 4三、解答题1. 求抛物线y = -2x² + 8x - 5的顶点坐标和对称轴方程。
解答:首先,我们知道抛物线的顶点坐标可以通过公式计算。
对于一般式的二次函数y = ax² + bx + c,顶点的横坐标为x = -b/2a,带入公式即可得到纵坐标。
在这个例子中,a = -2,b = 8,c = -5。
将这些值代入公式,我们可以计算出顶点的横坐标为x = -8/(-4) = 2。
将x = 2带入原方程,可以计算出顶点的纵坐标为y = -2(2)² + 8(2) - 5 = 7。
因此,抛物线y = -2x² + 8x - 5的顶点坐标为(2, 7)。
对称轴方程为x = 2。
2. 求抛物线y = x² - 4x + 3的焦点坐标。
解答:为了求解焦点坐标,我们需要先将方程转化为顶点形式。
通过配方可以将标准形式转化为顶点形式。
首先,我们可以将方程y = x²- 4x + 3写成完全平方式,即y = (x - 2)² - 1。
通过完全平方式转化后,我们可以得到抛物线的顶点坐标为(2, -1)。
抛物线习题精选(带答案)

抛物线习题精选一、选择题1.过抛物线焦点的直线与抛物线相交于,两点,若,在抛物线准线上的射影分别是,,则为().A.45°B.60°C.90°D.120°2.过已知点且与抛物线只有一个公共点的直线有().A.1条B.2条C.3条D.4条3.已知,是抛物线上两点,为坐标原点,若,且的垂心恰好是此抛物线的焦点,则直线的方程是().A.B.C.D.4.若抛物线()的弦PQ中点为(),则弦的斜率为()A.B.C.D.5.已知是抛物线的焦点弦,其坐标,满足,则直线的斜率是()A.B.C.D.6.已知抛物线()的焦点弦的两端点坐标分别为,,则的值一定等于()A.4 B.-4 C.D.7.已知⊙的圆心在抛物线上,且⊙与轴及的准线相切,则⊙的方程是()A.B.C.D.8.当时,关于的方程的实根的个数是()A.0个B.1个C.2个D.3个9.将直线左移1个单位,再下移2个单位后,它与抛物线仅有一个公共点,则实数的值等于()A.-1 B.1 C.7 D.910.以抛物线()的焦半径为直径的圆与轴位置关系为()A.相交 B.相离 C.相切 D.不确定11.过抛物线的焦点作直线交抛物线于,两点,如果,那么长是()A.10 B.8 C.6 D.412.过抛物线()的焦点且垂直于轴的弦为,为抛物线顶点,则大小()A.小于B.等于C.大于D.不能确定13.抛物线关于直线对称的曲线的顶点坐标是()A.(0,0)B.(-2,-2)C.(2,2)D.(2,0)14.已知抛物线()上有一点,它到焦点的距离为5,则的面积(为原点)为()A.1 B.C.2 D.15.记定点与抛物线上的点之间的距离为,到此抛物线准线的距离为,则当取最小值时点的坐标为()A.(0,0)B.C.(2,2)D.16.方程表示()A.椭圆 B.双曲线 C.抛物线 D.圆17.在上有一点,它到的距离与它到焦点的距离之和最小,则的坐标为()A.(-2,8)B.(2,8)C.(-2,-8)D.(-2,8)18.设为过焦点的弦,则以为直径的圆与准线交点的个数为()A.0 B.1 C.2 D.0或1或219.设,为抛物线上两点,则是过焦点的()A.充分不必要B.必要不充分C.充要D.不充分不必要20.抛物线垂点为(1,1),准线为,则顶点为()A.B.C.D.21.与关于对称的抛物线是()A.B.C.D.二、填空题1.顶点在原点,焦点在轴上且通径(过焦点和对称轴垂直的弦)长为6的抛物线方程是_________.2.抛物线顶点在原点,焦点在轴上,其通径的两端点与顶点连成的三角形面积为4,则此抛物线方程为_________.3.过点(0,-4)且与直线相切的圆的圆心的轨迹方程是_________.4.抛物线被点所平分的弦的直线方程为_________.5.已知抛物线的弦过定点(-2,0),则弦中点的轨迹方程是________.6.顶点在原点、焦点在轴上、截直线所得弦长为的抛物线方程为____________.7.已知直线与抛物线交于、两点,那么线段的中点坐标是__ _.8.一条直线经过抛物线()的焦点与抛物线交于、两点,过、点分别向准线引垂线、,垂足为、,如果,,为的中点,则 =__________.9.是抛物线的一条焦点弦,若抛物线,,则的中点到直线的距离为_________.10.抛物线上到直线的距离最近的点的坐标是____________.11.抛物线上到直线距离最短的点的坐标为__________.12.已知圆与抛物线()的准线相切,则 =________.13.过()的焦点的弦为,为坐标原点,则=________.14.抛物线上一点到焦点的距离为3,则点的纵坐标为__________.15.已知抛物线(),它的顶点在直线上,则的值为__________.16.过抛物线的焦点作一条倾斜角为的弦,若弦长不超过8,则的范围是________.17.已知抛物线与椭圆有四个交点,这四个交点共圆,则该圆的方程为__________.18.抛物线的焦点为,准线交轴于,过抛物线上一点作于,则梯形的面积为_______________.19.探照灯的反射镜的纵断面是抛物线的一部分,安装灯源的位置在抛物线的焦点处,如果到灯口平面的距离恰好等于灯口的半径,已知灯口的半径为30cm,那么灯深为_________.三、解答题1.知抛物线截直线所得的弦长,试在轴上求一点,使的面积为392.若的焦点弦长为5,求焦点弦所在直线方程3.已知是以原点为直角顶点的抛物线()的内接直角三角形,求面积的最小值.4.若,为抛物线的焦点,为抛物线上任意一点,求的最小值及取得最小值时的的坐标.5.一抛物线拱桥跨度为52米,拱顶离水面6.5米,一竹排上一宽4米,高6米的大木箱,问能否安全通过.6.抛物线以轴为准线,且过点,()求证不论点的位置如何变化,抛物线顶点的轨迹是椭圆,且离心率为定值.7.已知抛物线()的焦点为,以为圆心,为半径,在轴上方画半圆,设抛物线与半圆交于不同的两点、,为线段的中点.①求的值;②是否存在这样的,使、、成等差数列,若存在,求出的值;若不存在,说明理由.8.求抛物线和圆上最近两点之间的距离.9.正方形中,一条边在直线上,另外两顶点、在抛物线上,求正方形的面积.10.已知抛物线的一条过焦点的弦被焦点分为,两个部分,求证.11.一抛物线型拱桥的跨度为,顶点距水面.江中一竹排装有宽、高的货箱,问能否安全通过.12.已知抛物线上两点,(在第二象限),为原点,且,求当点距轴最近时,的面积.13.是抛物线上的动点,连接原点与,以为边作正方形,求动点的轨迹方程.参考答案:一、1.C;2.C;3.D;4.B;5.C;6.B;7.B;8.D;9.C10.C;11.B;12.C;13.C;14.C;15.C;16.C;17.B;18.B;19.C;20.A;21.D二、1.;2.;3.;4.5.;6.(在已知抛物线内的部分)7.或;8.(4,2);9.10.;11.;12.2;13.-414.2;15.0,,,;16.17.;18.3.14;19.36.2cm三、1.先求得,再求得或2.3.设,,则由得,,,于是当,即,时,4.抛物线的准线方程为,过作垂直准线于点,由抛物线定义得,,要使最小,、、三点必共线,即垂直于准线,与抛物线交点为点,从而的最小值为,此时点坐标为(2,2).5.建立坐标系,设抛物线方程为,则点(26,-6.5)在抛物线上,抛物线方程为,当时,,则有,所以木箱能安全通过.6.设抛物线的焦点为,由抛物线定义得,设顶点为,则,所以,即为椭圆,离心率为定值.7.①设、、在抛物线的准线上射影分别为、、,则由抛物线定义得,又圆的方程为,将代入得②假设存在这样的,使得,由定义知点必在抛物线上,这与点是弦的中点矛盾,所以这样的不存在8.设、分别是抛物线和圆上的点,圆心,半径为1,若最小,则也最小,因此、、共线,问题转化为在抛物线上求一点,使它到点的距离最小.为此设,则,的最小值是9.设所在直线方程为,消去得又直线与间距离为或从而边长为或,面积,10.焦点为,设焦点弦端点,,当垂直于轴,则,结论显然成立;当与轴不垂直时,设所在直线方程为,代入抛物线方程整理得,这时,于是,命题也成立.11.取抛物线型拱桥的顶点为原点、对称轴为轴建立直角坐标系,则桥墩的两端坐标分别为(-26,-6.5),(26,-6.5),设抛物线型拱桥的方程为,则,所以,抛物线方程为.当时,,而,故可安全通过.12.设,则,因为,所以,直线的方程为,将代入,得点的横坐标为(当且仅当时取等号),此时,,,,所以.13.设,,过,分别作为轴的垂线,垂足分别为,,而证得≌,则有,,即、,而,因此,即为所求轨迹方程.。
抛物线的练习题

抛物线的练习题一、选择题:1. 抛物线y = ax^2 + bx + c的顶点坐标为:A. (-b/2a, c - b^2/4a)B. (-b/a, c - b^2/4a)C. (-b/2a, c - b^2/2a)D. (-b/a, c - b^2/2a)2. 如果抛物线y = x^2 - 4x + 4的对称轴是:A. x = 1B. x = 2C. x = -2D. x = 03. 抛物线y = 2x^2 - 4x + 3的开口方向是:A. 向上B. 向下C. 向左D. 向右4. 抛物线y = -3x^2 + 6x - 5与x轴的交点个数是:A. 0B. 1C. 2D. 无穷多5. 对于抛物线y = x^2 + 2x + 1,其焦点坐标为:A. (0, 1/4)B. (1, 0)C. (-1, 0)D. (0, -1/4)二、填空题:6. 将抛物线y = 2x^2 - 8x + 7进行顶点式变换,得到y = 2(x - ______)^2 + ______。
7. 已知抛物线y = ax^2 + bx + c与y轴交于点(0, 5),且对称轴为x = -1,则b的值为______。
8. 当抛物线y = x^2 - 2x - 3的开口方向为向上时,其顶点的横坐标为______。
9. 抛物线y = 4x^2 - 12x + 9的焦点坐标为______。
10. 抛物线y = -x^2 + 4x - 3与x轴的交点坐标为______。
三、解答题:11. 已知抛物线y = ax^2 + bx + c经过点(1, 2)和(-1, -2),求抛物线的方程。
12. 抛物线y = 3x^2 - 6x + 5的顶点坐标是什么?并求出该抛物线与x轴的交点坐标。
13. 抛物线y = 2x^2 - 8x + 7的焦点坐标是什么?并求出其准线方程。
14. 已知抛物线y = -x^2 + 2x + 3,求其在x = 2时的函数值。
抛物线知识点归纳总结与经典习题

抛物线经典结论和例题1. 直线与抛物线的位置关系直线,抛物线* •廿,J"7 = fc+i才二2砂,消y得:+2(妬-p)x+护二0(1)当k=0时,直线I与抛物线的对称轴平行,有一个交点;(2)当k #0 时,A>0,直线I与抛物线相交,两个不同交点;Y0 ,直线丨与抛物线相切,一个切点;A<0,直线I与抛物线相离,无公共点。
(3)若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?(不一定)2. 关于直线与抛物线的位置关系问题常用处理方法直线I : y = kx • b 抛物线-■' ''-- :,(P一0)①联立方程法:y =kx +b 2 2 2丿2= k x +2(kb — p)x+b =0y =2px设交点坐标为A(x i, yj , B(X2, y2),则有:'0 ,以及X i,X2,X i X2,还可进一步求出% y2二b kx2 b 二k(x「x2) 2b ,2 2%丫2=(kx 「b)(kx 2 b)二 k X 1X 2 kb(x 〔 x ?) b在涉及弦长,中点,对称,面积等问题时,常用此法,比如二卫,即 kAB=JX i -X 2y i y2y o y o y o同理,对于抛物线X 2=2py(p =0),若直线丨与抛物线相交于 A 、M(xO,y O )是弦AB 的中点,则有隔二需瓷讦(注意能用这个公式的条件:1)直线与抛物线有两个不同的交点 斜率存在,且不等于零)一、抛物线的定义及其应用 例1、设P 是抛物线y2 = 4x 上的一个动点.⑴求点P 到点A(- 1,1)的距离与点P 到直线x = — 1的距离之和的最小值; ⑵a.相交弦AB 的弦长AB ==i k 2(论 x 2)2—4x^2 = i k 2yi - y 2 -「k!、® y 2)2—4y i y 2二 i Wb. 中点 M (x o , y o ), x oX i X 2 y i y 2丁,yo =W②点差法:设交点坐标为A(x i ,yj , B(X 2,y 2),代入抛物线方程,得y 22=2px 2将两式相减,可得(yi -y 2)(y i y 2)=2p(Xi -X 2)所以庶-池a. 在涉及斜率问题时,k AB2p y i y 2b. 在涉及中点轨迹问题时,设线段AB 的中点为M (X o , y °),B 两点,点,2)直线的若B(3,2),求|PB|+ |PF|的最小值.例2、设M(xO, y0)为抛物线C: x2二8y上一点,F为抛物线C的焦点,以F 为圆心、|FM|为半径的圆和抛物线C的准线相交,则yO的取值范围是()A. (0,2)B. [0,2]C. (2,+^) D . [2, +^)二、抛物线的标准方程和几何性质例3、抛物线y2= 2px(p>0)的焦点为F,准线为I,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK丄l,垂足为K,若|BC匸2|BF| , 且|AF| 4 ,贝U △AKF的面积是()A. 4B. 3C. 4 ;3D. 8例4、过抛物线y2= 2px(p>0)的焦点F的直线交抛物线于点A、B,交其准线I 于点C,若|BC| = 2|BF|,且|AF| = 3则此抛物线的方程为()3 9A. y2=尹B. y2= 9xC. y2= D . y2= 3x三、抛物线的综合问题例5、已知过抛物线y2= 2px(p>0)的焦点,斜率为2:2的直线交抛物线于A(X1, y", Bg y2)(X1<X2)两点,且|AB匸9.(1)求该抛物线的方程;(2)O为坐标T T T原点,C为抛物线上一点,若OC二OA+ XOB,求硝值.例6、已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.(1) 求动点P的轨迹C的方程;(2) 过点F作两条斜率存在且互相垂直的直线l i,12,设l i与轨迹C相交于点A,B, 12与轨迹C相交于点D , E,求AD •岸B的最小值例7、已知点M(1, y)在抛物线C:y2= 2px(p>0) 上, M点到抛物线C的焦点F1的距离为2,直线I: y = —-x+ b与抛物线C交于A, B两点.2(1)求抛物线C的方程;⑵若以AB为直径的圆与x轴相切,求该圆的方程•练习题1.已知抛物线x2= ay的焦点恰好为双曲线y2—x2^2的上焦点,则a等于()A. 1B. 4C. 8D. 162.抛物线-4x2上的一点M到焦点的距离为1,则点M的纵坐标是()1715715A.—B.—C.D.161616163. (2011辽宁高考)已知F是拋物线y2= x的焦点,A, B是该拋物线上的两点,7.设抛物线y 2= 8x 的焦点为F ,准线为I , P 为抛物线上一点,PA 丄I ,10.已知抛物线的顶点在原点,对称轴为y 轴,抛物线上一点Q(-3, m)到焦 点的距离是5,则抛物线的方程为 _________ .11 .已知抛物线y 2= 4x 与直线2x +y -4 = 0相交于A 、B 两点,抛物线的焦点|AF|+ |BF| = 3, 则线段AB 的中点到y 轴的距离为4. 5. 3 A- 4B. 15 c.— 47 D- 4已知抛物线 A .相离y 2二2px ,以过焦点的弦为直径的圆与抛物线准线的位置关系是B. 相交C. 相切 D .不确定已知F 为抛物线y 2 = 8x 的焦点,过F 且斜率为1的直线交抛物线于 点,则||FA| - |FB||的值等于B. 8C .D . 166.在y = 2x 2上有一点P ,它到A(1,3)的距离与它到焦点的距离之和最小 ,则点P 的坐标是A . (-2,1)B . (1,2)C . (2,1)D . (- 1,2)A 为垂足.如果直线AF 的斜率为-「3, 那么|PF 匸A. 4 .'3B . 8168.抛物线的顶点在原点,准线方程为 x = — 2,抛物线的方程 (A . y2= — 8xB . y2=8xC . y2 = — 4xD . y2= 4x9以抛物线x 2= 16y 的焦点为圆心,且与抛物线的准线相切的圆的方程为为 F ,那么 I F A | + | FB | = ____________ .12.过抛物线y2= 4x 的焦点作直线交抛物线于 A(x1 , y1), B(x2, y2)两点, 若x1 + x2 = 6,那么|AB|等于 _________ 13 .根据下列条件求抛物线的标准方程:(1)抛物线的焦点是双曲线16x 2— 9y 2= 144的左顶点; ⑵过点P(2, — 4).14.已知点A(— 1,0), B(1,— 1),抛物线C : y 2= 4x , O 为坐标原点,过点A 的动直线I 交抛物线C 于M , P 两点,直线MB 交抛物线C 于另一点Q.若向量解析一、抛物线的定义及其应用OM 与OP 的夹角为一,求厶POM 的面积.4例1、⑴如图,易知抛物线的焦点为F(1,0),准线是x =— 1.由抛物线的定义知:点P 到直线x 二一1的距离等于点P 到焦点F 的距离. 于是,问题转化为:在曲线上求一点P ,使点P 到点A(— 1,1)的距离与点P 到 F(1,0)的距离之和最小.显然,连结AF 交曲线于P 点,则所求的最小值为|AF|, 即为丐.(2)如图,自点B 作BQ 垂直准线于Q ,交抛物线于点P1,则|P1Q| = |P1F|.则有 |PB| + |PF| >|P1B| + |P1Q|= |BQ| = 4.即|PB|+ |PF|的最小值为 4.例2、解析:圆心到抛物线准线的距离为p ,即p = 4,根据已 知只要|FM|>4即 可•根据抛物线定|FM| = y0 + 2由y0 + 2>4,解得y0>2,故y0的取值范围是 (2,+^). 二、抛物线的标准方程和几何性质例3、设点A(X 1,y 1),其中y 1>0.由点B 作抛物线的准线的垂线,垂足为•则|BF|=|BB 1|;又|CB|= 2|FB|,因此有 |CB|= 2|BB|, cosZCBB 1 =1 n n p;,/CBB 1 = j.即直线AB 与x 轴的夹角为[.又|AF| = |AK| = X 1 +; = 4,因此因此△ AKF 的面积等于! |AK|y 1=:M X 2 ;3 = 4 '3.例4 .分别过点A 、B 作AA 1、BB 1垂直于I ,且垂足分别为B 1,由已知条件 |BC| = 2|BF|得 |BC| = 2|BB 1|,A/BCBi = 30。
(完整版)抛物线练习题(含答案)

抛物线练习题一、选择题1.在直角坐标平面内,到点(1,1)和直线 x+ 2y= 3 距离相等的点的轨迹是 ()A .直线B.抛物线C.圆D.双曲线2.抛物线 y2= x 上一点 P 到焦点的距离是 2,则 P 点坐标为 ()3,± 67,± 79,± 35,± 10A. 22B. 42C. 42D. 223.抛物线 y= ax2的准线方程是y= 2,则 a 的值为 ()11A. 8 B .-8C. 8D.- 84.设抛物线 y2= 8x 上一点 P 到 y 轴的距离是4,则点 P 到该抛物线焦点的距离是 ()A .4B . 6C. 8D. 125.设过抛物线的焦点 F 的弦为 AB,则以 AB 为直径的圆与抛物线的准线的地址关系是()A .订交B .相切C.相离D.以上答案都有可能6.过点 F(0,3)且和直线 y+ 3=0 相切的动圆圆心的轨迹方程为 ()A .y2= 12xB .y2=- 12x C. x2= 12y D .x2=- 12y7.抛物线 y2= 8x 上一点 P 到 x 轴距离为12,则点 P 到抛物线焦点 F 的距离为 ()A .20B .8C. 22D. 248.抛物线的极点在坐标原点,焦点是椭圆4x2+ y2= 1 的一个焦点,则此抛物线的焦点到准线的距离为 ()11A. 2 3 B. 3 C.2 3 D.4 39.设抛物线的极点在原点,其焦点F 在 y 轴上,又抛物线上的点(k,- 2)与 F 点的距离为4,则 k 的值是 ()A. 4 B . 4 或- 4C.- 2 D .2 或- 212的焦点坐标是 ()10.抛物线 y=m x (m<0)A.0,mB. 0,-mC. 0,1D. 0,-1 444m4m11.抛物线的极点在原点,对称轴是x 轴,抛物线上的点(-5,2 5) 到焦点的距离是6,则抛物线的方程为 ()A. y2=- 2x B .y2=- 4x C. y2= 2x D. y2=- 4x 或 y2=- 36x12.已知抛物线y2=2px(p>0) 的准线与圆 (x- 3)2+ y2= 16 相切,则p 的值为 () 1A. 2 B . 1C.2 D .4二、填空题13.过抛物线焦点 F 的直线与抛物线订交于A 、B 两点,若A 、B 在抛物线准线上的射影是A 1、B 1,则∠ A 1FB 1=。
抛物线练习题

抛物线练习题抛物线是二次函数的图像,它在数学中有着重要的应用。
本文将为您提供一些抛物线的练习题,帮助您更好地理解和应用抛物线的概念。
练习题一:抛物线的标准方程已知抛物线的顶点坐标为(2,3),经过点(1,0)。
求该抛物线的标准方程。
解答:由于已知抛物线的顶点坐标为(2,3),则抛物线的标准方程可以表示为:y = a(x - 2)^2 + 3又因为抛物线经过点(1,0),将该点代入方程中可得:0 = a(1 - 2)^2 + 30 = a + 3a = -3所以,该抛物线的标准方程为:y = -3(x - 2)^2 + 3练习题二:抛物线的焦点和准线已知抛物线的顶点坐标为(0,0),焦点为(2,0)。
求该抛物线的准线方程。
由于已知抛物线的顶点坐标为(0,0),准线方程可以表示为:y = -p又因为抛物线的焦点坐标为(2,0),代入焦准距离公式可得:p = 2所以,该抛物线的准线方程为:y = -2练习题三:抛物线的对称轴给定抛物线的焦点坐标为(3,0),顶点坐标为(1,2)。
求该抛物线的对称轴方程。
解答:由于已知抛物线的焦点坐标为(3,0),顶点坐标为(1,2),对称轴方程可以表示为:x = h其中,抛物线的对称轴与焦点的x坐标相等,所以对称轴方程为:x = 3练习题四:抛物线的焦点和顶点已知抛物线的焦点坐标为(0,1),顶点坐标为(1,4)。
求该抛物线的准线方程。
由于已知抛物线的焦点坐标为(0,1),顶点坐标为(1,4),首先可以求得焦准距离的值:p = 3根据抛物线性质可知,焦点的y坐标为顶点的y坐标减去焦准距离的绝对值,所以焦点的y坐标为:1 = 4 - |3|解得焦点的y坐标为1。
因此,该抛物线的准线方程为:y = 1练习题五:抛物线的焦点和顶点已知抛物线的焦点坐标为(2,-1),顶点坐标为(1,0)。
求该抛物线的准线方程。
解答:由于已知抛物线的焦点坐标为(2,-1),顶点坐标为(1,0),首先可以求得焦准距离的值:p = 1根据抛物线性质可知,焦点的y坐标为顶点的y坐标减去焦准距离的绝对值,所以焦点的y坐标为:-1 = 0 - |1|解得焦点的y坐标为-1。
抛物线同步练习题小题含答案

抛物线基础训练题1. 抛物线y 2=8x 的准线方程是( A )。
(A )x =-2 (B )x =2 (C )x =-4 (D )y =-22. 过抛物线y 2=4x 的焦点F ,作倾斜角为60°的直线,则直线的方程是( B )。
(A )y =33(x -1) (B )y =3 (x -1) (C )y =33(x -2) (D )y =3 (x -2) 3.已知抛物线的焦点是F (0,4),则此抛物线的标准方程是( A ) (A )x 2=16y (B )x 2=8y (C )y 2=16x (D )y 2=8x4. 若抛物线y =x 2与x =-y 2的图象关于直线l 对称,则l 的方程是(B )。
(A )x -y =0 (B )x +y =0 (C )x =0 (D )y =05.AB 是过抛物线y 2=4x 焦点F 的弦,已知A ,B 两点的横坐标分别是x 1和x 2,且x 1+x 2=6则|AB |等于( B ) (A )10 (B )8 (C )7 (D )66.经过(1,2)点的抛物线的标准方程是(C )(A )y 2=4x (B )x 2=21y (C ) y 2=4x 或x 2=21y (D ) y 2=4x 或x 2=4y 7. 过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1, y 1)、B (x 2, y 2)两点,如果AB 与x 轴成45°角,那么|AB |等于( B )。
(A )10 (B )8 (C )6 (D )48.抛物线的焦点在y 轴上,准线与椭圆4x 2+3y 2=1的左准线重合,并且经过椭圆的右焦点,那么它的对称轴方程是C(A )y =24 (B )y =26 或 y =-26 (C )y =26 (D )y =22或y =-229. 顶点在原点,焦点是F (6, 0)的抛物线的方程是2y 24x =。
10.抛物线x 2=4y 的焦点为F ,A 是抛物线上一点,已知|AF |=4+22,则AF 所在直线方程是21211-122y x y x ++=+=+或。
习题(23)-抛物线简单的几何性质(1)

习题(23)抛物线的简单几何性质(1)一、选择题:1.直线和抛物线有且仅有一个公共点是直线和抛物线相切的 ( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 2.已知F 是抛物线y 2=-12x 的焦点,直线l 过焦点F 且x l ⊥轴,若l 交抛物线于A ,B 两点,则|AB |=(即通径长)( )A. 3B. 6C. 12D. 243.过抛物线x 2=4y 焦点作直线交抛物线于),(11y x A ,),(22y x B ,若y 1+y 2=6,则|AB |=( ) A. 10 B. 8 C. 6 D. 4 4.设斜率为2的直线l 过抛物线y 2=ax )0(≠a 的焦点F ,且和y 轴交于点A ,若OAF ∆(O 为坐标原点)的面积为4,则抛物线方程为( )A. y 2=4xB. y 2=8xC. y 2=±4xD. y 2=±8x5.抛物线x 2=4y 截直线l : y =kx +1所得的弦长为316,则l 的倾斜角为( ) A. ︒60 B. ︒30 C. ︒60或︒120 D. ︒30或︒150 *6.已知抛物线C : y 2=8x 与点M (-2,2),过C 的焦点且斜率为k 的直线与C 交于A ,B 两点,若0=⋅MB MA ,则k =( ) A.21B.22 C .2 D .2二、填空题:7.已知抛物线y 2=2x 上两点A ,B 到焦点的距离之和为5,则线段AB 的中点M 到y 轴的距离为 .8.平面内动点P 到定点A (2,0)的距离比P 到y 轴的距离大2,则动点P 的轨迹方程为 . 9.过(0,2)的直线与抛物线y 2=8x 交于A ,B ,若线段AB 的中点的横坐标是2,则|AB |= . 10.已知点M (3,2),F 是抛物线y 2=2x 的焦点,P 是该抛物线上的点,则|PM |+|PF |的最小值是 ,此时P 点的坐标是 .11.过抛物线x 2=2py (p >0)的焦点F 作斜率为1的直线 与该抛物线交于A ,B 两点,A ,B 在x 轴上的射影分别 为D,C ,若梯形ABCD 的面积为212,则抛物线的焦 点F 的坐标为 .三、解答题:12.已知P (0,1)是抛物线y 2=x 上一点,直线l 经过点P 且与抛物线只有一个公共点,求直线l 的方程.13.已知直线l : y =-1及圆1)2(:22=-+y x C ,动圆M 与直线l 相切,且与圆C 相外切,求动圆圆心M 的轨迹方程.14.如图,在正方形OABC 中,O 为坐标原点,点A 的坐标为(10,0),点C 的坐标为(0,10).分别将线段OA 和AB 十等分,分点分别记为A 1, A 2, ……,A 9和B 1, B 2, ……,B 9,连结i OB ,过A 1做x 轴的垂线与i OB 交于点i OB ,i P )91*,(≤≤∈i N i .(1)求证:点i P )91*,(≤≤∈i N i 都在同一条抛物线上,并求该抛物线E 的方程;(2)过点C 做直线与抛物线E 交于不同的两点M ,N ,若OCM ∆与OCN ∆的面积比为1:4,求直线的方程.lCMOyx。
(完整版)抛物线练习题(含答案)

抛物线练习题一、选择题1.在直角坐标平面内,到点(1,1)和直线x +2y =3距离相等的点的轨迹是( )A .直线B .抛物线C .圆D .双曲线2.抛物线y 2=x 上一点P 到焦点的距离是2,则P 点坐标为( )A.⎝⎛⎭⎫32,±62B.⎝⎛⎭⎫74,±72C.⎝⎛⎭⎫94,±32D.⎝⎛⎭⎫52,±102 3.抛物线y =ax 2的准线方程是y =2,则a 的值为( )A.18 B .-18C .8D .-8 4.设抛物线y 2=8x 上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是( )A .4B .6C .8D .125.设过抛物线的焦点F 的弦为AB ,则以AB 为直径的圆与抛物线的准线的位置关系是( )A .相交B .相切C .相离D .以上答案都有可能6.过点F (0,3)且和直线y +3=0相切的动圆圆心的轨迹方程为( )A .y 2=12xB .y 2=-12xC .x 2=12yD .x 2=-12y7.抛物线y 2=8x 上一点P 到x 轴距离为12,则点P 到抛物线焦点F 的距离为( )A .20B .8C .22D .248.抛物线的顶点在坐标原点,焦点是椭圆4x 2+y 2=1的一个焦点,则此抛物线的焦点到准线的距离为( )A .2 3 B. 3 C.12 3 D.143 9.设抛物线的顶点在原点,其焦点F 在y 轴上,又抛物线上的点(k ,-2)与F 点的距离为4,则k 的值是( )A .4B .4或-4C .-2D .2或-210.抛物线y =1mx 2(m <0)的焦点坐标是( ) A.⎝⎛⎭⎫0,m 4 B.⎝⎛⎭⎫0,-m 4 C.⎝⎛⎭⎫0,14m D.⎝⎛⎭⎫0,-14m 11.抛物线的顶点在原点,对称轴是x 轴,抛物线上的点(-5,25)到焦点的距离是6,则抛物线的方程为( )A .y 2=-2xB .y 2=-4xC .y 2=2xD .y 2=-4x 或y 2=-36x12.已知抛物线y 2=2px (p >0)的准线与圆(x -3)2+y 2=16相切,则p 的值为( )A.12 B .1 C .2 D .4二、填空题13.过抛物线焦点F的直线与抛物线相交于A、B两点,若A、B在抛物线准线上的射影是A1、B1,则∠A1FB1= 。
抛物线练习题带答案,知识点总结(基础版)
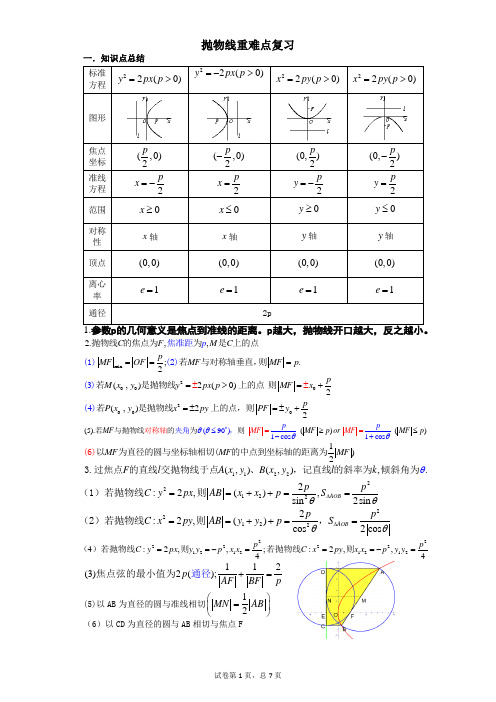
抛物线重难点复习一.知识点总结2.,,C F p M C 焦抛物线的焦点为为是准距上的点min ;.2pMF OF MF MF p ===(1)(2)若与对称轴垂直,则2000(,)2(0)23p M x y y px p MF x =>=±+±若是抛物线上的点则() 2000(,)224p P x y x py PF y =±=±+若是抛物线上的(点,则) (5).()(90)1cos s ()1co p MF MF pp or MF p MF MF θθθθ≥≤-+==≤ 若与抛物线的为则夹角,对称轴1)2MF MF MF 以为直径的圆与坐标轴相切(的中点到坐标轴的距离为(6)1122(,)(,),.F l A x y B x y l k θ3.过焦点的直线交抛物线于点、,记直线的斜率为倾斜角为221222:2,(),sin 2sin AOB p p C y px AB x x p S θθ∆==++==(1)若抛物线则221222:2,()cos 2cos AOB p p C x py AB y y p S θθ∆==++==(2)若抛物线则, 222222121212124:2,,;:2,,44p p C y px y y p x x C x py x x p y y ==-===-=()若抛物线则若抛物线则112(3)2();p AF BF p+=通焦点弦的最径小值为 (5)以AB 为直径的圆与准线相切12MN AB ⎛⎫=⎪⎝⎭(6)以CD 为直径的圆与AB 相切与焦点F1.已知抛物线22(0)y px p =>上横坐标为 3 的点到其焦点的距离为 4,则p =________. 【答案】2【解析】抛物线y 2=2px (p >0, ∵抛物线y 2=2px (p >04,∴p=2.故答案为2.2.已知F 是抛物线y 2=2x 的焦点,A ,B 是该抛物线上的两点,|AF |+|BF |=11,则线段AB 的中点到y 轴的距离为( ) A. 3 B. 4 C. 5 D. 7 【答案】C 【解析】∵F 是抛物线y 2=2x 的焦点∴F (12,0) ,准线方程x =−12, 设A (x 1,y 1),B (x 2,y 2)∴|AF |+|BF |=x 1+1+x 2+1=11x 1+x 2=10,∴线段AB 的中点横坐标为5∴线段AB 5,所以B 选项是正确的.3.已知抛物线C :的焦点为F ,()00A x y ,是C 上一点,则0x =( )A. 2B. 2±C. 4D. 4± 【答案】D【解析】28x y =,如图,由抛物线的几何意义,可知0022AF Al y y ===+,所以02y =, 所以04x =±,故选D 。
抛物线基础练习题

抛物线基础练习题1.动点P 到点A (0,2)的距离比到直线l :y =-4的距离小2,则动点P 的轨迹方程为A. x y 42=B. x y 82=C.y x 42=D.y x 82=2.已知直线l 与抛物线x y 82=交于A 、B 两点,且l 经过抛物线的焦点F ,A 点的坐标为(8,8),则线段AB 的中点到准线的距离是 ( ) A.425 B. 225 C. 825 D.25 3.已知抛物线的焦点在直线y x 2--4=0上,则此抛物线的标准方程是( )A.x y 162=B.y x 82-=C. x y 162=或y x 82-=D. x y 162=或y x 82=4.直线y =kx -2与抛物线x y 82=交于A 、B 两点,且AB 的中点横坐标为2,则k 的值是 ( ) A.-1 B.2 C.-1或2 D.以上都不是5.已知抛物线的顶点在原点,焦点在y 轴上,其上的点)3,(-m P 到焦点的距离为5,则抛物线方程为 ( )A .y x 82=B .y x 42=C .y x 42-=D .y x 82-=6.物线x y 122=截直线12+=x y 所得弦长等于 ( )A .15B .152C .215D .157.已知圆07622=--+x y x ,与抛物线)0(22>=p px y 的准线相切,则=p8.抛物线的准线方程为 _____________9.抛物线上的一点M 到焦点的距离为1,则点M 的纵坐标是( )A .B .C .D .010.抛物线的准线方程是 ____________11.抛物线在点M (,)处的切线的倾斜角是( )A .30°B .45°C .60°D .90°12.物线22x y =的焦点坐标是 ( )A .)0,1(B .)0,41(C .)81,0(D . )41,0( 13抛物线的焦点与椭圆的右焦点重合,则的值为( ) 22y x =24x y =161716158728x y =-2x y =214122y px =22162x y +=p。
高中数学抛物线经典例题

抛物线(1)抛物线——二次曲线【例1】P 为抛物线px y 22=上任一点,F 为焦点,则以PF 为直径的圆与y 轴( ).A 相交 .B 相切 .C 相离 .D 位置由P 确定【解析】如图,抛物线的焦点为,02p F ⎛⎫⎪⎝⎭,准线是 :2pl x =-.作PH ⊥l 于H ,交y 轴于Q ,那么PF PH =,且2pQH OF ==.作MN ⊥y 轴于N 则MN 是梯形PQOF 的中位线,()111222MN OF PQ PH PF =+==.故以PF 为直径的圆与y 轴相切,选B.【评注】相似的问题对于椭圆和双曲线来说,其结论则 分别是相离或相交的.(2)焦点弦——常考常新的亮点弦有关抛物线的试题,许多都与它的焦点弦有关.理解并掌握这个焦点弦的性质,对破解这些试题是大有帮助的.【例2】 过抛物线()022p px y =的焦点F 作直线交抛物线于()()1122,,,A x y B x y 两点,求证:(1)12AB x x p =++ (2)pBF AF 211=+ 【证明】(1)如图设抛物线的准线为l ,作1AA l ⊥11111,2pA BB l B AA x ⊥==+于,则AF ,122pBF BB x ==+.两式相加即得:12AB x x p =++(2)当AB ⊥x 轴时,有AF BF p ==,112AF BF p∴+=成立; 当AB 与x 轴不垂直时,设焦点弦AB 的方程为:2p y k x ⎛⎫=- ⎪⎝⎭.代入抛物线方程:2222p k x px ⎛⎫-= ⎪⎝⎭.化简得:()()222222014p k x p k x k -++=∵方程(1)之二根为x 1,x 2,∴1224k x x ⋅=.()122111212121111112224x x p p p p p AF BF AA BB x x x x x x +++=+=+=+++++ ()()121222121222424x x p x x p p p p p p x x p x x ++++===+++++. 故不论弦AB 与x 轴是否垂直,恒有p BF AF 211=+成立.(3)切线——抛物线与函数l XY FA(x,y)11B(x,y)22A 1B 1l【例3】证明:过抛物线22y px =上一点M (x 0,y 0)的切线方程是:y 0y=p (x+x 0)【证明】对方程22y px =两边取导数:22.py y p y y''⋅=∴=,切线的斜率 00x x p k y y ='==.由点斜式方程:()()20000001p y y x x y y px px y y -=-⇒=-+20021y px =,代入()即得: y 0y=p (x+x 0)(4)定点与定值——抛物线埋在深处的宝藏例如:1.一动圆的圆心在抛物线x y 82=上,且动圆恒与直线02=+x 相切,则此动圆必过定点 ( )()()()().4,0.2,0.0,2.0,2A B C D -显然.本题是例1的翻版,该圆必过抛物线的焦点,选B. 2.抛物线22y px =的通径长为2p ;3.设抛物线22y px =过焦点的弦两端分别为()()1122,,,A x y B x y ,那么:212y y p =-以下再举一例【例4】设抛物线22y px =的焦点弦AB 在其准线上的射影是A 1B 1,证明:以A 1B 1为直径的圆必过一定点【分析】假定这条焦点弦就是抛物线的通径,那么A 1B 1=AB=2p ,而A 1B 1与AB 的距离为p ,可知该圆必过抛物线的焦点.由此我们猜想:一切这样的圆都过抛物线的焦点.以下我们对AB 的一般情形给于证明. 【证明】如图设焦点两端分别为()()1122,,,A x y B x y , 那么:22121112.y y p CA CB y y p =-⇒⋅== 设抛物线的准线交x 轴于C ,那么.CF p =2111111.90A FB CF CA CB A FB ∴∆=⋅∠=︒中故.这就说明:以A 1B 1为直径的圆必过该抛物线的焦点.● 通法 特法 妙法(1)解析法——为对称问题解困排难解析几何是用代数的方法去研究几何,所以它能解决纯几何方法不易解决的几何问题(如对称问题等). 【例5】(07.四川文科卷.10题)已知抛物线 y=-x 2+3上存在关于直线x+y=0对称的相异两点 A 、B ,则|AB|等于( )A.3B.4C.32D.42 【分析】直线AB 必与直线x+y=0垂直,且线段 AB 的中点必在直线x+y=0上,因得解法如下.【解析】∵点A 、B 关于直线x+y=0对称,∴设直线AB 的方程为:y x m =+.由()223013y x m x x m y x =+⎧⇒++-=⎨=-+⎩设方程(1)之两根为x 1,x 2,则121x x +=-.11,22M ⎛⎫- ⎪⎝⎭. 设AB 的中点为M (x 0,y 0),则120122x x x +==-.代入x+y=0:y 0=12.故有从而1m y x =-=.直线AB 的方程为:1y x =+.方程(1)成为:220x x +-=.解得:2,1x =-,从而1,2y =-,故得:A (-2,-1),B (1,2).AB ∴=,选C.(2)几何法——为解析法添彩扬威 虽然解析法使几何学得到长足的发展,但伴之而来的却是难以避免的繁杂计算,这又使得许多考生对解析几何习题望而生畏.针对这种现状,人们研究出多种使计算量大幅度减少的优秀方法,其中最有成效的就是几何法.【例6】(07.全国1卷.11题)抛物线24y x =的焦点为F ,准线为l ,经过F x 轴XYAB FA 1B 11M CXOY ABMl x y +=ÿxyM(x,y)F 1(-c ,0)F 2(c,0)O H2:a l x c=-r 1r 2r 2上方的部分相交于点A ,AK l ⊥,垂足为K ,则AKF △的面积( ) A .4B .33C .43D .8【解析】如图直线AF 3AFX=60°. △AFK 为正三角形.设准线l 交x 轴于M ,则2,FM p == 且∠KFM=60°,∴234,43AKF KF S ∆===选C. 【评注】(1)平面几何知识:边长为a 的正三角形的面积用公式23S ∆=计算. (2)本题如果用解析法,需先列方程组求点A 的坐标,,再计算正三角形的边长和面积.虽不是很难,但决没有如上的几何法简单.(3)定义法——追本求真的简单一着许多解析几何习题咋看起来很难.但如果返朴归真,用最原始的定义去做,反而特别简单. 【例7】(07.湖北卷.7题)双曲线22122:1(00)x y C a b a b-=>>,的左准线为l ,左焦点和右焦点分别为1F 和2F ;抛物线2C 的线为l ,焦点为21F C ;与2C 的一个交点为M ,则12112F F MF MF MF -等于( )A .1-B .1C .12-D .12【分析】 这道题如果用解析法去做,计算会特别繁杂,而平面几何知识又一时用不上,那么就从最原始的定义方面去寻找出路吧.如图,我们先做必要的准备工作:设双曲线的半 焦距c ,离心率为e ,作 MH l H ⊥于,令 1122,MF r MF r ==.∵点M 在抛物线上, 1112222,MF MF r MH MF r e MH MF r ∴=====故,这就是说:12||||MF MF 的实质是离心率e.其次,121||||F F MF 与离心率e 有什么关系?注意到:()1212111122111F F e r r c e a e e MF r r r e +⋅⎛⎫====-=- ⎪⎝⎭. 这样,最后的答案就自然浮出水面了:由于()12112||||11||||F F MF e e MF MF -=-+=-.∴选 A..(4)三角法——本身也是一种解析三角学蕴藏着丰富的解题资源.利用三角手段,可以比较容易地将异名异角的三角函数转化为同名同角的三角函数,然后根据各种三角关系实施“九九归一”——达到解题目的.因此,在解析几何解题中,恰当地引入三角资源,常可以摆脱困境,简化计算.线x y 82=的【例8】(07.重庆文科.21题)如图,倾斜角为a 的直线经过抛物焦点F ,且与抛物线交于A 、B 两点。
高中数学抛物线练习题(含答案)

抛物线练习题一、选择题1.在直角坐标平面内,到点(1,1)和直线x +2y =3距离相等的点的轨迹是( )A .直线B .抛物线C .圆D .双曲线2.抛物线y 2=x 上一点P 到焦点的距离是2,则P 点坐标为( )A.⎝⎛⎭⎫32,±62B.⎝⎛⎭⎫74,±72C.⎝⎛⎭⎫94,±32D.⎝⎛⎭⎫52,±102 3.抛物线y =ax 2的准线方程是y =2,则a 的值为( )A.18 B .-18C .8D .-8 4.设抛物线y 2=8x 上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是( )A .4B .6C .8D .125.设过抛物线的焦点F 的弦为AB ,则以AB 为直径的圆与抛物线的准线的位置关系是( )A .相交B .相切C .相离D .以上答案都有可能6.过点F (0,3)且和直线y +3=0相切的动圆圆心的轨迹方程为( )A .y 2=12xB .y 2=-12xC .x 2=12yD .x 2=-12y7.抛物线y 2=8x 上一点P 到x 轴距离为12,则点P 到抛物线焦点F 的距离为( )A .20B .8C .22D .248.抛物线的顶点在坐标原点,焦点是椭圆4x 2+y 2=1的一个焦点,则此抛物线的焦点到准线的距离为( )A .2 3 B. 3 C.12 3 D.143 9.设抛物线的顶点在原点,其焦点F 在y 轴上,又抛物线上的点(k ,-2)与F 点的距离为4,则k 的值是( )A .4B .4或-4C .-2D .2或-210.抛物线y =1mx 2(m <0)的焦点坐标是( ) A.⎝⎛⎭⎫0,m 4 B.⎝⎛⎭⎫0,-m 4 C.⎝⎛⎭⎫0,14m D.⎝⎛⎭⎫0,-14m 11.抛物线的顶点在原点,对称轴是x 轴,抛物线上的点(-5,25)到焦点的距离是6,则抛物线的方程为( )A .y 2=-2xB .y 2=-4xC .y 2=2xD .y 2=-4x 或y 2=-36x12.已知抛物线y 2=2px (p >0)的准线与圆(x -3)2+y 2=16相切,则p 的值为( )A.12 B .1 C .2 D .4二、填空题13.过抛物线焦点F的直线与抛物线相交于A、B两点,若A、B在抛物线准线上的射影是A1、B1,则∠A1FB1= 。
初中抛物线经典练习题(含详细答案)

初中数学抛物线经典试题集锦【编著】黄勇权【第一组题型】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
3、在平面直角坐标系xOy中,已知抛物线的顶点C为(2,4),并在x轴上截得的长度为6。
(1)写出抛物线与x轴交点A、B的坐标(2)求该抛物线的表达式(3)写出抛物线与y轴交点P的坐标4、直线的解析式为y=2x+4,交x轴于点A,交y轴于点B,若以A 为顶点,,且开口向下作抛物线,交直线AB于点D,交y轴负半轴于点C,(1)若△ABC的面积为20,求此时抛物线的解析式(2)若△BDO的面积为8,求此时抛物线的解析式【答案】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
解:【第一问】因为函数y=x²+bx+c过点A(2,0),C(0, -8)分别将x=2,y=0代入y=x²+bx+c,得0=4+2b+c-----①将x=0,y=-8代入y=x²+bx+c,得-8=c-------------②将②代入①,解得:b=2--------------------------------------③此时,将②③代入y=x²+bx+c,所以:二次函数的解析式y=x²+ 2x -8【第二问】△ABP的面积= 12│AB│*│y p│----------------------④因为A、B两点在x轴上,令x²+ 2x -8=0(x-2)(x+4)=0解得:x1=2,x2= -4所以:│AB│=│X1- X2│=│2-(- 4)│=6------⑤又△ABP的面积=15-------------------------------------⑥由④⑤⑥,得:12*6*│y p│=15│y p│=5故有:y p= ±5即:p点的纵坐标为5或-5.把y=5代入y=x²+ 2x -8,即:5=x²+ 2x -8x²+ 2x -13=0解得:x= -1± 14那么,此时p点坐标(-1+ 14,5),(-1- 14,5)-------⑦把y=-5代入y=x²+ 2x -8,即:-5=x²+ 2x -8x²+ 2x -3=0(x-1)(x+3)=0解得:x= 1或x= -3那么,此时p点坐标(1,-5),(-3,-5)------------------⑧由⑦⑧得,使△ABP的面积为15,p点坐标是:(-1+ 14,5),(-1- 14,5),(1,-5),(-3,-5)2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
初中抛物线经典练习题(含详细答案)

【编著】 黄勇权【第一组题型】1、已知二次函数y=x ²+bx+c 过点A (2,0),C (0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p 使△ABP 的面积为15,请直接写出p 点的坐标。
2、在平面直角坐标系xOy 中,抛物线y=2x ²+mx+n 经过点A (5,0),B (2,-6).(1)求抛物线的表达式及对称轴(2)设点B 关于原点的对称点为C ,写出过A 、C 两点直线的表达式。
初中数学抛物线 经典试题集锦3、在平面直角坐标系xOy中,已知抛物线的顶点C为(2,4),并在x轴上截得的长度为6。
(1)写出抛物线与x轴交点A、B的坐标(2)求该抛物线的表达式(3)写出抛物线与y轴交点P的坐标4、直线的解析式为y=2x+4,交x轴于点A,交y轴于点B,若以A为顶点,,且开口向下作抛物线,交直线AB于点D,交y轴负半轴于点C,(1)若△ABC的面积为20,求此时抛物线的解析式(2)若△BDO的面积为8,求此时抛物线的解析式【答案】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
解:【第一问】因为函数y=x ²+bx+c 过点A (2,0),C (0, -8)分别将x=2,y=0代入y=x ²+bx+c , 得 0=4+2b+c-----①将x=0,y=-8代入y=x ²+bx+c ,得-8=c-------------②将②代入①,解得:b=2--------------------------------------③此时,将② ③代入y=x ²+bx+c ,所以:二次函数的解析式 y=x ²+ 2x -8【第二问】△ABP 的面积= 12│AB │*│y p │----------------------④ 因为A 、B 两点在x 轴上,令x ²+ 2x -8=0(x-2)(x+4)=0解得:x 1=2,x 2= -4所以:│AB │=│X 1- X 2│=│2-(- 4)│=6------⑤又△ABP 的面积=--------------------------⑥由 ④ ⑤ ⑥,得 : 12*6*│y p │=15│y p│=5故有:y p= ±5即:p点的纵坐标为5或-5.把y=5代入 y=x²+ 2x -8,即:5=x²+ 2x -8x²+ 2x -13=0解得:x= -1± 14那么,此时p点坐标(-1+ 14,5),(-1- 14,5)-------⑦把y=-5代入 y=x²+ 2x -8,即:-5=x²+ 2x -8x²+ 2x -3=0(x-1)(x+3)=0解得:x= 1或x= -3那么,此时p点坐标(1,-5),(-3,-5)------------------⑧由⑦⑧得,使△ABP的面积为15,p点坐标是:(-1+ 14,5),(-1- 14,5),(1,-5),(-3,-5)2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
初中数学抛物线经典习题及答案

初中数学抛物线经典试题集锦【第一组题型】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
3、在平面直角坐标系xOy中,已知抛物线的顶点C为(2,4),并在x轴上截得的长度为6。
(1)写出抛物线与x轴交点A、B的坐标(2)求该抛物线的表达式(3)写出抛物线与y轴交点P的坐标4、直线的解析式为y=2x+4,交x轴于点A,交y轴于点B,若以A 为顶点,,且开口向下作抛物线,交直线AB于点D,交y轴负半轴于点C,(1)若△ABC的面积为20,求此时抛物线的解析式(2)若△BDO的面积为8,求此时抛物线的解析式【答案】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
解:【第一问】因为函数y=x²+bx+c过点A(2,0),C(0, -8)分别将x=2,y=0代入y=x²+bx+c,得0=4+2b+c-----①将x=0,y=-8代入y=x²+bx+c,得-8=c-------------②将②代入①,解得:b=2--------------------------------------③此时,将②③代入y=x²+bx+c,所以:二次函数的解析式y=x²+ 2x -8【第二问】△ABP的面积= 12│AB│*│y p│----------------------④因为A、B两点在x轴上,令x²+ 2x -8=0(x-2)(x+4)=0解得:x1=2,x2= -4所以:│AB│=│X1- X2│=│2-(- 4)│=6------⑤又△ABP的面积=15-------------------------------------⑥由④⑤⑥,得:12*6*│y p│=15│y p│=5故有:y p= ±5即:p点的纵坐标为5或-5.把y=5代入y=x²+ 2x -8,即:5=x²+ 2x -8x²+ 2x -13=0解得:x= -1± 14那么,此时p点坐标(-1+ 14,5),(-1- 14,5)-------⑦把y=-5代入y=x²+ 2x -8,即:-5=x²+ 2x -8x²+ 2x -3=0(x-1)(x+3)=0解得:x= 1或x= -3那么,此时p点坐标(1,-5),(-3,-5)------------------⑧由⑦⑧得,使△ABP的面积为15,p点坐标是:(-1+ 14,5),(-1- 14,5),(1,-5),(-3,-5)2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
初中抛物线经典练习题(含详细答案)

初中抛物线经典练习题(含详细答案)初中数学抛物线经典试题集锦,编著者为黄勇权。
以下为题目和解答。
第一组题型】1、已知二次函数$y=x^2+bx+c$过点$A(2,0)$,$C(0,-8)$1)求此二次函数的解析式;2)在抛物线上存在一点$p$使$\triangle ABP$的面积为15,请直接写出$p$点的坐标。
解:第一问】因为函数$y=x^2+bx+c$过点$A(2,0)$,$C(0,-8)$,分别将$x=2$,$y=0$代入$y=x^2+bx+c$,得$0=4+2b+c$-----①。
将$x=0$,$y=-8$代入$y=x^2+bx+c$,得$-8=c$-------------②。
将②代入①,解得:$b=2$--------------------------------------③。
此时,将②③代入$y=x^2+bx+c$,所以二次函数的解析式为$y=x^2+2x-8$。
第二问】因为$A$、$B$两点在$x$轴上,令$x^2+2x-8=0$,解得:$x_1=2$,$x_2=-4$。
所以$|AB|=|x_1-x_2|=|2-(-4)|=6$。
又$\triangle ABP$的面积为15,所以$|y_p|\cdot 6=30$,即$|y_p|=5$。
故$p$点的纵坐标为5或-5,即$p(2,5)$或$p(2,-5)$。
2、在平面直角坐标系$xOy$中,抛物线$y=2x^2+mx+n$经过点$A(5,B)$,$B(2,-6)$。
1)求抛物线的表达式及对称轴;2)设点$B$关于原点的对称点为$C$,写出过$A$、$C$两点直线的表达式。
解:第一问】因为抛物线$y=2x^2+mx+n$经过点$A(5,B)$,$B(2,-6)$,分别将$x=5$,$y=B$代入$y=2x^2+mx+n$,得$B=50+5m+n$-----①。
将$x=2$,$y=-6$代入$y=2x^2+mx+n$,得$-6=8+2m+n$-------------②。
抛物线相交问题练习题

抛物线相交问题练习题一、基础题1. 已知抛物线 $y = x^2 4x + 3$ 与 $y = 2x^2 3x 1$,求两抛物线的交点坐标。
2. 抛物线 $y = x^2 + 6x 7$ 与 $y = x^2 8x + 15$ 相交于A、B两点,求线段AB的中点坐标。
3. 已知抛物线 $y = 2x^2 4x + 1$ 与 $y = x^2 + 2x + 3$,求两抛物线的交点个数。
4. 抛物线 $y = x^2 2x 3$ 与 $y = 2x^2 + 4x + 5$ 相交于C、D两点,求CD线段的长度。
5. 已知抛物线 $y = 3x^2 6x + 2$ 与 $y = 3x^2 + 6x 2$,求两抛物线的公共弦方程。
二、提高题1. 抛物线 $y = x^2 5x + 6$ 与 $y = 2x^2 + 8x 7$ 相交于E、F两点,若线段EF的中点在直线 $y = 3x 1$ 上,求EF的长度。
2. 已知抛物线 $y = 4x^2 12x + 9$ 与 $y = 2x^2 + 8x 7$,求两抛物线交点处的切线方程。
3. 抛物线 $y = x^2 4x + 3$ 与 $y = x^2 + 6x 7$ 相交于G、H两点,若GH线段的长度为4,求两抛物线的交点坐标。
4. 已知抛物线 $y = 2x^2 8x + 8$ 与 $y = x^2 + 4x 1$,求两抛物线交点处的切线夹角。
5. 抛物线 $y = x^2 2x 3$ 与 $y = 2x^2 + 8x 11$ 相交于I、J两点,若IJ线段的长度为 $\sqrt{5}$,求两抛物线的交点坐标。
1. 抛物线 $y = x^2 6x + 9$ 与 $y = 2x^2 + 12x 18$ 相交于K、L两点,求以KL为直径的圆的方程。
2. 已知抛物线 $y = 3x^2 12x + 11$ 与 $y = x^2 + 4x 3$,求两抛物线交点处的切线平行于直线 $y = 2x + 1$ 的交点坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.抛物线的定义满足以下三个条件的点的轨迹是抛物线:(1)在平面内;(2)动点到定点F 的距离与到定直线l 的距离相等;(3)定点不在定直线上.❶其中点F 叫做抛物线的焦点,直线l 叫做抛物线的准线. 若定点F 在定直线l 上,则动点的轨迹为过点F 且垂直于l 的一条直线. 1.若定点F 在定直线l 上,则动点的轨迹为过点F 且垂直于l 的一条直线. 2.焦点到准线的距离等于p ,焦点非零坐标是一次项除以4. 3.焦点与原点的距离都等于一次项系数的绝对值的14,即2p 4=p 2
4.通径:过焦点垂直于对称轴的弦,长等于2p ,通径是过焦点最短的弦.
设AB 是过抛物线y 2=2px (p >0)焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则
(1)x 1x 2=p 24,y 1y 2=-p 2; (2)|AF |=x 1+2p ,|BF |=x 2+2p ,弦长|AB |=x 1+x 2+p =2p sin 2α
(α为弦AB 的倾斜角); (3)1|FA |+1|FB |
=2p ; (4)以弦AB 为直径的圆与准线相切; (5)以AF 或BF 为直径的圆与y 轴相切; (6)过焦点弦的端点的切线互相垂直且交点在准线上.
一.抛物线定义:
1.一个动圆经过点F (-1,0),又与直线L:x=1相切,则动圆圆心的轨迹方程是( )
A.x y 42=
B.x y 22-=
C.x y 42-=
D.x y 82
-=
2.已知动圆圆心在抛物线x y 42=上,且动圆与直线x=-1相切,则动圆必过定点( )A.(2,0)B.(1,0)C.(0,1) (1)当Q (Q Q y x ,)为抛物线内任意一点,则存在PQ PF +的最小值,当P 、Q 两
点的纵坐标相等时,即2min p Q x EQ PQ PF +==+(内部连准线)
(2)当Q (Q Q y x ,)为抛物线外任意一点,存在PQ d +最小值,当Q 、P 、F 三点
共线时,()()2
2
2min Q p Q y x FQ PQ d +-==+(外部连焦点)
由此类比抛物线py x 22=的最值问题,把握内连准线,外找焦点。
3..(1)已知抛物线y 2=4x 的焦点是F ,点P 是抛物线上的动点,对于定点A (4,2),求|P A |+|PF |的最小值,并求出取最小值时的P 点坐标.
(2)已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点A (0,2)的距离与P 到该抛物线准线的距离之和的最小值为( )A .172 B .3C . 5 D .92
4.已知点P 为抛物线x y 42=上的一个动点,设点P 到y 轴的距离为d ,对于定点A (3,4),d PA +的最小值为( )
A.52
B.152-
C.152+
D.252-
5.已知抛物线方程为y 2=4x ,直线l 的方程为x -y+5=0,在抛物线上有一动点P 到y 轴的距离为d 1,到直线l 的距离为d 2.求d 1+d 2的最小值.
为 。
6.若点P 为抛物线x y 82
=上的动点,点Q 在以C (2,0)位圆心,半径为1的圆上运动,则PC PQ +的最小值为 。
二. 抛物线的焦点位置判断:焦点在一次项的坐标轴上,一次项的符号决定开口方向.
1已知抛物线)0(22≠=p px y 的准线与圆(x -3)2+y 2=16相切,则P 的值为( ) (A ) (B )1 (C )2 (D )4
2..设A 、B 为抛物线)0(22≠=p px y 上的点,且090=∠AOB (O 为原点),则直线AB 必过的定点坐标为__________.
12
2.顶点在原点,且过点P (-4,4)的抛物线标准方程是( )
A.x y 42-=
B.y x 42=
C.x y 42-=或y x 42=
D.x y 42=或y x 4-2
=
3.设抛物线的顶点在原点,且其准线方程为:x=2,则抛物线的方程为________.
4.抛物线)0(22>=p px y 的焦点为F ,倾斜角为 60的直线L 过点F 且与抛物线的一个交点为A ,3=AF ,则抛物线的方程为( )A.x y 32= B.x y 292= C.x y 232=或x y 2
92= D.x y 32=或x y 92= 抛物线的几何性值
5.过点(-1,0)且与抛物线x y =2
有且仅有一个公共点的直线有( )A.1条 B.2条 C.3条 D.4条
7.已知过抛物线x y 42=焦点F 的直线与抛物线交于A ,B 两点,且两点的横坐标之和为4,则线段AB 的长度为( )
A.4
B.5
C.6
D.8
8.已知过抛物线x y 42=焦点F 的直线与抛物线交于A ,B 两点(其中A 点在第一象限),3=,则直线L 的斜率为
9.过抛物线C:x y 42=的焦点F 的直线交抛物线于A ,B 两点,若BF AF 3=,则AB 斜率为 。
10.设抛物线C:x y 32
=的焦点为F ,过点F 且倾斜角为 30的直线交C 于A ,B 两点,则AB =( ) 11.已知抛物线的方程为x y =2,A ,B 为抛物线上两点,F 为抛物线焦点,若3=+BF AF ,则AB 的中点到y 轴
的距离为 。
12.抛物线y=-x 2上的点到直线4x +3y -8=0距离的最小值是 ( )A .43 B .75 C .85 D .3
13.(2017·邯郸质检)设F 为抛物线y 2=2x 的焦点,A 、B 、C 为抛物线上三点,若F 为△ABC 的重心,则|F A →|+|FB →|+|FC →|的值为( )A .1 B .2 C .3 D .4
14.已知抛物线y 2=2px (p >0),过点C (-2,0)的直线l 交抛物线于A 、B 两点,坐标原点为O , OA →·OB →=1 (1)求抛物线的方程;
(2)当以AB 为直径的圆与y 轴相切时,求直线l 的方程.
15.已知椭圆C :x 2a 2+y 2b 2=1(a>b>0)的离心率为√22,且以原点为圆心,椭圆的焦距为直径的圆与直线 x sin θ+y cos θ-1=0相切(θ为常数).
(1)求椭圆C 的标准方程;
(2)若椭圆C 的左、右焦点分别为F 1,F 2,过F 2作直线l 与椭圆交于M ,N 两点,求
·的最大值.。
