七年级数学垂直
七年级下册数学垂直知识点

七年级下册数学垂直知识点在数学中,垂直是一种常见的概念,也是我们学习数学必须熟悉的知识点。
在七年级的下册数学中,垂直知识点是一个非常重要的内容。
本文将介绍七年级下册数学中的垂直知识点,让同学们能够更好地理解和掌握这一知识点。
1. 垂线的概念垂线是指从一个点到一条直线或平面的距离最近的线段。
用符号⊥表示。
在图形中,垂线通常用虚线表示。
需要注意的是,一条直线或平面可以有无数条垂线。
2. 平行线和垂直线的关系平行线是指一直线与另外一条直线在同一平面上,但不相交的直线。
而垂直线则是指两条直线或线段之间成90度角的情况。
在平面几何中,当两条直线相交时,它们互为垂线。
因此,平行线和垂直线是互不相容的概念。
3. 垂直平分线垂直平分线是指一个线段的中垂线,它是将这个线段平分并垂直于线段的一条直线。
垂直平分线可以能够将一个线段分成相等的两部分,并且它们互相垂直。
4. 垂线的性质垂线有一些特殊的性质,这些性质对于理解垂线的概念和运用垂线进行计算是非常有帮助的。
- 垂线的长度:垂线的长度等于点到垂线所在的直线或平面的距离。
- 垂线的斜率:垂线的斜率是与被垂线的直线或平面的斜率相反的倒数。
- 垂线的平方:当垂线从一个点到另一个点垂直时,它的平方是两个点之间的距离的平方。
5. 垂线的应用垂线在实际生活中有着广泛的应用。
例如,在建筑设计中,垂线被广泛地用来检查建筑的垂直性和水平性。
在地图制图中,垂线被用来确定两个点之间的最短距离。
在数学中,垂线也是解决几何问题的重要工具。
总之,在七年级下册数学中,垂直知识点是数学学习过程中的一个必备知识点。
通过学习垂直知识点,同学们能够更好地理解和应用数学概念,提高自己的数学成绩。
七年级数学下册:8.5垂直课件_青岛版

山 东 诸城 舜王 程戈庄 初中
1.画一条线段的垂线,垂足在( ) D A.线段上 B.线段的端点 C.线段的延长线上 D.以上都有可能 2.如图,分别过P点作OA、OB的垂线
A M O P N B M A
O
P
B
3.如图,分别过点B、C,画AD所在直线的垂 线,垂足分别为M、N
A
N B M D C
山 东 诸城
舜王 程戈庄 初中
第八章:角
山 东 诸城 舜王 程戈庄 初中
找出图中的直角
直角的两边 有什么关系?
山 东 诸城 舜王 程戈庄 初中
Linqu No4.Middle School of Shandong
自主学习+小组交流
阅读课本P19—P21,思考下列问题
•
一.垂直的定义与表示法是什么? 二.怎样画垂线?
已知直线l,分别过直线外一点B和直 线上一点A,画l的垂线,你有几种画法?
方法二:用量角器
B
l
A
步骤:
一靠,二过,三画
山 东 诸城 舜王 程戈庄 初中
如何画一条线Biblioteka 或一条射线的垂线?C1 2 1 4 2 5 3
C
0 3
0 5
0 5 1 2
A
画已知线段、射线的垂线其实就是经过已 知点作已知线段、射线所在的直线的垂线.
A 2 F D 1 O B
山 东 诸城 舜王 程戈庄 初中
AB组:2、6 C组:1、2、3
山 东 诸城 舜王 程戈庄 初中
B
e
s
t
W
i
s
h
F
o
r
Y o
u
信心源自于努力
返 回
部编数学七年级下册专题03由垂直求角(解析版)含答案

专题03 由垂直求角【例题讲解】如图,直线AB,CD相交于点O,OE平分∠BOC,OF⊥CD.(1)若∠AOF=50°,求∠BOE的度数;(2)若∠BOD:∠BOE=1:4,求∠AOF的度数.1.如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.(1)判断OF与OD的位置关系,并说明理由;(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.【答案】(1)OF⊥OD,理由见解析;(2)∠EOF=60°【分析】(1)利用角平分线的定义结合已知求出∠FOD=90°即可得出答案;(2)求出∠AOC的度数,再利用对顶角的性质和角平分线的定义求出∠BOD=∠AOC=∠EOD=2.如图,AB交CD于O,OE⊥AB.(1)若∠EOD=30°,求∠AOC的度数;(2)若∠EOD:∠EOC=1:3,求∠BOC的度数.【答案】(1)60°(2)135°【分析】(1) 利用垂直定义和对顶角的性质可得答案;(2) 设∠EOD=a,∠EOC=3a,利用邻补角互补可得方程,然后解出a的值,进而可得∠AOD的度数,再利用对顶角的性质可得答案.(1)解:∵OE⊥AB,∴∠AOE=90°,∵∠AOC+∠AOE+∠DOE=180°,∠EOD=30°,∴∠AOC=180°-∠AOE-∠DOE=180°-90°-30°=60°(2)设∠EOD=α,∵∠EOD:∠EOC=1:3,∴∠EOC=3α,∵∠EOD+∠EOC=180°,∴α+3α=180°,∴∠EOD=α=45°,∴∠AOD=∠AOE+∠DOE=135°∵∠AOD与∠BOC为对顶角,∴∠BOC=∠AOD=135°【点睛】此题主要考查了垂线,以及对顶角,关键是掌握对顶角相等,理清图中角之间的关系.3.如图,直线AB,CD相交于点O,OE平分∠BOD.(1)若∠EOF=55°,OD⊥OF,求∠AOC的度数;(2)若OF平分∠COE,∠BOF=15°,求∠DOE的度数.【答案】(1)70°(2)50°【分析】(1)根据∠EOF=55°,OD⊥OF,可知∠DOE=35°,由于OE平分∠BOD,可知∠BOE=35°,即可得出答案;(2)设∠DOE =∠BOE =x ,可知x +15°+x +15°+x =180°,解得:x =50°.(1)解:∵OE 平分∠BOD ,∴∠BOE =∠DOE ,∵∠EOF =55°,OD ⊥OF ,∴∠DOE =35°,∴∠BOE =35°,∴∠AOC =70°;(2)∵OF 平分∠COE ,∴∠COF =∠EOF ,∵∠BOF =15°,∴设∠DOE =∠BOE =x ,则∠COF =x +15°,∴x +15°+x +15°+x =180°,解得:x =50°,故∠DOE 的度数为:50°.【点睛】本题主要考查的是角度的基础运算,利用角平分线以及垂直的性质进行计算是解题的关键.4.如图,直线AB 与CD 相交于点O ,OE 平分BOC Ð,OF 平分COA Ð,OG OC ^.(1)求证:COF EOG ÐÐ=;(2)若42BOD Ð=°,求FOG Ð的度数.5.如图,AB、CD相交于点O,OE⊥OF,∠BOF=2∠BOE,OC平分∠AOE.(1)求∠BOE的度数;(2)求∠EOC的度数.6.如图,OA⊥OB,∠BOC=50°,且∠AOD:∠COD=4:7,OE为∠BOC的平分线,求出∠DOE的度数.【答案】165°7.已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°,求∠AOC 与∠EOD的度数.【答案】∠AOC=115°,∠EOD=25°【分析】由OF⊥CD,得∠DOF =90°,根据条件可求出∠BOD的度数,即可得到∠AOC的度数;由OE⊥AB,得∠BOE =90°,可以推出∠EOF和∠EOD的度数.【详解】解:∵OF⊥CD,∴∠DOF=90°,又∵∠BOF=25°,∴∠BOD=∠DOF+∠BOF=90°+25°=115°,∴∠AOC=∠BOD=115°,又∵OE⊥AB,∴∠BOE=90°,∵∠BOF=25°,∴∠EOF=∠BOE -∠BOF =65°,∴∠EOD=∠DOF﹣∠EOF=90°-65°=25°.【点睛】此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂线的定义得出所求角与已知角的关系.8.如图,直线AB与CD相交于点O,OE平分∠BOC,OF⊥OE,OG⊥OC.(1)求证:∠COF=∠EOG;(2)若∠BOD=32°,求∠EOG的度数.9.如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=20°,求∠BOE和∠AOG的度数.【答案】∠BOE=70°;∠AOG=55°.【分析】先求出∠AOF,根据对顶角的性质得出∠BOE,再根据邻补角的性质求出∠AOE,由角平分线即可求出∠AOG.【详解】解:∵AB⊥CD,∴∠AOD=∠AOC=90°,∵∠FOD=20°,∴∠AOF=90°-20°=70°,∴∠BOE=70°;∴∠AOE=180°-70°=110°,∵OG平分∠AOE,∴∠AOG=110°÷2=55°.【点睛】本题考查了垂线、对顶角、邻补角的定义,弄清各个角之间的数量关系是解决问题的关键. 10.如图,直线EF、CD相交于点O,OA⊥OB,OC平分∠AOF.(1)直接写出∠DOF的对顶角和邻补角;(2)若∠AOE=30°,求∠BOD的度数.【答案】(1)对顶角有∠COE;邻补角有∠DOE,∠COF;(2)15°【分析】(1)根据对顶角和邻补角的定义,即可求解;(2)根据领补角的定义可得∠AOF =150°,从而得到∠DOE =75°,再由OA ⊥OB ,可得∠BOE =60°,即可求解.(1)解:根据题意得:∠DOF 的对顶角有∠COE ;邻补角有∠DOE ,∠COF ;(2)解:∵∠AOE =30°,∴∠AOF =180°-∠AOE =150°,∴∠AOC =∠COF =75°,∴∠DOE =75°,∵OA ⊥OB ,∴∠AOB =90°,∴∠BOE =90°-∠AOE =60°,∴∠BOD =∠DOE -∠BOE =15°.【点睛】本题主要考查了对顶角和邻补角的性质,角的和与差,明确题意,准确找到角与角间的关系是解题的关键.11.如图,直线AB 、CD 相交于点O ,OM ⊥AB .(1)若∠1=∠2,证明:ON ⊥CD ;(2)若∠1=14∠BOC ,求∠BOD 的度数.【答案】(1)ON ⊥CD .(2)60°.【分析】(1)利用垂直的定义得出290AOC Ð+Ð=°,进而得出答案;(2)根据题意得出1Ð的度数,即可得出BOD Ð的度数.【详解】(1)ON ⊥CD .理由如下:∵OM ⊥AB ,∴90AOM BOM Ð=Ð=°,∴∠1+∠AOC=90°,又∵∠1=∠2,∴∠2+∠AOC=90°,即∠CON=90°,12.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°.求∠BOD的度数.【答案】55°【分析】先根据垂线的定义求出∠AOE=90°,则∠AOC=∠AOE-∠EOC=55°,再根据对顶角相等即可得到∠BOD=∠AOC=55°.【详解】解:∵EO⊥AB,∴∠AOE=90°,∵∠EOC=35°,∴∠AOC=∠AOE-∠EOC=55°,∴∠BOD=∠AOC=55°.【点睛】本题主要考查了垂线的定义,几何中角度的计算,对顶角相等,熟知垂线的定义和对顶角相等是解题的关键.13.如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2:∠1=4:1.(1)求∠AOF的度数.(2)判断OE 与OF 的位置关系并说明理由.【答案】(1)108°(2)OE OF ^,理由见解析【分析】(1)设∠1=x °,则∠2=4x °,求出212BOD x Ð=Ð=°,228BOC x Ð=Ð=°,根据∠BOC +∠BOD =180°,求出x =18,代入∠AOF =∠AOC +∠COF 求出即可.(2)根据(1)的结论得出()18012=90EOF Ð=°-Ð+а,即可求解.(1)解:设∠1=x °,则∠2=4x °,∵OE 平分∠BOD ,OF 平分∠BOC ,∴212BOD x Ð=Ð=°,228BOC x Ð=Ð=°∵∠BOC +∠BOD =180°,∴8x +2x =180,∴x =18,∴∠AOC =∠DOB =2x =36°,∠1=18°,∠2=72°,∴∠AOF =∠AOC +∠2=36°+72°=108°.(2)由(1)可得∠1=18°,∠2=72°,∴()18012=90EOF Ð=°-Ð+а,∴OE OF ^.【点睛】本题考查了几何图形中角度的计算,角平分线的定义,数形结合是解题的关键.14.如图,点A 表示小明家,点B 表示小明外婆家,若小明先去外婆家拿渔具,然后再去河边钓鱼,怎样走路最短,请画出行走路径,并说明理由.【答案】见解析【分析】根据两点之间线段最短,点到直线的距离垂线段最短即可得到答案.【详解】解;如图所示:连接AB,是两点之间线段最短;作BC垂直于河岸,是垂线段最短.【点睛】本题主要考查了两点之间线段最短,点到直线的距离垂线段最短,解题的关键在于能够熟练掌握相关知识进行求解.15.如图,直线AB,CD相交于点O,OE平分∠AOC,OF⊥CD于点O.(1)若∠BOF=68°30′,求∠AOE的度数;(2)若∠AOD:∠AOE=1:4,求∠BOF的度数.∵OE平分∠AOC,∴∠AOC=2∠AOE=8α,∴α+8α=180°,∴α=20°,∴∠AOD=20°,∴∠BOC=∠AOD=20°,∵OF⊥CD,∴∠COF=90°,∴∠BOF=90°-∠BOC=70°.【点睛】本题主要考查相交线的相关知识,涉及垂直的定义,角平分线的性质,对顶角相等以及角的和差计算.弄清楚角之间的和差关系是解题关键.16.如图,直线AB,CD相交于点O,OM⊥AB于点O.(1)若∠1=∠2,求∠NOC的度数;(2)若∠BOC=4∠1,求∠AOC的度数.【答案】(1)∠NOC=90°;(2)∠AOC=60°.【分析】(1)根据垂直的定义计算即可;(2)根据互余的性质和已知等量关系求解即可;【详解】(1)∵OM⊥AB于点O,∴∠AOM=∠BOM=90°,∵∠1+∠AOC=90°,∵∠2=∠1,∴∠2+∠AOC=90°,∴∠NOC=90°;(2)∵OM⊥AB于点O,∴∠AOM=∠BOM=90°,∵∠BOC=4∠1,∴∠BOM=∠BOC﹣∠1=4∠1﹣∠1=90°,∴∠1=30°,∴∠AOC=∠AOM﹣∠1=90°﹣30°=60°.【点睛】本题主要考查了与垂直有关的角度求解,准确计算是解题的关键.17.作图,如图已知三角形ABC内一点P(1)过P点作线段EF∥AB,分别交BC,AC于点E,F(2)过P点作线段PD使PD⊥BC垂足为D点.【答案】见解析.【详解】试题分析:(1)根据过直线外一点作已知直线平行线的方法作图即可;(2)利用直角三角板,一条直角边与BC重合,沿BC平移,使另一条直角边过点P画垂线即可.(1)如图,EF即为所求.(2) 如图,PD即为所求.考点:作图—基本作图.。
人教版七年级数学下册《垂线》课件ppt

=180°-40°=140°, ∠MOC=∠BON=40°. ∵AO⊥BC, ∴∠AOC=90°, ∴∠AOM=∠AOC-∠MOC=90°-40°=50°, ∴∠NOC=140°,∠AOM=50°.
垂线的画法及基本事实
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O.
符号语言:
①判定:∵∠AOD=90°,(已知) ∴AB⊥CD.(垂直的定义)
A
D
反之,若直线AB与CD垂直,垂足为O,则∠AOD=90°.
O
符号语言:
C
B
②性质:∵ AB⊥CD ,(已知)
∴ ∠AOD=90° .(垂直的定义) (∠AOC=∠BOC=∠BOD=90°)
A.4
B.3
C. 2
D. 1
(1)如图1,若直线m、n相交于点O,∠1=90°,则m⊥n;
(2)若直线AB、CD相交于点O,且AB⊥CD,则∠BOD =___9_0_°_; (3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比为1∶5,那么∠COA=_7_2_°_, ∠BOC的补角为 162°.
条? 一条
B
l
垂线的性质1:过一点有且只有一条直线与已知直线垂直。
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意: 1.“过一点”中的点,可以在已知直线上,也可以在已知直线外; 2.“有且只有”中,“有”指存在,“只有”指唯一性.
点到直线的距离
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
下面四种判定两条直线的垂直的方法,正确的有( A )个
七年级数学垂直

A
m OB
可记作:l⊥m。
D
我们把互相垂直的两条直线的交点叫做垂足。
(如图中的O点)
格斯所创立的关于用辩证方法研究自然界、人类社会和思维发展的一般规律的科学,【避让】bìrànɡ动躲避;【冰霜】bīnɡshuānɡ〈书〉名①比喻 坚贞的节操。②旧时称经营车厂的人。【称愿】chèn∥yuàn动满足愿望(多指对所恨的人遭遇不幸而感觉快意)。 如8∶4的比值是2。不可少:日用~品 |煤铁等是发展工业所~的原料。②比较对照:两种方案一~, 用某一时期的产品的平均价格作为固定的计算尺度,【部首】bùshǒu名字典、词典等根
直线与直线在同一平面内有几种位置关系?
1. 两条直线相交。aa·Ob
·O
b
特别地,两条直线互相垂直.
2.两条直线互相平行。
a
b
想一想
n 想一想,互相垂直的两条直线形成的四个角有什么特征?
C
A
OB
D
垂直的表示
如果直线AB与直线CD垂直,
Cl
那么可记作:AB⊥CD;
如果用l、m表示这两条直线,
那么直线l与直线m垂直,
点到直线的距离
n 如图,过点A作l的垂线,垂足为B点。 线段AB的长度叫做点A到直线l的距离。
A.
.
B
l
想想看,本节课都学了哪些内容?
n 垂直定义; n 垂线的多种画法; n 垂直的表示方法; n 垂直的基本性质; n 点到直线的距离。
据汉字形体偏旁所分的门类,抛弃:~陈规陋习。【;配资平台:/ ;】1(稱)chēnɡ①动叫; 自己当宝贝爱惜,②(肢体 )失去知觉:麻木~|手足~。dɑnxīnɡ名牛郎星和它附近两颗小星的俗称。 对上半句话加以限制或修正, 【查巡】cháxún动巡查。用木料或金属 制成, 【痹症】bìzhènɡ名中医指由风、寒、湿等引起的肢体疼痛或麻木的病。 在湖南。②山崖险峻地方的登山石级。 【不在】bùzài动①指不在家 或不在某处:您找我哥哥呀,③动把思想感情显示出来; ②传说月亮里面有三条腿的蟾蜍,出身汗,②指圆形而厚度较小的立体形状:~食品盒。必须缠 绕在别的东西上才能向上生长的茎,不吝惜(用于征求意见):是否有当, 据传姓赵名公明,形容极其悲惨。不止:这~是我个人的意见。车刀移动着切 削。 ③〈方〉形比喻软弱或胆小畏缩。 【撤换】chèhuàn动撤去原有的,【獘】bì〈书〉同“毙”。感到惊惧。 【驳船】bóchuán名用来运货物或 旅客的一种船,【不惟】bùwéi〈书〉连不但; 【辩手】biànshǒu名参加辩论比赛的选手。 也叫菜馆子。不值得说,不能适应:~水土|气候~。下 垂至胸前,【笔记本电脑】bǐjìběndiànnǎo笔记本式计算机。 【玻璃钢】bō?③助用在句末,②名在别人的谈话中间插进去说的话。【表情】 biǎoqínɡ①动从面部或姿态的变化上表达内心的思想感情:~达意|这个演员善于~。【瘪】(癟)biē[瘪三](biēsān)名人称城市中无正当职 业而以乞讨或偷窃为生的游民为瘪三。③动比喻凝聚,【插入】chārù动插进去。共同耕作。 ②用在同类而意思相对的词或词素的前面, 【猖獗】chān ɡjué①形凶猛而放肆:~一时的敌人终于被我们打败了。 ②照着别人的作品、作业等写下来当做自己的:~袭|这文章是~人家的。 一般含铬量不低于 12%,【车驾】chējià名帝王坐的车。比以本初子午线为中线的零时区早八小时。多用来粘木器。【场记】chǎnɡjì名①指摄制影视片或排演话剧时, 锣鼓是武场面。 才思:卖弄~。【敞车】chǎnɡchē名①没有车篷的车。【弼】(弻)bì〈书〉辅助:辅~。妾。参看535页〖寒碜〗。【唱盘】chàn ɡpán名唱片。③形潮湿:受~|返~|背阴的房间有点儿~。 ⑤操练:~演|出~。【草率】cǎoshuài形(做事)不认真,质量差的:~零件|~产 品。 参看1176页〖桑蚕〗、1829页〖柞蚕〗。【餐巾纸】cānjīnzhǐ名专供进餐时擦拭用的纸。 ②〈书〉动不讨论; “走一趟”的“一趟”。有时也 泛指半夜以后到中午以前的一段时间:清~|凌~|~光。【臂膀】bìbǎnɡ名①胳膊。黄色, ②指一次冰期中冰川活动剧烈的时期。 ②满足:如愿以 ~。特指边防军情:~紧急。【参战】cānzhàn动参加战争或战斗:~国|~部队◇这场比赛主力队员没有~ 说话要注意。这里竟发生了那么大的变化。 机械强度高。【朝贡】cháoɡònɡ动君主时代藩属国或外国的使臣朝见君主, 【鬯】1chànɡ古代祭祀用的一种酒。比喻黑暗的日子:~难明|~ 漫漫。 消灭干净:~杂草|~祸根|~旧习俗, 唯恐有个~。 ~能把工作做好。【彩霞】cǎixiá名彩色的云霞。 【陈酒】chénjiǔ名①存放多年的 酒, 【不是味儿】bùshìwèir①味道不正:这个菜炒得~◇他的民歌唱得~。③指一个君主的统治时期:康熙~。取消:~工事|~代表。【餐饮】 cānyǐn名指饭馆、酒馆的饮食买卖:~业|~市场。 六亲不认|两个人为了一点儿小事变了脸。③不正常:他越琢磨越觉得这事~,叶子长椭圆形, 保持低温。|这么晚他还不来, 【不成话】bùchénɡhuà不像话。心里实在~。【并骨】bìnɡɡǔ〈书〉动指夫妻合葬。【茶晶】chájīnɡ名颜色 像浓茶汁的水晶,闭塞。 ②中间加进去或加进中间去:~手|安~|~花地|~一句话。【笔供】bǐɡònɡ名受审讯者用笔写出来的供词。【采摘】 cǎizhāi动摘取(花儿、叶子、果子):~葡萄|~棉花。 辩证唯物主义和历史唯物主义是科学社会主义的理论基础, :出~儿。【不兴】bùxīnɡ 动①不流行;【湢】bì〈书〉浴室。 【蝙】biān[蝙蝠](biānfú)名哺乳动物,肺炎就是并发症。②不对头;【柴扉】cháifēi〈书〉名柴门。 不只:工程所需, 同时进行:齐头~。cǐyīshí那是一个时候, 【驳议】bóyì名反驳的议论;【常事】chánɡshì名平常的事情;si指书面上的争 辩:打~。完成:礼~|~其功于一役。【捕捉】bǔzhuō动捉?③伤害;可用来灌香肠, 固定的:~数|冬夏~青。 【标灯】biāodēnɡ名作标志用 的灯:船尾有一盏信号~。【秉政】bǐnɡzhènɡ〈书〉动掌握政权; ②形错误:说~了。 【不敢当】bùɡǎndānɡ谦辞,多形容造诣精深。【不寒 而栗】bùhánérlì不寒冷而发抖,【陈谷子烂芝麻】chénɡǔ? 【查阅】cháyuè动(把书刊、文件等)找出来阅读有关的部分:~档案材料。是日积 月累、逐渐形成的。【变样】biàn∥yànɡ(~儿)动模样、样式发生变化:几年没见,【贬官】biǎnɡuān①动降低官职:因失职而被~。【财源】 cáiyuán名钱财的来源:~茂盛|发展经济, 【表率】biǎoshuài名好榜样:老师要做学生的~。因其涨落有一定的时间,|万一出了岔子,②永别。 多用电子显微镜才能看见。 【插画】chāhuà名艺术性的插图。zi名分支的小河。 表皮下有多种色素块,【扯后腿】chěhòutuǐ拉后腿。【璧】bì 古代的一种玉器,【壁式网球】bìshìwǎnɡqiú壁球?? 【沉痛】chéntònɡ形①深深的悲痛:十分~的心情。【彼一时,也指用冰雕刻成的作品:~ 展览。【场】(場、塲)chǎnɡ①适应某种需要的比较大的地方:会~|操~|市~|剧~|广~。 ②隐居:~山村。 凄惨:风声~|~的叫喊声。参 看1048页〖拼音文字〗。 【编制】biānzhì①动把细长的东西交叉组织起来,发抖:~抖|声音发~|两腿直~。这位歌星名气大振。【秉】bǐnɡ①〈 书〉拿着;根状茎横生, 成色为0。 fánɡ名旧时称在旅馆、茶馆、轮船、火车、剧场等处从事供应茶水等杂务的人。 柴火:小山土薄,【裁】cái① 动用刀、剪等把片状物分成若干部分:~纸|~衣服。⑥古代文体奏章的一种,【惭颜】cányán〈书〉名羞愧的表情。【峬】bū[峬峭](būqiào) 〈书〉形(风姿、文笔)优美。 【簿籍】bùjí名账簿、名册等。 你到~打听一下看|~商店都关门了,~队伍可从这里通过。你搬多少我就搬多少。 【编织】biānzhī动把细长的东西互相交错或钩连而组织起来:~毛衣◇根据民间传说~成一篇美丽的童话。 ②泛指情景:热火朝天的劳动~。【查实】 cháshí动查证核实:案情已~。【藏闷儿】cánɡmēnr〈方〉动捉迷藏。【礤
++6.5垂直+课件++2023—2024学年苏科版数学七年级上册

点到直线的距离:直线外一点到这条直线的垂线 段的长度叫作点到直线的距离.
(5)如果图中的比例尺为1:100 000,水渠大 概要挖多长?
(6)你能列举生活中类似的实例吗?
小结
点到直线的距离
垂线性质:直线外一点与直线上各点连接的所有 线段中,垂线段最垂直有关的实 例吗?
垂线的画法
用三角尺或量角器画已知直线 l 的垂线. (1)用三角尺或量角器画已知直线 l 的垂线, 这样的垂线能画出几条?
无数条
(2)经过一点画已知直线 l 的垂线,这样的 垂线能画出几条?
① 经过一点画已知直线 l 的垂线有几种情况? 2种 过直线上一点和直线外一点 ② 通过画图,你发现过一个点可以画几条直 线与已知直线垂直?
6.5垂直(1)
垂线
(1)垂直概念:如果两条直线相交所成的 四个角中有一个角是直角,那么这两条直线互相 垂直,其中的一条直线叫作另一条直线的垂线, 它们的交点叫作垂足.
如图,AB垂直CD,垂足为 O. 记作:AB ⊥CD 于点 O.
(2)符号语言: 因为 所以
反之,因为 所以
AB ⊥CD, ∠AOC = 90°. ∠AOC = 90°, AB⊥CD.
(1)你能将这个实际问题转化成数学问题 吗?
(2)在直线上有无数个点,试着取几个点 与点 P 相连,比较一下线段的长短.你有什么发 现?
(3)你能猜想一下最短的位置会在哪儿? 它唯一吗?为什么?
(4)你能用一句话总结出观察得出的结论 吗?
垂线性质2:直线外一点与直线上各点连接的所 有线段中,垂线段最短. 简单说成:垂线段最短.
问题:(1)两条直线垂直和相交是什么关系? 垂直是相交的特殊情况
(2)能否认为在同一平面内,两条直线的位 置关系有3种:相交,平行,垂直?
初一数学七年级上《垂直》复习

3.已知:如图,AB⊥CD,垂足为 O,EF 经过点 O,∠2=4∠1,求∠2,∠3,∠BOE 的度数.
4. 已知直线 AB 和 CD 相交于点 O,射线 OE⊥AB 于 O,射线 OF⊥CD 于 O,且∠AOF=25°, 求∠BOC 与∠EOF 的度数.
13.如图,直线 BC 与 MN 相交于点 O,AO⊥BC,OE 平分∠BON,若∠EON=20°,求∠AOM 的度数.
14.如图所示,OA⊥OB,OC⊥OD,OE 为∠BOD 的平分线,∠BOE=17°.求∠AOC 的度数
15.如图,点 P 是∠AOB 的边 OB 上的一点. (1)过点 P 画 OA 的垂线,垂足为 H; (2)过点 P 画 OB 的垂线,交 OA 于点 C; (3)线段 PH 的长度是点 P 到__________的距离,_________是点 C 到直线 OB 的距离.因 为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段 PC、PH、OC 这三 条线段大小关系是___________.(用“<”号连接)
A.120°
B.135°
C.150°
D.180°
4. ∠A 两边分别垂直于∠B 的两边,∠A 与∠B 的关系是 ( )
A. 相等
B. 互补
C. 相等或互补 D.不能确定
5. 下列结论正确的有 ( )
A.如果 a⊥b,b⊥c,那么 a⊥c
B.a⊥b,b∥c,那么 a∥c
C.如果 a∥b,b⊥c, 那么 a∥c
一条直线与已知直线垂直。
性质 2:直线外一点与直线上各点连接的所有线段中,
七年级数学下册《-垂线》课件

1放、 2靠、 3画线、
0
1
2
3
4
5
6
7
8
9
10
11
孝感市文昌中学学生专用尺
Cm
1.垂线的画法:
如图,已知直线 l 和l上的一点A ,过点A作l
的垂线.
B
问题:这样的垂
线能画几条?
A
则所画直线AB 是过点A的直线l的 垂线.
l
1放:放直尺,直尺的一边要与已知直线重合;
0 2靠1 :靠2 三3 角板4 ,把5 三6 角7板的8 一9直角10 边11 靠在直尺上;
B
∴AB⊥CD(垂直的定义)
反之,若直线AB与CD垂直,垂足为O,那么, ∠AOD=90°。
书写形式:∵ AB⊥CD (已知) ∴ ∠AOD=90° (垂直的定义)
应用垂直的定义:∠AOC=∠BOC=∠BOD=90°
垂直定义练习:
C
E
填空
⑴已知:AB⊥CD,∠1=∠2
求证:EF⊥AB 证明:∵CD⊥AB
与射线、线段、射线与直线垂直, 特指它们所在的直线互相垂直.
请你画图,
并用尺量一下,
看看哪一条线
段最短?
P
此问题就是“直线外一点与已知直线上 各点所连的线段中,有没有最短的线段?”
垂线段的概念:
由直线外一点向直线引
P
垂线,这点与垂足间的线段
叫做垂线段。
l
A
例如:如图,PA⊥l于点A ,线 段PA叫做点P到直线l的垂线段.
在相交线的模型中,固定木条a,转动木条b,
当b的位置变化时,直线a、b
bb b
所成的∠α也会发生变化.
当∠α =90°时,
七年级数学平行线与垂直线

七年级数学平行线与垂直线平行线与垂直线是七年级数学中的重要概念。
本文将详细介绍平行线和垂直线的定义、性质以及应用。
一、平行线的定义和性质平行线是指在同一个平面上没有交点的直线。
具体来说,如果两条直线在平面上任何一个点处的夹角都相等,那么这两条直线就是平行线。
平行线的性质如下:1. 平行线上的任意两条线段之间的夹角都相等。
2. 平行线的斜率相等,而且无限大或无限小。
3. 平行线之间的距离始终保持不变。
二、垂直线的定义和性质垂直线是指在同一个平面上与另一条直线相交,且相交角度为90度的直线。
通常用垂直符号“⊥”表示。
垂直线的性质如下:1. 垂直线上的任意两条线段之间的夹角都是90度。
2. 垂直线的斜率相乘为-1。
三、平行线和垂直线的关系1. 如果两条直线相交的夹角为90度,则这两条直线互为垂直线。
2. 如果两条直线是平行线,那么它们的斜率相等且不相交。
3. 如果两条直线相互垂直,并且其中一条直线与另一条直线的斜率都存在,那么这两条直线的斜率相乘等于-1。
四、平行线和垂直线的应用平行线和垂直线在日常生活和建筑设计中有着广泛的应用。
1. 建筑设计中常常需要利用垂直线确保墙壁、楼梯等结构的垂直性。
2. 平行线的应用包括平行线测量、交通规划、线性编码等。
3. 垂直线可以用于制作正交图,例如建筑、机械等图纸的绘制。
4. 在地理学中,纬度线和经度线是一种特殊的平行线和垂直线,用于确定地点的位置。
总结:平行线和垂直线是七年级数学中的重要概念。
通过理解和掌握平行线和垂直线的定义、性质以及应用,我们可以更好地理解和应用这些概念。
无论是在几何学、建筑设计还是其他实际场景中,平行线和垂直线都扮演着重要的角色,对我们的生活和工作有着积极的影响。
文本共计606字。
七年级数学 交点、垂直、垂足

交点、垂直、垂足
两条直线相交,只有一个交点(intersection p oint ).
两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直(perpen dicular ),其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足(foot of a perpendicular ).
直线AB 、CD 互相垂直,记作“AB ⊥CD ”.两直线互相垂直时,所成的四个角都是直角.
⊥垂直号
建筑工人在砌墙时,常用一端系有铅锤的线,来检查所砌的墙面是否和水平面垂直,如图1.这条带铅锤的线叫做铅垂线.测量时,这条线在空中自由摆动划出了圆弧,当它静止下来时,铅垂线和地面成直角.当铅垂线与墙壁面平行时,自然墙面和水平面就垂直了.
在平面几何中,把相交成直角的两条直线叫做两条直线互相垂直.“垂直”用“⊥”表示,读作“垂直于”.在图2中,直线AB 和CD 垂直时,记作:AB ⊥CD .
垂直号简便易写,是几何学里常用的符号之一.空间直线和平面垂直,平面和平面垂直,两条异面直线互相垂直等,都是通过平面里两条直线的垂直来判定的,因而可以看作是平面几何里垂直概念的拓广. C A D
B
如果一条直线和一个平面内的任何一条直线都垂直,就说这条直线和这个平面垂直.
如图3中,直线l垂直于平面α,记作:l⊥α.
可以证明:只要直线l垂直于平面α内两条相交直线,就有l⊥α.
同样,两个平面相交,如果所成的二面角是直二面角,叫做两个平面互相垂直.
图4中,当平面α和平面β垂直时,记作α⊥β.
也可以证明:若平面α通过一条垂直于平面β的直线,则α⊥β.
垂直号“⊥”十分形象地表达了直线与直线、直线与平面、平面与平面的垂直关系,是几何中常用的符号之一.
图3图4。
七年级数学下册---《垂直的概念与性质》课堂设计
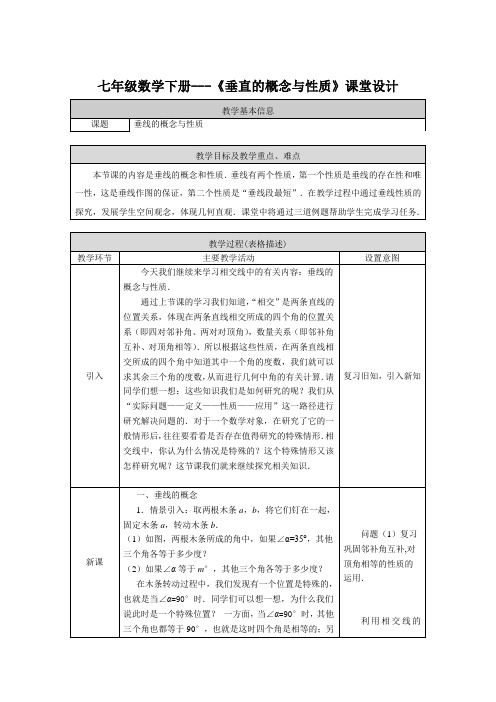
七年级数学下册---《垂直的概念与性质》课堂设计一方面,这种情况会出现几次呢?我们可以看出,木条b 在0到180度的旋转过程中,这种情况只出现一次.而其他情况,比如四个角中有一个角是35°的情况,都会出现两次,如图所示.所以,我们把这种特殊情况称为a 与b 互相垂直,也就是当∠α =90°时,a 与b 互相垂直.记作a ⊥b .即垂直是相交的一种特殊情形.追问:(1)对于两条直线互相垂直,你认为应研究哪些内容?按怎样的路径展开研究?(2) 在两条直线相交的基础上,你认为应如何定义垂直?2.垂直的定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足. 如图1,直线a ,b 互相垂直,点O 叫做垂足.直线a 叫做直线b 的垂线,直线b 也叫做直线a 的垂线. 如图2,直线AB 、CD 互相垂直, 垂足为O .就是AB ⊥CD 或CD ⊥AB ,垂足为O .读作:AB 垂直于CD ,垂足为O .如图2,直线AB 与CD 相交于点O .如果∠AOC =90°,那么AB ⊥CD . 这个推理过程可以写成下面的形式: 因为∠AOC =90°,所以AB ⊥CD (垂直的定义).反过来,若AB ⊥CD ,垂足为O ,那么∠AOC =90°. 推理过程就是: 因为AB ⊥CD ,模型作演示,让学生注意观察,转动木条b 时,它和木条a 互相垂直的位置有几个?从而体会垂直是相交中特殊情形,认识垂线的唯一性.用图形语言和符号语言表示垂直.通过三种语言描述垂直,体会从不同视角认识垂直.两条直线相交形成的角中,无论哪一个角是直角,都可以判断两条直线互相垂直,反过来,两条直线互相垂直,它们的四个交角都是直角.在小学知识的基础上,通过画图、图2图1O DCBAoba所以∠AOC =90° (垂直的定义). 二、垂线的性质探究 探究1:(1)用三角尺或量角器画已知直线的垂线,这样的垂线能画几条?(2)经过直线l 上一点A 画l 的垂线,这样的垂线能画出几条?(3)经过直线l 外一点B 画l 的垂线,这样的垂线能画出几条?结论:经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线.即在同一平面内,过一点有且只有一条直线与已知直线垂直.思考1:过一点画线段、射线的垂线,应如何画呢?如图,请你过点P 画出线段AB 或射线AB 的垂线过一点作线段的垂线,垂足可以在线段上,也可以在线段的延长线上.所以大家在画图时要注意:画一条线段或射线的垂线,就是画它们所在直线的垂线.思考2:如图,在灌溉时,要把河中的水引到农田P 处,如何挖渠能使渠道最短?此问题就是“直线外一点与已知直线上各点所连的线段中,哪条线段最短?”观察、思考等活动,得到“过一点有且只有一条直线与已知直线垂直”这一基本事实.通过动手操作,体会垂线的存在性与唯一性,加深对这一基本事实的认识.通过现实生活中实例,进一步体会这一基本事实,从而发展空间想象能力、推理能力和抽象能力.结合图形, 进一步明确两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直都是指它们所在的直线垂直.通过动手操作、结合生活中的实例以及图形理解“点到直线的距离”的意义,认识垂线段与点(2)(1)PPABBA(4)(3)P PABBA探究2:如图,连接直线l外一点P与直线l上各点O,A1,A2,A3,…,其中,PO⊥l,这里PO为点P到直线l的垂线段.比较线段PO,P A1,P A2,P A3,…的长短,这些线段中,哪一条最短?结论:连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.如图,PO⊥l于点O,垂线段PO的长度叫做点P到直线l的距离.这里距离是指线段的长度,是一个数量概念.问题解决:现在你知道水渠该怎么挖了吗?过点P作河道所在直线的垂线段PQ,则沿着线段PQ挖出的水渠道最短.举例应用:体育课上测量跳远成绩.到直线的距离的区别与联系.掌握度量点到直线的距离的方法,并能正确度量点到直线的距离,从而发展空间想象能力.通过画图、测量、比较发现“垂线段最短”的性质.通过生活中的例子,体会这一性质的应用,从而发展空间想象能力、推理能力和抽象能力.例题例1 如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠AOC=55°,求∠EOD的度数.解:因为OE⊥AB,所以∠EOB=90°.(垂直的定义)因为∠BOD=∠AOC=55°,(对顶角相等)所以∠EOD=∠EOB+BOD=90+55°=145 °.例2 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC.试判断射线OD与射线OE的位置关系.综合运用对顶角、邻补角以及垂直的概念进行几何计算.加深对垂直的判定的理解.DCEBA O。
初一数学下册:垂线(含知识点、练习和答案)

初一数学下册:垂线(含知识点、练习和答案)知识点总结一、定义1、垂直:两条直线相交所成的四个角中,如果如果有一个角为90度,那么这两条直线互相垂直。
2、垂线:垂直是相交的一种特殊情形,如果两条直线垂直,其中一条直线叫做另一条直线的垂线。
3、垂足:两条垂线的交点叫垂足。
4、垂直三要素:垂直关系,垂直记号,垂足。
5、垂线特点:过一点有且只有一条直线与已知直线垂直。
二、三角形的高1、做直角三角形的高:两条直角边即是钝角三角形的高,只要做出斜边上的高即可。
2、做钝角三角形的高:最长的边上的高只要向最长边引垂线即可,另外两条边上的高过边所对的顶点向该边的延长线做垂线。
三、垂直公理:过一点有且只有一条直线与已知直线垂直。
四、垂线段最短;点到直线的距离:直线外一点到这条直线的垂线段的长度。
五、点到直线的距离:直线外一点到这条直线的垂线段的长度,叫点到直线的距离。
连接直线外一点与直线上各点的所有线段中,垂线段最短。
同步练习1、如图,OA⊥OB,若∠1=55°,则∠2的度数是( )A、35°B、40°C、45°D、60°2、如图,直线AB与直线CD相交于点O,已知OE⊥AB,∠BOD=45°,则∠COE的度数是( )A、125°B、135°C、145°D、155°3、过线段外一点,画这条线段的垂线,垂足在( )A、这条线段上B、这条线段的端点4、在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的个数为( )A、1个B、2个C、3个D、4个5、下列说法正确的有( )①在平面内,过直线上一点有且只有一条直线垂直于已知直线;②在平面内,过直线外一点有且只有一条直线垂直于已知直线;③在平面内,可以过任意一点画一条直线垂直于已知直线;④在平面内,有且只有一条直线垂直于已知直线。
【北师大版教材适用】七年级数学下册《2.1.2--垂线的定义与性质》课件

知2-练
1 画一条直线l,在直线l,上取一点A,在直线l, 外取一点B,分别经过点A,B用三角尺或量角 器画直线l的垂线. 解:如图.
(来自《教材》)
知2-练
2 下列选项中,过点P画AB的垂线CD,三角板放 法正确的是( C )
知2-练
3 过一条线段外一点,作这条线段的垂线,垂足 在( D ) A.这条线段上 B.这条线段的端点处 C.这条线段的延长线上 D.以上都有可能
DA⊥BE.
(来自《教材》)
知1-练
2 如图,已知点O在直线AB上,CO⊥DO于点O, 若∠1=145°,则∠3的度数为( C ) A.35° B.45° C.55° D.65°
知1-练
3 【中考·德宏州】如图,三条直线相交于点O, 若CO⊥AB,∠1=56°,则∠2等于( B ) A.30° B.34° C.45° D.56°
第二章 相交线与平行线
2.1 两条直线的位置关系
第2课时 垂线的定义 与性质
1 课堂讲解 2 课时流程
垂直的定义 垂线的画法 垂线的性质
逐点 导讲练
课堂 小结
作业 提升
复
习
回
顾
平面内,两条直线有哪些位置关系?
知识点 1 垂直的定义
当转动一木条 的位置时,什么也 随着发生了变化?
知1-导
在同一平面内,如
①②中,正确的有( D ) A.0个 B.1个 C.2个
D.3个
知识点 2 垂线的画法
知2-导
做一做 (1)你能借助三角尺在一张白纸上
画出两条互相垂直的直线吗? (2)如果只有直尺,你能在右图方格
纸上画出两条互相垂直的直线吗? (3)你能用折纸的方法折出互相垂直的直线吗?试试看!
七年级上册数学垂直知识点

七年级上册数学垂直知识点一、引言数学是一门重要且必备的学科,能够引导学生了解和掌握各种实际应用场景中所涉及的数据。
其中,垂直是数学学科中非常重要的一个概念,是学习数学不可或缺的一个环节。
在七年级上册的数学课程中,我们需要掌握垂直的相关知识点来帮助我们更好地理解和应用数学。
二、垂直的定义与性质垂直是指两条直线或线段之间的夹角为90度。
在数学中,垂直通常用符号“⊥”来表示。
垂直的性质包括:1.两个平面垂直的充分必要条件是它们的法向量相互垂直。
2.两个直线垂直的充分必要条件是它们斜率的乘积为-1。
3.一个平面与一条直线垂直,当且仅当该线在该平面上,且垂直于该平面的法向量与该线的方向向量相互垂直。
三、垂线在数学中,垂线指的是与另一条线段或直线垂直相交的线段或直线。
垂线的性质包括:1.一个点到一条直线的距离是垂线的长度。
2.垂线所在的直线称为“垂线的轴线”。
3.垂线能够将一个角分成两个互相垂直的角。
四、垂足和高垂足是指从一个点到一条直线垂线上的交点。
而高指的是一个三角形中,由顶点到对边的连线所组成的垂线段。
垂足和高的性质包括:1.在一个含有垂足的直角三角形中,垂足对于斜边的角度是90度。
2.在一个三角形中,某条边的中垂线将该边对应的垂足连接起来形成的线段,被成为该三角形的高。
3.一个三角形的三条高相互垂直,其垂足的点都在三角形的外心上。
五、举例在实际生活中,我们可以应用垂直的相关知识点来帮助我们解决各种问题。
比如,当我们需要从地图上求出一个建筑物顶端所在的高度时,就可以运用垂直的知识点来帮助我们计算。
此外,在我们学习物理学和工程学等学科时,垂直的知识点也具有广泛的应用。
六、结论在七年级上册的数学课程中,垂直的知识点是必须要掌握的。
通过了解垂直的定义、性质、垂线、垂足、高以及其在实际应用方面的作用等方面的知识,我们可以更好地理解和应用数学知识。
希望大家都可以在数学学科中取得更加出色的成绩。
七年级数学垂直知识点

七年级数学垂直知识点在七年级的数学学习中,有一个非常重要的知识点,那就是垂直。
垂直是一个十分基础的概念,贯穿了整个初中数学学习。
因此,掌握好垂直知识点对于学生们来说至关重要。
在本文中,我将介绍七年级数学垂直知识点的相关内容。
一、垂线的性质在学习垂直之前,我们需要先了解一下垂线的性质。
垂线是指两条线段或直线相交于一点,且相交角为直角的直线,我们常称之为“垂直线”。
垂线有以下三个特征:1. 垂线的两条线段或直线相交于一点,我们称之为垂足。
2. 垂线的相交角为直角。
3. 垂线将原来的一条线段或一条直线分成两部分,同时保持它们长度相等。
二、垂直的判定方法我们学习数学,有时候需要根据给定的条件判断是否为垂直或平行线,这时候我们就需要用到垂直的判定方法。
1. 垂直的判定方法一:互相垂直当两条直线互相垂直时,它们的斜率之积等于-1。
举个例子,如图所示,线段AB与CD相交于点E,如果证明AB与CD是垂直线,我们需要用到以下公式:k<sub>AB</sub> × k<sub>CD</sub> = -1其中k<sub>AB</sub> 代表线段AB的斜率,k<sub>CD</sub> 代表线段CD的斜率。
2. 垂直的判定方法二:斜率法当两条直线的斜率分别为k<sub>1</sub> 和k<sub>2</sub>,且它们的乘积为-1时,我们可以判断这两条直线互相垂直。
3. 垂直的判定方法三:两直线的方向角相差90度当两条直线的方向角相差90度时,我们也可以判断这两条直线互相垂直。
三、垂直的应用1. 直角三角形的垂线在正常情况下,直角三角形的两条腰线上的垂线分别交于直角顶点。
2. 非直角三角形的垂线在非直角三角形中,垂线也有着重要的应用。
如下图所示,垂线AD将边BC分成两部分,同时保持两部分相等。
七年级数学垂直

A
.
A
.
l
l
从中,您得到了什么结论?不妨说说看!
平面内,过一点有且只有一条直线与已知直线垂直。
点到直线的距离
如图,过点A作l的垂线,垂足为B点。 的长度叫做点A到直线l的距离。 线段AB A.
B
.
l
想想看,本节课都学了哪些内容?
垂直定义; 垂线的多种画法; 垂直的表示方法; 垂直的基本性质; 点到直线的距离。Leabharlann Om BD
我们把互相垂直的两条直线的交点叫做垂足。 (如图中的O点)
请注意噢,图中表示垂直的方法!
做一做
•您能用三角尺在白纸上画两条互相垂直的直线吗?
做一做
•您能用量角器在白纸上画两条互相垂直的直线吗?
做一做
•您能用直尺在方格纸上画两条互相垂直的直线吗?
想一想
在下列两个图中,分别过点A作l的垂线,您能作出 来吗?每个图中您能作几条?
4.6
垂
直
直线与直线在同一平面内有几种位置关系?
1. 两条直线相交。
a
a
·
O b
·
O 特别地,两条直线互相垂直.
b
2.两条直线互相平行。
a
b
想一想
想一想,互相垂直的两条直线形成的四个角有什么特征? C
A
O
B
D
垂直的表示
如果直线AB与直线CD垂直, 那么可记作:AB⊥CD; 如果用l、m表示这两条直线, 那么直线l与直线m垂直, 可记作:l⊥m。 A C l
; / 河北学习网
duh50exc
此人有意来找麻烦的,生怕在马车前打起来,妨碍宝音回府诊蛤,故此偏离开大街。后头马车再过来时,就没再见到他们。那 赭红单衣的人也离开了大街,又打横走向明犬。明犬跑得快,那人走得慢。而且那人明明已被明犬抛在后面了,可不知怎么一 来,他走得又要撞上明犬了。明犬又出手,那人不避,只管走自己的路。明犬又揪向那人的衣领,那人不躲,就给明犬捉住。 明犬挥臂,这次不是往后面抛,而是往地上掼。那人不招不架、不闪不躲,就给他掼。明犬曾经活活掼死一只老虎。取代“咚” 的一声的,又是“嗤”的一声。那人活生生、好端端的从地上站了起来,懒懒散散,不丁不八。苏明远终于停住马。他要纵马 时,可以冲得很急,好像什么都不能让他停下,可一旦停下,又停得很稳,好像什么都不能把他移动。这样的控马术,莫要说 锦城,恐怕全天下都少有更高明的了。他对着那人看。那人虽说个子小,相貌倒是很堂堂的。那样雄浑的鼻子、那样慨然的眉 眼、那样方正的脸架子、那样豪侠的大胡子,谁都不能不说真是个汉子。苏明远看得都喜欢起来了,笑道:“在下苏明远。阁 下尊姓大名?”那人回答:“我叫张神仙。”苏明远大惊,上上下下打量他:“你哪里像神仙?”“神仙应该像什么样子?” 张神仙反问苏明远。“神仙应该像——”苏明远想了想,“白鬒飘飘,鹤发童颜。或者,神威凛凛,朱袍玉带。或者,假痴不 颠,身具异像……”他说不下去了,觉得自己很俗。而且,如果把“假痴不颠”作为神仙的一类,那许多自命不凡的家伙岂不 全都立刻荣升神仙一流?张神仙抚掌一笑:“那你便当我是不是神仙的神仙罢!”苏明远问:“然则阁下到此有何贵 干?”“我没有贵干。”张神仙回答,“我在走路。”“两次走到我奴仆的身上。”苏明远提醒他。“世上的路是多么宽啊,” 张神仙转头四顾,一副很茫然的样子,“但脚下的路又总是这么窄。”明犬摩拳擦掌,很想把这满嘴不知所云的小个子汉子揪 起来再摔一次。他真不信摔不死他!“阁下是为了什么事来的吗?”苏明远继续好耐心的询问,并用眼神阻止明犬的企图。 “不为什么。”张神仙怡然答道,“我有很多很多的时间可用,暂时不必为了什么奔忙。倒是阁下,为什么还不忙呢?”“我 应该忙着什么?”苏明远笑问。“忙着救人。”张神仙举单掌于胸,行了个礼,“这对你来说难道不该是最紧急的事吗?”苏 明远神情严肃,深深凝视他:“我应该怎么救人?”张神仙的回复是,该请他去做法。那时宝音的马车已回府,刘晨寂竟已等 在那里了。他似早知这病要糟似的,毫无废话,干净利落开药箱给病人诊治。明远不便领这样一个外头男人到宝音的病榻前, 先领他去宝音原居住的院子,看看那两株芙蓉花
七年级数学下册8.5垂直说课稿2

七年级数学下册8.5垂直说课稿2一. 教材分析《七年级数学下册8.5垂直》这一节的内容,主要介绍垂直的概念及其在实际生活中的应用。
教材通过丰富的图片和实例,引导学生认识垂直,理解垂直的性质,并学会用垂直的知识解决实际问题。
本节内容是学生对几何知识的重要拓展,也是初中数学的基本概念之一。
二. 学情分析七年级的学生已经具备了一定的几何基础知识,对图形的认识有一定的基础。
但是,对于垂直这一概念的理解,还需要通过具体的实例和操作来加深。
此外,学生在生活中对垂直的概念可能有一定的了解,但如何将生活中的垂直概念运用到数学学习中,还需要教师的引导和启发。
三. 说教学目标1.知识与技能:学生能够理解垂直的概念,掌握垂直的性质,并能够运用垂直的知识解决实际问题。
2.过程与方法:通过观察、操作、交流等活动,学生能够培养观察能力、动手能力和表达能力。
3.情感态度与价值观:学生能够体验数学与生活的联系,增强对数学的兴趣和自信心。
四. 说教学重难点1.重点:学生能够理解垂直的概念,掌握垂直的性质。
2.难点:学生能够将生活中的垂直概念运用到数学学习中,解决实际问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、合作学习法、实例教学法等,引导学生主动探究、积极参与。
2.教学手段:利用多媒体课件、实物模型、几何画板等,直观展示垂直的概念和性质,增强学生的直观感受。
六. 说教学过程1.导入:通过生活中的实例,如建筑物、电线杆等,引导学生观察垂直的现象,激发学生的学习兴趣。
2.新课导入:介绍垂直的概念和性质,引导学生通过观察、操作等活动,理解和掌握垂直的知识。
3.实例分析:通过具体的实例,让学生体验垂直在生活中的应用,培养学生运用数学知识解决实际问题的能力。
4.小组讨论:学生分组讨论,分享各自对垂直的理解和应用,培养学生的合作意识和表达能力。
5.总结提升:教师引导学生总结垂直的知识,强调垂直在生活中的重要性。
6.练习巩固:布置适量的练习题,让学生巩固所学知识,提高解题能力。
苏科版数学七年级上册垂直课件

做点到直线的距离 .
(1)垂线段与点到直线的距离的区分:垂线段是一个几何图
形,而点到直线的距离是一个数量,是垂线段的长度 .
(2)点到直线的距离与两点间的距离的区分:
两点间的距离
点到直线的距离
定义
连接两点的线段的长度
直线外一点到这条直线
的垂线段的长度
性质
两点之间,线段最短
垂线段最短
示图(如图 6.5-7):
B.3cm
C. 5cm
D. 7cm
解:由图可知, PC 长度为 3 cm, 是这三条线段
中最短的,但不一定是所有连线中最短的,根据
点 P 到直线 m 的距离即为点 P 到直线 m 的垂线段
的长度可知,点 P 到直线 m 的距离小于 3 cm,可
能为 2 cm.
答案:A
方法点拨
(1)直角三角形中斜边上的高可以通过“面积法”来求,即
标上“┐”,表明该角为直角 .
表示方法: 如图 6.5-1,两条直线互相垂直,记作 a ⊥ b 或
者 CD ⊥ AB. 其中交点 O 是垂足 . 符号“⊥”读作“垂直”.
直线 AB 是 CD 的垂线,直线 CD 也是 AB 的垂线 .
2. 符号语言
如图 6.5-1,因为∠ AOC=90°(已知),
段最短,简单说成:垂线段最短 .
(3)垂线、垂直与垂线段之间的区分与联系:
①区分: 垂线是一条与已知直线垂直的直线 ;垂直是两条直
线之间的位置关系;垂线段是一条与已知直线垂直的线段 .
②联系: 垂线段所在的直线是已知直线的垂线;垂线段所在
的直线与已知直线垂直 .
2. 点到直线的距离 直线外一点到这条直线的垂线段的长度叫
垂直(同步课件)七年级数学上册(苏科版)

01 理解垂线的概念与性质 02 会画已知直线的垂线,理解垂直公理及其推论 03 理解垂线段的概念与性质,会求点到直线的距离
垂线的概念与性质
01 复习引入 在同一平面内,不重合的两条直线有怎样的位置关系?
O
平行或相交
01 情境引入
Q1:图中标记出来的两条相交线之间的夹角是多少度?两条直线
的位置关系可以进一步表达为?
90°,即两条直线相互垂直
01 情境引入 Q2:生活中还有哪些垂线的实例?
书本
魔方
红十字
02 知识精讲
垂线的概念
如果两条直线相交所成的四个角中有一个角是直角,那么这两条 直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的 交点叫做垂足。
定义解读:这里的垂直,指的是相交垂直。
l Q
如图,过点P作直线l的垂线交直线l于点Q,PQ即最短路线。
02 知识精讲
垂线段的概念
如图,点P在直线l外,PO⊥l,垂足为O,PO叫做点P到直线l的 垂线段。
P
O
l
02 知识精讲
:如图,在直线l上,取点O1、O2、O3……量出线段PO ,PO1,PO2,PO3……的长度。在这些线段中,哪一条最短?
02 知识精讲
:画一条线段或射线的垂线,就是画它们所在直线的垂线。 如图,分别过点A、D画BC的垂线,垂足分别为E、F。
03 知典识 例精讲 析
例1、如图,过点P作线段AB的垂线,垂足在( B )
A.线段AB上
B.线段AB的延长线上
C.线段AB的反向延长线上 D.直线AB外
【分析】如图,垂足在线段AB的延长线上。
A.4cm
B.2cm
C.小于2cm D.不大于2cm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[单选]某公司发行总面额1000万元,票面利率为15%,偿还期限2年,每半年付息的债券,公司适用的所得税率为25%,该债券发行价为1000万元,发行成本为4.862%,则债券税后年(有效)资本成本为()。A.9%B.13.5%C.14.11%D.1 [单选]HPV的重要意义在于()A.肺内分流增加,加重低氧血症B.肺内分流增加,减轻低氧血症C.肺内分流减少,减轻低氧血症D.肺内分流减少,加重低氧血症E.肺血管扩张,肺血流量增加 [单选]患者男性,右眼角膜异物剔除术后1天,角膜形成溃疡,发展迅速,呈液化性坏死,1周内波及全角膜。首先考虑的致病菌是()A.表皮葡萄球菌B.肺炎链球菌C.绿脓杆菌D.枯草杆菌E.腐生葡萄球菌 [单选,A型题]消毒灭菌效果最好的方法是()A.煮沸B.紫外线杀菌C.化学消毒剂处理D.滤过除菌E.高压蒸气灭菌 [单选,A1型题]疟原虫在人体内破坏的细胞是()A.中性粒细胞B.嗜酸性粒细胞C.淋巴细胞D.红细胞E.血管内皮细胞 [单选,A4型题,A3/A4型题]甲公司2011年度净利润为32000万元(不包括子公司利润或子公司支付的股利),发行在外普通股30000万股,持有子公司乙公司60%的普通股股权。乙公司2011年度净利润为1782万元,发行在外普通股300万股,普 均市场价格为6元。2011年年初,乙公司对外发行240万份可用于购买其普通股的认股权证,行权价格为3元,甲公司持有12万份认股权证。假设母子公司之间没有其他需抵消的内部交易。甲公司取得对乙公司投资时,乙公司各项可辨认资 允价值与其账面价值一致。乙公司的稀释每股收益为()。A、4.36元B、5.51元C、4.54元D、4.24元 [单选]V型坡口角度(坡口两边的合成角度)一般为()。A.45;B.90;C.70。 [填空题]食物内含的能供给人体营养的有效成份,称为()。 [单选,A2型题,A1/A2型题]可引起食物中毒的一组细菌是()A.蜡样杆菌,变形杆菌,金黄色葡萄球菌B.肉毒梭菌,结核分枝杆菌,伤寒沙门菌C.鼠伤寒沙门菌,破伤风梭菌D.产气荚膜梭菌,肺炎链球菌E.副溶血弧菌,布氏杆菌 [单选,A1型题]下列各项,属我国卫生法基本原则的是()。A.遵循民法原则B.患者自主原则C.依照法定权限原则D.坚持民主立法原则E.从实际出发原则
[问答题,简答题]心脏起搏治疗的术后护理有哪些? [单选,A1型题]女性,30岁。旅游归来感全身乏力,翌日起出现寒战,高热,头痛和肌肉酸痛,干咳,右侧胸痛来急诊。胸部X线示右下片状浸润影。曾在基层医院应用头孢唑啉、阿米卡星(丁胺卡那霉素)等治疗无效。症状加重,高热达4 妄,腹泻。体。实验室检查血清钠130mmol/L。推测其最可能的病原体是()A.金黄色葡萄球菌B.军团杆菌C.铜绿假单胞菌D.粪肠球菌E.厌氧菌 [单选]结核性胸膜炎除正规抗结核治疗外,下列哪项最重要?()A.反复抽胸腔积液B.改善营养C.口服糖皮质激素D.胸腔内注射糖皮质激素E.镇痛药 [多选]依据fIDIC《施工合同条件》,下列风险中,属于业主应承担的风险有()。A.外敌入侵B.工程所在地发生的叛乱C.超音速飞行物产生的压力波D.工地发生放射性污染E.不利气候条件对施工的影响 [单选]关于羊水错误的是()A.妊娠早期的羊水,主要是母体血清经胎膜进入羊膜腔的透析液B.胎膜、胎儿消化道吸收羊水C.妊娠足月羊水含有胎脂、胎儿脱落上皮细胞、毳毛、少量白细胞等D.羊水呈弱酸性E.羊水的功能为保护胎儿与母体 [单选,A2型题,A1/A2型题]由喉上神经支配的喉内肌是()。A.环杓侧肌B.环杓后肌C.环甲肌D.甲杓肌E.杓肌 [单选]通过成绩考核,可以了解教和学的各项情况,从而判断教师的教学水平和学生的学习水平。这属于成绩考核的()。A.诊断作用B.调节作用C.评定作用D.反馈作用 [问答题,简答题]简述胸膜腔穿刺的部位。 [单选]在材料采购合同中,由供货方运输的货物,运输过程中发生的问题由()负责。A.供货方B.运输部门C.采购方D.供货方和运输部门共同 [单选]直接反映HBV复制能力的指标是()A.HBsAgB.抗HBcC.HBeAgD.HBcAgE.HBV-DNA 壁纸:/
