气象常用计算公式
气温的测量和计算公式

气温的测量和计算公式气温是指空气的热度,是天气的重要指标之一。
气温的测量和计算是气象学中的重要内容,也是人们日常生活中经常关注的话题。
本文将就气温的测量和计算公式进行详细介绍。
一、气温的测量方法。
1. 气温计测量法。
气温计是测量气温的常用工具,它根据不同的物理原理分为水银气温计、酒精气温计和电子气温计等。
水银气温计是最常见的一种,它利用水银的膨胀和收缩来测量气温。
酒精气温计则是利用酒精的膨胀和收缩来测量气温。
电子气温计则是利用电子元件来测量气温。
无论是哪种气温计,其测量原理都是利用物质的膨胀和收缩来间接测量气温。
2. 热电偶测量法。
热电偶是利用两种不同金属导线的热电势差来测量温度的一种仪器。
当两种不同金属导线的接触点温度发生变化时,它们之间的热电势差也会发生变化,通过测量这种热电势差的变化来间接测量温度。
3. 红外线测温法。
红外线测温法是一种非接触式的温度测量方法,它利用物体辐射出的红外线来测量物体的温度。
通过测量物体辐射出的红外线的强度和频率来计算出物体的温度。
二、气温的计算公式。
1. 摄氏度和华氏度的转换公式。
摄氏度和华氏度是两种常用的温度单位,它们之间的转换公式如下:摄氏度 = (华氏度 32) / 1.8。
华氏度 = 摄氏度 1.8 + 32。
通过这两个公式,可以方便地在摄氏度和华氏度之间进行转换。
2. 气温的平均值计算公式。
在气象学中,气温的平均值是一个重要的气象要素。
气温的平均值可以通过以下公式来计算:平均气温 = (最高气温 + 最低气温) / 2。
其中,最高气温和最低气温分别是一天中的最高温度和最低温度。
3. 气温的变化率计算公式。
气温的变化率是指单位时间内气温的变化量,可以通过以下公式来计算:气温变化率 = (终点气温起点气温) / 时间间隔。
其中,终点气温和起点气温分别是时间间隔内的气温值,时间间隔是指两次气温测量的时间间隔。
4. 气温的逐日变化趋势计算公式。
气温的逐日变化趋势可以通过气温的日变化率来计算,日变化率可以通过以下公式来计算:日变化率 = (当日最高气温当日最低气温) / 当日最低气温。
风量风速计算方法

风量风速计算方法风量和风速是气象学和风力学中常用的两个重要概念。
风量是指单位时间内通过一个垂直面积的风流量,通常用立方米每秒(m³/s)为单位表示。
而风速是指风流通过一定垂直面积的速度,通常用米每秒(m/s)为单位表示。
风量和风速的计算方法有多种,以下将介绍常用的几种计算方法。
一、风量的计算方法:1.数学模型法:这种计算方法基于流体力学原理建立了数学模型来计算风量。
最常用的数学模型是管道流动模型,它假设风流是通过一个管道流动,根据压差和流速的关系来计算风量。
其计算公式为:风量(m³/s)=面积(m²)×风速(m/s)2.物理模型法:这种计算方法基于实际物理模型来测量风量。
最常用的物理模型是风洞模型,通过在风洞中测量压差和流速来计算风量。
该方法适用于实际工程中需要准确测量风量的场合。
二、风速的计算方法:1.风速计仪器法:这是最常用的测量风速的方法,通过使用专用的风速计仪器(如风速计、风传感器等)来直接测量风流的速度。
风速计仪器根据不同的原理和结构,可以测量不同范围和精度的风速。
2.压差法:这种方法通过测量通过一个垂直面积的风流的压差来计算风速。
常用的压差计法有差压计法和双管法。
差压计法通过测量气流两侧的压差来计算风速,双管法通过测量气流两侧的流速差来计算风速。
3.线速度法:这种方法通过测量在一个平行于风流方向的线上经过的风流点的时间间隔和距离来计算风速。
一般使用光电传感器或激光测距仪来测量时间和距离,然后根据时间和距离的关系计算风速。
需要注意的是,风量和风速的计算方法会受到多种因素的影响,如风流的不均匀性、地形的影响、测量设备的精确度等。
因此,在实际应用中要根据具体情况选择适当的计算方法,并进行准确的数据处理和分析。
标准风速计算公式

标准风速计算公式风速的计算在我们的生活和科学研究中可有着不小的作用呢!比如说,搞气象研究的科学家们得靠它来预测天气,建筑师在设计高楼大厦时也得考虑风的影响,就连咱们平常放风筝,也能心里有个数,知道啥样的风合适。
那标准的风速计算公式是啥呢?其实啊,常用的风速计算公式是 V = 3.6 × L / T 。
这里的 V 表示的就是风速啦,单位是千米每小时;L 呢,代表的是一段距离,单位是米;T 则是通过这段距离所用的时间,单位是秒。
我给您举个例子啊。
有一次我去海边玩,正好碰到有人在做风速测量的实验。
他们在沙滩上固定了两个标杆,相距 50 米。
然后拿着一个特别的仪器,记录下一个小物件从一个标杆飘到另一个标杆所用的时间。
当时我就好奇地凑过去看,那个小物件在风的推动下,花了 10 秒钟从这头飘到了那头。
那按照咱们的公式来算,风速 V 就等于 3.6 × 50 ÷ 10 ,算下来就是 18 千米每小时。
这风不算太大,吹在脸上挺舒服的。
那为啥要搞清楚风速计算公式呢?这用处可大了去了。
比如说,在能源领域,风力发电就得靠它来确定合适的安装位置和风机的设计参数。
要是不知道风速情况,那风机可能发不了多少电,或者干脆被大风吹坏了。
再比如说,在交通运输中,飞机的起降就得考虑风速。
要是风速计算不准确,那飞机可能会遇到危险。
我就听说过有一次因为突然的强风,导致飞机在降落的时候晃得厉害,把乘客吓得够呛。
还有在农业方面,农民伯伯们也得根据风速来决定啥时候喷农药,要是风太大,农药都被吹跑了,起不到作用;风太小呢,又扩散不开。
总之,标准风速计算公式虽然看起来简单,但是背后的作用可真是不容小觑。
它就像是一个默默无闻的小卫士,在各个领域悄悄地发挥着重要的作用,保障着我们的生活和工作能够顺利进行。
希望通过我这一番不太专业但还算通俗的讲解,能让您对标准风速计算公式有个初步的了解。
以后再遇到跟风速有关的事儿,您也能心里有数啦!。
实际大气压计算公式

实际大气压计算公式大气压这东西,咱在生活中好像不怎么能直接感觉到,但它又实实在在地影响着咱们的生活。
你想想,为啥气球能鼓起来?为啥飞机能在天上飞?这里头都有大气压的作用呢!要说实际大气压的计算公式,咱们得先搞清楚啥是大气压。
简单来说,大气压就是大气对物体表面产生的压力。
那这压力咋算呢?咱们常用的实际大气压计算公式是:P = ρgh。
这里的 P 就是大气压啦,ρ 是大气的密度,g 是重力加速度,h 是高度。
比如说,咱在山上和在海边,感受到的大气压就不一样。
我记得有一次我去爬山,越往上爬,就感觉呼吸越费劲。
一开始我还纳闷呢,后来才反应过来,这是因为高度增加了,大气压变小啦!当时我那心跳都加快了,喘气也粗了,就想着赶紧爬到山顶,看看风景,缓解缓解这难受劲儿。
等到了山顶,放眼望去,那景色确实美,可我还是觉得有点不舒服,这就是大气压在“捣乱”。
那这个公式具体咋用呢?咱举个例子。
假如知道在某个高度的大气密度是 1.2 千克/立方米,重力加速度咱们一般取 9.8 米每秒平方,高度是 500 米。
那咱们就能算出来这地方的大气压是多少。
把数字带进公式里,P = 1.2×9.8×500 = 5880 帕斯卡。
这就得出了这个高度的大气压数值。
再比如说,气象站的工作人员,他们就得经常用这个公式来监测和预测天气变化。
因为大气压的变化和天气可是密切相关的,要是大气压突然降低,那很可能就要下雨啦。
还有啊,飞机飞行的时候,飞行员也得时刻关注大气压的变化,来调整飞行高度和速度,保证飞行安全。
总之,这个实际大气压的计算公式虽然看起来简单,但用处可大着呢!它能帮我们解释好多生活中的现象,也能在很多领域发挥重要作用。
不管是咱们日常感受的气候变化,还是那些高大上的科学研究和工程应用,实际大气压计算公式都像是一个隐藏在背后的小能手,默默发挥着它的作用,让我们的世界变得更加有序和可预测。
所以啊,可别小瞧了这个公式,多了解了解它,说不定能让咱对这个世界的认识更深刻呢!。
(整理)气象常用计算公式

1、资料和计算丰富、可靠的气象观测资料是研究和了解大气环流及气候特征的最重要的基础。
正是由于它们,才大大加深和扩大了我们对大气和气候运动本身的认识,并为理论研究和数值模拟提供了重要素材和基本保证。
没有这些宝贵的资料作为基础,任何关于大气或气候的研究都只能停留在空中楼阁亦或海市蜃楼的阶段。
虽然气象观测可以追溯到千年以前,但显然由于条件、认识、技术手段和科学发展水平的限制,在早期只是对发生在某些局部区域的大气中某些特殊天气现象的零星观测,还算不上是对大气环流的从地面到高空、从区域到全球、从单一到综合、从特殊到一般、从里到外、由外及里、从下到上、由上至下、从离散到连续的全方位、全视角的、系统的三维观测。
近半个多世纪以来,随着科学技术的迅速发展、监测手段的日益先进、社会需求的不断增加、国际协作的日渐密切,上述状况有了本质的改变。
各种新技术如气象雷达、气象卫星、红外及微波遥感、高速电子计算机等在气象观测中的广泛应用,使得气象观测水平有了史无前例的发展,观测的种类和质量有了前所未有的提高。
加之,由于人类本身生存和发展的需要,使得气象观测项目和种类大大丰富起来;由于国际间广泛紧密的合作,使得观测资料的协调度和统一性也大大提高了。
目前,已经形成了可同时监测全球天气情况的气象观测系统和气象通讯系统。
特别是,1991年美国国家环境预报中心(NCEP)和美国国家大气科学研究中心(NCAR)联手实施的全球再分析计划(NCEP/NCAR Global Reanalysis Project),把全球观测资料的质量提高到一个新的水平。
该计划在全球范围内,通过世界各国及各主要科研机构和业务部门,把能搜集到的资料包括地面观测资料、高空探测资料、航舶资料、卫星遥感资料、雷达资料、飞机资料、气球资料,浮标资料以及其它观测资料等统一进行编码、详细的订正预处理和复杂的质量控制,并用一个较完善的同化系统统一进行资料同化,使得观测资料的统一性、协调性、可靠性、完善性、代表性都有了显著的提高,引起了国际大气科学界的极大关注和反响。
大气压强和温度的关系计算公式

大气压强和温度的关系计算公式
大气压强和温度是气象领域中两个重要的物理量,它们之间的关系可以用以下计算公式表示:
P = P0 * exp(-Mgh/RT)
其中,P是大气压强,单位为帕斯卡(Pa);P0是海平面上的标准大气压,其取值约为101325 Pa;M是空气的平均分子量,其取值约为28.97 g/mol;g是重力加速度,取值约为9.8 m/s2;h是海拔高度,单位为米(m);R是气体常数,取值约为8.31 J/(mol·K);T 是温度,单位为开尔文(K)。
根据这个公式,可以看出大气压强和温度之间存在负相关关系,即温度升高,大气压强降低;温度下降,大气压强增加。
当海拔高度升高时,大气压强也会随之降低,这和大气的密度有关。
同时,空气中的水蒸气也会对大气压强产生影响,这个因素在气象预测和天气预报中也需要考虑到。
- 1 -。
气象常用计算公式

1、资料和计算丰富、可靠的气象观测资料是研究和了解大气环流及气候特征的最重要的基础。
正是由于它们,才大大加深和扩大了我们对大气和气候运动本身的认识,并为理论研究和数值模拟提供了重要素材和基本保证。
没有这些宝贵的资料作为基础,任何关于大气或气候的研究都只能停留在空中楼阁亦或海市蜃楼的阶段。
虽然气象观测可以追溯到千年以前,但显然由于条件、认识、技术手段和科学发展水平的限制,在早期只是对发生在某些局部区域的大气中某些特殊天气现象的零星观测,还算不上是对大气环流的从地面到高空、从区域到全球、从单一到综合、从特殊到一般、从里到外、由外及里、从下到上、由上至下、从离散到连续的全方位、全视角的、系统的三维观测。
近半个多世纪以来,随着科学技术的迅速发展、监测手段的日益先进、社会需求的不断增加、国际协作的日渐密切,上述状况有了本质的改变。
各种新技术如气象雷达、气象卫星、红外及微波遥感、高速电子计算机等在气象观测中的广泛应用,使得气象观测水平有了史无前例的发展,观测的种类和质量有了前所未有的提高。
加之,由于人类本身生存和发展的需要,使得气象观测项目和种类大大丰富起来;由于国际间广泛紧密的合作,使得观测资料的协调度和统一性也大大提高了。
目前,已经形成了可同时监测全球天气情况的气象观测系统和气象通讯系统。
特别是,1991年美国国家环境预报中心(NCEP)和美国国家大气科学研究中心(NCAR)联手实施的全球再分析计划(NCEP/NCAR Global Reanalysis Project),把全球观测资料的质量提高到一个新的水平。
该计划在全球范围内,通过世界各国及各主要科研机构和业务部门,把能搜集到的资料包括地面观测资料、高空探测资料、航舶资料、卫星遥感资料、雷达资料、飞机资料、气球资料,浮标资料以及其它观测资料等统一进行编码、详细的订正预处理和复杂的质量控制,并用一个较完善的同化系统统一进行资料同化,使得观测资料的统一性、协调性、可靠性、完善性、代表性都有了显著的提高,引起了国际大气科学界的极大关注和反响。
气象数据统计项目、单位和精度、非观测项目计算公式
附录 A
(规范性附录)
统计项目、单位和精度
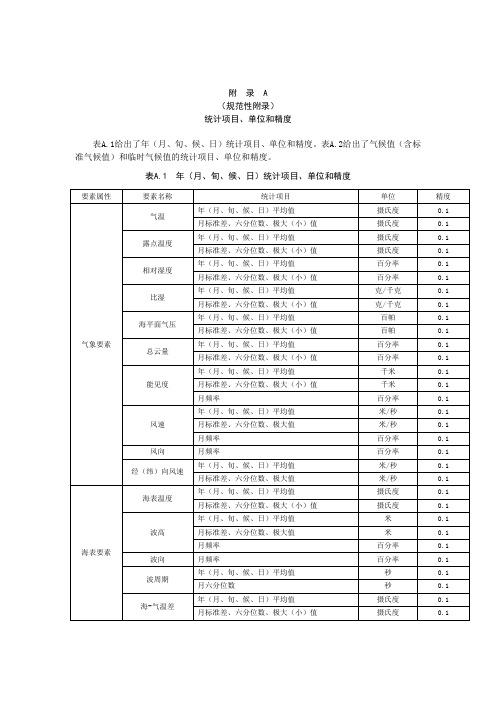
表A.1给出了年(月、旬、候、日)统计项目、单位和精度。
表A.2给出了气候值(含标准气候值)和临时气候值的统计项目、单位和精度。
表A.1 年(月、旬、候、日)统计项目、单位和精度
表A.2 气候值(含标准气候值)和临时气候值统计项目、单位和精度
附录 B
(规范性附录)
非观测项目计算公式
B.1 海-气温差
海-气温差计算见式(C.1):
=...................................... (B.1)
D-
S
A
式中:
D——海-气温差,单位为摄氏度(℃);
S——海表温度,单位为摄氏度(℃);
A——空气温度,单位为摄氏度(℃)。
B.2 相对湿度、比湿、经向风和纬向风
相对湿度、比湿、经向风和纬向风。
降水百分率计算公式

降水百分率计算公式
降水百分率是指在一定时间内,某地区的降水量占该地区平均降水量的百分比。
它是气象学中常用的一个指标,可以用来评估某地区的降水情况。
降水百分率的计算公式如下:
降水百分率 = 实际降水量 ÷ 平均降水量 × 100%
其中,实际降水量指某地区在一定时间内的降水量,平均降水量指该地区在同一时间段内的历史平均降水量。
例如,某地区在一年内的降水量为800毫米,而该地区历史上同一时间段内的平均降水量为1000毫米,则该地区的降水百分率为:降水百分率 = 800 ÷ 1000 × 100% = 80%
这意味着该地区的降水量只有历史平均降水量的80%。
降水百分率的应用
降水百分率可以用来评估某地区的降水情况,对于农业、水利、交通等领域都有重要的意义。
在农业方面,降水百分率可以用来评估某地区的灌溉需求。
如果降水百分率低于50%,则该地区需要增加灌溉量,以保证农作物的正
常生长。
在水利方面,降水百分率可以用来评估某地区的水资源状况。
如果降水百分率低于50%,则该地区的水资源可能会出现短缺,需要采取相应的节水措施。
在交通方面,降水百分率可以用来评估某地区的道路安全情况。
如果降水百分率高于50%,则该地区可能会出现道路湿滑、积水等情况,需要采取相应的交通安全措施。
降水百分率是一个重要的气象指标,可以用来评估某地区的降水情况,对于农业、水利、交通等领域都有重要的应用价值。
气象区域站平均间距计算公式

气象区域站平均间距计算公式一、基本概念。
气象区域站是为了获取更详细、更准确的气象数据而在一定区域内分布设立的站点。
计算气象区域站平均间距有助于评估气象观测网络的覆盖密度等情况。
二、简单的二维平面平均间距计算(假设站点均匀分布在一个平面区域内)1. 对于规则形状区域(如正方形区域)- 如果区域面积为A(单位:平方千米等面积单位),气象区域站的数量为n。
- 首先考虑正方形区域边长L=√(A)。
- 我们假设站点按照正方形网格排列(这是一种理想的均匀分布情况),那么在一条边上站点的数量m满足m = √(n)(这里是基于正方形区域内站点均匀分布的近似计算)。
- 平均间距d就可以近似为L/(m - 1)(因为m个站点有(m - 1)个间隔)。
- 综合起来得到公式:d=(√(A))/(√(n)- 1)2. 对于圆形区域。
- 设圆形区域半径为r,面积A=π r^2。
- 假设站点均匀分布在圆形区域内,将圆形区域近似看作是由多个小正方形组成(当站点密度较大时这种近似有一定合理性)。
- 首先计算圆形区域的等效正方形面积A_eq,根据经验A_eq≈(4)/(π)A(这个等效面积是为了将圆形区域转换为可类比正方形区域来计算间距)。
- 然后按照正方形区域的计算方法,用A_eq代替A计算平均间距,即d=frac{√(frac{4){π}A}}{√(n)-1}3. 不规则区域。
- 一种常用的方法是采用泰森多边形(Voronoi diagram)法。
- 首先构建泰森多边形,每个气象站为一个多边形的中心,多边形内的任意一点到该气象站的距离比到其他气象站的距离都近。
- 计算每个泰森多边形的面积A_i(i = 1,2,·s,n)。
- 然后计算平均面积¯A=(1)/(n)∑_i = 1^nA_i。
- 最后按照正方形区域计算间距的思路,假设这个平均面积对应的是一个正方形区域,得到平均间距d=frac{√(¯A)}{√(n)-1}。
风力的计算公式

风力的计算公式风力是指风对物体施加的力量,通常用牛顿(N)或千克力(kgf)表示。
风力的大小与风速、物体的面积和形状、空气密度等因素有关。
在工程设计和气象预报中,需要对风力进行精确的计算和预测。
本文将介绍风力的计算公式及其应用。
风力的计算公式风力的计算公式可以用牛顿第二定律表示:F = ma其中,F表示物体所受的合力,m表示物体的质量,a表示物体的加速度。
在风力作用下,物体的加速度可以表示为:a = F / m因此,风力可以表示为:F = ρAv²/2其中,ρ表示空气密度,A表示物体的投影面积,v表示风速。
这个公式也称为风力公式。
风力公式的推导风力公式的推导需要用到流体力学的基本原理。
在空气中运动的物体,会受到空气的阻力和升力。
阻力是垂直于运动方向的力,升力是垂直于物体表面的力。
在低速情况下,阻力和升力可以近似为线性关系。
因此,可以将阻力和升力表示为:Fz = 1/2ρv²CzAFx = 1/2ρv²CxA其中,Cz和Cx分别表示升力系数和阻力系数,A表示物体的投影面积,ρ表示空气密度,v表示风速。
这个公式也称为空气动力学公式。
将阻力和升力分解为水平和垂直方向,可以得到:Fh = Fx cosθ - Fz sinθFv = Fx sinθ + Fz cosθ其中,θ表示物体与风向的夹角。
在水平方向上,物体所受的合力为:Fh = Fx cosθ - Fz sinθ= 1/2ρv²A(Cx cosθ - Cz sinθ)在垂直方向上,物体所受的合力为:Fv = Fx sinθ + Fz cosθ= 1/2ρv²A(Cx sinθ + Cz cosθ)当物体与风向垂直时,θ=90°,此时水平方向上的力为零,垂直方向上的力最大。
因此,可以将垂直方向上的力称为风力。
F = Fv = 1/2ρv²A(Cx sinθ + Cz cosθ)当物体是一个平面板时,Cx=1,Cz=0,此时风力公式可以简化为:F = 1/2ρv²A这个公式也称为平板风力公式。
真风速计算公式

真风速计算公式一、引言真风速是指风在静止空气中的速度,通常用来描述风的强度。
在气象学、航空航天等领域,准确测量和计算真风速具有重要意义。
本文将介绍真风速计算公式及其应用。
二、背景知识在气象学中,测量风速常用的仪器是风速计。
然而,通过风速计测量得到的风速是指相对风速,即相对于风速计所在位置的风速。
为了得到真实的风速,需要进行修正计算。
三、真风速计算公式真风速计算公式是通过测量相对风速、温度、气压等参数,并结合大气物理学原理,推导出来的计算公式。
下面是常用的真风速计算公式之一:真风速 = 相对风速 / (1 - (温度 - 15) * (0.0065 + 0.004 * 相对湿度) / 273.15)其中,相对风速是通过风速计测量得到的风速;温度是指空气的温度,单位为摄氏度;相对湿度是指空气中水蒸气的含量与饱和水蒸气含量的比值,以百分数表示。
四、应用案例为了更好地理解真风速计算公式的应用,下面以一个应用案例进行说明。
假设某地气象站测量到的相对风速为20 m/s,温度为25摄氏度,相对湿度为50%。
我们可以利用真风速计算公式来计算该地的真风速。
根据公式,代入相应的数值进行计算:真风速= 20 / (1 - (25 - 15) * (0.0065 + 0.004 * 0.5) / 273.15)≈ 21.36 m/s因此,该地的真风速约为21.36 m/s。
五、注意事项在使用真风速计算公式时,需要注意以下几点:1. 温度的单位应为摄氏度,如果使用其他单位,需要进行转换。
2. 相对湿度应以百分数表示,如果使用其他形式的湿度表示,需要进行转换。
3. 公式中的常数值已经进行了近似处理,如果需要更精确的结果,可以使用更精确的常数值。
4. 公式中的温度差值和相对湿度差值的乘积应除以273.15,这是由于温度以开尔文为单位,需要进行单位转换。
六、总结真风速计算公式是通过测量相对风速、温度、相对湿度等参数,结合大气物理学原理,推导出来的计算公式。
气象常用计算公式

气象常用计算公式气象学是研究大气现象的科学,其中包含了大量的观测和计算。
以下是一些常用的气象计算公式。
1.水汽压和相对湿度的计算:- 饱和水汽压(es)的计算:es=6.112exp(17.67T/(243.5+T))- 已知温度(T)和相对湿度(RH),可以计算水汽压(e):e=RH/100*es2.气温和露点温度的计算:-已知水汽压(e)和相对湿度(RH),可以通过上面的公式计算得到露点温度(Td)- 温度(T)和露点温度(Td)之间的关系:Td=243.5log(RH/100)+((17.67T)/(243.5+T))/(17.67-2.11log(RH/100)) 3.位温的计算:-位温(θ)是衡量大气稳定性的一个指标,可通过以下公式计算:θ=T*(1000/P)^0.286-其中,T为温度(摄氏度),P为压强(百帕)4.风速和风向的计算:- 运算速率(U)的计算:U=sqrt(U₁²+U₂²)其中,U₁和U₂是风速在两个垂直方向上的成分- 风向(D)的计算:D=atan(U₁/U₂)-如果风速为0,则风向定义为0度5.湿绝热流和干绝热流的计算:-已知温度(T)和垂直速度(w)的情况下,可以计算湿绝热流(θw)和干绝热流(θ):θw=θ+0.608wθ=θw-0.608w6.气压的计算:-已知海平面上的气压(P₀)、海拔高度(h)和温度(T)的情况下,可以计算海平面以上其中一高度处的气压(P):P=P₀*(1-(0.0065*h)/(T+0.0065*h))这些公式是气象学中常用的计算方法,可以帮助气象学家研究和预测天气变化。
不同的计算公式适用于不同的气象参数和条件,因此在使用时需要注意选择合适的公式。
同时,在应用这些公式时,也需要考虑数据的准确性和可靠性,以获得较为准确的计算结果。
等雨量线法计算公式

等雨量线法计算公式等雨量线法是一种在气象学和水文学中常用的计算降水量的方法。
咱们先来了解一下啥是等雨量线。
简单说,等雨量线就是把降雨量相同的点连起来形成的线。
比如说,有一场雨下完了,咱们在地图上标注出不同地点的降雨量,然后把降雨量相同的点用线连起来,就得到了等雨量线。
那等雨量线法的计算公式又是咋回事呢?这计算公式啊,其实就是通过这些等雨量线来估算一个区域的平均降雨量。
公式大概是这样的:平均降雨量 = (f1×P1 + f2×P2 + ...... + fn×Pn)/ F这里面的f1、f2 一直到fn 表示的是相邻两条等雨量线之间的面积,P1、P2 到 Pn 表示的是相应的等雨量线代表的降雨量,F 就是整个计算区域的总面积。
听起来可能有点复杂,咱举个例子就清楚啦。
有一次我去一个山区考察降雨量。
那地方山连着山,地形复杂得很。
我们在不同的地点设置了雨量测量器,雨停之后,把各个测量点的数据标在地图上,然后开始画等雨量线。
我记得有一块区域,相邻的两条等雨量线分别代表 50 毫米和 80 毫米的降雨量,它们之间的面积大概是 10 平方公里。
按照公式,先算出这部分的降雨量贡献:(10×(50 + 80))/ 2 = 650 万立方米。
然后把整个区域这样一块一块地算出来,最后加在一起除以总面积,就能得到这个区域的平均降雨量啦。
在实际应用中,等雨量线法的计算可没这么简单。
比如说,测量点的分布要合理,如果太稀疏,画出来的等雨量线就不准确;还有,地形的影响也不能忽略,山区和平原的降雨分布差别很大。
有时候为了更精确,还得考虑风向、云层的移动等因素。
而且,这计算过程中还可能会出错。
我就有过一次,算完了之后怎么都觉得不对劲,回头一检查,原来是把一个测量点的数据标错位置了,那叫一个郁闷!重新算一遍,才得到了正确的结果。
总之,等雨量线法的计算公式虽然看起来有点头疼,但只要咱认真仔细,考虑周全,还是能比较准确地算出一个区域的降雨量,为农业生产、水利工程等提供有用的数据支持。
湿球温度计算公式

湿球温度计算公式
湿球温度是一个气象学术语,表示为Tw,是指通过湿度和气温相结合计算出来的一个温度值。
其中
Tw:湿球温度,单位为摄氏度;
T:气温,单位为摄氏度;
RH:相对湿度,单位为百分比。
下面我们来详细解释一下公式的各个参数:
1.湿球温度(Tw):湿球温度是通过测量湿度和气温相结合计算得到的一个温度值。
它是指气温下空气中水分子的蒸发导致的冷却效应。
2.气温(T):气温是指空气中的温度,通常使用摄氏度或华氏度来表示。
在湿球温度计算中,需要使用到的气温数据。
3.相对湿度(RH):相对湿度是指单位体积空气中所含水蒸气的质量与该温度下所能含有的最大水蒸气质量之比,通常以百分比表示。
相对湿度越高,空气中的水分含量越大。
4.公式说明:
5.计算过程:
首先,将Tw的值赋一个初始值,通常为气温(T)的值。
然后,通过迭代计算的方式,不断更新Tw的值,直到收敛(收敛条件为更新前后的Tw值之差小于一个设定值,通常为0.1摄氏度)。
在每次迭代计算中,使用公式右侧的表达式对湿球温度进行更新,直
到满足收敛条件为止。
需要注意的是,湿球温度计算公式是基于一些假设和近似推导得到的,因此,在实际应用中可能存在一定的误差。
此外,公式的计算结果也会受
到气温和相对湿度数据的精确性影响。
总之,湿球温度计算公式可以通过气温和相对湿度的数据来计算出湿
球温度的近似值,是气象学中常用的一个温度指标。
通过湿球温度的计算,可以更好地了解空气中的水分含量和蒸发冷却效应,对气象学研究和工程
应用具有重要的意义。
昼夜平均温度计算公式

昼夜平均温度计算公式在气象学和地球科学领域中,昼夜平均温度是一个重要的气候指标。
它反映了某一地区在一天内的温度变化情况,对于预测天气、研究气候变化等具有重要意义。
昼夜平均温度的计算涉及到一些复杂的因素,包括地理位置、季节、气候类型等。
下面我们将介绍昼夜平均温度的计算公式及其相关知识。
首先,昼夜平均温度是指一天内白天和夜晚的温度平均值。
一般来说,白天的温度较高,夜晚的温度较低,因此昼夜平均温度可以反映出一天内的温度变化情况。
昼夜平均温度的计算公式如下:昼夜平均温度 = (白天温度 + 夜晚温度) / 2。
其中,白天温度和夜晚温度分别是指一天内的最高温度和最低温度。
一般来说,白天温度是指在太阳升起后到太阳落下前的时间段内的最高温度,夜晚温度是指在太阳落下后到太阳升起前的时间段内的最低温度。
通过这个公式,我们可以得到一天内的昼夜平均温度。
在实际应用中,昼夜平均温度的计算还涉及到一些修正和调整。
首先,由于地球自转和公转的影响,不同地区的昼夜时间长度不同,因此需要考虑日照时间对昼夜平均温度的影响。
其次,地形、海洋、湖泊等地貌特征也会对昼夜温度产生影响,因此需要进行地形修正。
最后,气象站点的海拔高度、气候类型等因素也需要进行修正。
通过这些修正和调整,我们可以得到更加准确的昼夜平均温度。
昼夜平均温度对气候研究和天气预测具有重要意义。
首先,它可以反映出某一地区的气候特点,如炎热的沙漠地区昼夜温差大,而温和的海洋地区昼夜温差小。
其次,昼夜平均温度还可以用于天气预测,通过对历史数据的分析,可以预测出未来一段时间内的昼夜平均温度,从而指导人们的生活和生产。
除了昼夜平均温度,气象学和地球科学领域还有许多其他重要的气候指标,如气温、湿度、风速等。
这些指标都对我们的生活和工作产生着重要影响,因此我们需要加强对气候指标的研究和应用,以更好地适应气候变化的影响。
总之,昼夜平均温度是一个重要的气候指标,它反映了一天内的温度变化情况。
雨量计算公式

雨量计算公式
雨量计算公式是一种常见的气象研究方法,它可以帮助我们对不同地区和时期的降雨量进行准确的计算。
雨量计算公式源于熵原理,它表达了一个区域在一定时间内(例如一个小时)由雨水蒸发和滴落的总量。
根据该公式,雨量平均可以用以下公式表示:M=(m/M)V,其中M是当地一定时间(假设为1小时)内降雨量,M是雨水蒸发量,V是滴落量。
也就是说,
某个地区一小时内的降雨量就是雨水蒸发量和滴落量的总和。
除此之外,还有一种经典的雨量计算方法叫做Capstone方法,它针对多雨地区设计,并且可以更精确地衡量雨量。
该方法基于对不同尺度(如水文单位、地理单位和经济单位)降雨变化的分析,以及水文区分级的方法,它可以更精确地确定降雨的分布模式和时间位置。
这样从降水信息的微观、宏观以及行业角度可以给出更准确的雨量计算结果。
总而言之,雨量计算公式是利用熵原理和Capstone方法对降
雨量进行准确分析和计算的一种重要方法。
它不仅有助于对地区雨量的实时预报,还可以用于水资源分析、水文建模和气象预报等领域。
它的准确度和灵敏性也得到了广泛认可,并被用于制定水资源、气象灾害预警和灾害维护等重要的水资源利用决策。
降雨计算公式范文

降雨计算公式范文1. 税拉万公式(Traverse)税拉万公式是一种简单的方法,用于估算降雨量。
它基于一个假设,即降雨的强度在时间和空间上是均匀分布的。
税拉万公式的计算公式如下:降雨量=面积×强度其中面积为计算区域的面积,强度为单位时间内的降雨量。
2. 李希梅罗公式(Meierhofer)李希梅罗公式是一种根据实测数据来计算降雨量的公式。
公式的计算方法如下:降雨量=1.92×(雨量数据-补偿因子)其中补偿因子是一个经验值,用于考虑其他因素对降雨量的影响。
3. 哈里森公式(Harrison)哈里森公式是一种可以用来估算降雨量的经验公式。
公式的计算方法如下:降雨量=Σ(a×R^b)其中a和b是经验系数,R是一小时雨强。
4. 普里普莱特公式(Primitive)普里普莱特公式是一种常用的计算洪水流量的公式。
公式的计算方法如下:洪水流量=C×A×[(K×Q^m)/(K+Q^m)]其中C是经验系数,A是流域的面积,Q是实时的降雨量。
5. 四代冈利帕斯公式(Gumbel)四代冈利帕斯公式是一种用于估算极值降雨的公式。
公式的计算方法如下:极值降雨 = a + b × log(N)其中a和b是经验系数,N是计算区域的年频率。
6. 增色公式(Thiessen)增色公式是一种用于估算站点降雨量的公式。
公式的计算方法如下:站点降雨量=Σ(站点i的面积×站点i的降雨量)/Σ(站点i的面积)其中站点i是计算区域内的站点。
以上只是几个常见的降雨计算公式,实际上还有许多其他的公式和方法可以用于降雨量的计算和预测。
不同的公式适用于不同的情况和目的,选择适合的公式需要考虑到地理条件、气象要素和数据可靠性等因素。
相对湿度与温度计算公式

相对湿度与温度计算公式
相对湿度与温度是气象学中常用的两个参数,它们之间有一定的关系。
相对湿度指空气中实际水蒸气压与饱和水蒸气压的比值,通常以百分数表示。
而温度指的是物体的热度高低程度,通常以摄氏度或华氏度表示。
下面介绍相对湿度与温度计算公式。
首先,计算相对湿度的公式为:
相对湿度 = (实际水蒸气压 / 饱和水蒸气压) × 100%
其中实际水蒸气压是指空气中所含水蒸气的压强,饱和水蒸气压是指在该温度下,水蒸气达到饱和的压强。
其次,计算饱和水蒸气压的公式为:
当温度以摄氏度表示时,饱和水蒸气压 = 6.11 × 10^[(7.5 ×温度) / (温度 + 237.3)]
当温度以华氏度表示时,饱和水蒸气压 = 4.58 × 10^[(7.5 ×温度) / (温度 + 234.5)]
最后,计算实际水蒸气压的公式为:
实际水蒸气压 = 相对湿度×饱和水蒸气压 / 100%
通过以上公式的计算,我们可以得到相对湿度与温度之间的关系,进而为气象预测、农业生产等方面提供依据。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、资料和计算丰富、可靠的气象观测资料是研究和了解大气环流及气候特征的最重要的基础。
正是由于它们,才大大加深和扩大了我们对大气和气候运动本身的认识,并为理论研究和数值模拟提供了重要素材和基本保证。
没有这些宝贵的资料作为基础,任何关于大气或气候的研究都只能停留在空中楼阁亦或海市蜃楼的阶段。
虽然气象观测可以追溯到千年以前,但显然由于条件、认识、技术手段和科学发展水平的限制,在早期只是对发生在某些局部区域的大气中某些特殊天气现象的零星观测,还算不上是对大气环流的从地面到高空、从区域到全球、从单一到综合、从特殊到一般、从里到外、由外及里、从下到上、由上至下、从离散到连续的全方位、全视角的、系统的三维观测。
近半个多世纪以来,随着科学技术的迅速发展、监测手段的日益先进、社会需求的不断增加、国际协作的日渐密切,上述状况有了本质的改变。
各种新技术如气象雷达、气象卫星、红外及微波遥感、高速电子计算机等在气象观测中的广泛应用,使得气象观测水平有了史无前例的发展,观测的种类和质量有了前所未有的提高。
加之,由于人类本身生存和发展的需要,使得气象观测项目和种类大大丰富起来;由于国际间广泛紧密的合作,使得观测资料的协调度和统一性也大大提高了。
目前,已经形成了可同时监测全球天气情况的气象观测系统和气象通讯系统。
特别是,1991年美国国家环境预报中心(NCEP)和美国国家大气科学研究中心(NCAR)联手实施的全球再分析计划(NCEP/NCAR Global Reanalysis Project),把全球观测资料的质量提高到一个新的水平。
该计划在全球范围内,通过世界各国及各主要科研机构和业务部门,把能搜集到的资料包括地面观测资料、高空探测资料、航舶资料、卫星遥感资料、雷达资料、飞机资料、气球资料,浮标资料以及其它观测资料等统一进行编码、详细的订正预处理和复杂的质量控制,并用一个较完善的同化系统统一进行资料同化,使得观测资料的统一性、协调性、可靠性、完善性、代表性都有了显著的提高,引起了国际大气科学界的极大关注和反响。
该计划现已完成1948~1997年的资料再分析工作,并在实施新的计划内容。
NCEP/NCAR再分析资料反映了当代国际大气科学资料研究的水平,其代表性是不言而喻的。
由于所搜集的资料来自于世界各国,所以处理后的资料理应采取“取之于民,用之于民”的使用原则,事实也是如此。
因在资料使用上的高度开放性和高效性,目前该再分析资料已成为当今世界上应用最为普遍的大气环流和气候诊断资料。
所以,NCEP/NCAR再分析资料是世界各国集体团结协作的优秀结晶,是世界大气科学界的共同财富,可以预料,其巨大的价值必会随着时间的推移越加显现出来。
本套全球大气环流气候图集就是利用NCEP/NCAR的1958~1997年40年再分析资料进行统计处理的。
本套图集初步分为五册,具体是:第一册,气候平均态;第二册,变率;第三册,基本模态和遥相关型;第四册,能量、动量和各种输送;第五册,持续性和谱特征。
本书是其中的第一册,旨在用尽可能多的气象要素、从更多的角度来全面展示大气环流气候平均状态的三维结构和特征,包括环流的纬向对称性和随经度变化的纬向不均匀性(即纬向对称场的偏差场)。
1.1原始资料本书所用资料是NCEP/NCAR再分析数据集中月平均资料子集数据的最优月平均资料(月统计是按每日4个时次即0, 6, 12和18时的资料全部参加统计的最优平均),时间段为1958年1月~1997年12月共40年,包括常规要素资料、扩展要素资料和其它要素资料三类,具体由表1给出。
表1 本书中所用NCEP/NCAR1958~1997再分析资料一览表Table 1.List of NCEP/NCAR 1958-1997 reanalysis data used in this book.参数单位层次类型和层次值网格类型纬向风u m s-1p-L17 经纬度经向风v m s-1p-L17 经纬度垂直速度ωhPa s-1 p-L11 经纬度位势高度z gpm p-L17 经纬度温度T K p-L17 经纬度比湿q kg kg-1 p-L8 经纬度相对湿度r % p-L8 经纬度相对涡度ζs-1 p-L17 经纬度散度 D s-1 p-L17 经纬度流函数ψm2 s-1 p-L17 经纬度位势速度χm2 s-1p-L17 经纬度海平面气压P SL hPa SL 经纬度降水率P kg m-2 s-1 SFC 高斯可降水量W kg m-2TOT 经纬度对流性降水率P C kg m-2 s-1SFC 高斯云量C C, C CH, C CM和C CL% THML 高斯向下长波↓LWFW m-2 SFC 高斯向下短波↓SWF和↓TSWFW m-2ST 高斯向上长波↑LWF和↑TLWFW m-2ST 高斯向上短波↑SWF和↑TSWFW m-2ST 高斯净长波F LW W m-2SFC 高斯净短波F SW W m-2SFC 高斯潜热通量↑LHFW m-2SFC 高斯感热通量↑SHFW m-2SFC 高斯表中的一些符号的意义如下:p-L17:等压面, 共17层:1000, 925, 850, 700, 600, 500, 400, 300, 250, 200, 150, 100, 70, 50, 30, 20, 10hPa; p-L11:等压面, 共11层:1000, 850, 700, 600, 500, 400, 300, 250, 200, 150, 100hPa;p-L8:等压面, 共8层:1000, 925, 850, 700, 600, 500, 400, 300hPa;SL:平均海平面;SFC:地面;ST:地面及大气顶部;TOT:总大气柱;THML :总大气柱、高云、中云、低云;经纬度网格:2.5︒⨯2.5︒网格,纬向从东经0︒E 到西经2.5︒W ,经向从北纬90︒N 到南纬90︒S ;高斯网格:1.875︒⨯1.875︒网格,纬向从东经0︒E 到西经1.875︒W , 经向从北纬88.542︒N 到南纬88.542︒S 。
1.2计算本书中的气候平均采用统计中简单的等权平均(即算术平均)。
对任意量A 在第I 年第j 月(或季)的值记为j I A ,,其多年第j 月份(或季)的气候平均值为j A ,则∑==NI j I j A NA 11,, (1)其中N 为统计的总年数。
本书中N =40。
令水平空间场A 在离散网格点上的值已知,其在纬度为i 、经度为j 处的值记为ij A ,在纬度为i 处A 的纬向平均记为i A ][,则∑==mj iji A m A 11][, (n i ,Λ ,2 ,1=) (2) 其中m 为纬圈上的格点数,n 为经圈上的格点数。
本书中对经纬网格场m =144,n =73; 对高斯网格场m =192, n =94。
进一步,记A 在纬度为i 、经度为j 处的纬向偏差值为*ijA ,则iij ij A A A ][*-=, (3)其中n i ,Λ ,2 ,1=,m j ,Λ ,2 ,1=。
本书中在统计位势高度z 的纬向平均时已减去了相应等压面上标准大气的位势高度值SA z 。
这里标准大气的位势高度SA z 是根据1976美国标准大气得来,如表2所示。
表2 本书中所用不同等压面的标准大气位势高度值 (美国标准大气, 1976) Table 2. Values of the geopotential height of standard atmosphere at the different pressure levels used in this book. (U.S. Standard Atmosphere, 1976)气 压 p (hPa)位势高度 SA z (gpm)1 1 000 1102 925 7623 850 1 4574 700 3 0125 600 4 206 6 500 5 5747 400 7 1858 3009 164 9 250 10 363 10 200 11 784 11 150 13 608 12 100 16 180 13 70 18 442 14 50 20 576 153023 84916 20 26 481 171031 055对于位温θ是按下述熟知的公式计算的κθ⎪⎪⎭⎫ ⎝⎛p p T 00=, (4)其中p c R d =κ,00p 为参考面气压,一般取为00p =1000 hPa.相当位温e θ是根据下述关系式得到的⎪⎪⎭⎫⎝⎛=T c Lq pe sexp θθ,(5)其中L 是相变潜热,s q 是饱和比湿,满足p e q ss 622.0=, (6)这里s e 是饱和水汽压。
利用关于饱和水汽压随温度变化关系的Clapeyron-Clausius 方程可得⎪⎪⎭⎫⎝⎛-=T T R L e e 16.273622.0exp d s0s ,TT e )16.273(6.8s010-⋅=, (7)式中11.6s0=e hPa 是温度为0︒C (即T =273.16 K )时的饱和水汽压。
但由于上式算出的结果与实际情况不完全符合,所以在实际计算中一般采用Magnus 的如下经验公式⎪⎩⎪⎨⎧⋅⋅=++.,10,102655.9s02375.7s0s 对于冰面对于水面;t tt te e e(8)其中t =-T 273.16是摄氏温度。
一般地说,大气环流是处于斜压状态的。
根据绝对加速度的环流定理知,大气的斜压性是产生环流加速度的动力因素。
因此,计算表征大气斜压性大小的物理量有重要意义。
这一物理量可以由斜压矢量N (又称力管矢量)来表示,即N = ) grad ( curl p α-=p grad grad ⨯-α.(9)用Hamilton 算子表示就是N = ) ( p ∇⨯∇-α =p ∇⨯∇-α.(10)斜压矢量N 的大小代表了单位面积内力管数的多少。
因为力管的存在是大气斜压性的充要条件,所以单位面积上的力管数(即斜压矢量N )给出了大气斜压性大小的度量。
简单的推导可得斜压矢量N 的三个分量如下:()y pz z p y N x ∂∂∂∂-∂∂∂∂-=αα, (11)()z p x x p z N y ∂∂∂∂-∂∂∂∂-=αα, (12)()xp y y p x N z ∂∂∂∂-∂∂∂∂-=αα. (13)在实际大气中,一般来讲,斜压矢量N 的垂直分量远小于它的水平分量,因此斜压矢量N 是准水平的。
这表明,只需要考虑N 的水平分量N h 即可,它代表了垂直剖面上的力管数,表征了垂直剖面上大气斜压性的大小。
不难知,N h -=k ()ααh h ∇∂∂-∇∂∂⨯z p p z . (15) 为了给出p 坐标系中N h 的表达,需要应用准静力学方程,即 0=+∂∂g z pα. (16)由此可得,()()z pg z p ∂∂∇=+∂∂∇=ααh h 0 ()p z p z z p h h h ∇∂∂+∇∂∂-∇∂∂=ααα.(17)所以,N h -=k ()p z h ∇∂∂⨯α. (18)此式表明,水平斜压矢量N h 是由水平气压梯度力的垂直微分决定的。
