鲁教版平面图形的旋转(第一课时)
鲁教版(五四制)八年级数学上册第四章第二节图形的旋转第一课时PPT课件

4.2图形的旋转
第1课时
想一想
➢上面情景中的转动现象,有 什么共同的特征? ➢钟表的指针、秋千在转动过 程中,其形状、大小、位置是 否发生变化呢?
引入新知
在平面内,将一个图形绕一个顶点沿 某个方向转动一个角度,这样的图形运动 称为旋转,这个定点称为旋转中心,转动 的角称为旋转角.
.
O
例题解析
本图案可以看做是一个菱形通过几次旋 转得到的?每次旋转了多少度?
旋转5次得到,旋 转角度分别等于 60°,120°, 18边三角形,D是BC边上的一点, △ABD经过旋转后到达△ACE的位置 .
(1)旋转中心是哪一点?
A
(2)旋转了多少度?
例题解析
: 解 (1)它的旋转中心是钟表的轴心;
(2)分针匀速旋转一周需要60分,因 此旋转20分,分针旋转的角度为:
360 20 120
120
60
做一做:
在图中,正方形ABCD与正方形 EFGH边长相等,这个图案可以看做 是哪个“基本图案”通过旋转得到的?
做一做:
可以看做是正方形ABCD绕点O旋转45°前后的图形共同 组成的;也可以看做是△ABC绕点O分别旋转45°,90° 135°,180°,225°前后所有图形共同组成的。也可以 看做是△AOB绕点O分别旋转45°,90°,135°,180° 225°,270°,315°前后所有图形共同组成的. .
(3)如果M是AB上
中点,那么经过上述
M
的旋转后,点M到了
E
什么位置?
BD
C
本课作业
课后习题
注意:“将一个图形绕着某个方向旋 转一个角度”意味着图形上的每个点都同 时都按相同的方向转动相同的角度,因此, 旋转具有如下特征:
鲁教版七下《平面图形的旋转》精品示范课(实录说课教案)_张老师

登陆21世纪教育助您教考全无忧8.3平面图形的旋转教案设计学校:濮阳高新区实验学校8.3平面图形的旋转一、教学目标:(1)知识与技能:①经历对生活中与旋转现象有关的图形进行观察、思考、分析、概括、抽象等过程,进一步发展学生的空间观念。
②探索、理解旋转前后两个图形对应点到旋转中心的距离相等、对应点与旋转中心的连线所成的角彼此相等、旋转前后的图形大小不变的性质.(2)过程与方法:在探索图形旋转的性质过程中,让学生自主探索,学会有条理地思考、分析、解决问题,培养学生推理意识和能力,发展学生的空间观念.(3)情感与态度:培养学生勇于发现,大胆探索,合作创新的精神;体会数学在生活中的作用,增强学习数学的兴趣,树立学好数学的信心.二、教学重点、难点:(1)教学重点:旋转的基本要素及其性质.(2)教学难点:图形旋转的基本性质.三、教法分析:本节课以“情景——操作——讨论”的教学模式进行,主要采用“探索发现”的教学方法,并以小组讨论法相结合,将直观操作和简单说理结合起来.增强学生学习数学的兴趣,引导学生动手实践、自主探索、大胆猜想、合作交流,发现图形旋转的性质.四、教学过程(一)、导入:师:生活中很多现象都与数学有关,只要大家做个有心人,你会发现数学无处不在,无时不在,首先请同学们随老师欣赏一组图片.(学生欣赏图片)(二)、揭示课题我们发现生活中旋转的物体很多,今天让我们走进图形的旋转世界,你会发现,奥妙无穷!(板书:8.3平面图形的旋转)(三)、合作学习:活动一:师:请同学们拿出老师发给大家的含30°的三角板,按要求进行操作。
在练习本上描出点o ,将三角板的直角顶点与点O 重合,放在纸上画出它的外轮廓,然后将三角板绕着O 点旋转一定角度,画出旋转后三角板的外轮廓.(老师请一位同学到前 面黑板上演示画图)师:请同桌两个同学将你们所画的三角形重叠在一起,将旋转前的两个三角形重合,观察旋转前后的两个三角形的组合图形,它们也重合吗?为什么? 师:根据刚才的操作,你认为图形的旋转与哪些因素有关?旋转中心、旋转方向、旋转角度有一个不同,都会影响到旋转后的图形的位置。
七年级数学下册 8.3《平面图形的旋转》课件 鲁教版

特征一 : 都是绕着一个定点旋转一定的角度。 特征二 : 在旋转的过程中,它们的形状大小没有发生变化,
变化的只是它们上面每个点的位置。
你还能说出生活中 类似的例子吗?
在平面内,将一个图形绕一个定点旋转一定的角 度,这样的图形运动称为图形的旋转,这个定点称 为旋转中心,旋转的角度称为旋转角。 为了进一步了解图形旋转前后的点、线段、角之 间的关系,我们一起用几何画板做两个实验。 操作一 操作二
A
分析:
O
B
2.在课本94页完成操作2。
请你利用旋转图形的性质完成下列问题:
A
M
M’
E
B
D
C
如图,三角形ABC是等边三角形,D是BC上一点, 三角形ABD经过旋转后到达三角形ACE的位置。 (1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是 AB上一点,那么经过旋转后,点 M转到了什么位置?请在图中将点M的对应 点M’表示出来。 解: (1)旋转中心是点A;
(2)逆时针旋转了0度;
(3)如图。
课堂小结:
(1)什么是图形的旋转? (2)旋转图形有哪些性质?
E F
结论:
1.旋转前、后的图形全等; 2.对应点到旋转中心的距离相等;
B
D
C
O A
3.每一对对应点与旋转中心的连线 所成的角彼此相等。
以上的三个结论就是图形旋转时所具备的性质, 利用这些性质,我们可以画出图形绕某个点旋转 以后的图形。
试 一 试
1.已知线段AB和点O,试画出线段AB绕O点 o 按逆时针方向旋转100 后的图形。
鲁教版八年级上册 4.1 图形的平移与旋转 (第一课时) 课件(共25张PPT)

×
C E
√ ×
×
D F
合作探究
2.如下图∠ ABC 是∠O经过平移而得的角, 若∠O=65°,则∠ABC等于多少度?
A 解: ∠ ABC 是∠O平移过 B O D C 程中的对应角, 所以
∠ ABC=∠O=65°
合作探究
3、平移的作图: 将线段AB平移,使点A与点D对应。
A
D
B
1、连结AD。 4、连结CD。
平移的方向
移动的距离
创设情境 引入新知
1、平移的概念:
一点说明
把一个图形整体沿某一直线方向移动一定的距离,
图形的这种移动叫做平移变换,简称平移。
图形的平移不一定是水平的,也不一定是竖直的。
如左图的鸟的
飞行也是平移
观察分析 理解新知
1、平移的概念:
(1)做一做: (1) 下面两个图形的变换是不是平移?
5.某宾馆在重新装修后,准备在大厅的楼梯上铺上某种红 色地毯,已知这种地毯每平方米售价 30 元,主楼梯道宽 2 米, 504 元. 其侧面如图 28-4 所示,则购买地毯至少需要 ________
图 28-4
(2.6 5.8) 2 30 16.8 30 504(元)
拓展训练
一个长方形竹园长20米,宽12米,竹园有一条横 向宽度都为1.5米的小径(如图).你能求出这个 竹园中竹子的种植面积吗(除去小径的面积)? 请说明理由.
20米 12米 1.5米
课堂小结
1.通过本节课的学习, 谈谈你的收获? 2.你还有那些困惑?
请说明理由。
(2)“小小竹排水中游,巍巍青山两岸走”, 所蕴涵的图形变换是__________变换?
鲁教版八年级数学上册4.2图形的旋转说课课件(共21张PPT)

(3)如果M是AB的中点,那么经过上述旋转后,点M旋转
到了什么位置?
(4)线段AD与AE有何数量关系? ∠DAE 为多少度?
(四)分层推进,掌握作图
(1)已知点A与点O,画出点A绕着点O旋转100°后的点 A’ (2)已知线段AB与点O,画出线段AB绕着点O按逆时 针方向旋转100°后的图形。 (3)画出△ABC绕点A顺时针旋转90°后的对应三角形。
B
BB' ′
A
A B/
C/
B
A/
旋转的性质:
O
C
旋转前、后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
A
E
如图,△ABC是等边三角形,
△ABD经过旋转后到达△ACE的位置. B
(1)旋转中心是哪一点?线段AB的
D
C
对应线段是哪一条?
(2)旋转了多少度?如何描述此旋转?
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
三、学生情况分析
认知分析:学生已学习了平移、轴对称这两种图形基本变换,
有了一定的变换思想。
能力分析:初三学生已经有一定的观察、抽象和分析能力,他
义务教育实验教材 鲁教版《数学》八年级上册
图形的旋转
教材分析
说
课
教法与学法
流
教学情分析
程
教学过程
教学设计说明
一、教材分析
1、教材地位作用的分析
《图形的旋转》是鲁教版初 中数学第4章的内容。是继平移、 轴对称之后的又一种图形变换, 是义务教育阶段数学课程标准中 图形变换的一个重要组成部 分.同时“图形的旋转”是一个 重要的基础知识,隐含着重要的 变换思想,它不仅为本章后续学 习中心对称及中心对称图形做好 准备,而且也为今后学习学习 “圆”的知识内容做好铺垫。
鲁教版八年级数学上册4-2《图形的旋转》课件

(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把BQC旋转
得到?
A
R
P
B
C
Q
练习2.如图,△ABC为等边三角形,D是 △ABC内一点,若将△ABD经过旋转后到 △ACP位置,则旋转中心是__________, 旋转角等于_________度,△ADP是 ___________三角形. A
注意:图形的旋转不改变图形的形状、大小,只改变图形的位置.
想一想
△ABC绕点C旋转,在这
个过程中,你有什么发现? A
C B
C
A
旋转的基本性质
◆旋转前、后的图形全等. ◆对应点到旋转中心的距离相等. ◆每一对对应点与旋转中心的 连线所成的角彼此相等. ◆图形的旋转是由旋转中心和 旋转的角度决定.
例题1.
动.
A.2
B.3
C.4 D.5
随堂练习2.
香港特别行政区区旗中央的紫 荆花图案由5个相同的花瓣组成, 它是由其中一瓣经过几次旋转得 到的?
随堂练习3.
如图,如果正方形CDEF 旋转后能与正方形ABCD重合,那 么图形所在的平面上可以作为旋转 中心的点共有______个.
A
D
E
B C
F
检测反馈
练习1. 如图:P是等边ABC内的一点,把 ABP按不同的方向通过旋转得到BQC和 ACR,
4.2 图形的旋转
第一课时 图形的旋转
知识探究 下面这些图形是怎么来的呢?
『数学』
想一想、议一议
图中的三角形
B
是如何变化的,
你能描述一个
这个旋转的过
程吗?
C
B
C A
图形旋转的概念
八年级数学上册第四章图形的旋转第1课时旋转的认识pptx课件鲁教版五四制

例2 如图所示,△ABC是直角三角形,延长AB到D,使BD =BC,在BC上取BE=AB,连接DE.△ABC旋转后能与 △EBD重合,那么:旋转中心是__点__B__;旋转的角度是 ___9_0_°___;AC的对应边是___E_D____;∠A的对应角是 _∠__B__E_D__;点C的对应点是___点__D___.
这个定点称为旋转中心,转动的角称为旋转角.
A
B
旋转角
o 旋转中心
例2 下列运动属于旋转的是( B ) A.篮球的滚动 B.钟摆的摆动 C.气球升空的运动 D.一个图形沿某条直线对折的过程 导引:按旋转的定义判断.
归纳
判断一种运动是否是旋转的 前提条件是图形在同一平 面内 的运动,其次要紧扣旋转的“三 要素”,看是否同时具有:旋转 中心、旋转角、旋转方向.
知识点 2 旋转的性质 旋转的基本性质: (1)旋转不改变图形的大小和形状. (2)图形上的每一点都绕旋转中心沿相同方向转动 了相同的角度. (3)任意一对对应点与旋转中心的连线所成的角度 都是旋角. (4)对应点到旋转中心的距离相等.
特别提醒
旋转的性质的作用 1.可以用来判断线段或角是否相等. 2. 可以用来计算图形的面积、线段的长度或
导引:△DEC按顺时针方向旋转得到△DGA,点D的位置 未改变,即旋转中心是点D,△DEC与△DGA 能够 完全重合,进而找出对应线段与对应角.
解:根据图形旋转的性质可以得到: (1) △DEC是绕点D顺时针旋转90°后到达△DGA位置 的,所以点D为旋转中心,旋转角度是90°. (2) DE与DG,DC与DA,EC与GA是对应线段,∠CDE 与∠ADG,∠C与∠DAG,∠DEC与∠G是对应角. (3)有.相等线段有:DG=DE(答案不唯一); 相等角有:∠G=∠DEC(答案不唯一); 能够完全重合的两个三角形是△DEC与△DGA.
第四章《图形的旋转》 专题课件-2021-2022学年鲁教版(五四制)八年级数学上册

三、等腰直角三角形类型:
在等腰直角三角形△ABC中,∠C=90°, P为△ABC内一点,将△APC绕C点按逆时针 方向旋转90°,使得AC与BC重合。
经过这样旋转变化,在图(3-1-b)中, △P' CP为等腰直角三角形。
由旋转性质,可证A、F、D、E共线;
则OA+OB+OC= AE 勾股定理求得AB=2=2AC,得∠ABC=30°,得∠ABE=90°, 勾股定理求得AE,得解。
A
3.在边长为2的正方形ABCD内求一点P,使得PA+PB+PC
之和为最小,并求这个最小值.
【解析】将△BPC绕B点顺时针旋转60°,得△BEF,可
可得此时∠APB=∠CPB=∠APC=120°
P点即为“费马点”
2.已知Rt△ABC中,∠C=90°,AC=1,BC= 3,O为△ABC
A
内一点,且∠AOB=∠BOC=∠COA=120°,则
OA+OB+OC=
.
O
C
B
【解析】将△BOC绕B点逆时针旋转60°,得△BDE; 可得△BOD为等边三角形;
ABCD面积为
.
【解析】(方法一) 将△APB绕B点顺时针旋转90°得△CBM,连接PM,过C点作 CN⊥BM,交BM延长线于N点.
易得△PBM为等腰直角三角形,求得PM= 2 2
由PC2=PM2+CM2,得PM⊥CM,可得△CMN为等腰直角三角形, 求得CN,MN 由勾股定理可求BC,进而求得正方形面积。
A
D
P
B
C
鲁教版八年级4.2图形的旋转

4.2图形的旋转知识点1.在平面内,将一个图形绕一个定点按某个方向转动一个角度,图形的这种变化称为旋转,这个定点称为旋转中心,转动的角称为旋转角.旋转不改变图形的形状和大小.旋转三要素:旋转中心、旋转方向、旋转角。
注意:(1)旋转不是在空间中,而是在平面内,它不改变图形的形状个大小。
(2)旋转中心是点不是直线。
(3)旋转角值角,旋转角度指旋转角的度数,二者有区别。
例1.如图,可以看到点A旋转到点A’,∠AOB旋转到∠A’OB’,点B的对应点是;线段OB的对应线段是;线段AB的对应线段是;∠A的对应角是;∠B的对应角是;旋转中心是;旋转角是;2.旋转的性质:(1)对应线段相等,对应角相等;(2)对应点到旋转中心的距离相等;(3)任意一组对应点与旋转中心的连线所成的角都等于旋转角.例2.如图,在∆ABC中,AB=BC,将∆ABC绕点B顺时针旋转α度,得到∆A1BC1,A1B交AC 于点E,A1C1分别交AC,BC于点D,F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④A1D=CE,⑤A1F=CE.其中正确的是(写出正确结论的序号).3.旋转作图例3.如图,已知线段AB和线段AB所在直线外的一点O,画出线段AB绕点O按逆时针方向旋转450后的线段解:(1)连接OA,OB;(2)以OA为一边,在OA边的下方画∠AOC=450,并在OC上截取OM=OA;(3)以OB为一边在OB边的左侧画∠BOD=450,并在OD上截取ON=OB;(4)连接MN.线段MN就是线段AB绕点O按逆时针方向旋转450后的线段。
旋转作图步骤(1)确定旋转三要素:旋转中心、旋转方向、旋转角;(2)找到图形中的关键点;(3)连接图形的关键点与旋转中心,并按旋转的方向分别将它们旋转一个角,得到此关键点的对应点;(4)顺次连接所作的各个关键点的对应点,并标上相应的字母;(5)写出结论.例4.如图,∆ABC绕点C旋转后,顶点A的对应点为点D.试画出顶点B的对应点,以及旋转后的三角形.分析:因为点C为旋转中心,点A与点D是对应点,所以∠ACD是旋转角.假设顶点B的对应点为点E,则∠BCE=∠ACD,且CE=CB.解:(1)连接CD;(2)以CB为一边作∠BCF,使得∠BCF=∠ACD;(3)在射线CF上截取CE=CB;(4)连接DE.∆DEC就是∆ABC绕点C旋转后的三角形.练一练:1.如图,画出∆ABC绕点C逆时针旋转900后的图形.2.如图,四边形ABCD绕点O旋转后,顶点A的对应点为E,试确定B,C,D的对应点的位置以及旋转后的四边形。
鲁教版数学八年级上4.2《图形的旋转》ppt课件2
B
C
【解析】作法二 (1)以点C为圆心、CB长为半径画弧 , (2)以点D为圆心、AB长为半径画弧 , A (3)两弧的交点E 即为点B的 对应点. (4)连接 CE 、ED、DC. B C E
D
则△DEC就是△ABC绕C点旋转后的图形.
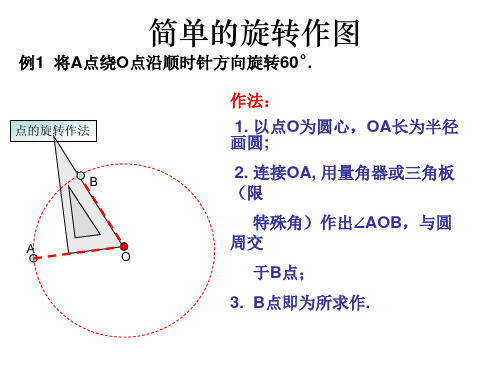
简单的旋转作图
例1 将A点绕O点沿顺时针方向旋转60˚. 作法:
点的旋转作法
1. 以点O为圆心,OA长为半径 画圆; 2. 连接OA, 用量角器或三角板 (限 特殊角)作出∠AOB,与圆 周交
O
B
A
于B点;
3. B点即为所求作.
简单的旋转作图
例2 将线段AB绕O点沿顺时针方向旋转60˚.
线段的旋转作法
作法:
C
1. 将点A绕点O顺时针 旋转60˚,得 点C;
2. 将点B绕点O顺时针 旋转60 ˚,得点D ; 3. 连接CD, 则线段CD即 为所求作.
B
A D
O
【例4】如图,△ABC绕C点旋转后,顶点A的对应点 为点D.试确定顶点B的对应位置,以及旋转后的三 角形. 分析: E D
1.明确旋转中心、旋转的方向 与大小;
2.假设顶点B的对应点为E, 则∠BCE 、∠ACD 都是旋 转角,且∠BCE =∠ACD 、
A
B
C
CE=CB 、CD=CA.
【解析】作法一(1)连接CD; (2)以CB 为一边作∠BCF,使 得∠BCF=∠ACD; F E D A
(3)在射线CF上截取CE=CB;
(4)连接DE . 则△DEC就是△ABC绕C点旋转后 的图形.
83平面图形的旋转个(课件)

A
B′
B
C
本环节的意图:
以上两个实践活动通过分组合作、讨 论交流、动手操作、问题探究等活动,让 学生更加直观的理解了图形旋转的概念, 并探究得出旋转角的确定方法,突破了本 节课的难点,提高了学生的合作意识和动 手操作能力,同时也为证明三角形全等奠 定了基础。
(四)变换图形运用新知
例1.如图所示,△ABC是等边三角形,D是BC
5、∠AOD与∠BOE有什么大小关系?
∠AOD=∠BOE
1、旋转中心; 2、对应点; 3、旋转角; 4、对应线段; 5、对应角。
旋转角就是对应点与旋转中心连线的夹角。
旋转的基本性质
1、旋转不改变图形的形状和大小,即旋转 前后的两个图形全等; 2、图形上的每一点都绕旋转中心沿相同方 向转动了相同的角度; 3、任意一对对应点与旋转中心的连线所成 的角度都是旋转角;
你能举出生活中旋转的例子吗?
(二)观察思考归纳概念
本环节的设计思路: 单摆运动 思考交流 归纳概念
具体设计: 观察单摆运动过程,并完成问题。
1.单摆上的小球是绕着哪一个点、按什么方向、
. 转动多大的角度由位置P转到位置P′的? O
.
P
. P′
1.单摆上的小球是绕着哪一个点、按什么方向、 转动多大的角度由位置P转到位置P′的?
4、对应点到旋转中心的距离相等。
活动二:小组交流、合作探究
如图所示,旋转中心在△ABC的外面任意一点O 处,将整个△ABC逆时针旋转60°后,会得到一个怎 样的三角形呢?(学生动手操作、展示)
O
A
B
C
C′
A′
O
A
B
C
请你找出旋转前后这两个三角形对应的顶点、
鲁教版七下数学《平面图形的旋转》精品示范课(实录说课教案)

濮阳市信息技术优质课大赛《平面图形的旋转》(鲁教版七年级下第八章第三节)参评单位:濮阳市第七中学参评教师:王继广参评时间: 2013年5月一、教学目标:知识与技能目标通过具体实例认识旋转,理解旋转的基本性质.过程与方法目标在认识和理解旋转的过程中,学会观察生活中的现象,掌握探究问题的基本方法,并能解决生活中的基本问题.情感态度价值观目标通过学生亲身体验数学活动,感受数学与生活的关系,进一步培养学生的合作意识及审美情趣.二、教学重难点:教学重点了解旋转的意义,理解旋转的性质.教学难点如何探究旋转的性质.三、教学准备:多媒体课件、投影、学生自制模型等四、教学过程安排:(一)观看现象,引入新知首先请同学们观看一段生活旋转现象,导入新课.(展示生活中旋转的图片,让学生观察,并提出问题:“你知道它们在做什么运动吗?”学生异口同声地回答:“旋转”。
从而引入课题——8.3 平面图形的旋转。
)(二)分析现象,归纳概念1. 观察:继续让学生观察刚才的两幅图片,并提出问题:“这些生活中的旋转现象,有什么共同特征?你能用你自己的语言来说说什么是旋转吗?”(请几名学生回答)(根据学生所说,具体展示生活中轮盘、拧螺丝帽、指针、叶片转动现象,学生通过观看动画演示,发现它们有什么共同特征?通过学生分析、描述、总结、类比图形平移的概念,归纳出图形旋转的概念在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转. 这个定点称为旋转中心.转动的角称为旋转角.(首先教师引导学生将钟表指针抽象成数学图形中的线段,指针旋转现象就可以看作成线段绕其中的一个端点旋转,由此抽象出数学模型,然后利用此图形让学生认识对应点、旋转角及对应点到旋转中心的距离相等的性质,使学生对于旋转的性质有了初步的理解。
)教师追问指针、叶片在转动过程中,其形状、大小、位置是否发生改变?学生交流感知并形成共识:旋转不改变图形的大小和形状.2.归纳:和学生一起得出旋转的概念,并强调旋转的“三要素”—' AA O—旋转中心、旋转方向、旋转角(教师板书)。
鲁教版八年级数学上册《图形的旋转》课件 ppt

B H
C
G
●
O
E
D
图4-26
例4 画一个腰长等于3的等腰直角三角形ABC,取一个
锐角为45°的三角尺,把三角尺的直角顶点放在
Rt△ABC的斜边BC的中点O处,并使三角尺的一条直角
边经过点A,另一条直角边经过点B(图4-27(1)).将三角
尺绕点O按顺时针方向旋转一个角度,记三角尺的两腰
AB,AC的交点分别为E,F(图4-27(2)).在三角尺按图
解:(1)旋转中心是点O,旋转角是∠AOD.
(2)点A,C,B分别旋转到点D,F, E.
(3) AO=DO,BO=EO,AC=DF,CB=FE.
(4)∠AOD=∠BOE, ∠A=∠D ,∠C=∠F , ∠B=∠E ,∠AOB=∠DOE.
随堂练习1
下列现象中属于旋转的有( D)个 ①地下水位逐年下降;②传送带的移 动;③方向盘的转动;④水龙头开关 的转动;⑤钟摆的运动;⑥荡秋千运 动. A.2 B.3 C.4 D.5
.
动手作图
1.点的旋转
试着找一找如图A点绕O点
顺时针旋转30°后所在的位
置A′.
2.线段的旋转
试着画一画线段AB绕O点
A
O
A' B′
逆时针旋转90°后所得的线 段(O点在线段外).
B
O
A
A′
C′
3.图形的旋转
C B′
试着画△ABC绕O点逆时针旋转 A
60°后所得的三角形.
O
例2 如图4-21,已知线段AB和线段AB所在直线外 的一点O,画出线段AB绕点O按逆时针方向旋转45° 后的线段.
4-27所示的方式绕点O旋转的过程中,线段AE与CF的长
鲁教版(五四制)八年级数学上册第四章图形的平移与旋转回顾与思考第一课时PPT课件

7.下列说法正确的是( B ) A.旋转改变图形的形状和大小 B.平移改变图形的位置 C.图形可以向某方向旋转一定距离 D.由平移得到的图形也一定可由旋转得到
8.如图,四边形EFGH是由四边形ABCD平 移得到的,已知AD=5,∠B=700,则( B)
A.FG=5,∠G=700 B.EH=5,∠F=700 C.EF=5,∠F=700 D.EF=5,∠E=700
(A) (B)
(C)
(D)
4.经过平移,△ABC的边AB移到了EF,作出 平移后的三角形。
A
E
B
F
C
5.在右图中作出“三角旗”绕O点按逆时 针旋转90°后的图案。
O
6.已知四边形ABCD和点O,画四边形 A'B'C'D'使它与已知四边形关于点O对称。
画法:
A'
B'
O C'
D'
D C
B A
四边形A'B'C'D'就是所求的四边形。
A
D
B E
G C
F
16.如图:在梯形ABCD中,AD∥BC, ∠B+∠C=90o,点E在AD上,先将AB 向右平移,使点A与点E重合,交BC于 F,再将DC向左平移,使点D与点E重 合,交BC于G,请判断ΔEFG的形状
C.ΔABD和ΔACE D.ΔACE和ΔADE
A E
D
B
C
13.在正方形ABCD中,E为DC边上的点,连 结BE,将△BCE绕点C顺时针方向旋转900得 到 △ DCF , 连 结 EF , 若 ∠ BEC=600 , 则 ∠EFD的度数为( B ) A.100 B.150 C.200 D.250
鲁教版数学七下8.3《平面图形的旋转》word教案

8.3平面图形的旋转教学目标1. 通过网上教学和学生网上冲浪,让学生自主地学习,培养他们利用网络获取知识的能力和分析问题、解决问题的能力。
2.经历对生活中的旋转现象有关图形进行观察、分析、欣赏等过程培养学生初步的审美能力,增强对图形欣赏的意识,培养创新能力。
3.通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心的距离相等、对应点与旋转中心的连线所成的角彼此相等的性质4.培养学生合作学习,探索学习的意识,追求成功的精神,增强学生自我价值感。
教学重点、难点重点:对生活中的旋转现象作数学上的分析研究,旋转定义,旋转的性质。
难点:对旋转现象的分析研究,旋转的性质的探索。
教具准备投影仪、电脑、时钟、小风车教学过程(一)网上冲浪——寻找生活中的旋转现象我们生活在一个充满旋转的世界里,旋转这种现象司空见惯,作用非凡,而其中包含着丰富的数学知识,你能举出生活中的实例吗?学生利用老师自制的《生活中的旋转》网站,及提供的一些相关网站和百度、google 搜索引擎,在网上搜索生活中旋转实例,在学生充分收集、观察、分析、欣赏的基础上,提出下列问题:1.在大家搜索到的旋转实例中,哪些部位作旋转?它们有什么共同特征?2.旋转的部位,其形状、大小、位置是否发生改变?学生交流、感知并形成共识,教师给出旋转定义平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
旋转不改变图形的大小和形状。
(二)小组活动——探索旋转的基本规律教师引导学生对旋转现象进行数学上的分析。
1.学生利用教学课件演示,观察思考,交流讨论。
2.然后教师提出以下问题:ABCDEF(1)旋转过程中旋转中心是什么?旋转角是什么?(2)经过旋转,点A、B、C分别移动到什么位置?(3)AO与DO的长有什么关系?BO与EO,OC与OF呢?(4)∠AOD、∠BOE、∠COF有什么大小关系?学生交流总结得出旋转性质:经过旋转,图形上的每一点都绕着旋转中心沿着相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本图案可以看做是一个菱形通过几次旋转得到 的?每次旋转了多少度? 每次旋转了多少度?
还可以看做是几个菱形通 还可以看做是几个菱形通 过几次旋转得到的? 过几次旋转得到的?每次 旋转了多少度? 旋转了多少度? 3个 个 1次 1800 次
本图案可以看做是一个菱形通过几次旋转得到 的?每次旋转了多少度? 每次看做是△ 绕点O分别旋转 也可以看做是△AOB绕点 分别旋转 °,90°, 绕点 分别旋转45° ° 135°,180°,225°270°,315°前后所有图形 ° ° ° ° ° 共同组成的. 共同组成的
.
O
做一做:
也可以看做是△ 绕点O分别旋转 也可以看做是△ABC绕点 分别旋转 °,90°, 绕点 分别旋转45° ° 135°,180°,225°前后所有图形共同组成的。 ° ° °前后所有图形共同组成的。
还可以看做是几个菱形通 还可以看做是几个菱形通 过几次旋转得到的? 过几次旋转得到的?每次 旋转了多少度? 旋转了多少度?
3个 个
1次 1800 次
2、如图E是正方形 如图E ABCD内一点 内一点, ABCD内一点,将 ABE绕点 绕点B △ABE绕点B顺时针 方向旋转到△ 方向旋转到△CBF, 其中EB=3cm, EB=3cm,则 其中EB=3cm,则 BF=_____cm , EBF=_____° ∠EBF=_____°
例1:钟表的分针匀速旋转一周需要60分. 钟表的分针匀速旋转一周需要60分 钟表的分针匀速旋转一周需要60 (1)指出它的旋转中心; 指出它的旋转中心; 20分 分针旋转了多少度? (2)经过20分,分针旋转了多少度? 经过20
解:(1)它的旋转中心是钟表的轴心; ( 它的旋转中心是钟表的轴心; 轴心 (2)分针匀速旋转一周需要60分,因此旋转 分针匀速旋转一周需要60分 60 20分 20分,分针旋转的角度为 360° × 20 = 120° 60
A
3、图形上的点A经过 图形上的点A 旋转变为B 旋转变为B,那么这 两点叫做这个旋转的 对应点。 对应点。
B
旋转角
o
旋转中心
旋转三要素: 旋转三要素: 图形的旋转由旋转中心和 图形的旋转由旋转中心和旋转 旋转中心 方向及旋转的角度所决定 所决定。 方向及旋转的角度所决定。
随堂练习1 随堂练习1 下列现象中属于旋转的有( )个 下列现象中属于旋转的有( C )个 ①地下水位逐年下降;②传送带的移 地下水位逐年下降; 动;③方向盘的转动;④水龙头开关 方向盘的转动; 的转动; 钟摆的运动; 的转动;⑤钟摆的运动;⑥荡秋千运 动. A.2 B.3 C.4 D.5
沙河中学初二数学组
图形的旋转
1、在平面内,将一个图形绕一个定点沿某个方 、在平面内,将一个图形绕一个定点沿某个方 定点沿某个
旋转。 向转动一个角度,这样的图形运动称为旋转。 转动一个角度,这样的图形运动称为旋转 角度 旋转不改变图形的形状和大小 不改变图形的形状和大小。 旋转不改变图形的形状和大小。 2、这个定点称为旋转中心, 这个定点称为旋转中心, 旋转中心 转动的角称为旋转角 旋转角。 转动的角称为旋转角。
如图∠C=30° ABC绕 3、如图∠C=30°,△ABC绕A点逆时 针旋转30 后得到△AB’C , 30° 针旋转30°后得到△AB C’,则图中 度数是30 的角还有__________ 30° 度数是30°的角还有__________
A
2
B
4
3
5
1
C'
C
B'
4、如图将 ABC绕 △ABC绕C点逆 时针旋转30 30° 时针旋转30° 后,点B落在 B′, 落在A B′,点A落在A’ 点位置, 点位置,若 C⊥AB, A’C⊥AB,求 C⊥AB ∠B’A’C的度数。 A C的度数。
议一议 如图,如果把钟表的指针看做四边形 如图,如果把钟表的指针看做四边形AOBC,它绕 点 ,它绕O点 旋转得到四边形DOEF. 在这个旋转过程中: 在这个旋转过程中: 旋转得到四边形 (1)旋转中心是什么 )旋转中心是什么? 旋转中心是点O 旋转中心是点
分别移动到什么位置? 和点E的位置 (2)经过旋转,点A、B分别移动到什么位置? D和点 的位置 )经过旋转, 、 分别移动到什么位置 点 和点 (3)旋转角是什么? ∠AOD和∠BOE都是旋转角 )旋转角是什么? ∠AOD和 BOE都是旋转角 (4)AO与DO的长有什么关系?BO与EO呢? ) 与 的长有什么关系? 与 呢 的长有什么关系 AO=DO,BO=EO , (5)∠AOD与∠BOE有什么大小关系? ) AOD与 BOE有什么大小关系? 有什么大小关系 ∠AOD=∠BOE
B'
B A'
E
C
A
※复习与回顾※
1、分析图中的旋转现象
(第1题) (第2题)
第2题 2、图中是否存在这样的两个三角形,其中一个是另一个通过 旋转得到的?
例题解析
本图案可以看做是一个菱形通过几次旋 转得到的?每次旋转了多少度?
旋转5次得到,旋 旋转 次得到, 次得到 转角度分别等于 60°120°180° ° ° ° 240°300° ° °
本图案可以看做是一个菱形通过几次旋转得到 的?每次旋转了多少度? 每次旋转了多少度?
也可以看做是二个相邻菱 也可以看做是二个相邻菱 形通过几次旋转得到的? 形通过几次旋转得到的? 每次旋转了多少度? 每次旋转了多少度? 2次 1200 , 2400 次
旋转的基本性质
(1)旋转不改变图形的大小和形状. 旋转不改变图形的大小和形状. (2)图形上的每一点都绕旋转中心沿 相同方向转动了相同的角度 (3)任意一对对应点与旋转中心的连 线所成的角都是旋转角,旋转角都相等. 线所成的角都是旋转角,旋转角都相等 (4)对应点到旋转中心的距离相等. 对应点到旋转中心的距离相等.
在图中,正方形ABCD与正方形EFGH边长 在图中,正方形ABCD与正方形EFGH边长 ABCD与正方形EFGH 相等,这个图案可以看作是哪个“基本 相等,这个图案可以看作是哪个“ 图案”通过旋转得到的. 图案”通过旋转得到的.
做一做:
可以看做是正方形ABCD绕点 旋转 °前 绕点O旋转 可以看做是正方形 绕点 旋转45° 后的图形共同组成的; 后的图形共同组成的;
平移和旋转的异同: 平移和旋转的异同: 1、相同:都是一种运动;运动前后 、相同:都是一种运动; 不改变图形的形状和大小 2、不同 、 运动方向 平移 旋转 直线 运动量的衡量 移动一定距离
顺时针或逆时针 转动一定的角 度
做一做: 做一做: 在图中,正方形ABCD与正方形 EFGH边长相等 , 这个图案可以看作 边长相等, 边长相等 是哪个“基本图案”通过旋转得到的? 是哪个“基本图案”通过旋转得到的
A E
D
B F
C
练习、
如图正方形CDEF CDEF旋转后能与正方形 1、如图正方形CDEF旋转后能与正方形 ABCD重合 重合, CD的中点那么图形上 ABCD重合,若O是CD的中点那么图形上 可以作为旋转中心的点是_________ 可以作为旋转中心的点是_________
A D O B C F E
.
.
O
思考题:香港区徽可以看作是什么“基本图案” 思考题:香港区徽可以看作是什么“基本图案” 通过怎样的旋转而得到的? 通过怎样的旋转而得到的?
可以看作是一个花瓣连续 次 可以看作是一个花瓣连续4次旋转所形 连续 成的,每次旋转分别等于72 成的,每次旋转分别等于 0 , 1440 , 2160 , 2880
