空间直角坐标系向量的坐标表示
空间向量的正交分解及其坐标表示(上课用)

注意: 1.空间向量的基底可以为零向量吗?
基向量不能为零向量
2.空间向量的基底唯一吗?
任意三个不共面的向量都可作为空间向量的一个基底。
三、平面向量的坐标表示
y
正交单a位 xi +y j
基底
yj
a 我们把(x,y)叫做向量 a 的
j
(直角)坐标,记作
O
x
i xi
a (x, y)
其中,x叫做 a 在x轴上的坐标, y叫做 a在y轴上的坐标, (x,y)叫做向量的坐标表示.
记作.P=(x,y,z)
e3
e1
O e2
y
x
三、空间向量的正交分解及其坐标表示
由空间向量基本定理,对
z
于空间任一向量 p 存在唯
一的 有序实数组 (x,y, z)使 p xi yj zk
记作 p =(x,y,z)
PP k
i Oj
y
空间向量 p
i, j, k 为基底
P′
一一对应
x 有序实数组 (x, y, z)
1 2 OA MN
23
O M
1
OA
2
ON
OM
2 3
A
Q
P
C
1
OA
2
ON
1
OA
2 3 2
1
OA
2
1
OB
OC
6 3 2
N B
1
OA
1
OB
1
OC
633
例题:
已知空间四边形OABC,其对角线为OB,AC,M,N,分
别是对边OA,BC的中点,点P,Q是线段MN三等分点,用基向
量OA,OB,OC表示向量OP,OQ.
空间向量的坐标表示与计算

空间向量的坐标表示与计算空间向量是三维空间中的一个重要概念,可以用来表示空间中的一个点或者空间中的两个点之间的位移向量。
为了方便计算和表示,我们可以使用坐标表示来描述和计算空间向量。
一、空间向量的坐标表示在三维坐标系中,可以使用三个坐标轴(通常是x轴、y轴、z轴)来表示一个空间向量的坐标。
这三个坐标轴是相互垂直的,构成一个直角坐标系。
对于一个空间向量v,可以使用v的起点在坐标原点的坐标表示来表示该向量。
假设v的坐标表示为(x, y, z),其中x、y、z分别表示v在x轴、y轴、z轴上的坐标值。
例如,对于一个空间向量v,如果它的起点在坐标原点,终点的坐标分别为(3, 4, 5),那么可以表示为v = (3, 4, 5)。
二、空间向量的计算1. 向量的加法空间向量的加法是指将两个向量相加得到一个新的向量。
假设有两个向量a和b,它们的坐标表示分别为(a1, a2, a3)和(b1, b2, b3)。
那么它们的和向量c的坐标表示为(c1, c2, c3),其中c1 = a1 + b1,c2 = a2 + b2,c3 = a3 + b3。
+ b的坐标表示为(c1, c2, c3) = (1 + 4, 2 + 5, 3 + 6) = (5, 7, 9)。
2. 向量的减法空间向量的减法是指将一个向量减去另一个向量得到一个新的向量。
假设有两个向量a和b,它们的坐标表示分别为(a1, a2, a3)和(b1, b2, b3)。
那么它们的差向量c的坐标表示为(c1, c2, c3),其中c1 = a1 - b1,c2 =a2 - b2,c3 = a3 - b3。
例如,对于向量a = (1, 2, 3)和向量b = (4, 5, 6),它们的差向量c = a - b的坐标表示为(c1, c2, c3) = (1 - 4, 2 - 5, 3 - 6) = (-3, -3, -3)。
3. 向量的数量积空间向量的数量积是指将两个向量相乘得到一个标量(即一个数)。
空间向量的坐标表示与数量积

空间向量的坐标表示与数量积空间向量是指具有大小和方向的量,可以用坐标表示。
在三维空间中,一个向量可以由其在坐标系中的坐标表示。
坐标表示的形式可以是直角坐标、柱坐标或球坐标等,而本文将主要讨论向量的直角坐标表示以及与数量积的关系。
一、直角坐标表示直角坐标系是三维空间中最常用的坐标系。
一个向量在直角坐标系中的坐标表示为(x, y, z),其中x、y、z分别表示向量在X轴、Y轴和Z轴上的投影长度。
向量的坐标表示使我们能够方便地进行向量运算,比如向量的加减、数量积等。
下面以一个具体的向量为例进行说明。
假设有向量A,它的起始点在原点O(0, 0, 0),终点在点P(x, y, z)。
根据直角坐标系的定义,我们可以得到向量A的坐标表示为A(x, y, z)。
这表示向量A在X轴上的投影长度为x,在Y轴上的投影长度为y,在Z轴上的投影长度为z。
二、数量积的计算数量积是一种向量运算,它可以衡量两个向量之间的相似程度。
数量积的计算公式为:A·B = |A||B|cosθ其中,A·B表示向量A和向量B的数量积,|A|和|B|分别表示向量A和向量B的长度,θ表示向量A与向量B之间的夹角。
具体地,我们可以通过向量的坐标来计算数量积。
设向量A的坐标表示为A(x1, y1, z1),向量B的坐标表示为B(x2,y2, z2)。
根据数量积的计算公式,我们可以得到:A·B = x1x2 + y1y2 + z1z2三、应用举例假设有向量A(1, 2, 3)和向量B(4, 5, 6),我们可以通过坐标表示计算它们的数量积。
首先,根据数量积的计算公式,我们可以得到:A·B = (1)(4) + (2)(5) + (3)(6)= 4 + 10 + 18= 32因此,向量A和向量B的数量积为32。
数量积的计算结果可以告诉我们这两个向量之间的相似程度。
如果数量积为正数,表示两个向量之间的夹角为锐角;如果数量积为负数,表示两个向量之间的夹角为钝角;如果数量积为零,表示两个向量垂直。
3.1.4 空间向量的坐标表示

与x轴、y轴、z轴方向相同的单位向量 i, rj, k
作为基向量,对于空间任意一个向量 a ,
根据空间向量基本定理,存在惟一的有序实数组
rrr r
(x,y,z ),使 a= xi+ yj+ zk. r 有序实数组(x,y,z )叫做向量 r a 在空间直角
坐标系O-xyz中的坐标,记 作 : a = (x , y , z) u u u r u u u r
对于空间任意一点A(x,y,z ),向 量 O A 坐 标 为 O A = ( x , y , z ) .
3.空间向量的坐标运算法则.
r
r
(1r )若ra = ( a 1 , a 2 , a 3 ) , b = ( b 1 , b 2 , b 3 ) ,
则 a + b = ( a 1 + b 1 , a 2 + b 2 , a 3 + b 3 ) ,
rr 解: a+b=(4, 7, 4) ,
rr a-b=(-2, -13, 12) ,
r 3a=(3, -9, 24)
例2 已知空间四点A(-2,3,1),B(2,-5,3),C(10,0, 10)和D(8,4,9),求证:四边形ABCD是梯形.
uuur uuur uuur
解: AB=OB- OA=(4, -8, 2) ,
rr a - b = ( a 1 - b 1 , a 2 - b 2 , a 3 - b 3 ) ,
r a = (a 1 , a 2 , a 3 ) (∈ R ) ,
r r
a b a 1 = b 1 , a 2 = b 2 , a 3 = b 3 ( ∈ R ) ,
数学应用
已知 a r = ( 1 , - 3 , 8 ) , b r = ( 3 , 1 0 , - 4 ) , 求 a r+ b r, a r+ b r, 3 a r.
空间向量的坐标表示与几何应用

空间向量的坐标表示与几何应用在三维空间中,空间向量是研究物体运动和位置的重要工具。
为了准确地描述和计算空间向量,我们需要用坐标来表示它们。
本文将详细介绍空间向量的坐标表示方法,并探讨其在几何应用中的重要性。
一、坐标表示方法1. 直角坐标系直角坐标系是最常用的表示空间向量的方法。
在直角坐标系中,我们以三个相互垂直的坐标轴为基准,分别表示x、y、z三个方向。
一个空间向量可以通过三个坐标值(x,y,z)来表示,分别表示它在x轴、y 轴和z轴上的投影长度。
例如,对于一个空间向量v,在直角坐标系中,我们可以表示为v=(x,y,z)。
2. 球坐标系球坐标系是另一种表示空间向量的方法,它是通过一个原点、一个偏离原点的距离、一个与z轴的夹角和一个与x轴的投影角来确定一个空间向量的位置。
在球坐标系中,一个空间向量的坐标通常表示为(r,θ,φ),其中r表示向量到原点的距离,θ表示向量与z轴的夹角,φ表示向量在x-y平面上的投影与x轴的夹角。
二、坐标表示的几何应用1. 向量的加法与减法通过坐标表示,我们可以方便地对空间向量进行加法与减法运算。
只需将对应坐标相加或相减即可得到结果。
例如,对于向量v=(x1,y1,z1)和向量w=(x2,y2,z2),它们的和可以表示为v+w=(x1+x2,y1+y2,z1+z2)。
2. 向量的数量积与夹角坐标表示还可以用于计算向量的数量积和夹角。
向量的数量积可以通过坐标之间的乘积运算得到。
例如,对于向量v=(x1,y1,z1)和向量w=(x2,y2,z2),它们的数量积可以表示为v·w=x1x2+y1y2+z1z2。
夹角可以通过向量的数量积公式求解:cosθ = (v·w) / (|v| |w|)其中,|v|和|w|分别表示向量v和w的模长。
3. 点与直线的相对位置通过点和直线的坐标表示,我们可以判断一个点与直线的相对位置关系。
以直线的方程和点的坐标为基础,我们可以计算点到直线的距离,从而判断点在直线上方、下方还是与直线相交。
空间向量的坐标和运算

空间向量的坐标和运算一、空间向量的坐标和运算1.空间直角坐标系在单位正方体$oabc$-$d$′$a$′$b$′$c$′中,以$o$点为原点,分别以射线$oa$,$oc$,$od$′的方向为正方向,以线段$oa$,$oc$,$od$′的长为单位长,建立三条数轴:$x$轴、$y$轴、$z$轴。
这时我们说建立了一个空间直角坐标系$oxyz$,其中点$o$叫做坐标原点,$x$轴、$y$轴、$z$轴叫做坐标轴。
通过每两个坐标轴的平面叫做坐标平面,分别称为$xoy$平面、$yoz$平面、$xoz$平面。
2.空间矢量的坐标一个向量在空间直角坐标系中的坐标等于表示向量的有向线段的终点坐标减去起点坐标。
如果$a(x_1,y_1,z_1)$,$B(x_2,y_2,z_2)$,那么$\overrightarrow{AB}=\overrightarrow{ob}-\overrightarrow{OA}$=$(x_2-x_1$,$y_2-y_1$,$z_2-z_1)$。
3、空间向量的坐标运算设置$\boldsymbol(x_1,y_1,z_1)$,$\boldsymbol B(x_2,y_2,z_2)$,然后(1)$\boldsymbola+\boldsymbolb$=$(x_1+x_2,y_1+y_2,z_1+z_2)$。
(2) $\boldsymbola-\boldsymbolb$=$(x_1-x_2,y_1-y_2,z_1-z_2)$(3)$\boldsymbola·\boldsymbolb$=$x_1x_2+y_1y_2+z_1z_2$。
(4) $|\boldsymbola |=\sqrt{x^2_1+y^2_1+z^2_1}$(5)$λ\boldsymbola=(λx_1,λy_1,λz_1)$。
4.平行(共线)和垂直空间向量的充要条件设非零向量$\boldsymbola(x_1,y_1,z_1)$,$\boldsymbolb(x_2,y_2,z_2)$,则$\boldsymbola∥\boldsymbolb\leftrightarrow\frac{x_1}{x_2}=\frac{y_1}{y_2}=\frac{z_1}{z_2}=λ(λ∈\mathbf{r})$$\boldsymbola⊥\boldsymbolb\leftrightarrow\boldsymbola·\boldsymbolb=0\leftrig htarrow$$x_1x_2+y_1y_2+z_1z_2=0$。
课件2:1.1.3 空间向量的坐标与空间直角坐标系

cos〈a,b〉=
a1b1+a2b2+a3b3 a21+a22+a23 b21+b22+b23
知识点四 空间直角坐标系
1.空间直角坐标系
以空间中两两__垂__直____且相交于一点 O 的三条直线分别
定义
为 x 轴、y 轴、z 轴,这时就说建立了空间直角坐标系 Oxyz,其中点 O 叫做坐标__原__点____,x 轴、y 轴、z 轴叫
【基础自测】
1.已知向量 a=(-3,2,5),b=(1,x,-1),且 a·b=2,
则 x 的值为( )
A.3
B.4
C.5
D.6
解析:∵a·b=-3×1+2x+5×(-1)=2,∴x=5. 答案:C
2.已知向量 a=(3,-2,1),b=(-2,4,0),则 4a+2b 等于( )
A.(16,0,4)
方法归纳 解决空间向量垂直、平行问题的思路 1.若有关向量已知时,通常需要设出向量的坐标,例如, 设向量 a=(x,y,z). 2.在有关平行的问题中,通常需要引入参数,例如,已 知 a∥b,则引入参数 λ,有 a=λb,再转化为方程组求解. 3.选择向量的坐标形式,可以达到简化运算的目的.
跟踪训练 3 (1)(变条件)若将本例(1)中“c∥B→C”改为 “c⊥a 且 c⊥b”,求 c.
做_坐__标__轴___.通过每两个坐标轴的平面叫做_坐__标__平__面_,
分别称为 xOy 平面、yOz 平面、___x_O_z___平面
画法
在平面上画空间直角坐标系 Oxyz 时,一般使∠xOy= __1_3_5_°___,∠yOz=90°
图示
说明
本书建立的坐标系都是___右__手___直角坐标系,即在空间 直角坐标系中,让右手拇指指向____x____轴的正方向, 食指指向____y____轴的正方向,中指指向____z____轴的 正方向,则称这个坐标系为右手直角坐标系
1.2空间直角坐标系-向量的坐标表示
例 8 设P 在x 轴上,它到P1(0, 2,3) 的距离为到 点 P2 (0,1,1)的距离的两倍,求点 P 的坐标.
解 因为P 在x 轴上,设P点坐标为 ( x,0,0),
PP1 x2 2 2 32 x2 11,
PP2 x2 12 12 x2 2,
B(0, y, z)
• M(x, y, z)
y
Q(0, y,0) A( x, y,0)
设空间两点A(x1, y1, z1), B(x2 , y2 , z2 ), 则点A与点B之间的距离| AB | 就是 向量AB (x2 x1, y2 y1, z2 z1)的模. 即:| AB || AB |
定点 o •
y 纵轴
横轴 x 空间直角坐标系
Ⅲ
yoz面
Ⅳ
xoy面
Ⅶ
x
Ⅷ
z zox 面
Ⅱ
o
yⅠ
Ⅵ Ⅴ
空间直角坐标系共有八个卦限
例4 在空间直角坐标系中,指出下列各
点在哪个卦限?
A(1,2,3), B(2,3,4), C(2,3,4), D(2,3,1) .
解答: A:Ⅳ; B:Ⅴ; C:Ⅷ; D:Ⅲ;
例 6 设 A( x1 , y1 , z1 )和B( x2 , y2 , z2 )为两已知 点,而在AB 直线上的点M 分有向线段AB 为
两部分AM 、MB,使它们的值的比等于某数
( 1),即 AM ,求分点的坐标.
MB
解 设 M( x, y, z)为直线上的点, z
B
AM {x x1, y y1, z z1} A M
非零向量
a
的方向角: 、
、
z
a M1M2 (ax , ay , az )
空间向量的表示与运算技巧

空间向量的表示与运算技巧在数学和物理学中,空间向量是描述三维空间中大小和方向的量。
它是由一组按照特定规则排列的数值组成,可以用于计算物体的位移、速度、加速度等各种物理量。
本文将介绍空间向量的表示和运算技巧。
一、空间向量的表示方法1. 直角坐标表示法直角坐标表示法是最常用的一种表示方法。
在三维直角坐标系中,一个空间向量可以用三个实数(x,y,z)表示,分别表示向量在x轴、y轴和z轴上的分量。
例如,向量A可以表示为A = (x,y,z)。
2. 分量表示法分量表示法将向量的分量按照一定顺序排列,形成一个有序数组。
例如,向量A可以表示为A = [x,y,z]。
3. 基向量表示法基向量表示法利用基向量来表示一个向量。
在三维空间中,通常使用标准单位向量i、j、k作为基向量。
例如,向量A可以表示为A =x*i + y*j + z*k。
二、空间向量的运算技巧1. 向量的加法向量的加法是将对应分量相加得到新的向量。
例如,向量A =(x1,y1,z1)和向量B = (x2,y2,z2),它们的和可以表示为A + B = (x1+x2, y1+y2, z1+z2)。
2. 向量的减法向量的减法是将对应分量相减得到新的向量。
例如,向量A =(x1,y1,z1)和向量B = (x2,y2,z2),它们的差可以表示为A - B = (x1-x2, y1-y2, z1-z2)。
3. 向量的数量积向量的数量积,又称为点积或内积,是将对应分量相乘后求和得到一个标量。
例如,向量A = (x1,y1,z1)和向量B = (x2,y2,z2),它们的数量积可以表示为A·B = x1*x2 + y1*y2 + z1*z2。
4. 向量的向量积向量的向量积,又称为叉积或外积,是通过对应分量的乘积得到一个新的向量。
向量A = (x1,y1,z1)和向量B = (x2,y2,z2)的向量积可以表示为A×B = (y1*z2 - z1*y2, z1*x2 - x1*z2, x1*y2 - y1*x2)。
空间向量的坐标表示与混合积的应用

空间向量的坐标表示与混合积的应用空间向量是三维空间中具有方向和长度的量,通常用坐标来表示。
本文将讨论空间向量的坐标表示以及混合积的应用。
一、坐标表示在空间直角坐标系中,一个空间向量可以表示为三个坐标的有序组(x, y, z),分别对应向量在x轴、y轴和z轴上的投影。
坐标表示的示例:对于向量AB,A点坐标为(x1, y1, z1),B点坐标为(x2, y2, z2),则向量AB的坐标表示为(x2 - x1, y2 - y1, z2 - z1)。
二、混合积混合积也称为标量三重积,是三个向量的乘积,其结果是一个数。
对于三个向量A、B和C,其混合积的计算公式如下:(A × B) · C = |A × B| × |C| × cosθ其中,A × B表示向量A和向量B的叉积,|A × B|表示叉积的模,|C|表示向量C的模,θ表示向量C相对于向量A × B的夹角。
混合积的应用示例:1. 体积计算:对于三个相交于一点的向量A、B和C,其混合积的绝对值| (A × B) · C |表示以这三个向量为棱所构成的平行六面体的体积。
2. 判断共线与共面关系:若三个向量A、B和C的混合积为0,则说明这三个向量共线或者共面。
3. 判断四面体的定向体积:对于四面体的四个顶点A、B、C和D,可以利用混合积来判断顶点的排列顺序是否与其定向体积一致。
三、应用示例以下是一些应用示例,展示了空间向量的坐标表示和混合积的应用:1. 三角形面积计算:已知三角形的三个顶点A(x1, y1, z1),B(x2, y2, z2),C(x3, y3, z3),可以将AB和AC两个向量进行叉积运算得到一个新向量D,其模即为三角形的面积:S = 0.5 |D|.2. 判断四点共面:已知四个点A(x1, y1, z1),B(x2, y2, z2),C(x3,y3, z3),D(x4, y4, z4),可以将AB和AC两个向量进行叉积运算得到一个新向量E,然后计算DE与DC的叉积F。
空间直角坐标系中的向量

空间直角坐标系中的向量在空间直角坐标系中,向量是一种既有大小又有方向的量,常用箭头来表示。
本文将讨论空间直角坐标系中向量的基本概念、表示方法以及向量运算等内容。
向量的基本概念在空间直角坐标系中,一个向量可以由起点和终点确定。
向量的模表示向量的大小,用 ||a|| 或 |AB| 表示,其中a为向量AB的模,AB为向量的名称。
向量的方向表示向量的朝向,可以用箭头表示。
向量既有大小,也有方向,所以向量是有向线段。
向量的表示方法向量的表示方法有两种:点表示法和分量表示法。
- 点表示法:用向量的起点和终点表示向量。
例如,向量AB用A 点和B点表示。
- 分量表示法:用向量在坐标轴上的投影表示向量。
空间直角坐标系中的向量可以表示为三个有序数对,即(x,y,z)。
其中x、y、z分别为向量在x轴、y轴和z轴上的分量。
向量的运算在空间直角坐标系中,向量的运算包括向量的加法、减法、数量乘法和数量除法。
- 向量的加法:向量的加法满足三角形法则,即将一个向量平移后与另一个向量首尾相接,用结果向量的起点和终点表示。
向量的加法满足交换律和结合律。
- 向量的减法:向量的减法可以看作是向量加法的逆运算,即将减去的向量取负。
例如,向量AB-向量AC可以表示为向量CB。
- 数量乘法:向量与实数的乘积,即将向量的模与实数相乘后保持方向不变。
- 数量除法:向量除以实数,即将向量的模除以实数后保持方向不变。
向量的坐标表示在空间直角坐标系中,向量的坐标表示为(x,y,z),其中x为向量在x 轴上的分量,y为向量在y轴上的分量,z为向量在z轴上的分量。
向量的数量乘法和数量除法的性质向量的数量乘法和数量除法满足以下性质:- 量的分配律:a(向量BC + 向量CD) = a向量BC + a向量CD,(a+b)向量AB = a向量AB + b向量AB。
- 量的结合律:a(b向量AB) = (ab)向量AB。
- 一对称性:-1向量AB = -向量AB。
空间坐标系与向量的表示

空间坐标系与向量的表示在数学和物理学中,空间坐标系和向量是两个重要的概念。
空间坐标系是为了描述物体在空间中的位置而建立的一种坐标系统,而向量则是用来表示空间中的大小和方向的量。
本文将介绍空间坐标系和向量的表示方法。
一、空间坐标系空间中常用的坐标系有直角坐标系和极坐标系。
直角坐标系是一种以直角为基础的坐标系,其中的三个坐标轴分别与空间中的三个方向相垂直。
我们通常用x、y和z分别表示直角坐标系的三个坐标轴。
在直角坐标系中,每个点的位置可以用一个有序的数对 (x, y, z) 来表示,其中x表示点在x轴上的投影长度,y表示点在y轴上的投影长度,z表示点在z轴上的投影长度。
另一种常用的空间坐标系是极坐标系。
极坐标系通常用于描述平面上的点,但也可以扩展到三维空间中。
在极坐标系中,点的位置由极径和极角确定。
将极径表示为r,极角表示为θ,那么可以用一个有序的数对(r, θ, z) 来表示空间中的点的位置。
二、向量的表示向量是空间中的一种几何量,它既有大小又有方向。
在空间中,向量通常用有序的组数来表示。
假设空间中有一个向量A,它的大小为|A|,方向为从点P指向点Q。
那么向量A可以表示为⃗PQ。
向量的表示方法有多种,常见的有分量表示法和坐标表示法。
1. 分量表示法分量表示法是将向量A在各个坐标轴上的投影长度表示为有序的数对 (Ax, Ay, Az)。
其中Ax表示向量在x轴上的投影长度,Ay表示向量在y轴上的投影长度,Az表示向量在z轴上的投影长度。
例如,向量A在直角坐标系中的分量表示为 (Ax, Ay, Az)。
2. 坐标表示法对于直角坐标系来说,向量A的坐标表示与分量表示是相同的。
即向量A的坐标表示为 (Ax, Ay, Az)。
而对于极坐标系来说,向量A的坐标表示为 (r, θ, z)。
其中r表示向量的大小,θ表示向量与正x轴的夹角,z表示向量在z轴上的投影长度。
三、总结本文介绍了空间坐标系和向量的表示方法。
空间坐标系包括直角坐标系和极坐标系,用来描述物体在空间中的位置。
高二寒假讲义03 空间向量及其运算的坐标表示
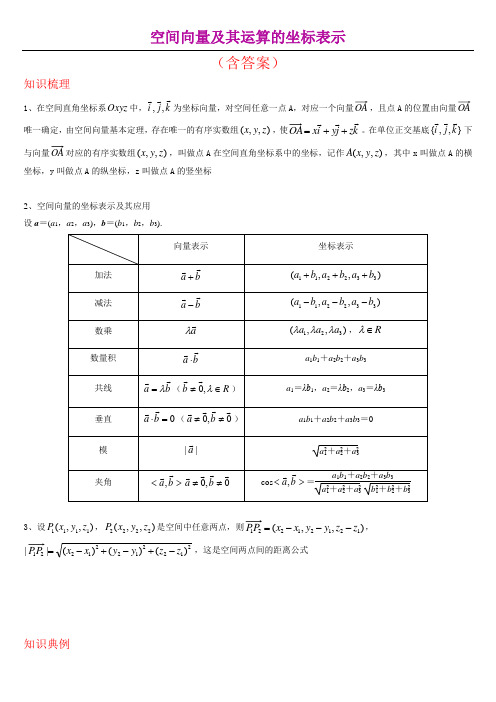
空间向量及其运算的坐标表示(含答案)知识梳理1、在空间直角坐标系Oxyz 中,k j i,,为坐标向量,对空间任意一点A ,对应一个向量OA ,且点A 的位置由向量OA唯一确定,由空间向量基本定理,存在唯一的有序实数组),,(z y x ,使k z j y i x++=。
在单位正交基底},,{k j i 下与向量对应的有序实数组),,(z y x ,叫做点A 在空间直角坐标系中的坐标,记作),,(z y x A ,其中x 叫做点A 的横坐标,y 叫做点A 的纵坐标,z 叫做点A 的竖坐标2、空间向量的坐标表示及其应用 设a =(a 1,a 2,a 3),b =(b 1,b 2,b 3).3、设),,(1111z y x P ,),,(2222z y x P 是空间中任意两点,则),,(12121221z z y y x x P P ---=,21221221221)()()(||z z y y x x P P -+-+-=,这是空间两点间的距离公式知识典例题型一 空间向量的坐标运算例1 设,x y R ∈,向量(,1,1),b (1,,1),c (2,4,2)a x y ===-,c a⊥,c b//,则||a b +=( ) A .22 B 10C .3D .4【答案】C 【分析】 根据,c a c b ⊥,结合向量的坐标运算可求得参数,x y 的值,再结合向量的加法与模长运算即可求解【详解】,241,2,(1,2,1)b c y y b ∴=-⨯∴=-∴=-,a c ⊥()214+20,a c x ∴⋅=+⋅-=1x ∴=,(1,1,1),(2,1,2)a a b ∴=∴+=-,222||2(1)23a b ∴+=+-+=,故选: C.巩固练习1、已知点()2,3,1B -,向量()3,5,2AB =-,则点A 坐标是( ) A .()1,2,3 B .()1,2,3-C .()5,8,1-D .()5,8,1--【答案】D 【分析】设点(),,A x y z ,由点A 和点B 表示出向量AB ,构造等式求解即可. 【详解】设点(),,A x y z ,则向量()()2,3y,1z 3,5,2AB x =----=-,所以233512x y z -=-⎧⎪--=⎨⎪-=⎩⇒581x y z =⎧⎪=-⎨⎪=-⎩,所以点()5,8,1A --. 故选:D2、(多选)对于任意非零向量()111,,a x y z =,()222,,b x y z =,以下说法错误的有( ) A .若a b ⊥,则1212120x x y y z z ++=B .若//a b ,则111222x y z x y z == C .121212222222111222cos ,x y z a zb x y =++⋅+>+<D .若1111===x y z ,则a 为单位向量 【详解】对于A 选项,因为a b ⊥,则1212120a b x x y y z z ⋅=++=,A 选项正确; 对于B 选项,若20x =,且20y ≠,20z ≠,若//a b ,但分式12x x 无意义,B 选项错误; 对于C 选项,由空间向量数量积的坐标运算可知121212222222111222cos ,x y z a z b x y =++⋅+>+<,C 选项正确;对于D 选项,若1111===x y z ,则2221113a =++=,此时,a 不是单位向量,D 选项错误. 故选:BD.题型二 向量坐标求解直线关系例 2 棱长为1的正方体ABCD-A 1B 1C 1D 1中,E ,F ,G 分别是DD 1,BD ,BB 1的中点. (1)求证:EF ⊥CF ;(2)求EF 与CG 所成角的余弦值; (3)求CE 的长.【答案】(1)证明见解析;(21535. 【分析】建立空间直角坐标系,得出,,,,D E C F G 的坐标,由坐标运算得出,,,EF CF CG CE 的坐标,根据数量积公式证明EF ⊥CF ;由数量积公式求出EF 与CG 所成角的余弦值;再由模长公式得出CE 的长. 【详解】建立如图所示的空间直角坐标系Dxyz则1111 (0,0,0),0,0,,(0,1,0),,,0,1,1,2222 D E C F G⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以1111111,,,,,0,1,0,,0,1,2222222EF CF CG CE⎛⎫⎛⎫⎛⎫⎛⎫=-=-==-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(1)证明:因为111110022222EF CF⎛⎫⎛⎫⋅=⨯+⨯-+-⨯=⎪ ⎪⎝⎭⎝⎭,所以EF CF⊥,即EF⊥CF. (2)因为22211111111310,222242222 EF CG EF⎛⎫⎛⎫⎛⎫⎛⎫⋅=⨯+⨯+-⨯==++-=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22215102CG⎛⎫=++=⎪⎝⎭1154cos,=1535EF CGEF CGEF CG⋅∴==⋅⨯.(3)()222150122CE⎛⎫=+-+=⎪⎝⎭巩固练习1、在正方体ABCD-A1B1C1D1中,E,F分别为A1D1,BB1的中点,则cos EAF∠=____,EF=____. 【答案】2562建立空间直角坐标系,利用向量法得出cos ,AE AF ,从而得出cos EAF ∠,最后由模长公式得出EF . 【详解】以A 为原点,AB ,AD,AA 1分别为x 轴、y 轴、z 轴建立直角坐标系设正方体棱长为1,则110,,1,1,0,22E F ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭11110,,1,1,0,,1,,2222AE AF EF ⎛⎫⎛⎫⎛⎫∴===-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭122cos ,=55522AE AF AE AF AE AF⋅∴==⨯ 2222116cos ,||1522EAF EF EF ⎛⎫⎛⎫∴∠===+-+-= ⎪ ⎪⎝⎭⎝⎭. 故答案为:25;6 2、如图,长方体1111ABCD A B C D -中,14AA AB ==,2AD =,E 、F 、G 分别是1DD 、AB 、1CC 的中点,则异面直线1A E 与GF 所成角的余弦值是( )A .0B .105C .22D .155【答案】A建立空间直角坐标系,表示1,A E GF ,然后利用空间向量的夹角公式计算即可. 【详解】 如图()()()()12,0,40,0,2,2,2,0,0,4,2A E F G ,所以()()12,0,2,2,2,2A E GF =--=--所以异面直线1A E 与GF 所成角的余弦值110⋅=A E GF A E GF故选:A巩固提升1、已知向量()1,1,1m λ=-,()2,2,3n λ=-,若()()m n m n +⊥-,则λ=__________ 【答案】7 【分析】根据空间向量的加法和减法的坐标运算,可求得m n +和m n -,结合空间向量垂直的坐标关系,即可求得λ的值. 【详解】向量()1,1,1m λ=-,()2,2,3n λ=- 则()32,3,4m n λ+=-,()1,1,2m n -=---因为()()m n m n +⊥- 所以()()0m n m n +⋅-=,代入可得()()32,3,41,1,20λ-⋅---=即23380λ---=,解得7λ= 故答案为: 72、已知a 、b 是异面直线,且a ⊥b ,12,e e 分别为取自直线a 、b 上的单位向量,且a =1223e e +,124b ke e =-,a b ⊥,则实数k 的值为___. 【答案】6 【分析】根据向量垂直其数量积为0,转化为基底的运算,即可得答案; 【详解】由a b ⊥,得a b ⋅=0,又12,e e 分别为取自直线a 、b 上的单位向量,∴120e e ⋅=∴(1223e e +)·(124ke e -)=0,∴2120k -=,∴6k =. 故答案为:6.3、在空间直角坐标系O xyz -中,(0,0,0),O E F ,B 为EF 的中点,C 为空间一点且满足||||3CO CB ==,若1cos ,6EF BC <>=,,则OC OF ⋅=( )A .9B .7C .5D .3【解析】设(,,)C x y z,B ,(,,)OC x y z =,()BC x y z =,(EF =-,由(()1cos ,436EF BC x y z EF BC EF BC⋅-⋅===⋅⋅,整理可得:2x y -=-, 由||||3CO CB ==化简得x y +=,以上方程组联立得x y ==, 则()(,,)3OC OF x y z =⋅==. 故选:D.4、设ABCD -A 1B 1C 1D 1是棱长为a 的正方体,则有( ) A.AB →·C 1A →=a 2B .AB →·A 1C 1→=2a 2C.BC →·A 1D →=a 2 D .AB →·C 1A 1→=a 2【答案】 C【解析】 建系如图.则AB →·C 1A →=(a,0,0)·(-a ,-a ,-a )=-a 2, AB →·A 1C 1→=(a,0,0)·(a ,a,0)=a 2, BC →·A 1D →=(0,a,0)·(0,a ,-a )=a 2,AB →·C 1A 1→=(a,0,0)·(-a ,-a,0)=-a 2,故只有C 正确.5、正方体ABCD -A 1B 1C 1D 1中,点E 为上底面A 1C 1的中心.若向量A E →=AA 1→+xAB →+yAD →,则实数x ,y 的值分别为( ) A .x =1,y =1 B .x =1,y =12C .x =12,y =12D .x =12,y =1【答案】 C【解析】A E →=AA 1→+xAB →+yAD →=,所以x=y=126、平行六面体ABCD -A 1B 1C 1D 1中,向量AB →,AD →,AA 1→两两的夹角均为60°,且|AB →|=1,|AD →|=2,|AA 1→|=3,则|AC 1→|等于( ) A .5 B .6 C .4 D .8【答案】 A【解析】 设AB →=a ,AD →=b ,AA 1→=c ,则AC 1→=a +b +c ,|AC 1→|2=a 2+b 2+c 2+2a ·b +2b ·c +2c ·a =25,因此|AC 1→|=5.故选A.。
空间向量的坐标表示

空间向量得坐标表示[本周重点]:空间右手直角坐标系,向量得坐标运算,夹角公式,距离公式。
[本周难点]:向量坐标得确定以及夹角公式,距离公式得应用。
[知识要点]:一、空间直角坐标系中空间向量得直角坐标表示在空间直角坐标系O一xyz中,以为单位正交基底, 对空间任一点A,对应向量,存在唯一一组有序实数组x、y、z,使,则在空间直角坐标系中,点A得坐标为(x,y,z),其中x叫做点A 得横坐标;y叫做点A得纵坐标;z叫做点A得竖坐标、向量得坐标为(x,y,z)。
(1)空间直角坐标系就是在仿平面直角坐标系得基础上,选取空间任意一点O与一个单位正交基底(按右手系排列)建立得坐标系,做题选择坐标系时,应注意点O得任意性,原点O得选择要便于解决问题,既有利于作图直观性,又要尽可能使各点得坐标为正。
(2)空间任一点P得坐标确定得办法如下:作P在XOY平面上得射影点,求出在XOY 平面内得坐标(x,y,0),求出并确定符号即z,得坐标P(x,y,z)。
二、空间向量得直角坐标运算:设则(1) + =(a1+b1,a2+b2,a3+b3);(2) - =(a1-b1,a2-b2,a3-b3);(3) =a1b1+a2b2+a3b3、(4) // 或、(5) a1b1+a2b2+a3b3=0、(6)A(x1,y1,z1),B(x2,y2,z2),则三、夹角与距离公式:1、向量与得夹角:设则、注意:(1)夹角公式可以根据数量积得定义推出:,其中θ得范围就是(2)用此公式求异面直线所成角等角度时,要注意这些角度与θ得关系(相等,互余,互补)。
2、两点距离公式:设A(x1,y1,z1),B(x2,y2,z2)为空间两点,则两点间距离公式就是模长公式得推广,首先根据向量得减法推出向量得坐标表示,然后再用模长公式推出。
3、平面得法向量:如果表示向量得有向线段所在得直线垂直于平面α,则称这个向量垂直于平面α,记作、如果,那么向量叫做平面α得法向量四、利用向量得坐标理论完成解题得程序:建立空间直角坐标系O-xyz,对空间图形中得向量进行量化处理,用坐标(x,y,z)进行表示、利用坐标运算与图形得数量关系、位置关系之间得对应,完成解题过程、重点例题讲解:例1.已知空间三点A(—2,0,2),B(—1,1,2),C(—3,0,4)。
高中数学1-3空间向量及其运算的坐标表示1-3-1空间直角坐标系课件新人教A版选择性必修第一册

2.向量的坐标: 给定向量 a,若O→A=a,a=xi+yj+zk,有序实数组_(_x_,__y_,__z_) _叫做 a 在空间直角坐标系 Oxyz 中的坐标,简记为 a=_(_x_,__y_,__z)__.
【预习自测】
1.在空间直角坐标系中,点 P(1,2,3)到平面 Ozx 的距离是
()
A.1
【答案】(2,-3,1) 【解析】点P(2,3,-1)关于坐标平面Oxy的对称点P1的坐标为(2, 3,1),点P1关于坐标平面Oyz的对称点P2的坐标为(-2,3,1),点P2关 于z轴的对称点P3的坐标是(2,-3,1).
3.如图,正方体AOCD-A′B′C′D′的棱 长为2,则图中的点M关于y轴对称的点的坐 标为________.
__x_轴__、__y_轴__、__z_轴___,它们都叫坐标轴,这时就建立了一个空间直角坐标
系Oxyz,O叫做原点,i,j,k都叫做_坐__标__向__量___,通过每两条坐标轴的
平面叫做__坐__标__平__面__,分别称为__O__x_y__平面,__O_y_z___平面,__O__z_x___ 平面,它们把空间分成__八__个__部__分__.
坐标互为相反数,所以点(2,3,2)关于平面Oxy的对称点的坐标为(2,
3,-2).
探究 3 求关于点对称的点
点A(3,-2,4)关于点(0,1,-3)的对称点的坐标是
A.(-3,4,-10)
B.(-3,2,-4)
()
C.32,-21,21
D.(6,-5,11)
【答案】A
【解析】由线段中点坐标公式,则A(3,-2,4)关于点(0,1,-3)
在空间直角坐标系 Oxyz 中,i,j,k 为坐标向量,对空间任意一点 A,
02 第二节 空间直角坐标系 向量的坐标

第二节空间直角坐标系向量的坐标本节将建立空间的点及向量与有序数组的对应关系,引进研究向量的代数方法,从而建立代数方法与几何直观的联系.分布图示★空间直角坐标系★坐标面与卦限★空间点与坐标的对应关系★空间两点间的距离公式★例1★例2★向量的坐标★向量的代数运算★例3★例4★向量的模与方向余弦★例5★例6★例7★例8★例9★向量在轴上的投影★例10★内容小结★课堂练习★习题8 –2 ★返回内容要点一、空间直角坐标系二、空间两点间的距离三、向量的坐标表示四、向量的代数运算五、向量的模与方向余弦六、向量在轴上的投影性质1(为向量与轴的夹角);性质2 ;性质3(为实数).例题选讲例1 求证以、、三点为顶点的三角形是一个等腰三角形.解从而原结论成立.空间两点间的距离例2 (E01)设P在x轴上, 它到的距离为到点的距离的两倍, 求点P的坐标.解因为在轴上,设点坐标为所求点为向量的代数运算例3 (E02) 设求在y轴上的分向量.解在轴上的坐标为13,在轴上的分向量为例4 (E03) 已知两点和以及实数试在有向线段上求一点,使.解如图,由于因此所以代入得故所求点为注: 本例中的点称为有向线段的定比分点,特别地,当为的中点,其坐标为例5 求平行于向量的单位向量.解所求向量有两个,一个与同向,一个反向.或向量的模与方向余弦例6 (E04) 已知两点和,求与向量平行的向量的单位向量.解所求向量有两个,一个与同向,一个与反向.因为所以故所求向量为例7 (E05) 已知两点和, 计算向量的模、方向余弦和方向角.解例8 设有向量, 已知它与x轴和y轴的夹角分别为和, 如果的坐标为(1, 0, 3), 求的坐标.解设向量的方向角为或设的坐标为的坐标为例9 设点位于第卦限, 向径与轴、轴的夹角依次为和,且求点的坐标.解由关系式因为在第卦限,知故于是点的坐标为向量在轴上的投影例10 (E06) 设立方体的一条对角线为OM, 一条棱为OA, 且求在方向上的投影解如图(见系统演示),记有于是课堂练习1. 给定两点: 在轴上有一点, 满足求点的坐标.2. 从点沿向量方向取长为34的线段, 求点的坐标.。
空间向量及其运算的坐标表示

平面向量
平面向量的坐标运算: a ( x1 , y1 ), b ( x2 , y2 ) a b ( x1 x2 , y1 y2 );
空间向量
空间向量的坐标运算: a ( x1 , y1 , z1 ), b ( x2 , y2 , z 2 ) a b ( x1 x2 , y1 y2 , z1 z 2 );
空间向量
空间向量的夹角: a ( x1 , y1 , z1 ), b ( x2 , y2 , z 2 ) ab cos a,b | a || b | x1 x2 y1 y2 z1 z 2 2 2 2 2 2 x1 y1 z12 x2 y2 z 2
垂直与平行: a ( x1 , y1 , z1 ), b ( x2 , y2 , z 2 ) x1 y1 z1 a // b (?) x2 y 2 z 2 a b x1 x2 y1 y2 z1 z 2 0
x1 x 2 y1 y 2 z1 z 2 (3)中点坐标公式: ( , , ) 2 2 2
2.两个向量夹角公式
a1b1 a2b2 a3b3 a b cos a, b ; 2 2 2 2 2 2 | a || b | a1 a2 a3 b1 b2 b3
垂直与平行: a ( x1 , y1 ), b ( x2 , y2 ) a // b x1 y2 x2 y1 0 a b x1 x2 y1 y2 0
对比表4
平面向量
平面向量基本定理: 如果e1 , e 2是同一平面内的两个不 共线 的向量,那么对于这个 平面内的任一 向量a,有且仅有一对实数 x, y,使a xe1 ye 2 .
空间向量及其运算的坐标表示 人教A版(2019)选择性必修第一册高中数学精品课件

A.30°
B.45°
C.60°
D.90°
→
→
→
设向量P→
1P2与P1P3的夹角为θ,因为P1P2=(3,1,0)-(1,-1,2)=(2,2,-2),P1P3=(0,1,3)-(1,
-1,2)=(-1,2,1),所以 cos θ=
→
P→
1P2·P1P3
=0.因为 0°≤θ≤180°,所以θ=90°.故选 D.
标为( D )
1
1
A.( ,1,- )
2
2
1
1
C.(- ,1, )
2
2
1
1
B.( ,-1, )
2
2
1
1
D.( ,1, )
2
2
由题可知,M 为 DC1 的中点,
1
1
1
1
→
→
→
→
→
→
→
→
→
→
→
→,
∴AM=AD+DM=AD+ (DD1+DC)=AD+ (AA1+AB)= AA1+AD+ AB
2
2
2
2
1
1
∴坐标为( ,1, ).
B
)
A. (0,-4,6)
B. (0,-2,3)
C. (0,2,3)
D. (0,-2,6)
【答案】B
−3+3 1−5 −4+10
【解析】根据线段的中点坐标公式可得线段 AB 的中点 M 的坐标是(
即(0,-2,3).故选 B.
2
,2 ,
2
),
例题解析
例 4.点 A(2,-3,1)关于原点的对称点 A′的坐标是(
空间直角坐标系,向量的坐标表

向量的坐标表示
空间直角坐标系
由三个互相垂直的坐标轴$x, y, z$构成的坐标系,每个轴上的 单位长度为1。
向量的坐标表示
在空间直角坐标系中,任意向量$overrightarrow{a}$可以表示 为$(x, y, z)$,其中$x, y, z$分别表示向量在$x, y, z$轴上的投 影。
向量的模长与夹角
分配律
$(vec{A} + vec{B}) cdot vec{C} = vec{A} cdot vec{C} + vec{B} cdot vec{C}$
交换律
$vec{A} cdot vec{B} cdot vec{C} = vec{B} cdot vec{A} cdot vec{C}$
结合律
$(vec{A} cdot vec{B}) cdot vec{C} = vec{A} cdot (vec{B} cdot vec{C})$
向量的模长
向量的模长可以通过坐标表示计算,即$|overrightarrow{a}| = sqrt{x^2 + y^2 + z^2}$。
向量的夹角
两个向量的夹角可以通过余弦公式计算,即$costheta = frac{overrightarrow{a} cdot overrightarrow{b}}{|overrightarrow{a}||overrightarrow{b}|}$,其中 $theta$为两个向量的夹角,$overrightarrow{a} cdot overrightarrow{b}$表示两 个向量的点积。
向量的模长
表示向量的大小,记作$|overrightarrow{AB}|$或$|overrightarrow{a}|$,计算公式为 $sqrt{x^2 + y^2 + z^2}$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间任给两个点M1 ,M2的坐标,可 得空间向量M1M2的坐标形式.
例5 : M1(1,2,3), M2 (10,1,3)
则OM 1
i
2
j 3k
(1,2,3),
• M2
OM 2 10i j 3k (10,1,3) M1•
M1M
2
OM
2
OM1
(10i j 3k ) (i 2 j 3k )
1.向量的模:
设向量 (x, y, z),作OM z
R(0,0, z)
C( x,o, z)
o
x P( x,0,0) 由右图知:向量的模为
| | x2 y2 z2
B(0, y, z)
• M(x, y, z)
y
Q(0, y,0) A( x, y,0)
设空间两点A(x1, y1, z1), B(x2 , y2 , z2 ), 则点A与点B之间的距离| AB | 就是 向量AB (x2 x1, y2 y1, z2 z1)的模. 即:| AB || AB |
6
k,)
11 11 11
2. 空间两向量的夹角的概念:
定义2.1.15
设有两个非零向量
a
0,
b 0,
规定不超过 的 AOB(设 AOB,0 )
称为向量a与向量b 的夹角,记作
b
(a,
b)
(b,
a)
a
类似地,可定义向量与一轴或空间两轴的夹角.
特殊地,当两个向量中有一个零向量时,规定 它们的夹角可在0与 之间任意取值.
(x2 x1)2 ( y2 y1)2 (z2 z1)2
空间两点间距离公式
例 7 求证以M1(4,3,1)、M 2 (7,1,2)、M 3 (5,2,3)
三点为顶点的三角形是一个等腰三角形.
解 M1M2 2 (7 4)2 (1 3)2 (2 1)2 14, M2M3 2 (5 7)2 (2 1)2 (3 2)2 6, M3M1 2 (4 5)2 (3 2)2 (1 3)2 6,
x
x1 ( x2
x)
x
x1 x2 1
,
y
y1 ( y2
y)
y
y1 y2 , 1
z z1 (z2 z)
z z1 z2 , 1
M 为有向线段AB 的定比分点. M 为中点时,
x x1 x2 , y y1 y2 , z z1 z2 .
2
ቤተ መጻሕፍቲ ባይዱ
2
2
1.2.3 向量的模与方向余弦
点在哪个卦限?
A(1,2,3), B(2,3,4), C(2,3,4), D(2,3,1) .
解答: A:Ⅳ; B:Ⅴ; C:Ⅷ; D:Ⅲ;
空间的点 11 有序数组( x, y, z)
特殊点的表示: 坐标轴上的点 P, Q, R,
坐标面上的点 A, B, C, O(0,0,0)
注意 : 借助空间直角
z
坐标系可表示向量
R(0,0, z)
C( x,o, z)
o x P( x,0,0)
B(0, y, z)
• M(x, y, z)
y
Q(0, y,0) A( x, y,0)
如:
OP
xi ,
OQ PA yj,
OR zk
2.向量 的坐标分解式 任给向量 ,对应点M,使 OM
以OM为对角线,三条坐标轴为棱作长方体
三个坐标轴的正方向 符合右手系.
z 竖轴
即以右手握住z 轴,
当右手的四个手指
从正向x 轴以 角
2
度转向正向y 轴
时,大拇指的指向
就是z 轴的正向.
定点 o •
y 纵轴
横轴 x 空间直角坐标系
Ⅲ
yoz面
Ⅳ
xoy面
Ⅶ
x
Ⅷ
z zox 面
Ⅱ
o
yⅠ
Ⅵ Ⅴ
空间直角坐标系共有八个卦限
例4 在空间直角坐标系中,指出下列各
OPAQ——RCMB,
z
有:
R(0,0, z)
C( x,o, z)
OM OP PA AM
o
xi yj zk
x P( x,0,0)
B(0, y, z)
• M(x, y, z)
y
Q(0, y,0) A( x, y,0)
定义1.13
若向量r的坐标分解式为r
r xi
r yj
r zk ,
则称xir
,
r yj
,
r zk
为向量r
沿三个坐标轴方向的分向量,
三元有序数组(x, y, z)称为向量r的坐标,记作
r
(x,
y,
z ); 若r
uuuur OM , (x,
y,
z )也称为点M 的坐标,
记作M (x, y, z).
结论: 在给定的空间直角坐标系下,空间的向量 (或点)与三元有序数组之间有一一对应的关系.
两部分AM 、MB,使它们的值的比等于某数
( 1),即 AM ,求分点的坐标.
MB
解 设 M( x, y, z)为直线上的点, z
B
AM {x x1, y y1, z z1} A M
o
y
MB {x2 x, y2 y, z2 z} x
由题意知: AM MB
{ x x1, y y1, z z1} { x2 x, y2 y, z2 z},
j
(az
b
{ax
bx
,
a
y
by ,
az
bz
}
bz
)k;
(ax bx )i (ay by ) j (az bz )k;
a
{a
x
, a
y
,
az }
(ax )i (ay ) j (az )k.
例 6 设 A( x1 , y1 , z1 )和B( x2 , y2 , z2 )为两已知 点,而在AB 直线上的点M 分有向线段AB 为
M2M3 M3M1 , 原结论成立.
例 8 设P 在x 轴上,它到P1(0, 2,3) 的距离为到 点 P2 (0,1,1)的距离的两倍,求点 P 的坐标.
解 因为P 在x 轴上,设P点坐标为 ( x,0,0),
PP1 x2 2 2 32 x2 11,
PP2 x2 12 12 x2 2,
11i 3 j 6k (11,3,6)
说明 : 借助向量的坐标分解式 ,可用代数的方法讨论
向量的运算
1.2.2 利用坐标作向量的线性运算
则
a设ab{a{xa,
x
ay
, az
bx,
},
a
y
b {bx , by , by , az bz }
bz
},
a
(ax
bx )i
(a y
by )
PP1 2 PP2 , x2 11 2 x2 2
x 1, 所求点为 (1,0,0), (1,0,0).
例9
求平行于向量a
6i
7
j
6k 的单位向
量的分解式.
解 所求向量有两个,一个与 a同向,一个反向
| a| 62 72 (6)2 11,
a0
|
a a|
( 6
i
7
j
